Abstract
This paper presents a novel methodology for short-term load forecasting in the context of significant shifts in the daily load curve due to the rapid and extensive adoption of Distributed Energy Resources (DERs). The proposed solution, built upon the Similar Days Method (SDM) and Artificial Neural Network (ANN), introduces several novelties: (1) selection of similar days based on hidden representations of day data using Autoencoder (AE); (2) enhancement of model generalization by utilizing a broader set of training examples; (3) incorporating the relative importance of training examples derived from the similarity measure during training; and (4) mitigation of the influence of outliers by applying an ensemble of ANN models trained with different data splits. The presented AE configuration and procedure for selecting similar days generated a higher-quality training dataset, which led to more robust predictions by the ANN model for days with unexpected deviations. Experiments were conducted on actual load data from a Serbian electrical power system, and the results were compared to predictions obtained by the field-proven STLF tool. The experiments demonstrated an improved performance of the presented solution on test days when the existing STLF tool had poor predictions over the past year.
1. Introduction
Digitalization and automation have significantly transformed the energy landscape in recent decades. Advanced Distribution Management Systems (ADMSs) and other digital innovations have revolutionized network operations across all voltage levels, from low-voltage to high-voltage (sub)transmission networks. The traditional ADMS algorithms require further development to address the new technical challenges introduced by Distributed Energy Resources (DERs), which have transformed the traditional network into an active network [1]. Examples of issues in distribution network operation include voltage rises near connection points, feeder overloads, and reverse power flows during periods of low demand and high generation [2,3]. Load forecasting engines, one of the crucial modules in ADMS, had to evolve to account for the significant number of consumers who also produce electricity, known as prosumers.
Moreover, to increase and stimulate green energy production, governments are heavily subsidizing the installation of DERs on residential and public buildings, significantly accelerating the adoption process. Taking the Republic of Serbia as an example, in the last year and a half, the number of prosumers increased seven times, with the installed power growing eight and a half times [4]. This rapid mass adoption, coupled with the weather-dependent nature of DERs, can significantly influence the network load and result in daily load curves with no historical reference. Consequently, during these transition periods, load forecast algorithms, particularly those based on the Similar Day Method (SDM), can produce poor predictions without clearly identifiable causes due to their reliance on historical data.
This paper focuses on improving the selection of the training dataset for Short-Term Load Forecasting (STLF) based on Artificial Neural Networks (ANNs) in the context of the rapid and extensive adoption of DERs. The proposed methodology is based on the concept of selecting similar days and is supported by a novel method for determining the importance of training examples.
The proposed solution searches for similar days based on the similarity of hidden features rather than the similarity of raw data. This is achieved by employing straightforward concepts that can be modified, upgraded, optimized for other datasets, and integrated into more complex architectures.
1.1. Related Work
The excellent performance of learning-based Artificial Intelligence (AI) models has been extensively recognized and researched, as noted in [5,6,7,8]. Artificial Neural Networks (ANNs) hold a special place in AI technologies. This well-established concept has proven particularly effective for load forecasting. A better understanding of how the ANN can be applied to load forecasting problems can be found in [9,10]. An Autoencoder (AE) is a special case of an ANN trained to reproduce the input. An AE consists of two components: an encoder that identifies and represents important input features as code during training and a decoder that uses this code to reconstruct the original inputs. The AE concept and its applications have been discussed in detail in [11,12]. The latent space representation of the input, or code, is the actual value that the AE concept brings. In reference [13], the authors employed the AE along with the similar day method to compare historical days with the forecasted day. This approach enabled them to identify an improved Artificial Neural Network (ANN) training set based on the similarity of codes.
The Similar Day Method (SDM) is a simple forecasting method that searches historical data for days with similar characteristics. The most similar day was then used as the forecast [14]. The concept of the SDM was used in [15,16] to develop a day similarity metric model for the STLF (DSMM-STLF tool) that performed well in practical applications. However, the methodology based on this method lacks good results when there are no similar days in the historical data or the forecasted day is a special day, like a national or religious holiday. Special days can be determined in advance, and deviations from the nonspecial day load profile are expected in these cases. In study [17], the authors introduced an enhancement to the DSMM-STLF tool, which considers the expected deviation from the nonspecial day load profile and applies it to special days. The issue of unexpected deviations or cases with no similar historical data remained unsolved. Training an ANN model on a small dataset can be challenging, and various training techniques are used to address common problems that may arise in this scenario, for example, overfitting [18] and local optimum [19].
1.2. Proposed Solution
In all the previously mentioned studies, certain issues have not been adequately addressed:
- The selection of similar days is based on the similarity of the raw data. However, in the context of significant and rapid shifts in the daily load curve, there are instances when algorithms fail to identify sufficiently similar days to generate accurate predictions. In such cases, hidden features, rather than raw data, can be employed to measure similarity. Hidden features capture essential data, data patterns, and complex relationships that are not obvious from the raw inputs [20].
- Only the most similar days were used to produce predictions. The discarded data contain a considerable amount of important hidden information and dependencies. Incorporating these data into the model creation process can improve the results.
- Similar days selected were used with equal importance. This approach can be effective when there are many similar days in history. However, when only a few similar days are available, the algorithm can be enhanced by incorporating the relative importance of these days, thereby assigning greater value to more similar days.
- The outlier phenomenon among the selected days was not addressed. In the context of significant and rapid changes, a similar day selection procedure can produce poor training examples. Training procedures can be improved to mitigate the influence of outliers on the resulting prediction.
This paper proposes a methodology that addresses these issues and introduces the following novelties and contributions:
- The proposed method selects similar days based on hidden representations of day data. This procedure searches historical data for days with similar hidden features and dependencies.
- The proposed solution leverages a broader set of training examples rather than relying solely on a relatively small number of similar days. Including valuable information from a more extensive dataset enhances the models’ generalization capabilities.
- The relative importance of training examples is introduced based on the similarity of the days. This is employed during the training phase to assign greater values to days more similar to the forecasted day.
- A solution to mitigate the influence of outliers is proposed. Ensemble training is employed to train multiple models with different splits of the training data, resulting in predictions with reduced impact from outliers.
Authors hypothesize that the proposed solution will effectively learn hidden features from historical data, enhance the selection of training datasets by comparing encoded inputs rather than raw inputs, and ultimately achieve lower forecasting errors than the STLF tool in scenarios involving unexpected deviations from load profiles. The hypothesis was tested using real-life data from a Serbian power system. Test examples were selected from days in the past year during which the DSMM-STLF tool produced high forecasting errors. Holidays and other predetermined special days were excluded from the experiment. The solution proposed in this paper is an improvement of the DSMM-STLF tool and methodologies presented in [15,16,17]. The process structure and flow of the proposed solution are illustrated in Figure 1.

Figure 1.
Process flow of the proposed solution.
This paper is organized as follows: Section 2 describes and defines the methods and materials used to create the proposed solution and conduct experiments. Section 3 describes the experiments and their results. Results and observations are discussed in Section 4. The main conclusions are given in Section 5. The literature used is listed in the last section.
2. Materials and Methods
This section presents the concepts of an autoencoder and artificial neural network. Furthermore, it describes a procedure for selecting similar days and details the unique architecture employed for training the ANN model for short-term load forecasting.
2.1. Autoencoder
The AE is one of the main building blocks of the proposed solution. In this study, an AE in its most original form is used, or as it is named in [9], The Basic AE. The AE is trained to reproduce the given input. However, copying the input to the output has no practical use. The latent representation (or code) of the input is more valuable than the actual output. The special case of AE, where the hidden layer is in a lower dimension than the input, is called under-complete [11,21]. In this case, the AE learns how to compress data and learns the most salient features of the input [11]. This type of encoding introduces errors in the reconstruction vector due to data loss resulting from compression. However, the precise design of autoencoders can minimize these errors and ensure that the encoded representation retains the essential information.
The AE’s structure integrates an encoder and a decoder as its main components. The encoder processes input data to the latent vector layer, and the decoder reconstructs data from the latent vector to the output layer. This study employed an Autoencoder (AE) with one hidden layer in both the encoder and decoder, resulting in the AE architecture shown in Figure 2.
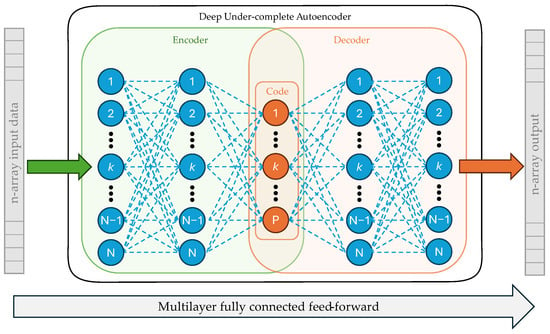
Figure 2.
An under-complete AE architecture with one hidden layer in both the encoder and decoder.
2.2. Selection of Similar Days
SDM is based on comparing the characteristics of historical days with the characteristics of the forecasted day. These characteristics can be weather data, the day of the week, date [14], or any other attribute that influences load consumption. In this study, each day from the available history data is coded using AE, and the codes are compared rather than the raw input data. The basic idea is presented in reference [13]. The further development and discussion of this idea are presented below.
The characteristics of the two days are captured in their respective latent-space representation vectors. To assess the similarity between the two days, a measurement of the similarity between these vectors is required. The Euclidian distance is used in [13] to measure the similarity of two vectors as follows:
where p and q are the vectors to be compared, and N is their dimension. The calculated distances can then be sorted, and the resulting diagram is shown in Figure 3. Based on this graphical representation, a knee-point can be identified. In Figure 3a, all available similar days are shown to represent the macro-level view. In this broader context, the graph can be analyzed as described in [13] and used to identify the macro-level knee-point at which the graph of distances begins to exhibit a more linear trend. Figure 3b provides a detailed micro-level view of the days most similar to the forecast day, showing the smallest distances. The knee-point at the micro-level can be identified using the same method. For this dataset, the macro-level knee-point typically occurs around the 100th day, while the micro-level knee-point is observed around the 20th day for almost every analyzed day.
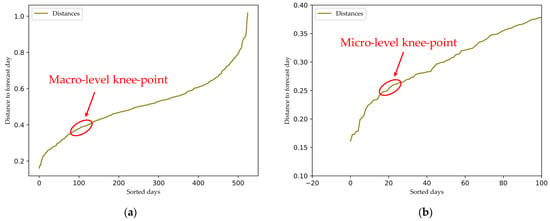
Figure 3.
Diagrams of Euclidian distances of selected days with (a) macro-level and (b) micro-level knee-points marked.
2.3. Artificial Neural Network Model
The proposed solution uses the ANN model to predict the load profile. According to [10], the multilayer feed-forward architecture is the most popular. The ability to learn the complex nonlinear relationships within the data distinguished it from linear models [10]. Throughout time, single models and several hybrid ANN-based methods have been established and used in theory and practice [6].
The Multilayer Perception (MLP) network is one of the simplest neural networks, consisting of an input layer, a hidden layer, and an output layer. However, deep ANN structures have more layers than MLP, particularly more hidden ones. Empirically, greater depth does seem to result in better generalization [21].
This study employs a feed-forward deep neural network model with multiple hidden layers. The architecture of the used ANN model is shown in Figure 4.
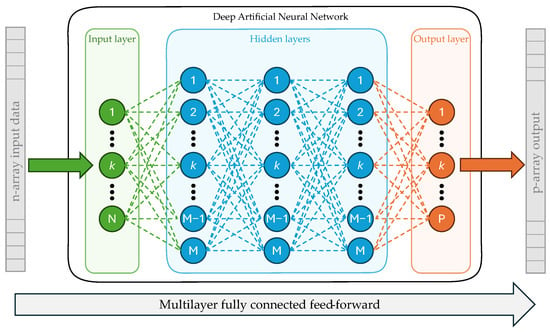
Figure 4.
ANN architecture for forecasting load profiles.
2.4. Training Procedure
In most cases, ANN training involves back-propagation to calculate the gradient. Methods such as Stochastic Gradient Descent (SGD) then use this gradient to update the model’s parameters during learning [21]. ANNs trained using a back-propagation algorithm are susceptible to overfitting [6,10]. According to [18], overfitting occurs when an algorithm fits the model too closely to its training data, which limits its ability to generalize and accurately predict outcomes on new datasets. Overfitting can be addressed by implementing early stopping [18,22], ensemble learning [18,23,24], and cross-validation [22,25].
2.4.1. Example Weights
The discussion in Section 2.2 clearly shows that not every day in history has the same value as the forecast procedure. Some days exhibit greater similarity, resulting in smaller Euclidean distances, whereas other days show less similarity, leading to larger distances. It is reasonable to prioritize more similar days with smaller distances. At this point, weights are introduced, which can be defined in a simple manner:
where d is the Euclidian distance calculated using Equation (1). With this definition, weights are larger for smaller distances and vice versa, assigning more importance to days that are more similar to the forecasted day. Furthermore, a more general weight equation can be defined based on the previous discussion as follows:
where d is the Euclidian distance, and a and b are independent parameters. It is important to note that if a = 1 and b = 0, the value of the weight factor is equal to 1 regardless of distance. In addition, if a = 1 and b = 1, (3) is reduced to (2). These two cases were used in this study to train the ANN model either without weights (w = 1) or with linear weights, as defined in Equation (2).
2.4.2. Weights of Examples in the Loss Function
It was previously discussed that days with lower distances should be more important in ANN training. As stated in [26], this is achieved by multiplying the loss of each example by its associated weight. In this study, the Mean Squared Error (MSE) was used as the loss function. If the weights are included, it is then transformed into a weighted mean square error loss function [27]:
All of the computer code for training the ANN in this research was written using the Keras [28] deep learning framework on top of TensorFlow [29].
2.4.3. Example Weights in Pre-Training and Fine-Tuning
Curriculum learning is described in [19] as an adaptive training strategy with analogies in the animal or human world, where infants learn simpler examples at first and then are introduced to more complicated ones. The authors emphasize the initiation of the learning procedure, proposing that a pre-trained model serves both to identify better local minima and to function as a regularizer [19]. This also requires a method for ranking the examples [30]. This learning approach inspired the two-stage learning procedure presented in this paper, where weights serve as a measure of the example’s difficulty. The first stage is the pre-training phase, in which the model is trained on simpler examples, positioning the solution within the parameter space of the final solution. The second stage is fine-tuning, where the model is trained on a small set of the most difficult days. In Section 2.2, two knee-points are marked in the diagrams: macro-level and micro-level. The days between the two knee-points are used for the pre-training stage, and then the model is fine-tuned with days ranked from 1 to micro-level knee-point. The major difference between the proposed method and curriculum learning is that in the curriculum learning method, all examples are included in the target training set.
2.4.4. Addressing Overfitting
Ensemble learning is a training technique that trains several models independently and then produces more accurate results by averaging the predictions [18]. This method also provides better generalization [23,24]. The presented methodology uses a small training set during the fine-tuning stage, which can lead to overfitting. This study employs ensemble learning during this stage, which helps to avoid the overfitting issue [23].
Cross-validation requires splitting the training dataset into k groups (k-fold cross-validation). One group is used as the validation set, and the rest of the data is used as the training set. Training is performed iteratively, and each group is used as a validation set [22,31]. The predictions are averaged to produce a k-fold estimate [25]. In this study, the concept of cross-validation was integrated with ensemble learning to train models on a small dataset during the fine-tuning phase. Each example in this small dataset contains valuable information. However, some examples have to be used as validation examples. By combining cross-validation with ensemble learning, each example is used for training and validation across different folds. The training set was divided into four groups to train the four models. Each model was trained on different training and validation sets. As shown in Figure 5, each model in this fine-tuning phase was started from the same pre-trained model.
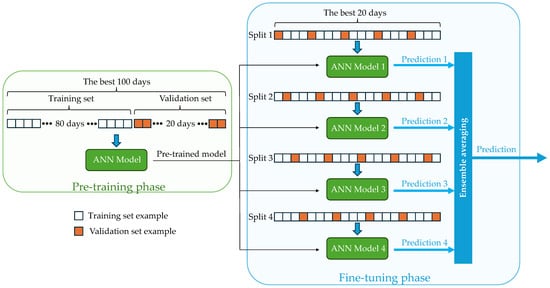
Figure 5.
Diagram of the fine-tuning training phase using validation sets of a sorted training set.
A hold-out [22,25] was used for the pre-training phase to create a validation set. Since two-stage training is employed, examples used for fine-tuning training are used as a validation set in pre-training. By validating the pre-training process in this manner, an effective starting model for the fine-tuning phase can be established.
Early stopping is a technique for preventing overfitting [18,22]. Both training loss and validation loss are tracked, and when a validation loss begins to degrade, training is stopped, and the best model is saved [22]. This method was used in every ANN training procedure in this study.
2.5. Metrics
This paper uses the Mean Absolute Percentage Error (MAPE) to compare results or determine forecast quality. This is also a widely used metric that is appropriate for engineering purposes. MAPE is defined as follows:
2.6. Data and Computer Code
The research and experiments were conducted using actual data from the Serbian electrical power system and weather data for Belgrade, the capital city of Serbia.
The data used in the experiments are publicly available. The historical electrical load data of the Serbian power system can be found on the Transparency platform of the European Network of Transmission System Operators for Electricity [32]. The weather data for Belgrade are available on a meteorology website designed and supported by Raspisaniye Pogodi Ltd., St. Petersburg, Russia [33]. This study uses actual measured data instead of weather forecast data for training purposes.
The computer code, training data, and saved models for each test example are available in a public GitHub repository [34] and Supplementary Materials.
3. Results
The experiments were conducted using the solution architecture described in the previous section using the following configurations and parameters:
- The AE inputs are the 24 h load from the previous day and the 24 h temperature forecast. Day in week is not an AE input but is used as a filter. The hidden layers of the encoder and decoder were in the exact dimensions as the input, 48 units. The code layer has 40 units.
- The ANN architecture was kept the same for each training. The input to the ANN is a 24 h temperature forecast. The output is a 24 h load profile. There are three hidden layers with 48 units between the input and output layers. The Adam optimizer [28] was used in every training with a learning rate of lr = 0.001 for pre-training and a variable learning rate from lr = 0.001 to lr = 0.0001 in the fine-tuning phase.
- The macro-level knee-point is set to 100, and the micro-level knee-point is set to 20 for every tested day.
Two experiments were conducted. The first experiment aimed to evaluate the design of the AE and the procedure for selecting similar days. The second experiment was designed to test the working hypothesis. Test examples were chosen from days in the previous 1-year period when the DSMM-STLF tool produced high forecasting errors, excluding pre-defined special days.
3.1. Experiment 1
Experiment 1 was conducted by training the ANN on the best 100 days (macro-level knee-point). There are two cases: training without weights and training with weights. In both cases, the test day was used for validation. The experiment aimed to verify whether the proposed AE configuration and procedure for selecting similar days can ultimately produce a training set for ANN training that provides better prediction than the existing DSMM-STLF tool. The experimental results are presented in Table 1.

Table 1.
Experiment 1 results: Comparison of ANN and DSMM-STLF tool errors.
Table 1 indicates that the ANN model generally provides better forecasts than the DSMM-STLF tool, except for the 14 May 2023 case, where the ANN error was larger in both training scenarios. On certain days, such as 19 June 2023, the error approached 1%, suggesting that the utilized dataset effectively captures dependencies necessary for achieving accurate forecasting results. Therefore, the AE configuration and procedure for selecting similar days were sufficient to produce a higher-quality dataset.
3.2. Experiment 2
The results of Experiment 1 clearly show that an ANN model capable of producing better forecasts can be obtained using the proposed methodology. However, the primary question was whether this could be achieved using only the available data. The validation set had to be carefully selected from the most similar days.
Experiment 2 was conducted in two stages: the first stage was pre-training the model with the days between two knee-points, days 20–100, and the second stage was fine-tuning employing ensemble learning and cross-validation. The fine-tuning phase was performed on the subsets of most similar days: first 20 days, first 16 days, first 12 days, first eight days, and first four days, consistently retaining the most similar days in each set. Four models were trained for each subset, and the final prediction was the mean value of their predictions. The training and validation days were selected as presented in Figure 5. The forecast errors of the proposed architecture compared with the DSMM-STLF tool errors are presented in Table 2.

Table 2.
Experiment 2 results. The error of the proposed solution compared to DSMM-STLF tool errors.
Table 2 shows that the proposed solution provided better results in 6 out of 9 cases. For days 16 July 2023, 17 July 2023, and 2 December 2023, the forecast error was higher than the DSMM-STLF tool. On certain days, such as 19 June 2023 and 25 February 2024, the errors closely align with those presented in Table 1. This observation suggests that the parameters configured in the algorithm are appropriate for these load curves and the utilized dataset. However, on days with substantial discrepancies in errors, such as 16 July 2023, further optimization of the parameters is necessary to reduce the error and bring it closer to the results shown in Table 1.
4. Discussion
The working hypothesis is defined in Section 1. This hypothesis was tested for ten days in two experiments. From the experimental results, two important conclusions can be drawn:
- The architecture of the AE and the approach of calculating distances as a measure of similarity between two days can produce a training set that leads to better predictions. Selecting days by comparing features in the form of hidden representations rather than raw data showed improved results.
- It is feasible to develop a training procedure that trains an ANN to forecast days with unexpected deviations from a typical daily curve using the training set prepared as described.
The hypothesis is supported based on these two conclusions derived from the experimental results.
Despite achieving the study’s primary goal, it may be beneficial to provide a few more observations and interpretations that came up front during the experiments. First, the best results were achieved using training with weight factors in all cases except for two days, observing the entire test set in Table 2. This observation should stimulate further research on the importance of days and provide a better definition of weight factors. Second, the importance of ensemble learning and k-fold cross-validation should be emphasized. Figure 6 shows that Model 2 produced significantly poorer predictions than the other three models. All four models are trained using the same pre-trained model, with the primary differences being the training and validation datasets. One potential cause of poor performance is the presence of training examples that are too distant from the forecasted day. If the training data lacks features relevant to the prediction task, the resulting predictions may be inaccurate. A second potential cause is the use of validation examples that are not closely related to the forecasted day. Since the training error is computed based on the validation set, irrelevant validation data can lead to the development of models that produce poor predictions. It is important to note that this stage of training is conducted on very small training sets, where a single bad training example can significantly affect the forecast. Ensemble learning plays a crucial role in mitigating the impact of these examples.
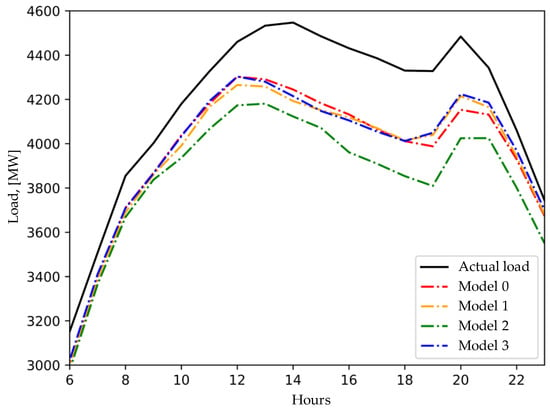
Figure 6.
Ensemble learning—predictions of individual models compared to the actual load.
Finally, the results of Experiment 2 indicate that the proposed solution was not entirely successful. To be precise, the error was higher for three test days. The first aspect of the discussion addresses the nature of an SDM forecast: if there are no similar days in the historical data, the prediction will not perform well. In addition, the nature of test days is crucial; these test days are instances where an established tool has already produced poor results. With this understanding, it was clear from the beginning of the study that the proposed solution was not expected to provide better predictions for every test day. The second aspect of the discussion is that the proposed architecture and methods were not optimized. For instance, the procedure for selecting similar days enabled the design of a very simple ANN with only 24 input nodes, thereby reducing the training execution time. However, since improved prediction accuracy is more valuable in this case than short execution time, incorporating additional parameters into the ANN input, such as another weather parameter like wind speed, might result in better forecasting.
4.1. Prediction Errors in STLF Context
In this paper, the error metric MAPE is used to evaluate and compare the prediction results. In the scientific community, all MAPE results smaller than 2% are considered acceptable [16,35,36,37]. The proposed algorithm is tested on days with unexpected deviations from typical daily patterns, and the results shown in Table 2 are comparable to this error threshold, highlighting the significance of the presented forecasting model.
Similar STLF methodologies, as examined in the reference [38], produced average errors ranging from 1.65% to 3.15% across various datasets. The similar day-based wavelet neural network methodology, tested on the New England dataset from 2006, achieved a MAPE value of 1.65%. An example of an LSTM model applied to the Belgian power transmission system over the course of one year, considering only standard days, reported a MAPE of 2.12%. Given that the results of this study, tested on days with unexpected deviations from typical daily patterns, are comparable to those of similar methodologies tested on all days, it can be concluded that the presented model produces relevant results.
A special day, such as a national or religious holiday, can be identified in advance, and deviations from the load profile of nonspecial days are anticipated in these cases. The methodology for forecasting special days, as presented in [17], yielded MAPE values of 1.39% for the SDRM-STLF model and 3.59% for the standard algorithm. The prediction errors reported in Table 2 are comparable to those of the SDRM-STLF and standard models, indicating that the results of this study are significant in the context of predicting nonstandard days.
The proposed work is the culmination of several years of research, with multiple papers published throughout this time [13,15,16,17,38,39,40,41]. Older models have been rigorously tested across diverse datasets, geographies, and power systems, and the current model represents the latest advancement in this ongoing development. The proposed solution addresses the issue of predicting days with unexpected deviations from typical daily patterns, a known limitation of the existing DSMM-STLF tool, as shown in Table 2. Consequently, the overall accuracy of the tool is improved.
4.2. Future Research
The proposed solution provides a solid foundation for further research. At this stage, several potential directions for further analysis can be identified:
- Further analysis of the AE design, especially related to the inputs and encoding dimension.
- Investigating and testing alternative measures of similarity. In this study, the Euclidean norm is used, which does not account for the position of the node in the latent vector. This information might be important for accurately assessing similarity.
- Defining a procedure for determining the knee-points that would be used instead of the graphical approach. It could provide optimal knee-points for each day instead of using the same numbers for all test examples.
- The weights are defined using the Equation (3). Parameters a and b can be varied, and defining the optimization procedure for weights for each forecast day based on the training set can improve prediction accuracy.
- Experiments with additional inputs to the ANN could provide more accurate prediction models.
- Further investigation of curriculum learning could lead to improvements. In this paper, only the idea of this method is used to define a two-stage training procedure. It would be very interesting to investigate the results if the procedure starts differently or to experiment with a multi-stage approach.
- Analyzing shifts in daily load curves and establishing a methodology to identify the root causes. This could serve as an additional filtering criterion for selecting similar days or as an input to the ANN.
5. Conclusions
This paper presents a novel methodology for short-term load forecasting that selects similar days based on hidden representations of day data. It enhances model generalization by utilizing a broader set of training examples and incorporating their relative importance during training. In addition, ensemble training mitigates the influence of outliers by using multiple models with different data splits, resulting in more robust predictions.
An autoencoder is utilized to define a training set of similar days extracted from a significantly broader historical dataset, facilitating a simple design of an ANN model for load profile prediction. Two experiments demonstrated that the proposed ANN-based methodology can be trained to provide better predictions on test examples than a field-proven DSMM-STLF tool. The application of adaptive training techniques, such as curriculum learning combined with ensemble learning, which mimics the progression from simple to complex learning observed in humans and animals, demonstrated potential in these applications.
The proposed methodology enhances the DSMM-STLF tool and provides a solid foundation for further research. The presented architecture is not limited to the STLF problem but can be considered a universal idea that can be applied to similar challenges.
Supplementary Materials
The supporting materials to help read and reproduce the results of the research, such as computer code and trained models, are uploaded to the public GitHub repository and can be downloaded at: https://github.com/zpajic-uns/AutoencoderDataSelectionAdaptiveTrainingSTLF (accessed on 28 June 2024).
Author Contributions
Conceptualization, Z.P. and Z.J.; methodology, Z.P.; software, Z.P.; validation, Z.P. and Z.J.; formal analysis, Z.P.; investigation, Z.P.; resources, Z.J.; data curation, Z.P.; writing—original draft preparation, Z.P.; writing—review and editing, Z.P., Z.J. and A.S.; visualization, Z.P.; supervision, A.S.; project administration, Z.P.; funding acquisition, Z.P. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Schneider Electric Novi Sad, Industrijska 3G, 21000 Novi Sad, Serbia.
Data Availability Statement
The original data presented in the study are openly available. Historical electrical load data on the Serbian power system can be found on the Transparency platform of the European Network of Transmission System Operators for Electricity (https://transparency.entsoe.eu/ (accessed on 28 June 2024)). The weather data for Belgrade are available on a meteorology website designed and supported by Raspisaniye Pogodi Ltd. (https://rp5.ru/Weather_archive_in_Belgrade (accessed on 28 June 2024)). The computer code and data used to train the models, as well as saved models for each test example, are available on the public GitHub repository (https://github.com/zpajic-uns/AutoencoderDataSelectionAdaptiveTrainingSTLF (accessed on 28 June 2024)).
Acknowledgments
The authors are grateful to Duško Bekut, a Technology board member at Schneider Electric LLC, Novi Sad, Serbia, for his administrative support within the company.
Conflicts of Interest
Author Zoran Janković was employed by the company Schneider Electric Novi Sad. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Ghiani, E.; Pisano, G. Chapter 2—Impact of Renewable Energy Sources and Energy Storage Technologies on the Operation and Planning of Smart Distribution Networks. In Operation of Distributed Energy Resources in Smart Distribution Networks; Zare, K., Nojavan, S., Eds.; Academic Press: Cambridge, MA, USA, 2018; pp. 25–48. ISBN 978-0-12-814891-4. [Google Scholar]
- Sajadi, A.; Strezoski, L.; Strezoski, V.; Prica, M.; Loparo, K.A. Integration of Renewable Energy Systems and Challenges for Dynamics, Control, and Automation of Electrical Power Systems. WIREs Energy Environ. 2019, 8, e321. [Google Scholar] [CrossRef]
- Strezoski, L.; Stefani, I.; Brbaklic, B. Active Management of Distribution Systems with High Penetration of Distributed Energy Resources. In Proceedings of the IEEE EUROCON 2019—18th International Conference on Smart Technologies, Novi Sad, Serbia, 1–4 July 2019; pp. 1–5. [Google Scholar]
- Vukadinović: Broj Kupaca-Proizvođača Električne Energije za Godinu i po Dana Povećan Sedam Puta. Available online: http://www.mre.gov.rs/vest/sr/4887/vukadinovic-broj-kupaca-proizvodjaca-elektricne-energije-za-godinu-i-po-dana-povecan-sedam-puta.php (accessed on 29 May 2024).
- Habbak, H.; Mahmoud, M.; Metwally, K.; Fouda, M.M.; Ibrahem, M.I. Load Forecasting Techniques and Their Applications in Smart Grids. Energies 2023, 16, 1480. [Google Scholar] [CrossRef]
- Al Mamun, A.; Sohel, M.; Mohammad, N.; Sunny, M.S.H.; Dipta, D.R.; Hossain, E. A Comprehensive Review of the Load Forecasting Techniques Using Single and Hybrid Predictive Models. IEEE Access 2020, 8, 134911–134939. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Sun, M.; Sun, C. Hybrid Policy-Based Reinforcement Learning of Adaptive Energy Management for the Energy Transmission-Constrained Island Group. IEEE Trans. Ind. Inform. 2023, 19, 10751–10762. [Google Scholar] [CrossRef]
- Raghav, L.P.; Kumar, R.S.; Raju, D.K.; Singh, A.R. Optimal Energy Management of Microgrids Using Quantum Teaching Learning Based Algorithm. IEEE Trans. Smart Grid 2021, 12, 4834–4842. [Google Scholar] [CrossRef]
- Peng, T.M.; Hubele, N.F.; Karady, G.G. Advancement in the Application of Neural Networks for Short-Term Load Forecasting. IEEE Trans. Power Syst. 1992, 7, 250–257. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural Networks for Short-Term Load Forecasting: A Review and Evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Chen, S.; Guo, W. Auto-Encoders in Deep Learning—A Review with New Perspectives. Mathematics 2023, 11, 1777. [Google Scholar] [CrossRef]
- Hubens, N. Deep Inside: Autoencoders. Available online: https://towardsdatascience.com/deep-inside-autoencoders-7e41f319999f (accessed on 18 May 2024).
- Pajić, Z.; Selakov, A. A Flexible Approach for Selection of the Training Set for ANN-Based Load Forecast Using Autoencoder and Similar Day Method. In Proceedings of the 2023 IEEE Belgrade PowerTech, Belgrade, Serbia, 25 June 2023; pp. 1–5. [Google Scholar]
- Feinberg, E.A.; Genethliou, D. Load Forecasting. In Applied Mathematics for Restructured Electric Power Systems; Chow, J.H., Wu, F.F., Momoh, J., Eds.; Power Electronics and Power Systems; Kluwer Academic Publishers: Boston, MA, USA, 2005; pp. 269–285. ISBN 978-0-387-23470-0. [Google Scholar]
- Janković, Z.; Selakov, A.; Bekut, D.; Đorđević, M. Day Similarity Metric Model for Short-Term Load Forecasting Supported by PSO and Artificial Neural Network. Electr. Eng. 2021, 103, 2973–2988. [Google Scholar] [CrossRef]
- Janković, Z.; Vesin, B.; Selakov, A.; Berntzen, L. Gab-SSDS: An AI-Based Similar Days Selection Method for Load Forecast. Front. Energy Res. 2022, 10, 844838. [Google Scholar] [CrossRef]
- Jankovic, Z.; Ilic, S.; Vesin, B.; Selakov, A. Special Day Regression Model for Short-Term Load Forecasting. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Novi Sad, Serbia, 10 October 2022; pp. 1–5. [Google Scholar]
- IBM. What Is Overfitting? Available online: https://www.ibm.com/topics/overfitting (accessed on 18 May 2024).
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum Learning. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14 June 2009; pp. 41–48. [Google Scholar]
- Berahmand, K.; Daneshfar, F.; Salehi, E.S.; Li, Y.; Xu, Y. Autoencoders and Their Applications in Machine Learning: A Survey. Artif. Intell. Rev. 2024, 57, 28. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Lin, D.C.-E. 8 Simple Techniques to Prevent Overfitting. Available online: https://towardsdatascience.com/8-simple-techniques-to-prevent-overfitting-4d443da2ef7d (accessed on 18 May 2024).
- Ganaie, M.A.; Hu, M.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble Deep Learning: A Review. Eng. Appl. Artif. Intell. 2022, 115, 105151. [Google Scholar] [CrossRef]
- Mienye, I.D.; Sun, Y. A Survey of Ensemble Learning: Concepts, Algorithms, Applications, and Prospects. IEEE Access 2022, 10, 99129–99149. [Google Scholar] [CrossRef]
- Blum, A.; Kalai, A.; Langford, J. Beating the Hold-out: Bounds for K-Fold and Progressive Cross-Validation. In Proceedings of the Twelfth Annual Conference on Computational Learning Theory, Santa Cruz, CA, USA, 6 July 1999; pp. 203–208. [Google Scholar]
- Example-Weighted Neural Network Training—Wolfram Language Documentation. Available online: https://reference.wolframcloud.com/language/tutorial/NeuralNetworksExampleWeighting.html (accessed on 20 May 2024).
- Chintalapati, R. Tensorflow: The Curious Case of Weighted Mean Square Error. Available online: https://www.rajashekar.org/wmse/ (accessed on 20 May 2024).
- Team Keras. Keras Documentation: About Keras 3. Available online: https://keras.io/about/ (accessed on 20 May 2024).
- TensorFlow. Available online: https://www.tensorflow.org/ (accessed on 20 May 2024).
- Lapedriza, A.; Pirsiavash, H.; Bylinskii, Z.; Torralba, A. Are All Training Examples Equally Valuable? arXiv 2013, arXiv:1311.6510. [Google Scholar]
- Aloqaily, A.A. Modelling, Data Mining and Visualisation of Genetic Variation Data. Ph.D. Thesis, University of Technology, Sydney, Australia, 2012. [Google Scholar]
- ENTSO-E Transparency Platform. Available online: https://transparency.entsoe.eu/ (accessed on 28 June 2024).
- Weather Archive in Belgrade. Available online: https://rp5.ru/Weather_archive_in_Belgrade (accessed on 28 June 2024).
- zpajic-uns Zpajic-Uns/AutoencoderDataSelectionAdaptiveTrainingSTLF. Available online: https://github.com/zpajic-uns/AutoencoderDataSelectionAdaptiveTrainingSTLF (accessed on 28 June 2024).
- Dong, X.; Qian, L.; Huang, L. Short-Term Load Forecasting in Smart Grid: A Combined CNN and K-Means Clustering Approach. In Proceedings of the 2017 IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju Island, Republic of Korea, 13–16 February 2017; pp. 119–125. [Google Scholar]
- Hossen, T.; Plathottam, S.J.; Angamuthu, R.K.; Ranganathan, P.; Salehfar, H. Short-Term Load Forecasting Using Deep Neural Networks (DNN). In Proceedings of the 2017 North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017; pp. 1–6. [Google Scholar]
- Amber, K.P.; Ahmad, R.; Aslam, M.W.; Kousar, A.; Usman, M.; Khan, M.S. Intelligent Techniques for Forecasting Electricity Consumption of Buildings. Energy 2018, 157, 886–893. [Google Scholar] [CrossRef]
- Janković, Z. Adaptive Time Series Forecasting Model in Intelligent Infrastructure Networks. Ph.D. Thesis, University of Novi Sad, Novi Sad, Serbia, 2022. [Google Scholar]
- Selakov, A.; Cvijetinović, D.; Milović, L.; Mellon, S.; Bekut, D. Hybrid PSO–SVM Method for Short-Term Load Forecasting during Periods with Significant Temperature Variations in City of Burbank. Appl. Soft Comput. 2014, 16, 80–88. [Google Scholar] [CrossRef]
- Savić, S.; Selakov, A.; Milošević, D. Cold and Warm Air Temperature Spells during the Winter and Summer Seasons and Their Impact on Energy Consumption in Urban Areas. Nat. Hazards 2014, 73, 373–387. [Google Scholar] [CrossRef]
- Selakov, A.; Ilic, S.; Vukmirovic, S.; Kulic, F.; Erdeljan, A.; Gorecan, Z.; Gorečan, Z. A Comparative Analysis of SVM and ANN Based Hybrid Model for Short Term Load Forecasting. In Proceedings of the PES T&D 2012, Orlando, FL, USA, 7–10 May 2012; pp. 1–5. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).