Application of the FDTD Method to Analyze the Influence of Brick Complexity on Electromagnetic Wave Propagation

Abstract

This article presents a numerical analysis of the effects related to the propagation of electromagnetic waves in an area containing a non-ideal, non-uniform, and absorbing dielectric. The analysis concerns the influence of electrical parameters, the structure of the building material, and the layering of the wall on the values of the electric field intensity. A multivariate analysis was carried out with different conductivity values. Homogeneous materials (e.g., solid brick) can be analyzed using the analytical method. In the case of complex materials containing, e.g., hollows (brick with hollows, hollow block), it is necessary to use the numerical method. The FDTD (finite difference time domain) method was used to assess the dependence of the electric field intensity on the layering, the length of hollows in bricks, and the material loss. In order to check the correctness of the adopted numerical assumptions, a series of tests related to the discretization of the model was carried out. The article also presents the influence of changing the length of hollows in bricks on the values of the electric field intensity at a frequency of 2.4 GHz. The instantaneous field distributions and maximum values of the electric field intensity are presented. In the model with a two-layer wall, regardless of the conductivity, the field values were the same for the two models, where the difference in the percentage of ceramic mass in the brick was 8%. A 12% decrease in the percentage of ceramic mass in the brick resulted in a 15% increase in the value of the area between a single-layer and a double-layer wall made of clinker bricks. At a conductivity of 0.04 S/m for a single-layer wall, the field values were similar for all brick variants.

1. Introduction

Wireless networks are a proven solution used in the creation of telecommunications systems. There is a noticeable dynamic development of technologies related to wireless communication, starting from remote communication between selected devices within personal networks with a range of up to several meters WPAN (wireless personal area network), through WLAN (wireless local area network) with a range of up to several hundred meters, to extensive WWAN (wireless wide area network) telecommunications networks, reaching up to several dozen kilometers. The group of wireless communication systems includes both networks based on communication using infrared, as well as networks in which data transmission takes place via radio in the microwave band. Wireless communication systems allow for the transfer of data between computers without the need to install complex cable installations. They also provide the possibility of joint use of one broadband connection. Thanks to the use of standard devices, the installation of wireless data transmission systems is in many cases easier and faster than the installation of cable networks. Technologies of this type are an important, constantly gaining in importance as a supplement to wired networks. They can be used where technical reasons make it difficult to lay wired networks [1,2,3,4,5].

Maintaining the proper quality of communication in the selected area remains a fundamental issue when installing wireless communication systems. The greatest problems with communication occur inside buildings, and for this reason, there are often areas with signal loss. The reason is the effects created by the propagation of electromagnetic waves in systems, especially those with complex geometry and material structure. Analyses of the functioning of networks in existing buildings are most often performed. However, problems that may arise with communication between devices can be predicted at the design stage (especially in single-family houses). When installing routers, for example, the building structure can also be taken into account to reduce the undesirable effects associated with EM wave propagation. Therefore, numerous analyses of the impact of different wall structures, the variety of materials used, and the values of electrical parameters on the quality of EM wave propagation are needed. The best tool for such multivariant analyses is the use of numerical methods, which are non-invasive and do not incur additional costs. It is easy to modify models, which allows for the collection of a large number of results for a detailed analysis of the issues discussed. When using numerical methods, in order to obtain correct results, important factors are:

-

correct model representation, taking into account the constraints imposed by the choice of method;

-

correct assumption and description of boundary conditions and assumptions regarding the analysis;

-

assignment of the correct values of electrical parameters for the building material.

The use of analytical methods leads to solutions that are fully based on the mathematical model and burdened with the smallest error [6]. However, their use is possible in systems with simple geometry. The limitations of analytical methods do not allow for considering issues related to the propagation of electromagnetic waves in complex real building structures [7]. Their use is limited to checking and comparing the approximate solution obtained using numerical methods, in the case of simple test models.

Due to the complex nature of the occurring physical phenomena and the significant diversity of geometry and material structures in building structures, the results of the works presented in the available literature are often fragmentary [8,9]. In selected cases, they concern systems that are largely theoretical in terms of geometry and materials used [10]. This is partly due to the choice of the method for calculating field phenomena [11,12]. Three basic groups of presented issues can be distinguished in the available publications.

-

Description of material data characterizing the electrical properties of building materials [13,14,15,16].

-

Analysis of building structures, including multilayer structural elements and composite materials (reinforced concrete), which influences the method of mathematical description of the structure and properties of composite materials within the models created [17,18,19,20].

-

Selection of the method used to determine the distribution of the electromagnetic field [9,21,22,23,24].

A particularly complex and rarely analyzed issue is the assessment of electromagnetic phenomena in building structures, including those containing multilayer materials and those with a periodic arrangement of components (e.g., hollow bricks, hollow blocks, reinforced concrete). Due to the large diversity of building materials and technologies used, this fundamental factor determines the scope and complexity of research.

The issues presented in publications [13,25] take into account the applied building materials and technologies to a limited extent. The analysis of available source materials [9,26,27,28,29] indicates that many issues have not been considered in a comprehensive manner so far, taking into account the internal structure of elements or the differentiation of material properties. In many publications, the authors focus more on the analysis of homogeneous materials (i.e., concrete, aerated concrete, solid brick) than on complex materials (e.g., bricks with cavities, hollow bricks). Many authors, when modeling structures, do not take into account cavities in the material. A wall composed of homogeneous material is modeled, and yet this percentage share of ceramic mass in the brick is, on average, about 78% [30]. It should be remembered that there is air inside the cavities, which does not constitute an obstacle to the propagation of electromagnetic (EM) waves. The article shows that cavities should be considered when modeling because they significantly impact the values of the EM field intensity. The article contains a detailed analysis of the effect of changing the length of cavities inside commonly used bricks on the quality of transmission and the formation of momentary signal amplifications and reductions.

In the literature, walls made of basic building materials are analyzed, which are often treated as uniform homogeneous structures [31,32,33,34,35]. Despite the diverse composition and properties of individual components, the particle sizes, e.g., aggregate; meet the conditions of quasistationarity. The dimensions of the model remain relatively large compared to unordered components, e.g., concrete [36]. The second reason for homogenizing the properties of a given material is related to the limited possibilities of mapping a complex structure due to the capabilities of a computer or software. For the reasons given, the analyzed walls are described in the form of homogeneous plates of various sizes, the properties of which are uniform, isotropic, and expressed by three parameters: ε_r, μ_r, and σ [35,37]. Few publications have analyzed the different variants of the composition of building materials, e.g., concrete [38]. A comparison of two types of concrete samples with different porosity of the structure was presented in [38]. The analysis of concrete, taking into account the relative water content expressed by the weight ratio (w/c), is included in [16,39]. An example of the application of the numerical method is presented in [40]. A concrete slab with a single layer of cross-reinforcement was analyzed at two frequencies (f ∈ {0.9, 1.8} GHz). The authors determined the reflection and transmission coefficients for different angles of electromagnetic wave incidence as a function of wall thickness in the range from 0.02 to 0.2 m for both homogeneous concrete slabs and those containing a metal mesh inside the structure. The article is an example of applying the FDTD method to the problems of modeling fields in building structures [41]. The publication considers a periodic one- and two-dimensional model of a concrete wall, taking into account the diversity of the structure, with special emphasis on reinforcing bars. The phenomena occurring at frequencies in the range from 0.5 to 2 GHz were analyzed. The publication [42] describes the analysis of the effect of reinforced concrete on signal attenuation, considering the rod diameter’s effect on the effects related to reflection. The analysis was performed in the frequency range from 0.1 to 6 GHz. It was shown that wave propagation through inhomogeneous materials, taking into account the thickness of the plate, is complex. The presented results prove that the nature of physical phenomena in the case of reinforced plates and inhomogeneous materials requires numerous analyses of special cases for specific frequencies. An EM wave passing through complex materials changes its wavefront, propagates at different speeds, and at different angles experiences multiple reflections, which overlap and result in momentary signal loss or amplification.

In the case of hollow bricks, it can often be noticed that the authors analyzed models of walls made of homogeneous material, e.g., solid bricks [15]. The considerations often concern random dimensions of walls or real dimensions used only in a given country [43]. Many authors analyze the dependence of, e.g., wall thickness on damping. In the article [44] a comparison of the results obtained by the FDTD method and the values obtained by measurements were presented. The analysis concerned one level of a seven-story office building consisting of several rooms modeled with different types of building materials and different wall thicknesses. All walls were modeled as homogeneous materials. The walls made of bricks did not contain hollows because it would have been impossible due to the implementation of the numerical model. It was shown that to obtain results consistent with the calculated measurements, it is necessary to create large FDTD (3D) models, which require a large amount of RAM and a long computation time.

In the literature, one can find models of walls made of hollow elements, not in bricks but in concrete, because such technology is mandatory in a given country [43]. Due to the specificity of construction technology used, for example, in England, the literature presents the analysis of concrete elements with hollows [45]. The authors investigated the use of ultra-wideband radar for detection through a wall composed of two homogeneous layers of concrete separated by an air gap. Two types of concrete blocks were considered: (a) with 12 cavities (3 in 4 rows); (b) with 3 cavities in one row. The aim was to investigate the effect of the air gap on the level of the radar signal power reflected from the target. The authors in [46] described the results of measurements and simulations performed in Ansys HFSS, where the object was a 50 cm thick hollow brick wall made of 25 × 50 cm Porotherm bricks. The analysis concerned the effectiveness of electromagnetic field shielding in the high-frequency range of 0.9–5 GHz. The authors in [43] presented a study on integrating frequency-selective surfaces (FSS) in some building construction systems. Penetration losses were assessed for different materials used in southern Europe, ranging from 800 MHz to 10 GHz. Three types of walls made of bricks with hollows of thicknesses 11 cm (with eight square hollows), 15 cm (with 12 square hollows), and 20 cm (with 16 square hollows) were considered. The article [43] presents the penetration loss curves dependent on the frequency (up to 40 GHz) for homogeneous materials (concrete, solid brick, plaster, wood, and glass). Different attenuation slopes were indicated. A significant difference is observed in the case of brick material, which in the International Telecommunication Union (ITU) document is valid only for frequencies up to 10 GHz. The authors noted that an individual analysis of walls made of non-homogeneous material is necessary, which causes changes in the propagation of EM waves due to its passage through different media.

Correct determination of electrical properties of materials is an important condition for correct, reliable representation of field phenomena in modeled building structures [13]. Basic ceramic and concrete materials are generally imperfect dielectrics. For this reason, the values of the parameters of modeled materials, including: electric permittivity, magnetic permeability, and conductivity, are subject to detailed discussion.

The analysis of the wave propagation in the high-frequency range is connected with the necessity to research the effects of the construction itself and the building materials with different electrical properties, i.e., the electric permittivity (ε = ε₀ε_r) and conductivity (σ) [8]. Both the periodic structures and singular elements of specific material properties (reinforcement) cause the resistance of the wireless transmission channel to be subjected to interference, signal delays, and signal loss. Some of the factors are random in nature and connected to the changes in wave propagation conditions. However, the construction of resistible communication networks requires, at the stage of designing the system, to take into account the elements influencing the field distribution (among others, the geometry of the building, complex material structures in the path between the transmitter, and receiver). The mentioned problems are especially visible in low-range wireless networks (like Wi-Fi), used in buildings.

The review of source materials shows that the issues discussed in this work constitute an important, still explored issue. This is aimed, among others, at helping design and assess wireless communication systems’ operating conditions. Most studies focus on the analysis of the impact of the arrangement of walls and other construction elements on the propagation of electromagnetic waves [9,13]. The following issues are considered to a lesser extent:

-

complex construction and structure of wall materials;

-

modeling of walls with dimensions consistent with construction techniques;

-

diversity of building materials used (i.e., types of bricks).

The article presents the results of a multivariant impact analysis:

-

wall structure (single-layer and double-layer);

-

lengths of hollows inside bricks;

-

values of electrical parameters adopted to describe the building material for the values of electric field intensity.

The finite difference time domain (FDTD) method was used for the analysis, which allows for the observation of phenomena occurring at selected moments in time [47,48,49]. It is also possible to obtain the maximum electric field values for the final evaluation. In the case of all methods, the biggest problem is the description of the model, assigning the appropriate boundary conditions, and checking their correctness. For this reason, the article also presents the impact of improper matching of the adopted conditions (model discretization) on the results. Based on the comparison of results from the analytical and numerical analysis, a multivariate analysis was then carried out at the frequency used in the set of standards created for the construction of wireless computer networks, e.g., Wi-Fi (2.4 GHz). A particular application of this network is the construction of local networks based on WLAN radio communication. The range of the network is from several meters to several kilometers.

The analysis of the electric field distribution in selected wall structures also took into account the variability of the brick conductivity. The reason was two issues.

(1)

A review of many publications found a large discrepancy in the values assigned to electrical parameters (e.g., for brick, the conductivity is in the range from 0.0174 S/m to 0.244 S/m) [15,16,43,50].

Depending on weather conditions, geographical location, and the method of making the building material, the walls of the structure may have different losses, which require a detailed analysis.

Section 2 presents a description of the most commonly used building material, bricks in this case. The ranges of the electrical parameters used for these materials are also presented. Section 3 discusses mathematical relationships describing the analyzed field problems. Equations that are the basis for formulating the FDTD numerical scheme are determined. Section 4 presents the analyzed models, the system’s geometry, the adopted assumptions and variants of the walls made of hollow bricks. Section 5 contains the results of a detailed analysis of the selection of the differential mesh size. Section 6 contains the results and discussion related to the analysis of the influence of layering, material loss, and the length of hollows contained in bricks on the values of the electric field intensity.

2. Building Material–Bricks

In the available literature, the walls are mainly considered as homogeneous plates of various sizes, whose properties are uniform, isotropic, and expressed by three parameters: relative electric permittivity (ε_r), relative magnetic permeability (μ_r), and conductivity (σ). Building structures are created based on basic building materials, the internal structure of which, its complexity, and variability of material parameters have an impact on building and electrical properties.

In recent years, the most commonly used technology is brickwork. Loads are transferred by reinforced concrete ceilings, which allows for any shaping of the space inside the building. The main building material is ceramics (e.g., in the form of bricks and hollow blocks). Walls can also be multilayered depending on the materials used and the function they are to perform (e.g., partition, load-bearing, protective, and protective wall).

Lime-sand products are made of lime, sand, and water [51]. Silicate materials, like building ceramics, are characterized by high bulk density resulting from the small amount of free space in the material. Bricks are made of clay or other clay raw materials with the addition of sand and then dried and fired at high temperatures. The division of finished products concerns geometric features, compressive strength, degree of firing, and raw materials used [52,53]. Ceramic elements are created by firing a mixture of natural ingredients, in which clay plays the dominant role, and the remaining ingredients include, among others, clay, shale, or kaolin. Currently, their production process is automated [54]. Masses of various consistencies are obtained based on the proper ingredient dosage and humidity control. Products with diverse properties and applications are obtained through appropriate shaping, drying, and then repeated firing at temperatures reaching 1000–1450 °C. Ceramic elements available on the construction market can be divided according to their application:

-

structural: bricks, hollow blocks, roof tiles, pipes, lintel, and sewage fittings;

-

finishing and decorative: ceramic tiles;

-

sanitary products-washbasins, urinals, toilet bowls.

When considering the elements for building walls, we can distinguish solid bricks, perforated bricks, traditional blocks, porous blocks, polished blocks, and acoustic blocks. From the point of view of the structural designer, it is important to divide masonry elements according to the size and direction of drilling holes, i.e., divide them into groups according to [55,56], as well as their possible application.

Ceramic bricks are the oldest and most common masonry elements used in construction. Despite the continuous development of technology for erecting buildings from other formats of masonry elements, it is still a solution that is used in some applications. Recently, there has been a return to red burnt brick as a great decorative accent for interiors and building facades. The high demand for bricks is also influenced by the fashion for revitalizing old buildings. The dimensions of bricks, depending on the country where they were produced, differed in dimensions. Until now, in Poland, a standard solid building brick with traditional dimensions had a length, width and height of 250 × 120 × 65 mm, respectively. There is no strict dimensioning of the hollows. Only the volumetric density, the function that the wall is to fulfill, the manufacturing tolerance, external dimensions, and the application are specified. Figure 1 shows examples of types of building materials made of ceramics.

In numerical analysis, the authors of available publications do not use hollow modeling. They only focus on the problem of a wall made of bricks and assign only different values of electrical parameters (

Table 1. Example values of the electrical properties of bricks [21,22,43,50].

No.	f (GHz)	εr′	εr2	σ (S/m)
1	1.7–2.6	4.44	-	0.01
2	1.7–18.0	4.62–4.11	-	0.0174–0.0364
3	2.0	4.44	-	-
4	3.0; 9.0; 24.0 9.0 24.0	3.7–19	0.12–3.7	-
5	5.0	4.12	0.16	0.0445
6	60.0	3.95	0.073	0.244

) [43]. The main reasons are the time-consuming modeling of hollows and the limitations of computing power. The authors of the publication [21] measured the electrical parameters for three types of solid bricks (red, brown, and with a groove) with water content close to zero. The analysis concluded that at frequencies of 3 GHz, 9 GHz, and 24 GHz, the value of ε_r′ is similar and is within the range from 3.7 to 4.44. Depending on the frequency, in the available literature, one can find the value of relative permittivity in the range of 2.82–19, while conductivity takes values from 0.00278 to 0.244 S/m.

3. Analysis Methods

When modeling electromagnetic phenomena in the considered wall systems, the relative measure of the size of the analyzed model should be the size of the linear dimensions of the system in relation to the length of the propagating electromagnetic wave. The choice of the calculation method is largely dictated by the relative size of the model and the resulting approximations in the representation of physical phenomena. The issues considered in electromagnetic wave propagation belong to the group of open problems. Despite the relatively small range of operation of local wireless communication systems (e.g., within buildings), the representation of field phenomena is associated with the reproduction of wave propagation phenomena in an open, theoretically infinite area. In local wireless communication systems, the boundaries of wave propagation are not limited to the building area; hence, the complexity and size of the considered area should be taken into account, as well as the adoption of such boundary conditions that will well reflect the modeled system.

The dimensions of the modeled building structures at the frequency of 2.4 GHz are larger than the length of electromagnetic waves [48]. Due to the failure to meet the quasistationarity condition, the analyzed task comes down to solving the boundary-initial problem presented by differential equations [27,48,49]. The materials present in the studied systems are treated as continuous media, characterized by means of homogenized electrical parameters ε_r, μ_r, and σ.

In order to analyze the field distribution, the finite-difference time-domain method (FDTD) was used [48,49]. The time-domain algorithm (FDTD) is an explicit scheme in which the model representation is reduced to a matrix description of the material distribution in the model domain. This set is sequentially searched in each time-scheme step. The calculated field value is a linear combination of the appropriate factors determined in previous iterations over time. Determining the field value using the FDTD scheme requires first calculating the unsteady state. To determine the field intensity amplitude distribution (the so-called envelope), a sequence of calculations in the time domain after reaching the steady state is also necessary. The method is based on Maxwell’s equations in time and space [48]:

$$\nabla \times E=-{\displaystyle \frac{\partial B}{\partial t}},$$

(1)

$$\nabla \times H=J_P+J_D+J_I,$$

(2)

$$\nabla ·D=\rho .$$

(3)

$$\nabla ·B=0,$$

(4)

$$\nabla ·J=-{\displaystyle \frac{\partial \rho }{\partial t}},$$

(5)

where E is a vector of the electric field and H is the magnetic field (vector). The sources of these fields are electric charges and electric currents, which can be expressed as local densities, namely charge density ρ and current density J. The density of conduction current J_P and displacement current J_D are presented by:

$$J_P=\sigma \hspace{0.17em}E,$$

(6)

$$J_D={\displaystyle \frac{\partial D}{\partial t}}.$$

(7)

The FDTD method allows the analysis of complex structures in which every material has a corresponding electrical properly material. Description issues by Equations (1)–(5) allow for the determination of the field distribution in the nonstationary state and steady state in the appearance of time-varying field excitations. After putting in a decomposition, Equations (1) and (2) are presented in six conjugate differential equations of the first order that describe the field components of electric and magnetic [48,49]:

$${\displaystyle \frac{\partial E_x}{\partial t}}={\displaystyle \frac{1}{\epsilon }}\left({\displaystyle \frac{\partial H_z}{\partial y}}-{\displaystyle \frac{\partial H_y}{\partial z}}-\sigma E_x\right),$$

(8)

$${\displaystyle \frac{\partial E_y}{\partial t}}={\displaystyle \frac{1}{\epsilon }}\left({\displaystyle \frac{\partial H_x}{\partial z}}-{\displaystyle \frac{\partial H_z}{\partial x}}-\sigma E_y\right),$$

(9)

$${\displaystyle \frac{\partial E_z}{\partial t}}={\displaystyle \frac{1}{\epsilon }}\left({\displaystyle \frac{\partial H_y}{\partial x}}-{\displaystyle \frac{\partial H_x}{\partial y}}-\sigma E_z\right),$$

(10)

$${\displaystyle \frac{\partial H_x}{\partial t}}={\displaystyle \frac{1}{\mu }}\left({\displaystyle \frac{\partial E_y}{\partial z}}-{\displaystyle \frac{\partial E_z}{\partial y}}\right),$$

(11)

$${\displaystyle \frac{\partial H_y}{\partial t}}={\displaystyle \frac{1}{\mu }}\left({\displaystyle \frac{\partial E_z}{\partial x}}-{\displaystyle \frac{\partial E_x}{\partial z}}\right),$$

(12)

$${\displaystyle \frac{\partial H_z}{\partial t}}={\displaystyle \frac{1}{\mu }}\left({\displaystyle \frac{\partial E_x}{\partial y}}-{\displaystyle \frac{\partial E_y}{\partial x}}\right).$$

(13)

In a formulation of this method, the Yee cell is used (Figure 2). It contains six appropriately placed component vectors of field intensity: electrical {E_x, E_y, E_z} and magnetic {H_x, H_y, H_z}. In order to calculate the area, the entire considered area must be divided into Yee cells. This is one of the main factors determining correct results. In this paper, in Section 4, the impact of the Yee cell size on the correctness of the results is presented. Determined spatial distributions of E_x, E_y, E_z, H_x, H_y, and H_z are assigned in definite points of the area (x, y, and z), taking into account the finite size of the step of integration on the field (Δ_x, Δ_y, and Δ_z).

Iterative integration of Equations (1) and (2) in the time domain is constructed on the two-step scheme. The physical quantities are functions of the spatial variables (x, y, z) and the time variable (t). Following, put in Euler’s scheme of the central differences to approximate the partial derivatives are new Equations (8)–(13) in the form:

$${\displaystyle \frac{{}_{i,j,k}{}^{n+1}E_x-{}_{i,j,k}{}^{n}E_x}{{\Delta }_t}}={\displaystyle \frac{1}{{\epsilon }_{i,j,k}}}\left({\displaystyle \frac{{}_{i,j+\frac{1}{2},k}{}^{n+\frac{1}{2}}H_z-{}_{i,j-\frac{1}{2},k}{}^{n+\frac{1}{2}}H_z}{{\Delta }_y}}-{\displaystyle \frac{{}_{i,j,k+\frac{1}{2}}{}^{n+\frac{1}{2}}H_y-{}_{i,j,k-\frac{1}{2}}{}^{n+\frac{1}{2}}H_y}{{\Delta }_z}}-{\sigma }_{i,j,k} {}_{i,j,k}{}^{n+{\displaystyle \frac{1}{2}}}E_x\right),$$

(14)

$${\displaystyle \frac{{}_{i,j,k}{}^{n+1}E_y-{}_{i,j,k}{}^{n}E_y}{{\Delta }_t}}={\displaystyle \frac{1}{{\epsilon }_{i,j,k}}}\left({\displaystyle \frac{{}_{i,j,k+\frac{1}{2}}{}^{n+\frac{1}{2}}H_x-{}_{i,j,k-\frac{1}{2}}{}^{n+\frac{1}{2}}H_x}{{\Delta }_z}}-{\displaystyle \frac{{}_{i+\frac{1}{2},j,k}{}^{n+\frac{1}{2}}H_z-{}_{i-\frac{1}{2},j,k}{}^{n+\frac{1}{2}}H_z}{{\Delta }_x}}-{\sigma }_{i,j,k} {}_{i,j,k}{}^{n+{\displaystyle \frac{1}{2}}}E_y\right),$$

(15)

$${\displaystyle \frac{{}_{i,j,k}{}^{n+1}E_z-{}_{i,j,k}{}^{n}E_z}{{\Delta }_t}}={\displaystyle \frac{1}{{\epsilon }_{i,j,k}}}\left({\displaystyle \frac{{}_{i+\frac{1}{2},j,k}{}^{n+\frac{1}{2}}H_y-{}_{i-\frac{1}{2},j,k}{}^{n+\frac{1}{2}}H_y}{{\Delta }_x}}-{\displaystyle \frac{{}_{i,j+\frac{1}{2},k}{}^{n+\frac{1}{2}}H_x-{}_{i,j-\frac{1}{2},k}{}^{n+\frac{1}{2}}H_x}{{\Delta }_y}}-{\sigma }_{i,j,k} {}_{i,j,k}{}^{n+{\displaystyle \frac{1}{2}}}E_z\right),$$

(16)

$${\displaystyle \frac{{}_{i,j,k}{}^{n+\frac{1}{2}}H_x-{}_{i,j,k}{}^{n-\frac{1}{2}}H_x}{{\Delta }_t}}={\displaystyle \frac{1}{{\mu }_{i,j,k}}}\left({\displaystyle \frac{{}_{i,j,k+\frac{1}{2}}{}^{n}E_y-{}_{i,j,k-\frac{1}{2}}{}^{n}E_y}{{\Delta }_z}}-{\displaystyle \frac{{}_{i,j+\frac{1}{2},k}{}^{n}E_z-{}_{i,j-\frac{1}{2},k}{}^{n}E_z}{{\Delta }_y}}\right),$$

(17)

$${\displaystyle \frac{{}_{i,j,k}{}^{n+\frac{1}{2}}H_y-{}_{i,j,k}{}^{n-\frac{1}{2}}H_y}{{\Delta }_t}}={\displaystyle \frac{1}{{\mu }_{i,j,k}}}\left({\displaystyle \frac{{}_{i+\frac{1}{2},j,k}{}^{n}E_z-{}_{i-\frac{1}{2},j,k}{}^{n}E_z}{{\Delta }_x}}-{\displaystyle \frac{{}_{i,j,k+\frac{1}{2}}{}^{n}E_x-{}_{i,j,k-\frac{1}{2}}{}^{n}E_x}{{\Delta }_z}}\right),$$

(18)

$${\displaystyle \frac{{}_{i,j,k}{}^{n+\frac{1}{2}}H_z-{}_{i,j,k}{}^{n-\frac{1}{2}}H_z}{{\Delta }_t}}={\displaystyle \frac{1}{{\mu }_{i,j,k}}}\left({\displaystyle \frac{{}_{i,j+\frac{1}{2},k}{}^{n}E_x-{}_{i,j-\frac{1}{2},k}{}^{n}E_x}{{\Delta }_y}}-{\displaystyle \frac{{}_{i+\frac{1}{2},j,k}{}^{n}E_y-{}_{i-\frac{1}{2},j,k}{}^{n}E_y}{{\Delta }_x}}\right).$$

(19)

The values ${}_{i,j,k}{}^{n+{\displaystyle \frac{1}{2}}}E$ are approximated by the arithmetic average of solutions in the following steps n and n + 1, e.g.,

$${}_{i,j,k}{}^{n+{\displaystyle \frac{1}{2}}}E_z={\displaystyle \frac{{}_{i,j,k}{}^{n+1}E_z+{}_{i,j,k}{}^{n}E_z}{2}}.$$

(20)

After substituting Equation (20) to the Equation (16) is obtained form:

$${}_{i,j,k}{}^{n+1}E_z={\displaystyle \frac{1-\frac{{\sigma }_{i,j,k}{\Delta }_t}{2{\epsilon }_{i,j,k}}}{1+\frac{{\sigma }_{i,j,k}{\Delta }_t }{2{\epsilon }_{i,j,k}}}}·{}_{i,j,k}{}^{n}E_z+{\displaystyle \frac{\frac{{\Delta }_t}{{\epsilon }_{i,j,k}}}{1+\frac{{\sigma }_{i,j,k}{\Delta }_t}{2{\epsilon }_{i,j,k}}}}·\left({\displaystyle \frac{{}_{i+\frac{1}{2},j,k}{}^{n+\frac{1}{2}}H_y-{}_{i-\frac{1}{2},j,k}{}^{n+\frac{1}{2}}H_y}{{\Delta }_x}}-{\displaystyle \frac{{}_{i,j+\frac{1}{2},k}{}^{n+\frac{1}{2}}H_x-{}_{i,j-\frac{1}{2},k}{}^{n+\frac{1}{2}}H_x}{{\Delta }_y}}\right).$$

(21)

In Figure 3, the algorithm using molecular notation (determine the, e.g., ${}_{i,j,k}{}^{n+1}E_z$ in the time step n + 1) is shown:

The final form of Equations (1) and (2) is:

$${}_{i,j,k}{}^{n+1}E_x=c_{i,j,k}^{ee}·{}_{i,j,k}{}^{n}E_x+c_{i,j,k}^{eh}·\left({}_{i,j+{\displaystyle \frac{1}{2}},k}{}^{n+{\displaystyle \frac{1}{2}}}H_z-{}_{i,j-{\displaystyle \frac{1}{2}},k}{}^{n+{\displaystyle \frac{1}{2}}}H_z-{}_{i,j,k+{\displaystyle \frac{1}{2}}}{}^{n+{\displaystyle \frac{1}{2}}}H_y+{}_{i,j,k-{\displaystyle \frac{1}{2}}}{}^{n+{\displaystyle \frac{1}{2}}}H_y\right),$$

(22)

$${}_{i,j,k}{}^{n+1}E_y=c_{i,j,k}^{ee}·{}_{i,j,k}{}^{n}E_y+c_{i,j,k}^{eh}·\left({}_{i,j,k+{\displaystyle \frac{1}{2}}}{}^{n+{\displaystyle \frac{1}{2}}}H_x-{}_{i,j,k-{\displaystyle \frac{1}{2}}}{}^{n+{\displaystyle \frac{1}{2}}}H_x-{}_{i+{\displaystyle \frac{1}{2}},j,k}{}^{n+{\displaystyle \frac{1}{2}}}H_z+{}_{i-{\displaystyle \frac{1}{2}},j,k}{}^{n+{\displaystyle \frac{1}{2}}}H_z\right),$$

(23)

$${}_{i,j,k}{}^{n+1}E_z=c_{i,j,k}^{ee}·{}_{i,j,k}{}^{n}E_z+c_{i,j,k}^{eh}·\left({}_{i+{\displaystyle \frac{1}{2}},j,k}{}^{n+{\displaystyle \frac{1}{2}}}H_y-{}_{i-{\displaystyle \frac{1}{2}},j,k}{}^{n+{\displaystyle \frac{1}{2}}}H_y-{}_{i,j+{\displaystyle \frac{1}{2}},k}{}^{n+{\displaystyle \frac{1}{2}}}H_x+{}_{i,j-{\displaystyle \frac{1}{2}},k}{}^{n+{\displaystyle \frac{1}{2}}}H_x\right),$$

(24)

$${}_{i,j,k}{}^{n+{\displaystyle \frac{1}{2}}}H_x=c_{i,j,k}^{hh}·{}_{i,j,k}{}^{n-{\displaystyle \frac{1}{2}}}H_x+c_{i,j,k}^{he}·\left({}_{i,j,k+{\displaystyle \frac{1}{2}}}{}^{n}E_y-{}_{i,j,k-{\displaystyle \frac{1}{2}}}{}^{n}E_y-{}_{i,j+{\displaystyle \frac{1}{2}},k}{}^{n}E_z+{}_{i,j-{\displaystyle \frac{1}{2}},k}{}^{n}E_z\right),$$

(25)

$${}_{i,j,k}{}^{n+{\displaystyle \frac{1}{2}}}H_y=c_{i,j,k}^{hh}·{}_{i,j,k}{}^{n-{\displaystyle \frac{1}{2}}}H_y+c_{i,j,k}^{he}·\left({}_{i+{\displaystyle \frac{1}{2}},j,k}{}^{n}E_z-{}_{i-{\displaystyle \frac{1}{2}},j,k}{}^{n}E_z-{}_{i,j,k+{\displaystyle \frac{1}{2}}}{}^{n}E_x+{}_{i,j,k-{\displaystyle \frac{1}{2}}}{}^{n}E_x\right),$$

(26)

$${}_{i,j,k}{}^{n+{\displaystyle \frac{1}{2}}}H_z=c_{i,j,k}^{hh}·{}_{i,j,k}{}^{n-{\displaystyle \frac{1}{2}}}H_z+c_{i,j,k}^{he}·\left({}_{i,j+{\displaystyle \frac{1}{2}},k}{}^{n}E_x-{}_{i,j-{\displaystyle \frac{1}{2}},k}{}^{n}E_x-{}_{i+{\displaystyle \frac{1}{2}},j,k}{}^{n}E_y+{}_{i-{\displaystyle \frac{1}{2}},j,k}{}^{n}E_y\right).$$

(27)

The building of the numerical model need write the table of coefficients {$c_{i,j,k}^{ee}$, $c_{i,j,k}^{ehx}$, $c_{i,j,k}^{ehy}$, $c_{i,j,k}^{ehz}$, $c_{i,j,k}^{hh}$, $c_{i,j,k}^{hex}$, $c_{i,j,k}^{hey}$, $c_{i,j,k}^{hez}$} describing each Yee cells, where:

$$c_{i,j,k}^{ee}={\displaystyle \frac{{\epsilon }_{i,j,k}-{\sigma }_{i,j,k} {\Delta }_t}{{\epsilon }_{i,j,k}+{\sigma }_{i,j,k} {\Delta }_t}},$$

(28)

$$c_{i,j,k}^{ehy}={\displaystyle \frac{2{\Delta }_t}{2{\epsilon }_{i,j,k}+{\sigma }_{i,j,k}{\Delta }_t}}·{\displaystyle \frac{1}{{\Delta }_x}},$$

(29)

$$c_{i,j,k}^{ehx}={\displaystyle \frac{2{\Delta }_t}{2{\epsilon }_{i,j,k}+{\sigma }_{i,j,k}{\Delta }_t}}·{\displaystyle \frac{1}{{\Delta }_y}}.$$

(30)

Please note that calculation errors using the differential method are influenced by the following factors:

• the size of the mesh discretizing the area, where the solution is approximated by linear functions;
• the construction of the mesh discretizing the area, including possible local changes in its distribution related to the change of the mesh size;
• limitations of the method resulting from the condition of using a cuboid (rectangular) mesh, which leads to a less accurate representation of irregular surfaces, e.g., rounded surfaces;
• simplification of the representation of the real model;
• imperfect limitation of the space by means of absorption boundary conditions, which in the case of Mura boundary conditions [48,49] requires the use of first-order differential approximations. Consequently, the resultant order of approximations in the model is subject to local changes.

For the above reasons, it is necessary to reduce or minimize factors that may interfere with correct results.

4. Construction of Numerical Models

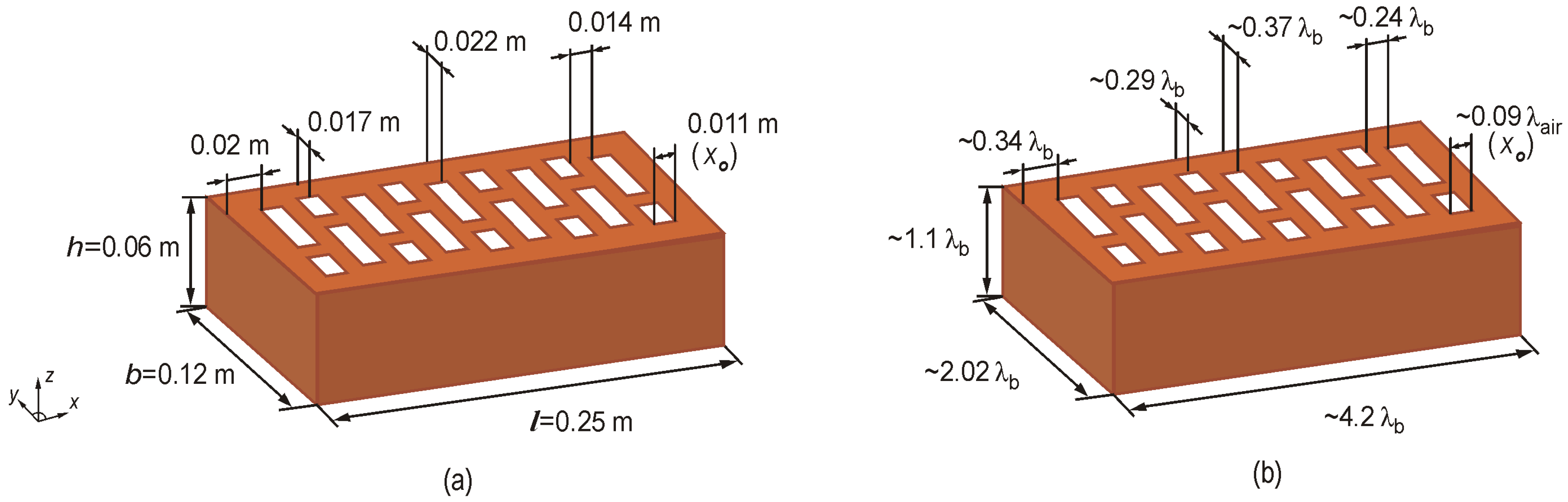
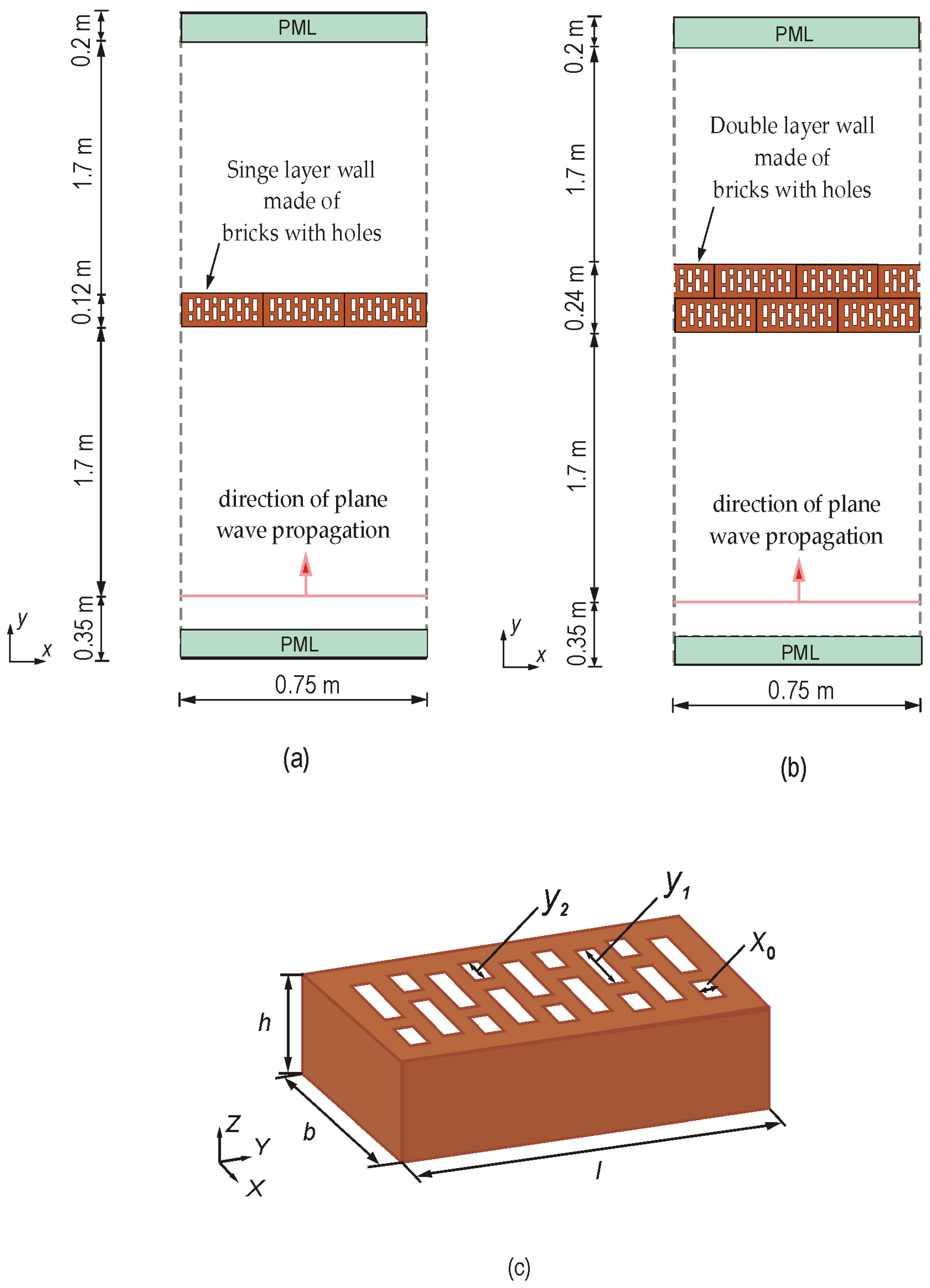
The subject of the analysis is a system consisting of a wall made of bricks (Figure 4). The external dimensions of the bricks are h = 0.06 m (height), b = 0.12 m (width), l = 0.25 m (length). Figure 4b shows the electrical representation of the dimensions of the analyzed bricks, assuming that the relative electrical permittivity of the material is 4.44 and the conductivity is 0 S/m. The dimensions of the ceramic elements were related to the wavelength in the brick λ_b = 0.0593 m.

For the analysis, walls made of a non-homogeneous material, i.e., brick with hollows, were assumed for calculations. Two variants of walls were considered: single-layer (1w_B) (Figure 5a) and double-layer (2w_B) (Figure 5b). The changed hollow sizes are shown in Figure 5c. In addition to the influence of layers on the values of the electric field intensity (E_z) the influence of the change in the hollow length inside the bricks (y₁, y₂) in the models under consideration was also analyzed. Because different values of electrical parameters of building materials are found in the literature, the analysis also took into account the variability of the conductivity value, which ranges from 0 to 0.2 S/m.

It was assumed that on both sides of the wall, there is an open space with air properties that are devoid of other elements that can disturb the propagating electromagnetic wave and affect the field distribution in the system. By omitting the phenomena occurring at the ends of the wall, it was possible to reduce the model’s size by applying periodicity conditions. The adopted assumptions allow, in accordance with the goal, the determination of the effect of a wall composed of inhomogeneous material on the electromagnetic field distribution, omitting other factors. The dimensions and general construction of the adopted model are shown in Figure 5.

The adopted analysis area allowed for taking into account possible deformations in the field distribution related to the non-uniform structure of the materials under consideration and field changes at a certain distance from the wall. The forcing field in the system was a harmonic plane wave, linearly polarized, propagating in the direction consistent with the Oy axis (k = 1_y):

$$E\left(x,y,t\right)=E_z{\overrightarrow{1}}_z=\sin \left(\omega t\right)·1\left(t\right)·{\overrightarrow{1}}_z$$

(31)

To represent the conditions of the open problem, two types of absorption conditions are used interchangeably in the FDTD algorithm formulation [48,49]: absorbing boundary condition (ABC) and perfectly matched layer (PML). In the case of PML conditions, the main limitation of their adoption is the necessity of creating an additional area, which is used to represent the propagation of the wave to infinity. It is assumed that the thickness of the PML layer should be no less than 0.25 wavelengths in air [49]. This results in an increase in the size of the model due to a larger number of differential meshes. The created PML layer is to dampen the penetrating wave by a gradual, selected increase in conductivity. In the analysis, the absorption of propagating waves was obtained by adopting PML conditions. Numerical errors are influenced by, among other things, the type of boundary conditions adopted. In the analysis, the ABC conditions were not chosen because they result in an imperfect limitation of space. First-order differential approximations are often used with ABC. Therefore, the resultant order of approximations in the model is subject to local changes.

The area of the models under consideration was subject to discretization by entering a uniform Yee cell grid. Based on the additional tests carried out (Section 5), it was assumed that the maximum linear size of the Yee cell was at most Δ = 0.5 mm. With the adopted differential grid resolution, the wave phenomena on a section of one wavelength in a brick (λ_b) were modeled using 118 cells.

5. Mesh Size Selection Analysis

Additionally, tests were carried out to illustrate the influence of Yee cell size on the accuracy of calculations. Two models were considered: a single-layer wall (1w_B) and a double-layer wall (2w_B), at a frequency of 2.4 GHz for different sizes of differential grid elements Δ ∈ {0.5, 1, 1.5, 2, 3, 4, 5, 6} mm.

Table 2. Average number of Yee cells per wavelength at f = 2.4 GHz.

Δ [mm]	Relative Electrical Permittivity					Air
	εr′ = 5 (λb = 0.0559 m)	εr′ = 6 (λb = 0.051 m)	εr′ = 7 (λb = 0.0472 m)	εr′ = 8 (λb = 0.0442 m)	εr′ = 1 (λp = 0.125 m)	εr′ = 1 (λp = 0.125 m)
0.5	111	102	94	88	250	250
1.0	56	51	47	44	125	125
1.5	35	34	31	29	83	83
2.0	28	25	23	22	62	62
3.0	18	16	15	14	41	41
4.0	14	13	12	11	31	31
5.0	11	10	9	8	25	25
6.0	9	8	7	7	20	20

presents a comparison of the average number of Yee cells per wavelength in the dielectric.

The value of λ_b was determined assuming that the equivalent value of permittivity corresponds to the case of a non-dissipative dielectric (σ = 0 S/m, ε_r′′ = 0):

$${\lambda }_{\mathrm{b}}={\displaystyle \frac{{\lambda }_0}{\sqrt{{{\epsilon }_{\mathrm{r}}}^{\prime }·{\mu }_{\mathrm{r}}}}}.$$

(32)

One of the possible reasons for the discrepancy in the results may be the incorrect assumption of the Yee cell size, which may result in an inaccurate representation of the phenomena during the calculations. For this purpose, the electric field distribution was additionally analyzed for different Yee cell sizes Δ ∈ {0.5, 1, 1.5, 2, 3, 4, 5, 6} mm. To quantitatively characterize the differences between the results obtained by the numerical method and from the analytical relationship, the parameter δ_Δ describing the error in calculating the field value was used:

$${\mathsf{\delta }}_{\Delta }=\left|{\displaystyle \frac{\max \left(\mathrm{result}\_\mathrm{numeric}\right)}{\max \left(\mathrm{result}\_\mathrm{analytical}\right)}}\right|·100\%.$$

(33)

Due to the numerical dispersion effects of the differential grid and the desire to increase the precision of spatial mapping of field changes, in practice, the following condition is adopted:

$$\max \left({\Delta }_x,{\Delta }_y,{\Delta }_z\right)\le {\displaystyle \frac{\lambda }{10}}.$$

(34)

The maintenance of condition (34) limits the effects of numerical dispersion to the level of 15% compared to the actual values of the field in the model systems [48]. Further increase of the grid resolution by adopting the value max(Δ) ≈ λ/20 contributes to the reduction of the error to the value of about 5%, but it is associated with a significant increase of the size of the numerical model (N_DOF number). For this reason, the construction of the adapted grid and gradual adaptation of the local size of the grid elements to the wavelength in the materials leads to a reduction of the size of the numerical models even when the condition (34) is met.

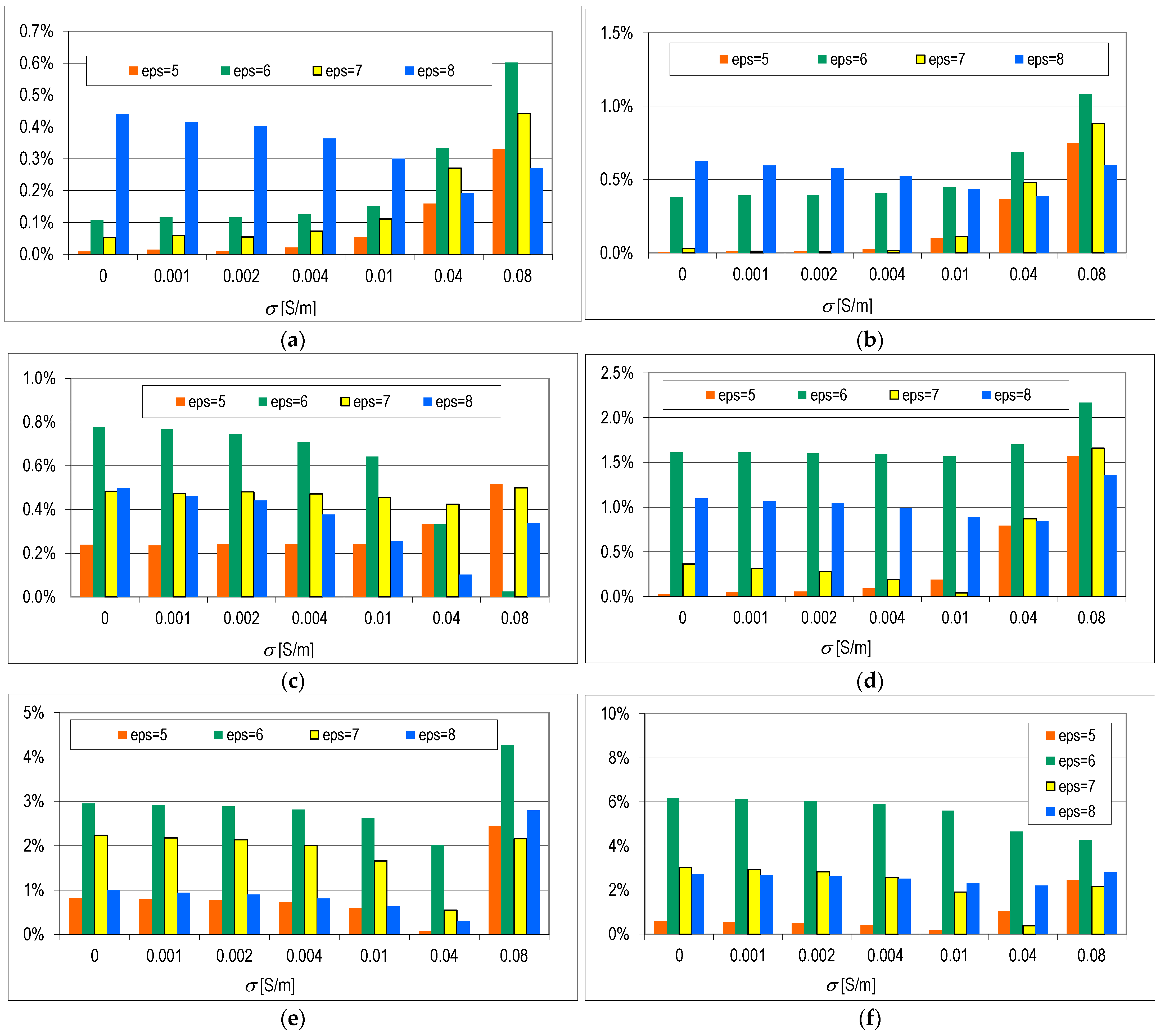
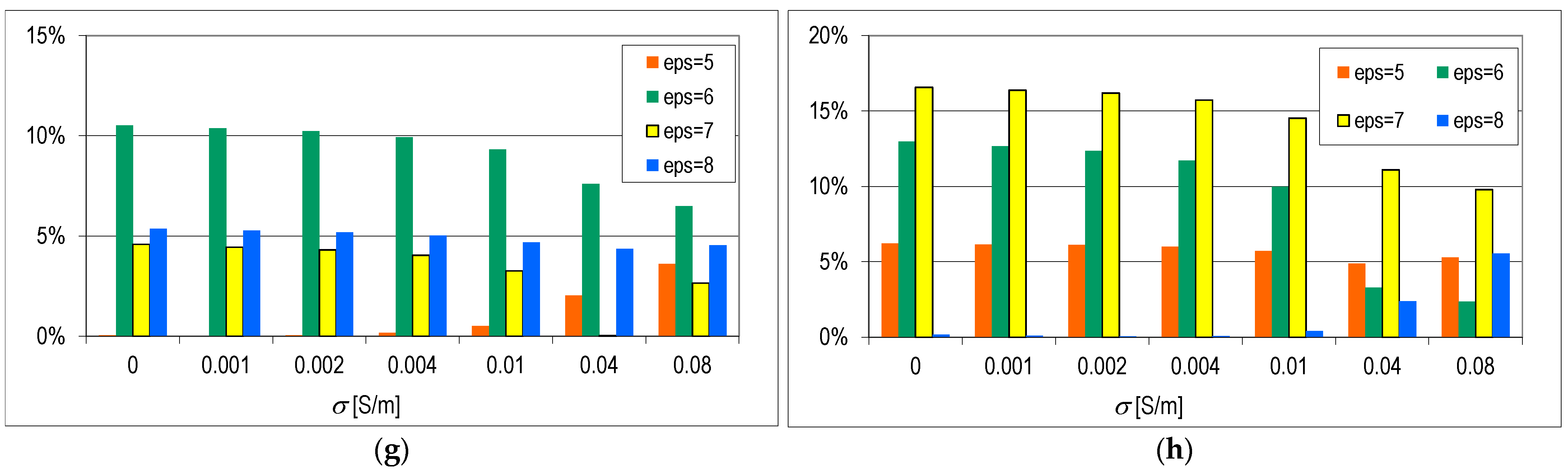
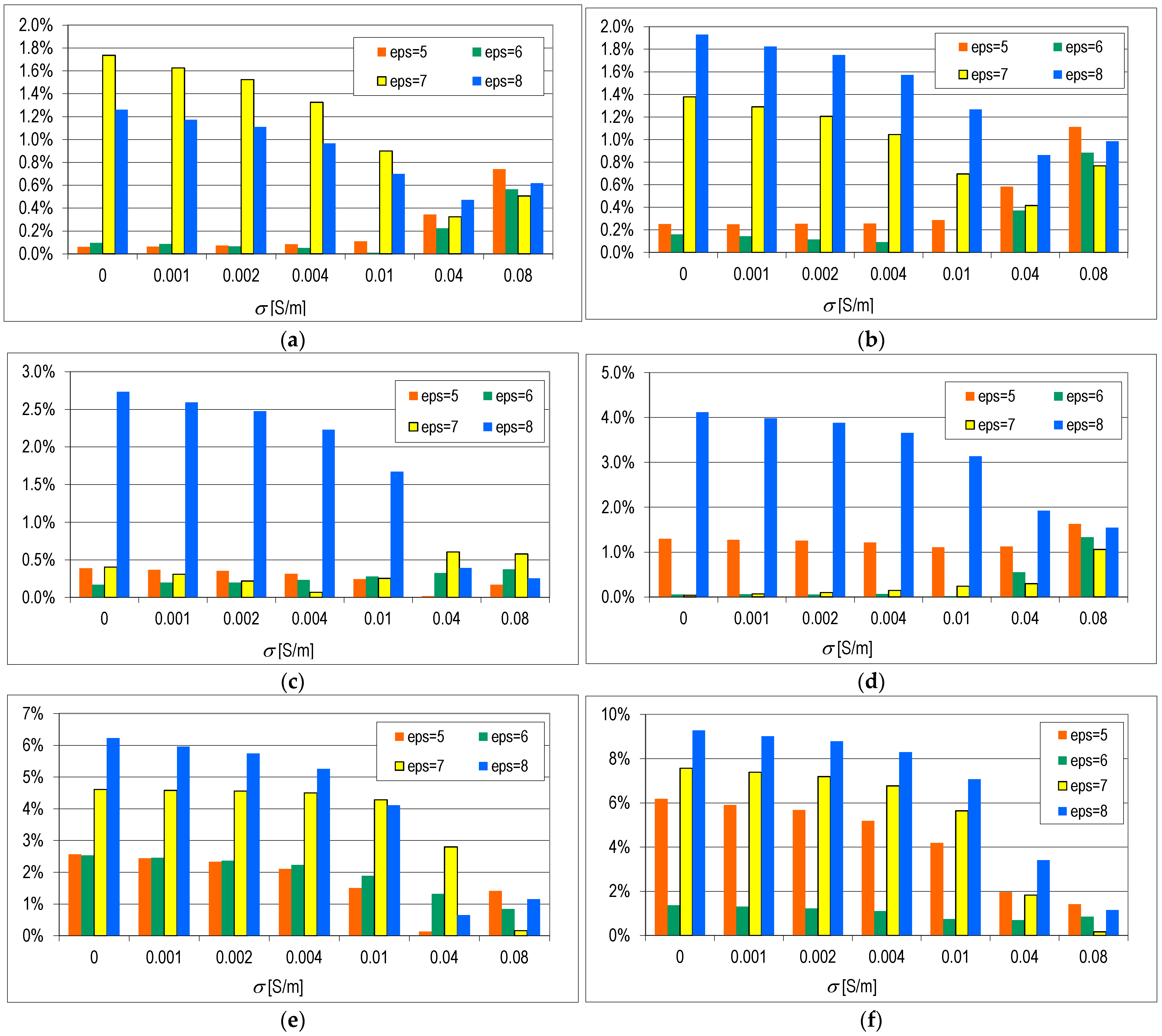
Figure 6 and Figure 7 show the percentage values of the error in calculating the electric field intensity for the single-layer model (Figure 6) and the two-layer model (Figure 7), taking into account the variability of the relative values of the concrete permittivity ε_r′ ∈ {5, 6, 7, 8}. In numerical calculations, in order to obtain reliable results, it is assumed that the number of Yee cells per wavelength in the dielectric should not be less than 10, according to Equation (34) [48]. Therefore, in the 1w_B model, the above assumption is met when Δ ≤ 4 mm. The error depends on the assumed value of conductivity and relative permittivity. With the conductivity often assumed in the literature equal to 0.01 S/m:

• ε_r′ = 5, the maximum value of the error δ_Δ is 0.2%;
• ε_r′ = 6, the maximum value of the error δ_Δ is 5.6%;
• ε_r′ = 7, the maximum value of the error δ_Δ is 1.9%;
• ε_r′ = 8, the maximum value of the error δ_Δ is 2.3%.

For further calculations, Δ = 0.5 mm was assumed, where the error did not exceed 0.3% for σ = 0.01 S/m, for example:

• ε_r′ = 5, the maximum value of the error δ_Δ is 0.2%;
• ε_r′ = 6, the maximum value of the error δ_Δ is 0.1%;
• ε_r′ = 7, the maximum value of the error δ_Δ is 0.1%;
• ε_r′ = 8, the maximum value of the error δ_Δ is 0.3%.

In the analysis of the model with a single-layer wall, according to the relationship (34), the number of cells per wavelength causes an error of about 3% on average. However, a three-fold increase in the number of cells is a safe assumption in order to obtain reliable results with a small error (up to 1%). Unfortunately, with the increase in the model and frequency, it is necessary to take into account the capabilities of computers processing many unknowns that increase with the decrease in cell size [48].

In the model with a two-layer wall, when Δ ≤ 4 mm, the error value was in the range depending on the conductivity and relative electrical permittivity. At a conductivity of 0.01 S/m:

• ε_r′ = 5, the maximum value of the error δ_Δ is 4.2%;
• ε_r′ = 6, the maximum value of the error δ_Δ is 0.7%;
• ε_r′ = 7, the maximum value of the error δ_Δ is 5.6%;
• ε_r′ = 8, the maximum value of the error δ_Δ is 7.1%.

For further calculations, Δ = 0.5 mm was assumed, where the error did not exceed 0.9% for σ = 0.01 S/m, for example:

• ε_r′ = 5, the maximum value of the error δ_Δ is 0.1%;
• ε_r′ = 6, the maximum value of the error δ_Δ is 0.0%;
• ε_r′ = 7, the maximum value of the error δ_Δ is 0.9%;
• ε_r′ = 8, the maximum value of the error δ_Δ is 0.7%.

For better analysis, the results are presented in the form of tables.

Table 3. Tabulated summary of the δ_Δ error for model 1w_B, with ε_r′ = 5.

εr′ = 5	δΔ (%)
	σ (S/m)
Δ [mm]	0	0.001	0.002	0.004	0.01	0.04	0.08
0.5	0.0	0.0	0.0	0.0	0.1	0.2	0.3
1.0	0.0	0.0	0.0	0.0	0.1	0.4	0.7
1.5	0.2	0.2	0.2	0.2	0.2	0.3	0.5
2.0	0.0	0.0	0.1	0.1	0.2	0.8	1.6
3.0	0.8	0.8	0.8	0.7	0.6	0.1	2.5
4.0	0.6	0.5	0.5	0.4	0.2	1.0	2.5
5.0	0.0	0.0	0.0	0.2	0.5	2.0	3.6
6.0	6.2	6.1	6.1	6.0	5.7	4.9	5.3

,

Table 4. Tabulated summary of the δ_Δ error for model 1w_B, with ε_r′ = 6.

εr′ = 6	δΔ (%)
	σ (S/m)
Δ [mm]	0	0.001	0.002	0.004	0.01	0.04	0.08
0.5	0.1	0.1	0.1	0.1	0.2	0.3	0.6
1.0	0.4	0.4	0.4	0.4	0.4	0.7	1.1
1.5	0.8	0.8	0.7	0.7	0.6	0.3	0.0
2.0	1.6	1.6	1.6	1.6	1.6	1.7	2.2
3.0	3.0	2.9	2.9	2.8	2.6	2.0	4.3
4.0	6.2	6.1	6.0	5.9	5.6	4.6	4.3
5.0	10.5	10.4	10.2	9.9	9.3	7.6	6.5
6.0	13.0	12.7	12.4	11.7	10.0	3.3	2.4

,

Table 5. Tabulated summary of the δ_Δ error for model 1w_B, with ε_r′ = 7.

εr′ = 7	δΔ (%)
	σ (S/m)
Δ [mm]	0	0.001	0.002	0.004	0.01	0.04	0.08
0.5	0.1	0.1	0.1	0.1	0.1	0.3	0.4
1.0	0.0	0.0	0.0	0.0	0.1	0.5	0.9
1.5	0.5	0.5	0.5	0.5	0.5	0.4	0.5
2.0	0.4	0.3	0.3	0.2	0.0	0.9	1.7
3.0	2.2	2.2	2.1	2.0	1.7	0.5	2.2
4.0	3.0	2.9	2.8	2.6	1.9	0.4	2.2
5.0	4.6	4.4	4.3	4.0	3.3	0.0	2.6
6.0	16.6	16.4	16.2	15.7	14.5	11.1	9.8

and

Table 6. Tabulated summary of the δ_Δ error for model 1w_B, with ε_r′ = 8.

εr′ = 8	δΔ (%)
	σ (S/m)
Δ [mm]	0	0.001	0.002	0.004	0.01	0.04	0.08
0.5	0.4	0.4	0.4	0.4	0.3	0.2	0.3
1.0	0.6	0.6	0.6	0.5	0.4	0.4	0.6
1.5	0.5	0.5	0.4	0.4	0.3	0.1	0.3
2.0	1.1	1.1	1.0	1.0	0.9	0.8	1.4
3.0	1.0	0.9	0.9	0.8	0.6	0.3	2.8
4.0	2.7	2.7	2.6	2.5	2.3	2.2	2.8
5.0	5.4	5.3	5.2	5.0	4.7	4.3	4.5
6.0	0.2	0.1	0.1	0.1	0.4	2.4	5.5

present a summary of the error values for the single-layer model, and

Table 7. Tabulated summary of the δ_Δ error for model 2w_B, with ε_r′ = 5.

εr′ = 5	δΔ (%)
	σ (S/m)
Δ [mm]	0	0.001	0.002	0.004	0.01	0.04	0.08
0.5	0.1	0.1	0.1	0.1	0.1	0.3	0.7
1.0	0.3	0.2	0.3	0.3	0.3	0.6	1.1
1.5	0.4	0.4	0.4	0.3	0.2	0.0	0.2
2.0	1.3	1.3	1.3	1.2	1.1	1.1	1.6
3.0	2.6	2.4	2.3	2.1	1.5	0.1	1.4
4.0	6.2	5.9	5.7	5.2	4.2	2.0	1.4
5.0	10.4	10.1	9.7	9.1	7.5	3.3	1.5
6.0	15.4	14.6	13.9	12.5	9.1	0.2	5.9

,

Table 8. Tabulated summary of the δ_Δ error for model 2w_B, with ε_r′ = 6.

εr′ = 6	δΔ (%)
	σ (S/m)
Δ [mm]	0	0.001	0.002	0.004	0.01	0.04	0.08
0.5	0.1	0.1	0.1	0.1	0.0	0.2	0.6
1.0	0.2	0.1	0.1	0.1	0.0	0.4	0.9
1.5	0.2	0.2	0.2	0.2	0.3	0.3	0.4
2.0	0.1	0.1	0.1	0.1	0.0	0.6	1.3
3.0	2.5	2.5	2.4	2.2	1.9	1.3	0.8
4.0	1.4	1.3	1.2	1.1	0.7	0.7	0.8
5.0	0.8	0.9	1.0	1.1	1.4	1.7	0.9
6.0	4.0	3.8	3.7	3.3	2.3	2.3	7.2

,

Table 9. Tabulated summary of the δ_Δ error for model 2w_B, with ε_r′ = 7.

εr′ = 7	δΔ (%)
	σ (S/m)
Δ [mm]	0	0.001	0.002	0.004	0.01	0.04	0.08
0.5	1.7	1.6	1.5	1.3	0.9	0.3	0.5
1.0	1.4	1.3	1.2	1.0	0.7	0.4	0.8
1.5	0.4	0.3	0.2	0.1	0.3	0.6	0.6
2.0	0.0	0.1	0.1	0.1	0.2	0.3	1.1
3.0	4.6	4.6	4.6	4.5	4.3	2.8	0.2
4.0	7.6	7.4	7.2	6.8	5.6	1.8	0.2
5.0	13.0	12.5	12.1	11.3	9.1	2.6	0.7
6.0	24.2	23.5	22.9	21.6	18.4	10.3	10.2

and

Table 10. Tabulated summary of the δ_Δ error for model 2w_B, with ε_r′ = 8.

εr′ = 8	δΔ (%)
	σ (S/m)
Δ [mm]	0	0.001	0.002	0.004	0.01	0.04	0.08
0.5	1.3	1.2	1.1	1.0	0.7	0.5	0.6
1.0	1.9	1.8	1.7	1.6	1.3	0.9	1.0
1.5	2.7	2.6	2.5	2.2	1.7	0.4	0.3
2.0	4.1	4.0	3.9	3.7	3.1	1.9	1.6
3.0	6.2	6.0	5.7	5.3	4.1	0.7	1.2
4.0	9.3	9.0	8.8	8.3	7.1	3.4	1.2
5.0	8.9	8.7	8.5	8.0	7.0	3.5	0.6
6.0	4.4	4.5	4.6	4.9	5.5	7.0	10.7

for the two-layer model.

The following assumptions were made based on the analysis of the influence of mesh size on the correct results and the numerical conditions for further multivariant analysis.

-

The Nyquist condition (34) was satisfied by assuming a cubic Yee cell with dimensions Δ = 0.5 mm.

-

The Courant–Friedrichs–Lewy condition (CFL condition) [48,49] was maintained by assuming a time step size of Δ_t = 0.0537 ns. Thus, the stability of the method was maintained.

6. Results and Discussion

For the purposes of further numerical analysis, the brick dimensions were determined as average values based on the measurements performed. The method of determining the test parameters is specified in the standard [46], which specifies the number of samples required to test each property of the masonry element as 3 or 10 pieces. In this work, it was decided to perform its own measurement on a randomly selected sample of 30 bricks from two sources. The reason was the lack of standards regarding the dimensions of hollows inside bricks. The standards include permissible deviations of external dimensions resulting from the production process (e.g., drying) [15,46]. Tests defined in this way are the basis for accepting a given batch of material. Due to the assessment of electrical properties, it is necessary to consider the distribution and size of hollows.

In order to determine the effect of changes in the dimensions of the hollows on the field distribution, calculations were made with the change of the length of hollows in the axis consistent with the shortest dimension of the brick. The dimensions changed in the tests were y₁ and y₂ (Figure 5c).

Table 11. Instantaneous distributions of the relative value of the E_z component in the entire area containing a single-layer wall, taking into account the variation of the length of hollows.

Model M1	Model M2	Model MW	Model M3	Model M4
y1 = 0.031 m (from model MW: y1 − 0.012 m)	y1 = 0.037 m (from model MW: y1 − 0.006 m)	y1 = 0.043 m	y1 = 0.048 m (from model MW: y1 + 0.005 m)	y1 = 0.051 m (from model MW: y1 + 0.008 m)
y2 = 0.009 m (from model MW: y2 − 0.012 m)	y2 = 0.015 m (from model MW: y2 − 0.006 m)	y2 = 0.021 m	y2 = 0.026 m (from model MW: y2 + 0.005 m)	y2 = 0.029 m (from model MW: y2 + 0.008 m)

presents the considered models of one-dimensional walls and the changed dimensions (y₁, y₂). The results for the two-layer wall are presented in

Table 12. Instantaneous distributions of the relative value of the E_z component in the entire area containing the two-layer wall, taking into account the variation of the length of hollows.

Model M1	Model M2	Model MW	Model M3	Model M4
y1 = 0.031 m (from model MW: y1 − 0.012 m)	y1 = 0.037 m (from model MW: y1 − 0.006 m)	y1 = 0.043 m	y1 = 0.048 m (from model MW: y1 + 0.005 m)	y1 = 0.051 m (from model MW: y1 + 0.008 m)
y2 = 0.009 m (from model MW: y2 − 0.012 m)	y2 = 0.015 m (from model MW: y2 − 0.006 m)	y2 = 0.021 m	y2 = 0.026 m (from model MW: y2 + 0.005 m)	y2 = 0.029 m (from model MW: y2 + 0.008 m)

. The typical size of a brick is x₀ = 0.011 m, y₁ = 0.043 m, and y₂ = 0.021 m (model marked as MW).

6.1. Qualitative Assessment of Instantaneous Values of Electric Field Intensity in the Models Considered

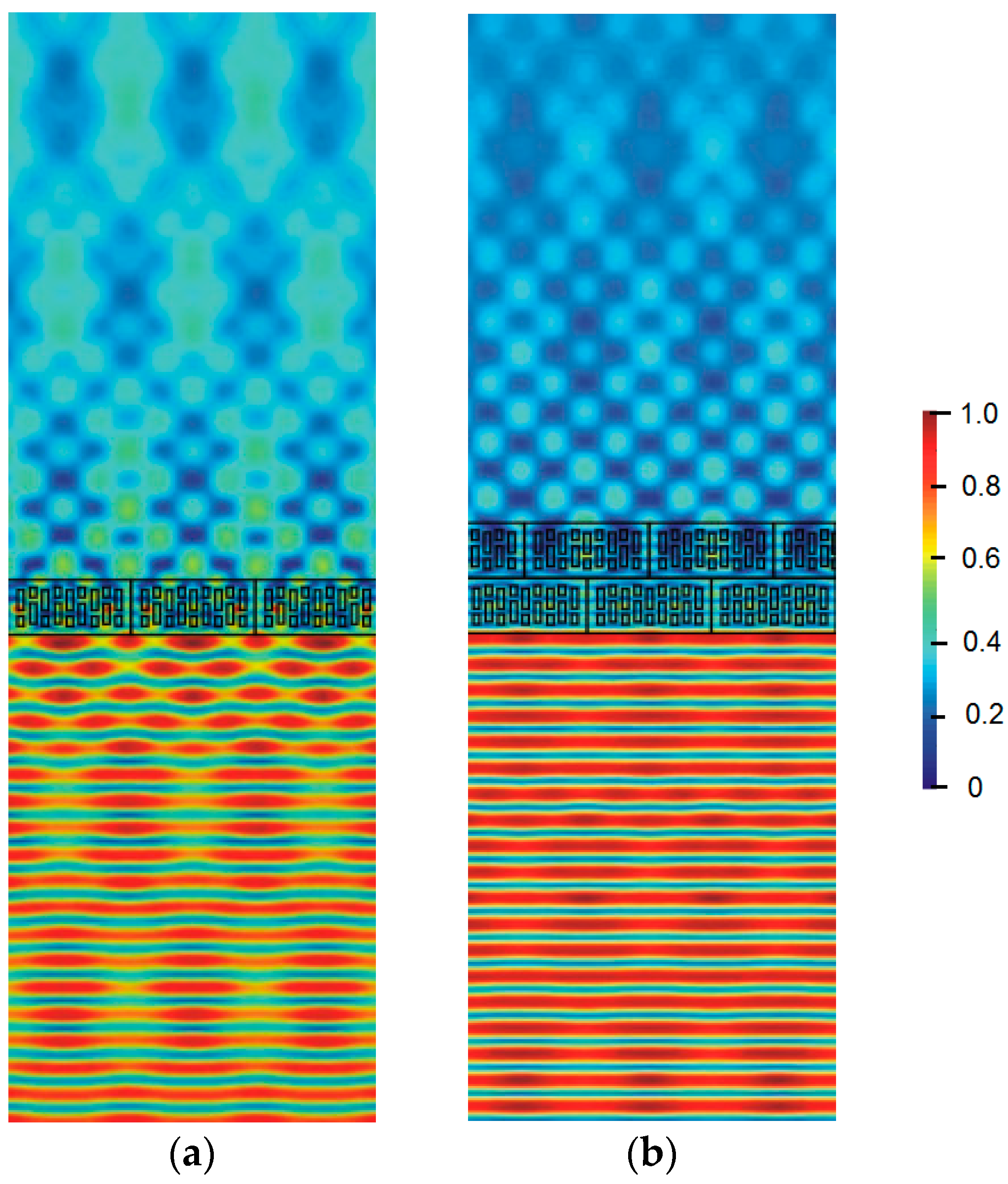
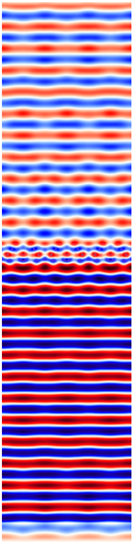
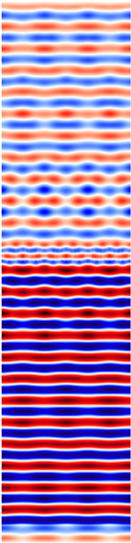
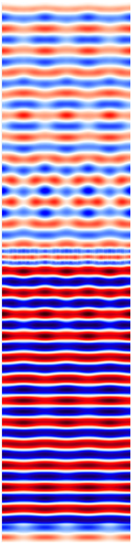
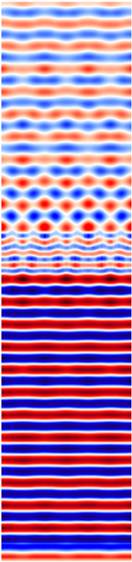
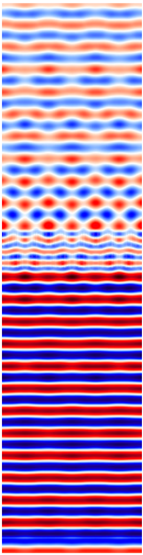
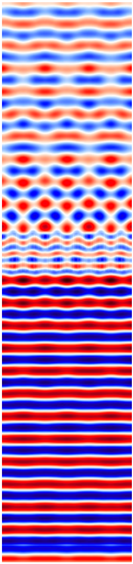
Calculations of hollow brick systems indicate local field changes due to wave propagation in a material with a complex structure. Table 11 and Table 12 show the distribution of the E_z component for the same selected moment after reaching the steady state. The results are for the same electrical parameters of the bricks (σ = 0.01 S/m, ε_r = 4.44).

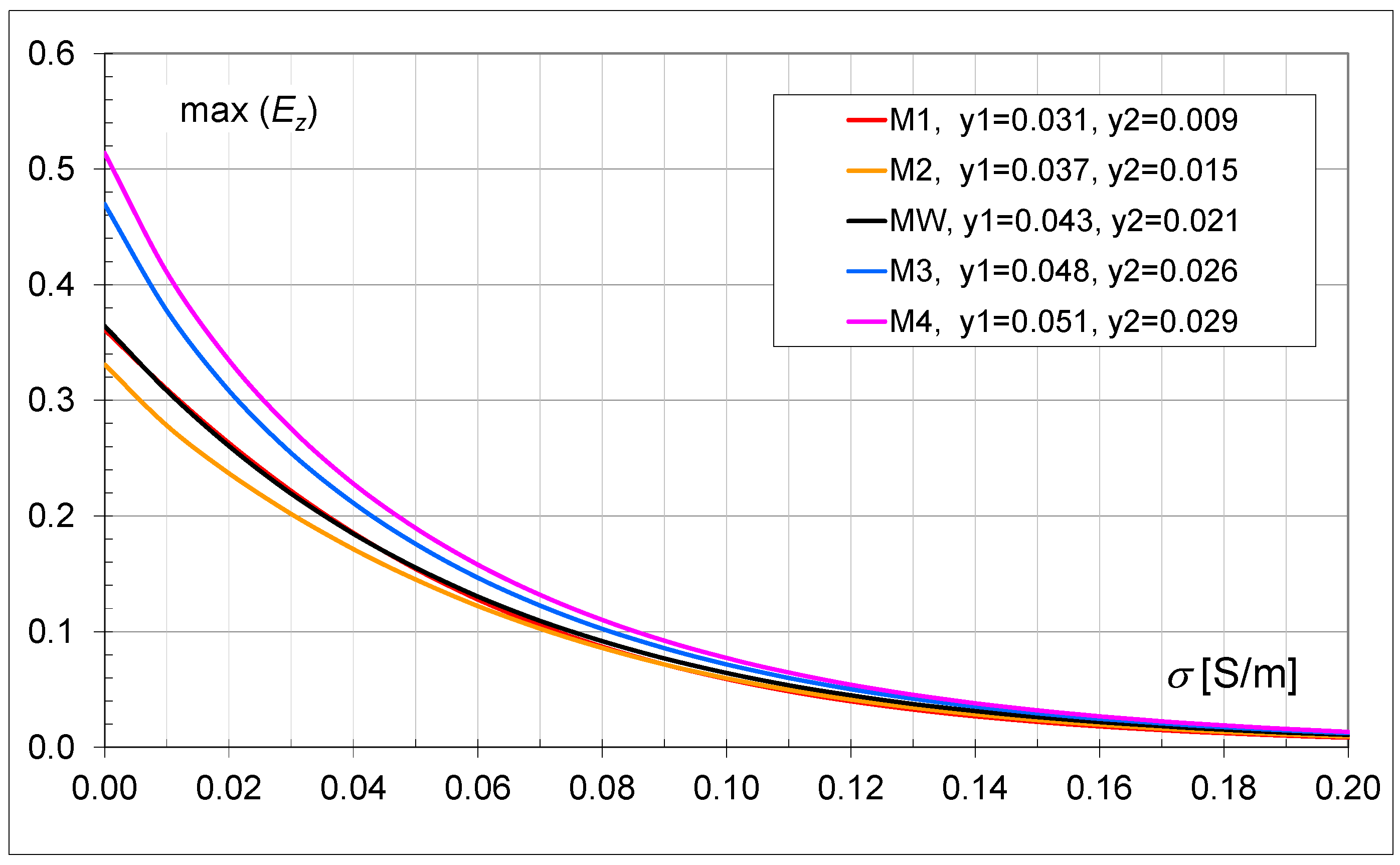
For both single- and double-layer walls, a decrease in the electric field intensity value resulting from the ceramic mass loss (σ = 0.01 S/m) is noticeable in the area behind the wall. The propagation of an electromagnetic wave in the brick area is complex. The porosity of the brick in the electromagnetic sense affects the appearance of multiple reflections at the air-ceramic mass boundary. The number and size of holes in the brick changes the field image in the area close to the wall. The local change in the wave speed when passing through subsequent air and ceramic mass areas is reflected in the field distributions and the occurrence of interference. Due to the larger surface area of the cavities and boundary surfaces, the indicated effect is particularly visible when assessing the phenomena occurring behind the wall in the M4 model. The range of field changes, in this case, takes on larger values. The effects of wave reflections from the wall, causing momentary minima and maxima formation, are particularly visible at a distance of 0.6 m in front of the wall in the models.

A larger ceramic surface (e.g., in the M1 model) causes less wavefront distortion in the area behind the wall. This results from the greater resultant homogeneity of the material. However, due to attenuation, this has a negative effect on the maximum field values. For example, in a system with a single-layer wall, the field values in the M4 model are higher by about 15% than the values achieved in the M1 model. The distribution of the ceramic mass and its relative share influence the limitation of the resultant effects of wave reflection. The indicated factors simultaneously guarantee higher values of the electric field intensity in the area behind the wall. Two layers of bricks cause greater wavefront distortion and a greater number of minima and maxima than in systems with a single layer of bricks. The electric field values behind the wall are lower than in the case of single-layer walls.

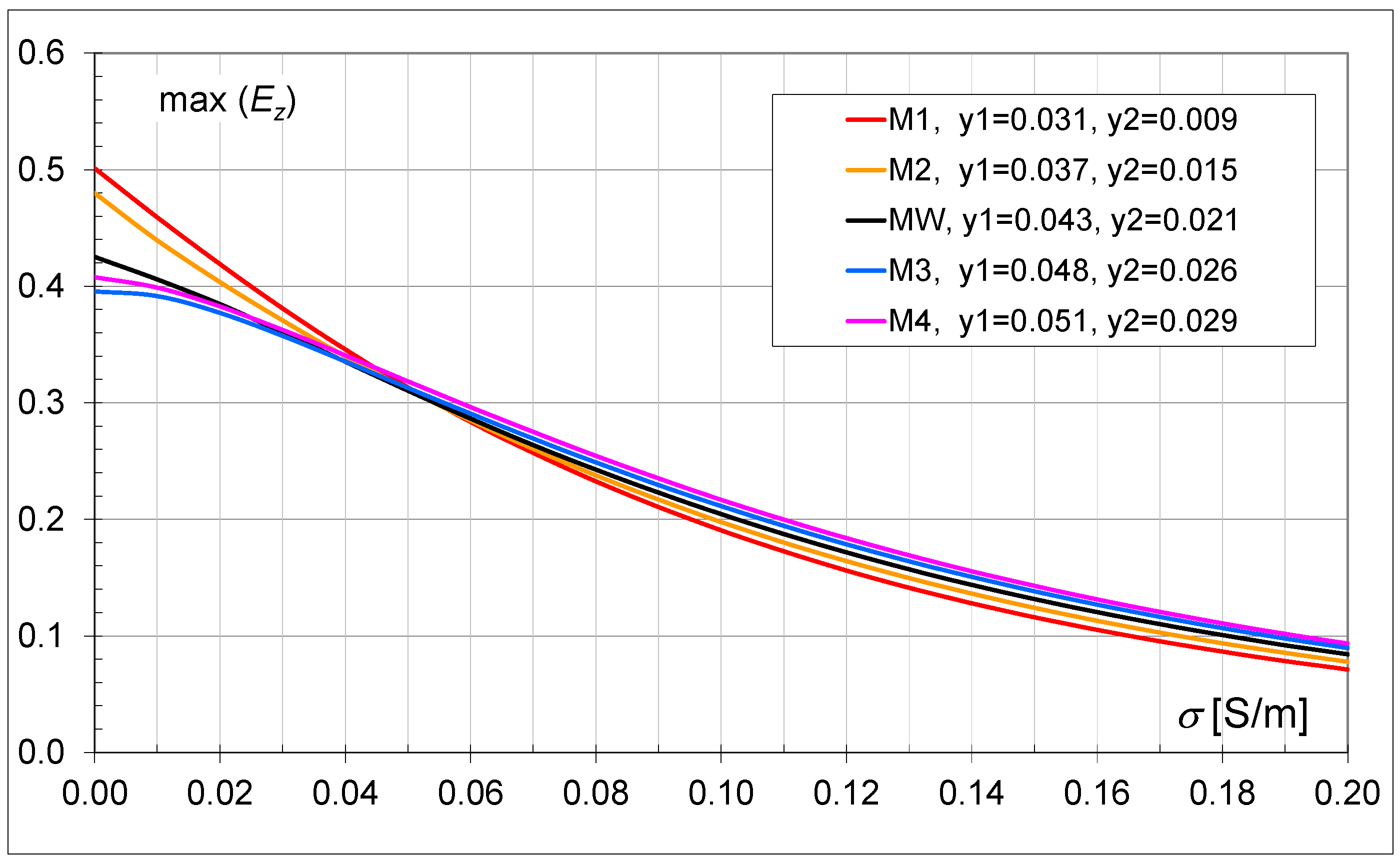
In order to perform the field envelope, it was necessary to develop an additional algorithm and a program written in C++. The algorithm aimed to determine a map describing the maximum field values because of processing the sequence of instantaneous field distributions calculated at equal time intervals. The above-described conclusions regarding the analysis of instantaneous distributions are also confirmed by the presented maximum values of the E_z component, assuming that the conductivity of the ceramic mass is 0.01 S/m (Figure 8). The figure shows envelopes for a model with a single-layer and two-layer wall of typical dimensions (MW).

The distribution of the ceramic mass and its relative share influence the limitation of the resultant effects of wave reflection. The indicated factors simultaneously guarantee higher values of the electric field intensity in the area behind the wall. In both variants of the wall (1w_B, 2w_B) made of typical bricks (MW), it can be seen that the field values are high in the area in front of the wall. The two-layer wall causes a more uniform field distribution, similar to the distribution in the case of a homogeneous material, e.g., solid bricks. This effect is related to the numerous reflections of the EM wave from the wall itself and inside the hollows. It can be assumed that the two-layer wall is a greater obstacle, and another layer of bricks will cause almost 80% wave reflection. However, when considering the area behind the wall, the higher values are this time for the single-layer wall. Numerous hollows transmit more energy, thanks to which the signal quality is better.

However, in the two-layer wall model, more areas have a low field value, which can result in a worse range. However, as you can see, these are temporary decreases, so they are not a major problem, especially since they occur in the area up to half a meter behind the wall. As can be seen in Figure 8, there are no dead zones for the single- and two-layer models.

The greatest risk of signal loss is posed by metal elements in structures, such as reinforcement. In the case of walls made of ceramics, the problem is layering. In the case of areas in front of the wall, with increasing layers, walls made of hollow bricks may have a field distribution similar to walls with homogeneous material. The larger the size of the gaps, the greater the wavefront distortions. In the case of the possible location of routers, it would be advisable to place them on the side of the wall where the maximum use of data transmission is assumed. Taking into account the ceilings and related physical phenomena, routers should be placed approx. 0.5 m below the ceilings.

6.2. Cumulative Analysis of the Maximum Values of the Electric Field Intensity Behind a Wall Made of Single- and Double-Layer Walls

The FDTD method allows obtaining instantaneous images of the field (Table 11 and Table 12). In order to obtain the maximum values of the field (Figure 9 and Figure 10 and

Table 13. Maximum values of the E_z component behind the different wall with the same values of electrical parameters of bricks.

Type of a Wall	Name of Model	Figure of Analyzed Wall	Maximum Values of the Ez Component (-)
single-layer wall	M1 (from model MW: y1 − 0.012 m, y2 − 0.012 m)		0.465
	M2 (from model MW: y1 − 0.006 m, y2 − 0.006 m)		0.445
	MW		0.415
	M3 (from model MW: y1 + 0.005 m, y2 + 0.005 m)		0.391
	M4 (from model MW: y1 + 0.008 m, y2 + 0.008 m)		0.409
double-layer wall	M1 (from model MW: y1 − 0.012 m, y2 − 0.012 m)		0.315
	M2 (from model MW: y1 − 0.006 m, y2 − 0.006 m)		0.279
	MW		0.313
	M3 (from model MW: y1 + 0.005 m, y2 + 0.005 m)		0.379
	M4 (from model MW: y1 + 0.008 m, y2 + 0.008 m)		0.411

), it was necessary to develop an algorithm written in C++. The algorithm searched for the maximum values from any number of files with instantaneous values of the electric field component. The files were saved at regular intervals to trace the phenomena of wave propagation within one wavelength.

Figure 9 and Figure 10 show the influence of the variation of the length of the hollows in the bricks on the electric field intensity values (models: M1, M2, MW, M3, and M4). The analysis also took into account the variation of the conductivity values in the range from 0 to 0.2 S/m.

The above-described conclusions concerning the analysis of instantaneous distributions are also confirmed by the presented maximum values of the E_z component, assuming the conductivity of the ceramic mass is 0.01 S/m (Figure 9 and Figure 10). In the single-layer model, in the range of small conductivity values (σ < 0.04 S/m), the smaller the amount of ceramic mass (i.e., larger hollows), the field values decrease. However, in the two-layer model, the situation is reversed. That is, models M3 and M4 have higher values than the other models, and this is in the entire range of conductivity. Such an inverted relationship is also present in the single-layer model, but only at higher conductivity values, i.e., above 0.04 S/m. For this value, in the 1wB models, the field values are similar for all variants of the length of hollows. The observed effects should be associated with the complexity of field phenomena during wave propagation in a porous material.

Increasing the size of the gaps (air area) at the expense of the dissipative dielectric reduces the resultant wave attenuation. The characteristics are monotonic. Regardless of the wall model, smaller differences between the field values are visible for different values of the conductivity of the ceramic mass than for the single-layer wall. The electric field values are similar for the M1 and MW models in the two-layer model.

Table 13 presents the maximum field values for each wall variant, considering the hollows’ variability. For σ = 0.01 S/m, when comparing single-layer wall systems with double-layer ones, it can be seen that in models with a greater length of hollows (M3, M4), increasing the wall thickness practically does not affect the change in the field intensity value. However, in the remaining models, increasing the wall layering causes a decrease in the field value (e.g., for: M1 by 32%, M2 by 36%, MW by 24%).

The porosity of the brick in the electromagnetic sense affects the appearance of multiple reflections at air–ceramic mass boundary. The number and size of holes in the brick change the field image in the area close to the wall. The local change in the wave speed when passing through subsequent air and ceramic mass areas is reflected in the field distributions and the occurrence of interference. The differences in the analyzed field values can be explained in macroscopic terms by taking into account the share of ceramic mass in the volume of the brick. A higher mass value causes less distortion of the wavefront in the area behind the wall. This results from the greater resultant homogeneity of the material. However, attenuation negatively affects the maximum field values.

6.3. Comparison of Field Values Between Single- and Double-Layer Walls with Different Brick Variants

Table 14. Percentage difference in the max(E_z) component value between single and double layer walls at σ = 0.01 S/m.

Name of Model	Type of Brick	Percentage of Ceramic Mass in Brick	σ = 0.01 S/m	σ = 0.04 S/m
M1		86.80%	reduction by 34%	reduction by 45%
M2		82.84%	reduction by 36%	reduction by 48%
MW		78.88%	reduction by 24%	reduction by 45%
M3		75.58%	reduction by 5%	reduction by 36%
M4		73.60%	increase by 4.8%	reduction by 30%

shows the percentage difference between the field values obtained for a single-layer wall and a double-layer wall with the same types of bricks. The values are for two conductivity values (0.01 S/m and 0.04 S/m). The table also includes the percentage of ceramic mass in a given type of brick. The percentage of ceramic mass decreases with the increase in the length of the hollows. The double-layer wall causes a smaller decrease in the field value with the increase in the length of the hollows.

At a conductivity of 0.04 S/m for a single-layer wall, the field values are similar for all brick variants and average 0.34. In the case of a double-layer wall, the field values decrease with the increase in conductivity. The characteristics have a similar course. Doubling the bricklayer causes a 45% decrease in the field value in the M1 model. A 12% decrease in the percentage of ceramic mass in the brick causes a 15% increase in the field value between 1w_B and 2w_B.

The exception is the model with the largest dimensions of the hollows and, at the same time, the smallest percentage of the ceramic mass (M4). In this case, the second layer causes the field values to be higher than for a single-layer wall. Such a relationship was observed for conductivity of 0.01 S/m. Such arrangement of hollows and their sizes caused the occurrence of numerous reflections inside the bricks, which overlapped and increased the field values in the 2w_B model. Generally, two layers cause a decrease in the field value. Increasing the percentage of the ceramic mass in the brick causes smaller differences between the field values obtained for single- and double-layer walls.

7. Conclusions

The article presents the effect of changing the length of the brick holes and the layering of the wall on the values of the electric field intensity. Based on the multivariate analysis using the time-based method (FDTD), it was possible to observe where and in what places in the area with the wall there are local maxima and minima that can interfere with data transmission. The second layer of bricks causes an increase in such areas compared to a single-layer wall. Such interferences are also particularly visible when the wall contains a larger surface of air holes, i.e., when the holes are longer. The greatest distortions are after the EM wave passes through the wall. However, such a phenomenon is also visible in front of the wall, i.e., before the wave passes through the lossiness medium. In this case, higher values of field amplification and weakening were observed, but only in the area up to 1 m in front of the wall.

The article’s main objective was to analyze the influence of changing the length of the hollows on the electric field values. In the single-layer model, in the range of small conductivity values (σ < 0.04 S/m), the smaller the amount of ceramic mass (i.e., larger hollows), the field values decrease. In the two-layer model, the larger the hollow surface, the higher the field intensity values in the entire range of the considered conductivities (0–0.2 S/m). Such a relationship also occurs in the single-layer model, but only at higher conductivity values (0.04–0.2 S/m). Increasing the percentage of ceramic mass in the brick causes smaller inhomogeneities in the field distribution. A 12% decrease in the percentage share of ceramic mass in the brick causes a 15% increase in the field value between models 1w_B and 2w_B. The increase in the material lossiness causes the wave to be attenuated when passing through the dielectric. On the other hand, the porosity of the medium in electromagnetic terms results in the occurrence of multiple reflections and deflections with relatively small attenuation. The main conclusion is that small deviations from the standard dimensions of the hollows do not significantly affect the field values further away from the wall. Only in the zone close to the wall do they cause wavefront distortions.

The proposed method has a major limitation resulting from the condition of using a cuboid (rectangular) mesh, which leads to a less accurate representation of irregular surfaces, e.g., rounded surfaces. It can be approximated by significantly reducing the mesh size. However, this is associated with a large number of degrees of freedom and increased requirements for computational units. It is planned to eliminate this problem by using an adaptive mesh. In the case of large analysis zones or rounded surfaces, such a solution would allow for the analysis of large-scale systems without the need to homogenize material parameters and complex structures. It would also be helpful to add a function that allows for the obtaining of the field envelope without the need to save n-files and search for maximum values using an additional algorithm. It is also possible to use parallel programming, allowing for accurate analysis of larger areas, e.g., covering one floor of a building.