Abstract
Due to its simple structure and stable operation, the Organic Rankine Cycle (ORC) has gained significant attention as a primary solution for low-grade thermal power generation. However, the economic challenges associated with development difficulties in hot dry rock (HDR) geothermal power systems have necessitated a better balance between performance and cost effectiveness within ORC systems. This paper establishes a game pattern of the Organic Rankine Cycle with performance as the master layer and economy as the slave layer, based on the Stackelberg game theory. The optimal working fluid for the ORC is identified as R600. At the R600 mass flow rate of 50 kg/s, the net system cycle work is 4186 kW, the generation efficiency is 14.52%, and the levelized cost of energy is 0.0176 USD/kWh. The research establishes an optimization method for the Organic Rankine Cycle based on the Stackelberg game framework, where the network of the system is the primary optimization objective, and the heat transfer areas of the evaporator and condenser serve as the secondary optimization objective. An iterative solving method is utilized to achieve equilibrium between the performance and economy of the ORC system. The proposed method is validated through a case study utilizing hot dry rock data from Qinghai Gonghe, allowing for a thorough analysis of the working fluid and system parameters. The findings indicate that the proposed approach effectively balances ORC performance with economic considerations, thereby enhancing the overall revenue of the HDR power system.
1. Introduction
With the rapid development of the world’s economy and population growth, the shortage of fossil energy and the environmental problems caused by greenhouse gas emissions have become the key factors restricting the sustainable and healthy development of the world. As a new type of clean energy, hot dry rock (HDR) is not affected by seasons and weather, giving it excellent development prospects. China is rich in geothermal resources [1], about 1/6 of the world’s resources. Hot dry rock resources in the Gonghe Basin of Qinghai province are equivalent to t of standard coal [2]. Its temperature is around 236 °C, which belongs to the medium-low temperature heat source. HDR has considerable stock as an environmentally friendly renewable energy source, with sizeable thermal energy density and wide distribution. HDR has become an important research direction in clean energy [3]. However, due to the difficulty of underground engineering of HDR power stations [4] and high investment [5], the unit kilowatt development cost has remained high for a long time. The economy has become the main bottleneck restricting HDR geothermal energy’s large-scale development and utilization [6]. A novel power generation system optimization method is urgently needed. There are three common ways to generate electricity from HDR: flash steam system, Organic Rankine Cycle (ORC) system, and Kalina cycle system [7]. Due to the low temperature of HDR, flash steam systems are usually not considered. Rodríguez CEC has conducted a comparative analysis of the ORC system and the Kalina Cycle performance for low- and medium-temperature power generation. The thermal analysis of the ORC system cycle with 15 different organic working fluids and the Kalina cycle with three different concentrations of ammonia mixtures (65%, 75%, and 84% by mass, respectively) shows that the ORC system cycle has a higher thermal efficiency than the Kalina cycle [8]. Comparing ten power generation cycles, Yu, S.C. et al. [9] found that the ORC system had the highest performance at 450–500 K. Loni, R. et al. [10] pointed to the ORC system’s high flexibility and compatibility with low- and medium-temperature heat sources and that the ORC system is a promising technology for power generation. Al-Rawashdeh, H.A. et al. utilized ORC to participate in waste heat recovery in a cement plant, and the results showed that the thermal efficiency is higher with ORC power generation technology at a low-temperature heat source [11]. The above literature indicates that the ORC system is a hot research topic in the world’s low- and medium-temperature power generation.
In early research, the ORC system optimization goal was usually maximum thermal efficiency or output power. With the development of research, the economy of the ORC system, including total cost, payback period (PBP), and net present value (NPV), has attracted more and more attention. The study’s results show that it is difficult for different optimization objectives to reach the optimum simultaneously [12]. Gomaa, M. et al. analyze and optimize the components of an ORC system using solar collectors and waste heat recovery, using R245fa as the ORC working fluid. The results show that ORC is beneficial for solving environmental problems. And it saves USD 280,000 per year [13]. Pan W et al. used a particle swarm algorithm to optimize the ORC thermal efficiency and cost. The optimization results show that the thermal efficiency of ORC can reach 12.76%, and the investment cost is about 8539.66 USD/kW [14]. Wang et al. used an evolutionary algorithm for multi-objective optimization of ORC systems with exergy efficiency and total investment cost exergy as optimization objectives. R134a is the power generation work mass, and the final optimal exergy efficiency and total investment cost exergy were 13.98%, and USD [15]. Muhammad Imran et al. used a genetic algorithm for the multi-objective optimization of ORC systems, single-stage regenerative ORC systems, and two-stage regenerative ORC systems, with the optimization objectives of maximizing thermal efficiency and minimizing specific investment costs. This resulted in R245fa as the optimal power-generating fluid [16]. Gimelli A. et al. optimized the ORC system using a multi-objective optimization algorithm with electrical efficiency and heat transfer area as the optimization objectives to derive the Pareto boundaries, which yielded the optimal electrical efficiency ranging from 14.1% to 18.9%. The optimal heat transfer area ranged from 446 m2 to 1079 m2 [17]. José C. Jiménez-García et al. proposed that multi-objective optimization is a future research direction for ORC systems [18]. Zhang, C. et al. [19] pointed out that the heat exchanger area accounts for a large proportion of the total cost of the ORC system.
Based on the above research, conventional thermodynamic parameter analysis methods are not optimal and cannot obtain optimal solutions. The existing optimization methods based on the fundamental theorem of thermodynamics do not consider the influence of equipment structure on thermodynamic performance. In existing ORC system optimization research, balancing the system’s network and the heat exchanger’s area is challenging. Game theory can profoundly reveal the system’s internal contradictions and achieve an equilibrium of optimization objectives, which is very suitable for solving the contradiction between performance and cost in ORC system optimization. Therefore, based on game theory, we propose an ORC system optimization method that balances the network representing performance and the heat exchanger area representing cost in the game for the HDR dynamic system. Firstly, the ORC Stackelberg game pattern is established based on the performance of the thermal cycle and the economy of the thermal cycle. Secondly, the ORC system’s thermodynamic and heat exchanger area models are established based on the game pattern. Then, the optimization method and solution method of the Stackelberg game ORC based on the network of the system and the heat exchange area of the heat exchanger are proposed. Finally, the accuracy and effectiveness of the ORC optimization method are verified by taking the construction of hot dry rock resources in the Gonghe Basin of Qinghai Province as an example.
2. Stackelberg Game Pattern of ORC Optimization
2.1. System Components and Thermal Processes
The ORC system consists of an evaporator, a turbine, a condenser, and an industrial pump. High-temperature fluid moves through the evaporator, heating the power generation process. After the temperature is reduced, the power generation process is heated to a gaseous high-temperature and high-pressure power generation process into the expansion of the turbine to perform the work. The process drives the motor to generate electricity. After expansion through the turbine, the low-temperature, low-pressure steam enters the condenser, which is condensed into a liquid state by the condensate and then pumped to the evaporator through the mass pump to start the next round of the power generation process as shown in Figure 1. Therefore, the evaporator, condenser, pump, and turbine are the core components of the ORC system. Subsequent sections will also focus on discussing these four components.

Figure 1.
ORC system flowchart.
2.2. Framework of the Stackelberg Game Pattern
In ORC system optimization, a high network indicates strong performance but also requires a larger heat exchanger area and incurs higher costs. HDR is a medium-low temperature heat source, so the network performance dominates ORC system optimization. So, in the application scenario of HDR, ORC system performance dominates, while cost follows, making it suitable for research using Stackelberg game theory. Based on the Stackelberg game, the ORC system optimization can consider the cycle’s network to be the leader and the heat exchanger’s area to be the follower. In our study, based on the Stackelberg game method, the players are the system network, the heat exchanger area of the evaporator, and the condenser, which represents the requirement of maximizing the thermal cycle performance of the turbine and minimizing the system cost. Based on the above analysis, the Stackelberg game pattern for ORC system optimization is shown in Figure 2.

Figure 2.
Schematic diagram of Stackelberg game pattern for ORC system optimization.
3. Thermodynamic Model of ORC
It can be seen in 1.2 that the two levels of the game in ORC system optimization are the heat exchanger area and the network of the system. Therefore, we focus on establishing the model of the heat exchanger area and the network of the system.
In this paper, based on the careful consideration of the investment cost as well as the parameters of the work quality, the thermodynamic model is established with the basic structure of shell and tube heat exchanger with the best economy as the evaporator and condenser of the ORC system. The shell and tube heat exchanger are shown in Figure 3. In modeling the system, the following assumptions and conditions are made.

Figure 3.
Shell and tube heat exchanger geometry.
- The ORC system is always in a steady state;
- We neglect the evaporator and condenser pressure drop losses, piping resistance losses, and heat losses;
- The isentropic efficiency of both the pump and the turbine is 0.85;
- We assume that the pinch point temperature is 10 °C and the condensate inlet temperature is 20 °C;
- We assume that the atmospheric pressure is 0.1 MPa.
3.1. Geometric Design of Shell and Tube Heat Exchangers
(m) indicates the outer diameter of the heat exchanger tube, (m) indicates the heat exchanger tube center spacing, (m) indicates the outer diameter of the outermost heat exchanger tube, (m) indicates the outer diameter of the shell, (m) indicates the center diameter of the outermost heat exchanger tube, (°) indicates the outer angle at the folding plate, (°) indicates the inner angle at the folding plate, (m) indicates the folding plate spacing, and (m) indicates the center distance from the opening of the folding plate to the inner wall of the tube. The above parameters can fully describe the geometry of the shell and tube heat exchanger and are the optimization variables for the subsequent study of heat exchanger design. Therefore, before modeling the evaporator and condenser heat exchangers, the geometrical model of the shell and tube heat exchanger is first given [20] in Figure 3.
In the above equation, (m) indicates the clearance between the shell and the outermost tube, indicates the proportion of tubes in the window, indicates the cross-section bundle ratio, (m2) indicates the bypass flow area, (m2) indicates the shell center cross area, (m2) indicates the leakage area between the tube and the folding plate, (m2) indicates the leakage area between the shell and the folding plate, indicates the lateral pipe spacing, and indicate the tube and shell gap, respectively, is the number of bundles, and denotes the bundle constant.
3.2. Models of Evaporator Area
Based on obtaining the geometrical model of the shell and tube heat exchanger, this paper adopts the moving boundary method combined with the average logarithmic temperature difference method to construct the mathematical model of the evaporator. Figure 4 shows the heat exchange process of the evaporator.

Figure 4.
Schematic diagram of heat exchange process of evaporator.
The tube side of the evaporator is a high-temperature fluid, and the shell side is an organic power generation medium. Since the high-temperature fluid on the tube side does not undergo a phase change, the evaporator is divided into a preheating zone, phase change zone, and superheating zone according to the phase change process of the organic working fluids on the shell side using the moving boundary method. Then, the heat transfer model is established using the mean logarithmic temperature difference method. The heat transfer model using the mean logarithmic temperature difference method can be expressed as [20]
In the above equation, (kW) denotes the amount of heat exchanged for each heat transfer process, denotes the heat transfer coefficient of the heat exchanger, denotes the heat transfer area of the heat exchanger, F is the correction factor, (K) is the mean logarithmic temperature difference, and i is the number of subparagraphs. In this paper, the heat exchange process is divided into preheating section, phase change section, and superheating section. It is used to calculate the heat transfer coefficient of the heat exchanger. (kW/(m2·K)) indicates the heat transfer coefficient of the fluid in the tube, indicates the heat transfer coefficient of the fluid outside the tube, is the heat transfer coefficient of the bundle, and and indicate the inner and outer diameters of the tube bundle, respectively. The above equation gives the calculation of the mean logarithmic temperature difference, and and indicate the high-temperature side (tube side) and low-temperature side (shell side) temperatures, respectively.
The heat transfer coefficients modeled for each heat transfer zone on the tube and shell sides are below, respectively.
3.2.1. Models of Tube-Side Heat Transfer Coefficient
The heat transfer coefficients are modeled as follows since no phase change occurs in the high-temperature fluid on the tube side [21]:
In the above equation, is the tube-side heat transfer coefficient, is the Nussell number, k denotes the thermal conductivity, Re is the Reynolds number, and Pr is the Prandtl number.
3.2.2. Models of Shell-Side Heat Transfer Coefficient
The basic model of the shell-side heat transfer coefficient is as follows [22]:
In the above equation, is the shell-side heat transfer coefficient, is the ideal heat transfer coefficient of the shell side, and are the correction factors, and is the area factor.
The heat transfer properties of the power generation medium are greatly affected by the phase change, resulting in the shell side ideal heat transfer coefficient needing to be calculated separately for the phase change area and the non-phase change area. In addition, the shell-side non-phase-change region also needs to consider the influence of the arrangement between the tube bundles on the heat transfer area, commonly used in the engineering arrangement of 30°, 45°, 60°, and 90°, as shown in Figure 5. Among them, 30°, 45°, and 60° can use the same calculation model.
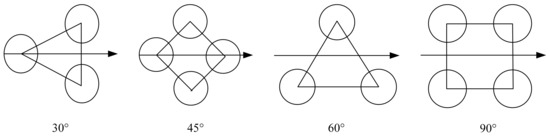
Figure 5.
Schematic diagram of tube bundle arrangement.
The calculation model for the preheating and superheating zones on the shell side is as follows when the tube bundles are aligned at 90° [22]:
Similarly, we can obtain the model for calculating the heat transfer coefficient for tube bundles arranged at 30°, 45°, and 60° as follows:
where indicates the hydraulic diameter, indicates the Lévêque number, indicates the Hagen number Pr indicates the Prandtl number, Red indicates the Reynolds number, indicates the transverse pipe spacing, indicates the longitudinal pipe spacing, indicates the bundle of pipe constant, and and are two dimensionless constants.
When the organic working fluid exchanges heat with the heat source during the phase transition stage, there is a significant difference in the heat transfer coefficient calculation compared to the non-phase transition stage. The calculation model for the heat transfer coefficient during the phase transition stage is as follows [23]. The in the model is a constant, generally taken as 250:
where (kPa) is the evaporation pressure, (kPa) is the critical pressure of the power generation medium, is the temperature of the high-temperature side corresponding to the gas saturation point of the evaporator, is the temperature of the high-temperature side corresponding to the liquid saturation point of the evaporator, and is the saturation temperature of the evaporation side.
3.3. Models of Condenser Area
3.3.1. Models of Condenser Tube-Side Heat Transfer Coefficient
The condenser and evaporator use a shell and tube heat exchanger of the same physical structure, with cold water on the tube side and power generation media on the shell side. Figure 6 shows the schematic diagram of the condenser heat transfer process. The condenser tube side heat transfer coefficient is modeled as follows:
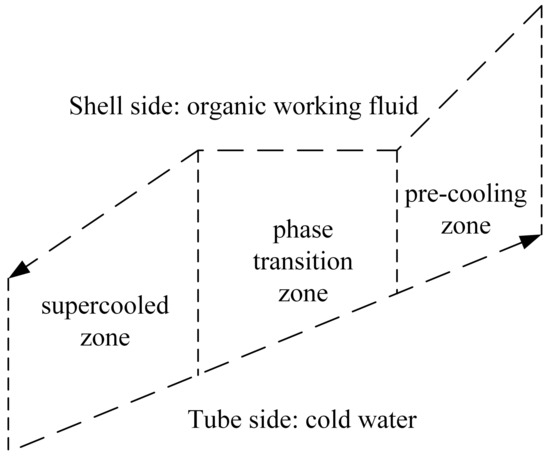
Figure 6.
Schematic diagram of condenser heat exchange process.
In the above equation, is the condenser tube side heat transfer coefficient, is the Nussell number, denotes the thermal conductivity, is the Reynolds number, and is the Prandtl number.
3.3.2. Models of Condenser Shell-Cide Heat Transfer Coefficient
The basic model for the heat transfer coefficient in the non-phase change region on the shell side of the condenser is as follows:
In the above equation, is the condenser shell-side heat transfer coefficient, and is the condenser ideal heat transfer coefficient of the shell side.
The condenser shell-side non-phase-change region also needs to consider the influence of the arrangement between the tube bundles on the heat transfer area, commonly used in the engineering arrangement of 30°, 45°, 60°, and 90° as shown in Figure 5. Among them, 30°, 45°, and 60° can use the same calculation model.
The calculation model for the precooling and subcooling zones on the shell side is as follows when the tube bundles are arranged at 90°:
Similarly, we can obtain the model for calculating the heat transfer coefficient for tube bundles arranged at 30°, 45° and 60° as follows:
where indicates the hydraulic diameter, indicates the Lévêque number, indicates the Reynolds number, indicates the Prandtl number, indicates the Reynolds number, indicates the transverse pipe spacing, indicates the longitudinal pipe spacing, indicates the bundle of pipe constant, and and are two dimensionless constants.
The shell-side phase change process for the exothermic condensation of high-temperature organic matter vapor into a liquid state differs in its heat transfer principle from boiling heat transfer. Therefore, its heat transfer calculation model differs from the evaporator phase change stage. The following is the condenser shell-side phase change area heat transfer coefficient calculation model [22]:
where is the constant-pressure specific heat capacity of the organic mass, h is the specific enthalpy, g is the gravitational acceleration, is the saturation temperature on the condensing side, and is the dynamic viscosity.
3.4. Models of Turbine
The following equation gives the thermodynamic model of the turbine:
where (kg/s) is the mass flow rate of the power generation medium, represents the evaporator outlet temperature, and is the condenser inlet temperature.
3.5. Models of Pump
The following equation gives the thermodynamic model of the work pump:
where and are the evaporator inlet temperature and condenser outlet temperature, respectively.
3.6. Net Circulating Work and Thermal Efficiency
4. A Bi-Level Stackelberg Game Approach for ORC System Optimization
4.1. Game Model of Leader
According to the Stackelberg game pattern identified in Figure 2, the leader’s strategy set and payment are, respectively,
where and .
4.2. Game Model of Follower
The follower’s strategy set and payment are, respectively,
The above ORC Stackelberg game pattern can be further transferred to a two-layer optimization model iteratively solved by optimizing X to maximize the network of the system given :
The minimum heat transfer area is obtained by optimizing and , respectively, given :
4.3. Constraints and Solving Method
In ORC system optimization, some constraints need to be added in order to prevent some parameters from being too high and damaging the equipment as follows (applicable to the organic working fluids selected herein):
where indicates the evaporator high-temperature side pressure, indicates the condenser condensate side pressure, and indicates the pressure ratio of the turbine. It is the ratio of the pressure of the organic working fluid on the evaporating side of the evaporator and the condensing side of the condenser.
The parameters, as well as the optimization variables, are first defined, followed by designing the initial values of thermodynamic parameter operating points to run the operating points with the optimization objective of the net system work, followed by developing the heat exchanger structural parameter operating point dispositions to optimize the evaporator and condenser structural parameters with the aim of a minimal heat exchanger area. The optimization results are stored in the system network, and the heat exchanger area reaches equilibrium. If the system network and heat exchanger area reach equilibrium, the optimization results are stored; if the heat exchanger area and network do not reach equilibrium, the optimized thermodynamic and heat exchanger structural parameters are input to continue the iteration until the heat exchanger area and network reach equilibrium. Figure 7 gives the flowchart of the ORC system design optimization method based on the Stackelberg game.
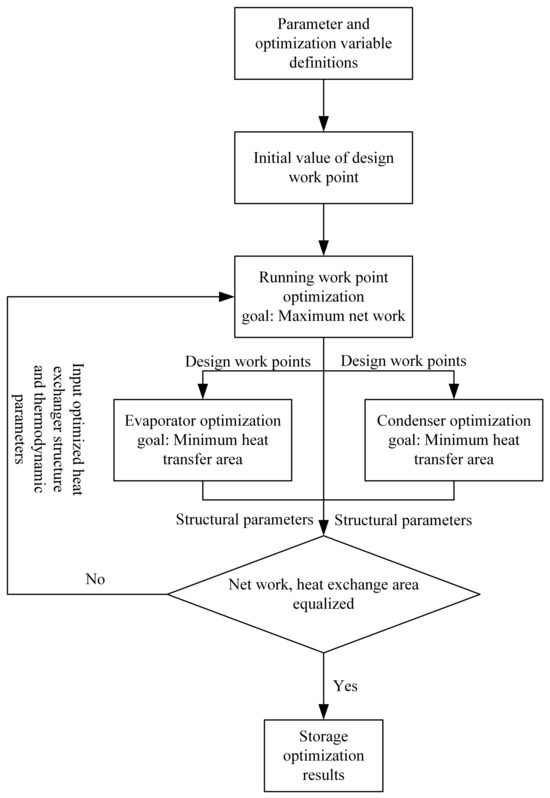
Figure 7.
ORC system optimization Stackelberg game approach.
The mathematical model of the ORC system established above contains many non-linear dimensionless models. At the same time, it is also necessary to call the external black-box physical properties database to calculate the enthalpy, density, saturation temperature, kinetic viscosity, other physical parameters of the workpiece, etc. This paper uses MATLAB software 2019 to establish the optimization model and the gradient-free optimization function, FMINCOM, to call the physical properties database software REFPROP 9.1 to solve the game problem.
5. Case Study
5.1. Parameters of Case
The development of hot dry rock power plants is quite challenging, and their economic viability is currently relatively weak. In hot dry rock power generation, ORC is the optimal power generation system comparing three standard power generation systems. Therefore, the ORC optimization method based on the Stackelberg game proposed in this paper is simulated in a hot dry rock scenario to solve the problem of hot dry rock power plant economics.
Currently, the potential high-quality HDR in China is mainly concentrated in Gonghe Basin, where the temperature of HDR is 236 °C at 3600 m underground. According to the operation data of the Sult HDR power station [24], the predicted temperature range at the wellhead of the Gonghe HDR resource production wellhead is 200–210 °C. Combined with the best working temperature of a low-grade thermal power generation system, the outlet temperature of the production well is 200 °C as a typical parameter construction case of a high-quality HDR power station. The case parameters of the HDR power station are shown in Table 1.

Table 1.
Parameter table of calculation example of HDR power station.
5.2. ORC Optimization Results
In order to compare and analyze the optimization results, we evaluate the game balance solution using a levelized cost of energy.
Models of levelized costs of energy are given as follows [25]:
where is the full-cycle cost correction factor, is the system operation and management costs, taken as 1.5% of the total investment cost of the system, (USD) is the total investment cost, and is the annual operating time of the system, taken as 8000 h.
The full-cycle cost correction factor is calculated as follows:
where i is the annual interest rate, taken as 0.05, and is the operational life, taken as 20 years.
The total investment cost is calculated as follows [26]:
where and are the chemical plant cost indices for 2024 and 2001, 674.316 [27] and 397 [28], respectively, and includes the equipment costs for heat exchangers, process pumps, and turbines.
ORC system equipment costs are calculated as follows:
where is the baseline cost of equipment, are coefficients, Z is the characteristic parameter of each component (for the heat exchanger, Z is the heat transfer area; for the expansion machine of the mass pump, Z is the power consumption of the mass pump and the expansion work of the expansion machine), is the pressure correction coefficient, and p is the operating pressure of each component so that the calculation of the cost of the equipment of the evaporator, condenser, circulating pumps, and the expansion machine is .
According to the existing research on ORC system working fluids, the heat source temperature is 190–210 °C. In this paper, R600 is chosen as the organic working fluid to derive the optimization results of ORC under different mass flow rates. The results of the optimized design of the ORC system for different mass flow rates of heat sources are given in Table 2.

Table 2.
Alternative organic working fluids list of ORC system (this table is for different values of the mass flow rate of the working fluid).
It can be seen that with the increase in heat source mass flow, the increase in the total heat exchange capacity of the thermodynamic cycle leads to the gradual growth of the heat exchange area of the evaporator and condenser. The network is improved, and the investment cost of the system is also increased.
5.3. Parametric Analysis
The selection of organic working fluids has a significant impact on the performance of the ORC system. Therefore, before the optimization design of the thermal cycle, the power generation materials should be selected from the economic point of view. When choosing organic working fluids, the matching with the heat source should be considered first, and the critical temperature of organic working fluids should be matched with the heat source. Satisfactory efficiency and network cannot be obtained by a critical temperature that is too high or too low. Secondly, environmental protection is also crucial for selecting organic working fluids. Generally, the working medium’s ozone depletion potential (ODP) is required to be 0, the global warming potential (GWP) is less than 10, and the ORC system is provided with high thermal efficiency. Finally, the availability of organic working fluids should be considered [29]. This paper chooses six organic working fluids as alternative power generation materials [30]. As shown in Table 3.

Table 3.
Alternative organic working fluids list of ORC system (: critical pressure; : critical temperature).
Based on a typical high-quality HDR power plant from Table 1, the ORC system optimization is conducted using various organic working fluids to evaluate the net system power, levelized cost of energy, and heat exchanger area per kilowatt. This analysis aimed to determine suitable organic working fluids for HDR development. The optimal network of the ORC system obtained using different organic working fluids is given in Figure 8. It can be seen that R600, R1233zd, and R245fa have better performance in the optimal network. The optimal network reflects the overall operational performance of the system but does not fully reflect the system’s heat exchanger efficiency and economy. Therefore, it is also necessary to screen the alternative work masses further through the heat exchanger area and the levelized cost of energy. Figure 9 gives the minimum heat exchanger area (condenser + evaporator) corresponding to different organic working fluids.

Figure 8.
Optimal network of organic working fluids.
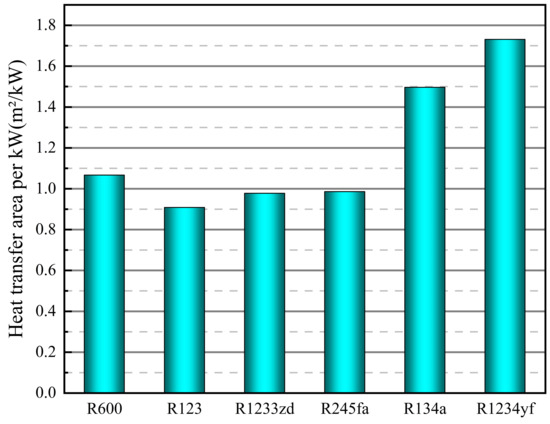
Figure 9.
Minimum heat transfer area per kW for organic working fluids.
It is reflected that R123 has high heat transfer efficiency in the low-power scene. While R134a and R1234yf have larger heat exchanger areas, indicating that they are not well matched with the heat source. In contrast, R600, R123, and R1233zd also have advantages in heat transfer efficiency, and the comparison results of the levelized cost of energy are given in Figure 10 by combining the network and heat exchanger area.
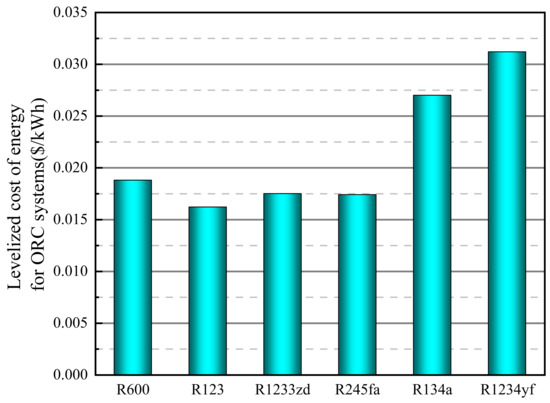
Figure 10.
Levelized cost of energy for organic working fluids.
R123 has a clear advantage in terms of cost. Still, its optimal net power is small, and it can be considered that the ORC system with R123 is more suitable for occasions where the stand-alone power is small. It is necessary to take advantage of the distributed resources. In addition, R600, R1233zd, and R245fa all have good economics, while R1233zd has a higher cost of its own and is currently mainly used as an additive. According to the ODP and GWP indices, the eco-environmental protection policy requires that the R245fa class of ORCs be discontinued entirely in 2030. Finally, butane (R600), as a power generation fluid, can obtain a sizeable network and has good economy. Therefore, by analyzing the six organic working fluids, this paper finally adopts butane (R600) as the organic working fluid for the ORC system.
After selecting the ORC system medium, it is also necessary to determine the tube bundle arrangement of the evaporator and condenser in the ORC system to reduce the heat exchanger area further and lower the investment cost to improve the economy. According to the four ways of tube bundle arrangement of shell and tube heat exchanger given in Figure 5, there are 16 combinations of evaporator and condenser in the ORC system. The effects of the 16 tube bundle arrangements on the evaporator area, condenser area, and total heat transfer area are given in Figure 11. The evaporator–condenser tube bundle arranged at 60°-60° has a smaller heat transfer area with higher efficiency. Therefore, the evaporator and condenser tube bundles are selected to be placed at 60°. (Note: The former of the horizontal coordinate tube bundle arrangement angles in Figure 11 is the evaporator angle, and the latter is the condenser angle. AC represents the condenser heat transfer area, and AE represents the evaporator heat transfer area).

Figure 11.
Relationship between tube bundle arrangement and heat transfer area.
6. Conclusions
According to the typical application scenarios of HDR in Qinghai province, this paper establishes the Stackelberg game pattern of the circulating network and heat exchanger area. The optimization method of the ORC system based on the Stackelberg game is established by constructing the detailed thermodynamic model of the ORC system. The leading layer takes the maximum network of the system as the optimization goal, and the secondary layer takes the minimum heat exchanger area as the optimization goal. Afterwards, an iterative solution method is proposed. Finally, the Stackelberg game method is verified by the Gonghe hot dry rock data in Qinghai Province. The analysis of this study shows that the network is gradually increasing with the gradual increase in the organic work fluids mass flow rate. Still, the power generation efficiency is slowly decreasing, and the levelized cost of energy is also gradually increasing. This indicates that the heat exchanger area dominates the cost of the ORC system. By optimizing the ORC system with the method proposed in this paper, the following conclusions can be drawn:
- The ORC optimization method based on the Stackelberg game can balance the net system work and heat transfer area during optimization;
- The organic working fluid R600 is the best ORC performance working fluid;
- The total heat transfer area is minimized when the evaporator and condenser tube bundle angles are 60°; Heat transfer area of 4466 m2;
- At R600 of 50 kg/s, the net system cycle work is 4186 kW, the generation efficiency is 14.52%, and the levelized cost of energy is 0.0176 USD/kWh.
The effect of heat exchangers and piping on pressure was not considered in this study, and more refined modeling needs to be carried out in the future so that more accurate results can be obtained through this approach.
Author Contributions
Conceptualization, Y.S. and Z.H.; methodology, Y.S.; software, Y.S.; validation, Z.H.; writing—original draft preparation, Z.H. and Y.S.; writing—review and editing, Z.H. and W.W.; supervision, Y.S.; project administration, Y.S.; funding acquisition, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Basic Research Project of Qinghai Province (NO. 2024-ZJ-725).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
All authors have declared that in this study, no conflict of interest could affect the impartiality and objectivity of the results.
References
- Zhao, X.-G.; Wan, G. Current situation and prospect of China’s geothermal resources. Renew. Sustain. Energy Rev. 2014, 32, 651–661. [Google Scholar] [CrossRef]
- Zhu, G.; Zhang, L.; Deng, Z.; Feng, Q.; Niu, Z.; Xu, W. Three-Dimensional Geological Modeling and Resource Estimation of Hot Dry Rock in the Gonghe Basin, Qinghai Province. Energies 2023, 16, 5871. [Google Scholar] [CrossRef]
- Lu, S.-M. A global review of enhanced geothermal system (EGS). Renew. Sustain. Energy Rev. 2018, 81, 2902–2921. [Google Scholar] [CrossRef]
- Zhang, Y.-J.; Li, Z.-W.; Guo, L.-L.; Gao, P.; Jin, X.-P.; Xu, T.-F. Electricity generation from enhanced geothermal systems by oilfield produced water circulating through reservoir stimulated by staged fracturing technology for horizontal wells: A case study in Xujiaweizi area in Daqing Oilfield, China. Energy 2014, 78, 788–805. [Google Scholar] [CrossRef]
- Brown, D.; DuTeaux, R.; Kruger, P.; Swenson, D.; Yamaguchi, T. Fluid circulation and heat extraction from engineered geothermal reservoirs. Geothermics 1999, 28, 553–572. [Google Scholar] [CrossRef]
- Quick, H.; Michael, J.; Huber, H.; Arslan, U. History of international geothermal power plants and geothermal projects in Germany. In Proceedings of the World Geothermal Congress, Bali, Indonesia, 25–30 April 2010; pp. 25–29. [Google Scholar]
- Varma, G.P.; Srinivas, T. Power generation from low temperature heat recovery. Renew. Sustain. Energy Rev. 2017, 75, 402–414. [Google Scholar] [CrossRef]
- Rodríguez, C.E.C.; Palacio, J.C.E.; Venturini, O.J.; Lora, E.E.S.; Cobas, V.M.; Dos Santos, D.M.; Dotto, F.R.L.; Gialluca, V. Exergetic and economic comparison of ORC and Kalina cycle for low temperature enhanced geothermal system in Brazil. Appl. Therm. Eng. 2013, 52, 109–119. [Google Scholar] [CrossRef]
- Yu, S.C.; Chen, L.; Zhao, Y.; Li, H.X.; Zhang, X.R. Thermodynamic analysis of representative power generation cycles for low-to-medium temperature applications. Int. J. Energy Res. 2015, 39, 84–97. [Google Scholar] [CrossRef]
- Loni, R.; Najafi, G.; Bellos, E.; Rajaee, F.; Said, Z.; Mazlan, M. A review of industrial waste heat recovery system for power generation with Organic Rankine Cycle: Recent challenges and future outlook. J. Clean. Prod. 2021, 287, 125070. [Google Scholar] [CrossRef]
- Al-Rawashdeh, H.A.; Gomaa, M.R.; Mustafa, R.J.; Hasan, A.O. Efficiency and exergy enhancement of ORC powered by recovering flue gases-heat system in cement industrials: A case study. Int. Rev. Mech. Eng 2019, 13, 185–197. [Google Scholar] [CrossRef]
- Hu, S.; Yang, Z.; Li, J.; Duan, Y. A review of multi-objective optimization in organic Rankine cycle (ORC) system design. Energies 2021, 14, 6492. [Google Scholar] [CrossRef]
- Gomaa, M.; Mustafa, R.; Al-Dhaifallah, M.; Rezk, H. A low-grade heat organic rankine cycle driven by hybrid solar collectors and a waste heat recovery system. Energy Rep. 2020, 6, 3425–3445. [Google Scholar] [CrossRef]
- Pan, W.; Li, J.; Zhang, G.; Zhou, L.; Tu, M. Multi-Objective Optimization of Organic Rankine Cycle (ORC) for Tractor Waste Heat Recovery Based on Particle Swarm Optimization. Energies 2022, 15, 6720. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Z.; Wang, M.; Li, M.; Dai, Y. Multi-objective optimization of an organic Rankine cycle (ORC) for low grade waste heat recovery using evolutionary algorithm. Energy Convers. Manag. 2013, 71, 146–158. [Google Scholar] [CrossRef]
- Imran, M.; Park, B.S.; Kim, H.J.; Lee, D.H.; Usman, M.; Heo, M. Thermo-economic optimization of Regenerative Organic Rankine Cycle for waste heat recovery applications. Energy Convers. Manag. 2014, 87, 107–118. [Google Scholar] [CrossRef]
- Gimelli, A.; Luongo, A.; Muccillo, M. Efficiency and cost optimization of a regenerative Organic Rankine Cycle power plant through the multi-objective approach. Appl. Therm. Eng. 2017, 114, 601–610. [Google Scholar] [CrossRef]
- Jiménez-García, J.C.; Ruiz, A.; Pacheco-Reyes, A.; Rivera, W. A comprehensive review of organic rankine cycles. Processes 2023, 11, 1982. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, C.; Wang, S.; Xu, X.; Li, Q. Thermo-economic comparison of subcritical organic Rankine cycle based on different heat exchanger configurations. Energy 2017, 123, 728–741. [Google Scholar] [CrossRef]
- Hu, S.; Li, J.; Yang, F.; Yang, Z.; Duan, Y. Multi-objective optimization of organic Rankine cycle using hydrofluorolefins (HFOs) based on different target preferences. Energy 2020, 203, 117848. [Google Scholar] [CrossRef]
- Petukhov, B.S.; Popov, V.N. Theoretical calculation of heat exchange and frictional resistance in turbulent flow in tubes of an incompressible fluid with thermophysical properties. Teplofizika Vysokikh Temperatur 1963, 1, 69–83. [Google Scholar]
- Walraven, D.; Laenen, B.; D’haeseleer, W. Optimum configuration of shell-and-tube heat exchangers for the use in low-temperature organic Rankine cycles. Energy Convers. Manag. 2014, 83, 177–187. [Google Scholar] [CrossRef]
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.I. Handbook of Heat Transfer; Mcgraw-Hill: New York, NY, USA, 1998; Volume 3. [Google Scholar]
- Hettkamp, T.; Teza, D.; Baumgaertner, J.; Gerard, A.; Baria, R. The European Hot Dry Rock research project at Soultz-sous-Forets; Stand des europaeischen Hot Dry Rock-Forschungsprojektes Soultz-sous-Forets. In Geothermische Fachtagung: 20 Jahre Tiefe Geothermie in Deutschland; HydroTherm Consult GmbH: Walldorf, Germany, 2002; pp. 48–55. [Google Scholar]
- Feng, Y.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Comparison between regenerative organic Rankine cycle (RORC) and basic organic Rankine cycle (BORC) based on thermoeconomic multi-objective optimization considering exergy efficiency and levelized energy cost (LEC). Energy Convers. Manag. 2015, 96, 58–71. [Google Scholar] [CrossRef]
- Li, J.; Yang, Z.; Hu, S.; Yang, F.; Duan, Y. Effects of shell-and-tube heat exchanger arranged forms on the thermo-economic performance of organic Rankine cycle systems using hydrocarbons. Energy Convers. Manag. 2020, 203, 112248. [Google Scholar] [CrossRef]
- Anugraha, R.P.; Renanto, R.; Maulana, R.A.; Kusumo, R.D. Techno-economical study on the production of high octane gasoline in light naphtha plant. J. Chem. Technol. Metall. 2024, 59, 81–86. [Google Scholar] [CrossRef]
- de Oliveira Neto, R.; Sotomonte, C.A.R.; Coronado, C.J.; Nascimento, M.A. Technical and economic analyses of waste heat energy recovery from internal combustion engines by the Organic Rankine Cycle. Energy Convers. Manag. 2016, 129, 168–179. [Google Scholar] [CrossRef]
- Bahrami, M.; Pourfayaz, F.; Kasaeian, A. Low global warming potential (GWP) working fluids (WFs) for Organic Rankine Cycle (ORC) applications. Energy Rep. 2022, 8, 2976–2988. [Google Scholar] [CrossRef]
- Wang, D.; Ling, X.; Peng, H.; Liu, L.; Tao, L. Efficiency and optimal performance evaluation of organic Rankine cycle for low grade waste heat power generation. Energy 2013, 50, 343–352. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).