A Joint Estimation Method of Distribution Network Topology and Line Parameters Based on Power Flow Graph Convolutional Networks
Abstract
1. Introduction
- (1)
- This paper introduces a novel convolutional network for power flow, leveraging the topological dependencies and complex-valued convolution properties of AC power flow equations. The proposed network enhances line parameter identification accuracy and offers physical interpretability and adaptability to varying topologies.
- (2)
- The proposed topology identification method combines the dual correlation of node voltage magnitudes and their trends, ensuring strong robustness and improved identification accuracy.
- (3)
- This method relies solely on power and voltage magnitude data, eliminating the need for voltage phase angle measurements, which avoids the high costs of PMU deployment and greatly enhances practicality.
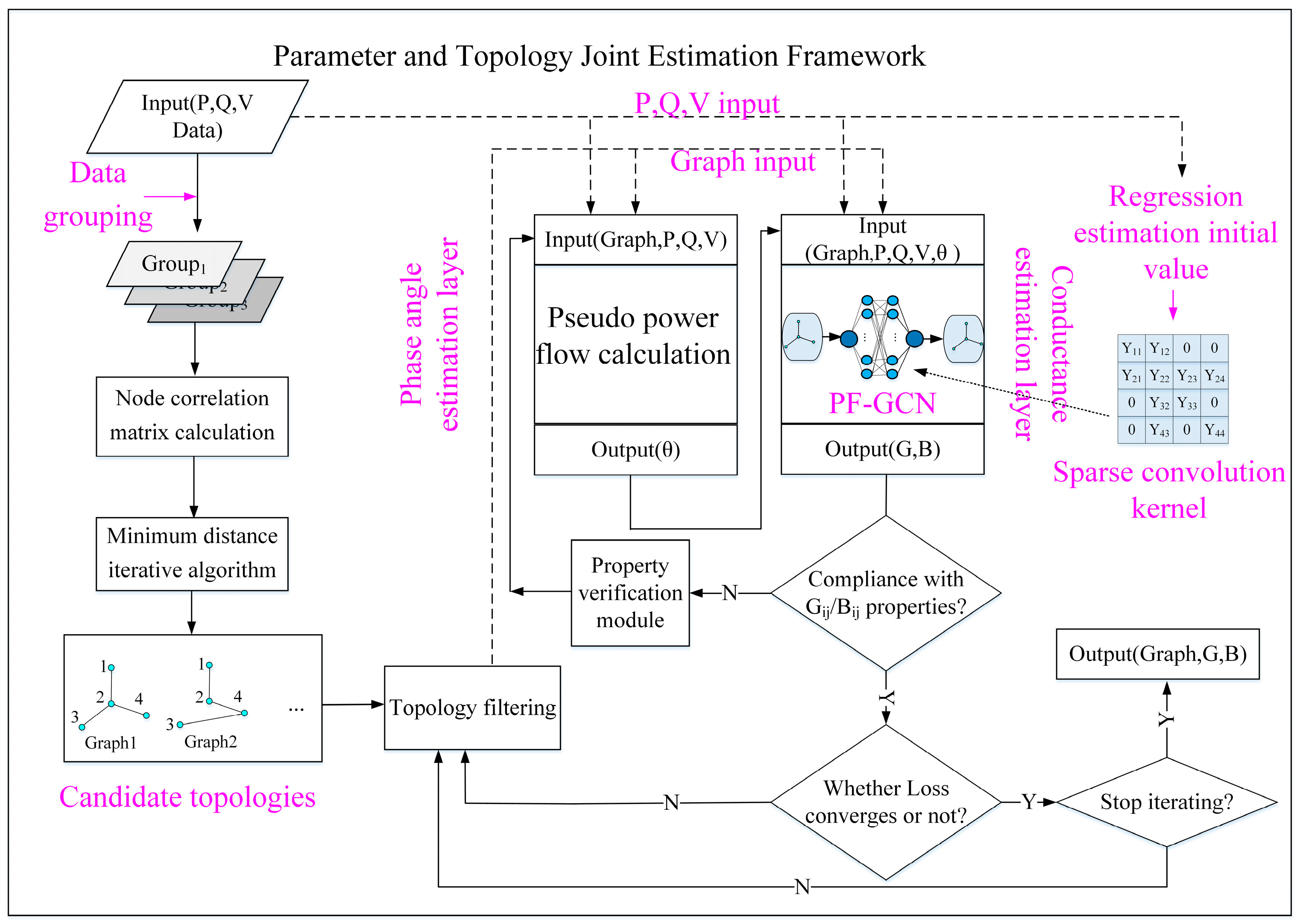
2. A Framework for Joint Estimation of Topology and Line Parameters
3. Candidate Topology Generation
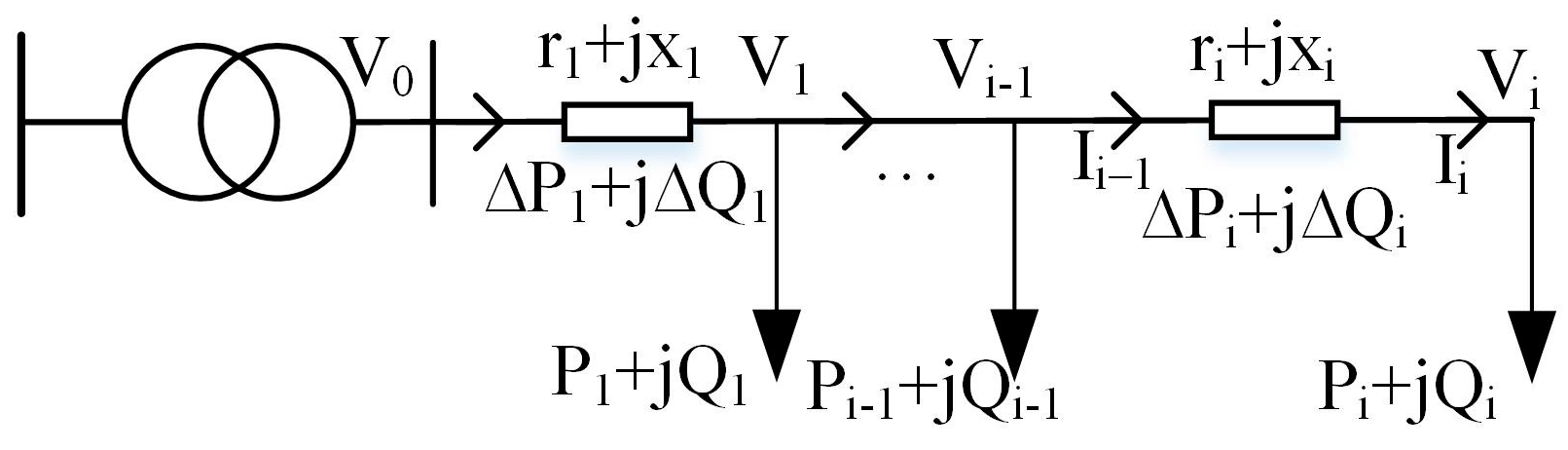
3.1. Definition of Graphs and the Principle of Node Correlation
3.2. Node Correlation Matrix Calculation
3.3. Minimum Distance Iteration Algorithm
| Algorithm 1: Minimum Node Distance Iterative Algorithm |
| Input: Correlation Matrix for U nodes |
| Output: Node adjacency matrix |
| 1:Initialize node pool = [0, 1, .., U − 1];Initialize line pool = []; Initialize node adjacency matrix , all elements = 0 |
| 2.Sort matrix in ascending order of rows to obtain an index matrix |
| 3.Traverse matrix : |
| 4. If and : |
| 5. Establish a connection between node i and node j, update |
| 6. If : |
| 7. Establish a connection for ’s corresponding node based on the minimum distance, update |
| 8.Remove nodes in from |
| 9.While ( > 0): |
| 10. Traverse , establish a connection between node k and ’s corresponding node, update , remove nodes in from |
| 11. Update by , return |
4. Line Parameter Estimation Model Based on PF-GCN
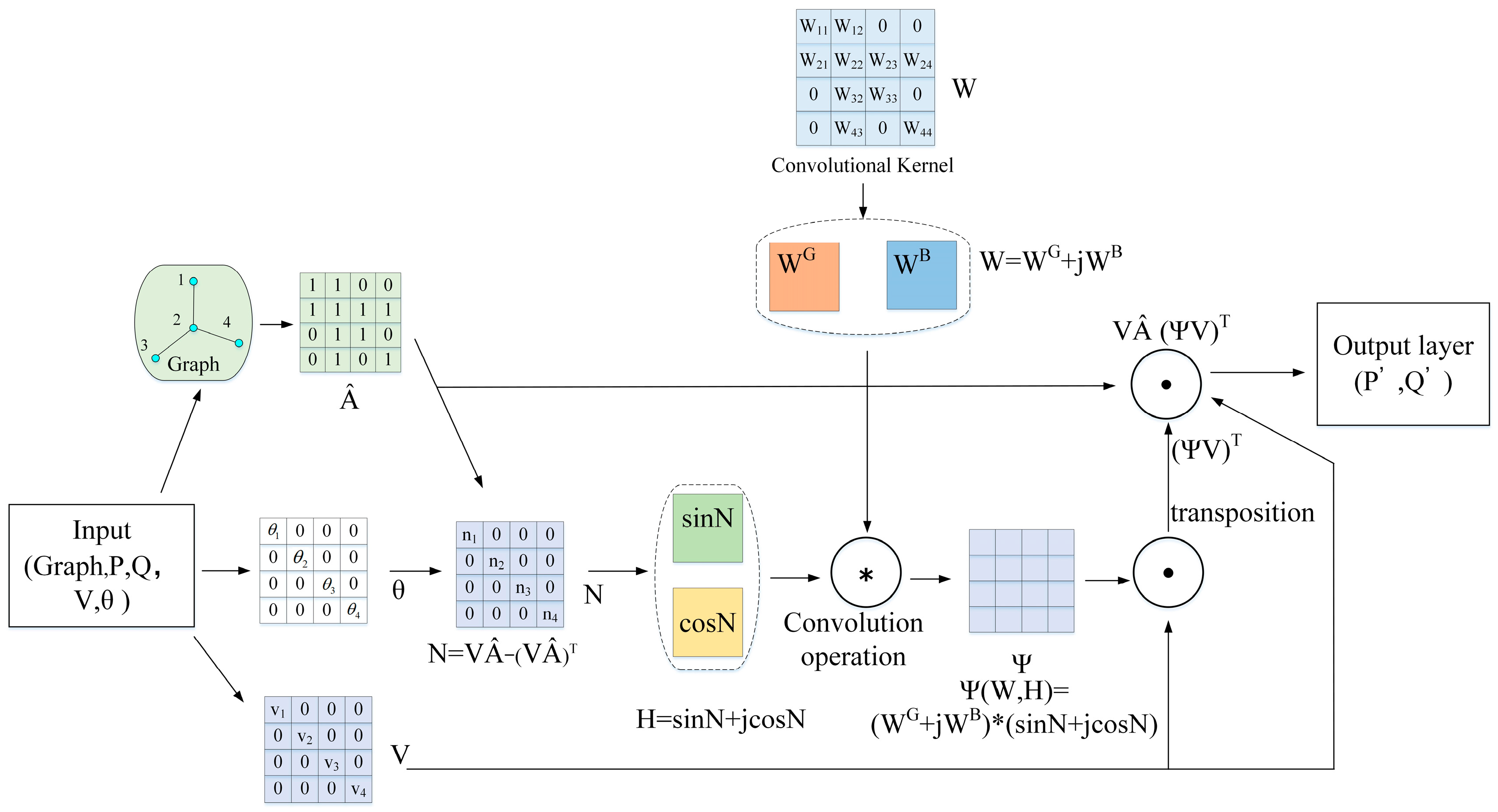
4.1. Theoretical Foundations of CV-GCN
4.2. Principles and Framework of PF-GCN Parameter Estimation Models
4.3. Loss Function Design for Parameter Estimation Layer
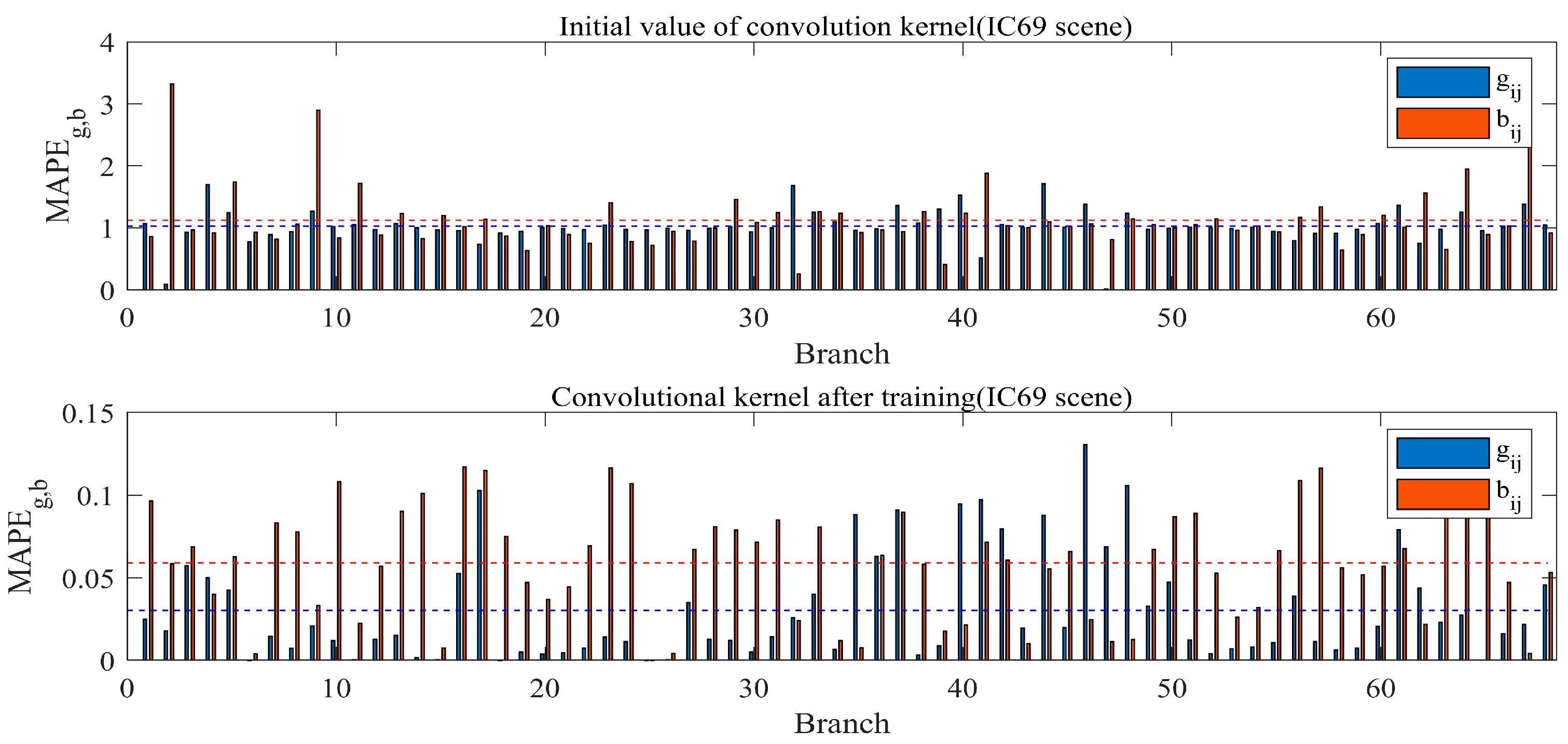
4.4. Convolution Kernel Iteration Initial Value Calculation
5. Results
5.1. Introduction to Experiments
- C33: IEEE-33 system, 600 measurements, random error = 0;
- IC69: Improved IEEE-69 system, 600 measurements, random error = 0.
5.2. Evaluation Indicators
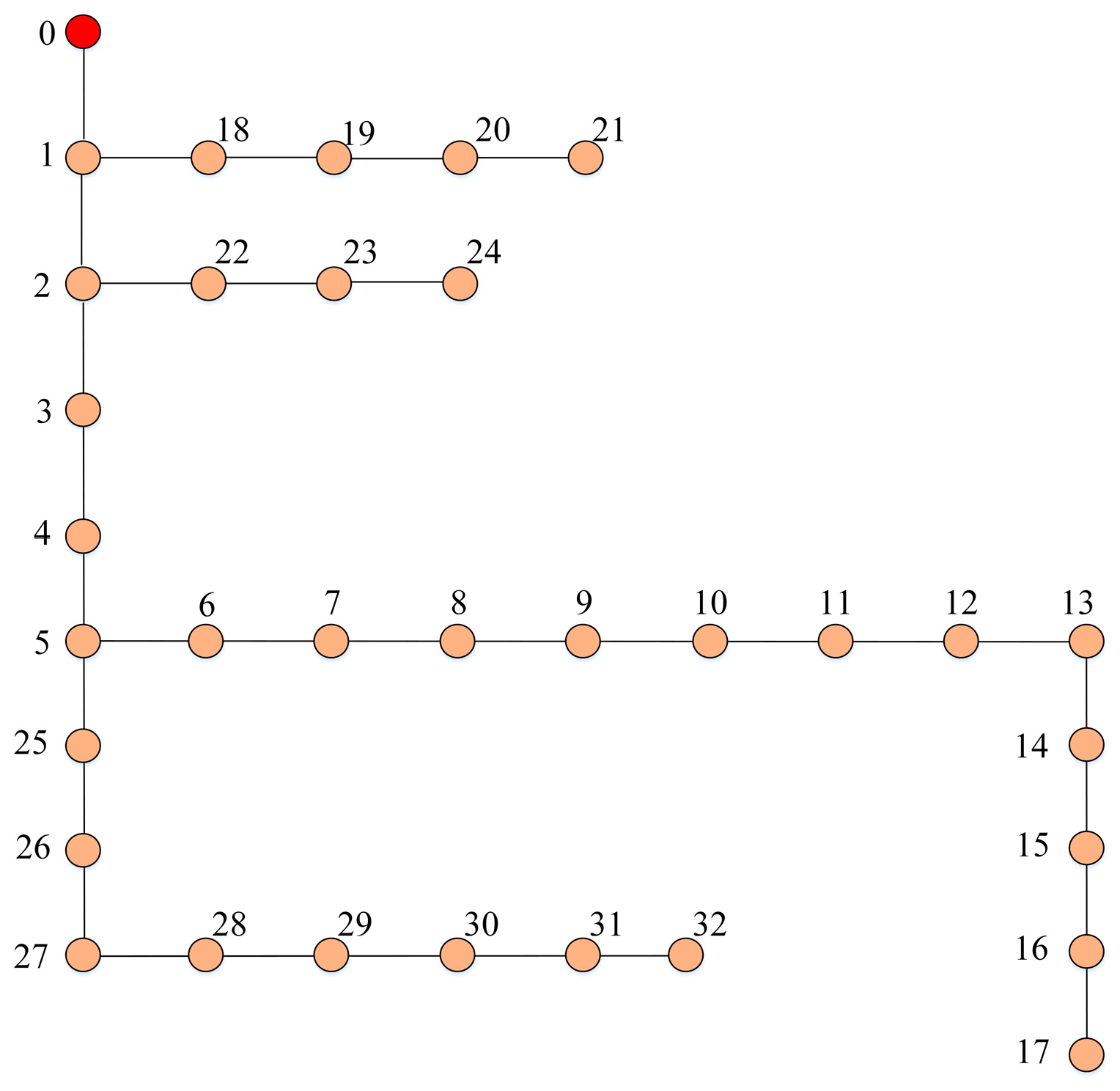
5.3. IEEE-33 System Test Results
5.3.1. Candidate Topology Identification Results
5.3.2. Parameter Estimation Results
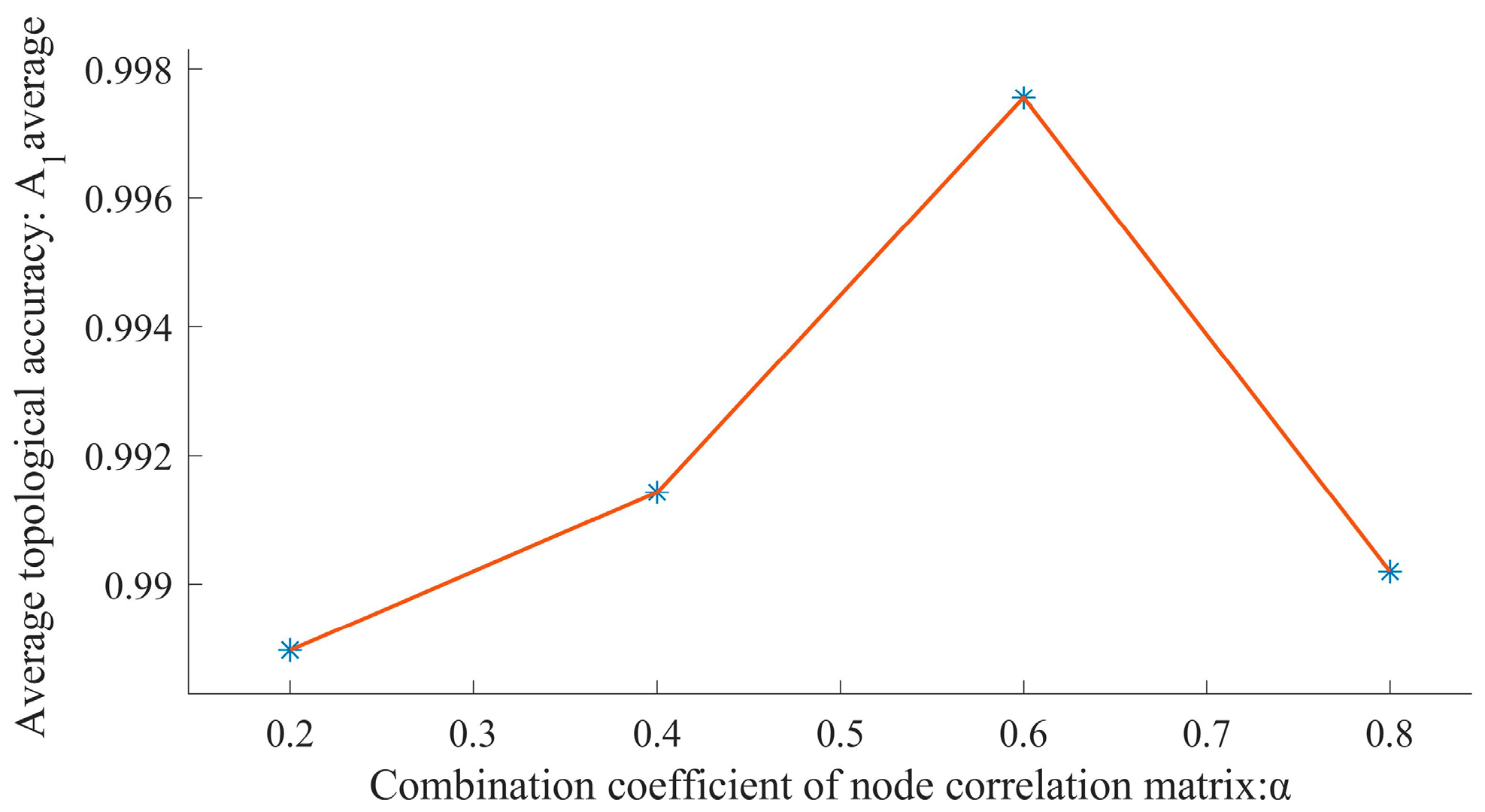
5.3.3. Impact Analysis of Parameter
5.4. Improved IEEE-69 System Test Results
5.4.1. Analysis of Topology Identification Results
5.4.2. Analysis of Parameter Estimation Results
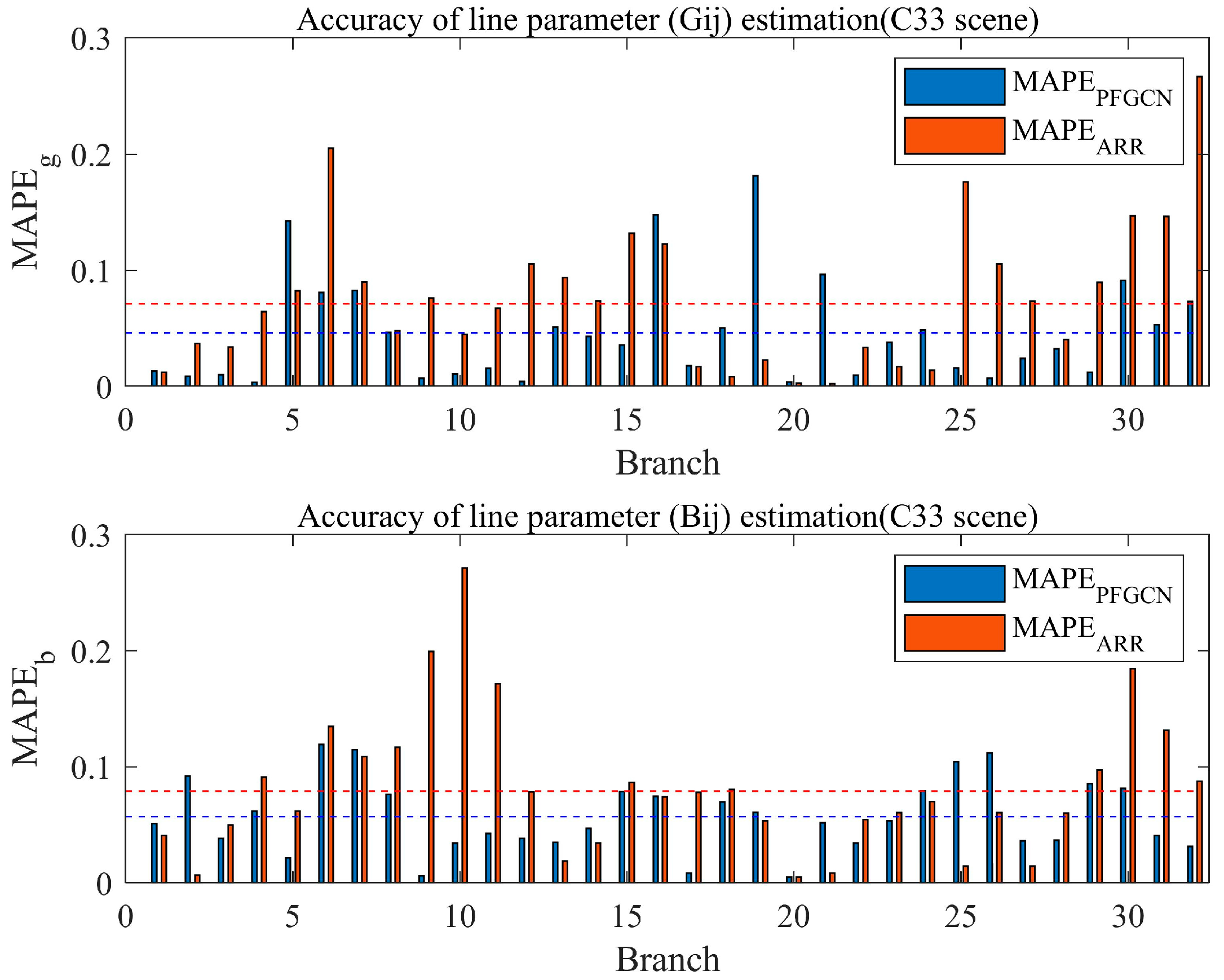
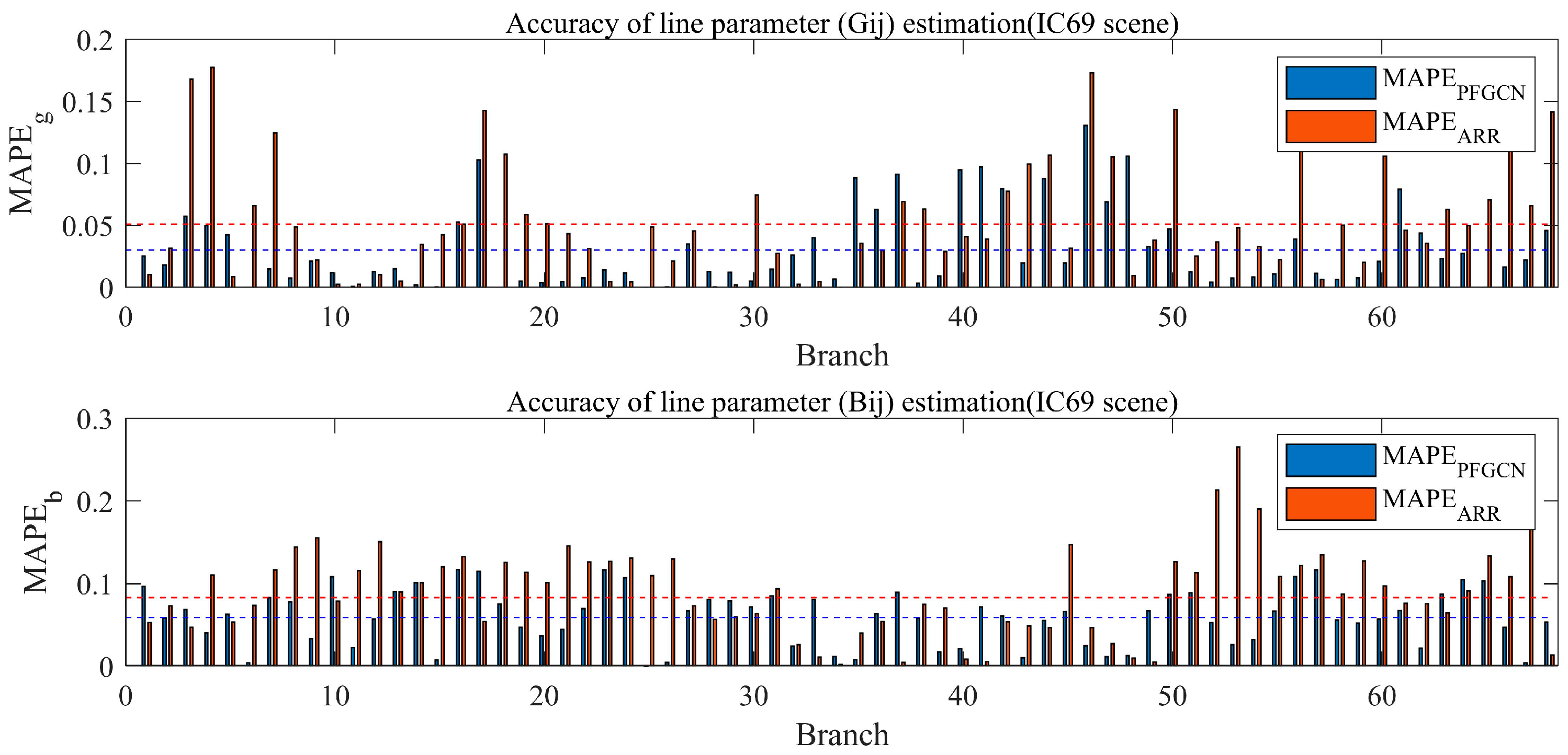
5.5. Algorithm Comparison
5.6. Error Sensitivity Analysis
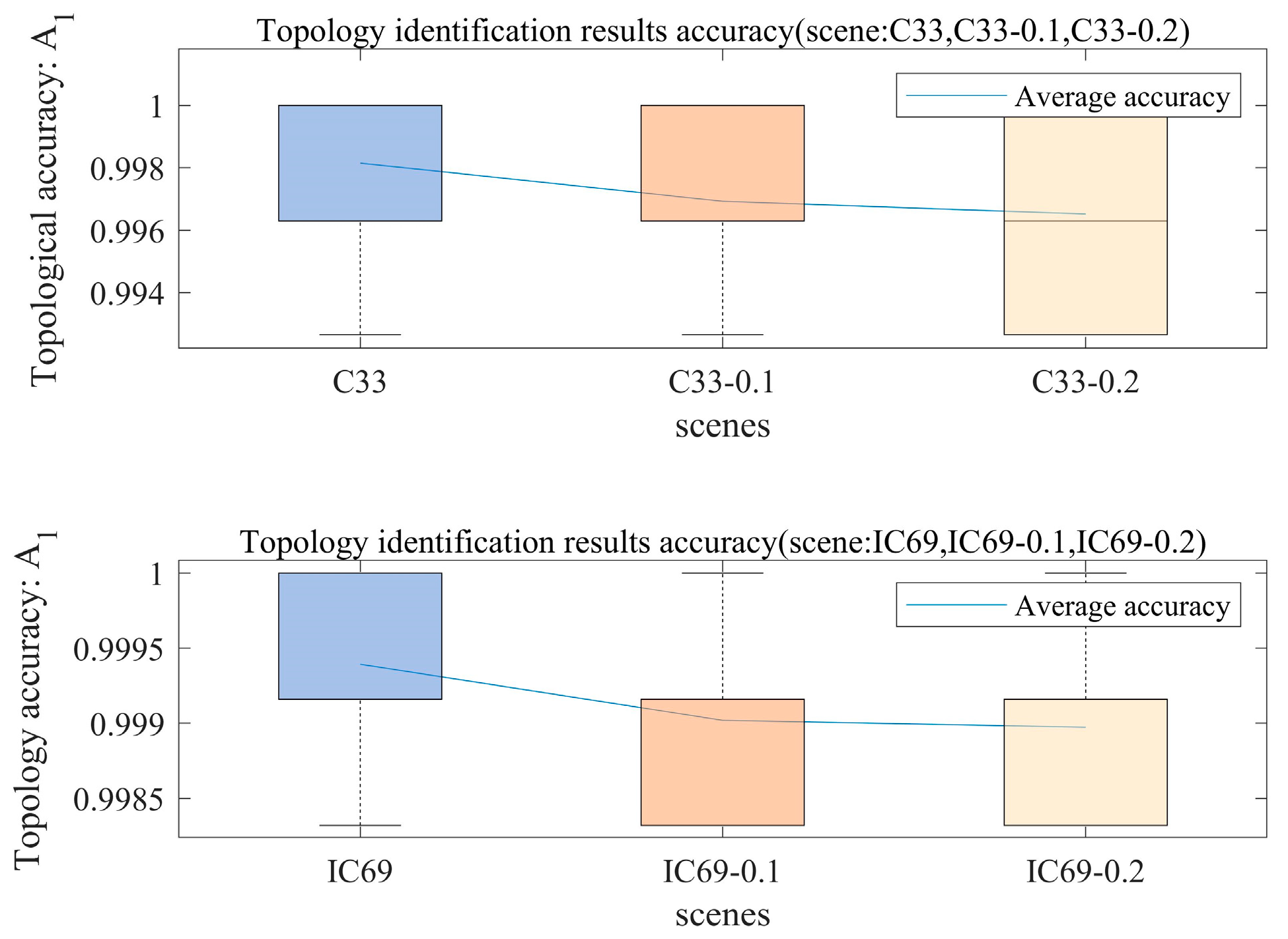
- C33_0.1: IEEE-33 system, 600 measurements, random error = 0.1%;
- C33_0.2: IEEE-33 system, 600 measurements, random error = 0.2%;
- IC69_0.1: Improved IEEE-69 system, 600 measurements, random error = 0.1%.
- IC69_0.2: Improved IEEE-69 system, 600 measurements, random error = 0.2%.
5.6.1. Error Sensitivity Analysis of Topology Identification Methods
5.6.2. Error Sensitivity Analysis of Parameter Estimation Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Zhao, Y.; Zhou, Y. A Data-Driven Topology and Parameter Joint Estimation Method in Non-PMU Distribution Networks. IEEE Trans. Power Syst. 2024, 39, 1681–1692. [Google Scholar] [CrossRef]
- Park, S.; Deka, D.; Chertkov, M. Exact Topology and Parameter Estimation in Distribution Grids with Minimal Observability. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018. [Google Scholar]
- Dehghanpour, K.; Wang, Z.; Wang, J.; Yuan, Y.; Bu, F. A Survey on State Estimation Techniques and Challenges in Smart Distribution Systems. IEEE Trans. Smart Grid 2019, 10, 2312–2322. [Google Scholar] [CrossRef]
- Dong, X.; Kang, C.; Sun, H.; Zhang, N. Analysis of Power Transfer Limit Considering Thermal Balance of Overhead Conductor. IET Gener. Transm. Distrib. 2015, 9, 2007–2013. [Google Scholar] [CrossRef]
- Cavraro, G.; Arghandeh, R. Power Distribution Network Topology Detection with Time-Series Signature Verification Method. IEEE Trans. Power Syst. 2018, 33, 3500–3509. [Google Scholar] [CrossRef]
- Pappu, S.J.; Bhatt, N.; Pasumarthy, R.; Rajeswaran, A. Identifying Topology of Low Voltage Distribution Networks Based on Smart Meter Data. IEEE Trans. Smart Grid 2018, 9, 5113–5122. [Google Scholar] [CrossRef]
- Deka, D.; Backhaus, S.; Chertkov, M. Structure Learning in Power Distribution Networks. IEEE Trans. Control Netw. Syst. 2017, 5, 1061–1074. [Google Scholar] [CrossRef]
- Zhao, J.; Li, L.; Xu, Z.; Wang, X. Full-Scale Distribution System Topology Identification Using Markov Random Field. IEEE Trans. Smart Grid 2020, 11, 4714–4726. [Google Scholar] [CrossRef]
- Ma, L.; Wang, L. Topology Identification of Distribution Networks Using a Split-EM Based Data-Driven Approach. IEEE Trans. Power Syst. 2021, 37, 2019–2031. [Google Scholar] [CrossRef]
- Pegoraro, P.A.; Brady, K.; Muscas, C. Line Impedance Estimation Based on Synchrophasor Measurements for Power Distribution Systems. IEEE Trans. Instrum. Meas. 2018, 68, 1002–1013. [Google Scholar] [CrossRef]
- Dutta, R.; Patel, V.S.; Chakrabarti, S.; Sharma, A. Parameter Estimation of Distribution Lines Using SCADA Measurements. IEEE Trans. Instrum. Meas. 2020, 70, 1–11. [Google Scholar] [CrossRef]
- Lave, M.; Reno, M.J.; Peppanen, J. Distribution System Parameter and Topology Estimation Applied to Resolve Low-Voltage Circuits on Three Real Distribution Feeders. IEEE Trans. Sustain. Energy 2019, 10, 1585–1592. [Google Scholar] [CrossRef]
- Srinivas, V.L.; Wu, J. Topology and Parameter Identification of Distribution Network Using Smart Meter and μPMU Measurements. IEEE Trans. Instrum. Meas. 2022, 71, 1–14. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Weng, Y.; Zhang, N. Topology Identification and Line Parameter Estimation for Non-PMU Distribution Network: A Numerical Method. IEEE Trans. Smart Grid 2020, 11, 4440–4453. [Google Scholar] [CrossRef]
- Wang, C.; Lou, Z.; Li, M.; Zhu, C.; Jing, D. Identification of Distribution Network Topology and Line Parameter Based on Smart Meter Measurements. Energies 2024, 17, 830. [Google Scholar] [CrossRef]
- Ni, J.; Tang, Z.; Liu, J.; Zeng, P.; Baldorj, C. A Topology Identification Method Based on One-Dimensional Convolutional Neural Network for Distribution Network. Energy Rep. 2023, 9, 355–362. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, J.; Liu, F.; Tang, J. Hybrid Data and Model-driven Joint Identification of Distribution-network Topology and Parameters. IET Gener. Trans. Distrib. 2022, 16, 4846–4866. [Google Scholar] [CrossRef]
- Sun, J.; Xia, M.; Chen, Q. A Classification Identification Method Based on Phasor Measurement for Distribution Line Parameter Identification Under Insufficient Measurements Conditions. IEEE Access 2019, 7, 158732–158743. [Google Scholar] [CrossRef]
- Wang, Z.; Xia, M.; Lu, M.; Pan, L.; Liu, J. Parameter Identification in Power Transmission Systems Based on Graph Convolution Network. IEEE Trans. Power Deliv. 2021, 37, 3155–3163. [Google Scholar] [CrossRef]
- Li, H.; Blasch, E. Distribution Grid Topology and Parameter Estimation Using Deep-Shallow Neural Network with Physical Consistency. IEEE Trans. Smart Grid 2023, 15, 655–666. [Google Scholar] [CrossRef]
- Wang, W.; Yu, N. Estimate Three-Phase Distribution Line Parameters with Physics-Informed Graphical Learning Method. IEEE Trans. Power Syst. 2022, 37, 3577–3591. [Google Scholar] [CrossRef]
- Liu, S.; Wu, C.; Zhu, H. Topology-Aware Graph Neural Networks for Learning Feasible and Adaptive AC-OPF Solutions. IEEE Trans. Power Syst. 2023, 38, 1–11. [Google Scholar] [CrossRef]
- Sinaga, K.P.; Hussain, I.; Yang, M.-S. Entropy K-Means Clustering with Feature Reduction Under Unknown Number of Clusters. IEEE Access 2021, 9, 67736–67751. [Google Scholar] [CrossRef]
- Luczak, M. Hierarchical Clustering of Time Series Data with Parametric Derivative Dynamic Time Warping. Expert Syst. Appl. 2016, 62, 116–130. [Google Scholar] [CrossRef]
- Liang, H.; Ma, J. Develop Load Shape Dictionary Through Efficient Clustering Based on Elastic Dissimilarity Measure. IEEE Trans. Smart Grid 2021, 12, 442–452. [Google Scholar] [CrossRef]
- Niepert, M.; Ahmed, M.; Kutzkov, K. Learning Convolutional Neural Networks for Graphs. arXiv 2016, arXiv:1605.05273. [Google Scholar] [CrossRef]
- Trabelsi, C.; Bilaniuk, O.; Zhang, Y.; Serdyuk, D.; Subramanian, S.; Santos, J.F.; Mehri, S.; Rostamzadeh, N.; Bengio, Y.; Pal, C.J. Deep Complex Networks. arXiv 2017, arXiv:1705.09792. [Google Scholar]

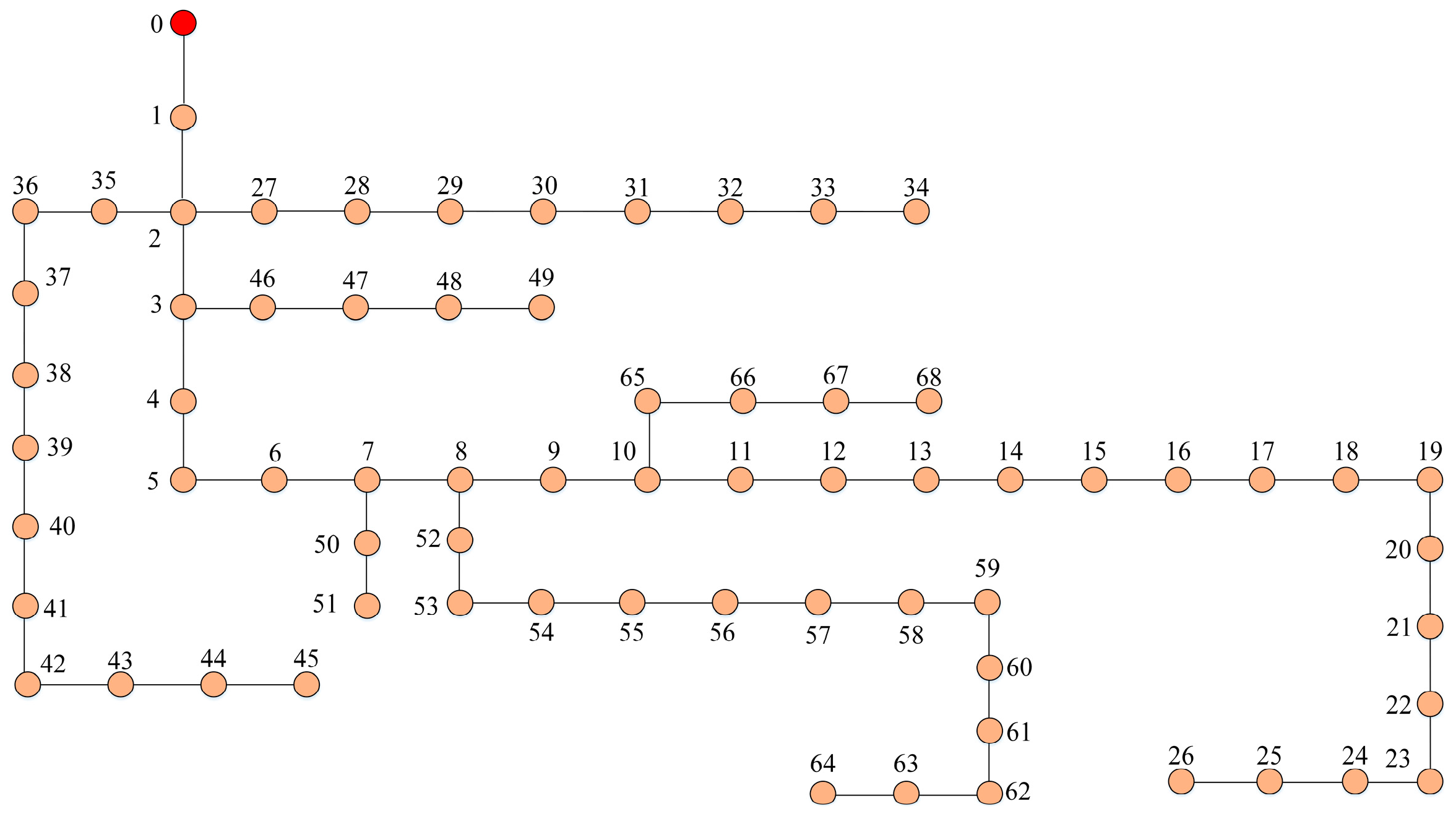

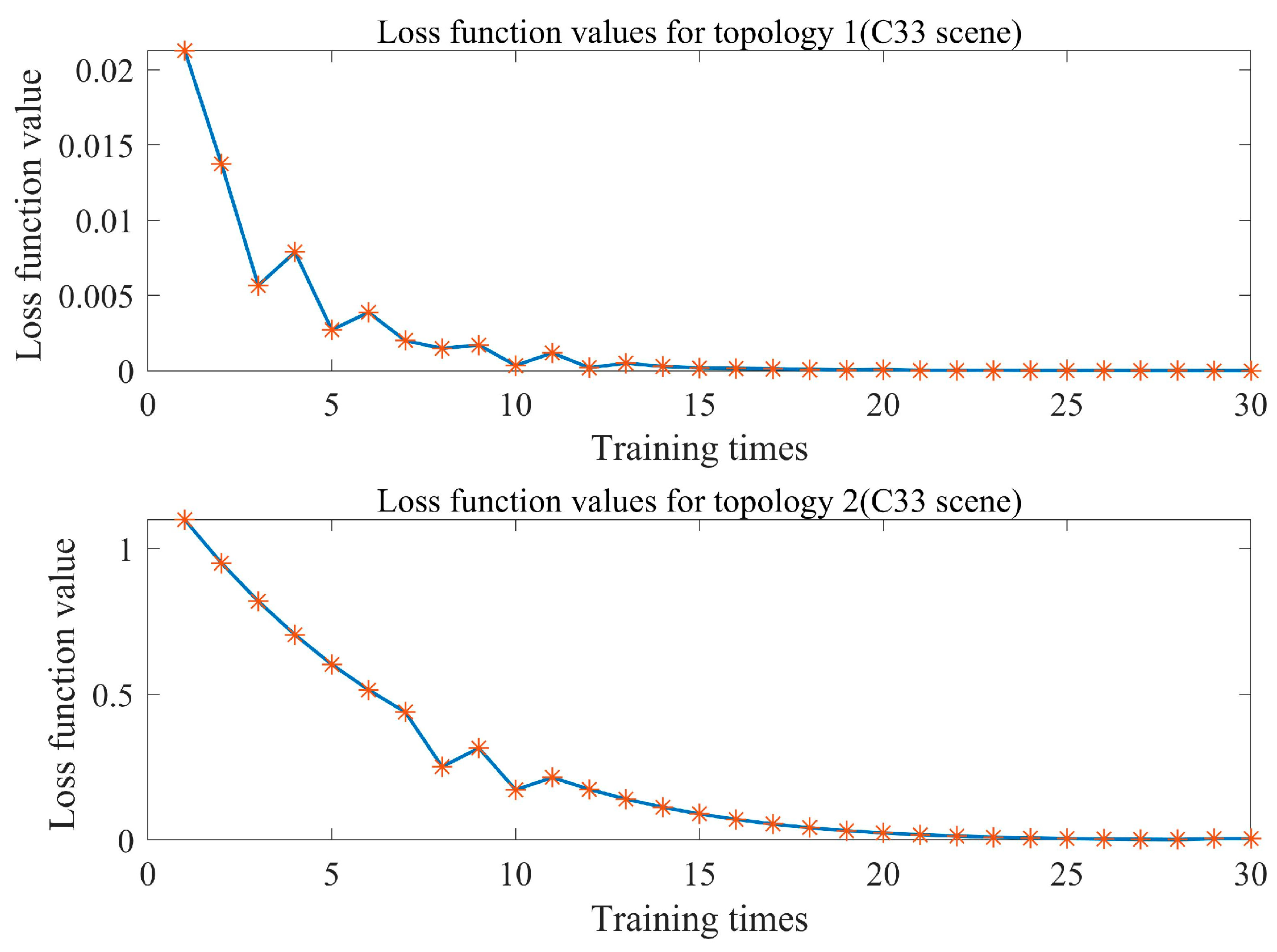
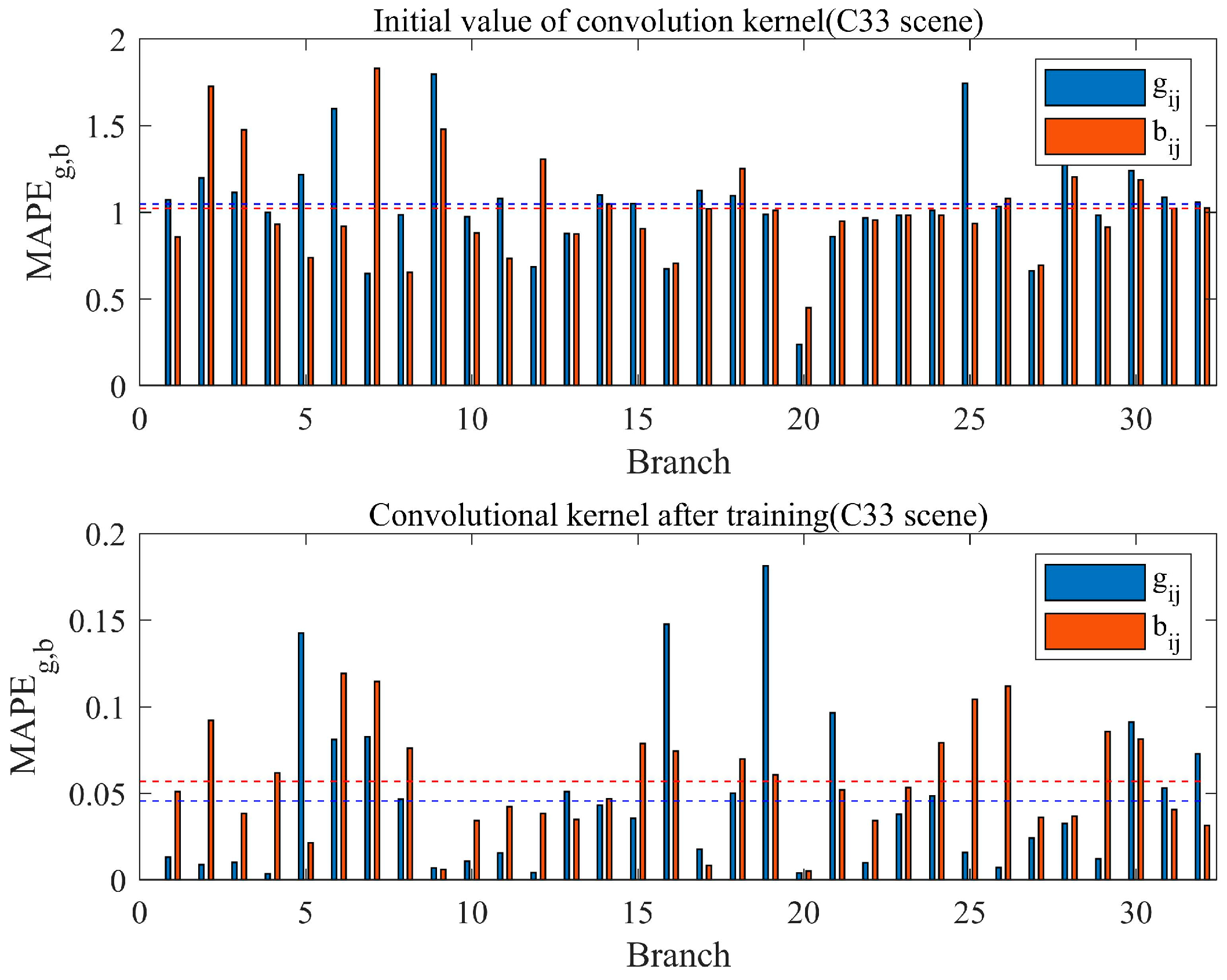
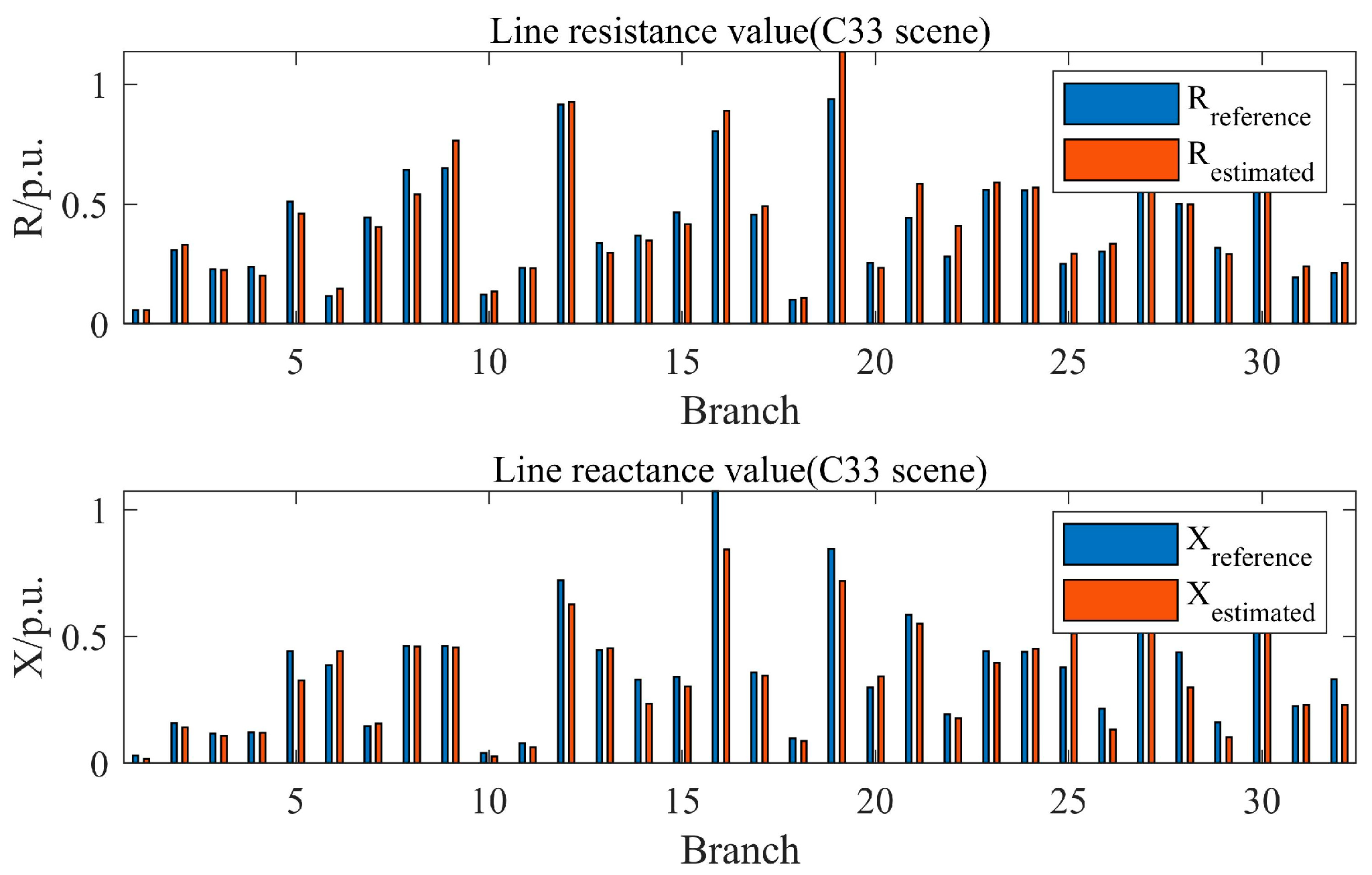

| Group | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.9963 | 1 | 0.9963 |
| Group | Topology 1 | Topology 2 |
|---|---|---|
| 1 | 0.9963 | |
| 1.03 × 10−5 | 4.47 × 10−3 |
| Group | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.9992 | 1 | 0.9983 | 0.9992 |
| Scene | CV-GCN | ARR | |
|---|---|---|---|
| C33 | 0.046 | 0.071 | |
| 0.057 | 0.079 | ||
| 2.605 | 5.053 | ||
| 3.748 | 5.223 | ||
| 0.081 | 0.158 | ||
| 0.117 | 0.163 | ||
| 0.999 | 0.998 | ||
| 0.996 | 0.992 | ||
| IC69 | 0.030 | 0.051 | |
| 0.059 | 0.083 | ||
| 15.892 | 37.296 | ||
| 21.616 | 30.204 | ||
| 0.234 | 0.548 | ||
| 0.318 | 0.444 | ||
| 0.999 | 0.991 | ||
| 0.997 | 0.993 |
| Scene | C33 | C33_0.1 | C33_0.2 | IC69 | IC69_0.1 | IC69_0.2 |
|---|---|---|---|---|---|---|
| 0.046 | 0.061 | 0.059 | 0.030 | 0.063 | 0.076 | |
| 0.057 | 0.075 | 0.088 | 0.059 | 0.084 | 0.091 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Shen, X.; Tang, X.; Liu, J. A Joint Estimation Method of Distribution Network Topology and Line Parameters Based on Power Flow Graph Convolutional Networks. Energies 2024, 17, 5272. https://doi.org/10.3390/en17215272
Wang Y, Shen X, Tang X, Liu J. A Joint Estimation Method of Distribution Network Topology and Line Parameters Based on Power Flow Graph Convolutional Networks. Energies. 2024; 17(21):5272. https://doi.org/10.3390/en17215272
Chicago/Turabian StyleWang, Yu, Xiaodong Shen, Xisheng Tang, and Junyong Liu. 2024. "A Joint Estimation Method of Distribution Network Topology and Line Parameters Based on Power Flow Graph Convolutional Networks" Energies 17, no. 21: 5272. https://doi.org/10.3390/en17215272
APA StyleWang, Y., Shen, X., Tang, X., & Liu, J. (2024). A Joint Estimation Method of Distribution Network Topology and Line Parameters Based on Power Flow Graph Convolutional Networks. Energies, 17(21), 5272. https://doi.org/10.3390/en17215272






