Optimal Dispatching Strategy for Textile-Based Virtual Power Plants Participating in GridLoad Interactions Driven by Energy Price
Abstract
1. Introduction
- This paper first establishes a bi-level dispatching strategy for VPP targeting textile industrial parks to specially address the coupling characteristics of electricity and steam.
- Considering the impact on the user behavior brought by the energy prices, this strategy is modeled as where VPPO aims to maximize its own revenue in the upper level, while multiple textile industry users aim to minimize total operational costs in the lower level, finally resulting in an economic increase of the overall system.
- Considering that the textile industry users utilize electrically-driven industrial steam boilers under decarbonization, the storage-like characteristics of the steam accumulator (SA) is specially addressed.
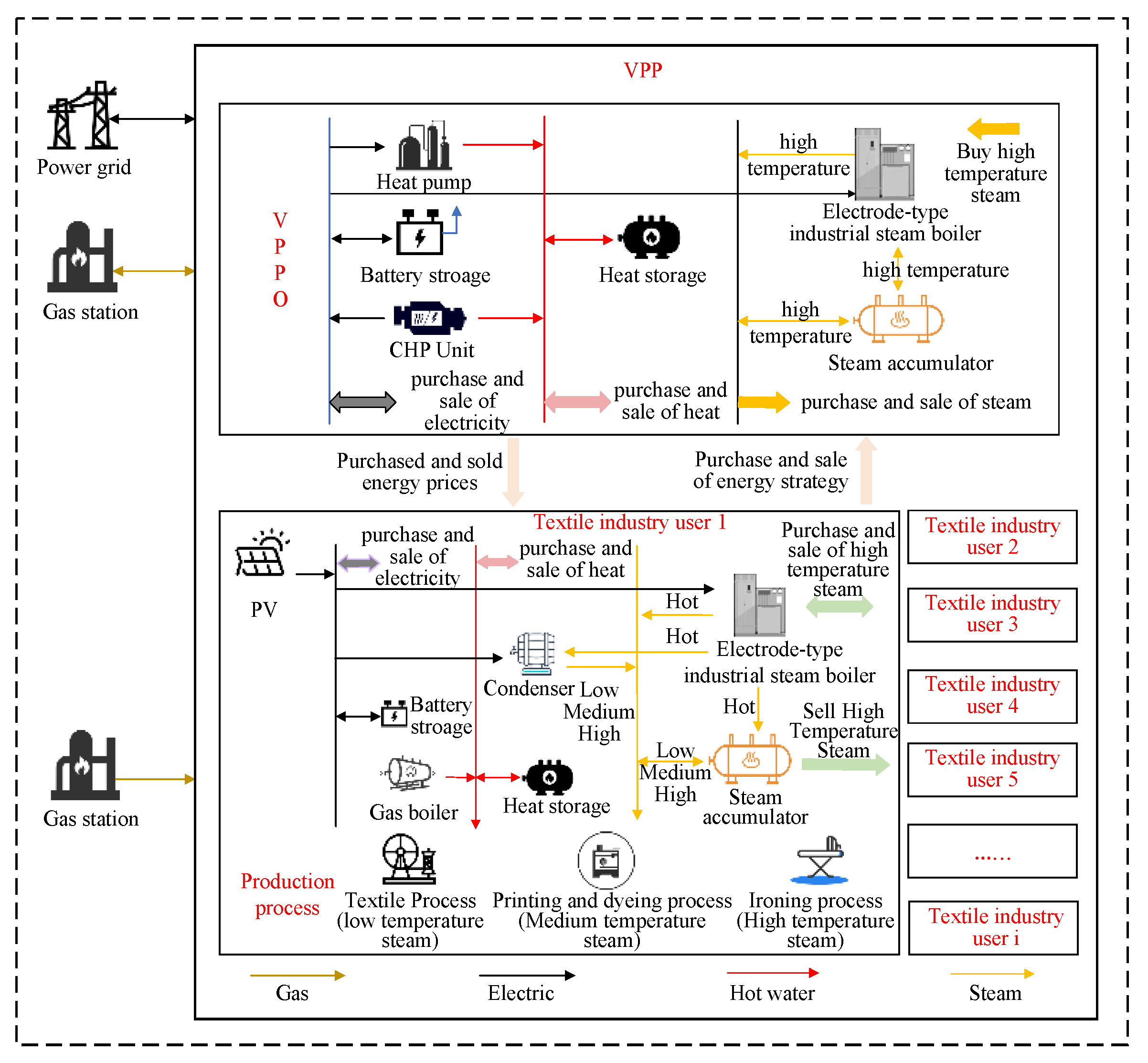
2. Bi-Level Dispatching Framework for VPP
3. The Bi-Level Optimal Dispatching Model for VPPO and Users
3.1. The VPPO-Level Optimal Dispatching Model
3.1.1. VPPO-Level Objective Function
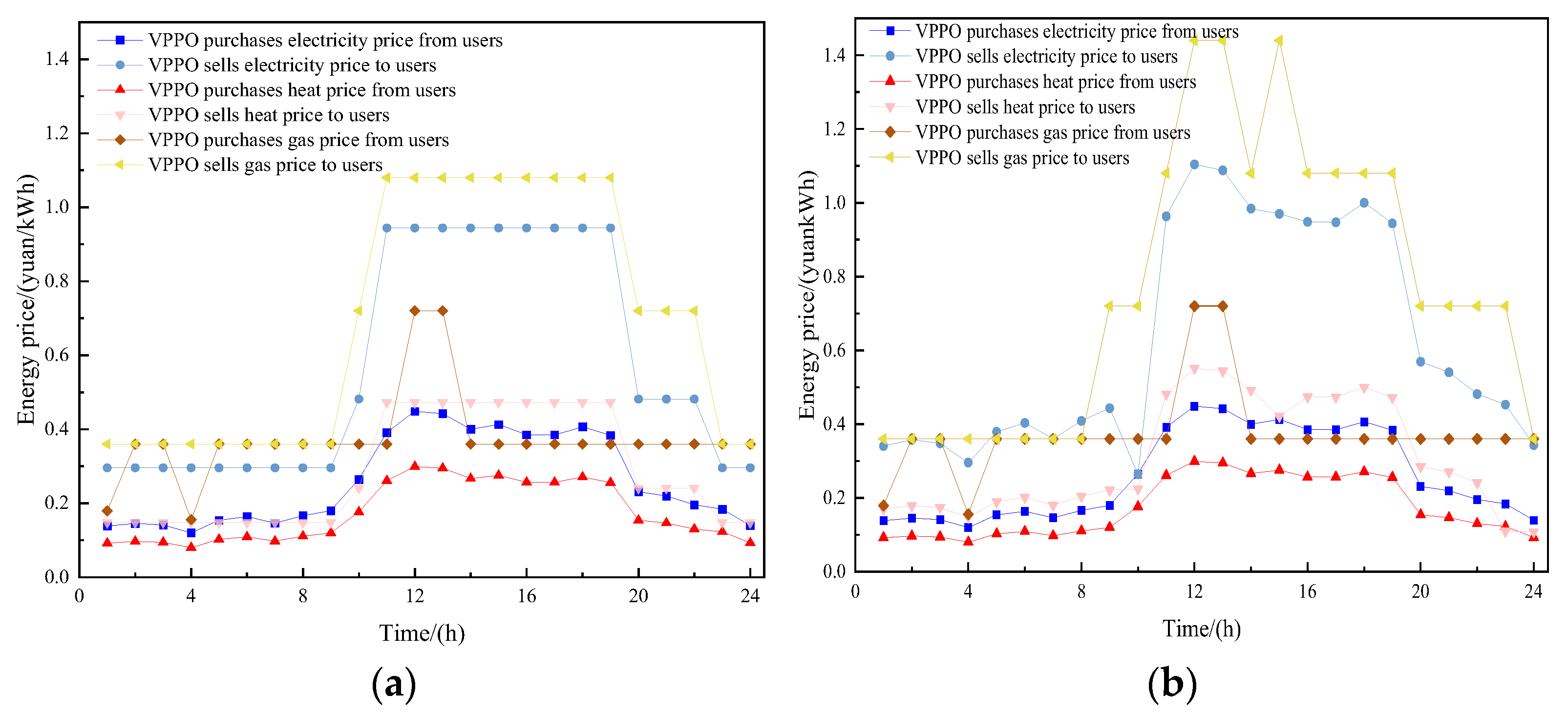
3.1.2. Energy Price Constraint
3.1.3. VPPO’s Constraints on Multi-Energy Transaction Volumes with Users
3.1.4. VPPO-Level Power Balance Constraint
3.2. User-Level Optimal Dispatching Model
3.2.1. User-Level Objective Function
3.2.2. Constraints on Purchasing and Selling Electricity, Heat, and Steam Power
3.2.3. User-Level Power Balance Constraint
3.3. Solution Process
4. Constraints on the Operation of Various Types of Equipment
4.1. Modeling of Multi-Energy Coupling Devices by VPPO
4.1.1. Electrode Industrial Steam Boilers
4.1.2. Steam Accumulator
4.2. Multi-Energy Coupling Equipment Model for Textile Industry Users
4.2.1. Electrode Industrial Steam Boiler for Users
4.2.2. User’s Condenser
4.2.3. User’s Steam Accumulator
5. Result Analysis
5.1. Basic Data
5.2. Strategy Results Analysis
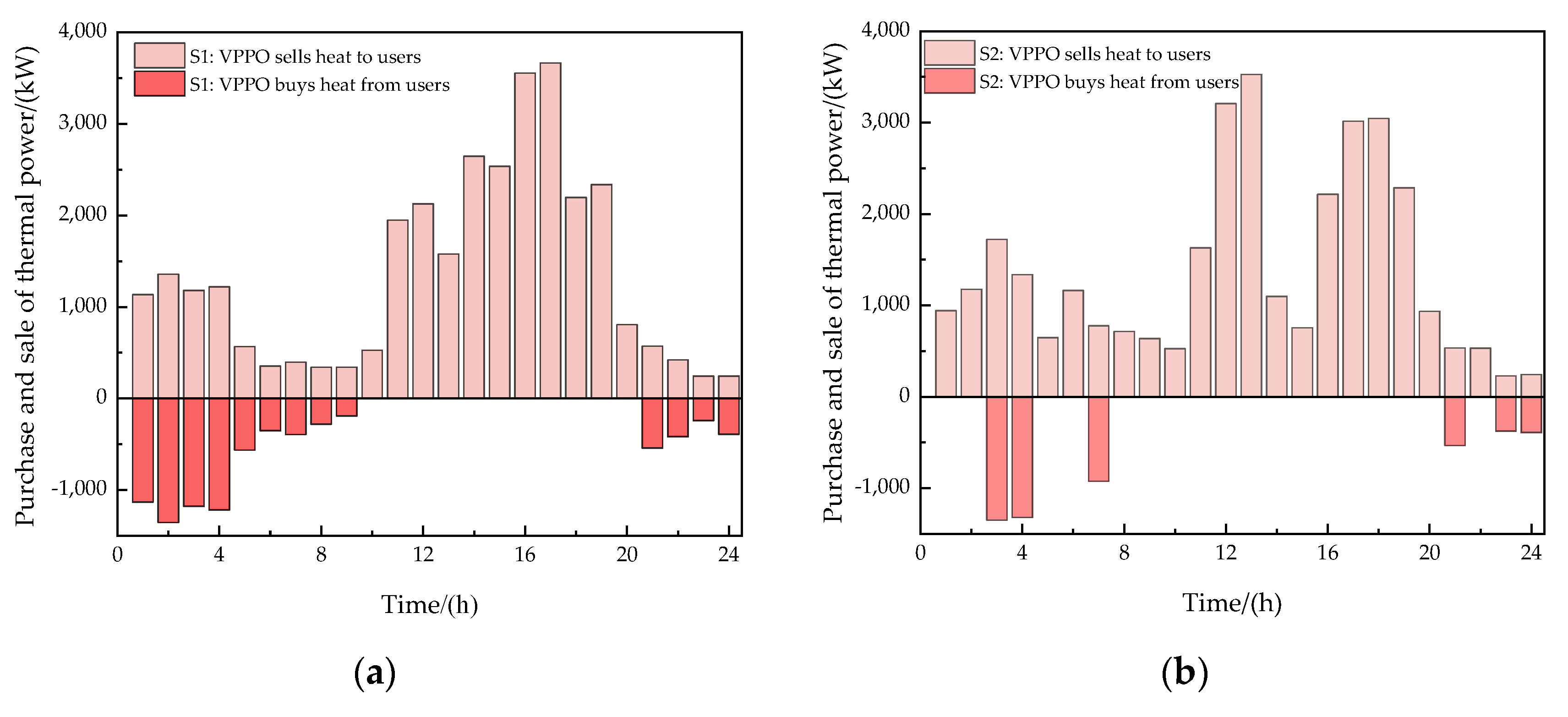
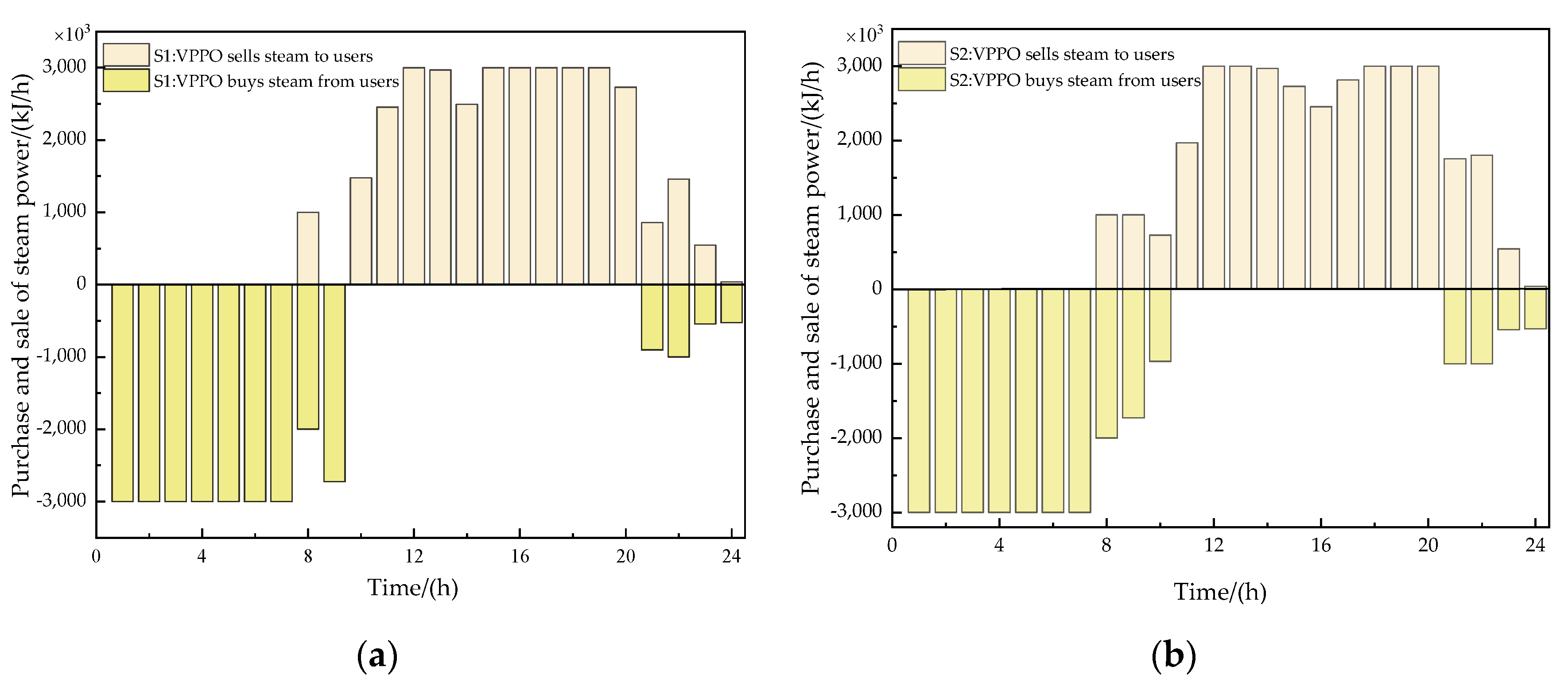
5.3. Analysis of Energy Trading Outcomes
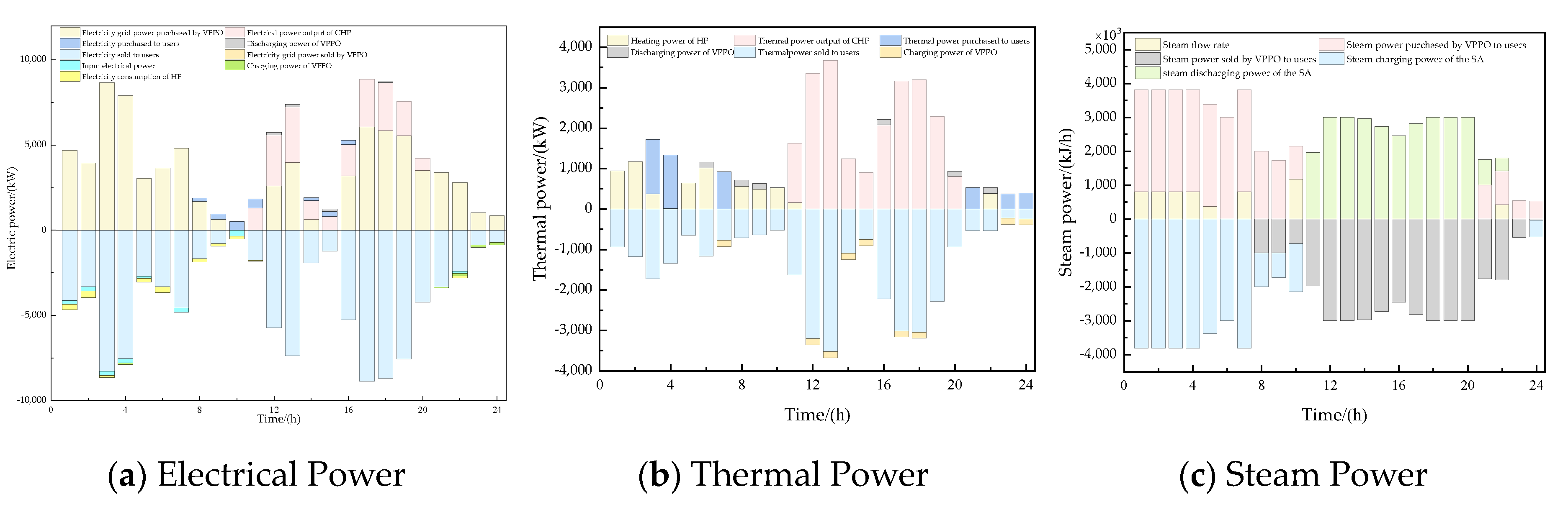
5.4. Analysis of Optimal Dispatching Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, C.; Guan, Y. Cluster Convergence: Pioneering the Future -Symposium on Advancing the Modernization of Textile Industry Clusters. Text. Appar. Wkly. 2024, 10, 21. [Google Scholar]
- Liu, J.; Peng, J.; Deng, J.; Liu, S. Two-stage Robust Optimization-based Economic Dispatch of Virtual Power Plants Considering Cogeneration. J. Syst. Simul. 2023, 35, 1799–1813. [Google Scholar]
- Bhuiyan, E.A.; Hossain, M.Z.; Muyeen, S.M. Towards Next Generation Virtual Power Plant: Technology Review and Frameworks. Renew. Sustain. Energy Rev. 2021, 150, 111358. [Google Scholar] [CrossRef]
- Gao, C. Conceptual reflection on virtual power plants. Distrib. Util. 2023, 40, 2–6. [Google Scholar]
- Xie, B.; Zhang, L.; Hao, P. Real-time Pricing Demand Response Mechanism of Virtual Power Plant Based on Stackelberg Game. Chin. J. Manag. Sci. 2024, 1–18. [Google Scholar] [CrossRef]
- Tao, W.; Ai, Q.; Li, X. Research Status and Prospects of Collaborative Dispatching and Market Trading of Virtual Power Plants. South Power Syst. Technol. 2024, 1–15. Available online: http://kns.cnki.net/kcms/detail/44.1643.tk.20240318.1018.008.html (accessed on 27 September 2024).
- Hao, J.; Huang, T.; Xu, Q.; Sun, Y. Virtual power plant multi-objective optimal dispatching strategy with multiple energy suppliers. Distrib. Util. 2023, 40, 32–42. [Google Scholar]
- Li, B.; Gu, C.; Du, J.; Tian, K.; Chen, S. Virtual power plant resource dispatching optimization strategy considering electrothermal conversion. Distrib. Util. 2023, 40, 16–21. [Google Scholar]
- Yu, H.; Lu, W.; Tang, L.; Zhang, Y.; Zou, X. Economic dispatch and profit distribution strategy for multi-agent virtual power plants considering risk preference. Integr. Intell. Energy 2024, 46, 66–77. [Google Scholar]
- Liao, S.; He, C.; Li, L.; Xu, J.; Sun, Y. Solution Method of Regulatory Boundary for Industrial Park Type Virtual Power Plant Considering Power Network Constraints. Autom. Electr. Power Syst. 2024, 48, 66–75. [Google Scholar]
- Wang, J.; Shen, X.; Xu, Y. Ancillary service for frequency regulation based on multi-energy virtual power plant aggregating factory load. In Proceedings of the 11th IET International Conference on Advances in Power System Control, Operation and Management (APSCOM 2018), Hong Kong, China, 11–15 November 2018. [Google Scholar]
- Yu, S.; Zhang, J.; Yuan, Z.; Fang, F. Resilience Enhancement Strategy of Combined Heat and Power-Virtual Power Plant Considering Thermal Inertia. Power Gener. Technol. 2023, 44, 758–768. [Google Scholar]
- Jiang, Z.; Zhang, F.; Hu, F.; Sun, Y.; Jiang, W. Evaluation method of aggregated responsiveness of distributed resources in virtual power plant. Electr. Power Eng. Technol. 2022, 41, 39–49. [Google Scholar]
- Zhang, N.; Zhu, H.; Yang, L.; Hu, C. Optimal Dispatching Strategy of Multi-Energy Complementary Virtual Power Plant Considering Renewable Energy Consumption. Power Gener. Technol. 2023, 44, 625–633. [Google Scholar]
- Wang, J.; Niu, Y.; Chen, Y.; Du, M. Master-slave game optimal dispatching of virtual power plant. Electr. Power Autom. Equip. 2023, 43, 235–242. [Google Scholar]
- Li, Q.; Zhu, D.; Huang, D.; Wu, S.; Yang, Y. Stackelberg game pricing strategy between virtual power plant operators and electric vehicle users. Electr. Power Eng. Technol. 2022, 41, 183–191. [Google Scholar]
- Cang, H.; Liu, H. Economic research on virtual power plant source-load coordination based on electricity price linkage. Mod. Electron. Tech. 2022, 45, 149–155. [Google Scholar]
- Qiang, L.; Jiale, T.; Ke, Z. Pricing Strategy for a Virtual Power Plant Operator with Electric Vehicle Users Based on the Stackelberg Game. World Electr. Veh. J. 2023, 14, 72. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, Y.C.; Wei, F.C. Multi-time scale dispatching for virtual power plants: Integrating the flexibility of power generation and multi-user loads while considering the capacity. Appl. Energy 2024, 362, 122980. [Google Scholar] [CrossRef]
- Zhang, Y. On Low-Carbon Optimization Operation of Integrated Energy Systems Considering Hydrogen Energy Coupling and Master-Slave. Master’s Thesis, Nanchang University, Nanchang, China, 2023. [Google Scholar]
- Ehsan, H.-F.; Saeed, H.; Seifeddine, B.-E. Virtual Power Plant Operational Strategies: Models, Markets, Optimization, Challenges, and Opportunities. Sustainability 2022, 14, 12486. [Google Scholar] [CrossRef]
- Hua, Y.; Wang, Y.; Bai, H.; Han, D.; Pu, F. Interval master-slave game optimal dispatching of virtual power plant with electric vehicle. Therm. Power Gener. 2022, 51, 163–170. [Google Scholar]
- Tang, F. Optimal Dispatching of Combined Heat and Power of Virtual Power Plant Based on Hybrid Energy Storage. Master’s Thesis, North China Electric Power University, Beijing, China, 2021. [Google Scholar]
- Liang, A.; Zeng, S.; Ren, J.; Zhang, X.; Cao, F. Intelligent Operation Dynamic Characteristics of Heat Pump System in Integrated Electric-thermal Cooperative Grid Based on Game Optimization Algorithm. J. Refrig. 2024, 45, 109–111. [Google Scholar]
- Sun, W.; Wu, J.; Zhang, Q. Coordinated optimization of a distribution network and multi-integrated energy microgrid based on a double-layer game. Power Syst. Prot. Control 2024, 52, 26–38. [Google Scholar]
- Maddah, H.; Sadeghzadeh, M.; Ahmadi, M.H.; Kumar, R.; Shamshirband, S. Modeling and Efficiency Optimization of Steam Boilers by Employing Neural Networks and Response-Surface Method (RSM). Mathematics 2019, 7, 629. [Google Scholar] [CrossRef]
- Bai, Z.; Miao, C.; Wang, W.; Sun, F.; Zhang, P. The Value of Thermal Storage Technology in Integrated Energy System. Distrib. Util. 2019, 36, 20–26. [Google Scholar]






| Time Interval | Time Range |
|---|---|
| Peak period | 11:00~19:00 |
| off-peak period | 10:00, 20:00~22:00 |
| valley period | 1:00~9:00, 23:00~24:00 |
| Scenario | VPPO Earnings/(yuan) | Total Operating Costs for Textile Industry Users/(yuan) | Overall Economic Costs of the VPP/(yuan) |
|---|---|---|---|
| S1 | 5 471.167 1 | 88 800.828 7 | 83 329.661 6 |
| S2 | 10 258.255 5 | 90 145.685 1 | 79 887.429 6 |
| Scenario | Cost for User 1 | Cost for User 2 | Cost for User 3 |
|---|---|---|---|
| S1 | 22 075.684 1 | 30 818.277 9 | 35 906.866 7 |
| S2 | 22 218.254 9 | 31 329.119 6 | 36 598.310 5 |
| cost volatility | −0.646% | −1.658% | −1.926% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, T.; Liu, C.; Xu, Y.; Ding, M.; Li, M.; Yang, H.; Dou, X. Optimal Dispatching Strategy for Textile-Based Virtual Power Plants Participating in GridLoad Interactions Driven by Energy Price. Energies 2024, 17, 5142. https://doi.org/10.3390/en17205142
Chai T, Liu C, Xu Y, Ding M, Li M, Yang H, Dou X. Optimal Dispatching Strategy for Textile-Based Virtual Power Plants Participating in GridLoad Interactions Driven by Energy Price. Energies. 2024; 17(20):5142. https://doi.org/10.3390/en17205142
Chicago/Turabian StyleChai, Tingyi, Chang Liu, Yichuan Xu, Mengru Ding, Muyao Li, Hanyu Yang, and Xun Dou. 2024. "Optimal Dispatching Strategy for Textile-Based Virtual Power Plants Participating in GridLoad Interactions Driven by Energy Price" Energies 17, no. 20: 5142. https://doi.org/10.3390/en17205142
APA StyleChai, T., Liu, C., Xu, Y., Ding, M., Li, M., Yang, H., & Dou, X. (2024). Optimal Dispatching Strategy for Textile-Based Virtual Power Plants Participating in GridLoad Interactions Driven by Energy Price. Energies, 17(20), 5142. https://doi.org/10.3390/en17205142







