A Novel Point of Common Coupling Direct Power Control Method for Grid Integration of Renewable Energy Sources: Performance Evaluation among Power Quality Phenomena
Abstract
1. Introduction
- (1)
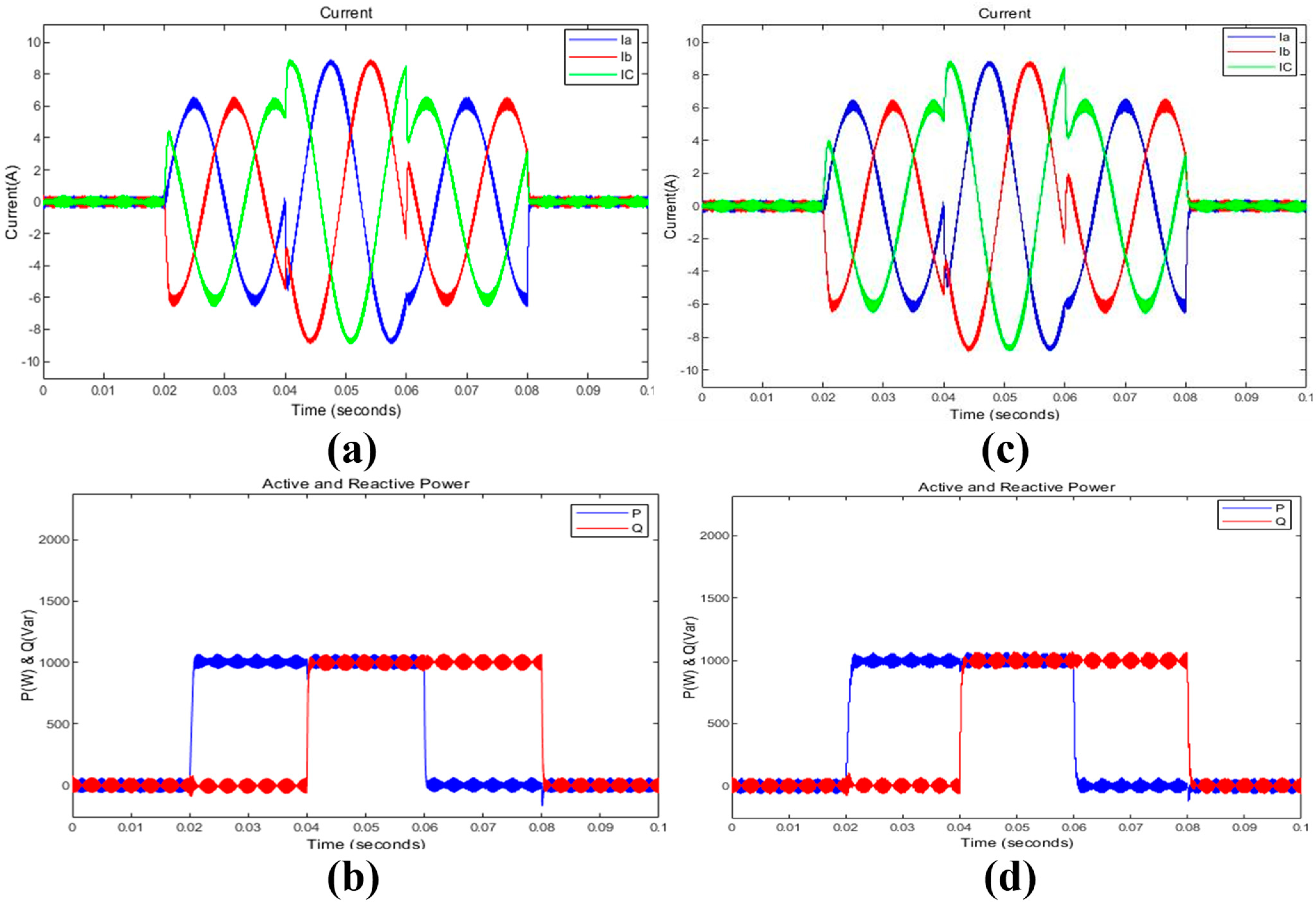
- They assess whether PCC-DPC will be efficient enough to keep track strictly over specified power references throughout a sudden disturbance on the network, ensuring uninterrupted supply even when there are transients.
- (2)
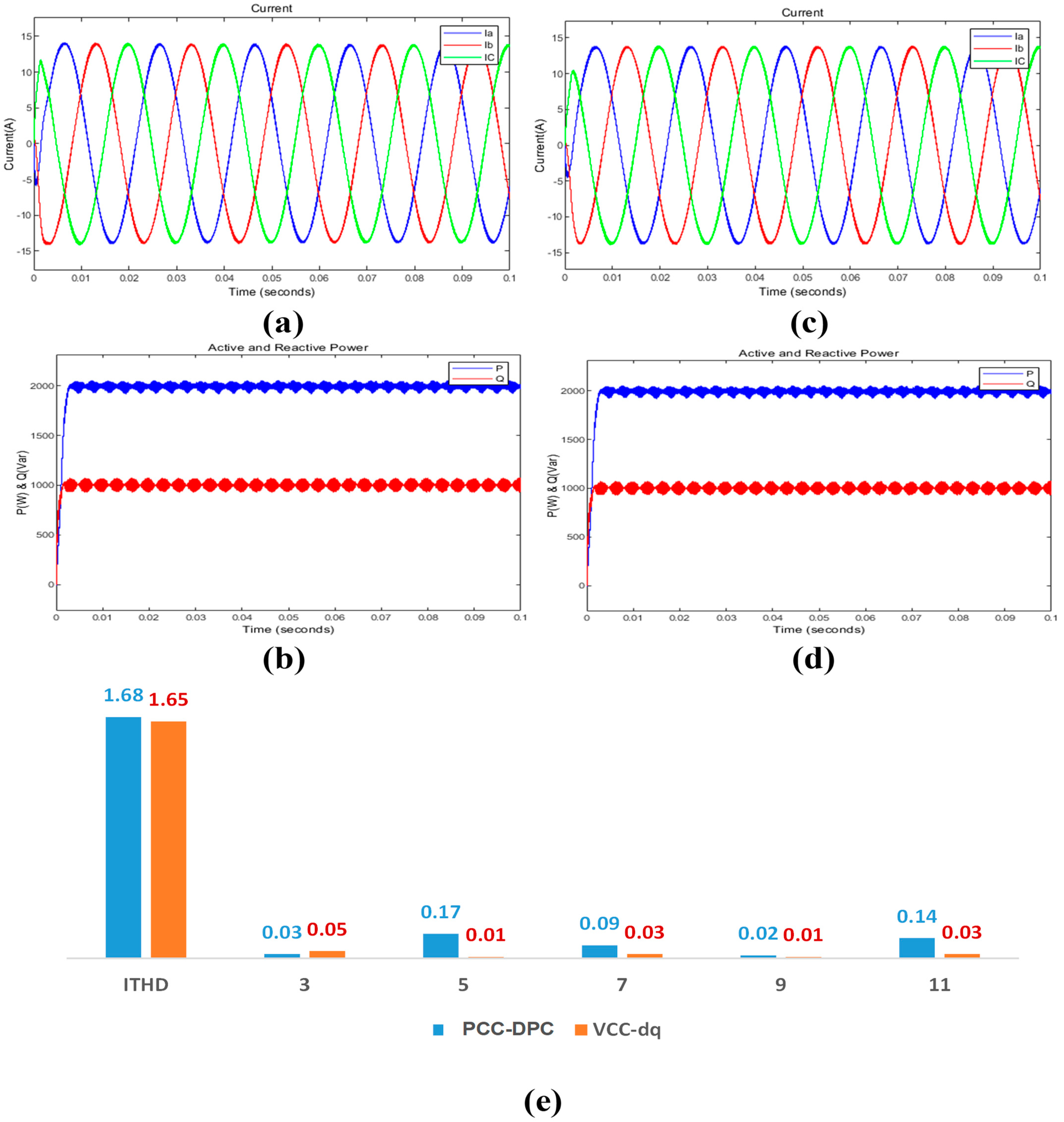
- They examine the Total Harmonic Distortion (THD) caused by PCC-DPC and a Vector Current Controller (VCC) during steady-state operation. It investigates how each of these control methods impact on power quality in terms of THD when there are no disturbances like voltage sags.
- (3)
- These cases evaluate LVRT/HVRT capabilities. The idea is to see whether PCC-DPC can still be operational even if there are certain conditions that may cause a fault on the grid.
- (4)
- This case study illustrates how PCC-DPC ensures uninterrupted supply and prevents minor changes in frequency resulting in grid disconnections.
- (5)
- These cases address power quality analysis for imbalanced grids. These simulations involve several scenarios where Vmin and Vmax perturbations occur in an individual phase. This investigation has been carried out to ensure that minimal detrimental effect would be observed on power quality as a result of deviation from the equilibrium.
2. Research Methodology
3. Results and Discussion
4. Discussion
- Enhanced tracking performance: accelerated reaction and potentially enhanced stability in comparison to VCC-dq.
- Minimized steady-state harmonics: it demonstrates excellent harmonic performance in accordance with grid standards (comparable to VCC-dq), while additional research is needed to address specific harmonics.
- Grid resilience: it ensures stable functioning and power control even in the presence of voltage drops and increases, and slight fluctuations in frequency.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| d-q | dq-frame (rotating reference frame) |
| DPC | Direct Power Control |
| f | Grid Voltage Frequency |
| GVM-DPC | Voltage Modulation Direct Power Control |
| LTI | Linear Time-Invariant |
| LUT | Look-up Table |
| MG | Microgrid |
| MIMO | Multi input Multi Output |
| MPC-DPC | Model Predictive Control Direct Power Control |
| PCC | Point of Common Coupling |
| PCC-DPC | Point of Common Coupling Modulation of Direct Power Control |
| —frame (saturation reference frame) | |
| PLL | Phase-locked loop |
| PWM | Pulse width modulation |
| PBC-DPC | Predictive Direct Power Control |
| SMC-DPC | Sliding Mode Direct Power Control |
| SVM | Space vector modulation |
| THD | Total harmonic distortion |
| VCC | Vector Current Controller |
| Vdc | DC source voltage |
| VSI | Voltage Source Inverter |
| VSC | Voltage Source Converter |
| ω | Grid Voltage Angular Frequency |
References
- Jia, J.; Yang, G.; Nielsen, A.H. A Review on Grid-Connected Converter Control for Short-Circuit Power Provision under Grid Unbalanced Faults. IEEE Trans. Power Deliv. 2018, 33, 649–661. [Google Scholar] [CrossRef]
- Wei, B.; Gui, Y.; Trujillo, S.; Guerrero, J.M.; Vasquez, J.C.; Marzabal, A. Distributed Average Integral Secondary Control for Modular UPS Systems-Based Microgrids. IEEE Trans. Power Electron. 2019, 34, 6922–6936. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Liserre, M.; Chen, Z.; He, J.; Li, Y. An active damper for stabilizing power electronics-based AC systems. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 1131–1138. [Google Scholar] [CrossRef]
- Kazmierkowski, M.; Malesani, L. Current control techniques for three-phase voltage-source PWM converters: A survey. IEEE Trans. Ind. Electron. 1998, 45, 691–703. [Google Scholar] [CrossRef]
- Reyes, M.; Rodriguez, P.; Vazquez, S.; Luna, A.; Teodorescu, R.; Carrasco, J.M. Enhanced decoupled double synchronous reference frame current controller for unbalanced grid-voltage conditions. IEEE Trans. Power Electron. 2012, 27, 3934–3943. [Google Scholar] [CrossRef]
- Diaz, N.L.; Luna, A.C.; Vasquez, J.C.; Guerrero, J.M. Centralized Control Architecture for Coordination of Distributed Renewable Generation and Energy Storage in Islanded AC Microgrids. IEEE Trans. Power Electron. 2017, 32, 5202–5213. [Google Scholar] [CrossRef]
- Mortezaei, A.; Simoes, M.; Savaghebi, M.; Guerrero, J.; Al-Durra, A. Cooperative control of multi-master-slave islanded microgrid with power quality enhancement based on conservative power theory. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar] [CrossRef]
- Arcos-Aviles, D.; Pascual, J.; Guinjoan, F.; Marroyo, L.; Sanchis, P.; Marietta, M.P. Low complexity energy management strategy for grid profile smoothing of a residential grid-connected microgrid using generation and demand forecasting. Appl. Energy 2017, 205, 69–84. [Google Scholar] [CrossRef]
- Mensou, S.; Essadki, A.; Nasser, T.; Idrissi, B.B. A direct power control of a DFIG based-WECS during symmetrical voltage dips. Prot. Control. Mod. Power Syst. 2020, 5, 5. [Google Scholar] [CrossRef]
- Boubzizi, S.; Abid, H.; El Hajjaji, A.; Chaabane, M. Comparative study of three types of controllers for DFIG in wind energy conversion system. Prot. Control. Mod. Power Syst. 2018, 3, 21. [Google Scholar] [CrossRef]
- Zhang, Y.; Qu, C. Direct power control of a pulse width modulation rectifier using space vector modulation under unbalanced grid voltages. IEEE Trans. Power Electron. 2015, 30, 5892–5901. [Google Scholar] [CrossRef]
- Noguchi, T.; Tomiki, H.; Kondo, S.; Takahashi, I. Direct power control of PWM converter without power-source voltage sensors. IEEE Trans. Ind. Appl. 1998, 34, 473–479. [Google Scholar] [CrossRef]
- Bouafia, J.G.; Krim, F. Predictive direct power control of three-phase pulse width modulation (PWM) rectifier using space-vector modulation (SVM). IEEE Trans. Power Electron. 2010, 25, 228–236. [Google Scholar] [CrossRef]
- Cheng, P.; Nian, H. Direct power control of voltage source inverter in a virtual synchronous reference frame during frequency variation and network unbalance. IET Power Electron. 2016, 9, 502–511. [Google Scholar] [CrossRef]
- Li, L.; Nian, H.; Ding, L.; Zhou, B. Direct power control of dfig system without phase-locked loop under unbalanced and harmonically distorted voltage. IEEE Trans. Energy Convers. 2018, 33, 395–405. [Google Scholar] [CrossRef]
- Nian, H.; Li, L. Direct power control of doubly fed induction generator without phase-locked loop under harmonically distorted voltage conditions. IEEE Trans. Power Electron. 2018, 33, 5836–5846. [Google Scholar] [CrossRef]
- Antoniewicz, P.; Kazmierkowski, M.P. Virtual-flux-based predictive direct power control of ac/dc converters with online inductance estimation. IEEE Trans. Ind. Electron. 2008, 55, 4381–4390. [Google Scholar] [CrossRef]
- Vazquez, S.; Marquez, A.; Aguilera, R.; Quevedo, D.; Leon, J.I.; Franquelo, L.G. Predictive optimal switching sequence direct power control for grid-connected power converters. IEEE Trans. Ind. Electron. 2014, 62, 2010–2020. [Google Scholar] [CrossRef]
- Choi, D.-K.; Lee, K.-B. Dynamic performance improvement of AC/DC converter using model predictive direct power control with finite control set. IEEE Trans. Ind. Electron. 2014, 62, 757–767. [Google Scholar] [CrossRef]
- Hu, J. Improved Dead-Beat Predictive DPC Strategy of Grid-Connected DC–AC Converters with Switching Loss Minimization and Delay Compensations. IEEE Trans. Ind. Inform. 2013, 9, 728–738. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, Z.Q. Improved voltage-vector sequences on dead-beat predictive direct power control of reversible three-phase grid-connected voltage-source converters. IEEE Trans. Power Electron. 2013, 28, 254–267. [Google Scholar] [CrossRef]
- Gui, Y.; Kim, C.; Chung, C.C.; Guerrero, J.M.; Guan, Y.; Vasquez, J.C. Improved direct power control for grid-connected voltage source converters. IEEE Trans. Ind. Electron. 2018, 65, 8041–8051. [Google Scholar] [CrossRef]
- Gui, Y.; Wang, X.; Blaabjerg, F. Vector Current Control Derived from Direct Power Control for Grid-Connected Inverters. IEEE Trans. Power Electron. 2019, 34, 9224–9235. [Google Scholar] [CrossRef]
- Gui, Y.; Wang, X.; Blaabjerg, F.; Pan, D.; Gui, Y.; Wang, X.; Blaabjerg, F.; Pan, D.; Gui, Y.; Wang, X.; et al. Control of Grid-Connected Voltage-Source Converters: The Relationship between Direct-Power Control and Vector-Current Control. IEEE Ind. Electron. Mag. 2019, 13, 31–40. [Google Scholar] [CrossRef]
- Gui, Y.; Wei, B.; Li, M.; Guerrero, J.M.; Vasquez, J.C. Passivity-based coordinated control for islanded AC microgrid. Appl. Energy 2018, 229, 551–561. [Google Scholar] [CrossRef]
- Gui, Y.; Wang, X.; Wu, H.; Blaabjerg, F. Voltage-Modulated Direct Power Control for a Weak Grid-Connected Voltage Source Inverters. IEEE Trans. Power Electron. 2019, 34, 11383–11395. [Google Scholar] [CrossRef]
- Almatani, N.O.; Alhussainy, A.A.; Alghamdi, S.; Kotb, H.; AboRas, K.M.; Vellingiri, M.; Rawa, M. Assessment of a High-Order Stationary Frame Controller for Two-Level and Three-Level NPC Grid-Connected Inverters. Energies 2022, 15, 9313. [Google Scholar] [CrossRef]
- Ahmad, S.; Rashid, T.; Ferdowsy, C.S.; Islam, S.; Mahmood, A.H. A technical comparison among different PV-MPPT algorithms to observe the effect of fast changing solar irradiation. In Proceedings of the 2015 IEEE International WIE Conference on Electrical and Computer Engineering (WIECON-ECE), Dhaka, Bangladesh, 19–20 December 2015; pp. 155–158. [Google Scholar]
- Pan, D.; Ruan, X.; Wang, X.; Yu, H.; Xing, Z. Analysis and Design of Current Control Schemes for LCL-Type Grid-Connected Inverter Based on a General Mathematical Model. IEEE Trans. Power Electron. 2017, 32, 4395–4410. [Google Scholar] [CrossRef]
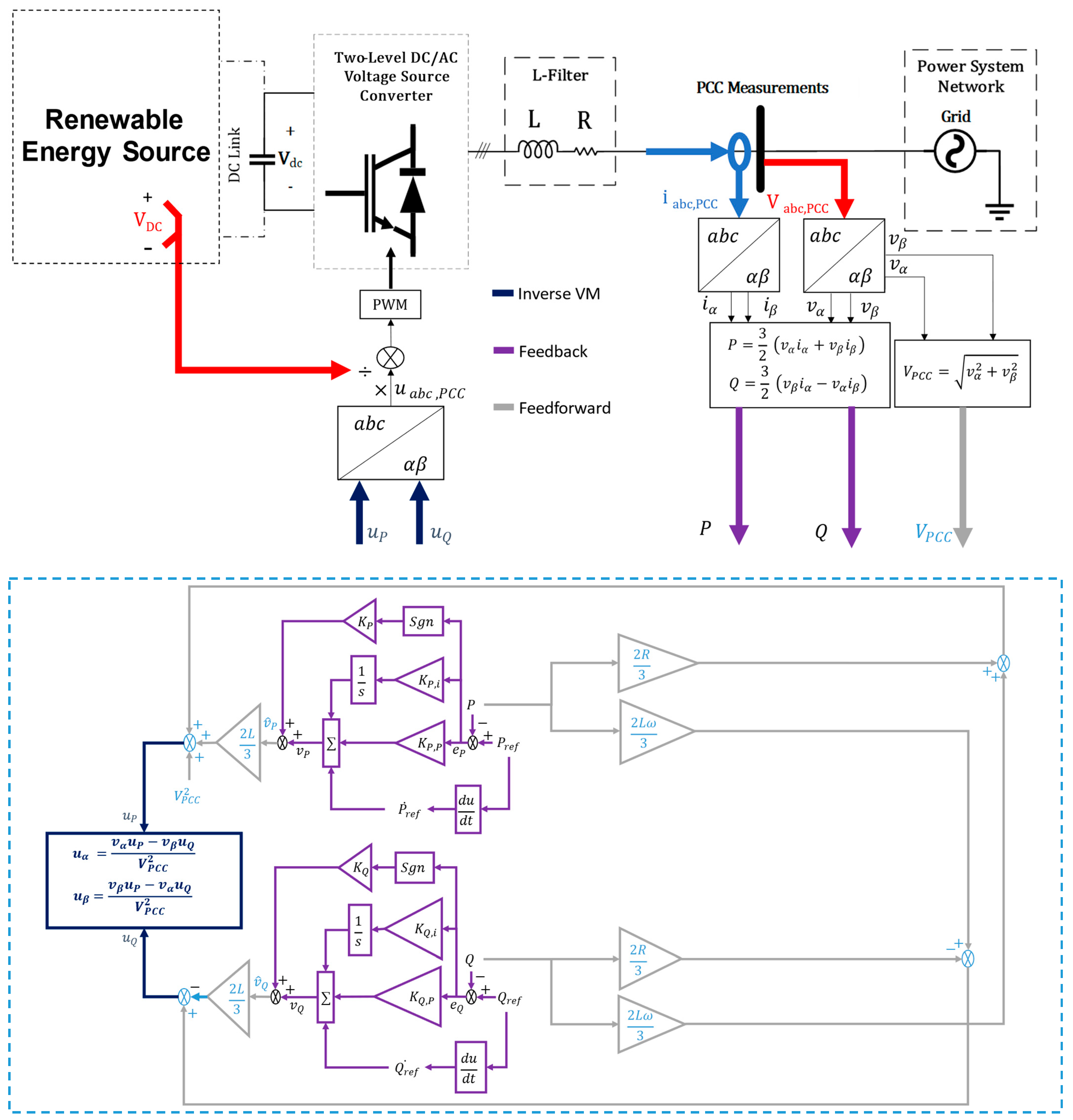
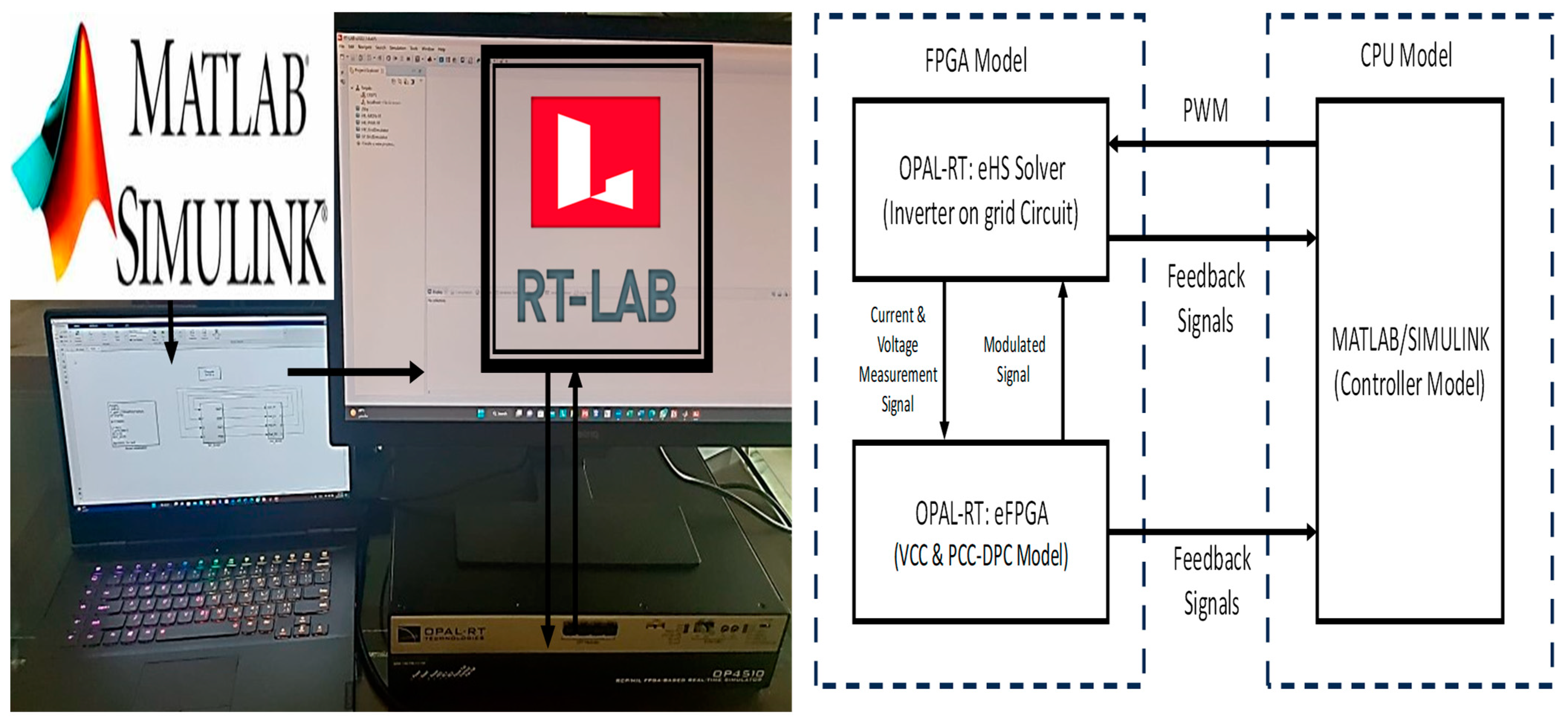




| Feature | Vector Control (VCC) | Direct Power Control (DPC) | Grid Voltage Modulation DPC (GVM-DPC) |
|---|---|---|---|
| Control Method | Indirect control of real and reactive power through d–q transformation | Direct control of real and reactive power | Direct control of grid voltage |
| Grid Synchronization PLL | Required | Not required | Not required |
| Power Quality | Introduce current harmonics due to complex calculations and require additional filtering to meet grid standards | Potential for high Total Harmonic Distortion (THD) due to variable switching frequency | Aims to reduce harmonic distortion by directly controlling grid voltage |
| Transient Response | Slower response due to indirect control | Faster response due to Direct Power Control | Can achieve fast transient response |
| Steady-State Performance | Generally good steady-state performance | Potential for power fluctuations due to variable switching frequency | Aims for improved steady-state performance by minimizing voltage variations |
| Computational Burden | Moderate | Can be high due to complex calculations and potential need for online calculations (predictive DPC) | Lower compared to DPC due to simpler structure |
| Robustness | Generally robust | Less robust due to unpredictable harmonic spectrum | Considered more robust compared to other DPC methods (SMC-DPC, PBC-DPC) |
| Variations | Several improved VCC approaches with additional PI regulators | Predictive DPC, Model Predictive Control DPC (MPC-DPC), virtual synchronous reference frame DPC | - |
| Recent Developments | Focus on improving robustness and stability | Focus on reducing harmonic distortion, fixed switching frequency | - |
| Parameter | Value |
|---|---|
| DC/AC voltage source converter | |
| Line to line voltage (rms) | 133 V |
| Resistance filter (Ra,b,c) | 0.16 Ω |
| Inductive filter (La,b,c) | 4 mH |
| AC frequency | 50 Hz |
| Switching frequency | 10 kHz |
| Sampling frequency | 10 kHz |
| Power rate | 2 kVA |
| controller frame | |
| 40 | |
| 1608.8 | |
| 10 | |
| 50,000 | |
| Voltage-Modulated Direct Power Control | |
| 5000 | |
| 300 | |
| 10 | |
| Case Study | Focus | PCC-DPC Performance | VCC-dq Frame Performance | Key Observations |
|---|---|---|---|---|
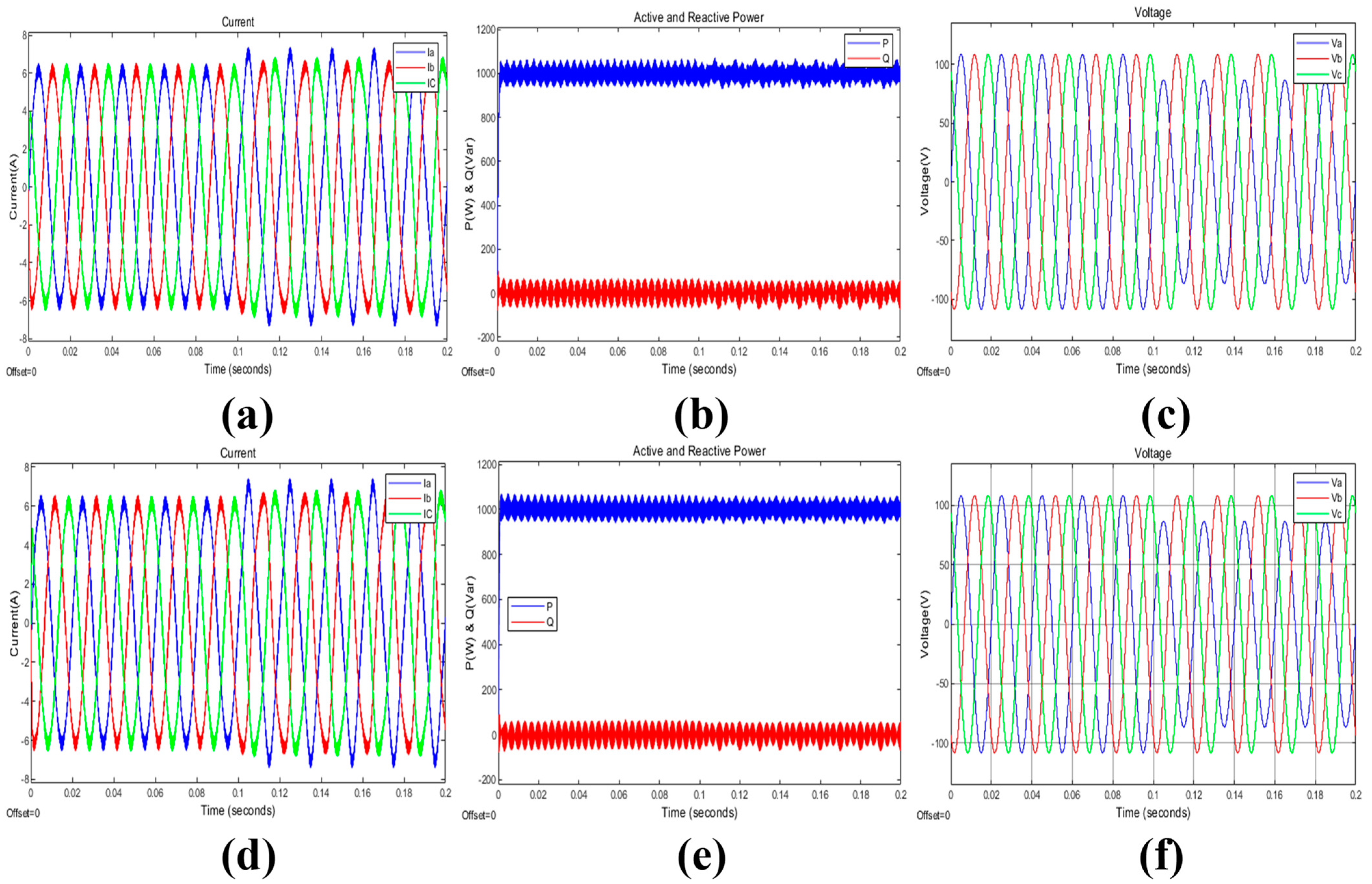
| Tracking Performance (Transient Mode) | Ability to track active and reactive power references | Significantly reduced ripples in active and reactive power, faster tracking of active power, and smaller overshoot in reactive power | Similar performance with reduced ripples | PCC-DPC offers faster response and potentially better stability |
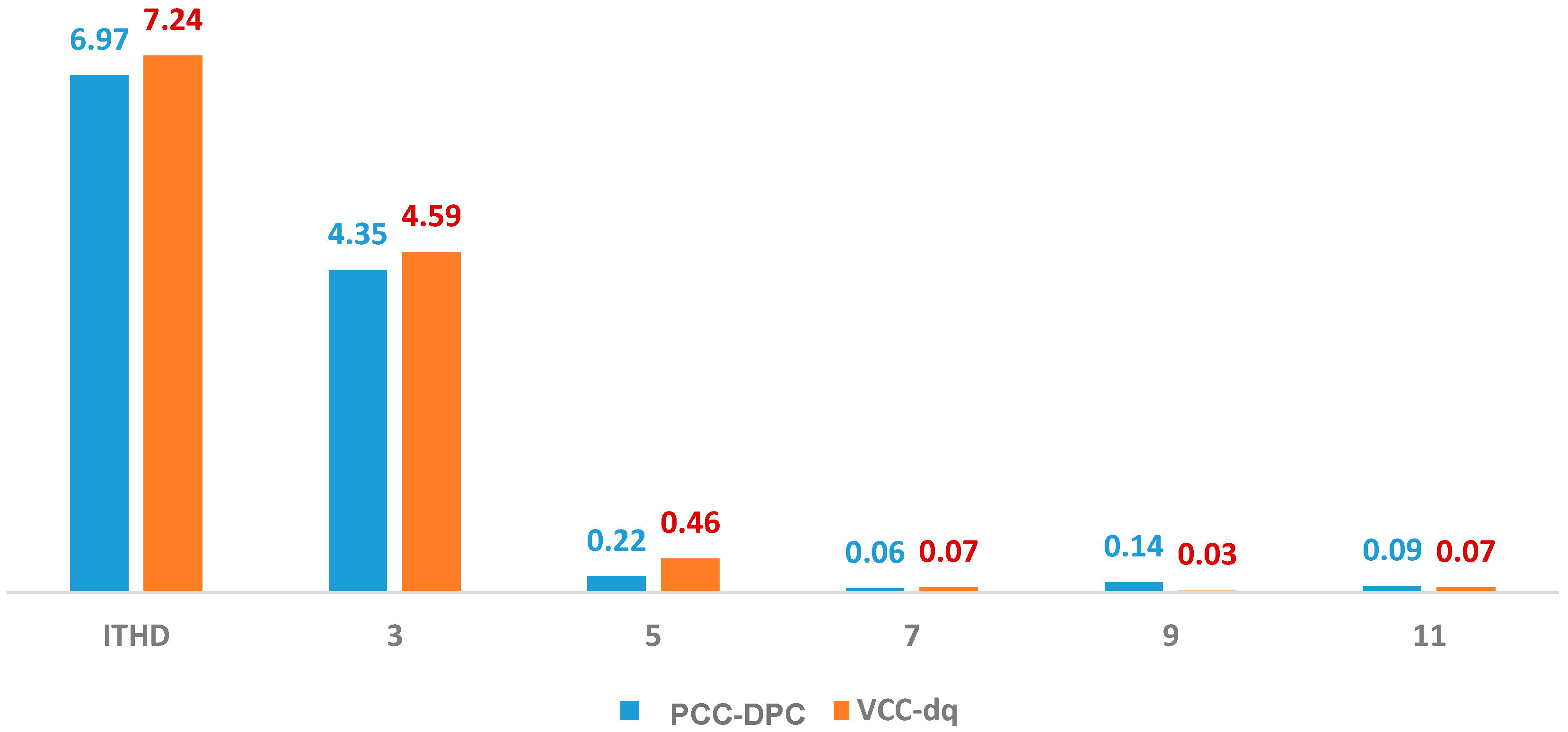
| Harmonics Analysis (Steady-State) | Harmonic content in output currents | THD (total harmonic distortion) of 1.68% (within grid standards)—slight increase in fifth, seventh, and eleventh harmonics (needs further investigation) | THD of 1.65% | PCC-DPC achieves good harmonic performance similar to VCC-dq but requires further investigation for specific harmonics |
| Low-Voltage Ride-Through (LVRT) | Response to voltage sags | Maintains power reference with small overshoot in active power—regulates reactive power without overshoot | Similar behavior with small overshoot in active power | Both methods demonstrate robustness during voltage sags |
| High-Voltage Ride-Through (HVRT) | Response to voltage swells | Maintains power reference with small overshoot in active power—regulates reactive power without overshoot | Similar behavior with small overshoot in active power | Both methods demonstrate robustness during voltage swells |
| Grid Frequency Variation | Response to minor frequency changes | No impact on active or reactive power, or output currents | Similar behavior | Both methods demonstrate robustness to minor grid frequency variations |
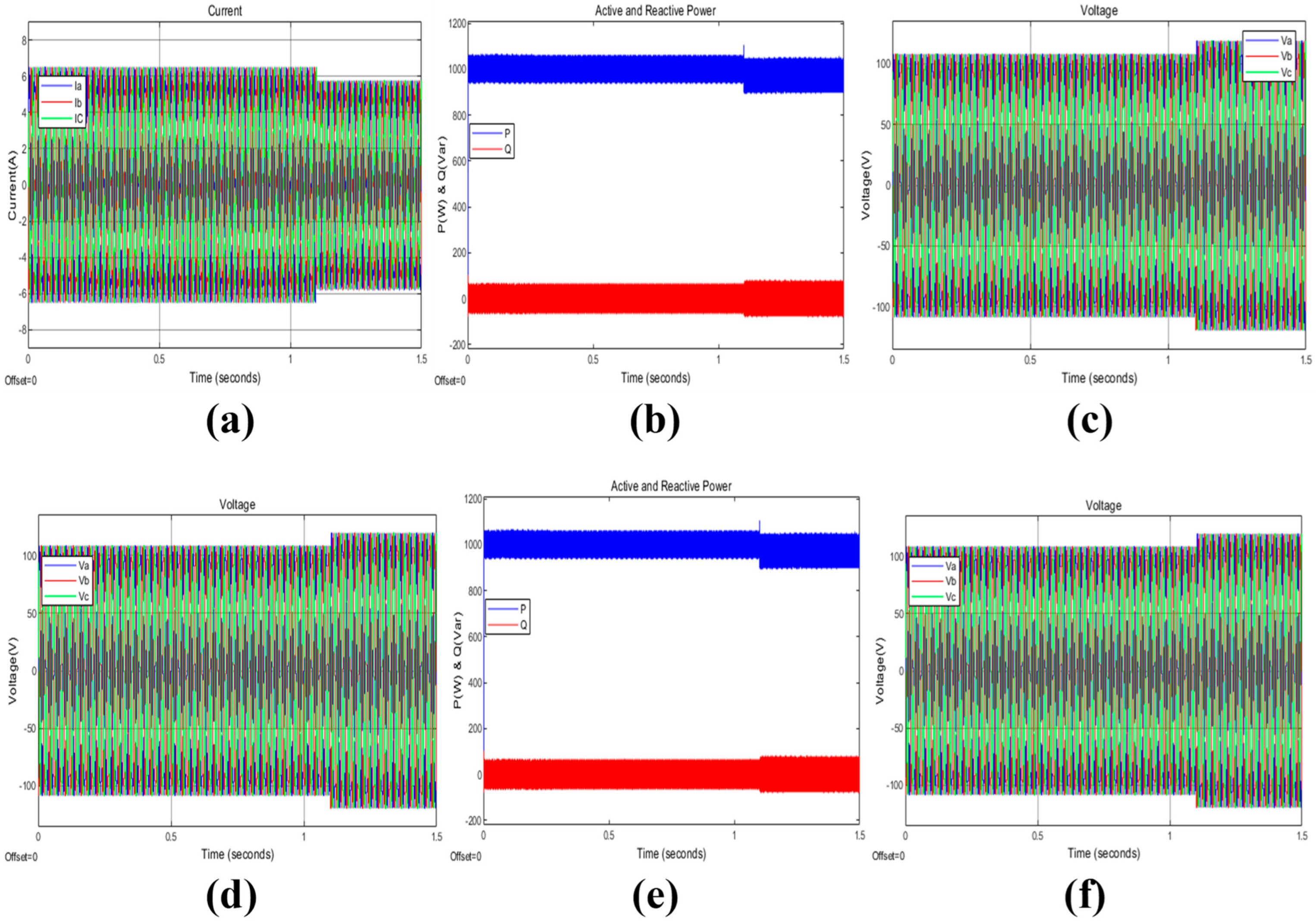
| Unbalanced Grid (20% Sag in Phase A) | Performance under unbalanced voltage | Maintains power reference without compensation—increased current THD (7.81%) | Better performance in power regulation and violated current THD standard | PCC-DPC prioritizes power regulation but needs improvement for THD under unbalanced conditions |
| Unbalanced Grid (20% Swell in Phase A) | Performance under unbalanced voltage | Maintains power reference without compensation—increased current THD (6.97%) | Better performance in power regulation and violated current THD standard | Similar to case 6, PCC-DPC prioritizes power regulation but needs improvement for THD under unbalanced conditions |
| Performance Evaluation | Case Study | Rise Time | Settling Time | Settling Min/Max | Over/Undershoot | Peak | Peak Time |
|---|---|---|---|---|---|---|---|
| PCC-DPC | Tracking Performance (Transient Mode) | 2.9247 × 10−7 | 0.1000 | −128.5664/1.0672 × 10+3 | 1.0155 × 10+4/8.5122 × 10+4 | 1.0672 × 10+3 | 0.0314 |
| Harmonics Analysis (Steady-State) | 0.0018 | 0.0989 | 1.7627 × 10+3/2.0580 × 10+3 | 3.1665/0.3377 | 2.0580 × 10+3 | 0.0077 | |
| VCC-dq | Tracking Performance (Transient Mode) | 5.7426 × 10−7 | 0.1000 | −168.7826/1.0741 × 10+3 | 6.8514 × 10+3/4.4237 × 10+4 | 1.0741 × 10+3 | 0.0315 |
| Harmonics Analysis (Steady-State) | 0.0013 | 0.0992 | 1.8081 × 10+3/2.1117 × 10+3 | 5.1031/0.0017 | 2.1117 × 10+3 | 0.0047 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alturki, Y.A.; Alhussainy, A.A.; Alghamdi, S.M.; Rawa, M. A Novel Point of Common Coupling Direct Power Control Method for Grid Integration of Renewable Energy Sources: Performance Evaluation among Power Quality Phenomena. Energies 2024, 17, 5111. https://doi.org/10.3390/en17205111
Alturki YA, Alhussainy AA, Alghamdi SM, Rawa M. A Novel Point of Common Coupling Direct Power Control Method for Grid Integration of Renewable Energy Sources: Performance Evaluation among Power Quality Phenomena. Energies. 2024; 17(20):5111. https://doi.org/10.3390/en17205111
Chicago/Turabian StyleAlturki, Yusuf A., Abdullah Ali Alhussainy, Sultan M. Alghamdi, and Muhyaddin Rawa. 2024. "A Novel Point of Common Coupling Direct Power Control Method for Grid Integration of Renewable Energy Sources: Performance Evaluation among Power Quality Phenomena" Energies 17, no. 20: 5111. https://doi.org/10.3390/en17205111
APA StyleAlturki, Y. A., Alhussainy, A. A., Alghamdi, S. M., & Rawa, M. (2024). A Novel Point of Common Coupling Direct Power Control Method for Grid Integration of Renewable Energy Sources: Performance Evaluation among Power Quality Phenomena. Energies, 17(20), 5111. https://doi.org/10.3390/en17205111







