An Experimental Investigation of Pressure Drop in Two-Phase Flow during the Condensation of R410A within Parallel Microchannels

Abstract

In this study, the flow condensation of R-410A within 18 square microchannels arranged horizontally in parallel was experimentally investigated. All components of pressure drop, including expansion, contraction, deceleration, and friction, were quantified specifically for microchannels. The test conditions included saturation temperature, vapor quality, and mass flux, ranging from 18.86 to 24.22 bar, 0.09 to 0.92, and 200 to 445 kg/m²·s, respectively. The frictional pressure loss made up approximately 92.89% of the overall pressure reduction. The findings demonstrate that the pressure drop rises with higher mass flux and a lower saturation temperature. By comparing with correlations and semi-empirical models outlined in the literature across various scales, specimen types, and refrigerant media, correlations developed for two-phase adiabatic flows in multi-channel configurations can effectively predict the pressure drop in microchannel condensation processes. The model introduced by Sakamatapan and Wongwises demonstrated the highest predictive accuracy, with a mean absolute deviation of 8.4%.

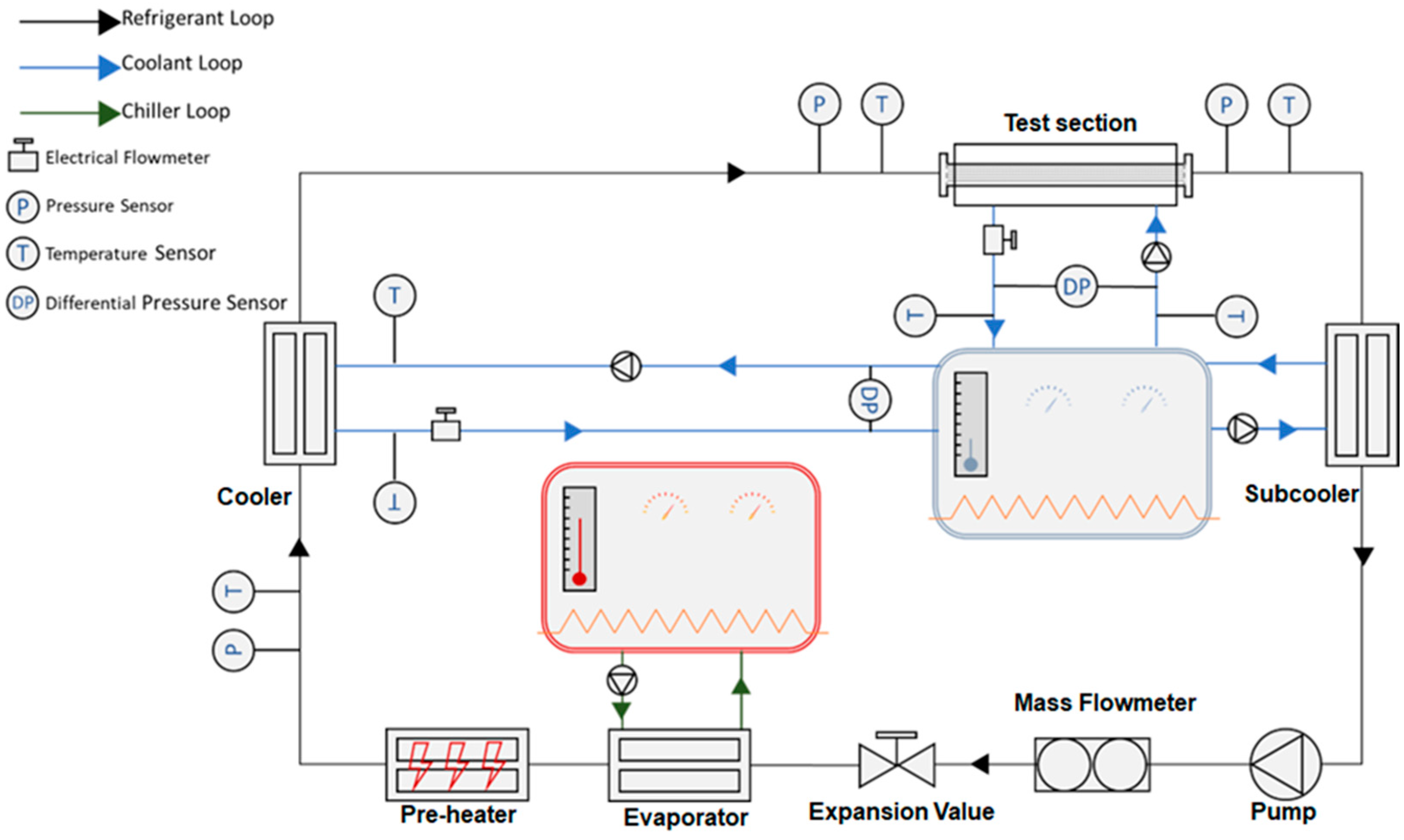
1. Introduction

Over the past few decades, the pursuit of more efficient energy utilization brought widespread attention to heat exchangers as critical components of thermal systems across various industries. Especially in scenarios where space and material usage are constrained, the development of more efficient and compact heat exchange technologies became crucial. Microchannel and minichannel heat exchangers, known for their superior heat transfer performance and advantages in reducing weight and volume [1], show great potential in applications such as automotive air conditioning [2], electronic cooling [3], and spacecraft thermal control [4], and are considered the future direction of heat exchange technology.

Research on two-phase flow within microchannels, particularly its potential to significantly enhance heat transfer efficiency and reduce environmental impact, became a focal point of international studies. Unlike single-phase flow, the heat transfer process in two-phase flow involves both sensible and latent heat, resulting in a higher heat transfer coefficient. Moreover, microchannel technology contributes to the reduction in environmentally unfriendly refrigerants used in large-scale heat exchange equipment [5], making it more environmentally friendly. However, the flow characteristics in microchannels differ markedly from those in macrochannels [6], especially the dominant role of surface tension in microchannel condensation, which leads to significant differences in flow patterns, pressure drop, and heat transfer coefficients in contrast to traditional large-diameter pipes.

The design of microchannels heavily relies on the pressure drop as a key factor; it directly affects the system’s energy efficiency and performance. In microchannels, even minor changes in pressure can lead to significant alterations in flow and heat transfer performance due to the reduced size. Therefore, accurately predicting and controlling the pressure drop in microchannels is essential for optimizing heat exchanger design. Microchannel condensation is a key element in enhancing heat exchanger efficiency. Extensive research into microchannel condensation was conducted by scholars such as Ghiaasiaan [7] and Garimella [5]. However, the process of phase change within micro geometries remains incompletely understood. Liu et al. [8] conducted an experimental study on the rise of a single Taylor bubble in stagnant and downward-flowing non-Newtonian fluids. The experimental results show that the bubble velocity increases with the inclination angle and decreases with increasing liquid viscosity. Luo et al. [9] performed a comprehensive analysis of the pressure gradient in a visualization pipeline. To better predict the pressure gradient in horizontal wells, they proposed a new liquid holdup correlation based on the Mukherjee-Brill model. The validation against experimental and field data demonstrated that the established two-phase flow model can accurately predict the pressure gradient over different pressure ranges and gas–liquid velocities. The disagreement on heat transfer and pressure drop models is evident from the varying results reported by different authors. The majority of models for pressure drop in microchannels during two-phase flow were derived from two conventional tube models: the homogeneous flow model and the separated flow model. In the homogeneous flow model, it is assumed that the two phases are thoroughly mixed, and the pressure drop is determined by considering the two phases as a unified entity inside the channel. In the separated flow approach, each phase is assumed to flow separately within the channel, with coupling parameters for vapor and liquid flow. The Lockhart and Martinelli parameter [10], as well as the Chisholm parameter [11] proposed by Lockhart and Martinelli and Chisholm, respectively, illustrate the connection between the two phases.

In air conditioning systems, R410A is extensively utilized. Comprising a balanced 50%/50% mixture of R125 and R32, R410A exhibits a temperature glide of 0.1 °C at atmospheric conditions and is classified as a near-azeotropic blend [12]. In recent studies, Li et al. [13] investigated the condensation heat transfer characteristics of R32 and R410A in four horizontal circular tubes through experimental research. They examined how mass flux, vapor quality, refrigerant type, and saturation temperature influence heat transfer during the condensation process. Furthermore, they introduced the specific sensitivity factor (SSF) to evaluate the impact of these parameters on heat transfer and pressure drop. Tang et al. [14] examined how the material affects the evaporative and condensing heat transfer characteristics of R410A in horizontal tubes made of aluminum and stainless steel with an inner diameter of 6 mm. Their findings suggest that material and surface roughness have a minimal impact on the thermal performance during the condensation process.

Although extensive research was conducted on microchannel condensation and two-phase flow, most studies focused on larger diameter single tubes, with a few studies focused on microchannels with a limited range of conditions and geometries. Detailed experimental data on the condensation of R410A in parallel multi-channel microchannels remain scarce. Pressure drops, being one of the key parameters for refrigerant performance in heat exchangers, requires further investigation. There are also applications such as data center cooling [15]; R410A is still a commonly used refrigerant and there are currently no suitable substitutes. Therefore, further exploration of the pressure drop characteristics of R410A not only helps optimize its application, but also provides a reference for the development of alternative refrigerants in the future. Existing pressure drop prediction models (such as the Friedel model) are widely used for macro channels or single microchannel designs, but their applicability to parallel multi-channel microchannel systems remains to be validated. This study aims to fill this gap by analyzing the pressure drop observed during the convective condensation of R410A within an 18-channel horizontal microchannel flat tube. By experimentally measuring the pressure drop characteristics under different mass flow rates and saturation temperatures, the study quantifies pressure drop components such as frictional pressure drop and momentum pressure drop. The experimental conditions, including saturated pressure (Psat), vapor quality (x), and mass flux (G), are presented in Section 3 of the paper. The study further evaluates the impact of saturated temperature, vapor quality, and mass flux on the frictional pressure drop, comparing and analyzing the experimental findings against empirical and semi-empirical models presented in the literature. These new experimental data provide important validation for existing two-phase flow pressure drop models in microchannels and offer a deeper examination of their accuracy.

2. Literature Review—Pressure Drop

In microchannel environments, dominant surface tension forces significantly influence two-phase flows, leading to the predominance of annular flows over gravity-influenced flows such as stratified ones. With increased fluid velocities, the impact of shear forces intensifies because the gravitational influence on the liquid film within microchannels is minimal, in contrast to conventional channels. This results in a notable increase in pressure drop. Elevated pressure drops can indirectly affect two-phase heat transfer by lowering the system operating pressure and reducing the associated corresponding saturation temperature, which results in a great amount of vapor remaining uncondensed at lower temperatures. Consequently, a reduced cooling temperature is required for effective condensation. Additionally, it highlights the complex interaction between flow dynamics and thermal transfer in two-phase microchannel systems.

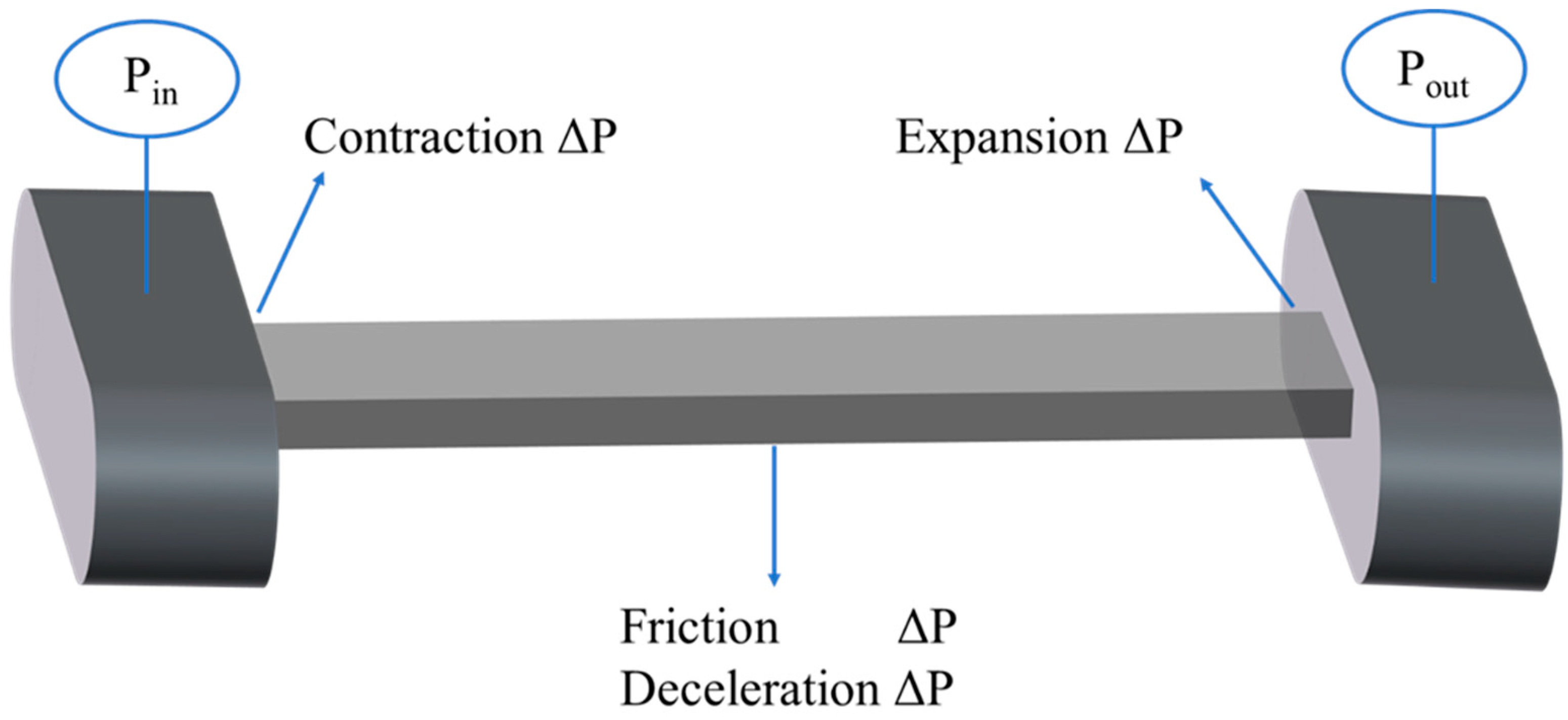
Typically, the overall pressure drop in a two-phase flow is comprised of several components: momentum or acceleration (ΔP_m), gravitational (ΔP_g), local (ΔP_l), and frictional (ΔP_f) pressure drops, as described in the following equation:

∆P_total = ∆P_momentum + ∆P_{gravitational} + ∆P_local + ∆P_frictional.

(1)

It should be noted that in two-phase flow dynamics, “local pressure drop” typically refers to the pressure changes caused by sudden variations in fluid flow, such as through valves, bends, contractions, or expansions. Local pressure drops require careful consideration in engineering design, as they can lead to significant changes in fluid dynamic performance, affecting the overall efficiency and operational stability of the system.

The frictional pressure drop is the primary contributor to the total pressure drop, and the current models used for estimating two-phase frictional pressure drops in microchannels/minichannels can be summarized into four main types [16]: i. direct empirical correlations dominated by flow parameters; ii. flow pattern-specific empirical correlations; iii. homogeneous equilibrium models (HEMs) are developed similarly to single-phase flow equations but with continuously adjusted two-phase flow parameters such as the friction factor; and iv. separated flow models (SFMs), which handle the vapor and liquid phases separately for calculation and then combine the results using a parameter ratio.

This section reviews the latest correlations for frictional pressure drops in two-phase microchannel flows, including those that account for condensation. Additionally, it incorporates well-established traditional correlations for two-phase pressure drops in larger pipes, such as those proposed by Lockhart and Martinelli [10], Friedel [17], and the homogeneous model. The experimental data will be compared and analyzed against these correlations in Section Four of the results.

2.1. Homogeneous Equilibrium Model

$${\left({\displaystyle \frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{Z}}}\right)}_{\mathrm{F}}={\displaystyle \frac{2{\mathrm{f}}_{\mathrm{t}\mathrm{p}}{\mathsf{\rho }}_{\mathrm{t}\mathrm{p}}{\mathrm{u}}^2}{{\mathrm{D}}_{\mathrm{h}}}}$$

(2)

where

$${\mathrm{f}}_{\mathrm{t}\mathrm{p}}=\left\{\begin{array}{c}16\mathrm{R}{\mathrm{e}}_{\mathrm{t}\mathrm{p}}^{-1} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{R}{\mathrm{e}}_{\mathrm{t}\mathrm{p}}<2000\\ 0.079\mathrm{R}{\mathrm{e}}_{\mathrm{t}\mathrm{p}}^{-0.25} \mathrm{f}\mathrm{o}\mathrm{r} 2000\le \mathrm{R}{\mathrm{e}}_{\mathrm{t}\mathrm{p}}<20000\\ 0.046\mathrm{R}{\mathrm{e}}_{\mathrm{t}\mathrm{p}}^{-0.2} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{R}{\mathrm{e}}_{\mathrm{t}\mathrm{p}}\ge 20000\end{array}\right..$$

(3)

In fluid dynamics, the homogeneous model treats the system as a single-phase entity, often employing the Blasius equations. For accurate Reynolds number calculations, it is essential to precisely determine the two-phase density ${\mathsf{\rho }}_{\mathrm{t}\mathrm{p}}$ and viscosity ${\mathsf{\mu }}_{\mathrm{t}\mathrm{p}}$.

$${\mathrm{R}\mathrm{e}}_{\mathrm{t}\mathrm{p}}={\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{t}\mathrm{p}}{\mathrm{u}}_{\mathrm{t}\mathrm{p}}{\mathrm{D}}_{\mathrm{h}}}{{\mathsf{\mu }}_{\mathrm{t}\mathrm{p}}}}$$

(4)

Homogeneous models typically utilize a uniform approach to determine density, as specified in Equation (5).

$${\mathsf{\rho }}_{\mathrm{t}\mathrm{p}}={\left({\displaystyle \frac{1-\mathrm{x}}{{\mathsf{\rho }}_{\mathrm{l}}}}+{\displaystyle \frac{\mathrm{x}}{{\mathsf{\rho }}_{\mathrm{v}}}}\right)}^{-1}$$

(5)

For viscosity calculations using the homogeneous model, this paper will employ the McAdams et al. model [18], which is expressed as follows:

$${\displaystyle \frac{1}{{\mathsf{\mu }}_{\mathrm{t}\mathrm{p}}}}={\displaystyle \frac{\mathrm{x}}{{\mathsf{\mu }}_{\mathrm{v}}}}+{\displaystyle \frac{1-\mathrm{x}}{{\mathsf{\mu }}_{\mathrm{l}}}}.$$

(6)

In two-phase flow, the homogeneous model is a classic model used for predicting pressure drop. However, studies by Venkatesan et al. [19] and Choi and Kim [20] indicate that the homogeneous flow model is primarily applicable to bubbly flow. This model is valid under conditions of high flow rates and when the steam content is less than 0.1.

2.2. Lockhart and Martinelli Model

The Lockhart and Martinelli [10] correlation, as detailed in Equation (7), utilizes the two-phase multiplier (${\mathsf{\phi }}^2$) outlined in Equation (8). This multiplier effectively quantifies the ratio of a two-phase pressure drop (either in liquid or vapor form) to that of a single-phase. Specifically, ${\mathsf{\phi }}^2$ is formulated as:

$${\left({\displaystyle \frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{Z}}}\right)}_{\mathrm{F}}={\mathsf{\phi }}^2{\left({\displaystyle \frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{z}}}\right)}_{\mathrm{l}},$$

(7)

where ${\mathsf{\phi }}^2$ is defined by the relation:

$${\mathsf{\phi }}^2=1+{\displaystyle \frac{\mathrm{C}}{\mathrm{X}}}+{\displaystyle \frac{1}{{\mathrm{X}}^2}}.$$

(8)

Here, C varies with the flow regime, and X denotes the Martinelli parameter. The equations for determining C and the Martinelli parameter X are provided in Equations (9) and (10), respectively.

$$\mathrm{C}=\left\{\begin{array}{cc}\hfill 20,& \mathrm{L}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{d}:\mathrm{T}\mathrm{u}\mathrm{r}\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{t}/\mathrm{V}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{r}:\mathrm{T}\mathrm{u}\mathrm{r}\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{t}\hfill \\ \hfill 12,& \mathrm{L}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{d}:\mathrm{L}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}/\mathrm{V}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{r}:\mathrm{T}\mathrm{u}\mathrm{r}\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{t}\hfill \\ \hfill 10,& \mathrm{L}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{d}:\mathrm{T}\mathrm{u}\mathrm{r}\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{t}/\mathrm{V}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{r}:\mathrm{L}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}\hfill \\ \hfill 5,& \mathrm{L}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{d}:\mathrm{L}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}/\mathrm{V}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{r}:\mathrm{L}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}\hfill \end{array}\right.$$

(9)

$$\mathrm{X}={\left[{\displaystyle \frac{{\left(\frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{z}}\right)}_{\mathrm{l}}}{{\left(\frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{z}}\right)}_{\mathrm{v}}}}\right]}^{1/2}$$

(10)

Chen and Spedding [21] pointed out in their study that the Lockhart and Martinelli correlation is not only one of the earliest systematic representations of gas–liquid two-phase flow, but also one of the most widely used. The major drawback of this correlation is that it neglects at least one crucial factor: flow pattern. Its predictive performance is insufficient for stratified and annular flow.

2.3. Friedel Model

Friedel [17] developed a correlation derived from an extensive dataset of 25,000 observations collected from adiabatic flow within channels, each having a hydraulic diameter (D_h) exceeding 1 mm. The factors ${\mathrm{f}}_{\mathrm{v}\mathrm{o}}$ and ${\mathrm{f}}_{\mathrm{l}\mathrm{o}}$ are calculated according to Equation (3), representing the friction factors for vapor-only or liquid-only flow, respectively.

$${\left({\displaystyle \frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{Z}}}\right)}_{\mathrm{F}}={\mathsf{\phi }}_{\mathrm{l}\mathrm{o}}^2{\left({\displaystyle \frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{z}}}\right)}_{\mathrm{l}\mathrm{o}}$$

(11)

$${\mathsf{\phi }}_{\mathrm{l}\mathrm{o}}^2=\mathrm{E}+{\displaystyle \frac{0.32\mathrm{F}\mathrm{H}}{{\mathrm{F}\mathrm{r}}_{\mathrm{t}\mathrm{p}}^{0.045}{\mathrm{W}\mathrm{e}}_{\mathrm{t}\mathrm{p}}^{0.035}}}$$

(12)

$$\mathrm{E}=(1-\mathrm{x}{)}^2+{\mathrm{x}}^2{\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{l}}{\mathrm{f}}_{\mathrm{v}\mathrm{o}}}{{\mathsf{\rho }}_{\mathrm{v}}{\mathrm{f}}_{\mathrm{l}\mathrm{o}}}}$$

(13)

$$\mathrm{F}={\mathrm{x}}^{0.78}{\left(1-\mathrm{x}\right)}^{0.24}$$

(14)

$$\mathrm{H}={\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{l}}}{{\mathsf{\rho }}_{\mathrm{v}}}}\right)}^{0.91}{\left({\displaystyle \frac{{\mathsf{\mu }}_{\mathrm{l}}}{{\mathsf{\mu }}_{\mathrm{v}}}}\right)}^{0.19}{\left(1-{\displaystyle \frac{{\mathsf{\mu }}_{\mathrm{v}}}{{\mathsf{\mu }}_{\mathrm{l}}}}\right)}^{0.7}$$

(15)

$${\mathrm{W}\mathrm{e}}_{\mathrm{t}\mathrm{p}}={\displaystyle \frac{{\mathrm{G}}^2{\mathrm{D}}_{\mathrm{h}}}{\mathsf{\sigma }{\mathsf{\rho }}_{\mathrm{t}\mathrm{p}}}}$$

(16)

Whalley [22], in previous work, recommended using the (${\mathsf{\mu }}_{\mathrm{l}}/{\mathsf{\mu }}_{\mathrm{v}}$) < 1000 condition to predict the frictional pressure drop in two-phase flow. However, Wang et al. [23] found that the Friedel correlation is not applicable when the liquid mass flux is low.

2.4. Cavallini et al. Model

Cavallini et al. [24] conducted an experimental investigation into the pressure drop during condensation within an 8 mm D_h circular tube, studying refrigerants R22, R32, R236ea, R134a, R125, R410A, and R407C. Their research accounted for mass fluxes ranging from 100 to 750 kg/m²s and saturation temperatures varying from 30 to 50 °C. They recommended modifications to the existing Friedel correlation to better suit the microchannel condensation flows of these refrigerants. It should be mentioned that the E parameter (Equation (13)) within Friedel’s correlation remains consistent. The formula is given below:

$${\left({\displaystyle \frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{Z}}}\right)}_{\mathrm{F}}={\mathsf{\phi }}_{\mathrm{l}\mathrm{o}}^2{\left({\displaystyle \frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{z}}}\right)}_{\mathrm{l}\mathrm{o}}$$

(17)

$${\mathsf{\phi }}_{\mathrm{l}\mathrm{o}}^2=\mathrm{E}+{\displaystyle \frac{1.262\mathrm{F}\mathrm{H}}{{\mathrm{W}\mathrm{e}}^{0.1458}}}$$

(18)

$$\mathrm{F}={\mathrm{x}}^{0.6978}$$

(19)

$$\mathrm{H}={\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{l}}}{{\mathsf{\rho }}_{\mathrm{v}}}}\right)}^{0.3278}{\left({\displaystyle \frac{{\mathsf{\mu }}_{\mathrm{l}}}{{\mathsf{\mu }}_{\mathrm{v}}}}\right)}^{1.181}{\left(1-{\displaystyle \frac{{\mathsf{\mu }}_{\mathrm{v}}}{{\mathsf{\mu }}_{\mathrm{l}}}}\right)}^{3.477}.$$

(20)

2.5. Son and Oh Model

Building on the research by Lockhart and Martinelli [10], Son and Oh [25] conducted experiments to study the condensation behavior of R134a, R22, and R410A within a minichannel, utilizing a tube characterized by a D_h of 1.77 mm. From their experimental findings, they developed a novel correlation to estimate the pressure drop during condensation, employing the superposition model. Within this model, they introduced a new Chisholm factor (C), which they derived dependently on both the two-phase Reynold number (Re_tp) and the two-phase Weber number (We_tp).

$$\mathrm{C}=2485{\mathrm{W}\mathrm{e}}_{\mathrm{t}\mathrm{p}}^{-0.407}{\mathrm{R}\mathrm{e}}_{\mathrm{t}\mathrm{p}}^{-0.34}$$

(21)

$${\mathsf{\mu }}_{\mathrm{t}\mathrm{p}}={\left({\displaystyle \frac{\mathrm{x}}{{\mathsf{\mu }}_{\mathrm{v}}}}+{\displaystyle \frac{1-\mathrm{x}}{{\mathsf{\mu }}_{\mathrm{l}}}}\right)}^{-1}$$

(22)

2.6. Sakamatapan and Wongwises Model

Sakamatapan and Wongwises [26] carried out an experimental investigation into the condensation flow of R134a through two distinct configurations of multi-port microchannels: one set comprising fourteen channels with a D_h of 1.1 mm and another set of eight channels having a D_h of 1.2 mm. Their results show that the friction factor plays a major role in the total pressure loss. Notably, they observed an increase in the friction factor with higher mass flux and vapor quality, while a rise in saturation temperature and channel diameter results in a decrease. Consequently, they developed a correlation utilizing the equivalent Reynolds number (Re_eq) to estimate the friction factor for condensation flows at microscales.

$${\left({\displaystyle \frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{Z}}}\right)}_{\mathrm{F}}={\displaystyle \frac{2{\mathrm{f}}_{\mathrm{t}\mathrm{p}}{\mathrm{R}\mathrm{e}}_{\mathrm{e}\mathrm{q}}^2{\mathsf{\mu }}_{\mathrm{l}}^2}{{\mathsf{\rho }}_{\mathrm{l}}{\mathrm{D}}_{\mathrm{h}}^3}}$$

(23)

$${\mathrm{f}}_{\mathrm{t}\mathrm{p}}=6977{\mathrm{R}\mathrm{e}}_{\mathrm{e}\mathrm{q}}^{-0.337}{\mathrm{x}}^{-0.031}{\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{l}}}{{\mathsf{\rho }}_{\mathrm{v}}}}\right)}^{6.51}{\left({\displaystyle \frac{{\mathsf{\mu }}_{\mathrm{l}}}{{\mathsf{\mu }}_{\mathrm{v}}}}\right)}^{-11.883}$$

(24)

$${\mathrm{R}\mathrm{e}}_{\mathrm{e}\mathrm{q}}={\displaystyle \frac{{\mathrm{G}}_{\mathrm{e}\mathrm{q}}{\mathrm{D}}_{\mathrm{h}}}{{\mathsf{\mu }}_{\mathrm{l}}}}$$

(25)

$${\mathrm{G}}_{\mathrm{e}\mathrm{q}}=\mathrm{G}\left[\left(1-\mathrm{x}\right)\mathrm{x}{\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{l}}}{{\mathsf{\rho }}_{\mathrm{v}}}}\right)}^{{\displaystyle \frac{1}{2}}}\right]$$

(26)

2.7. Andresen et al. Model

Andresen et al. [27] carried out experiments to evaluate the condensation pressure drop of refrigerants R410A and R404A under near-critical pressures. They conducted tests on sections with D_h varying between 0.76 and 9.4 mm. They discovered that existing correlations failed to accurately predict pressure drops at reduced pressures of 0.8 and 0.9, particularly considering the variations in tube size and mass flux ranges. Consequently, they introduced a new correlation for pressure drop that demonstrated good predictive performance in comparison with experimental data.

$${\mathsf{\phi }}^2=1+{\displaystyle \frac{24{\mathrm{R}\mathrm{e}}_{\mathrm{l}}^{-0.3}{\mathrm{N}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}^{-0.4}}{\mathrm{X}}}+{\displaystyle \frac{1}{{\mathrm{X}}^2}}$$

(27)

$${\mathrm{N}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}={\displaystyle \frac{{\left[\frac{\mathsf{\sigma }}{\mathrm{g}\left({\mathsf{\rho }}_{\mathrm{l}}-{\mathsf{\rho }}_{\mathrm{v}}\right)}\right]}^{\frac{1}{2}}}{{\mathrm{D}}_{\mathrm{h}}}}$$

(28)

2.8. Kim and Mudawar Model

Kim and Mudawar [28] identified that models and correlations previously used to predict the pressure drops in adiabatic and condensing mini/microchannels are only applicable to a limited range of working fluids and narrow parameter scopes. To address this, they assembled a comprehensive database from 36 sources, comprising 7115 data points related to adiabatic and condensing flows in mini/microchannels, covering 17 different working fluids. The dataset covers D_h ranging from 0.0695 to 6.22 mm, with mass flux values spanning from 4.0 to 8528 kg/m²s. Utilizing this extensive collection, they developed a universal methodology for predicting two-phase frictional pressure drops, which demonstrated excellent predictive accuracy against the newly integrated database.

$${\left({\displaystyle \frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{z}}}\right)}_{\mathrm{l}}={\displaystyle \frac{2{\mathrm{f}}_{\mathrm{l}}{\mathrm{v}}_{\mathrm{l}}{\mathrm{G}}^2{\left(1-\mathrm{x}\right)}^2}{{\mathrm{D}}_{\mathrm{h}}}}$$

(29)

$${\left({\displaystyle \frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{z}}}\right)}_{\mathrm{v}}={\displaystyle \frac{2{\mathrm{f}}_{\mathrm{v}}{\mathrm{v}}_{\mathrm{v}}{\mathrm{G}}^2{\mathrm{x}}^2}{{\mathrm{D}}_{\mathrm{h}}}}$$

(30)

The values of ${\mathrm{f}}_{\mathrm{l}}$ and ${\mathrm{f}}_{\mathrm{v}}$ can be derived using the calculation methods found in the mean value model, which is particularly pertinent for laminar flow in rectangular channels. This can be computed using the following formula:

$${\mathrm{f}}_{\mathrm{k}}{\mathrm{R}\mathrm{e}}_{\mathrm{k}}=24\left(1-1.3553\mathsf{\beta }+1.9467{\mathsf{\beta }}^2-1.7012{\mathsf{\beta }}^3+0.9564{\mathsf{\beta }}^4-0.2537{\mathsf{\beta }}^5\right)$$

(31)

where k can be l or v, the selection of C depends on the flow patterns of the vapor and liquid phases in two-phase flow. The parameter β represents the aspect ratio of the rectangular channel.

The specific formula can be referenced as follows:

$$\mathrm{C}=\left\{\begin{array}{cc}\hfill 0.39{\mathrm{R}\mathrm{e}}_{\mathrm{l}\mathrm{o}}^{0.03}{\mathrm{S}\mathrm{u}}_{\mathrm{v}\mathrm{o}}^{0.1}{\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{l}}}{{\mathsf{\rho }}_{\mathrm{v}}}}\right)}^{0.35},& \mathrm{L}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{d}:\mathrm{T}\mathrm{u}\mathrm{r}\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{t}/\mathrm{V}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{r}:\mathrm{T}\mathrm{u}\mathrm{r}\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{t}\hfill \\ \hfill {0.0015\mathrm{R}\mathrm{e}}_{\mathrm{l}\mathrm{o}}^{0.59}{\mathrm{S}\mathrm{u}}_{\mathrm{v}\mathrm{o}}^{0.19}{\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{l}}}{{\mathsf{\rho }}_{\mathrm{v}}}}\right)}^{0.36},& \mathrm{L}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{d}:\mathrm{L}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}/\mathrm{V}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{r}:\mathrm{T}\mathrm{u}\mathrm{r}\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{t}\hfill \\ \hfill 8.7\times {10}^{-4}{\mathrm{R}\mathrm{e}}_{\mathrm{l}\mathrm{o}}^{0.17}{\mathrm{S}\mathrm{u}}_{\mathrm{v}\mathrm{o}}^{0.5}{\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{l}}}{{\mathsf{\rho }}_{\mathrm{v}}}}\right)}^{0.14},& \mathrm{L}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{d}:\mathrm{T}\mathrm{u}\mathrm{r}\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{t}/\mathrm{V}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{r}:\mathrm{L}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}\hfill \\ \hfill 3.5\times {10}^{-5}{\mathrm{R}\mathrm{e}}_{\mathrm{l}\mathrm{o}}^{0.44}{\mathrm{S}\mathrm{u}}_{\mathrm{v}\mathrm{o}}^{0.5}{\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{l}}}{{\mathsf{\rho }}_{\mathrm{v}}}}\right)}^{0.48},& \mathrm{L}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{d}:\mathrm{L}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}/\mathrm{V}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{r}:\mathrm{L}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}\hfill \end{array}\right..$$

(32)

2.9. Jige et al. Model

Jige et al. [29] investigated the condensation heat transfer and pressure drop characteristics of four refrigerants (R134a, R410A, R32, and R1234ze(E)) within horizontal multi-port rectangular channels at mass fluxes ranging from 100 to 400 kg/m²s, under saturated temperatures of 60 °C and 40 °C. The study elucidated the impact of various factors such as mass flux, vapor quality, saturated pressure, refrigerant composition, and the D_h of the rectangular channels on condensation characteristics. Based on these influences, they proposed a new correlation for predicting the frictional pressure drop of condensation flows in small channels, as follows:

$${\left({\displaystyle \frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{Z}}}\right)}_{\mathrm{F}}=\left[{\mathrm{x}}^{1.8}+(1-\mathrm{x}{)}^{1.8}{\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{v}}{\mathrm{f}}_{\mathrm{l}\mathrm{o}}}{{\mathsf{\rho }}_{\mathrm{l}}{\mathrm{f}}_{\mathrm{v}\mathrm{o}}}}+0.65{\mathrm{x}}^{0.68}(1-\mathrm{x}{)}^{0.43}{\left({\displaystyle \frac{{\mathsf{\mu }}_{\mathrm{l}}}{{\mathsf{\mu }}_{\mathrm{v}}}}\right)}^{1.25}{\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{v}}}{{\mathsf{\rho }}_{\mathrm{l}}}}\right)}^{0.75}\right]\left({\displaystyle \frac{2{\mathrm{f}}_{\mathrm{v}\mathrm{o}}{\mathrm{G}}^2}{{\mathrm{D}}_{\mathrm{h}}{\mathsf{\rho }}_{\mathrm{v}}}}\right).$$

(33)

The expression for ${\mathrm{f}}_{\mathrm{k}\mathrm{o}}$ is as follows, where k can be l or v:

$${\mathrm{f}}_{\mathrm{k}\mathrm{o}}=\left\{\begin{array}{c}\mathsf{\lambda }/\left(\mathrm{G}{\mathrm{D}}_{\mathrm{h}}/{\mathsf{\mu }}_{\mathrm{k}}\right), \mathrm{for} \left(\mathrm{G}{\mathrm{D}}_{\mathrm{h}}/{\mathsf{\mu }}_{\mathrm{k}}\right)\le 1500\\ 0.046/(G{\mathrm{D}}_{\mathrm{h}}/{\mathsf{\mu }}_{\mathrm{k}}{)}^{0.2}, \mathrm{for} (G{\mathrm{D}}_{\mathrm{h}}/{\mathsf{\mu }}_{\mathrm{k}})>1500\end{array}\right..$$

(34)

In circular channels, $\mathsf{\lambda }=16$. For rectangular channels, refer to the calculation method of ${\mathrm{f}}_{\mathrm{k}}{\mathrm{R}\mathrm{e}}_{\mathrm{k}}$ as described by Kim and Mudawar [28].

3. Experimental Setup and Data Reduction

To determine the pressure drop characteristics of multi-port flat tubes with a D_h of 0.78 mm, a test apparatus featuring a novel transition section was established for two-phase flows. The experimental section utilizes extruded aluminum multi-port flat tubes, with a total length of 100 mm, incorporating parallel channels that have a rectangular cross-sectional shape. Operational parameters were varied across a broad range to ensure high reliability and comparability of the pressure drop correlations. Specific test parameters are detailed in

Table 1. Operation conditions.

Test Fluid	R410A
Mass flux $\left[\mathrm{k}\mathrm{g}{\mathrm{m}}^{-2}{\mathrm{s}}^{-1}\right]$	200, 250, 300
Vapor quality $\left[\text{-}\right]$	0.09–0.92
Saturation temperature $\left[\mathrm{℃}\right]$	30–40

.

3.1. Test Method

Figure 1 shows the schematic diagram of the test loop and its main components, where the overall heat source and sink of the system are managed by two water tanks (the test water tank and the auxiliary water tank). The conditions on the refrigerant side are controlled by adjusting water flow and temperature. The refrigerant circuit is powered by a gear pump, with mass flux primarily regulated by the pump’s frequency. The pump’s minimum stable output is 6 kg/h, but it can be fine-tuned using an expansion valve to further reduce the refrigerant velocity. The refrigerant passes through an OVAL flow meter, which verifies the required mass flow rate and helps dampen any flow fluctuations caused by the pump, with the expansion valve also serving to mitigate these fluctuations. Next, the refrigerant enters a plate evaporator and a heating section to heat the refrigerant from a subcooled or saturated state to a superheated state. To meet specific experimental conditions, the vapor quality required is adjusted by the condenser, ensuring the refrigerant is saturated before entering the test section. The system logic automatically adjusts the water temperature and flow in the test heat exchanger to ensure the refrigerant exits in a subcooled state. Finally, the subcooler’s function is to make sure the refrigerant is sufficiently subcooled before it enters the pump cycle. Primarily to prevent any phase change due to temperature differences between the refrigerant and the external environment, thus completing the entire cycle of the condensation experiment.

Once the testing circuit is established, a static pressure test is performed with pure nitrogen, setting the pressure 10% above the maximum operating level. If the pressure loss is less than 1 kPa over a 3 h period, it is considered acceptable. The test loop is then evacuated using a vacuum pump until the pressure drops below 10 kPa, as detected by the sensors. This vacuum state is maintained for 30 min to confirm the absence of any form of gas in the test loop. This procedure is repeated each time the test section is altered and can also be applied directly to the test section.

3.2. Test Line

Figure 2 displays the design of the test line, which primarily consists of two platinum resistance thermometers (pt100), a pressure acquisition system, a heating jacket, and a parameter sampling kit. The pt100 thermometers are specifically used for measuring the inlet and outlet temperatures of the refrigerant fluid, each with a length of 15 cm. During system operation, a pressure acquisition module is mounted above the tips of the temperature sensors, ensuring consistency between the pressure and temperature readings at the inlets and outlets. The heating jacket circulates water internally and uniformly transfers heat to the microchannel flat tubes through aluminum material. Notably, after transitioning from a circular tube to a cavity and then to a flat tube, a change in geometry causes a pressure variation, which will be discussed in detail in subsequent sections. Once the refrigerant in the tooling cavity is thoroughly mixed, it immediately enters the test section. However, within a “measurement flange”, it is only possible to determine the average temperature and pressure drop across all channels. At this stage, the separation of microchannels is yet to be achieved, and due to thermal effects from the environment, the pressure drop within the flat tube should be considered a sum of momentum and frictional pressure drops.

3.3. Test Section

This study examined a flat microchannel featuring a D_h of 0.78 mm. The relevant physical parameters (dimensions and roughness) were measured using a metallographic microscope and a roughness gauge, with the arithmetic mean detailed in

Table 2. Characteristics of Diverse D_h Microchannels.

Number	Tube
Channel number	18
Tube width [mm]	25.3
Tube thickness [mm]	1.26
Hole width [mm]	0.95
Hole height [mm]	0.66
D [mm]	0.78
Wall thickness [mm]	0.29

. The selected test section length was 10 cm, and the microchannel flat tube was made of aluminum material. Additionally, a layer of thermally conductive silicone grease was applied between the thermocouples and the heating jacket to fill any gaps between them.

3.4. Data Reduction

3.4.1. Pressure Drop

The local pressure drops observed in the experimental system are depicted in Figure 3. The pressures at the inlet and outlet, for both single-phase and saturated (two-phase) refrigerants, were monitored using two absolute pressure sensors positioned at the inlet and outlet mixers. The overall pressure drop across the test section comprises several components: the pressure drop due to contraction between the inlet plenum and microchannel entry, as well as the deceleration and frictional pressure drops inside the microchannel, and the expansion pressure drop between the microchannel outlet and the outlet plenum. By calculating the local pressure drop between the inlet plenum and the microchannel inlet, the pressure at the microchannel inlet can be inferred. Similarly, the pressure at the microchannel outlet is determined by the pressure measured in the outlet plenum, adjusted by the local pressure drop between the microchannel outlet and the outlet plenum.

In this study, the region between the microchannel entry and the inlet plenum is fully insulated. The steam within the plenum is maintained in a saturated state, controlled by a front-end condenser, and verified using pressure transducers and thermocouples. Therefore, the compression section’s pressure drop is characterized as a two-phase flow. As condensation occurs inside the microchannel, the associated pressure drop is modeled as two-phase flow. If complete condensation occurs, the pressure change from the microchannel exit to the outlet mixer should be treated as single-phase flow; otherwise, the two-phase flow model remains applicable.

The pressure drop (PD in kPa/m) is calculated by dividing the differential pressure measurement by the length of the tube.

$$\mathrm{P}\mathrm{D}={\displaystyle \frac{\mathrm{D}\mathrm{P}}{\mathrm{L}}}$$

(35)

The contraction pressure drop during phase transition can be estimated using the slip flow model, which assumes the absence of vena contracta [30].

$$\mathsf{\Delta }{\mathrm{P}}_{\mathrm{C}\mathrm{o}\mathrm{n}}={\displaystyle \frac{{\mathrm{G}}^2}{2{\mathsf{\rho }}_{\mathrm{l}}}}\left\{{\left({\displaystyle \frac{1}{{\mathrm{C}}_{\mathrm{c}}}}-1\right)}^2+\left(1-{\mathsf{\sigma }}^2\right)\right\}\left(1+\mathrm{x}{\displaystyle \frac{\left({\mathsf{\rho }}_{\mathrm{l}}-{\mathsf{\rho }}_{\mathrm{v}}\right)}{{\mathsf{\rho }}_{\mathrm{l}}}}\right)$$

(36)

$${\mathrm{C}}_{\mathrm{c}}=1-{\displaystyle \frac{1-\mathsf{\gamma }}{2.08\left(1-\mathsf{\gamma }\right)+0.5371}}$$

(37)

$$\mathsf{\gamma }={\displaystyle \frac{{\mathrm{A}}_{\mathrm{s}}}{{\mathrm{A}}_{\mathrm{l}}}}$$

(38)

In this model, G represents the mass flux in the smaller sectional area. The variables ${\mathsf{\rho }}_{\mathrm{t}\mathrm{p}}$, ${\mathsf{\rho }}_{\mathrm{l}}$, ${\mathsf{\rho }}_{\mathrm{v}}$, and ${\mathsf{\rho }}^{″}$ denote the homogeneous density, liquid density, vapor density, and mixture density, respectively. The parameter $\mathsf{\alpha }$ refers to the void fraction, and $\mathsf{\gamma }$ signifies the ratio of the smaller sectional area to the larger one.

In microchannels, as steam condenses, the vapor quality diminishes along the axial path; consequently, the resulting deceleration pressure drop is characterized as follows [31]:

$$\mathsf{\Delta }{\mathrm{P}}_{\mathrm{D}\mathrm{e}}={\left[{\displaystyle \frac{{\mathrm{G}}^2{\mathrm{x}}^2}{{\mathsf{\rho }}_{\mathrm{v}}\mathsf{\alpha }}}+{\displaystyle \frac{{\mathrm{G}}^2(1-\mathrm{x}{)}^2}{{\mathsf{\rho }}_{\mathrm{l}}\left(1-\mathsf{\alpha }\right)}}\right]}_{\mathrm{x}={\mathrm{x}}_{\mathrm{i}\mathrm{n}}}-{\left[{\displaystyle \frac{{\mathrm{G}}^2{\mathrm{x}}^2}{{\mathsf{\rho }}_{\mathrm{v}}\mathsf{\alpha }}}+{\displaystyle \frac{{\mathrm{G}}^2(1-\mathrm{x}{)}^2}{{\mathsf{\rho }}_{\mathrm{l}}\left(1-\mathsf{\alpha }\right)}}\right]}_{\mathrm{x}={\mathrm{x}}_{\mathrm{o}\mathrm{u}\mathrm{t}}}$$

(39)

$$\mathsf{\alpha }={\left[1+{\left({\displaystyle \frac{1-\mathrm{x}}{\mathrm{x}}}\right)}^{0.74}\cdot {\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{v}}}{{\mathsf{\rho }}_{\mathrm{l}}}}\right)}^{0.65}\cdot {\left({\displaystyle \frac{{\mathsf{\mu }}_{\mathrm{l}}}{{\mathsf{\mu }}_{\mathrm{v}}}}\right)}^{0.13}\right]}^{-1}.$$

(40)

Single phase expansion pressure drop would be [32]:

$$\mathsf{\Delta }{\mathrm{P}}_{\mathrm{E}\mathrm{x}\mathrm{p}}={\mathrm{K}}_{\mathrm{e}}\cdot {\displaystyle \frac{\mathsf{\rho }\cdot {\mathrm{u}}_{\mathrm{s}}^2}{2}}+{\displaystyle \frac{\mathsf{\rho }\cdot {\mathrm{u}}_{\mathrm{s}}^2\cdot \left({\mathsf{\gamma }}^2-1\right)}{2}}$$

(41)

$${\mathrm{K}}_{\mathrm{e}}=\left\{\begin{array}{c}0.8,400\le {\mathrm{R}\mathrm{e}}_{\mathrm{s}}\le 11000\\ -0.2154+0.0043{\mathrm{R}\mathrm{e}}_{\mathrm{s}}-5\times {10}^6{\mathrm{R}\mathrm{e}}_{\mathrm{s}}^2,{\mathrm{R}\mathrm{e}}_{\mathrm{s}}<400\end{array}\right..$$

(42)

Here, ${\mathrm{K}}_{\mathrm{e}}$ is considered the coefficient of expansion loss, while ${\mathrm{R}\mathrm{e}}_{\mathrm{s}}$ and ${\mathrm{u}}_{\mathrm{s}}$ represent the average values within the smaller channel.

Considering the evaluations of localized pressure drop, the total frictional pressure drop for two-phase flow within the microchannel can be outlined as follows:

$$\mathsf{\Delta }{\mathrm{P}}_{\mathrm{f}}=\mathsf{\Delta }{\mathrm{P}}_{\mathrm{m}\mathrm{e}\mathrm{a}}-\mathsf{\Delta }{\mathrm{P}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{o}\mathrm{n}}+\mathsf{\Delta }{\mathrm{P}}_{\mathrm{D}\mathrm{e}}-\mathsf{\Delta }{\mathrm{P}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s},\mathrm{e}\mathrm{x}\mathrm{p}}.$$

(43)

3.4.2. Evaluation of Measurement Uncertainty

To ensure the study’s reliability, the operating system underwent calibration. Thermistors were adjusted in an oil bath using a platinum resistance thermometer, achieving an uncertainty of less than 0.01 K. Pressure sensors and flow meters were similarly calibrated using standard pressure gauges and corresponding calibration setups. The accuracy of the experiment was further verified by considering the heat balance between the heat transfer rate from the refrigerant and the total rate removed by the cooling water, typically within a margin of less than 10.83%, indicating the experiment’s effective thermal insulation and measurement precision. Traditional error propagation analysis was employed to assess the maximum uncertainties of indirect experimental parameters [33]. The uncertainties related to the working parameters are shown in

Table 3. Measurement Accuracy and Calculation Parameter Uncertainties.

Measurement	Range	Brand	Uncertainty
T (thermistors)	−20–80 °C	SAILING	0.01 °C
Pressure sensors	0–5 kPa	MIRCO	0.055%
${\dot{\mathrm{m}}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$	0–40 kg/h	OVAL	0.1%
Diameter	0–150 mm	Deli	0.1 mm
PD	0–10 kPa	YOKOGAWA	0.19–1.57%
xin	-	-	0.89–23.96%

.

4. Results

Measurements of convective condensation flows were conducted in 18 parallel microchannels, covering a total of 81 test conditions. The range of parameters examined (including mass flux, vapor quality, heat flow rate, saturation temperature, absolute pressure, vapor superheating, and Reynolds numbers based on liquid and vapor flows within the microchannel) can be outlined as follows:

• $200\le G \left[\mathrm{k}\mathrm{g}/{\mathrm{m}}^2\mathrm{s}\right]\le 300$;
• $0.09\le x \left[\text{-}\right]\le 0.92$;
• $35\le Q \left[\mathrm{W}\right]\le 432$;
• $30\le T_{sat} \left[\mathrm{℃}\right]\le 40$;
• $0.15\le T_{sub,out} \left[\mathrm{℃}\right]\le 0.48$;
• $1.886\le P_{sat} \left[\mathrm{k}\mathrm{P}\mathrm{a}\right]\le 2.422$;
• $1402<{Re}_{lo}<2427$;
• $10443<{Re}_{vo}<16637$.

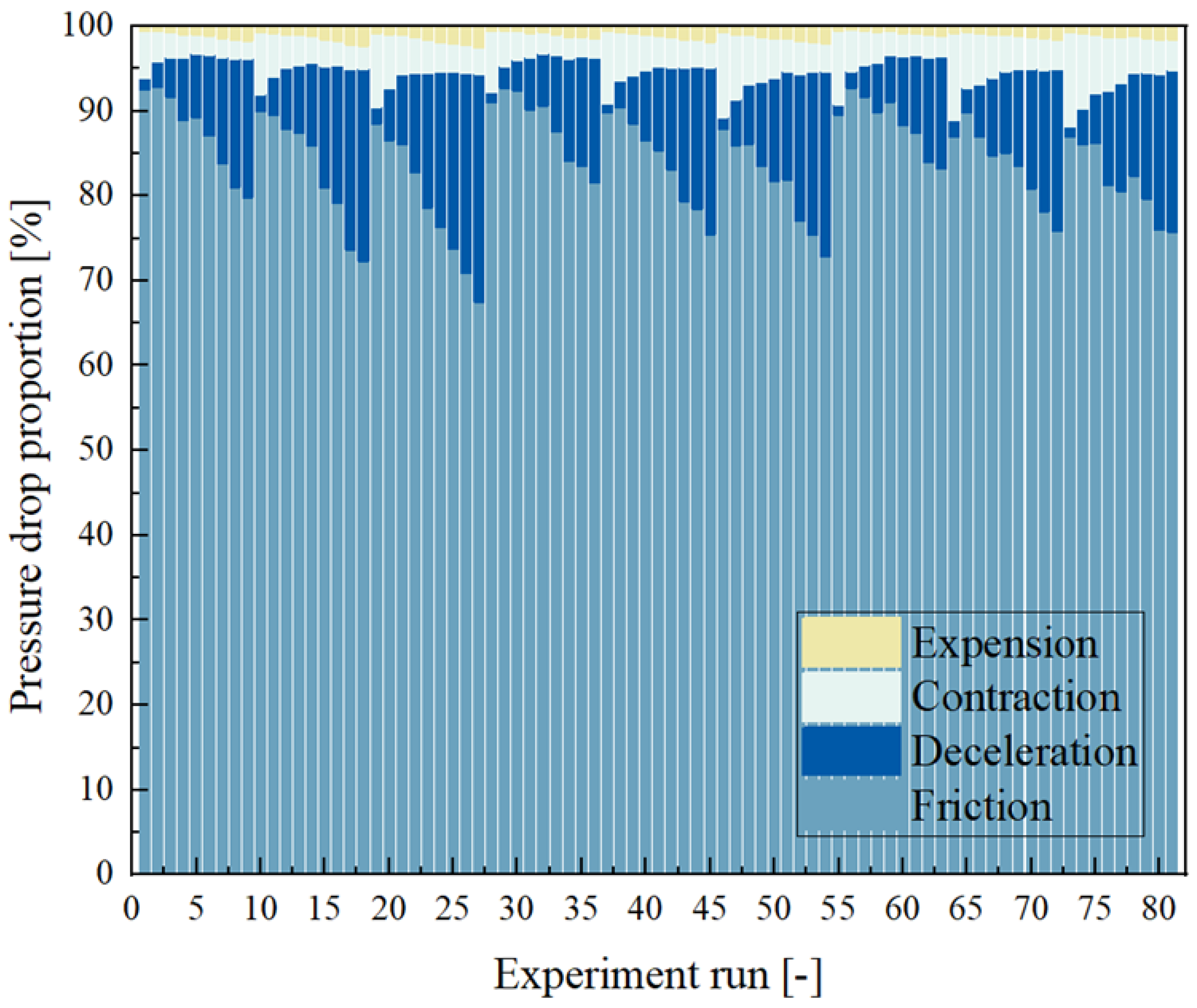
The impact of each factor on the overall pressure drop is detailed in Figure 4. Contraction and expansion pressure drops within the microchannels are minimal. The percentage impact of contraction pressure drops varies between 2.06% and 11.06% under different operating conditions, while the percentage impact of expansion pressure drops ranges from 0.46% to 2.50%. The results indicate that two-phase frictional pressure drop remains the predominant pressure drop mechanism within the microchannels.

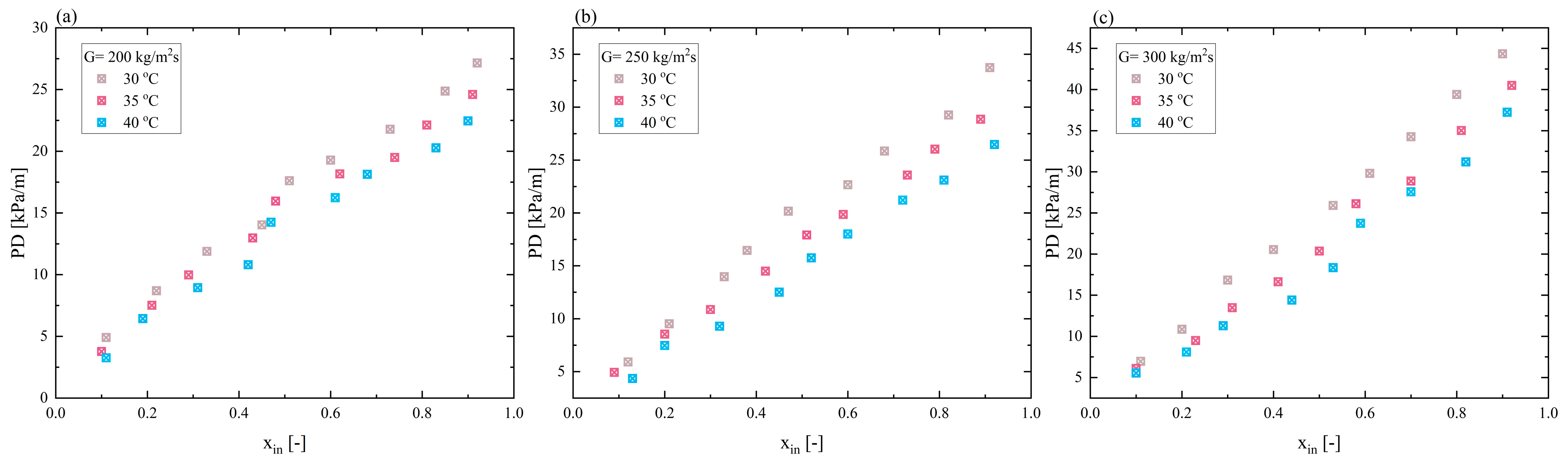
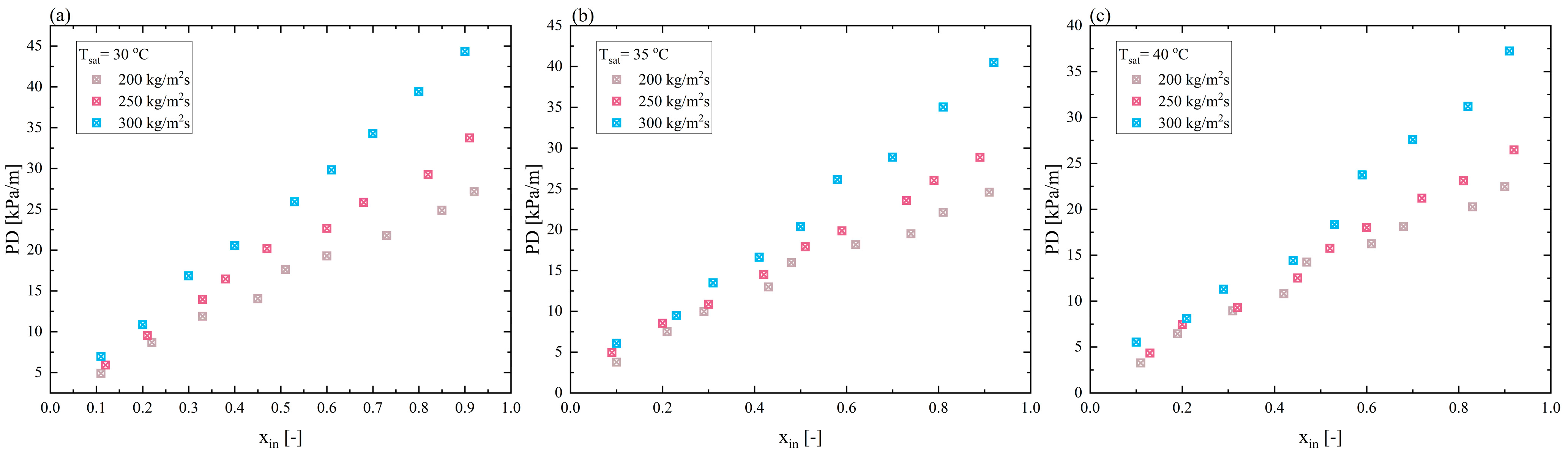
4.1. Mass Flux Effect

Figure 5a–c shows three different pressure gradient trends under three different mass flux conditions, with a consistent overall trend of increasing pressure gradients as mass flux increases. For example, at a saturation temperature of 30 °C, when the mass flux increases from 200 kg/m²·s to 250 kg/m²·s, the pressure gradient at a vapor quality of about 0.85 increases by 17.63%, and when the mass flux increases from 250 kg/m²·s to 300 kg/m²·s, the pressure gradient at a vapor quality of about 0.8 increases by 34.67%. Thus, under high vapor quality, the pressure gradient is more sensitive to changes in mass flux. The pressure drop also increases with the increase in vapor quality because as the vapor continuously condenses into liquid, the increase in vapor quality intensifies the phase change reactions, resulting in heightened frictional interaction between the vapor and liquid phases. Additionally, flow patterns predominantly shift to annular and mist flow [34], where the liquid adheres to the microchannel walls in a film, while the gas flows rapidly at the center. This mode enhances the effects of surface tension and shear forces, resulting in more significant pressure drops.

4.2. Saturation Temperature Effect

In this section, data from 81 experimental measurements are illustrated in Figure 6 to explain the influence of saturation temperature (pressure) on frictional pressure drops. The results are presented as a function of inlet vapor quality, x_in. The experimental data are categorized into three groups based on mass flux: G = 300 kg/m²·s, G = 250 kg/m²·s, and G = 200 kg/m²·s. The figure for these three cases exhibits two general trends: firstly, the frictional pressure drop decreases as the saturation temperature increases; secondly, the pressure drop increases with increasing vapor quality. The observed differences in frictional pressure drops can be explained as follows: the explanation for the first trend was discussed in the previous section and is largely influenced by flow patterns and the shear forces between the vapor and liquid phases. Regarding the second trend, as the saturation temperature rises, so does the corresponding saturation pressure, which increases the saturated vapor density. From an energy conservation perspective, this reduces the slip speed between the gas and liquid phases, thereby decreasing shear forces and reducing the frictional pressure drop. For instance, at a mass flux of G = 300 kg/m²·s, when the saturation temperature is increased from 30 °C to 35 °C (an increase of 16.67%), the saturated vapor density increases to about 87.98 kg/m³ (an approximate increase of 15.9%), which corresponds to a reduction in the pressure drop of about 14.82%; however, when the saturation temperature is raised from 35 °C to 40 °C (an increase of 14.29%), the saturated vapor density increases to about 102.17 kg/m³ (an approximate increase of 16.12%), resulting in a pressure drop reduction of about 10.64%. During steam condensation, as the vapor mass along the microchannel axis decreases, the vapor density at high vapor quality is more significantly affected by the saturation pressure (temperature) at the microchannel entry.

5. Pressure Drop Predictions

The measurement results of two-phase frictional pressure drop were compared with those obtained through traditional correlation methods. These traditional methods include the Lockhart and Martinelli model [10], homogeneous model, Friedel model [17], and Cavallini model [24], which are commonly used to predict adiabatic flows in macrochannels. More recent studies on minichannel, such as those by Son and Oh [25], Sakamatapan and Wongwises [26], and Jige et al. [29], as well as transition studies from microchannel to macrochannel by Andresen et al. [27] and Kim and Mudawar [28], were also compared. 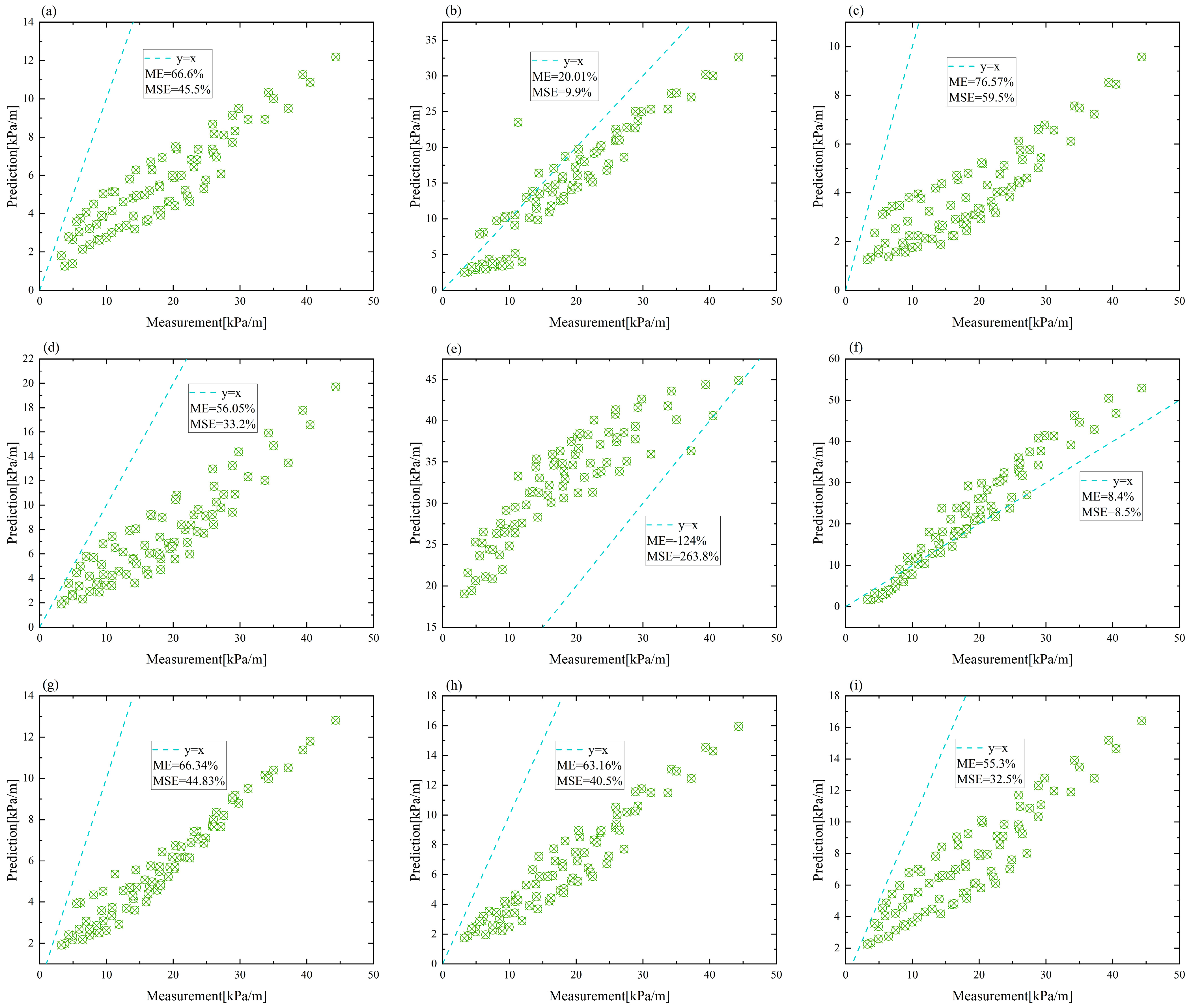The results are presented in Figure 7. The best prediction was achieved using the correlation by Sakamatapan and Wongwises, with a mean error (ME) of 8.4% and a mean squared error (MSE) of 8.5%, as shown in Equations (44) and (45).

$$\mathrm{\%}\mathrm{M}\mathrm{E}={\displaystyle \frac{1}{\mathrm{n}}}\left({\displaystyle \frac{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}-\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}}\right)\times 100\mathrm{\%}$$

(44)

$$\mathrm{\%}\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{1}{\mathrm{n}}}\left({\displaystyle \frac{{\left(\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}-\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right)}^2}{{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}^2}}\right)\times 100\mathrm{\%}$$

(45)

Figure 7f demonstrates that the correlation by Sakamatapan and Wongwises [26] exhibits higher accuracy in regions of low pressure drop compared to high pressure drop regions. The fact that the %MSE is slightly higher than the %ME also confirms this trend, amplifying the impact of larger error regions, specifically in areas of high pressure drop.

This correlation was specifically developed for multiport minichannels using the concept of equivalent mass flux (refer to Equation (26)). Although originally developed for the refrigerant R134a, experimental studies showed that it also accurately predicts pressure drops within this range for R410A in parallel microchannel flat tube experiments. Therefore, it is recommended to use Sakamatapan and Wongwises for predicting pressure drops of R410A in experimental settings of parallel microchannels. Surprisingly, the Lockhart and Martinelli model [10], which was developed for macrochannels, also performed well in these experiments, with an ME of about 20%, and the MSE is about 9.9%, indicating that the Lockhart and Martinelli model did not consistently deviate from the experimental values, meaning there were not many large deviations in the dataset. This may be due to the predominance of laminar flow in the liquid phase (Reynolds number generally less than 2000), while the vapor phase is turbulent, making the use of a C value of 12 appropriate. This indicates that certain correlations derived from two-phase adiabatic flow in macroscopic pipes can reasonably forecast convective condensation pressure drops in microchannels. In contrast, the Son and Oh model [25] significantly overestimated the experimental values and deviated considerably, with an ME of −124% and MSE of 263.8%. This correlation was derived from experiments using single mini copper tubes, and hence, it is not recommended for predicting frictional pressure drops in parallel microchannels within the scope of this work. Despite the comprehensive coverage of conditions and geometric information of experimental specimens by the Kim and Mudawar model [28], the predicted results (ME = 63.16%) are not satisfactory. Therefore, when selecting a correlation, it is advisable to choose one that is highly accurate within a specific range.

6. New Correlation for Prediction

To further enhance the predictive accuracy of the model, this study aims to revise the correlation formula by Sakamatapan and Wongwises [26]. Although the current model demonstrates certain predictive capabilities within the experimental dataset, there are still shortcomings, particularly in regions of high pressure drop where the predictive accuracy is less than ideal. The revised friction factor can be seen in Equation (46).

$${\mathrm{f}}_{\mathrm{t}\mathrm{p}}=122376{\mathrm{R}\mathrm{e}}_{\mathrm{e}\mathrm{q}}^{-1.37}{\mathrm{x}}^{0.36}{\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{l}}}{{\mathsf{\rho }}_{\mathrm{v}}}}\right)}^{2.74}{\left({\displaystyle \frac{{\mathsf{\mu }}_{\mathrm{l}}}{{\mathsf{\mu }}_{\mathrm{v}}}}\right)}^{-4.78}$$

(46)

The performance and comparative analysis of the proposed correlation are detailed in Figure 8. After the revision, the model’s MSE improved from 8.5% to 1.1%. It is evident from the figure that the revised model significantly improves alignment with the experimental data. Future work will focus on further validating the revised model under a broader range of conditions and exploring the potential of applying this method to other types of fluid dynamics models.

7. Conclusions

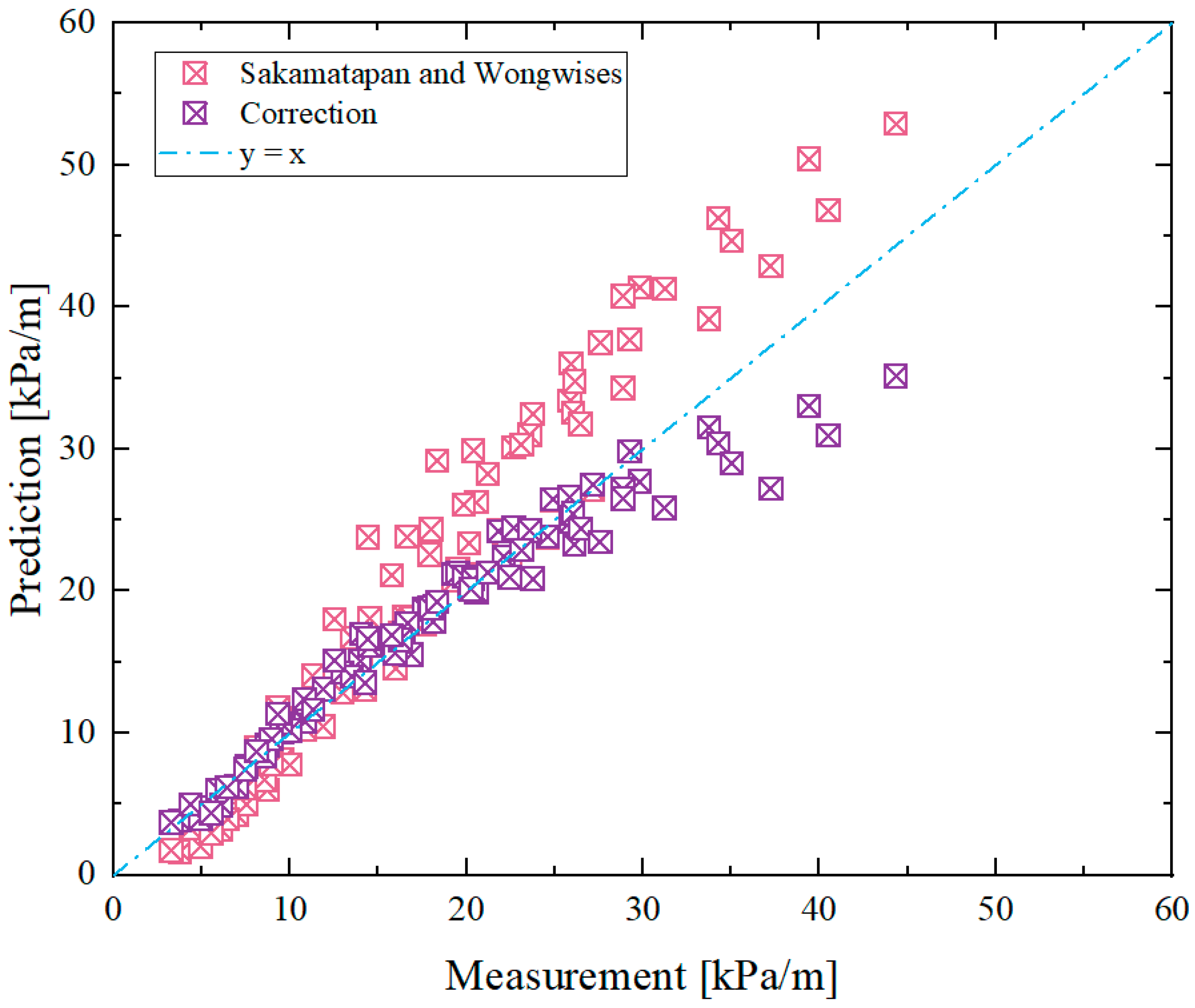
R410A is a near-azeotropic mixture composed of R32 and R125. This experiment primarily investigated the flow condensation behavior of R410A within 18 microchannel tubes (D_h of 0.78 mm). The experiment measured the pressure gradients of R410A under varying mass fluxes (200–300 kg/m²s), saturation pressures (1.886 kPa–2.422 kPa), and vapor qualities (0.09–0.92), and calculated the pressure drop losses due to contraction, expansion, friction, and deceleration. The contributions from contraction and expansion to the pressure drop were found to be very minor, with the lowest contraction pressure drop constituting only 2.06% and the lowest expansion drop at just 0.46%, both of which could essentially be neglected. The experiment also found that the deceleration pressure drop, which reached up to 26.88% of the total, increased with heat flux, indicating that frictional pressure drop remains the primary component of total pressure loss. Key flow parameters identified as contributors to a higher frictional pressure gradient were a rise in mass flux, vapor quality, and a reduction in channel saturation temperature. The measured frictional pressure gradients were also compared with nine empirical correlations, covering everything from single to multi-port channels, and from microchannels to macroscopic channels. Results show that the Lockhart and Martinelli model, originally developed for macroscopic channels, performed well, with an average error of about 20%. The Sakamatapan and Wongwises correlation method exhibited the best performance, with a mean error (ME) of 8.4%. Thus, it is recommended for predicting the frictional pressure gradient under the conditions studied in this research. To further enhance the predictive performance of the model, this study revised the correlation by Sakamatapan and Wongwises [26], improving the model’s MSE to 1.1%. The plan is to continue validating and developing new correlations for accurately predicting condensation pressure drops in microchannels. Additionally, future work should extend to exploring the geometric configurations of microchannels, investigating the condensation characteristics of alternative refrigerants, and developing high-precision predictive models tailored to parallel-flow microchannel systems. An in-depth analysis of various flow patterns is also necessary, focusing particularly on optimizing these regimes to enhance the overall efficiency of microchannel heat exchangers.