The Application of the Particle Element Method in Tubular Propellant Charge Structure: Lumped Element Method and Multiple-Element Method
Abstract
:1. Introduction
2. Lumped Element Method and Multiple-Element Method
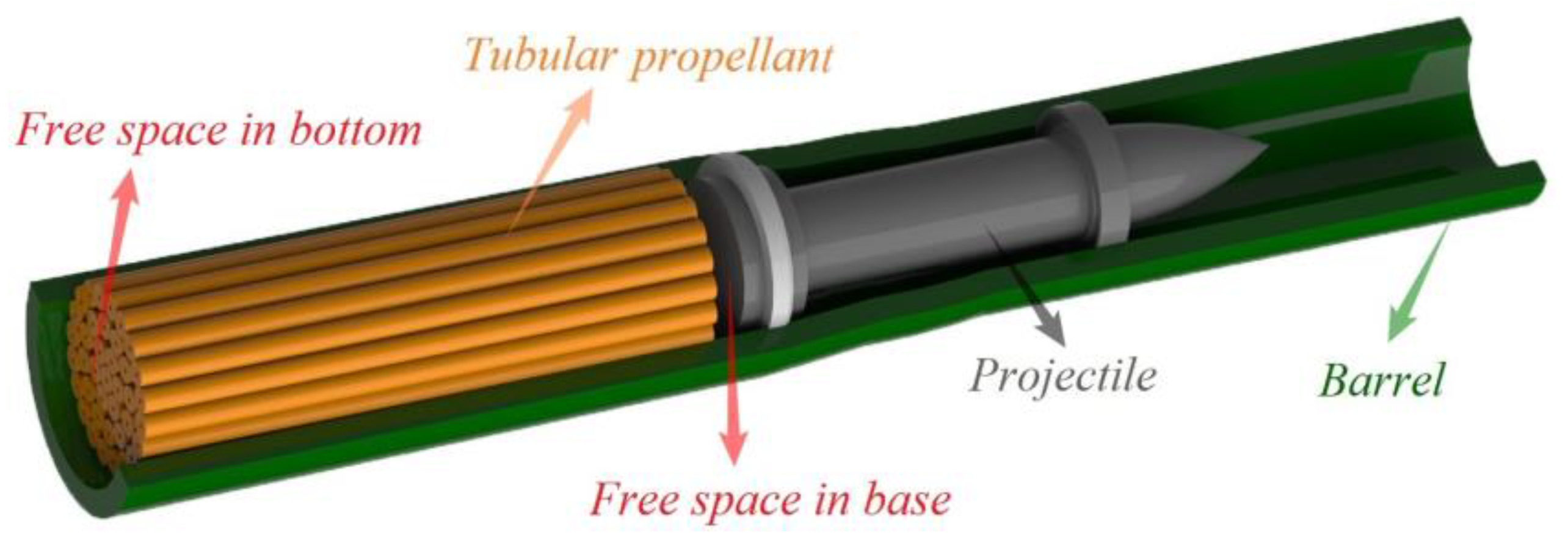
2.1. Physical Model
- (1)
- Each tubular propellant within the same bundle shares identical shape, dimensions, and properties, with identical combustion and motion laws.
- (2)
- Surface ignition temperature criterion is adopted for the tubular propellant, ensuring simultaneous ignition inside and outside the tube on the same cross-section.
- (3)
- The tubular propellants are treated as incompressible.
- (4)
- The thermodynamic characteristics of the propellant gas remain constant and adhere to the Nobel–Abel state equation.
- (5)
- The flow in the chamber is assumed to be inviscid.
2.2. Particle Element Method
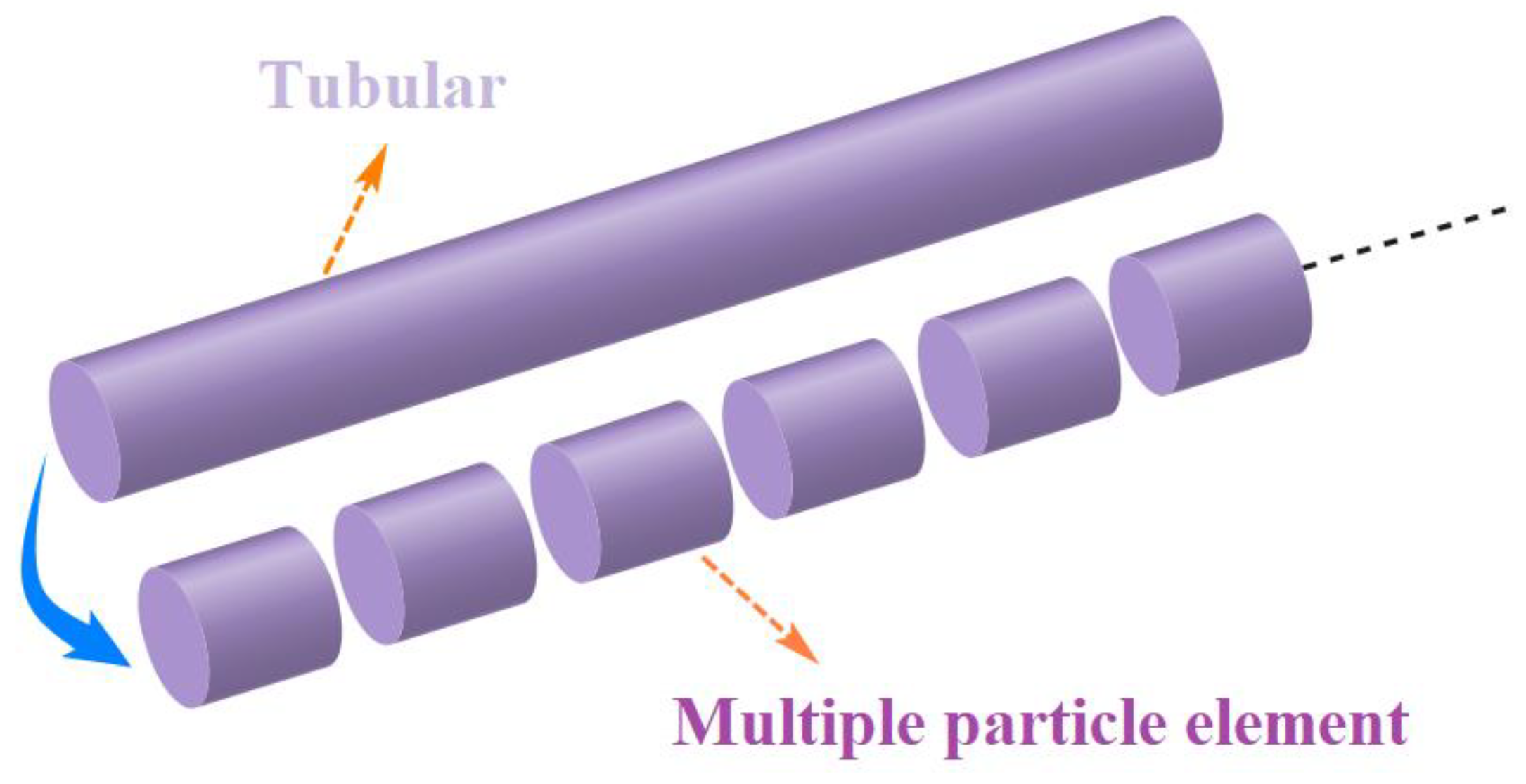
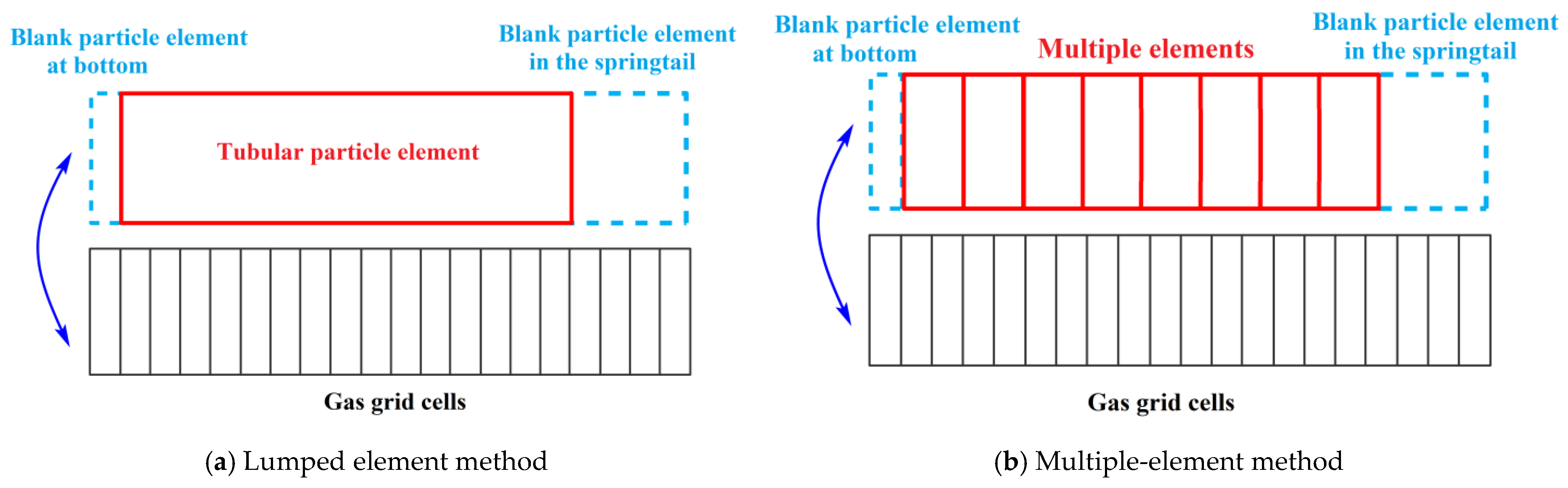
2.2.1. Lumped Element Method
2.2.2. Multiple-Element Method
2.3. Gas Phase Flow Field Equation
2.4. Auxiliary Equation
- (1)
- Inter-phase resistance equation of tubular propellant.
- (2)
- Combustion equation of tubular propellant.
2.5. Coupling and Parameter Transfer between Particle Elements and Flow Field Grid Cells
- (1)
- Flow field computation.
- (2)
- Particle element computation.
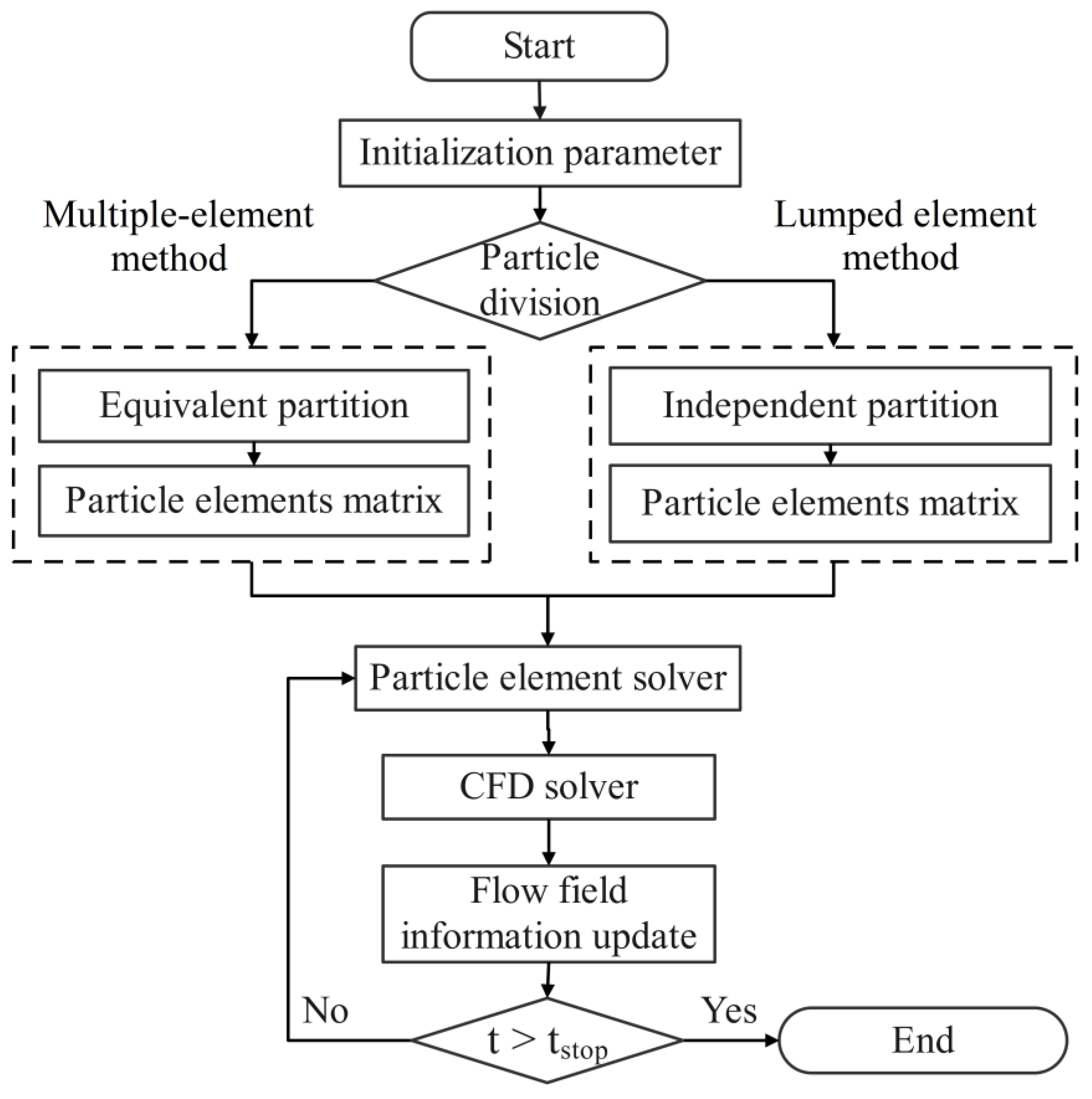
3. Numerical Calculation Method
3.1. Numerical Method
3.2. Calculation Condition
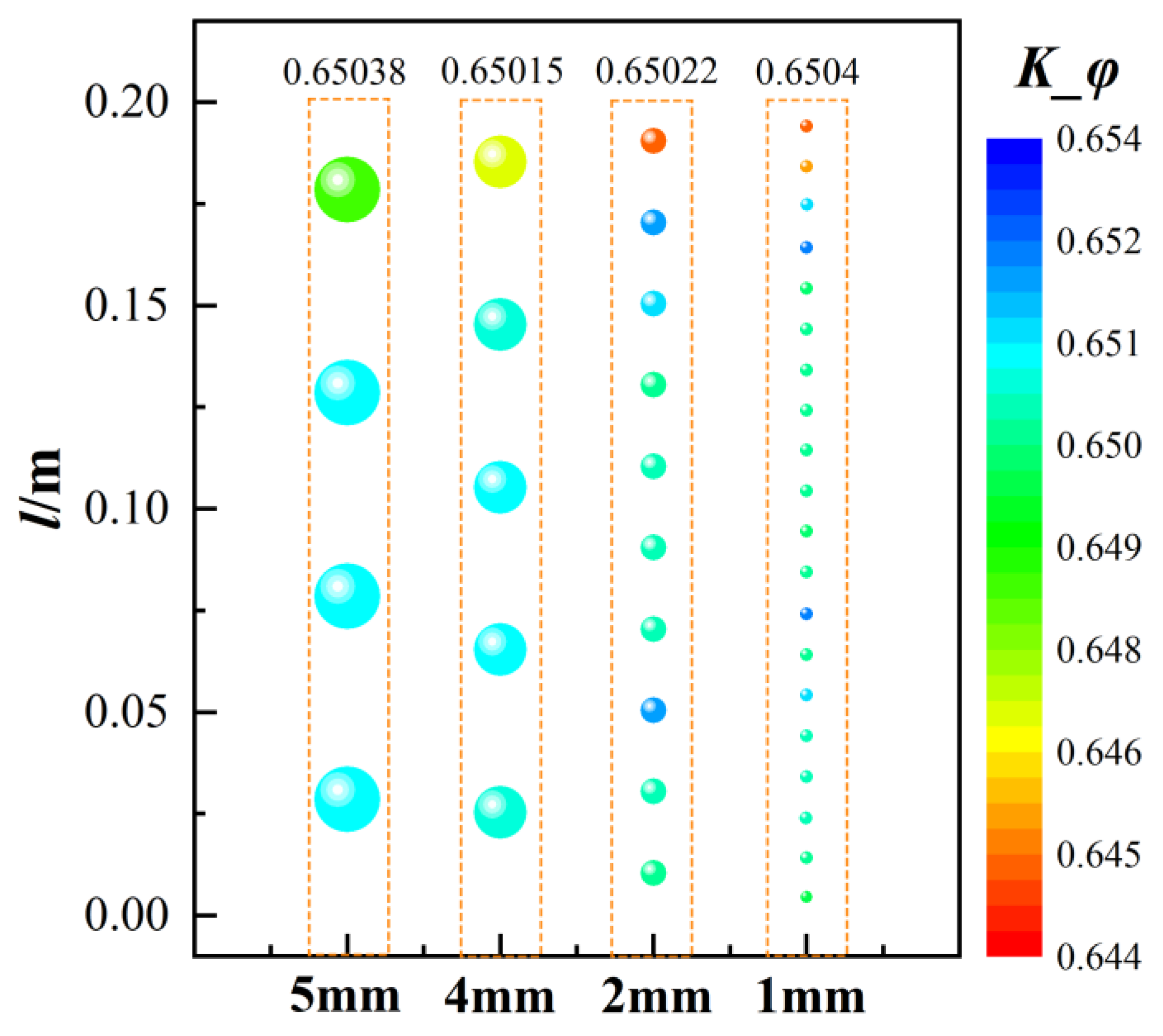
3.3. Mesh Generation
3.4. Calculation Process
4. Results and Discussion
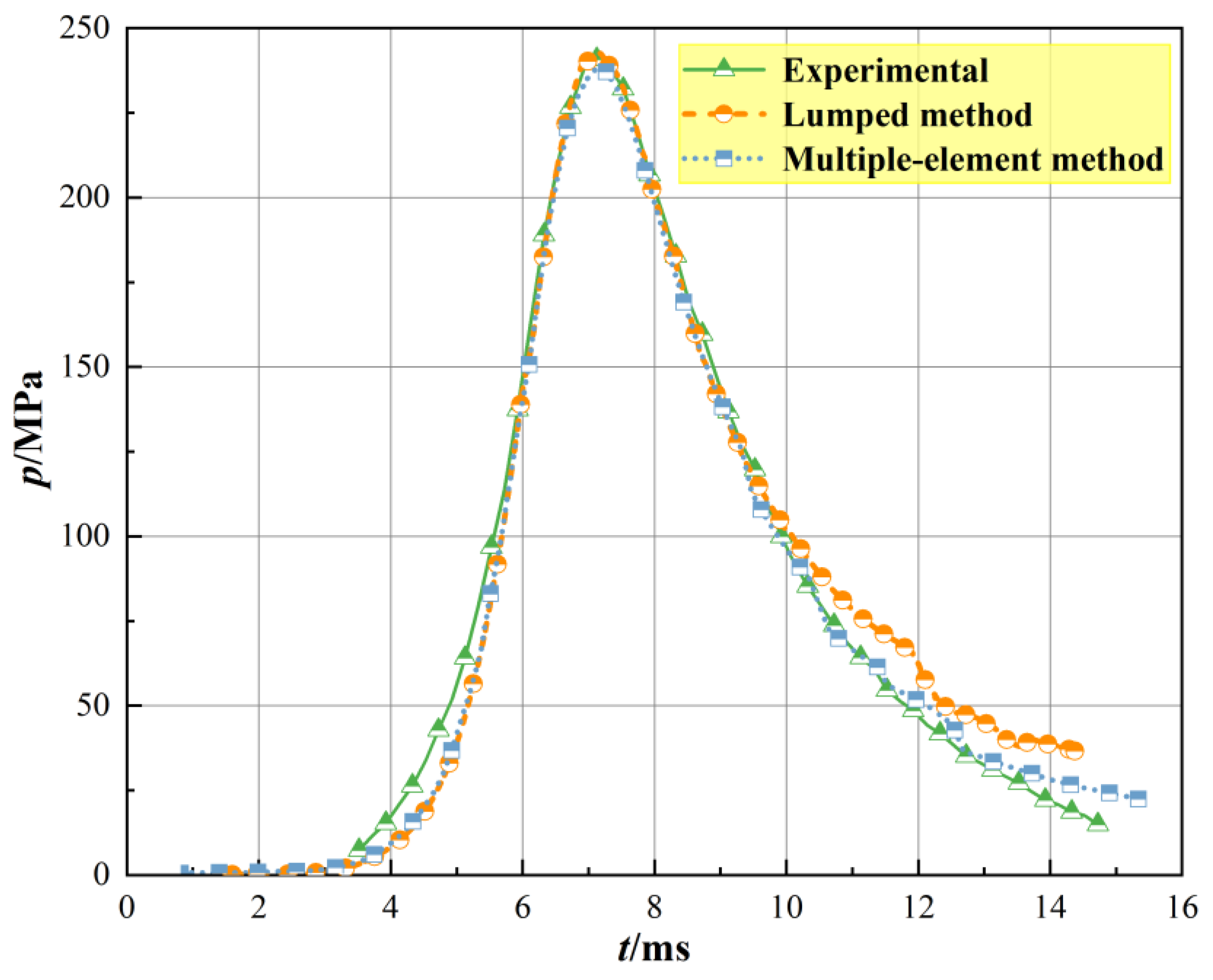
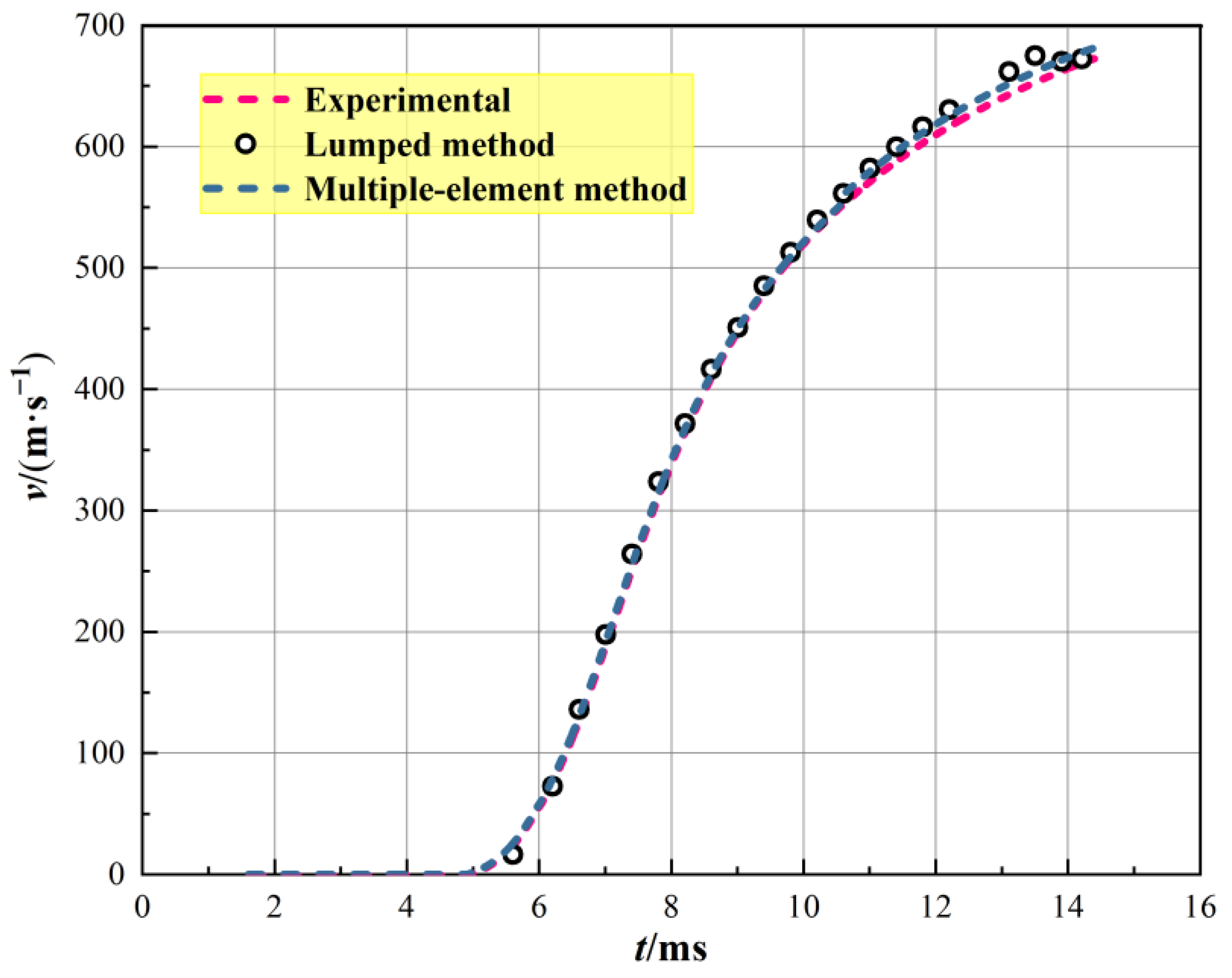
4.1. Comparison of Experimental and Numerical Simulation Results
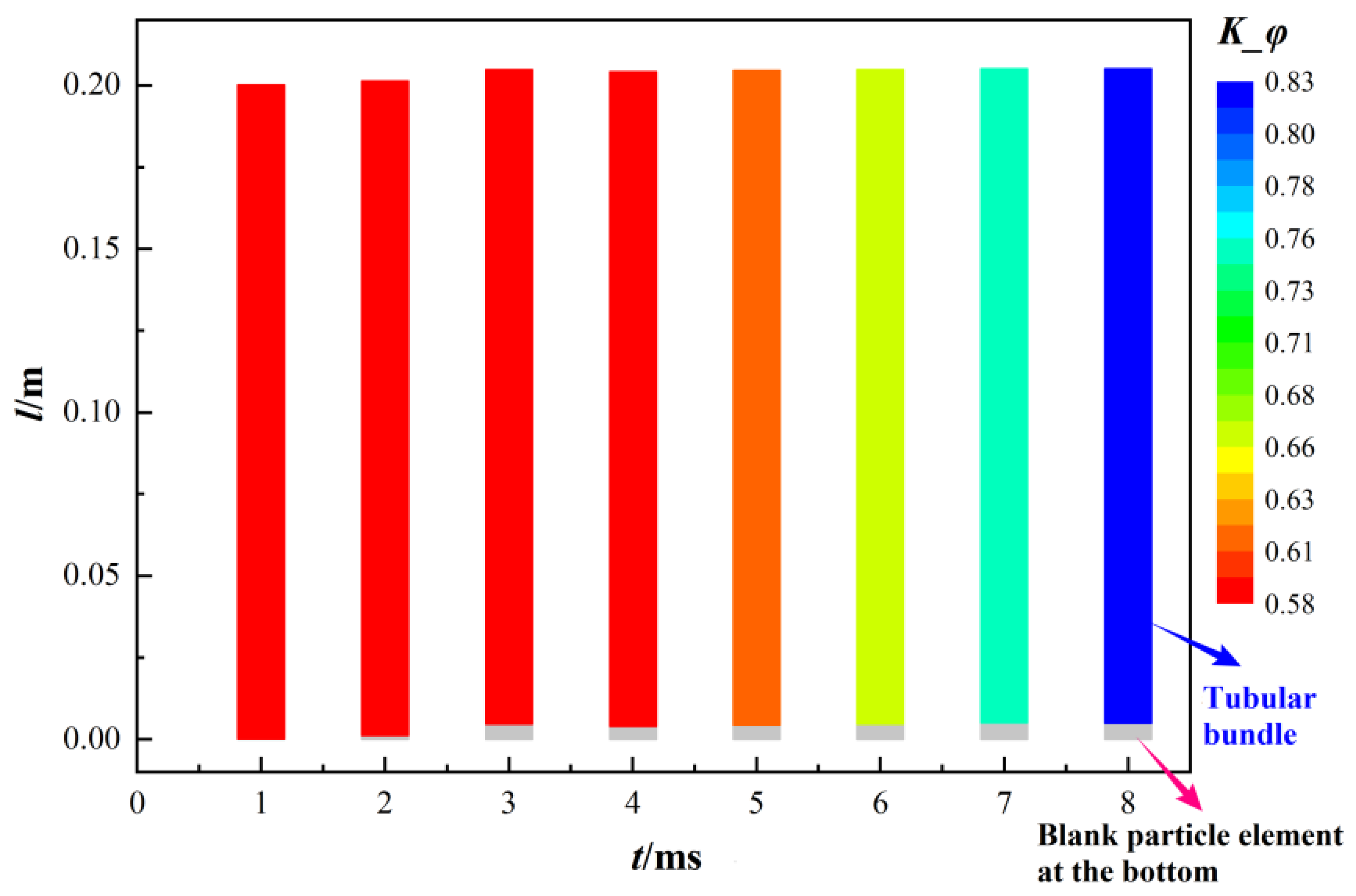
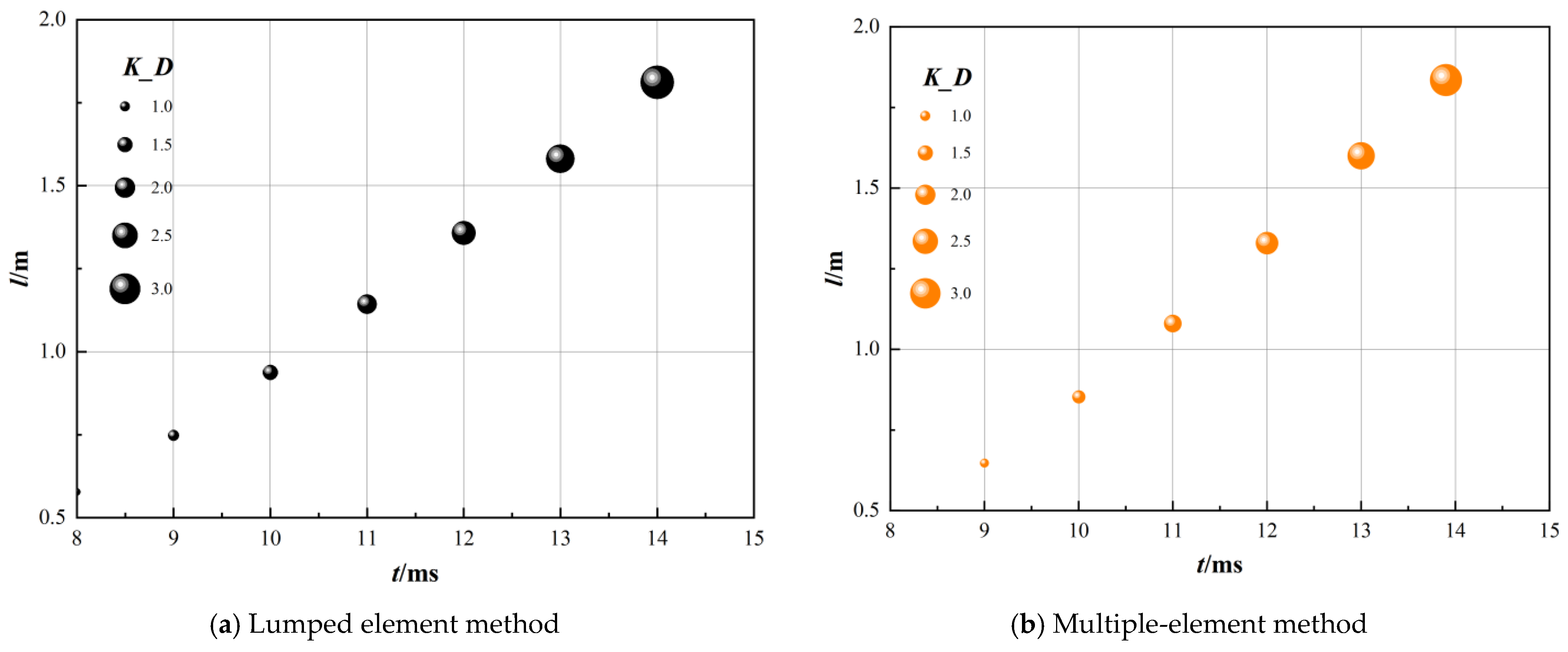
4.2. Analysis of the Tubular Propellant Movement
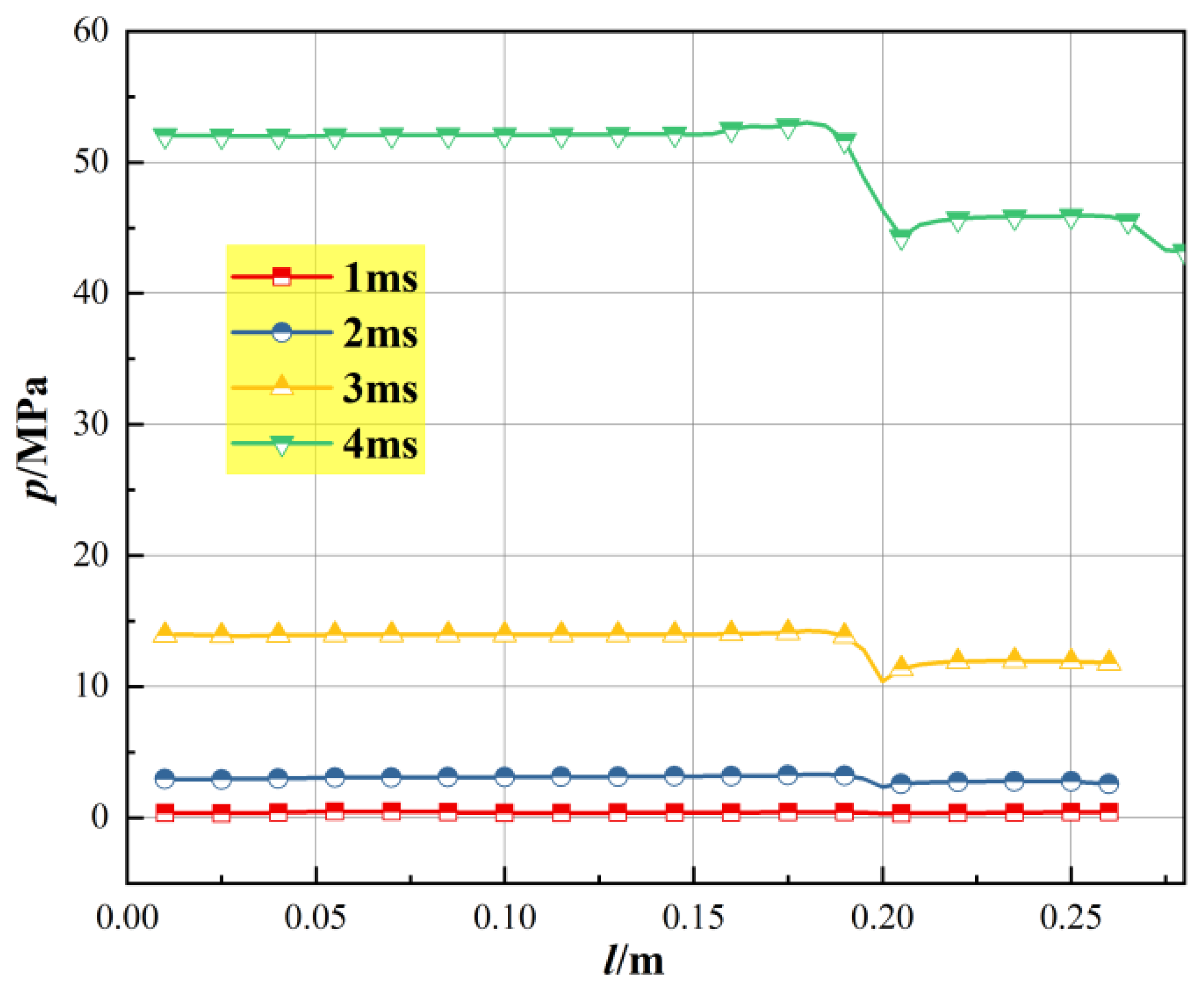
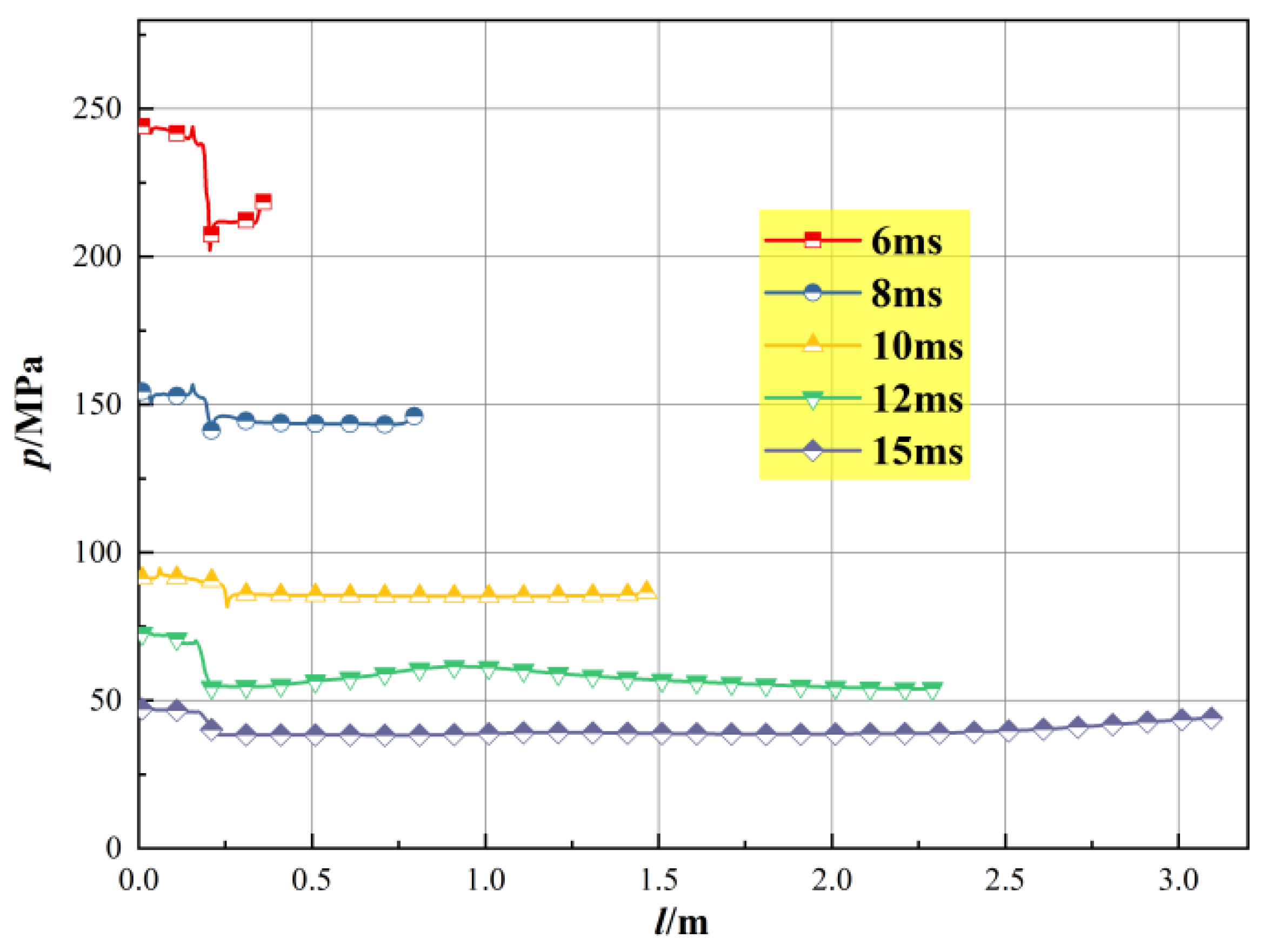
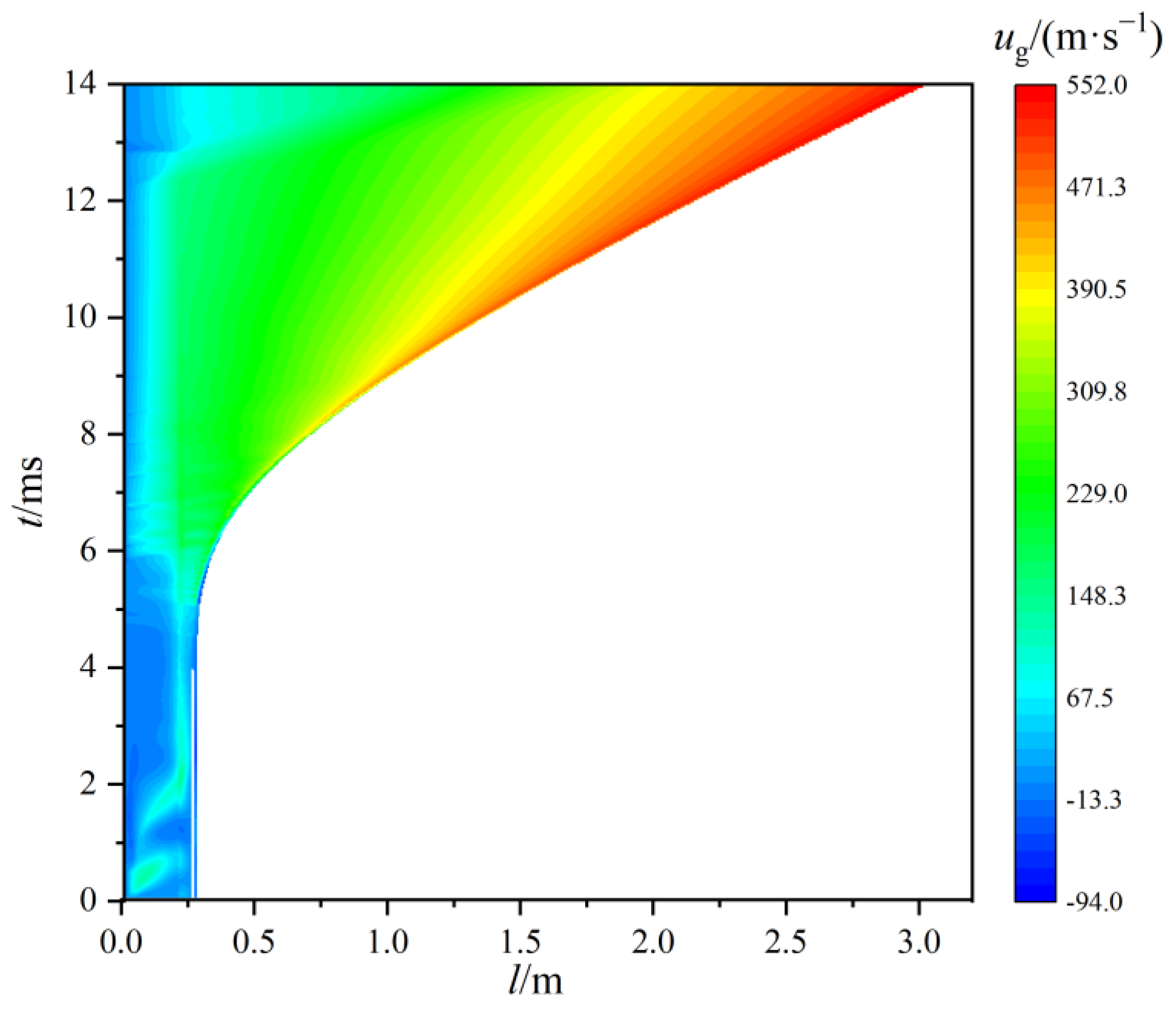
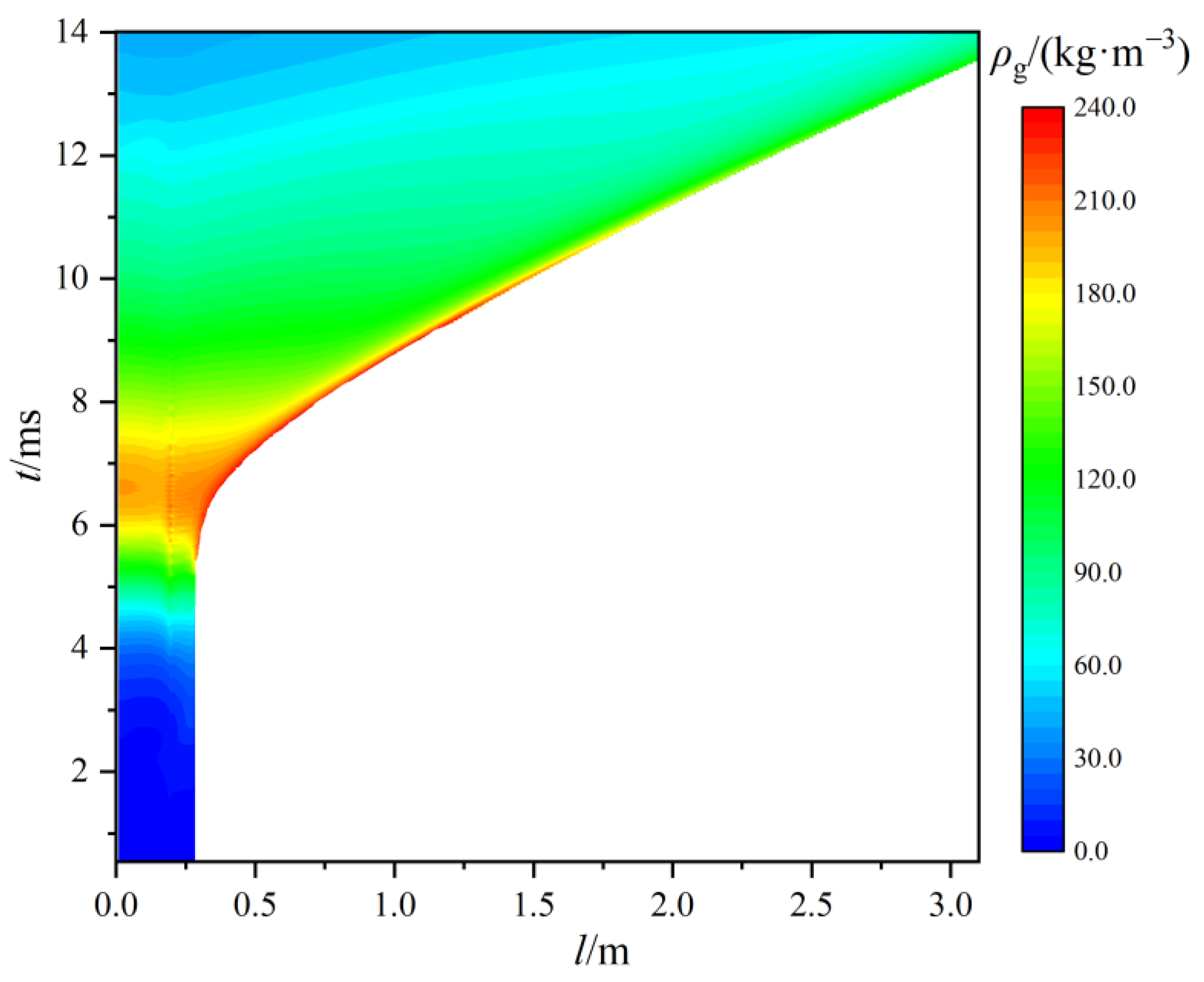
4.3. Analysis of Flow Field
5. Conclusions
- (1)
- The multiple-element method has high accuracy and can be highly consistent with the test curve. However, the lumped element is large, and the pressure capture in the chamber is not fine enough, which leads to a certain error between the lumped element method and the test.
- (2)
- The tubular propellant bundle vibrates back and forth in the chamber, but the speed is relatively small, the maximum speed is not more than 8 m/s, in the initial period, the movement of the bundle is very small, and the blank particle element at the bottom of the chamber is almost invisible. With the movement of the tubular bundle, the void space gradually appeared in the bottom of the chamber, and the blank particle element in the bottom of the chamber gradually expanded.
- (3)
- The free space causes the gas to expand easily, and the pressure in the propellant region is significantly higher than that in the free region, resulting in an obvious interfacial pressure gap. Fluid flows through the solid particle bed due to the porous structure, resulting in low flow rate. While free space flow rate distribution is relatively uniform, the fluid in free space can reach higher speeds.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Area of the barrel section | Cf | drag coefficient |
| dp | Perforation diameter of a propellant grain | eg | Internal energy of gas phase |
| ep | energy of propellant grain | f | Interphase heat transfer |
| fs | Interphase drag | M | mass of bundle |
| mc | Generation rate of gas by propellant | mp | Mass of Particle element |
| n | Burning rate index | N | Number of particle elements |
| p | Pressure | Qp | Interphase heat transfer |
| re0 | initial outside diameter of propellant | ri0 | inside diameter of propellant |
| re | outer diameter at any time | ri | inner diameter at any time |
| Rp | Interparticle stress | T | Time |
| u1 | the burning rate coefficient | ug | Gas velocity |
| up | Solid velocity vector | uign | Gas velocity of ignition |
| xl | The left end of the bundle | xR | The Right end of the bundle |
| φ | Gas porosity | ρg | Gas density |
| ρp | Propellant density | Δt | Time step |
| λ* | global maximum eigenvalue | dx | the grid cell scale |
References
- Miura, H.; Matsuo, A.; Nakamura, Y. Numerical Prediction of Interior Ballistics Performance of Projectile Accelerator Using Granular or Tubular Solid Propellant. Propellants Explos. Pyrotech. 2013, 38, 204–213. [Google Scholar] [CrossRef]
- Woodley, C.; Carriere, A.; Franco, P.; Gröger, T.; Hensel, D.; Nussbaum, J.; Kelzenberg, S.; Longuet, B. Comparisons of internal ballistics simulations of the AGARD gun. In Proceedings of the 22nd International Symposium on Ballistics, Vancouver, BC, Canada, 14–18 November 2005; Volume 1, pp. 339–345. [Google Scholar]
- Jang, J.; Oh, S.; Roh, T. Comparison of the characteristics of granular propellant movement in interior ballistics based on the interphase drag model. J. Mech. Sci. Technol. 2014, 28, 4547–4553. [Google Scholar] [CrossRef]
- Xiao, Z.; Xu, F. Relationship between slivering point and gas generation rules of 19-perforation TEGDN propellants with different length/outside diameter ratios and perforation diameters. J. Energetic Mater. 2016, 36, 141–151. [Google Scholar] [CrossRef]
- El Sadek, H.; Zhang, X.; Rashad, M. Interior ballistic study with different tools. Int. J. Heat Technol. 2014, 32, 141e6. [Google Scholar]
- Cheng, S.; Jiang, K.; Xue, S.; Tao, R.; Lu, X. Performance analysis of internal ballistic multiphase flow of composite charge structure. Energies 2023, 16, 2127. [Google Scholar] [CrossRef]
- López-Munoz, C.; García-Cascales, J.; Velasco, F.; Otón-Martínez, R. An Energetic Model for Detonation of Granulated Solid Propellants. Energies 2019, 12, 4459. [Google Scholar] [CrossRef]
- Xue, X.; Ye, Q.; Yu, Y. Three-dimensional heat transfer characteristics of complex structure with nineteen tubular propellants under different heating rates. Int. Commun. Heat Mass Transf. 2022, 139, 106491. [Google Scholar] [CrossRef]
- Ongaro, F.; Robbe, C.; Papy, A.; Stirbu, B.; Chabotier, A. Modelling of internal ballistics of gun systems: A review. Def. Technol. 2024; in press. [Google Scholar] [CrossRef]
- Otón-Martínez, R.A.; Velasco, F.J.; Nicolás-Pérez, F.; García-Cascales, J.R.; Mur-Sanz de Galdeano, R. Three-Dimensional Numerical Modeling of Internal Ballistics for Solid Propellant Combinations. Mathematics 2021, 9, 2714. [Google Scholar] [CrossRef]
- Gough, P.S.; Zwarts, F.J. Modeling Heterogeneous Two-Phase Reacting Flow. AIAA J. 1979, 17, 17–25. [Google Scholar] [CrossRef]
- Gough, P.S. Some Fundamental Aspects of the Digital Simulation of Convective Burning in Porous Beds; AIAA: Orlando, FL, USA, 1977; pp. 77–855. [Google Scholar]
- Gough, P.S. Formulation of a Next-Generation Interior Ballistic Code; PGA-TR-91-3; Paul Gough Associates: Portsmouth, UK, 1993. [Google Scholar]
- Gough, P.S. Modeling arbitrarily packaged multi-increment solid propellant charges of various propellant configurations. In Proceedings of the 33rd JANNAF Combustion Meeting, Monterey, CA, USA, 4–8 November 1996; CPIA Publication: Washington, DC, USA, 1996; pp. 421–435. [Google Scholar]
- Ma, H.; Zhao, Y.; Cheng, Y. CFD-DEM modeling of rod-like particles in a fluidized bed with complex geometry. Powder Technol. 2019, 344, 673–683. [Google Scholar] [CrossRef]
- Yao, L.; Liu, Y.; Liu, J.; Xiao, Z.; Xie, K.; Cao, H.; Zhang, H. An optimized CFD-DEM method for particle collision and retention analysis of two-phase flow in a reduced-diameter pipe. Powder Technol. 2022, 405, 117547. [Google Scholar] [CrossRef]
- Lin, Z.; Sun, X.; Yu, T.; Zhang, Y.; Li, Y.; Zhu, Z. Gas–solid two-phase flow and erosion calculation of gate valve based on the CFD-DEM model. Powder Technol. 2020, 366, 395–407. [Google Scholar] [CrossRef]
- Hu, C.; Luo, K.; Yang, S.; Wang, S.; Fan, J. A comprehensive numerical investigation on the hydrodynamics and erosion characteristics in a pressurized fluidized bed with dense immersed tube bundles. Chem. Eng. Sci. 2016, 153, 129–145. [Google Scholar] [CrossRef]
- Cheng, C.; Zhang, X. Numerical Investigation on the Transient Ignition Behavior Using CFD-DEM Approach. Combust. Sci. Technol. 2014, 186, 1115–1137. [Google Scholar] [CrossRef]
- Lu, L.; Morris, A.; Li, T.; Benyahia, S. Extension of a coarse grained particle method to simulate heat transfer in fluidized beds. Int. J. Heat Mass Transf. 2017, 111, 723–735. [Google Scholar] [CrossRef]
- Lu, L.; Yoo, K.; Benyahia, S. Coarse-grained-particle method for simulation of liquid–solids reacting flows. Ind. Eng. Chem. Res. 2016, 55, 10477–10491. [Google Scholar] [CrossRef]
- Cheng, S.; Tao, R.; Xue, S.; Lu, X. The Particle Element Method to Obtain Parameter Distributions of Two-phase Reactive Flow in a Propulsion Combustion System. Combust. Sci. Technol. 2024, 196, 730–752. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, H.; Xue, S.; Tao, R. Application and Research of the Particle Element Model in Ignition Process of Large-Particle High-Density Charge. Combust. Sci. Technol. 2022, 194, 1850–1871. [Google Scholar] [CrossRef]
- Cheng, S.; Tao, R.; Lu, X.; Xue, S.; Jiang, K. Efficient two-dimension particle element method of interior ballistic two-phase flow. Combust. Theory Model. 2023, 27, 558–583. [Google Scholar]

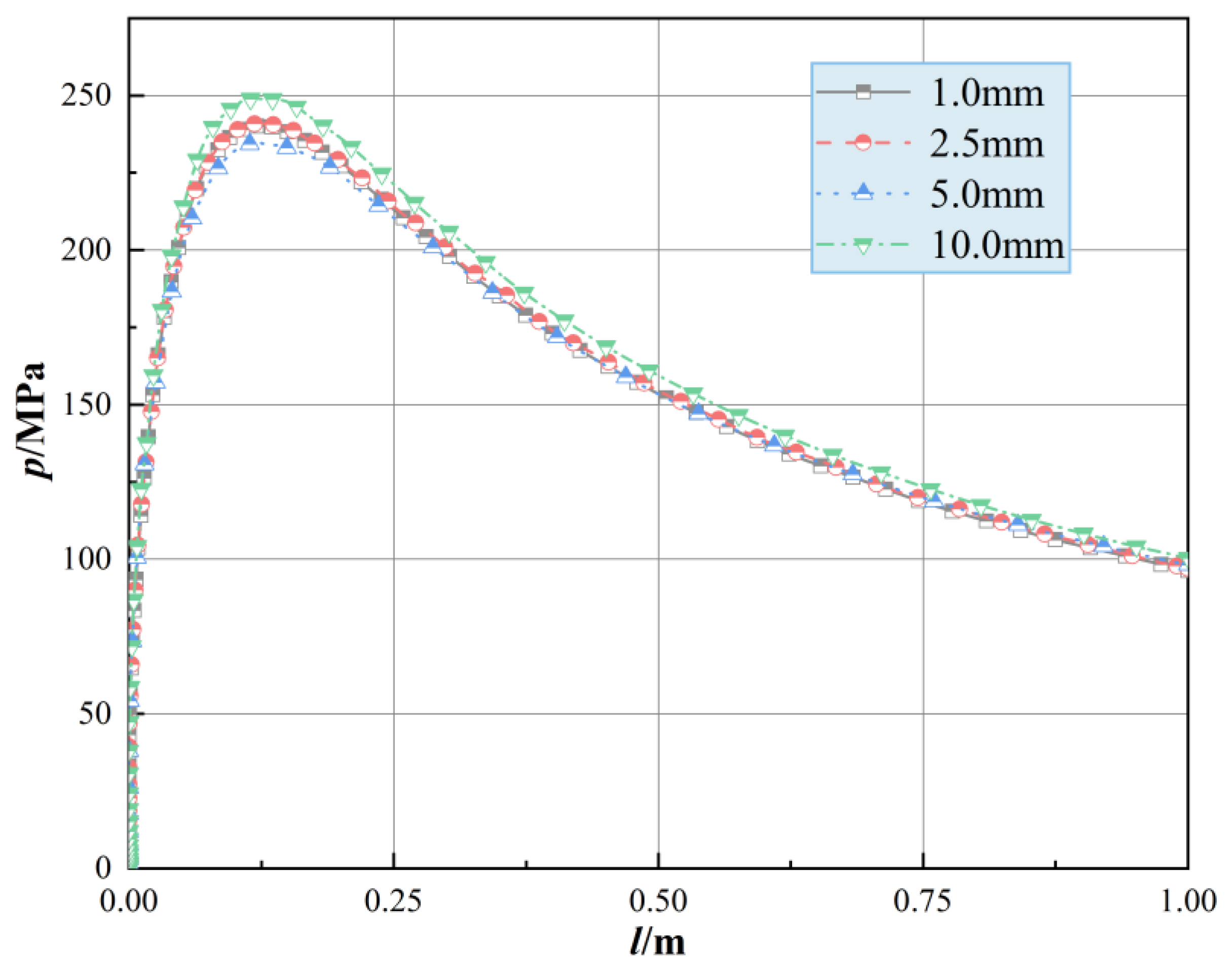



| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Caliber A/mm | 50 | Ratio of specific heats γ | 1.232 |
| Projectile travel l/mm | 3195 | Powder density ρp/(kg·m−3) | 1615 |
| Projectile mass m/kg | 2.5 | Covolume α/(m3/kg) | 0.001 |
| Ignition mass mign/g | 4.5 | Burn rate index n | 0.874 |
| Main charge mass m/kg | 0.5 | Burn rate coefficient a/(cm·MPa−n·s−1) | 0.2299 |
| Detonation temperature/K | 3133 | Tubular propellant size/mm | Φ 6.35 × 200 |
| powder impetus f/(kJ/kg) | 1036 | Diameter of chamber/mm | 2.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, R.; Cheng, S.; Lu, X.; Xue, S.; Cui, X. The Application of the Particle Element Method in Tubular Propellant Charge Structure: Lumped Element Method and Multiple-Element Method. Energies 2024, 17, 4384. https://doi.org/10.3390/en17174384
Tao R, Cheng S, Lu X, Xue S, Cui X. The Application of the Particle Element Method in Tubular Propellant Charge Structure: Lumped Element Method and Multiple-Element Method. Energies. 2024; 17(17):4384. https://doi.org/10.3390/en17174384
Chicago/Turabian StyleTao, Ruyi, Shenshen Cheng, Xinggan Lu, Shao Xue, and Xiaoting Cui. 2024. "The Application of the Particle Element Method in Tubular Propellant Charge Structure: Lumped Element Method and Multiple-Element Method" Energies 17, no. 17: 4384. https://doi.org/10.3390/en17174384
APA StyleTao, R., Cheng, S., Lu, X., Xue, S., & Cui, X. (2024). The Application of the Particle Element Method in Tubular Propellant Charge Structure: Lumped Element Method and Multiple-Element Method. Energies, 17(17), 4384. https://doi.org/10.3390/en17174384






