Research on a Thirteen-Level Switched Capacitor Inverter with Low Switching Loss
Abstract
1. Introduction
2. Working Modes of Proposed Topology
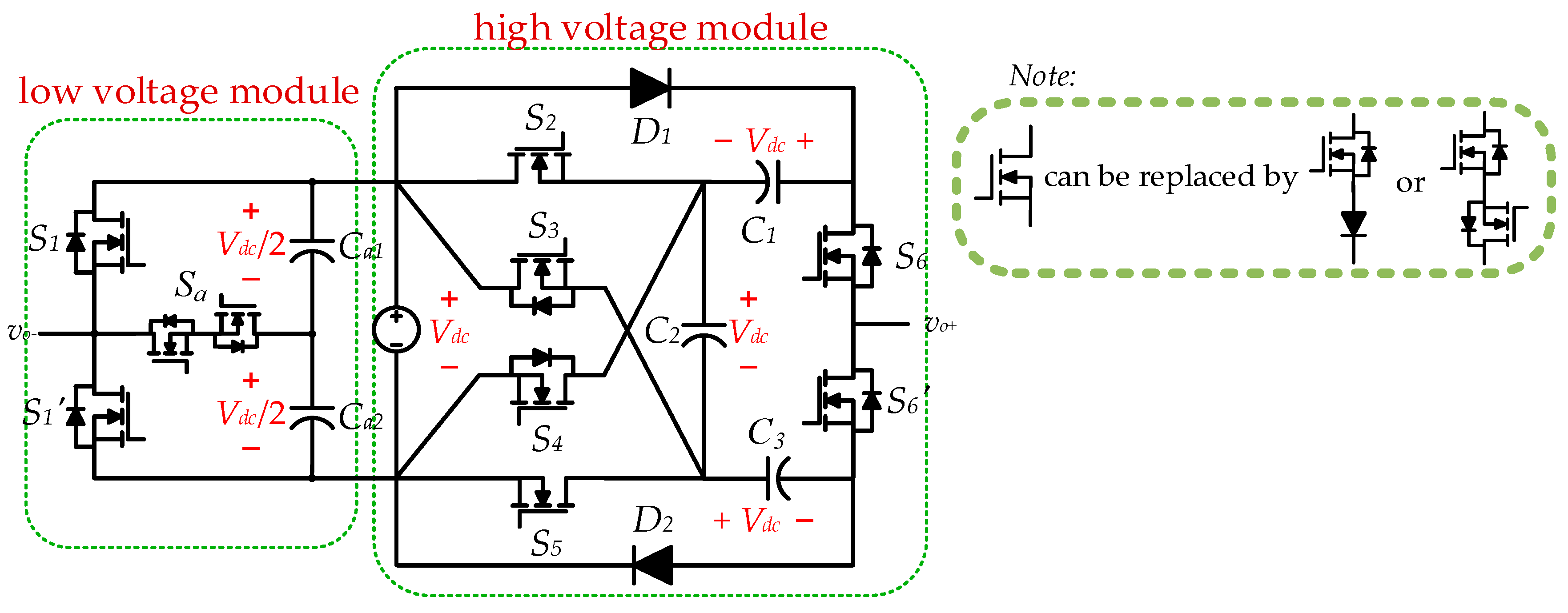
2.1. Structure of Proposed Topology
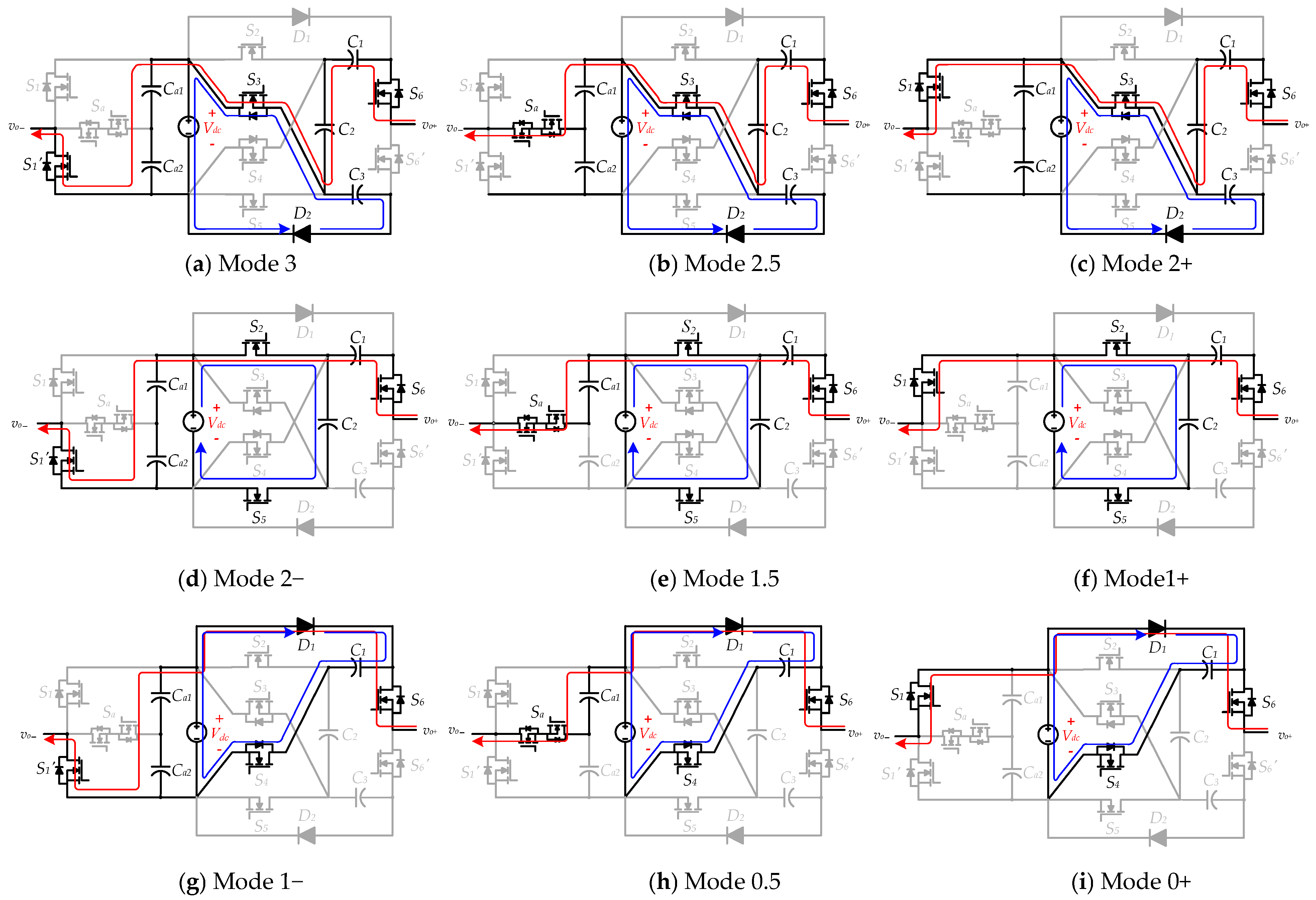
2.2. Working Mode Analysis
- (1)
- Modes 3, 2.5, and 2+: In these three states, switches S3 and S6 turn on in the high-voltage module. As S3 switches on, the diode D2 is conducted so that the charging loop for C3 is formed. As for the low-voltage module, S1′, Sa, and S1 are switched on in turn to generate 3Vdc, 2.5Vdc, and 2Vdc, respectively.
- (2)
- Mode 2−, 1.5 and 1+: Similarly, the switching states in the high-voltage module are completely the same, and switches in the low-voltage module are conducted alternately. By turning on S2 and S5, the capacitor C2 can be charged to the input source voltage.
- (3)
- Mode 1−, 0.5 and 0+: S4 is turned on in these states and D1 conducts so that C1 can be charged to Vdc. As for the low-voltage module, one of three switches is turned on to generate different output levels.
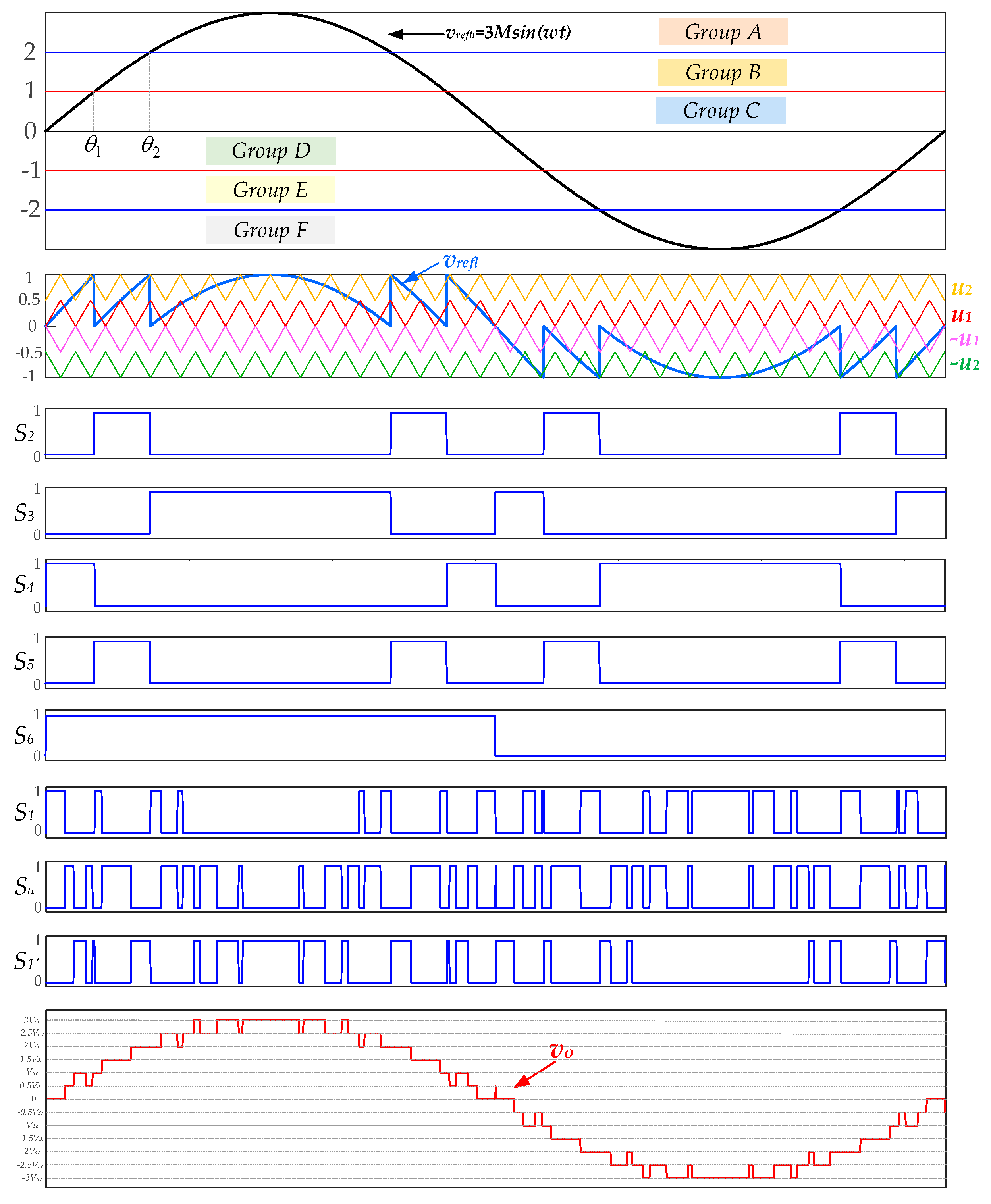
3. Proposed Modulation Method
3.1. Step Waveform Modulation for High-Voltage Module
3.2. LS-PWM for Low-Voltage Module
4. Self-Balance Analysis and Capacitance Calculation
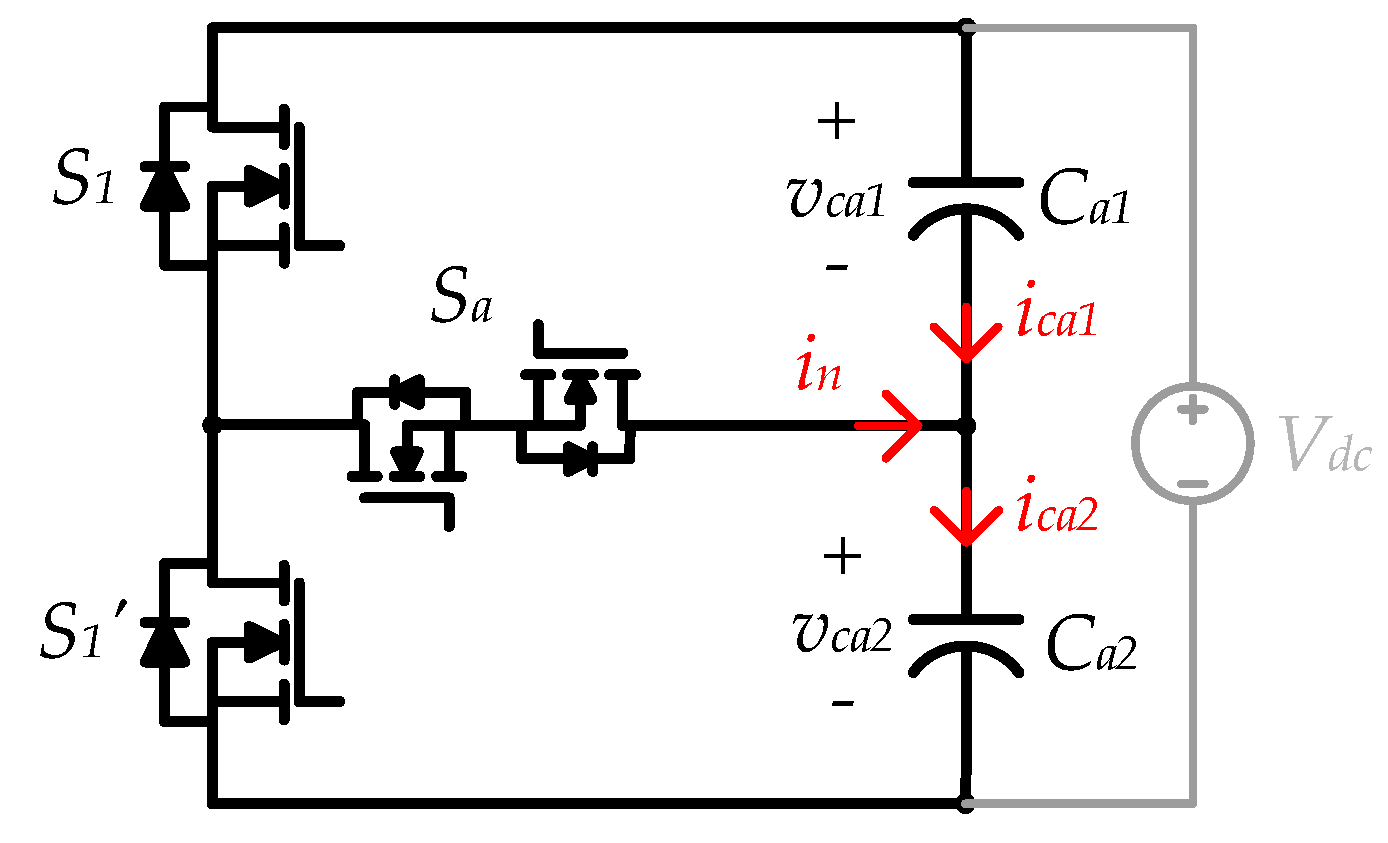
4.1. Self-Balance Analysis
4.2. Capacitance Calculation
5. Loss Analysis and Comparative Study
5.1. Loss Analysis
5.2. Comparative Study
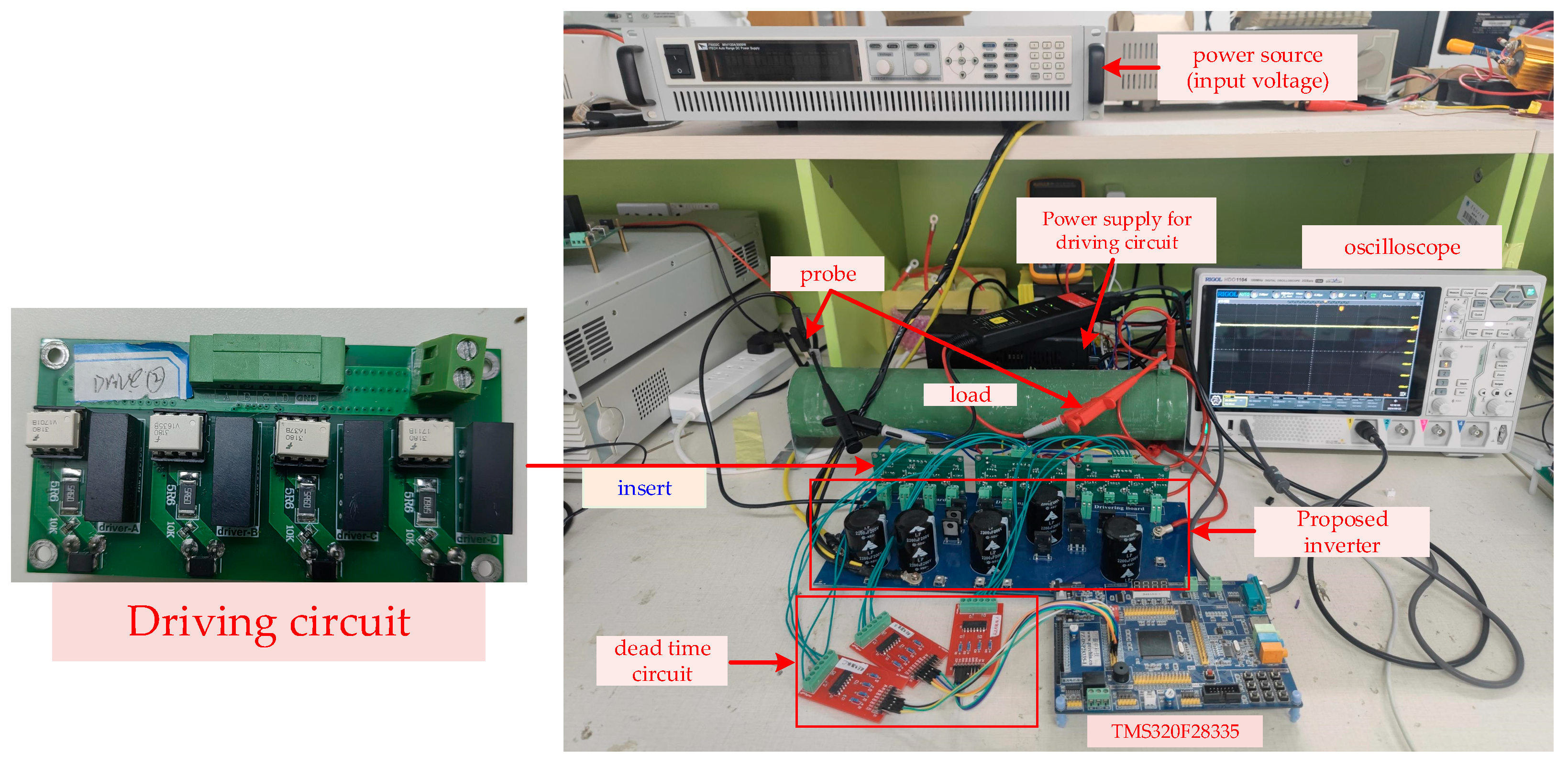
6. Simulation and Experimental Results
6.1. Simulation Results
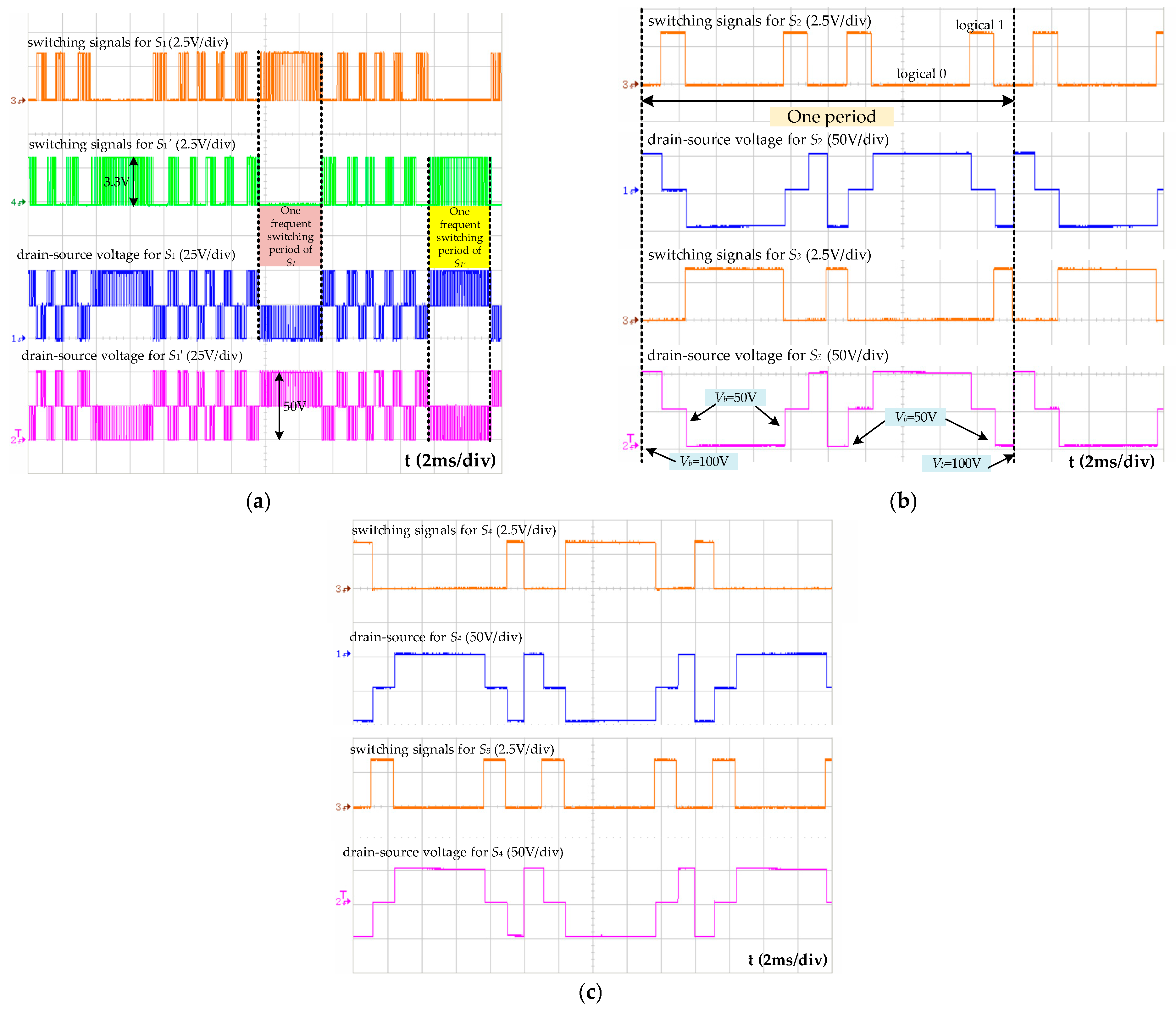
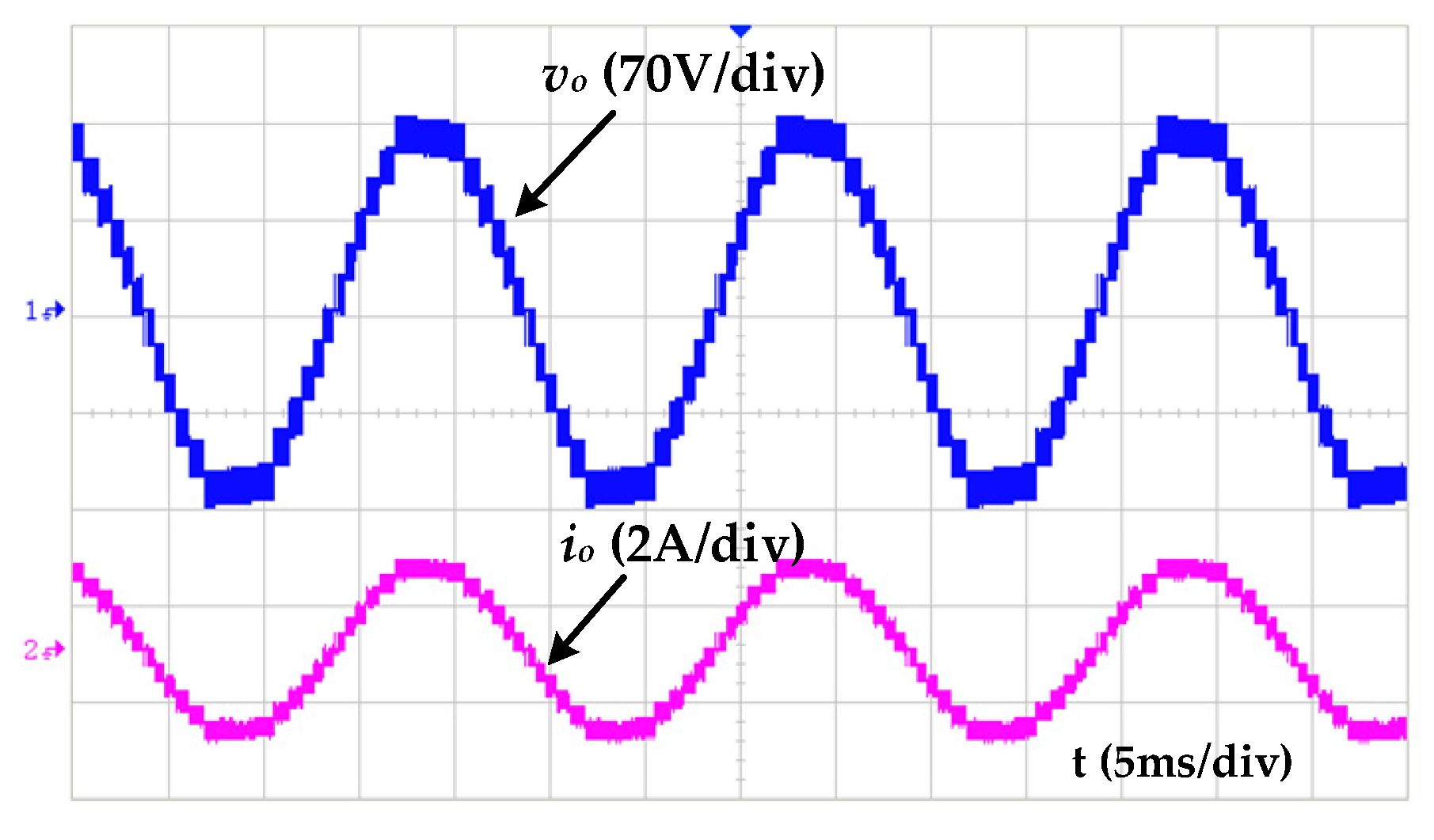
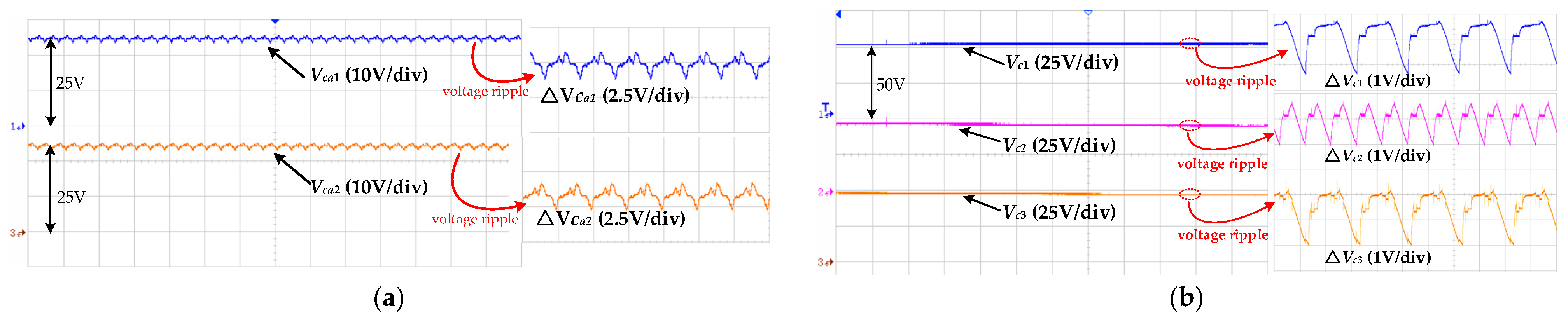
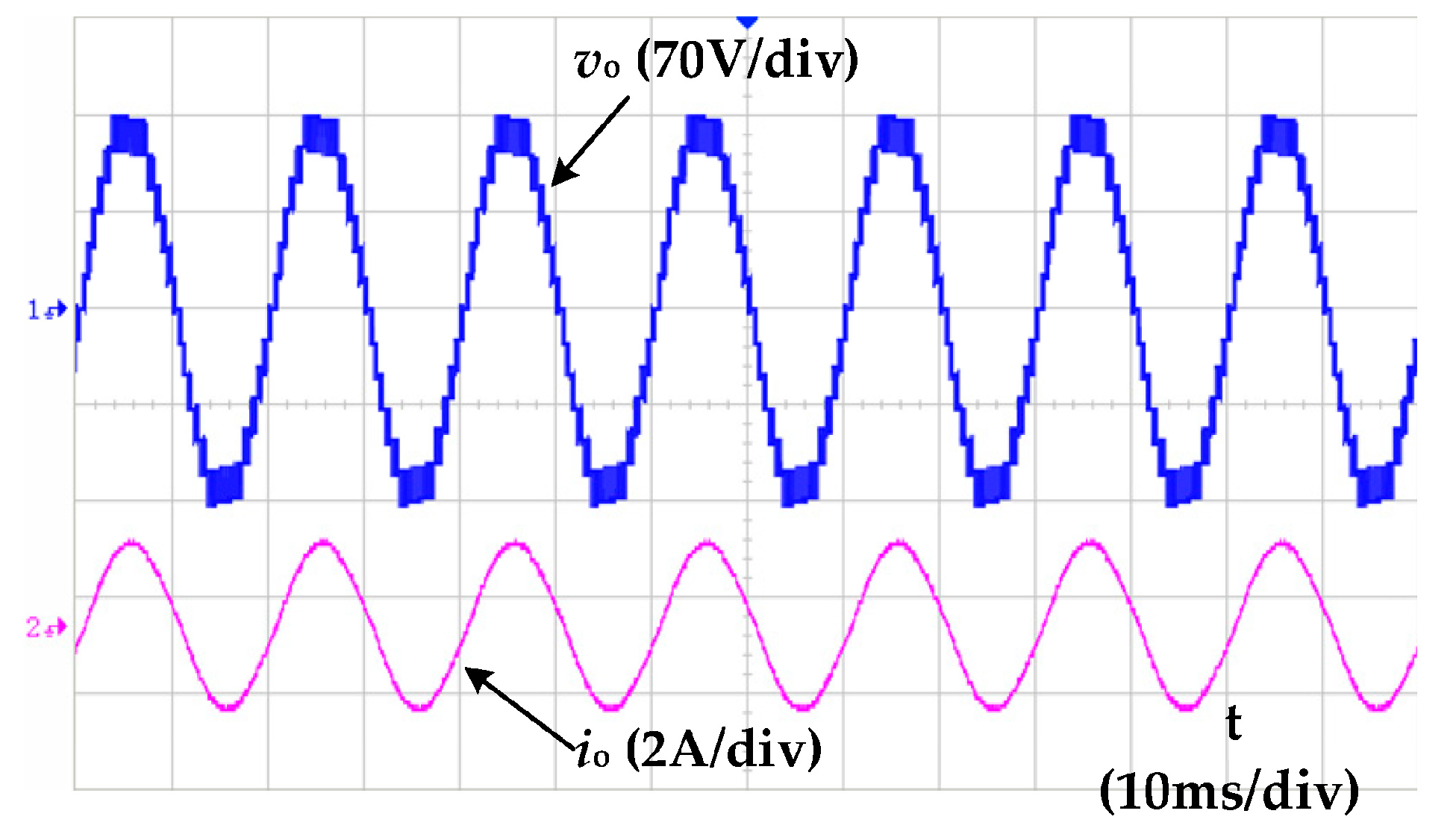
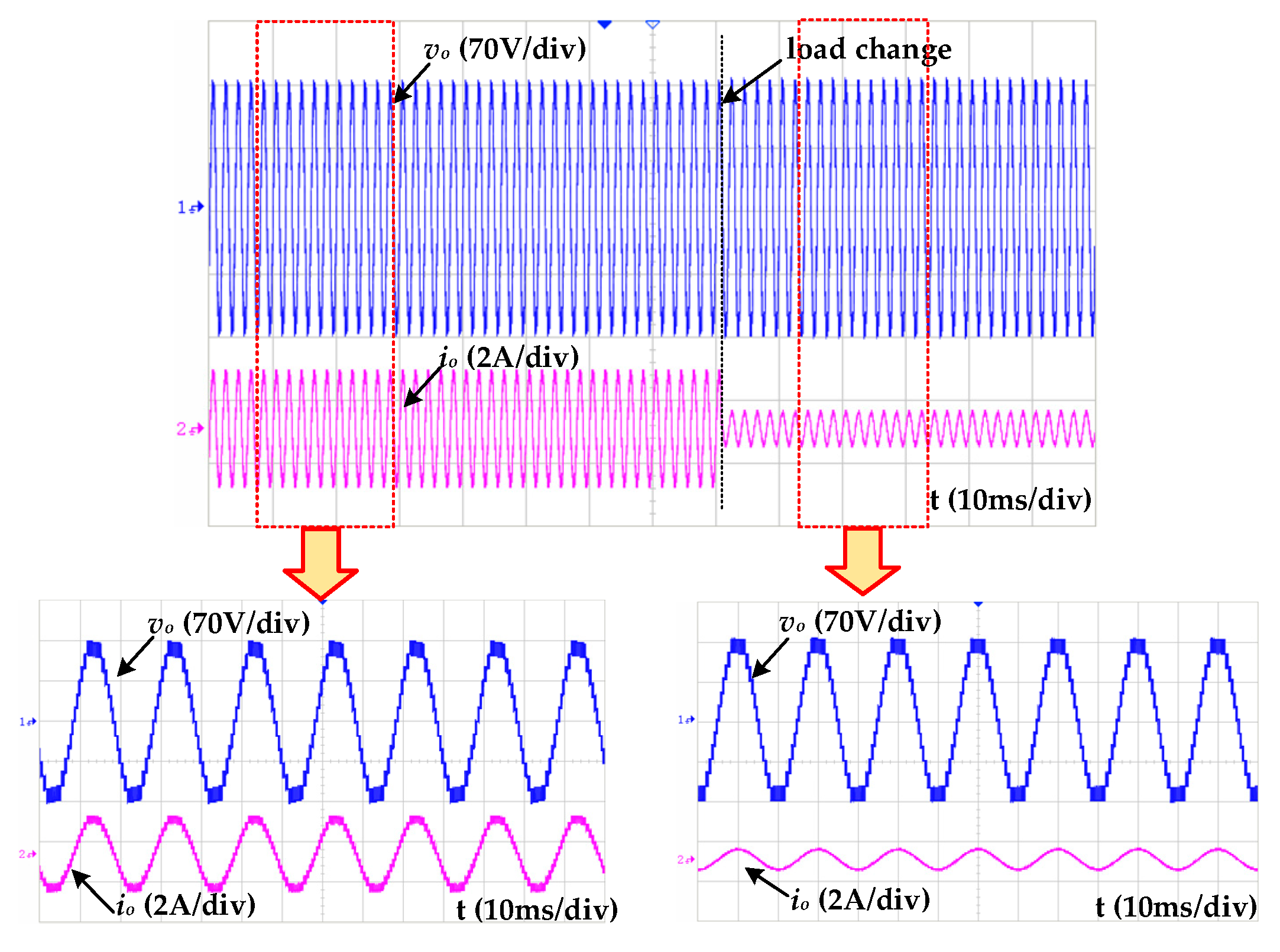
6.2. Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Hsieh, C.-H.; Liang, T.-J.; Chen, S.-M.; Tsai, S.-W. Design and Implementation of a Novel Multilevel DC–AC Inverter. IEEE Trans. Ind. Appl. 2016, 52, 2436–2443. [Google Scholar] [CrossRef]
- Xiao, B.; Hang, L.; Mei, J.; Riley, C.; Tolbert, L.M.; Ozpineci, B. Modular Cascaded H-Bridge Multilevel PV Inverter with Distributed MPPT for Grid-Connected Applications. IEEE Trans. Ind. Appl. 2015, 51, 1722–1731. [Google Scholar] [CrossRef]
- Sheir, A.; Youssef, M.Z.; Orabi, M.A. Novel Bidirectional T-Type Multilevel Inverter for Electric Vehicle Applications. IEEE Trans. Power Electron. 2019, 34, 6648–6658. [Google Scholar] [CrossRef]
- Yu, Y.; Konstantinou, G.; Hredzak, B.; Agelidis, V.G. Power Balance of Cascaded H-Bridge Multilevel Converters for Large-Scale Photovoltaic Integration. IEEE Trans. Power Electron. 2016, 31, 292–303. [Google Scholar] [CrossRef]
- Ye, Z.; Lei, Y.; Liao, Z.; Pilawa-Podgurski, R.C.N. Investigation of Capacitor Voltage Balancing in Practical Implementations of Flying Capacitor Multilevel Converters. IEEE Trans. Power Electron. 2022, 37, 2921–2935. [Google Scholar] [CrossRef]
- Guo, X.; Cavalcanti, M.C.; Farias, A.M.; Guerrero, J.M. Single-Carrier Modulation for Neutral-Point-Clamped Inverters in Three-Phase Transformerless Photovoltaic Systems. IEEE Trans. Power Electron. 2013, 28, 2635–2637. [Google Scholar] [CrossRef]
- Iqbal, A.; Siddique, M.D.; Reddy, B.P.; Maroti, P.K. Quadruple Boost Multilevel Inverter (QB-MLI) Topology With Reduced Switch Count. IEEE Trans. Power Electron. 2022, 36, 7372–7377. [Google Scholar] [CrossRef]
- Akbari, A.; Ebrahimi, J.; Jafarian, Y.; Bakhshai, A. A Multilevel Inverter Topology with an Improved Reliability and a Reduced Number of Components. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 553–563. [Google Scholar] [CrossRef]
- Samadaei, E.; Sheikholeslami, A.; Gholamian, S.A.; Adabi, J. A Square T-Type (ST-Type) Module for Asymmetrical Multilevel Inverters. IEEE Trans. Power Electron. 2018, 33, 987–996. [Google Scholar] [CrossRef]
- Roy, T.; Sadhu, P.K.; Dasgupta, A. Cross-Switched Multilevel Inverter Using Novel Switched Capacitor Converters. IEEE Trans. Ind. Electron. 2019, 66, 8521–8532. [Google Scholar] [CrossRef]
- Samadaei, E.; Kaviani, M.; Bertilsson, K. A 13-Levels Module (K-Type) With Two DC Sources for Multilevel Inverters. IEEE Trans. Ind. Electron. 2019, 66, 5186–5196. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Hu, C.; Shen, W.; Holmes, D.G.; Yu, X. A Nine-Level Inverter for Low-Voltage Applications. IEEE Trans. Power Electron. 2020, 35, 1659–1671. [Google Scholar] [CrossRef]
- Liu, J.; Wu, J.; Zeng, J.; Guo, H. A Novel Nine-Level Inverter Employing One Voltage Source and Reduced Components as High-Frequency AC Power Source. IEEE Trans. Power Electron. 2017, 32, 2939–2947. [Google Scholar] [CrossRef]
- Ye, Y.; Cheng, K.W.E.; Liu, J.; Ding, K. A Step-Up Switched-Capacitor Multilevel Inverter with Self-Voltage Balancing. IEEE Trans. Ind. Electron. 2014, 61, 6672–6680. [Google Scholar] [CrossRef]
- Zeng, J.; Wu, J.; Liu, J.; Guo, H. A Quasi-Resonant Switched-Capacitor Multilevel Inverter with Self-Voltage Balancing for Single-Phase High-Frequency AC Microgrids. IEEE Trans. Ind. Inform. 2017, 13, 2669–2679. [Google Scholar] [CrossRef]
- Zeng, J.; Lin, W.; Cen, D.; Liu, J. Novel K-Type Multilevel Inverter with Reduced Components and Self-Balance. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 4343–4354. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Guo, Y.; Wang, K.; Liang, J. An X-type Boost Multilevel Inverter Based on Switched Capacitor Cells with Low Voltage Stress and High Frequency Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 11, 3623–3632. [Google Scholar] [CrossRef]
- Lee, S.S.; Bak, Y.; Kim, S.-M.; Joseph, A.; Lee, K.-B. New Family of Boost Switched-Capacitor Seven-Level Inverters (BSC7LI). IEEE Trans. Power Electron. 2019, 34, 10471–10479. [Google Scholar] [CrossRef]
- Alyami, S.; Ali, J.S.M.; Almakhles, D.; Almutairi, A.M. Obeidat. Seven Level T-Type Switched Capacitor Inverter Topology for PV Applications. IEEE Access 2021, 9, 85049–85059. [Google Scholar] [CrossRef]
- Lee, S.S. Single-Stage Switched-Capacitor Module (S3CM) Topology for Cascaded Multilevel Inverter. IEEE Trans. Power Electron. 2018, 33, 8204–8207. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, K.W.E.; Ye, Y. A Cascaded Multilevel Inverter Based on Switched-Capacitor for High-Frequency AC Power Distribution System. IEEE Trans. Power Electron. 2014, 29, 4219–4230. [Google Scholar] [CrossRef]
- Roy, T.; Sadhu, P.K. A Step-Up Multilevel Inverter Topology Using Novel Switched Capacitor Converters with Reduced Components. IEEE Trans. Ind. Electron. 2021, 68, 236–247. [Google Scholar] [CrossRef]
- Lin, W.; Zeng, J.; Liu, J.; Yan, Z.; Hu, R. Generalized Symmetrical Step-Up Multilevel Inverter Using Crisscross Capacitor Units. IEEE Trans. Ind. Electron. 2020, 67, 7439–7450. [Google Scholar] [CrossRef]
- Anand, V.; Singh, V. A 13-Level Switched-Capacitor Multilevel Inverter with Single DC Source. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1575–1576. [Google Scholar] [CrossRef]
- Bhatnagar, P.; Singh, A.K.; Gupta, K.K.; Siwakoti, Y.P. A Switched-Capacitors-Based 13-Level Inverter. IEEE Trans. Power Electron. 2022, 37, 644–658. [Google Scholar] [CrossRef]
- Ye, Y.; Chen, S.; Zhang, X.; Yi, Y. Half-Bridge Modular Switched-Capacitor Multilevel Inverter with Hybrid Pulsewidth Modulation. IEEE Trans. Power Electron. 2020, 35, 8237–8247. [Google Scholar] [CrossRef]
- Ye, Y.; Chen, S.; Wang, X.; Cheng, K.-W.E. Self-Balanced 13-Level Inverter Based on Switched Capacitor and Hybrid PWM Algorithm. IEEE Trans. Ind. Electron. 2021, 68, 4827–4837. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, G.; Wang, X.; Yi, Y.; Cheng, K.W.E. Self-Balanced Switched-Capacitor Thirteen-Level Inverters with Reduced Capacitors Count. IEEE Trans. Ind. Electron. 2022, 69, 1070–1076. [Google Scholar] [CrossRef]
- Boora, K.; Kumar, J. A Novel Cascaded Asymmetrical Multilevel Inverter with Reduced Number of Switches. IEEE Trans. Ind. Appl. 2019, 55, 7389–7399. [Google Scholar] [CrossRef]
- Laib, A.; Krama, A.; Sahli, A.; Kihal, A.; Abu-Rub, H. Reconfigurable Model Predictive Control for Grid Connected PV Systems Using Thirteen-Level Packed E-Cell Inverter. IEEE Access 2022, 10, 102210–102222. [Google Scholar] [CrossRef]
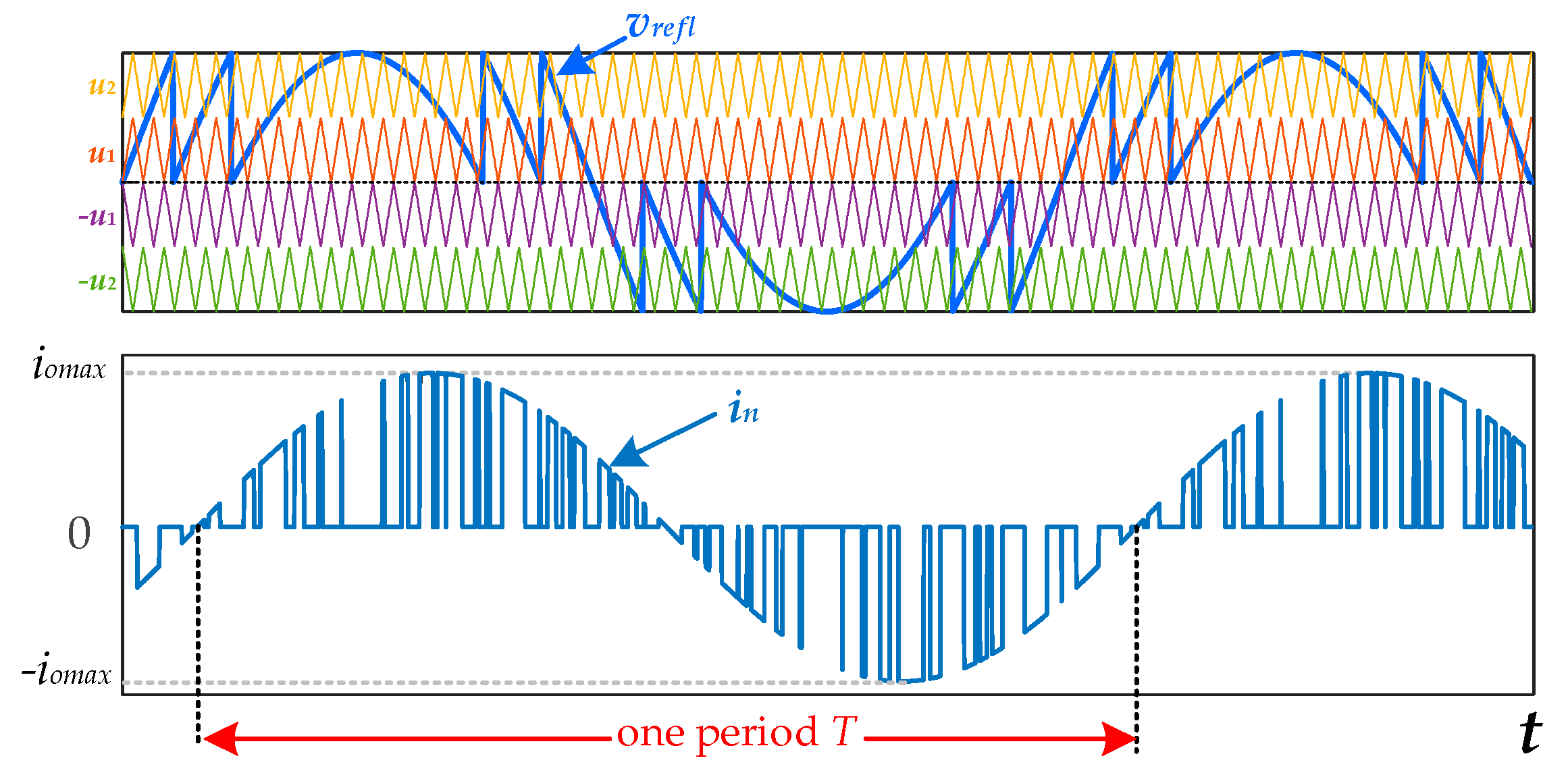
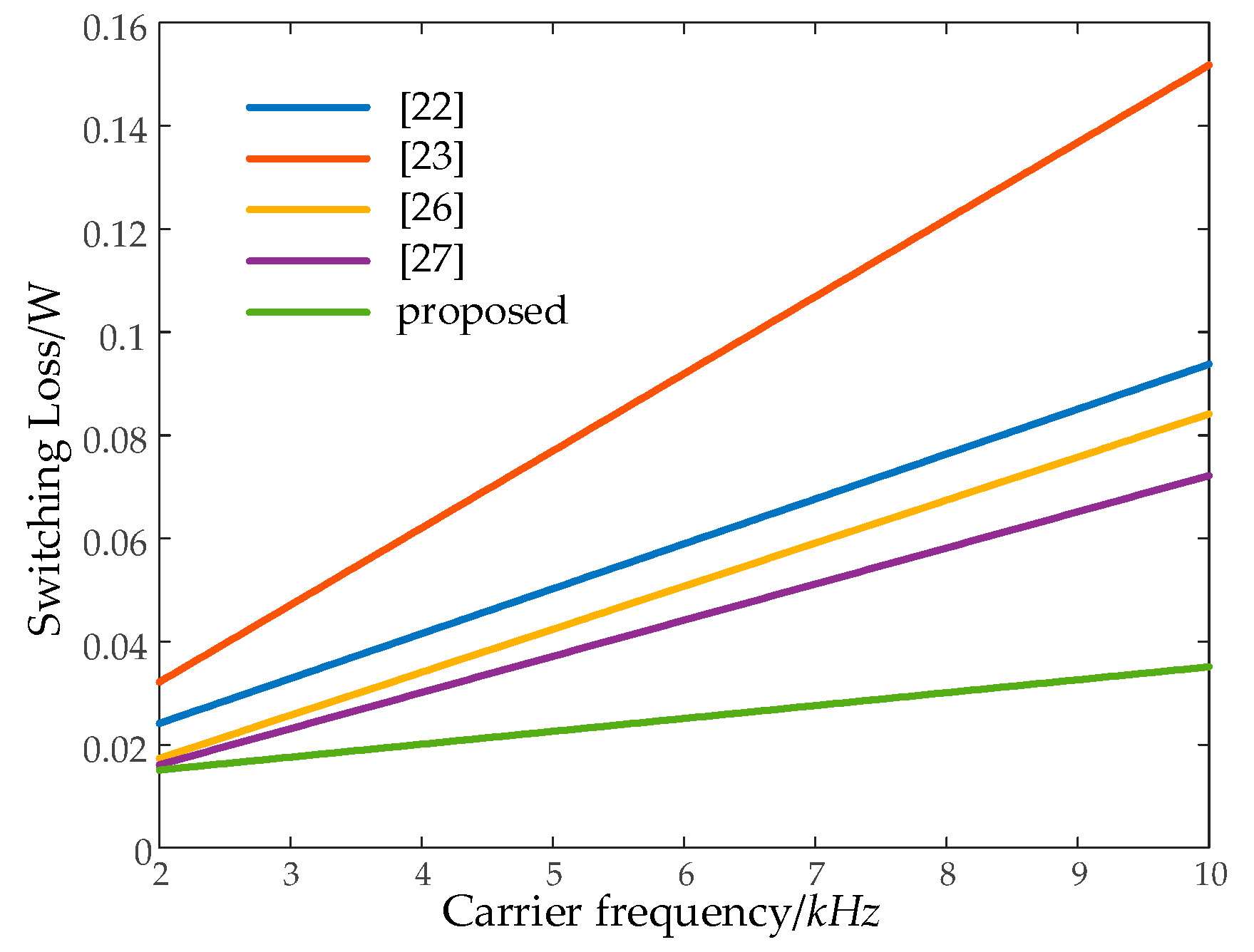
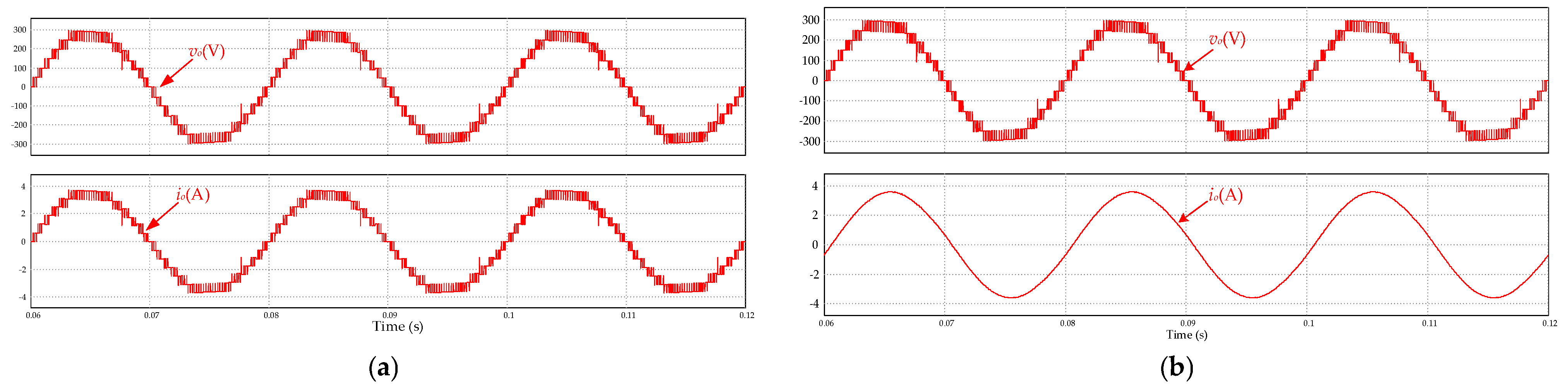
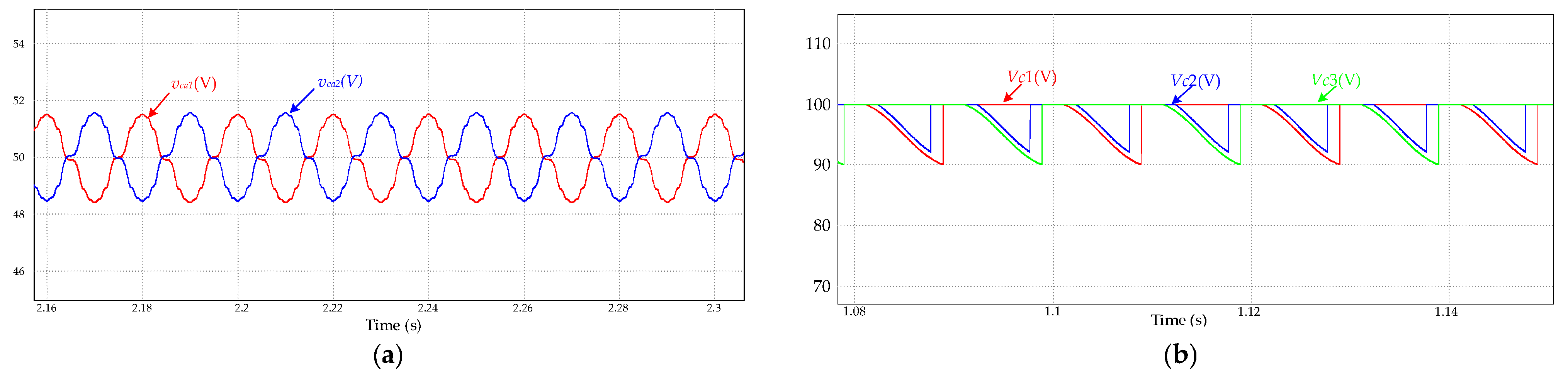

| Group | Mode | S1 | Sa | S1′ | S2,3,4,5,6 | C1 | C2 | C3 | vo |
|---|---|---|---|---|---|---|---|---|---|
| A | 3 | 0 | 0 | 1 | 3Vdc | ||||
| 2.5 | 0 | 1 | 0 | 01001 | D | D | C | 2.5Vdc | |
| 2+ | 1 | 0 | 0 | 2Vdc | |||||
| B | 2− | 0 | 0 | 1 | 2Vdc | ||||
| 1.5 | 0 | 1 | 0 | 10011 | D | C | N | 1.5Vdc | |
| 1+ | 1 | 0 | 0 | Vdc | |||||
| C | 1− | 0 | 0 | 1 | Vdc | ||||
| 0.5 | 0 | 1 | 0 | 00101 | C | N | N | 0.5Vdc | |
| 0+ | 1 | 0 | 0 | 0 | |||||
| D | 0− | 0 | 0 | 1 | 0 | ||||
| −0.5 | 0 | 1 | 0 | 01000 | N | N | C | −0.5Vdc | |
| (−1)+ | 1 | 0 | 0 | −Vdc | |||||
| E | (−1)− | 0 | 0 | 1 | −Vdc | ||||
| −1.5 | 0 | 1 | 0 | 10010 | N | C | D | −1.5Vdc | |
| (−2)+ | 1 | 0 | 0 | −2Vdc | |||||
| F | (−2)− | 0 | 0 | 1 | −2Vdc | ||||
| −2.5 | 0 | 1 | 0 | 00100 | C | D | D | −2.5Vdc | |
| −3 | 1 | 0 | 0 | −3Vdc |
| State | Group | S2,3,4,5,6 |
|---|---|---|
| vrefh > 2 | A | 01001 |
| 1 < vrefh < 2 | B | 10011 |
| 0 < vrefh < 1 | C | 00101 |
| −1 < vrefh < 0 | D | 01000 |
| −2 < vrefh < −1 | E | 10010 |
| vrefh < −2 | F | 00100 |
| State | S1 Sa S1′ |
|---|---|
| vrefl > u2 | 001 |
| u1 < vrefl < u2 | 010 |
| 0 < vrefl < u1 | 100 |
| −u1 < vrefl < 0 | 001 |
| −u2 < vrefl < −u1 | 010 |
| vrefl < −u2 | 100 |
| Swtiches | Switching Frequency | Blocking Voltage |
|---|---|---|
| S1 and S1′ | 5fo + fc/2 | Vdc/2 |
| Sa | fc | Vdc/2 |
| S2 and S5 | 4fo | Vdc |
| S3 and S4 | 3fo | 2Vdc, Vdc |
| S6 and S6′ | fo | 3Vdc |
| Reference | Ns | Nsw | NDR | ND | NC | Nlevel | TSV(×Vstep) | H Bridge | CF | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| α = 0.5 | α = 1 | α = 1.5 | |||||||||
| [10] | 2 | 16 | 16 | 2 | 4 | 13 | 34 | No | 8.46 | 11.08 | 13.69 |
| [11] | 2 | 14 | 11 | 0 | 2 | 13 | 39 | No | 7.15 | 10.15 | 13.15 |
| [14] | 1 | 10 | 8 | 10 | 5 | 13 | 59 | Yes | 4.81 | 7.08 | 9.35 |
| [15] | 1 | 14 | 6 | 6 | 6 | 13 | 48 | Yes | 4.31 | 6.25 | 8 |
| [27] | 1 | 10 | 10 | 4 | 4 | 13 | 36 | No | 3.54 | 4.92 | 6.31 |
| [28] | 1 | 12 | 12 | 4 | 3 | 13 | 36 | No | 3.76 | 5.15 | 6.53 |
| [21] | 2 | 14 | 14 | 2 | 4 | 13 | 36 | No | 8 | 10.77 | 13.54 |
| [24] | 1 | 15 | 15 | 0 | 3 | 13 | 35 | No | 3.88 | 5.23 | 6.58 |
| [23] | 1 | 19 | 18 | 0 | 4 | 13 | 40 | No | 4.69 | 6.23 | 7.77 |
| [29] (one basic unit) | 3 | 8 | 8 | 0 | 0 | 17 | 28 | No | 5.29 | 7.76 | 10.23 |
| [30] | 1 | 10 | 8 | 0 | 4 | 13 | 28 | No | 3 | 3.84 | 4.92 |
| Proposed | 1 | 10 | 8 | 4 | 5 | 13 | 37 | No | 3.5 | 4.92 | 6.34 |
| Items | Value |
|---|---|
| Input voltage Vdc | 50 V |
| Capacitance | 2200 μF |
| Output frequency fo | 50 Hz |
| Carrier wave frequency | 10 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Liu, Y.; Li, T.; Fang, M.; Liu, J.; Huang, C. Research on a Thirteen-Level Switched Capacitor Inverter with Low Switching Loss. Energies 2024, 17, 5104. https://doi.org/10.3390/en17205104
Wu Z, Liu Y, Li T, Fang M, Liu J, Huang C. Research on a Thirteen-Level Switched Capacitor Inverter with Low Switching Loss. Energies. 2024; 17(20):5104. https://doi.org/10.3390/en17205104
Chicago/Turabian StyleWu, Zhipeng, Yuanhuang Liu, Tianchu Li, Ming Fang, Junfeng Liu, and Chunyan Huang. 2024. "Research on a Thirteen-Level Switched Capacitor Inverter with Low Switching Loss" Energies 17, no. 20: 5104. https://doi.org/10.3390/en17205104
APA StyleWu, Z., Liu, Y., Li, T., Fang, M., Liu, J., & Huang, C. (2024). Research on a Thirteen-Level Switched Capacitor Inverter with Low Switching Loss. Energies, 17(20), 5104. https://doi.org/10.3390/en17205104








