Identification of Sub-Synchronous Oscillation Mode Based on HO-VMD and SVD-Regularized TLS-Prony Methods
Abstract
1. Introduction
2. Fundamental Principles of the Identification Algorithm
2.1. Ideal Mathematical Model of SSO
2.2. Principles and Shortcomings of the VMD Algorithm
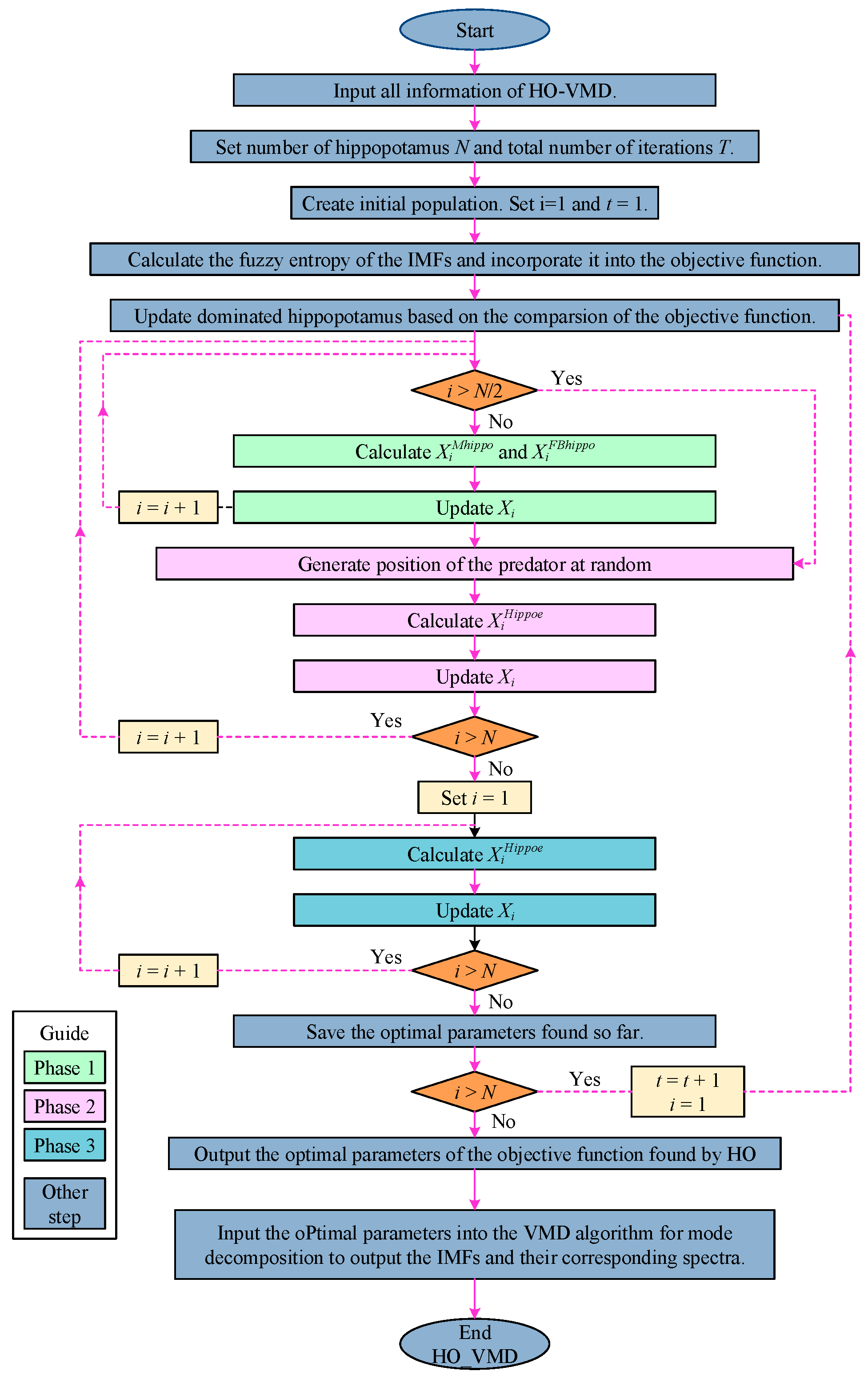
2.3. VMD Algorithm Improved Based on HO Algorithm
2.4. Improved Prony Identification Algorithm
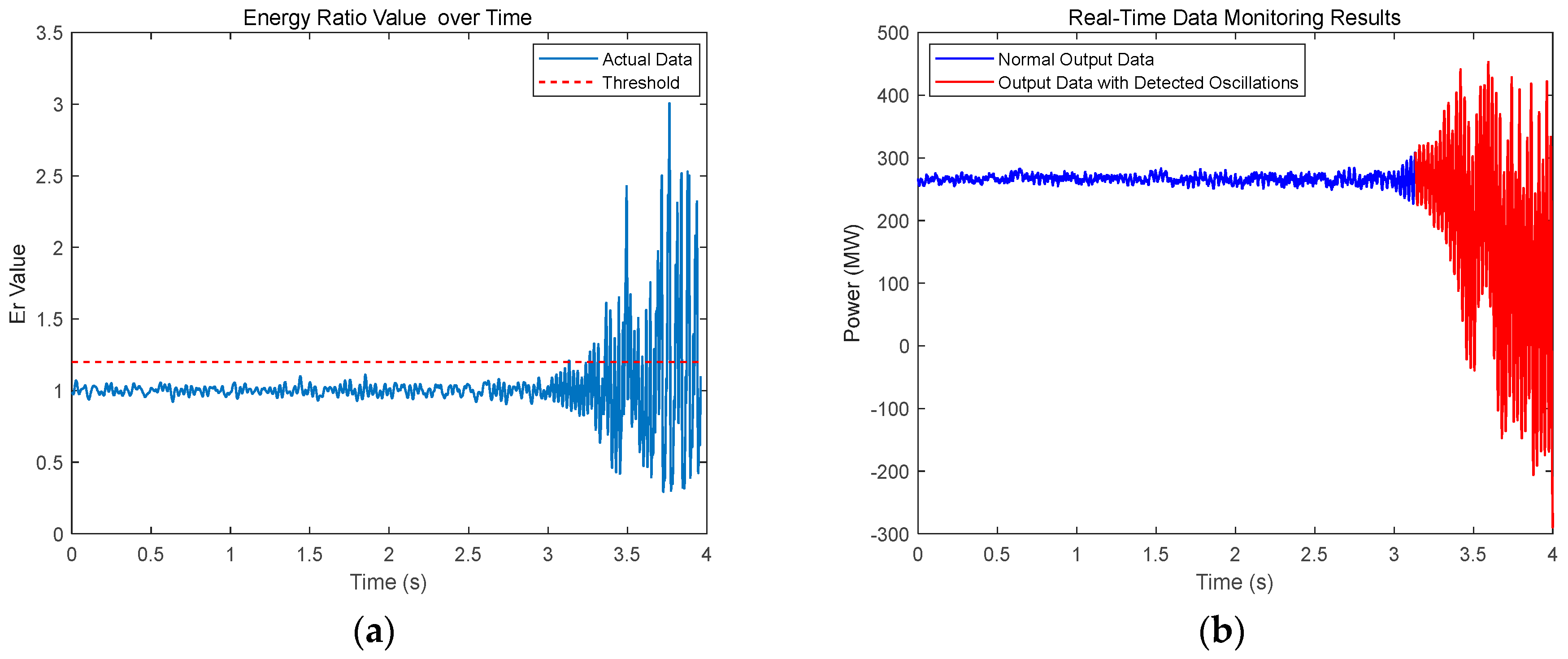
2.5. Energy Ratio Function
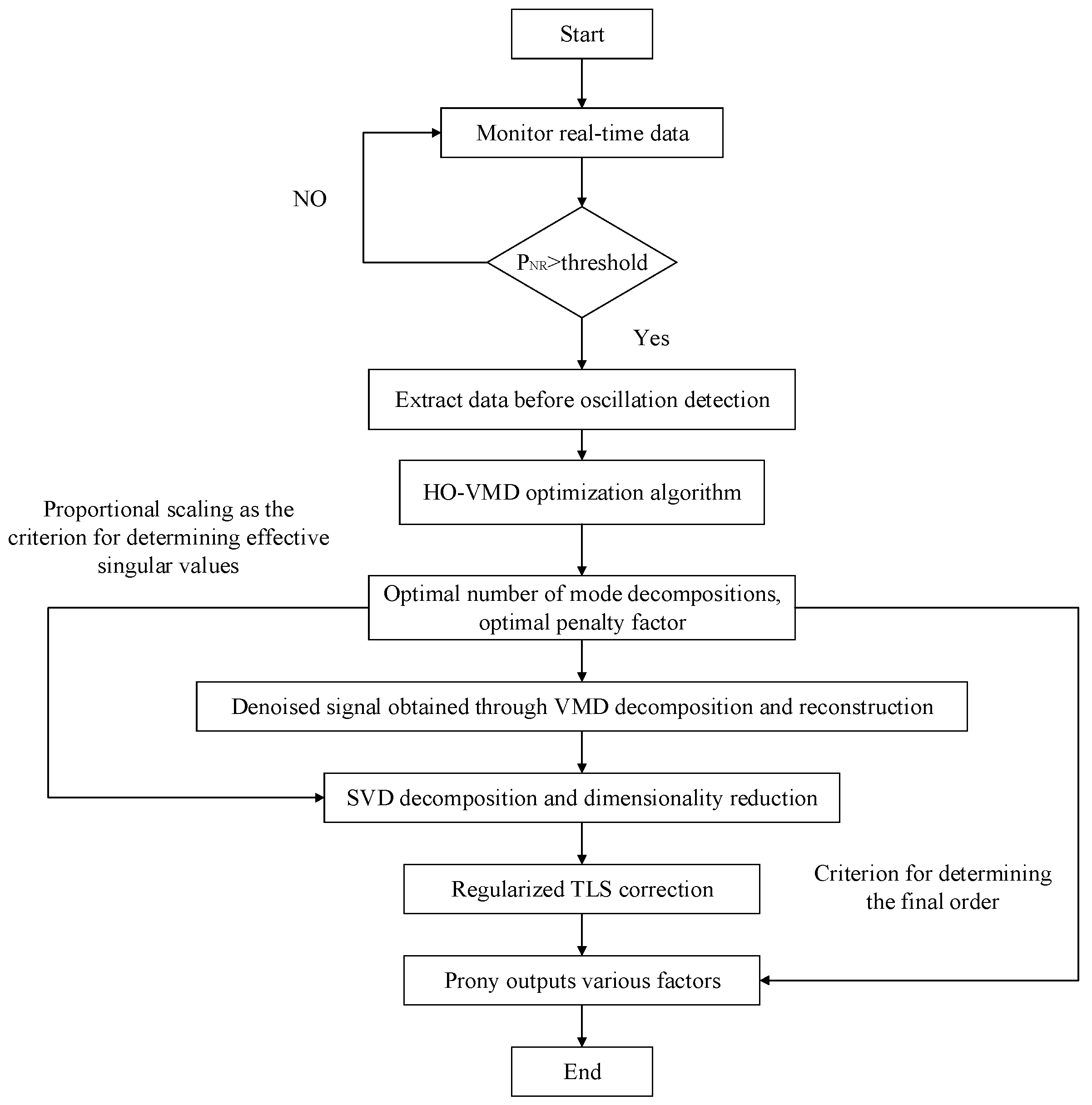
3. Specific Stages of the HO-VMD and SVD-RTLS-Prony Algorithms
4. Case Study
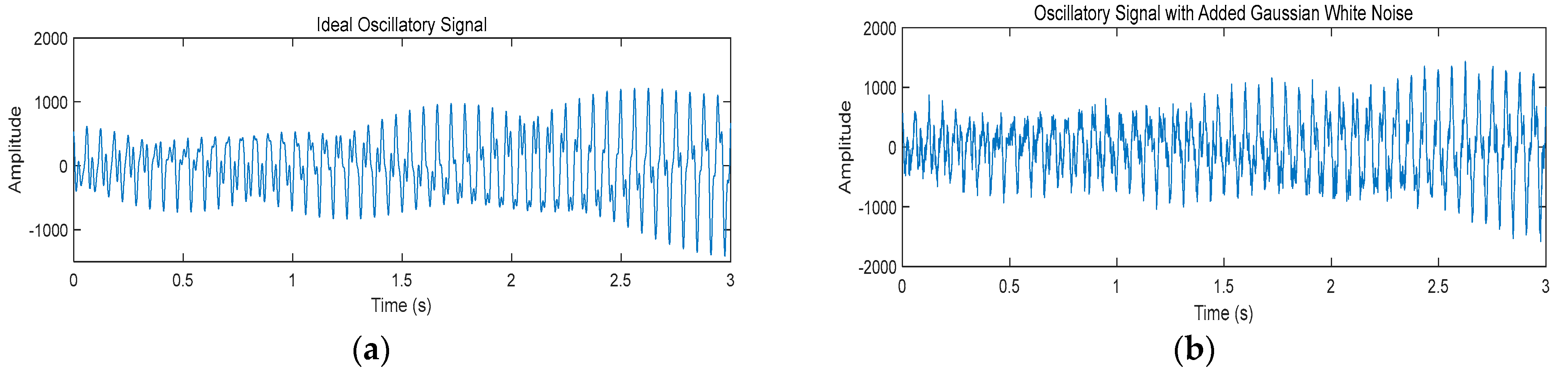
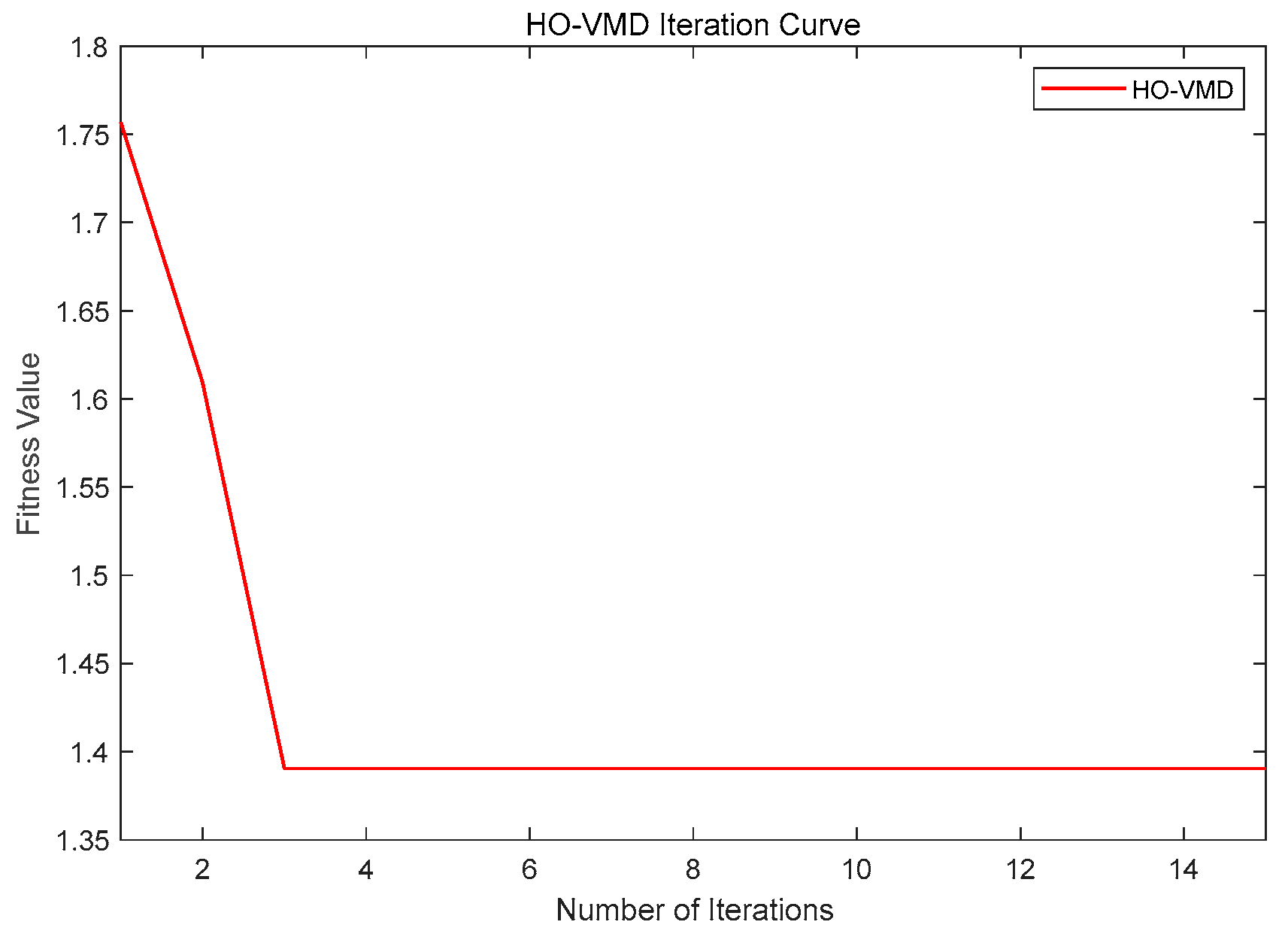
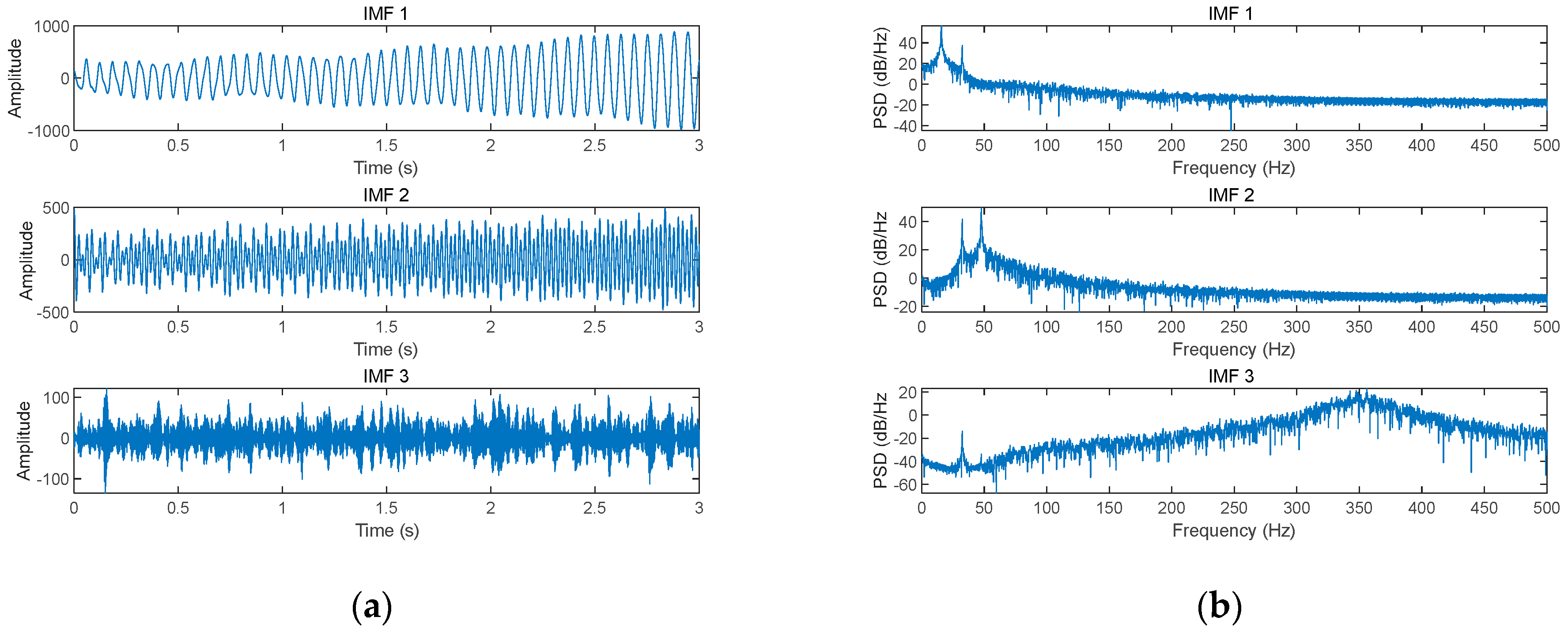
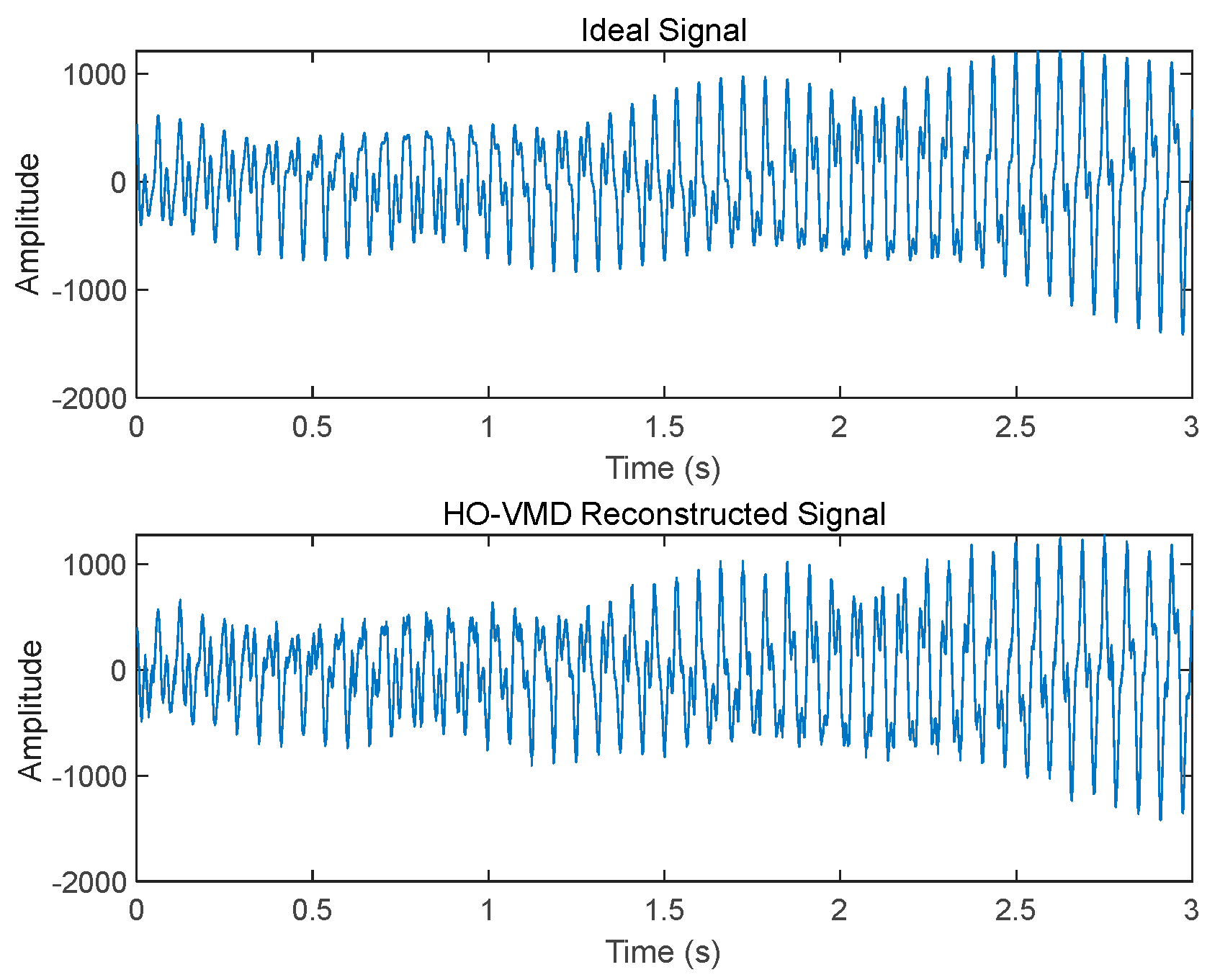
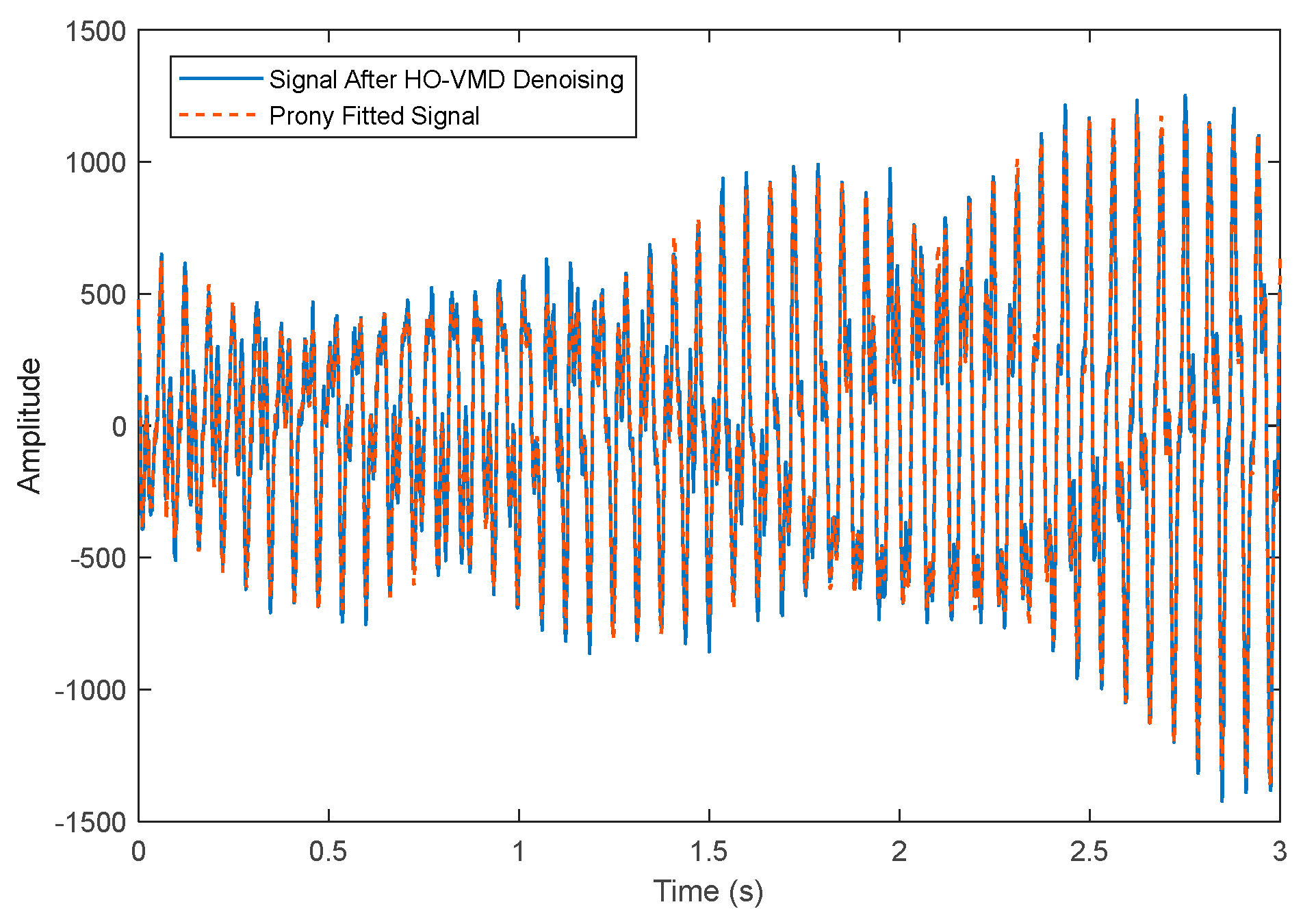
4.1. Ideal Signal Case Study
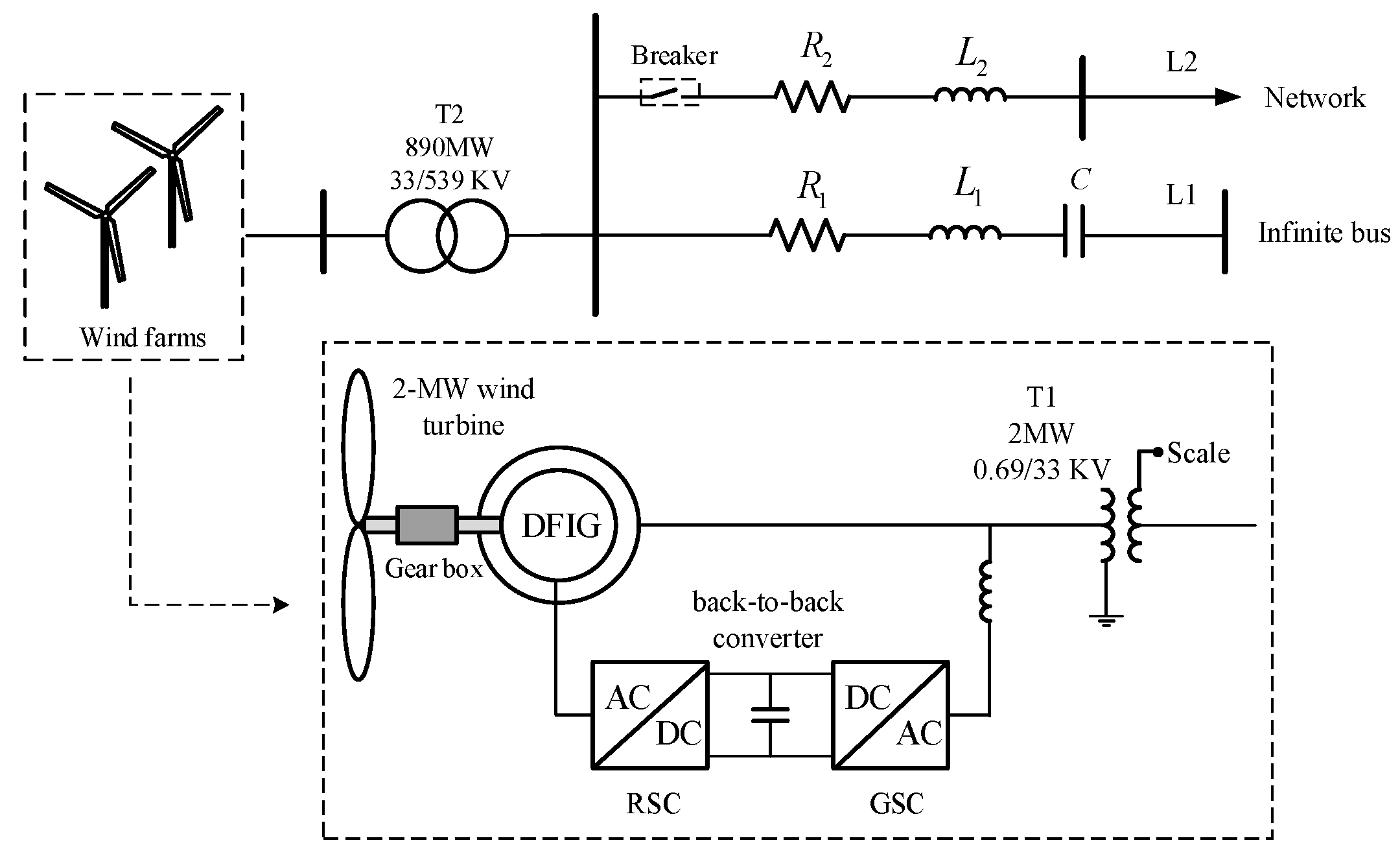
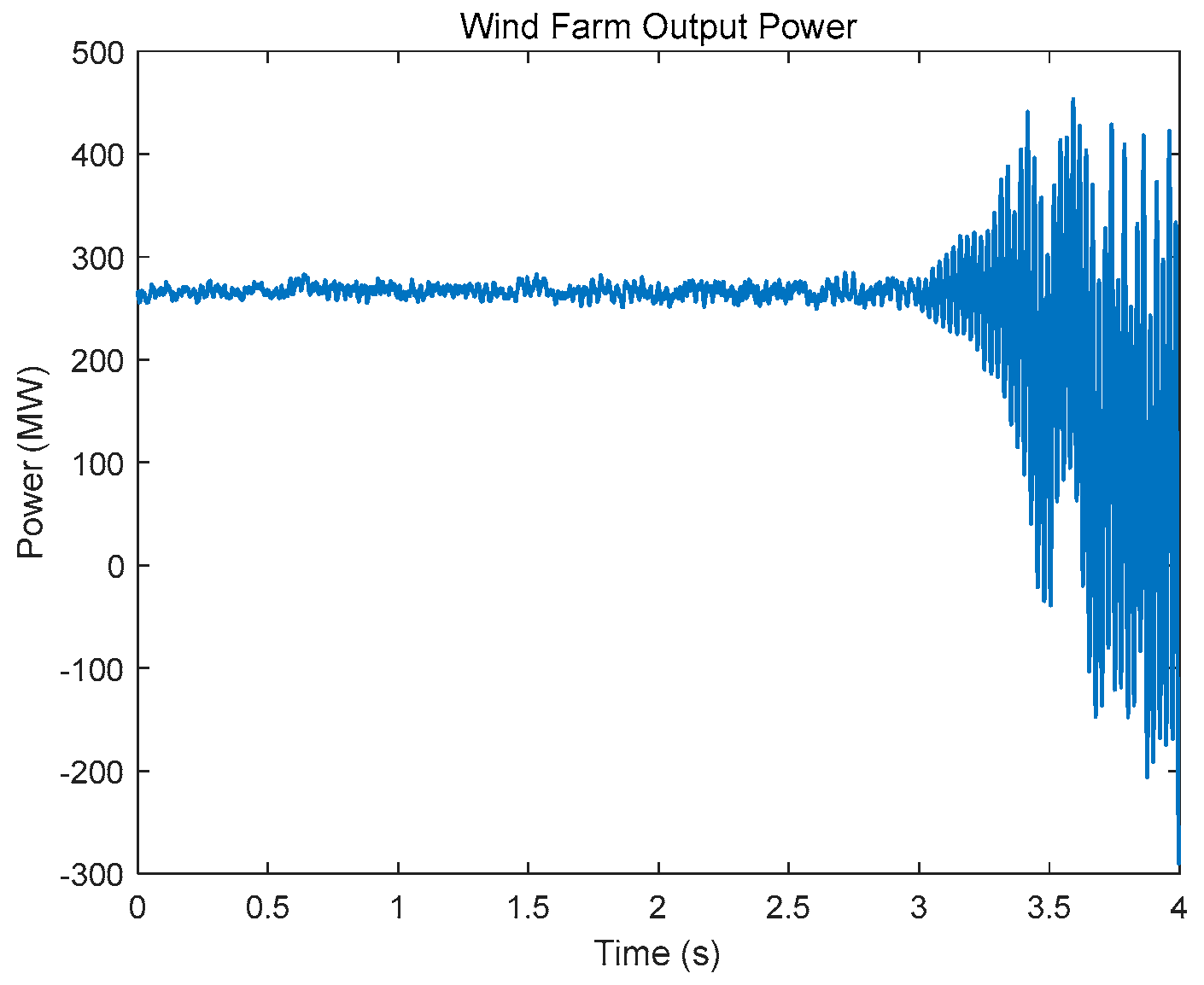
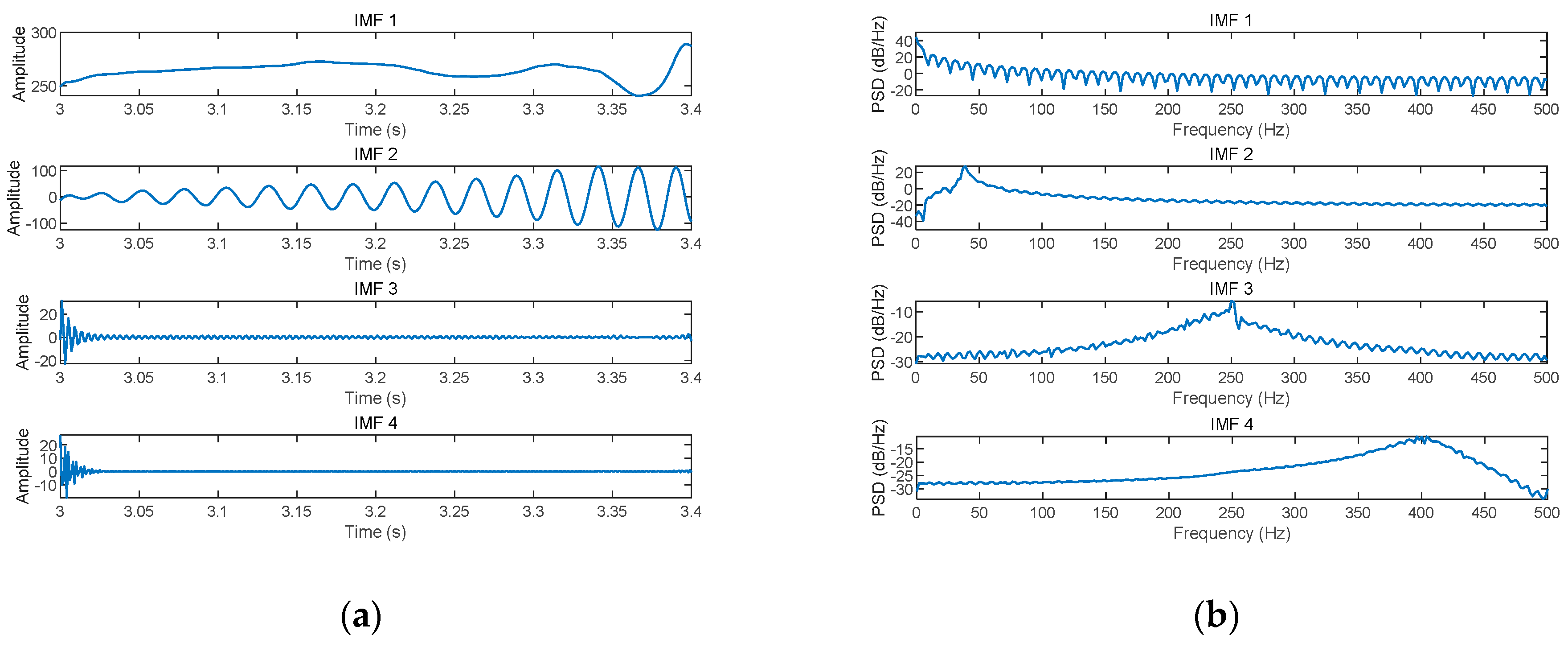
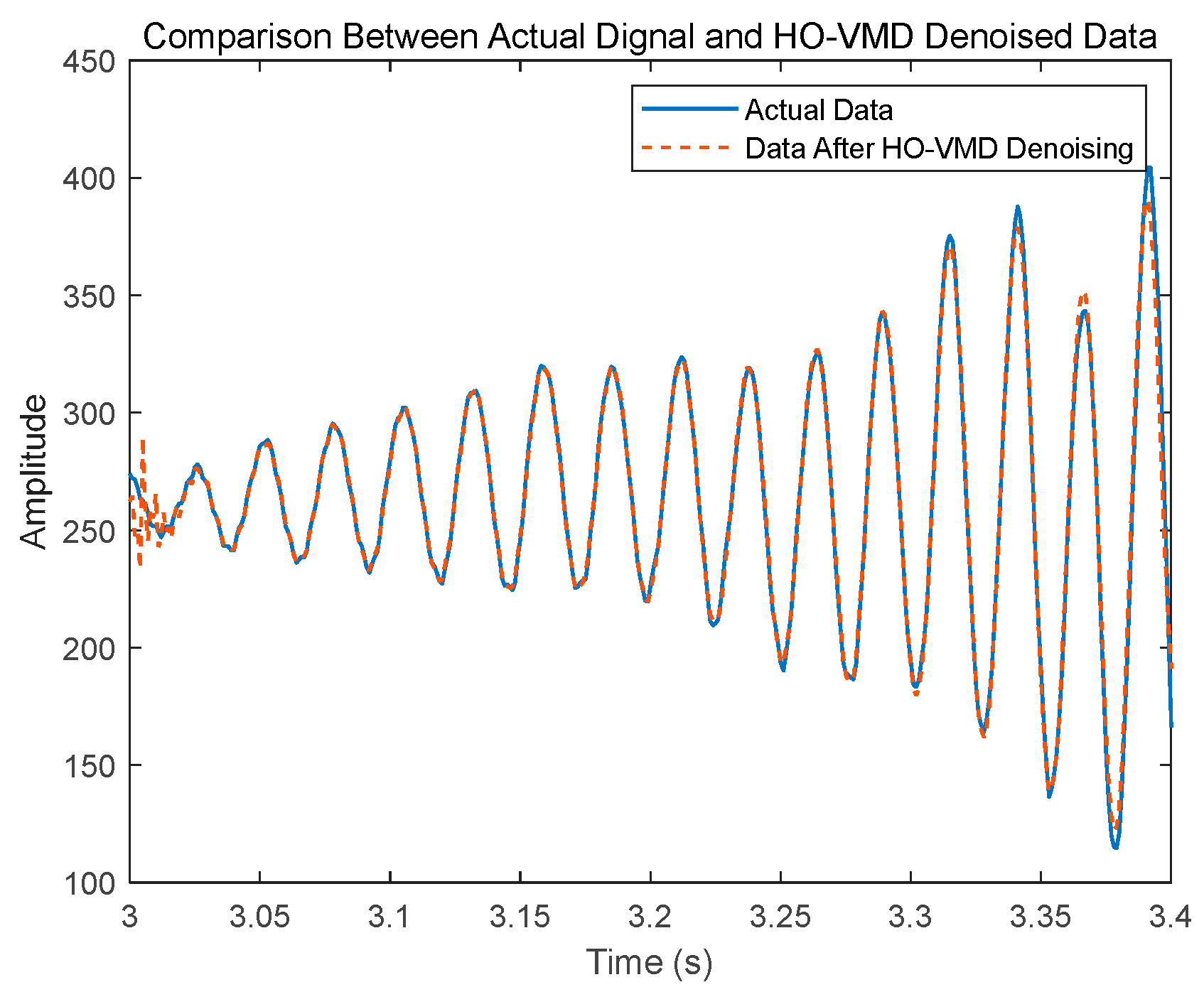
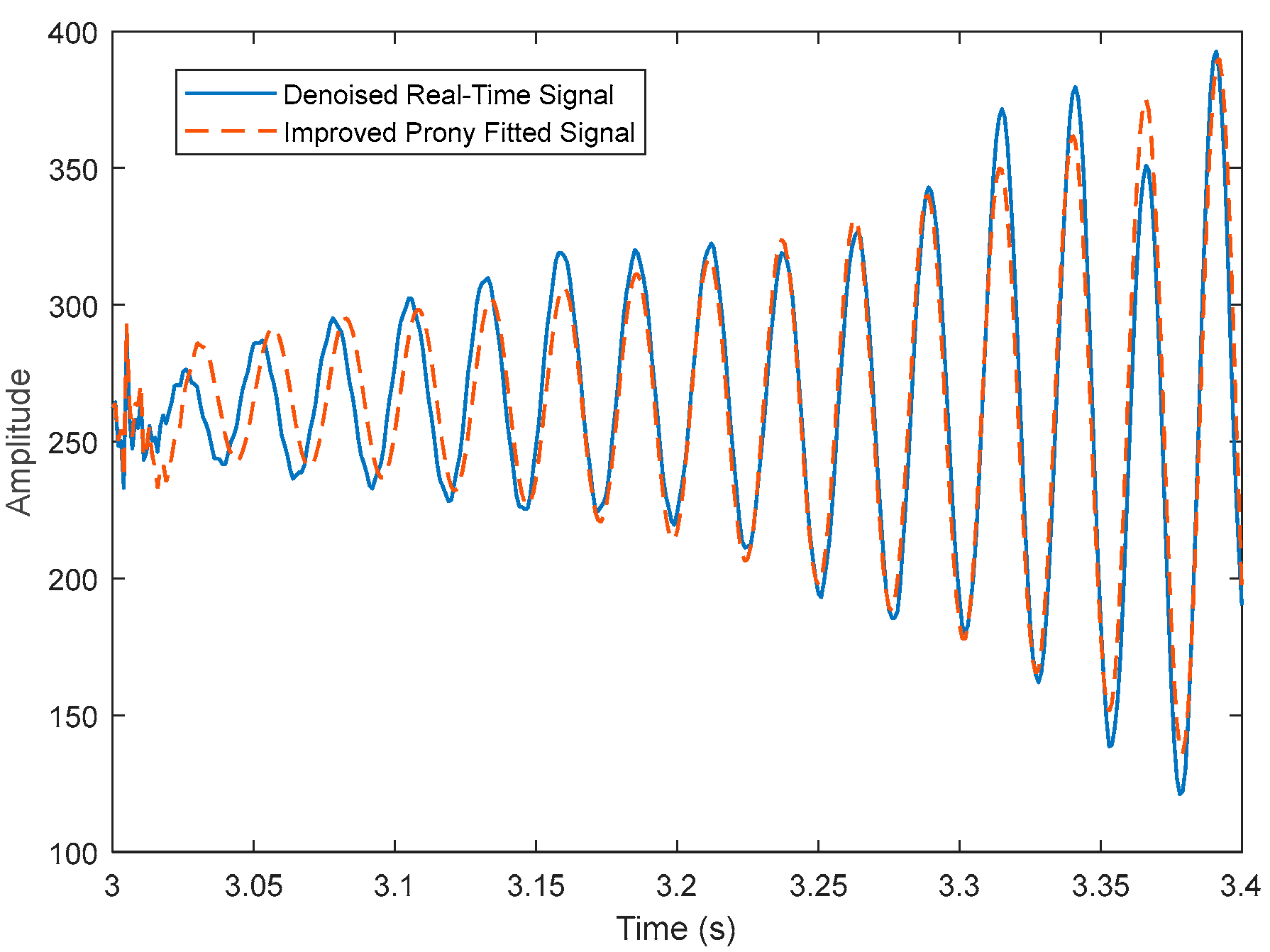
4.2. Practical Signal Case Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Rated Power: | 2 MW |
| Rated Voltage: | 0.69 kV |
| Frequency: | 60 Hz |
| Stator Resistance: | 0.00488 pu |
| Rotor Resistance: | 0.005491 pu |
| Stator Leakage Inductance: | 0.09231 pu |
| Rotor Leakage Inductance: | 0.09955 pu |
| Stator-Rotor Mutual Inductance: | 3.95279 pu |
| DC Side Capacitance: | 0.104 F |
| Rotor Inertia Constant: 0.4 s | Wind Turbine Inertia Constant: 4 s |
| Stiffness Coefficient: 0.3 pu | Damping Coefficient: 0.01 pu |
References
- Cheng, Y.Z.; Fan, L.L.; Rose, J.; Huang, S.H.; Schmall, J.; Wang, X.Y.; Xie, X.R.; Shair, J.; Ramamurthy, J.R.; Modi, N.; et al. Real-World Subsynchronous Oscillation Events in Power Grids With High Penetrations of Inverter-Based Resources. IEEE Trans. Power Syst. 2023, 38, 316–330. [Google Scholar] [CrossRef]
- Liu, G.; Liu, J.; Liu, A.D. Mitigating sub-synchronous oscillation using intelligent damping control of DFIG based on improved TD3 algorithm with knowledge fusion. Sci. Rep. 2024, 14, 14692. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, J.; Kemmetmüller, W.; Kugi, A. Modeling and static optimization of a variable speed pumped storage power plant. Renew. Energy 2017, 111, 38–51. [Google Scholar] [CrossRef]
- Ma, X.; Wu, D.; Wang, D.X.; Huang, B.W.; Desomber, K.; Fu, T.; Weimar, M. Optimizing pumped storage hydropower for multiple grid services. J. Energy Storage 2022, 51, 104440. [Google Scholar] [CrossRef]
- Shafiullah, G.M.; Oo, A.M.T.; Ali, A.; Wolfs, P. Potential challenges of integrating large-scale wind energy into the power grid-A review. Renew. Sustain. Energy Rev. 2013, 20, 306–321. [Google Scholar] [CrossRef]
- Obi, M.; Bass, R. Trends and challenges of grid-connected photovoltaic systems—A review. Renew. Sustain. Energy Rev. 2016, 58, 1082–1094. [Google Scholar] [CrossRef]
- Sun, B.; Ju, P.; Shahidehpour, M.; Pan, X.P. Calculation of Stable Domain of DFIG-Based Wind Farm in Series Compensated Power Systems. IEEE Access 2020, 8, 34900–34908. [Google Scholar] [CrossRef]
- Philip, J.G.; Jung, J.S.; Onen, A. Empirical Wavelet Transform Based Method for Identification and Analysis of Sub-synchronous Oscillation Modes Using PMU Data. J. Mod. Power Syst. Clean Energy 2024, 12, 34–40. [Google Scholar] [CrossRef]
- Chen, X.; Wu, X.; Zhou, J.Y.; Li, Q.F.; Wu, C.Y.; Li, Q.; Ren, B.X.; Xu, K. Ambient data-driven SSO online monitoring of type-3 wind turbine generator integrated power systems based on MMPF-KF method. Sci. Rep. 2023, 13, 15813. [Google Scholar] [CrossRef]
- Touti, E.; Abdeen, M.; El-Dabah, M.A.; Kraiem, H.; Agwa, A.M.; Alanazi, A.; Alanazi, T.I. Sub-Synchronous Oscillation Mitigation for Series-Compensated DFIG-Based Wind Farm Using Resonant Controller. IEEE Access 2024, 12, 66185–66195. [Google Scholar] [CrossRef]
- Xie, X.; Wang, L.; He, J.; Liu, H.; Wang, C.; Zhan, Y. Analysis of Subsynchronous Resonance/Oscillation Types in Power Systems. Power Syst. Technol. 2017, 41, 1043–1049. [Google Scholar]
- Yan, Y.B.; Yuan, X.M.; Hu, J.B. Stationary-Frame Modeling of VSC Based on Current-Balancing Driven Internal Voltage Motion for Current Control Timescale Dynamic Analysis. Energies 2018, 11, 374. [Google Scholar] [CrossRef]
- Song, R.; Guo, J.; Li, B.; Zhou, P.; Du, N.; Yang, D. Mechanism and Characteristics of Subsynchronous Oscillation in Direct-Drive Wind Power Generation System Based on Input-Admittance Analysis. Proc. Chin. Soc. Electr. Eng. 2017, 37, 4662–4670. [Google Scholar]
- Vieto, I.; Li, G.H.; Sun, J. Behavior, Modeling and Damping of a New Type of Resonance Involving Type-III Wind Turbines. In Proceedings of the 19th IEEE Workshop on Control and Modeling for Power Electronics (COMPEL), Padua, Italy, 25–28 June 2018. [Google Scholar]
- Liu, H.K.; Xie, X.R.; He, J.B.; Xu, T.; Yu, Z.; Wang, C.; Zhang, C.Y. Subsynchronous Interaction Between Direct-Drive PMSG Based Wind Farms and Weak AC Networks. IEEE Trans. Power Syst. 2017, 32, 4708–4720. [Google Scholar] [CrossRef]
- Ma, J.J.; Lyu, L.; Man, J.F.; Chen, M.Q.; Cheng, Y.J. Noise-like-Signal-Based Sub-Synchronous Oscillation Prediction for a Wind Farm with Doubly-Fed Induction Generators. Electronics 2024, 13, 2200. [Google Scholar] [CrossRef]
- Ma, Y.; Huang, Q.; Zhang, Z.Y.; Cai, D.S. Application of Multisynchrosqueezing Transform for Subsynchronous Oscillation Detection Using PMU Data. IEEE Trans. Ind. Appl. 2021, 57, 2006–2013. [Google Scholar] [CrossRef]
- Hauer, J.F.; Demeure, C.J.; Scharf, L.L. Initial Results in Prony Analysis of Power-System Response Signals. IEEE Trans. Power Syst. 1990, 5, 80–89. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, S.N. Exact Model Order ESPRIT Technique for Harmonics and Interharmonics Estimation. IEEE Trans. Instrum. Meas. 2012, 61, 1915–1923. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT—Estimation of signal parameters via rotational invariance techniques. In Proceedings of the Program of the Institute for Mathematics and Its Applications: Signal Processing, University of Minnesota, The Institute of Mathematics and Its Applications, Minneapolis, MN, USA, 27 June–5 August 1989; pp. 369–411. [Google Scholar]
- Zhang, C.Y.; Chen, Z.T.; Wang, M.H.; Jia, L.; Zi, P. A Novel Identification Method of Power System Oscillation based on Dynamic Mode Decomposition. In Proceedings of the Power System and Green Energy Conference (PSGEC), Electr Network, Shanghai, China, 20–22 August 2021; pp. 713–717. [Google Scholar]
- Wang, Y.; Jiang, X.L.; Xie, X.R.; Yang, X.M.; Xiao, X.Y. Identifying Sources of Subsynchronous Resonance Using Wide-Area Phasor Measurements. IEEE Trans. Power Deliv. 2021, 36, 3242–3254. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.N.; Srikanth, N. A Comparative Study of Empirical Mode Decomposition-Based Short-Term Wind Speed Forecasting Methods. IEEE Trans. Sustain. Energy 2015, 6, 236–244. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Shao, Y.; Gong, W.W.; Zhang, Z.W.; Wu, J.W. Research on combined diagnosis of mechanical fault vibration-sound signal of high voltage circuit breaker based on EEMD-Energy Entropy feature. In Proceedings of the International Conference on Sensors and Instruments (ICSI), Qingdao, China, 28–30 May 2021. [Google Scholar]
- Wang, X.L.; Zhou, F.C.; He, Y.L.; Wu, Y.J. Weak fault diagnosis of rolling bearing under variable speed condition using IEWT-based enhanced envelope order spectrum. Meas. Sci. Technol. 2019, 30, 035003. [Google Scholar] [CrossRef]
- Chegini, S.N.; Bagheri, A.; Najafi, F. Application of a new EWT-based denoising technique in bearing fault diagnosis. Measurement 2019, 144, 275–297. [Google Scholar] [CrossRef]
- Keyhani, A.; Mohammadi, S. Structural modal parameter identification using local mean decomposition. Meas. Sci. Technol. 2018, 29, 025003. [Google Scholar] [CrossRef]
- Naik, J.; Satapathy, P.; Dash, P.K. Short-term wind speed and wind power prediction using hybrid empirical mode decomposition and kernel ridge regression. Appl. Soft Comput. 2018, 70, 1167–1188. [Google Scholar] [CrossRef]
- Wei, P.; Li, Q.S.; Sun, M.M.; Huang, J.X. Modal identification of high-rise buildings by combined scheme of improved empirical wavelet transform and Hilbert transform techniques. J. Build. Eng. 2023, 63, 105443. [Google Scholar] [CrossRef]
- Lu, T.; Yu, F.Q.H.; Wang, J.R.; Wang, X.Y.; Mudugamuwa, A.; Wang, Y.F.; Han, B.K. Application of adaptive complementary ensemble local mean decomposition in underwater acoustic signal processing. Appl. Acoust. 2021, 178, 107966. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Li, T.X.; Zhang, F.D.; Lin, J.; Bai, X.Y.; Liu, H.Z. Fading noise suppression method of Φ-OTDR system based on non-local means filtering. Opt. Fiber Technol. 2023, 81, 103572. [Google Scholar] [CrossRef]
- Liu, B.; Liu, C.F.; Zhou, Y.; Wang, D.H. A chatter detection method in milling based on gray wolf optimization VMD and multi-entropy features. Int. J. Adv. Manuf. Technol. 2023, 125, 831–854. [Google Scholar] [CrossRef]
- Du, H.R.; Wang, J.X.; Qian, W.J.; Zhang, X.N. An Improved Sparrow Search Algorithm for the Optimization of Variational Modal Decomposition Parameters. Appl. Sci. 2024, 14, 2174. [Google Scholar] [CrossRef]
- Meng, Z.; Wang, X.Y.; Liu, J.B.; Fan, F.J. An adaptive spectrum segmentation-based optimized VMD method and its application in rolling bearing fault diagnosis. Meas. Sci. Technol. 2022, 33, 125107. [Google Scholar] [CrossRef]
- Guo, Y.Y.; Ho, Y.K.; Zhao, X.Z.; Zhang, C.L.; Long, S.B. An IGSA-VMD method for fault frequency identification of cylindrical roller bearing. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2024, 238, 9307–9320. [Google Scholar] [CrossRef]
- Amiri, M.H.; Hashjin, N.M.; Montazeri, M.; Mirjalili, S.; Khodadadi, N. Hippopotamus optimization algorithm: A novel nature-inspired optimization algorithm. Sci. Rep. 2024, 14, 5032. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.Y.; Li, X.C.; Liu, Z.L.; Liu, Y. Application of Underdetermined Blind Source Separation Algorithm on the Low-Frequency Oscillation in Power Systems. Energies 2023, 16, 3571. [Google Scholar] [CrossRef]
- Wang, D.M.; Sun, Y.; Xiao, J.L.; Lu, J.Y. Research on pipeline leakage signal denoising using variational mode decomposition and energy value. Pet. Sci. Technol. 2023, 1–17. [Google Scholar] [CrossRef]
- Yang, C.; Shi, Q.H. An interval perturbation method for singular value decomposition (SVD) with unknown-but-bounded (UBB) parameters. J. Comput. Appl. Math. 2024, 436, 115436. [Google Scholar] [CrossRef]
- Liu, K.; Hu, X.; Li, X.; Han, X. Sub-Synchronous Oscillation Modal Identification Method Based on Emd and Tls-Pronyalgorithm and Voltage Feedback Suppression Strategy. Acta Energiae Solaris Sin. 2023, 44, 294–302. [Google Scholar]
- Fan, L.L.; Kavasseri, R.; Miao, Z.L.; Zhu, C.X. Modeling of DFIG-Based Wind Farms for SSR Analysis. IEEE Trans. Power Deliv. 2010, 25, 2073–2082. [Google Scholar] [CrossRef]
- Leon, A.E. Integration of DFIG-Based Wind Farms Into Series-Compensated Transmission Systems. IEEE Trans. Sustain. Energy 2016, 7, 451–460. [Google Scholar] [CrossRef]
| SNR | MSE | |
|---|---|---|
| 3-order EMD | 3.25 | 104,627.47 |
| 3-order VMD (α = 500) | 16.98 | 4439.01 |
| 5-order EMD | 11.76 | 14,770.51 |
| 5-order VMD (α = 1000) | 15.12 | 6808.60 |
| 7-order EMD | 10.29 | 20,685.75 |
| 7-order EMD (α = 2000) | 14.65 | 7593.49 |
| Mode | Amplitude | Frequency | Damping Factor | Damping Ratio |
|---|---|---|---|---|
| 1 | 277.36 | 15.60 | 0.41 | −0.41 |
| 2 | 221.07 | 32.40 | −0.18 | 0.09 |
| 3 | 162.78 | 47.60 | 0.26 | −0.09 |
| Mode | Amplitude | Frequency | Damping Factor | Damping Ratio |
|---|---|---|---|---|
| 1 | 269.4425 | 0.00 | −0.10 | 100.00 |
| 2 | 34.2672 | 0.00 | −64.22 | 100.00 |
| 3 | 18.65 | 39.82 | 4.99 | −2.04 |
| 4 | 28.36 | 243.17 | −106.35 | 6.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wu, F.; Shi, L.; Li, Y.; Qi, P.; Guo, X. Identification of Sub-Synchronous Oscillation Mode Based on HO-VMD and SVD-Regularized TLS-Prony Methods. Energies 2024, 17, 5067. https://doi.org/10.3390/en17205067
Chen Y, Wu F, Shi L, Li Y, Qi P, Guo X. Identification of Sub-Synchronous Oscillation Mode Based on HO-VMD and SVD-Regularized TLS-Prony Methods. Energies. 2024; 17(20):5067. https://doi.org/10.3390/en17205067
Chicago/Turabian StyleChen, Yuzhe, Feng Wu, Linjun Shi, Yang Li, Peng Qi, and Xu Guo. 2024. "Identification of Sub-Synchronous Oscillation Mode Based on HO-VMD and SVD-Regularized TLS-Prony Methods" Energies 17, no. 20: 5067. https://doi.org/10.3390/en17205067
APA StyleChen, Y., Wu, F., Shi, L., Li, Y., Qi, P., & Guo, X. (2024). Identification of Sub-Synchronous Oscillation Mode Based on HO-VMD and SVD-Regularized TLS-Prony Methods. Energies, 17(20), 5067. https://doi.org/10.3390/en17205067






