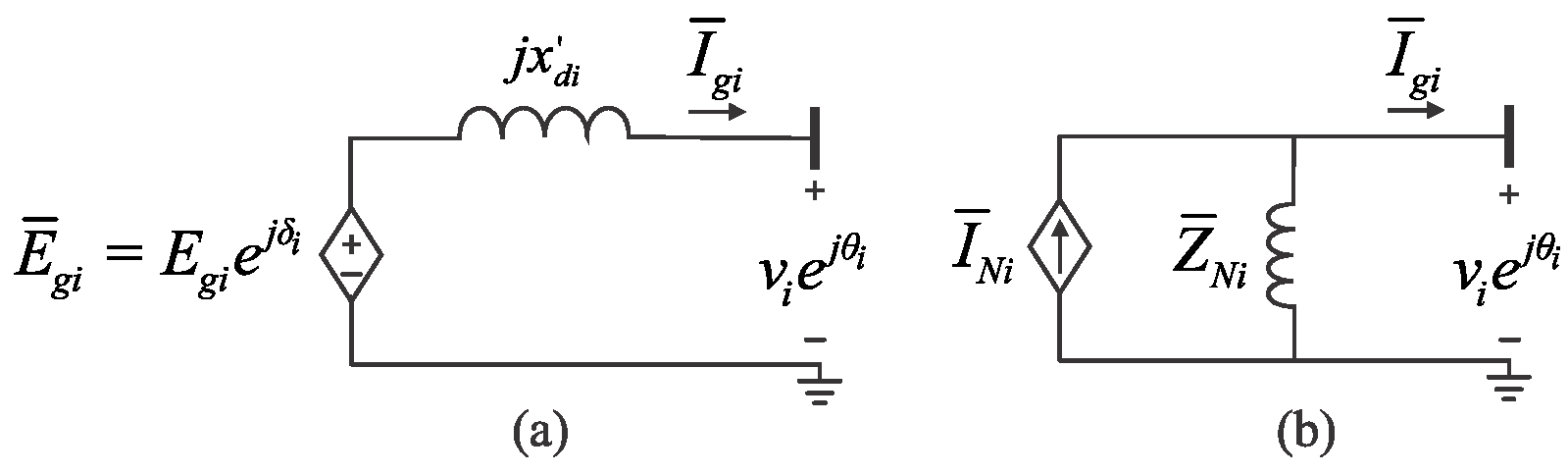Computing the Network’s Equilibrium Point at the Fault Clearing Instant in Transient Stability Studies

Abstract

This paper proposes an approach for computing the network’s equilibrium point related to the fault clearing time in transient stability studies. The computation of this point is not a trivial task, particularly when the algebraic network’s equations are expressed in the power balance form. A natural attempt to solve this problem is using Newton’s method. However, convergence issues are found because of the lack of a general strategy for initializing nodal voltages at the clearing time. This problem has not been widely discussed in the existing literature and, therefore, is comprehensively analyzed in this paper. Furthermore, the paper proposes the use of a network’s model based on current injections and an extended admittance matrix to overcome the problem. This model is efficiently solved via the fixed-point iteration method, which involves factorization of the extended admittance matrix into the product of a lower triangular matrix [L] and an upper triangular matrix [U]. This solution executes a just once and only forward–backward substitution during the iterative solution process. Case studies clearly demonstrate the proposal’s effectiveness in computing the equilibrium point in operating conditions where Newton’s method fails to converge.

1. Introduction

The power system’s ability to withstand a large disturbance without generators losing synchronism is routinely evaluated at control centers. This evaluation can be performed through Lyapunov-based and non-Lyapunov-based transient stability approaches [1]. In the latter category, the methods that have received the most attention are time-domain (TD) simulation [2], the extended equal area criterion [3,4], and data-driven techniques [1,5,6].

In the context of the conventional TD simulation method, the transient stability problem is formulated through a system of nonlinear differential-algebraic equations (DAEs), where the algebraic network’s equations can be expressed either in the current balance or power balance form [7]. This DAE system is directly solved by means of a numerical integration process. Different TD approaches have been proposed to increase the efficiency of that integration process, such as the use of the dishonest Newton method [8] and a mix of explicit and implicit integration methods [9]. The decomposition of DAEs into equivalent linear subsystems for the purpose of parallel computing was proposed in [5,10], while the use of a semi-implicit formulation to reduce the computational burden and to simplify the formulation of the transient stability problem is reported in [11]. Lastly, an analytical method to solve the set of DAEs using differential transformation is detailed in [12]. Despite these outstanding contributions, the conventional TD simulation is still the most used approach in the power engineering industry for performing transient stability analysis [5,9].

In the conventional TD simulation method, the DAEs are commonly solved by means of an explicit partitioned integration approach when the current balance form is considered. On the other hand, when the power balance form is adopted, a simultaneous-implicit (SI) integration approach is generally used [5]. When comparing both approaches, the power balance form has the advantage of being a general framework for modeling all devices used in different power system studies [7,8], including renewable energy sources [1,13]. In addition, this approach may be faster and numerically more stable for stiff systems [5,14]. Therefore, this work has focused on this SI approach.

The SI approach solves the transient stability problem in a single frame of reference, where the set of DAEs is algebraized by the trapezoidal integration method. The resulting nonlinear discrete equations are solved by means of Newton’s method at each integration step. Therefore, an accurate initial condition of the dynamic and algebraic state variables is crucial in avoiding an ill-conditioned Jacobian matrix and the loss of Newton’s method convergence [7]. Unlike dynamic state variables, algebraic state variables instantaneously change after a disturbance occurs. In this case, the TD simulation must be paused to compute the values of algebraic states that determine the network’s equilibrium point immediately after the disturbance occurrence [14]. The TD simulation is then continued by considering this equilibrium point as the initial condition for the first integration step of the post-disturbance period. However, the TD simulation cannot be completed if the computation of such an equilibrium point fails due to the lack of an accurate initial condition, which is the problem addressed in this paper, as detailed below.

The post-disturbance equilibrium point associated with the inception of a fault can be obtained by directly solving the set of nonlinear algebraic equations of the network in power balance form through Newton’s method [14]. Care must be exercised, however, when this approach is used to compute the equilibrium point at the fault clearing instant [7]. In this case, one intuitive initialization for solving those nonlinear algebraic equations is using the values of algebraic state variables calculated just before the fault clearing. However, when the disturbance is a short circuit and the voltage magnitudes’ adjustments are divided by their corresponding voltage magnitudes, this initialization leads to a singular Jacobian matrix so that Newton’s method fails to converge [15]. If voltage adjustments are not weighted, the iterative solution of the algebraic equations results in a zero voltage magnitude at the faulted bus immediately after clearing the fault. Furthermore, this null value remains for the rest of the TD simulation [7]. Another option is to initialize the algebraic states to their prefault values or with a flat initialization profile. These initializations, however, could steer Newton’s method to an eventual loss of convergence because the longer the fault clearing time, the further away the initial guess is from the algebraic variables’ actual values immediately after clearing the fault [16]. In these circumstances, Newton’s method fails to compute the network’s equilibrium point at the fault clearing instant, and therefore, the TD simulation cannot be continued.

To the best of the authors’ knowledge, a strategy for addressing the above numerical problems has not been reported in the literature for transient stability studies of power systems. In addition, in a review of the technical documentation of existing commercial and open-source software for transient stability analyses, no guidelines to solve those numerical issues have been found. This lack of guidelines may be because existing commercial software formulates the transient stability problem by expressing the algebraic network’s equations in the current balance form, where the initialization of the algebraic variables at the fault clearing instant do not produce that failure of the TD simulation.

In this context, this paper provides a comprehensive analysis to clarify the failure of Newton’s method in calculating the network equilibrium point at the fault clearing instant when the algebraic network’s equations are in power balance form, which is also illustrated by numerical examples. Furthermore, an approach is proposed to solve the algebraic state variables just after clearing a fault by overcoming those drawbacks in the SI approach. To this aim, the generator and load models are transformed into current injections that are related to the network’s nodal voltages through a constant extended network admittance matrix. Hence, this LU-factorized matrix, which is constant throughout the solution process, is used to solve the current injection-based system model by performing only one forward and backward substitution in each iteration of the fixed-point iteration method.

This paper is organized as follows: First, the power balance-based transient stability problem and the failure of Newton’s method in the SI approach are described in Section 2. Next, the proposed approach is given in detail in Section 3. Several case studies are then presented in Section 4 to illustrate the failure of the SI approach and to demonstrate the effectiveness of the proposed approach. Lastly, conclusions are presented in Section 5.

2. Problem Statement for the Computation of the Equilibrium Point at ${\mathbf{t}}_{\mathbf{c}\mathbf{l}}^{\mathbf{+}}$

In this section, the problem for computing the network’s equilibrium point at the fault clearing instant is comprehensively formulated. For this purpose, the transient stability problem is formulated by a set of DAEs expressed in the power balance form, and these equations are discretized by the SI approach. These discretized equations are then used to clarify how the initialization of algebraic variables at $t_{cl}^{+}$ leads to the misperformance of Newton’s method in computing that equilibrium point.

The power system’s dynamics are given by the set of DAEs

$$\begin{array}{l}\dot{\mathit{x}}=\mathit{f}(\mathit{x},\mathit{y},\mathit{\beta })\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \mathit{f}:{ℝ}^{n_x+n_y+n_p}\to {ℝ}^{n_x}\\ \mathbf{0}=\mathit{g}(\mathit{x},\mathit{y},\mathit{\beta })\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \mathit{g}:{ℝ}^{n_x+n_y+n_p}\to {ℝ}^{n_y}\\ \mathit{x}\in {ℝ}^{n_x}\hspace{1em} \mathit{y}\in {ℝ}^{n_y}\hspace{1em} \mathit{\beta }\in {ℝ}^{n_p}\end{array},$$

(1)

where x and y denote the vectors of dynamic and algebraic state variables, while β is the vector of input parameters. The algebraic variables correspond to the bus voltages expressed in polar or D-Q rectangular coordinates: y = [${\mathit{v}}^T$ ${\mathit{\theta }}^T$]^T = [${\mathit{v}}_1$,…,${\mathit{v}}_n$,${\theta }_1$,…,${\theta }_n$]^T or y = [$v_D^T$ $v_Q^T$]^T = [$v_{D1}$,…,$v_{Dn}$,$v_{Q1}$,…,$v_{Qn}$]^T, where T is the transposed operator. Furthermore, the rate of change of x given by f(∙) is restricted to comply with the nodal power balance g(∙) = 0.

2.1. TD Simulation via a Simultaneous-Implicit Approach

The dynamics of x and y are obtained for a study time period T by discretizing (1) through the trapezoidal rule and iteratively solving the resulting discretized equations for each discrete time using Newton’s method, as follows. At the (k + 1)-th time step, the discretized equations are linearized: [J^k+1]ⁱ [∆χ^k+1]ⁱ = −[Ф^k+1]ⁱ, where the Jacobian matrix J^k+1 is given by (2) and ∆χ^k+1 = [∆x^T ∆y^T]^k+1,T. Note that the Jacobian submatrices correspond to (3), and I denotes an identity matrix. Furthermore, Ф^k+1 = [φ(·)^T g(·)^T]^k+1,T, where the vector φ(·)^k+1 corresponds to the discretization of f(∙) via the trapezoidal rule in the time interval [k, k + 1], as given by (4) and g(·)^k+1 = g(x^k+1, y^k+1, β):

$${\mathit{J}}^{k+1}=\left[\begin{array}{cc}\mathit{I}-0.5\Delta t{\mathit{f}}_x{(\cdot )}^{k+1}& -0.5\Delta t{\mathit{f}}_{\mathit{y}}{(\cdot )}^{k+1}\\ {\mathit{g}}_x{(\cdot )}^{k+1}& {\mathit{g}}_{\mathit{y}}{(\cdot )}^{k+1}\end{array}\right],$$

(2)

$$\begin{array}{l}{\mathit{f}}_x^{k+1}=\partial \mathit{\phi }{(\cdot )}^{k+1}/\partial {\mathit{x}}^{k+1} ,\hspace{1em} {\mathit{f}}_{\mathit{y}}^{k+1}=\partial \mathit{\phi }{(\cdot )}^{k+1}/\partial {\mathit{y}}^{k+1}\\ {\mathit{g}}_x^{k+1}=\partial \mathit{g}{(\cdot )}^{k+1}/\partial {\mathit{x}}^{k+1} ,\hspace{1em} {\mathit{g}}_{\mathit{y}}^{k+1}=\partial \mathit{g}{(\cdot )}^{k+1}/\partial {\mathit{y}}^{k+1}\end{array}$$

(3)

$$\mathit{\phi } {(\cdot )}^{k+1}=x^{k+1}-{\mathit{x}}^k-0.5\Delta t\left(\mathit{f}{(\cdot )}^{k+1}-\mathit{f}{(\cdot )}^k\right)=0.$$

(4)

Lastly, the linearized equations are solved at each iteration i of Newton’s method to obtain [∆χ^k+1]ⁱ and to update the values of the variables according to [x^k+1]ⁱ⁺¹ = [x^k+1]ⁱ + [Δx^k+1]ⁱ and [y^k+1]ⁱ⁺¹ = [y^k+1]ⁱ + [Δy^k+1]ⁱ, until a convergence criterion is satisfied. This solution method is applied to the entire study time period defined from the initial time $t_0^{+}=0$ to the time t_f of the fault inception, from t_f to the fault clearing time t_cl, and from t_cl to the end of the study time period t_end: T = [$t_0^{+}$, t_f] $\cup$ (t_f, t_cl] $\cup$ (t_cl, t_end].

2.2. Explicit Formulation of the Nonlinear Power Balance Equations at $t_{cl}^{+}$

The DAEs in (1) must reflect any network disturbance, including the clearing of faults. Hence, at the first time step after clearing the fault, k + 1 = $t_{cl}^{+}$, the step size must be set as Δt = 0 to calculate the instantaneous change in state variables’ values. According to (4), setting Δt = 0 directly yields x^k+1 = x^k, where x^k represents the values of the dynamic state variables at the last time step before clearing the fault: k = $t_{cl}^{-}$. Hence, the values of the dynamic state variables are known for k + 1 = $t_{cl}^{+}$ but not the values of algebraic state variables y^k+1 that correspond to the network’s equilibrium point immediately after clearing the fault.

An intuitive approach for attempting to obtain the value of the algebraic state variables y^k+1 is to use Newton’s method for solving the nonlinear power balance equations related to that time step k + 1 = $t_{cl}^{+}$: g(∙)^k+1 = 0. For this purpose, however, an initial condition of those variables is unknown because the values of the algebraic state variables instantaneously change from $t_{cl}^{-}$ to $t_{cl}^{+}$. In this context, the application of Newton’s method is difficult, as detailed below based on the explicit formulation of those nonlinear power balance equations.

Since the values of the variables x^k+1 and input parameters β are known, the nonlinear power balance equations can be expressed only in terms of the variables y^k+1: g(y)^k+1 = 0. For a system of nb buses, the set of power balance equations is given in explicit form by (5), where the equation for the nth bus is the product of multiplying the corresponding voltage phasor $v_n{e}^{j{\theta }_n}$ by the sum of the N_n complex conjugated currents injected at that bus [7]:

$$\mathit{g}{(\mathit{y})}^{k+1}={\left[\left(v_1{e}^{j{\theta }_1}\right)\left({\displaystyle \sum _{l=1}^{N_1}{\overline{I}}_{1 l}^{*}\left(\mathit{y}\right)}\right),\cdots ,\left(v_{nb}{e}^{j{\theta }_{nb}}\right)\left({\displaystyle \sum _{l=1}^{N_{nb}}{\overline{I}}_{nb l}^{*}\left(\mathit{y}\right)}\right)\right]}^{k+1,T}=\mathbf{0}.$$

(5)

For the sake of simplicity, (5) is expressed in compact form by (6), where $I_n{(\mathit{y})}^{k+1}$ is given by (7):

$$\mathit{g}{(\mathit{y})}^{k+1}={\left[v_1{I}_1(\mathit{y}),\cdots ,v_{nb}{I}_{nb}(\mathit{y})\right]}^{k+1,T}=\mathbf{0};$$

(6)

$$I_n{(\mathit{y})}^{k+1}={\left[\left(e^{j{\theta }_n}\right)\left({\displaystyle \sum _{l=1}^{N_n}{\overline{I}}_{n l}^{*}\left(\mathit{y}\right)}\right)\right]}^{k+1}; n=1,\dots ,nb.$$

(7)

The set of Equation (6) must be linearized around an initial condition y⁰ for their solution. Therefore, Taylor’s series theorem is applied, which yields (8), where A_n and B_n are given in (9) and (10), respectively. It should be noted that y^k+1 = [v^T θ^T]^k+1,T, ${\mathit{v}}_l^{k+1}\in {\mathit{v}}^{k+1}$, and ${\theta }_l^{k+1}\in {\theta }^{k+1}$ for l = 1,…, nb:

$$-{\left[\mathit{g}(\mathit{y})\right]}^{k+1,i}=-{\left[\begin{array}{c}{v}_1{I}_1(\mathit{y})\\ ⋮\\ v_{nb}{I}_{nb}(\mathit{y})\end{array}\right]}^{k+1,i}={\left[\begin{array}{c}{I}_1(\mathit{y})\Delta v_1\\ ⋮\\ I_{nb}(\mathit{y})\Delta v_{nb}\end{array}\right]}^{k+1,i}+{\left[\begin{array}{c}{v}_1{A}_1\\ ⋮\\ v_{nb}{A}_{nb}\end{array}\right]}^{k+1,i}+{\left[\begin{array}{c}{v}_1{B}_1\\ ⋮\\ v_{nb}{B}_{nb}\end{array}\right]}^{k+1,i}$$

(8)

$$A_n={\displaystyle \sum _{l=1}^{n_b}\frac{\partial I_n(\mathit{y})}{\partial v_l}}\Delta v_l; n=1,\dots ,nb,$$

(9)

$$B_n={\displaystyle \sum _{l=1}^{n_b}\frac{\partial I_n(\mathit{y})}{\partial {\theta }_l}}\Delta {\theta }_l; n=1,\dots ,nb.$$

(10)

To simplify and speed up the calculation of partial derivatives w.r.t. voltage magnitudes, the terms I_n(·)$\Delta v_n$ and (∂I_n(·)/$\partial v_l$)$\Delta v_l$ in (8) and (9) can be multiplied by the voltage magnitudes $v_n$ and $v_l$, respectively. To maintain the validity of (8), however, the increments $\Delta v_n$ and $\Delta v_l$ must be properly divided by those voltage magnitudes, which yields

$$-{\left[\mathit{g}(\mathit{y})\right]}^{k+1,i}=-{\left[\begin{array}{c}{v}_1{I}_1(\mathit{y})\\ ⋮\\ v_{nb}{I}_{nb}(\mathit{y})\end{array}\right]}^{k+1,i}={\left[\begin{array}{c}{v}_1{I}_1(\mathit{y})\Delta v_1/v_1\\ ⋮\\ v_{nb}{I}_{nb}(\mathit{y})\Delta v_{nb}/v_{nb}\end{array}\right]}^{k+1,i}+{\left[\begin{array}{c}{v}_1{C}_1\\ ⋮\\ v_{nb}{C}_{nb}\end{array}\right]}^{k+1,i}+{\left[\begin{array}{c}{v}_1{B}_1\\ ⋮\\ v_{nb}{B}_{nb}\end{array}\right]}^{k+1,i}$$

(11)

$$C_n={\displaystyle \sum _{l=1}^{n_b}{v}_l\frac{\partial I_n(\mathit{y})}{\partial v_l}}{\displaystyle \frac{\Delta v_l}{v_l}}; n=1,\dots ,nb$$

(12)

After some algebraic manipulation, either the linearized system (8) or (11) can be expressed as in (13) to attempt to solve (6) at the time step k + 1 = $t_{cl}^{+}$ via Newton’s method:

$${\left[{\mathit{J}}^{k+1}\right]}^i{\left[\Delta {\mathit{y}}^{k+1}\right]}^i=-{\left[\mathit{g}{(\mathit{y})}^{k+1}\right]}^i.$$

(13)

The iterative solution of (13) requires a proper initialization y⁰ = [${\mathit{v}}^{0,T}$${\mathit{\theta }}^{0,T}$]^k+1,T of the variables y^k+1 to compute the network’s equilibrium point just after the fault clearing. However, a strategy to assess that initial condition has not been reported in the existing literature for transient stability studies of power systems. This is not trivial because some nodal voltages change their values abruptly after clearing the fault. In this context, an intuitive way to overcome this initialization problem consists of setting the initial values at their corresponding values to the prefault conditions, y⁰ = ${\mathit{y}}^{t_0^{+}}$, or just before the fault clearing time, y⁰ = ${\mathit{y}}^{t_{cl}^{-}}$. Another option is to perform a flat initialization, y⁰ = [1^T 0^T]^0,T, where vectors 1 and 0 represent the flat voltage profile in polar coordinates. These initialization procedures, however, may lead to the Newton method’s misperformance, as discussed in the next section.

2.3. Newton Method’s Misperformance at $t_{cl}^{+}$

Assuming the occurrence of a solid short circuit at the nth bus of a power system, the corresponding voltage magnitude $v_n$ ∈ y becomes 0 during the fault period (t_f, $t_{cl}^{-}$). After clearing the fault at time step k + 1 = $t_{cl}^{+}$, $v_n$ recovers positive values for the post-fault period [$t_{cl}^{+}$, t_end]. To assess the power system’s transient response under this contingency scenario through Newton’s method, the algebraic state variables could be initialized to the values they have just before the fault is cleared, y⁰ = ${\mathit{y}}^{t_{cl}^{-}}$, which is called ${\mathit{y}}^{t_{cl}^{-}}$ initialization. This implies that (8) must be evaluated by considering $v_n^{k+1}=0$ at the first iteration of the solution process, such that the linearized equation in (8) related to the faulted bus n becomes ${\left[I_n(\mathit{y})\Delta v_n\right]}^{k+1,i}=0$ because the terms multiplied by $v_n^{k+1}$ are canceled out. Hence, the solution of (13) yields $\Delta v_n^{k+1}=0$, and therefore, the value of $v_n^{k+1}$ is not updated for the next iteration. In this case, $v_n^{k+1}$ will remain 0 for all further iterations of the solution process. Furthermore, this null value remains for the rest of the time-domain simulation [7], leading to an inaccurate computation of the power system’s transient behavior.

On the other hand, if the $t_{cl}^{-}$ initialization is used along with the linearized system (11) instead of (8), the consideration of $v_n^{k+1}=0$ in the first iteration cancels out the linearized equation corresponding to the nth row in (11), which leads to an ill-conditioned Jacobian matrix in (13). In this case, Newton’s method fails to converge to the equilibrium point associated with the fault clearing time. After that, the time-domain simulation cannot continue computing the system state variables evolution.

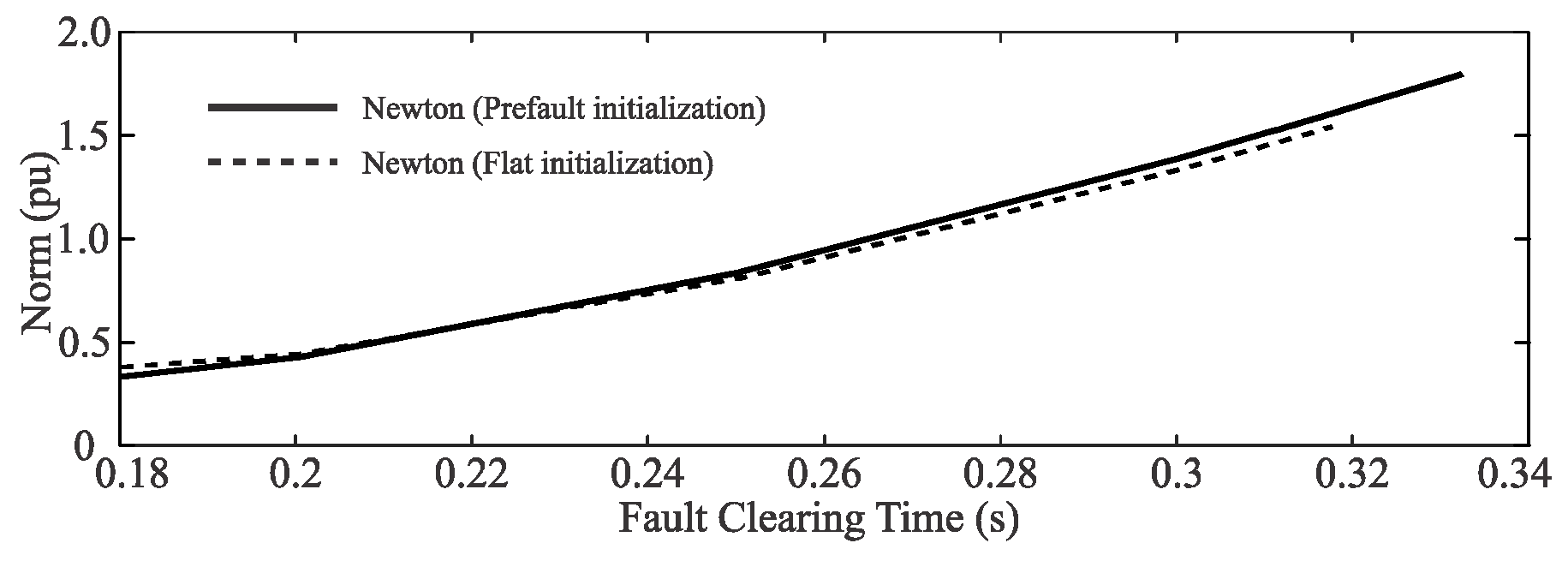
Lastly, it is well known that Newton’s method convergence is sensitive to the initial guess of the unknown variables [16]. Hence, the method may fail to converge when an initialization based on the prefault operating conditions or a flat voltage profile is used because, as the fault clearing time is longer, the solution of the algebraic state variables at time step k + 1 = $t_{cl}^{+}$ moves away from the initialization of y⁰. This statement is numerically demonstrated in Section 4.

3. Proposed Approach

Based on the preceding discussion, an approach to compute the value of the algebraic state variables y^k+1 at the time step k + 1 = $t_{cl}^{+}$ is proposed in this section. For this purpose, a current injection-based power system model is formulated. This model relates current injections to nodal voltages through an extended admittance matrix assembled by adding the equivalent admittances of generators and loads to the traditional network admittance matrix. Those equivalent admittances are directly derived from the current injection models of generators and loads. Lastly, the vector value y^k+1 is obtained from the solution of a proposed current injection-based model using a fixed-point method, as reported below.

3.1. Current Injection Generator Model

The injected current by the ith generator is obtained by transforming its Thévenin’s equivalent circuit into Norton’s equivalent circuit, as depicted in Figure 1.

From Kirchhoff’s voltage law, the voltage source behind the transient reactance $x_{di}^{\prime }$ in terms of the generators’ d-q reference frame is given by (14), where ${\delta }_i$ is the generator rotor angle [14]:

$$E_{gi}{e}^{j{\delta }_i}=v_i{e}^{j{\theta }_i}+j{x}_{di}^{\prime }{\overline{I}}_{gi}=[(v_{di}+j{v}_{qi})+j{x}_{di}^{\prime }(I_{di}+j{I}_{qi})]e^{j({\delta }_i-\pi /2)}$$

(14)

The current source and impedance associated with Norton’s circuit are directly derived from (14):

$$\begin{array}{c}{\overline{I}}_{Ni}=\left((v_{di}+j{v}_{qi})e^{j({\delta }_i-\pi /2)}+j{x}_{di}^{\prime }(I_{di}+j{I}_{qi})e^{j({\delta }_i-\pi /2)}\right)/j{x}_{di }^{\prime },\\ {\overline{Z}}_{Ni}=j{x}_{di}^{\prime }\end{array},$$

(15)

where $v_{wi}$ and I_wi (w = d, q) are as given in (16) [14]. Where ${\mathit{v}}_{Di}$ ∈ ${\mathit{v}}_D$ and ${\mathit{v}}_{Qi}$ ∈ ${\mathit{v}}_Q$ correspond to the voltage at the generator terminals in D-Q rectangular coordinates, ${\psi }_{\alpha i}$(α = 1d, 2q) are flux linkages, and $E_{wi}^{\prime }$(w = d, q) represent the internal voltages:

$$\begin{array}{l}{v}_{di}=v_{Di}\sin \left({\delta }_i\right)-v_{Qi}\cos \left({\delta }_i\right), v_{qi}=v_{Di}\cos \left({\delta }_i\right)+v_{Qi}\sin \left({\delta }_i\right),\\ I_{di}=k_{1i}{E}_{qi}^{\prime }+k_{2i}{\psi }_{1di}+k_{3i}{v}_{qi} , I_{qi}=k_{4i}{E}_{di}^{\prime }+k_{5i}{\psi }_{2qi}+k_{6i}{v}_{di}\end{array}.$$

(16)

The stator algebraic Equation (14) through (16) can represent different generator models by properly setting the coefficients k_εi (ε = 1,…,6), as given in

Table 1. Coefficients for currents in generators’ $d-q$ reference frame.

Coefficient	Model
	Classical	4th Order	6th Order
k1i	$1/x_{di}^{\prime }$	$1/x_{di}^{\prime }$	$\left(x_{di}^{″}-x_{lsi}\right)/x_{di}^{″}\left(x_{di}^{\prime }-x_{lsi}\right)$
k2i	0	0	$\left(x_{di}^{\prime }-x_{di}^{″}\right)/x_{di}^{″}\left(x_{di}^{\prime }-x_{lsi}\right)$
k3i	$-1/x_{di}^{\prime }$	$-1/x_{di}^{\prime }$	$-1/x_{di}^{″}$
k4i	0	$-1/x_{qi}^{\prime }$	$-\left(x_{qi}^{″}-x_{lsi}\right)/x_{qi}^{″}\left(x_{qi}^{\prime }-x_{lsi}\right)$
k5i	0	0	$\left(x_{qi}^{\prime }-x_{qi}^{″}\right)/x_{qi}^{″}\left(x_{qi}^{\prime }-x_{lsi}\right)$
k6i	$1/x_{di}^{\prime }$	$1/x_{qi}^{\prime }$	$1/x_{qi}^{″}$

. Furthermore, since the dynamic states do not change instantaneously, the values of ${\psi }_{\alpha i}$(α = 1d, 2q), $E_{wi}^{\prime }$(w = d, q), and ${\delta }_i$ are known at $t_{cl}^{+}$ from their corresponding values computed at $t_{cl}^{-}$.

Based on (15) and (16), the current source ${\overline{I}}_{Ni}$ is expressed in terms of D-Q rectangular coordinates:

$$\begin{array}{l}{I}_{N Qi}=I_{Qi}^{const}-B_{ai}{v}_{Di}-G_{ai}{v}_{Qi}\\ I_{N Di}=I_{Di}^{const}+G_{ai}{v}_{Di}+B_{bi}{v}_{Qi}\end{array},$$

(17)

where the constant terms in (17) are given by

$$\begin{array}{l}{I}_{Di}^{const}=k_{1i}{E}_{qi}^{\prime }\sin ({\delta }_i)+k_{2i}{\psi }_{1di}\sin ({\delta }_i)+k_{4i}{E}_{di}^{\prime }\cos ({\delta }_i)+k_{5i}{\psi }_{2qi}\cos ({\delta }_i) ,\\ I_{Qi}^{const}=-k_{1i}{E}_{qi}^{\prime }\cos ({\delta }_i)-k_{2i}{\psi }_{1di}\cos ({\delta }_i)+k_{4i}{E}_{di}^{ \prime }\sin ({\delta }_i)+k_{5i}{\psi }_{2qi}\sin ({\delta }_i) ,\\ G_{ai}=\left(k_{3i}+k_{6i}\right)\sin (2{\delta }_i)/2 ,\hspace{1em}{B}_{ai}=1/x_{di}^{\prime }+k_{3i}\cos {({\delta }_i)}^2-k_{6i}\sin {({\delta }_i)}^2,\\ B_{bi}=1/x_{di}^{\prime }+k_{3i}\sin {({\delta }_i)}^2-k_{6i}\cos {({\delta }_i)}^2.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\end{array}$$

(18)

By applying Kirchhoff’s current law to the Norton circuit, the total current ${\overline{I}}_{gi}$ injected by the generator is given by (17) plus the current through the impedance ${\overline{Z}}_{Ni}$. This results in

$$\left[\begin{array}{c}{I}_{g Qi}\\ I_{g Di}\end{array}\right]=\left[\begin{array}{c}{I}_{Qi}^{const}\\ I_{Di}^{const}\end{array}\right]+\left[\begin{array}{cc}-B_{ai}& -G_{ai}\\ G_{ai}& B_{bi}\end{array}\right]\left[\begin{array}{c}{v}_{Di}\\ v_{Qi}\end{array}\right]-\left[\begin{array}{cc}-1/x_{di}^{\prime }& 0\\ 0& 1/x_{di}^{\prime }\end{array}\right]\left[\begin{array}{c}{v}_{Di}\\ v_{Qi}\end{array}\right].$$

(19)

Lastly, the current injection model for the ng generators embedded in the system is directly obtained from (19):

$$\left[\begin{array}{c}{\mathit{I}}_{g Q}\\ {\mathit{I}}_{gD}\end{array}\right]=\left[\begin{array}{c}{\mathit{I}}_Q^{const}\\ {\mathit{I}}_D^{const}\end{array}\right]+\left[\begin{array}{cc}-{\mathit{B}}_a& -{\mathit{G}}_a\\ {\mathit{G}}_a& {\mathit{B}}_b\end{array}\right]\left[\begin{array}{c}{\mathit{v}}_D\\ {\mathit{v}}_Q\end{array}\right]-\left[\begin{array}{cc}{\mathit{B}}_N& \mathbf{0}\\ \mathbf{0}& -{\mathit{B}}_N\end{array}\right]\left[\begin{array}{c}{\mathit{v}}_D\\ {\mathit{v}}_Q\end{array}\right],$$

(20)

where the elements of G_a = diag(G_a1,…,G_ang), B_a = diag(B_a1,…,B_ang), and B_b = diag(B_b1,…,B_bng) are calculated from (18), while B_N = diag(−1/$x_{d1}^{\prime }$, …,−1/$x_{dng}^{\prime }$).

3.2. Current Injection Load Model

The complex power drawn by the load connected at the ith bus is given by the ZIP load model [14]. Thus, the total current demanded by the load equals the complex conjugate of the ratio of that power to the voltage at the connection bus. This current can be expressed in terms of the D-Q coordinates:

$$\begin{array}{l}{I}_{L Qi}=I_{LN Qi}(v_{Di},v_{Qi })+B_{zi }{v}_{Di}+G_{zi }{v}_{Qi}\\ I_{L Di}=I_{LN Di}(v_{Di},v_{Qi })+G_{zi }{v}_{Di}-B_{zi }{v}_{Qi}\end{array},$$

(21)

where I_{LN Qi}(·) and I_{LN Di}(·) are nonlinear terms given by (22). Furthermore, the coefficients of the last two linear terms in (21) are given by (23). Note that v_0i, P_0i, and Q_0i are known steady-state values of the voltage magnitude at the connection bus as well as the active and reactive power demanded by the load, respectively. Finally, p_γi and q_γi (for γ = z,c,p) are the ZIP parameters, and ${\theta }_i={\tan }^{-1}\left({\mathit{v}}_{Qi}/{\mathit{v}}_{Di}\right)$:

$$\begin{array}{l}{I}_{LN Di}(\cdot )=G_{ci}\cos ({\theta }_i)+B_{ci}\sin ({\theta }_i)+(G_{pi}{v}_{Di}+B_{pi}{v}_{Qi })/(v_{Di }^2+v_{Qi }^2),\\ I_{LN Qi}(\cdot )=G_{ci}\sin ({\theta }_i)-B_{ci}\cos ({\theta }_i)+(-B_{pi}{v}_{Di }+G_{pi}{v}_{Qi })/(v_{Di }^2+v_{Qi }^2),\\ G_{ci}=p_{ci}{P}_{0i}/v_{0i}, G_{pi}=p_{pi}{P}_{0i}, B_{ci}=q_{ci}{Q}_{0i}/v_{0i}, B_{pi}=q_{pi}{Q}_{0i},\end{array}$$

(22)

$$G_{zi } =p_{zi}{P}_{0i}/v_{0i}^2, B_{zi}=-q_{zi}{Q}_{0i}/v_{0i}^2.$$

(23)

Lastly, the current injection model for all nl loads of the system is obtained from (21) to (23):

$$\left[\begin{array}{c}{\mathit{I}}_{L Q}\\ {\mathit{I}}_{L D}\end{array}\right]=\left[\begin{array}{c}{\mathit{I}}_{LN Q}(\cdot )\\ {\mathit{I}}_{LN D}(\cdot )\end{array}\right]+\left[\begin{array}{cc}{\mathit{B}}_z& {\mathit{G}}_z\\ {\mathit{G}}_z& -{\mathit{B}}_z\end{array}\right]\left[\begin{array}{c}{\mathit{v}}_D\\ {\mathit{v}}_Q\end{array}\right],$$

(24)

where the elements of the diagonal matrices G_z and B_z are given by (23).

3.3. Current Injection-Based System Model

The general form of the system’s current injection model for time step k + 1 = $t_{cl}^{+}$ is given by $\overline{\mathit{I}}={\overline{\mathit{Y}}}_{bus}\overline{\mathit{v}}$, which is expressed in D-Q coordinates by

$${\left[\begin{array}{c}{\mathit{I}}_Q\\ {\mathit{I}}_D\end{array}\right]}^{k+1}={\left[\begin{array}{c}{\mathit{I}}_{g Q}-{\mathit{I}}_{L Q}\\ {\mathit{I}}_{gD}-{\mathit{I}}_{L D}\end{array}\right]}^{k+1}={\left[\begin{array}{cc}\mathit{B}& \mathit{G}\\ \mathit{G}& -\mathit{B}\end{array}\right]}^{k+1}{\left[\begin{array}{c}{\mathit{v}}_D\\ {\mathit{v}}_Q\end{array}\right]}^{k+1}={\left[{\mathit{Y}}_{bus}^{DQ}\right]}^{k+1}{\left[\begin{array}{c}{\mathit{v}}_D\\ {\mathit{v}}_Q\end{array}\right]}^{k+1},$$

(25)

where G and B are conductance and susceptance submatrices related to the real and imaginary parts of the network admittance matrix ${\mathit{Y}}_{bus}^{DQ}$ corresponding to the time step k + 1 = $t_{cl}^{+}$, respectively. This matrix is diagonal dominant because of the location of susceptance submatrices. Substituting (20) and (24) into (25) results in the proposed current injection model:

$${\left[\begin{array}{c}{\mathit{I}}_Q^{const}-{\mathit{I}}_{LN Q}(\cdot )\\ {\mathit{I}}_D^{const}-{\mathit{I}}_{LN D}(\cdot )\end{array}\right]}^{ k+1}= {\left[\begin{array}{cc}\mathit{B}+{\mathit{B}}_a+{\mathit{B}}_N+{\mathit{B}}_z& \mathit{G}+{\mathit{G}}_a+{\mathit{G}}_z\\ \mathit{G}-{\mathit{G}}_a+{\mathit{G}}_z& -\mathit{B}-{\mathit{B}}_b-{\mathit{B}}_N-{\mathit{B}}_z\end{array}\right]}^{ k+1}{\left[\begin{array}{c}{\mathit{v}}_D\\ {\mathit{v}}_Q\end{array}\right]}^{ k+1},$$

(26)

where the current injections and nodal voltages are related by the matrix referred to as the extended admittance matrix: Y_ext. In addition, note that in transit nodes, generators and loads current injections do not exist such that the corresponding elements in the current vector are 0. Furthermore, the elements of Y_ext associated with these transit nodes only correspond to the elements of ${\mathit{Y}}_{bus}^{DQ}$. Lastly, the proposed model (26) is nonlinear because of the terms I_{LN Q}(·) and I_{LN D}(·). A suitable solution method for (26) is given below.

3.4. Algorithm for Computing Algebraic State Variables

The computation of algebraic state variables just after clearing a fault is performed by solving the proposed model (26) for y^k+1 = [${\mathit{v}}_D^T$ ${\mathit{v}}_Q^T$]^k+1,T through the fixed-point iteration method. For applying this method, (26) is rewritten as given in (27), where the superscript k + 1 has been omitted to simplify the notation. The iterative solution process is depicted in Figure 2 and detailed below:

$$\left[\begin{array}{c}{\mathit{I}}_Q^{const}\\ {\mathit{I}}_D^{const}\end{array}\right]-{\left[\begin{array}{c}{\mathit{I}}_{LN Q}(\mathit{y})\\ {\mathit{I}}_{LN D}(\mathit{y})\end{array}\right]}^i=\left[{\mathit{Y}}_{ext}\right]{\left[\mathit{y}\right]}^{i+1}.$$

(27)

The procedure starts by assembling the Y_ext matrix and computing its LU factors, while the terms ${\mathit{I}}_Q^{const}$ and ${\mathit{I}}_D^{const}$ are evaluated from (18) by using the known values of dynamic state variables x at $t_{cl}^{-}$. Furthermore, the initial estimation of the algebraic variables is performed using one of the initialization processes described in Section 2.2, which results in y⁰ = [${\mathit{v}}^{0,T}$ ${\mathit{\theta }}^{0,T}$]^T. After that, the initial values are transformed into rectangular coordinates: y⁰ ↦ y⁰ = [${\mathit{v}}_D^{0,T}$ ${\mathit{v}}_Q^{0,T}$]^T. Furthermore, the iteration index is set as i = 0 to start the iterative solution process by evaluating I_{LN Q}(·) and I_{LN D}(·) from (22) and assembling the set of equations (27). Lastly, (27) is solved by using the LU factors of Y_ext in a forward and backward substitution to obtain a new value yⁱ⁺¹. If the maximum absolute difference between yⁱ⁺¹ and yⁱ satisfies a given tolerance Tol, yⁱ⁺¹ is transformed into polar coordinates, and the result is set as the solution of the algebraic state variables at time step k + 1 = $t_{cl}^{+}$. If not, yⁱ⁺¹ is set as the initial value yⁱ, the method returns to evaluate the terms I_{LN Q}(·) and I_{LN D}(·) from (22) in the i + 1 iteration, and the procedure is repeated.

It is important to note that Y_ext, ${\mathit{I}}_Q^{const}$, and ${\mathit{I}}_D^{const}$ are constants because they do not depend on the variables to be solved. Hence, their corresponding values and the LU factors of Y_ext are computed only once at the beginning of the solution process. In this sense, the computational burden at each iteration is mainly due to the forward and backward substitution executed to obtain a new value of yⁱ = [${\mathit{v}}_D^T$ ${\mathit{v}}_Q^T$]^i,T. In this way, the proposed approach efficiently solves the current injection model (26). Finally, if all loads are represented by pure constant impedances, the ZIP parameters p_γi and q_γi (for γ = c,p) in (22) are 0 and thus cancel out the nonlinear terms I_{LN Q}(·) and I_{LN D}(·). In this case, (26) becomes linear, and the proposal will require just one iteration for its solution.

On the other hand, when the initializing nodal voltages have the same values as just before clearing a short circuit at the ith bus, the voltages v_Di and v_Qi must be initialized with 1 and 0, respectively, to avoid a division by 0 in (22).

Lastly, for application purposes, the TD simulation by the SI approach described in Section 2.1 must be paused just after clearing the fault to obtain y^k+1 by using the proposed approach. This solution establishes the network’s equilibrium point at k + 1 = $t_{cl}^{+}$ and, together with the known value x^k+1 of the dynamic state variables, χ^k+1 = [x^T y^T]^k+1,T, yields the initial guess of the system state variables to continue the TD simulation for the post-disturbance period.

4. Case Studies

The proposed approach’s performance is numerically evaluated by executing transient stability studies on the WSCC 3-machine, 9-bus system [4], the New England 10-machine, 39-bus system [17], and the Mexican 46-machine, 190-bus equivalent system [18]. The objective of these TD simulations is twofold: a) to show Newton’s method misperformance in computing the network’s equilibrium point just after clearing faults in the SI approach and b) to demonstrate the proposed approach’s effectiveness in overcoming the Newton method drawback regarding that computation. The TD simulations are performed according to the approach given in Section 2.1, where the linearized power balance equations correspond to those given by (11). Within this context, the numerical integration is performed with a given step size, Δt, for a specified time period, T, but this simulation is paused at the clearing time, t_cl, to execute the proposed approach.

4.1. Example of the Newton’s Method Misperformance

The WSCC system is subjected to a three-phase solid-to-ground fault at bus 7 to demonstrate the theoretical concepts described in Section 2.3. To this aim, the TD simulation is performed by considering the generator model and contingency scenario reported in row 1 of

Table 2. Systems, generator models, and contingency scenarios for TD simulations.

System	Generator Models	Faulted Node	Fault Inception Time (ms)	Tripped Line Connecting Nodes
WSCC	Classic	7	100	7 and 5
New England	6th order	29	100	28 and 29
Mexican	4th order	182	100	182 and 86

. The fault at bus 7 is applied at t_f = 100 ms and cleared at t_cl = 180 ms by tripping the line connecting buses 5 and 7. The study time period and the step size were set as T = [0 s, 1 s] and Δt = 1 ms, respectively. The TD simulation was paused at $t_{cl}^{+}=180$ ms to compute the algebraic state variables by solving (11) and considering the $t_{cl}^{-}$ initialization. In this case, however, the Jacobian matrix in (13) becomes ill-conditioned, and no solution is obtained for the algebraic state variables. This failure in Newton’s convergence also prevented the system’s dynamic evolution from being further calculated for the rest of the study period T, as verified by the evolution of the voltage magnitude at bus 7 shown in Figure 3.

The TD simulation reported above is repeated but considering the prefault and flat voltage initializations for ${\mathit{y}}^0$. As reported in Section 2.3, Newton’s method fails to converge to a solution of (11) from an initial guess that is relatively distant from that solution. Hence, in these simulations, the clearing time was gradually increased from t_cl = 180 ms until a clearing time $t_{cl}^{+}$ where no convergence is achieved. The Euclidean norm between the solution of ${\mathit{y}}^{k+1}$ and initial conditions, ${\mathit{y}}^0$, is reported in Figure 4 for each clearing time. Note that the loss of convergence occurs at t_cl = 333 ms and t_cl = 317 ms for the prefault and flat voltage initializations, respectively, which does not happen in the proposed approach, as shown in the next section.

4.2. Effectiveness of the Proposed Approach

The proposed approach’s effectiveness is numerically demonstrated based on results obtained from three case studies: one for each system, generator model, and contingency scenario indicated in Table 2. In these studies, large fault clearing times are used to show the robustness of the proposal even if severe simulation conditions are considered.

All case studies were performed for two different fault clearing times, t_cl = 180 ms and t_cl = 500 ms, as well as the three different types of initializations reported in the paper. In all cases, the study time lasted 1 s and the step size was set as in Δt = 1 ms. The voltage magnitude trajectories at the faulted bus are shown in Figure 5, Figure 6 and Figure 7, from which it is clear that in all cases the proposed approach can compute the network’s equilibrium point, ${\mathit{y}}^{k+1}={[{\mathit{v}}^T {\mathit{\theta }}^T]}^{k+1,T}$, immediately after clearing the fault, k + 1 = $t_{cl}^{+}$. This fact, in turn, allows TD simulation to continue using the SI approach to compute the system’s transient evolution for the remaining study period. These results demonstrate that the effectiveness of the proposed approach is not affected by the following factors: the system’s scale, the generator model, the use of any of the intuitive initialization schemes mentioned above, nor the clearing of the fault at any desired point in time after the critical clearing time.

As a comparison, the results associated with TD simulations, where ${\mathit{y}}^{k+1}$ at k + 1 = $t_{cl}^{+}$ is computed based on Newton’s method and initialization at the prefault conditions, are also shown in Figure 5, Figure 6 and Figure 7. From a comparative analysis, it is clear that the same results are obtained from Newton’s method and the proposed approach. Newton’s method, however, fails to compute ${\mathit{y}}^{k+1}$ when t_cl is increased to 500 ms, making it impossible to continue the TD simulation.

To show the computational time performance of the proposed approach, the CPU times taken by the proposed approach and Newton’s method to compute ${\mathit{y}}^{k+1}$ in the cases illustrated in Figure 5a, Figure 6a, and Figure 7a for prefault initialization were measured and compared. The resulting CPU times for both methods are shown in column 2 and 3 of

Table 3. Comparison of CPU times.

System	CPU Times (ms)
	Proposed Approach	Newton’s Method
WSCC	0.09	1.30
New England	0.53	5.16
Mexican	4.47	23.95

, respectively. It should be noted that the proposed approach is faster than Newton’s method because only backward and forward substitutions are performed during the iterative solution process.

The solutions of (26) for different initializations were used to evaluate the power flow mismatch equations $\mathit{g}{(\cdot )}^{t_{cl}^{+}}$ at $t_{k+i}=t_{cl}^{+}$. All these solutions always satisfied the constraints $\mathit{g}{(\cdot )}^{t_{cl}^{+}}=0$, $\forall t_{cl}^{+}\in T_{cl}$. This statement is demonstrated by the results in

Table 4. Summary of maximum active and reactive power mismatch errors.

System	Generator Model	Prefault Values Initialization		Flat Values Initialization		${\mathit{t}}_{\mathit{c}\mathit{l}}^{-}$ Initialization
		ΔP	ΔQ	ΔP	ΔQ	ΔP	ΔQ
WSCC	Classical	7 · 10−9	2 · 10−8	6 · 10−9	1 · 10−8	9 · 10−9	2 · 10−8
	4th order	9 · 10−9	2 · 10−8	5 · 10−9	1 · 10−8	7 · 10−9	2 · 10−8
	6th order	8 · 10−9	2 · 10−8	8 · 10−9	2 · 10−8	3 · 10−9	8 · 10−9
Mexican	Classical	3 · 10−8	4 · 10−8	5 · 10−8	8 · 10−8	1 · 10−8	2 · 10−8
	4th order	1 · 10−7	2 · 10−7	1 · 10−7	1 · 10−7	1 · 10−7	2 · 10−7

, which correspond to the maximum power mismatch errors obtained in the entire set of TD simulations for the three types of initializations of the algebraic variables. Lastly, the same values of algebraic variables were obtained for a given fault clearing time, independently of the adopted initial conditions for solving (26). This is illustrated in Figure 8, when t_cl equals the critical clearing time (t_CCT) of the WSCC system. For this case study, no convergence is obtained with any of the three types of initializations when Newton’s method is applied for solving $\mathit{g}{(\cdot )}^{t_{cl}^{+}}=0$, as illustrated in Figure 8, when initializing algebraic variables at their prefault values.

Finally, for validation purposes, a transient stability study of the New England system considering the prefault initialization scheme and t_cl = 500 ms was performed with the proposed approach and DSATools software version 20.0 [19]. The transient behavior of the voltage magnitude at the faulted bus is shown in Figure 9 for both simulations. Even though how the DSATools software applies and clears the fault is unknown to us due to ownership rights, it is important to note that the discrepancy between the two trajectories is negligible. This naturally implies that the network’s equilibrium point just after the fault clearance is suitably computed by the proposed approach.

5. Conclusions

This paper proposes a fundamentally different and general approach for solving algebraic state variables just after clearing a fault in the power balance-based transient stability problem. The results show that the network’s equations expressed in the power balance form cannot be effectively solved using Newton’s method when the $t_{cl}^{-}$ initialization of the algebraic state variables is used. The initialization of those variables based on the prefault operating conditions, or a flat voltage profile, may mitigate this problem but does not ensure the success of Newton’s method in the SI approach at the fault clearing instant.

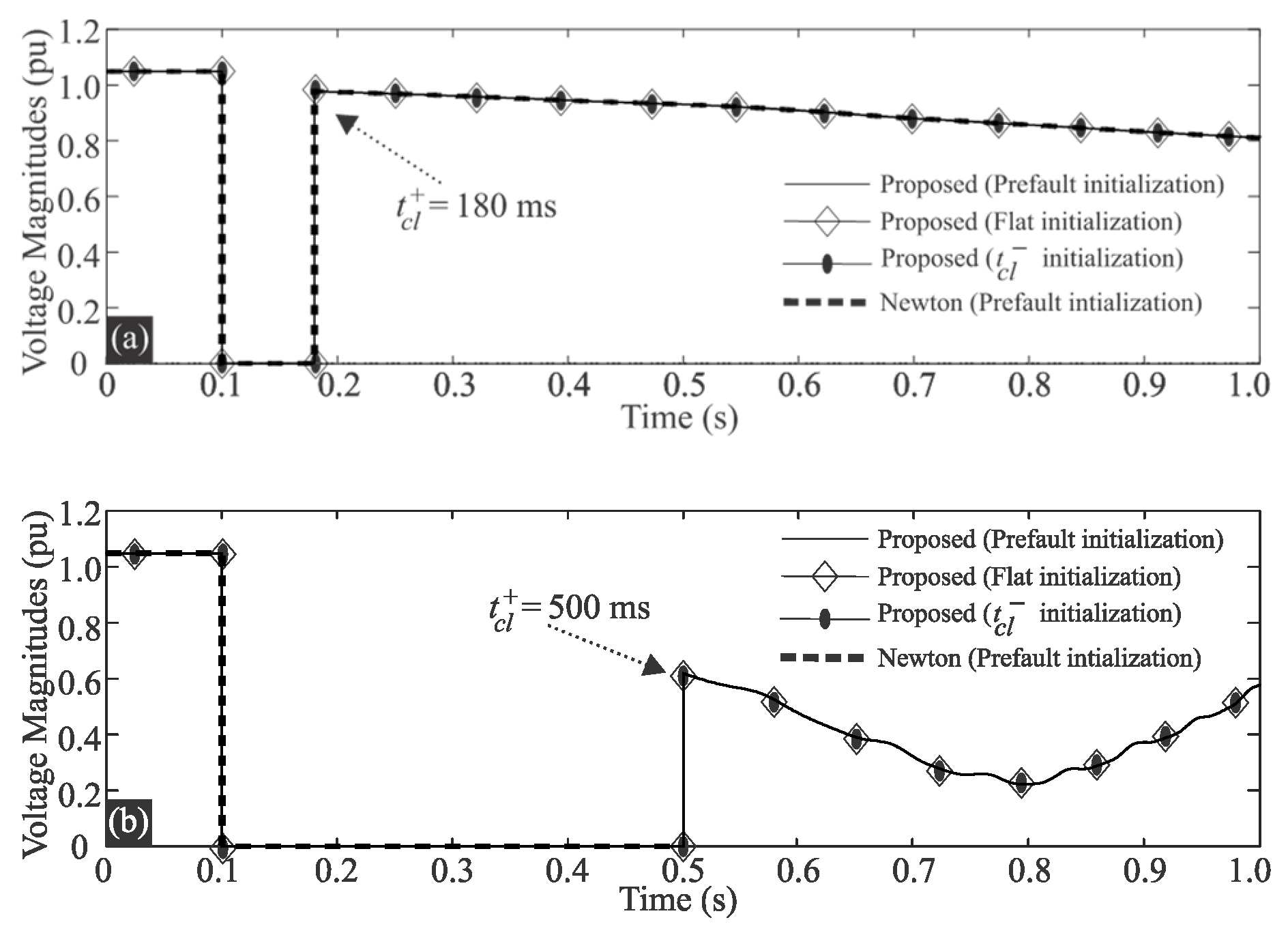
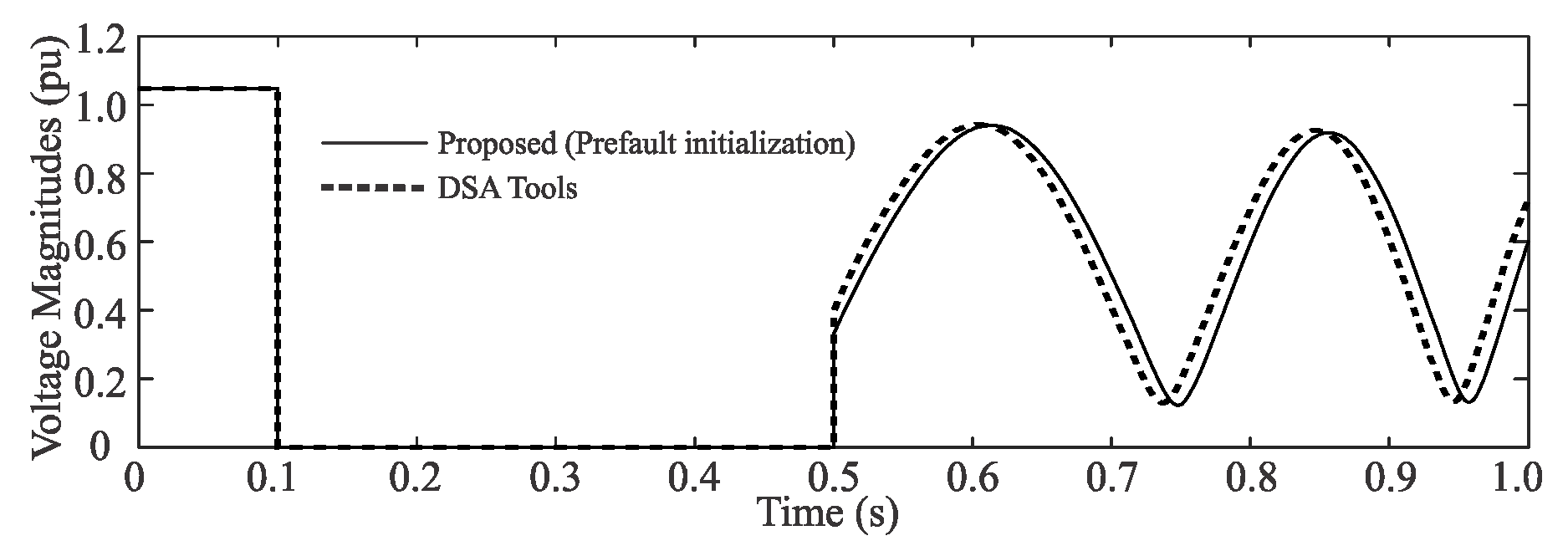
Accordingly, an approach was proposed in this paper to successfully compute the network’s equilibrium point in transient stability studies just after clearing a fault. For this purpose, a current injection-based system model has been derived, where current injections of generators and loads are related to nodal voltages by a constant extended admittance matrix. Hence, only one triangular factorization is needed at the beginning of the solution process to then compute nodal voltages through forward and backward substitutions. Numerical examples demonstrate the generality, robustness, low computation time, and high accuracy of the proposed approach, as well as how it overcomes the non-convergence problem of Newton’s method to compute the network’s equilibrium point immediately after the fault is cleared. In this way, the proposal can be used to assist the SI approach in computing the network’s equilibrium point at the fault clearing instant.

Finally, as future research work, it is proposed to explore the application of the proposed approach to perform TD simulations integrating the uncertainty of renewable resources. These simulations directly provide Jacobian matrices required to perform dynamic trajectory sensitivity analysis with respect to power system parameters.