Abstract
In the context of constructing new power systems, the intermittency and volatility of high-penetration renewable generation pose new challenges to the stability and secure operation of power systems. Enhancing the ramping capability of power systems has become a crucial measure for addressing these challenges. Therefore, this paper proposes a bi-level peak regulation optimization model for power systems considering ramping capability and demand response, aiming to mitigate the challenges that the uncertainty and volatility of renewable energy generation impose on power system operations. Firstly, the upper-level model focuses on minimizing the ramping demand caused by the uncertainty, taking into account concerned constraints such as the constraint of price-guided demand response, the constraint of satisfaction with electricity usage patterns, and the constraint of cost satisfaction. By solving the upper-level model, the ramping demand of the power system can be reduced. Secondly, the lower-level model aims to minimize the overall cost of the power system, considering constraints such as power balance constraints, power flow constraints, ramping capability constraints of thermal power units, stepwise ramp rate calculation constraints, and constraints of carbon capture units. Based on the ramping demand obtained by solving the upper-level model, the outputs of the generation units are optimized to reduce operation cost of power systems. Finally, the proposed peak regulation optimization model is verified through simulation based on the IEEE 39-bus system. The results indicate that the proposed model, which incorporates ramping capability and demand response, effectively reduces the comprehensive operational cost of the power system.
1. Introduction
The integration of high proportions of renewable energy into power systems poses unprecedented challenges to their secure and stable operation. The variability and intermittency of generation outputs from renewable energy units significantly increase the demand for peak regulation (PR) [1]. However, with the gradual reduction in the share of traditional thermal power generation, the PR ability of the power system has become constrained, making it difficult to rapidly respond to changing load demands and the uncertainty of renewable energy outputs. This not only reduces the economic efficiency and reliability of the power system but also raises concerns about the power system stability [2,3]. Consequently, enhancing PR ability of the power system is essential to better accommodate the variability and intermittency of renewable energy, improve response speed and flexibility, and ensure the secure and stable operation of the power system.
Flexible ramping capacity of the power system refers to the capability of the power system to respond to sustained disturbances caused by net load fluctuations and uncertainties within a 5–15 min timescale. Numerous power markets, both domestically and internationally, are actively exploring and developing market-based mechanisms for procuring ramping flexibility of the power system. Zhang et al. [4] proposed a comprehensive bidding strategy for virtual power plants to participate in power markets, addressing the synergy between flexible ramping product (FRP) and energy markets and managing wind power uncertainty through a two-stage distributionally robust optimization model and the use of flexible resources. Chen et al. [5] proposed a stochastic economic dispatch model incorporating the trading of FRPs to enhance system flexibility and ensured fair compensation for flexible resource providers, validated through wind power scenario simulations generated using the copula function and quasi-Monte Carlo methods. To address the limitations of current FRP models, such as the neglect of spatiotemporal correlations among uncertainty sources and the omission of security constraints like transmission limits, Fang et al. [6] proposed a deliverable FRP approach based on a distributionally robust chance-constrained multi-interval optimal power flow model that considers the spatiotemporal correlation of wind power and demand uncertainties and introduced a novel uncertainty-contained locational marginal price derived from the proposed asymmetrical affine policy. Kwon et al. [7] proposed a flexible ramping capacity model that accounted for the practical ramping capability of generation resources and net load uncertainty, integrating ramping constraints into unit commitment and economic dispatch processes. Yang et al. [8] proposed a day-ahead optimal dispatch model for a coupled system of renewable energy sources and thermal power units, considering ladder-type ramping rate and flexible spinning reserve constraints.
To address the challenges posed by the increased load demand and the integration of renewable energy, extensive research has been conducted on the peak regulation ability of the power system. Wei et al. [9] proposed an optimization model for the deep PR, addressing the challenges posed by the large-scale integration of wind power. The proposed model minimized thermal power unit fuel injection cost by considering energy storage accident standby and unplanned disconnection risks. Yang et al. [10] proposed a two-layer optimization dispatching model to enhance the utilization of renewable energy by addressing the imbalance in PR resources among provincial power grids. Wu et al. [11] proposed a deep PR optimization model for wind and thermal power based on cooperative game theory, by introducing a modified Shapley value method for profit allocation that considers cooperative fairness and deep PR ability. Yue et al. [12] introduced a collaborative optimization method combining electrolytic aluminum load regulation with thermal-power deep peak shaving to reduce renewable energy curtailment. Yang et al. [13] proposed a unit commitment model, which aimed at minimizing total cost by employing the particle swarm optimization algorithm. In addition, the trade-off between deep PR of thermal units and wind power curtailment was explored.
Existing studies have made significant progresses in power system PR optimization and ramping capacity analysis, but there are still some research gaps. Firstly, the impact of customer-side demand response on the ramping demand and its positive effect on the reduction in the ramping demand are seldom considered in the existing ramping demand and ramping capacity assessment methods. Secondly, the existing models on PR optimization do not fully consider the uncertainty of the ramping demand due to load forecast errors and renewable energy forecast errors.
To address the above deficiencies, this paper proposes the calculation method for the ramping demand of the power system and a two-layer optimization model for the PR considering the ramping capacity and demand response. The proposed model not only considers the uncertainty in the calculation of the ramping demand and the impact of customer-side demand response on the ramping demand but also takes into account the positive effects of the energy storage and carbon capture units on reducing the comprehensive operation cost of the power system. The upper and lower models proposed in this paper are formulated as the linear programming and mixed-integer second-order conic programming problems, respectively, which are efficiently solved using the GUROBI 11.0.2 solver on the AMPL modeling platform.
2. Calculation Method for Ramping Demand
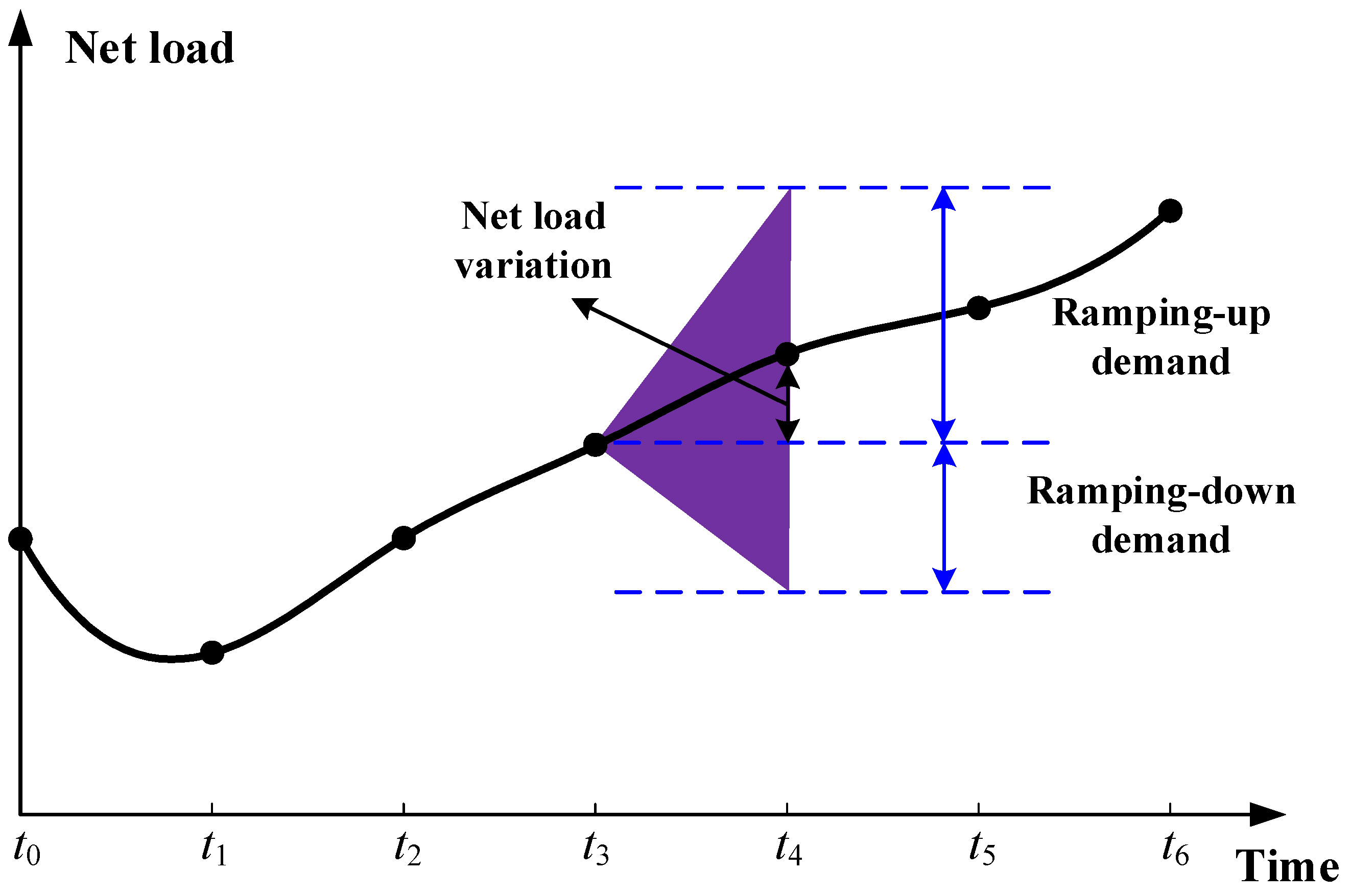
The ramping demand in power systems is typically determined by the predicted net load variation and forecast errors, as illustrated in Figure 1.
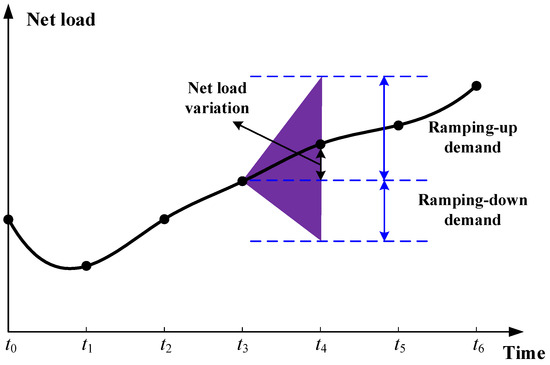
Figure 1.
Illustration of ramping demands.
The x-axis of Figure 1 represents the time periods, and the y-axis represents the net load. The ramping demand in a power system primarily includes ramping-up and ramping-down demands. In Figure 1, the net load variation refers to the difference in the net load between two adjacent time periods. In the actual operation of power systems, to effectively take into account the volatility and uncertainty of power demands and generation outputs of renewable energy, it is necessary to determine the maximum ramping-up and ramping-down demands between two adjacent time periods, as indicated by the shaded areas in Figure 1.
2.1. Deterministic Ramping Demand
The deterministic ramping-up and ramping-down demands are determined by the net load variation. The net load can be defined as the difference between the power demand and the generation outputs of the renewable energy. The calculation method of the net load considering the demand response is shown in (1).
where represents the set of the time horizons, which is set to 24 h (one day) in this study. represents the net load of the power system at time period t. represents the forecasted power demand of the power system at time period t. represents the power changes due to demand response at time period t. represents the forecasted outputs of renewable energy in the power system at time period t.
The calculation methods for the deterministic ramping-up and ramping-down demands of the power system are shown in (2)–(4):
where represents the net load variation in the power system at time period t. and represent the deterministic ramping-up demand and ramping-down demand of the power system at time period t, respectively.
Equation (2) represents the calculation method for the net load variation. Equations (3) and (4) represent the calculation method of the deterministic ramping-up demand and ramping-down demand.
2.2. Ramping Demand Considering Uncertainty
The uncertainty of the ramping demand primarily arises from load forecasting errors and renewable generation output forecasting errors in the power system. If the deterministic ramping demand belongs to ramping-up demand, the method for calculating the ramping-up demand considering the uncertainty is presented by (5):
where represents the ramping-up demand of the power system considering uncertainty at time period t. represents the upper bound of the load forecasting error for the power system at time period t. represents the lower bound of the renewable generation output forecasting error for the power system at time period t.
If the deterministic ramping demand of the power system is the ramping-down demand, the method for calculating the ramping-down demand considering the uncertainty is given by (6).
where represents the ramping-down demand of the power system considering uncertainty at time period t. represents the lower bound of the load forecasting error for the power system at time period t. represents the upper bound of the renewable generation output forecasting error for the power system at time period t.
In this work, extensive historical data on load demands and renewable energy generation outputs are employed to determine the lower bound and the upper bound of the load forecasting error and the renewable generation output forecasting error. The probability distribution function of forecasting errors at each time period can be derived from the historical data. At each time period, the lower and upper bounds of the forecasting errors are defined as the 5th and 95th percentiles of the corresponding probability distribution functions.
3. Bi-Level Peak Regulation Optimization Model
3.1. Upper-Level Model
The objective function of the upper-level model is to minimize the ramping demand of the power system, as shown in (7).
The following constraints should be satisfied:
- Constraints of the load adjustment amount
Equation (8) indicates that the sum of load adjustment at the scheduling time periods equals zero, which means that the total load demand remains unchanged.
- 2.
- Constraints of price-driven demand response
The price-driven demand response strategy uses price signals to guide users to adjust their electricity consumption patterns, thereby optimizing the load curve. By introducing the demand response, peak shaving and valley filling can be achieved, and peak regulation can be alleviated. The proposed price-driven demand response model can be described as follows:
where represents the demand price elasticity coefficient between time periods t and τ. represents the electricity price at time period τ before customers participate in demand response. represents the change in electricity price at time period τ after customers participate in demand response. and represent the minimum and maximum electricity prices at time period t after customers participate in demand response, respectively.
Equation (9) represents the calculation method for the demand price elasticity coefficient. Equation (10) indicates that the electricity price after customers participate in demand response remains within a certain range.
- 3.
- Constraints of electricity usage satisfaction and electricity cost satisfaction
Equation (11) represents the constraint of electricity usage satisfaction. Equation (12) represents the constraint of electricity cost satisfaction.
3.2. Lower-Level Model
The objective function of the lower-level model is to minimize the total cost of the power system, as shown in (13).
where Gi represents the set of generators connected to bus i. N denotes the set of buses. Ci represents the set of carbon capture units connected to bus i. F is the total cost of the power system. FP is the operation cost of thermal power units. FO is the start-up cost of thermal power units. FV is the cost of ethanolamine solution. FY is the carbon trading cost. ag, bg, and cg represent the cost coefficients for power generation by generator g at time period t. represents the active power output of generator g at time period t. is a binary variable representing the operational status of generator g at time period t, which equals 1 if the generator is in operation during time period t. Sg denotes the startup cost of generator g. KS represents the cost coefficient for ethanolamine solution. represents the operation coefficient of ethanolamine solution. represents the net CO2 capture amount of carbon capture unit c at time period t. represents the carbon trading price at time period t. mg represents the carbon emission intensity coefficient. represents the carbon trading coefficient. represents the total CO2 capture amount of carbon capture unit c at time period t.
The following constraints should be satisfied:
- Power balance constraints
Equations (18) and (19) represent the active power balance equation and the reactive power balance equation, respectively.
- 2.
- Power flow constraints
Equations (20) and (21) provide the calculation for power flow though the lines. Equation (22) represents the second-order cone relaxation constraint associated with auxiliary variables. Equation (23) specifies that the power flow though the lines remains within the threshold range.
- 3.
- Voltage constraints
- 4.
- Thermal power unit ramping capability constraints
Equation (25) indicates that the total ramping-up capability provided by all units should not be smaller than the ramping-up demand. Equation (26) specifies that ramping-up capability provided by all units should not be smaller than the ramping-down demand. Equation (27) indicates that the ramping-up capability of a unit does not exceed its ramping-up rate. Equation (28) indicates that the ramping-down capability of a unit does not exceed its ramping-down ramping rate. Equation (29) stipulates that the ramping-up capability of a unit does not exceed the difference between the unit’s maximum generation output and its current generation output. Equation (30) stipulates that the ramping-down capability of a unit does not exceed the difference between its current generation output and its minimum generation output.
- 5.
- Stepwise ramping rate constraints of thermal power units
The different ramping rates of thermal power units under different peak-shaving conditions are considered in this paper, and the ramping-up and ramping-down rates are calculated by (31) and (32), respectively.
where , , , and represent the power interval range parameters for different peak-shaving states of the thermal power unit. , , and represent the ramping-up rates of the thermal power unit under different peak-shaving states.
Equations (31) and (32) are conditional constraints. To improve the solving efficiency of the proposed model, (31) and (32) can be linearized, as shown in (33)–(40), respectively:
where , , , , , and are binary variables introduced for linearizing (31) and (32).
- 6.
- System reserve constraints
- 7.
- Generation output constraints of thermal power units
Equation (42) indicates that the power generation outputs of the thermal power unit are not less than its minimum value and not greater than its maximum value.
- 8.
- Logical constraints
Equation (43) represents the logical relationships among the three binary variables. Equation (44) indicates that the sum of the start-up state variable and the shut-down state variable for unit g does not exceed 1. Equations (45) and (46) enforces the minimum up time constraint and minimum down-time constraint, respectively.
- 9.
- Operation constraints of carbon capture units
Due to the CO2 capture function of carbon capture units, the power output of the carbon capture unit comprises the net power output of the carbon capture unit and the power due to the carbon capture consumption, as shown in (47).
where represents the power output of carbon capture unit c at time period t. represents power demand due to the carbon capture consumption.
The net power output of the carbon capture unit should meet the following constraints:
where and represent the upper and lower limits of net power output of the carbon capture unit c, respectively. λ is the energy consumed per unit of CO2 captured. is the carbon emission intensity of the carbon capture unit. η is the carbon capture efficiency. is the maximum flue gas diversion ratio at time t. is the fixed power demand of the carbon capture unit.
The power demand due to the carbon capture consumption for the carbon capture unit should meet the following constraints:
where represents the operating power demand of the carbon capture unit at time period t. represents the amount of CO2 provided by the storage tank at time period t. represents the split ratio of the carbon capture plant at time period t. represents the volume of solution required to capture the CO2 provided by the storage tank at time period t. and represent the molar masses of ethanolamine solution and CO2, respectively. represents the desorption amount in the regenerator. represents the concentration of the ethanolamine solution. represents the density of the ethanolamine solution.
Equation (50) indicates that the power demand due to the carbon capture consumption of the carbon capture unit is equal to the sum of operating power demand and fixed power demand of the carbon capture unit. Equation (51) calculates the operating power demand of the carbon capture unit. Equation (52) shows that the total CO2 capture amount of carbon capture unit is derived from the product of the carbon emission intensity and operating power demand of the carbon capture unit. Equation (53) indicates that the net CO2 capture amount of carbon capture unit c at time period t is equal to the sum of CO2 capture amount of carbon capture unit c itself and the amount of CO2 supplied by the storage tank at time period t. Equation (54) specifies the minimum and maximum limits of the net CO2 capture amount of carbon capture unit c at time period t. Equation (55) calculates the volume of solution required to capture the CO2 provided by the storage tank at time period t.
- 10.
- Operation constraints of energy storage
Equation (56) calculates the energy of the energy storage station at bus i at time period t. Equation (57) shows the minimum and maximum energy levels of the energy storage station.
The charging and discharging power of the energy storage system should satisfy the following constraints:
In the equations, the notation is as follows: and represent the upper limits for charging and discharging rates of the energy storage station, respectively. is a binary variable indicating the charging state of the energy storage station at time period t, which equals 1 if the device is charging. is a binary variable indicating the discharging state of the energy storage station at time period t, which equals 1 if the device is discharging. Variables and should satisfy the following constraint.
Equation (60) represents the logical constraint for charging and discharging states, which means that the energy storage station cannot be simultaneously in charging and discharging states.
where and represent the energy of the energy storage station at the first and last time period in the scheduling horizon, respectively.
Equation (61) ensures that the energy of the energy storage station remains unchanged at the first and last time period in the scheduling horizon.
4. Case Study
In this section, an improved IEEE 39-bus test system is employed for simulation analysis to demonstrate the effectiveness of the proposed method. The program is performed on the AMPL platform, and the commercial solver GUROBI 11.0.2 is employed to solve the model. The simulation is conducted on a desktop computer with an Intel(R) Core(TM) i7-10700 processor and 16 GB of memory. The total computational time of the proposed method for the 39-bus power system is 75.95 s.
4.1. Case Study Parameters
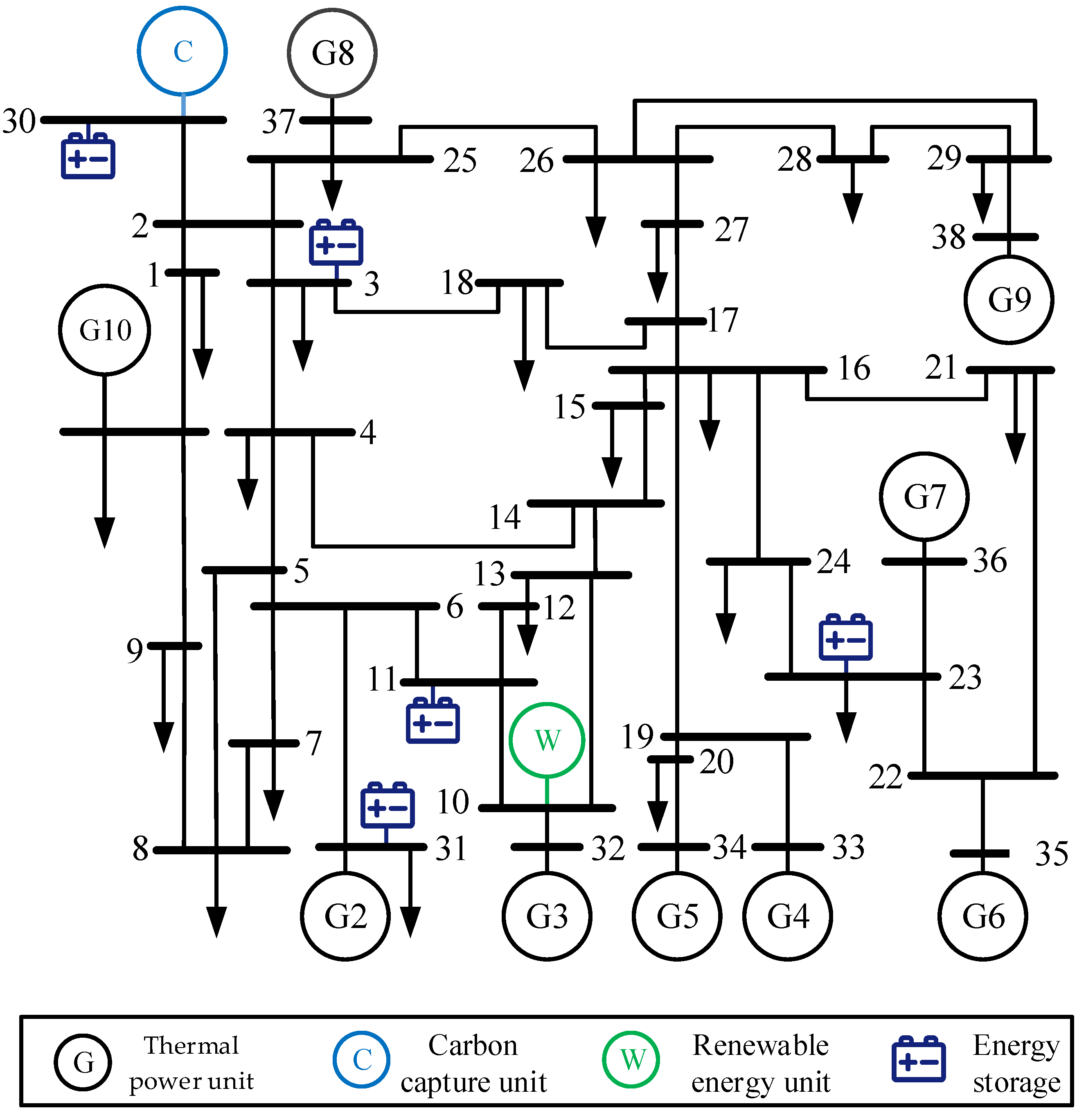
The time resolution considered in the model in this paper is 15 min, resulting in a total of 96 periods. The modified IEEE 39-bus system includes nine thermal power units, one carbon capture unit, one wind farm, and three energy storage stations. The topology of the modified IEEE 39-bus system is illustrated in Figure 2. The relevant parameters of the thermal power units are detailed in Table 1, and the parameters of the carbon capture unit are provided in Table 2.
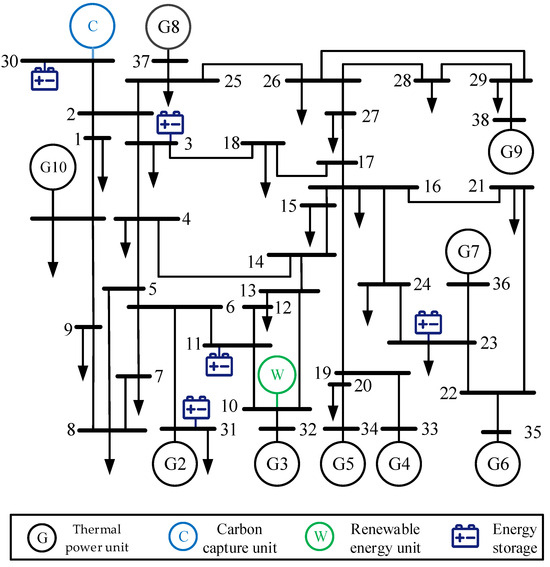
Figure 2.
Topology of the modified IEEE 39-bus system.

Table 1.
Parameters of thermal power units.

Table 2.
Parameters of carbon capture units.
4.2. Optimization Results of Price-Driven Demand Response
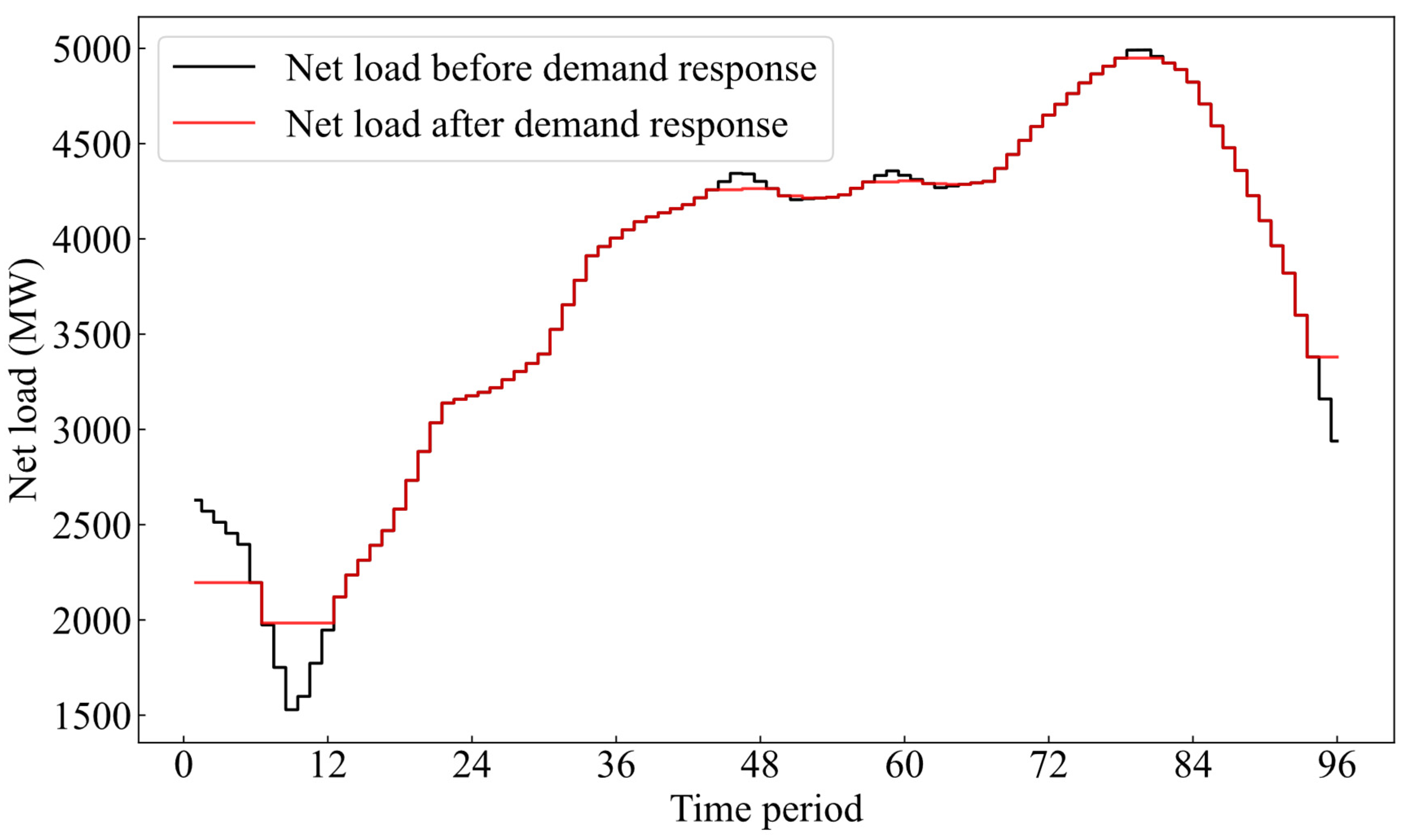
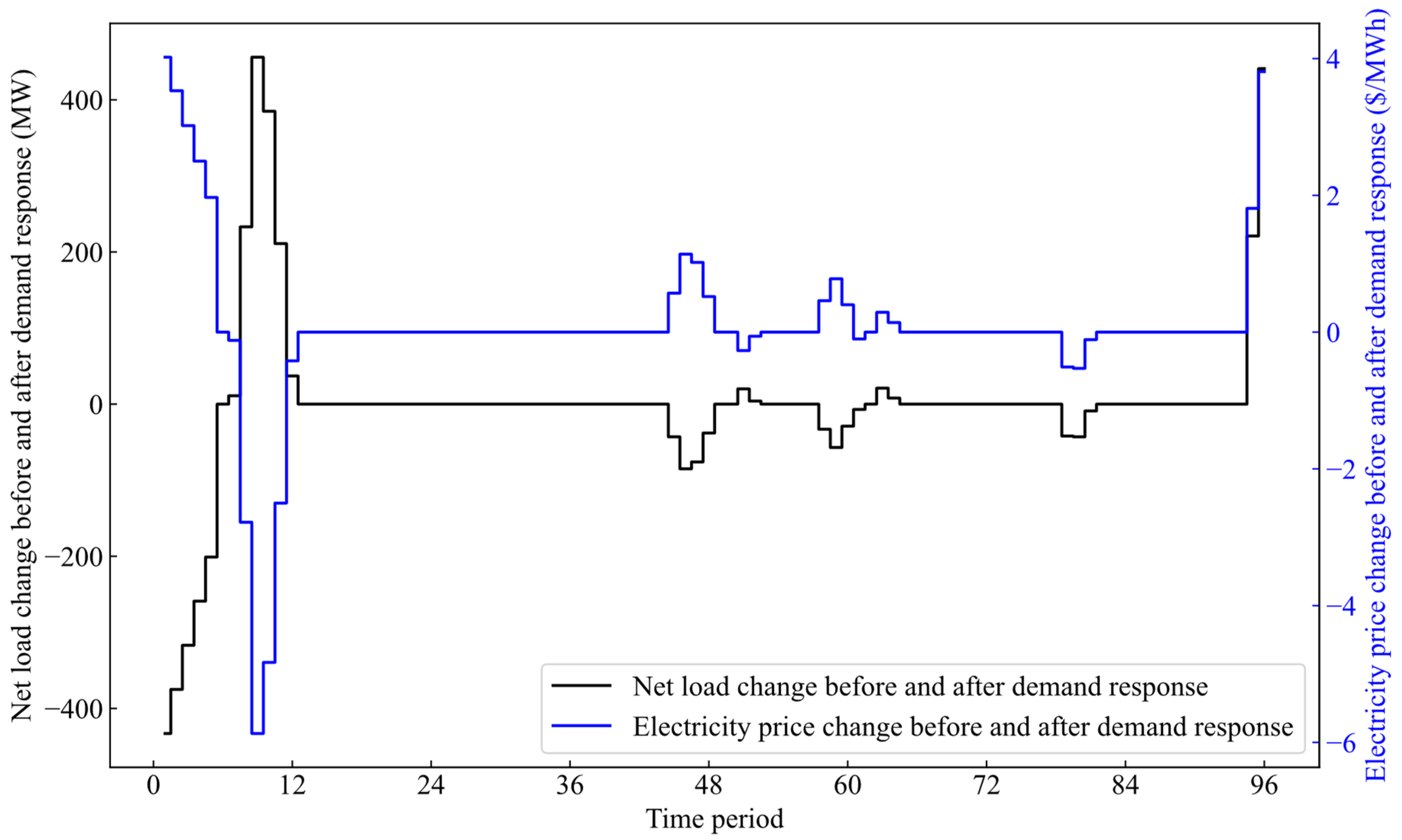
This section presents the optimization results of price-driven demand response. The net load curves before and after demand response are shown in Figure 3. In Figure 3, the black line represents the net load before demand response, while the red line represents the net load after demand response. It should be pointed out that the black lines and red lines overlap at some time periods; this is because the net loads before demand response and after demand response are identical at these time periods. The net load change and electricity price change before and after demand response are shown in Figure 4. It is seen from Figure 3 and Figure 4 that the demand response can effectively smooth the net load of the power system. During peak load periods, the increase in electricity prices leads to a reduction in peak load through demand-side response. During low load periods, the decrease in electricity prices encourages the load demand to increase. Therefore, the total ramping demand can be reduced, and the pressure on peak regulation can be alleviated.
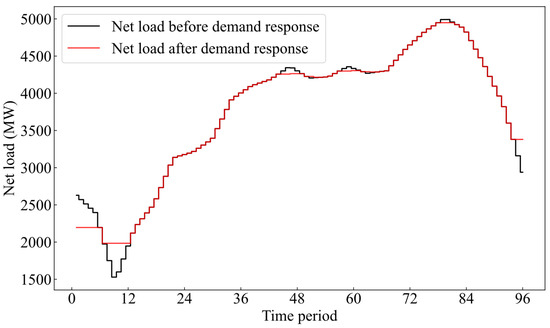
Figure 3.
Net load curves before and after demand response.
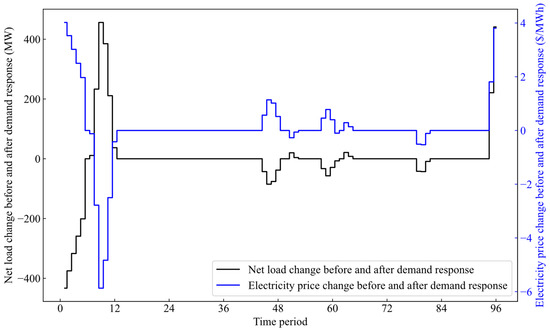
Figure 4.
Net load change and electricity price change curves before and after demand response.
4.3. Ramping Demand and Peak Regulation Optimization Results
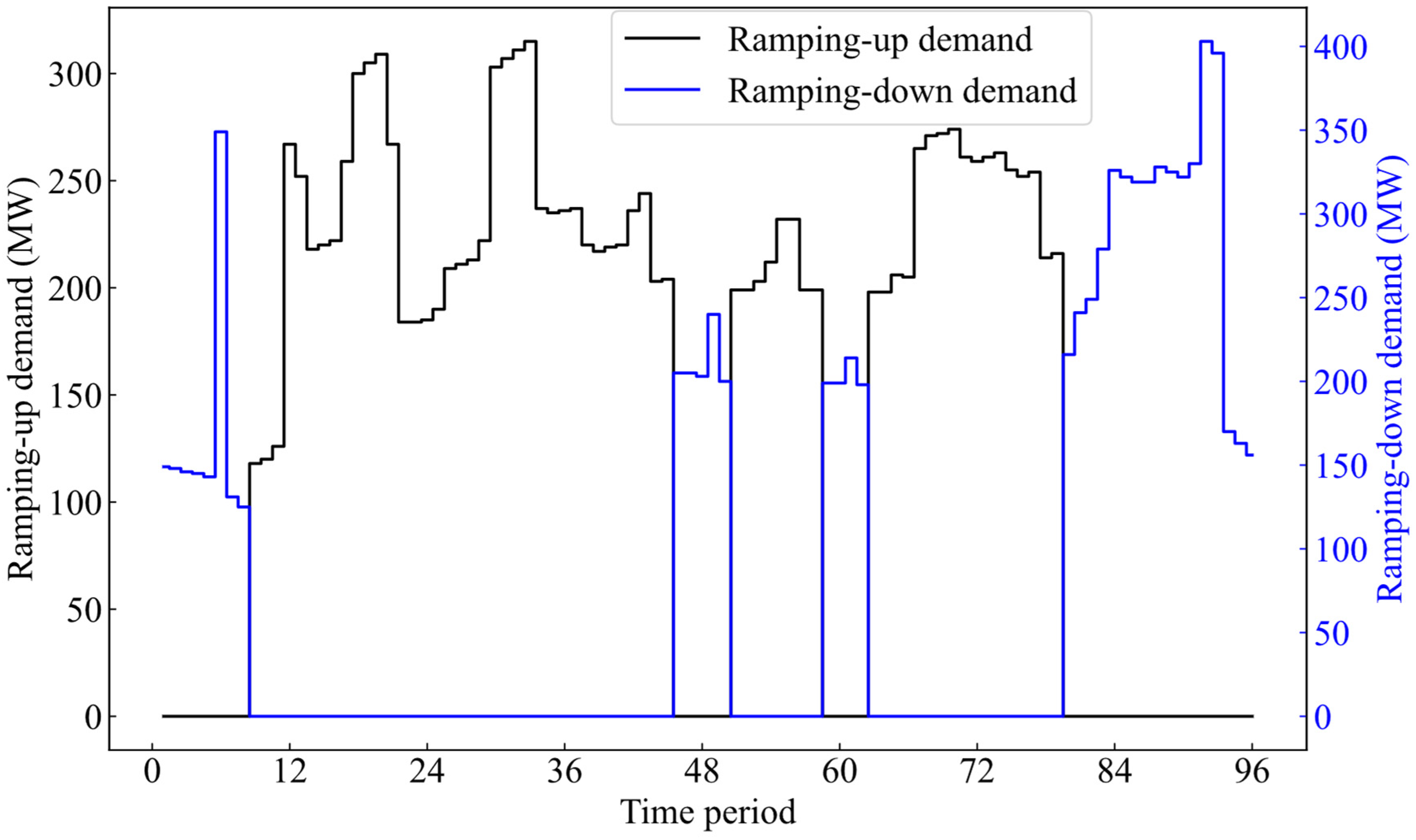
The ramping-up and ramping-down demand curves obtained by using the method proposed in this paper are shown in Figure 5.
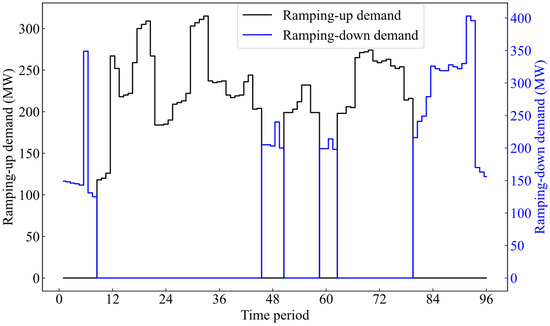
Figure 5.
Ramping-up and ramping-down demand curves of the power system.
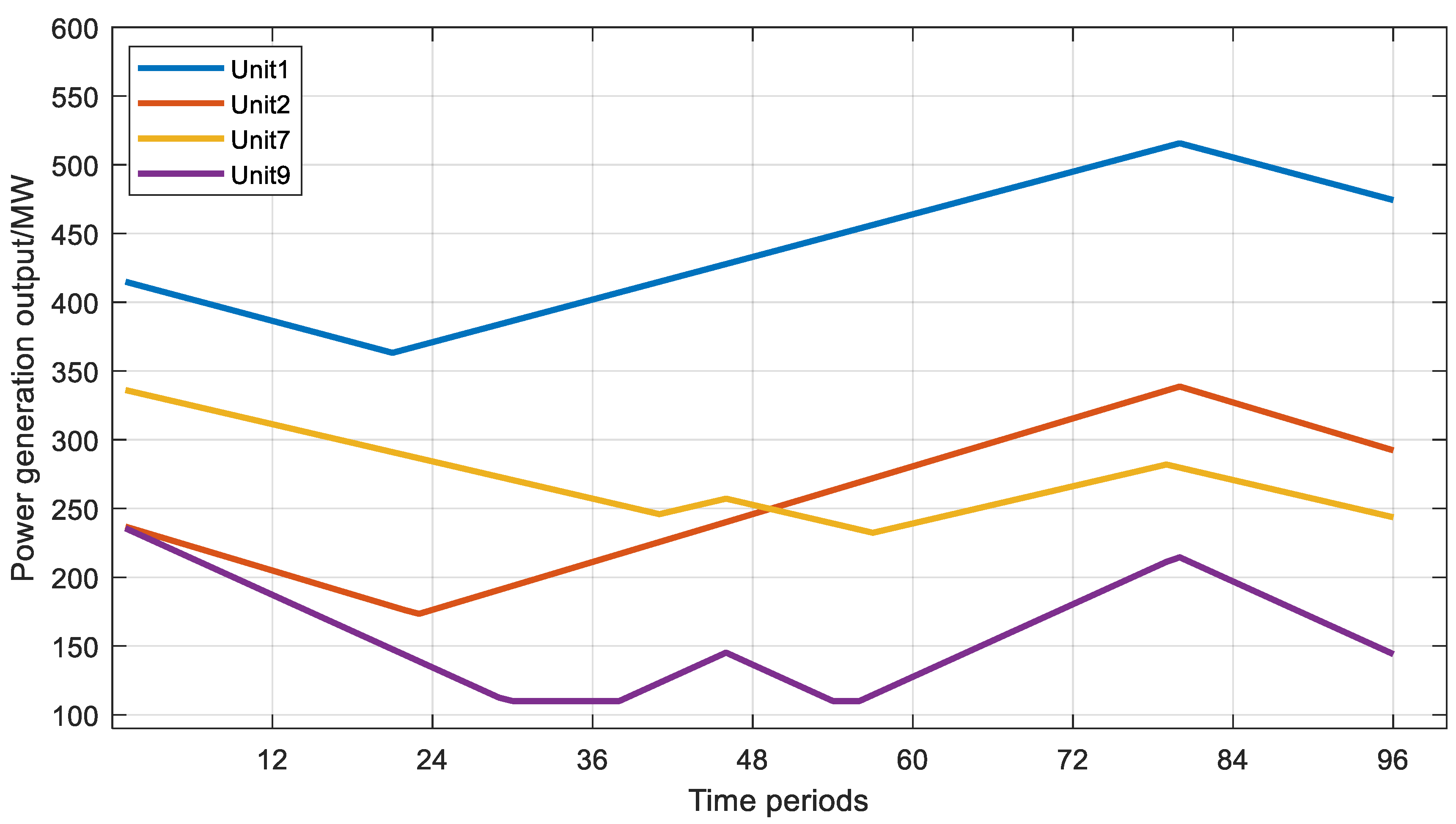
It is seen from Figure 5 that there are ramping-up demands at the time periods [11, 46], [50, 58], and [62, 80] and there are ramping-down demands at the time periods [0, 11], [46, 50], [58, 62], and [80, 96]. The ramping-up and ramping-down demands are determined by the combination of the power load curve, the wind power output curve, and concerned predicted errors. For example, at the time period [11, 14], the power demand increases while the wind power generation output decreases. This results in the ramping-up demand in the power system, which shows a gradually increasing trend. At the time period [15, 18], both the power load and wind power generation output increase. Since the increase in power load is greater than the increase in wind power generation output, the power system still has the ramping-up demand, which shows a gradually decreasing trend. The generation output curve of selected thermal power units obtained by using the proposed method is shown in Figure 6. It can be seen from Figure 6 that at the time period [1, 20], the overall generation outputs of thermal power units show a declining trend due to the decrease in the load demand in the power system in this period. At the time period [30, 46], the generation outputs of most thermal power units show an increasing trend, which are mainly attributed to the increase in the load demand in the power system in this period.
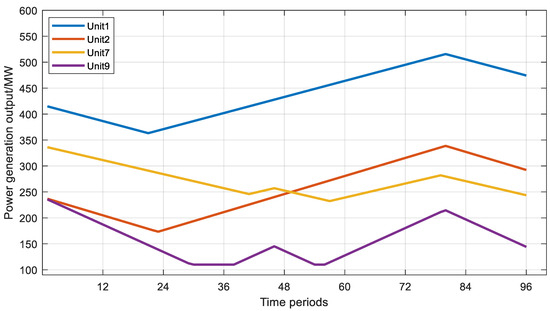
Figure 6.
Generation output curve of selected thermal power units.
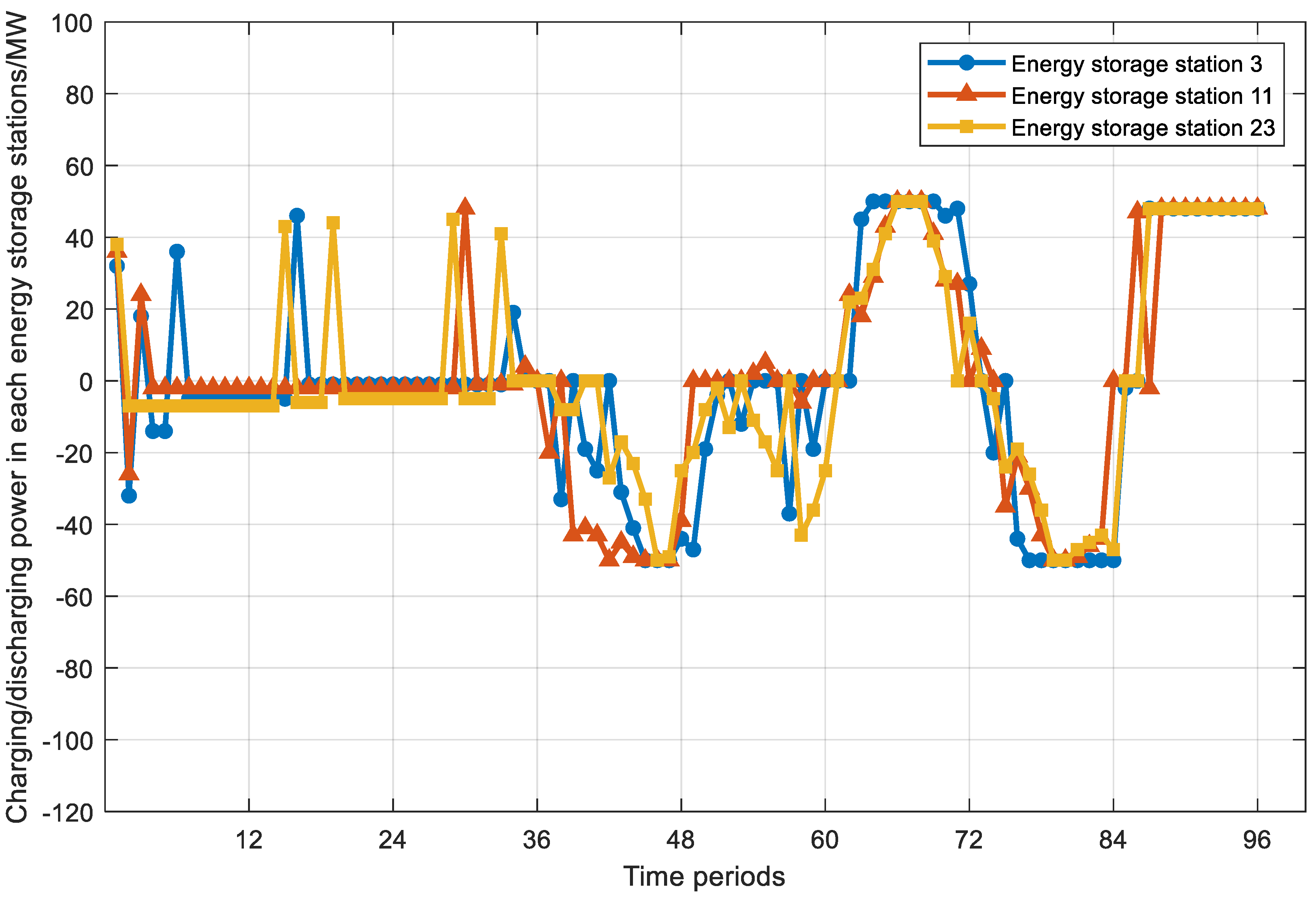
The charging and discharging power curves of energy storage stations are shown in Figure 7. It is seen from Figure 7 that the energy storage stations primarily engage in charging at the nighttime periods and discharging at the peak time periods. In the nighttime, the residential and commercial power demand is relatively low, the energy storage stations charge, and the stored energy is used to discharge in peak periods in the daytime. At the peak time periods, the power demand increases, and the energy storage stations discharge to meet the power demand and reduce the impact of the peak loads on the secure operation of power systems. Note that at the time period 60, most energy storage stations begin to charge and then discharge at the time period 72. The charging action at the time periods [60, 72] helps to ensure that sufficient energy is available for discharging in the peak load period following the time period 72 to alleviate the sharp increase in power demands.
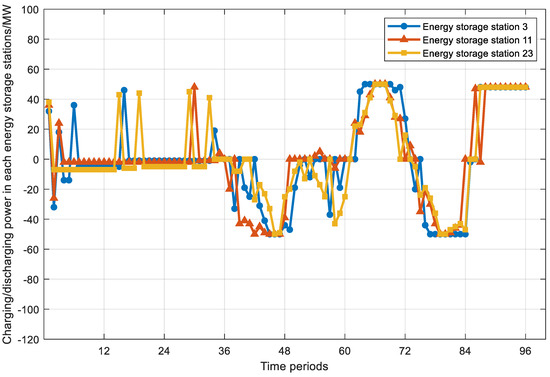
Figure 7.
The charging and discharging power curves of energy storage stations.
The effectiveness of the proposed model is validated by comparing the solutions of different scenarios. The following scenarios are introduced and analyzed.
Scenario 1: The demand response and energy storage are not considered.
Scenario 2: The demand response is considered; however, the energy storage is not considered.
Scenario 3: The energy storage is considered; however, the demand response is not considered.
Scenario 4: The demand response and energy storage are considered, which represents the method proposed in this paper.
Comparisons of peak regulation solutions in different scenarios are shown in Table 3. Scenario 1 is defined to evaluate the peak regulation solution of the power system without any flexible resources involved. This scenario helps identify the limitations of traditional peak regulation methods. Demand response is an important flexibility resource that optimizes power system scheduling by adjusting users’ consumption behavior. Scenario 2 is used to assess the contribution of demand response to peak regulation, particularly to validate the impact of demand response on power system operation in the absence of energy storage. Scenario 3 is used to evaluate the effect of energy storage on peak regulation and examine the impact of energy storage on power system operation without the demand response. Scenario 4 incorporates both demand response and energy storage for peak regulation. Scenario 4 integrates both flexibility resources to verify the proposed bi-level optimization model. It helps to analyze how the synergy between demand response and energy storage achieves optimal operation of the power system during peak periods. It is seen from Table 3 that in Scenario 1, the operation cost of thermal power units, the carbon trading cost, and the total cost are the highest among those in all scenarios, indicating insufficient economic efficiency in the power system operation. Compared to Scenario 1, the demand response is considered in Scenario 2, and the operation cost of thermal power units, the carbon trading cost, and the total cost are lower than those in Scenario 1. This indicates that incorporating demand response into the peak regulation process helps to optimize generation scheduling and improve power system operation efficiency. In Scenario 3, the energy storage is introduced for peak regulation optimization, and the associated costs are lower than those in Scenario 1. This demonstrates that energy storage plays a positive role in peak shaving and reducing both generation and carbon trading cost. In Scenario 4, both the demand response and energy storage are considered, and the operation cost of thermal power units, the carbon trading cost, and the total cost reach their minimal values. Therefore, the proposed method in this paper is beneficial for significantly reducing the total cost and enhancing the economic operation efficiency of the power system.

Table 3.
Comparisons of peak regulation solutions in different scenarios.
4.4. Sensitivity Analysis
4.4.1. Impact of Renewable Energy Generation Forecasts on Scheduling Results
The impact of variations in renewable energy generation forecasts on power system scheduling results is illustrated in Table 4. It is seen from Table 4 that both the ramping-up and ramping-down capacities of the power system increase with the increase in renewable energy generation forecasts. Specifically, when the variation in renewable energy generation forecasts increases from −20% to 20%, the ramping-up capacity increases from 11,500.3 MW to 12,677.4 MW, and the ramping-down capacity increases from 7952.2 MW to 8188.3 MW. This indicates that as renewable energy generation forecasts increase, the power system requires more ramping capacity to deal with the fluctuations of renewable energy generation output. In addition, it is seen from Table 4 that as renewable energy generation forecasts increase, the total cost of the power system gradually decreases. When the variation in renewable energy generation forecasts increases from −20% to 20%, the total cost of the power system decreases from $871,928.2 to $845,717.3. Therefore, the increase in renewable energy generation can enhance the economic efficiency of power system operation due to the reduction in fossil fuel power generation output.

Table 4.
Impact of renewable energy generation forecasts on scheduling results.
4.4.2. Impact of Carbon Prices on Associated Costs
The impact of carbon prices on associated costs is shown in Table 5. It is seen from Table 5 that as the carbon trading price increases, the operation cost of thermal power units, carbon trading cost, and total cost of the power system increase. Therefore, the carbon trading price is a crucial factor influencing the operation cost of power systems. This underscores the importance of establishing reasonable carbon trading prices in the carbon trading market to ensure the economic operation of the power system. The long-term implications of changes in carbon pricing on power system operational strategies mainly lie in adjustment of generation mix. As carbon prices increase, the cost of traditional fossil fuel-based generation increases substantially, driving the power system towards adopting low-carbon generation technologies. The resulting pricing signal encourages the rapid development and deployment of renewable energy and energy storage technologies, gradually replacing high-carbon fossil fuel units and reducing the operational costs of the power system.

Table 5.
Impact of carbon prices on associated costs.
5. Conclusions
This paper presents a bi-level optimization model for power system peak regulation taking the ramping capability and demand response into account. The proposed upper- and lower-level models aim to minimize ramping demands considering uncertainty factors and the overall operation cost of the power system, respectively. A modified IEEE 39-bus system is employed to verify the effectiveness of the proposed peak regulation optimization model. It is concluded from the simulation results that (1) the demand response strategy based on price incentives can flatten the net load curve of the power system, effectively mitigating peak regulation burden and improving operation efficiency of the power system, and (2) the proposed peak regulation optimization model, which considers the ramping capability and demand response, effectively reduces the total operation cost of the power system and enhances economic performance.
It should be pointed out that the optimization of cutting parameters and accuracy improvement in forecasting errors are not considered in this paper. Studying how to optimize the cutting parameters and improve the accuracy of the forecasting errors are our research directions for the future.
Author Contributions
Methodology, L.F. and Y.S.; Software, Z.Y.; Formal analysis, W.P. and L.X.; Investigation, H.L.; Resources, Y.L.; Writing—original draft, L.S.; Writing—review & editing, W.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [State Grid Anhui Electric Power Co., LTD. Enterprise Management Project] grant number [B61205240009].
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author/s.
Conflicts of Interest
Authors Linbo Fang, Wei Peng, Youliang Li, Zi Yang, Yi Sun, Hang Liu and Lei Xu were employed by the State Grid Anhui Electric Power Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Khatami, R.; Parvania, M.; Narayan, A. Flexibility Reserve in Power Systems: Definition and Stochastic Multi-Fidelity Optimization. IEEE Trans. Smart Grid 2020, 11, 644–654. [Google Scholar] [CrossRef]
- Li, J.; Pan, Y.; Mu, G.; Chen, G.; Zhu, X.; Yan, G.; Li, C.; Jia, C. A Hierarchical Demand Assessment Methodology of Peaking Resources in Multi-Areas Interconnected Systems with a High Percentage of Renewables. Appl. Energy 2024, 367, 123371. [Google Scholar]
- Yang, J.; Dong, Z.; Wen, F.; Chen, Q.; Liang, B. Spot Electricity Market Design for a Power System Characterized by High Penetration of Renewable Energy Generation. Energy Convers. Econom. 2021, 2, 67–78. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H.; Li, B. Distributionally Robust Comprehensive Declaration Strategy of Virtual Power Plant Participating in the Power Market Considering Flexible Ramping Product and Uncertainties. Appl. Energy 2023, 343, 121133. [Google Scholar]
- Chen, H.; Huang, J.; Lin, Z.; Huang, F.; Li, M. Stochastic Economic Dispatch Based Optimal Market Clearing Strategy Considering Flexible Ramping Products under Wind Power Uncertainties. CSEE J. Power Energy Syst. 2024, 10, 1525–1535. [Google Scholar]
- Fang, X.; Sedzro, K.S.; Yuan, H.; Ye, H.; Hodge, B.-M. Deliverable Flexible Ramping Products Considering Spatiotemporal Correlation of Wind Generation and Demand Uncertainties. IEEE Trans. Power Syst. 2020, 35, 2561–2574. [Google Scholar] [CrossRef]
- Kwon, H.; Park, J.-K.; Kim, D.; Yi, J.; Park, H. A Flexible Ramping Capacity Model for Generation Scheduling with High Levels of Wind Energy Penetration. Energies 2016, 9, 1040. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, N.; Zhou, G.; Chi, Y.; Chen, N.; Wang, L.; Wang, Q.; Chang, D. Day-Ahead Optimal Dispatch Model for Coupled System Considering Ladder-Type Ramping Rate and Flexible Spinning Reserve of Thermal Power Units. J. Mod. Power Syst. Clean Energy 2022, 10, 1482–1493. [Google Scholar] [CrossRef]
- Wei, W.; Ye, Z.; Wang, Y.; Dai, S.; Chen, L.; Liu, X. An Economic Optimization Method for Demand-Side Energy-Storage Accident Backup Assisted Deep Peaking of Thermal Power Units. Chin. J. Electr. Eng. 2022, 8, 62–74. [Google Scholar] [CrossRef]
- Yang, T.; Lou, S.; Zhang, M.; Li, Y.; Feng, W.; Liu, J. Research on a Two-Layer Optimal Dispatching Method Considering the Mutual Aid of Peak Regulating Resources among Regional Power Grids. Energies 2024, 17, 667. [Google Scholar] [CrossRef]
- Wu, W.; Zhu, J.; Chen, Y.; Luo, T.; Shi, P.; Guo, W.; Shi, P.; Jiang, C. Modified Shapley Value-Based Profit Allocation Method for Wind Power Accommodation and Deep Peak Regulation of Thermal Power. IEEE Trans. Ind. Applicat. 2023, 59, 276–288. [Google Scholar] [CrossRef]
- Yue, X.; Liao, S.; Xu, J.; Ke, D.; Wang, H.; Yang, J.; He, X. Collaborative Optimization of Renewable Energy Power Systems Integrating Electrolytic Aluminum Load Regulation and Thermal Power Deep Peak Shaving. Appl. Energy 2024, 373, 123869. [Google Scholar] [CrossRef]
- Yang, B.; Cao, X.; Cai, Z.; Yang, T.; Chen, D.; Gao, X.; Zhang, J. Unit Commitment Comprehensive Optimal Model Considering the Cost of Wind Power Curtailment and Deep Peak Regulation of Thermal Unit. IEEE Access 2020, 8, 71318–71325. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).