Abstract
As the evolution of smart grids accelerates, distributed energy resources (DERs) emerge as key elements in the transformation of global energy systems. However, the integration of these technologies introduces significant cybersecurity vulnerabilities, notably false data injection (FDI) and a direct load-altering attack (DLAA). Traditional load-altering attacks require a huge attack load and, thus, are not practical to implement. In contrast, in modern DER environments where households become “prosumers” with high-power energy generation, the implications of such attacks are substantially amplified. This paper considers a hybrid cyberattack that includes both FDI and a DLAA, and presents a hierarchical, optimal load adjustment framework that addresses these security concerns. A centralized optimizer first calculates the ideal load-shedding strategies for each substation, which are then securely broadcast to households. To address the complexities at the individual household level, we introduce a novel reinforcement learning algorithm termed Mean Field Deep Deterministic Policy Gradients (MF-DDPG). This algorithm employs mean-field game theory to enable decentrally coordinated decision-making among each household, making it particularly effective in zero-trust scenarios. Through this multifaceted approach, we offer a robust countermeasure against load-altering attacks, thereby enhancing the resilience and stability of advanced smart grids.
1. Introduction
As the world increasingly gravitates toward more sustainable and greener energy solutions [1,2,3], the role of distributed energy resources (DERs) [4,5] in smart grids has become paramount. This change is not just an incremental improvement, but a cornerstone of the global transformation of energy systems [3]. Parallel to the rise of DERs is the development of the transactive energy market (TEM) [6,7], which brings with it the need for intelligent devices that are price sensitive and capable of sophisticated energy management and grid stability.
Although the promises of DERs have been hailed as revolutionary, they come with a set of challenges that must be addressed, chief among them being cybersecurity vulnerabilities [8,9,10,11,12]. Historically, load-altering attacks have targeted the integrity of information, i.e., false data injections (FDIs), rather than direct load-altering attacks (DLAAs), primarily because the latter do not pose a significant threat to bulk power grids. In [13,14,15], false data were injected into different parts such as SCADA, meters, transmission lines, etc. Specifically for the TEM, the price can also be a critical false information to attack, i.e., [16,17]. Moreover, renewable energies such as the wind turbine system is also vulnerable to the FDI attack [18] The solution to FDI does not usually require load shedding since the demand is not directly altered. The direct load-altering attack seems unrealistic due to the capacity of the bulk system, which requires a feasible attack to control a very large amount of load. After the rise of IoT appliances, direct load-altering attacks become more and more realistic. In a work [19] presented at the USENIX Security Symposium, the researchers demonstrated that 200–300 compromised consumers per MW can cause sudden generation tripping in a 9-bus WSCC system. In [20], it is shown that the 1% demand increase attack (210 MW approximately equals 210,000 AC) will cause the frequency to drop to 59.875 Hz in the Polish power grid. If the attacked demand has an increase of 10%, load shedding will be initiated throughout the system. Although IoT systems make it easier for attackers to perform attacks, 210,000 AC is still an impractical number to achieve.
However, the advent of high-power residential prosumers, which act like DERs, significantly alters this scenario. In modern smart grid settings where households evolve into “prosumers” [21], generating their own energy via local residential resources like solar panels or storage solutions such as Tesla’s Powerwall, the risk and impact of cyberattacks escalate substantially. For instance, a Tesla Powerwall+ can contribute a peak output of 22 kW to the grid, while a single Tesla Super Charging station can draw as much as 250 kW. New large-scale charging facilities, such as the Harris Ranch Tesla Supercharger station in California, which boasts 98 supercharger stations, further amplify this risk. A security breach targeting only one of these charging facilities or even a smaller scale, say 1000 prosumer DERs, could successfully induce frequency imbalances in the power grid. Consequently, direct load attacks have become increasingly viable in today’s context.
The combination of a DLAA and FDI creates even more catastrophic consequences. This paper offers a multifaceted examination of the challenges and solutions related to load-altering attacks that have both DLAA and FDI components. Recognizing the inherent risks associated with compromised communication channels, be it between household DER controllers and substations or within the grid’s internal communication channels, we propose a hierarchical, optimal load adjustment framework that promotes optimal load shedding (for DLAAs) without reliable communications between households or households and substations (for FDI). The first layer of this framework involves a centralized optimizer that calculates ideal load-shedding strategies at the substation level, connected with each corresponding bus in the network. The high-level information is then securely transmitted to individual households through a dedicated emergency communication channel, bypassing compromised routine communication routes.
As an effective protection method, the emergency optimal load shedding problem has been an active research area for a long time. Traditional optimization techniques have been well studied and listed in the review papers [22,23,24], which suffer from several trade-offs such as accuracy and computational complexity. Reinforcement learning (RL) algorithms have been proven to be a promising solution for optimal control tasks in various applications [25,26,27]. In [28,29], deep Q learning is introduced to quickly determine the optimized load shedding scheme. Other RL algorithms, such as soft actor-critic [30], safe augmented random search [31], etc., are also explored. The common formulation for most RL algorithms requires the system to be formulated into a Markov Decision Process, which indicates a discrete state and action space. However, such a compromise in load shedding has the cost of reduced accuracy. The Deep Deterministic Policy Gradient (DDPG) algorithm [32] is known for handling continuous state and action space problems. In fact, it has been explored and proved to be effective for optimal load shedding [33,34]. In [33], the authors treated the power system as a multi-agent system and employed a multi-agent DDPG to find the optimal coordination among different areas. This approach is plausible, but one question remains unanswered, i.e., how does the consumer inside each area decide the amount of load to be curtailed? The ultimate answer to this question would be to let each household participate in free market competition (such as the TEM) and model this as a game with certain constrains. Thus, the proper coordination of this game is critical so that it will benefit the load shedding process.
To solve the game with consumers being the players on the market, two problems are especially difficult to tackle: (1) the number of players is usually large in realistic power systems, causing infeasible computational complexity (the nondeterministic polynomial (NP) problem) to solve in emergency; (2) under the circumstances of an FDI attack, the communications between players are not reliable and trustworthy due to the compromised channel. Instead of traditional multi-agent DDPG algorithms, mean field games (MFGs) [35] are notably successful in addressing those two concerns. In MFG theory, a large-scale multi-agent game is converted into a two-player game by invoking a virtual agent that represents the team. Instead of playing with other agents, each player only plays with the virtual “team agent” represented by the state distribution of all agents. In this case, the NP problem is reduced to a two-player game, which is a P problem. Moreover, the state distribution that represents the virtual “team agent” can be solved locally via the Fokker–Plack–Komogrov (FPK) equation [36]. Thus, no communication is required. Although useful, solving MFGs proved to be a difficult task since the FPK equation is a forward partial differential equation (PDE) and the Bellman equation from RL is a backward PDE. DDPG provides an improved numerical solution to the Bellman equation using the discrete-time iterative TD error to replace the PDE. However, this introduced an additional incompatibility, since the genetic FPK is a continuous-time PDE.
In this paper, we aim to extend the genetic MFG and DDPG to introduce a specialized discrete-time continuous state and action space reinforcement learning algorithm, termed Mean Field Deep Deterministic Policy Gradients (MF-DDPG). This algorithm is specifically designed for the hybrid FDI and DLAA model. The solution mandates zero-trust, leveraging the principles of mean field game theory to facilitate decentralized but coordinated decision-making processes among households.
1.1. Summary of Gaps
- The emerging power increase for residential DERs introduces new vulnerabilities to the power grid;
- Current protection algorithms against DLAAs and FDI are not well prepared for a combined hybrid attack. A decentralized zero-trust algorithm that coordinates high-power DERs is desperately needed.
1.2. Contributions and Novelties
- 1.
- A novel hybrid type of cyber threat combining FDI and a DLAA against DERs is identified in this paper. Compared with traditional DLAA and FDI attacks, the hybrid DLAA-FDI attack is more realistic since significantly less attacking load is required when the communication of the DERs is disrupted;
- 2.
- To handle the hybrid attack, mean field game theory is leveraged to enable a decentralized coordination of power adjustments among high-power residential DERs in a zero-communication fashion;
- 3.
- Traditional mean field game theory is extended from continuous-time to discrete-time so that it is compatible with a popular and proven successful reinforcement learning algorithm, namely, Deep Deterministic Policy Gradients (DDPG). The developed MF-DDPG algorithm is the first deep reinforcement learning framework to solve discrete-time mean field games online.
2. Hybrid Attack
In dynamic load-altering attacks (DLAA) on power grids [37,38], a high-volume attack load is vital and, thus, unrealistic in a traditional power grid. However, a novel threat arises when the residential DERs’ power increases. Once the high-power but more vulnerable residential DERs are attacked and their communication is compromised, this novel threat becomes practical.
2.1. Power Flow Modelling
Consider the power flow in a power grid system with high-power residential DERs and traditional generators, the power injection of a traditional generator bus i is:
where and are the sets of all generator and load buses, is the imaginary part of the admittance value between bus i and bus j, is the voltage phase angle of the i generator bus, and is the voltage phase angle of the load bus.
If i is a load bus, the power injection becomes negative, i.e.,
Following [38], the generators are modelled by the swing equations:
where is the rotor angular frequency deviation (), is the motor inertia, is the mechanical power input, and is the damping coefficient of the generator.
In each power system, a Load Frequency Controller (LFC) is employed to regulate the bus frequency to the desired value (60 Hz for US). The performance of this LFC system becomes a critical target for direct load-altering attacks (DLAAs), as any abrupt increase or decrease in the load could destabilize the system. Conventional LFCs often rely on Proportional-Integral-Derivative (PID) controllers, as mentioned in [39]. However, PID controllers may not provide an optimal response for global power flow control, particularly in the context of a potential large-scale multi-input multi-output system. Alternative centralized control methods, such as pole placement or Linear Quadratic Regulator (LQR) controllers [40], offer more sophisticated options. In this paper, we focus on a centralized pole placement-based LFC, denoted as , as a key component of our analysis and discussions.
Substituting the generator bus power injection function (1) and the LFC control into the swing Equation (3), one obtains
2.2. DLAA and FDI Attack
In the current power grid, the Load Frequency Controller (LFC) and dispatch between buses will work together to adjust the frequency of the generators to hold system (8) stable, i.e., maintaining in a fixed range.
In a direct load-altering attack (DLAA), the attacker abruptly changes the load at one or more grid substations (buses), pushing several buses into frequency imbalance. A popular type of attacking mechanism is to design an precise attack signal that generates a disturbance load signal on the original that interferes the LFC’s performance. For example, ref. [38] utilized a PI controller to generate a disturbance load signal on the original PI LFC controller so that the system poles are moved to the unstable side. This type of attack requires a large (1–2 p.u. in [38]) but very precise attacking signal, and, thus, it is not feasible in the real world compared to the capacity of the bulk system. Another type of DLAA creates a sudden load increase or decrease so that one or more generator buses exceed the maximum power output. Given a large input on the load , the LFC controller will be pushed out of the stable range and cause frequency deviation. The value of the attack load can be calculated by an LQR or controller.
On the other hand, the false data injection (FDI) attack is another common option for attacking power grids by injecting false data through SCADA or sensors. Traditional FDI attacks typically involve compromising the signals transmitted through the power grid communication infrastructure, which is often safeguarded by on-site cybersecurity experts. Thus, it is also not realistic in the real world.
Nevertheless, while both DLAA and FDI attacks individually face challenges in the traditional power grid. This paper evaluates an innovative hybrid attack that is made possible by an increasing number of high-power residential DERs. The residential DERs are more vulnerable against all attacks but the power is non-negligible comparable to the capacity of the bulk system. Due to the special vulnerability, both DLAA and FDI can be performed at the same time to enhance the attack consequences. Instead of injecting a false signal in the traditional FDI, the attacker just needs to disrupt the communication signal between DERs and the substations. Then, the following DLAA will require significantly less attacking load since the dispatch and the LFCs lose feedback from the DERs. The overall threat structure is illustrated in Figure 1.
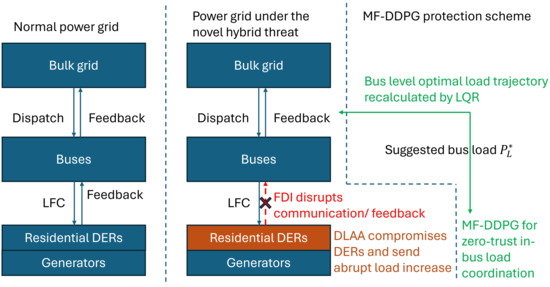
Figure 1.
The overall diagram of the hybrid attack and the developed protection scheme.
Considering the power flow dynamics in Equation (8), the goal of the hybrid attack is to (1) alter the load such that the frequency enters an unsafe region for the power grid and to (2) disrupt the DERs’ communication so that the LFC operates in a open-loop scheme and the dispatch target cannot be achieved.
3. Zero-Trust Defence
To avert a full-scale system breakdown, it is imperative to swiftly devise and disseminate an optimal load-shedding plan to all connected households. Due to the FDI attack, the development of a decentralized optimal load-shedding strategy for individual households is crucial.
3.1. Optimal Load Shedding at the Bus Level
Consider a hybrid DLAA-FDI attack that happens in the power grid. Recalling the power flow dynamics in Equation (8), and letting denote the target state (frequency), one can derive the dynamics for the frequency error as:
where is a newly added optimal load adjustment guidance to each load bus. The needs to be solved such that goes to zero, i.e., the current frequency meets the target frequency. Let
where is the unknown controller that needs to be calculated. The solution for is now converted to solve . The frequency error dynamics can now be written as the following state space representation:
To solve such that goes to zero, an objective function is formulated as:
when the minimum is found. By applying LQR control [25], we obtain the optimal solution for as
where Q and R are weight coefficients for different buses. And, is the Kalman Gain of power flow control subject to the solution of the algebraic Riccati equation (ARE) [25], i.e.,
.
Once the is obtained, can be solved by invoking Equation (9). Thus, the actual optimal load for the load buses can be obtained by solving
The will be broadcast to substations via the emergency channel. The next step is to develop a decentralized optimal coordination on the individual power consumption for each DER household, particularly under zero-trust zero-communication conditions.
3.2. Optimal Load Shedding within a Bus
Assuming that an optimal load-shedding schedule has already been obtained at an arbitrary bus, and all households have received the corresponding total power consumption recommendations via a system-wide emergency broadcast, the broadcast optimal consumption vector is denoted as , where denotes the target power consumption for load bus i. Individual households have to calculate the optimal power consumption considering the optimal total power consumption assigned to each substation. In approaching this computational challenge, two primary obstacles are encountered:
- Communication is inhibited between households and the associated substation, rendering data exchange impractical;
- The sheer number of households linked to a single substation introduces substantial computational complexity.
To model these issues, we begin by formulating a power consumption model tailored for an individual household. In the rest of the paper, all discussions are limited to residential DERs within the same bus. The power adjustment rate can be modelled as:
where i is the household index, and g is a scalar coefficient.
The defensive strategy deployed at each bus aims to accomplish three objectives:
- 1.
- The first objective, which is primarily of interest to utility companies, seeks to ensure that the aggregate power consumption aligns closely with the pre-determined target consumption, . If the total power consumption, denoted as , exceeds , the system risks shutdown due to under frequency. Conversely, would signify an over-frequency scenario. Thus, the performance of this objective is quantified through the minimization problem ;
- 2.
- The second objective arises under the assumption that the system is under attack and the communication system is untrustable. In this context, individual consumers are compelled to vie for a larger share of the limited power supply. The corresponding objective function for each consumer in this competitive scenario is ;
- 3.
- The third objective targets minimal deviation from normal power consumption levels for each household, expressed as , where quantifies the intervention to the consumer’s regular consumption pattern.
Combining the three objectives yields the following cost function:
Minimizing Equation (11) yields the optimal power adjustment rate . According to the Bellman’s principle of optimality [25], the cost function yields the discrete time Bellman equation:
As indicated by the Hamilton–Jacobi–Bellman (HJB) equation, presented as Equation (12), the determination of an individual’s power adjustment rate necessitates access to the consumption data of all other consumers in the system. However, under conditions of a cyberattack-induced zero-trust environment, secure communication among consumers is compromised, rendering such data unreliable. To circumvent this limitation, we propose employing mean field game theory, a concept elaborated upon in the next section, as an optimal resolution strategy.
3.3. Mean Field Game Formulation
The cornerstone of mean field game (MFG) theory lies in its ability to estimate the states of other agents based on their associated probability density functions (PDFs). Given that these PDFs can be approximated utilizing local information, the MFG framework emerges as particularly apt for facilitating optimal decision-making in environments defined by zero-trust. Concurrently, it is noteworthy that each bus harbours a large number of consumers.
The merits of employing MFG theory for the purpose of optimal load curtailment can be summarized as follows:
- Decentralized decision-making: the framework is well suited for zero-trust environments, particularly when the conventional data communication systems are compromised;
- Scalability: due to the substantial number of consumers connected to the power grid, computing a centralized solution becomes computationally infeasible, making the decentralized nature of MFG advantageous.
Denoting the PDF of the power consumption as at time k, the Mean Field type cost function can be derived as
where N is the number of consumers in the bus, and is the feasible state (power consumption) space. Equation (13) is obtained by substituting the PDF into the original cost function Equation (12). All residential DER power consumption is replaced by the PDF .
Next, the PDF of all consumers’ power consumption can be derived using the change of variables as
where is the inverse of the power adjustment dynamics in Equation (10). To solve Equation (14), the power adjustment rate is required and solved by the Bellman equation, i.e., Equation (13). On the other hand, to solve Equation (13), the PDF is required and solved by Equation (14). Therefore, the solution of the coupled Equations (13) and (14) yields the coordinated optimal power adjustment rate for all consumers connected to the bus. Moreover, the inverse function of Equation (10) is also difficult to derive if the optimal adjustment rate is a complex function.
In the MFG formulation, assumptions are made to facilitate the implementation and effectiveness of this approach.
We assume that consumers act rationally and their aggregated behaviour can be modelled using probability density functions (PDFs). This assumption is grounded in the economic theory of rational choice, which posits that individuals seek to optimize their utility given the constraints and information available to them. In the context of energy systems, this means that consumers respond predictably to price signals and other incentives, making it feasible to represent their collective behaviour through MFG theory. This assumption has been validated in several studies on transactive energy markets and demand response programs, where consumer actions are shown to follow predictable patterns.
The MFG framework operates under a zero-trust and zero-communication scenario, assuming that each consumer has access to the power consumption at the time when the attack happens. This local information is used to estimate the Mean Field, which represents the average state of all agents.
3.4. Mean Field DDPG
In the developed MF-DDPG algorithm, each household will maintain three neural networks, i.e., (1) the actor neural network to approximate the optimal load adjustment strategy; (2) the critic neural network to approximate the optimal cost function; and (3) the mass neural network to approximate the PDF of all households’ power consumptions.
With mild assumptions that the weights of the neural network exist, the following forms of neural networks are designed:
where , and are the parameters for the critic, actor, and mass neural networks.
The loss function for the critic neural network is defined as the residual error of the Bellman equation.
The actor neural network maximizes the expected optimal value function. Thus, the loss function is defined as follows:
Both neural networks are updated through target networks to stabilize training. The target networks are soft-updated using:
where is a hyper-parameter between 0 and 1.
The mass neural network is updated based on sampled actions (power adjustment rates). Given a set of uniformly sampled power consumption for agent i denoted as , the next predicted power consumption can be derived as:
where is the one step prediction of the power consumption. Substituting the system dynamics sample and into the PDF propagation, i.e., Equation (14), yields the following vector form:
Equation (20) will not hold until the correct is selected. The residual error is then defined as the loss function for the mass neural network.
Given the three loss functions, i.e., Equations (18), (19), and (21), the three neural networks’ parameters can be updated through applying gradient descend:
where , , and are the learning rates for the critic, actor, and mass neural networks.
Similar to the genetic DDPG where the approximation accuracy of the actor neural network depends on the accuracy of the critic neural network, in MF-DDPG, the accuracy of the mass neural network relies on the actor neural network’s performance.
The complete pseudocode for an individual consumer is given in Algorithm 1.
| Algorithm 1 Mean Field DDPG. |
|
It is worth noting that the developed MF-DDPG algorithm is a decentralized multi-agent reinforcement learning algorithm designed to operate without communications. Each agent independently executes this algorithm, culminating in an optimal solution that approximates an -Nash Equilibrium among all participating consumers. This framework, characterized as a zero-trust, zero-communication algorithm, is particularly advantageous in smart grid environments vulnerable to cyberattacks.
4. Case Studies
In this section, the proposed algorithm is tested in the IEEE 39-bus system. MATLAB 2023a was used to simulate the IEEE 39-bus physical system. Python 3.6 was used for the learning and implementation stages of the Mean Field DDPG algorithm. The simulation was run on a workstation with a Nvidia 4090 GPU (Nvidia, St. Clara, CA, USA).
4.1. Case Study for the Hybrid Attack
4.1.1. System Parameters
The parameters of the transmission lines, the inertia, and the damping coefficients of generators were selected from the standard IEEE 39-bus system [41,42]. The load vector for the 29 load buses was generated randomly between 0 and 2 p.u. The initial frequencies of the system were also randomly generated ranging from 40 Hz to 80 Hz. The initial frequencies between 70 and 55 Hz were pruned because their differences from the nominal 60 Hz were not significant enough. Note that the these frequencies were only used to test the LFC’s ability to push the power grid toward the target 60 Hz, and thus the over- or under-frequency tripping was not enforced before the actual attack happened.
To further strengthen the robustness of the LFC, unlike the common assumptions, we assumed the load at each bus was a dynamic and fast-changing process. To accommodate that, The LFC was designed using pole placement to drive the system to stability before the attack happened. We selected the poles at for all generator buses to further emphasis robustness. We also assumed that the maximum power output of each generator was 2.5 p.u. and the systematic failure would be observed when the frequency was below 58 Hz or beyond 62 Hz. Figure 2 demonstrates evolution of the system frequency being pushed to stability from a randomly initiated environment after 80 s.
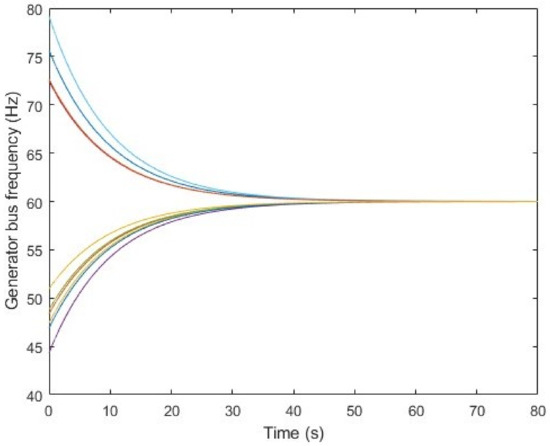
Figure 2.
Ten generator bus frequency plots before the attack happens. Each colored curve represents a generator bus’ frequency.
4.1.2. DLAA Attack
Rather than relying on precise control signal injection, our DLAA model employs a more practical approach: injecting a step function into the load that causes one or more generators to fail. Specifically, we introduced additional attack loads of 3 p.u., 5 p.u., and 2 p.u. on generator buses 10, 12, and 20 at t = 80 s. Figure 3 depicts the time evolution of the 10 generators’ bus outputs controlled by the LFC, and also the system frequency. In the upper part of Figure 3, the frequency of generator bus 12 and 13 becomes asynchronous. Bus 12 reached bus failure 3.6 s after the DLAA was injected due to under frequency. The lower part of Figure 3 demonstrates the controlled LFC output of the 10 generators’ buses. It is clear that bus 12 and 13 reached the maximum output power (marked with the red dashed line). However, injecting 5 p.u. is not a feasible method because the power requirement is huge.
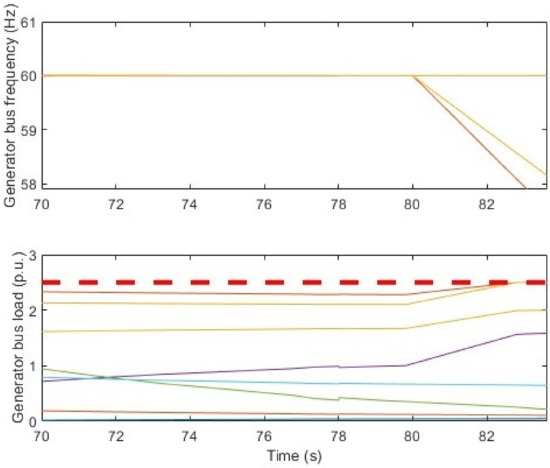
Figure 3.
Ten generator bus frequency plots and generator load outputs in the colored lines for the DLAA only. The red dashed line is the generators’ maximum output.
4.1.3. Hybrid Attack
By combining the DLAA and FDI as hybrid attacks, the required load to attack was significantly reduced. In the hybrid attack, we employed a 1.5 p.u., 2.2 p.u., and 1.5 p.u. additional attack load on generator buses 10, 12, and 20 at 80 s. To simulate the basic FDI attack, we assumed that the communications were disrupted from 80 s to 90 s. Figure 4 illustrates the time evolution of the frequency and the Load Frequency Controller (LFC) output during the hybrid attack. Several buses in the upper part of the figure become asynchronous, leading to an under-frequency condition that triggers line tripping approximately 9.43 s after the hybrid attack was initiated. This result underscores the effectiveness of the hybrid attack in achieving the desired destabilizing effect on the power grid while requiring significantly lower attack loads, making it a potent threat to the stability of the power grid.
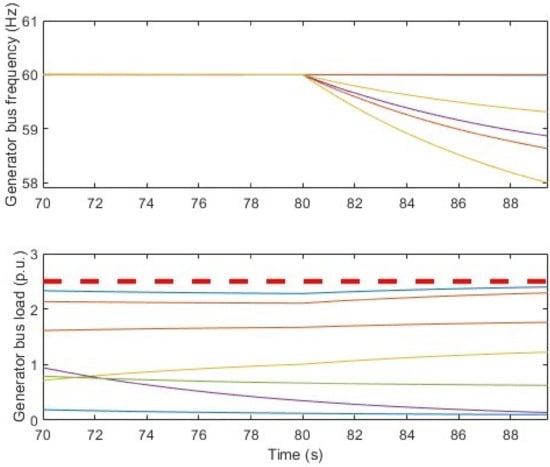
Figure 4.
Ten generator bus frequency plots and generator load outputs in colored lines for the hybrid DLAA-FDI attack. The red dashed line is the generators’ maximum output.
To further compare DLAA and the hybrid attack under the same attack pattern, we set the attack parameters for the DLAA to be the same as for the hybrid attack, i.e., a 1.5 p.u., 2.2 p.u., and 1.5 p.u. additional attack load on generator buses 10, 12, and 20 at 80 s. The frequencies of the power grid under both attacks are depicted in Figure 5. When employing the same amount as the DLAA, the hybrid attack successfully triggered under-frequency tripping near 90 s. On the other hand, the DLAA alone could be easily managed by the LFC.
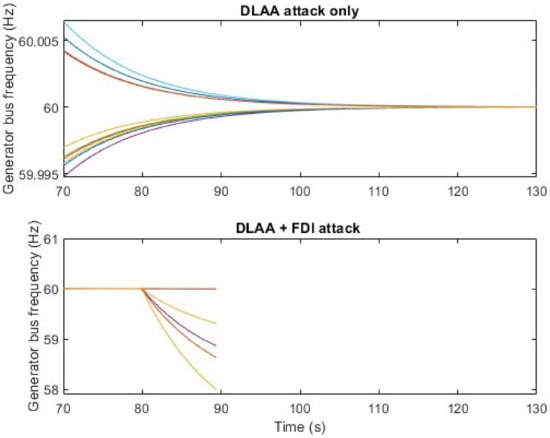
Figure 5.
DLAA and hybrid attack comparison. The colored lines represent the generator frequencies for different buses. The hybrid attack triggers under frequency tripping but DLAA along does not. The 1.5 p.u., 2.2 p.u., and 1.5 p.u. additional attack load are placed on generator buses 10, 12, and 20 at 80 s.
4.2. Case Studies for MF-DDPG Zero-Trust Defence
In this section, the performance of the developed MF-DDPG algorithm is evaluated using the IEEE 39-bus system, which is a widely utilized benchmark. The defence scheme consists of two distinct steps: (1) bus-level load shedding; and (2) decentralized household load shedding for each bus.
We continued to use the same set of parameters and the system that was used in the case studies for the hybrid attack. To test the performance of the proposed MF-DDPG algorithm in a more challenging setup, the attack load was increased as shown in Table 1.

Table 1.
Attack load in different buses.
4.2.1. LQR for Optimal Bus-Level Defence
Our approach began by computing the optimal load adjustments for each bus using Linear Quadratic Regulator (LQR) control with R and Q set as the identity matrices with proper dimensions. The attack load was injected at 80 s into the three buses described above. The frequency evolution of the 10 generator buses in the IEEE 39-bus system is plotted in Figure 6. It is clear that the system’s frequency became asynchronous due to the Load Frequency Control (LFC) saturation. However, the LQR controller calculated the optimal load adjustment rates for each bus, as is evident in Figure 6 and Figure 7, illustrating that the minimum bus frequency following the attack temporarily dropped to approximately 58.6 Hz but remarkably began to recover just 1.01 s after the attack’s onset. These plots collectively demonstrate the effectiveness of our designed bus-level defence mechanism in safeguarding the power grid against severe under-frequency tripping.
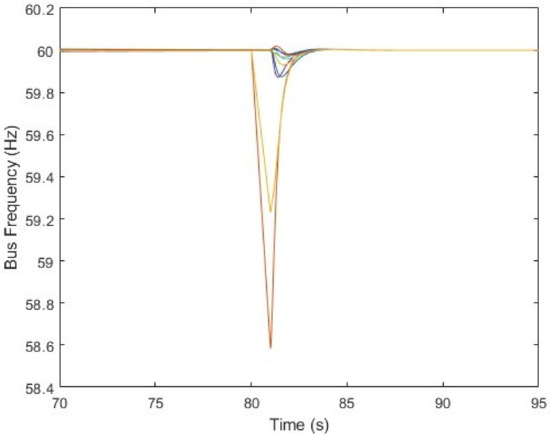
Figure 6.
Bus level frequency plot using LQR for defence against the hybrid DLAA-FDI attack. The hybrid attack was injected at 80 s. Each color line represent the frequency of each bus in the 10 generator buses in the IEEE 39-bus system.

Figure 7.
Bus level defence input plot for each bus . The color lines are the defense input load for each bus. The defence input was sampled to 1 s for the MF-DDPG algorithm.
Next, the calculated optimal bus-level adjustments were then broadcast to each household, forming the foundation of a decentralized collective load shedding scheme.
4.2.2. Decentralized Optimal Load Shedding Using MF-DDPG
After receiving the recommended bus-level load shedding amounts through an emergency broadcast, individual household DERs must collectively determine the optimal load adjustments. However, due to the presence of a false data injection (FDI) attack, the communication channels are compromised. Therefore, a decentralized but collectively coordinated approach is required to establish a zero-trust defence mechanism.
In this experiment, we assumed the dynamic optimal bus load was broadcast every one second, and the MF-DDPG model was updated to track the target during each second. It is worth noting that while training the model from scratch can be slow, the incremental model update is fast.
To illustrate the capabilities of the MF-DDPG algorithm, we selected a specific scenario involving bus 31 at time 83 s. And, the calculated load adjustment was to reduce by 0.0379 per unit (p.u.). The original load at bus 31 was 1.4850 p.u., necessitating a reduction to 1.4471 p.u. at this bus. In this simulation, we incorporated 1000 household DERs connected to this bus, with their initial power consumption values being randomly generated according to a uniform distribution ranging from 0 to 0.002 p.u. The exploration rate for action selection was set as 0.995. The learning rates for the actor NN and critic NN were set at 0.0001 and 0.001. The size of the experience pool was set as 450 entries. The discount factor was 0.8. The actor and critic NNs have a hidden layer with 40 neurons.
The metrics to evaluate the performance of the MF-DDPG algorithm are presented as follows:
Mean Adjusted Power Consumption: Figure 8 plotted the mean adjusted power consumption in bus 31. It is evident that the average power consumption stabilized at approximately 0.00147 p.u.
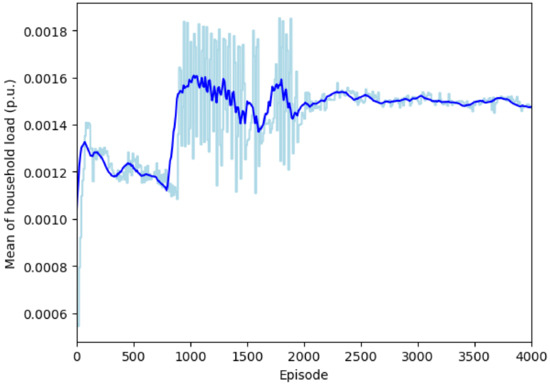
Figure 8.
Mean power consumption for the household DERs in bus 31 after receiving the broadcast signal at 83 s. The light blue line is the actual mean for each episode and the deep blue curve is the smoothed average over 100 episodes.
Time Evolution of 100 Households’ Load: Figure 9 presents the time evolution of the load for 100 households. This plot clearly illustrates that the MF-DDPG algorithm effectively achieved a collective load adjustment in 4 s. Thus, the MF-DDPG model would be able to produce an increment update every 4 s, i.e., achieving the suggested bus load every four broadcasts.
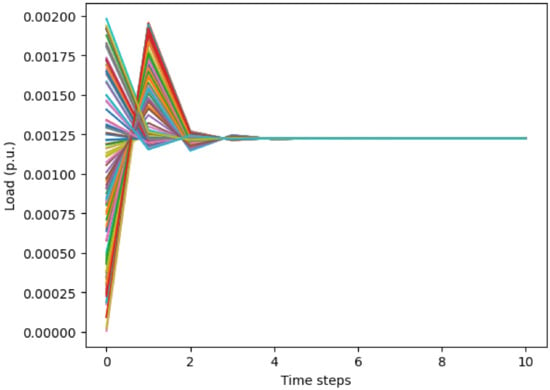
Figure 9.
Sampled actual load of 100 households in bus 31 after receiving the broadcast signal at 83 s. Each household’s power consumption is coordinated in a decentralized manner by Mean Field Games.
These results demonstrates the algorithm’s ability to coordinate and adapt household load adjustments in response to specific load reduction requirements, demonstrating its utility in real-world power grid scenarios. Note that during the MF-DDPG’s coordination process, no information was exchanged between the residential DERs.
To further assess the performance of the three neural networks, we conducted an in-depth analysis and present our findings as follows:
Critic Neural Network’s Average Episodic Loss (Figure 10): It is evident from the plot that the critic neural network’s average episodic loss gradually diminished, reaching nearly zero after approximately 3500 episodes. The convergence of the loss to zero indicates the successful convergence to a unique solution in the mean field game. This outcome also signifies the discovery of the Nash Equilibrium for load adjustments within bus 31.
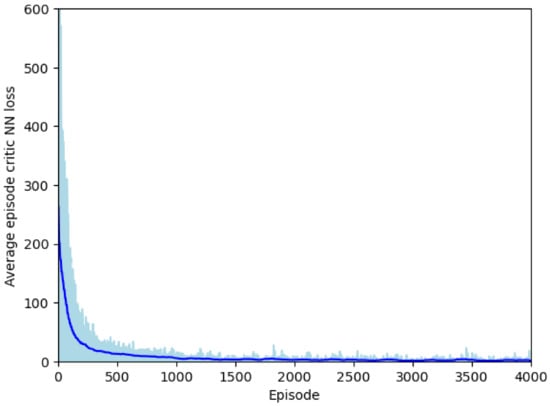
Figure 10.
Average episode critic NN’s loss.
Actor Neural Network’s Average Reward (Figure 11): To gain a more comprehensive understanding of the reinforcement learning process, we evaluated the actor neural network by initiating 10 random tests after each episode. The average reward, although negative due to the adaptation to the machine learning library, demonstrates a significant increase after around 1000 episodes. This growth in reward suggests that the actor neural network was learning effective policies for achieving desirable load adjustments.
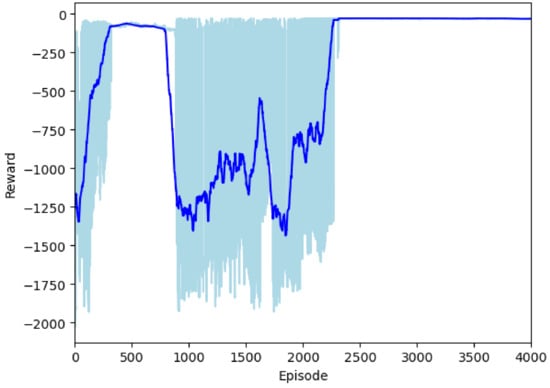
Figure 11.
Episode reward averaged over 10 random tests.
These observations collectively highlight the successful training and convergence of the neural networks, affirming their efficacy in optimizing load adjustments within the power grid system. The reduction in critic neural network loss and the increase in the actor neural network reward demonstrates that the optimal decision model was successfully learned. Since no communication is required in the online learning process, the developed MF-DDPG is a zero-trust and zero-communication algorithm.
4.3. Comparison Discussions
To the best of our knowledge, the joint threat of a DLAA and FDI has neither been addressed nor discussed. Due to the new trend in large-scale residential DERs, the combination of a DLAA and FDI made attacking the power grid realistic in the real world. When applied to a power grid with high-power residential DERs, most protection algorithms for a DLAA, such as [38], require information exchange between the DERs, which can be easily compromised due to the nature of the lower security level in residential equipment. Therefore, the developed MF-DDPG algorithm is the first algorithm that can protect the power grid against a DLAA in a completely decentralized setup.
5. Limitations
Although powerful in handling the hybrid attacks, the MFDDPG algorithm has several limitations, which originate from both the algorithm itself and the impact on the DER devices.
5.1. Limitations of MFDDPG
The mean field game approximates all DERs’ power consumption through local information only. And thus, the MFDDPG’s ability to adapt to system uncertainties is greatly limited. For example, if one high-power residential DER goes offline, the MFDDPG will still provide load shedding guidance as the device is still online. This could cause inaccurate protection, especially in highly complex and uncertain attacking scenarios. Moreover, the nature of mean field games requires all DERs to be operated under the same consumption pattern, i.e., the same parameters for Equation (10). In current residential DERs, most equipment is approximately similar, so the algorithm will work. However, when the DER types increase and become completely different, this algorithm will invite approximation errors.
5.2. Impacts on the DER Equipment
The MFDDPG algorithm is a type of online machine learning algorithm that requires a computational intensive unit (e.g., a GPU). Depending on the model and specifications, a GPU suitable for these tasks can range from $500 to $1500 or more. This requirement will increase the cost of the residential DER equipment and hinder the deployment in residential areas. Some residential DERs are already equipped with intensive computing units. The MFDDPG algorithm deployed in this advanced DER equipment will slow down the original DER control algorithms such as a solar panel controller.
Moreover, it also requires the DER equipment to have the ability to connect to the bus control centre and yield control over the centre once under attack. In transactive energy market research [6], such smart devices are already being developed. It will require effort to tailor these devices to DER equipment.
Lastly, once the attack happens, the residential DERs will not be able to continue their original duties, i.e., store or sell electricity based on the price. The MFDDPG protection protocol will be utilized to help the bus to recover from frequency anomaly.
5.3. Impacts of the Grid Inertia
The integration of renewable energy resources such as wind and solar has led to a significant reduction in grid inertia, which poses new challenges for maintaining grid stability and executing effective protective actions. Low-inertia systems are more susceptible to rapid frequency deviations, reducing the response time available for traditional protective mechanisms. In systems with reduced inertia, the grid’s ability to absorb and respond to disturbances diminishes, potentially requiring faster and more precise control actions. Conversely, higher inertia can delay the response time of protective measures but provides more stability against sudden frequency changes. In this context, our proposed hierarchical defence framework must adapt to the faster dynamics and heightened vulnerability of low-inertia grids. Future research should explore the integration of advanced prediction models and faster response control mechanisms within the MF-DDPG algorithm to ensure robustness in low-inertia scenarios.
5.4. Comparison with Filtering
Recent studies on dynamic sum-based event-triggered filtering for networked systems, such as TS fuzzy wind turbine systems [18], have demonstrated advanced capabilities in mitigating deception attacks through precise control and real-time system adjustments. These methods effectively counteract false data injection by dynamically adjusting the control inputs based on the system’s real-time conditions, thereby enhancing the robustness of the control system under cyberattacks. However, these approaches typically assume the availability of accurate and continuous communication, which may not be feasible in scenarios involving severe communication disruptions like denial-of-service (DoS) attacks. In contrast, our proposed hierarchical defence framework, which employs reinforcement learning and mean field game (MFG) theory, is designed to operate under zero-trust and zero-communication conditions, making it more resilient in scenarios where communication channels are compromised. By enabling decentralized decision-making among households based on local information, our method ensures coordinated grid stability without relying on centralized control or continuous data exchange. This decentralized approach provides a complementary perspective to filtering techniques, offering a robust and scalable solution for smart grids facing hybrid attacks that obstruct communication and disrupt system integrity.
6. Conclusions
In this paper, we present a thorough analysis of a novel hybrid attack that encompasses both direct load-altering attacks (DLAA) and false data injection (FDI) attacks. Traditional DLAA methods face significant challenges, as they typically require an attack load comparable to the generator bus output or precise control over a relatively large attack load. Similarly, FDI attacks are not feasible due to the stringent data injection requirements imposed by professionally protected Supervisory Control and Data Acquisition (SCADA) systems. However, in this hybrid attack mode, attackers can achieve their objectives by injecting a significantly smaller amount of attack load and simply disrupting communication between buses and households. To defend against this hybrid attack, we devised a hierarchical solution that leverages two key components: (1) LQR-based bus-level load shedding and (2) a decentralized MF-DDPG algorithm. This approach transforms the load shedding problem within each bus into a mean field game, reflecting our commitment to enforcing a zero-trust policy. Our comprehensive case studies encompass both attack and defence scenarios, serving as empirical evidence of the effectiveness of the proposed framework in safeguarding critical power grid systems.
In the future, we will focus on expanding the framework to handle more complex cyber-physical attacks, including advanced DoS scenarios. We also aim to integrate adaptive control techniques and test the approach with real-world data to validate its effectiveness in practical smart grid environments.
Author Contributions
Conceptualization, Z.Z., D.D. and H.X.; methodology, Z.Z. and H.X.; software, D.D.; resources, D.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by NASA grant number 231878A0001.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DERs | Distributed Energy Resources |
| DLAA | Direct Load Altering Attack |
| FDI | False Data Injection |
| MF-DDPG | Mean Field Deep Deterministic Policy Gradient |
| DDPG | Deep Deterministic Policy Gradient |
| TEP | Transactive Energy Market |
| SCADA | Supervisory Control and Data Acquisition |
| FPK | Fokker–Planck–Komogrov |
| PDE | Partial Differential Equation |
| MFG | Mean Field Games |
| LFC | Load Frequency Controller |
| PID | Proportional-Integral-Derivative |
| LQR | Linear Quadratic Regulator |
References
- Haegel, N.M.; Kurtz, S.R. Global Progress Toward Renewable Electricity: Tracking the Role of Solar. IEEE J. Photovoltaics 2021, 11, 1335–1342. [Google Scholar] [CrossRef]
- Mai, T.; Hand, M.M.; Baldwin, S.F.; Wiser, R.H.; Brinkman, G.L.; Denholm, P.; Arent, D.J.; Porro, G.; Sandor, D.; Hostick, D.J.; et al. Renewable Electricity Futures for the United States. IEEE Trans. Sustain. Energy 2014, 5, 372–378. [Google Scholar] [CrossRef]
- Elavarasan, R.M.; Shafiullah, G.; Padmanaban, S.; Kumar, N.M.; Annam, A.; Vetrichelvan, A.M.; Mihet-Popa, L.; Holm-Nielsen, J.B. A Comprehensive Review on Renewable Energy Development, Challenges, and Policies of Leading Indian States with an International Perspective. IEEE Access 2020, 8, 74432–74457. [Google Scholar] [CrossRef]
- Jiayi, H.; Chuanwen, J.; Rong, X. A review on distributed energy resources and MicroGrid. Renew. Sustain. Energy Rev. 2008, 12, 2472–2483. [Google Scholar] [CrossRef]
- Xu, S.; Xue, Y.; Chang, L. Review of power system support functions for inverter-based distributed energy resources-standards, control algorithms, and trends. IEEE Open J. Power Electron. 2021, 2, 88–105. [Google Scholar] [CrossRef]
- Huang, Q.; Amin, W.; Umer, K.; Gooi, H.B.; Eddy, F.Y.S.; Afzal, M.; Shahzadi, M.; Khan, A.A.; Ahmad, S.A. A review of transactive energy systems: Concept and implementation. Energy Rep. 2021, 7, 7804–7824. [Google Scholar] [CrossRef]
- Zia, M.F.; Benbouzid, M.; Elbouchikhi, E.; Muyeen, S.; Techato, K.; Guerrero, J.M. Microgrid transactive energy: Review, architectures, distributed ledger technologies, and market analysis. IEEE Access 2020, 8, 19410–19432. [Google Scholar] [CrossRef]
- Onunkwo, I.; Wright, B.J.; Cordeiro, P.G.; Jacobs, N.; Lai, C.F.; Johnson, J.T.; Hutchins, T.; Stout, W.M.; Chavez, A.D.; Richardson, B.T.; et al. Cybersecurity Assessments on Emulated DER Communication Networks; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2019.
- Zografopoulos, I.; Ospina, J.; Liu, X.; Konstantinou, C. Cyber-Physical Energy Systems Security: Threat Modeling, Risk Assessment, Resources, Metrics, and Case Studies. IEEE Access 2021, 9, 29775–29818. [Google Scholar] [CrossRef]
- Aljohani, T.; Almutairi, A. A comprehensive survey of cyberattacks on EVs: Research domains, attacks, defensive mechanisms, and verification methods. Def. Technol. 2024; in press. [Google Scholar] [CrossRef]
- Pinto, S.J.; Siano, P.; Parente, M. Review of cybersecurity analysis in smart distribution systems and future directions for using unsupervised learning methods for cyber detection. Energies 2023, 16, 1651. [Google Scholar] [CrossRef]
- Hasan, M.K.; Habib, A.A.; Shukur, Z.; Ibrahim, F.; Islam, S.; Razzaque, M.A. Review on cyber-physical and cyber-security system in smart grid: Standards, protocols, constraints, and recommendations. J. Netw. Comput. Appl. 2023, 209, 103540. [Google Scholar] [CrossRef]
- Zhang, H.; Meng, W.; Qi, J.; Wang, X.; Zheng, W.X. Distributed load sharing under false data injection attack in an inverter-based microgrid. IEEE Trans. Ind. Electron. 2018, 66, 1543–1551. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, X.; Lin, J.; Yu, W. On false data injection attacks against the dynamic microgrid partition in the smart grid. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 7222–7227. [Google Scholar]
- Chlela, M.; Joos, G.; Kassouf, M.; Brissette, Y. Real-time testing platform for microgrid controllers against false data injection cybersecurity attacks. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Krishnan, V.; Zhang, Y.; Kaur, K.; Hahn, A.; Srivastava, A.; Sindhu, S. Cyber-security analysis of transactive energy systems. In Proceedings of the 2018 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Denver, CO, USA, 16–19 April 2018; pp. 1–9. [Google Scholar]
- Majumder, R.; Bag, G.; Kim, K.H. Power Sharing and Control in Distributed Generation with Wireless Sensor Networks. IEEE Trans. Smart Grid 2012, 3, 618–634. [Google Scholar] [CrossRef]
- Yan, S.; Yang, X.; Gu, Z.; Xie, X.; Yang, F. Dynamic sum-based event-triggered H∞ filtering for networked TS fuzzy wind turbine systems with deception attacks. Fuzzy Sets Syst. 2024, 493, 109084. [Google Scholar] [CrossRef]
- Soltan, S.; Mittal, P.; Poor, H.V. {BlackIoT}:{IoT} botnet of high wattage devices can disrupt the power grid. In Proceedings of the 27th USENIX Security Symposium (USENIX Security 18), Baltimore, MD, USA, 15–17 August 2018; pp. 15–32. [Google Scholar]
- Huang, B.; Cardenas, A.A.; Baldick, R. Not everything is dark and gloomy: Power grid protections against {IoT} demand attacks. In Proceedings of the 28th USENIX Security Symposium (USENIX Security 19), Santa Clara, CA, USA, 14–16 August 2019; pp. 1115–1132. [Google Scholar]
- Dasgupta, R.; Sakzad, A.; Rudolph, C. Cyber attacks in transactive energy market-based microgrid systems. Energies 2021, 14, 1137. [Google Scholar] [CrossRef]
- Xu, D.; Girgis, A.A. Optimal load shedding strategy in power systems with distributed generation. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No. 01CH37194), Columbus, OH, USA, 28 January–1 February 2001; Volume 2, pp. 788–793. [Google Scholar]
- Bakar, N.N.A.; Hassan, M.Y.; Sulaima, M.F.; Na’im Mohd Nasir, M.; Khamis, A. Microgrid and load shedding scheme during islanded mode: A review. Renew. Sustain. Energy Rev. 2017, 71, 161–169. [Google Scholar] [CrossRef]
- Lu, M.; ZainalAbidin, W.; Masri, T.; Lee, D.; Chen, S. Under-frequency load shedding (UFLS) schemes—A survey. Int. J. Appl. Eng. Res. 2016, 11, 456–472. [Google Scholar]
- Lewis, F.L.; Vrabie, D. Reinforcement learning and adaptive dynamic programming for feedback control. IEEE Circuits Syst. Mag. 2009, 9, 32–50. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Pei, Y.; Yang, J.; Wang, J.; Xu, P.; Zhou, T.; Wu, F. An emergency control strategy for undervoltage load shedding of power system: A graph deep reinforcement learning method. IET Gener. Transm. Distrib. 2023, 17, 2130–2141. [Google Scholar] [CrossRef]
- Wei, Y.; Bugaje, A.A.B.; Bellizio, F.; Strbac, G. Reinforcement learning based optimal load shedding for transient stabilization. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Novi Sad, Serbia, 10–12 October 2022; pp. 1–5. [Google Scholar]
- Zhang, J.; Luo, Y.; Wang, B.; Lu, C.; Si, J.; Song, J. Deep reinforcement learning for load shedding against short-term voltage instability in large power systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 4249–4260. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Sun, X.; Lee, M.H.; Moon, J. Deep Reinforcement Learning Based Active Network Management and Emergency Load-Shedding Control for Power Systems. IEEE Trans. Smart Grid 2023, 15, 1423–1437. [Google Scholar] [CrossRef]
- Vu, T.L.; Mukherjee, S.; Yin, T.; Huang, R.; Tan, J.; Huang, Q. Safe reinforcement learning for emergency load shedding of power systems. In Proceedings of the 2021 IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Yan, Z.; Xu, Y. A Multi-Agent Deep Reinforcement Learning Method for Cooperative Load Frequency Control of a Multi-Area Power System. IEEE Trans. Power Syst. 2020, 35, 4599–4608. [Google Scholar] [CrossRef]
- Chen, C.; Cui, M.; Li, F.; Yin, S.; Wang, X. Model-Free Emergency Frequency Control Based on Reinforcement Learning. IEEE Trans. Ind. Inform. 2021, 17, 2336–2346. [Google Scholar] [CrossRef]
- Gomes, D.A.; Saúde, J. Mean field games models—A brief survey. Dyn. Games Appl. 2014, 4, 110–154. [Google Scholar] [CrossRef]
- Achdou, Y.; Cardaliaguet, P.; Delarue, F.; Porretta, A.; Santambrogio, F.; Achdou, Y.; Laurière, M. Mean field games and applications: Numerical aspects. In Mean Field Games: Cetraro, Italy 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 249–307. [Google Scholar]
- Su, Q.; Li, S.; Gao, Y.; Huang, X.; Li, J. Observer-based detection and reconstruction of dynamic load altering attack in smart grid. J. Frankl. Inst. 2021, 358, 4013–4027. [Google Scholar] [CrossRef]
- Amini, S.; Pasqualetti, F.; Mohsenian-Rad, H. Dynamic Load Altering Attacks Against Power System Stability: Attack Models and Protection Schemes. IEEE Trans. Smart Grid 2018, 9, 2862–2872. [Google Scholar] [CrossRef]
- Glover, J.D.; Sarma, M.S.; Overbye, T. Power System Analysis & Design, SI Version; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Pillai, A.G.; Rita Samuel, E. PSO based LQR-PID output feedback for load frequency control of reduced power system model using balanced truncation. Int. Trans. Electr. Energy Syst. 2021, 31, e13012. [Google Scholar] [CrossRef]
- Moeini, A.; Kamwa, I.; Brunelle, P.; Sybille, G. Open data IEEE test systems implemented in SimPowerSystems for education and research in power grid dynamics and control. In Proceedings of the 2015 50th International Universities Power Engineering Conference (UPEC), Stoke on Trent, UK, 1–4 September 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Brunelle, P. 10-Machine New-England Power System IEEE Benchmark; Retrieved 10 October 2023; MATLAB Central File Exchange: Natick, MA, USA, 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).