A Digital Iterative Learning Based Peak Current Mode Control for Interleaved Totem Pole PFC Circuit
Abstract
1. Introduction
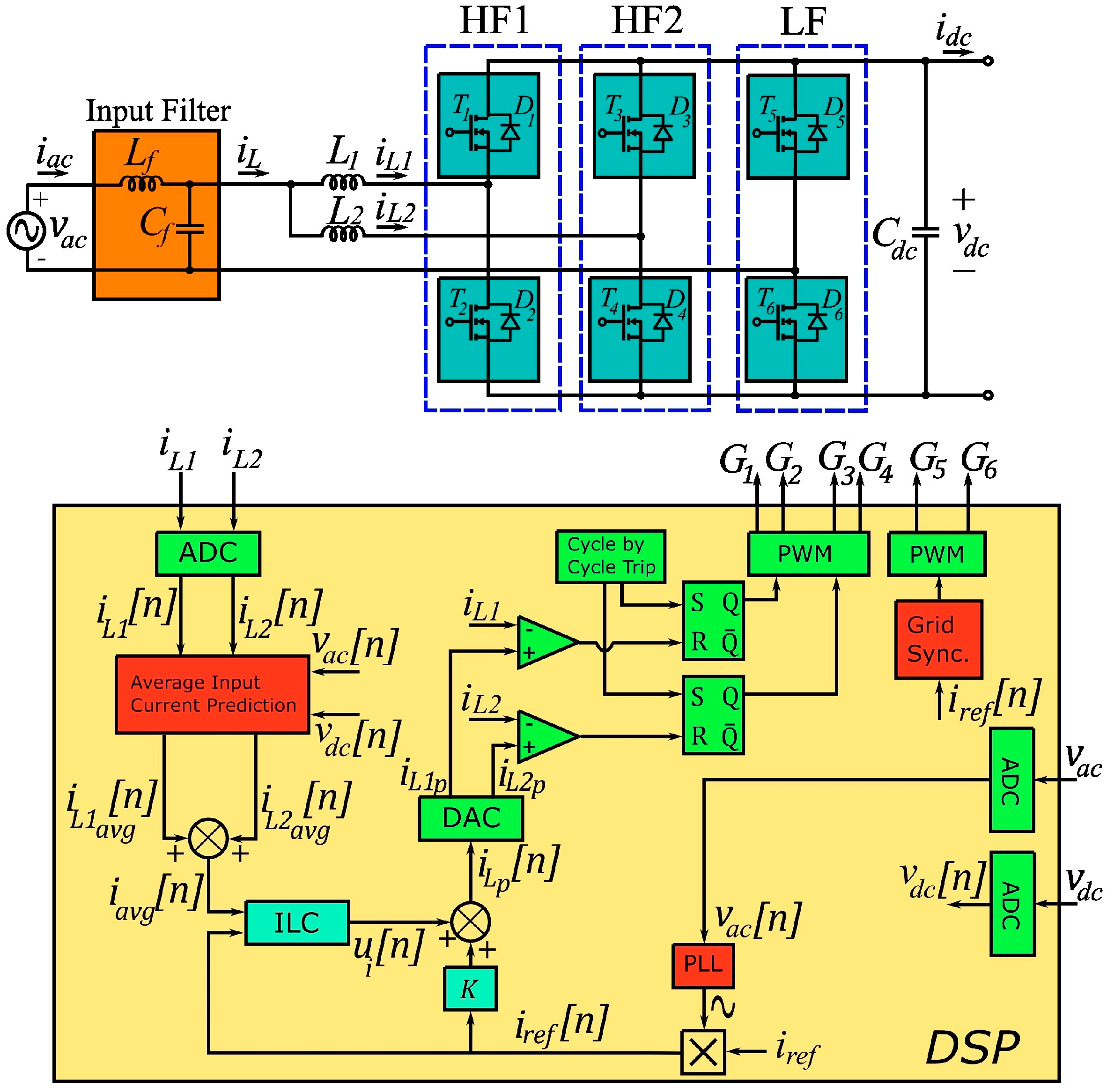
2. Digital PCMC in Interleaved Totem Pole PFC
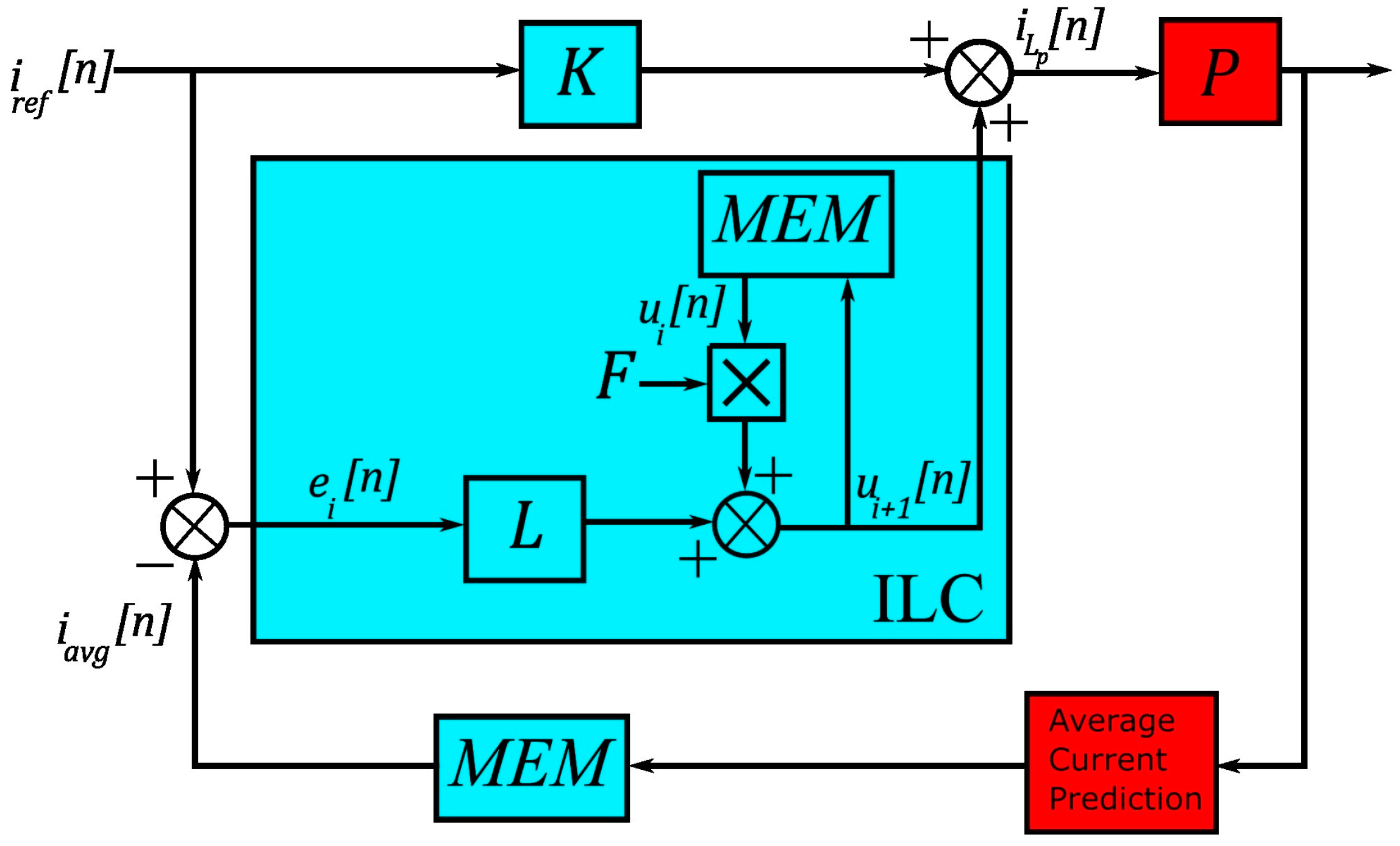
- The ILC method is used to minimize the error between the predicted average current and the reference current to ensure perfect reference tracking despite non-idealities and variations. The output of the ILC is added to the average current value calculated for the PCMC in each phase leg to achieve the compensated peak current value.
- The compensated peak current value is loaded into the digital-to-analog converter (DAC) and cycle-by-cycle current control is performed using fast comparators in the DSP.
- The outer voltage controller is not performed to analyze the performance of the proposed current controller. The grid synchronization of the input current is performed with the digital phase locked loop (PLL) algorithm.
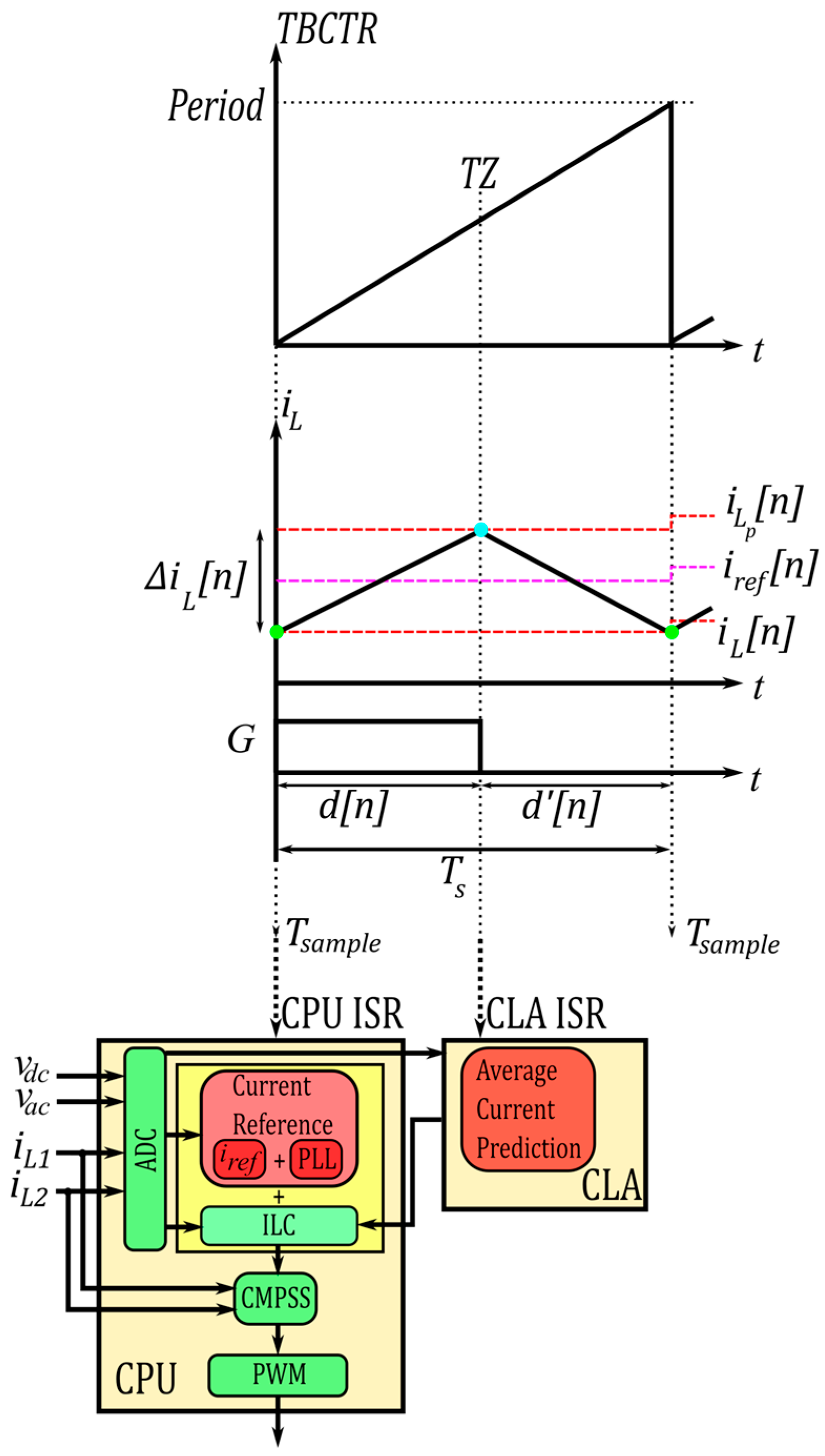
2.1. Average Input Current Prediction
2.2. Investigation of Non-Idealities and Disruptive Effects
2.2.1. Effect of Inductance Variation
2.2.2. Difficulty of Current Prediction in DCM Mode
2.2.3. Zero Crossing Distortion
2.2.4. Digital Computational Burden
3. Analysis of the Proposed ILC Method
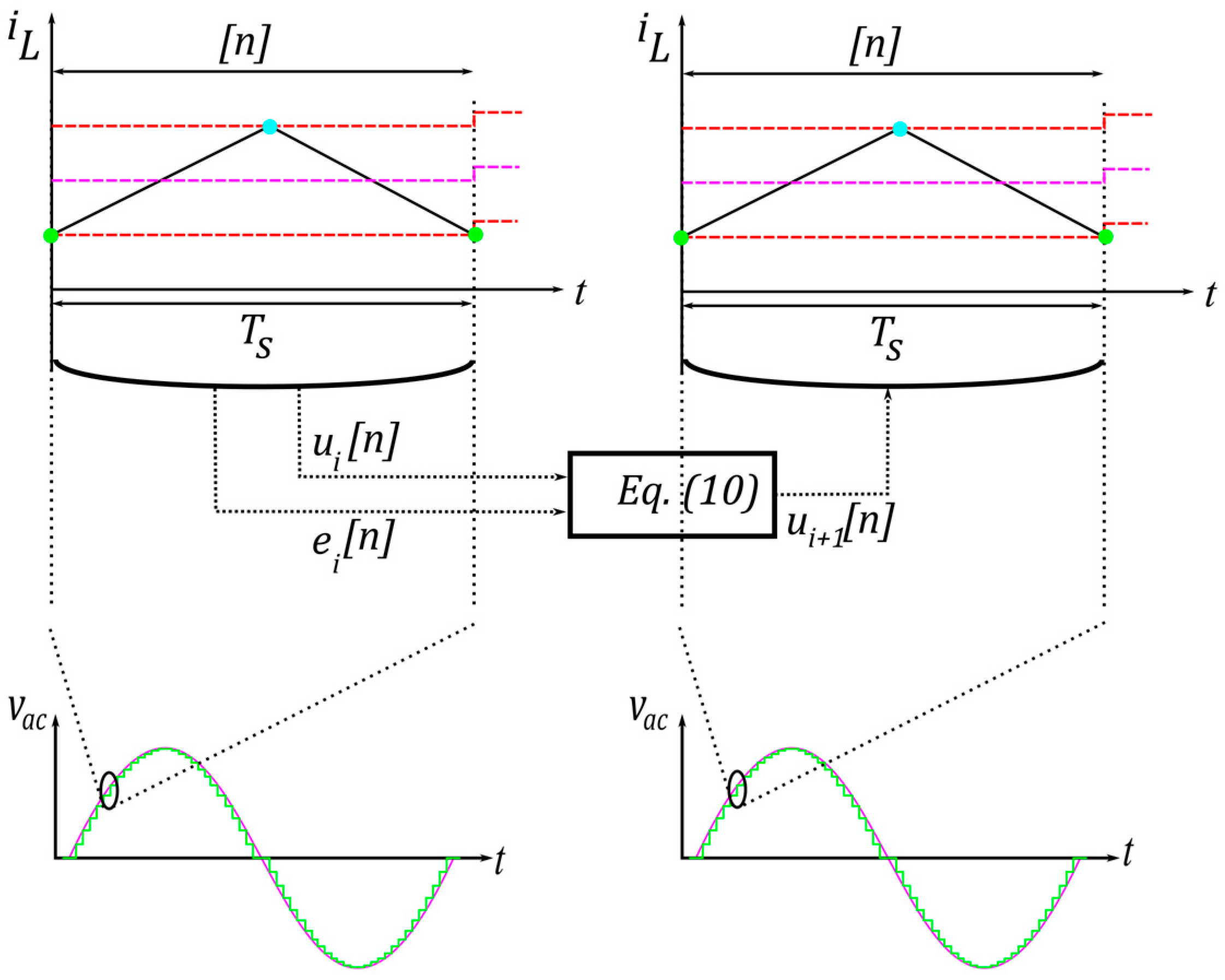
3.1. Implementation of the ILC Method for Digital PCMC
3.2. Convergence and Stability Analysis of the ILC
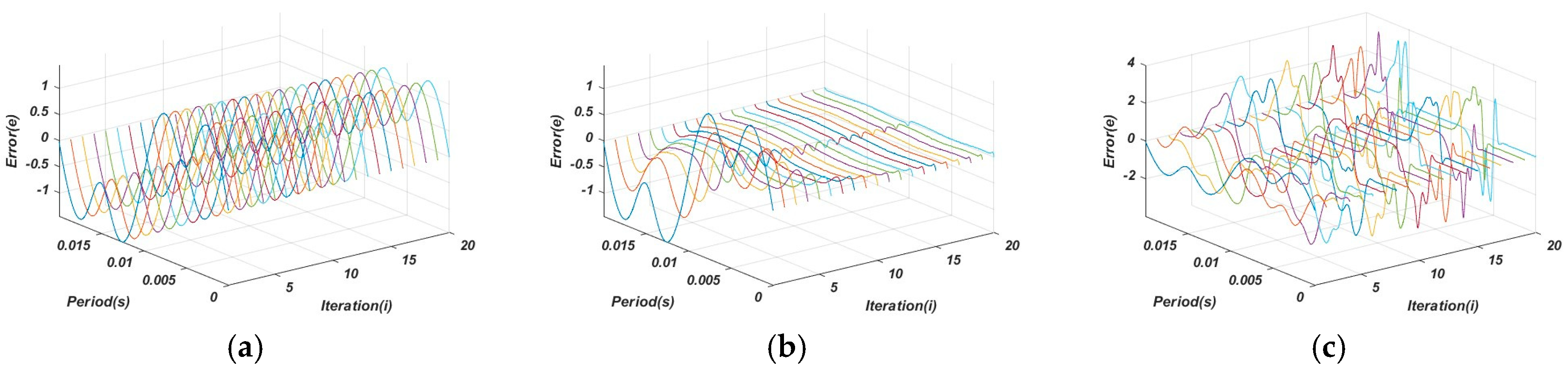
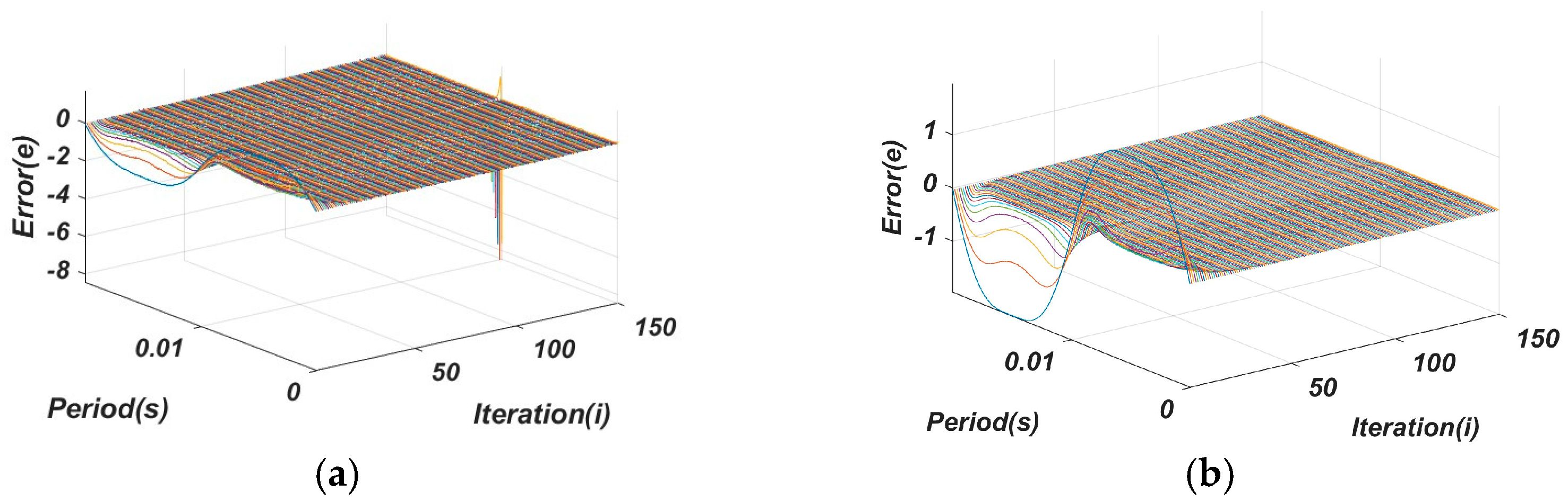
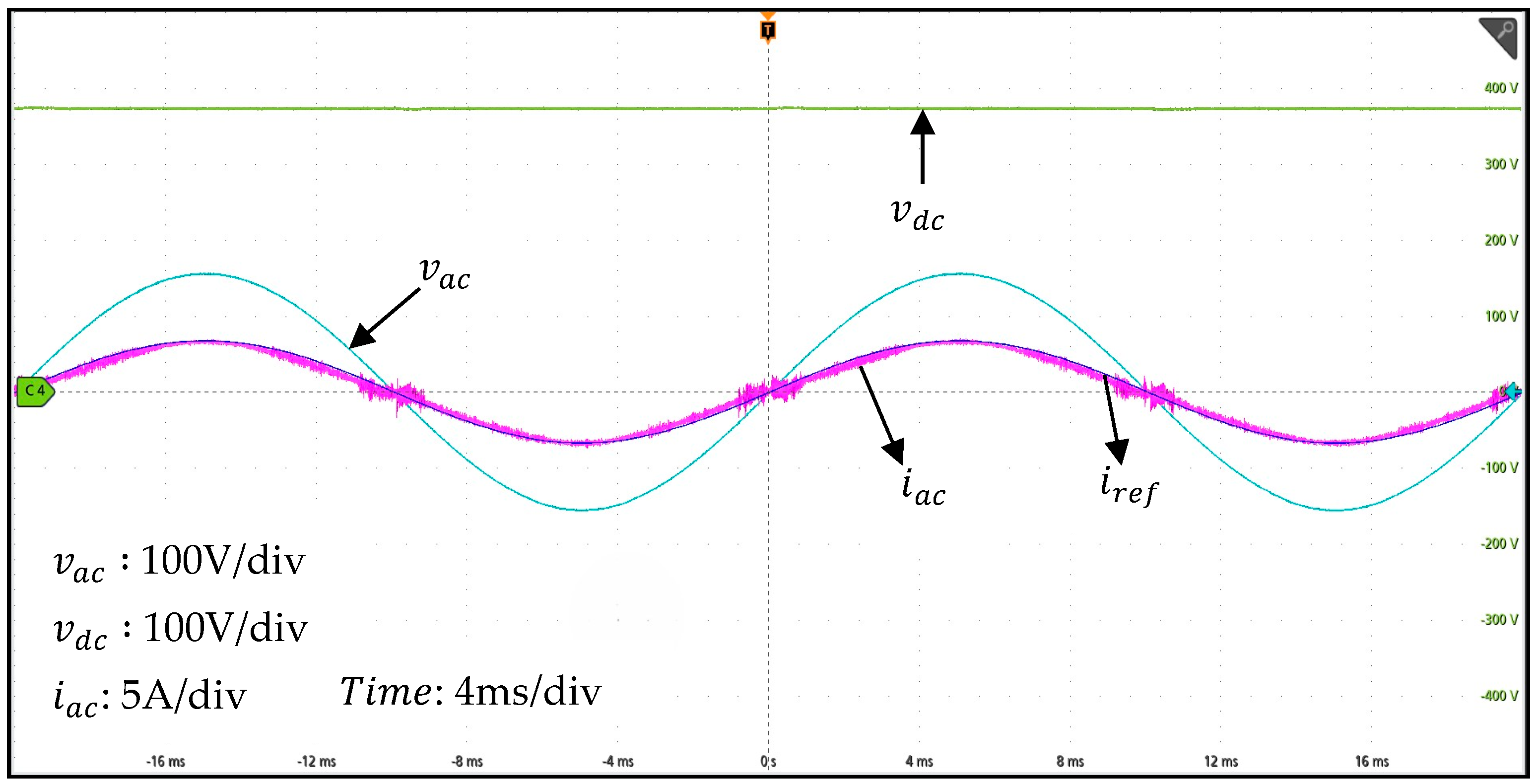
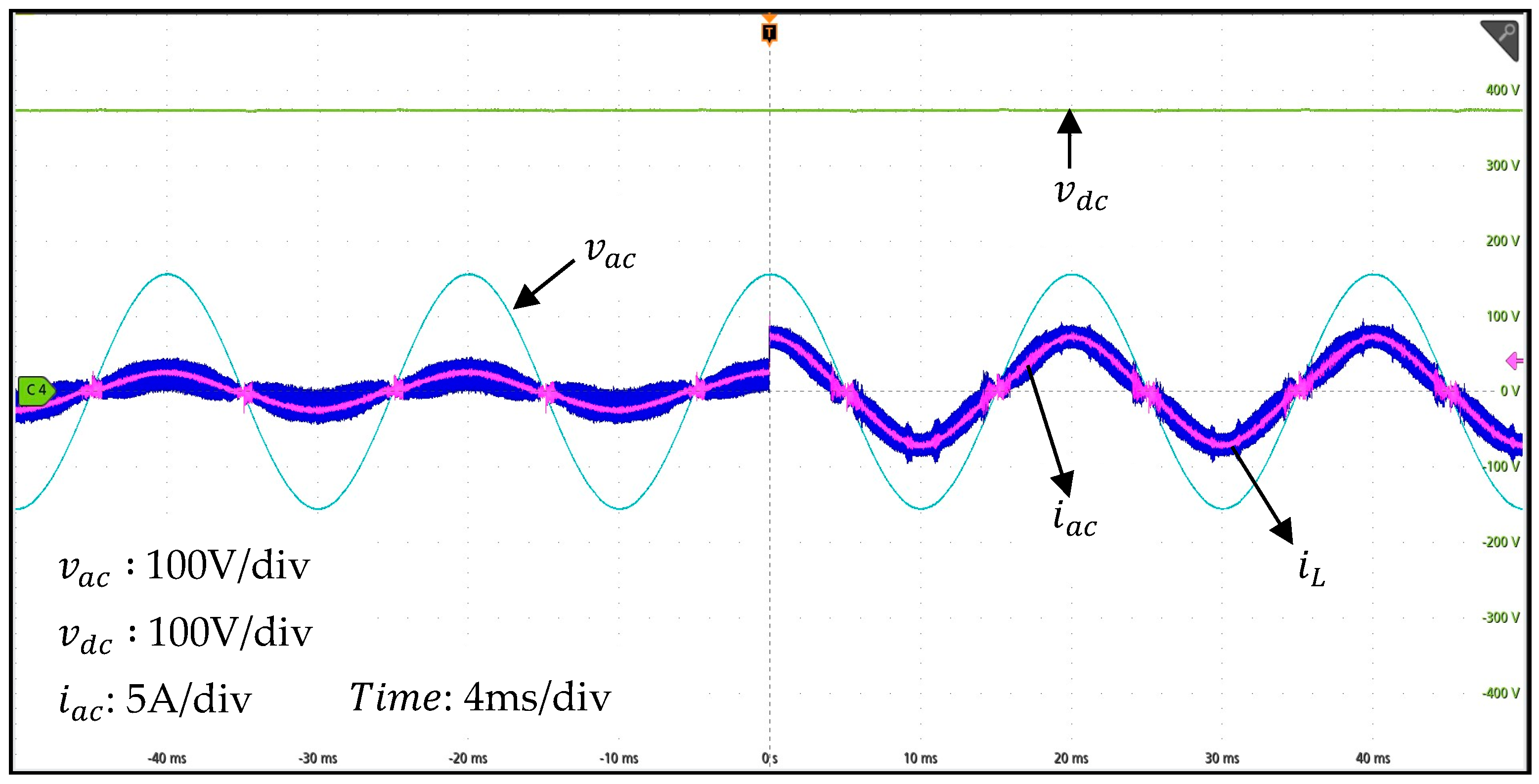
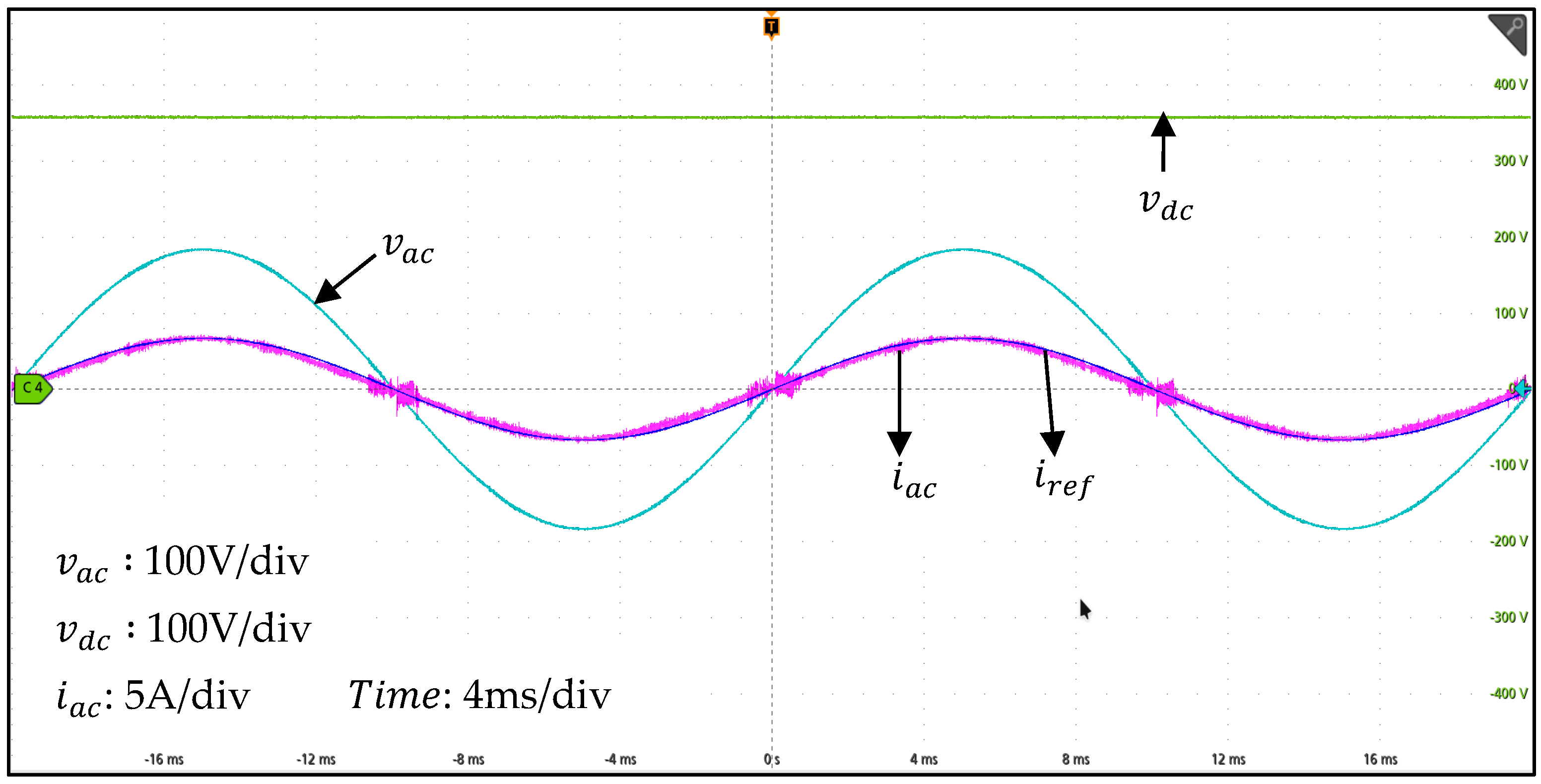
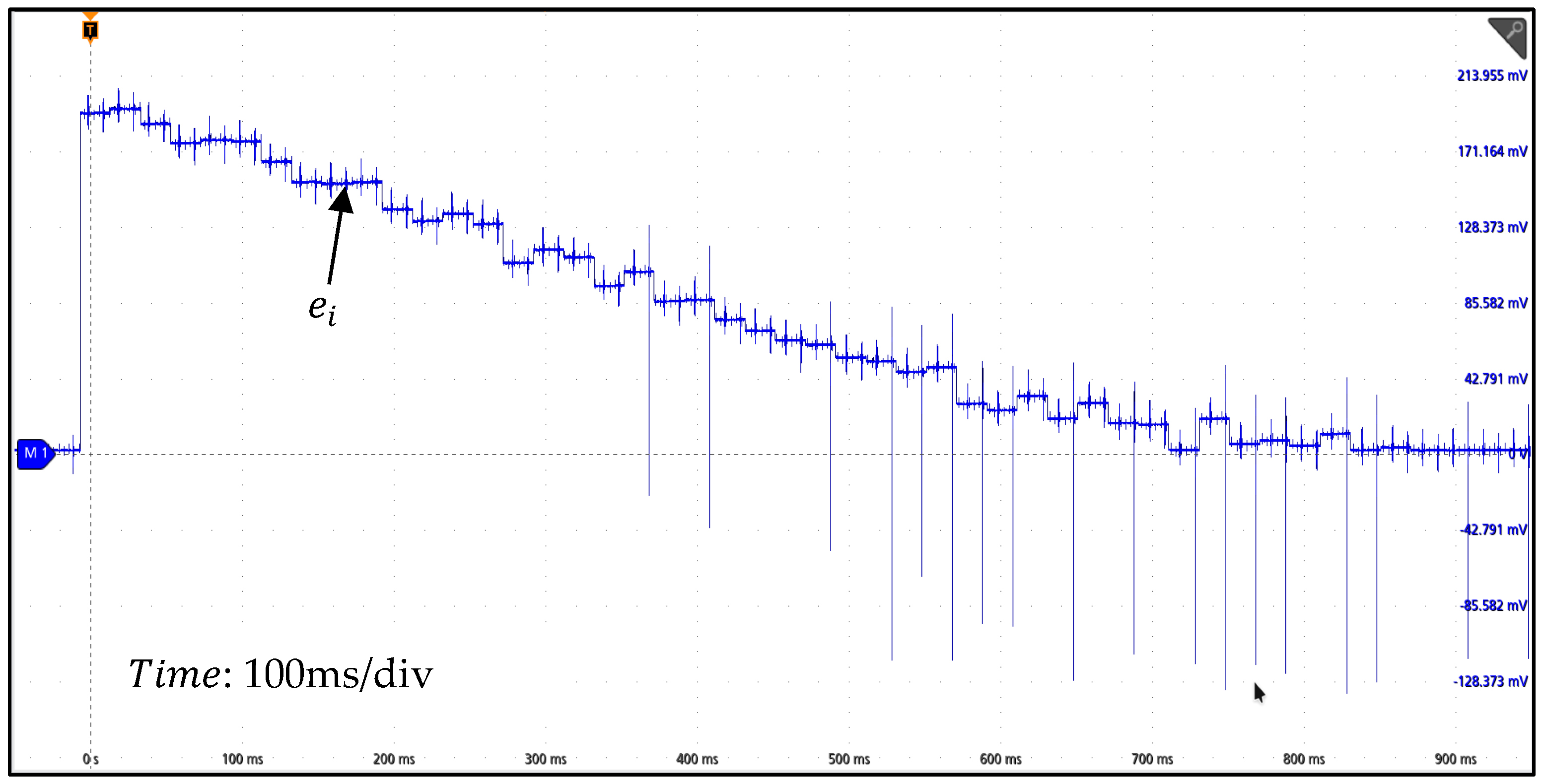
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEC 61000-3-2; Limits for Harmonic Current Emissions (Equipment Input Current <16 A per Phase). International Standard Organization: Geneva, Switzerland, 2001. Available online: https://webstore.iec.ch/en/publication/18726 (accessed on 5 October 2024).
- 80 PLUS Program. Available online: http://www.80plus.org/ (accessed on 20 December 2023).
- Environmental Protection Agency (EPA) Energy Star Program, Version 5.0 Computer Specifications. Available online: http://www.energystar.gov/ (accessed on 8 February 2023).
- Van de Sype, D.M.; De Gusseme, K.; Van den Bossche, A.P.; Melkebeek, J.A.A. A sampling algorithm for digitally controlled boost PFC converters. IEEE Trans. Power Electron. 2004, 19, 649–657. [Google Scholar] [CrossRef]
- Van de Sype, D.M.; De Gusseme, K.; Van den Bossche, A.P.; Melkebeek, J.A.A. Duty-Ratio Feedforward for Digitally Controlled Boost PFC Converters. IEEE Trans. Ind. Electron. 2005, 52, 108–115. [Google Scholar] [CrossRef]
- Ye, Z.Z.; Jovanovic, M.M. Implementation and Performance Evaluation of DSP-Based Control for Constant-Frequency Discontinuous-Conduction-Mode Boost PFC Front End. IEEE Trans. Ind. Electron. 2005, 52, 98–107. [Google Scholar] [CrossRef]
- Shin, J.W.; Cho, B.H. Digitally Implemented Average Current-Mode Control in Discontinuous Conduction Mode PFC Rectifier. IEEE Trans. Power Electron. 2012, 27, 3363–3373. [Google Scholar] [CrossRef]
- Hwu, K.I.; Chen, H.W.; Yau, Y.T. Fully Digitalized Implementation of PFC Rectifier in CCM Without ADC. IEEE Trans. Power Electron. 2012, 27, 4021–4029. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, G.; Lui, Y.F.; Wu, B. A Digital Power Factor Correction Control Strategy Optimized for DSP. IEEE Trans. Power Electron. 2004, 19, 1474–1485. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, G.; Lui, Y.F.; Wu, B. A New Duty Cycle Control Strategy for Power Factor Correction and FPGA Implementation. IEEE Trans. Power Electron. 2006, 21, 1745–1753. [Google Scholar] [CrossRef]
- Gusseme, K.; Van de Sype, D.M.; Van den Bossche, A.P.M.; Melkebeek, J.A. Digitally Controlled Boost Power-Factor-Correction Converters Operating in Both Continuous and Discontinuous Conduction Mode. IEEE Trans. Ind. Electron. 2005, 52, 88–97. [Google Scholar] [CrossRef]
- Chen, J.; Prodic, A.; Erickson, R.W.; Maksimovic, D. Predictive Digital Current Programmed Control. IEEE Trans. Power Electron. 2003, 18, 411–419. [Google Scholar] [CrossRef]
- Gusseme, K.; Van de Sype, D.M.; Van den Bossche, A.P.M.; Melkebeek, J.A. Input-Current Distortion of CCM Boost PFC Converters Operated in DCM. IEEE Trans. Ind. Electron. 2007, 54, 858–865. [Google Scholar] [CrossRef]
- Chen, M.; Mathew, A.; Sun, J. Nonlinear Current Control of Single-Phase PFC Converters. IEEE Trans. Power Electron. 2007, 22, 2187–2194. [Google Scholar] [CrossRef]
- Yao, K.; Ruan, X.; Mao, X.; Ye, Z. Variable-Duty-Cycle to Achive High Input Power Factor for DCM Boost PFC Converter. IEEE Trans. Ind. Electron. 2011, 58, 1856–1865. [Google Scholar] [CrossRef]
- Lim, S.F.; Khambadkone, A.M. A Simple Digital DCM Control Scheme for Boost PFC Operating in Both CCM and DCM. IEEE Trans. Ind. Appl. 2011, 47, 1802–1812. [Google Scholar] [CrossRef]
- Clark, C.W.; Musavi, F.; Eberle, W. Digital DCM Detection and Mixed Conduction Mode Control for Boost PFC Converters. IEEE Trans. Power Electron. 2014, 29, 347–355. [Google Scholar] [CrossRef]
- Park, J.; Kim, D.J.; Lee, K. Predictive Control Algorithm Including Conduction-Mode Detection for PFC Converter. IEEE Trans. Ind. Electron. 2016, 63, 5900–5911. [Google Scholar] [CrossRef]
- Chen, F.; Maksimovic, D. Digital Control for Improved Efficiency and Reduced Harmonic Distortion Over Wide Load Range in Boost PFC Rectifiers. IEEE Trans. Power Electron. 2010, 25, 2683–2692. [Google Scholar] [CrossRef]
- Luo, H.; Xu, J.; Luo, Y.; Sha, J. A Digital Pulse Train Controlled High Power Factor DCM Boost PFC Converter Over a Universal Input Voltage Range. IEEE Trans. Ind. Electron. 2019, 66, 2814–2824. [Google Scholar] [CrossRef]
- Choi, Y.; Kim, T.; Kim, R. An Active Partial Switching Method in Tertiary Loop for a High-Efficiency Predictive Current-Mode Control PFC Converter. IEEE Trans. Ind. Electron. 2018, 65, 7818–7828. [Google Scholar] [CrossRef]
- Luo, H.; Xu, J.; He, D.; Sha, J. Pulse Train Control Strategy for CCM Boost PFC Converter with Improved Dynamic Response and Unity Power Factor. IEEE Trans. Ind. Electron. 2020, 6, 10377–10387. [Google Scholar] [CrossRef]
- Moon, S.; Corradini, L.; Maksimovic, D. Autotuning of digitally Controlled Boost Power Factor Correction Rectifiers. IEEE Trans. Power Electron. 2011, 26, 3006–3018. [Google Scholar] [CrossRef]
- Li, S.; Lu, W.; Yan, S.; Zhao, Z. Improving Dynamic Performance of Boost PFC Converter Using Current-Harmonic Feedforward Compensation in Synchronous Reference Frame. IEEE Trans. Ind. Electron. 2020, 67, 4857–4866. [Google Scholar] [CrossRef]
- Nair, H.S.; Lakshminarasamma, N. An Improved Digital Algorithm for Boost PFC Converter Operating in Mixed Conduction Mode. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 4235–4245. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q.; Min, R.; Liu, K.; Tong, Q.; Lyu, D. A Current Reshaping Strategy to reduce Parasitics-Induced Current Distortion in Discontinuous Conduction Mode Boost Power Factor Correction Converter. IEEE Trans. Ind. Electron. 2021, 68, 2215–2224. [Google Scholar] [CrossRef]
- Bi, Y.; Zhao, T.; Li, H.; Xu, J.; Shu, G.; Wang, Y. Modified Deadbeat PRedictive Current Control Method for Single-Phase AC-DC PFC Converter in EV Charging System. IEEE Trans. Ind. Electron. 2023, 70, 286–297. [Google Scholar] [CrossRef]
- Lu, W.; Li, S.; Chen, W. Current-Ripple Compensation Control Technique for Switching Power Converters. IEEE Trans. Ind. Electron. 2018, 65, 4197–4206. [Google Scholar] [CrossRef]
- Wang, W.; Tzou, Y. Using Repetitive Control for Light Load THD and Efficiency Improvement for Boost Digital PFC Converters. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012. [Google Scholar]
- Cho, Y.; Lai, J. Digital Plug-In Repetitive Controller for Single-Phase Bridgeless PFC Converters. IEEE Trans. Power Electron. 2013, 28, 165–175. [Google Scholar]
- Ali, M.S.; Wang, L.; Alquhayz, H.; Ur Rehman, O.; Chen, G. Performance Improvement of Three-Phase Boost Power Factor Correction Rectifier Through Combined Parameters Optimization of Proportional-Integral and Repetitive Controller. IEEE Access 2021, 9, 58893–58909. [Google Scholar] [CrossRef]
- Nair, H.; Lakshminarasamma, N. A Computationally Simple Predictive CCM Average Current Controller with Nearly Zero Tracking Error for Boost PFC Converter. IEEE Trans. Ind. Appl. 2020, 56, 5083–5094. [Google Scholar] [CrossRef]
- Youn, H.; Park, J.; Park, K.; Baek, J.; Moon, G. A Digital Predictive Peak Current Control for Power Factor Correction with Low-Input Current Distortion. IEEE Trans. Power. Electron. 2016, 31, 900–912. [Google Scholar] [CrossRef]
- Fernandes, R.; Trescases, O. A Multimode 1-MHz PFC Front End with Digital Peak Current Modulation. IEEE Trans. Power. Electron. 2016, 31, 5694–5708. [Google Scholar] [CrossRef]
- Chandwani, A.; Dey, S.; Mallik, A. Parameter-Variation-Tolerant Robust Current Sensorless Control of a Single-Phase Boost PFC. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 3, 933–945. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Zaman, S.; Cao, R.; Gao, X.; Cao, M. Precise Correction of Current Zero-Crossing Distortion of Totem Pole PFC Converter. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference, Nanjing, China, 29 November–2 December 2020. [Google Scholar]
- Roman, R.C.; Precup, R.E.; Hedrea, E.L.; Preitl, S.; Zamfirache, I.A.; Bojan-Dragos, C.A.; Petriu, E.M. Iterative Feedback Tuning Algorithm for Tower Crane Systems. In Proceedings of the 8th International Conference on Information Technology and Quantitative Management, Chengdu, China, 9–11 July 2021. [Google Scholar]
- Radac, M.B.; Precup, R.E. Data-driven model-free slip control of anti-lock braking systems using reinforcement Q-learning. Neurocomputing 2018, 275, 317–329. [Google Scholar] [CrossRef]
- Zamfirache, I.A.; Precup, R.E.; Petriu, E.M. Q-Learning, Policy Iteration and Actor-Critic Reinforcement Learning Combined with Metaheuristic Algorithms in Servo System Control. Facta Univ. Ser. Mech. Eng. 2023, 21, 615–630. [Google Scholar] [CrossRef]
- Killingsworth, N.J.; Krstic, M. PID tuning using extremum seeking: Online, model-free performance optimization. IEEE Control Syst. Mag. 2006, 26, 70–79. [Google Scholar]
- Kim, J.H.; Park, J.H.; Lee, S.W.; Cheng, E.K.P. A two layered fuzzy logic controller for systems with deadzones. IEEE Trans. Ind. Electron. 1994, 41, 155–162. [Google Scholar]
- Lewis, F.L.; Liu, K.; Selmić, R.R.; Wang, L.X. Adaptive fuzzy logic compensation of actuator deadzones. J. Robot. Syst. 1997, 14, 501–512. [Google Scholar] [CrossRef]
- O’Donovan, J.G.; Roche, P.J.; Kavanagh, R.C.; Egan, M.G.; Murphy, J.M.G. Neural network based torque ripple minimisation in a switched reluctance motor. In Proceedings of the IECON’94: 20th International Conference on Industrial Electronics, Control, and Instrumentation, Bologna, Italy, 5–9 September 1994. [Google Scholar]
- Xu, J.X.; Panda, S.K.; Pan, Y.J.; Lee, T.H.; Lam, B.H. A modular control scheme for PMSM speed control with pulsating torque minimization. IEEE Trans. Ind. Electron. 2004, 51, 526–536. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Panda, S.K.; Xu, J.X. Indirect torque control of switched reluctance motors using iterative learning control. IEEE Trans. Power Electron. 2005, 20, 200–208. [Google Scholar] [CrossRef]
- Deng, H.; Oruganti, R.; Srinivasan, D. Analysis and Design of Iterative Learning Control Strategies for UPS Inverters. IEEE Trans. Ind. Electron. 2007, 54, 1739–1751. [Google Scholar] [CrossRef]
- Xu, J.X.; Panda, S.K.; Lee, T.H. Real Time Iterative Learning Control, 1st ed.; Springer: London, UK, 2009; pp. 7–27. [Google Scholar]



| Symbol | Quantity | Value |
|---|---|---|
| vac | Input Voltage | 110 Vac |
| vdc | Output Voltage | 380 Vdc |
| Po | Output Power | 250 W |
| L1, L2 | Boost Inductors | 220 µH |
| fL | Grid Frequency | 50 Hz |
| fs | Switching Frequency | 100 kHz |
| Cdc | Output Capacitor | 940 µF |
| Lf | Filter Inductor | 22 µH |
| Cf | Filter Capacitor | 1.5 µF |
| F | Forgetting Factor | 0.99 |
| L | Learning Gain | 0.01 |
| Current Controller | Affected by Changes in Parameters | Tracking Error | Requirement of Controller Design | Complexity | Dynamic Response | Computational Burden |
|---|---|---|---|---|---|---|
| PI controller [6] | Yes | Large | Yes | Simple | Low | Low |
| Ideal Predictive Controller [10,12,18] | Yes | Large | No | Simple | Medium | Medium |
| Predictive Current Controller with PI Feedback action [19] | Minimal | Small | Yes | Simple | Low | Medium |
| Predictive Average Mode Current Controller [32] | Minimal | Very Small | No | Simple | Very High | Low |
| Predictive Peak Current Mode Controller [33] | Minimal | Small | No | Hard | Medium | High |
| Proposed Current Controller | No | Very Small | No | Simple | Very High | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dudak, A.T.; Bakan, A.F. A Digital Iterative Learning Based Peak Current Mode Control for Interleaved Totem Pole PFC Circuit. Energies 2024, 17, 5026. https://doi.org/10.3390/en17205026
Dudak AT, Bakan AF. A Digital Iterative Learning Based Peak Current Mode Control for Interleaved Totem Pole PFC Circuit. Energies. 2024; 17(20):5026. https://doi.org/10.3390/en17205026
Chicago/Turabian StyleDudak, Ahmet Talha, and Ahmet Faruk Bakan. 2024. "A Digital Iterative Learning Based Peak Current Mode Control for Interleaved Totem Pole PFC Circuit" Energies 17, no. 20: 5026. https://doi.org/10.3390/en17205026
APA StyleDudak, A. T., & Bakan, A. F. (2024). A Digital Iterative Learning Based Peak Current Mode Control for Interleaved Totem Pole PFC Circuit. Energies, 17(20), 5026. https://doi.org/10.3390/en17205026







