The Early Detection of Faults for Lithium-Ion Batteries in Energy Storage Systems Using Independent Component Analysis with Mahalanobis Distance
Abstract
1. Introduction
1.1. A Brief Review of Fault Detection Approaches for LIBs
1.2. Preliminary
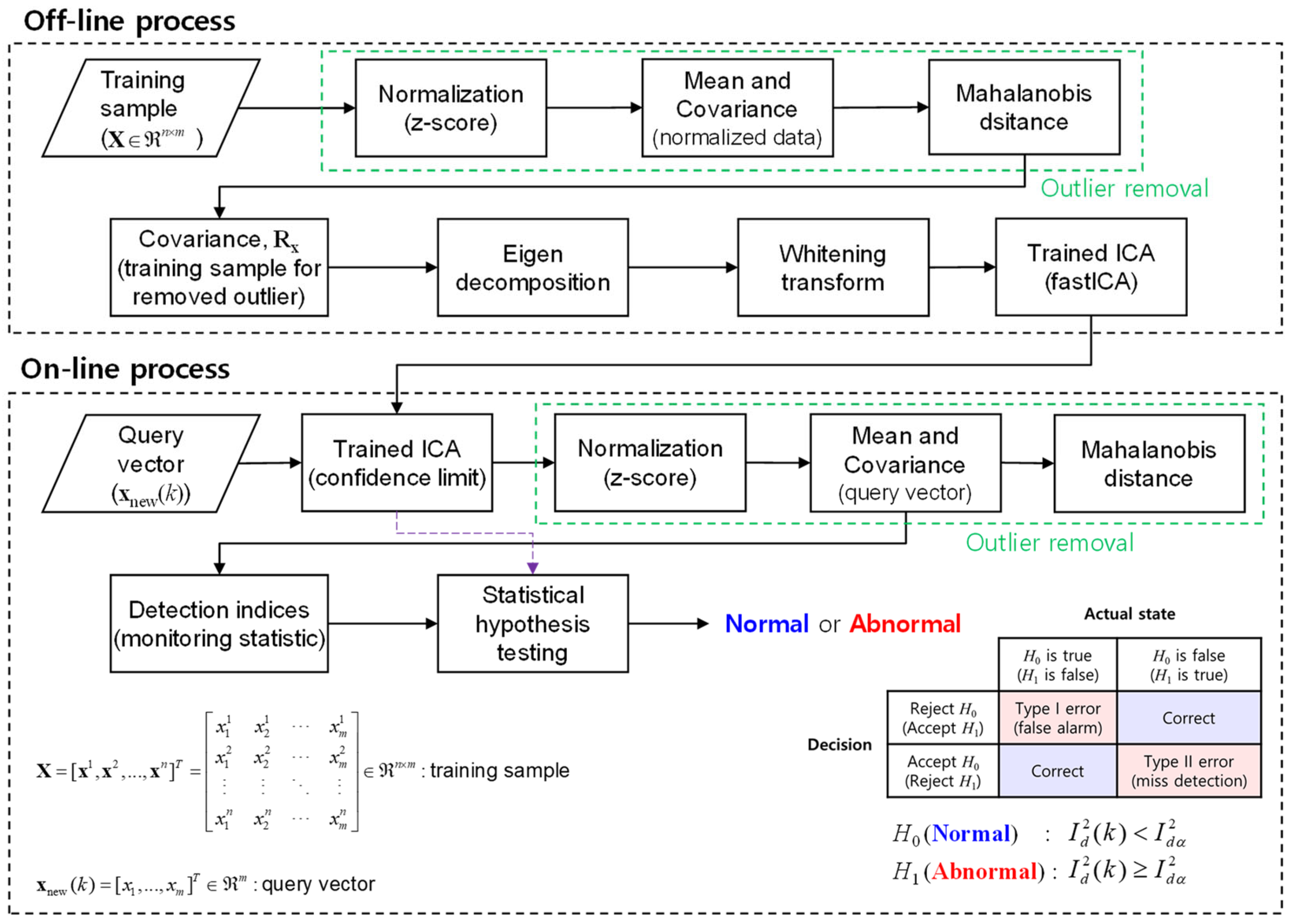
2. The Fault Detection of LIBs in an ESS Using MD and ICA
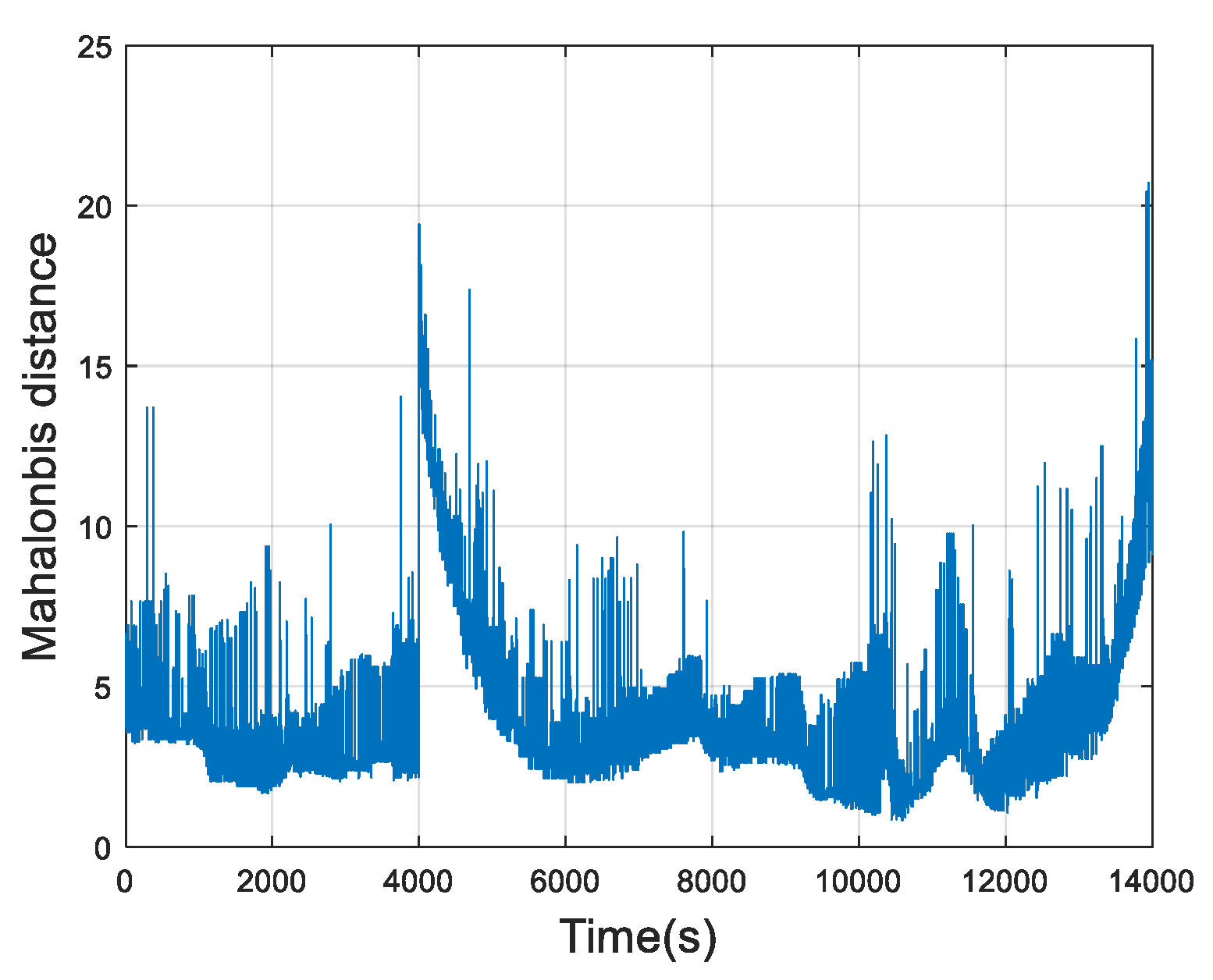
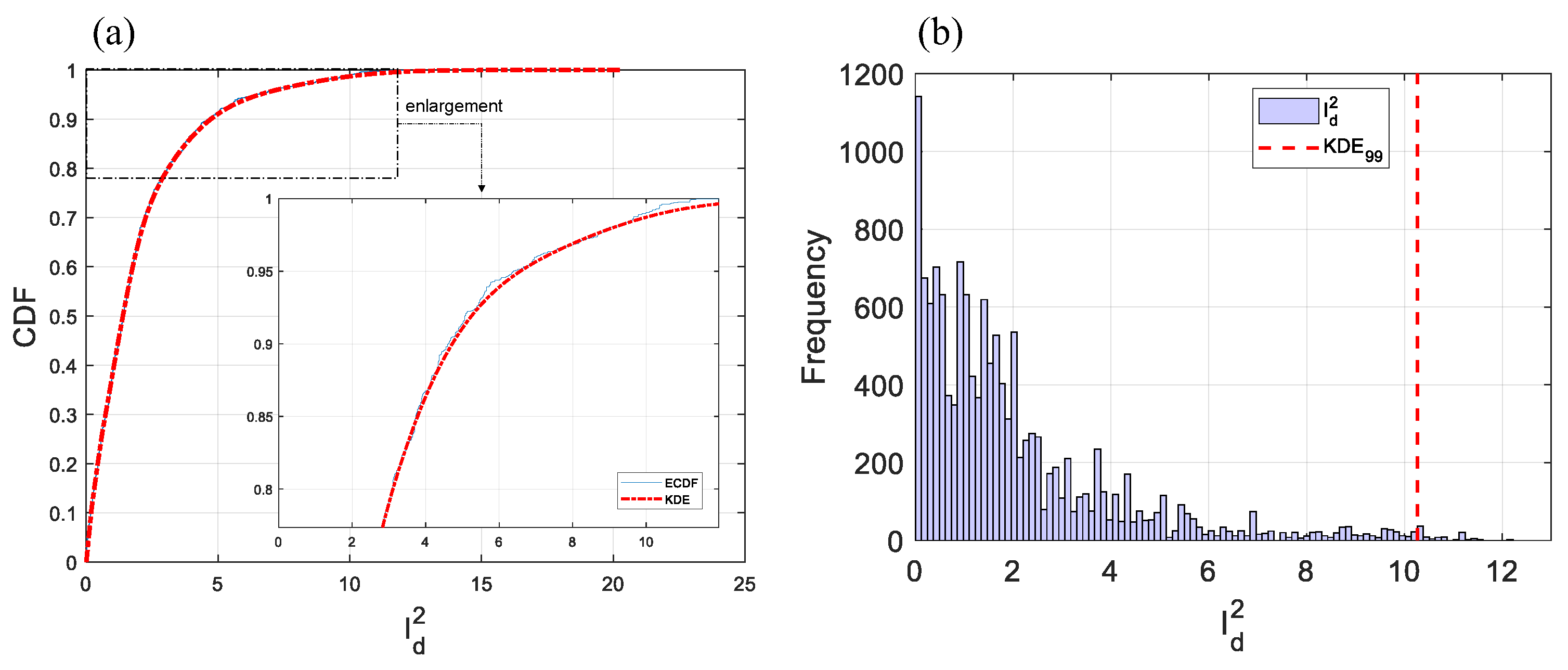
2.1. Outlier Removal Using Mahlanobis Distance
2.2. Fault Detection Based on ICA
2.2.1. ICA Algorithm
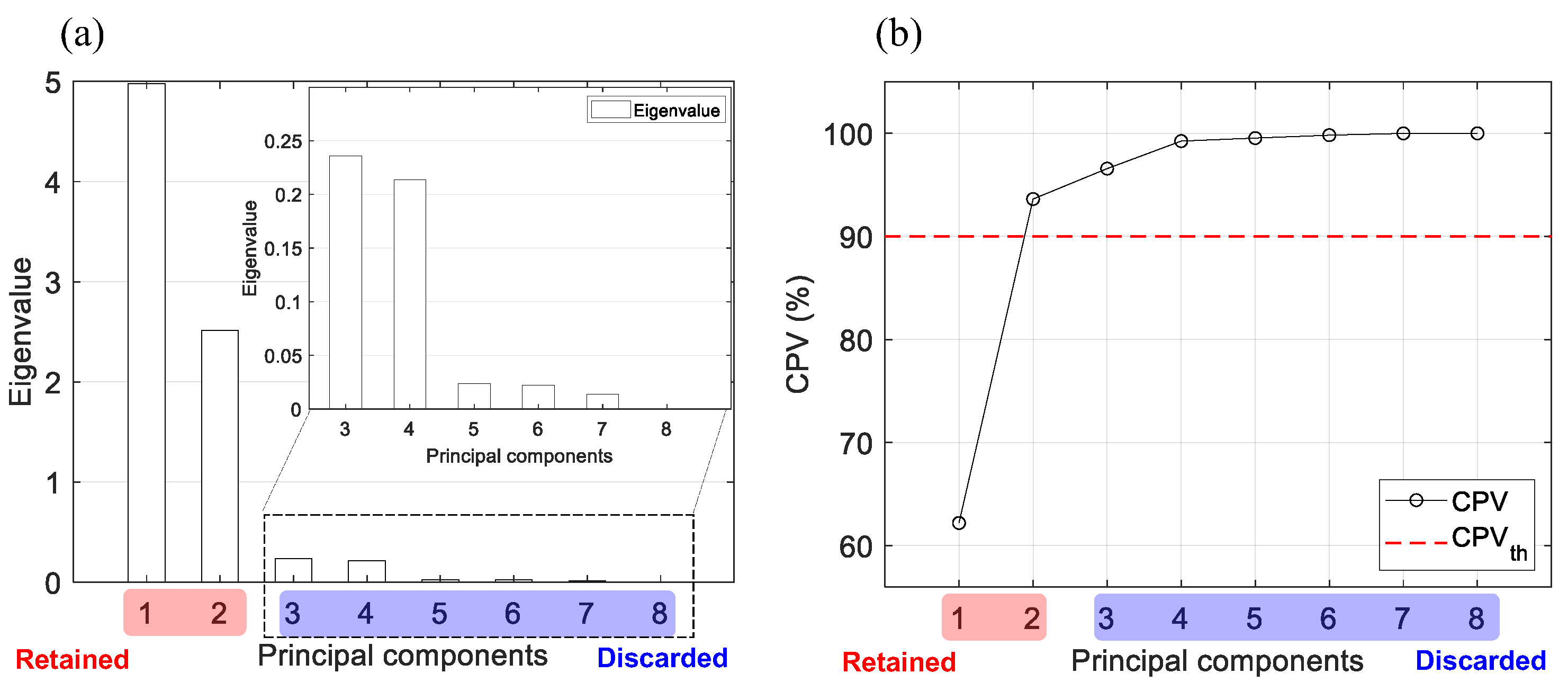
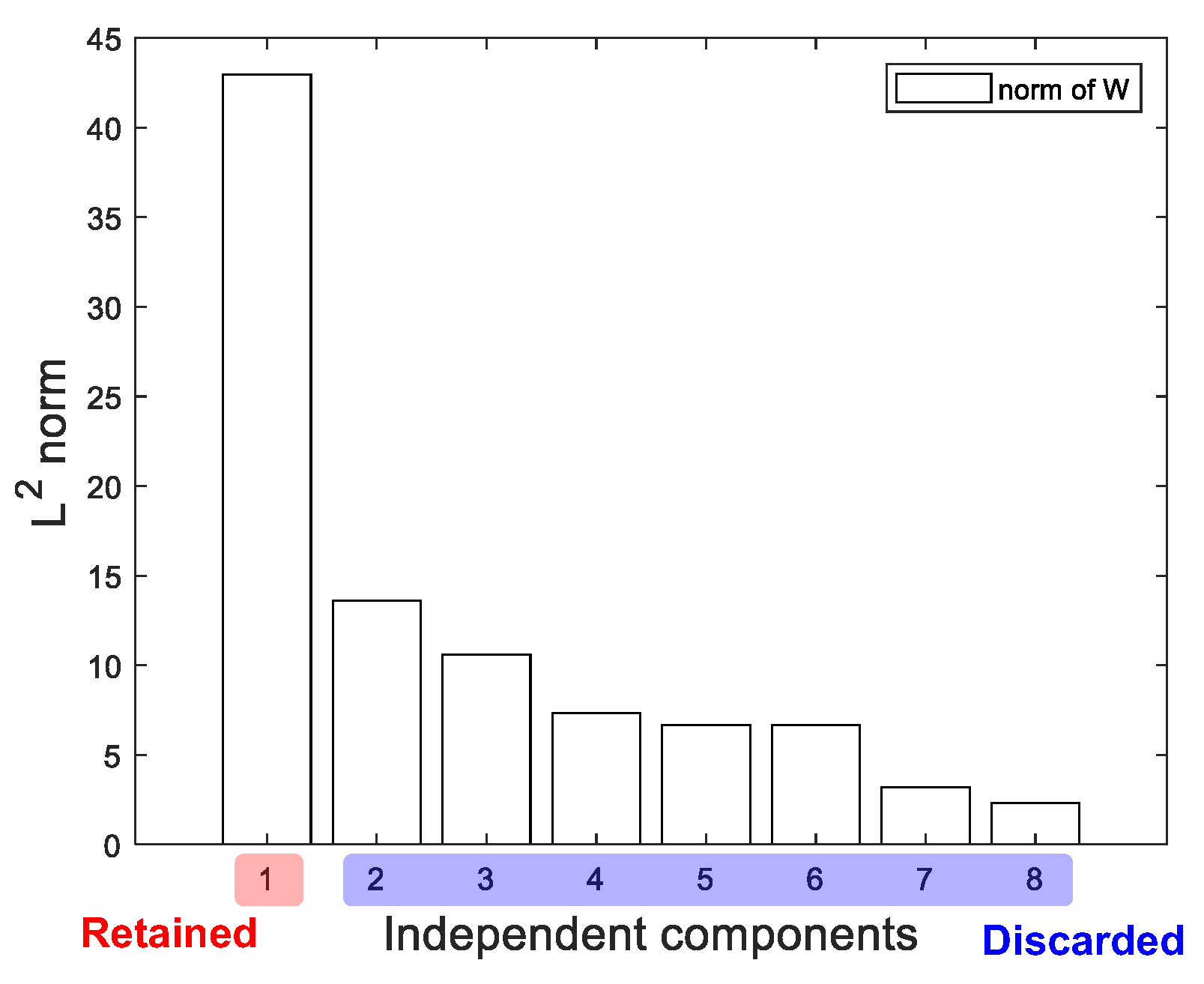
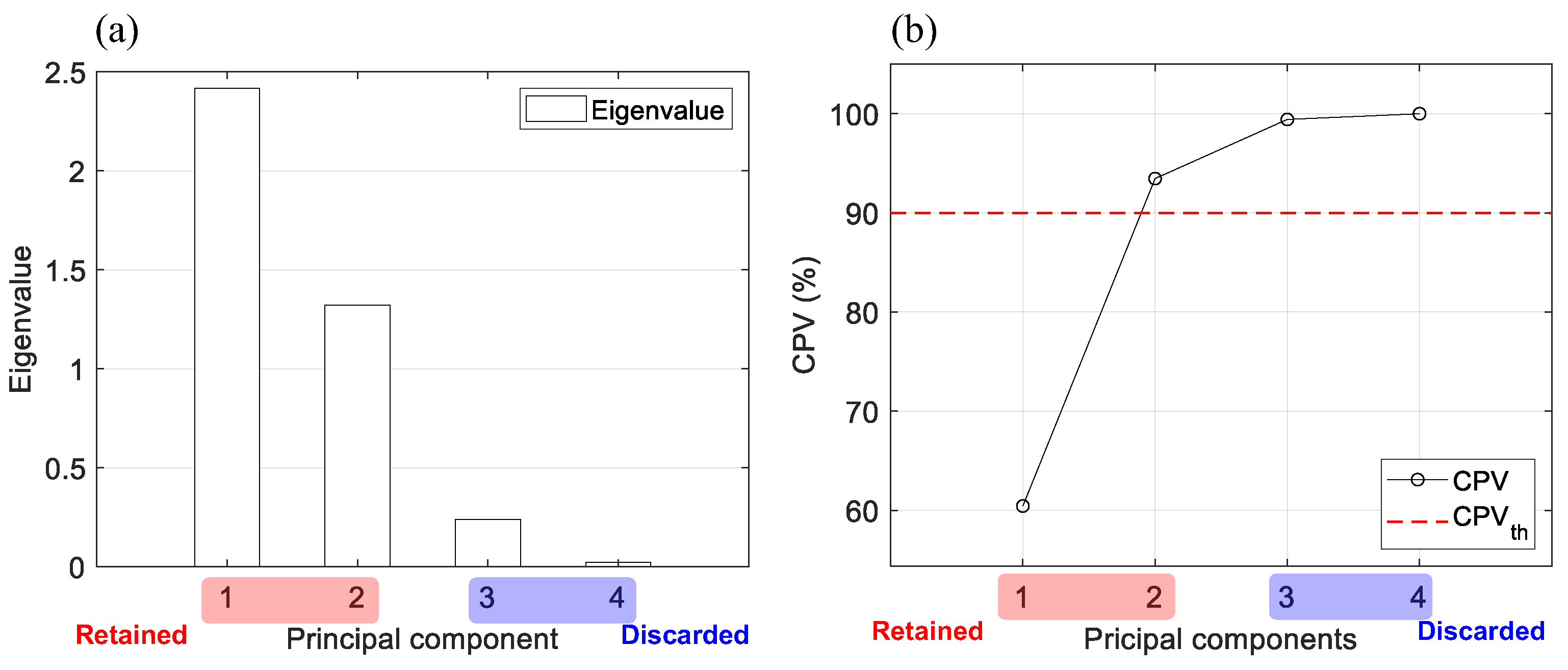
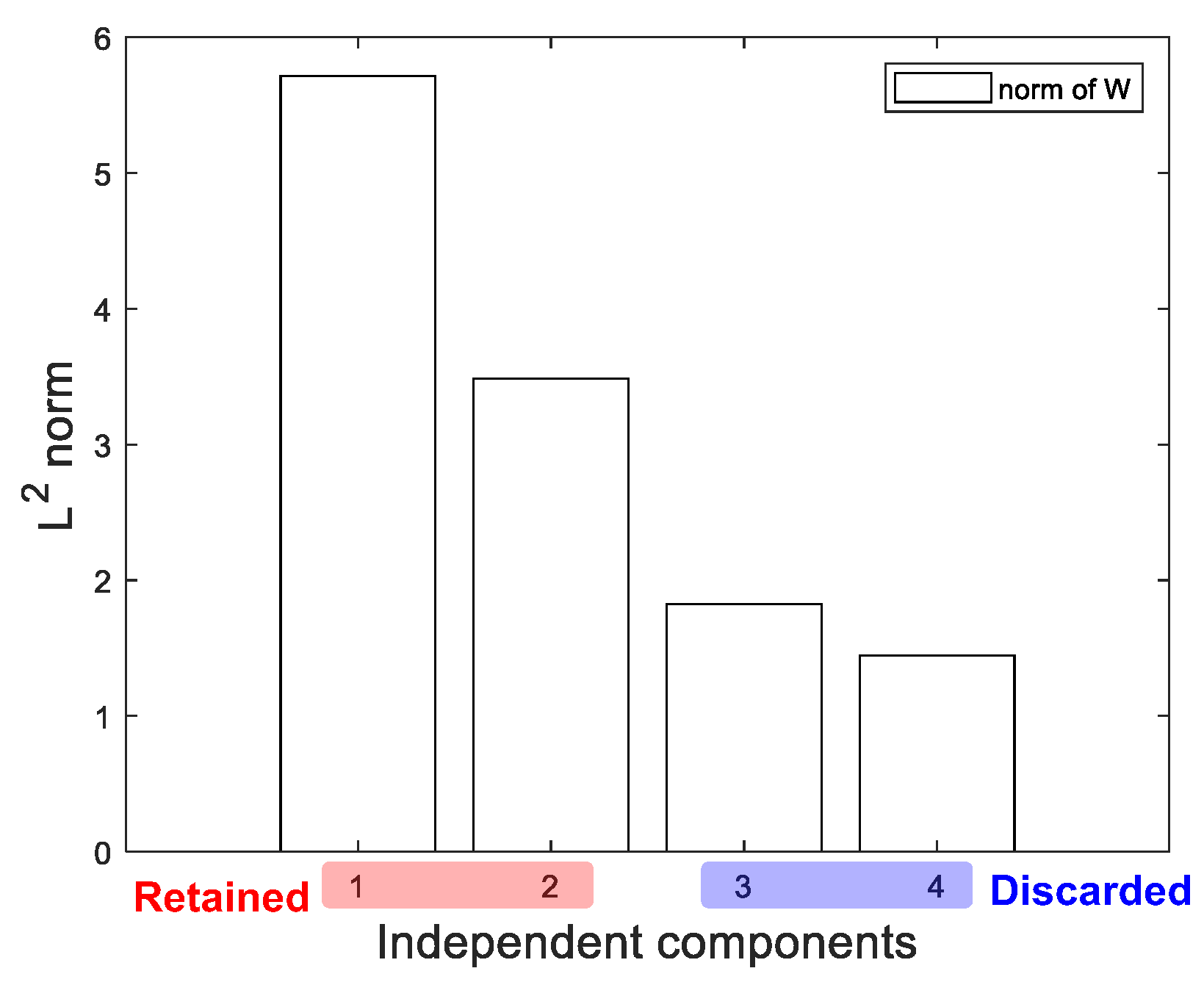
2.2.2. Determine the Number of ICs
2.2.3. Detection Indices
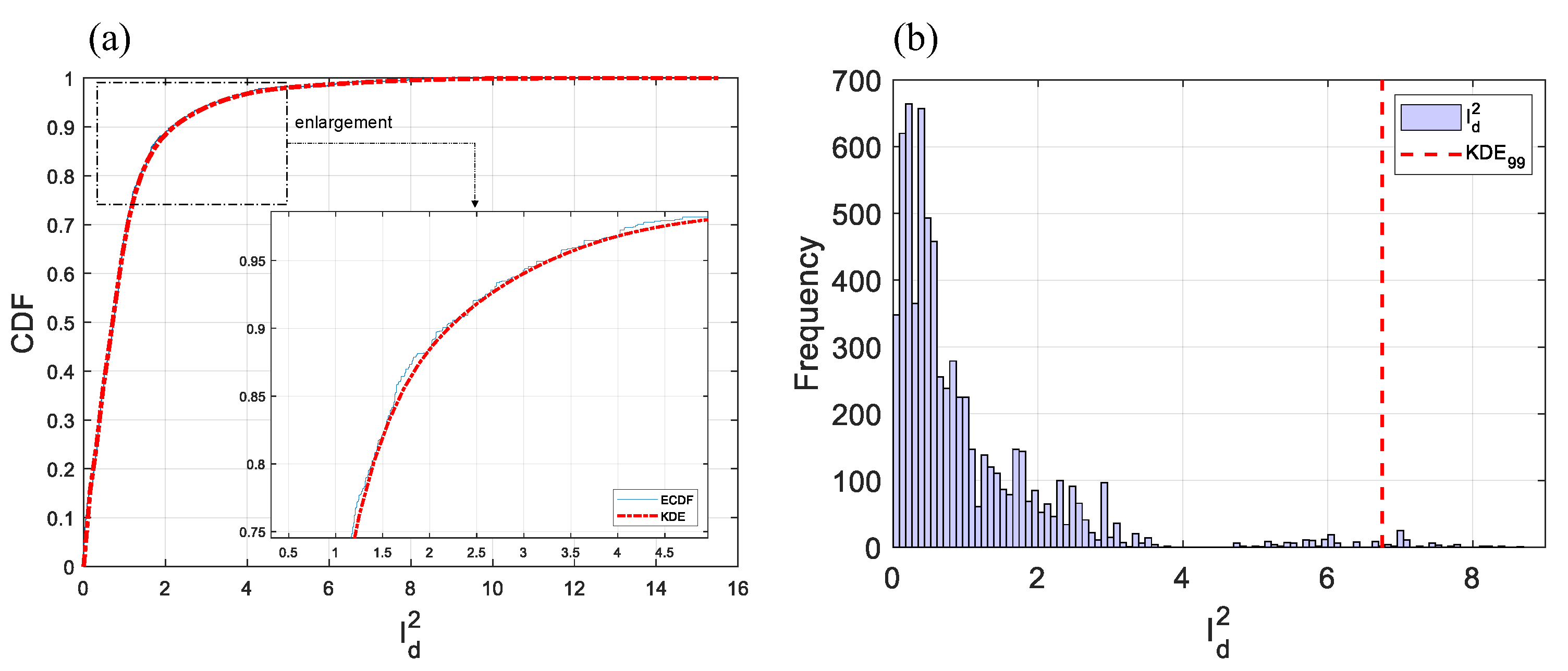
2.2.4. Confidence Limits
2.3. Performance Indices
3. Data Acquisition
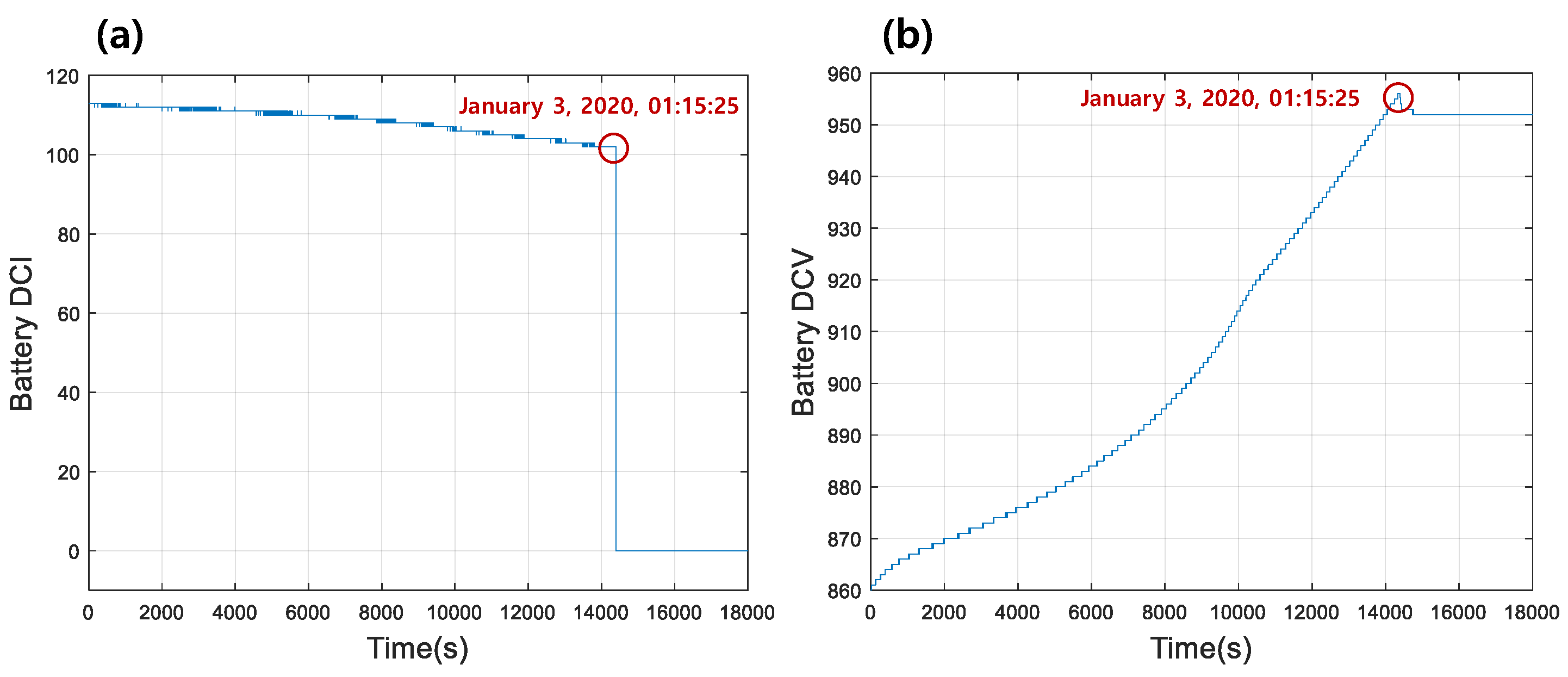
3.1. Fault Alarm 1: Battery Overvoltage
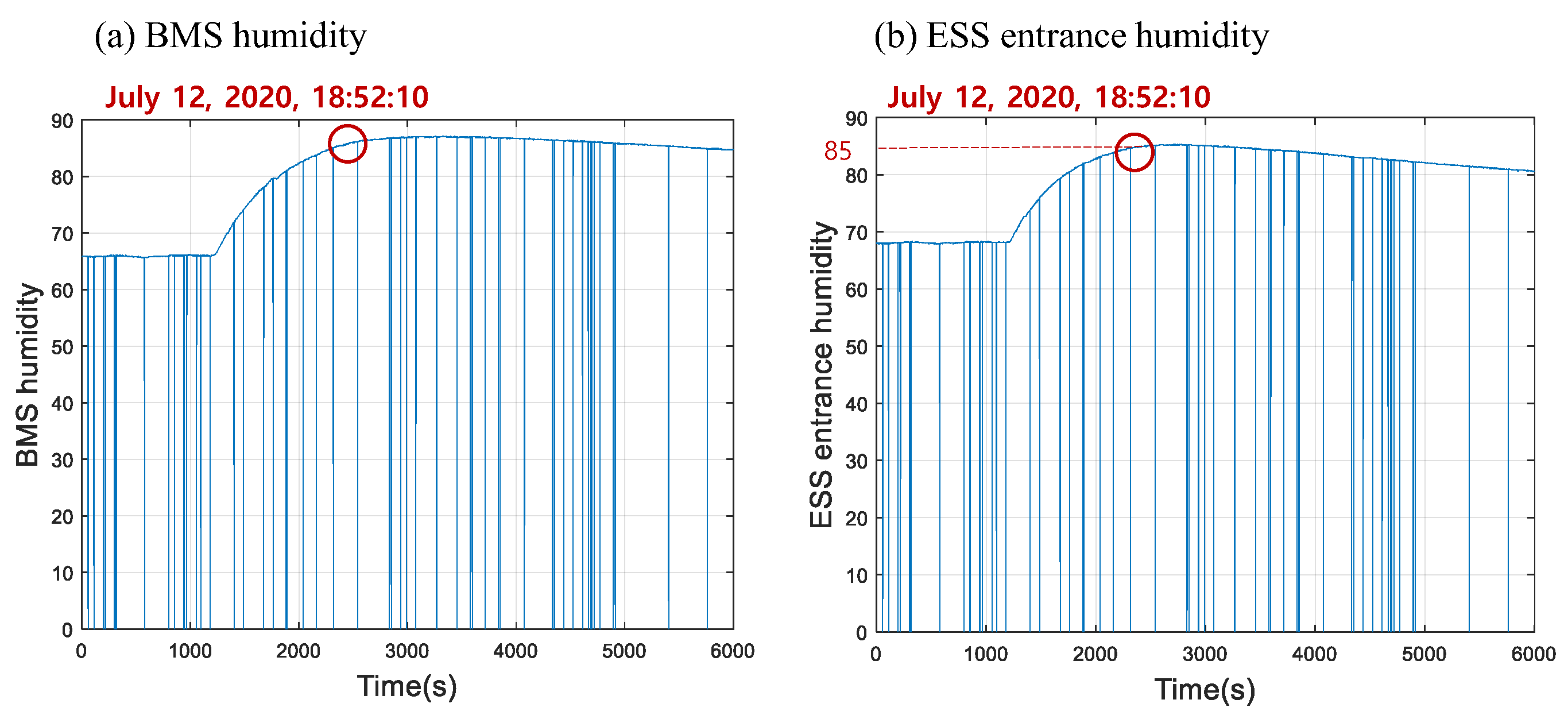
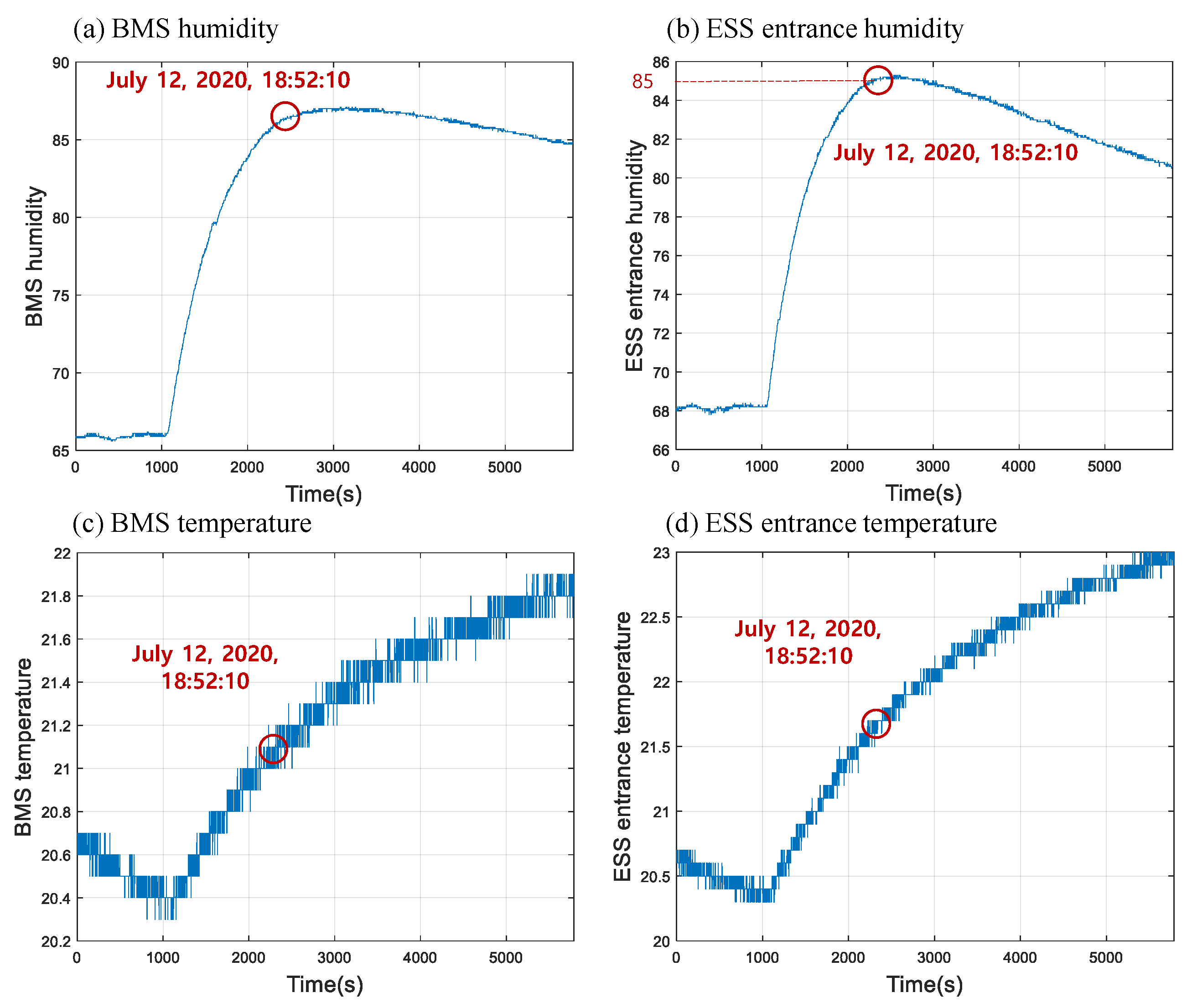
3.2. Fault Alarm 2: Humidity Anomaly
4. Experimental Results and Discussion
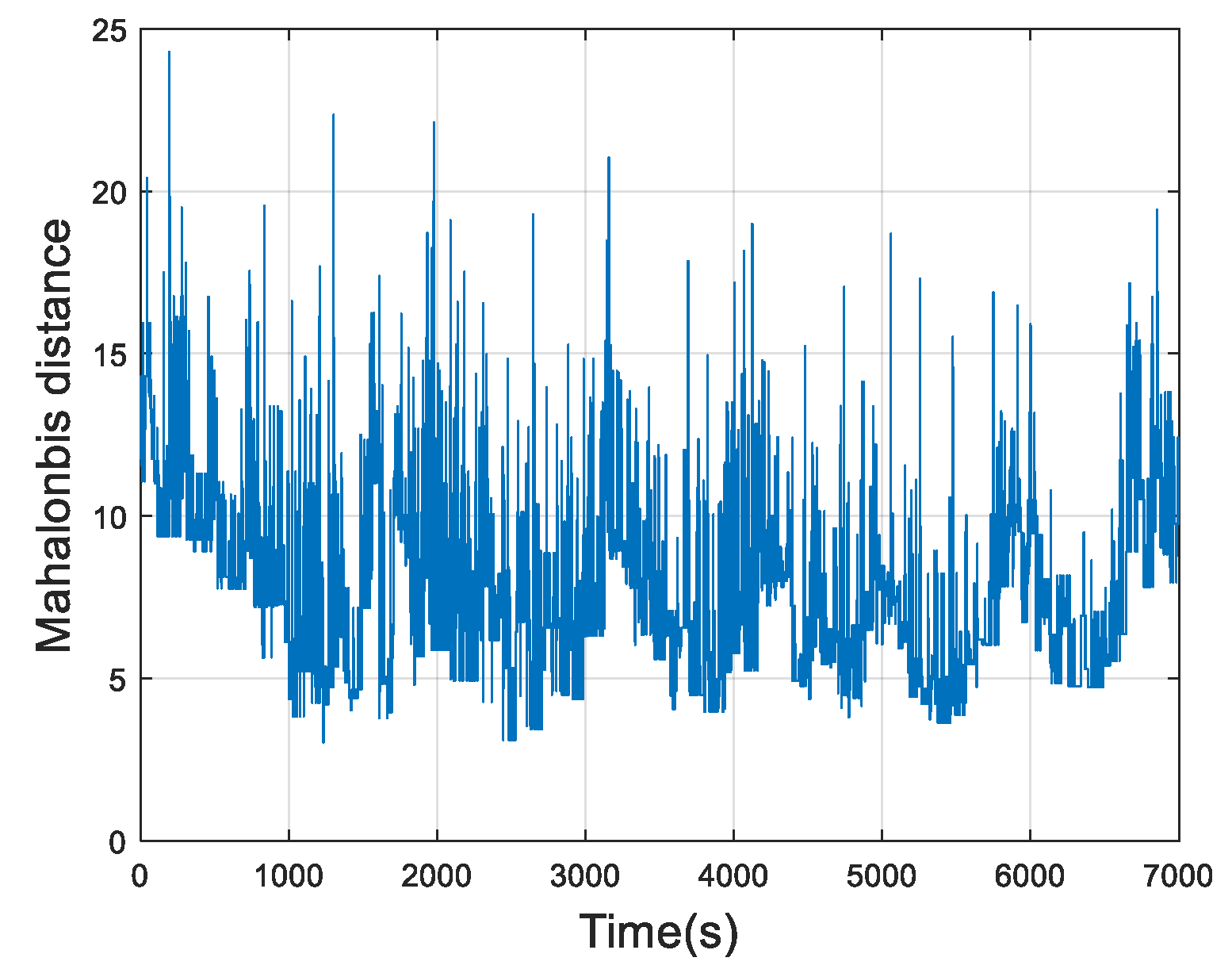
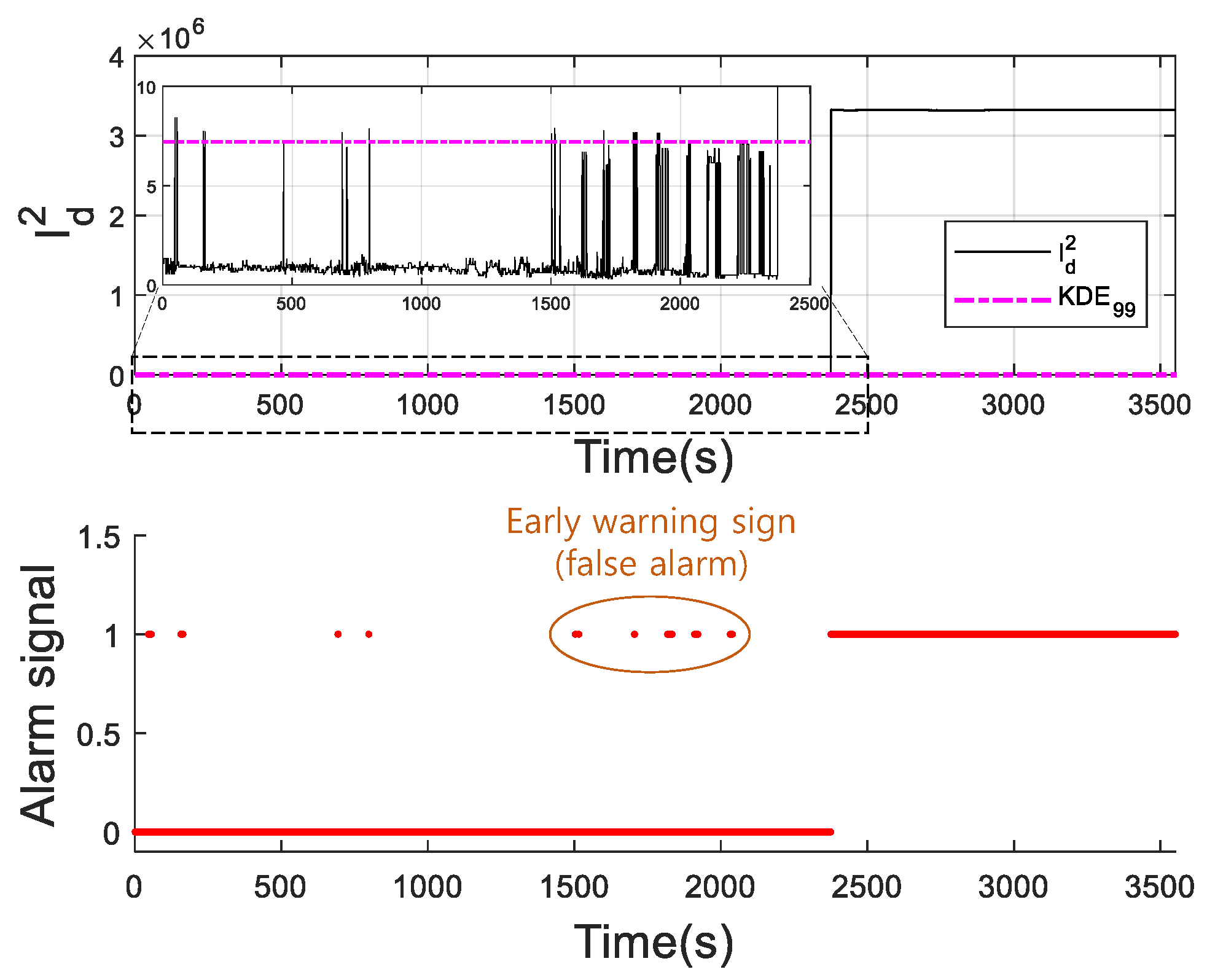
4.1. Battery Overvoltage Alarm
4.2. Humidity Anomaly
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nasiri, F.; Ooka, R.; Haghighat, F.; Shirzadi, N.; Dotoli, M.; Carli, R.; Scarabaggio, P.; Behzadi, A.; Rahnama, S.; Afshari, A.; et al. Data analytics and information technologies for smart energy storage systems: A state-of-the-art review. Sustain. Cities Soc. 2022, 84, 104004. [Google Scholar] [CrossRef]
- Rahman, F.; Rehman, S.; Abdul-Majeed, M.A. Overview of energy storage systems for storing electricity from renewable energy sources in Saudi Arabia. Renew. Sustain. Energy Rev. 2012, 16, 274–283. [Google Scholar] [CrossRef]
- Evans, A.; Strezov, V.; Evans, T.J. Assessment of utility energy storage options for increased renewable energy penetration. Renew. Sustain. Energy Rev. 2012, 16, 4141–4147. [Google Scholar] [CrossRef]
- Chavan, S.; Rudrapati, R.; Manickam, S. A comprehensive review on current advances of thermal energy storage and its applications. Alex. Eng. J. 2022, 61, 5455–5463. [Google Scholar] [CrossRef]
- Selvakumar, R.D.; Wu, J.; Ding, Y.; Alkaabi, A.K. Melting behavior of an organic phase change material in a square thermal energy storage capsule with an array of wire electrodes. Appl. Therm. Eng. 2023, 228, 120492. [Google Scholar] [CrossRef]
- Tran, M.K.; Mevawalla, A.; Aziz, A.; Panchal, S.; Xie, Y.; Fowler, M. A review of lithium-ion battery thermal runaway modeling and diagnosis approaches. Processes 2022, 10, 1192. [Google Scholar] [CrossRef]
- Wang, Q.; Mao, B.; Stoliarov, S.I.; Sun, J. A review of lithium ion battery failure mechanisms and fire prevention strategies. Prog. Energy Combust. Sci. 2019, 73, 95–131. [Google Scholar] [CrossRef]
- Qi, C.; Zhu, Y.; Gao, F.; Yang, K.; Jiao, Q. Mathematical model for thermal behavior of lithium ion battery pack under overcharge. Int. J. Heat Mass Transf. 2018, 124, 552–563. [Google Scholar] [CrossRef]
- Lystianingrum, V.; Hredzak, B.; Agelidis, V.G. Multiple model estimator based detection of abnormal cell overheating in a Li-ion battery string with minimum number of temperature sensors. J. Power Sources 2015, 273, 1171–1181. [Google Scholar] [CrossRef]
- Pan, Y.; Feng, X.; Zhang, M.; Han, X.; Lu, L.; Ouyang, M. Internal short circuit detection for lithium-ion battery pack with parallel-series hybrid connections. J. Clean. Prod. 2020, 255, 120277. [Google Scholar] [CrossRef]
- Dong, G.; Lin, M. Model-based thermal anomaly detection for lithium-ion batteries using multiple-model residual generation. J. Energy Storage 2021, 40, 102740. [Google Scholar] [CrossRef]
- Feng, X.; Pan, Y.; He, X.; Wang, L.; Ouyang, M. Detecting the internal short circuit in large-format lithium-ion battery using model-based fault-diagnosis algorithm. J. Energy Storage 2018, 18, 26–39. [Google Scholar] [CrossRef]
- Tran, M.K.; Panchal, S.; Chauhan, V.; Brahmbhatt, N.; Mevawalla, A.; Fraser, R.; Fowler, M. Python-based scikit-learn machine learning models for thermal and electrical performance prediction of high-capacity lithium-ion battery. Int. J. Energy Res. 2022, 46, 786–794. [Google Scholar] [CrossRef]
- Haider, S.N.; Zhao, Q.; Li, X. Data driven battery anomaly detection based on shape based clustering for the data centers class. J. Energy Storage 2020, 29, 101479. [Google Scholar] [CrossRef]
- Yao, L.; Xiao, Y.; Gong, X.; Hou, J.; Chen, X. A novel intelligent method for fault diagnosis of electric vehicle battery system based on wavelet neural network. J. Power Sources 2020, 453, 227870. [Google Scholar] [CrossRef]
- Tran, M.K.; Fowler, M. A review of lithium-ion battery fault diagnostic algorithms: Current progress and future challenges. Algorithms 2020, 13, 62. [Google Scholar] [CrossRef]
- Ma, M.; Li, X.; Gao, W.; Sun, J.; Wang, Q.; Mi, C. Multi-fault diagnosis for series-connected lithium-ion battery pack with reconstruction-based contribution based on parallel PCA-KPCA. Appl. Energy 2022, 324, 119678. [Google Scholar] [CrossRef]
- Yao, L.; Wang, Z.; Ma, J. Fault detection of the connection of lithium-ion power batteries based on entropy for electric vehicles. J. Power Sources 2015, 293, 548–561. [Google Scholar] [CrossRef]
- Xiong, J.; Banvait, H.; Li, L.; Chen, Y.; Xie, J.; Liu, Y.; Wu, M.; Chen, J. Failure detection for over-discharged Li-ion batteries. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–5. [Google Scholar]
- Kang, Y.; Duan, B.; Zhou, Z.; Shang, Y.; Zhang, C. A multi-fault diagnostic method based on an interleaved voltage measurement topology for series connected battery packs. J. Power Sources 2019, 417, 132–144. [Google Scholar] [CrossRef]
- Ma, M.; Wang, Y.; Duan, Q.; Wu, T.; Sun, J.; Wang, Q. Fault detection of the connection of lithium-ion power batteries in series for electric vehicles based on statistical analysis. Energy 2018, 164, 745–756. [Google Scholar] [CrossRef]
- Gajjar, S.; Palazoglu, A. A data-driven multidimensional visualization technique for process fault detection and diagnosis. Chemom. Intell. Lab. Syst. 2016, 154, 122–136. [Google Scholar] [CrossRef]
- Sun, X.; Marquez, H.J.; Chen, T.; Riaz, M. An improved PCA method with application to boiler leak detection. ISA Trans. 2005, 44, 379–397. [Google Scholar] [CrossRef] [PubMed]
- Dong, G.; Wei, J.; Zhang, C.; Chen, Z. Online state of charge estimation and open circuit voltage hysteresis modeling of LiFePO4 battery using invariant imbedding method. Appl. Energy 2016, 162, 163–171. [Google Scholar] [CrossRef]
- Kim, S.J.; Lee, S.Y.; Cho, K.S. Design of high-performance unified circuit for linear and non-linear SVM classifications. JSTS J. Semicond. Technol. Sci. 2012, 12, 162–167. [Google Scholar] [CrossRef]
- Lucu, M.; Martinez-Laserna, E.; Gandiaga, I.; Liu, K.; Camblong, H.; Widanage, W.D.; Marco, J. Data-driven nonparametric Li-ion battery ageing model aiming at learning from real operation data-Part B: Cycling operation. J. Energy Storage 2020, 30, 101410. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Yao, Y. Fault prognosis of battery system based on accurate voltage abnormity prognosis using long short-term memory neural networks. Appl. Energy 2019, 251, 113381. [Google Scholar] [CrossRef]
- Yao, Q.; Lu, D.D.C.; Lei, G. A simple internal resistance estimation method based on open circuit voltage test under different temperature conditions. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–4. [Google Scholar]
- Badmos, O.; Kopp, A.; Bernthaler, T.; Schneider, G. Image-based defect detection in lithium-ion battery electrode using convolutional neural networks. J. Intell. Manuf. 2020, 31, 885–897. [Google Scholar] [CrossRef]
- Qiu, Y.; Dong, T.; Lin, D.; Zhao, B.; Cao, W.; Jiang, F. Fault diagnosis for lithium-ion battery energy storage systems based on local outlier factor. J. Energy Storage 2022, 55, 105470. [Google Scholar] [CrossRef]
- Kumar, S.; Chow, T.W.; Pecht, M. Approach to fault identification for electronic products using Mahalanobis distance. IEEE Trans. Instrum. Meas. 2009, 59, 2055–2064. [Google Scholar] [CrossRef]
- Lee, J.M.; Yoo, C.; Lee, I.B. Statistical monitoring of dynamic processes based on dynamic independent component analysis. Chem. Eng. Sci. 2004, 59, 2995–3006. [Google Scholar] [CrossRef]
- Martin, E.; Morris, A. Non-parametric confidence bounds for process performance monitoring charts. J. Process Control 1996, 6, 349–358. [Google Scholar] [CrossRef]
- Hyvarinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.M.; Yoo, C.; Lee, I.B. Statistical process monitoring with independent component analysis. J. Process Control 2004, 14, 467–485. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Cheung, Y.M.; Xu, L. An empirical method to select dominant independent components in ICA for time series analysis. In Proceedings of the IJCNN’99. International Joint Conference on Neural Networks. Proceedings (Cat. No. 99CH36339), Washington, DC, USA, 10–16 July 1999; Volume 6, pp. 3883–3887. [Google Scholar]
- Hyvarinen, A. Survey on independent component analysis. Neural Comput. Surv. 1999, 2, 94–128. [Google Scholar]
- Yu, J.; Yoo, J.; Jang, J.; Park, J.H.; Kim, S. A novel hybrid of auto-associative kernel regression and dynamic independent component analysis for fault detection in nonlinear multimode processes. J. Process Control 2018, 68, 129–144. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Routledge: Milton Park, UK, 2018. [Google Scholar]
- Wand, M.P.; Jones, M.C. Kernel Smoothing; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Barsukov, Y. Secondary Batteries–Lithium Rechargeable Systems|Hazards and Protection Circuits. In Encyclopedia of Electrochemical Power Sources; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2009; Volume 5, pp. 177–183. [Google Scholar]





| Decision | |||
|---|---|---|---|
| Reject H0 (Accept H1) | Accept H0 (Reject H1) | ||
| Truth | H0 is true (H1 is false) | FAR (Type I error) | Correct decision |
| H0 is false (H1 is true) | Correct decision | MDR (Type II error) | |
| No. | Variables | Description | Unit |
|---|---|---|---|
| 1 | PCS_PCS4_BAT_Cmd_DCI | Battery DC current | A |
| 2 | PCS_PCS4_BAT_Cmd_DCV | Battery DC voltage | V |
| 3 | PCS_PCS4_BAT_Cmd_SOC | Battery state of charge | % |
| 4 | PCS_PCS4_DCI | PCS DC current | A |
| 5 | PCS_PCS4_DCV | PCS DC voltage | V |
| 6 | PCS_PCS4_GridIa | Phase current R | A |
| 7 | PCS_PCS4_GridIb | Phase current S | A |
| 8 | PCS_PCS4_GridIc | Phase current T | A |
| No. | Variables | Description | Unit |
|---|---|---|---|
| 1 | SENSOR.Sensor03.Humi | BMS humidity in ESS room | % |
| 2 | SENSOR.Sensor03.Temp | BMS temperature in ESS room | °C |
| 3 | SENSOR.Sensor04.Humi | ESS room entrance humidity | % |
| 4 | SENSOR.Sensor04.Temp | ESS room entrance temperature | °C |
| Fault Type | Indices | MD | LOF | PCA | ICA | AAKR | MD + ICA |
|---|---|---|---|---|---|---|---|
| MD | LOF | T2 | SPE | ||||
| Battery overvoltage | FAR | 34.82 | 100 | 38.95 | 2.44 | 99.83 | 1.54 |
| MDR | 0 | 0 | 0 | 0 | 0 | 0 |
| Fault Type | Indices | MD | LOF | PCA | ICA | AAKR | MD + ICA |
|---|---|---|---|---|---|---|---|
| MD | LOF | T2 | SPE | ||||
| Humidity anomaly | FAR | 1.4 | 100 | 0 | 0.7 | 93.08 | 1.37 |
| MDR | 3.22 | 0 | 4.9 | 4.46 | 0 | 1.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, S.; Kim, M.; Kim, E.; Kim, B.; Kim, J.; Cho, K.-H.; Park, H.-A.; Kim, S. The Early Detection of Faults for Lithium-Ion Batteries in Energy Storage Systems Using Independent Component Analysis with Mahalanobis Distance. Energies 2024, 17, 535. https://doi.org/10.3390/en17020535
Jung S, Kim M, Kim E, Kim B, Kim J, Cho K-H, Park H-A, Kim S. The Early Detection of Faults for Lithium-Ion Batteries in Energy Storage Systems Using Independent Component Analysis with Mahalanobis Distance. Energies. 2024; 17(2):535. https://doi.org/10.3390/en17020535
Chicago/Turabian StyleJung, Seunghwan, Minseok Kim, Eunkyeong Kim, Baekcheon Kim, Jinyong Kim, Kyeong-Hee Cho, Hyang-A Park, and Sungshin Kim. 2024. "The Early Detection of Faults for Lithium-Ion Batteries in Energy Storage Systems Using Independent Component Analysis with Mahalanobis Distance" Energies 17, no. 2: 535. https://doi.org/10.3390/en17020535
APA StyleJung, S., Kim, M., Kim, E., Kim, B., Kim, J., Cho, K.-H., Park, H.-A., & Kim, S. (2024). The Early Detection of Faults for Lithium-Ion Batteries in Energy Storage Systems Using Independent Component Analysis with Mahalanobis Distance. Energies, 17(2), 535. https://doi.org/10.3390/en17020535











