Designing a High-Order Sliding Mode Controller for Photovoltaic- and Battery Energy Storage System-Based DC Microgrids with ANN-MPPT
Abstract
1. Introduction
1.1. Background and Challenges
1.2. Literature Review
1.3. Motivation, Contributions, and Layout of This Paper
- A novel ANN-MPPT-based PID-HOSMC approach is proposed for a PV-dominant DC microgrid, designed using the nonlinear model with external disturbances and integrating a DPRL to effectively address the chattering issues inherent in conventional SMC methods.
- Theoretical analysis demonstrates that the proposed controller’s convergence time is significantly less than traditional reaching law-based SMC methods. Additionally, a method for selecting the sliding surface coefficients is also presented.
- Simulation analysis and PIL results demonstrate the robustness of the PID-HOSMC in comparison to an existing SMC approach under sudden changes in load demands and solar irradiance.
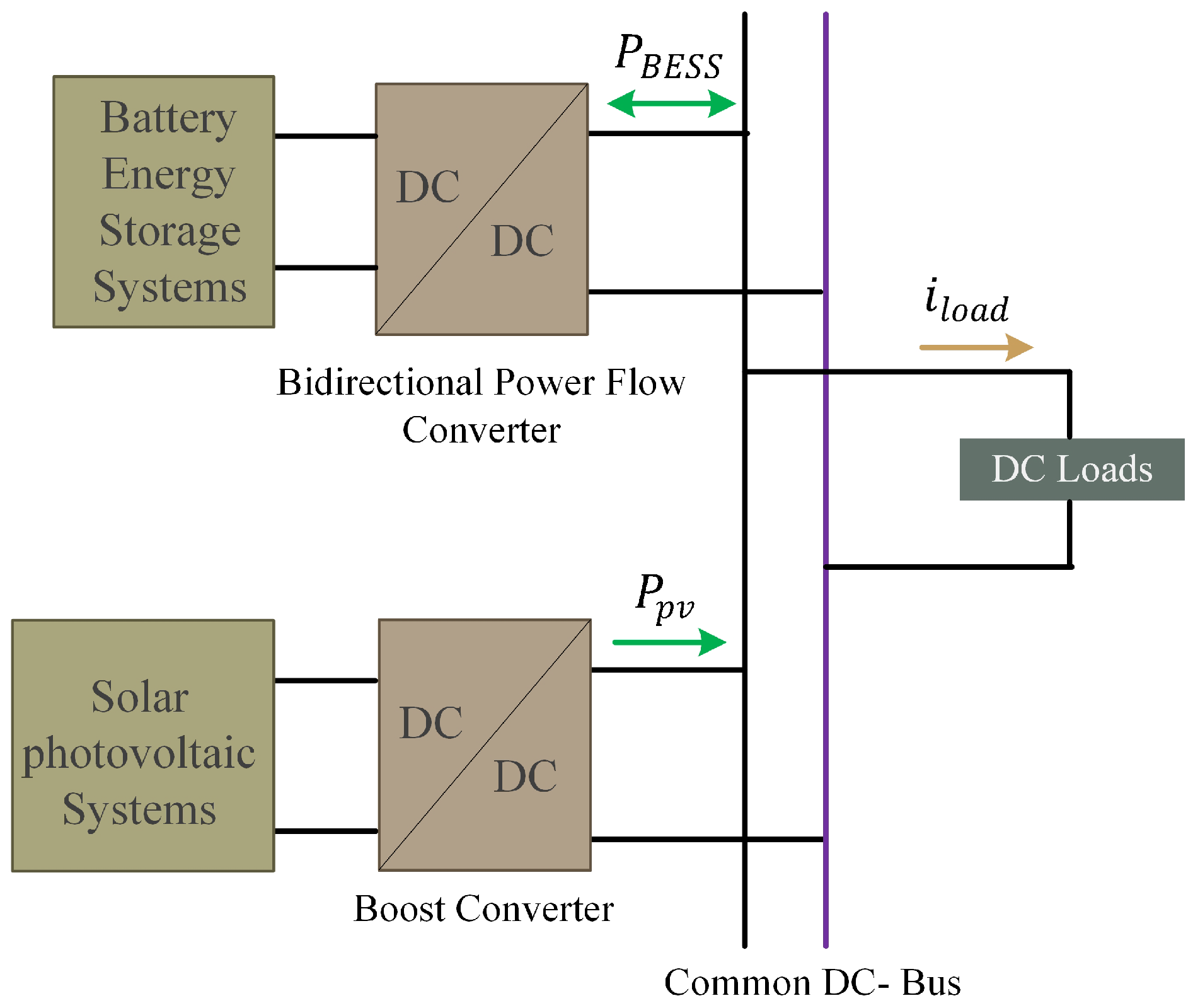
2. Overview on the Proposed DC Microgrid
2.1. Configuration and System Description
- symbolizes the net power of the system, representing the overall balance between power generation and power consumption.
- denotes the power output from the SPV system, serving as the primary power generation source.
- represents the power output from the BESS, which plays a crucial role in stabilizing the system and supplementing power as needed.
- stands for the power consumed by the various DC loads within the microgrid.
2.2. Operational Modes
3. Dynamical Modeling and Problem Formulation
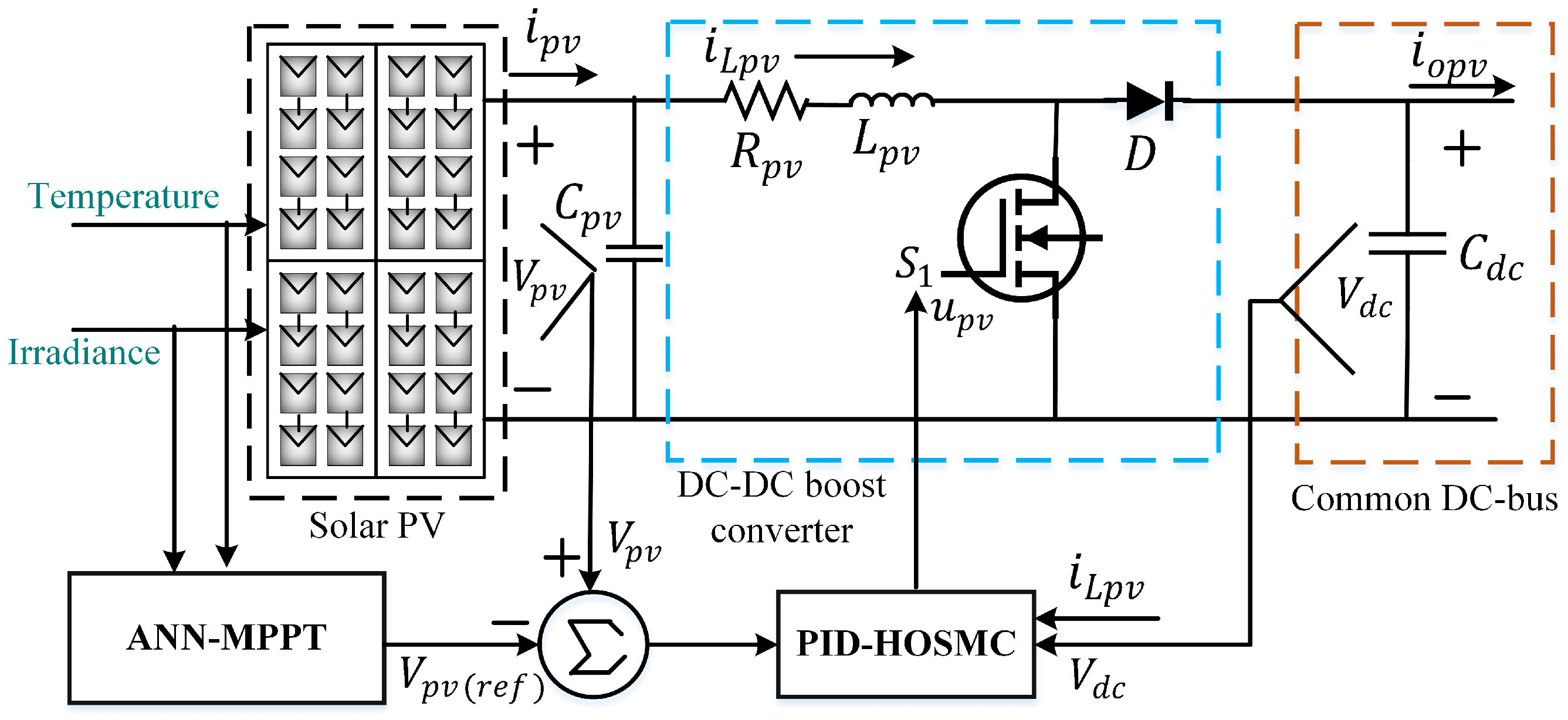
3.1. Modeling of a PV Unit with a DDBC
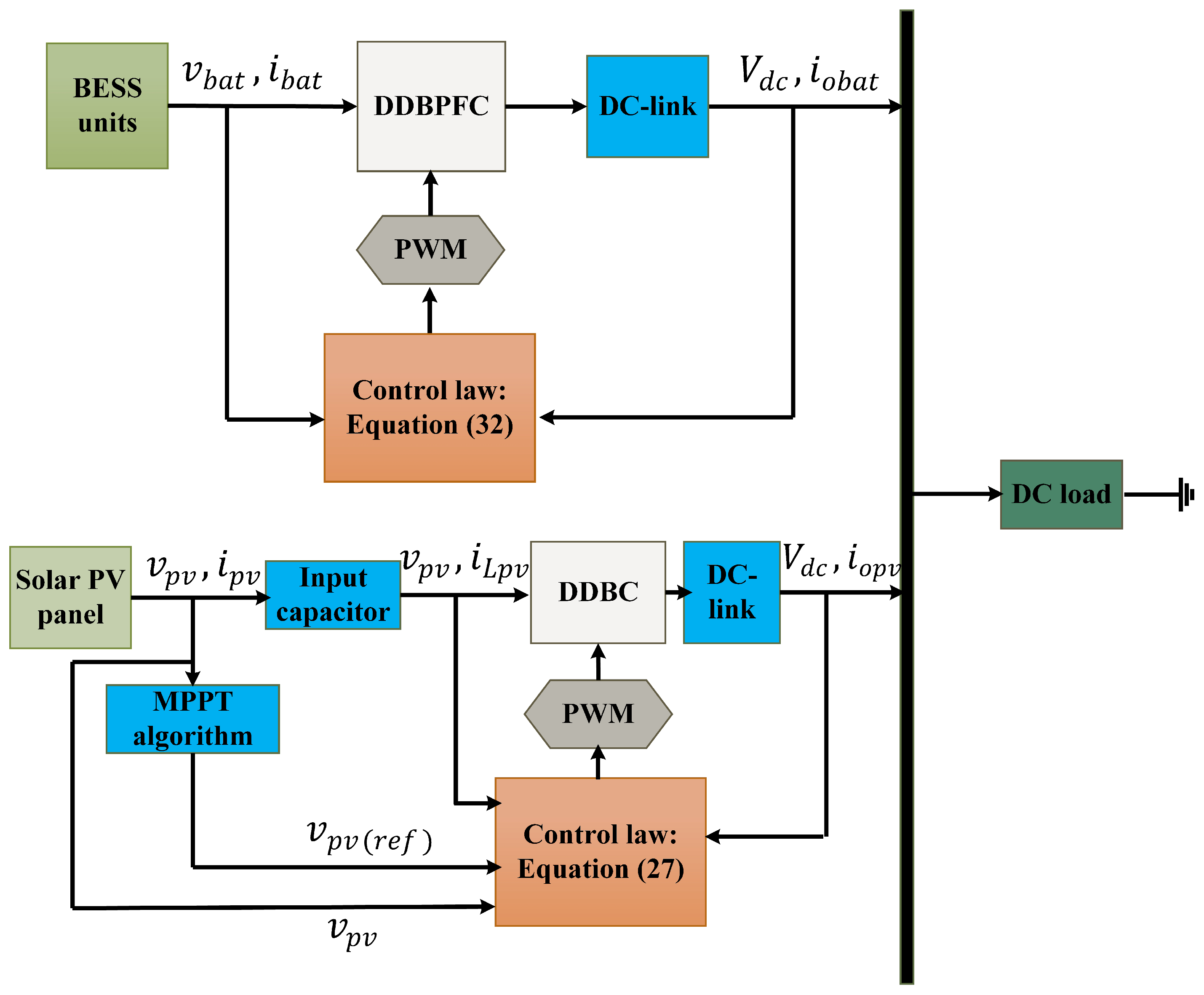
3.2. Modeling of a BESS Unit with a DDBPFC
3.3. Problem Formulation
4. Proposed PID-HOSMC Design
4.1. PID-HOSMC Design for the Solar PV and BESS Units
4.2. Analysis of Convergence
4.3. Determination of Sliding Surface Coefficients
5. Controller Performance Evaluation
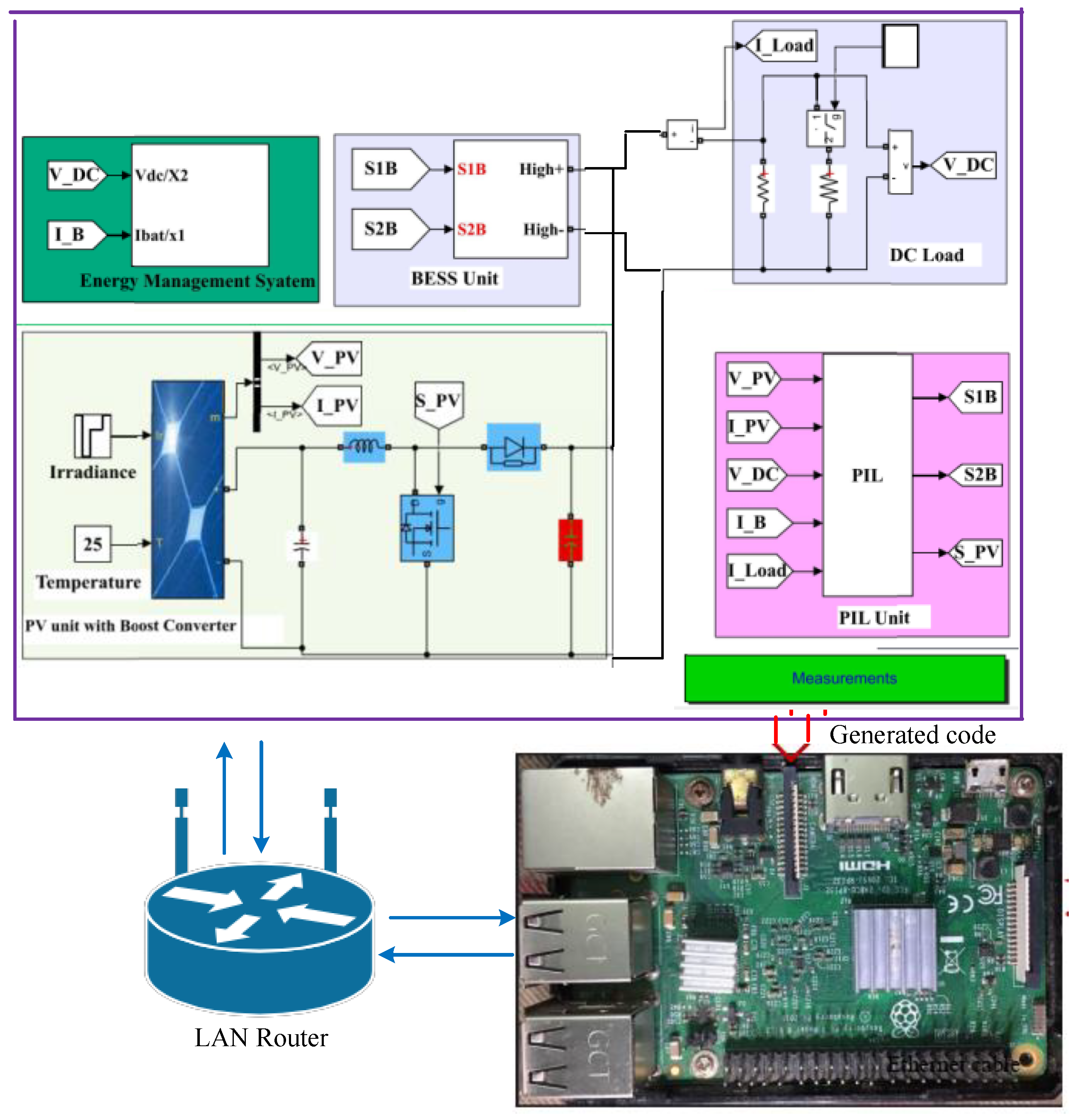
5.1. Test System Description
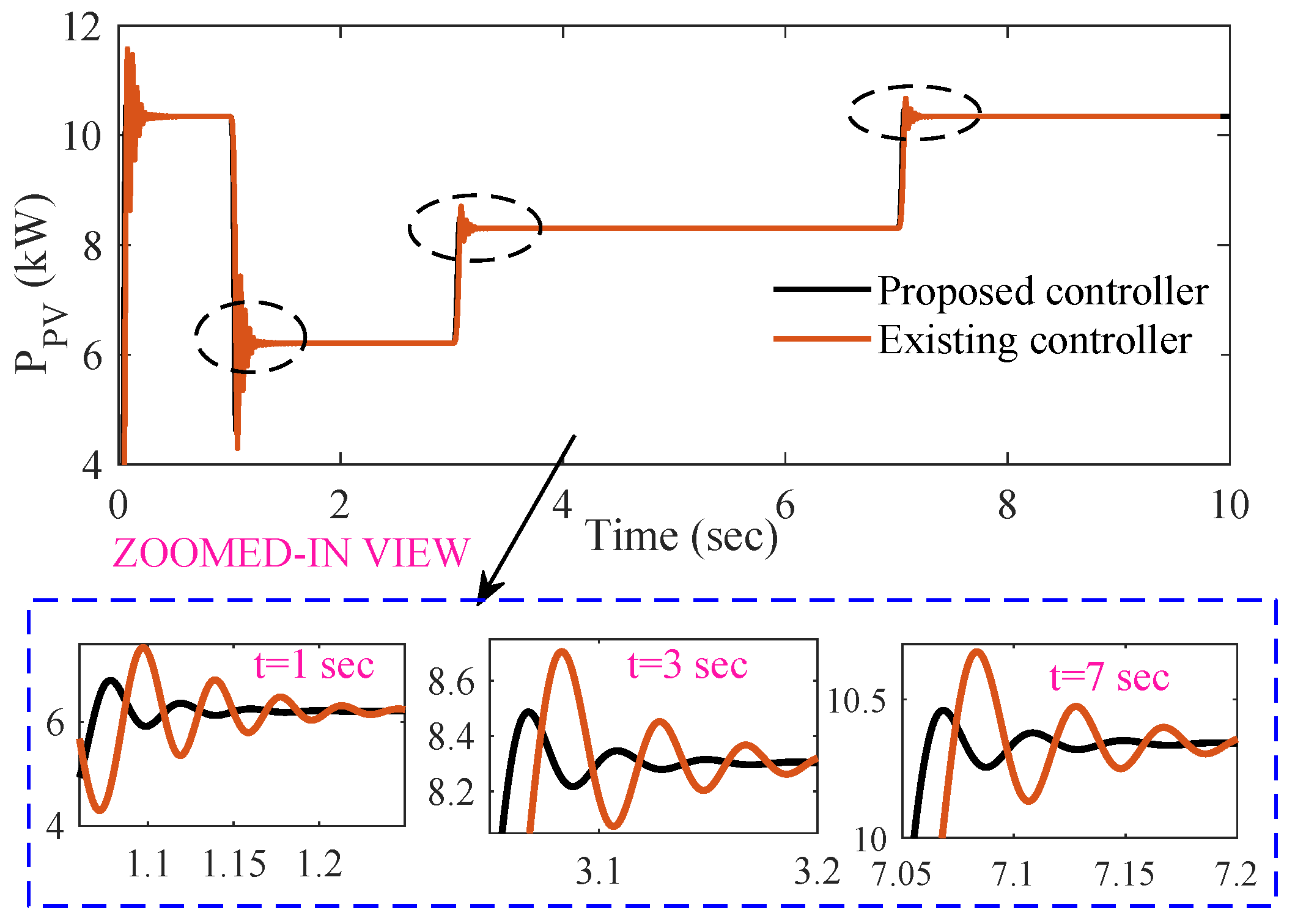
5.2. Simulation Results
5.3. Experimental Results in PIL
6. Conclusions
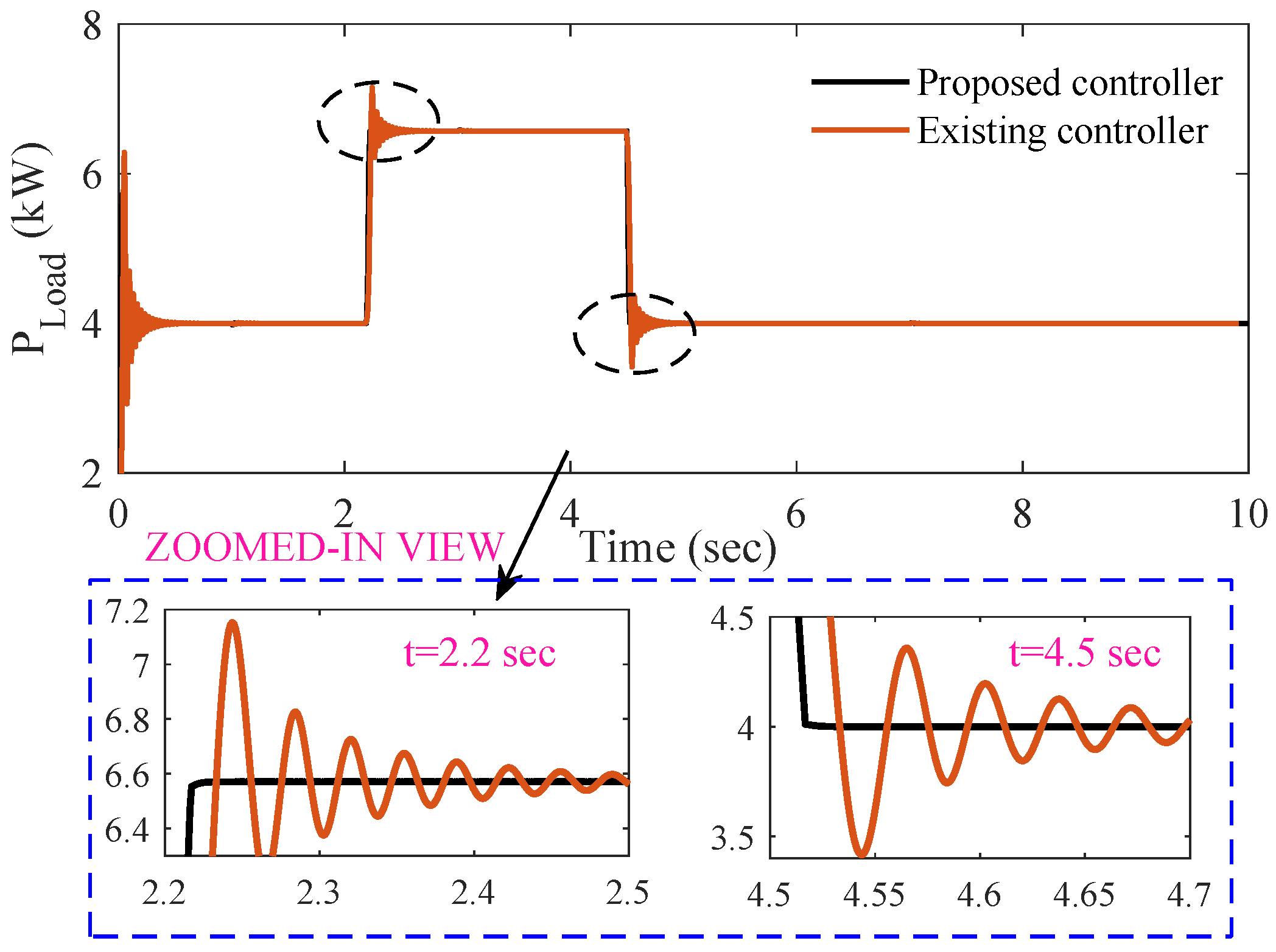
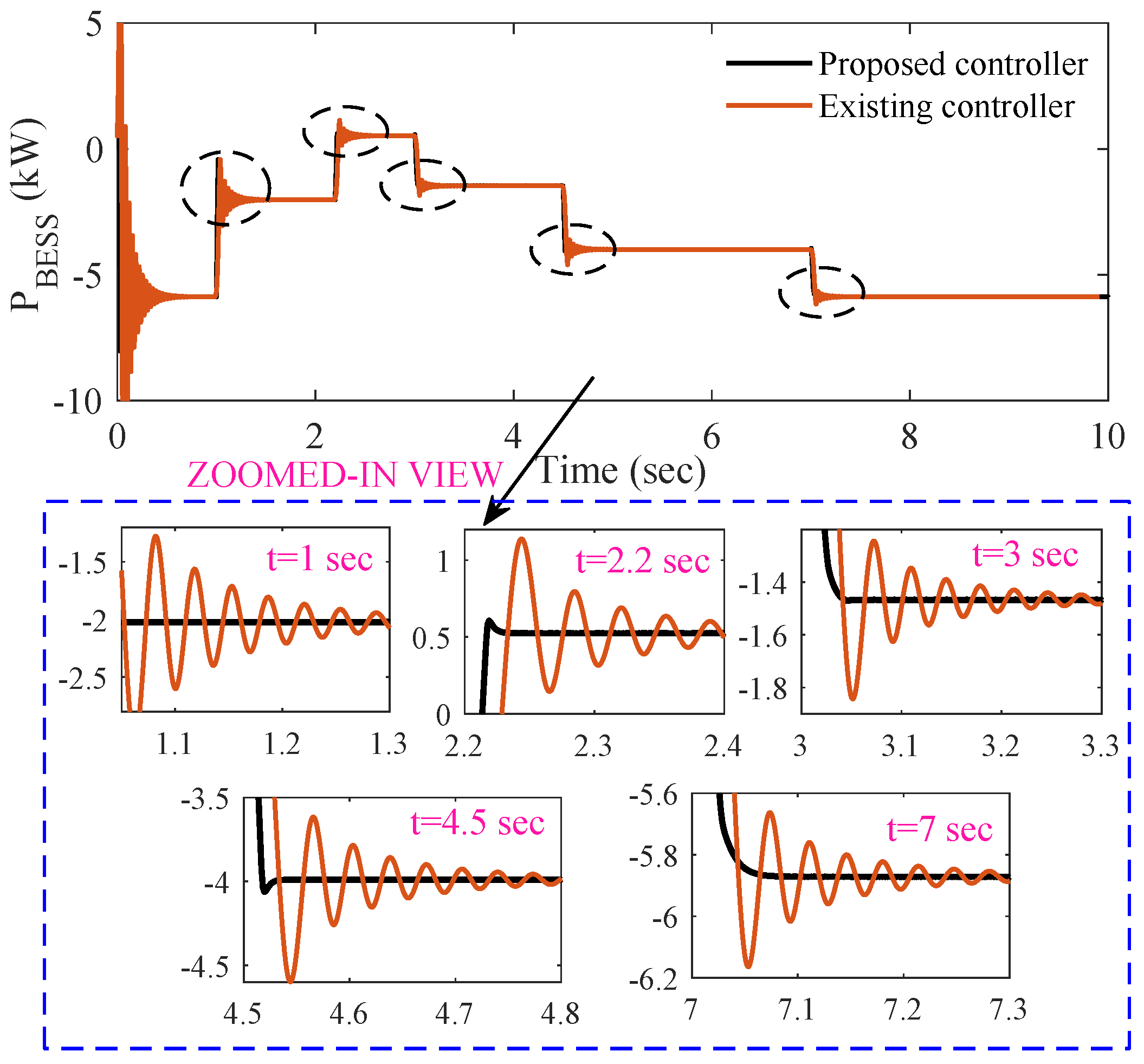
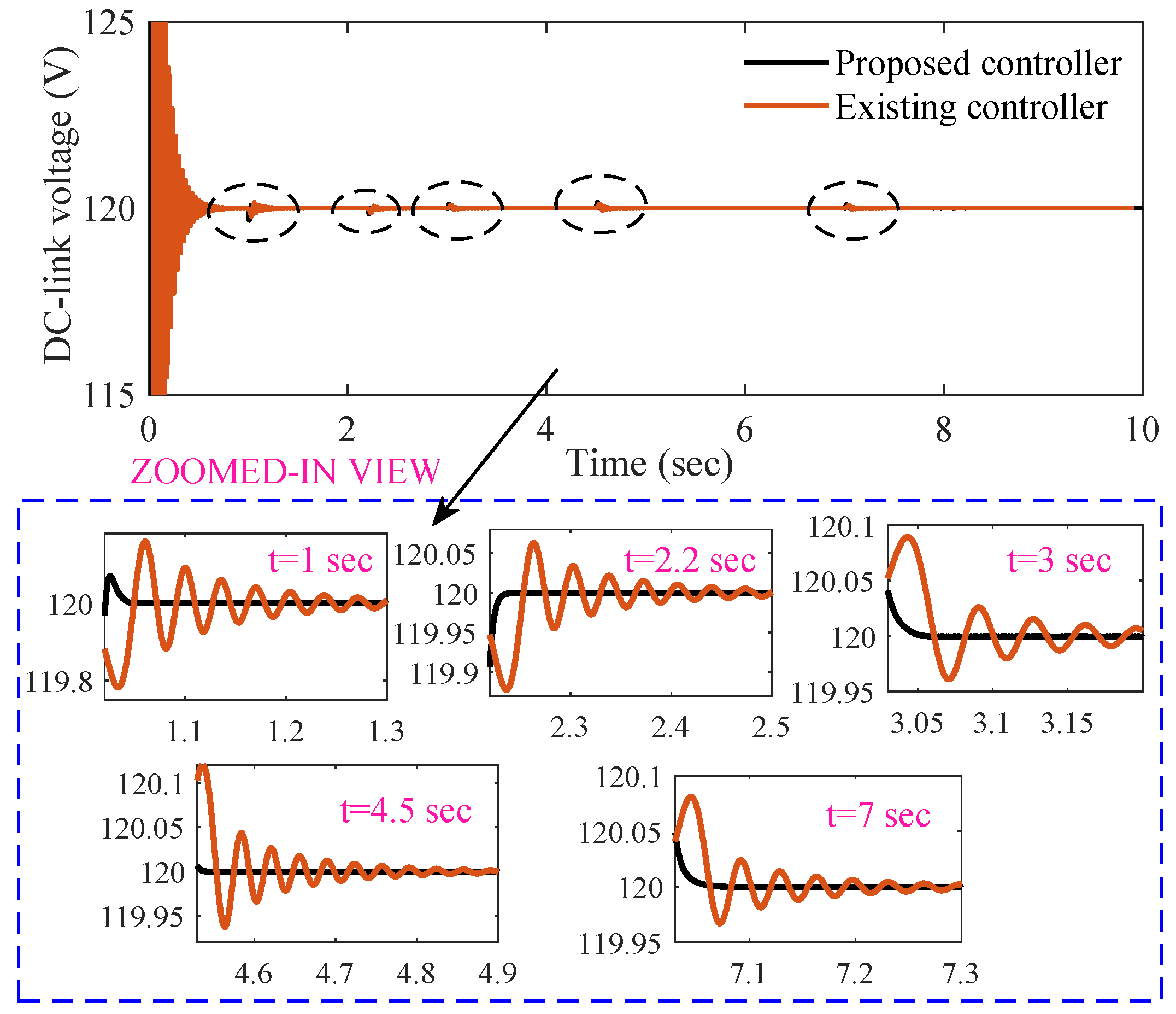
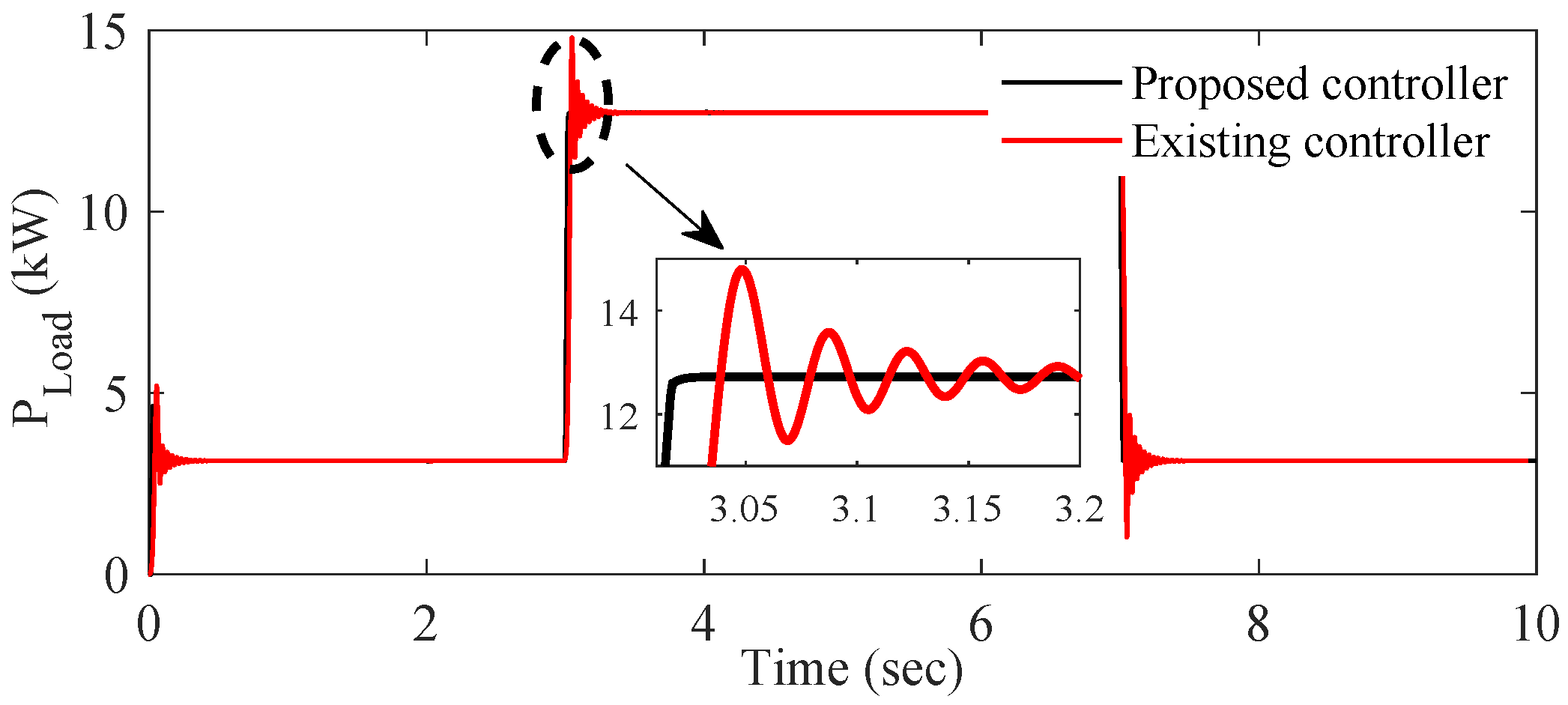
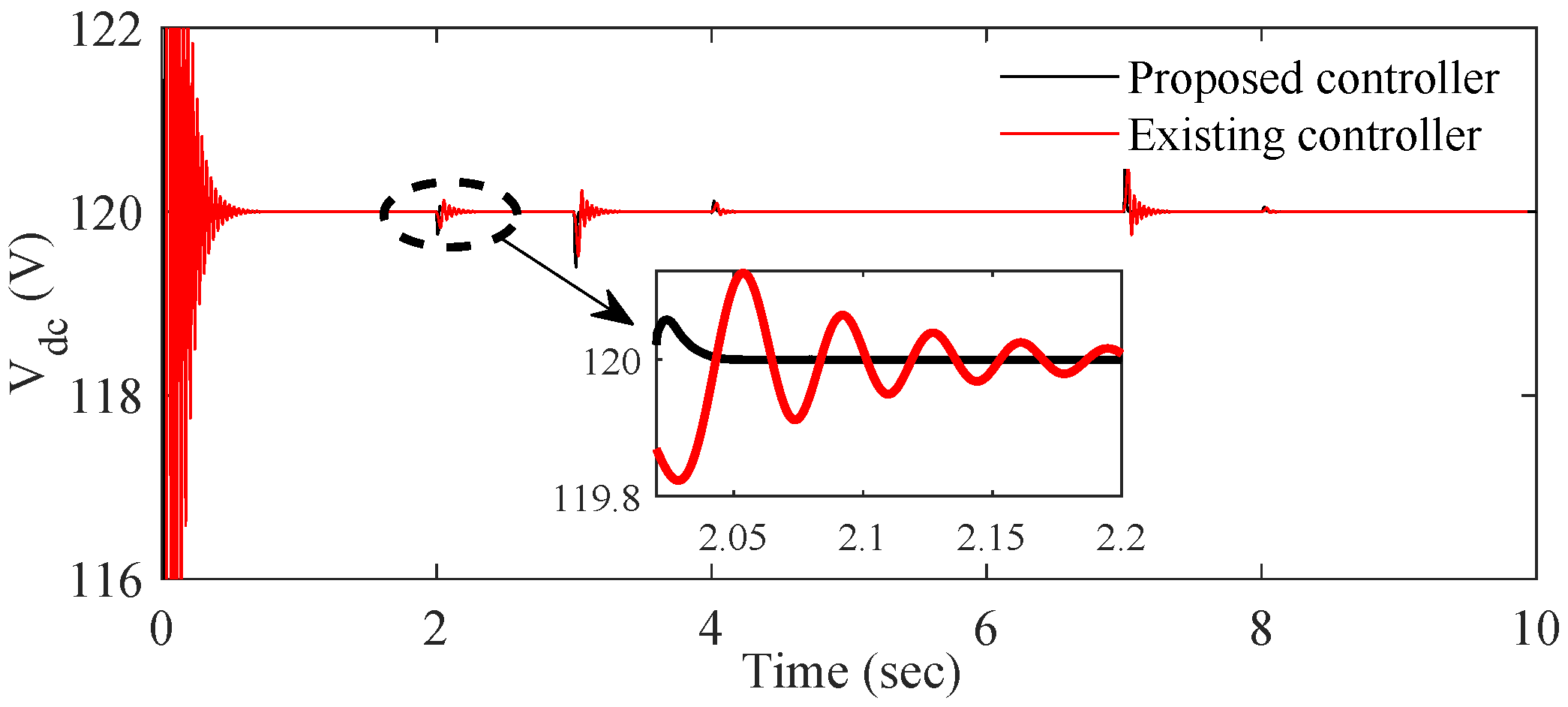
- The designed controller’s performance is far better compared to the existing controller in reducing transient and undesirable spikes and oscillations.
- In terms of quantitative (e.g., overshoot and settling time) analysis, the percentage of all responses is lowest when the proposed controller is used. It is obvious that the proposed controller shows a 58% improvement in settling time and a 82% improvement in overshoot compared to the existing controller.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| BESS | Battery energy storage system |
| BSC | Backstepping controller |
| CRRL | Constant rate reaching law |
| DPRL | Double power reaching law |
| DG | Distributed generator |
| DDBPFC | DC-DC converter bidirectional power flow converter |
| DDBC | DC-DC boost converter |
| ESS | Energy storage system |
| FBLC | Feedback linearization controller |
| LCF | Lyapunov control function |
| MPC | Model predictive controller |
| NSFT | Nonsingular fast terminal |
| PID-HOSMC | Proportional integral derivative higher-order sliding mode control |
| SPV | Solar photovoltaic |
| HOSMC | Higher-order sliding mode controller |
| SoC | State of charge |
References
- Ghosh, S.K.; Roy, T.K.; Pramanik, M.A.H.; Sarkar, A.K.; Mahmud, M.A. An energy management system-based control strategy for DC microgrids with dual energy storage systems. Energies 2020, 13, 2992. [Google Scholar] [CrossRef]
- Bayod-Rújula, Á.A.; Tejero-Gómez, J.A. Analysis of the hybridization of PV plants with a BESS for annual constant power operation. Energies 2022, 15, 9063. [Google Scholar] [CrossRef]
- Fan, L.; Miao, Z.; Shah, S.; Koralewicz, P.; Gevorgian, V. Solar PV and BESS plant-level voltage control and interactions: Experiments and analysis. IEEE Trans. Energy Convers. 2023, 38, 1040–1049. [Google Scholar] [CrossRef]
- Roy, T.K.; Pramanik, M.A.H.; Ghosh, S.K. Design of an integral terminal-based sliding mode controller for PV and BESS-based DC microgrids. Energy Nexus 2022, 7, 100130. [Google Scholar] [CrossRef]
- Roy, T.K.; Ghosh, S.K.; Saha, S. Stability enhancement of battery energy storage and renewable energy-based hybrid AC/DC microgrids using terminal sliding mode backstepping control approaches. ISA Trans. 2023, 142, 40–56. [Google Scholar] [CrossRef] [PubMed]
- Eghtedarpour, N.; Farjah, E. Distributed charge/discharge control of energy storages in a renewable-energy-based DC micro-grid. IET Renew. Power Gener. 2014, 8, 45–57. [Google Scholar] [CrossRef]
- Franzese, P.; Ribera, M.; Cervone, A.; Iannuzzi, D. Optimized control strategy for single-phase multilevel cascaded converter in a distributed PV-BESS system. Electr. Power Syst. Res. 2023, 214, 108818. [Google Scholar] [CrossRef]
- Ye, Q.; Mo, R.; Li, H. Low-frequency resonance suppression of a dual-active-bridge DC/DC converter enabled DC microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 982–994. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, L.; Wang, P. Review of voltage control strategies for DC microgrids. Energies 2023, 16, 6158. [Google Scholar] [CrossRef]
- Sevostyanov, N.A.; Gorbunov, R.L. Control strategy to mitigate voltage ripples in droop-controlled DC microgrids. IEEE Trans. Power Electron. 2023, 38, 15377–15389. [Google Scholar] [CrossRef]
- Korompili, A.; Monti, A. Review of modern control technologies for voltage regulation in DC/DC converters of DC microgrids. Energies 2023, 16, 4563. [Google Scholar] [CrossRef]
- Massenio, P.R.; Tipaldi, M.; Rizzello, G.; Brescia, E.; Cascella, G.L.; Naso, D. Gain-scheduled structured control in DC microgrids. IEEE Trans. Control. Syst. Technol. 2023, 31, 2571–2583. [Google Scholar] [CrossRef]
- Vigneysh, T.; Kumarappan, N. Autonomous operation and control of photovoltaic/solid oxide fuel cell/battery energy storage based microgrid using fuzzy logic controller. Int. J. Hydrogen Energy 2016, 41, 1877–1891. [Google Scholar] [CrossRef]
- Roy, T.K.; Mahmud, M.A.; Oo, A.M.T.; Haque, M.E.; Muttaqi, K.M.; Mendis, N. Nonlinear adaptive backstepping controller design for islanded DC microgrids. IEEE Trans. Ind. Appl. 2018, 54, 2857–2873. [Google Scholar] [CrossRef]
- Basantes, J.A.; Paredes, D.E.; Llanos, J.R.; Ortiz, D.E.; Burgos, C.D. Energy management system (EMS) based on model predictive control (MPC) for an isolated DC microgrid. Energies 2023, 16, 2912. [Google Scholar] [CrossRef]
- Guo, Q.; Bahri, I.; Diallo, D.; Berthelot, E. Model predictive control and linear control of DC–DC boost converter in low voltage DC microgrid: An experimental comparative study. Control Eng. Pract. 2023, 131, 105387. [Google Scholar] [CrossRef]
- Mardani, M.M.; Khooban, M.H.; Masoudian, A.; Dragičević, T. Model predictive control of DC-DC converters to mitigate the effects of pulsed power loads in naval DC microgrids. IEEE Trans. Ind. Electron. 2018, 66, 5676–5685. [Google Scholar] [CrossRef]
- Dragičević, T. Dynamic stabilization of DC microgrids with predictive control of point-of-load converters. IEEE Trans. Power Electron. 2018, 33, 10872–10884. [Google Scholar] [CrossRef]
- Ansari, S.; Zhang, J.; Singh, R.E. A review of stabilization methods for DCMG with CPL, the role of bandwidth limits and droop control. Prot. Control Mod. Power Syst. 2022, 7, 2. [Google Scholar] [CrossRef]
- Mahmud, M.A.; Roy, T.K.; Saha, S.; Haque, M.E.; Pota, H.R. Robust nonlinear adaptive feedback linearizing decentralized controller design for islanded DC microgrids. IEEE Trans. Ind. Appl. 2019, 55, 5343–5352. [Google Scholar] [CrossRef]
- Roy, T.K.; Mahmud, M.A. Active power control of three-phase grid-connected solar PV systems using a robust nonlinear adaptive backstepping approach. Sol. Energy 2017, 153, 64–76. [Google Scholar] [CrossRef]
- Roy, T.K.; Mahmud, M.A. Dynamic stability analysis of hybrid islanded DC microgrids using a nonlinear backstepping approach. IEEE Syst. J. 2017, 12, 3120–3130. [Google Scholar] [CrossRef]
- Panda, S.K.; Subudhi, B. An extended state observer based adaptive backstepping controller for microgrid. IEEE Trans. Smart Grid 2024, 15, 171–178. [Google Scholar] [CrossRef]
- Mi, Y.; Zhang, H.; Fu, Y.; Wang, C.; Loh, P.C.; Wang, P. Intelligent power sharing of DC isolated microgrid based on fuzzy sliding mode droop control. IEEE Trans. Smart Grid 2018, 10, 2396–2406. [Google Scholar] [CrossRef]
- Zhang, G.; Tong, D.; Chen, Q.; Zhou, W. Sliding mode control against false data injection attacks in DC microgrid systems. IEEE Syst. J. 2023, 17, 6159–6168. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, G.; Yu, J.; Yue, W.; Ning, J.; Liu, B. Harmonic analysis of sliding-mode-controlled buck converters imposed by onmodeled dynamics of hall sensor. Energies 2023, 16, 6124. [Google Scholar] [CrossRef]
- Ortiz-Castrillón, J.R.; Saldarriaga-Zuluaga, S.D.; Muñoz-Galeano, N.; López-Lezama, J.M.; Benavides-Córdoba, S.; Cano-Quintero, J.B. Optimal sliding-mode control of semi-bridgeless boost converters considering power factor corrections. Energies 2023, 16, 6282. [Google Scholar] [CrossRef]
- Liang, C.; Zhang, Y.; Ji, X.; Meng, X.; An, Y.; Yao, Q. DC bus voltage sliding-mode control for a DC microgrid based on linearized feedback. In Proceedings of the Chinese Automation Congress, Hangzhou, China, 22–24 November 2019; pp. 5380–5384. [Google Scholar]
- Esmaeli, A. RETRACTED: Stability analysis and control of microgrids by sliding mode control. Int. J. Electr. Power Energy Syst. 2016, 78, 22–28. [Google Scholar] [CrossRef]
- Kalla, U.K.; Singh, B.; Murthy, S.S.; Jain, C.; Kant, K. Adaptive sliding mode control of standalone single-phase microgrid using hydro, wind, and solar PV array-based generation. IEEE Trans. Smart Grid 2017, 9, 6806–6814. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Fulwani, D.; Guerrero, J.M. Adaptive-SMC based output impedance shaping in DC microgrids affected by inverter loads. IEEE Trans. Sustain. Energy 2020, 11, 2940–2949. [Google Scholar] [CrossRef]
- Gudey, S.K.; Gupta, R. Recursive fast terminal sliding mode control in voltage source inverter for a low-voltage microgrid system. IET Gener. Transm. Distrib. 2016, 10, 1536–1543. [Google Scholar] [CrossRef]
- Kumar, V.; Mohanty, S.R.; Kumar, S. Event trigger super twisting sliding mode control for DC micro grid with matched/unmatched disturbance observer. IEEE Trans. Smart Grid 2020, 11, 3837–3849. [Google Scholar] [CrossRef]
- Amine, H.M.; Mouaz, A.K.; Messaoud, H.; Othmane, A.; Saad, M. The impacts of control systems on hybrid energy storage systems in remote DC-microgrid system: A comparative study between PI and super twisting sliding mode controllers. J. Energy Storage 2022, 47, 103586. [Google Scholar] [CrossRef]
- Khan, T.A.; Ullah, A.; Hafeez, G.; Khan, I.; Murawwat, S.; Ali, F.; Ali, S.; Khan, S.; Rehman, K. A fractional order super twisting sliding mode controller for energy management in smart microgrid using dynamic pricing approach. Energies 2022, 15, 9074. [Google Scholar] [CrossRef]
- Zeb, K.; Busarello, T.D.C.; Ul Islam, S.; Uddin, W.; Raghavendra, K.V.G.; Khan, M.A.; Kim, H.J. Design of super twisting sliding mode controller for a three-phase grid-connected photovoltaic system under normal and abnormal conditions. Energies 2020, 13, 3773. [Google Scholar] [CrossRef]
- Yeasmin, S.; Roy, T.K.; Ghosh, S.K. Design of robust integral terminal sliding mode controllers with exponential reaching laws for solar PV and BESS-based DC microgrids with uncertainties. Sustainability 2022, 14, 7802. [Google Scholar] [CrossRef]
- Xiang, C.; Cheng, Q.; Zhu, Y.; Zhao, H. Sliding mode control of ship DC microgrid based on an improved reaching law. Energies 2023, 16, 1051. [Google Scholar] [CrossRef]
- Armghan, H.; Yang, M.; Ali, N.; Armghan, A.; Alanazi, A. Quick reaching law based global terminal sliding mode control for wind/hydrogen/battery DC microgrid. Appl. Energy 2022, 316, 119050. [Google Scholar] [CrossRef]
- Abdalla, Y.S.; Ali, N.; Alanazi, A.; Alanazi, M.; Armghan, H.; Sharaf, M.A.; Boudabbous, A.R.; Armghan, A. Fast reaching law based integral terminal sliding mode controller for photovoltaic-fuel cell-battery-super capacitor based direct-current microgrid. J. Energy Storage 2022, 56, 105915. [Google Scholar] [CrossRef]



| Ref. No. | Year | Control Approach | Contributions | Limitations |
|---|---|---|---|---|
| [8] | 2017 | Active damping controller |
|
|
| [9,10] | 2023, 2023 | Droop controller |
|
|
| [11,12,13] | 2023, 2016 | Fuzzy logic controller |
|
|
| [17,18] | 2018, 2018 | MPC |
|
|
| [19] | 2022 | FBLC |
|
|
| [20,21] | 2019, 2017 | Adaptive FBLC |
|
|
| [22] | 2017 | BSC |
|
|
| [23] | 2024 | Adaptive BSC |
|
|
| [24,25] | 2018, 2021 | SMC |
|
|
| [28] | 2019 | Adaptive SMC |
|
|
| Solar PV Panel with a DDBC | |
|---|---|
| Parameters | Values |
| 10 kW | |
| 0.05 | |
| 0.352 mH | |
| 2200 F | |
| BESS unit with a DDBPFC | |
| 48 V | |
| 150 Ah | |
| 0.053 | |
| 0.3 mH | |
| Parameters of the DC bus | |
| 120 V | |
| 1000 F | |
| PV Panel with a DDBC | |
|---|---|
| Parameters | Values |
| , , | 10, 5, 20 |
| , | 250, 450 |
| , | 1.5, 0.9 |
| BESS unit with a DDBPFC | |
| , , | 300, 250, 500 |
| , | 200, 250 |
| , | 1.5, 0.85 |
| Transient Time (s) | Settling Time (ms) | Overshoot/Undershoot (%) | ||
|---|---|---|---|---|
| Existing Controller | Proposed Controller | Existing Controller | Proposed Controller | |
| 1 | 290 | 120 | 19.42 | 10 |
| 3 | 300 | 140 | 6.81 | 2 |
| 7 | 305 | 140 | 3.532 | 1.504 |
| Transient Time (s) | Settling Time (ms) | Overshoot/Undershoot (%) | ||
|---|---|---|---|---|
| Existing Controller | Proposed Controller | Existing Controller | Proposed Controller | |
| 2.2 | 700 | 0 | 9.09 | 0.0 |
| 4.5 | 300 | 0 | 12.50 | 0.0 |
| Transient Time (s) | Settling Time (ms) | Overshoot/Undershoot (%) | ||
|---|---|---|---|---|
| Existing Controller | Proposed Controller | Existing Controller | Proposed Controller | |
| 1 | 400 | 60 | 40 | 0.0 |
| 2.2 | 424 | 20 | 140 | 5.0 |
| 3 | 313 | 50 | 28.57 | 0.0 |
| 4.5 | 300 | 20 | 12.50 | 0.0 |
| 7 | 305 | 50 | 6.89 | 0.0 |
| Transient Time (s) | Settling Time (ms) | Overshoot/Undershoot (%) | ||
|---|---|---|---|---|
| Existing Controller | Proposed Controller | Existing Controller | Proposed Controller | |
| 1 | 250 | 20 | 0.16 | 0.04 |
| 2.2 | 300 | 15 | 0.10 | 0.0 |
| 3 | 320 | 50 | 0.08 | 0.04 |
| 4.5 | 250 | 30 | 0.10 | 0.0 |
| 7 | 270 | 40 | 0.08 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, T.K.; Oo, A.M.T.; Ghosh, S.K. Designing a High-Order Sliding Mode Controller for Photovoltaic- and Battery Energy Storage System-Based DC Microgrids with ANN-MPPT. Energies 2024, 17, 532. https://doi.org/10.3390/en17020532
Roy TK, Oo AMT, Ghosh SK. Designing a High-Order Sliding Mode Controller for Photovoltaic- and Battery Energy Storage System-Based DC Microgrids with ANN-MPPT. Energies. 2024; 17(2):532. https://doi.org/10.3390/en17020532
Chicago/Turabian StyleRoy, Tushar Kanti, Amanullah Maung Than Oo, and Subarto Kumar Ghosh. 2024. "Designing a High-Order Sliding Mode Controller for Photovoltaic- and Battery Energy Storage System-Based DC Microgrids with ANN-MPPT" Energies 17, no. 2: 532. https://doi.org/10.3390/en17020532
APA StyleRoy, T. K., Oo, A. M. T., & Ghosh, S. K. (2024). Designing a High-Order Sliding Mode Controller for Photovoltaic- and Battery Energy Storage System-Based DC Microgrids with ANN-MPPT. Energies, 17(2), 532. https://doi.org/10.3390/en17020532










