Abstract
The Multiple Microgrid System (MMG) facilitates synergistic complementarity among various energy sources, reduces carbon emissions, and promotes the integration of renewable energy generation. In this context, we propose a two-stage robust cooperative scheduling model for MMGs based on non-cooperative game theory and a benefit allocation mechanism. In the first stage, considering electricity price fluctuations and uncertainties in wind and solar power outputs, a robust optimization approach is applied to establish an electric energy management model for MMGs. This model enables point-to-point energy sharing among microgrids. In the second stage, addressing the benefit allocation problem for shared electric energy, we introduce a Cost Reduction Ratio Distribution (CRRD) model based on non-cooperative game theory. The generalized Nash equilibrium is utilized to determine the benefit distribution for shared electric energy. Finally, through case studies, the proposed model is validated, ensuring fair returns for each microgrid. The results indicate that the proposed model optimizes the operational states of individual microgrids, reduces operational costs for each microgrid, and lowers the overall total operational costs of the MMG system. Additionally, an investigation is conducted into the impact of electricity price uncertainty coefficients and confidence levels of wind and solar uncertainties on the operational costs of microgrids.
1. Introduction
1.1. The Motivation of the Paper
In the context of an increasingly evident global energy crisis, microgrids are considered a key strategic initiative to address energy challenges. This study aims to enhance energy utilization efficiency through optimized scheduling and electric energy sharing among multiple microgrids. In this paper, the superiority of each microgrid is demonstrated by maintaining independent operational loads while concurrently reducing the overall operational costs of the entire microgrid system.
1.2. Description of the Background and Research Gaps
As microgrid technology continues to advance, the emergence of multiple adjacent microgrids within the same distribution area forms a Multiple Microgrid System. These systems possess flexibility and sustainability advantages, adapting well to varying energy demands and changing energy supply conditions. When a microgrid system includes electric loads, heating loads, and cooling loads, it constitutes a Combined Cooling, Heating, and Power (CCHP) microgrid system, enhancing the overall efficiency of multi-energy usage. The literature [1] has proposed a scheduling optimization model for CCHP microgrids, although the game relationship between microgrids and loads has not been taken into account. Although [2] introduced a non-cooperative game-based optimization model for CCHP microgrids, demonstrating the existence of the Nash equilibrium in non-cooperative games, there is a lack of consideration for uncertainties within the microgrid system. In addressing system uncertainties, ref. [3] proposed a predictive control dynamic optimization strategy. There is a deficiency in contemplating planning and design methods. Furthermore, ref. [4] presented a dual-level planning design for determining microgrid device types and capacities. The impact of electricity price mechanisms on market demand has not been considered. Finally, ref. [5] introduced a non-cooperative game optimization model for CCHP-based multi-districts, considering the impact of dynamic electricity pricing mechanisms on market demand. There is a lack of research on point-to-point electric energy sharing among multiple microgrids.
Energy interactions among multiple microgrids often involve electric energy sharing. Sharing electric energy enhances the integration of new energy sources, mitigates wind and solar energy curtailment, and improves the efficiency of various energy sources. In [6], considering the uncertainty of new energy output, a regional MMG distribution network energy trading model was proposed to minimize the overall operating cost of the MMG system. The interests of individual microgrids have not been taken into account. For regional MMGs, ref. [7] developed an optimization scheduling model considering both economic and comprehensive energy efficiency, aiming to improve the economic efficiency of the MMG system while ensuring a certain level of comprehensive energy efficiency. There is a deficiency in considering the economic viability of individual microgrids. Establishing a shared energy medium through a public energy storage station, ref. [8] demonstrated effective enhancement of energy usage efficiency, facilitating renewable energy integration and reducing the operating costs of MMG systems. Optimizing the multi-microgrid system as a collective entity overlooks the interrelations among individual microgrids, preventing the assurance that each microgrid benefits within the multi-microgrid system as a whole.
Currently, energy-sharing management modeling is categorized into single-stage and two-stage models. Single-stage energy-sharing management models predominantly focus on the global energy management of multiple microgrids [9,10]. The scheduling and settlement of individual microgrid dispatches and sharing are not sufficiently clear. Two-stage models typically optimize the energy sharing of multiple microgrids in the first stage, akin to single-stage models. In the second stage, settlement is performed for the optimal energy sharing determined in the first stage, considering the costs of energy sharing [11,12,13,14,15]. The earliest use of a two-stage energy-sharing management model is presented in [12]. Refs. [13,14] introduced power flow considerations into two-stage energy management modeling, enhancing microgrid safety and reliability. The settlement of energy-sharing costs in the second stage often employs non-cooperative game models to determine Nash equilibrium points [13,14,15,16]. The above-mentioned literature predominantly focuses on deterministic optimization models, with limited consideration for uncertainties in renewable energy output and minimal contemplation of the impact of electricity price fluctuations on electric energy sharing management.
1.3. Contributions of the Paper
In this context, this paper focuses on the study of electric energy-sharing transactions in microgrids and constructs a two-stage robust collaborative scheduling model for multiple microgrids based on non-cooperative game theory and profit allocation mechanisms. In the first stage, robust optimization is applied to address electricity price fluctuations and uncertainties in wind and solar power output. This establishes an electric energy management model for multiple microgrids, facilitating point-to-point energy sharing among individual microgrids. An analysis comparing the operational conditions of microgrids before and after electric energy sharing is conducted. In the second stage, addressing the clearance and settlement of shared electric energy, a Cost Reduction Ratio (CRR) model based on non-cooperative game theory is formulated. The generalized Nash equilibrium is utilized to determine the clearance and settlement of shared electric energy. Considering the interdependence and mutual influence of electric energy-sharing payments, this model ensures fairness in determining electric energy-sharing payments. This means that each microgrid can achieve the maximum cost reduction, and the cost reduction is as close as possible to the ideal situation. This model not only ensures the benefits of each microgrid within the model but also reduces the overall operating costs of the MMG system. The first-stage problem is solved using the Column and Constraint Generation (C&CG) method, while the second-stage problem is addressed using the Alternating Direction Method of Multipliers (ADMM). Finally, through case studies, the proposed model is validated, ensuring fair returns for each microgrid. The results indicate that the proposed model optimizes the operational states of individual microgrids, reduces operational costs for each microgrid, and lowers the overall total operational costs of the MMG system. Additionally, an investigation is conducted into the impact of electricity price uncertainty coefficients and confidence levels of wind and solar uncertainties on the operational costs of microgrids.
2. Multi-Microgrid Operational Architecture
Figure 1 illustrates the framework for electric energy-sharing transactions and energy management in a multi-microgrid setting. Each microgrid comprises various components, including renewable energy sources, electric storage (ES), thermal storage (TS), and four types of energy conversion devices: a ground-source heat pump (HP), gas turbine (GT), absorption cooler (AC), and electric cooler (EC). Photovoltaic (PV) and wind turbine (WT) units, as depicted in Figure 1, fall under the category of renewable energy sources. The load demands from internal end-users encompass electric loads, heating loads, and cooling loads.
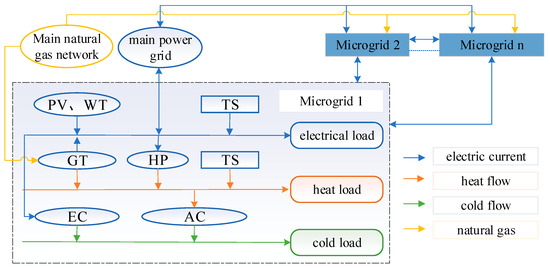
Figure 1.
Multi-microgrid power sharing and energy management framework.
Assuming each microgrid can engage in the buying and selling of electric energy with the main power grid and purchase natural gas from the main natural gas network, microgrids are interconnected through power interconnection lines, enabling real-time point-to-point sharing of electric energy transactions. A set of multiple microgrids is defined as , N microgrids. Simultaneously, the optimization periods are defined as , where the optimization period spans 24 h, and optimization is conducted every hour. Therefore, T = 24.
3. Optimization Scheduling and Trading Model for Multi-Microgrid Systems
3.1. Scheduling Model for Multi-Microgrid Systems
Gas Turbine (GT) Model [17]:
where: is the amount of natural gas consumed by microgrid I for GT operation in period t; and are the electric and thermal outputs of microgrid I from GT operation in period t; and are the efficiencies of GT in converting to electric and thermal energy for microgrid I in period t; is the heating value of natural gas; and are the maximum electric and thermal outputs of GT for microgrid I in period t.
Ground Source Heat Pump (HP) Model [17]:
where: is the thermal output of microgrid I from HP operation in period t; is the electric to the thermal conversion efficiency of HP for microgrid I in period t; is the electric power consumed by microgrid I for HP operation in period t; is the maximum electric power for HP operation for microgrid I in period t.
Electric Cooler (EC) Model [17]:
where: is the cooling output of microgrid I from EC operation in period t; is the electric to cooling conversion efficiency of EC for microgrid I in period t; is the electric power consumed by microgrid I for EC operation in period t; is the maximum electric power for EC operation for microgrid I in period t.
Absorption Cooler (AC) Model [17]:
where: is the cooling output of microgrid I from AC operation in period t; is the thermal to cooling conversion efficiency of AC for microgrid I in period t; is the thermal power consumed by microgrid I for AC operation in period t; is the maximum thermal power for AC operation for microgrid I in period t.
Energy Storage Device Model [17]:
Energy storage devices include Thermal Storage (TS) and Electric Storage (ES). Since the models for thermal and electric energy storage devices are similar, we will illustrate the model using the example of an electric energy storage device.
Storing excess electric energy in the electric storage device and releasing electric energy when the generated energy is insufficient to meet the electric load is modeled as follows:
where: represents the current capacity value of microgrid i’s electric storage device in period t; and are the efficiencies of the electric storage device for charging and discharging in period t; and are the charging and discharging powers of microgrid i’s electric storage device in period t; and are the minimum and maximum states of the charge ratios of microgrid i’s electric storage device; represents the total capacity of microgrid i’s electric storage device; and represent the initial and final stored electric energy in microgrid i’s electric storage device for a day, as electric storage devices operate in a cyclical manner over a day; and are auxiliary binary variables representing the charging and discharging states of microgrid i’s electric storage device in period t, and these states are mutually exclusive; and are the maximum charging and discharging powers of microgrid i’s electric storage device in period t.
Load Side Model [17]:
The user-side load of a microgrid includes the electrical load, thermal load, and cooling load. The electrical load can be divided into two categories: fixed load and transferable load. Users participate in demand response within the microgrid by adjusting their transferable load.
Fixed Load: These loads are considered crucial as they cannot be transferred. They cannot participate in any demand response programs and need to be serviced by the microgrid.
Transferable Load: These loads are controllable and can be shifted from one time interval to another but cannot be reduced. They can only participate in price-based demand response programs.
The price-based demand response plan for electric loads involves transferring transferable loads out of the microgrid during periods of high grid electricity prices and moving these loads back to the microgrid during periods of lower grid electricity prices. The sum of the transferred transferable loads at each moment should be equal to the sum of the received transferable loads at each moment. This approach aims to reduce users’ electricity costs and alleviate energy supply pressure during peak demand periods. A price-based demand response indirectly influences thermal and cooling loads through various energy conversion devices, as illustrated in Figure 1.
The model is described as follows:
where: is the initial electric load demand of microgrid I in period t; is the electric load demand of microgrid I after load demand response in period t; represents the electric load transferred into microgrid i at time t; represents the electric load transferred out of microgrid i at time t; and are auxiliary binary variables representing the transfer-in and transfer-out states of electric loads in microgrid i during time interval t, and the states of transferring in and out are mutually exclusive; is the coefficient representing the proportion of transferred-in electric load in microgrid i within the initial load at time t; is the coefficient representing the proportion of the transferred-out electric load in microgrid i within the initial load at time t; in this paper, and are both set to 15%; represents the cost reduction of the price-based demand response for electric loads in microgrid i; represents the electricity purchase price from the main grid for microgrid i at time t.
3.2. Multi-Microgrid Electric Energy Trading Model
3.2.1. Electric Energy Trading Model between Microgrids and the Main Power Grid
Each microgrid purchases electric energy from the main power grid when there is an electricity deficit and sells excess electric energy to the main power grid when there is a surplus. The cost for a microgrid to purchase electric energy from the main power grid is defined as follows [18]:
where: is the cost for microgrid I to purchase electric energy from the main power grid; and are the buying and selling prices, respectively, of electric energy between microgrid I and the main power grid in period t; and are the buying and selling electric power, respectively, between microgrid I and the main power grid in period t; is the penalty cost for electricity price uncertainty, which will be explained in Section 3.2.
Transactions between microgrid I and the main power grid must adhere to the following constraints:
where: is the maximum buying or selling electric power capacity for microgrid I in transactions with the main power grid.
3.2.2. Electric Energy Trading Model between Microgrids
Microgrids achieve point-to-point electric energy sharing through power interconnection lines. In period t, the electric energy sharing between microgrids must satisfy the following [18]:
where: represents the electric quantity purchased by microgrid i from microgrid j in period t; represents the unit price for the shared electric energy transactions between microgrid i and microgrid j, and it satisfies Price ; and represent the minimum and maximum hourly shared electric energy between microgrid i and microgrid j, respectively.
Therefore, the total cost of shared electric energy for microgrid I can be expressed as:
Due to Equations (23) and (25), the sum of the costs of shared electric energy for each microgrid system is zero:
4. System Fluctuations Due to the Uncertainty Model
4.1. Uncertainty Model for Wind and Solar Power
To address the uncertainty in wind and solar power outputs, a robust approach is employed. By solving the decision variables , the goal is to find the worst-case probability distribution for K discrete scenarios. This process enables obtaining the maximum expected cost.
where: is the cost of internal operations for microgrid I; Ω is the feasible domain of real-time operational scenarios; is the probability value for each discrete scenario; is the cost of purchasing natural gas for microgrid I; is the cost of demand response for microgrid; is the cost of operation and maintenance for the equipment of microgrid I.
where: is the purchase price of natural gas; is the amount of natural gas consumed by microgrid I for GT operation in period t.
where: is the price compensation coefficient for transferring the electric load.
where are the equipment operation and maintenance costs for GT, HP, EC, AC, ES, HS, PV, and WT, respectively.
In the solving process, it is necessary to find the probability distribution values for discrete scenarios that maximize the expected objective function. To ensure that the obtained probability distribution values are as close as possible to the actual data, a combined norm of 1-norm and ∞-norm is used to constrain the probability distribution values for discrete wind power and photovoltaic power scenarios [19]. The corresponding feasible domains are denoted as and . This ensures that the obtained probability distribution values reasonably match real-world situations.
The above formula represents the initial probability value for the k-th discrete scenario obtained from actual operational data; and represent the 1-norm and ∞-norm constraint conditions, respectively, and and represent the maximum allowable deviations under the worst-case robust conditions, as per the constraints.
According to references [20,21], the confidence levels constrain the probability distribution of discrete scenarios:
Letting the right-hand side of the inequalities be confidence levels and , respectively, Equation (33) can be transformed into Equation (34):
From Equations (33) and (34), Equation (35) is derived:
4.2. Electricity Price Uncertainty Model
The electricity market significantly influences the decisions of microgrids. However, accurately obtaining the distribution of electricity prices is a challenging task due to the complexity of the market. In such cases, robust optimization methods can be employed to describe the uncertainty brought about by electricity price fluctuations [22].
To handle the uncertainty brought about by electricity price fluctuations, a penalty cost is introduced and denoted as a penalty . Additionally, a price deviation coefficient is introduced, representing the degree of uncertainty for microgrid I. A larger numerical value indicates more periods of electricity price uncertainty. When is 0, it signifies that the microgrid does not consider electricity price fluctuations. When is 24, it means that uncertainty in electricity prices is considered at every moment. Here, T represents the number of periods in the scheduling cycle, and the range of k is [0, T]. The penalty term is activated only during periods of electricity price uncertainty, limited by , .
Considering electricity price uncertainty, the overall objective is to determine the optimal collaborative operation strategy for microgrids, minimizing the total operational cost. The objective involves a min-max formulation, utilizing robust optimization to address electricity price uncertainty. The goal is to identify the worst-case scenario for electricity prices, as generated by Equation (36). To simplify computations, auxiliary variables are introduced, transforming the penalty term for price deviation into the following form:
In these equations, represents the electricity price uncertainty parameter for each microgrid, and and are the dual variables for Equations (38) and (39), respectively. According to the strong duality theory, Equations (37)–(39) are transformed into the following minimization problem:
In these formulations, the introduction of an auxiliary variable serves to linearize the minimization problem. This transformation changes the objective function’s form from a Min-Max problem to a Min-Min problem.
5. Distributed Collaborative Energy Management for Multiple Microgrids
5.1. Phase 1: Energy Management Model for Multiple Microgrids
5.1.1. Microgrid Model without Considering Electricity Sharing
In the scenario where electricity sharing between microgrids is not considered, and for each microgrid I, the following electrical, thermal, and cooling load balance constraints must be satisfied:
where , , and are the electrical, thermal, and cooling loads for microgrid I at time t; Additionally, and denote the predicted output of renewable energy sources (photovoltaic and wind power) for microgrid I at time t.
In this case, the energy management model for microgrid i is represented as:
where is the operational cost for microgrid I without considering electricity sharing.
5.1.2. Microgrid Model Considering Electricity Sharing in Multiple Microgrids
As discussed in Section 3.2.2 of this paper, when considering electricity sharing between microgrids, the electrical load balance Equation (46) for microgrid I will include the electricity sharing term . Thus, for microgrid I involved in the set during period t, the power balance constraint considering electricity sharing is given by:
As per Equation (27), the total expenditure and income from sharing within the multiple microgrid system are equal throughout the day. Therefore, the cost of electricity sharing between microgrids is balanced in internal transactions within the multiple microgrid system. Hence, the objective function for the total operational cost considering electricity sharing in the multiple microgrid system is:
Here, represents the total operational cost considering electricity sharing, is the operational cost for microgrid i considering electricity sharing.
Therefore, the objective function for the operational cost of microgrid i becomes:
The first part of the model, , involves the cost of purchasing and selling electricity from/to the main grid by microgrid I (considering the penalty cost for electricity price uncertainty). The second part of the model, , considers the actual output of wind and photovoltaic power generation and optimizes for the uncertainty of discrete scenario probability distribution, adapting to different scenarios of wind and photovoltaic power output. This design can address challenges arising from uncertainty.
The proposed model is solved using the C&CG algorithm, which divides it into a Master Problem (MP) and Subproblems (SP). By iteratively solving the MP and SP, with feedback from the SP results to the MP, the optimization process is conducted, as depicted in Figure 2. The MP seeks the optimal result under the worst probability distribution scenario (considering constraints). The result provides data for the SP iteration. For Equation (52), it establishes a lower bound:
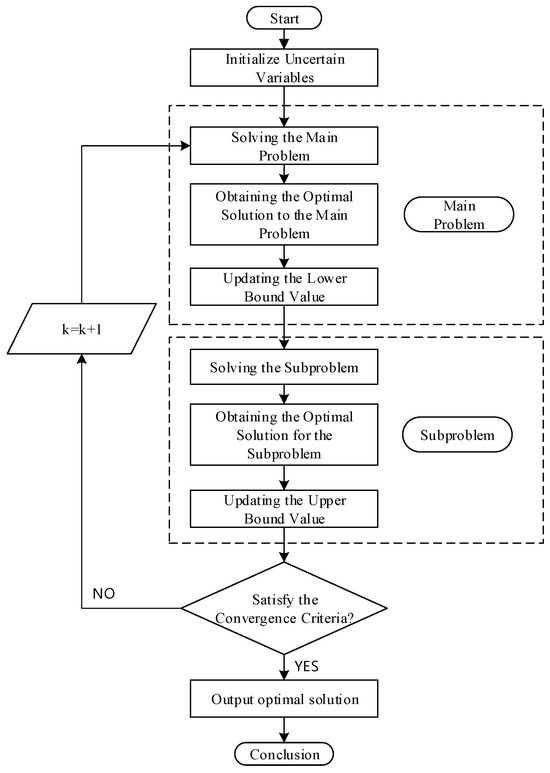
Figure 2.
C&CG algorithm flowchart.
In the formulas, represents the robust decision variables for the Master Problem; represents the variables for the Subproblem under the k-th scenario; represents the number of iterations. Equation (54) pertains to the second part of Equation (52), where W is the maximum value for the worst-case scenario.
Given the variables in the MP, the SP iterates and finds the worst probability distribution scenario under the current MP situation. The SP results are then fed back to the MP for iteration. The SP’s solution to Equation (52) provides an upper bound:
Within the innermost minimization term in Equation (55), problems for each scenario are independent. The inner minimization function can be represented as a parallel solution denoted by . Thus, Equation (55) can be rewritten in parallel solution form:
In summary, the MP and SP models for Equation (52) alternate in solving through iterations and variable updates via Equations (53), (54) and (56) until a predetermined accuracy is achieved, concluding the iterative process. Through continuous iteration and updating, the problem can be gradually optimized, approaching the optimal solution.
5.2. Second Stage: Non-Cooperative Game-Based Clearance and Settlement of Shared Electricity
After completing the first stage of electricity sharing, the second stage involves calculating the clearance and settlement of shared electricity models for each microgrid. As each microgrid pursues an individual optimal trend based on this paper’s optimization objectives, it is essential that each microgrid benefits from electricity sharing. A non-cooperative game-based model is established to determine the clearance and settlement of shared electricity, achieving a Nash equilibrium state where each microgrid’s operational cost is reduced, consequently lowering the total operational cost of the multi-microgrid system. This model is considered fair for all microgrids.
The incentive for participation: for each microgrid i, the operational cost reduction after electricity sharing must be greater than zero to motivate participation:
Call a microgrid I with reduced operating costs. The reduced operating cost ratio of a microgrid is defined as the ratio of the difference between the actual reduced operating cost and the maximum reduced operating cost to the maximum reduced operating cost. This reduction rate is formulated to minimize the squared sum of the reduction rates, subject to the constraints defined in Equation (27) within the microgrid inter-energy trading model. The objective is to minimize the squared sum of the reduction rates, aiming to bring the actual reduction in the operational costs of microgrid I as close as possible to the maximum reduction. This payment determination method is referred to as the Cost Reduction Ratio Distribution (CRRD) model, ensuring fairness among all microgrids. Each microgrid benefits from this model, and consequently, it is accepted by all microgrids. The specific formulation is provided below.
Firstly, incentivize each microgrid to participate in energy sharing, thereby reducing the operational costs for each microgrid. A feasible range for the transaction unit price of energy sharing, denoted as , can be determined. If all microgrids engage in energy sharing with a payment unit price within this range, the incentive condition in Equation (57) can be satisfied, encouraging the participation of all microgrids in energy sharing:
Subject to:
where and represent the maximum and minimum transaction unit prices, respectively, for the shared energy by the microgrid. The variable denotes the purchased electricity by microgrid I during period t.
The optimization problem above is to find the feasible upper bound for and the feasible lower bound for . Equation (59) addresses the worst-case scenario, ensuring all microgrids benefit from energy sharing, where microgrid I purchases energy at the maximum transaction unit price when buying and sells it at the minimum unit price when selling during energy sharing.
Equation (61) represents the idealized scenario for energy sharing payments, where microgrid I buys energy at the minimum transaction unit price when purchasing and sells it at the maximum unit price when selling during energy sharing. Evaluating the maximum cost reduction involves computing the idealized scenario, considering the constraints presented in Equation (27). However, it is impractical for all microgrids to achieve the idealized scenario in energy-sharing transactions.
Each microgrid participating in the game aims to maximize the reduction in its own operating costs, i.e., minimizing the rate of cost reduction. The variable is introduced to represent the cost reduction rate of the microgrid:
Subject to:
Note that the above optimization problem is strictly convex, therefore having a unique optimal solution when the feasible region is non-empty [23]. By substituting (63) into (27), we obtain the following constraint on to replace the coupling of in constraint (27):
Therefore, the decision variables include , , and , and the unique coupling constraint among them is (63). Let , so the regularized Lagrangian optimization function for the non-cooperative game is:
Based on the above formulas, the CRRD model can be solved in a distributed manner, such as using the ADMM framework. The algorithm process is shown in Table 1.

Table 1.
Retail electricity prices and feed-in tariffs on the main grid.
In Table 1, the variables and in Steps 3 and 4 are extracted from for minimizing the relevant objective functions and . Let and represent the optimal solution of the CRRD model.
Note that both Figure 2 (C&CG) and Algorithm 1 (ADMM) can be implemented in a distributed manner supported by a point-to-point energy-sharing platform. The local decision updates for each microgrid do not require any private information from other microgrids, and the updates to auxiliary variables only necessitate limited information from the microgrids. This approach ensures the privacy of microgrids.
| Algorithm 1 Solving the CRRD Model in the ADMM Framework |
| 1: Initialize , , , , |
| 2: repeat |
| 3: Every microgrid , updates : |
| 4: update : |
| 5: update : |
| 6: |
| 7: until |
After the execution of Figure 2 and Algorithm 1, once the energy-sharing configuration and payments are completed, actual energy sharing will take place in the energy management of microgrids. Payments will be facilitated through the point-to-point energy-sharing platform.
6. Case Study and Results
In the example of a nine-node microgrid system, the electrical system decomposition diagram is illustrated in Figure 3. The microgrid system comprises wind turbines (W), photovoltaic devices (P), gas turbines (G), and energy storage (E).
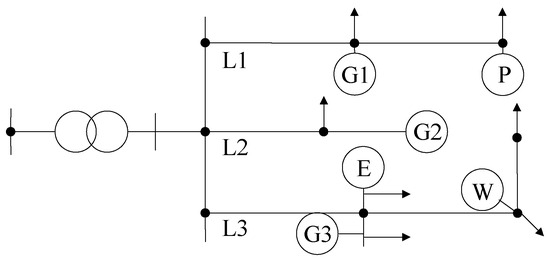
Figure 3.
Microgrid Electrical System Structure.
Power network constraints [24]: The power grid is modeled using the non-convex formulation of the branch flow model. Constraints (67)–(70) represent the branch power flow equations. Constraints (71) and (72) impose square limits on the voltage and current magnitudes.
In the equation: represents the active power flow of line (m, n); is the reference active power of node n; is the sum of active power flows from node n to all outgoing lines; represents the resistance of the line (m, n); is the square of the current magnitude of line (m, n); is the line from bus m to bus n in the power network; is the reactive power flow of line (m, n); is the reference reactive power of node n; is the sum of reactive power flows from node n to all outgoing lines; is the reactance of line (m, n); and are the square of the voltage magnitude at nodes n and m, respectively; and are the minimum and maximum values of the square of the voltage magnitude at node n; is the maximum value of the square of the current magnitude at node n.
To validate the feasibility and effectiveness of the proposed model, three microgrids are taken as examples. Table 1 provides the retail electricity price and grid electricity price of the main grid. The electric, heating, and cooling loads of the three microgrids are illustrated in Figure 4, Figure 5 and Figure 6, respectively. Microgrid 1 exclusively considers wind power generation as the form of renewable energy, while microgrids 2 and 3 exclusively consider solar power generation (with different solar resources for the two microgrids). Figure 7, Figure 8 and Figure 9 illustrate the generation resources of renewable energy within each microgrid, simulated using a dataset spanning 10 days. At different time points, surplus energy can be mutually utilized through complementary means. By employing game theory and profit distribution mechanisms, collaborative scheduling among multiple microgrids is realized to optimize energy utilization efficiency and system performance.
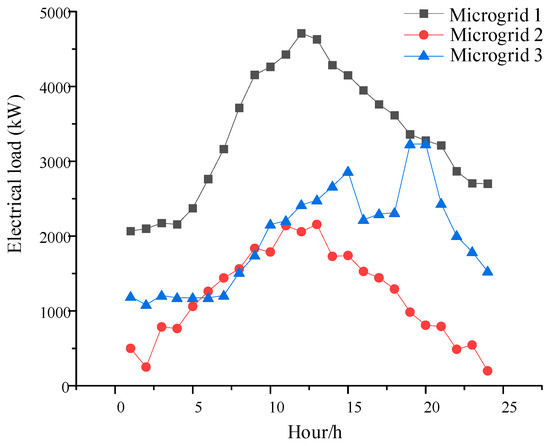
Figure 4.
Microgrid reference electrical load curve.
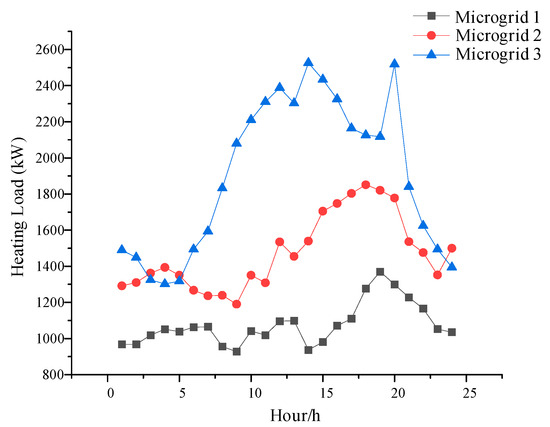
Figure 5.
Microgrid reference heating load curve.
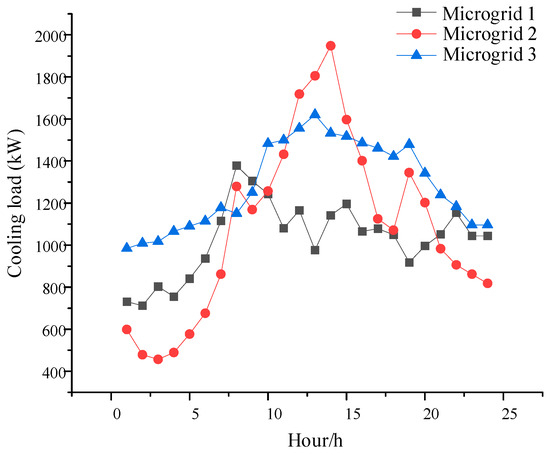
Figure 6.
Microgrid reference cooling load curve.
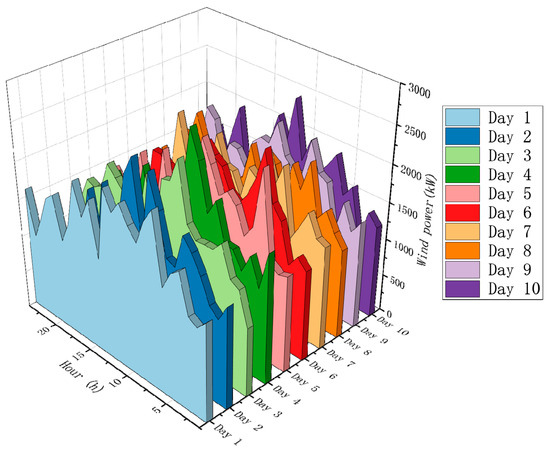
Figure 7.
Microgrid 1 reference wind power generation.
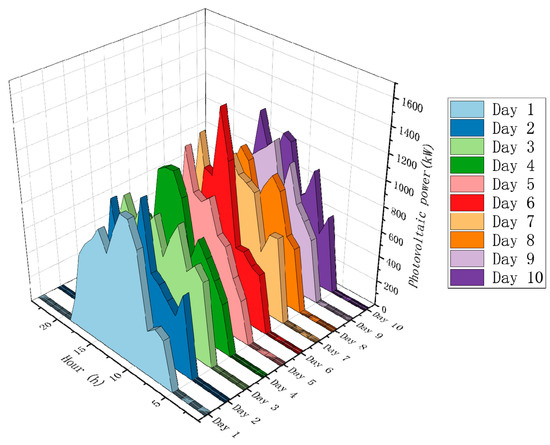
Figure 8.
Microgrid 2 reference PV generation.
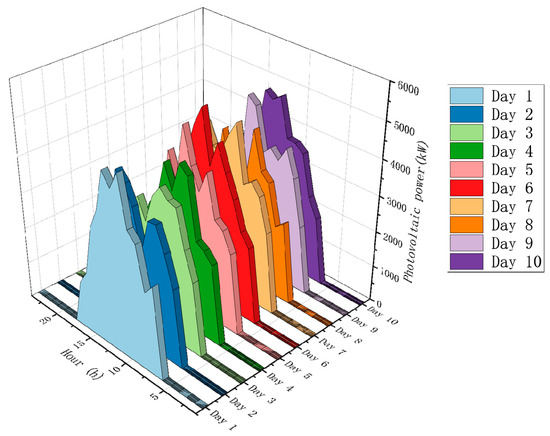
Figure 9.
Microgrid 3 reference PV generation.
In the text, the price deviation coefficient () is set to 0.1; the electricity price uncertainty parameter () is set to 5; the confidence intervals for wind and solar uncertainties are set at α = 0.95 and β = 0.99, respectively. The natural gas price is assumed to be 2.2 CNY/m3 in the Jiangsu region, with a heating value of 9.7 kW·h/m3. The power for buying and selling electricity between microgrids and the main grid is set at ±2000 kW, and the power for energy sharing among microgrids is ±2000 kW. The main parameters of each device and the node parameters of the microgrid can be found in references [8,21,24].
6.1. Energy Sharing Transaction Results among Microgrids
The results of energy transactions among Microgrid 1, Microgrid 2, and Microgrid 3 are illustrated in Figure 10. It is evident from the figure that the power of electricity transactions among the microgrids is in a real-time balanced state, achieving effective energy sharing and trading.
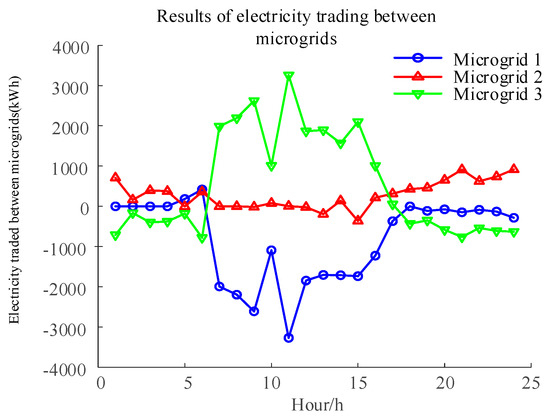
Figure 10.
Multi−microgrid power sharing transaction results.
Microgrid 1 sells electricity externally from 04:00 to 06:00, demonstrating characteristics of a surplus electricity microgrid. From 07:00 to 24:00, it buys electricity externally, indicating a deficit electricity microgrid. It does not engage in electricity transactions from 00:00 to 4:00, representing a self-sufficient microgrid.
Microgrid 2 sells electricity externally from 00:00 to 07:00 and 16:00 to 24:00, showing characteristics of a surplus electricity microgrid. It engages in minimal external electricity transactions from 07:00 to 15:00.
Microgrid 3 buys electricity externally from 00:00 to 06:00 and 18:00 to 24:00, indicating characteristics of a deficit electricity microgrid. From 08:00 to 17:00, it sells electricity externally, representing a surplus electricity microgrid.
To illustrate the optimization results of electric, heating, and cooling power dispatch before and after electricity sharing, we can take Microgrid 1 as an example.
Figure 11 shows that after electricity sharing, there is a significant increase in shared electricity compared to before sharing, with a focus on the period from 07:00 to 17:00. This concentration is due to the fact that the renewable energy source of the other two microgrids is photovoltaic power generation, and during periods of high photovoltaic generation in these microgrids, shared electricity is absorbed to enhance the efficiency of renewable energy utilization. Simultaneously, this practice significantly reduces the amount of electricity purchased from the main grid. The price-based electricity load demand response plan involves shifting the transferrable electrical load from high-price periods to low-price periods. Calculated using Formula (19), Microgrid 1 is projected to save ¥1472.06 by implementing this price-based electricity load demand response plan. During the fixed load phase, Microgrid 1 adopts a strategy to reduce electricity purchases and increase gas turbine power generation during high−price periods to counteract the high cost of electricity purchases. Based on grid selling prices, shared electricity costs, along with its own electricity load, and renewable energy output, Microgrid 1 adjusts the distribution of its electrical load to achieve the optimal state of electrical energy output. Energy storage primarily charges during low-price periods and discharges during high-price periods.
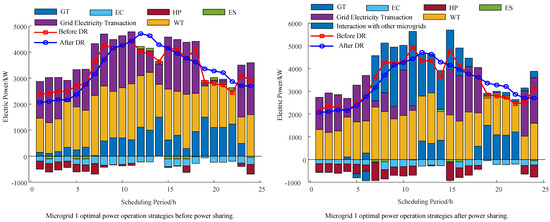
Figure 11.
Comparison of electric power dispatch optimization results before and after microgrid 1 electric power sharing.
As depicted in Figure 12, a substantial reduction in gas turbine-based heating is observed after the implementation of electricity sharing compared to before. This reduction is attributed to the dual functionality of the gas turbine, capable of generating both electricity and heat. The introduction of a significant amount of shared electricity, as shown in Figure 10, results in a decreased workload for the gas turbine, consequently influencing a decrease in the heat generation capacity of the gas turbine. Microgrid 1 is primarily supplied with heating from a gas turbine and a ground-source heat pump. The gas turbine generates heat during power generation, while the ground-source heat pump consumes electricity to produce heat. Through their respective constraints and considering shared electricity, a balance is achieved. A portion of the heating load is provided by an absorption chiller. Thermal energy storage is charged when thermal energy is abundant and discharged during periods of high heating costs.
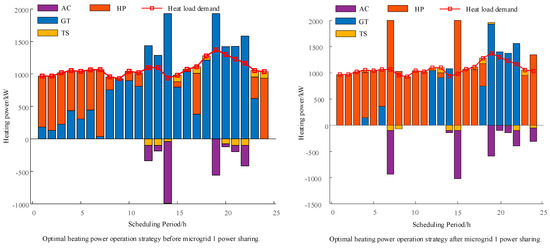
Figure 12.
Comparison of heating power dispatch optimization results before and after microgrid 1 electric power sharing.
As shown in Figure 13, after the implementation of electricity sharing, there is a significant decrease in the electricity-driven cooling provided by the electric chiller compared to the period before electricity sharing. Simultaneously, there is a substantial increase in the absorption chiller’s operation. Microgrid 1’s cooling system consists mainly of an electric chiller and an absorption chiller. During the cooling process, the absorption chiller provides cooling during periods of relatively low thermal energy costs, while the electric chiller achieves cooling by consuming electricity. Considering their respective constraints and shared electricity, Microgrid 1 adjusts the operation of the two cooling devices to achieve a balance between cooling load and cooling capacity.
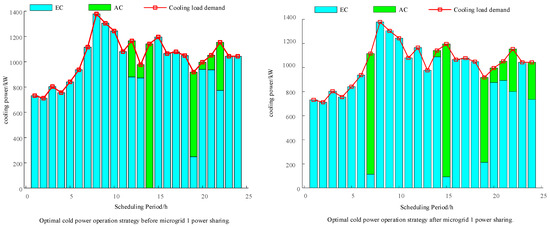
Figure 13.
Comparison of cooling power dispatch optimization results before and after microgrid 1 electric power sharing.
6.2. Microgrid System Cost and Revenue Analysis
A comparison of the cost results for multiple microgrids is presented in Table 2 for scenarios with and without considering energy sharing. In the scenario allowing energy sharing, the total operating cost of multiple microgrids is lower than in the scenario without energy sharing. The total costs for the three microgrids decreased by CNY 2046.7708, CNY 1241.1888, and CNY 1959.6289, with reduction rates of 4.55%, 4.70%, and 6.34%, respectively. The post-transaction total cost decreased by CNY 5247.5885, with a reduction rate of 5.13%. It can be observed that the costs for each microgrid significantly decrease under the new planning, reflecting the fairness in profit distribution. This indicates that the proposed energy-sharing trading mechanism can simultaneously improve the economic benefits of both society and individuals. This is because each microgrid cannot only focus on its own interests but must also consider the balance of energy-sharing payments, reflected in the almost zero-sum of all energy-sharing payments. The error is caused by the precision of Formula (65) and the accuracy of Algorithm 1.

Table 2.
The operation cost of microgrids.
The payment settlement method of the Cost Reduction Ratio Distribution (CRRD) is employed in this study. The calculated maximum transaction price for shared energy is CNY 0.79057, and the minimum transaction price is CNY 0.60198. Within this range of shared energy transaction prices, each microgrid can benefit from energy sharing. That is, within this range of transaction prices, each microgrid is incentivized to participate in trading. Therefore, the CRRD model is both economical and fair and can be accepted by each microgrid. In conclusion, this further validates the economic efficiency and fairness of this framework.
6.3. Impact Analysis of Electricity Price Uncertainty Coefficient on Microgrids
Based on the data in Table 3, the following results can be observed: as the electricity price deviation coefficient increases, the operating costs of each microgrid and the multi-microgrid system gradually increase. It can be seen that the penalty costs caused by electricity price fluctuations lead to an increase in the operating costs of each microgrid and the multi-microgrid system.

Table 3.
The influence of the electricity price deviation coefficient on the multi-microgrid system.
According to the data in Table 4, it can be observed that under different numbers of periods of electricity price uncertainty, the costs of the multi-microgrid system after cooperation gradually increase. This implies that with an increase in the number of periods of electricity price uncertainty, the electricity price fluctuates at more time intervals, leading to an increase in the costs of each microgrid and consequently causing the costs of the multi-microgrid system after cooperation to gradually rise.

Table 4.
The impact of electricity price uncertainty periods on the multi-microgrid system.
6.4. Impact Analysis of Wind and Solar Uncertainty Confidence Levels
In this section, an analysis is conducted by evaluating the computational results of the multi-microgrid system using a historical data count of 100 and a discrete scenario count of 10 for different confidence intervals ( and ).
As observed from Table 5, with the increase in the confidence interval values, the operating costs of the multi-microgrid system gradually increase. When the confidence interval increases, the uncertainty of photovoltaic and wind power output also increases, requiring more energy from other sources to compensate for this uncertainty. This, in turn, leads to an increase in the overall costs. This observation aligns with the pattern revealed in Equation (35), further validating the correctness of the computational results.

Table 5.
Comparison of results at different confidence levels.
7. Conclusions
This study explores the collaborative management and cost settlement of shared electrical energy in multi-microgrids, employing a two-stage collaborative scheduling model. In the first stage of the model, considering electricity price fluctuations and uncertainties in wind and photovoltaic power outputs, point-to-point energy sharing among microgrids is allowed, and a multi-microgrid energy management model is established. Fo solving, the C&CG algorithm is employed. In the second stage of the model, addressing the issue of shared energy payment distribution, a Cost Reduction Ratio Distribution (CRRD) model based on non-cooperative game theory is proposed. The Nash equilibrium is utilized to determine the transaction settlement of shared energy, and the ADMM algorithm is applied for solving. Finally, the feasibility and effectiveness of the proposed method and model are verified through case analysis.
The main conclusions of this work are summarized as follows:
1. In the proposed model, the sharing of electrical energy among microgrids reduces the overall operating costs of the multi-microgrid system.
2. A CRRD model based on non-cooperative game theory is established for point-to-point transactions, ensuring fairness in shared transactions and reducing the operating costs of each microgrid.
3. Considering uncertainties in wind and photovoltaic power outputs as well as electricity price fluctuations enhances the stability of the developed model, facilitating the integration of renewable energy generation.
4. Variations in the deviation coefficient, electricity price uncertainty periods, and the confidence intervals ( and ) of wind and solar power output have an impact on the total operating costs of the multi-microgrid system, leading to cost increases.
Author Contributions
Conceptualization, X.G. and X.Z.; methodology, X.G.; software, X.G.; validation, X.G. and X.Z.; formal analysis, X.G.; investigation, X.G.; resources, X.G.; data curation, X.G.; writing—original draft preparation, X.G.; writing—review and editing, X.G.; visualization, X.G.; supervision, X.Z.; project administration, X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Xinjiang Uygur Autonomous Region (2021D01C044).
Data Availability Statement
Most of the data has been shown in the article. Some core data are private to our lab.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, C.; Hong, B.; Guo, L.; Zhang, D.; Liu, W. A General Modeling Method for Optimal Dispatch of Combined Cooling, Heating and Power Microgrid. Proc. CSEE 2013, 33, 26–33+3. [Google Scholar]
- Lin, K.; Wu, J.; Hao, L.; Liu, D.; Li, D.; Yan, H. Optimization of Operation Strategy for Micro-energy Grid with CCHP Systems Based on Non-cooperative Game. Autom. Electr. Power Syst. 2018, 42, 25–32. [Google Scholar]
- Gu, W.; Wang, Z.; Wu, Z.; Luo, Z.; Tang, Y.; Wang, J. An online optimal dispatch schedule for CCHP microgrids based on model predictive control. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 2332–2342. [Google Scholar]
- Li, G.; Liu, W.; Cai, J.; Hong, B.; Wang, C. A two-stage optimal planning and design method for combined cooling, heat and power microgrid system. Energy Convers. Manag. 2013, 74, 433–445. [Google Scholar]
- Xu, Q.; Li, L.; Sheng, Y.; Huo, X.; Zhao, B. Day-Ahead Optimized Economic Dispatch of Active Distribution Power System with Combined Cooling, Heating and Power-Based Microgrids. Power Syst. Technol. 2018, 42, 1726–1735. [Google Scholar]
- Tan, S.; Liu, Y.; Xu, L.; Wang, H. Energy Transaction Mode in the Regional Multi-microgrid Connected Distribution Network Considering Wind Power Accommodation. Electr. Power Constr. 2019, 40, 1–9. [Google Scholar]
- Wang, S.; Wu, Z.; Yuan, S.; Zhuang, J. Method of Multi-objective Optimal Dispatching for Regional Multi-microgrid System. Proc. CSU-EPSA 2017, 29, 14–20. [Google Scholar]
- Wu, S.; Liu, J.; Zhou, Q.; Wang, C.; Chen, Z. Optimal Economic Scheduling for Multi-microgrid System with Combined Cooling, Heating and Power Considering Service of Energy Storage Station. Autom. Electr. Power Syst. 2019, 43, 10–18. [Google Scholar]
- Li, P.; Wu, D.; Li, Y.; Liu, H.; Wang, N.; Zhou, X. Optimal Dispatch of Multi-microgrids Integrated Energy System Based on Integrated Demand Response and Stackelberg game. Proc. CSEE 2021, 41, 1307–1321+1538. [Google Scholar]
- Yang, Z.; Ai, X. Distributed Optimal Scheduling for Integrated Energy Building Clusters Considering Energy Sharing. Power Syst. Technol. 2020, 44, 3769–3778. [Google Scholar]
- Cui, S.; Wang, Y.; Xiao, J. Peer-to-Peer Energy Sharing Among Smart Energy Buildings by Distributed Transaction. IEEE Trans. Smart Grid 2019, 10, 6491–6501. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Sun, Q.; Zhang, Y.; Liu, Z.; He, J. Multi-agent Real-time Collaborative Optimization Strategy for Integrated Energy System GroupBased on Energy Sharing. Autom. Electr. Power Syst. 2022, 46, 56–65. [Google Scholar]
- Wang, H.; Huang, J. Incentivizing Energy Trading for Interconnected Microgrids. IEEE Trans. Smart Grid 2018, 9, 2647–2657. [Google Scholar] [CrossRef]
- Li, J.; Zhang, C.; Xu, Z.; Wang, J.; Zhao, J.; Zhang, Y. Distributed transactive energy trading framework in distribution networks. IEEE Trans. Power Syst. 2018, 33, 7215–7227. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.; Bahrami, S.; Wong, V. Direct Energy Trading of Microgrids in Distribution Energy Market. IEEE Trans. Power Syst. 2020, 35, 639–651. [Google Scholar] [CrossRef]
- Xu, D.; Zhou, B.; Liu, N.; Wu, Q.; Nikolai, V.; Li, C.; Evgeny, B. Peer-to-Peer Multienergy and Communication Resource Trading for Interconnected Microgrids. IEEE Trans. Ind. Inform. 2021, 17, 2522–2533. [Google Scholar] [CrossRef]
- Li, J.; Zhao, X.; Zheng, Y.; Zhang, D. Optimal configuration of a regional integrated energy system considering energy sharing based on Nash negotiation. Power Syst. Prot. Control. 2023, 51, 22–32. [Google Scholar]
- Feng, C.; Ren, D.; Shen, J.; Wen, F.; Zhang, Y. Distributed Coordinated Optimal Scheduling of Interconnected Micro-energy GridsConsidering Multi-energy Sharing. Autom. Electr. Power Syst. 2022, 46, 47–57. [Google Scholar]
- Shui, Y.; Liu, J.; Gao, H.; Qiu, G.; Xu, W.; Guo, J. Two-stage Distributed Robust Cooperative Dispatch for Integrated Electricity and Natural Gas Energy Systems Considering Uncertainty of Wind Power. Autom. Electr. Power Syst. 2018, 42, 43–50+75. [Google Scholar]
- Zhao, C.; Guan, Y. Data-Driven Stochastic Unit Commitment for Integrating Wind Generation. IEEE Trans. Power Syst. 2016, 31, 2587–2596. [Google Scholar] [CrossRef]
- Ding, T.; Yang, Q.; Yang, Y.; Li, C.; Bie, Z.; Frede, B. A Data-Driven Stochastic Reactive Power Optimization Considering Uncertainties in Active Distribution Networks and Decomposition Method. IEEE Trans. Smart Grid 2018, 9, 4994–5004. [Google Scholar] [CrossRef]
- Du, J.; Han, X.; Li, T.; Yin, Z.; Bai, H. Optimization Strategy of Multi Microgrid Electric Energy Cooperative Operation Considering Electricity Price Uncertainty and Game Cheating Behaviors. Power Syst. Technol. 2022, 46, 4217–4230. [Google Scholar] [CrossRef]
- Cui, S.; Wang, Y.; Shi, Y.; Xiao, J. A New and Fair Peer-to-Peer Energy Sharing Framework for Energy Buildings. IEEE Trans. Smart Grid 2020, 11, 3817–3826. [Google Scholar] [CrossRef]
- Coelho, A.; Iria, J.; Soares, F.; Lopes, J.P. Real-time management of distributed multi-energy resources in multi-energy networks. Sustain. Energy Grids Netw. 2023, 34, 101022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).