Model-Free Approach to DC Microgrid Optimal Operation under System Uncertainty Based on Reinforcement Learning
Abstract
1. Introduction
1.1. Related Work
1.2. Contributions
- Propose a novel model-free approach for solving the LVDCMG optimal switching problem
- Demonstrate the ability of a reinforcement learning algorithm to solve LVDCMG optimal switching problem under measurement noise and imprecise power system mode
- Provide a minimal working example for applying reinforcement learning parameters in the LVDCMG optimal switching problem
2. Operation Control of DC Microgrids
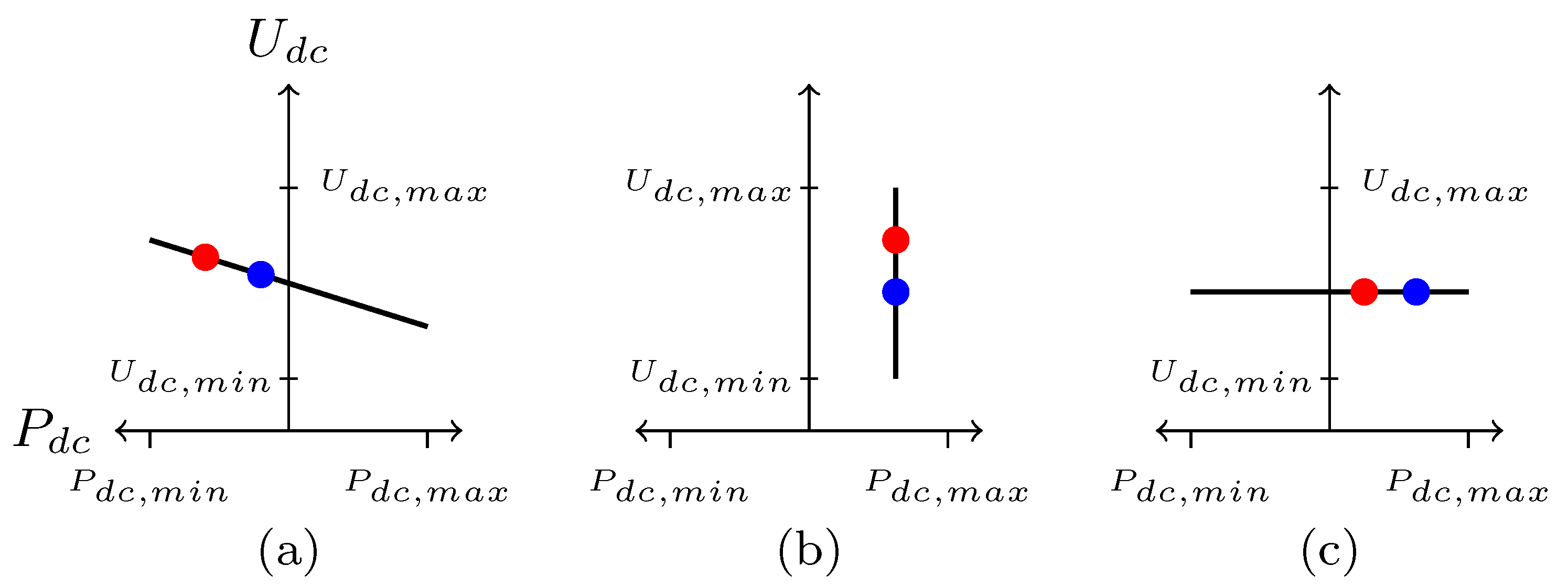
2.1. Models of DC Microgrids
2.2. Problem Statement
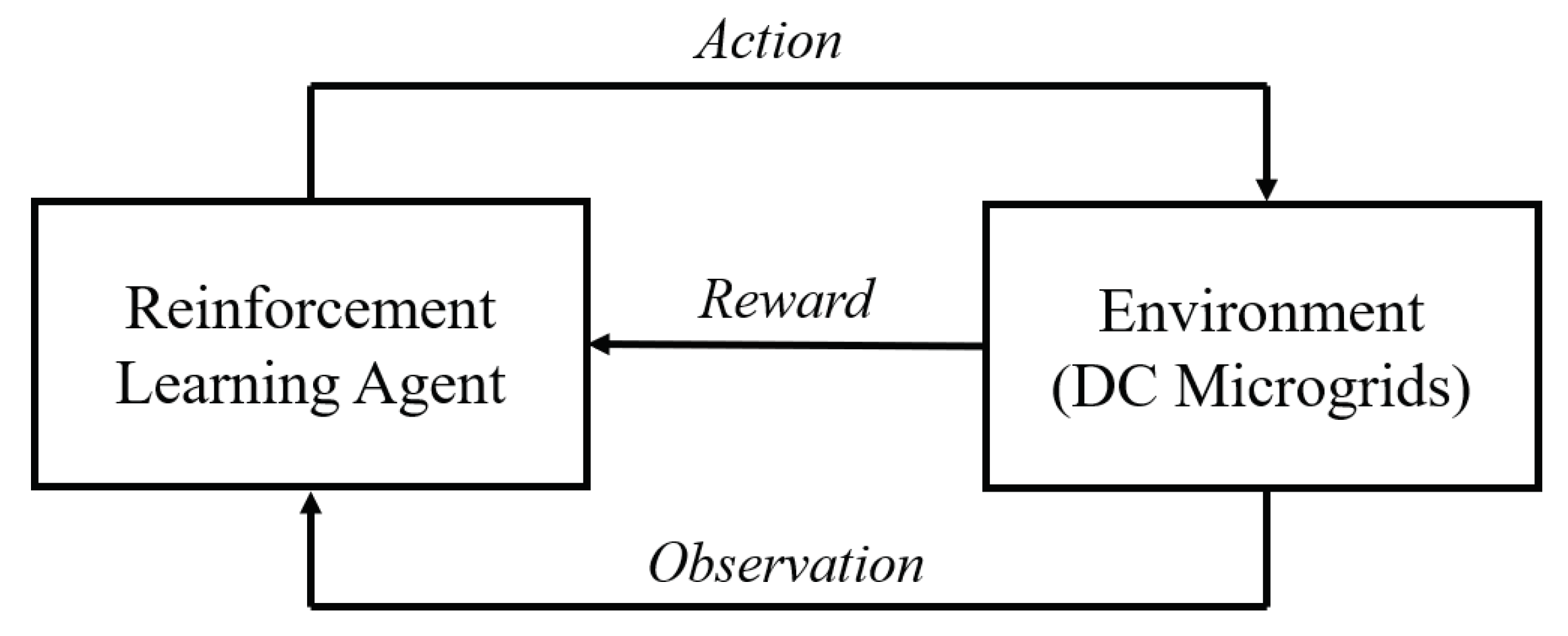
3. Reinforcement-Learning-Based Operation Control
3.1. DC Microgrids as a Markov Decision Process
- the future state only depends on the current state , not the previous state history,
- the system accepts a finite set of actions at every step,
- the system will provide state information and reward at every step.
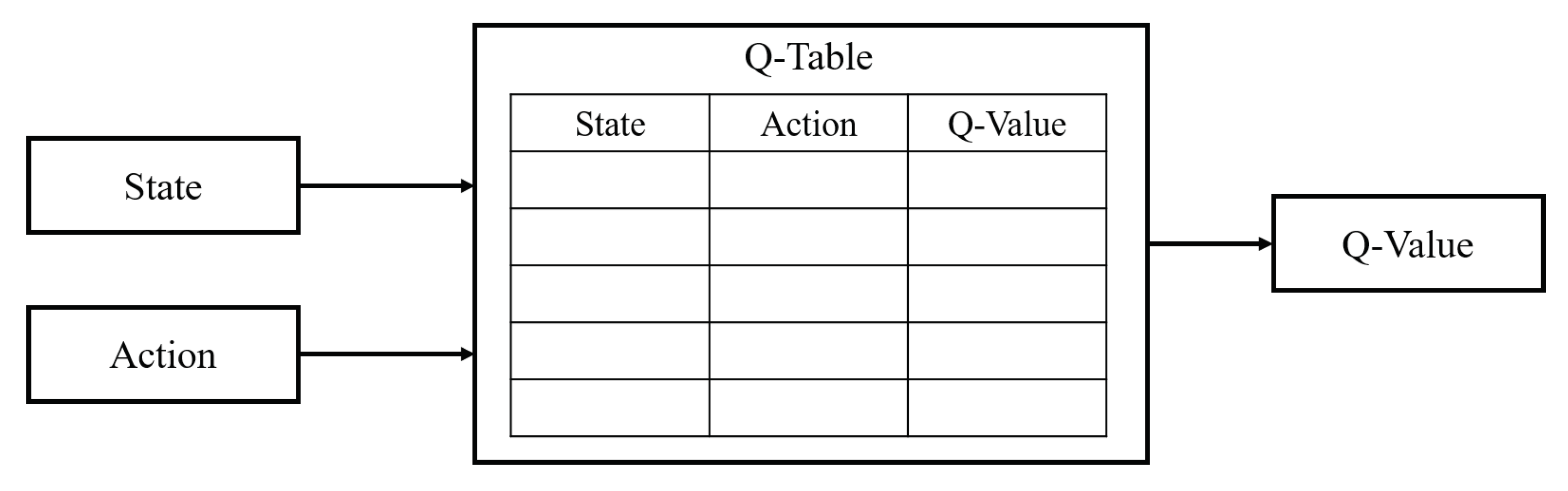
3.2. Q-Learning for Near-Optimal Operation Control
3.3. Q-Network for Operation Control under Uncertainty
4. Methodologies
- A simple environment: a simplified version of DC microgrid system consisting of a single source and a single load connected via a transmission line (). The system can be operated in 2 different modalities (). The number of update steps in a single episode of operation is set to be . For simplicity, the state equation matrices are simplified and assumed to be for mode and for mode .
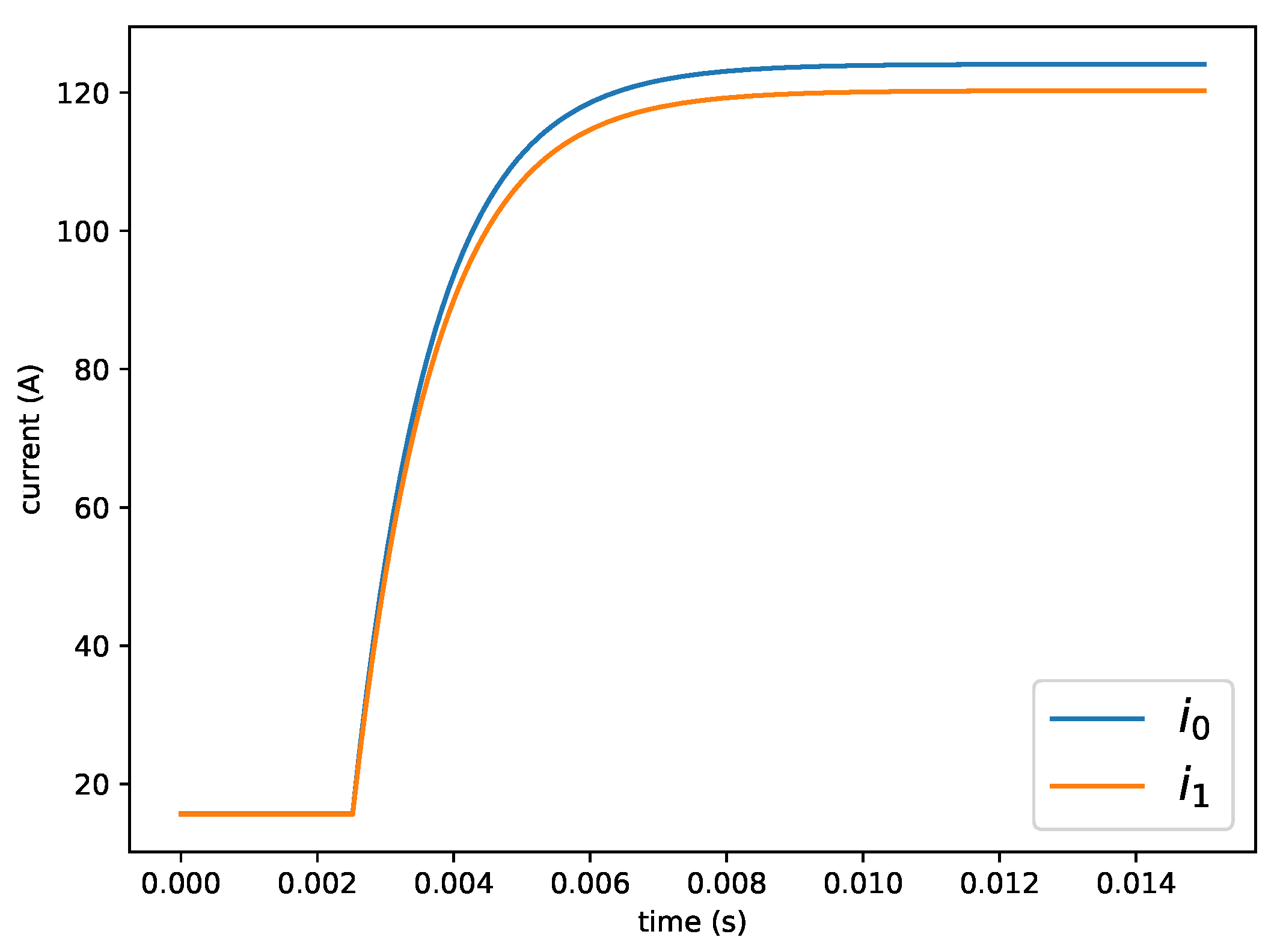
- A complex environment: a more realistic DC microgrid system consisting of 3 nodes. Each node consists of a source and/or a load. Two transmission lines () connect Node 1 and Node 2 as well as Node 2 and Node 3 as shown in Figure 6. The system can be operated in 2 different modalities (). The number of update steps in a single episode of operation is set to be . In this environment, it is assumed that the system’s mode of operation can only be updated once every 1 s. The state equation matrices used in this environment are derived from (16)–(22).
5. Results
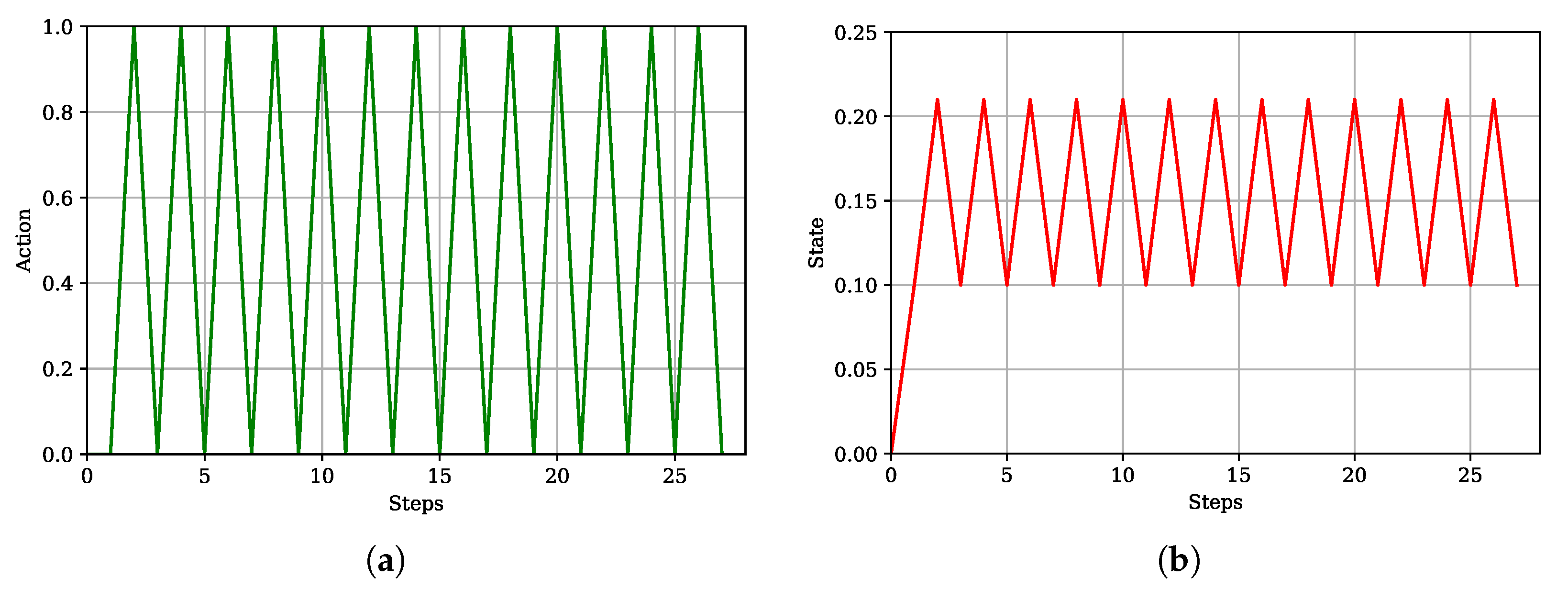
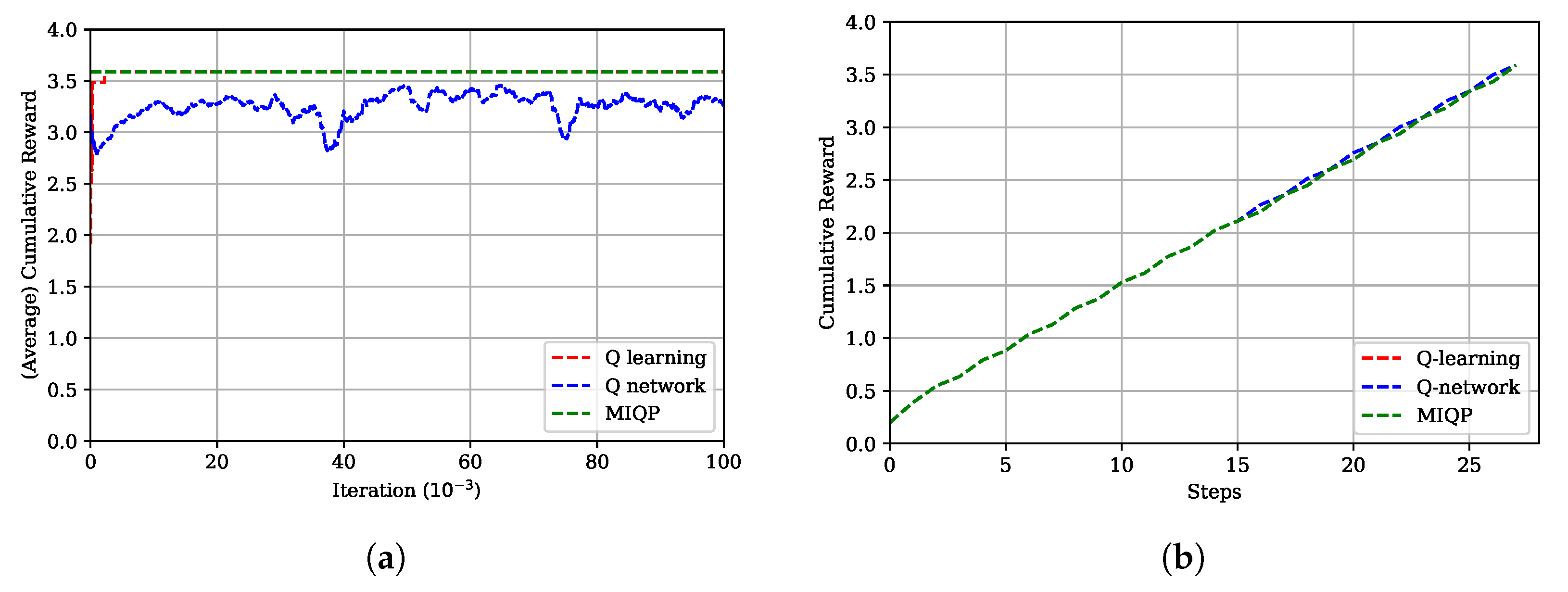
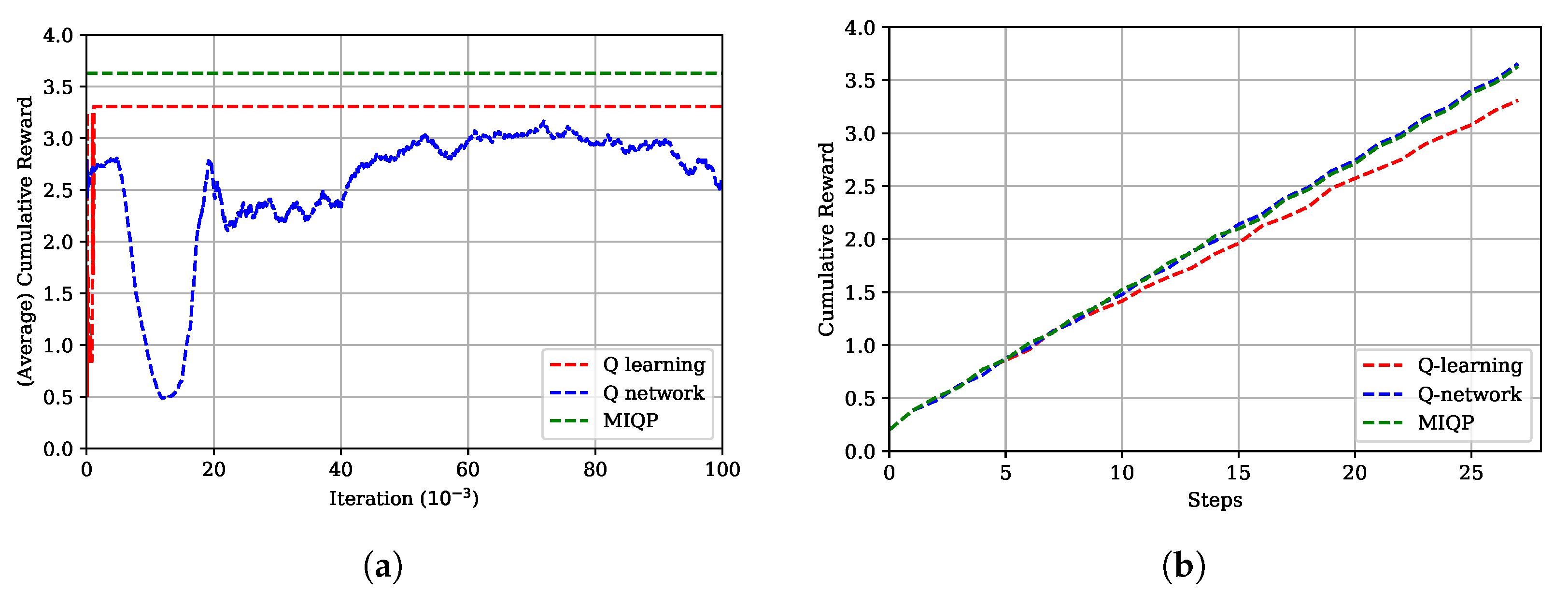
5.1. Simple Environment
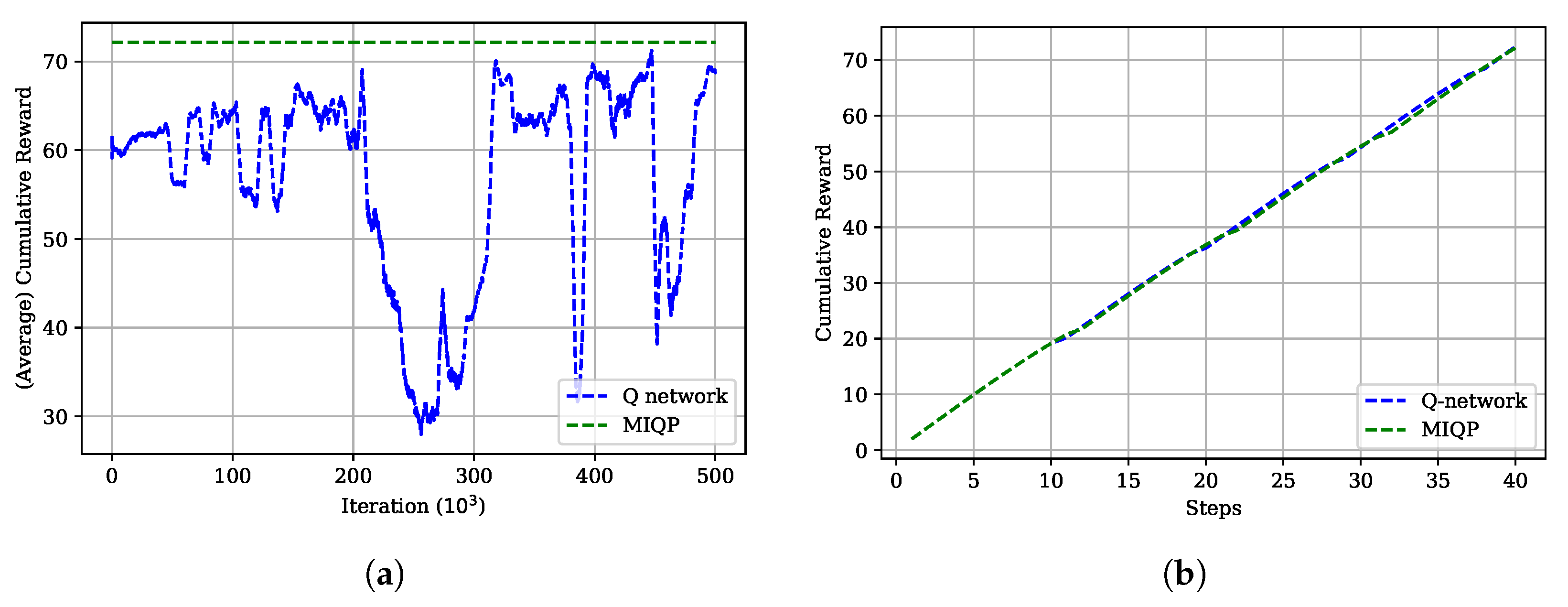
5.2. Complex Environment
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | alternating current |
| ACMG | AC microgrids |
| ADP | adaptive dynamic programming |
| BESS | battery energy storage system |
| CPS | constant power source |
| CPL | constant power load |
| DC | direct current |
| DCMG | DC microgrids |
| DOD | depth of discharge |
| DVS | droop-controlled voltage source |
| ESS | energy storage system |
| GA | genetic algorithm |
| HVAC | high voltage AC |
| KCL | Kirchoff’s current law |
| KVL | Kirchoff’s voltage law |
| LVDCMG | low-voltage DCMG |
| MDP | Markov decission process |
| MILP | mixed-integer linear programming |
| MIQP | mixed-integer quadratic programming |
| MVAC | medium voltage AC |
| PMU | phasor measurement unit |
| PSO | particle swarm optimization |
| PV | photo-voltaic |
| RL | reinforcement learning |
| SC | supervisory control |
| SOC | atate of charge |
| TS | tabu search |
| VVC | Volt/Var control |
References
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galván, E.; PortilloGuisado, R.C.; Prats, M.M.; León, J.I.; Moreno-Alfonso, N. Power-electronic systems for the grid integration of renewable energy sources: A survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuna, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Hou, N.; Li, Y. Communication-Free Power Management Strategy for the Multiple DAB-Based Energy Storage System in Islanded DC Microgrid. IEEE Trans. Power Electron. 2021, 36, 4828–4838. [Google Scholar] [CrossRef]
- Irnawan, R.; da Silva, F.F.; Bak, C.L.; Lindefelt, A.M.; Alefragkis, A. A droop line tracking control for multi-terminal VSC-HVDC transmission system. Electr. Power Syst. Res. 2020, 179, 106055. [Google Scholar] [CrossRef]
- Peyghami, S.; Mokhtari, H.; Blaabjerg, F. Chapter 3—Hierarchical Power Sharing Control in DC Microgrids. In Microgrid; Mahmoud, M.S., Ed.; Butterworth-Heinemann: Oxford, UK, 2017; pp. 63–100. [Google Scholar] [CrossRef]
- Shuai, Z.; Fang, J.; Ning, F.; Shen, Z.J. Hierarchical structure and bus voltage control of DC microgrid. Renew. Sustain. Energy Rev. 2018, 82, 3670–3682. [Google Scholar] [CrossRef]
- Abhishek, A.; Ranjan, A.; Devassy, S.; Kumar Verma, B.; Ram, S.K.; Dhakar, A.K. Review of hierarchical control strategies for DC microgrid. IET Renew. Power Gener. 2020, 14, 1631–1640. [Google Scholar] [CrossRef]
- Chouhan, S.; Tiwari, D.; Inan, H.; Khushalani-Solanki, S.; Feliachi, A. DER optimization to determine optimum BESS charge/discharge schedule using Linear Programming. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Maulik, A.; Das, D. Optimal operation of a droop-controlled DCMG with generation and load uncertainties. IET Gener. Transm. Distrib. 2018, 12, 2905–2917. [Google Scholar] [CrossRef]
- Dragičević, T.; Guerrero, J.M.; Vasquez, J.C.; Škrlec, D. Supervisory Control of an Adaptive-Droop Regulated DC Microgrid With Battery Management Capability. IEEE Trans. Power Electron. 2014, 29, 695–706. [Google Scholar] [CrossRef]
- Massenio, P.R.; Naso, D.; Lewis, F.L.; Davoudi, A. Assistive Power Buffer Control via Adaptive Dynamic Programming. IEEE Trans. Energy Convers. 2020, 35, 1534–1546. [Google Scholar] [CrossRef]
- Massenio, P.R.; Naso, D.; Lewis, F.L.; Davoudi, A. Data-Driven Sparsity-Promoting Optimal Control of Power Buffers in DC Microgrids. IEEE Trans. Energy Convers. 2021, 36, 1919–1930. [Google Scholar] [CrossRef]
- Ma, W.J.; Wang, J.; Lu, X.; Gupta, V. Optimal Operation Mode Selection for a DC Microgrid. IEEE Trans. Smart Grid 2016, 7, 2624–2632. [Google Scholar] [CrossRef]
- Anand, S.; Fernandes, B.G. Reduced-Order Model and Stability Analysis of Low-Voltage DC Microgrid. IEEE Trans. Ind. Electron. 2013, 60, 5040–5049. [Google Scholar] [CrossRef]
- Alizadeh, G.A.; Rahimi, T.; Babayi Nozadian, M.H.; Padmanaban, S.; Leonowicz, Z. Improving Microgrid Frequency Regulation Based on the Virtual Inertia Concept while Considering Communication System Delay. Energies 2019, 12, 2016. [Google Scholar] [CrossRef]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction. IEEE Trans. Neural Netw. 2005, 16, 285–286. [Google Scholar] [CrossRef]
- Glavic, M. (Deep) Reinforcement learning for electric power system control and related problems: A short review and perspectives. Annu. Rev. Control 2019, 48, 22–35. [Google Scholar] [CrossRef]
- Wang, W.; Yu, N.; Gao, Y.; Shi, J. Safe off-policy deep reinforcement learning algorithm for volt-var control in power distribution systems. IEEE Trans. Smart Grid 2019, 11, 3008–3018. [Google Scholar] [CrossRef]
- Hadidi, R.; Jeyasurya, B. Reinforcement learning based real-time wide-area stabilizing control agents to enhance power system stability. IEEE Trans. Smart Grid 2013, 4, 489–497. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. A Multi-Agent Deep Reinforcement Learning Method for Cooperative Load Frequency Control of a Multi-Area Power System. IEEE Trans. Power Syst. 2020, 35, 4599–4608. [Google Scholar] [CrossRef]
- Bellman, R.E.; Dreyfus, S.E. CHAPTER XI. Markovian Decision Processes. In Applied Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 31 December 1962; pp. 297–321. [Google Scholar] [CrossRef]
- Goldwaser, A.; Thielscher, M. Deep Reinforcement Learning for General Game Playing. Proc. AAAI Conf. Artif. Intell. 2020, 34, 1701–1708. [Google Scholar] [CrossRef]
- Ibarz, J.; Tan, J.; Finn, C.; Kalakrishnan, M.; Pastor, P.; Levine, S. How to Train Your Robot with Deep Reinforcement Learning; Lessons We’ve Learned. arXiv 2021, arXiv:2102.02915. [Google Scholar]
- Graesser, L.; Keng, W. Foundations of Deep Reinforcement Learning: Theory and Practice in Python; Addison-Wesley Data & Analytics Series; Pearson Education: Londun, UK, 2019. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.A.; Fidjeland, A.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]






| Paper | Systems | Methods | ||
|---|---|---|---|---|
| Algorithm | Objective | Unknown | ||
| [11] | DCMG | PSO | Economic, Environment | Droop |
| [12] | DCMG | SC | Stability | Mode |
| [15] | DCMG | MILP | Economic, Stability | Mode |
| [13] | DCMG | ADP | Stability | Policy |
| [14] | DCMG | RL, TS | Topology, Stability | Edge, Policy |
| [17] | ACMG | GA | Stability, Frequency | Generation |
| [20] | AC | RL | Economic, Stability | Tap Changer |
| [21] | AC | RL | Stability | Control Signal |
| Ours | DCMG | RL | Economic, Stability | Mode |
| Paper | Voltage Level | Data Challenge | ||
| Delay | Noise | Error | ||
| [11] | LV | - | - | - |
| [12] | LV | - | - | - |
| [15] | LV | - | - | - |
| [13] | LV | - | - | - |
| [14] | LV | - | - | - |
| [17] | LV | ✓ | - | - |
| [20] | MV | - | - | - |
| [21] | HV | - | - | - |
| [22] | HV | - | - | - |
| Ours | LV | - | ✓ | ✓ |
| Param | Values | Units | |
|---|---|---|---|
| Simple | Complex | ||
| 0.9 | 0.9 | - | |
| 0.2 | 0.2 | - | |
| 0.99 | 0.99 | - | |
| 0.01 | 0.001 | - | |
| 0.2 | 2 | - | |
| 0 | 0 | ampere | |
| 0.01 | 0.1 | ampere | |
| 0.1 | 0.0001 | second | |
| 30 | 10 | % | |
| 1 | 0.00001 | - | |
| 0.1 | 1 | - | |
| 28 | 40 | - | |
| 30,000 | 50,000 | - | |
| 10,000 | 250,000 | - | |
| 0.02 | 0.02 | - | |
| System | Model Error | Noise | Best Reward/Cost per Episode | ||
|---|---|---|---|---|---|
| Q-Learning | Q-Network | MIQP | |||
| Simple | x | x | 3.5867 | 3.5867 | 3.5871 |
| ✓ | x | 3.3092 | 3.6554 | 3.6293 | |
| ✓ | ✓ | x | 3.6685 | 3.6667 | |
| Complex | x | x | 74.2707 | 74.4254 | 75.0489 |
| ✓ | x | 72.4335 | 72.3714 | 72.1596 | |
| ✓ | ✓ | x | 72.3714 | 72.1596 | |
| System Multiplier | Number of Nodes | Training Time (s) |
|---|---|---|
| 1 | 3 | 13.949822300113738 |
| 100 | 300 | 28.190732199931517 |
| 1000 | 3000 | 125.25556980003603 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irnawan, R.; Rizqi, A.A.A.; Yasirroni, M.; Putranto, L.M.; Ali, H.R.; Firmansyah, E.; Sarjiya. Model-Free Approach to DC Microgrid Optimal Operation under System Uncertainty Based on Reinforcement Learning. Energies 2023, 16, 5369. https://doi.org/10.3390/en16145369
Irnawan R, Rizqi AAA, Yasirroni M, Putranto LM, Ali HR, Firmansyah E, Sarjiya. Model-Free Approach to DC Microgrid Optimal Operation under System Uncertainty Based on Reinforcement Learning. Energies. 2023; 16(14):5369. https://doi.org/10.3390/en16145369
Chicago/Turabian StyleIrnawan, Roni, Ahmad Ataka Awwalur Rizqi, Muhammad Yasirroni, Lesnanto Multa Putranto, Husni Rois Ali, Eka Firmansyah, and Sarjiya. 2023. "Model-Free Approach to DC Microgrid Optimal Operation under System Uncertainty Based on Reinforcement Learning" Energies 16, no. 14: 5369. https://doi.org/10.3390/en16145369
APA StyleIrnawan, R., Rizqi, A. A. A., Yasirroni, M., Putranto, L. M., Ali, H. R., Firmansyah, E., & Sarjiya. (2023). Model-Free Approach to DC Microgrid Optimal Operation under System Uncertainty Based on Reinforcement Learning. Energies, 16(14), 5369. https://doi.org/10.3390/en16145369







