Classification Algorithm for DC Power Quality Disturbances Based on SABO-BP
Abstract
1. Introduction
2. Direct Current Energy Mass Disturbance Problem
2.1. DC Voltage Interruption
2.2. DC Voltage Dip
2.3. DC Voltage Temporarily Rise
2.4. DC Voltage Fluctuation
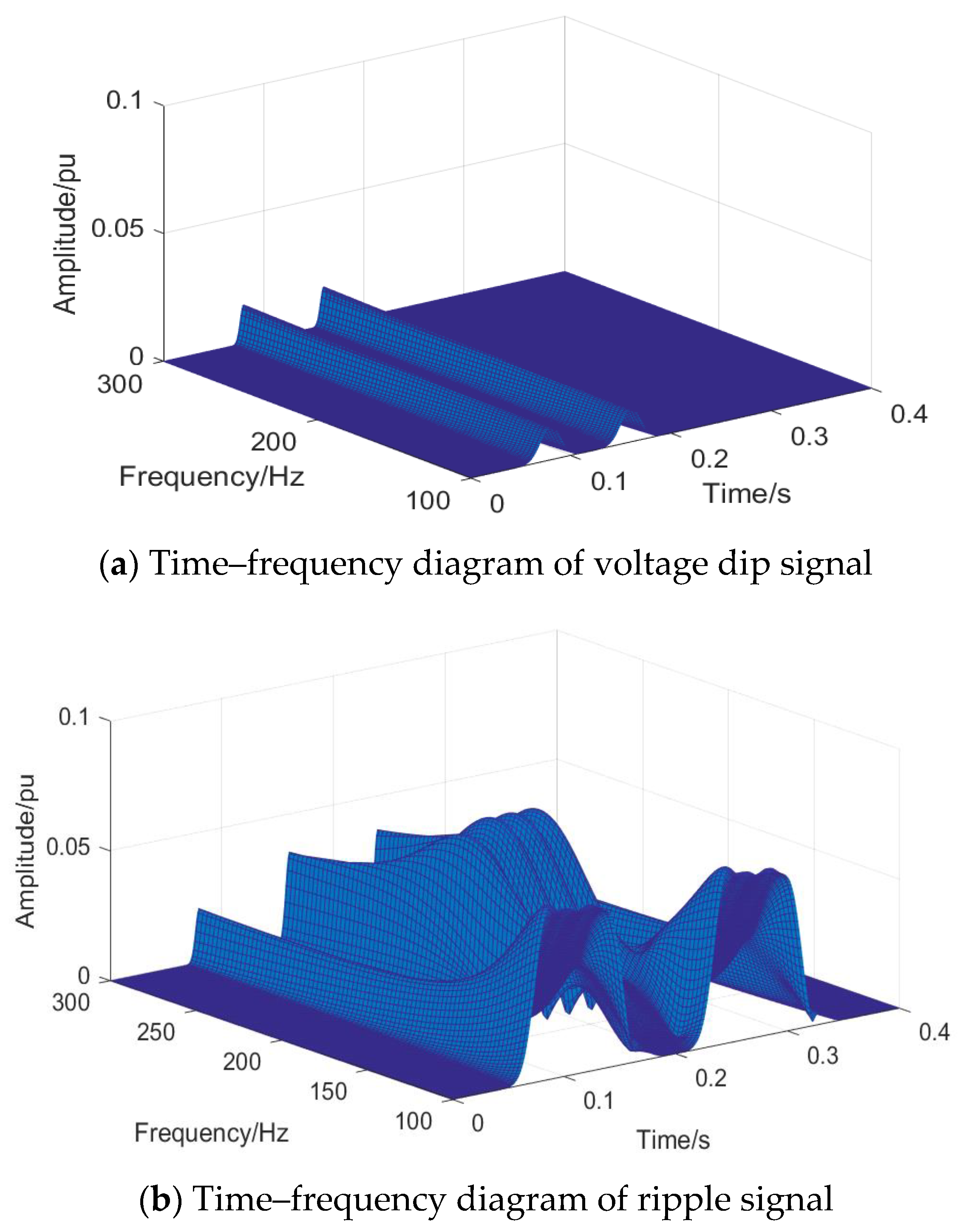
2.5. DC Voltage Ripple
3. Feature Extraction
3.1. S-Transform
3.2. Characteristic Index
3.2.1. Rectangle Coefficient
3.2.2. Standard Deviation of Waveform
3.3. Feature Extraction Rule
4. SABO-BP Algorithm
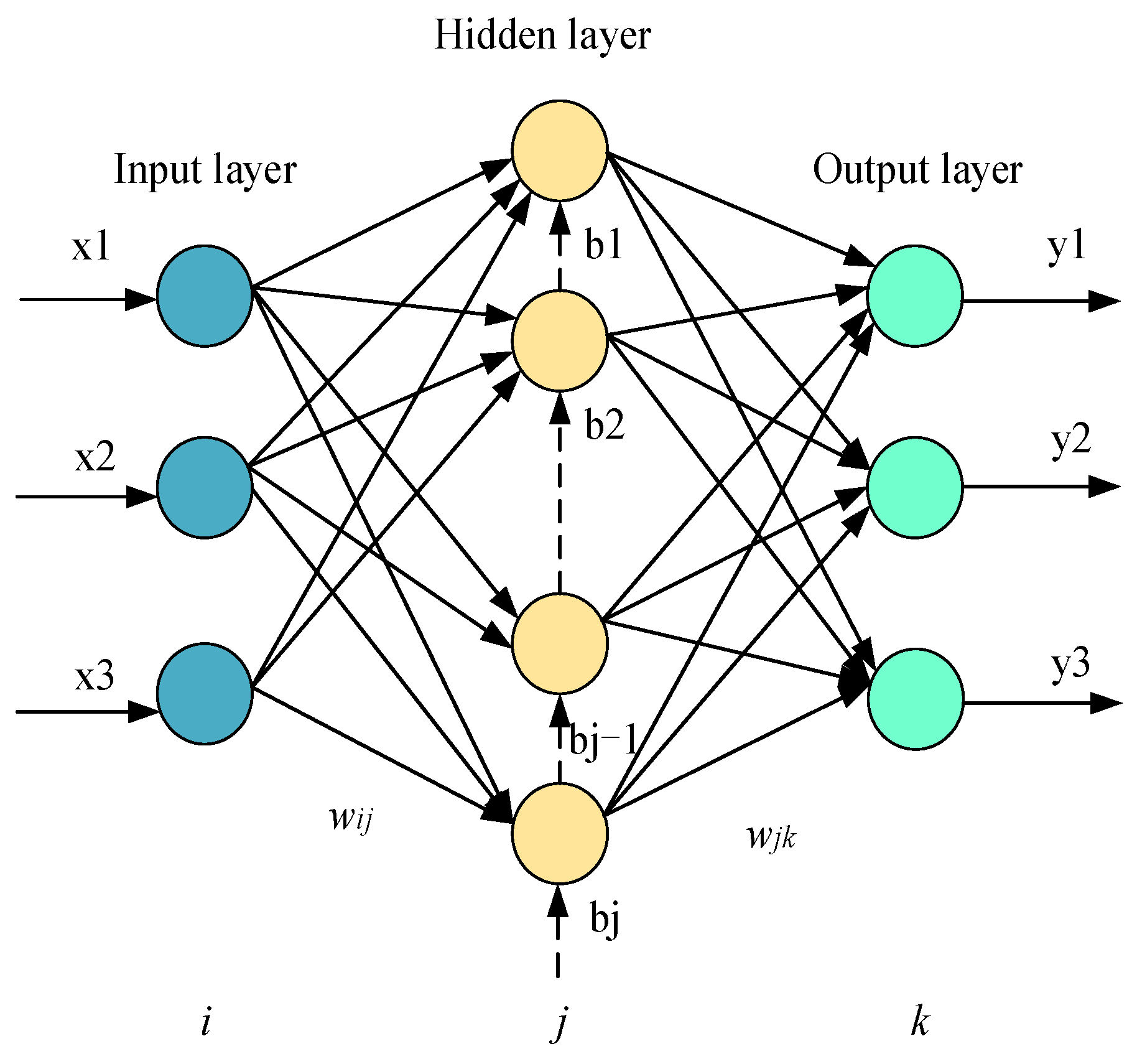
4.1. BP Neural Network
4.2. SABO Algorithm
4.2.1. Algorithm Initialization
4.2.2. SABO Algorithm Flow
- 1.
- The SABO algorithm introduces “-v”, referred to as the “v-difference” between search agents A and B, defined as follows:
- 2.
- The displacement of Xi in the search space is computed by taking the arithmetic mean of the “v-differences” obtained through subtraction with each search agent Xj.
- 3.
- Location update:
4.3. Establishment of the SABO-BP Model
5. Experimental Results and Analysis
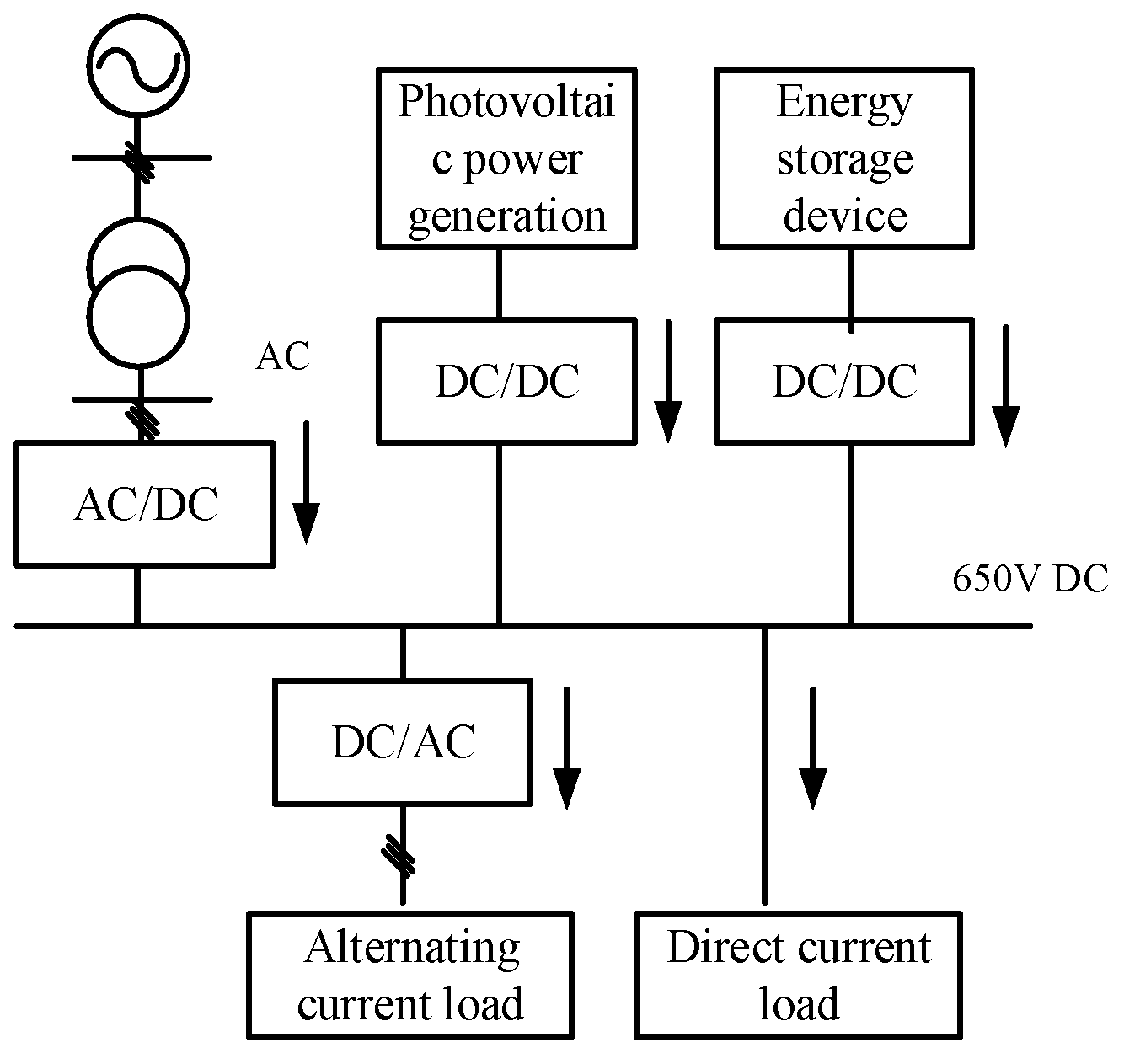
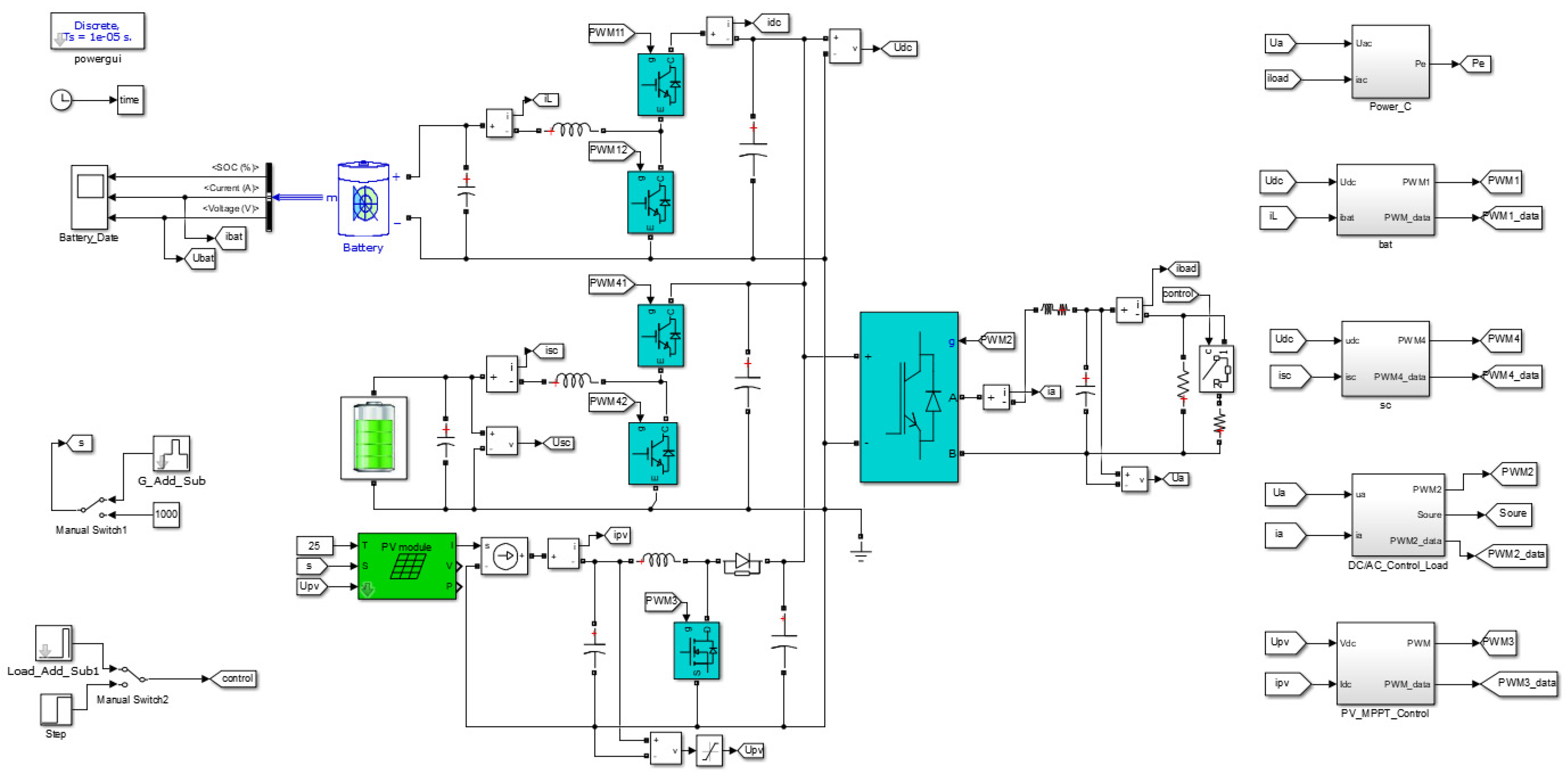
5.1. Experimental Model
5.2. Experimental Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Justo, J.; Mwasilu, F.; Lee, J.; Jung, J. AC-Microgrids versus DC-Microgrids with Distributed Energy Resources: A Review. Renew. Sustain. Energy Rev. 2013, 24, 387–405. [Google Scholar] [CrossRef]
- Elsayed, A.; Mohamed, A.; Mohammed, O. DC Microgrids and Distribution Systems: An Overview. Electr. Power Syst. Res. 2015, 119, 407–417. [Google Scholar] [CrossRef]
- Planas, E.; Andreu, J.; Garate, J.; de Alegria, I.; Ibarra, E. AC and DC Technology in Microgrids: A Review. Renew. Sustain. Energy Rev. 2015, 43, 726–749. [Google Scholar] [CrossRef]
- Alsaedi, A.; Alharbi, F.; Alahdal, A.; Alahmadi, A.; Ammous, A.; Ammous, K. Low Voltage Direct Current Supplies Concept for Residential Applications. Energy Explor. Exploit. 2022, 40, 1078–1097. [Google Scholar] [CrossRef]
- Al-Ismail, F. DC Microgrid Planning, Operation, and Control: A Comprehensive Review. IEEE Access 2021, 9, 36154–36172. [Google Scholar] [CrossRef]
- Barros, J.; de Apráiz, M.; Diego, R. Power Quality in DC Distribution Networks. Energies 2019, 12, 848. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Davoudi, A.; Aminifar, F.; Jatskevich, J.; Kakigano, H. Guest Editorial: Special Section on Smart DC Distribution Systems. IEEE Trans. Smart Grid 2014, 5, 2473–2475. [Google Scholar] [CrossRef]
- Tao, H.; Wang, P.; Chen, Y.; Stojanovic, V.; Yang, H. An Unsupervised Fault Diagnosis Method for Rolling Bearing Using STFT and Generative Neural Networks. J. Frankl. Inst. 2020, 357, 7286–7307. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.; Chen, X. Wavelets for Fault Diagnosis of Rotary Machines: A Review with Applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Shang, Y.; Miao, L.; Shan, Y.; Gnyawali, K.; Zhang, J.; Kattel, G. A Hybrid Ultra-Short-Term and Short-Term Wind Speed Forecasting Method Based on CEEMDAN and GA-BPNN. Weather Forecast. 2022, 37, 415–428. [Google Scholar] [CrossRef]
- Luo, D.; Wu, T.; Li, M.; Yi, B.; Zuo, H. Application of VMD and Hilbert Transform Algorithms on Detection of the Ripple Components of the DC Signal. Energies 2020, 13, 935. [Google Scholar] [CrossRef]
- Gou, J.; Ma, H.; Ou, W.; Zeng, S.; Rao, Y.; Yang, H. A Generalized Mean Distance-Based k-Nearest Neighbor Classifier. Expert Syst. Appl. 2019, 115, 356–372. [Google Scholar] [CrossRef]
- Tan, Z.; De, G.; Li, M.; Lin, H.; Yang, S.; Huang, L.; Tan, Q. Combined Electricity-Heat-Cooling-Gas Load Forecasting Model for Integrated Energy System Based on Multi-Task Learning and Least Square Support Vector Machine. J. Clean. Prod. 2020, 248, 119252. [Google Scholar] [CrossRef]
- Mishra, D.; Samantaray, S.; Joos, G. A Combined Wavelet and Data-Mining Based Intelligent Protection Scheme for Microgrid. IEEE Trans. Smart Grid 2016, 7, 2295–2304. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Y.; Chen, T. Back Propagation Neural Network with Adaptive Differential Evolution Algorithm for Time Series Forecasting. Expert Syst. Appl. 2015, 42, 855–863. [Google Scholar] [CrossRef]
- Mahbooba, B.; Timilsina, M.; Sahal, R.; Serrano, M. Explainable Artificial Intelligence (XAI) to Enhance Trust Management in Intrusion Detection Systems Using Decision Tree Model. Complexity 2021, 2021, 6634811. [Google Scholar] [CrossRef]
- Patil, M.; Tagade, P.; Hariharan, K.; Kolake, S.; Song, T.; Yeo, T.; Doo, S. A Novel Multistage Support Vector Machine Based Approach for Li Ion Battery Remaining Useful Life Estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
- Zayed, M.E.; Aboelmaaref, M.M.; Chazy, M. Design of Solar Air Conditioning System Integrated with Photovoltaic Panels and Thermoelectric Coolers: Experimental Analysis and Machine Learning Modeling by Random Vector Functional Link Coupled with White Whale Optimization. Therm. Sci. Eng. Prog. 2023, 44, 102051. [Google Scholar] [CrossRef]
- Almodfer, R.; Zayed, M.E.; Elaziz, M.A.; Aboelmaaref, M.M.; Mudhsh, M.; Elsheikh, A.H. Modeling of a Solar-Powered Thermoelectric Air-Conditioning System Using a Random Vector Functional Link Network Integrated with Jellyfish Search Algorithm. Case Stud. Therm. Eng. 2022, 31, 101797. [Google Scholar] [CrossRef]
- Bashir, T.; Chen, H.; Tahir, M.; Zhu, L. Short Term Electricity Load Forecasting Using Hybrid Prophet-LSTM Model Optimized by BPNN. Energy Rep. 2022, 8, 1678–1686. [Google Scholar] [CrossRef]
- Tang, X.; Shi, L.; Wang, B.; Cheng, A. Weight Adaptive Path Tracking Control for Autonomous Vehicles Based on PSO-BP Neural Network. Sensors 2023, 23, 412. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Wu, T.; Wang, Z.; Lin, X.; Cai, Y. A Novel Hybrid BPNN Model Based on Adaptive Evolutionary Artificial Bee Colony Algorithm for Water Quality Index Prediction. Ecol. Indic. 2023, 146, 109882. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, B.; Xu, D.; Cheng, M.; Xu, L. DC-Link Current Ripple Mitigation for Current-Source Grid-Connected Converters Under Unbalanced Grid Conditions. IEEE Trans. Ind. Electron. 2016, 63, 4967–4977. [Google Scholar] [CrossRef]
- Kapoor, R.; Gupta, R.; Son, L.H.; Jha, S.; Kumar, R. Detection of Power Quality Event Using Histogram of Oriented Gradients and Support Vector Machine. Measurements 2018, 120, 52–75. [Google Scholar] [CrossRef]
- Sacli, M.; Ayan, O.; Silsüpür, M.; Türkay, B. Investigation of Power Quality Analysis of Three-Phase Inverter Topologies for Renewable Energy Systems. In Proceedings of the 2017 10th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 30 November–2 December 2017; pp. 1445–1449. [Google Scholar]
- Kumar, D.; Zare, F.; Ghosh, A. DC Microgrid Technology: System Architectures, AC Grid Interfaces, Grounding Schemes, Power Quality, Communication Networks, Applications, and Standardizations Aspects. IEEE Access 2017, 5, 12230–12256. [Google Scholar] [CrossRef]
- Serdyukov, A.S.; Azarov, A.V.; Yablokov, A.V.; Shilova, T.V.; Baranov, V.D. Research Note: Reconstruction of Seismic Signals Using S-Transform Ridges. Geophys. Prospect. 2021, 69, 891–900. [Google Scholar] [CrossRef]
- Lou, Z.; Li, P.; Ma, K.; Teng, F. Harmonics and Interharmonics Detection Based on Synchrosqueezing Adaptive S-Transform. Energies 2022, 15, 4539. [Google Scholar] [CrossRef]
- Oliveira, R.A.D.; Bollen, M.H.J. Deep Learning for Power Quality. Electr. Power Syst. Res. 2023, 214, 108887. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, J.; Liu, Y.; Ma, D.; Li, M.; Xiang, B. Comparison of GA-BP and PSO-BP Neural Network Models with Initial BP Model for Rainfall-Induced Landslides Risk Assessment in Regional Scale: A Case Study in Sichuan, China. Nat. Hazards J. Int. Soc. Prev. Mitig. Nat. Hazards 2020, 100, 173–204. [Google Scholar] [CrossRef]
- Li, Z.-J.; Chen, W.-G.; Shan, J.; Yang, Z.-Y.; Cao, L.-Y. Enhanced Distributed Parallel Firefly Algorithm Based on the Taguchi Method for Transformer Fault Diagnosis. Energies 2022, 15, 3017. [Google Scholar] [CrossRef]
- Irfan, M.M.; Malaji, S.; Patsa, C.; Rangarajan, S.S.; Hussain, S.M.S. Control of DSTATCOM Using ANN-BP Algorithm for the Grid Connected Wind Energy System. Energies 2022, 15, 6988. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Subtraction-Average-Based Optimizer: A New Swarm-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics 2023, 8, 149. [Google Scholar] [CrossRef] [PubMed]






| Signal Detection Method | Peculiarity |
|---|---|
| Short-time Fourier transform (STFT) | It is good at analyzing stationary signals, but there may be issues with spectrum aliasing and leakage during use. |
| Wavelet transform (WT) | It can provide the characteristics of different scales of the disturbed signal, but it is very susceptible to noise. |
| Hilbert yellow transform (HHT) | It is suitable for analyzing abrupt signals, but its real-time performance is poor. |
| Variational mode decomposition (VMD) | It has good robustness, but the mode number K needs to be set manually, so it is not suitable for analyzing abrupt signals. |
| s-transform (ST) | It addresses the limitation of a fixed window width, exhibits superior time–frequency characteristics, and is not easily influenced by noise. |
| Pattern Recognition Scheme | Peculiarity |
|---|---|
| k-nearst neighbors (KNN) | It is simple in construction but computationally heavy. |
| support vector machines (SVM) | It is efficient in training, but difficult to train large-scale samples. |
| Decision Trees (DT) | It is easy to construct and understand, but it is prone to overfitting. |
| Extreme learning machines (ELM) | The hidden layer does not require iteration and has a fast learning speed. However, its controllable performance is poor and it is prone to overfitting. |
| Back propagation (BP) | It has high classification accuracy and strong processing power, but sometimes it is prone to falling into local optima. |
| Features | Extraction Rule | Design Purpose |
|---|---|---|
| F1 | The part of the fundamental wave amplitude time curve greater than 0.1 p.u. accounts for the time proportion of the whole detection time | Recognition of voltage interruption |
| F2 | The part of the fundamental amplitude time curve greater than 0.02 and less than 0.04 p.u. accounts for the time proportion of the whole detection time | Identifies voltage ups and downs |
| F3 | The part of the fundamental amplitude time curve less than 0.015p.u. accounts for the time proportion of the whole detection time | Identifies voltage fluctuation |
| F4 | Sum of standard deviations of waveform | Describes the degree of dispersion of the waveform amplitude |
| F5 | The rectangular coefficient of the waveform | Describes the deviation of voltage RMS value during the disturbance start-stop time |
| DC Bus Voltage | 650 V | Rated Capacity of the Supercapacitor | 20 F |
| Rated capacity of battery | 100 Ah | Boost switching frequency | 1 kHz |
| Battery voltage | 200 V | Buck-boost switching frequency | 10 kHz |
| Load power | 7 KW | Single inverter switching frequency | 10 kHz |
| Disturbance Class | F1 | F2 | F3 | F4 | F5 |
|---|---|---|---|---|---|
| DC voltage interruption | 0.9827 | 0.5461 | 0.3915 | 0.9278 | 22.3781 |
| DC voltage dip | 0 | 0.5511 | 0.7962 | 0.8925 | 22.5016 |
| DC voltage temporarily rise | 0.1275 | 0.8553 | 0.8905 | 0.6595 | 22.0067 |
| DC voltage fluctuation | 0.0926 | 0.4535 | 0.8553 | 0.2767 | 26.6732 |
| DC voltage ripple | 0.1287 | 0.4678 | 0.4559 | 0.2787 | 25.8180 |
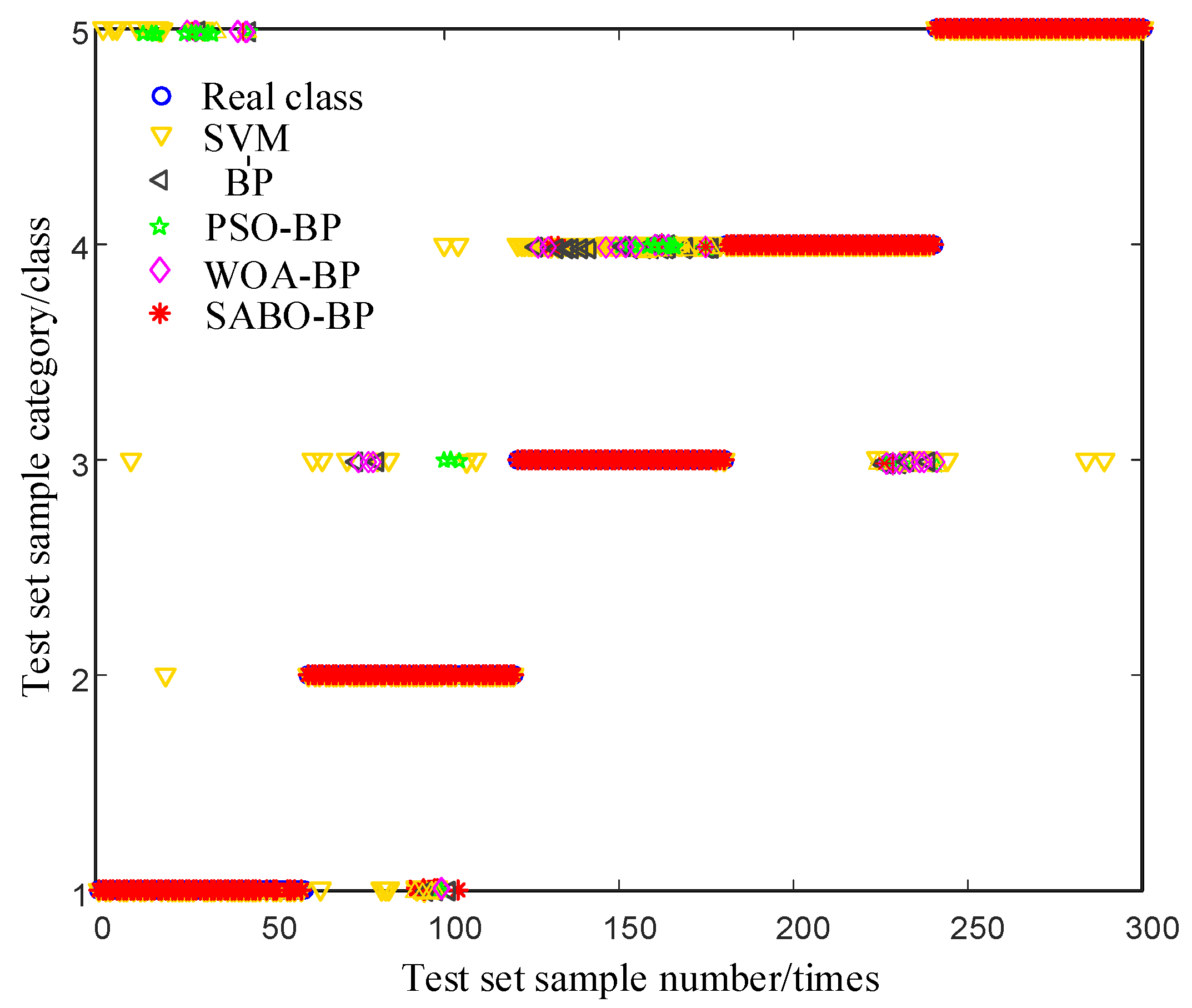
| Classifier | Average Running Time | Training Set Classification Accuracy | Test Set Classification Accuracy |
|---|---|---|---|
| ELM | 16.77 s | 54.327% | 45.278% |
| SVM | 10.36 s | 77.637% | 77.425% |
| BP | 10.86 s | 90.432% | 89.976% |
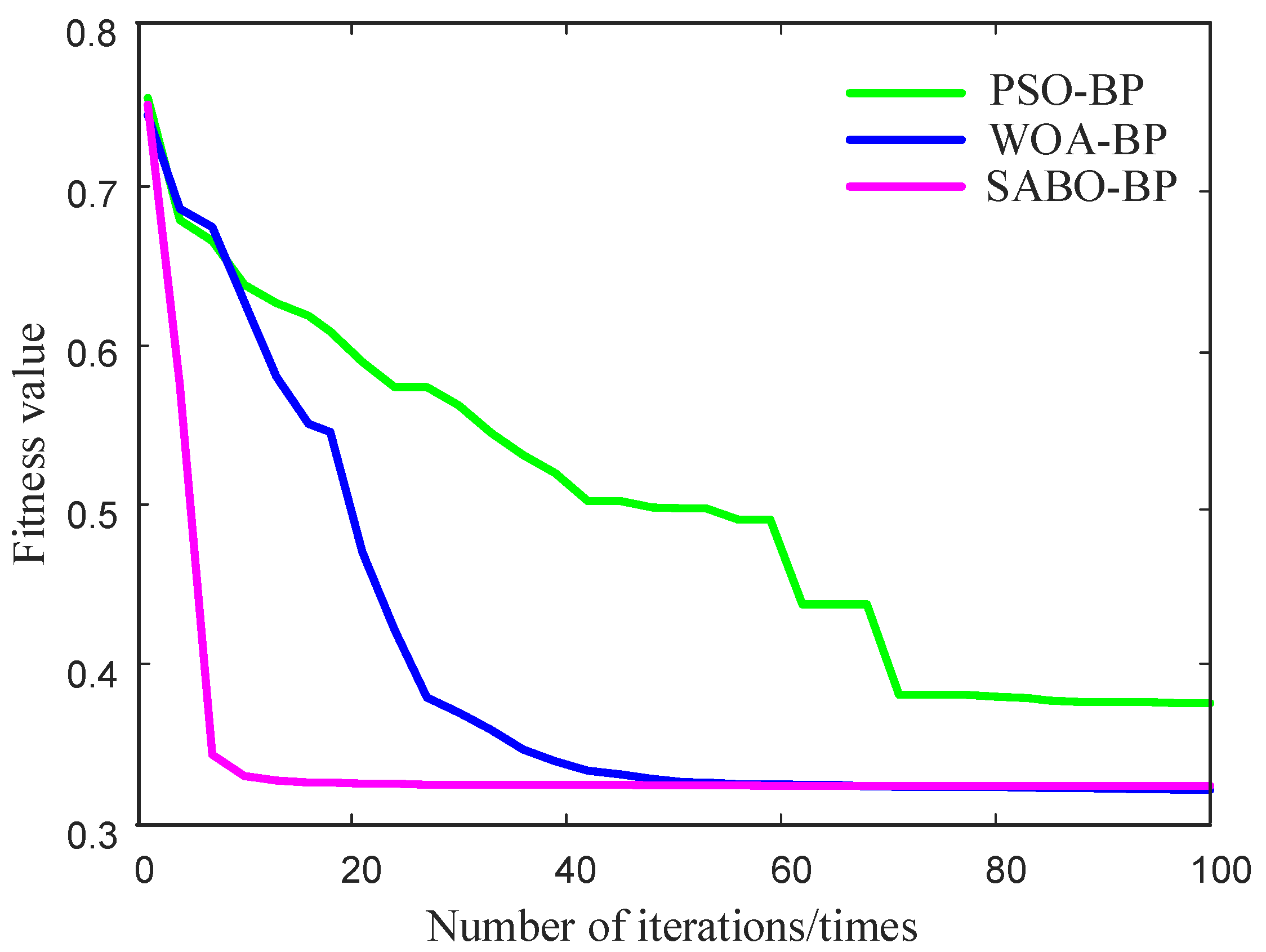
| PSO-BP | 19.71 s | 92.086% | 90.562% |
| WOA-BP | 29.54 s | 94.167% | 94.462% |
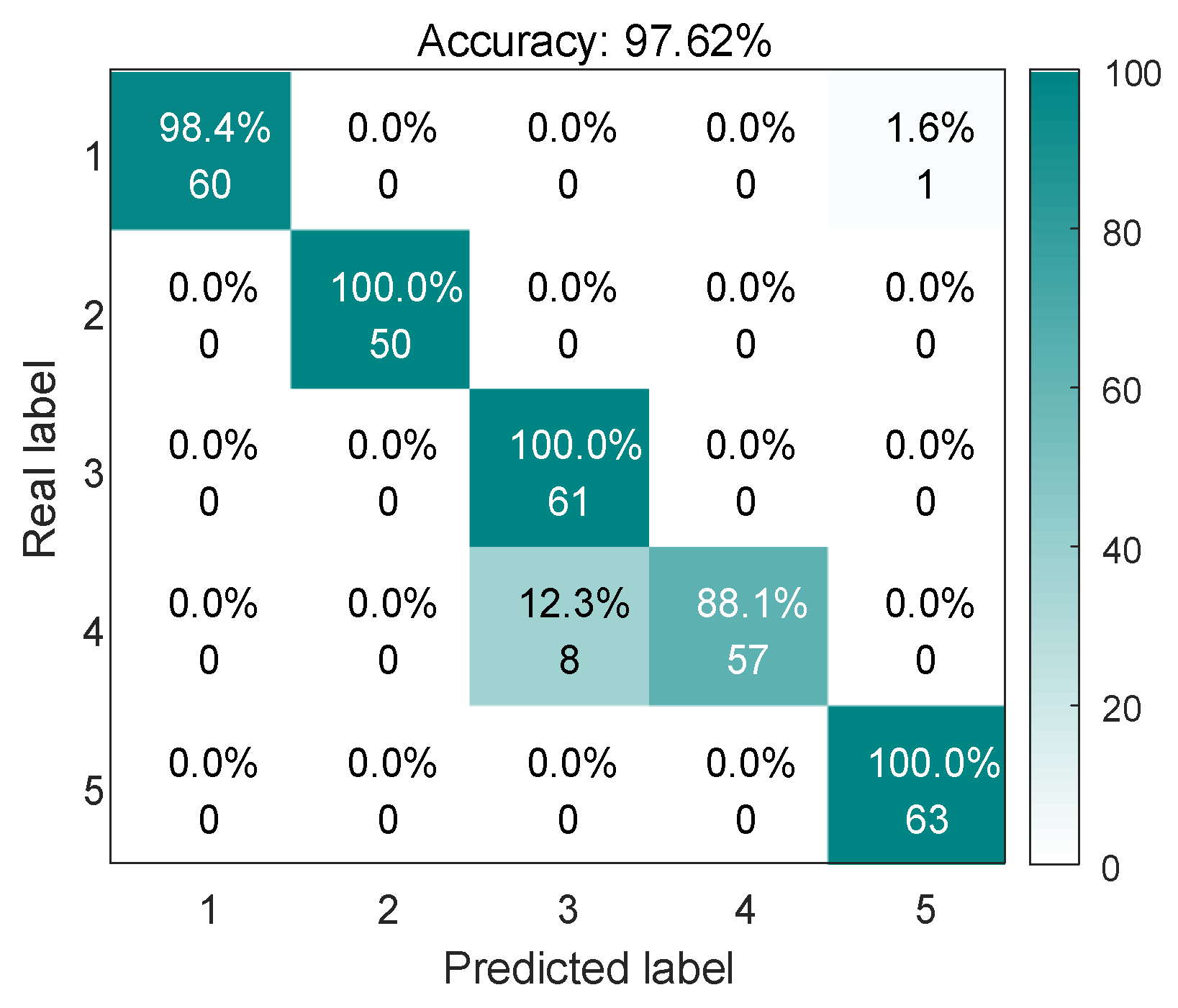
| SABO-BP | 20.73 s | 97.352% | 98.183% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, X.; Cen, W.; He, P.; Zhao, S.; Li, Q.; Xu, S.; Geng, A.; Duan, Y. Classification Algorithm for DC Power Quality Disturbances Based on SABO-BP. Energies 2024, 17, 361. https://doi.org/10.3390/en17020361
Duan X, Cen W, He P, Zhao S, Li Q, Xu S, Geng A, Duan Y. Classification Algorithm for DC Power Quality Disturbances Based on SABO-BP. Energies. 2024; 17(2):361. https://doi.org/10.3390/en17020361
Chicago/Turabian StyleDuan, Xiaomeng, Wei Cen, Peidong He, Sixiang Zhao, Qi Li, Suan Xu, Ailing Geng, and Yongxian Duan. 2024. "Classification Algorithm for DC Power Quality Disturbances Based on SABO-BP" Energies 17, no. 2: 361. https://doi.org/10.3390/en17020361
APA StyleDuan, X., Cen, W., He, P., Zhao, S., Li, Q., Xu, S., Geng, A., & Duan, Y. (2024). Classification Algorithm for DC Power Quality Disturbances Based on SABO-BP. Energies, 17(2), 361. https://doi.org/10.3390/en17020361





