Current-Sensorless Method for Photovoltaic System Using Capacitor Charging Characteristics

Abstract

The installed capacity of photovoltaic (PV) systems has increased significantly over the past few decades, and related technologies have advanced significantly. The electrical characteristics of a PV system change nonlinearly based on irradiation and temperature, and the I–V characteristic curve, expressed in terms of the voltage and current, is used to verify these characteristics. The maximum power point tracking (MPPT) control method was applied to maximize the performance of the PV system. Voltage and current sensors are used to control the I–V characteristic curve and MPPT; however, current sensors have various disadvantages in terms of price and system configuration. Therefore, this study presents a method for calculating the current of a PV system using the charging characteristics of a capacitor. The method presented in this paper analyzes the I–V characteristic curve’s qualities through simulations and experiments under normal, shaded, and mismatched conditions of the PV module.

1. Introduction

Solar energy is among the most sustainable and promising renewable energy sources. Although solar power has many advantages in terms of cleanliness and renewability, it has several disadvantages, such as low output efficiency, environmental dependence, and nonlinear electrical characteristics. In addition, it is necessary to improve the lifespan of solar power systems and optimize their monitoring, operation, and maintenance strategies to increase the economic feasibility of PV systems [1,2].

The electrical characteristics of PV systems change nonlinearly based on irradiation and temperature. The best approach to check these characteristics of a PV system is to examine the I–V characteristic curve [2,3,4,5,6,7,8]. This is because it shows all the operating points that represent the behavior of the PV system under specific temperature and irradiation conditions. To verify the characteristics of PV systems, a variable load method is generally used, including variable resistors, DC-DC converters, electronic loads, and capacitive loads. Since all these methods measure the voltage and current to display the I–V characteristic curve, using voltage and current sensors is essential [8,9,10,11,12].

Maximum power point tracking (MPPT) control is essential for maximizing the performance of PV systems. Many methods for identifying MPP have been developed over the past few decades. The most common and widely used techniques include perturbation and observation (P&O) and incremental conductance (IncCond). The MPPT algorithm requires both voltage and current sensors to simultaneously measure the voltage and current in the PV module. Consequently, implementing algorithms based on these sensors complicates the hardware configuration and increases costs.

Generally, sensors for measuring voltage can be easily implemented through a resistive potential distribution circuit; however, sensors for measuring current are not easy to implement. A variety of methods exist for measuring the PV current; however, the most frequently used methods use resistive shunts or Hall effect sensors. Hall effect sensors have no added loss components in series with the current to be measured but suffer from problems such as thermal drift, gain error, nonlinearity, and offset. In contrast, resistive shunts have no offset and exhibit good linearity; however, the resistive element causes significant power loss [13,14,15,16].

Methods such as observers, buck-boost converters, and adaptive model predictive controllers have been proposed for current-sensorless control in solar power generation systems. However, these approaches involve complex formulas or complicate the system configuration [17,18,19].

Therefore, this study proposes current-sensorless control using a capacitive load as one of the methods for representing the I–V characteristic curve. A capacitive load has the characteristic of storing voltage and has a time constant at which the voltage changes based on the resistance and the capacitive load. Therefore, this study proposes a method to measure changes in voltage using a voltage sensor and to calculate the current using the measured voltage and time constant characteristics of the capacitive load.

The feasibility of the method presented in this paper is demonstrated through simulations and experiments investigating the PV module’s I–V characteristic curve under normal, shaded, and mismatched conditions.

The remainder of this paper is organized as follows: Section 2 describes a method for obtaining the I–V characteristic curve of a PV system, Section 3 describes a current-sensorless method using capacitor charging characteristics, Section 4 includes simulation and experimental results, and Section 5 presents the conclusion.

2. Methods for Obtaining I–V Characteristic Curves of PV Systems

To obtain the I–V characteristics of a solar power generation system, an operating point, expressed as the voltage and current values from the short-circuit current to the open-circuit voltage, is required. The variable load method is generally used to change the voltage and current.

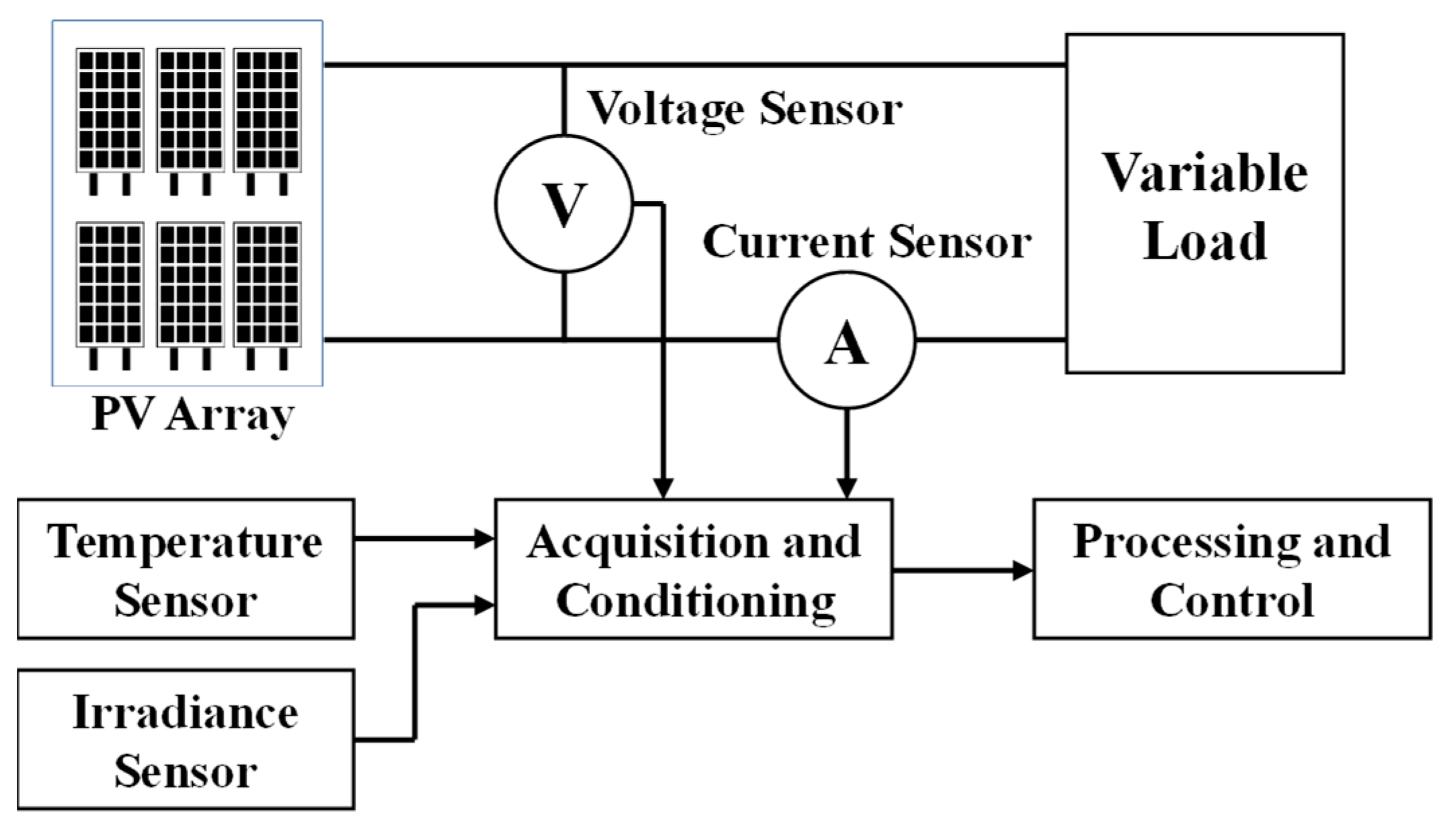
Figure 1 depicts a block diagram for measuring the I–V curve of a PV system. To measure the I–V curve, a variable load, a sensor to measure the voltage and current, an analog signal acquisition and conditioning block, and a processing and control block are required. Additionally, external sensors such as temperature and irradiation sensors are required to reference the measured values.

The variable loads used to measure the I–V characteristic curve of a PV system include a variable resistance, DC-DC converter, electronic load, and capacitive load.

2.1. I–V Characteristic Curve Measurement Using Variable Resistance

Figure 2 shows the measurement of the I–V curve using a variable resistor. The variable resistance method uses the voltage and current measured while changing the resistance from zero to infinity. However, in reality, no variable resistor with these characteristics exists, and the power consumed by the resistor causes losses or limits the characteristics of the measurement equipment.

Figure 3 shows a method for measuring the I–V curve by constantly changing the resistance by connecting multiple resistors in series or in parallel. However, many resistors are required to obtain a precise I–V curve using this method.

2.2. Method Using DC-DC Converter and Resistive Load

The DC-DC converter can vary the voltage through PWM control. As shown in Figure 4, by connecting the PV module to the converter and the resistive load to the output, the I–V curve can be measured by changing the voltage using a DC-DC converter. The method using a DC-DC converter can measure a precise I–V curve by adjusting the duty ratio. However, there is a problem in that the measurement system becomes complicated depending on the converter configuration.

2.3. How to Use Electronic Loads

Electronic loading is a method that uses semiconductor devices such as BJTs, MOSFETs, and IGBTs. Figure 5 shows the I–V characteristics of a PV module using a MOSFET. In the case of MOSFETs, the current flowing is limited based on the size of the voltage input to the gate, and an I–V curve can be obtained using this characteristic.

2.4. I–V Characteristic Curve Measurement Method Using Capacitive Load

Figure 6 shows the I–V curve measured using a capacitor, which is a capacitive load. Capacitors can store electrical energy. When a voltage is applied to a capacitor in the discharged state, charging begins, and the current flows like a short circuit. When the capacitor voltage continues to increase and charging is complete, no current flows and the capacitor operates as an open circuit. Using the characteristics of these capacitors, the I–V characteristic curve of the PV module can be obtained.

3. Current-Sensorless Method Using Capacitor Charging Characteristics

In Section 2, various methods for measuring the I–V curve of a PV system were described. These methods measure the voltage and current and display the respective characteristic curves using the measured results. The method using resistance can calculate the current by using a variable resistor or connecting the resistors in series or parallel. However, an additional device is required to control the variable resistor or the series/parallel connection of the resistors.

The method using the duty ratio of the DC-DC converter and the semiconductor also requires additional control algorithms to control the duty ratio and voltage.

Therefore, this paper proposes a method to calculate the current of the PV system with a simple configuration and formula by using the characteristics of the changing charge voltage of the capacitor. When using a capacitor, a resistor is required to discharge the charged voltage of the capacitor for continuous measurement, but it can be configured relatively simply compared to other methods.

The resistance of the PV system ($R_{pv}$) can be calculated from its voltage ($V_{pv}$) and current ($I_{pv}$).

Figure 7 shows the resistance characteristics displayed by the voltage and current of the PV system. The resistance of a PV system changes nonlinearly, owing to the nonlinear characteristics of the PV voltage and current. So, a method to calculate the PV system resistance is necessary. The current of the PV system can be calculated by the resistance using Equation (1).

Equation (1) shows how the current is calculated using the voltage and resistance as follows:

$${\mathrm{I}}_{\mathrm{p}\mathrm{v}}={\displaystyle \frac{{\mathrm{V}}_{\mathrm{p}\mathrm{v}}}{{\mathrm{R}}_{\mathrm{p}\mathrm{v}}}}$$

(1)

The method of measuring the I–V curve using a capacitive load utilizes the charging characteristics of a capacitor. The charging voltage of the capacitor (${\mathrm{V}}_{\mathrm{C}}$) based on time ($\mathrm{t}$) can be expressed using Equation (2) as follows:

$${\mathrm{V}}_{\mathrm{C}}={\mathrm{V}}_{\mathrm{p}\mathrm{v}}(1-{\mathrm{e}}^{-{\displaystyle \frac{\mathrm{t}}{{\mathrm{R}}_{\mathrm{p}\mathrm{v}}\mathrm{C}}}})$$

(2)

The charging voltage of the capacitor can be expressed in terms of the resistance as follows:

$${\displaystyle \frac{{\mathrm{V}}_{\mathrm{C}}}{{\mathrm{V}}_{\mathrm{p}\mathrm{v}}}}=1-{\mathrm{e}}^{-{\displaystyle \frac{\mathrm{t}}{{\mathrm{R}}_{\mathrm{p}\mathrm{v}}\mathrm{C}}}}$$

(3)

$${\displaystyle \frac{1}{{\mathrm{R}}_{\mathrm{p}\mathrm{v}}}}=-\ln \left(1-{\displaystyle \frac{\Delta {\mathrm{V}}_{\mathrm{C}}}{{\mathrm{V}}_{\mathrm{p}\mathrm{v}}}}\right)\times {\displaystyle \frac{\mathrm{C}}{\Delta \mathrm{t}}}$$

(4)

According to Equations (1) and (4), the current in the PV system can be calculated as follows:

$${\mathrm{I}}_{\mathrm{p}\mathrm{v}}={\mathrm{V}}_{\mathrm{p}\mathrm{v}}\times \left[-\ln \left(1-{\displaystyle \frac{\Delta {\mathrm{V}}_{\mathrm{C}}}{{\mathrm{V}}_{\mathrm{p}\mathrm{v}}}}\right)\times {\displaystyle \frac{\mathrm{C}}{\Delta \mathrm{t}}}\right]$$

(5)

Figure 8 shows the block diagram and the algorithm for calculating the PV system current. The current (${\mathrm{I}}_{\mathrm{p}\mathrm{v}}$) of the PV system is calculated using the capacitor ($\mathrm{C}$) used for measurement, the short-circuit current (${\mathrm{I}}_{\mathrm{s}\mathrm{c}}$) of the PV system, and the measured voltage (${\mathrm{V}}_{\mathrm{p}\mathrm{v}}$) of the PV system. Since the short-circuit current (${\mathrm{I}}_{\mathrm{s}\mathrm{c}}$) of the PV system is the maximum current of the PV system, if the calculated value exceeds this, the calculation is limited to the short-circuit current.

4. Simulation and Experimental Results

4.1. Simulation Results

Figure 9 shows the PSIM (12.0.4) circuit diagram for the I–V curve measurement.

Table 1. PV module specifications under the standard test condition (STC).

Index	Value
Model	SCM 100 WS
Voltage at maximum power point ($V_{mpp}$)	17.5 V
Current at maximum power point ($I_{mpp}$)	5.75 A
Open-circuit voltage ($V_{oc}$)	21 V
Short-circuit current ($I_{sc}$)	6.05 A
Maximum power ($P_{mpp}$)	100 W

shows the PV module specifications used in the simulation and the experiment. The key parameters of the current-sensorless control proposed in the paper are the capacitor and sampling time. The simulation was conducted with the parameters described in

Table 2. Conditions for simulations.

	Capacitor	Sampling Time	Conditions
Case 1	1 mF	1 μs	No Shaded
Case 2	2 mF	1 μs	No Shaded
Case 3	2 mF	1 μs	Partial Shaded
Case 4	2 mF	1 μs	PV Module Mismatch
Case 5	2 mF	10 μs	No Shaded
Case 6	2 mF	100 μs	No Shaded

. Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 show the simulation results according to Table 2 using the circuit in Figure 9.

Figure 10 illustrates the simulation results for case 1. Figure 10a shows the results measured using a current sensor, while Figure 10b presents the magnitude of the current calculated using the method proposed in the paper. Figure 10c illustrates the error between the value measured by the sensor and the current calculated by the method proposed in the paper. In the section where the current instantaneously rises to the short-circuit current, the current error initially appears large due to a delay in the calculation time. However, after that, it quickly decreases and approaches zero.

Figure 11 shows the simulation results for case 2. As the size of the capacitor doubles, the time constant doubles, and the current measurement time becomes approximately twice as long, as seen in Figure 10. As shown in Figure 10, initial errors occur but are almost 0 in most sections.

Figure 12 presents the simulation results for case 3 and illustrates the current characteristics when a shadow occurs on one of the four modules, as depicted in Figure 12a. The I–V curve of a PV system provides the quickest and most efficient means to detect mismatches resulting from partial shading and differences in electrical characteristics.

As depicted in Figure 12b,c, when shading occurs in one module, the output current changes according to the voltage variation. Even under shading conditions, the current can be calculated using the method proposed in the paper.

Figure 13 shows the mismatch characteristics of case 4, where the electrical characteristics of one module among the four PV modules are different.

PV modules with different electrical characteristics occur due to PV module failure or performance degradation due to PV module aging.

Figure 14 shows the characteristics when the sampling time is changed. Figure 14a is the current calculated using the proposed method when the sampling time is 10 us, and Figure 14b shows the current error in Figure 14a. Figure 14c is the current value calculated using the method proposed in the paper when the sampling time is 100 us, and Figure 14d shows the current error in Figure 14c. When the sampling time is increased, the initial error increases, but it quickly stabilizes in the subsequent period, resulting in the current error approaching zero.

4.2. Experimental Results

Figure 15 shows the configuration for the experiment. It consists of four PV modules: an oscilloscope for data collection, a voltage differential probe, a current probe, and a capacitor.

The sensorless experiment based on capacitor charging characteristics was conducted as follows:

• Step 1: Connect the PV module and capacitor in parallel through a switch.
• Step 2: Close the switch to charge the capacitor using the PV module.
• Step 3: Measure the capacitor’s voltage and current with an oscilloscope.
• Step 4: Calculate the current using the proposed method based on the measured capacitor voltage.
• Step 5: Compare the error between the current calculated by the proposed method and the measured current.

The capacitance of the capacitor and the sampling time used in the experiment and simulation were integer multiples to analyze their respective effects.

The specifications of the main components are shown in

Table 3. Specification of the main components for experiment.

	Model	Specification
Oscilloscope	Tektronix DPO 3034	Bandwidth: 300 Mhz Sampling rate: 2.5 GSa/s
Voltage differential probe	GWINSTEK GDP-025	Bandwidth: 25 Mhz Accuracy: ±2%
Current probe	GWINSTEK GCP-530	Bandwidth: 50 Mhz Accuracy: ±1%

. The experiment was conducted for cases 1 to 3, as listed in Table 2.

Figure 16 shows the experimental results for case 1, Figure 17 shows case 2, and Figure 18 shows the experimental results for case 3. Because of the ripple of the value measured through the voltage sensor and external noise, ripple occurs in the current calculated by the method suggested in the paper.

However, the experimental results for cases 1, 2, and 3 in Figure 16, Figure 17 and Figure 18 appear similar to the simulation results. In the current error of Figure 16, Figure 17 and Figure 18, the current calculated by the method presented throughout the paper became almost zero except for the initial error.

Therefore, it is possible to check the I–V characteristics of the PV system without using a current sensor through the method proposed in the paper.

5. Conclusions

This study proposed a current-sensorless control method for PV systems. The electrical characteristics of PV systems change nonlinearly based on temperature and solar radiation, and voltage and current sensors are used to measure these characteristics. However, current sensors have disadvantages, such as price and power loss. Therefore, this study introduced a method for calculating the current by measuring the voltage using the charging characteristics of the capacitor. The method proposed in this paper was used to conduct simulations and experiments under varying conditions, including capacitor size (1 mF, 2 mF), sampling time (10 μs, 10 μs, 1 μs), and PV module states (normal, shaded, and mismatched). Even when these conditions were changed, the results measured using the current sensor and those calculated using the method proposed in this paper were almost identical. These results confirmed that current-sensorless control is possible. When the method proposed in the paper is applied to a PV system, the number of current sensors can be reduced or eliminated, which is expected to provide advantages regarding system configuration, price, and efficiency. The method proposed in this paper is a simple approach for calculating current based on the charging characteristics of a capacitor. However, it is highly dependent on the capacitor size and sampling time, which poses a limitation. For example, the capacitor must have a large capacity, and the sampling time must be short to ensure accurate calculations.