1. Introduction
At present, the large-scale collection and storage of data has become a reality. Time-series data are widely prevalent in fields such as finance, weather forecasting, and health monitoring. However, within time-series data, there are often anomalies—data points that significantly deviate from the main pattern. These anomalies may be caused by various factors, such as sensor malfunctions or unexpected events. Consequently, the detection of outliers in time-series data is important.
Energy consumption data can be viewed as time series. Equipment failures or inefficient energy usage patterns can lead to abnormal energy consumption data. Implementing appropriate energy management measures to reduce the occurrence of such anomalies can effectively achieve energy savings. With the advancement in data collection and analysis technologies, algorithms for detecting anomalies in energy consumption data have rapidly evolved. From traditional statistical methods to machine learning-based approaches, various techniques have been proposed and applied specifically to anomaly detection in energy consumption data, providing support for energy management and optimization.
Classical time-series anomaly detection methods primarily include statistical-based anomaly detection algorithms, clustering and classification-based anomaly detection algorithms, and proximity-based anomaly detection algorithms. Statistical-based time-series anomaly detection algorithms encompass techniques such as the 3-sigma rule, quartile method, and other statistical measures. For instance, in Reference [
1], a hyperspectral anomaly detection problem in remote sensing was addressed by treating third- and fourth-order matrices as statistical features to highlight anomalous peaks, making anomalies easier to detect. Reference [
2] successfully employed the quartile method to identify wind-power anomaly data. Clustering-based anomaly detection methods are considered unsupervised learning techniques. For example, Reference [
3] introduced an improved streaming K-means clustering algorithm designed for detecting abnormal electricity consumption behavior in large-scale power data streams, drawing inspiration from the CluStream streaming-data clustering algorithm. In Reference [
4], model normality scores were first used to determine model clustering indices, with outliers identified based on these indices. Classification-based anomaly detection algorithms, on the other hand, can be viewed as supervised learning techniques. Reference [
5], for example, proposed a method to measure the confidence of classification results, identifying outliers by constructing classifiers. Proximity-based anomaly detection methods mainly include density-based and distance-based approaches. Reference [
6] preprocessed aggregated active power output and corresponding wind speed values, and then calculated weighted distances based on the similarity between each object in the data and the local outlier factor (LOF), to identify anomalies. Reference [
7] proposed an improved LOF algorithm for detecting abnormal electricity consumption behavior in users.
Classical time-series anomaly detection methods are widely applied, but their effectiveness is limited when used on unstable, nonlinear, or multivariate time series. Energy consumption sequences are generally unstable and nonlinear [
8]. In recent years, researchers have begun exploring deep learning-based methods for time-series anomaly detection, with significant attention given to methods based on prediction residuals (Residual = Actual Value − Predicted Value). For instance, in Reference [
9], a study was conducted on a method that combines random forests with statistical algorithms for anomaly detection. The study first utilized a random forest algorithm to predict building energy consumption, followed by the application of an improved statistical algorithm to the prediction residuals for anomaly detection, demonstrating high detection accuracy. In Reference [
10], the long short-term memory (LSTM) algorithm was used to predict energy consumption data, and anomaly scores were calculated based on the prediction results to ultimately identify anomalies. In reference [
11], the GNN-GRU–Attention algorithm was used to model and predict energy-consumption time series, and an improved random forest algorithm was subsequently employed to detect anomalies in the residuals. Experimental results indicated that this approach outperformed other anomaly detection algorithms based on prediction residuals, as well as classical time-series anomaly detection methods. In Reference [
12], a seasonal threshold approach was introduced to improve the accuracy of prediction-based outlier detection systems, especially for energy management systems in buildings. Reference [
13] presents an AI-based anomaly detection method for electricity consumption in smart cities, using data from households in northeastern Mexico. It first predicts energy consumption with deep learning algorithms and then detects outliers by analyzing the residuals with the Isolation Forest algorithm.
The method of using deep learning algorithms to predict sequences, calculate residuals, and then analyze these residuals to identify anomalies can be considered a hybrid approach. The foundation of this approach lies in establishing highly accurate time-series prediction models. The data that significantly deviate from the predicted values can be identified as outliers. The advancement in deep learning technology has significantly enhanced the accuracy of prediction models, laying a solid foundation for the implementation of time-series anomaly detection algorithms based on prediction errors. In recent years, with the introduction of the Transformer algorithm [
14], the accuracy and generalization capabilities of time-series prediction models have greatly improved. Building on this, the Informer [
15] and Autoformer [
16] algorithms have been proposed, making the model architecture more suitable for unstable and nonlinear time series.
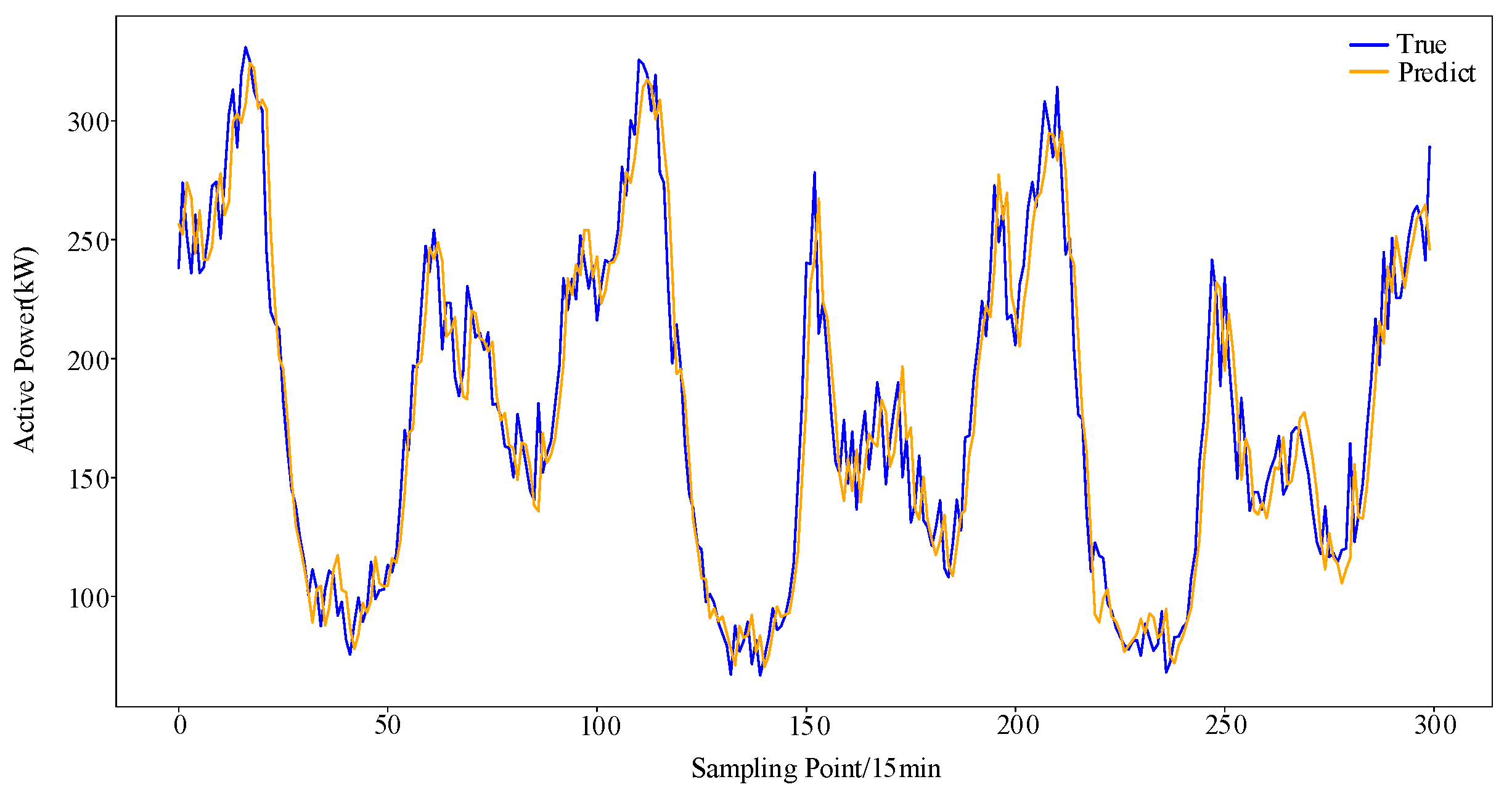
This paper proposes a time-series anomaly detection model, AF-GS–RandomForest, based on the Autoformer algorithm. The model first employs the Autoformer algorithm to predict the time series, and then the residuals are analyzed using a random forest algorithm optimized through Grid Search (Grid Search, GS) parameter tuning. The accuracy and robustness of the algorithm were validated on public datasets, and the model was subsequently applied to detect abnormal energy consumption in an office building. The results demonstrated that the F1 score of the detection model reached 0.998, outperforming existing commonly used anomaly detection algorithms.
2. Algorithm Design
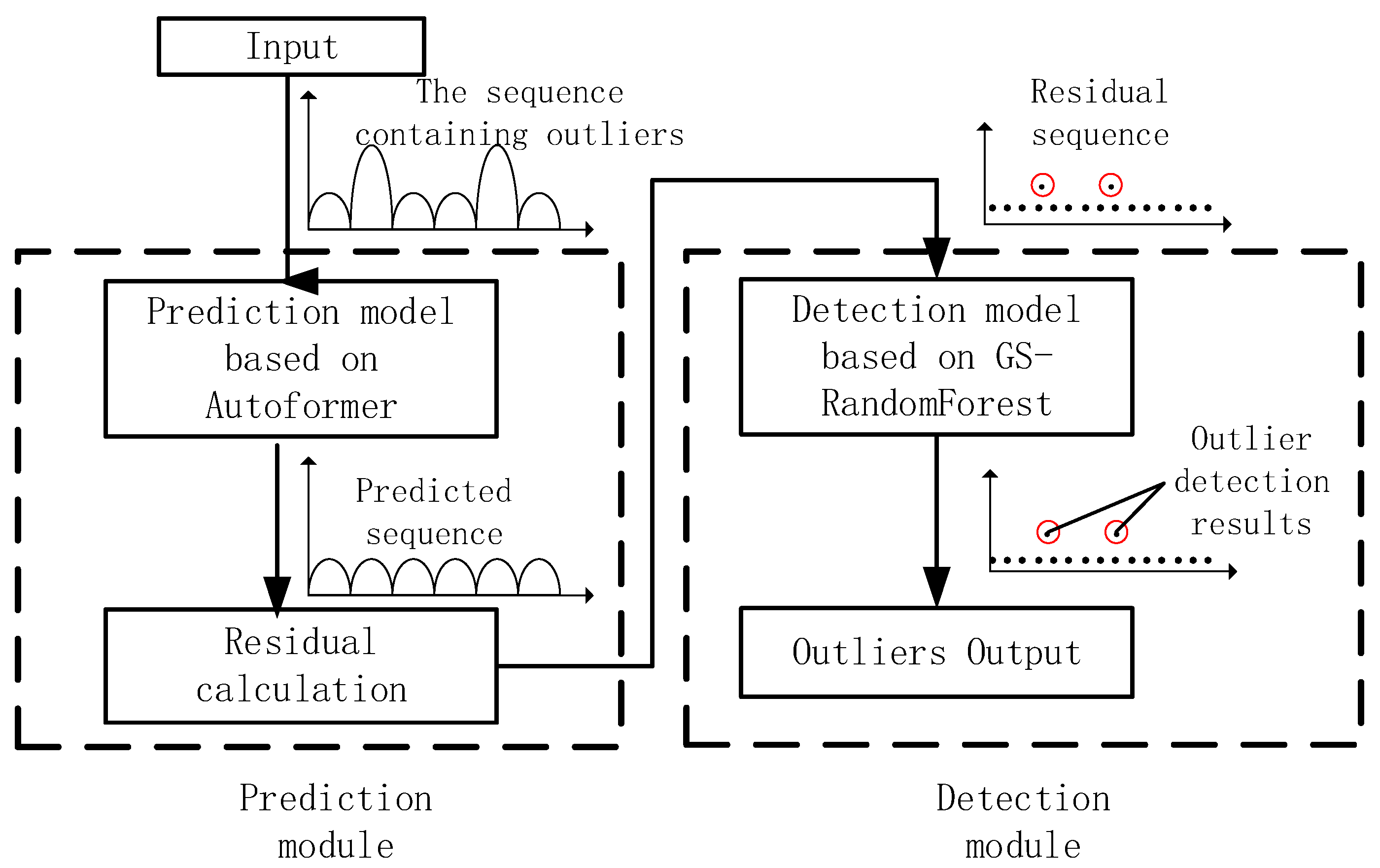
The structure of the AF-GS–RandomForest model consists of two components. The first component is the prediction module, which includes the sequence prediction and reconstruction module. This module employs the Autoformer algorithm to predict the time series and obtain the residuals. The second component detects anomalies in the residual sequence using the random forest algorithm optimized through Grid Search. The overall structure and workflow of the algorithm are illustrated in
Figure 1, where a simple, univariate sequence without trends is used as an example to demonstrate the detection process.
2.1. Autoformer Algorithm
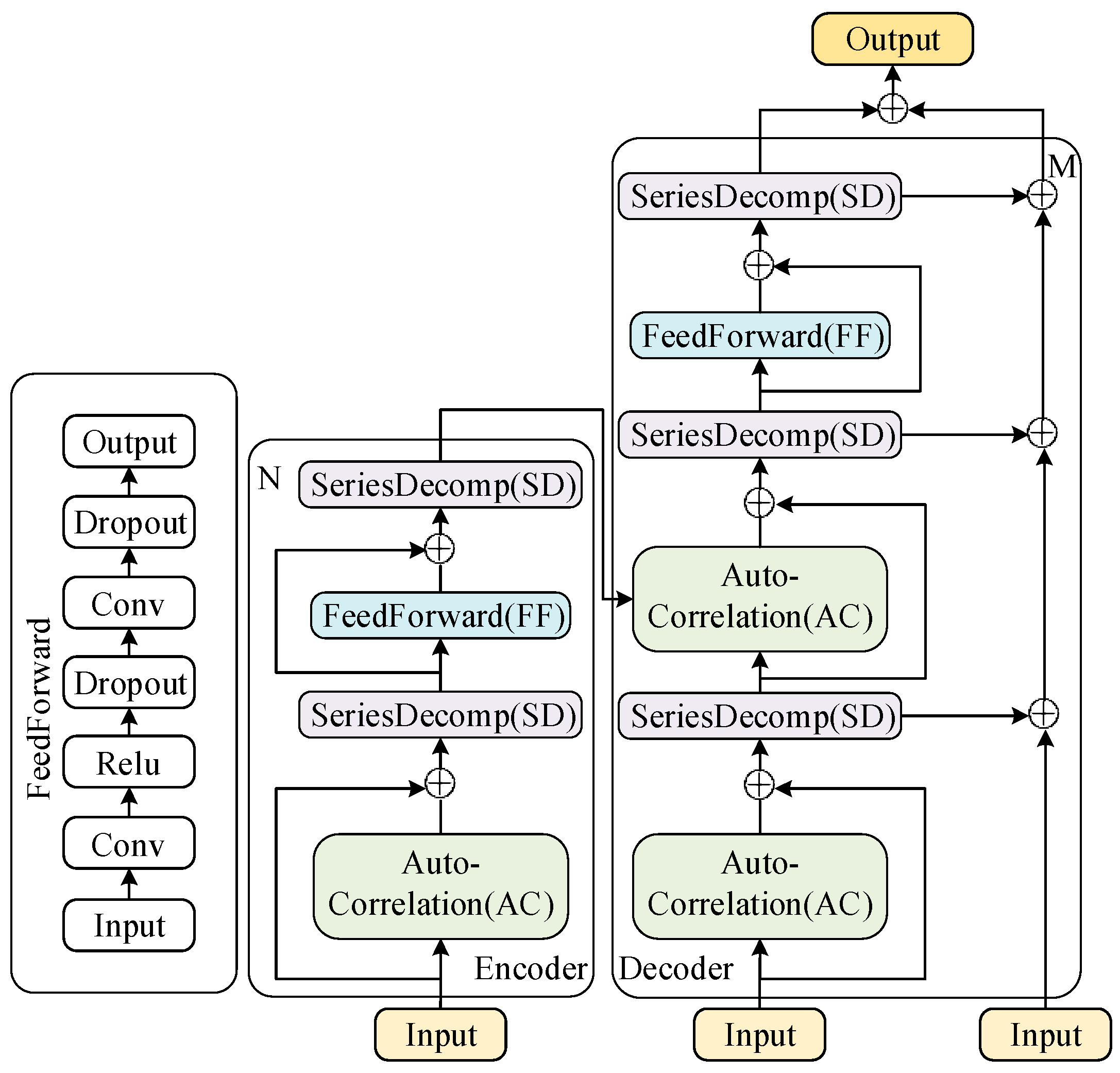
The structure of the time-series prediction model based on Autoformer is shown in
Figure 2. As can be seen from the figure, the Autoformer algorithm is built around the encoder–decoder architecture, which integrates the processes of decomposition and auto-correlation for more accurate time-series predictions. The Decomposition Block gradually separates long-term trend information, while the auto-correlation mechanism identifies the similarity of subsequences based on the periodicity of the sequence, and aggregates similar subsequences. Since energy consumption sequences are typically long, often exhibit seasonal trends, and are closely related to human activity patterns, they possess subsequence similarity. Therefore, these modules of Autoformer enable the algorithm to achieve higher accuracy when predicting such sequences [
16,
17].
In detail, the input to the algorithm is a time-series sequence, which is first fed into the encoder. The encoder processes the input sequence N (the length of the input time series), decomposing it into trend and seasonal components. The Decomposition Block (SD) is responsible for this process, which is further enhanced by the auto-correlation (AC) mechanism that identifies and aggregates similar subsequences from different periods. This mechanism is crucial for handling periodic patterns in energy consumption data.
The processed output from the encoder is then passed to the decoder, which reconstructs the sequence into the final predicted output M (the length of the output sequence). The decoder applies similar steps by modeling the trend and seasonal components separately and combining them to produce the final predictions. The FeedForward (FF) layer further enhances the model’s ability to process the time series efficiently.
The encoder and decoder are connected by the decomposition and auto-correlation processes. After the encoder extracts meaningful representations, the decoder reconstructs them into the final prediction. The auto-correlation mechanism ensures that both encoder and decoder are able to capture long-term dependencies and periodicities, enhancing prediction accuracy.
2.1.1. Decomposition Block
Based on the concept of moving averages, the original sequence is decomposed into a seasonal component (1) and a trend component (2):
where
x represents the original sequence,
xs represents the seasonal component, and
xt represents the trend component. Equations (1) and (2) are combined into Equation (3).
2.1.2. Auto-Correlation Mechanism
Typically, similar phases within different periods exhibit similar sub-processes. The model employs an auto-correlation mechanism to achieve efficient sequence-level connections, which includes two main components: period-based dependencies discovery and time-delay aggregation.
In the period-based dependencies module, based on the theory of random processes, the auto-correlation coefficient
Rxx(
τ) for a real discrete-time process {
x} can be calculated as shown in Equation (4).
where the auto-correlation coefficient
Rxx(
τ) represents the similarity between the sequence {
xt} and its
τ-lagged version {
xt−τ}. We regard this time-lagged similarity as the unnormalized confidence of the period estimate, that is to say, the confidence
R(
τ) for a period length of
τ.
The purpose of time-delay aggregation is to aggregate similar subsequence information to achieve sequence-level connections. To accomplish this, the Roll() operation is first used to align the information based on the estimated period length, followed by information aggregation. This process utilizes the parameters query (Q), key (K), and value (V), where Q and K are used to calculate the weights. Specifically, the auto-correlation coefficients of Q and K are first calculated using Equation (4), and then they are combined with V and weighted to obtain the final encoded output. This auto-correlation process is described by Equations (5)–(7).
where
k =
c × log
L,
L represents the length of the sequence and
c is a hyperparameter.
2.1.3. Encoder–Decoder Framework
In the encoder part, the original sequence xen to be predicted is first vectorized to obtain , which is then used as input. The trend components are gradually removed, resulting in the seasonal components and . This periodic characteristic is utilized to construct the auto-correlation mechanism, allowing the aggregation of similar sub-prcesses across different periods, thereby achieving information integration.
In the decoder part, models for the trend and seasonal components are established separately. For the seasonal component, modeling is performed based on the periodic properties of the sequence, with the auto-correlation mechanism aggregating subsequences that exhibit similar processes across different periods. For the trend component, a step-by-step accumulation method is employed to extract trend information from the predicted original sequence.
The latter half of the original sequence xen of length L is first decomposed into the seasonal component xens and the trend component xent. Then, xens and xent are concatenated with the all-zero sequence (x0) and the mean value sequence of the original sequence (xMean), respectively, to obtain the input sequences xdes and xdet for the decoder. The seasonal and trend components are modeled separately, ultimately yielding the model’s predicted values.
2.2. GS–RandomForest Algrithm
Random forest is an ensemble learning method constructed by combining multiple decision trees. Each decision tree in a random forest is built based on training data, and is used for prediction and classification. The advantage of random forests is that they mitigate the overfitting tendency of decision trees during classification, reducing the probability of overfitting by using multiple trees, which introduces randomness in variable selection, further increasing the model’s robustness and prediction accuracy.
To further enhance the performance of the random forest algorithm, a grid search algorithm is introduced to optimize the parameters of the random forest. Essentially, grid search is an exhaustive method that examines all possible combinations of parameters required in the model, comparing, analyzing, and validating each combination to select the optimal model and hyperparameter configuration.
The grid search algorithm assumes that the model has two hyperparameters, with each hyperparameter having a set of candidate parameters, which are considered in parallel. The algorithm then arranges all combinations into a two-dimensional grid or a grid in higher-dimensional space. The model traverses all nodes in the grid to select the optimal solution, which is the grid search process [
18].
Overall, the prediction module of the algorithm reconstructs the original sequence into a residual sequence, which can eliminate potential trend components in the original sequence, making outliers easier to detect using the grid search-optimized random forest algorithm. The improved random forest algorithm, through parameter optimization and the combination of multiple decision trees, effectively enhances the accuracy and stability of outlier detection [
19].
2.3. Model Evaluation Criteria
2.3.1. Evaluation Criteria for the Algorithm’s Prediction Module
The expressions for Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and the Coefficient of Determination (R
2) are provided in Equations (8)–(11). Among them, the smaller the MAE, MSE, and RMSE, the higher the prediction accuracy of the model. And the closer R
2 is to 1, the higher the prediction accuracy of the model. These metrics can be used to evaluate the prediction accuracy of the prediction module.
where n is the number of data points in the sequence,
is the i-th predicted value of the sequence, and
is the i-th actual value in the sequence.
2.3.2. Module Evaluation Criteria for the Algorithm’s Detection Module
Outlier detection can essentially be viewed as a binary classification problem. Therefore, precision, recall, and F1 score can be used to evaluate the accuracy of outlier detection. Their expressions are provided in Equations (12)–(14).
where TP (True Positive) represents the positive samples correctly predicted by the model, FP (False Positive) represents the negative samples incorrectly predicted as positive by the model, and FN (False Negative) represents the positive samples incorrectly predicted as negative by the model.
4. Conclusions
This study proposes a time-series anomaly detection model, AF-GS–RandomForest, for detecting anomalies in the time series of power consumption data. The main contributions of this work include the following: (1) the prediction component of the model, based on the Autoformer algorithm, effectively utilizes the sequence decomposition module, auto-correlation mechanism, and encoder–decoder modules to extract feature vectors from energy consumption data, enhancing the selection of critical information and fully leveraging historical data to predict energy consumption, thereby accurately reconstructing the residual sequence; and (2) an empirical analysis of the AF-GS–RandomForest algorithm was conducted, validating its effectiveness on typical datasets, and was successfully applied to a real dataset for detecting anomalies in energy consumption data.
This research primarily focuses on the detection of point anomalies. In future studies, methods for detecting and identifying anomalous time periods could be further explored. Additionally, as the methods chosen in this study rely heavily on high-accuracy prediction models, future research could focus on improving the structure of the prediction module to further enhance the algorithm’s prediction accuracy and robustness.