Impact of Data Corruption and Operating Temperature on Performance of Model-Based SoC Estimation
Abstract
1. Introduction
1.1. Contributions
- (a)
- Analyzed the impact of complex temperature environments on the performance of model-based SOC estimation to prove that the battery parameters can support estimating the SoC accurately.
- (b)
- Analyzed the impact of different data sampling times on the performance of model-based SOC estimation methods such as CLCS, DCLCS, and EKF. The experiments show how various data sampling times, used to simulate the adverse effect of data corruption inside EVs, significantly affect the SoC estimation accuracy. The experiments also show which method is suitable for accurately estimating the SoC of the data corruption.
- (c)
- Analyzed the SoC estimation results at different temperatures, 10 °C, 25 °C, and 40 °C, which are validated under a dynamic load profile, and analyzed the performance of different model-based methods at different data sampling times to demonstrate that an automatic data sampling time correction is necessary for the EV system.
1.2. Paper Structure
2. Model-Based SoC Estimation Methods
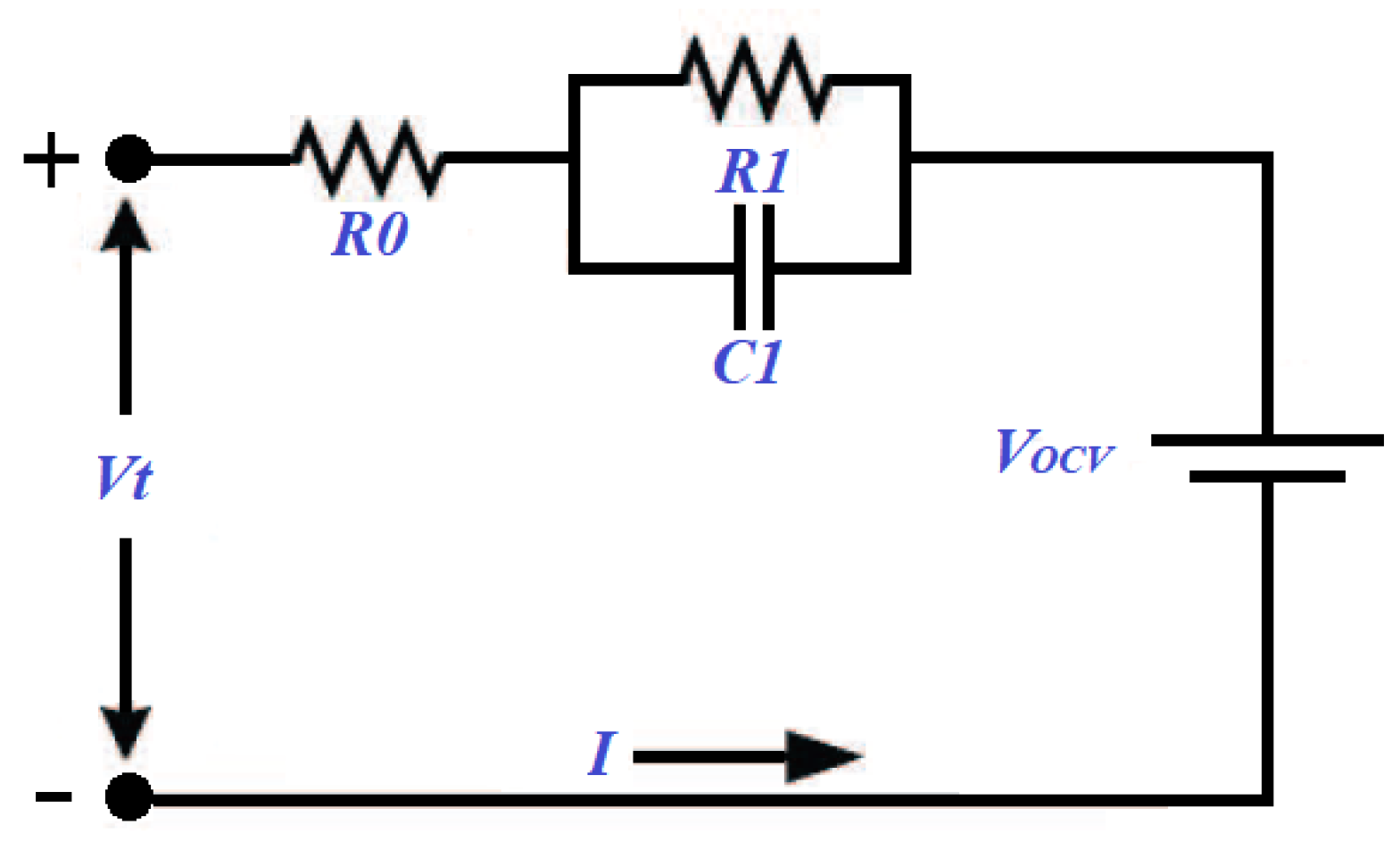
2.1. 1-RC Battery Modelling
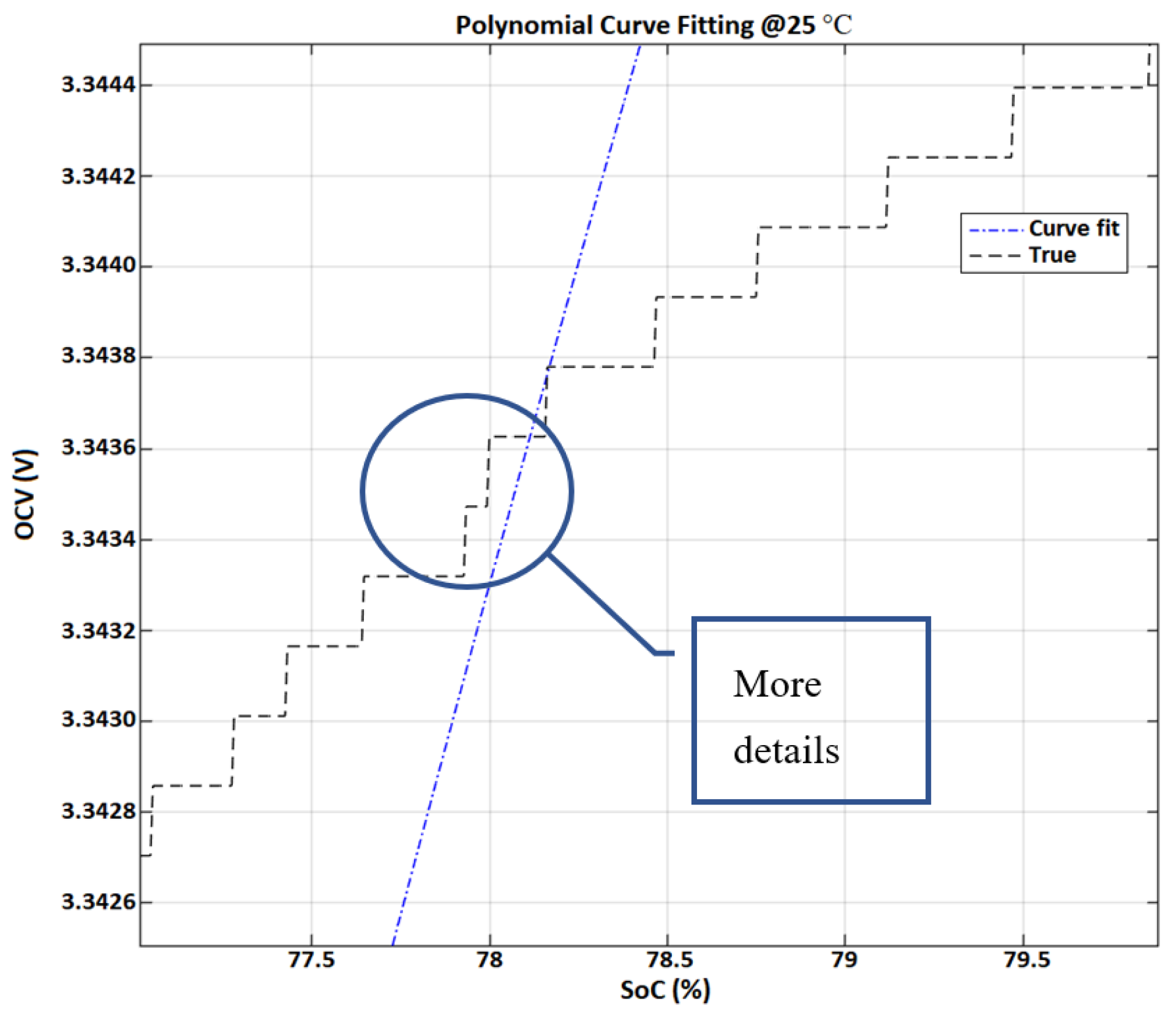
2.2. The OCV and SoC Relationship
3. SoC Estimation Methods
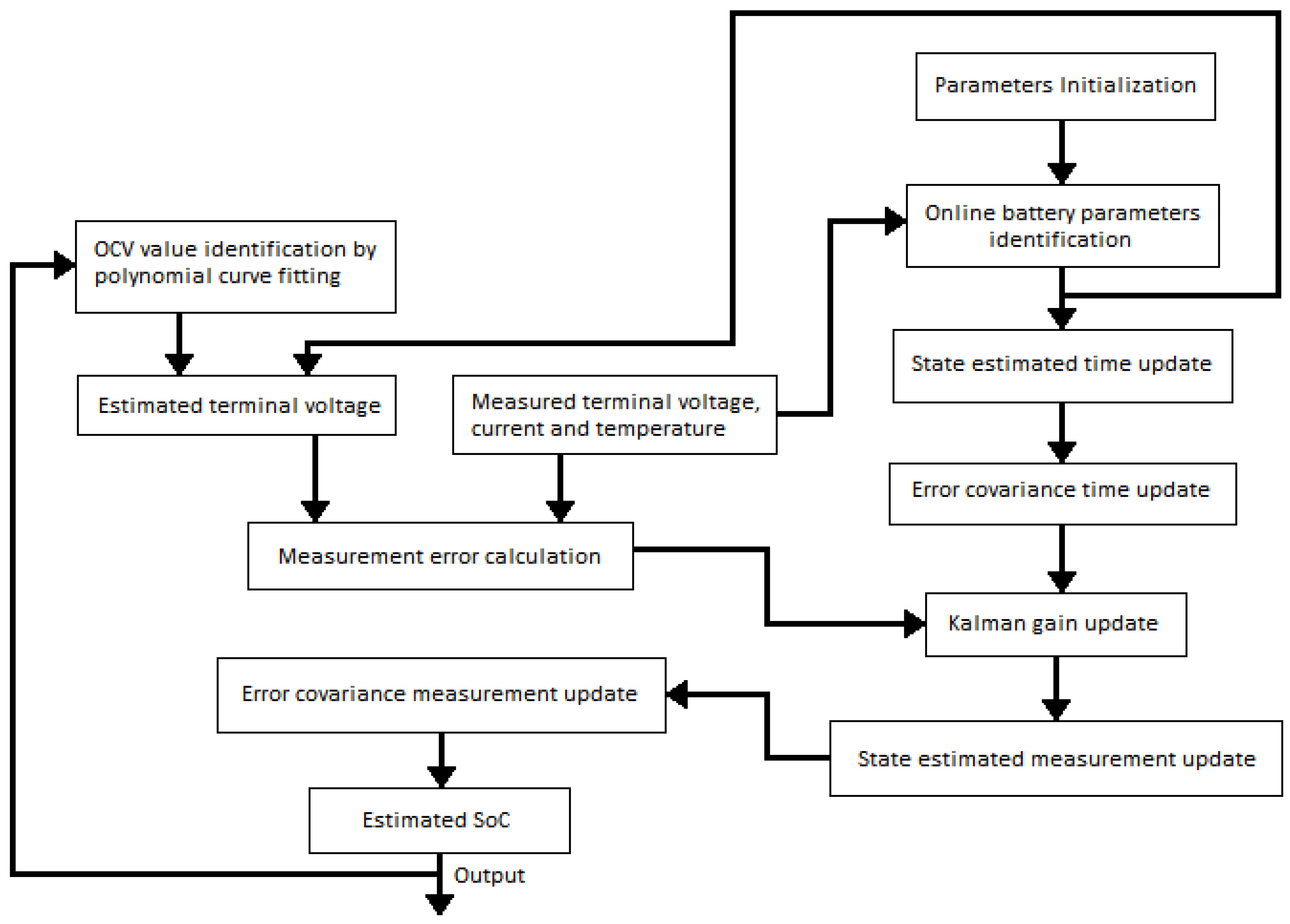
3.1. Using EKF
3.1.1. The Measurement Process of EKF
3.1.2. The Process Noise and Measurement Noise Covariance Consideration
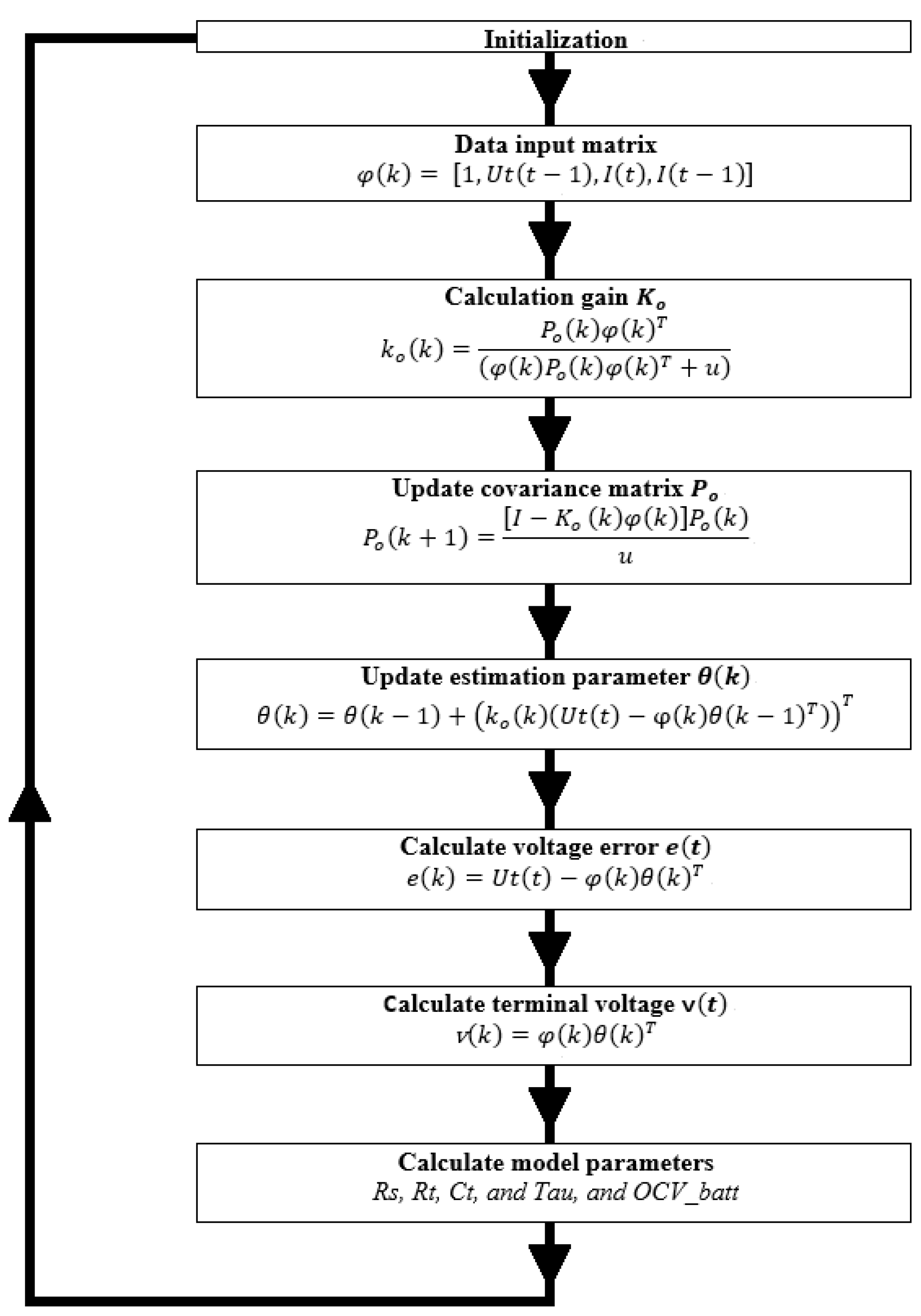
3.2. Using Traditional Mixed Method (Closed-Loop Control System)
3.3. Using Improved Mixed Method (Dual Closed-Loop Control System)
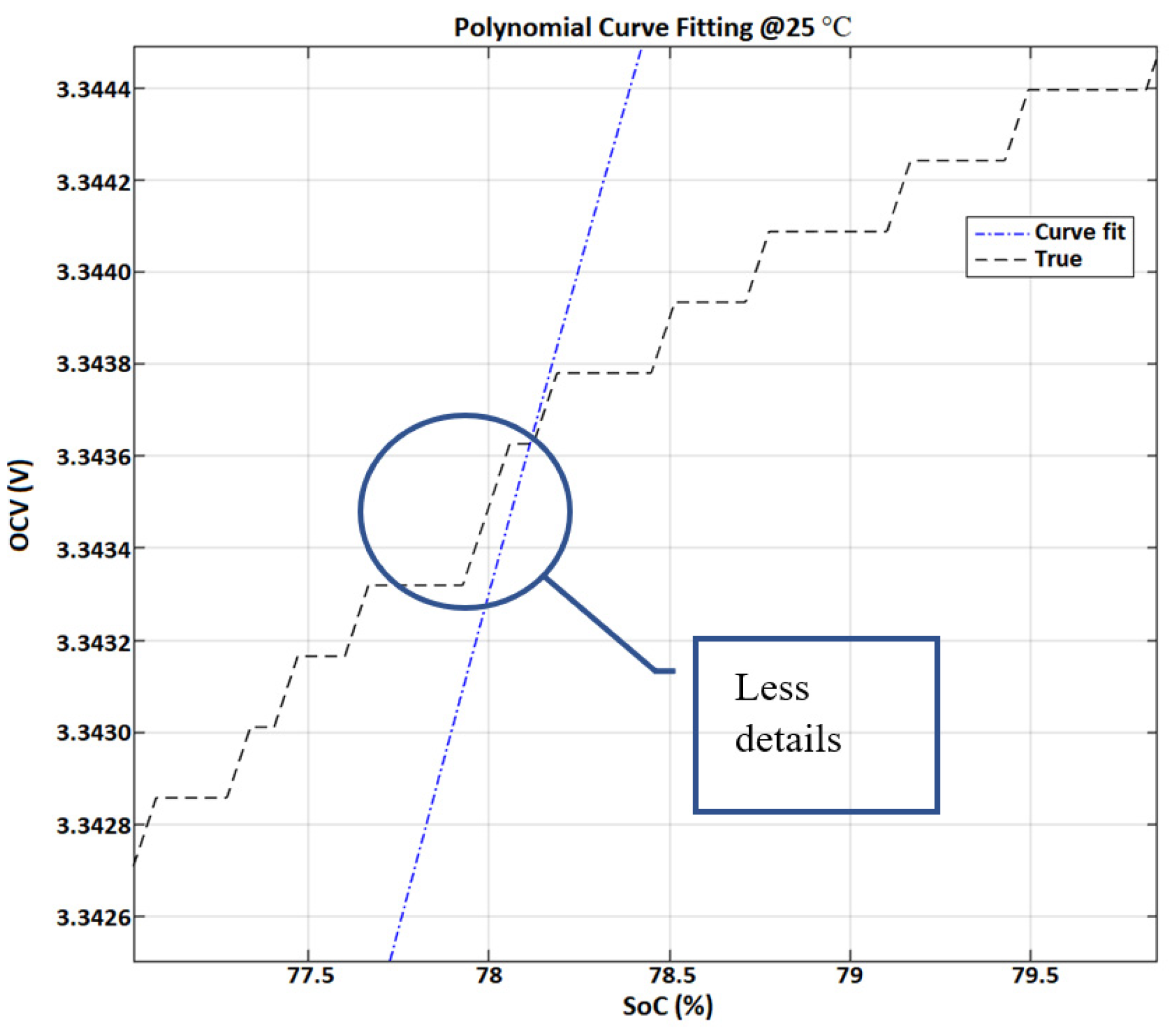
3.4. The Contour of the OCV-SoC Curve at a Low Data Sampling Time Situation
4. Experiments Setup
4.1. Battery Capacity Test at Different Temperatures
4.2. Dynamic Drive Cycle Test Profile
4.3. Software Structure for Data Measurement at Different Data Sampling Times
4.4. Evaluation Matrices—The Equation of the SoC RMSE
5. Results and Discussion
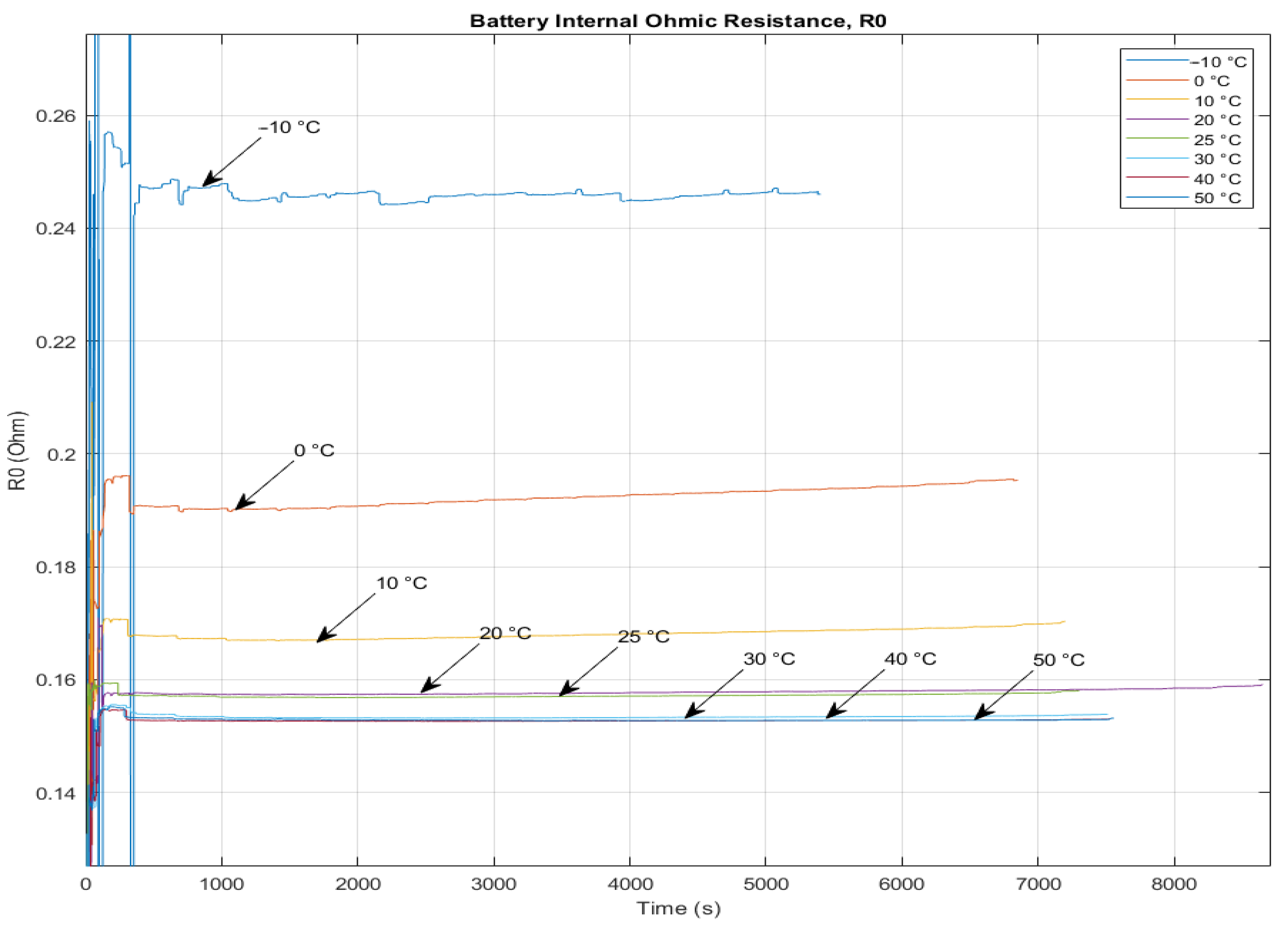
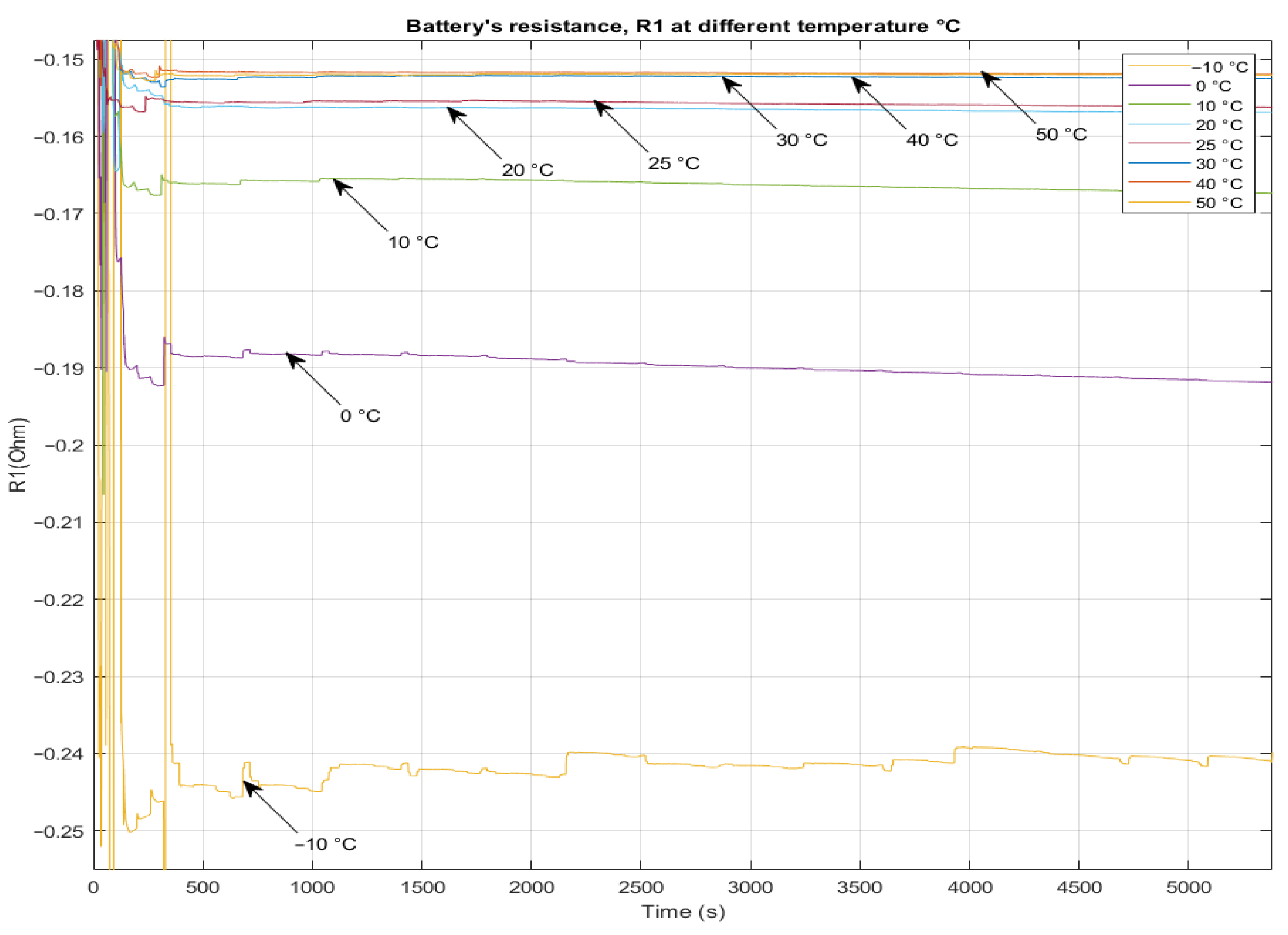
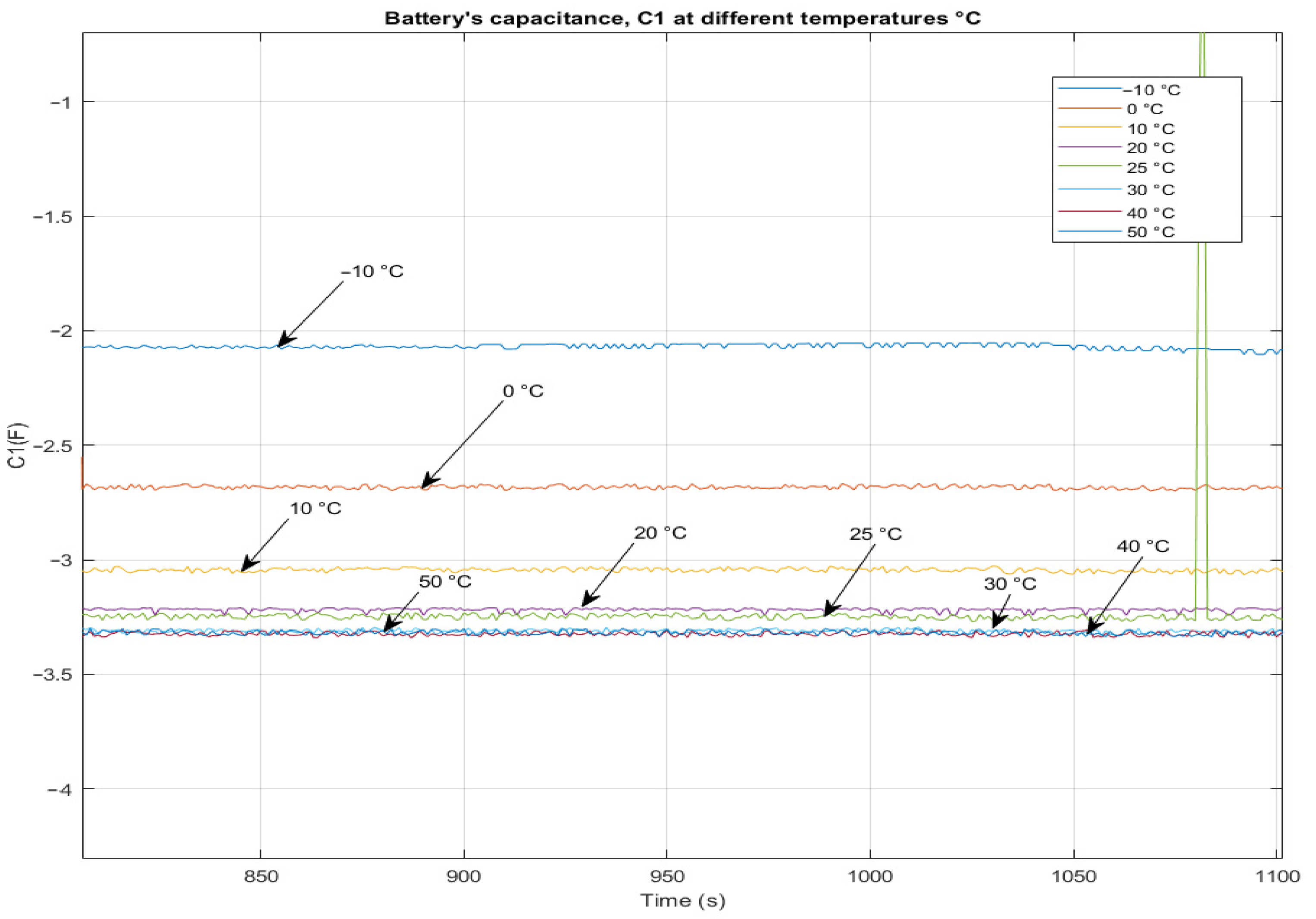
5.1. The Variation of Battery Parameters at Different Temperatures
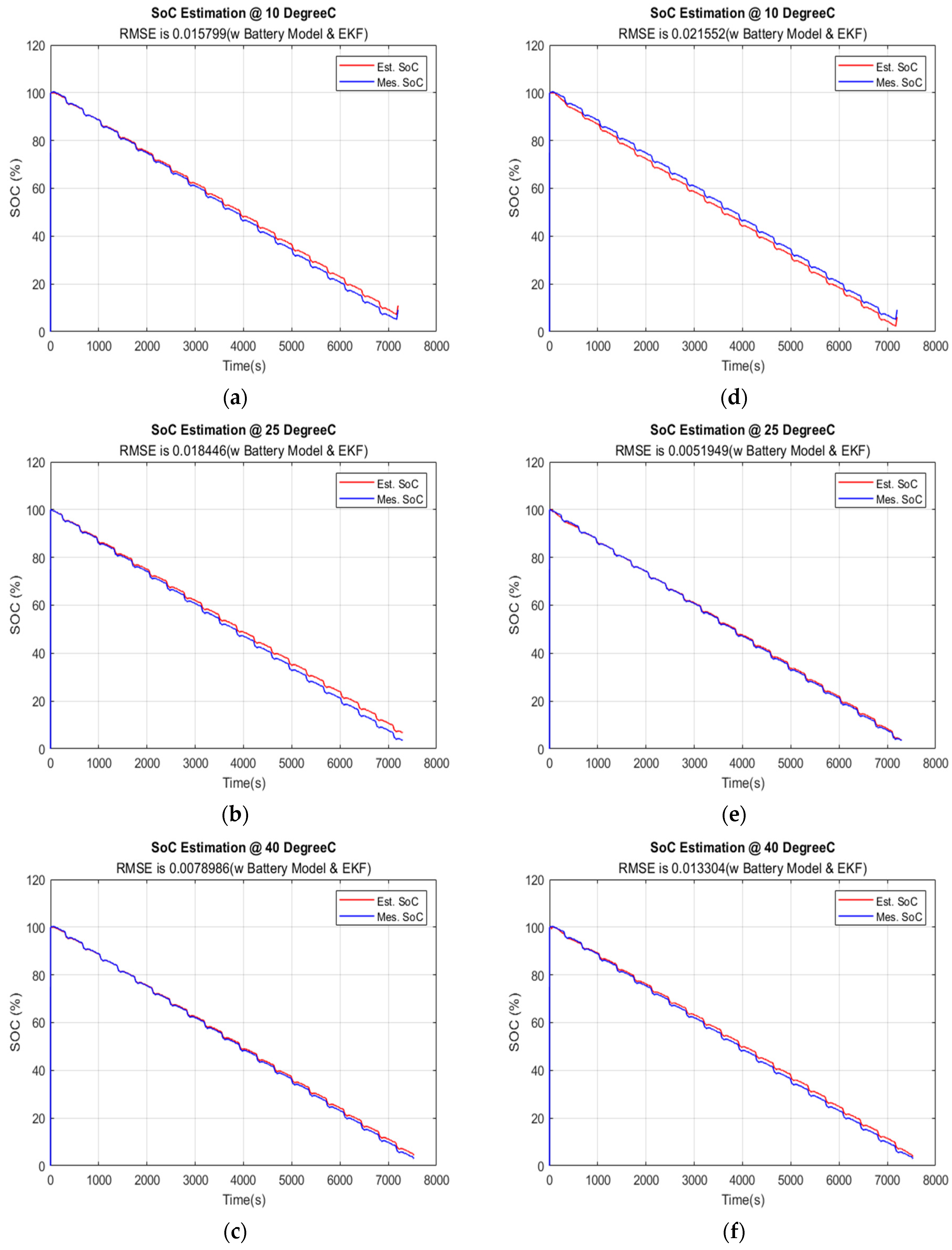
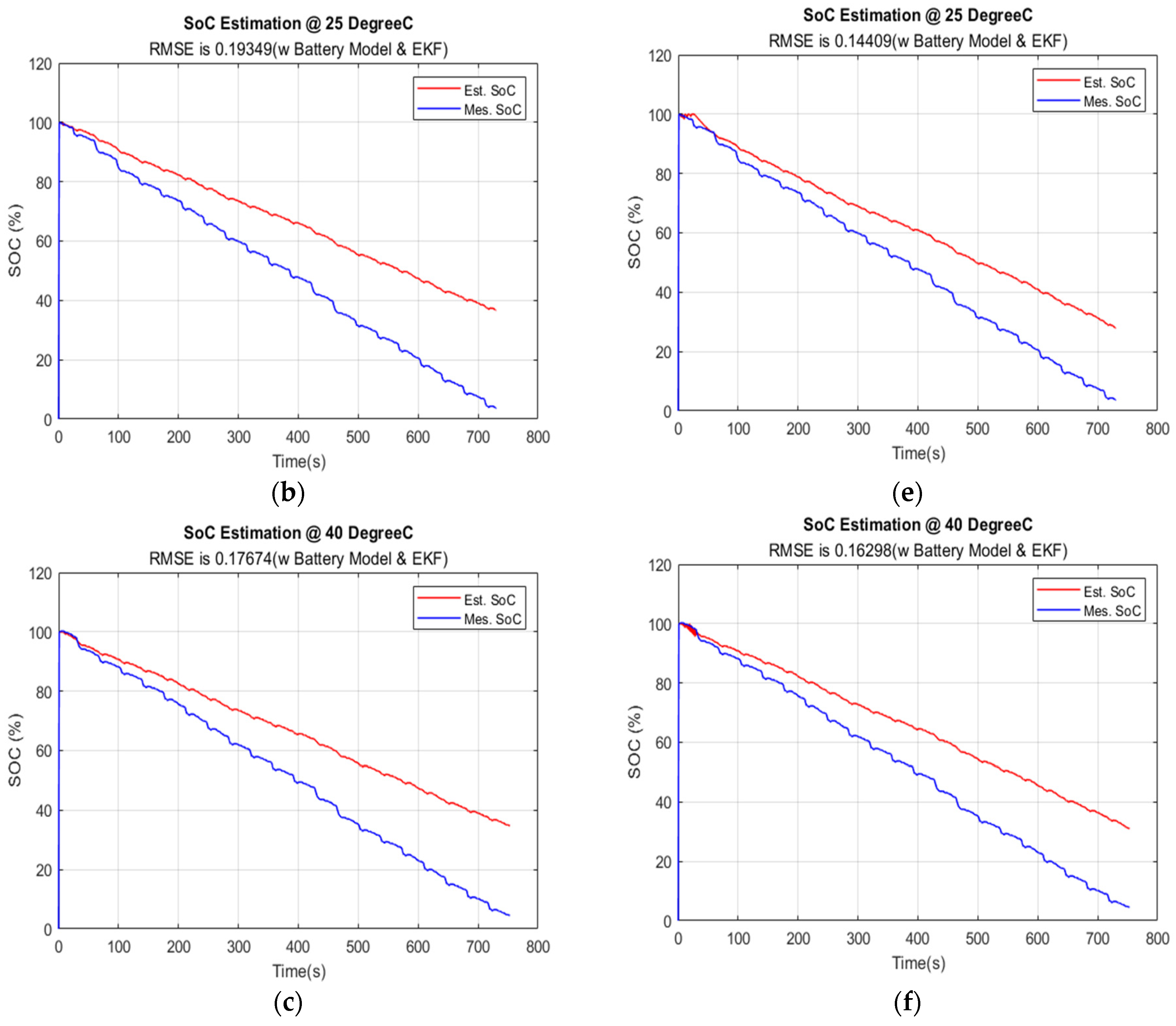
5.2. The SoC Estimation Results at Temperatures 10 °C, 25 °C, and 40 °C by EKF
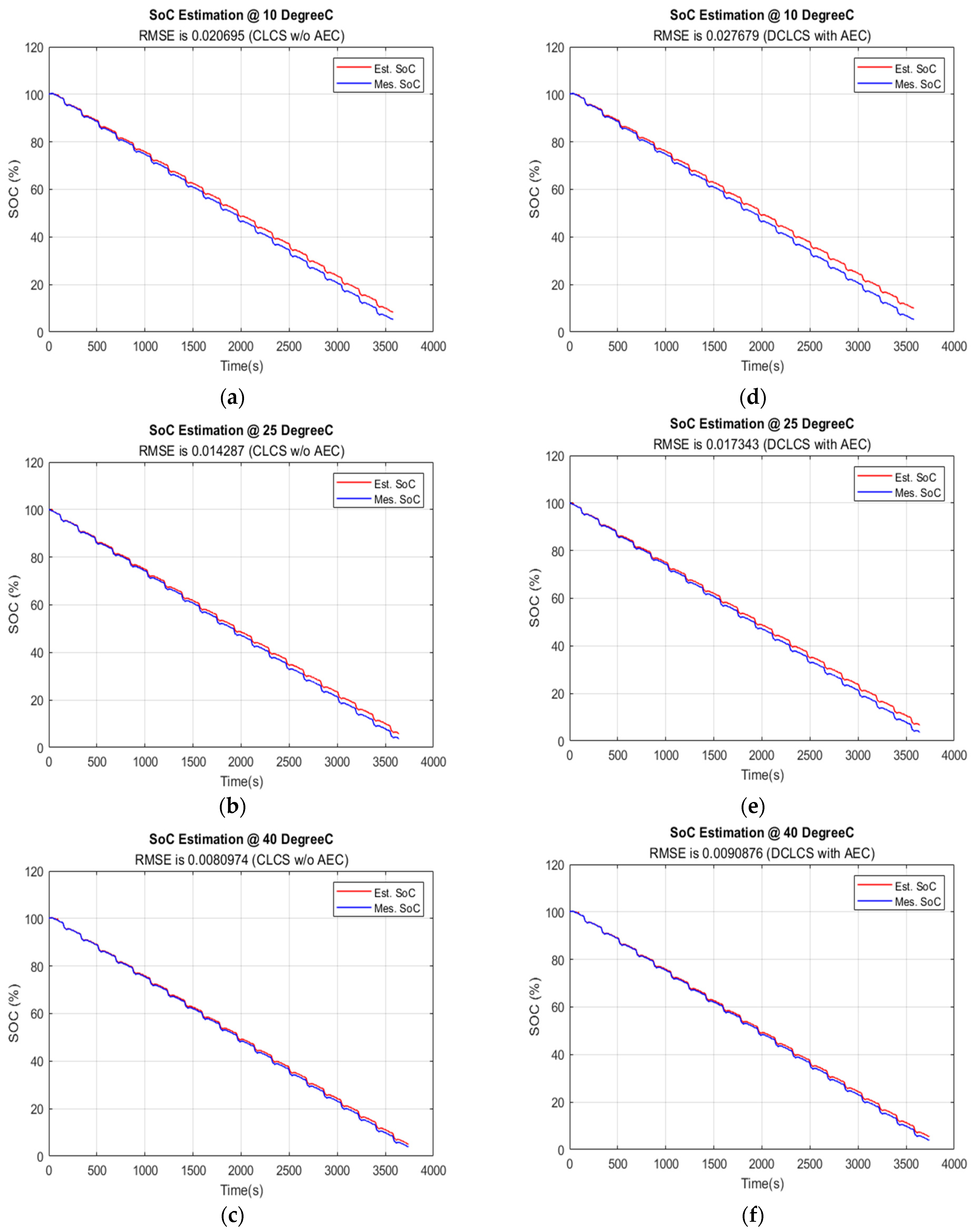
5.3. The SoC Estimation Result at Temperatures 10 °C, 25 °C, and 40 °C by CLCS and DCLCS with AEC
5.4. The SoC Results at Different Data Sampling Times and Temperatures 10 °C, 25 °C, and 40 °C by EKF
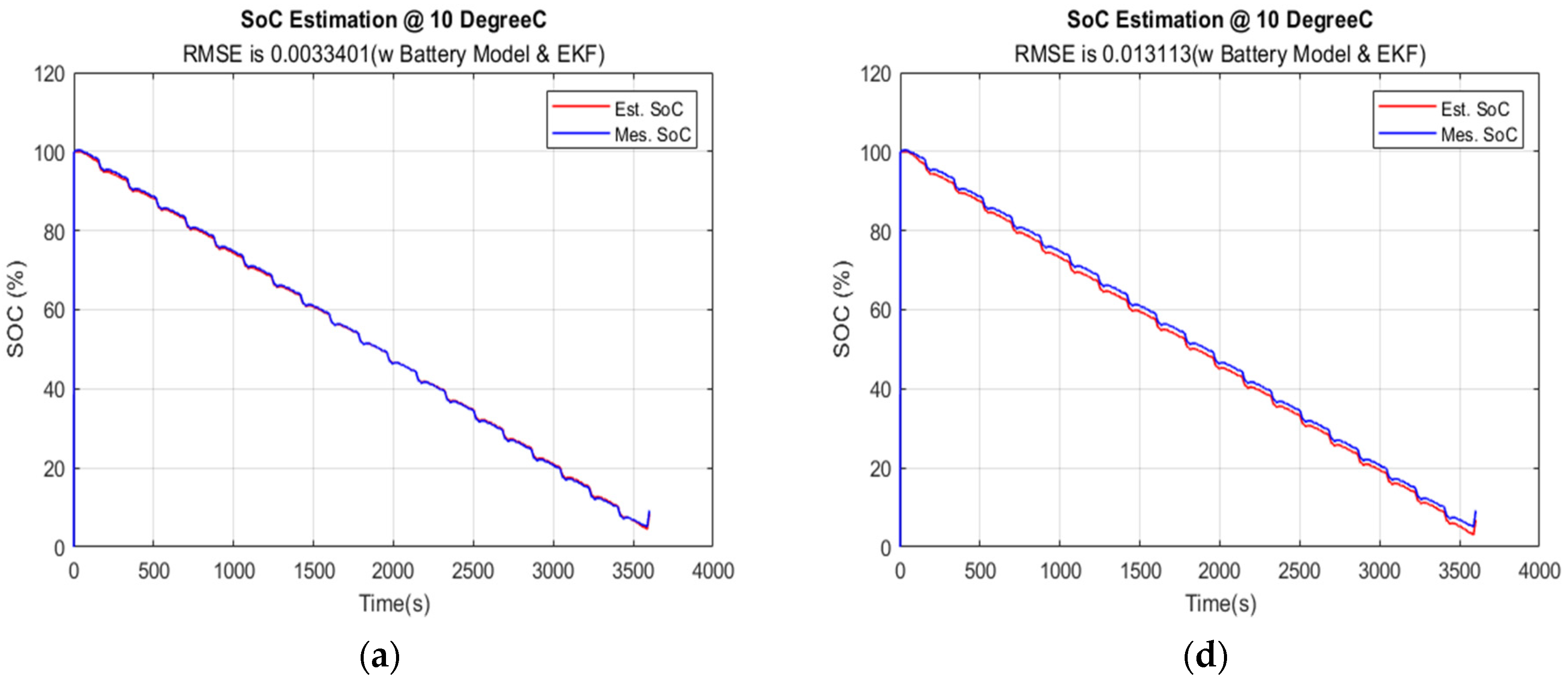
5.4.1. Data Sampling Time at 2 s
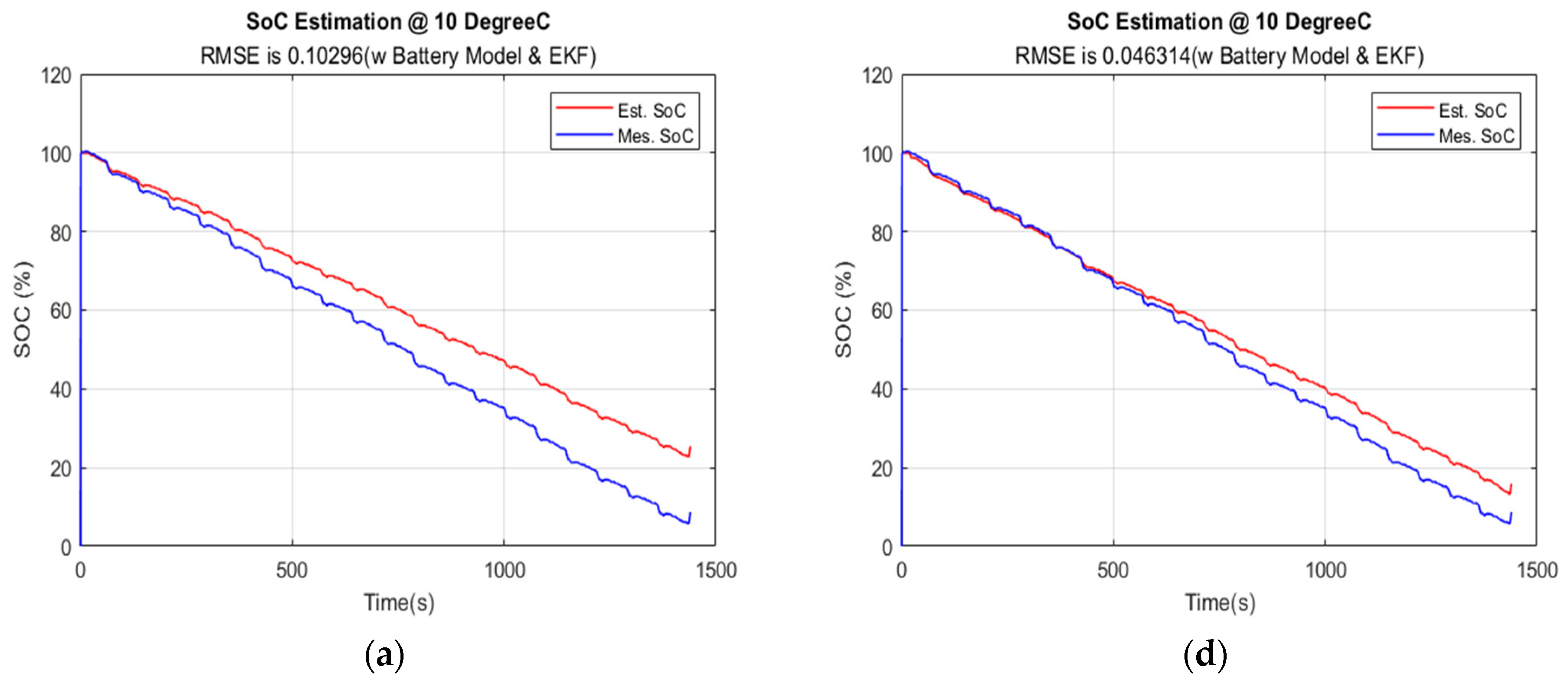
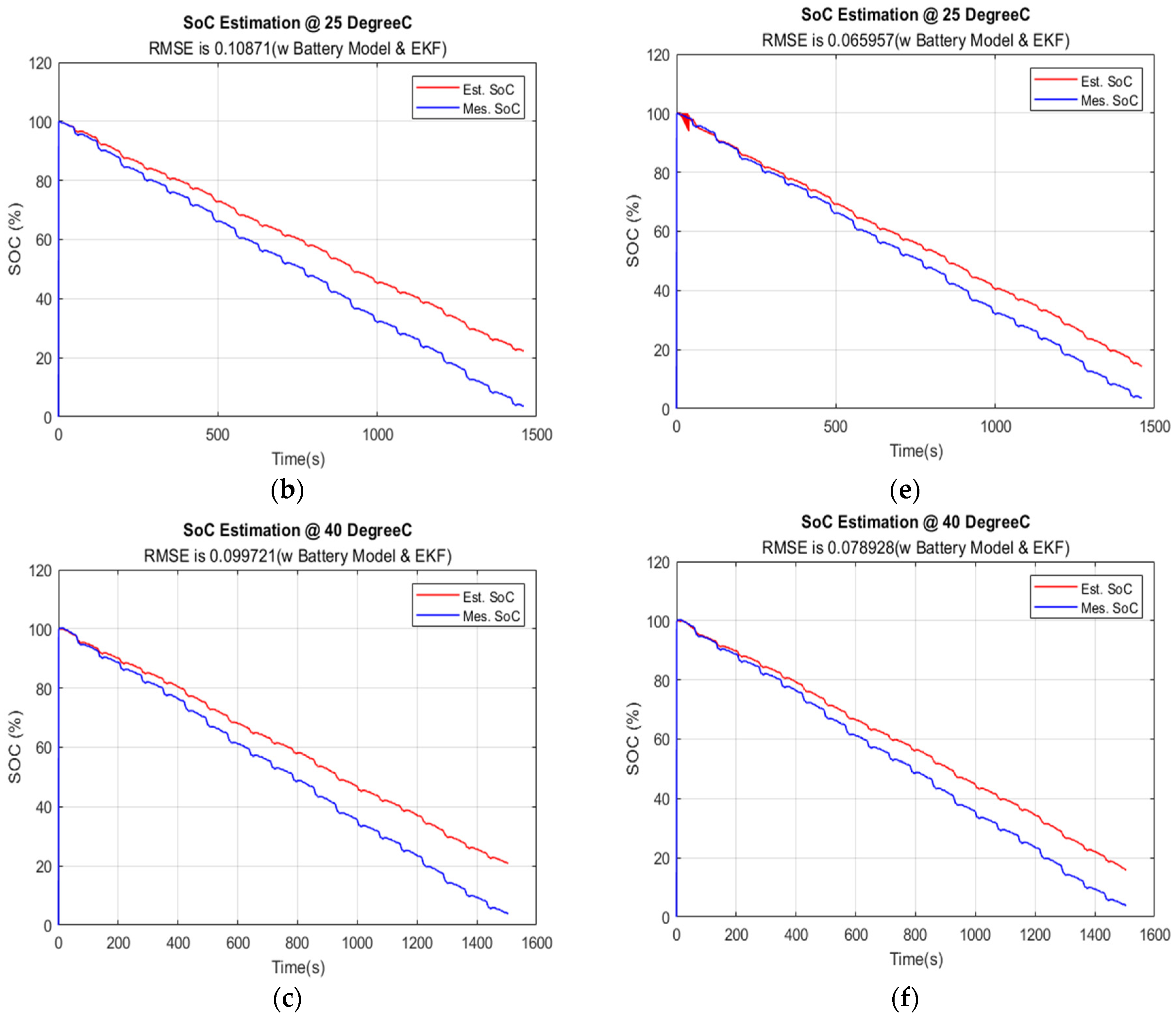
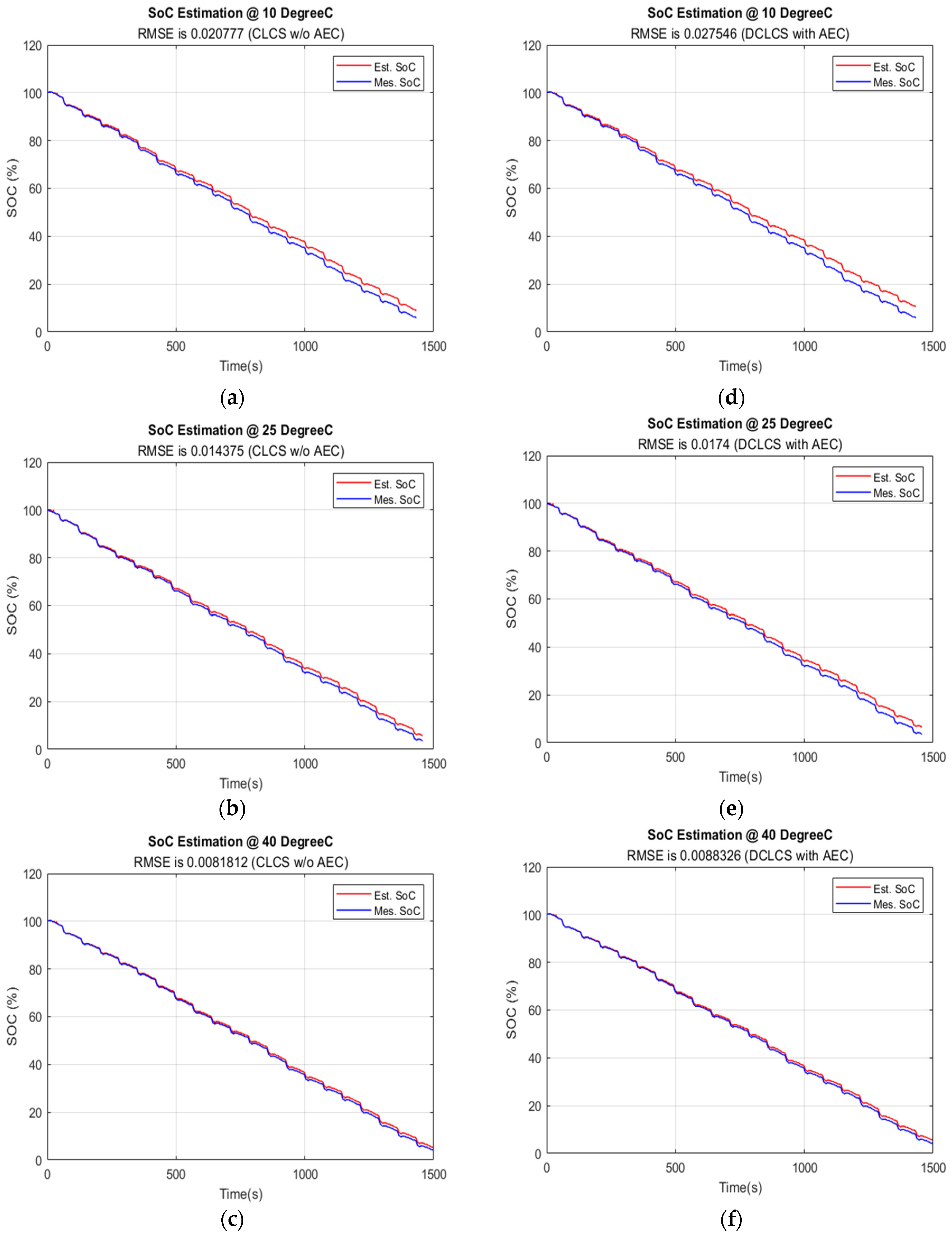
5.4.2. Data Sampling Time at 5 s
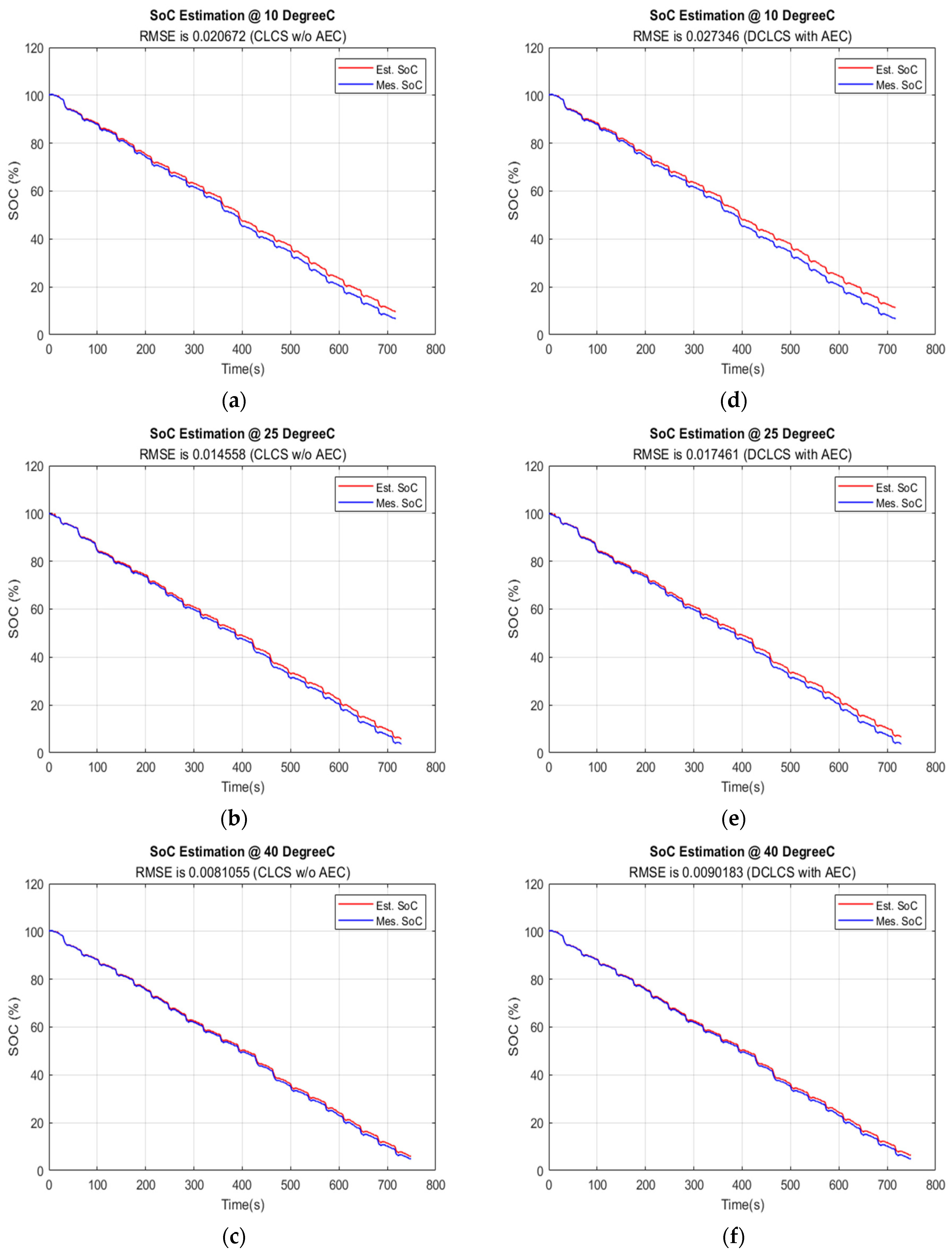
5.4.3. Data Sampling Time at 10 s
5.5. The SoC Results at Different Data Sampling Times and Temperatures 10 °C, 25 °C, and 40 °C by CLCS and DCLCS
5.5.1. Data Sampling Time at 2 s
5.5.2. Data Sampling Time at 5 s and 10 s
5.6. Discussion of Estimation Results of Model-Based Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EV | Electric Vehicle | CAN | Control Area Network |
| EVs | Electric Vehicles | VCU | Vehicle Control Unit |
| LIB | Lithium Battery | CCM | Coulomb Counting Method |
| BMS | Battery Management System | OCVM | Open Circuit Voltage Method |
| SoC | State of Charge | LFP | LifePO4 |
| KF | Kalman Filter | MBM | Model-Based Method |
| EMI | Electromagnetic interference | MM | Mixed Method |
| EKF | Extended Kalman Filter | CLCS | Closed-loop control system |
| OCV | Open-Circuit Voltage | ICC-AEC | Improved Coulomb Counting Method with an Adaptive Error Correction |
| 1-RC | First-Order | DCLCS | Dual closed-loop control system |
| 2-RC | Second-Order | Terminal Voltage | |
| ECM | Equivalent Circuit Model | Ohmic Resistance | |
| FF-RLS | Forgetting Factor-Based Recursive Least Squares Algorithm | Polarization Resistance | |
| DST | Dynamic Stress Test | Polarization Capacitance | |
| CCC | Climate Change Committee | Vocv | Voltage Source |
| HGVs | Heavy-Goods Vehicles | MCU | Microcontroller |
| MSD | Manual Service Disconnect | PLL | Phase Lock Loop |
| EMF | Electric and Magnetic Field | PC | Personal Computer |
| AC | Alternative Current | ISR | Interrupt Service Routine |
| DC | Direct Current | ASTC | Automatic Data Sampling Time Correction |
| PCF | Polynomial Curve Fitting | s | second |
References
- Sun, A. Why China’s Electric Vehicle Market Is at Full Throttle, Schroders. Available online: https://www.schroders.com/en/global/individual/insights/why-chinas-electric-vehicle-market-is-at-full-throttle/ (accessed on 30 October 2023).
- Briefing Document: The UK’s Transition to Electric Vehicles. The UK. 2020. Available online: https://www.theccc.org.uk/wp-content/uploads/2020/12/The-UKs-transition-to-electric-vehicles.pdf (accessed on 31 October 2023).
- Lin, X.; Stefanopoulou, A.G.; Perez, H.E.; Siegel, J.B.; Li, Y.; Anderson, R.D. Quadruple Adaptive Observer of the Core Temperature in Cylindrical Li-ion Batteries and their Health Monitoring. In Proceedings of the 2012 American Control Conference (ACC), Montréal, QC, Canada, 27–29 June 2012. [Google Scholar] [CrossRef]
- Rodríguez-Iturriaga, P.; Anseán, D.; López-Villanueva, J.A.; González, M.; Rodríguez-Bolívar, S. A method for the lifetime sensorless estimation of surface and core temperature in lithium-ion batteries via online updating of electrical parameters. J. Energy Storage 2023, 58, 106260. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, M.; Fu, C.; Cao, K.; Su, Z.; Yang, Z. State of charge estimation for lithium-ion batteries based on temperature-dependent second-order RC model. Electronics 2019, 8, 1012. [Google Scholar] [CrossRef]
- Madani, S.S.; Schaltz, E.; Kær, S.K. Review of parameter determination for thermal modeling of lithium ion batteries. Batteries 2018, 4, 20. [Google Scholar] [CrossRef]
- Sarrafan, K.; Muttaqi, K.; Sutanto, D. Real-time estimation of model parameters and state-of-charge of lithiumion batteries in electric vehicles using recursive least-square with forgetting factor. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems, PEDES 2018, Chennai, India, 18–21 December 2018; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Rzepka, B.; Bischof, S.; Blank, T. Implementing an extended Kalman filter for SoC estimation of a Li-ion battery with hysteresis: A step-by-step guide. Energies 2021, 14, 3733. [Google Scholar] [CrossRef]
- Zhu, M.; Qian, K.; Liu, X. A three-time-scale dual extended Kalman filtering for parameter and state estimation of Li-ion battery. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 238, 1352–1367. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Y.; Gu, T. A hierarchical adaptive extended Kalman filter algorithm for lithium-ion battery state of charge estimation. J. Energy Storage 2023, 62, 106831. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.S.; Fiori, F. Susceptibility to EMI of a Battery Management System IC for electric vehicles. In Proceedings of the 2015 IEEE International Symposium on Electromagnetic Compatibility (EMC), Dresden, Germany, 16–22 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 749–754. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Y.; Hu, Z.; Zhang, Y.; Zhang, J. A Battery SOC Estimation Method Based on AFFRLS-EKF. Sensors 2021, 21, 5698. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Ker, P.J.; Mahlia, T.M.I.; Mansor, M.; Ayob, A.; Saad, M.H.; Dong, Z.Y. Toward Enhanced State of Charge Estimation of Lithium-ion Batteries Using Optimized Machine Learning Techniques. Sci. Rep. 2020, 10, 4687. [Google Scholar] [CrossRef]
- Lee, J.; Won, J. Enhanced Coulomb Counting Method for SoC and SoH Estimation Based on Coulombic Efficiency. IEEE Access 2023, 11, 15449–15459. [Google Scholar] [CrossRef]
- Mohammadi, F. Lithium-ion battery State-of-Charge estimation based on an improved Coulomb-Counting algorithm and uncertainty evaluation. J. Energy Storage 2022, 48, 104061. [Google Scholar] [CrossRef]
- Codecà, F.; Savaresi, S.M.; Manzoni, V. The Mix Estimation Algorithm for Battery State-of-Charge Estimator: Analysis of the Sensitivity to Model Errors. 2009. Available online: http://asmedigitalcollection.asme.org/DSCC/proceedings-pdf/DSCC2009/48920/97/2770601/97_1.pdf (accessed on 31 October 2023).
- Kadem, O.; Kim, J. Real-Time State of Charge-Open Circuit Voltage Curve Construction for Battery State of Charge Estimation. IEEE Trans. Veh. Technol. 2023, 72, 8613–8622. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, L.; Liu, S.; Wang, L.; Loh, P.C. A generalized SOC-OCV model for lithium-ion batteries and the SOC estimation for LNMCO battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, T.; Li, X. SOC Estimation of Lithium-Ion Battery Based on Equivalent Circuit Model with Variable Parameters. Energies 2022, 15, 5829. [Google Scholar] [CrossRef]
- Aktas, A. Design and implementation of adaptive battery charging method considering the battery temperature. IET Circuits Devices Syst. 2020, 14, 72–79. [Google Scholar] [CrossRef]
- Hossain, M.; Saha, S.; Arif, M.T.; Oo, A.M.T.; Mendis, N.; Haque, M.E. A Parameter Extraction Method for the Li-Ion Batteries with Wide-Range Temperature Compensation. IEEE Trans. Ind. Appl. 2020, 56, 5625–5636. [Google Scholar] [CrossRef]
- Nissing, D.; Mahanta, A.; Van Sterkenburg, S. Thermal Model Parameter Identification of a Lithium Battery. J. Control Sci. Eng. 2017, 2017, 9543781. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S.; Adnan, S.B.R.S. Model-based state of X estimation of lithium-ion battery for electric vehicle applications. Int. J. Energy Res. 2022, 46, 10704–10723. [Google Scholar] [CrossRef]
- Wu, K.H.; Seyedmahmoudian, M.; Mekhilef, S.; Shrivastava, P.; Stojcevski, A. Lithium-ion battery state of charge estimation using improved coulomb counting method with adaptive error correction. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 09544070231210562. [Google Scholar] [CrossRef]
- Rajanna, B.V.; Kumar, M.K. Comparison of one and two time constant models for lithium ion battery. Int. J. Electr. Comput. Eng. 2020, 10, 670–680. [Google Scholar] [CrossRef]
- Yang, S.; Deng, C.; Zhang, Y.; He, Y. State of charge estimation for lithium-ion battery with a temperature-compensated model. Energies 2017, 10, 1560. [Google Scholar] [CrossRef]
- Yu, D.X.; Gao, Y.X. SOC estimation of Lithium-ion battery based on Kalman filter algorithm. Appl. Mech. Mater. 2013, 347–350, 1852–1855. [Google Scholar]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S.; Adnan, S.B.R.S. Combined State of Charge and State of Energy Estimation of Lithium-Ion Battery Using Dual Forgetting Factor-Based Adaptive Extended Kalman Filter for Electric Vehicle Applications. IEEE Trans. Veh. Technol. 2021, 70, 1200–1215. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.B.; Mekhilef, S. Lithium-ion Battery Model Parameter Identification Using Modified Adaptive Forgetting Factor-Based Recursive Least Square Algorithm. In Proceedings of the Energy Conversion Congress and Exposition—Asia, ECCE Asia 2021, Singapore, 24–27 May 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 2169–2174. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, Z. State of charge estimation at different temperatures based on dynamic thermal model for lithium-ion batteries. J. Energy Storage 2022, 48, 104011. [Google Scholar] [CrossRef]
- Singh, Y.; Mehra, R.; Scholar, M.E. Relative Study of Measurement Noise Covariance R and Process Noise Covariance Q of the Kalman Filter in Estimation. IOSR J. Electr. Electron. Eng. 2015, 10, 112–116. Available online: https://www.iosrjournals.org/iosr-jeee/Papers/Vol10-issue6/Version-1/P01061112116.pdf (accessed on 31 October 2023).




| Battery Model | A123 Lithium-Ion Battery |
|---|---|
| Chemistry | LiFePO4 (LFP) |
| Nominal Capacity | 1100 mAh |
| Voltage Range | 2.0 V to 3.6 V |
| Nominal Voltage | 3.3 V |
| Cell Length | 65 mm |
| Diameter | 18 mm |
| Temperature Range | −10 °C to 50 °C |
| Covariances | Temperature | |||
|---|---|---|---|---|
| Q | R | 10 °C | 25 °C | 40 °C |
| 0.015799 | 0.0184460 | 0.0078986 | ||
| 0.021552 | 0.0051949 | 0.0133040 | ||
| Different Temperatures Condition | Closed Loop Control System | Dual Closed Loop Control System with AEC |
|---|---|---|
| 10.0 °C | 0.0209 | 0.0130 |
| 25.0 °C | 0.01432 | 0.0060 |
| 40.0 °C | 0.00812 | 0.0078 |
| Model-Based Methods | ||||
|---|---|---|---|---|
| Data Sampling Times | EKF [Q] [R] | EKF [Q] [R] | MM with CLCS | DCLCS with AEC |
| 1 s | 0.0157990 | 0.0215520 | 0.0208840 | 0.0130400 |
| 2 s | 0.0033401 | 0.0131130 | 0.0206950 | 0.0276790 |
| 5 s | 0.1029600 | 0.0463140 | 0.0207770 | 0.0275460 |
| 10 s | 0.1716100 | 0.1260700 | 0.0206720 | 0.0273460 |
| Model-Based Methods | ||||
|---|---|---|---|---|
| Data Sampling Times | EKF [Q] [R] | EKF [Q] [R] | MM with CLCS | DCLCS with AEC |
| 1 s | 0.0184460 | 0.0051949 | 0.0143190 | 0.0060284 |
| 2 s | 0.0183020 | 0.0071460 | 0.0142870 | 0.0173430 |
| 5 s | 0.1087100 | 0.0659570 | 0.0143750 | 0.0174000 |
| 10 s | 0.1934900 | 0.1440900 | 0.0145580 | 0.0174610 |
| Model-Based Methods | ||||
|---|---|---|---|---|
| Data Sampling Times | EKF [Q] [R] | EKF [Q] [R | MM with CLCS | DCLCS with AEC |
| 1 s | 0.0078986 | 0.0133040 | 0.0081164 | 0.0078327 |
| 2 s | 0.0080993 | 0.0168310 | 0.0080974 | 0.0090876 |
| 5 s | 0.0997210 | 0.0789280 | 0.0081812 | 0.0088326 |
| 10 s | 0.1767400 | 0.1629800 | 0.0081055 | 0.0090183 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, K.H.; Seyedmahmoudian, M.; Mekhilef, S.; Shrivastava, P.; Stojcevski, A. Impact of Data Corruption and Operating Temperature on Performance of Model-Based SoC Estimation. Energies 2024, 17, 4791. https://doi.org/10.3390/en17194791
Wu KH, Seyedmahmoudian M, Mekhilef S, Shrivastava P, Stojcevski A. Impact of Data Corruption and Operating Temperature on Performance of Model-Based SoC Estimation. Energies. 2024; 17(19):4791. https://doi.org/10.3390/en17194791
Chicago/Turabian StyleWu, King Hang, Mehdi Seyedmahmoudian, Saad Mekhilef, Prashant Shrivastava, and Alex Stojcevski. 2024. "Impact of Data Corruption and Operating Temperature on Performance of Model-Based SoC Estimation" Energies 17, no. 19: 4791. https://doi.org/10.3390/en17194791
APA StyleWu, K. H., Seyedmahmoudian, M., Mekhilef, S., Shrivastava, P., & Stojcevski, A. (2024). Impact of Data Corruption and Operating Temperature on Performance of Model-Based SoC Estimation. Energies, 17(19), 4791. https://doi.org/10.3390/en17194791











