Flow Characteristics of Oil-Carrying by Water in Downward-Inclined and Horizontal Mobile Pipeline
Abstract
1. Introduction
2. Mathematical Model
3. Methodology
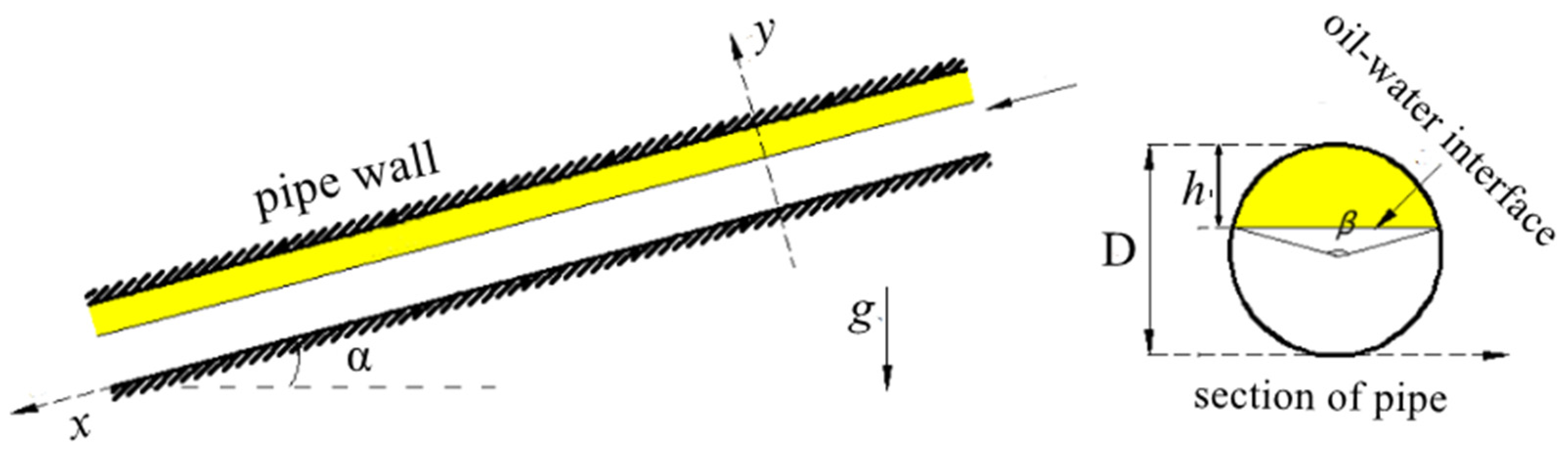
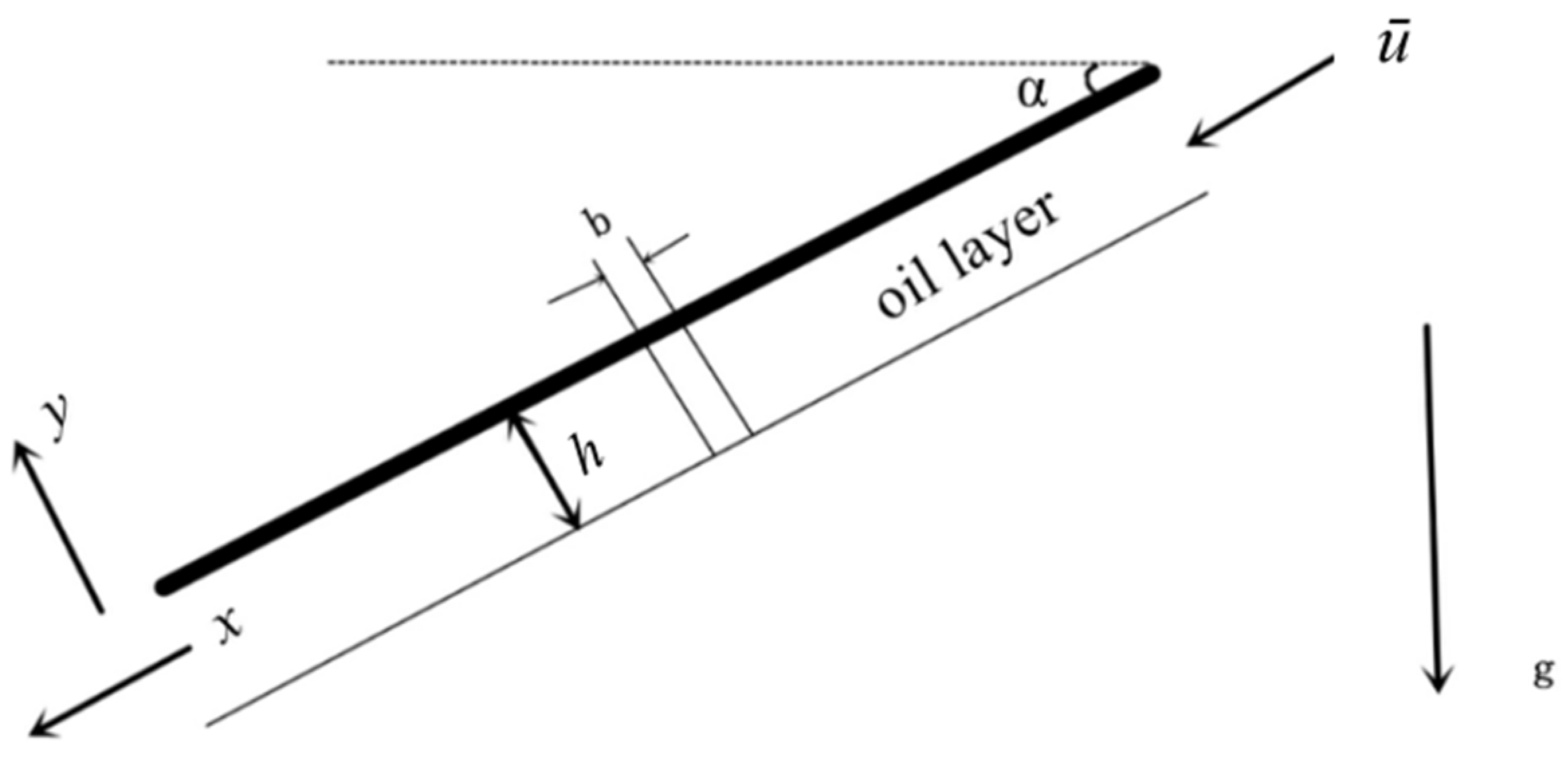
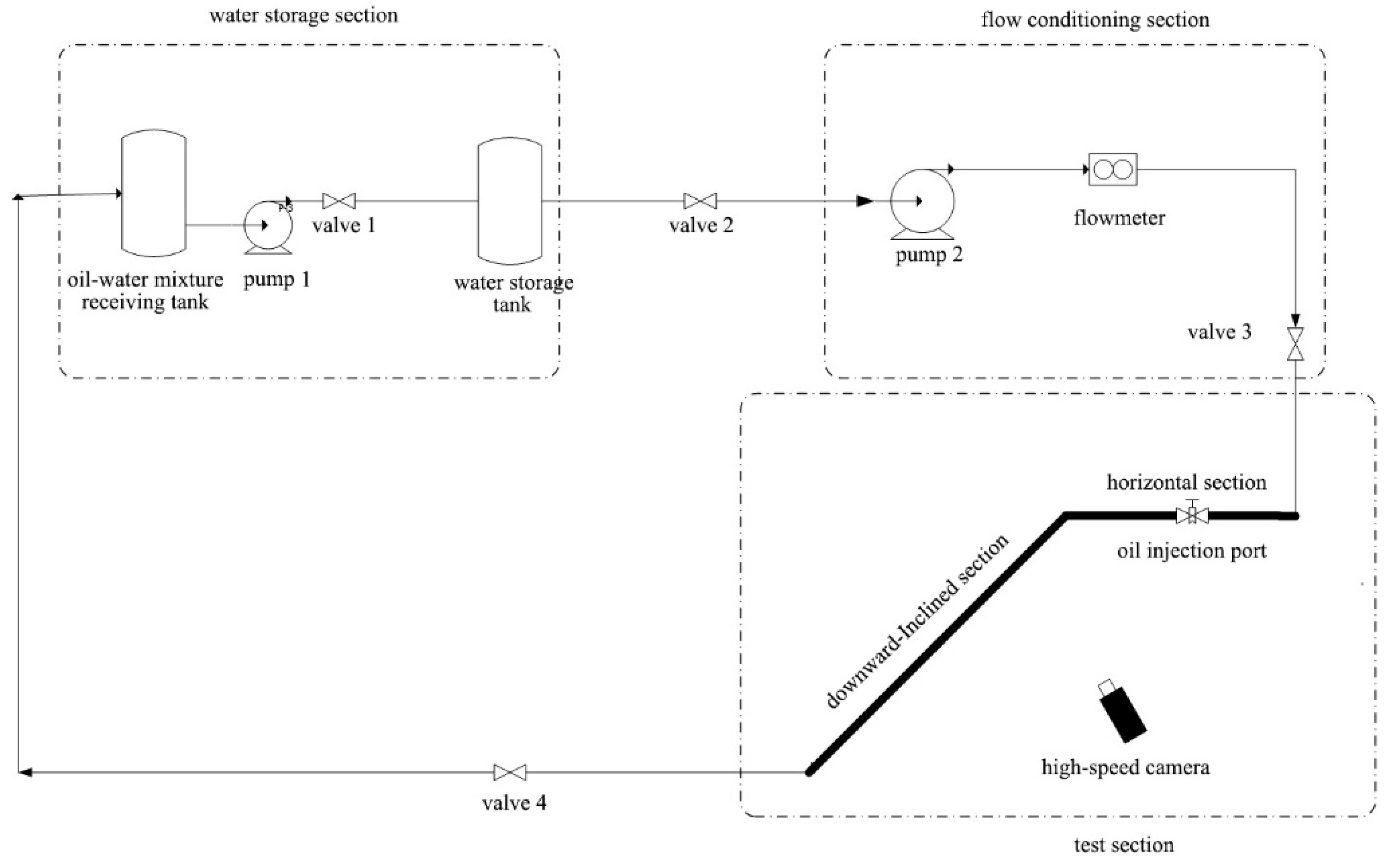
3.1. Geometric Model
3.2. Physical Properties
3.3. Computational Parameters
3.4. Initial Conditions
3.5. Boundary Conditions
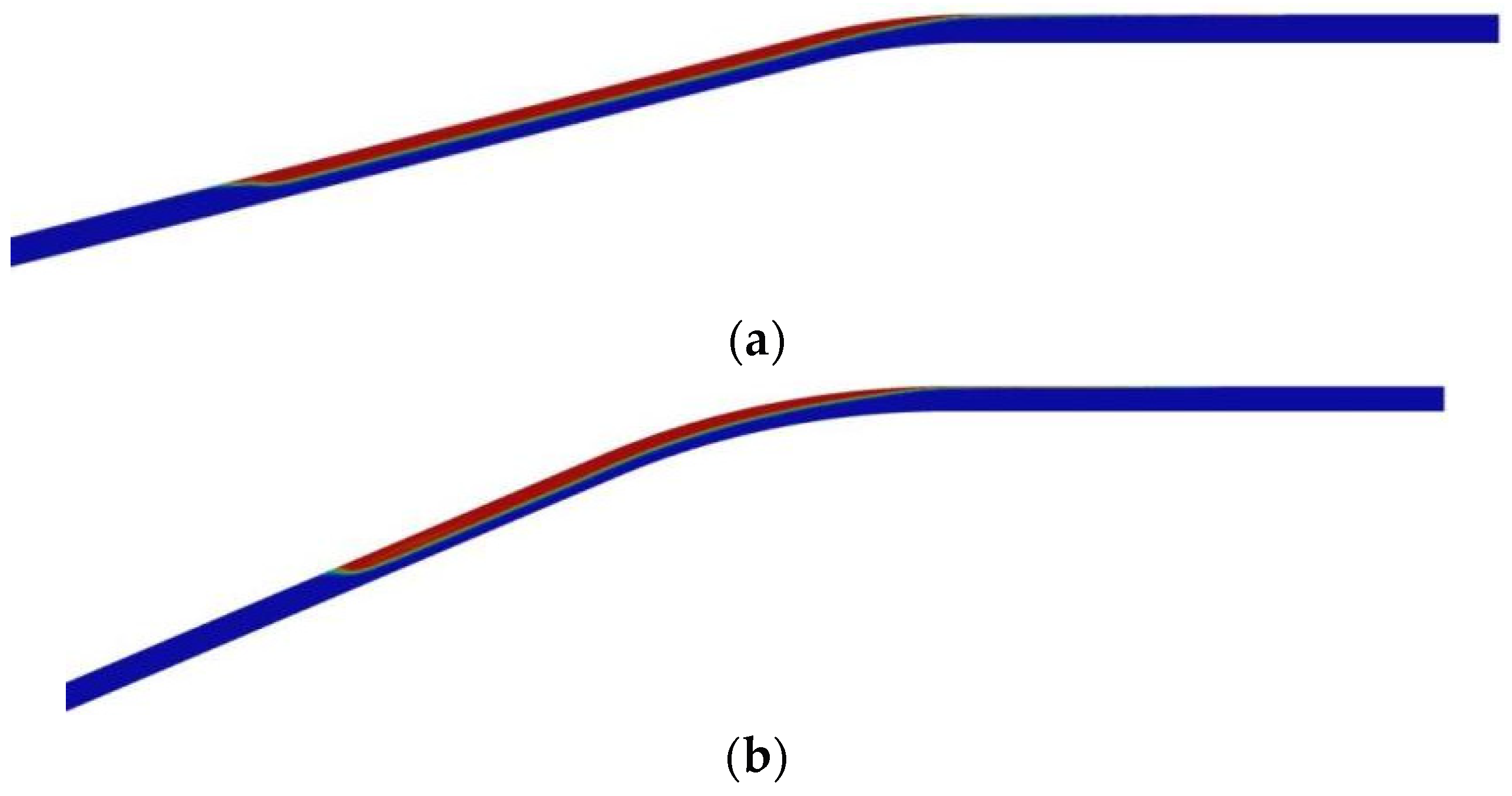
3.6. Model Verification
4. Results and Discussion
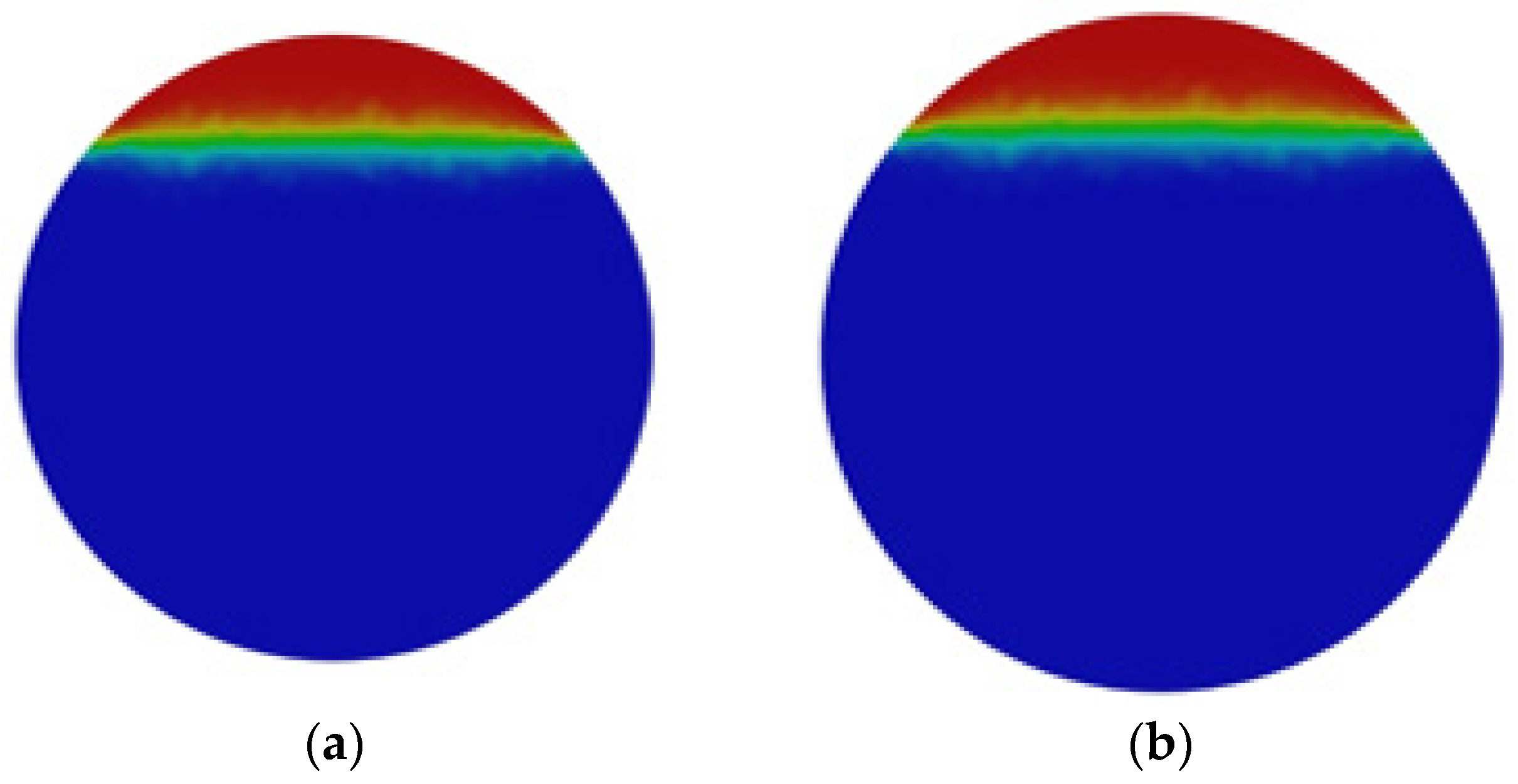
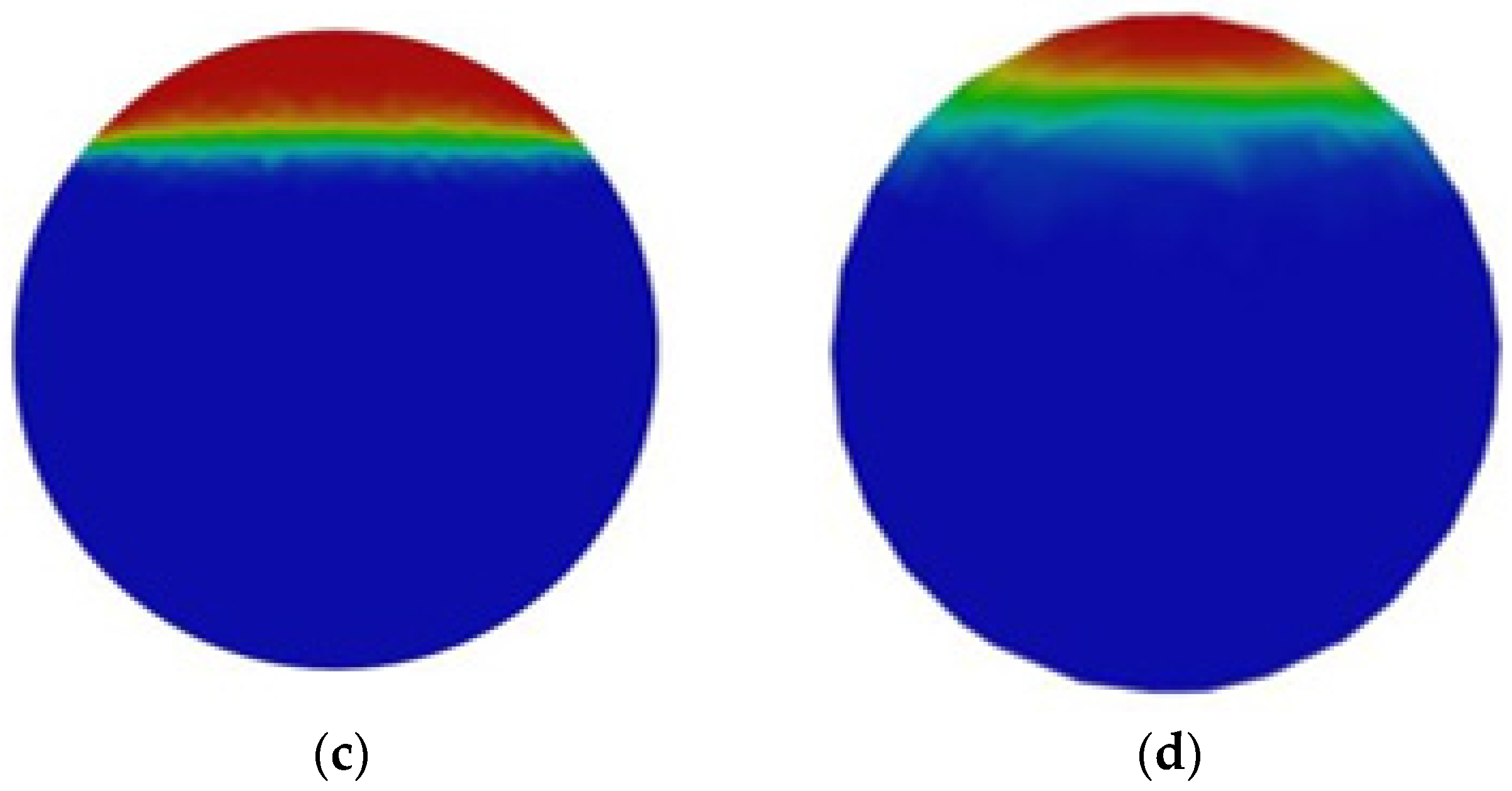
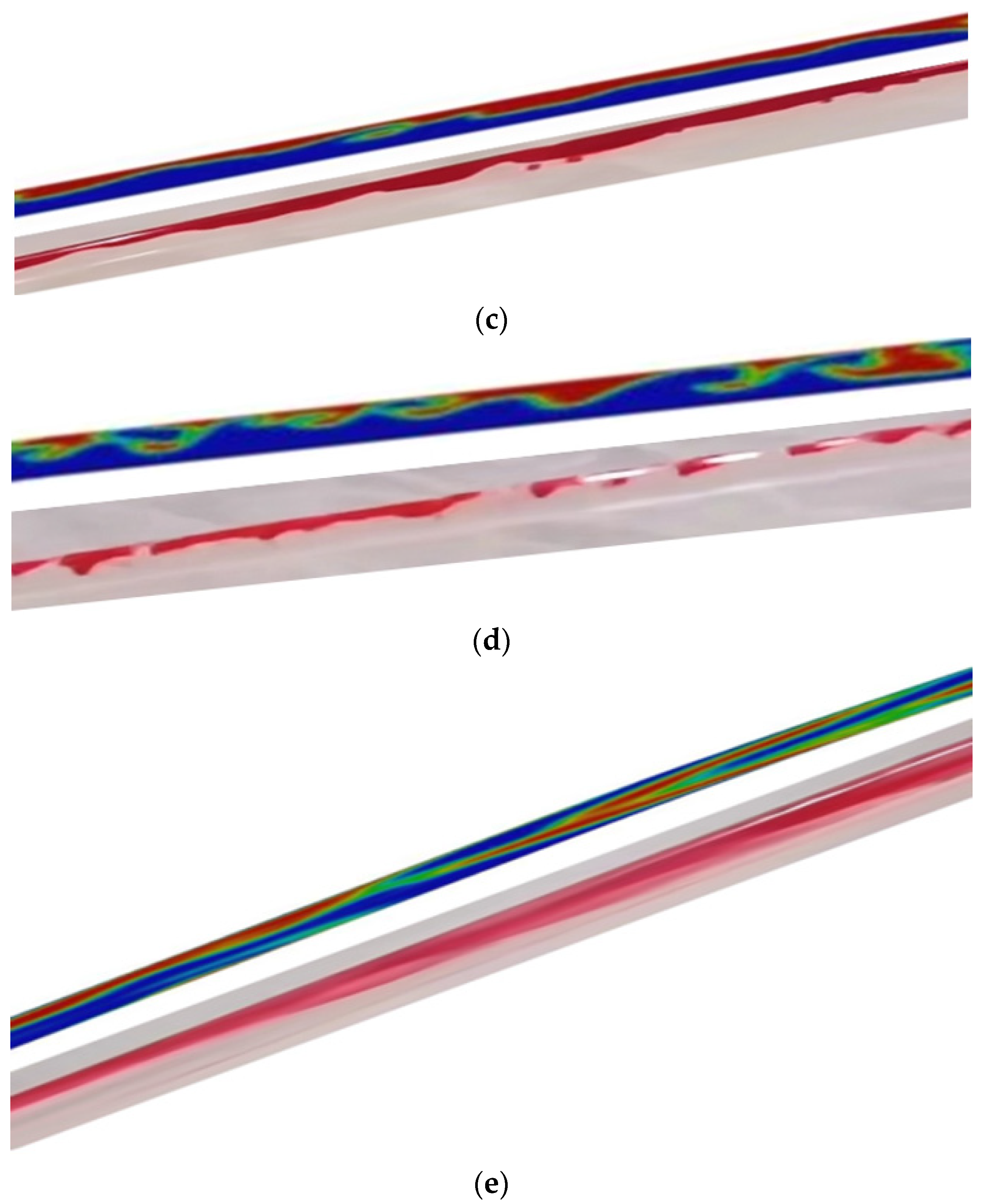
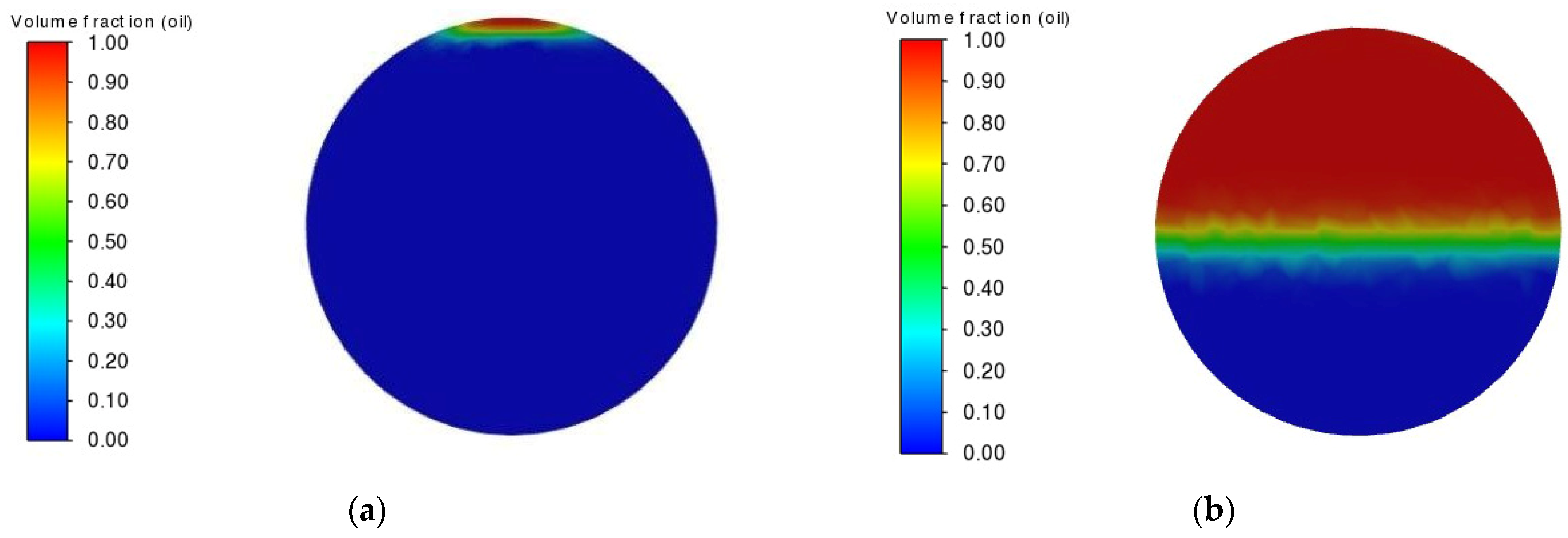
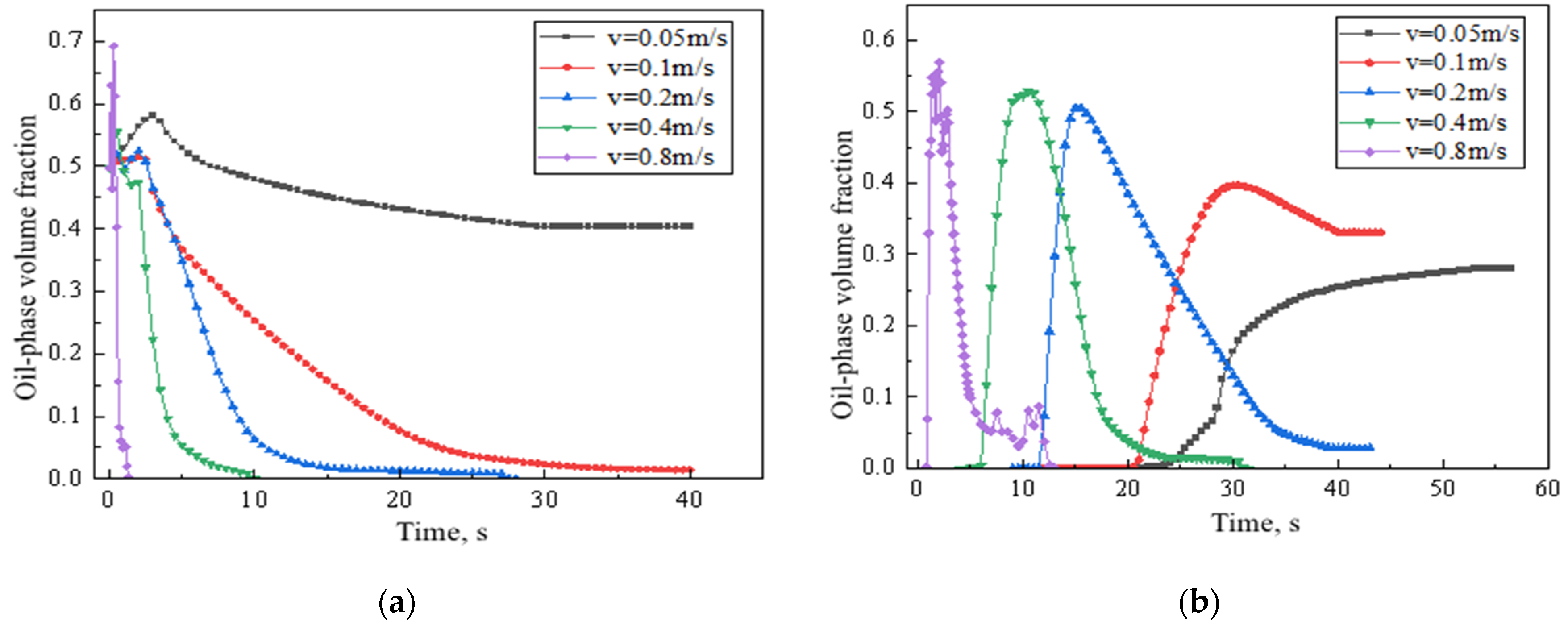
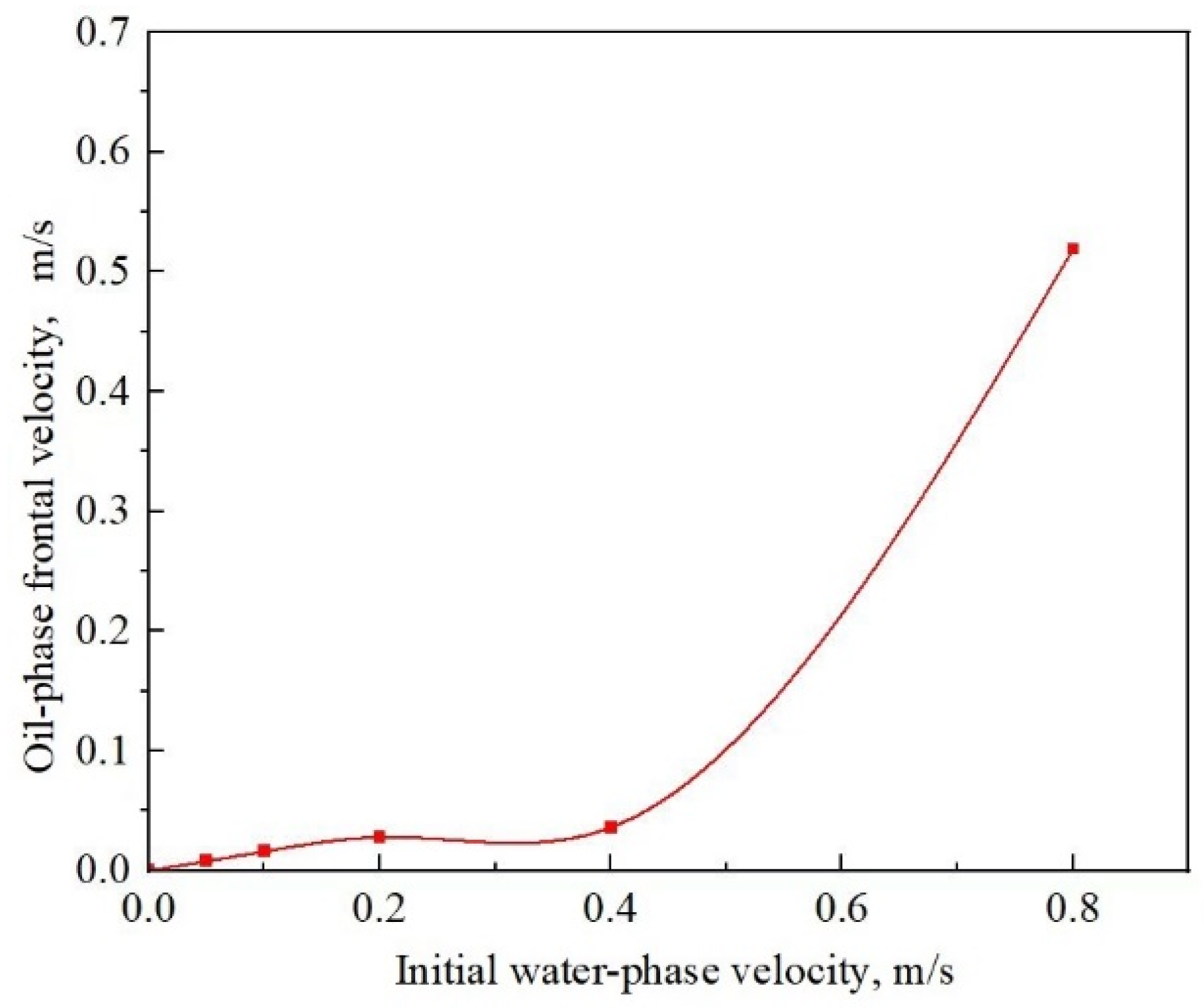
4.1. The Impact of Initial Water Phase Velocity
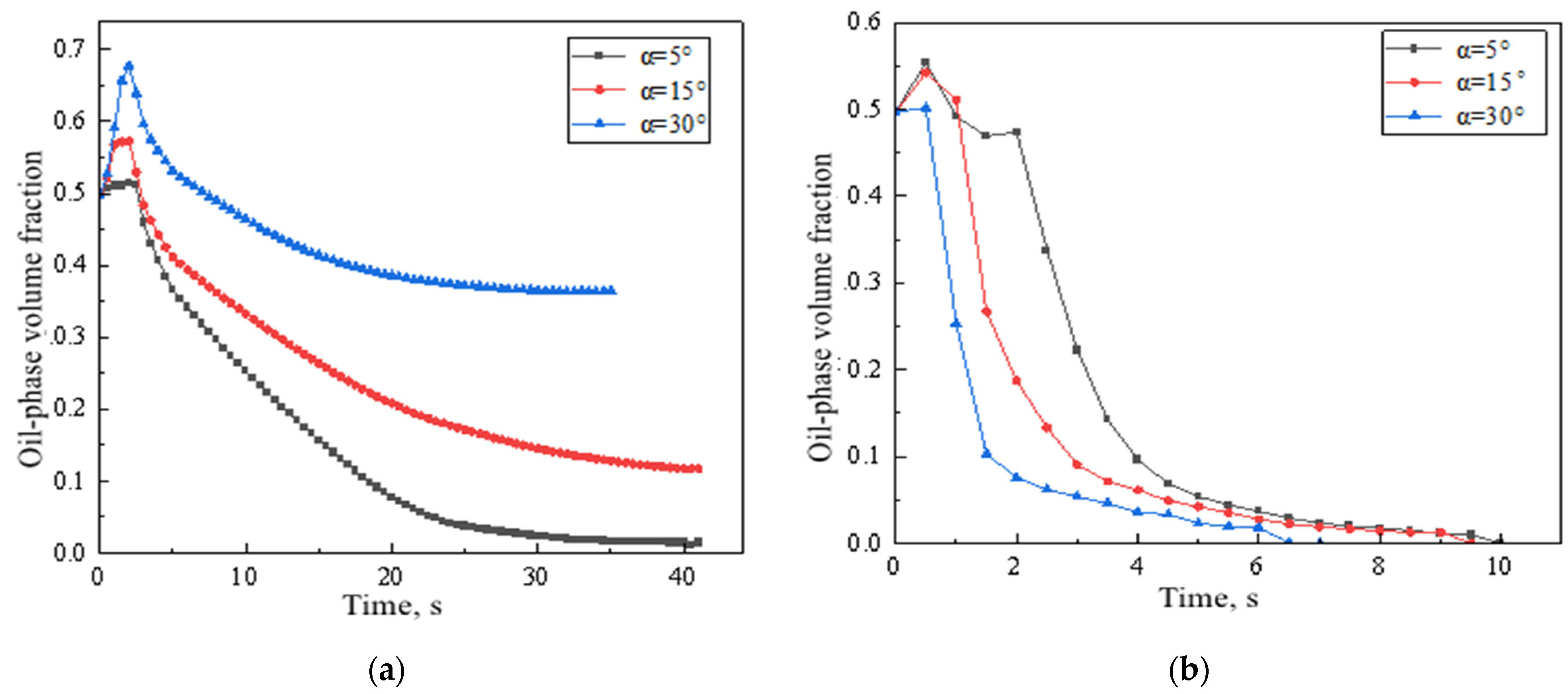
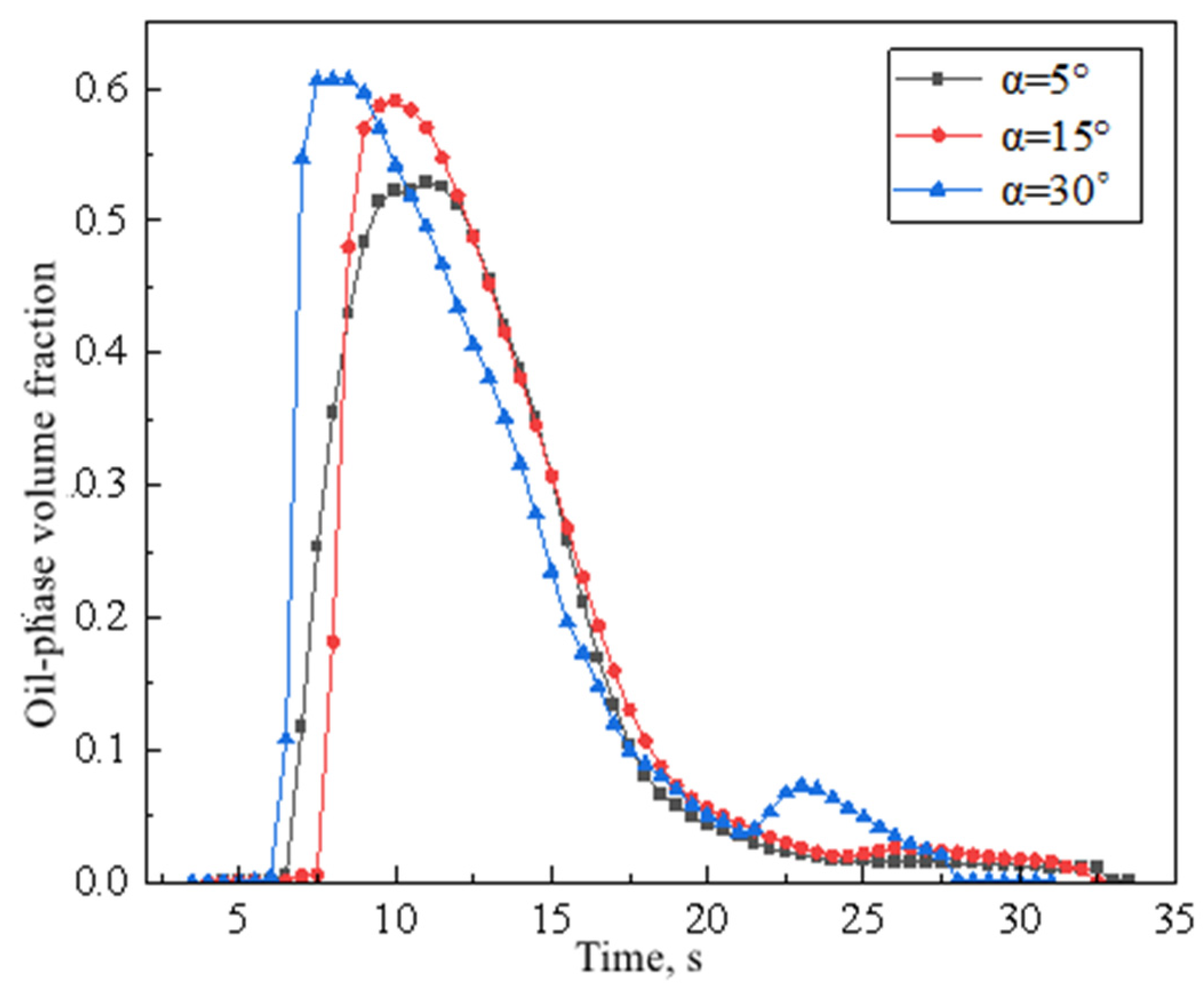
4.2. The Impact of Inclination Angle
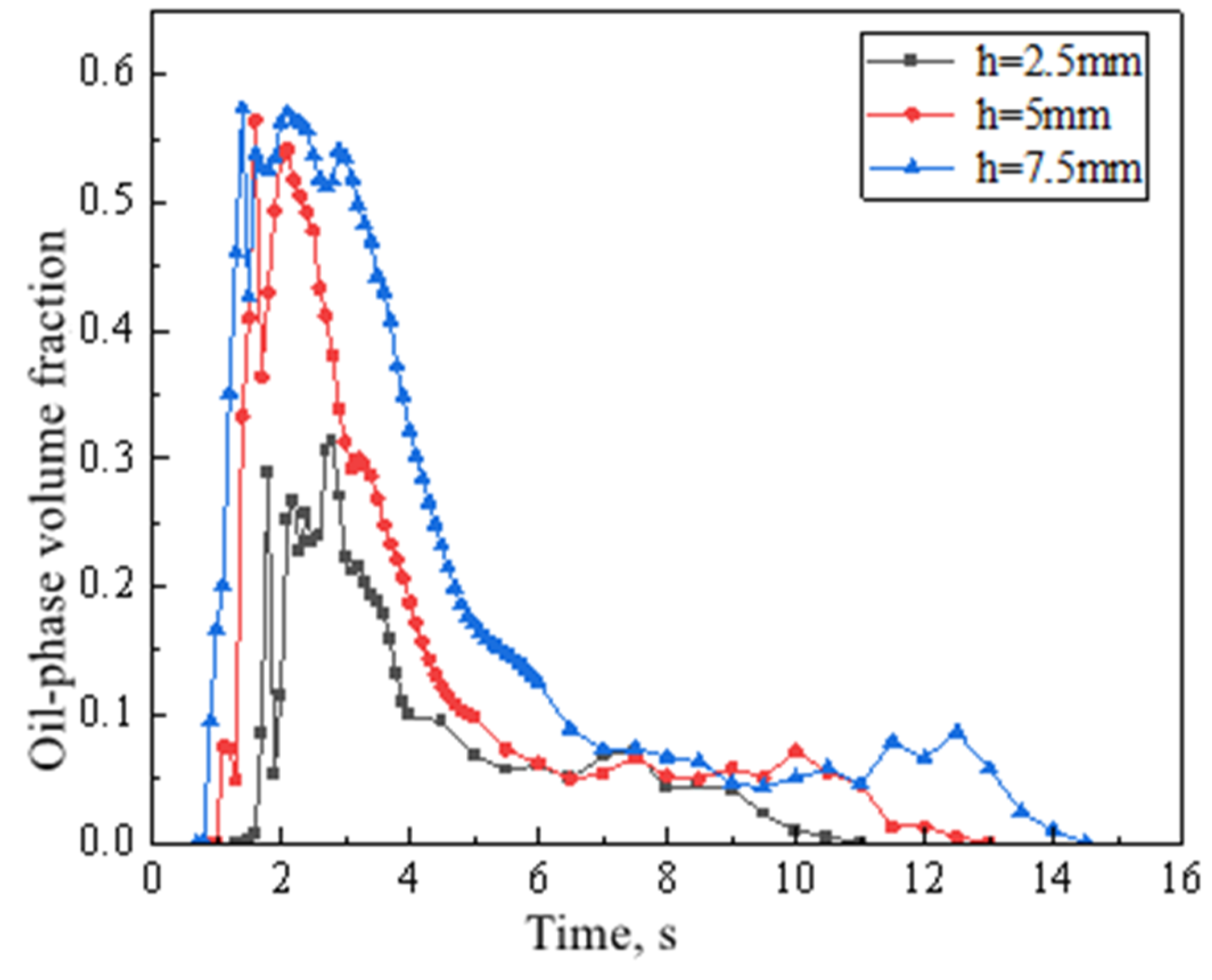
4.3. The Impact of Initial Oil Phase Thickness
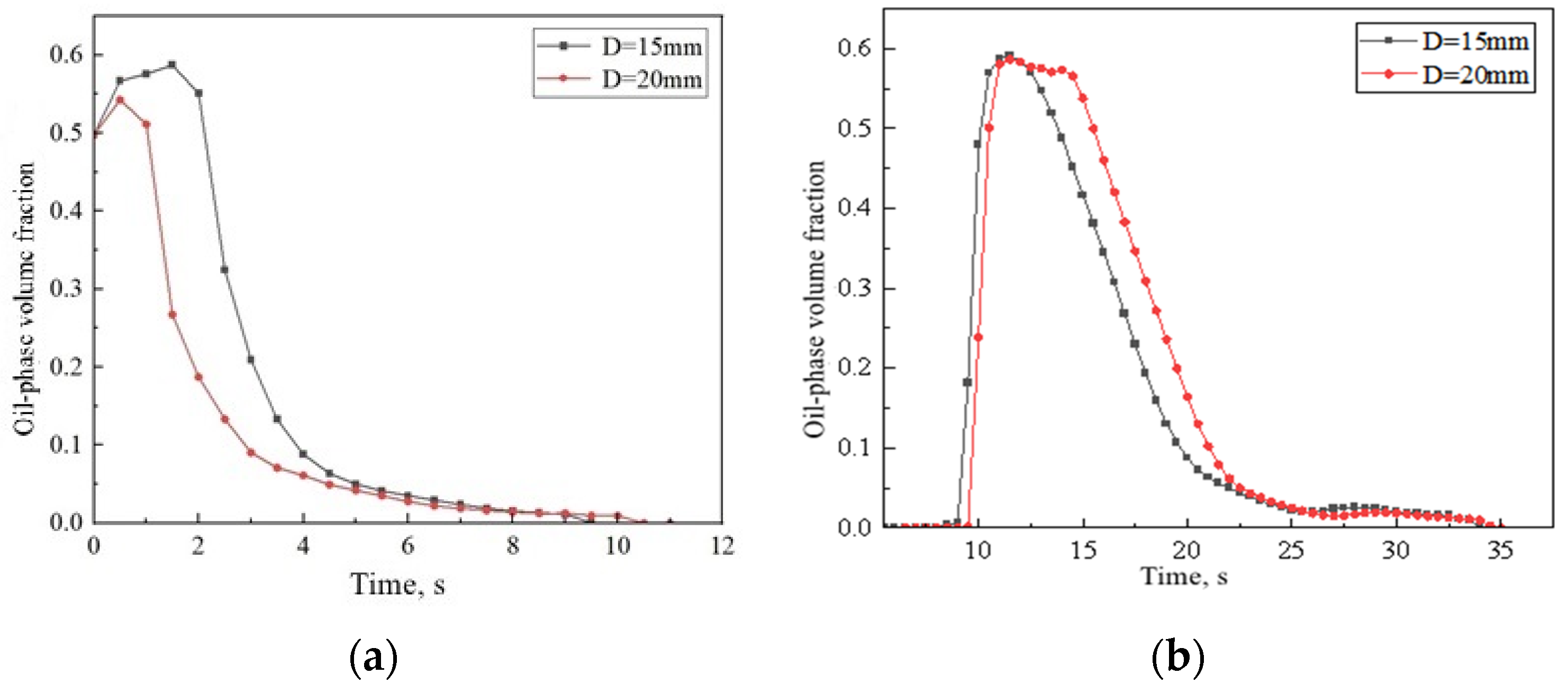
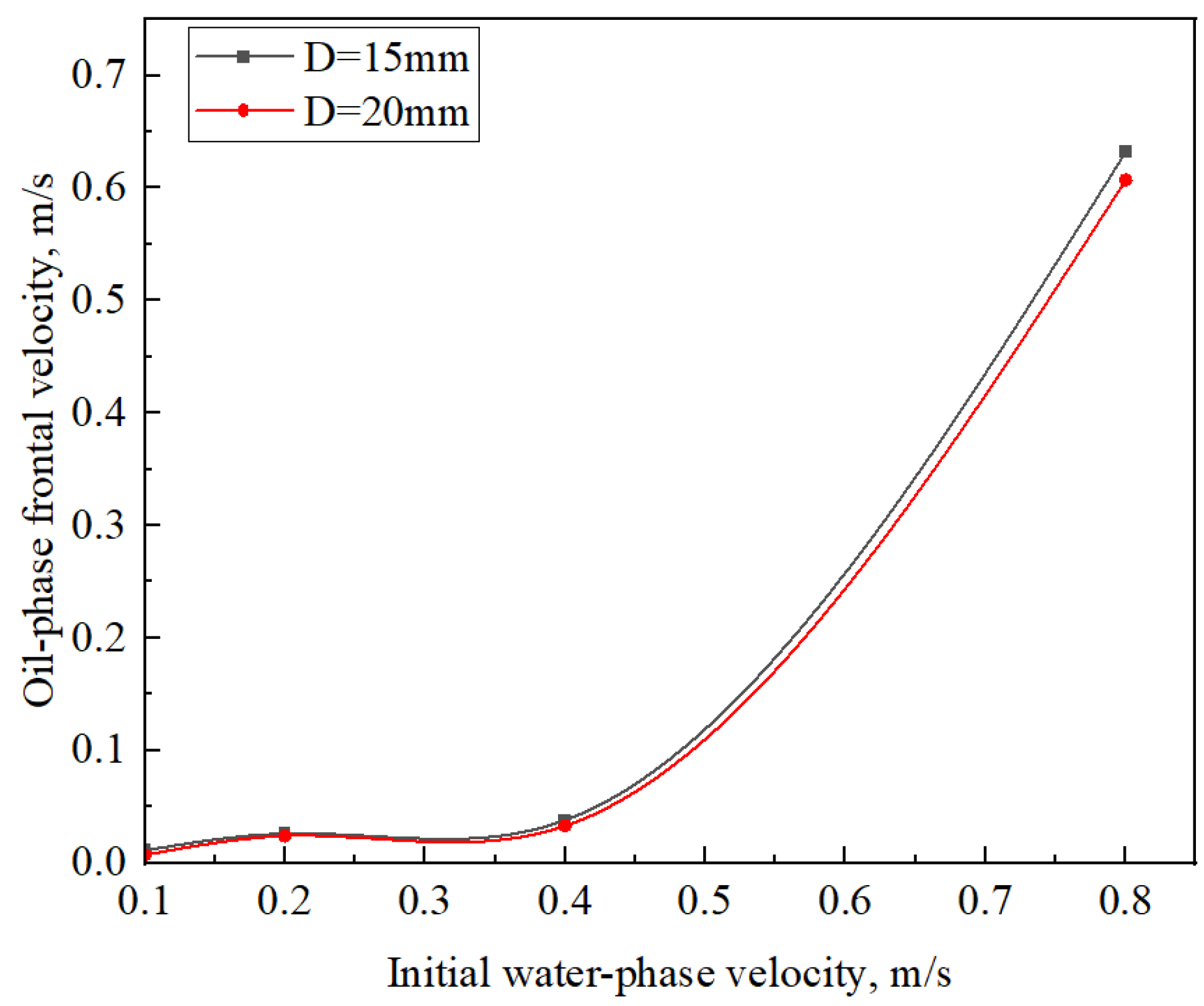
4.4. The Impact of Pipe Diameter
5. Conclusions
- (1)
- The initial water phase velocity has a facilitating effect on water’s oil-carrying capacity and oil frontal velocity; although it is more difficult for the water flow to carry the oil phase out of the downward-inclined pipe section, there exists a critical water phase velocity under certain conditions that can completely displace the oil phase from the pipe;
- (2)
- When the initial velocity of the water phase is below the critical velocity, an increase in the angle of the inclined pipe will weaken the water’s oil-carrying capacity and oil frontal velocity. Conversely, when the initial velocity of the water phase exceeds the critical velocity, an increase in the angle of the inclined pipe section will enhance the oil-carrying capacity and the frontal velocity of the oil phase;
- (3)
- The initial oil phase thickness does not directly affect the oil-carrying capacity of the water in the downward-inclined and horizontal mobile pipeline, but it can increase the oil frontal velocity;
- (4)
- Increasing the pipe diameter, both the water’s oil-carrying capacity and the frontal velocity of oil will be reduced.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Zhang, W.; Jia, D.; Yu, J. Study on the Manifold for Oil–water Mixture Cut during Mobile Pipeline Evacuation. J. Logist. Eng. Univ. 2013, 29, 30–35. [Google Scholar]
- Ming, Y.; Jiang, J.; Yong, Q.; Sun, Y. Analysis of the Current Situation of New Pipe Application and Its Implications for Motorized Pipelines Inspiration for the Development of Lightweighting. Ship Electron. Eng. 2023, 43, 134–138. [Google Scholar]
- Jiang, J.; Zhang, Z.; Li, J.; Chen, Y.; Chen, M.; Jiang, W. Resistance Characteristics of Oil-gas Two-phase Flow for Mobile Pipeline Evacuation Operation. Acta Armamentarii 2021, 42, 888–896. [Google Scholar]
- Duan, J.; Tan, G.; Ma, Z.; Liu, H.; Li, J.; Gu, K.; Lin, K.; Wang, J. Research Progress in Flow Characteristics of Liquid-carrying in the Draining Process in Mobile Pipelines. Contemp. Chem. Ind. 2021, 50, 1591–1596. [Google Scholar]
- Tan, G.; Xiao, D.; Li, M.; He, M.; Lin, K.; Liu, H.; Duan, J. Research Progress of Oil–water Two-phase Flow Characteristics of Displacement Flow of Oil by Water in Mobile Pipelines. Contemp. Chem. Ind. 2020, 49, 2290–2300. [Google Scholar]
- Guo, R.; Zhang, W.; Jiang, J.; Liu, Z. Numerical Simulation of Mobile Pipeline Gas-Gap Emptying Based on OLGA. J. Chem. Eng. Chin. Univ. 2017, 31, 337–345. [Google Scholar]
- Ashoorian, S.; Javadi, A.; Hosseinpour, N.; Husein, M. Evolution of adsorbed layers of asphaltenes at oil–water interfaces: A novel experimental protocol. J. Colloid Interface Sci. 2021, 594, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Dewangan, S.K.; Senapatı, S.K.; Deshmukh, V. CFD prediction of oil–water two-phase stratified flow in a horizontal channel: Coupled level set-VOF approach. Sigma J. Eng. Nat. Sci. 2020, 38, 1–19. [Google Scholar]
- Li, Z.; Fan, C. A novel method to identify the flow pattern of oil–water two-phase flow. J. Pet. Explor. Prod. Technol. 2020, 10, 3723–3732. [Google Scholar] [CrossRef]
- Xu, G. Investigation on the Mechanism of Deposuted Water Displaced by Flowing Oil in Inclined Products Oil Pipeline. Ph.D. Thesis, China University of Petroleum, Qingdao, China, 2011. [Google Scholar]
- Xu, G.; Liu, T.; Niu, Z.; Cai, L.; Wang, M. Analysis of the velocity and shear stress of the local water-diesel flow system. In Proceedings of the ASME Asia Pacific Pipeline Conference, Qingdao, China, 15–19 May 2019; p. V001T11A002. [Google Scholar]
- Xu, G.; Cai, L.; Ullmann, A.; Brauner, N. Experiments and simulation of water displacement from lower sections of oil pipelines. J. Pet. Sci. Eng. 2016, 147, 829–842. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, J.; Li, W.; Jiang, H.; Gong, J. Research on Oil–Water Displacement in Upward Inclined Pipes. Nat. Gas Oil 2019, 37, 8–14. [Google Scholar]
- Xiong, K. Study on Two-Phase Flow Characteristics of Diesel Oil Carrying Water; Southwest Petroleum University: Chengdu, China, 2017. [Google Scholar]
- Song, X.; Xiong, K.; Zhu, J.; Yu, D. Influence of water carrying capacity of oil products on internal corrosion of pipelines. Oil Gas Storage Transp. 2015, 34, 834–838. [Google Scholar]
- Yang, W. Study on Flow Law and Position Prediction of Lowlying Water in Topographic Relief Oil Pipeline; China University of Petroleum: Qingdao, China, 2019. [Google Scholar]
- Xu, G.; Zhang, G.; Zhao, S. An experiment on dewatering for lower location of pipeline. Oil Gas Storage Transp. 2011, 30, 369–372. [Google Scholar]
- Li, G.; Fang, G.; Kou, Z.; Chen, S.; Duan, J.; Chen, Y. Oil–Water Hydrodynamics Model during Oil Displacement by Water in Down-Hill Mobile Pipeline. Processes 2024, 12, 880. [Google Scholar] [CrossRef]
- Brauner, N.; Maron, D.M.; Rovinsky, J. A two-fluid model for stratified flows with curved interfaces. Int. J. Multiph. Flow 1998, 24, 975–1004. [Google Scholar] [CrossRef]
- Ullmann, A.; Zamir, M.; Ludmer, Z.; Brauner, N. Stratified laminar countercurrent flow of two liquid phases in inclined tubes. Int. J. Multiph. Flow 2003, 29, 1583–1604. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, H.; Cai, X.; Gou, Q.; Jiang, L.; Chen, K.; Chen, Z.; Jiang, S. Current Status and Future Trends of In Situ Catalytic Upgrading of Extra Heavy Oil. Energies 2023, 16, 4610. [Google Scholar] [CrossRef]
- Pang, Z.; Wang, L.; Wu, Z.; Wang, X. An investigation into propagation behavior of the steam chamber during expanding-solvent SAGP (ES-SAGP). SPE J. 2019, 24, 413–430. [Google Scholar] [CrossRef]









| uw (m/s) (D = 15 mm) | uw (m/s) (D = 20 mm) | uw (m/s) (D = 100 mm) | uw (m/s) (D = 150 mm) |
|---|---|---|---|
| 0.05 | 0.06 | 0.13 | 0.16 |
| 0.10 | 0.12 | 0.26 | 0.32 |
| 0.20 | 0.23 | 0.52 | 0.63 |
| 0.40 | 0.46 | 1.03 | 1.27 |
| 0.80 | 0.92 | 2.07 | 2.53 |
| Grid ID | Grid Size (mm) | Grid Number | Average Grid Quality |
|---|---|---|---|
| 1 | 0.2 | 1,478,991 | 0.849 |
| 2 | 0.5 | 678,342 | 0.802 |
| 3 | 1.0 | 225,980 | 0.779 |
| 4 | 1.5 | 128,972 | 0.718 |
| Parameters | Water | 0# Diesel |
|---|---|---|
| density (kg/m3) | 998.2 | 833.5 |
| viscosity (mPa·s) | 1.003 | 3.500 |
| Boundary Type | Boundary Condition | Parameter Settings |
|---|---|---|
| Velocity Inlet | Inlet Velocity | 0.2 m/s |
| Turbulence Intensity | 5% | |
| Turbulence Viscosity Ratio | 10 | |
| Flow Direction Specification Method | Normal to Boundary | |
| Coordinate System | Absolute Coordinates | |
| Pressure Outlet | Total Pressure | 0 |
| Turbulence Intensity | 5% | |
| Turbulence Viscosity Ratio | 10 | |
| Flow Direction Specification Method | Normal to Boundary | |
| Coordinate System | Absolute Coordinates | |
| Wall | Wall Type | No-slip Wall |
| Shear Condition | No-slip | |
| Wall Roughness Height (m) | 0.0002 | |
| Wall Roughness Constant | 0.5 |
| D (mm) | Dip Angle (°) | (m/s) | (m/s) |
|---|---|---|---|
| 15 | 5 | 0.166 | 0.202 |
| 15 | 0.148 | 0.280 | |
| 30 | 0.122 | 0.326 | |
| 45 | 0.102 | 0.356 | |
| 20 | 5 | 0.192 | 0.234 |
| 15 | 0.172 | 0.322 | |
| 30 | 0.142 | 0.378 | |
| 45 | 0.118 | 0.412 |
| h (mm) | uw1 (m/s) | uw2 (m/s) |
|---|---|---|
| 2.5 mm | 0.153 | 0.269 |
| 5 mm | 0.156 | 0.274 |
| 7.5 mm | 0.157 | 0.274 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, G.; Li, G.; Kou, Z.; Liu, H.; Duan, J.; Chen, Y. Flow Characteristics of Oil-Carrying by Water in Downward-Inclined and Horizontal Mobile Pipeline. Energies 2024, 17, 4779. https://doi.org/10.3390/en17194779
Fang G, Li G, Kou Z, Liu H, Duan J, Chen Y. Flow Characteristics of Oil-Carrying by Water in Downward-Inclined and Horizontal Mobile Pipeline. Energies. 2024; 17(19):4779. https://doi.org/10.3390/en17194779
Chicago/Turabian StyleFang, Gang, Guang Li, Zhi Kou, Huishu Liu, Jimiao Duan, and Yan Chen. 2024. "Flow Characteristics of Oil-Carrying by Water in Downward-Inclined and Horizontal Mobile Pipeline" Energies 17, no. 19: 4779. https://doi.org/10.3390/en17194779
APA StyleFang, G., Li, G., Kou, Z., Liu, H., Duan, J., & Chen, Y. (2024). Flow Characteristics of Oil-Carrying by Water in Downward-Inclined and Horizontal Mobile Pipeline. Energies, 17(19), 4779. https://doi.org/10.3390/en17194779





