Abstract
Photovoltaic (PV) power generation is highly stochastic and intermittent, which poses a challenge to the planning and operation of existing power systems. To enhance the accuracy of PV power prediction and ensure the safe operation of the power system, a novel approach based on seasonal division and a periodic attention mechanism (PAM) for PV power prediction is proposed. First, the dataset is divided into three components of trend, period, and residual under fuzzy c-means clustering (FCM) and the seasonal decomposition (SD) method according to four seasons. Three independent bidirectional long short-term memory (BiLTSM) networks are constructed for these subsequences. Then, the network is optimized using the improved Newton–Raphson genetic algorithm (NRGA), and the innovative PAM is added to focus on the periodic characteristics of the data. Finally, the results of each component are summarized to obtain the final prediction results. A case study of the Australian DKASC Alice Spring PV power plant dataset demonstrates the performance of the proposed approach. Compared with other paper models, the MAE, RMSE, and MAPE performance evaluation indexes show that the proposed approach has excellent performance in predicting output power accuracy and stability.
1. Introduction
As socio-economic development continues, a growth in energy demand is observed. However, meeting the sustainable development requirements of human society with existing fossil fuels is difficult, and more renewable energy sources need to be discovered and utilized. Solar energy is a clean and friendly renewable energy source. As an essential method of utilizing solar energy, PV power generation is technologically mature. However, PV power generation is susceptible to seasonal variations [1], weather conditions [2], solar radiation intensity [3], and PV module equipment [4], which are all highly stochastic and intermittent [5]. Accurate and reliable PV power prediction is crucial for ensuring rational electricity dispatch arrangements and the stable operation of PV grids [6,7].
PV power prediction can be categorized into three types based on the temporal resolution: ultra-short-term prediction, short-term prediction, and medium- to long-term prediction [8]. Medium- to long-term prediction refers to predictions made more than three days in advance, typically ranging from a week to a month or even a year. This type of prediction mainly provides assessment support for power system scheduling and facilitates long-term decision-making and planning. Short-term prediction refers to predictions made one to three days in advance, primarily to ensure the reliability of power system operations. Ultra-short-term prediction involves predictions made within one day and can guide real-time grid dispatching. The focus of this paper is on ultra-short-term prediction of photovoltaic power.
Nowadays, the existing PV power prediction methods mainly focus on two aspects: white-box modeling prediction and black-box modeling prediction. White-box modeling prediction belongs to a mathematical method known as the physical modeling method [9]. It analyzes the factors that affect the magnitude of the PV power output. Then, mathematical calculations derive the relationship between the factors and power generation to establish a prediction model. Although physical methods can achieve satisfactory predictions under stable weather conditions, most of these data are difficult to obtain, which requires strong domain expertise on the part of the modeler, and the predictions are susceptible to weather variations [10]. On the other hand, black-box modeling is based on a data-driven approach that uses machine learning and deep learning algorithms to build prediction models [11]. The models built using this approach have low interpretability but perform well in many tasks such as fault detection, image processing, and time series prediction and have undoubtedly evolved into a new research hotspot.
With continuous research, abundant models have been built for predicting PV power, such as ARIMA [12,13], BPNN [14,15], GRU [16,17], LSTM [18,19], and BiLSTM [20,21,22,23,24]. Many improvement methods have been proposed to enhance the model prediction accuracy. Reference [25] introduced the self-attention mechanism (SAM) to further select the optimal features of PV power. Reference [26] innovatively used multiple PV power plants’ output series as inputs to the prediction model without meteorological data. Reference [27] uses ensemble learning that stacks multiple models to predict PV power at the same time. Furthermore, PV power prediction models can be affected by many free parameters with large impacts. How to choose the method of parameter optimization is extremely relevant to improve the performance of the prediction model [28]. Reference [29] proposed a hybrid algorithm combining a genetic algorithm (GA) and a particle swarm optimization (PSO) algorithm. Reference [30] used an improved PSO algorithm to search for the ideal parameters of the extreme learning machine (ELM), which was finally applied to the online prediction process.
Moreover, numerous research has been performed on data processing. For example, signal decomposition algorithms are used to reduce the complexity of the input data. The typical decomposition algorithms are WT [31,32], EMD [33,34], and VMD [35,36]. Reference [37] combines ensemble empirical mode decomposition (EEMD) and variational mode decomposition (VMD) for multi-step decomposition of data. Reference [38] employs robust mean decomposition (RLMD) to capture the physical effects of atmospheric variables. Clustering algorithms find the similarities between data and categorizes them; commonly used clustering algorithms are the FCM clustering algorithm [39], K-means clustering algorithm [40], and similar day analysis (SDA) [41]. Reference [42] uses a clustering algorithm to filter irrelevant features and divides relevant features into independent subsets, thus reducing redundancy. Reference [43] clusters historical weather data to find combinations with similar weather patterns.
PV power generation is characterized by strong seasonality and periodicity, and the impact of both on prediction performance has been extensively discussed in previous research. Commonly used methods for seasonal factors are seasonal modeling or seasonal decomposition. References [44,45] use a seasonal decomposition algorithm based on locally estimated scatterplot smoothing (LOESS) to divide the data into multiple components, which reduces the complexity of the data and effectively improves the ability of the model to capture seasonal information. Reference [46] presents seasonal decomposition combined with the least squares support vector regression method, which effectively handles the effects brought about by seasons. The above methods require the assumption of a fixed time interval, the choice of which is important for the impact on the prediction performance and is usually based on manual experience or automatic detection. The prevalent approach for periodic factors is the application of attention mechanisms. Attention mechanisms are used to accurately extract relationships between nonlinear features by assigning different weights. Different types of attention mechanisms have been proposed in the field of time series forecasting, such as self-attention mechanism [47], dual-attention mechanism [48], integrated attention mechanism [49], variable attention mechanism [50], multi-head attention mechanism [51], etc. Due to the extensive data requirements for training, this approach results in increased computational complexity and poor performance when the external periodic patterns are not well defined.
In a word, an excellent PV power prediction model is forced to consider the effects caused by seasonal and periodic factors. However, few studies have paid full attention to the joint impact caused by these two factors to make targeted improvements. Therefore, a novel approach based on seasonal division and PAM is proposed in this paper. It aims to improve the performance of prediction by exploring these two regularity factors. Firstly, the dataset is divided into four categories according to seasons and performs seasonal decomposition, respectively. This will first give the model a large regularity interval estimated on a seasonal scale. Secondly, the ameliorated PAM assigns a daily period-based weight to the data, thereby giving an accurate, small regularity interval. Finally, an improved NRGA algorithm is used for model optimization. The proposed approach effectively improves the prediction performance of the model.
The rest of the paper is structured as follows: Section 2 describes the implementation process of the proposed approach, the relevant theory, and the improvement part. Section 3 verifies the performance of the proposed approach through the designed experiments. Finally, the ultimate conclusion is given in Section 4.
2. Proposed Approach
In this section, the implementation of the modeling approach and the processing details of the model will be described step by step. Compared with the traditional PV power prediction methods, the hybrid model proposed in this paper has the following advantages:
- (a)
- The approach considers the influence of seasonal characteristics on the performance of PV power prediction in the time series dataset, which effectively solves the problem of the prediction model being insensitive to seasonal information.
- (b)
- The ameliorated PAM is added to the model, which helps the model effectively capture the nonlinear relationship of the data at different time points in the same daily period, and the prediction accuracy and stability are improved.
- (c)
- The model parameter optimization adopts the improved NRGA. By enriching the ability of the algorithm to find the optimal parameters both globally and locally, and the predictive performance of the model is thus enhanced.
- (d)
- The approach allows the model to have better performance in the prediction of different output time steps.
The framework of the proposed model is shown in Figure 1.
2.1. Step1: Data Process
PV power characterization data are processed for missing values and outliers, and the missing values are filled using cubic spline interpolation [52] to ensure the integrity of the data. Outliers are removed directly. Then, the Pearson coefficient is used to screen out the features with a strong correlation with PV power. Next, the features are divided into four subdatasets according to the FCM. Finally, the SD of the divided dataset is performed to obtain the three types of components, namely, trend, period, and residual, to complete the data processing process.
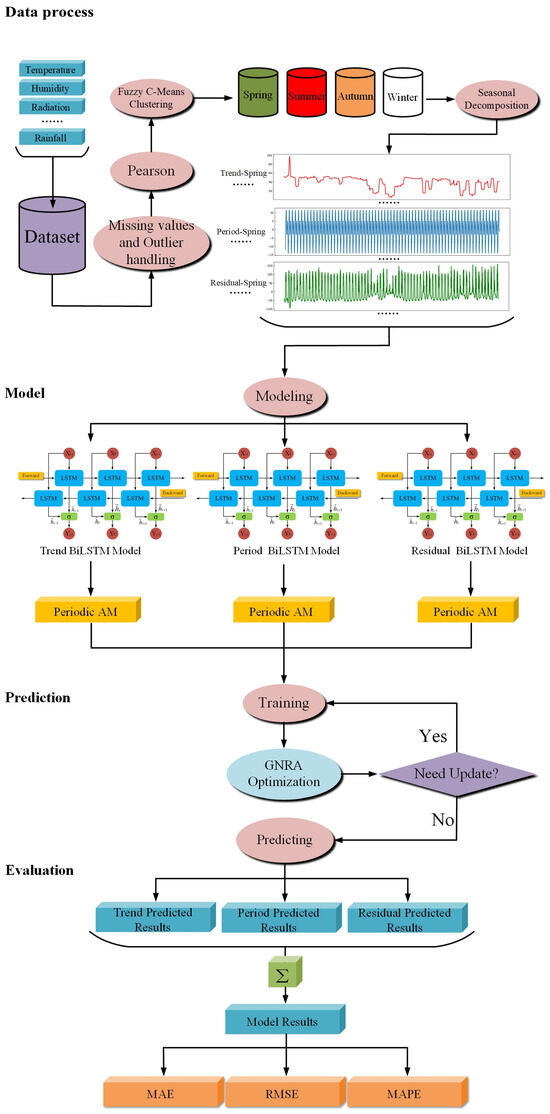
Figure 1.
Framework of the proposed model.
FCM belongs to a soft clustering method, which can deal with fuzzy or uncertain data point classification and better capture the complex seasonal structure. To address the bias of the current fixed seasonal classification methods, we first divide the original data into four sub-datasets (i.e., spring, summer, fall, and winter) according to the date. Then, we use the FCM to recluster the initially divided datasets. Assume that the data samples are , and the old categories are , which will be reclustered into new categories , with the center of clustering of each type being . represents the membership degrees of concerning . It is required that the sum of the membership degrees of all data samples is 1. The specific formula is as follows:
where represents the objective function of the algorithm, which requires repeated computation of the membership degrees and the clustering centers to find an optimal classification that minimizes . represents the Euclidean distance between the th sample and the center of the th class. is a weighting parameter that controls the degree of fuzzyness. j represents the number of features of the data samples.
There are two decomposition models for seasonal decomposition, namely the additive and multiplicative models. The former is suitable when the data do not change proportionally over time, while the latter is more suitable when the data change proportionally over time [53].
- (i)
- SD additive model, where the total series is the sum of the subseries:
- (ii)
- SD multiplicative model, where the total series is the product of the subseries:where represents the actual value of the feature at moment t. , , and represents the values of the trend component, period component, and residual component of the feature at moment t, respectively.
The components are calculated using the moving average method with the following formulas:
where represents the level estimate of the feature at moment t. m is the set periodicity length. , , and are three smoothing parameters, all of which take values between 0 and 1, which are automatically chosen by the model based on the characteristics and periodicity of the feature data.
2.2. Step2: Model
Three BiLSTM models are constructed from the three types of components processed, respectively, and the models are trained. In order to make the model pay more effective attention to the daily periodicity of the input data, this paper adds a novel periodicity component to the attention mechanism. It enables the model to better capture the patterns of the input data. The specific calculation formula is as follows:
where A and X represent the output and input vector sets of the attention mechanism, respectively. N represents the number of vector sets, and represents the correlation score or energy associated with the th input vector , which determines how much importance the model attaches to that vector. represents the time series of the input data. is the specified period of attention, which implies that the model will focus on finding the relationship between the data at the same time points in different periods. It needs to be computed based on the time step of the data and its potential periodicity. For example, in this paper, the time step of the dataset is 5 min, and if we need to focus on the periodicity within a day, we need to set to 288.
2.3. Step3: Prediction
NRGA is used to optimize the parameters of the BiLSTM model. During the training process, the iterative search is repeated until the optimal parameters of the model are found. Then, the optimized parameters are used for prediction, and the optimal results of the three components are predicted.
NRGA is an improved algorithm. First, the initial estimated solution is arbitrarily generated. Of course, it is only completely random when the algorithm begins. Then, the initial estimated solution will be continuously optimized to find the optimal parameters of the model through the Newton–Raphson formula, as shown in Equation (11):
where is the estimate for the next iteration, and is the estimate for the current iteration. represents the value of the fitness function parameter at , and is the first-order derivative at of the fitness function.
The Newton–Raphson formula is an optimization method that converges quickly with high accuracy, and it gradually approximates the solution of the equations by continuously updating the estimated solution [54]. The local convergence of the formula allows it to find the optimal solution rapidly and precisely, especially when the initial estimated solution is close to the actual solution. However, the effectiveness can be extremely dependent on the choice of the initial estimated solution and the nature of the fitness function.
In addition, to enhance the global optimization capability of the algorithm, an adaptive accelerated regularization penalty term and constraints are introduced, as shown in Equations (12)–(14):
where is the fitness function and model optimization, which are used to find the minimum of the fitness function. is a set of search parameters that affect the performance of the model, and and are the weights of the two different errors, respectively. and are the adaptive weighting coefficients of the regularization terms and , respectively, which change with the increase in iterations to speed up the convergence of the algorithm, improve the searching efficiency. MAE and RMSE are the mean absolute errors and root mean square errors, respectively, calculated as given in Equations (24) and (25).
The first iteration of the algorithm will be judged to be completed when the maximum number of iterations is reached or the fitness function does not decrease within a set number of times. Next, according to the elite selection strategy [55], the current optimal solution, i.e., the elite, is captured and directly added to the next generation population. Then, the subsequent crossover and mutation operations are performed. The mutation process will introduce the Cauchy mutation model to determine the direction of gene mutation [56]. The formula of the Cauchy mutation model is as follows:
where x is a random variable. represents the location parameter, which reflects the median of the Cauchy distribution. is the scale parameter, which controls the width of the tails of the Cauchy distribution. The random variable x range should be adjusted explicitly according to the specific parameters. With the introduction of the Cauchy variation model, the search range of NRGA’s population is expanded, the diversity is increased, and the global search capability of the algorithm is improved.
The parameters for optimization include batch size, the number of iterations, the number of neurons in the BiLSTM layer, the number of neurons in the fully connected layer, the dropout rate, the values of regularization, the weights of the Huber loss function, and the initial learning rate. The NRGA pseudo-code is shown in Algorithm 1.
| Algorithm 1 Newton–Raphson Genetic Algorithm (NRGA) |
|
In Algorithm 1, the selection operation is realized by the Roulette Wheel Selection [57], as follows:
where is the probability of chromosome p being selected. represents the sum of fitness of all chromosomes in the population, and P represents the total number of chromosomes in the population.
The crossover operation is performed as follows:
where represents the crossover transformation performed on this chromosome, is the weights at the crossover, and represent the maximum or minimum value of the corresponding parameter on the two chromosomes, and and represent the maximum and minimum values of the different parameters in the population, respectively.
The mutation operation is calculated as follows:
where represents the mutation rate, which determines whether each gene on the chromosome is changed or not, and determines the direction of the mutation of the gene, usually a random number. is the mutation model already given in Equation (15).
2.4. Step4: Evaluation
Three prediction result components are combined to obtain the final result of the PV power prediction model, and the prediction effect is evaluated using the three errors, MAE, RMSE, and MAPE, as the evaluation metrics. The calculation formula is as follows:
where y and are the actual and predicted values of the sample, respectively. is the total number of samples.
3. Case Study
3.1. Experimental Design
In order to verify the effectiveness of the proposed approach, this paper will conduct an experimental analysis from the following five aspects:
- (a)
- By assessing the predictive performance of two seasonal decomposition models before and after seasonal division, we further analyze the impact of seasonal division and seasonal decomposition on the prediction results.
- (b)
- The NRGA, GA, and PSO algorithms were used to optimize the parameters of BiLSTM, LSTM, GRU, and BPNN prediction models, and the effectiveness of each algorithm in finding the optimal parameters was evaluated.
- (c)
- The role of PAM in the different prediction models was verified through ablation experiments.
- (d)
- The prediction results in this paper are compared and analyzed with other references to verify the performance of the proposed model. Then, the prediction performance of the proposed model at different temporal resolutions was analyzed.
- (e)
- The datasets from different locations were selected to validate the generalization performance of the proposed approach.
3.2. Dataset
In this paper, the experiment dataset comes from the 1A PV power generation system at the DKASC Alice Springs in Australia. The description of the measurement equipment is shown in Table 1. The data interval is selected from 0:00 a.m. on 1 April 2016 to 11:55 p.m. on 31 March 2023, which spans about seven years, and the time step is 5 min. Each piece of data contains real-time measured power plant data and meteorological data such as temperature, weather relative humidity, global and diffuse horizontal radiation, current phase average, wind speed, wind direction, active power, and weather daily rainfall. These data are used to train and test the proposed model. The temporal resolution in this paper is set to 5 min. The PV active power profile of DKASC is shown in Figure 2.

Table 1.
The descriptions of the measurement equipment.
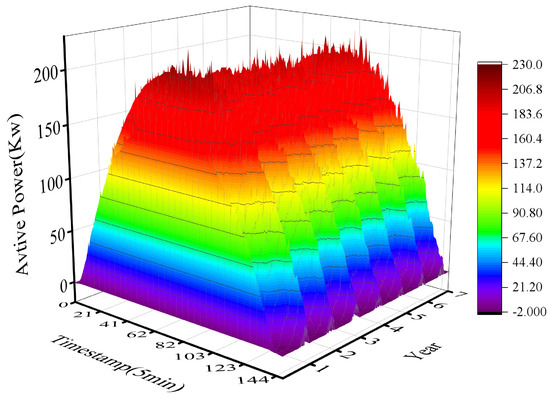
Figure 2.
PV active power profile of DKASC.
3.3. Results and Discussion
There are 16 features in the DKASC dataset, as shown in Table 2. Although they all affect the magnitude of PV output power to a certain extent, the degree of effect is different. In this regard, this paper calculates the Pearson coefficients of the 16 features with each other and uses the Pearson coefficients to categorize all the features and search for those that show a high correlation with PV active power among them to input into the model. The results are shown in Figure 3. It can be seen from Figure 3 that the values of the Pearson coefficients between the three features, namely, the current phase average, the global horizontal radiation and the radiation global tilted, and the output power of PV are as high as 0.99, 0.97 and 0.99, which present highly positive correlation characteristics. Therefore, the above three features and the PV output power itself are selected as the input features of the prediction model.

Table 2.
Definition of the features.
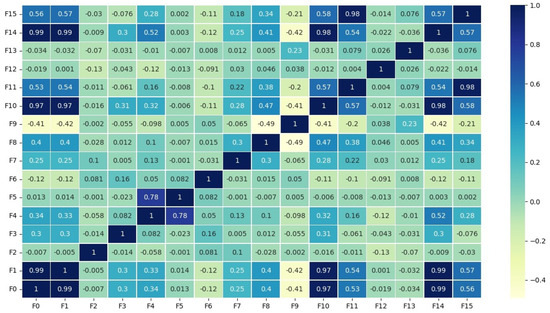
Figure 3.
Heat map of Pearson coefficient results.
In order to explore the impact of different seasons on PV power prediction, this paper first divides the dataset after feature selection into four sub-datasets according to the seasons: spring, summer, autumn, and winter. The method of seasonal division is as follows: spring (March to May), summer (June to August), autumn (September to November), and winter (December to February). Secondary clustering is then performed using the FCM algorithm. The sequence of characteristics of different seasons after seasonal division are shown in Figure 4. These results show that the change trends of the selected feature data are roughly the same, which is the reason why they have a high correlation with each other. In addition, the global horizontal radiation in autumn and winter is higher than that in spring and summer, obviously, because this paper divides the seasons according to the rules of the northern hemisphere. However, the collection site of the dataset is located in Australia in the southern hemisphere, and the northern hemisphere in spring and summer is precisely the southern hemisphere in autumn and winter.
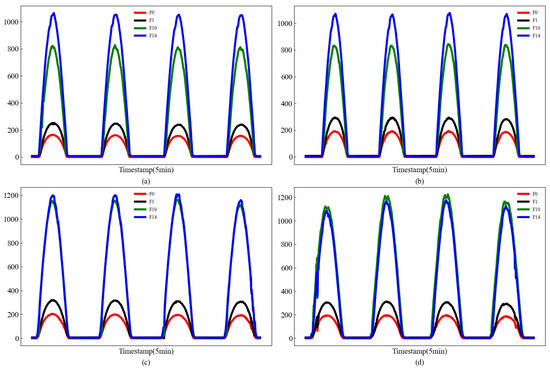
Figure 4.
Sequence of characteristics of different seasons after seasonal division (a) spring, (b) summer, (c) autumn, (d) winter.
After the season division, the SD method decomposes all input features in the sub-dataset into three components: trend, period, and residual. To accurately assess the impact of seasonal division and decomposition on PV power prediction, both additive and multiplicative models of SD decomposition are applied to the dataset with (D1) and without (D2) seasonal division. The prediction results are shown in Table 3. It can be observed from Table 3 that for different seasons, all three evaluation metrics for autumn and winter are higher than those for spring and summer. This is due to the increased absolute error caused by the higher power values in the autumn and winter seasons. Furthermore, the analysis of the prediction results indicates that the multiplicative model of SD performs better than the additive model, reducing prediction errors to some extent whether or not the season is divided. The MAE, RMSE, and MAPE values of the multiplicative model before seasonal division are reduced by 14.7%, 4.49%, and 3.24%, respectively, compared to the additive model. After seasonal division, they are reduced by 16.3%, 3.42%, and 6.92%. Because the selected feature trends in this study are roughly similar and exhibit a proportional relationship. The multiplicative model can better fit the multiplicative relationship present in the data, thereby reducing prediction errors. Therefore, the subsequent experiments in this paper will use the multiplicative model. The decomposition results of spring feature F0 are shown in Figure 5 After seasonal division, the prediction model can more easily discover the underlying data patterns in different seasons, thus improving prediction accuracy. The three errors obtained after seasonal division are 0.14123 Kw, 0.23149 Kw, and 0.04522 Kw, which are reduced by 8.26%, 2.42%, and 8.66% compared to predictions without division.

Table 3.
Error comparison of seasonal decomposition models in different seasons.
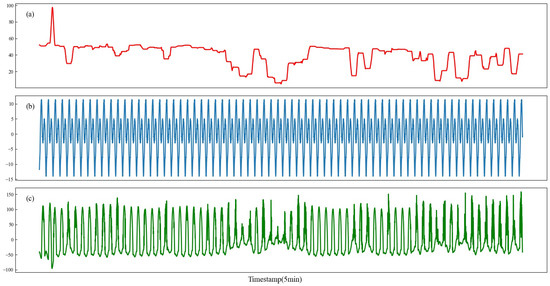
Figure 5.
The decomposition results of spring feature F0. (a) Trend component, (b) period component, (c) residual component.
Different optimization algorithms have different effects. To verify the prediction performance of the proposed algorithm, NRGA, GA, and PSO optimization algorithms are used to find the optimal parameters of the BiLSTM, LSTM, GRU, and BPNN prediction models, respectively, and to calculate their errors. The experimental results are shown in Table 4 and Figure 6.

Table 4.
Error comparison of each model under different algorithms.
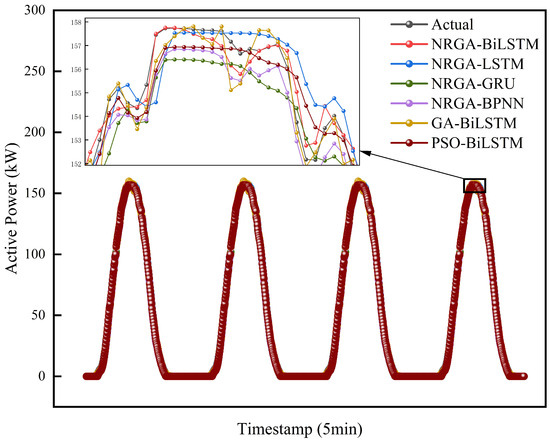
Figure 6.
Predictive effectiveness of each model under different algorithms.
These results show that the prediction accuracy of the NRGA-BiLSTM method is generally higher than the other comparative models. BiLSTM has the lowest error for the other models under NRGA optimization, with a reduction of 18.4%, 19.5%, and 42.7% in MAE, 22.4%, 28.3%, and 37.7% in RMSE, 18.1%, 23%, and 49% in MAPE, respectively, when compared with the LSTM, GRU, and BPNN models. It has been attributed to the unique bidirectional temporal memory structure of BiLSTM, with a better ability to extract multiple time series features. In addition, the model prediction error after NRGA optimization is lower than that after both GA and PSO algorithms. In the BiLSTM model, the MAE after NRGA algorithm optimization is lower than that after GA and PSO algorithm optimization by 1.41% and 2.35%, the RMSE is lower by 2.41% and 5.58%, the MAPE is reduced by 5.18% and 7.58%, respectively, and the trends presented in the other models are more or less the same. In summary, PSO is more likely to fall into local optimality than GA, leading to a more significant prediction error. While NRGA is optimized based on GA, the ability of global and local optimality search is improved.
To explore the effect of the PAM on the prediction model, a comparative experiment was conducted with or without adding the PAM as an experimental variable. The results are summarized in Table 5. According to the results, adding the PAM has led to a certain degree of improvement in the accuracy of all four models. During the BiLSTM, the MAE, RMSE, and MAPE have been diminished by 7.41%, 6.94%, and 5.30%, respectively. Since the PV power data are highly cyclic, the PAM makes the model focus on finding the pattern of the PV power data in the set period, thus obtaining better prediction results. In addition, the BiLSTM model has the most accurate prediction, with the accuracy in descending order of BiLSTM > LSTM > GRU > BPNN.

Table 5.
Effect of the PAM on different model prediction accuracies.
To further validate the prediction accuracy of the proposed model in this paper, we have selected the prediction models in the references for comparative studies to demonstrate the superiority of the proposed method. These papers all use the same dataset DKASC as this paper, and the output time step is 5 min. Since MAPE is not calculated in some of the comparative research, only MAE and RMSE are compared and analyzed. The final results are shown in Table 6. From the results, the proposed model has the lowest MAE, and the RMSE is only higher than reference [58]. The reason for the improved prediction accuracy can be explained in three ways. Firstly, the seasonal division puts the data of the same season together and inputs them into the model for prediction, which makes it easier for the model to find the patterns. Secondly, the model parameters are well-optimized by the NRGA. Finally, the PAM makes the model focus on finding the relationship between the data at the same time points in different periods. The value of RMSE is higher than the research [58] because this paper does not consider the impact of the inclement weather factor. Adverse weather conditions can result in significant fluctuations in PV output power that deviate from the daily period, thereby amplifying the RMSE. A greater amount of severe weather leads to an increase in the RMSE of the model. Furthermore, compared with other traditional model parameter optimization algorithms such as grid search, random search, and Bayesian, NRGA can find the optimal solution more efficiently and can be adapted to a variety of application scenarios, but it has the limitation of higher computational overhead.

Table 6.
Error comparison with other published papers on the same dataset.
The above experiments were conducted with a 5 min temporal resolution. Consequently, the prediction performance of different models (BiLSTM, LSTM, GRU, and BPNN) for 10 min and 15 min temporal resolutions is shown in Table 7. The prediction accuracy of each model gradually decreases from the highest 5 min temporal resolution to the 15 min temporal resolution, which is because the uncertainty of the PV power increases with the increase in the output time step and leads to a gradual decrease in the prediction accuracy of all the different models. In addition, among the results given for different temporal resolutions, BiLSTM has the most accurate prediction, with MAE of 0.14123 Kw, 0.21722 Kw, and 0.30254 Kw, RMSE of 0.23149 Kw, 0.32873 Kw, and 0.45943 Kw, and MAPE of 0.04522 Kw, 0.07649 Kw, and 0.10471 Kw for the three output time steps, respectively. These results show the advantage of the BiLSTM model in PV power prediction. Finally, the predictive performance of different models in different case studies is presented in Table 8. It can be observed that the BiLSTM consistently demonstrates reliable predictive performance across different datasets, indicating the proposed approach possesses strong generalization capabilities.

Table 7.
Prediction performance of different models in different temporal resolution.

Table 8.
Prediction performance of different models in different case studies.
4. Conclusions
This study proposes a hybrid prediction approach to address the challenges posed by the stochastic and intermittent nature of PV power. The proposed approach is based on FCM, SD, PAM, and NRGA. First, the pre-processed and feature-selected dataset is divided into different seasons under FCM. Then, the divided dataset is decomposed using the SD multiplicative model, which decomposes the input sequence into feature sequences composed of trend, period, and residual components for predicting PV output power. BiLSTM, which performs well in time series prediction, is used for the prediction model, and the PAM is added to assign different weights to the input data. Therefore, the prediction model will focus on finding the relationship between the data at the same time points in different periods. Finally, regarding parameter optimization, the improved NRGA is implemented, which enhances the global and local search capabilities of the algorithm. At the same time, it effectively prevents the algorithm from converging to a locally optimal solution and helps the model find the optimal parameters faster. Seven years of DKASC Alice Springs power plant data were selected to design experiments to verify the performance of the approach. The final results demonstrate that compared with LSTM, GRU, and BPNN, and previous research findings, the proposed approach in this paper has improvements in MAE, RMSE, and MAPE with higher accuracy, as well as comparatively superior performance at different output time steps for PV power prediction. The MAE, RMSE, and MAPE are 0.14123 Kw, 0.23149 Kw, and 0.04522 Kw.
Overall, the proposed approach effectively captures the periodic and seasonal characteristics of PV data, thus improving the PV power prediction accuracy. It is expected to support the secure and steady operation of the PV grid and provide a significant reference for practical application.
Author Contributions
H.W. conceptualization, methodology, software, validation, writing—original draft, visualization. H.L. conceptualization, methodology, software, writing—original draft, writing—review and editing, supervision, resources, project administration. H.J. supervision, project administration, funding acquisition. Y.H. validation, formal analysis, data curation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (NSFC) (62163019), the Applied Basic Research Project of Yunnan Province (202101AT070096), and the Major Science and Technology Special Plan of Yunnan Province (202202AC080008).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the corresponding authors upon request due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Abbreviations | |
| ARIMA | autoregressive integrated moving average |
| BiLSTM | bidirectional long short-term memory |
| BPNN | backpropagation neural network |
| DKASC | desert knowledge Australia solar centre |
| ELM | extreme learning machine |
| EMD | empirical mode decomposition |
| EEMD | ensemble empirical mode decomposition |
| FCM | fuzzy c-means clustering |
| GA | genetic algorithm |
| GRU | gated recurrent units |
| LOESS | locally estimated scatterplot smoothing |
| LSTM | long short-term memory |
| MAE | mean absolute error |
| MAPE | mean absolute percentage error |
| NRGA | Newton–Raphson genetic algorithm |
| PAM | periodic attention mechanism |
| PSO | particle swarm optimization |
| PV | photovoltaic |
| RLMD | robust mean decomposition |
| RMSE | root mean square error |
| SAM | self-attention mechanism |
| SD | seasonal decomposition |
| SDA | similar day analysis |
| THD | total harmonic distortion |
| VMD | variational mode decomposition |
| WT | wavelet decomposition |
| Symbols | |
| a | Old clustering categories |
| b | New clustering categories |
| The direction of the mutation | |
| c | Crossover rate |
| d | The estimate of NRGA |
| e | Correlation score |
| Mutation rate | |
| p | The set of chromosomes |
| w | Weighting parameter |
| x | Data samples |
| A | The input vector sets of the attention mechanism |
| I | Iterations counter |
| J | The objective function of the FCM algorithm |
| The level estimate of the feature at moment t | |
| Regularization terms | |
| N | The number of vector sets |
| The actual value of the feature at moment t | |
| The crossover transformation | |
| The values of the period component at moment t | |
| The specified period of attention | |
| Q | The probability of chromosomes being selected. |
| The values of the residual component at moment t | |
| The values of the trend component at moment t | |
| X | Output vector sets of the attention mechanism |
| Y | The set of parameters optimized by the NRGA |
| , , | Smoothing parameters |
| The scale parameter of the Cauchy mutation model | |
| , | Adaptive weighting coefficients |
| Membership degrees | |
| Clustering center | |
| Euclidean distance | |
| Fuzzyness parameter | |
| The Fitness function of NRGA |
References
- Bett, P.E.; Thornton, H.E.; Troccoli, A.; De Felice, M.; Suckling, E.; Dubus, L.; Saint-Drenan, Y.M.; Brayshaw, D.J. A simplified seasonal forecasting strategy, applied to wind and solar power in Europe. Clim. Serv. 2022, 27, 100318. [Google Scholar] [CrossRef] [PubMed]
- Sharma, N.; Puri, V.; Mahajan, S.; Abualigah, L.; Zitar, R.A.; Gandomi, A.H. Solar power forecasting beneath diverse weather conditions using GD and LM-artificial neural networks. Sci. Rep. 2023, 13, 8517. [Google Scholar] [CrossRef]
- Ye, H.; Yang, B.; Han, Y.; Chen, N. State-Of-The-Art Solar Energy Forecasting Approaches: Critical Potentials and Challenges. Front. Energy Res. 2022, 10, 875790. [Google Scholar] [CrossRef]
- Wang, M.; Peng, J.; Luo, Y.; Shen, Z.; Yang, H. Comparison of different simplistic prediction models for forecasting PV power output: Assessment with experimental measurements. Energy 2021, 224, 120162. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bâra, A. A stacked ensemble forecast for photovoltaic power plants combining deterministic and stochastic methods. Appl. Soft Comput. 2023, 147, 110781. [Google Scholar] [CrossRef]
- Khan, U.A.; Khan, N.M.; Zafar, M.H. Resource efficient PV power forecasting: Transductive transfer learning based hybrid deep learning model for smart grid in Industry 5.0. Energy Convers. Manag. X 2023, 20, 100486. [Google Scholar] [CrossRef]
- Klyve, Ø.S.; Nygård, M.M.; Riise, H.N.; Fagerström, J.; Marstein, E.S. The value of forecasts for PV power plants operating in the past, present and future Scandinavian energy markets. Sol. Energy 2023, 255, 208–221. [Google Scholar] [CrossRef]
- Wang, F.; Lu, X.; Mei, S.; Su, Y.; Zhen, Z.; Zou, Z.; Zhang, X.; Yin, R.; Duić, N.; Shafie-khah, M.; et al. A satellite image data based ultra-short-term solar PV power forecasting method considering cloud information from neighboring plant. Energy 2022, 238, 121946. [Google Scholar] [CrossRef]
- Mayer, M.J.; Gróf, G. Extensive comparison of physical models for photovoltaic power forecasting. Appl. Energy 2021, 283, 116239. [Google Scholar] [CrossRef]
- Ma, W.; Qiu, L.; Sun, F.; Ghoneim, S.S.M.; Duan, J. PV Power Forecasting Based on Relevance Vector Machine with Sparrow Search Algorithm Considering Seasonal Distribution and Weather Type. Energies 2022, 15, 5231. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, J.; Liu, H.; Tong, J.; Sun, Z. Prediction of energy photovoltaic power generation based on artificial intelligence algorithm. Neural Comput. Appl. 2021, 33, 821–835. [Google Scholar] [CrossRef]
- Sharadga, H.; Hajimirza, S.; Balog, R.S. Time series forecasting of solar power generation for large-scale photovoltaic plants. Renew. Energy 2020, 150, 797–807. [Google Scholar] [CrossRef]
- Fara, L.; Diaconu, A.; Craciunescu, D.; Fara, S. Forecasting of Energy Production for Photovoltaic Systems Based on ARIMA and ANN Advanced Models. Int. J. Photoenergy 2021, 2021, 6777488. [Google Scholar] [CrossRef]
- Zhong, J.; Liu, L.; Sun, Q.; Wang, X. Prediction of Photovoltaic Power Generation Based on General Regression and Back Propagation Neural Network. Energy Procedia 2018, 152, 1224–1229. [Google Scholar] [CrossRef]
- Harendra Kumar Yadav, Y.P.; Tripathi, M.M. Short-term PV power forecasting using empirical mode decomposition in integration with back-propagation neural network. J. Inf. Optim. Sci. 2020, 41, 25–37. [Google Scholar] [CrossRef]
- Sabri, M.; El Hassouni, M. A Novel Deep Learning Approach for Short Term Photovoltaic Power Forecasting Based on GRU-CNN Model. E3S Web Conf. 2022, 336, 00064. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, Y.; Leng, M.; Yang, X.; Zhou, Q. LOWESS smoothing and Random Forest based GRU model: A short-term photovoltaic power generation forecasting method. Energy 2022, 256, 124661. [Google Scholar] [CrossRef]
- Xiao, Z.; Huang, X.; Liu, J.; Li, C.; Tai, Y. A novel method based on time series ensemble model for hourly photovoltaic power prediction. Energy 2023, 276, 127542. [Google Scholar] [CrossRef]
- Huang, Z.; Huang, J.; Min, J. SSA-LSTM: Short-Term Photovoltaic Power Prediction Based on Feature Matching. Energies 2022, 15, 7806. [Google Scholar] [CrossRef]
- Cao, W.; Zhou, J.; Xu, Q.; Zhen, J.; Huang, X. Short-Term Forecasting and Uncertainty Analysis of Photovoltaic Power Based on the FCM-WOA-BILSTM Model. Front. Energy Res. 2022, 10, 926774. [Google Scholar] [CrossRef]
- Wang, S.; Ma, J. A novel GBDT-BiLSTM hybrid model on improving day-ahead photovoltaic prediction. Sci. Rep. 2023, 13, 15113. [Google Scholar] [CrossRef]
- Bourakadi, D.E.; Ramadan, H.; Yahyaouy, A.; Boumhidi, J. A novel solar power prediction model based on stacked BiLSTM deep learning and improved extreme learning machine. Int. J. Inf. Technol. 2023, 15, 587–594. [Google Scholar] [CrossRef]
- Tahir, M.F.; Tzes, A.; Yousaf, M.Z. Enhancing PV power forecasting with deep learning and optimizing solar PV project performance with economic viability: A multi-case analysis of 10 MW Masdar project in UAE. Energy Convers. Manag. 2024, 311, 118549. [Google Scholar] [CrossRef]
- Rai, A.; Shrivastava, A.; Jana, K.C. A CNN-BiLSTM based deep learning model for mid-term solar radiation prediction. Int. Trans. Electr. Energy Syst. 2021, 31, e12664. [Google Scholar] [CrossRef]
- Khan, Z.A.; Hussain, T.; Baik, S.W. Dual stream network with attention mechanism for photovoltaic power forecasting. Appl. Energy 2023, 338, 120916. [Google Scholar] [CrossRef]
- Zhen, H.; Niu, D.; Wang, K.; Shi, Y.; Ji, Z.; Xu, X. Photovoltaic power forecasting based on GA improved Bi-LSTM in microgrid without meteorological information. Energy 2021, 231, 120908. [Google Scholar] [CrossRef]
- Guo, X.; Gao, Y.; Zheng, D.; Ning, Y.; Zhao, Q. Study on short-term photovoltaic power prediction model based on the Stacking ensemble learning. Energy Rep. 2020, 6, 1424–1431. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, L.; Gao, P.; Yang, B.; Han, Y.; Lian, C. Short-Term Power Generation Forecasting of a Photovoltaic Plant Based on PSO-BP and GA-BP Neural Networks. Front. Energy Res. 2022, 9. [Google Scholar] [CrossRef]
- Semero, Y.K.; Zhang, J.; Zheng, D. PV power forecasting using an integrated GA-PSO-ANFIS approach and Gaussian process regression based feature selection strategy. CSEE J. Power Energy Syst. 2018, 4, 210–218. [Google Scholar] [CrossRef]
- Chen, X.; Ding, K.; Zhang, J.; Han, W.; Liu, Y.; Yang, Z.; Weng, S. Online prediction of ultra-short-term photovoltaic power using chaotic characteristic analysis, improved PSO and KELM. Energy 2022, 248, 123574. [Google Scholar] [CrossRef]
- Eseye, A.T.; Zhang, J.; Zheng, D. Short-term photovoltaic solar power forecasting using a hybrid Wavelet-PSO-SVM model based on SCADA and Meteorological information. Renew. Energy 2018, 118, 357–367. [Google Scholar] [CrossRef]
- Mishra, M.; Byomakesha Dash, P.; Nayak, J.; Naik, B.; Kumar Swain, S. Deep learning and wavelet transform integrated approach for short-term solar PV power prediction. Measurement 2020, 166, 108250. [Google Scholar] [CrossRef]
- Khelifi, R.; Guermoui, M.; Rabehi, A.; Taallah, A.; Zoukel, A.; Ghoneim, S.S.M.; Bajaj, M.; AboRas, K.M.; Zaitsev, I. Short-Term PV Power Forecasting Using a Hybrid TVF-EMD-ELM Strategy. Int. Trans. Electr. Energy Syst. 2023, 2023, 6413716. [Google Scholar] [CrossRef]
- Majumder, I.; Behera, M.K.; Nayak, N. Solar power forecasting using a hybrid EMD-ELM method. In Proceedings of the 2017 International Conference on Circuit, Power and Computing Technologies (ICCPCT), Kollam, India, 20–21 April 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, S.; Liu, S.; Guan, X. Ultra-Short-Term Power Prediction of a Photovoltaic Power Station Based on the VMD-CEEMDAN-LSTM Model. Front. Energy Res. 2022, 10, 945327. [Google Scholar] [CrossRef]
- Wang, S.; Wei, L.; Zeng, L. Ultra-short-term Photovoltaic Power Prediction Based on VMD-LSTM-RVM Model. IOP Conf. Ser. Earth Environ. Sci. 2021, 781, 042020. [Google Scholar] [CrossRef]
- Lin, W.; Zhang, B.; Li, H.; Lu, R. Multi-step prediction of photovoltaic power based on two-stage decomposition and BILSTM. Neurocomputing 2022, 504, 56–67. [Google Scholar] [CrossRef]
- Ngoc-Lan Huynh, A.; Deo, R.C.; Ali, M.; Abdulla, S.; Raj, N. Novel short-term solar radiation hybrid model: Long short-term memory network integrated with robust local mean decomposition. Appl. Energy 2021, 298, 117193. [Google Scholar] [CrossRef]
- Gu, B.; Shen, H.; Lei, X.; Hu, H.; Liu, X. Forecasting and uncertainty analysis of day-ahead photovoltaic power using a novel forecasting method. Appl. Energy 2021, 299, 117291. [Google Scholar] [CrossRef]
- Lin, P.; Peng, Z.; Lai, Y.; Cheng, S.; Chen, Z.; Wu, L. Short-term power prediction for photovoltaic power plants using a hybrid improved Kmeans-GRA-Elman model based on multivariate meteorological factors and historical power datasets. Energy Convers. Manag. 2018, 177, 704–717. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, Y.; Luo, Q.; Huang, H.; Wei, X. Prediction of photovoltaic power output based on similar day analysis using RBF neural network with adaptive black widow optimization algorithm and K-means clustering. Front. Energy Res. 2022, 10. [Google Scholar] [CrossRef]
- Nejati, M.; Amjady, N. A New Solar Power Prediction Method Based on Feature Clustering and Hybrid-Classification-Regression Forecasting. IEEE Trans. Sustain. Energy 2022, 13, 1188–1198. [Google Scholar] [CrossRef]
- Rana, M.; Koprinska, I.; Agelidis, V.G. Solar power forecasting using weather type clustering and ensembles of neural networks. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 4962–4969. [Google Scholar] [CrossRef]
- Bin, F.; He, J. A short-term photovoltaic power prediction model using cyclical encoding and STL decomposition based on LSTM. In Proceedings of the 2023 3rd International Conference on Electronic Information Engineering and Computer Communication (EIECC), Wuhan, China, 8–10 December 2023; pp. 260–266. [Google Scholar] [CrossRef]
- Kumar, S.J.S.; Sam, K.N. Multi-Hybrid STL-LSTM-SDE-MA Model Optimized with IWOA for Solar PV-Power Forecasting. In Proceedings of the 2023 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Kerala, India, 17–20 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Lin, K.P.; Pai, P.F. Solar power output forecasting using evolutionary seasonal decomposition least-square support vector regression. J. Clean. Prod. 2016, 134, 456–462. [Google Scholar] [CrossRef]
- Hu, Z.; Gao, Y.; Ji, S.; Mae, M.; Imaizumi, T. Improved multistep ahead photovoltaic power prediction model based on LSTM and self-attention with weather forecast data. Appl. Energy 2024, 359, 122709. [Google Scholar] [CrossRef]
- Aslam, M.; Kim, J.S.; Jung, J. Multi-step ahead wind power forecasting based on dual-attention mechanism. Energy Rep. 2023, 9, 239–251. [Google Scholar] [CrossRef]
- Lei, X. A Photovoltaic Prediction Model with Integrated Attention Mechanism. Mathematics 2024, 12, 2103. [Google Scholar] [CrossRef]
- Wang, H.; Yan, J.; Zhang, J.; Liu, S.; Liu, Y.; Han, S.; Qu, T. Short-term integrated forecasting method for wind power, solar power, and system load based on variable attention mechanism and multi-task learning. Energy 2024, 304, 132188. [Google Scholar] [CrossRef]
- Fu, H.; Zhang, J.; Xie, S. A Novel Improved Variational Mode Decomposition-Temporal Convolutional Network-Gated Recurrent Unit with Multi-Head Attention Mechanism for Enhanced Photovoltaic Power Forecasting. Electronics 2024, 13, 1837. [Google Scholar] [CrossRef]
- He, Y.; Li, H.; Wang, S.; Yao, X. Uncertainty analysis of wind power probability density forecasting based on cubic spline interpolation and support vector quantile regression. Neurocomputing 2021, 430, 121–137. [Google Scholar] [CrossRef]
- Prema, V.; Rao, K.U. Development of statistical time series models for solar power prediction. Renew. Energy 2015, 83, 100–109. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Farakhor, A.; Khadem Haghighian, S. Novel algorithm of MPPT for PV array based on variable step Newton-Raphson method through model predictive control. In Proceedings of the 2013 13th International Conference on Control, Automation and Systems (ICCAS 2013), Gwangju, Republic of Korea, 20–23 October 2013; pp. 1577–1582. [Google Scholar] [CrossRef]
- Kong, D.; Chang, T.; Dai, W.; Wang, Q.; Sun, H. An improved artificial bee colony algorithm based on elite group guidance and combined breadth-depth search strategy. Inf. Sci. 2018, 442–443, 54–71. [Google Scholar] [CrossRef]
- Liu, Z.F.; Li, L.L.; Tseng, M.L.; Lim, M.K. Prediction short-term photovoltaic power using improved chicken swarm optimizer–Extreme learning machine model. J. Clean. Prod. 2020, 248, 119272. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Li, N.; Li, L.; Huang, F.; Liu, X.; Wang, S. Photovoltaic power prediction method for zero energy consumption buildings based on multi-feature fuzzy clustering and MAOA-ESN. J. Build. Eng. 2023, 75, 106922. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Togneri, R.; Datta, A.; Arif, M.D. Computationally expedient Photovoltaic power Forecasting: A LSTM ensemble method augmented with adaptive weighting and data segmentation technique. Energy Convers. Manag. 2022, 258, 115563. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. Photovoltaic power forecasting based LSTM-Convolutional Network. Energy 2019, 189, 116225. [Google Scholar] [CrossRef]
- Chen, B.; Lin, P.; Lai, Y.; Cheng, S.; Chen, Z.; Wu, L. Very-Short-Term Power Prediction for PV Power Plants Using a Simple and Effective RCC-LSTM Model Based on Short Term Multivariate Historical Datasets. Electronics 2020, 9, 289. [Google Scholar] [CrossRef]
- Huang, X.; Li, Q.; Tai, Y.; Chen, Z.; Liu, J.; Shi, J.; Liu, W. Time series forecasting for hourly photovoltaic power using conditional generative adversarial network and Bi-LSTM. Energy 2022, 246, 123403. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network. Appl. Energy 2019, 251, 113315. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).