Author Contributions
Conceptualization, R.B., M.R., A.L. and M.M.; methodology, R.B., M.R., A.L. and M.M.; software, R.B. and V.C.; validation, R.B., M.R., A.L. and M.M.; investigation, R.B., M.R., A.L. and M.M.; data curation, R.B. and A.L.; writing—original draft preparation, R.B.; writing—review and editing, R.B., M.R., A.L. and M.M.; visualization, R.B. and V.C.; supervision, M.R. and M.M.; project administration, M.R. and M.M.; funding acquisition, M.R. and M.M. All authors have read and agreed to the published version of the manuscript.
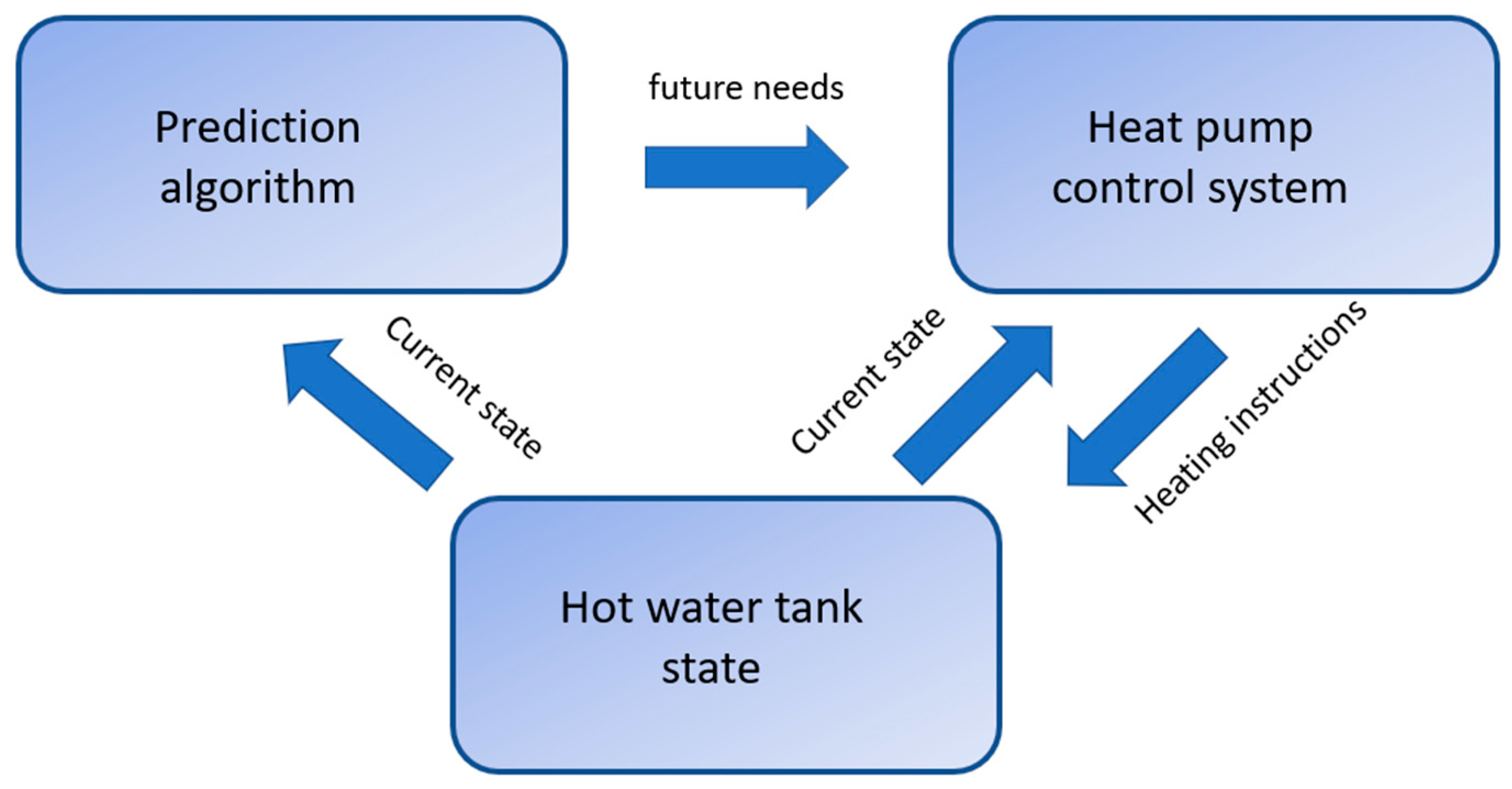
Figure 1.
Schematic view of a smart domestic hot water management system.
Figure 1.
Schematic view of a smart domestic hot water management system.
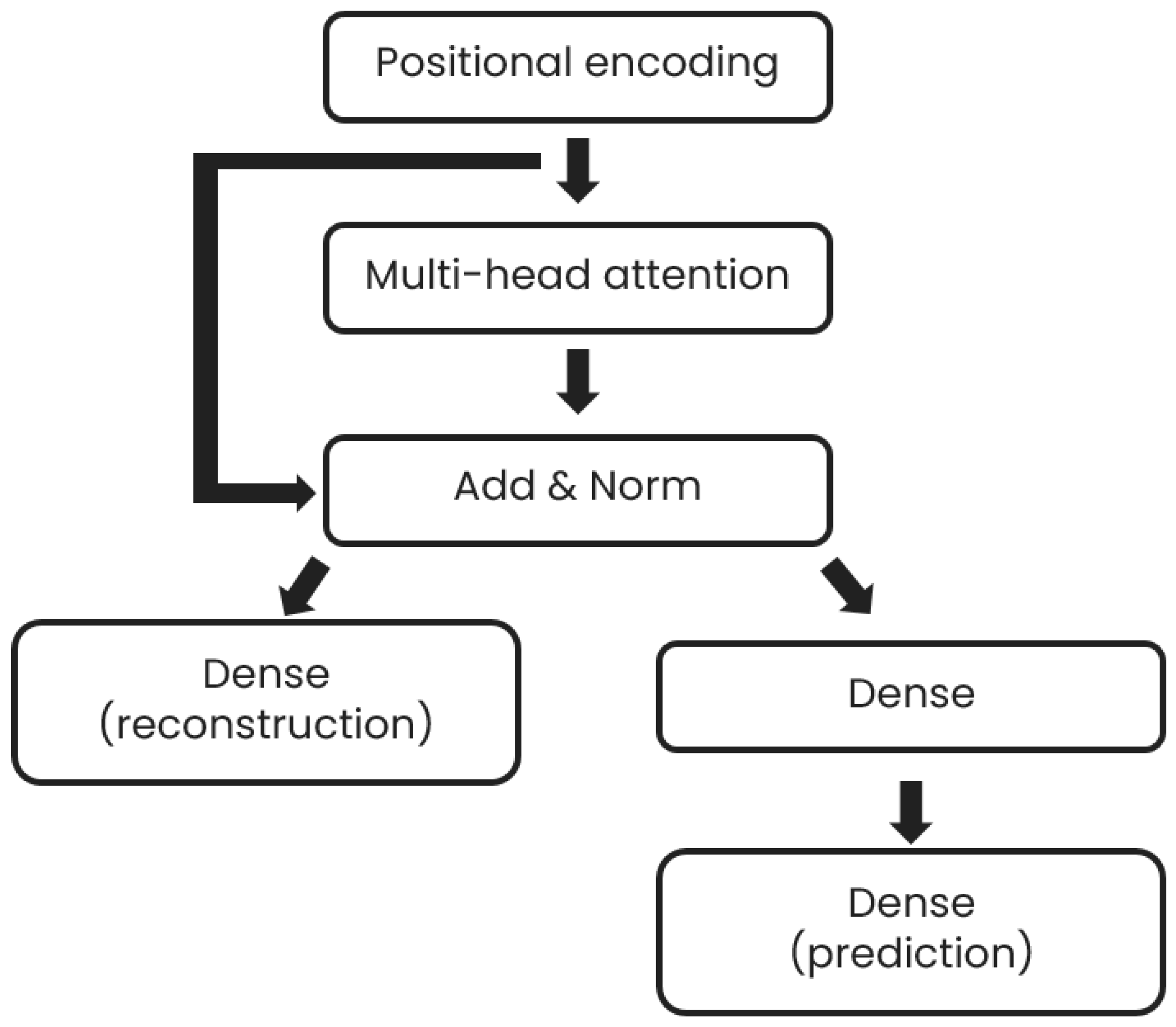
Figure 2.
Prediction model architecture.
Figure 2.
Prediction model architecture.
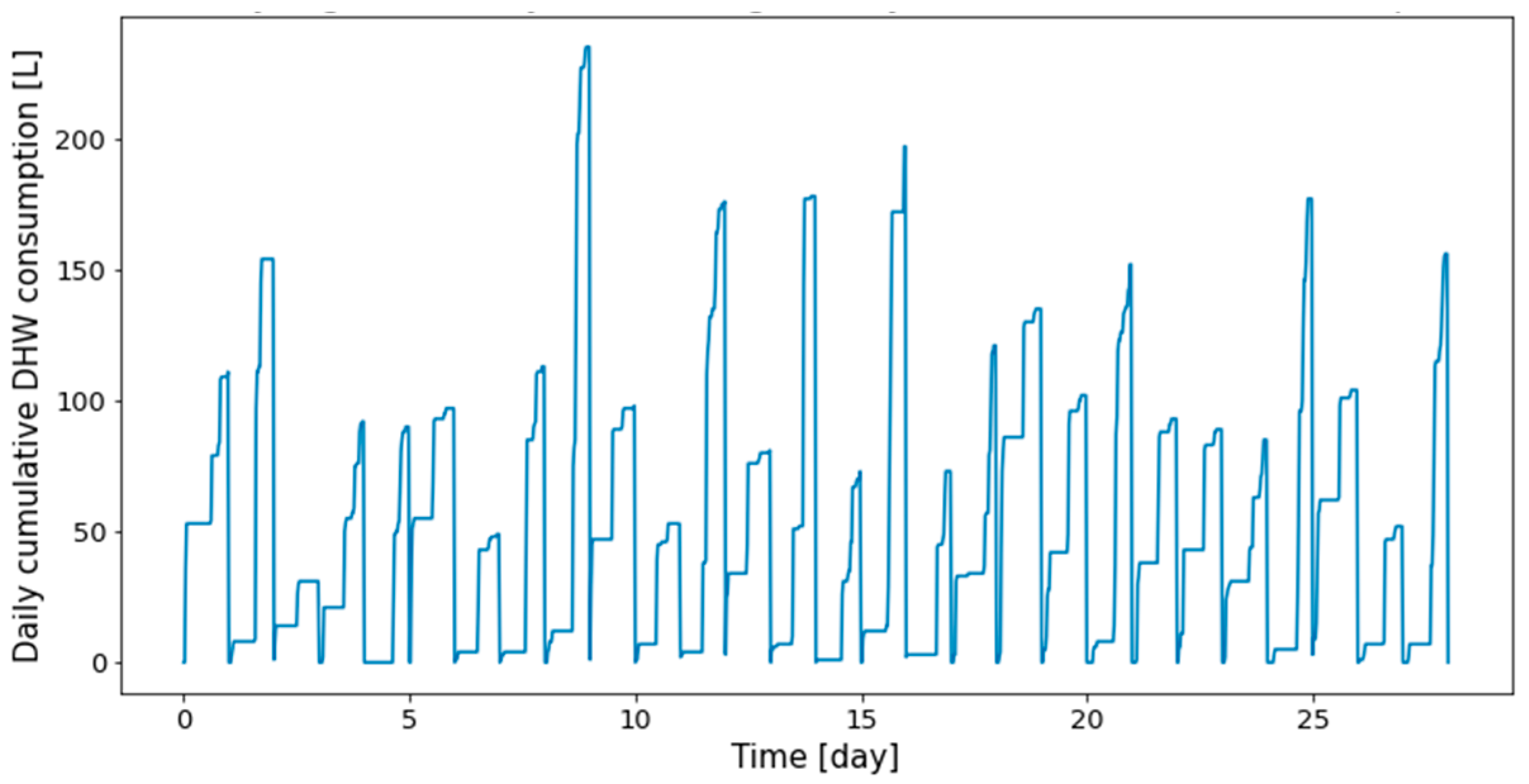
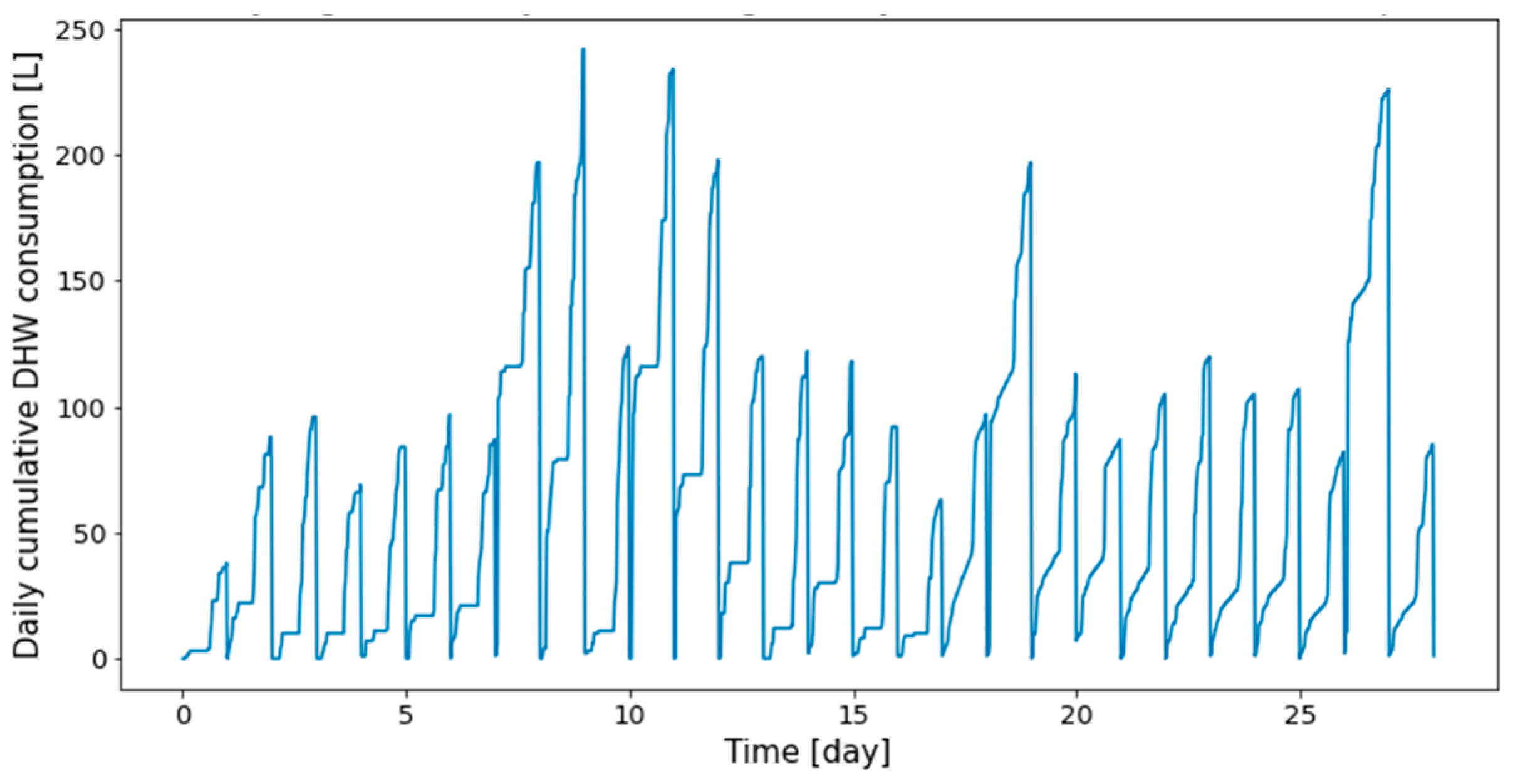
Figure 3.
First twenty-eight days of Dwelling A daily cumulative DHW consumption.
Figure 3.
First twenty-eight days of Dwelling A daily cumulative DHW consumption.
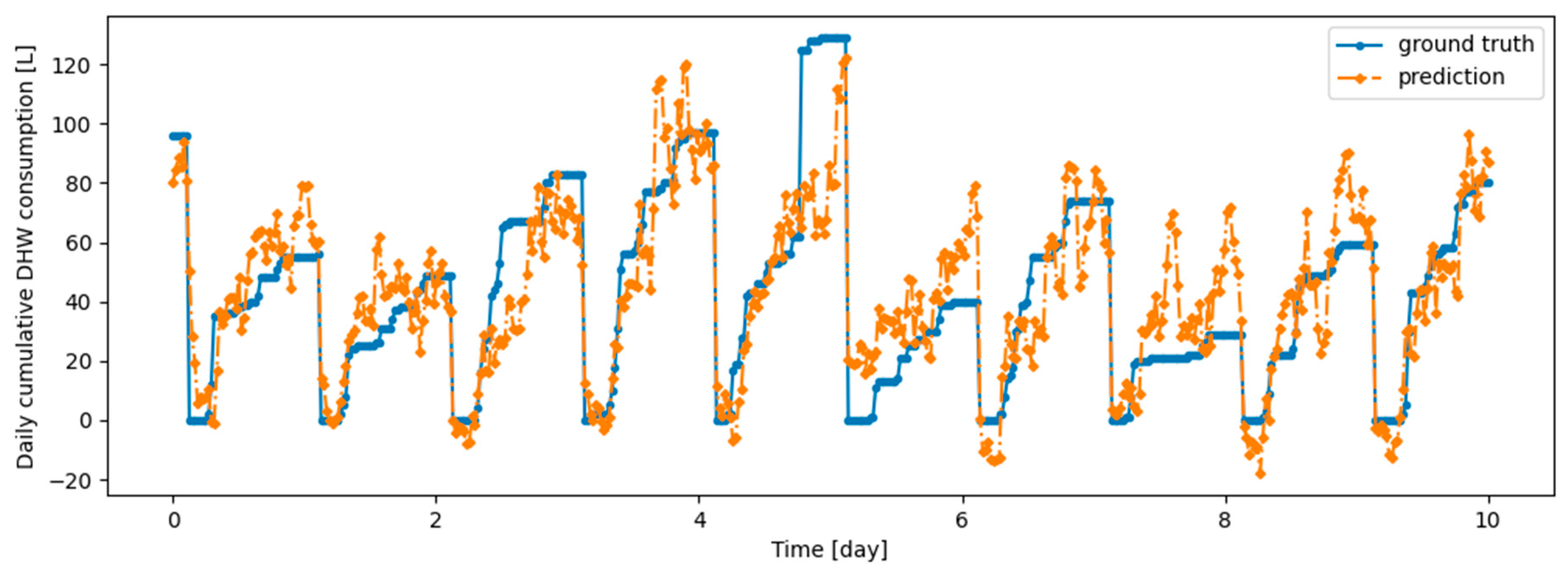
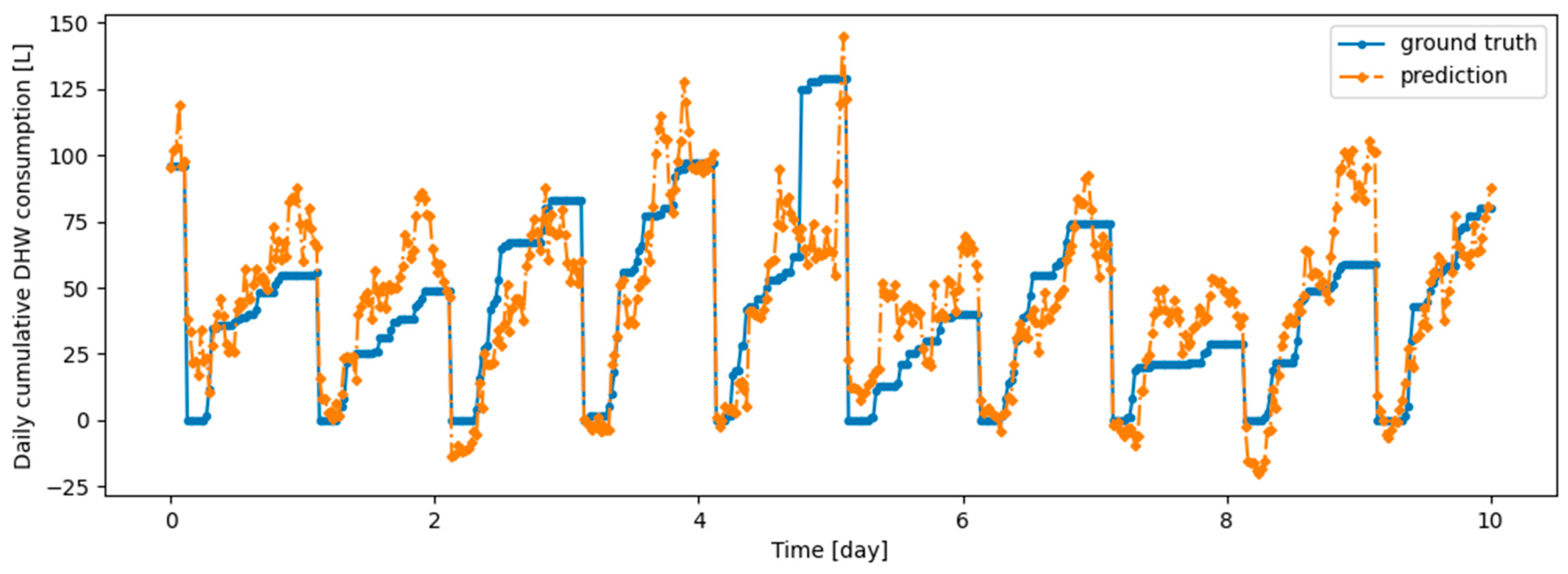
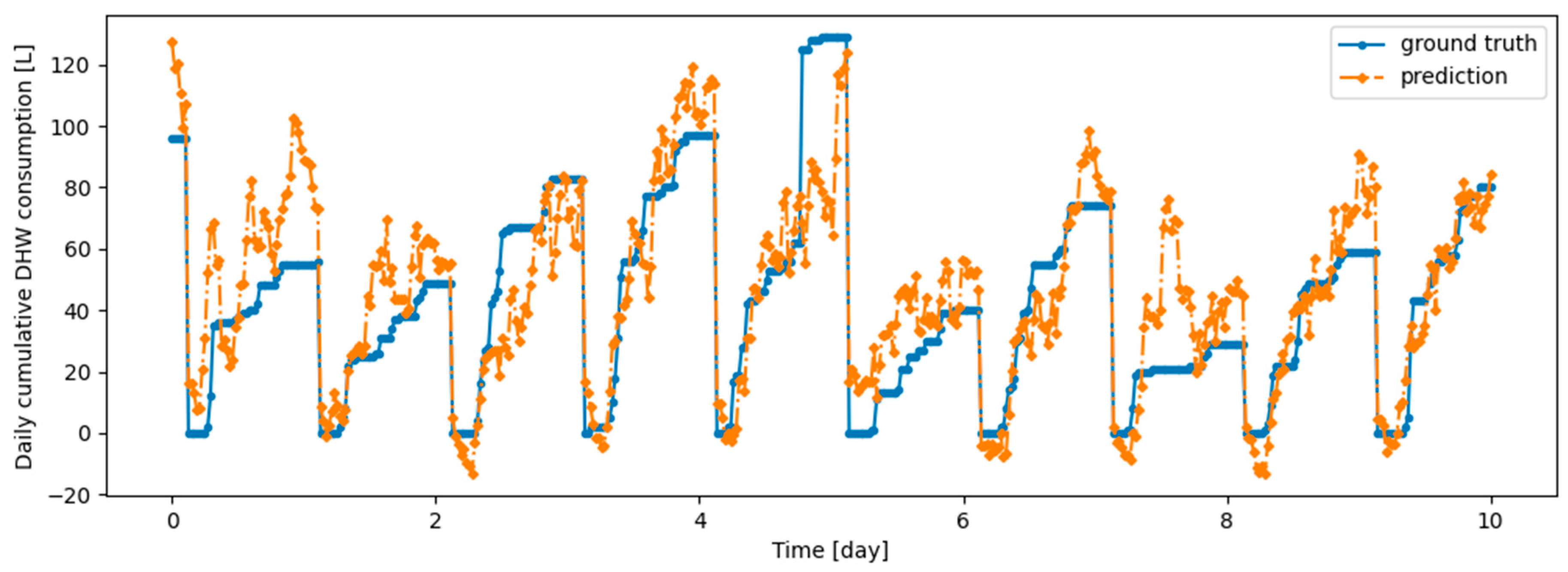
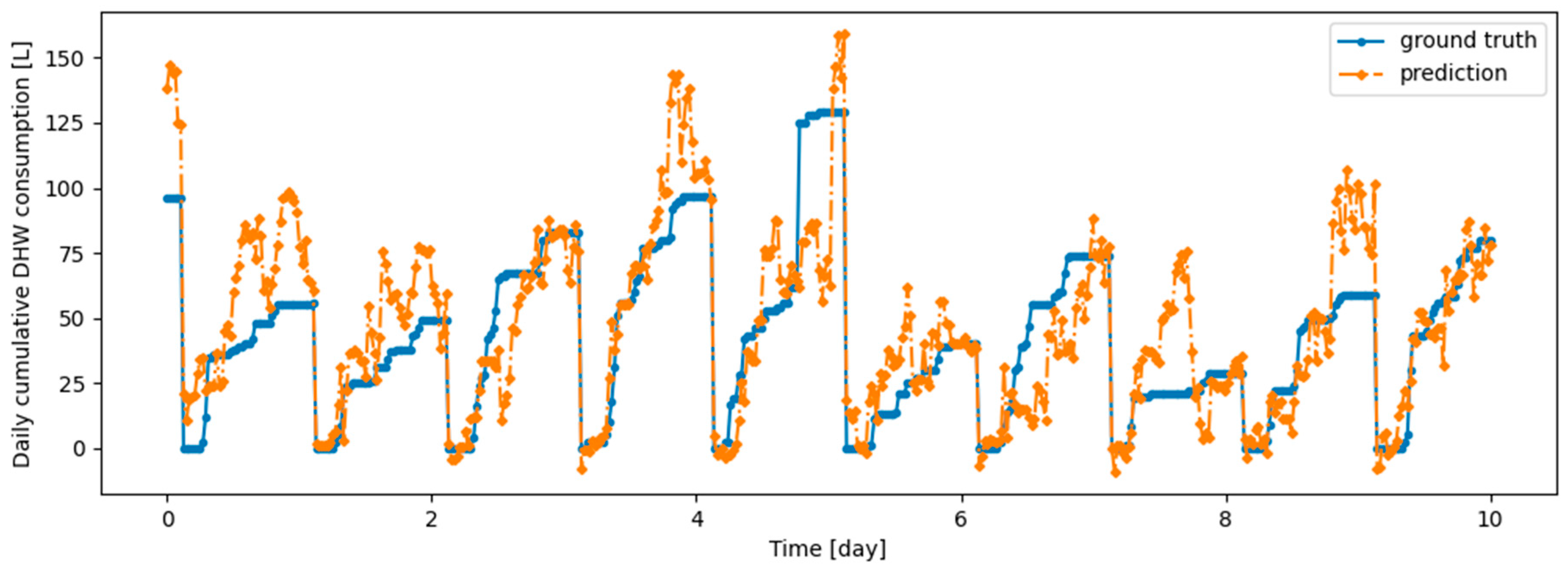
Figure 4.
First twenty-eight days of Dwelling B daily cumulative DHW consumption.
Figure 4.
First twenty-eight days of Dwelling B daily cumulative DHW consumption.
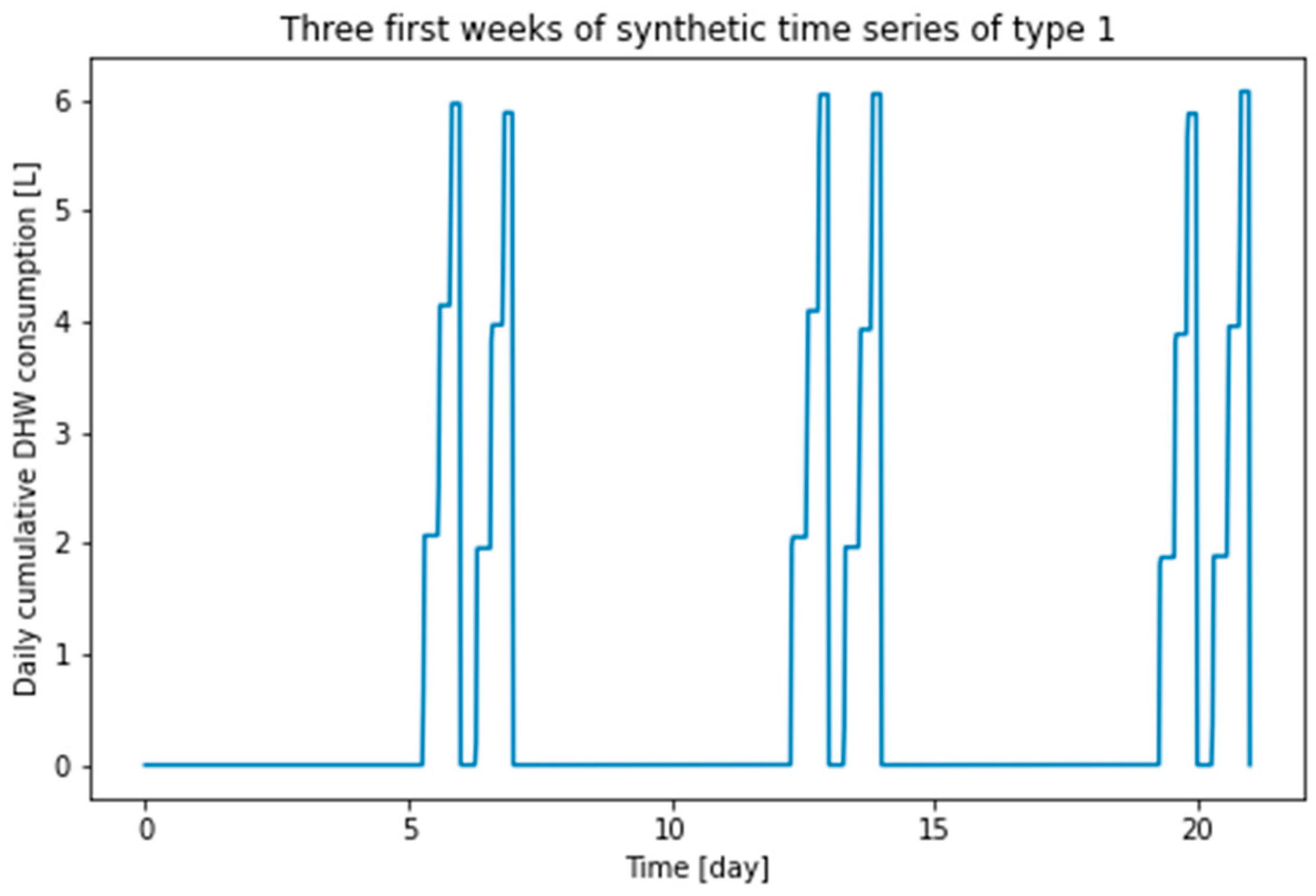
Figure 5.
First three weeks of type 1 synthetic time series.
Figure 5.
First three weeks of type 1 synthetic time series.
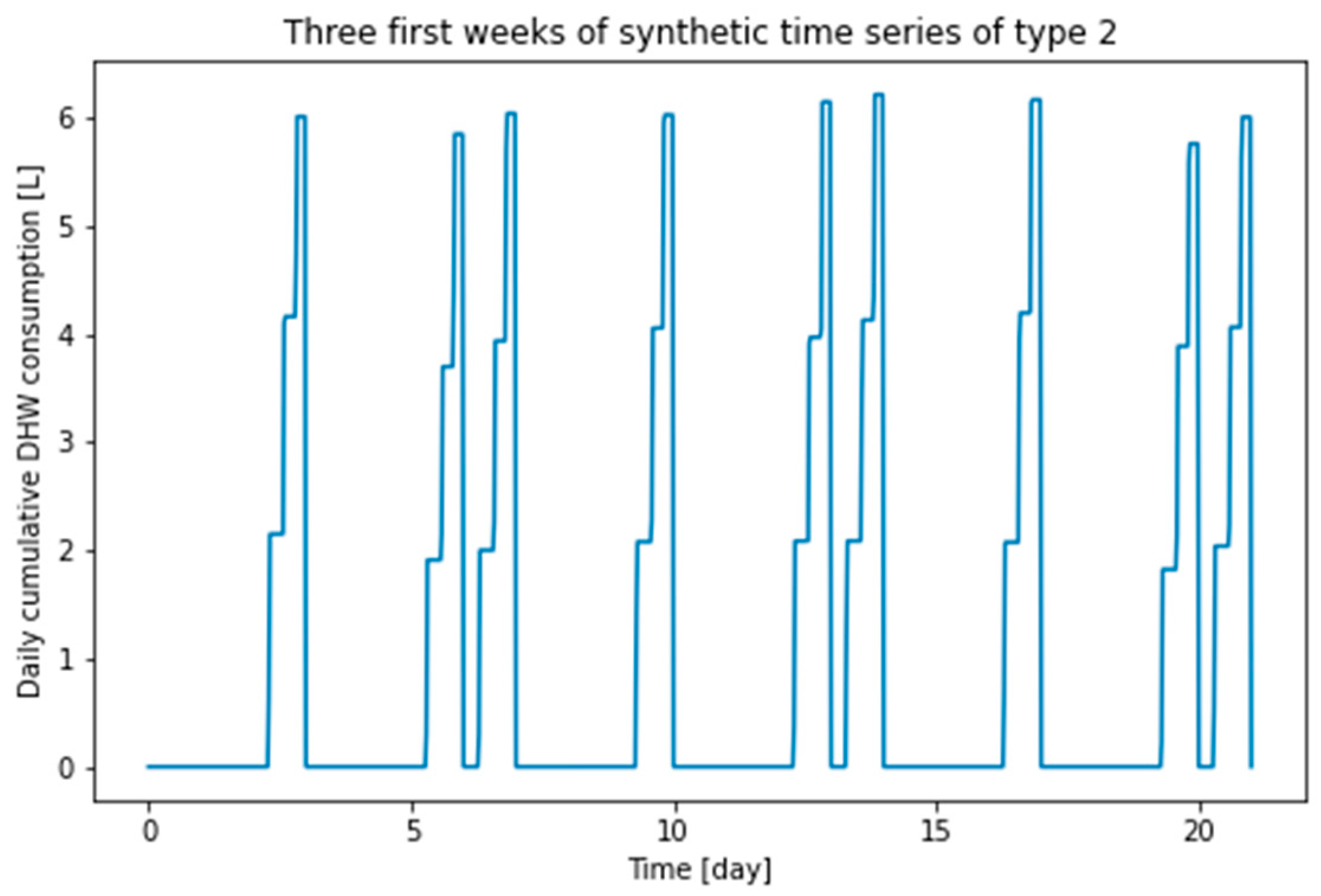
Figure 6.
First three weeks of type 2 synthetic time series.
Figure 6.
First three weeks of type 2 synthetic time series.
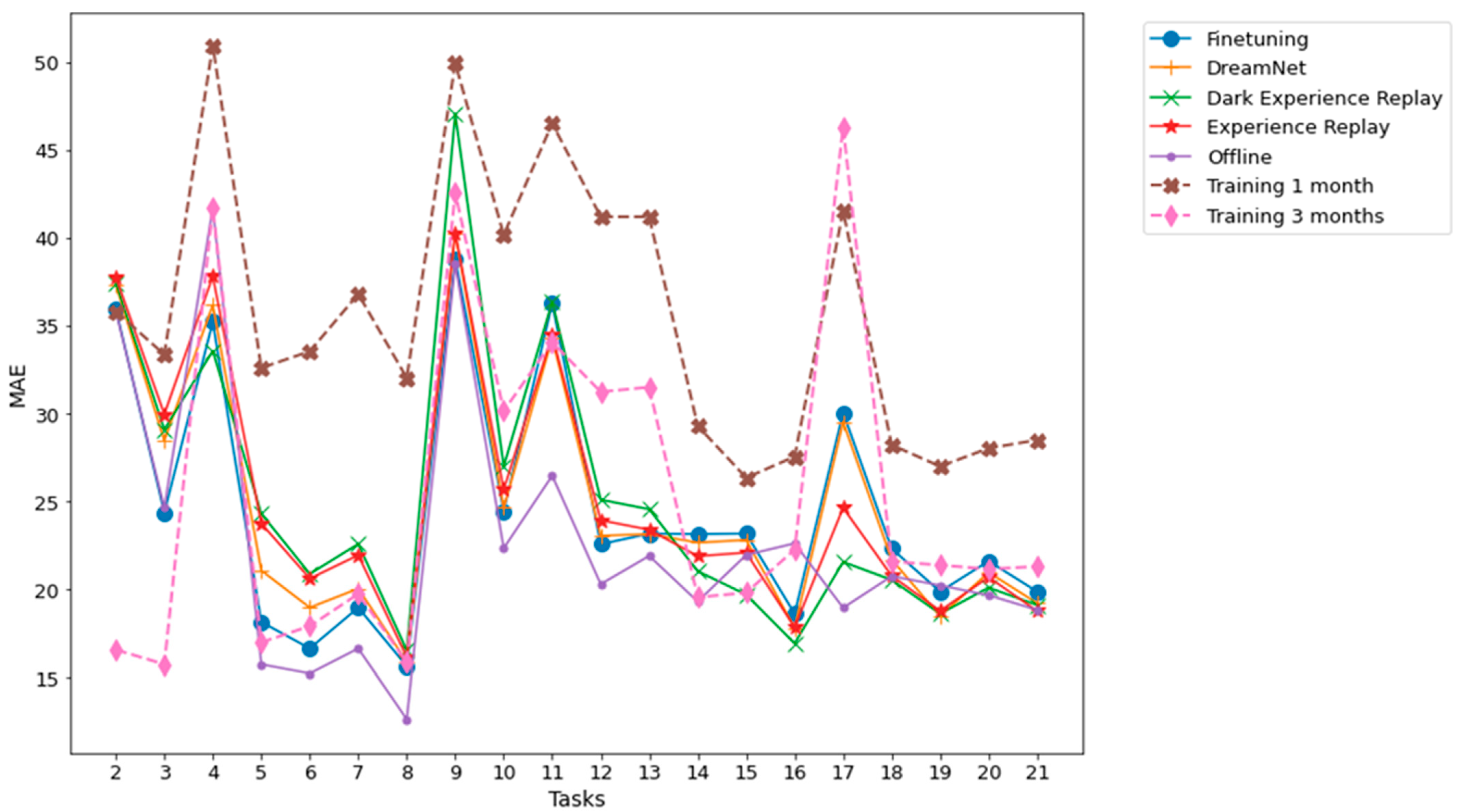
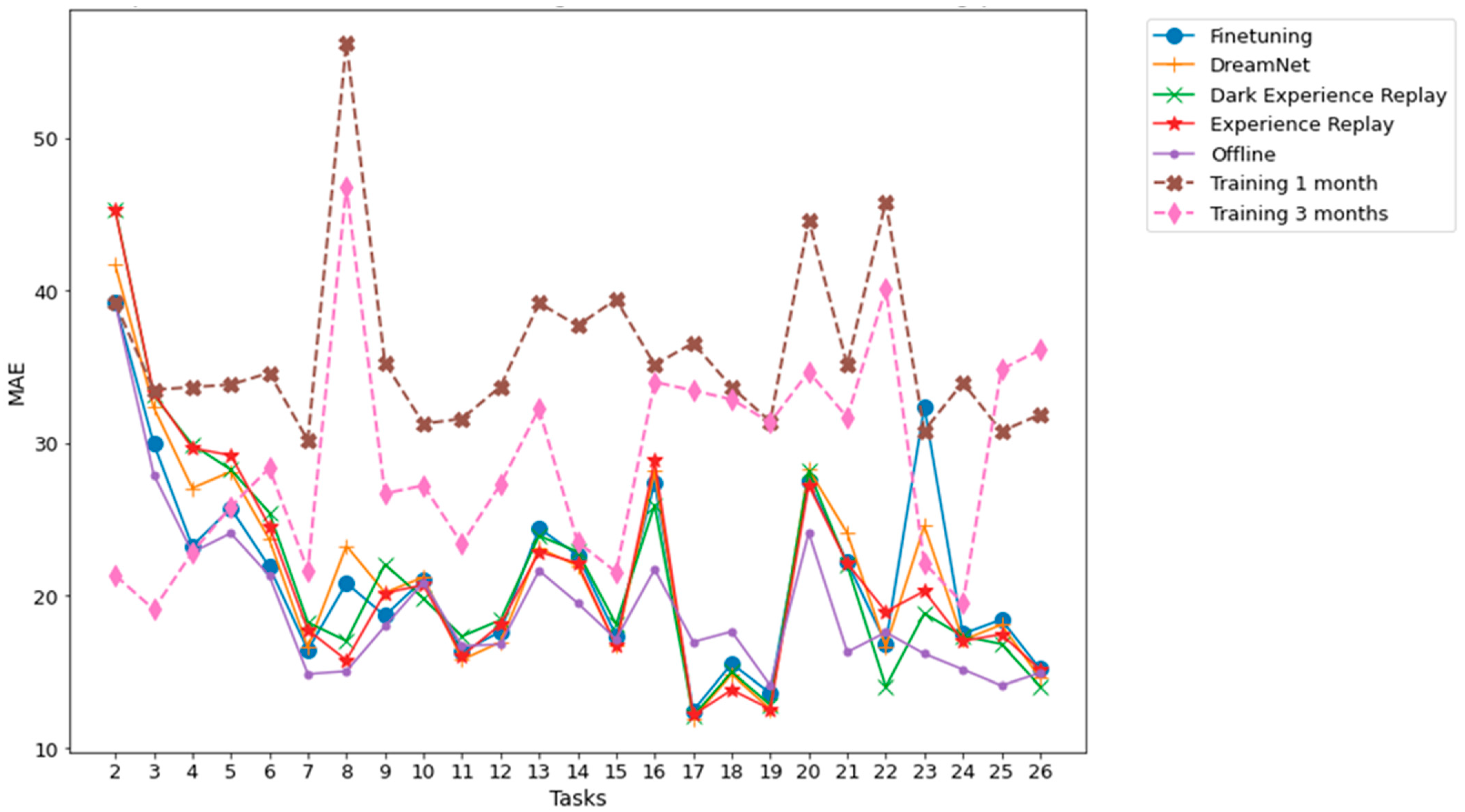
Figure 7.
Dwelling A MAE between multiple time horizon predictions and their associated ground truth for each task. The prediction time horizons are 0.5 h, 1 h, 2 h, 6 h, 12 h, 18 h, 24 h. The results shown are obtained from an average of 5 runs.
Figure 7.
Dwelling A MAE between multiple time horizon predictions and their associated ground truth for each task. The prediction time horizons are 0.5 h, 1 h, 2 h, 6 h, 12 h, 18 h, 24 h. The results shown are obtained from an average of 5 runs.
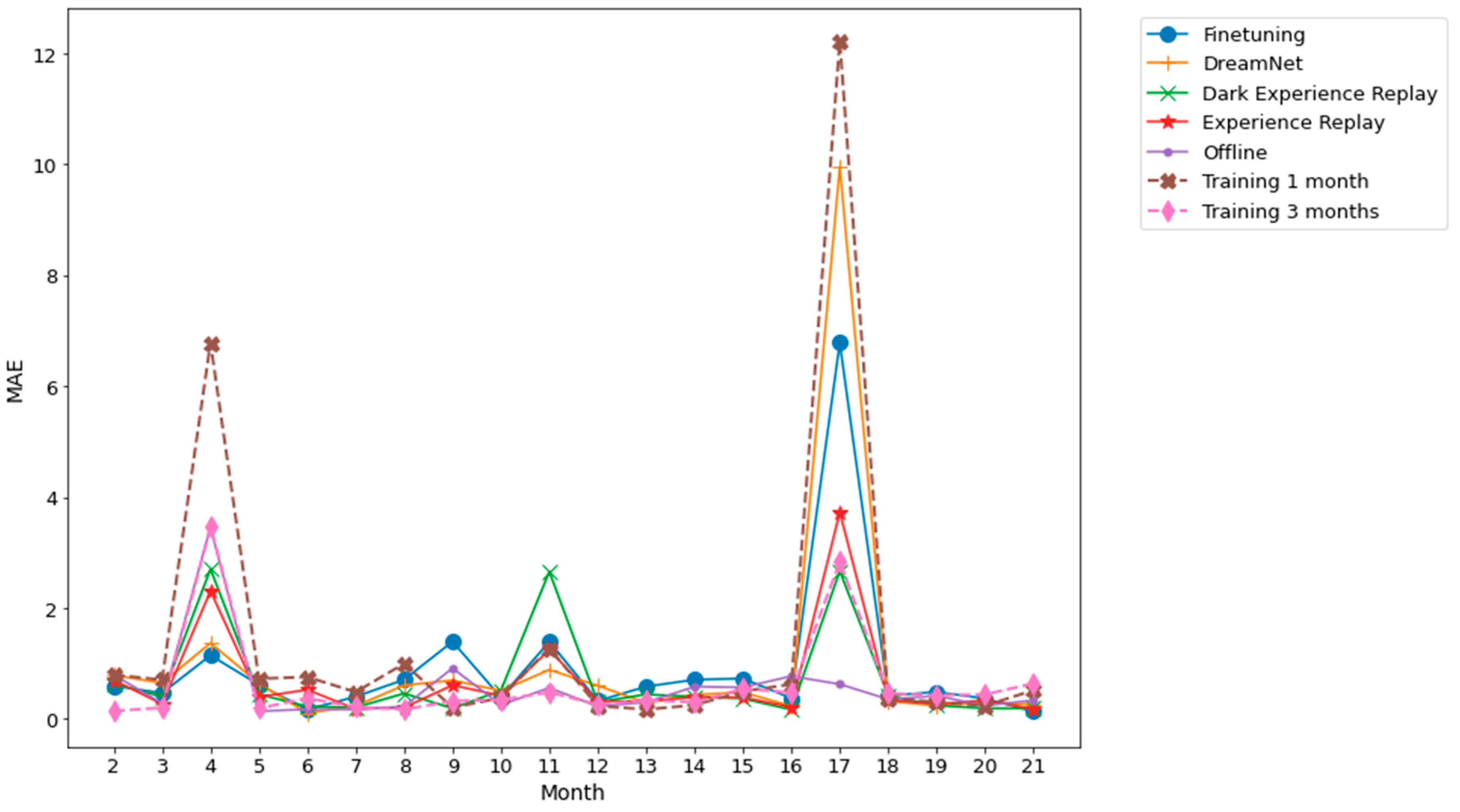
Figure 8.
Dwelling B MAE between multiple time horizon predictions and their associated ground truth for each task. The prediction time horizons are 0.5 h, 1 h, 2 h, 6 h, 12 h, 18 h, 24 h. The results shown are obtained from an average of 5 runs.
Figure 8.
Dwelling B MAE between multiple time horizon predictions and their associated ground truth for each task. The prediction time horizons are 0.5 h, 1 h, 2 h, 6 h, 12 h, 18 h, 24 h. The results shown are obtained from an average of 5 runs.
Figure 9.
Dwelling A standard deviation associated with the 5 runs whose mean is shown in
Figure 7.
Figure 9.
Dwelling A standard deviation associated with the 5 runs whose mean is shown in
Figure 7.
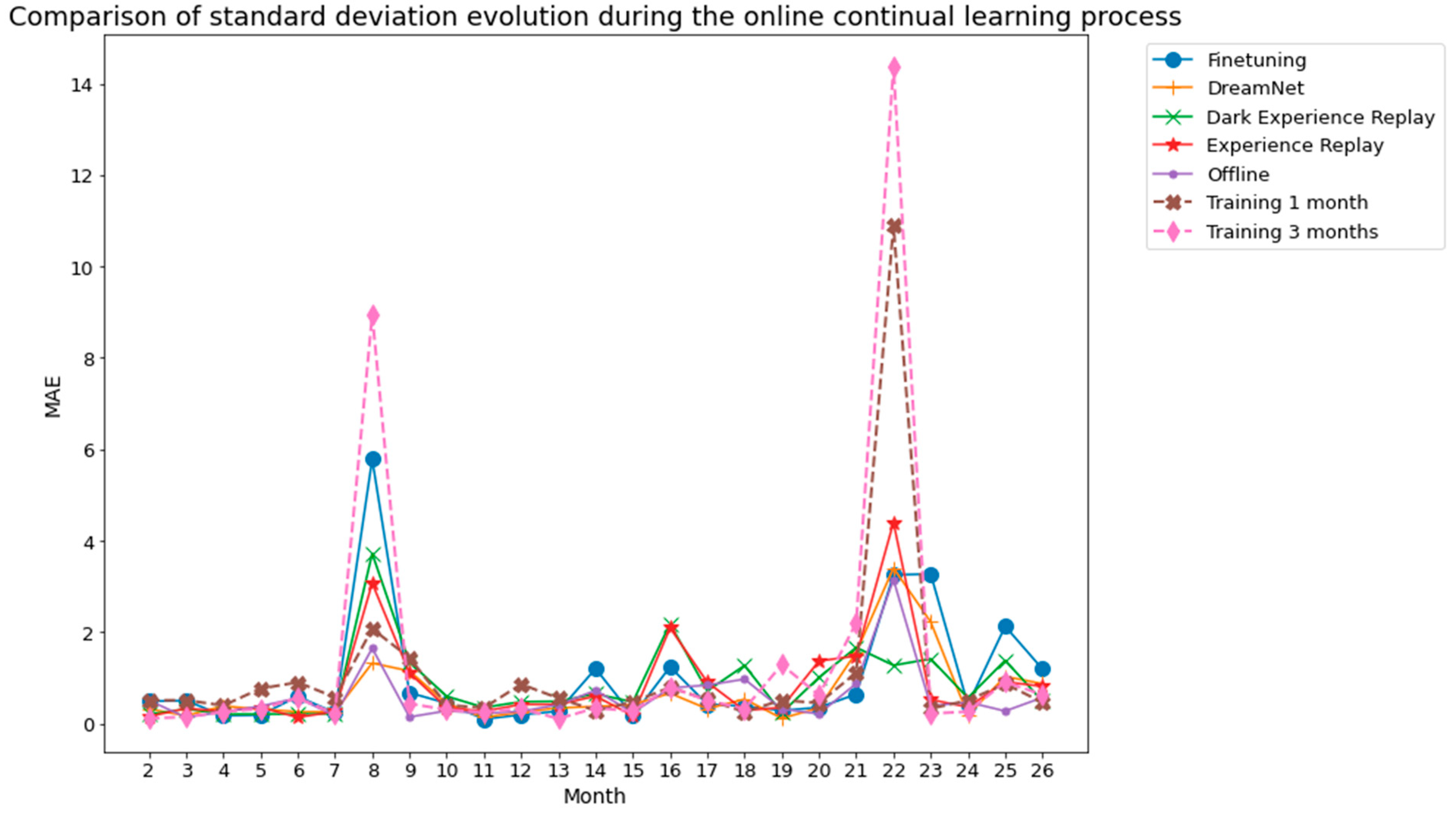
Figure 10.
Dwelling B standard deviation associated with the 5 runs whose mean is shown in
Figure 8.
Figure 10.
Dwelling B standard deviation associated with the 5 runs whose mean is shown in
Figure 8.
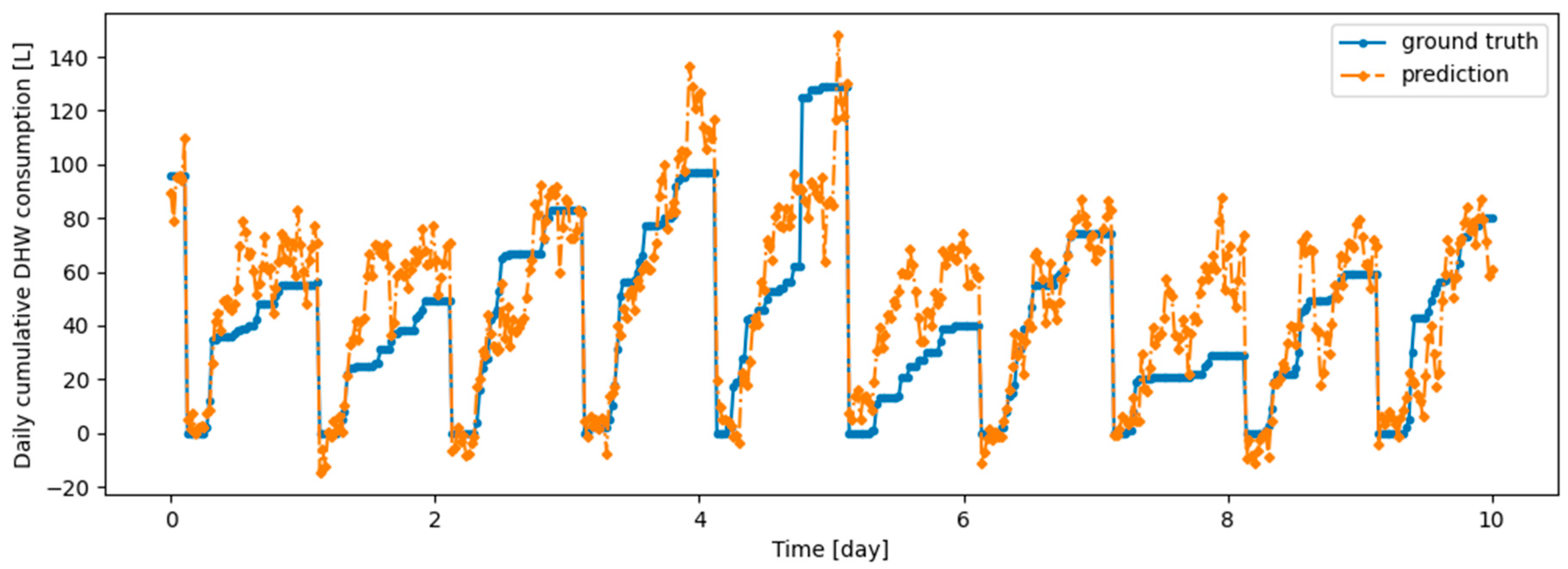
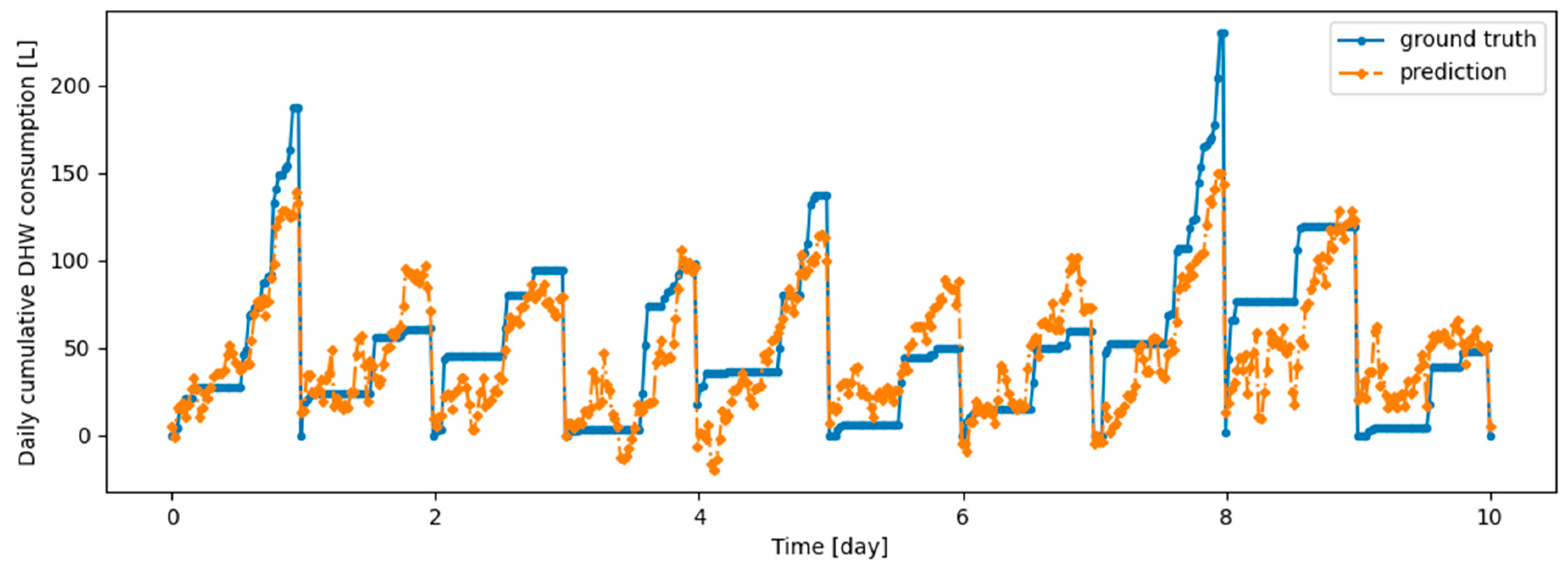
Figure 11.
Example of 6-h prediction versus ground truth for 10 days in the last task of Dwelling A’s DHW consumption with a model continuously trained with the Dream Net algorithm.
Figure 11.
Example of 6-h prediction versus ground truth for 10 days in the last task of Dwelling A’s DHW consumption with a model continuously trained with the Dream Net algorithm.
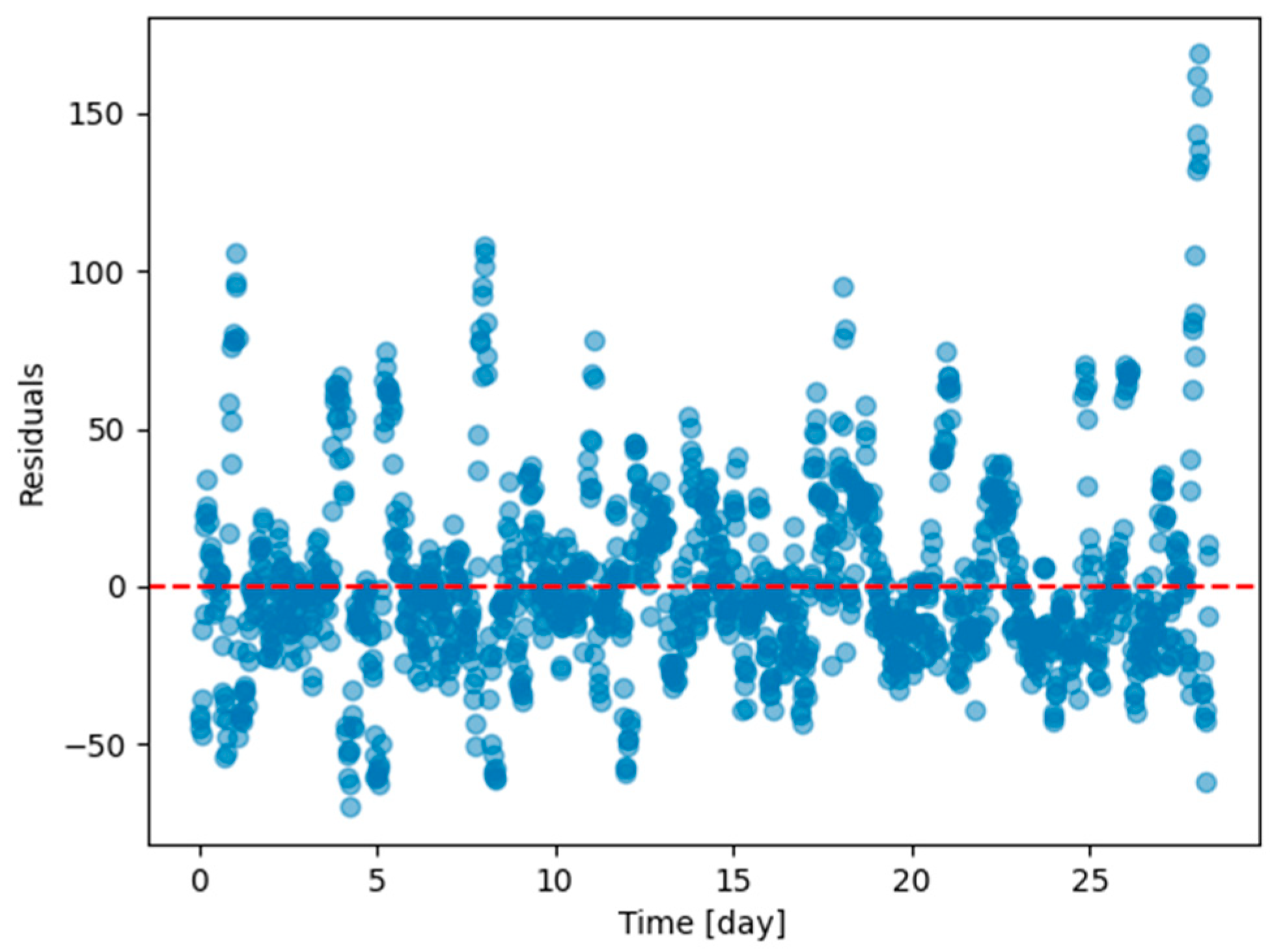
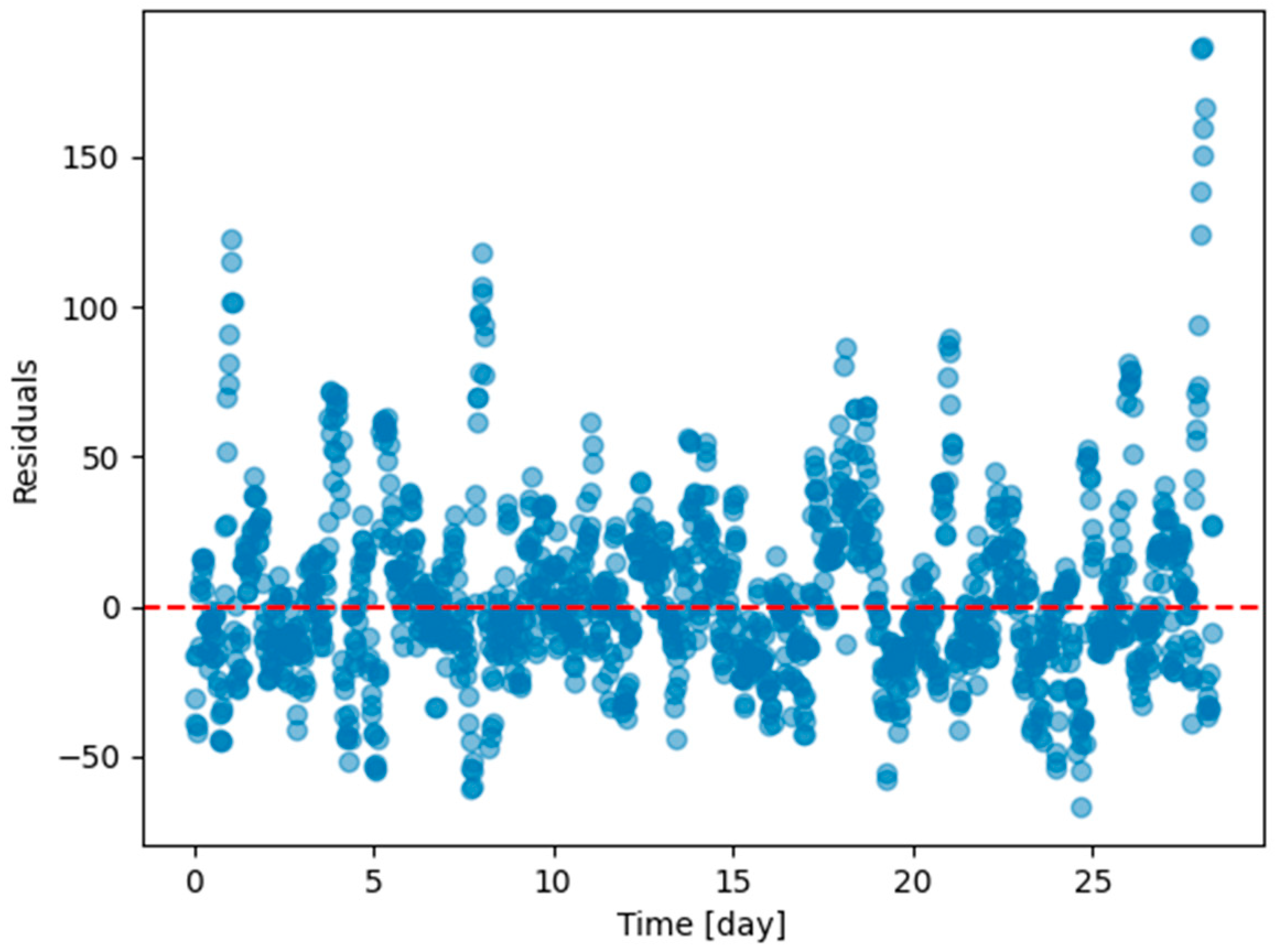
Figure 12.
Residual plot (ground truth minus predicted value) of the last task of Dwelling A DHW consumption with a model continuously trained with Dream Net with all tasks except the last one of Dwelling A.
Figure 12.
Residual plot (ground truth minus predicted value) of the last task of Dwelling A DHW consumption with a model continuously trained with Dream Net with all tasks except the last one of Dwelling A.
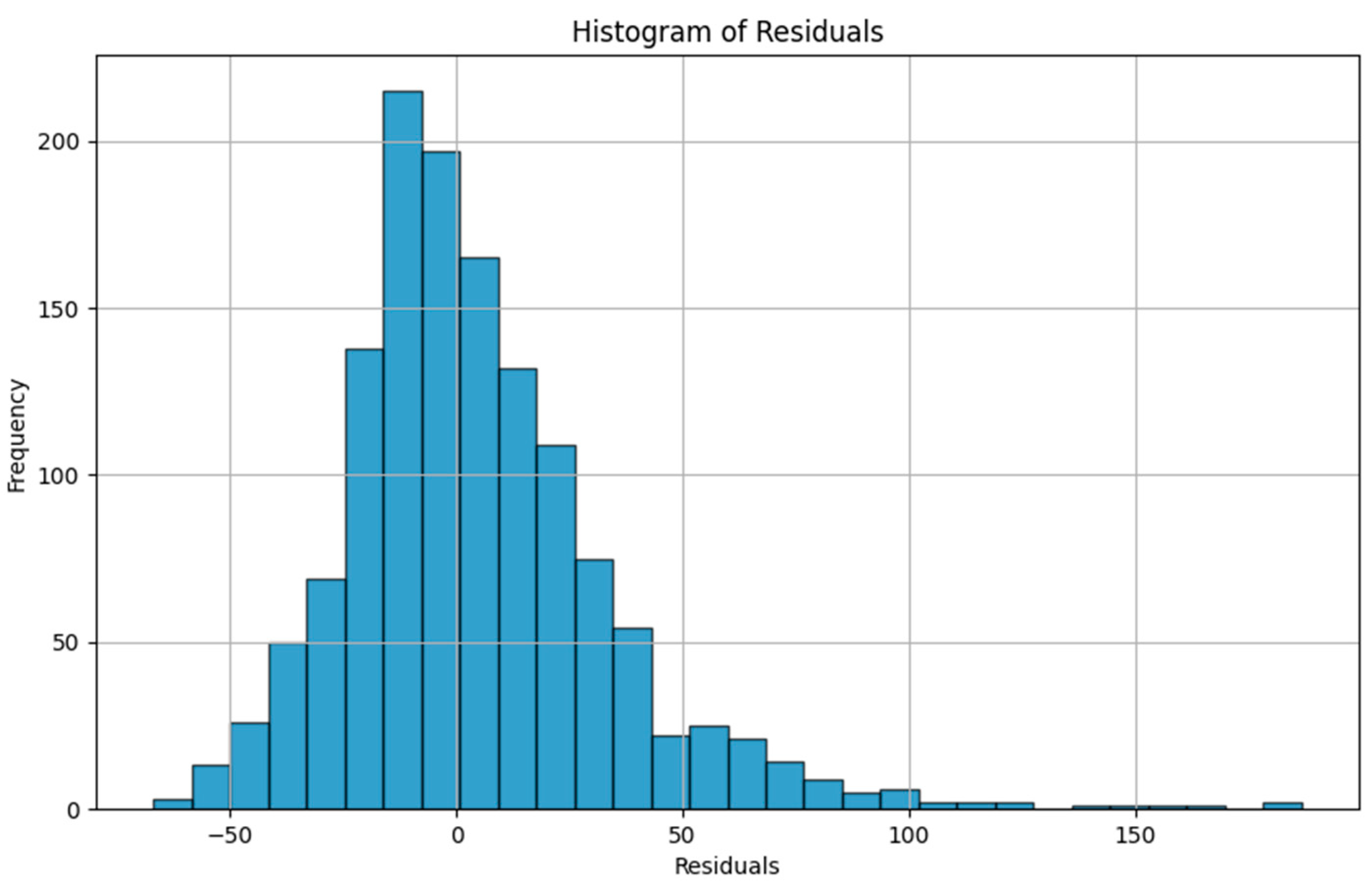
Figure 13.
Residual plot (ground truth minus predicted value) histogram of the last task of Dwelling A DHW consumption with a model continuously trained using the Dream Net algorithm with all tasks except the last one in Dwelling A.
Figure 13.
Residual plot (ground truth minus predicted value) histogram of the last task of Dwelling A DHW consumption with a model continuously trained using the Dream Net algorithm with all tasks except the last one in Dwelling A.
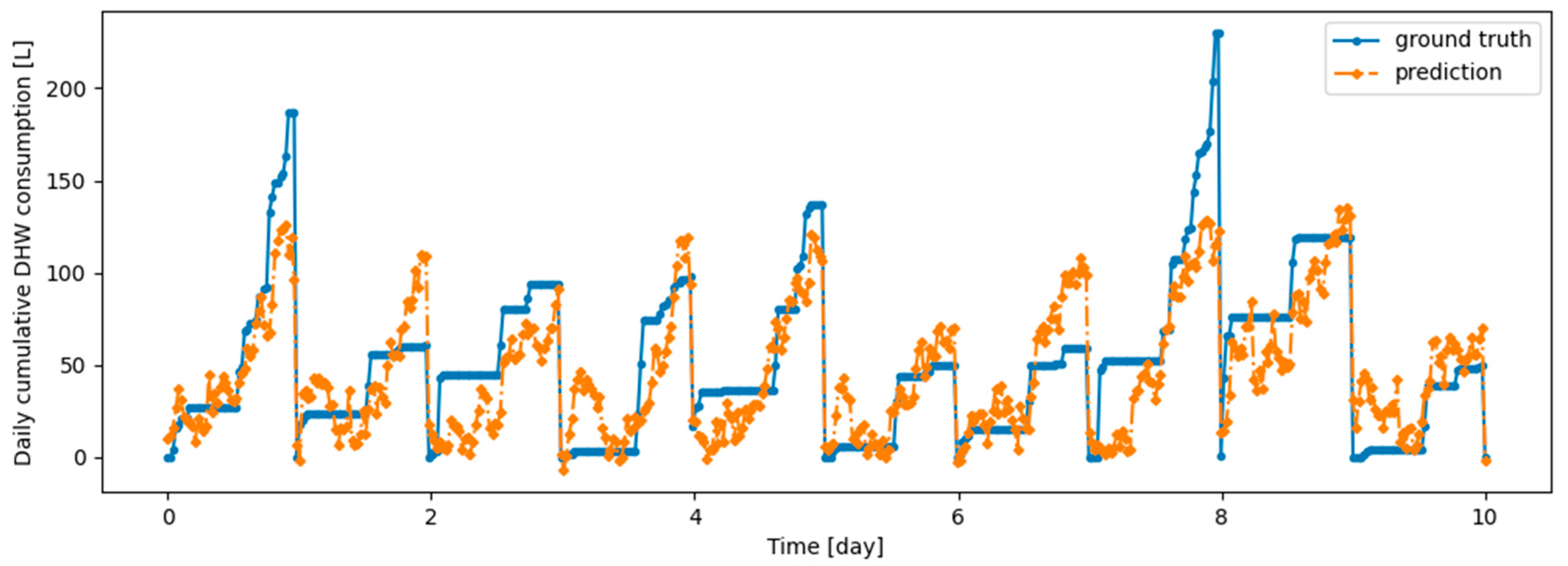
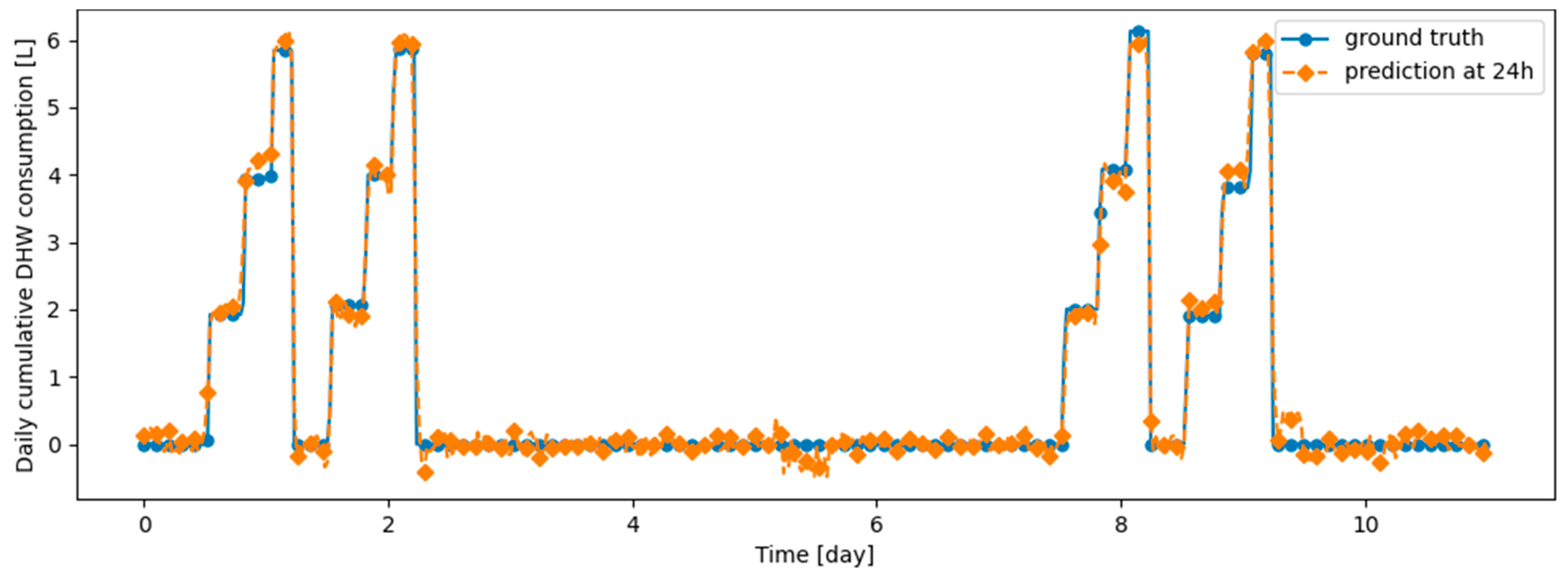
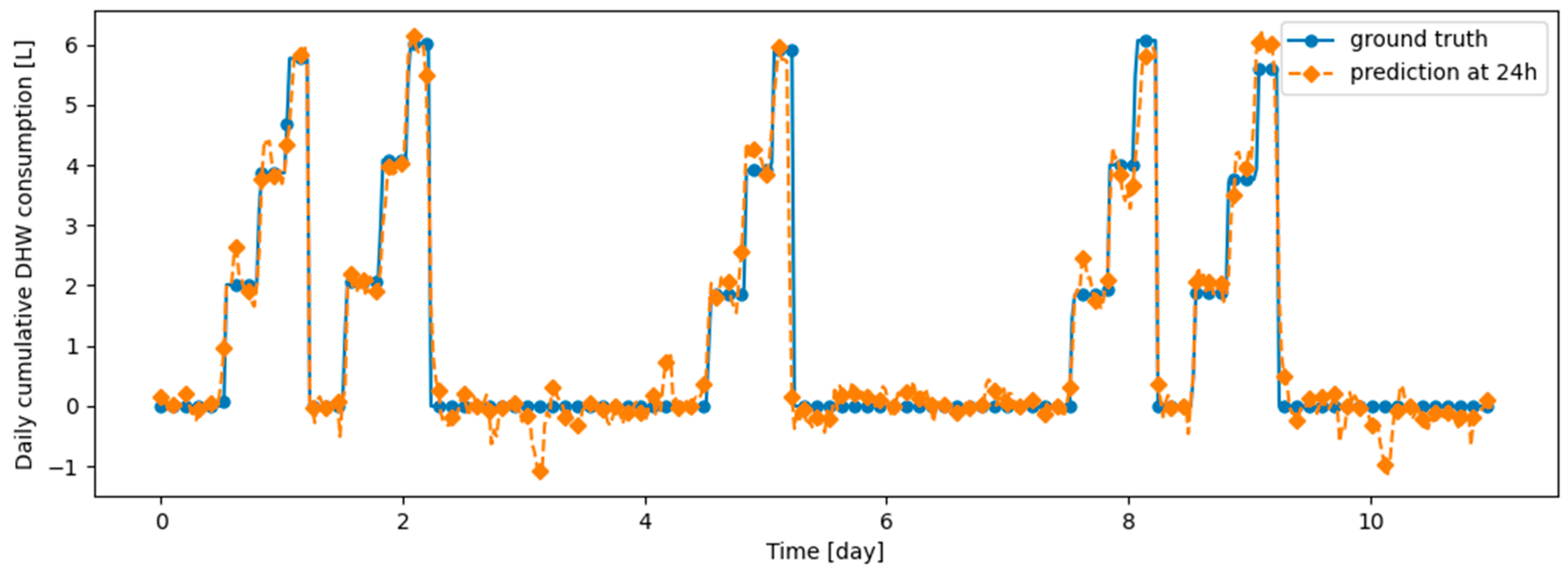
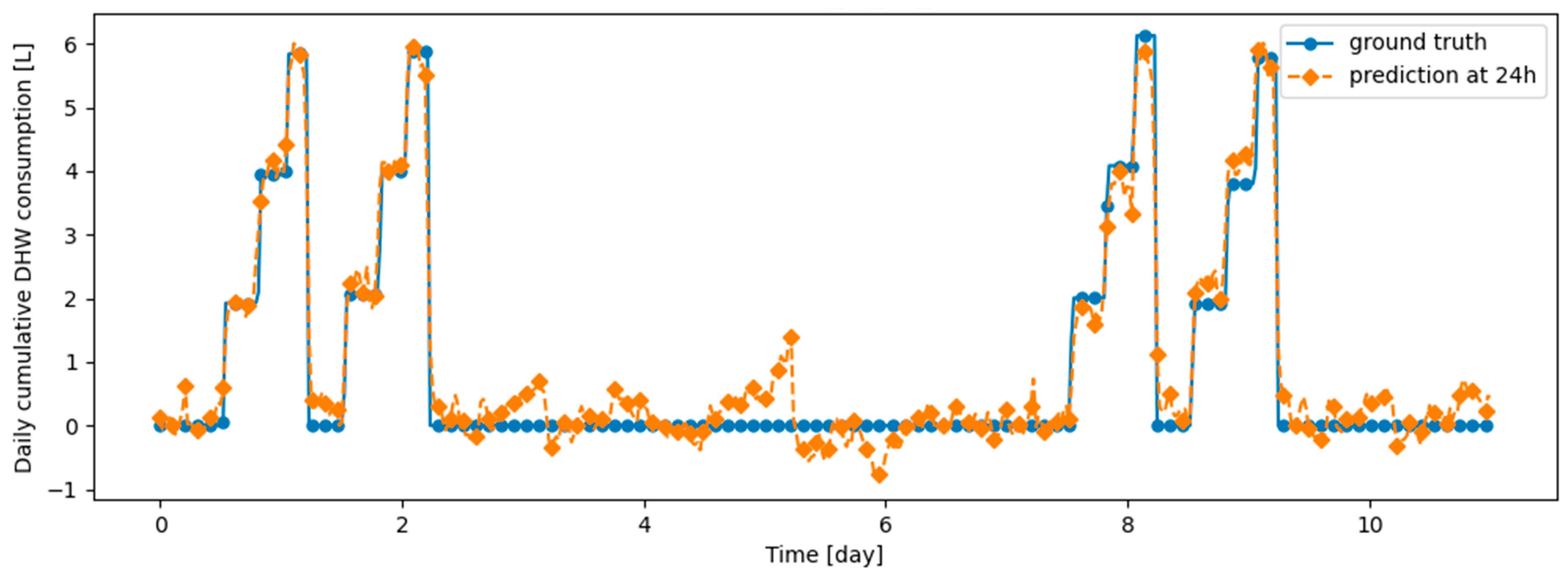
Figure 14.
Example of 24-h prediction versus ground truth for 11 days of d1_test, after training the model on d1_train.
Figure 14.
Example of 24-h prediction versus ground truth for 11 days of d1_test, after training the model on d1_train.
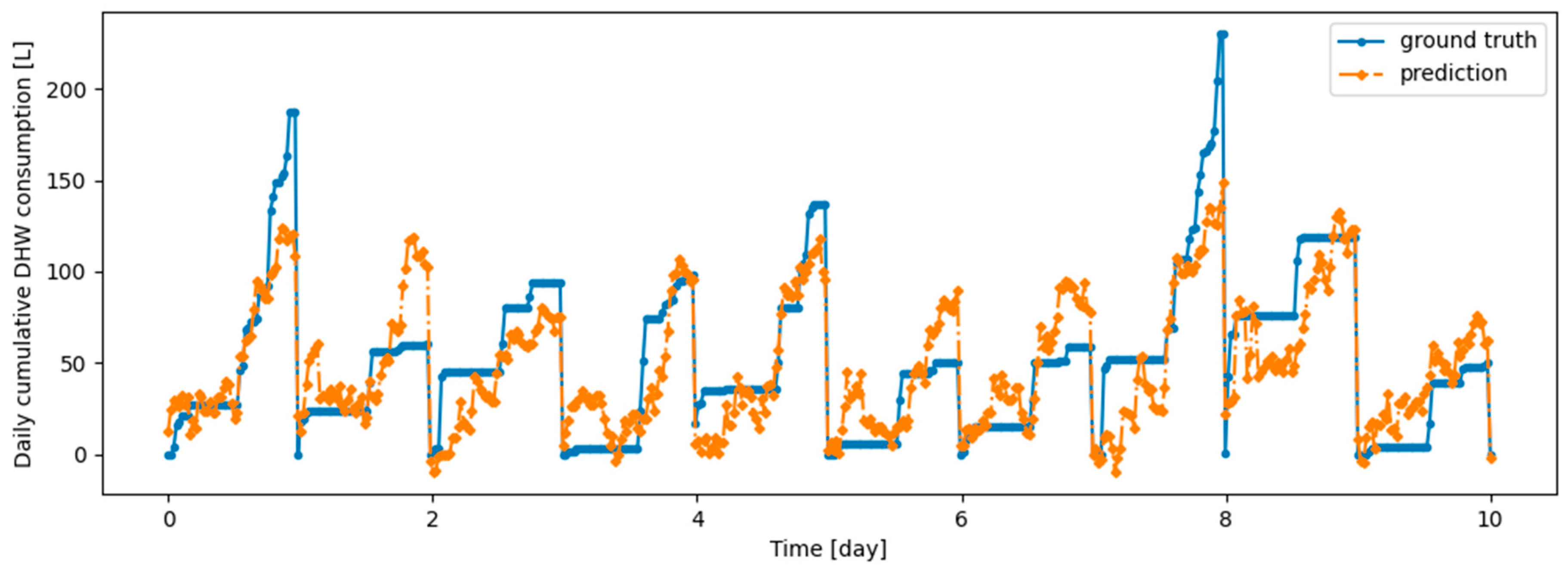
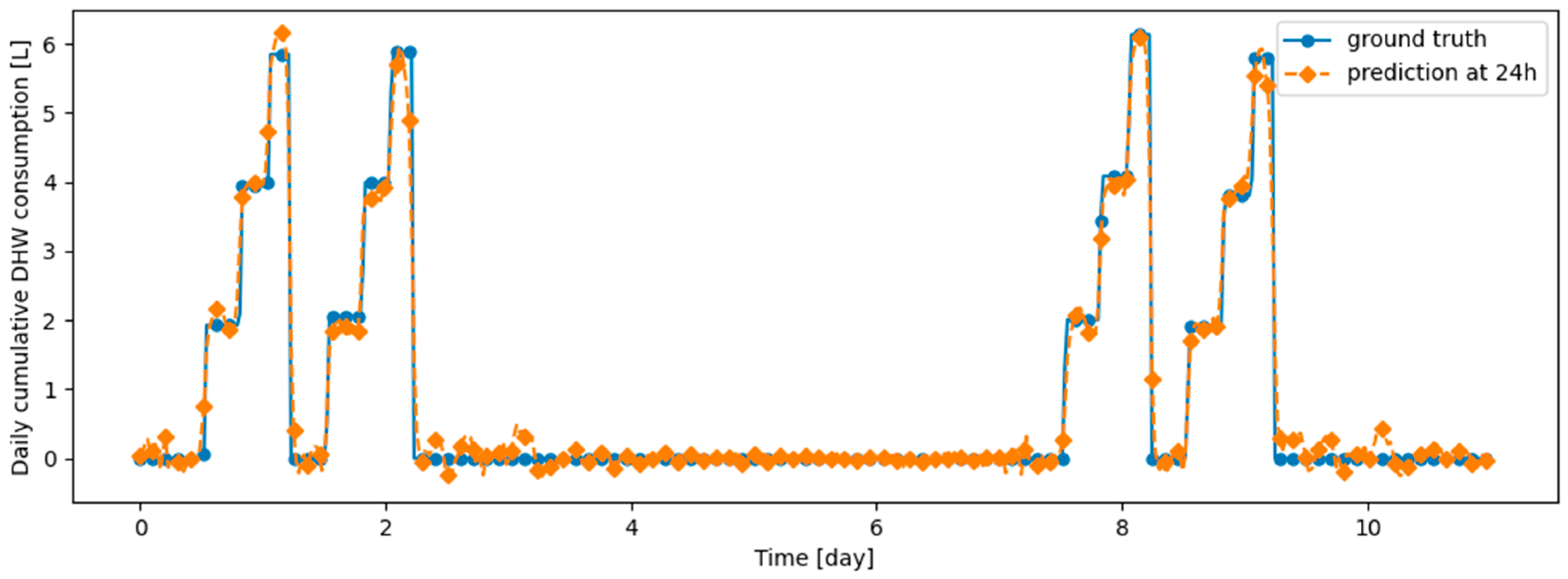
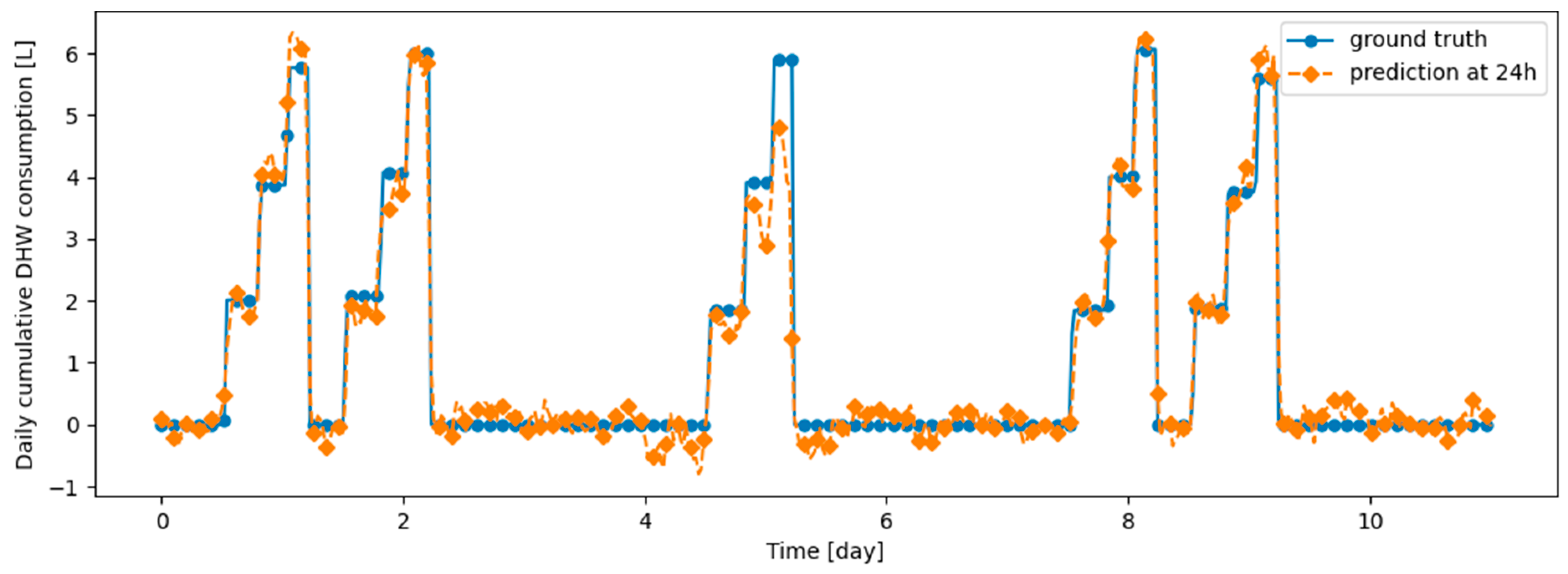
Figure 15.
Example of 24-h prediction versus ground truth for 11 days of d2_test, after training the model on d1_train.
Figure 15.
Example of 24-h prediction versus ground truth for 11 days of d2_test, after training the model on d1_train.
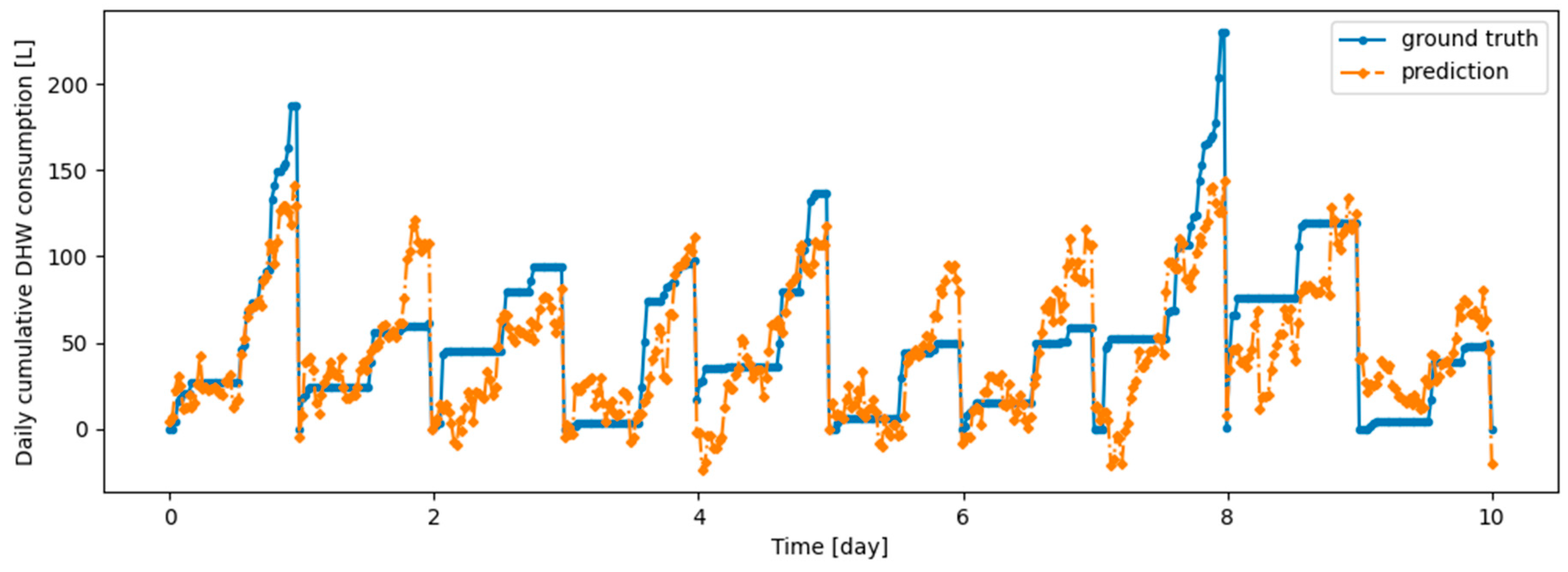
Figure 16.
Example of 24-h prediction versus ground truth for 11 days of d1_test, after first training the model on d1_train and then finetuning the model on d2_train, with no particular continual learning strategy.
Figure 16.
Example of 24-h prediction versus ground truth for 11 days of d1_test, after first training the model on d1_train and then finetuning the model on d2_train, with no particular continual learning strategy.
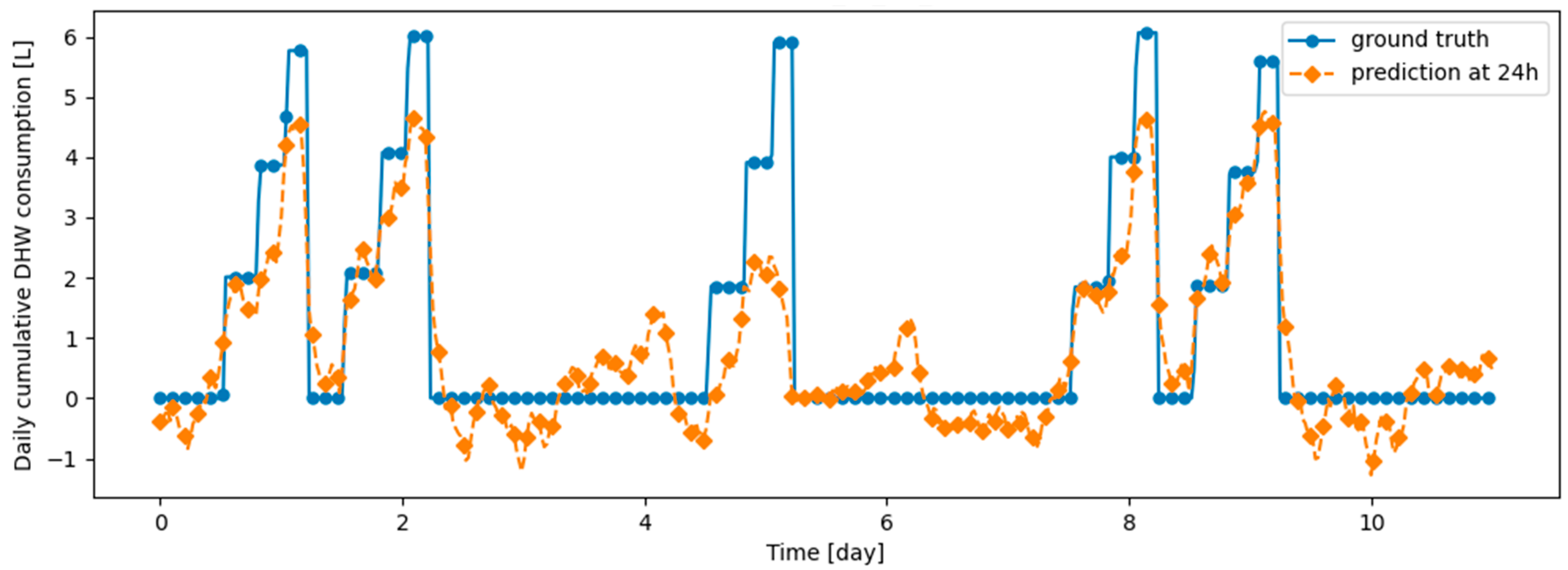
Figure 17.
Example of 24-h prediction versus ground truth for 11 days of d2_test, after first training the model on first d1_train and then finetuning the model on d2_train, with no particular continual learning strategy.
Figure 17.
Example of 24-h prediction versus ground truth for 11 days of d2_test, after first training the model on first d1_train and then finetuning the model on d2_train, with no particular continual learning strategy.
Figure 18.
Example of 24-h prediction versus ground truth for 11 days of d1_test, after training the model first on d1_train and then on d2_train using Dream Net.
Figure 18.
Example of 24-h prediction versus ground truth for 11 days of d1_test, after training the model first on d1_train and then on d2_train using Dream Net.
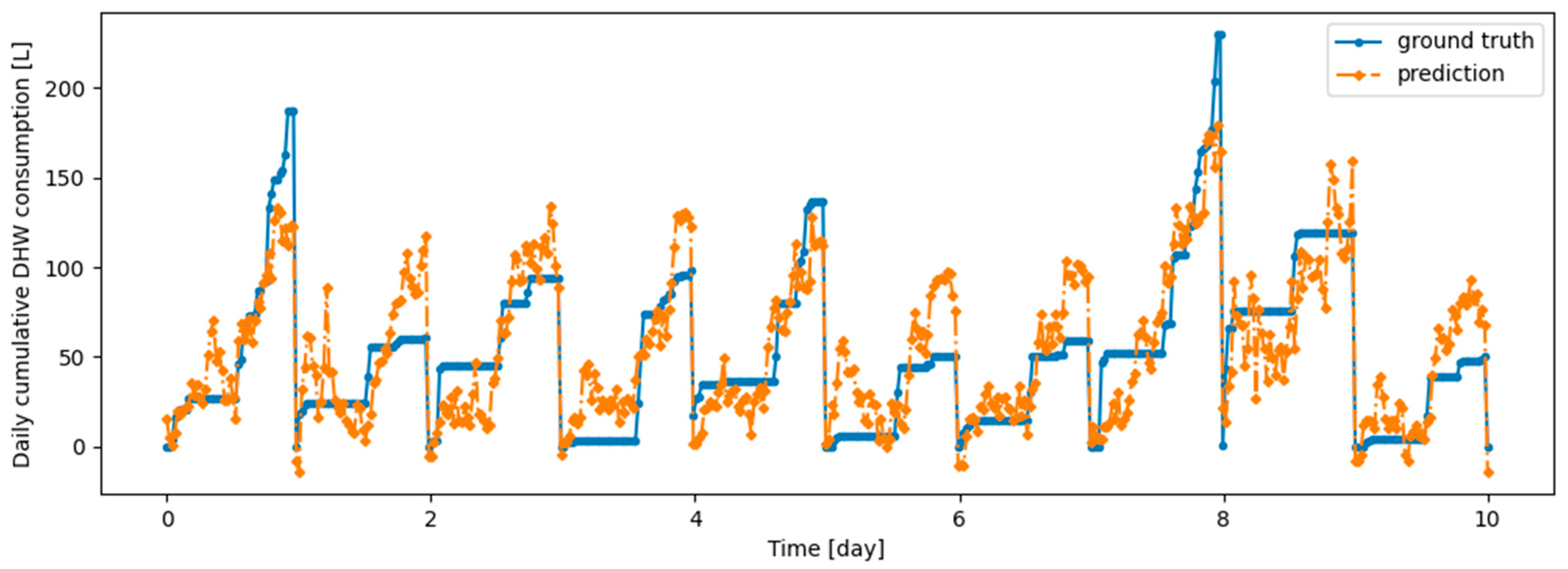
Figure 19.
Example of 24-h prediction versus ground truth for 11 days of d2_test, after training the model first on d1_train and then on d2_train using Dream Net.
Figure 19.
Example of 24-h prediction versus ground truth for 11 days of d2_test, after training the model first on d1_train and then on d2_train using Dream Net.
Table 1.
Parameters used for the j-th day of the week DHW consumption profile.
Table 1.
Parameters used for the j-th day of the week DHW consumption profile.
| Symbols | Names & Description |
|---|
| Number of DHW consumption of day j of the week () |
| Amplitude of the i-th consumption of the j-th day of the week () |
| Standard deviation of the noise for amplitude for the i-th consumption of the j-th day of the week |
| Random increment for amplitude of the i-th consumption of the j-th day of the week, |
| Slope of the i-th consumption of the j-th day of the week |
| Centre of the i-th consumption of the j-th day of the week |
| Standard deviation of the noise for centre for the i-th consumption of the j-th day of the week |
| Random increment for centres of the i-th consumption of the j-th day of the week, |
| Sigmoid function, |
| Time index |
Table 2.
Parameters used for constructing synthetic time series of type 1 and 2.
Table 2.
Parameters used for constructing synthetic time series of type 1 and 2.
| Parameters | of Week of Type 1 | of Week of Type 2 |
|---|
| 3 | 3 |
| 2 L, if
0 L, else | 2 L, if
0 L, else |
| 0.1 | 0.1 |
| | |
| 10 | 10 |
|
|
|
| 0.1 | 0.1 |
| | |
Table 3.
Hyperparameters tested in the grid search and optimal for the prediction model on the Dwelling A dataset.
Table 3.
Hyperparameters tested in the grid search and optimal for the prediction model on the Dwelling A dataset.
| Hyperparameters | Tested Value | Optimal Value from Grid Search |
|---|
| Key dimension | [1, 2, 4, 8] | 8 |
| Number of heads | [1, 2, 4, 8] | 4 |
| Penultimate_ratio | [1, 2, 4, 8] | 8 |
Table 4.
Hyperparameters tested in the grid search and optimal hyperparameters for the Dream Net algorithm on the Dwelling A dataset.
Table 4.
Hyperparameters tested in the grid search and optimal hyperparameters for the Dream Net algorithm on the Dwelling A dataset.
| Dream Net Hyperparameters | Tested Value | Optimal Value from Grid Search |
|---|
| Epochs | [30, 50, 70] | 70 |
| Reinjection number | [2, 5, 7] | 7 |
| Real example batch size | [32, 64, 128] | 32 |
| Pseudo example batch size | [128, 256, 512] | 128 |
Table 5.
Hyperparameters tested in the grid search and optimal hyperparameters for the DER/ER algorithms on the Dwelling A dataset.
Table 5.
Hyperparameters tested in the grid search and optimal hyperparameters for the DER/ER algorithms on the Dwelling A dataset.
| DER/ER Hyperparameters | Tested Value | Optimal Hyperparameters for ER | Optimal Hyperparameters for DER |
|---|
| Epochs | [30, 50, 70] | 70 | 70 |
| Buffer size | [500 | 500 | 500 |
| [0, 0.5, 1] | 0 | 0.5 |
| [0, 0.5, 1] | 0.5 | 0.5 |
| Batch size of current task examples | [50, 200] | 50 | 50 |
| Batch size of examples from the buffer | [50, 200] | 200 | 200 |
Table 6.
Mean and standard deviation over all months (over the 5 runs) for the DHW consumption of Dwelling A and Dwelling B. The MAE is averaged for the difference prediction horizons.
Table 6.
Mean and standard deviation over all months (over the 5 runs) for the DHW consumption of Dwelling A and Dwelling B. The MAE is averaged for the difference prediction horizons.
| Continual Learning Algorithm | Mean MAE on Dwelling A | MAE Standard Deviation on Dwelling A | Mean MAE on Dwelling B | MAE Standard Deviation on Dwelling B |
|---|
| Dream Net | 24.805 | 6.929 | 21.559 | 6.737 |
| DER | 25.084 | 7.744 | 21.457 | 7.328 |
| ER | 25.041 | 6.967 | 21.492 | 7.352 |
| Finetuning | 24.423 | 6.822 | 21.351 | 6.212 |
| Offline | 22.695 | 7.449 | 19.365 | 5.377 |
| First month training (MAE on second month excluded) | 35.513 | 7.546 | 35.950 | 5.736 |
| First three months training (MAE on second to fourth month excluded) | 26.376 | 9.249 | 29.458 | 6.617 |
Table 7.
Hyperparameters tested in the grid search and optimal hyperparameters for the Dream Net algorithm.
Table 7.
Hyperparameters tested in the grid search and optimal hyperparameters for the Dream Net algorithm.
| Dream Net Hyperparameters | Tested Value | Optimal Value from Grid Search |
|---|
| Epochs | [30, 50, 70] | 50 |
| Reinjection number | [2, 5, 7] | 7 |
| Real example batch size | [32, 64, 128] | 64 |
| Pseudo example batch size | [128, 256, 512] | 512 |
Table 8.
Hyperparameters tested in the grid search and optimal hyperparameters for the DER and ER algorithms.
Table 8.
Hyperparameters tested in the grid search and optimal hyperparameters for the DER and ER algorithms.
| DER/ER Hyperparameters | Tested Value | Optimal Hyperparameters for ER | Optimal Hyperparameters for DER |
|---|
| Epochs | [30, 50, 70] | 50 | 70 |
| Buffer size | [500] | 500 | 500 |
| [0, 0.5, 1] | 0 | 0.5 |
| [0, 0.5, 1] | 0.5 | 1 |
| Batch size of current task examples | [50, 200] | 200 | 200 |
| Batch size of examples from the buffer | [50, 200] | 200 | 200 |
Table 9.
MAE and associated standard deviation over 5 runs on synthetic validation data, after learning d1_train and updating the model with a continual learning algorithm or finetuning it on d2_train. The MAE and associated standard deviation on the joint learning setup, where d1_train and d2_train are learned simultaneously, are also shown.
Table 9.
MAE and associated standard deviation over 5 runs on synthetic validation data, after learning d1_train and updating the model with a continual learning algorithm or finetuning it on d2_train. The MAE and associated standard deviation on the joint learning setup, where d1_train and d2_train are learned simultaneously, are also shown.
| Learning Setup | MAE on d1_val | MAE on d1_val Standard Deviation | MAE on d2_val | MAE on d2_val Standard Deviation |
|---|
| d1_train only | 0.1517 | 0.007415 | 0.9064 | 0.01876 |
| Joint | 0.1595 | 0.0028 | 0.1785 | 0.0044 |
| Finetuning | 0.6796 | 0.0354 | 0.1344 | 0.0012 |
| Dream Net | 0.4266 | 0.0622 | 0.4578 | 0.0288 |
| DER | 0.1933 | 0.0052 | 0.2386 | 0.0039 |
| ER | 0.2483 | 0.0092 | 0.2411 | 0.0054 |
Table 10.
MAE and associated standard deviation over 5 runs on synthetic test data, after learning d1_train and updating the model with a continual learning algorithm or finetuning it on d2_train. The MAE and associated standard deviation on the joint learning setup, where d1_train and d2_train are learned simultaneously, are also shown.
Table 10.
MAE and associated standard deviation over 5 runs on synthetic test data, after learning d1_train and updating the model with a continual learning algorithm or finetuning it on d2_train. The MAE and associated standard deviation on the joint learning setup, where d1_train and d2_train are learned simultaneously, are also shown.
| Learning Setup | MAE on d1_Test | MAE on d1_Test Standard Deviation | MAE on d2_Test | MAE on d2_Test Standard Deviation |
|---|
| d1_train only | 0.1502 | 0.0064 | 0.9131 | 0.0482 |
| Joint | 0.1413 | 0.0044 | 0.1579 | 0.0062 |
| Finetuning | 0.6874 | 0.0102 | 0.1162 | 0.0037 |
| Dream Net | 0.4050 | 0.0323 | 0.4071 | 0.0258 |
| DER | 0.2117 | 0.0066 | 0.2299 | 0.0040 |
| ER | 0.2415 | 0.00188 | 0.2034 | 0.0054 |