Abstract
This article presents the evaluation of the performance of the distance relay (ANSI function 21) when integrating Distributed Energy Resources (DERs) in a Local Distribution System (LDS). The aim is to understand the impacts of and the necessary modifications required in the operation of distance relays, considering different levels of DER aggregation, and identifying any threshold levels before issues arise. To achieve this, first, a comprehensive review was carried out to analyze the impacts generated in the protection systems. Second, by using the DigSilent Power Factory software, the implementation of the distance relay using a IEEE 13 Node Test Feeder was validated. The aggregation of the three fundamental types of DG, synchronous machines, solar panels, and wind turbines, was evaluated. The threshold at which distributed generation power injection begins to compromise distance protection performance was identified. This study compares the outcomes of using mho and quadrilateral protection schemes.
1. Introduction
The change in social dynamics due to the emerging climate crisis has led to the adoption of another philosophy of societal development, one that is more in harmony with the concept of sustainable development and kindness to the natural environment. Since the generation of electric energy through conventional sources is one of the great contributors to the acceleration of climate change [1], the energy sector has found in innovation in non-conventional renewable energy sources an opportunity to make real change in social development, since the costs of incorporating devices that convert energy from renewable sources have decreased considerably, which has been reflected in renewable electricity accounting for 30% of the total electricity generated in 2022 [2]. Distributed energy resources—DERs—play an important role in obtaining energy in a clean way [3].
However, this has led to new challenges for system operators, since the incorporation of DERs proposes new dynamics and transients in the operation of power systems [4]. The traditional centralized system has shifted to a distributed system that has many variables, leading to multiple changes and impacts at both component and system levels.
Based on the experience of power system operators, it is clear that the large-scale integration of DERs in the LDS is affecting the operation of the ANSI 21 function in RST/NST networks, especially when there is a risk of reversal power flow from a lower voltage level to a higher one. Thus, it is necessary to determine the response of function 21 in the RST/NST to the integration of DERs, as well as to define the threshold according to the amount of DER installed in the LDS by which the response of function 21 in the RST/NST is impacted (considering the different types of DER).
The contributions of the proposed research work are the following:
- A comprehensive review of the main effects caused by the aggregation of DERs in the protection systems commonly used in local distribution systems.
- A comparison of relay operations under different operating configurations (quadrilateral and mho), with varying levels of aggregation of distributed generation technologies.
- An analysis of and introduction to the aggregation limits of DERs for each technology before disturbances occur in impedance estimation, zone displacement, or relay operation delays.
The rest of this article is organized as follows: Section 2 introduces the impact assessment for distributed generation aggregation in the protection of local distribution systems. Section 3 presents the advantages of distance relay implementation as the main protection in local distribution systems during the presence of reversal power flow. In Section 4, the simulation framework and distance relay configuration are explained. Section 5 presents the results and discussion, while Section 6 comprises the conclusions.
2. Impacts on the Protection Systems Due to the Integration of Distributed Generation in the LDS
One of the new challenges arising from the integration of distributed energy resources, particularly distributed generation, is the direction of power flow. It is evident that with the injection of dispersed and variable energy throughout the day, power flow can become multidirectional, as energy now flows from end users back to substations [5]. This represents a shift in protection performance, since traditional radial protection philosophies may operate inadequately, resulting in the unpredictable operation of existing protections and potentially leading to coordination loss.
Essentially, the integration of DERs introduces two fundamental issues in distribution systems. The first is increased short-circuit levels; in the event of a fault, the fault could be fed by both the power system and distributed generation. This could technically overwhelm breaker capacities, necessitating recalculations and the reallocation of protection device settings due to integrated distributed generation [6]. The second issue involves islanding operation scenarios in which part of the network remains energized after a breaker opens to clear a fault, which is sustained by distributed generation at that point. Such operations are considered undesirable due to technical reasons such as difficulty in controlling voltage and frequency, poor quality of energy supplied to the isolated system, safety concerns, challenges in reconnecting the isolated part of the network, and dealing with arc faults if distributed generation remains connected [7].
In response to all these situations, multiple solutions have been proposed. The implementation of directional protections is proposed in [8], which would require voltage transformers that are not installed at most points in distribution systems and adaptive protection systems. These systems automatically adjust relay settings when the system transitions between interconnected and isolated modes and vice versa. However, some issues have also been identified when implementing these new protection schemes:
- Prior to implementing these protection schemes, all possible operational configurations must be known in advance;
- Short-circuit levels can be challenging to calculate with different modes of operation in isolated systems;
- Updating currently used protection devices in distribution networks;
- The high costs associated with implementing communication systems.
In the integration of DERs into distribution systems, four types of distributed generators can be identified: synchronous generators directly connected to the grid, such as small hydro turbines or thermal generators with heat concentration systems; asynchronous generators directly connected to the grid, such as squirrel cage or wound rotor types; asynchronous generators with double-fed induction and a power converter in the rotor circuit, often used in rural contexts due to their lower equipment cost, and typically seen in small-scale hydro-generation-like run-of-river systems; and, finally, generators with electronic power converter interfaces, with or without a rotor, such as photovoltaic solar panels, battery systems like V2G [9], and fully controlled wind turbine generators [10,11]. These generators are classified based on their contribution to the fault current, in [12], as follows:
- Synchronous generators with independent excitation contribute fault currents between 500% and 1000% of their nominal current for the first cycles, reducing thereafter to between 200% and 400%;
- Asynchronous generators contribute fault currents between 500% and 1000% of their nominal current for the first few cycles, decreasing to negligible amounts within the next 10 cycles;
- Generators with inverter interfaces contribute fault currents between 100% and 400% of their nominal current, sometimes falling below 100% for certain inverters. However, [13] notes that the fault current contribution capability is typically less than 50% of the nominal current, except in cases in which inverters are specifically designed to provide much higher fault currents. Therefore, the fault current duration depends on the technologies and controller configurations.
According to the abovementioned information, it is worth mentioning how the integration of DERs impacts the various protections used in distribution systems, and emphasizing in particular how protection operations can fail.
In this regard, ref. [8] examines two protection functions alongside overcurrent protection, which is the prevailing protection in distribution systems. The first is differential protection, or function 87, which operates by comparing currents entering and leaving a specific protected zone. It is triggered when a significant difference in measured currents exceeds a predetermined threshold in the protection configuration. It is noted that one advantage of using differential protection is its insensitivity to bidirectional power flow and reductions in fault current, which contrasts with the operation mode of overcurrent protection. However, there is a possibility of communication system failure being integrated into differential protection, necessitating the inclusion of a secondary protection system compounded by the potential high cost of establishing communication systems. Furthermore, challenges arise from unbalanced loads, adding to the difficulties posed by transients during distributed generation connection.
Consideration is also given to schemes incorporating distance protection, typically used in transmission lines. Distance protection operates by calculating impedance (thereby being independent of current), offering an advantage over overcurrent relays. Distance relays are designed to operate only for faults occurring between the relay and the point of reach, triggering when the measured impedance falls below a set threshold. Additionally, errors may occur due to fault resistance in admittance measurement, which is particularly challenging in short distribution lines [8]. The subsequent section is dedicated entirely to the impacts on distance protection operation.
Regarding overcurrent relays, which are predominant in distribution systems, a particular review is introduced. The literature proposes that with the integration of distributed generation, as previously mentioned, the fault current is now supplied by both the distributed generator and the power system grid. However, the grid’s contribution diminishes with the increasing size of the distributed generator (or, in other words, reduction depends on the relative short-circuit impedance of the main source and the distributed generation, as well as the feeder impedance to the fault point).
Therefore, the overcurrent measured by function 51 would be smaller than the configured threshold for relay operation, causing the fault not to be cleared [13]. This type of misoperation is known as “blinding” [14]. Figure 1 illustrates the aforementioned points, where Isc Grid is the short circuit current given by the grid, which is now smaller than the previous DG aggregation and is surpassed in magnitude by the DG short-circuit contribution (Isc DG).
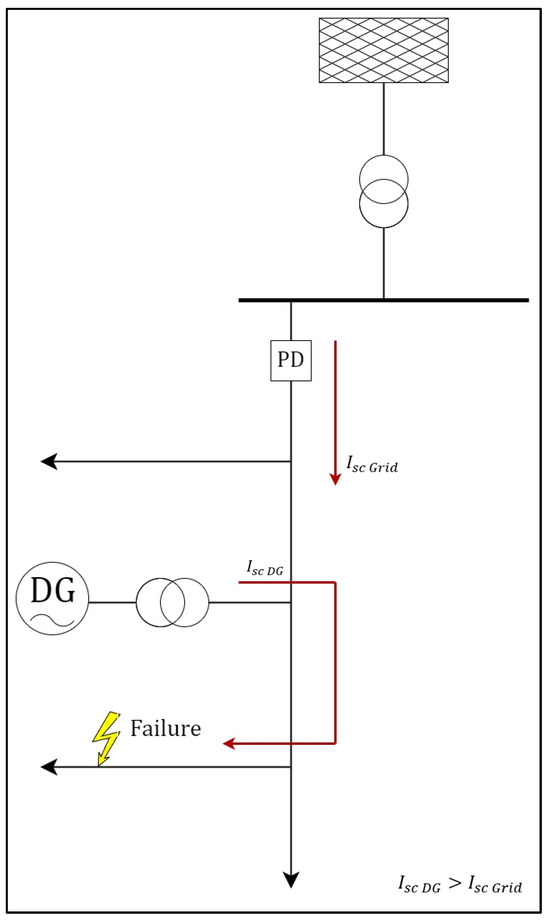
Figure 1.
Protection blinding due to distributed generation integration.
Another case of relay misoperation occurs when a fault happens upstream of the protective device, occurring in a feeder adjacent to where the distributed generation is located. In this scenario, the protective device of the unaffected feeder detects the high fault current provided by the distributed generation and trips, disconnecting the unaffected feeder from operation and thereby reducing the reliability of the distribution system. This occurs particularly with electromechanical relays that lack directional characteristics. This type of misoperation is known as false tripping [15]. Figure 2 illustrates this situation, where Isc DG is the short circuit current given by the DG to feed the fault on the adjacent feeder due to the novel multidirectional power flow capability.
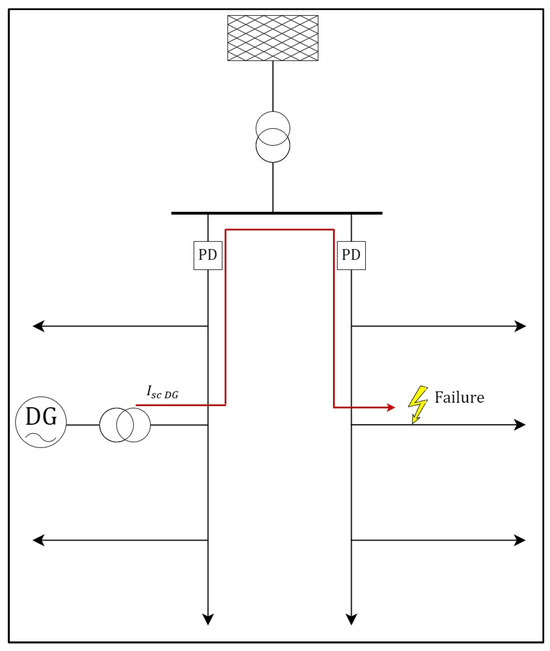
Figure 2.
False tripping of the protection due to the integration of distributed generation.
On the other hand, integrating distributed generation at an intermediate point would result in continuing to feed a fault current, potentially leading to coordination loss between the recloser–fuse and the fuse for transient faults. Typically, in the event of a fault, the recloser operates first to clear the fault temporarily and then attempts to close again if the fault is temporary. If the fault is permanent, the recloser remains closed using its time-delay curve, and it is the fuse’s responsibility to completely clear the fault. This protection scheme can potentially fail with the integration of distributed generation, since, for example, during a transient fault, the constant contribution of the short-circuit current from the distributed generation added between the recloser and the fuse can directly cause the fuse to blow. Figure 3 illustrates this situation.
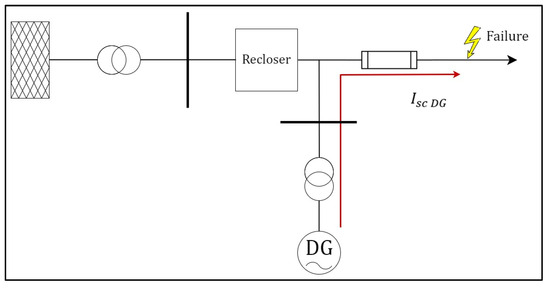
Figure 3.
Blowing of the fuse due to transient faults caused by constant short-circuit current contribution from DG.
Therefore, it is proposed that distributed generation be disconnected promptly to prevent it from continuing to feed the fault, thereby avoiding the improper operation of the network protection system; however, the speed at which distributed generation disconnects from the grid during a fault also impacts the distribution system, because disconnecting either too quickly or too slowly can be dangerous [5]. Nevertheless, this practice is not desirable as it leads to unnecessary blackouts, making distributed generation deliver energy unreliably. Additionally, due to the increased contribution of distributed generation to grid resilience, indiscriminate disconnection is neither desirable nor acceptable in a competitive and regulated energy market. However, in [12], the authors propose that, in the event of a distribution system fault, isolating or fracturing the network can be beneficial, provided there is sufficient distributed generation capacity to supply that zone. This is because loads can be supplied by these generators without waiting for the distribution system fault to be repaired, that is only reconnection is required to restore service. The authors indicate that this approach would certainly increase the reliability of the fractured area, since there would be no outages, and there would also be no loss of fault-free distributed generation, which would continue to supply power.
3. Benefits of Implementing Distance Relay in Distribution Systems
In the previous section, the weaknesses of protections in distribution systems were detailed. These are primarily composed of reclosers, fuses, and overcurrent relays, with the integration of DERs and, in particular, DG posing significant challenges. These issues represent decreases in the safety and reliability of the distribution system, becoming limitations on its expansion and modernization with the addition of new technologies. Therefore, in response to these challenges, many authors propose the implementation of the distance relay as a new philosophy for protection systems, as it offers greater technical and economic benefits compared to other ANSI function implementations, as an alternative solution to the new challenges and demands in the SDL [16].
In this sense, the benefits of the distance relay include increased sensitivity, selectivity, and precision, as well as its operational characteristic [17]. Additionally, the operational principle of the distance relay based on impedance estimation makes it immune to changes in network topology. As mentioned in [18], for example, variations in the current source located behind the relay naturally cause changes in short-circuit current contributions at any feeder location; however, the impedance remains constant, since the voltage–current relationship also remains constant. This inherent aspect of the distance relay ensures its operation remains undisturbed. It can be ensured that implementing the distance relay in distribution systems with added GD enhances their operation and protection [19,20].
To illustrate this point, many integrations involve electronic converter interfaces (mainly photovoltaic panels and wind turbines), which are characterized by their significantly low contribution to short-circuit currents. As shown in the previous section, this reduction poses a serious problem for fault clearance in systems with conventional protections like fuses, reclosers or the ANSI 51 function.
Therefore, using the distance relay becomes an interesting option for networks with low or negligible short-circuit levels. For instance, in Smart Grids capable of islanding, it is known that their short-circuit levels are considerably reduced, affecting the operation of conventional protections. A solution to this is implementing distance protection, which is virtually independent of impedance source variations. That is, in the face of reduced short-circuit current levels, distance protection ensures effective operations by relying solely on network impedance estimation [21].
Lastly, in consideration of all the aforementioned points, it is worth asking how and where to place distance protection in distribution systems. As synthesized in [19], a straightforward approach to implementing distance protection in overhead distribution lines is replacing the recloser with a distance relay at the feeder’s start. Additionally, [22] proposes that the ANSI 27 function can be replaced by an ANSI 21 function, provided that certain considerations are made regarding compensations for resistance in faults, which will be discussed later.
4. Simulation Results and Validation
To carry out the simulation and performance evaluation of the distance relay concerning the integration of distributed energy resources, particularly distributed generation, the IEEE 13 node test feeder in the DigSilent Power Factory 2023 software libraries was used [23]. Specifically, the “Study Distributed Generation 2018”, which includes distributed generation units from renewable energy resources, was directly modeled and incorporated.
It is important to note that certain changes were necessary in the system structure, such as replacing the autotransformers with a three-phase transformer of the same power rating. Figure 4 depicts the system used and the changes made to it.
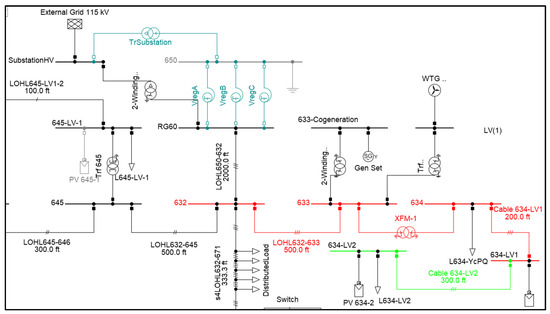
Figure 4.
IEEE 13 node test feeder study case with distributed generation.
Generally, the distance relay is typically characterized as either mho or quadrilateral [24]. However, the quadrilateral characteristic is preferred over mho due to its advantages, particularly in terms of its flexibility in covering faults with ground resistance [19], allowing adaptive boundary configurations to ensure proper operation under such conditions [24]. The relay operates by assigning zones determined as percentages of impedance, considering factors such as power factor, fault resistance, and changes in distance configuration [17].
To show these features and advantages, the same distance relay was performed with both mho and quadrilateral characteristics. In the simulation scenario, three relays were installed (referred to as relay G, J, and K, respectively) for the analysis of these characteristics to understand the impacts generated by the location and type of distributed generator. All were configured with current transformers at a ratio of 120:1 and voltage transformers at a ratio of 20,000:110. The configuration parameters for the distance relay with the mho characteristic are presented in Table 1 and Figure 5a,b.

Table 1.
Distance relay configuration parameters with hmo characteristic.
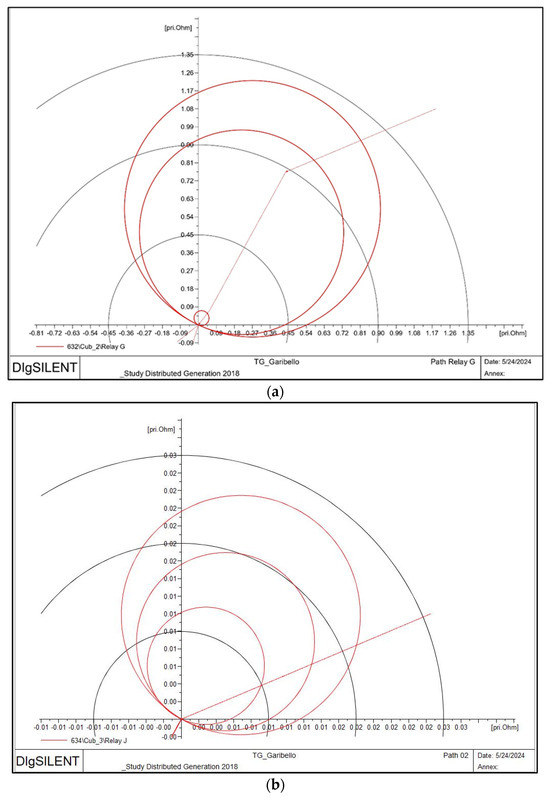
Figure 5.
(a) mho characteristic for relay G; (b) mho characteristic for relay J.
Following the recommendations in the literature, for Zone 1 instantaneous protection, a reach of 80% of the line impedance was configured. Zone 2 was set with a reach of 100% of the main line plus 20% of the adjacent line, with an operating time of 0.3 s. Zone 3 was configured with a reach of 100% of the main line plus 50% of the adjacent line [25,26]. Load encroachment limiters, known as Load Encroachment, were not considered in any of the characteristics, as this assumption is made when the load is balanced, which is not the case in this distribution system. This could pose a problem for three-phase faults with significant ground resistance, but this was not addressed in this study [19,27]. Reach margins were maintained to mitigate errors induced by voltage and current transformers, as well as impedance measurement [28].
The quadrilateral characteristic was implemented in the system version simulating voltage levels of 57.5 kV and 0.48 kV. The configured reaches were like those established with the mho characteristic. Although it is known that the quadrilateral characteristic offers flexibility to extend protection reaches in the presence of ground resistance during faults, for instance, in [19], the resistive reach was configured at four times the reactive reach. However, in this case, the overestimation of the resistive reach was omitted, as faults with ground resistance, which only increase impedance along the resistive axis, were not considered. Relay K was omitted, since the results obtained with the mho characteristic showed no significant changes compared to the system operation without DG integration. This will be detailed in the results and analysis section. The configuration parameters for the distance relay with the quadrilateral characteristic are presented in Table 2 and Figure 6a,b.

Table 2.
Distance relay configuration parameters with quadrilateral characteristic.
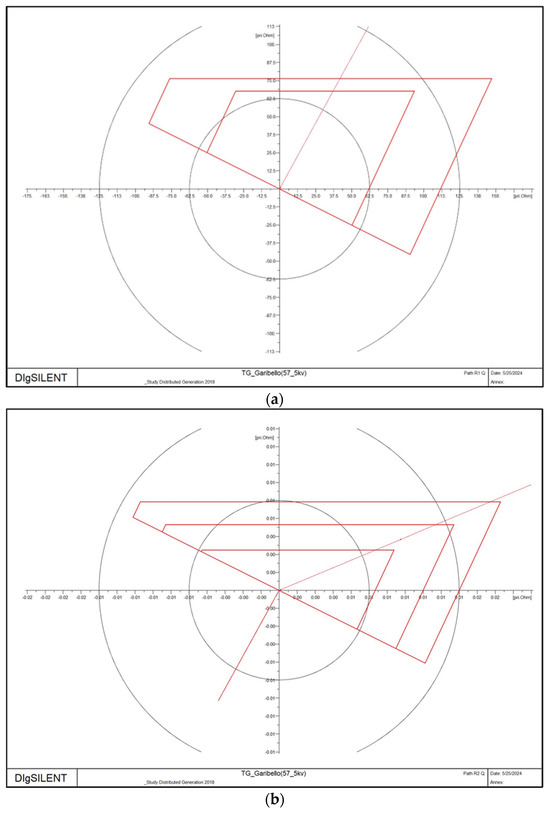
Figure 6.
(a) Quadrilateral characteristic for relay G; (b) quadrilateral characteristic for relay J.
From the experience of modeling the distance relay in the distribution system, it is worth highlighting the encountered issues to illustrate the reasons why the relay operation can naturally fail.
The first and most impactful, as also found in the literature, is low impedance values. These necessitate that the relay has a resolution in the impedance estimation for zone setting, which it sometimes lacks. Trying to configure it in the relay parameters can lead to phase–phase or phase–ground detection issues. As noted in [29], short lines can generate overreach errors in impedance estimation due to the low X/R ratio, ultimately affecting the fault current magnitude.
In [17], the authors specify that single line-to-ground faults (SLGs) can cause significant ground fault currents, leading the distance relay to trip rapidly, impacting system stability before voltage and/or frequency protections operate. Additionally, an interesting result is how the connection of transformers, typically with a Delta-Y configuration, causes SLG faults to be seen as line-to-line faults, thereby affecting relay operation reliability.
Lastly, this study confirmed according to [21] that when a relay is installed at a certain location with a short-circuit current source disconnected, during fault occurrence, the relay will not detect the fault because no current flows through it, resulting in blind operation and a loss of reliability and selectivity due to non-operation.
5. Simulation Case Studies and Discussion
To assess the impacts of integrating DERs into the SDL, particularly distributed generation, various tests were conducted using the three most commonly found types of distributed generators: synchronous generators, wind turbines, and photovoltaic solar panels. These tests varied the installed power, fault location, and fault type, as well as their impact on the relay. Additionally, the performance of all the generators was evaluated using both mho and quadrilateral characteristics.
5.1. Test with Synchronus Generator
For the case of the synchronous generator (SG) operating with an integrated distance relay using mho characteristics, tests were conducted by varying its power from a threshold value (which differed for three-phase and single-phase faults) up to a maximum value that did not exceed the DER definition limit of 10 MW installed [30,31]. The methodology involved initially measuring the fault impedances in the system section evaluated without DG integration, followed by repeating the faults with different installed power values. The results obtained were then used to calculate the error propagation relative to the installed power. The transformer connection was maintained as Dy7 for all the cases.
From the results obtained in the simulation and presented Figure 7a,b, it was observed that delays in trip times (and, consequently, displacement in protection zones) occurred primarily for zones 2 and 3. This was evident with errors exceeding 0.86% for the quadrilateral characteristic and 0.49% for the mho characteristic.
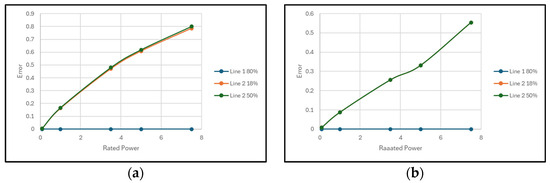
Figure 7.
(a) Error propagation in impedance measurement with integration of SG in relay with mho characteristic; (b) error propagation in impedance measurement with integration of SG in relay with quadrilateral characteristic.
5.2. Test with Solar PV Generator
For the testing of the photovoltaic solar panel, the same methodology as was employed with the synchronous generator was followed; however, in this case, increases in the installed power were achieved not by directly changing the number of panels or their peak power, but rather by altering the number of inverters in parallel. These modifications resulted in changes in the current and power supplied by the solar farm, impacting both load-flow and short-circuit analyses. It is worth mentioning that in the load flow with seven inverters, the generated power overloaded the distribution line, creating an interesting scenario for analysis.
In the case of the solar photovoltaic generators, zone displacements were observed only for zone 3 in both the quadrilateral and mho characteristic relays, with error percentages exceeding 5.26%. Figure 8a,b shows the findings described above.
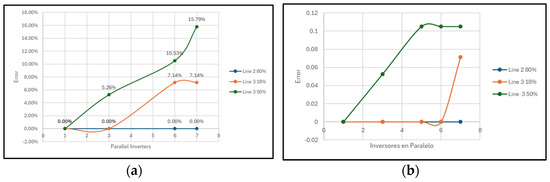
Figure 8.
(a) Error propagation in impedance measurement with integration of solar PV generator in relay with quadrilateral characteristic; (b) error propagation in impedance measurement with integration of solar PV generator in relay with mho characteristic.
5.3. Test with Wind Turbine
Similarly to what occurred with the PV systems, the contributions of the wind turbines varied as long as the number of turbines connected in parallel was changed. Similarly, the installed power was adjusted so as not to exceed the DER definition. For the wind turbines, it was observed that the error propagation behaved more linearly, resulting in zone displacements for error values exceeding 4.55% and 9.11% in the relays with quadrilateral and mho characteristics, respectively. Figure 9a,b shows the findings described above.
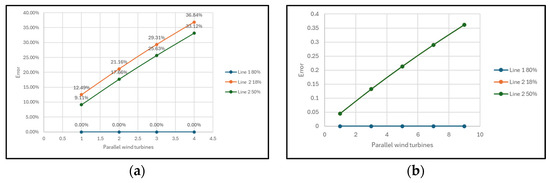
Figure 9.
(a) Error propagation in impedance measurement with integration of wind turbines in relay with mho characteristic; (b) error propagation in impedance measurement with integration of wind turbines in relay with quadrilateral characteristic.
5.4. Results Discussion
It should be highlighted that in each case presented, a reduction in the short-circuit current contribution from the grid was observed, with the distributed generator’s contribution being predominant. This result is corroborated by the findings in [18]. Considering that the distance relay was primarily located at the beginning of the line, it is interesting to describe the impacts this would have on impedance measurement and estimation, as well as the relay’s response during operation. According to [32], in the presence of distributed generation, impedance estimation tends to be lower, differing from the actual values, which can lead to improper relay operation, since these impedance values are now closer to operational thresholds.
Therefore, the challenge lies in the fact that the integration of DG promotes a reduction in the operational reach of the distance relay for fault clearing, primarily causing an inability to detect faults with the configurations defined prior to DG integration. This occurs because, as explained in [33], in the event of a fault downstream from the bus where DG is connected, the relay located upstream will measure a lower impedance than the actual fault impedance, disrupting the relay’s zone settings. This could result in trips in smaller zones leading to more line disconnections or, conversely, delays, or even failure to operate [34,35].
This phenomenon was particularly evident for zones 2 and 3 of the relay, regardless of their operational characteristic. As expected, and as mentioned above, there was a reduction and zone displacement, respectively, from zone 2 to zone 3, and non-operation due to faults located in zone 3. On the other hand, zone 1 was not affected in any of the cases because, during the faults in this zone, the short-circuit current levels (and, therefore, the voltage–current relationship) were not altered by contributions from distributed generation. However, when changing the location of the DG, for instance, to the bus where the distance relay was located, there were also no impacts on the operation of zone 1 despite the increase in short-circuit current, as the voltage–current relationship remained constant (see Figure 10).
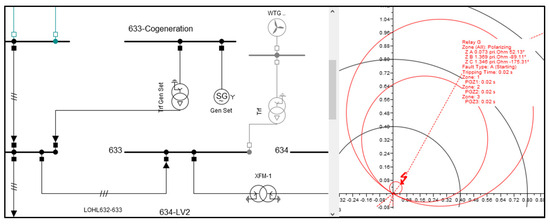
Figure 10.
Invariant zone 1 due to DG aggregation on the relay bar.
The mentioned effects are observable for both three-phase and single-phase faults with or without earth resistance [36]. In addition to this, interesting findings are reported in [29], where it was discovered that changes in impedance measured by the distance relay can also be attributed to the transformer connection, typically of the Yd type. This causes faults of the SLG type to be perceived by the relay as line-to-line faults, emphasizing the need for phase angle compensation due to the transformer connection to mitigate this impact.
Nevertheless, regardless of the transformer connection type used for DG integration, all effects are known as the “infeed effect” [22,29,33,34]. Figure 11 illustrates this effect.
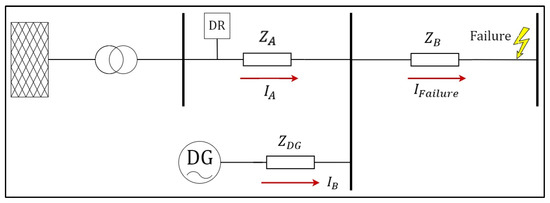
Figure 11.
Infeed effect.
The Infeed effect is described by equation (1), which helps to recognize the reason for the increase in impedance estimated by the relay upon DG integration, regardless of whether the fault is earthed. It has been noted that these faults also cause a reduction in reach in all relays [34]. The identification of this factor in the increase in the estimated impedance explains the increased measurement errors, as increasing the installed power of distributed generation increases the ratio, thereby increasing the impedance of the faulted line.
Another effect, called Outfeed, is caused by increased load, as in the aggregation of higher distributed demand seen in electric vehicles. The Outfeed effect results in an opposite effect, causing overreach, which translates to a displacement towards the source in the protection zones due to reduced estimated impedance. Regarding the simulations conducted in this study, a scenario was proposed in which the power delivered by distributed generation was significantly large (up to 10 generators of 10 MVA in parallel), and no similar impacts were observed compared to changes in demanded power. However, it was observed that other elements of the distribution system (transformer, line) were overloaded first, before any reduction in impedance measured by the relay occurred. Figure 12 illustrates these points.
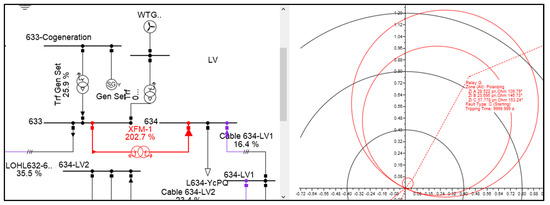
Figure 12.
Absence of alterations in the operation of the DR with load increased.
It is worth comparing the relay operation’s performance when configured with mho or quadrilateral characteristics. It is particularly notable that for all the added technologies, the impacts on the error propagation and operational zones were evidently smaller with a quadrilateral configuration. This was observed in the error propagation in the impedance magnitude estimation for the synchronous generator, in which, the quadrilateral characteristic, the error gap between the operational zones was practically negligible, representing lesser impacts on relay performance. This also applied to the wind turbine and photovoltaic panel.
Another advantage is evident in the thresholds for distributed generation aggregation. For instance, for solar aggregations, it was found that with the mho characteristic, impacts were observed directly from one parallel inverter, compared to the quadrilateral characteristic, in which, with the same number of solar panels, peak power, and short-circuit current, the threshold increased to two parallel inverters. Table 3 summarizes the integration thresholds according to the technology added in percentages of bus power without GD aggregation.

Table 3.
Thresholds of distributed generation aggregation before affecting the operation of the distance relay.
6. Conclusions
This work introduces the effects of integrating DERs into protection systems in distribution networks, initially by analyzing the implications for overcurrent relays, reclosers, and fuses, as these are primarily used. It can be said that it is essential to review installed capacity and aggregation locations to mitigate the impacts generated without needing major modifications to protection settings.
The simulation results indicate a direct impact of DER technology and quantity on distance relay operation, the identification of aggregation thresholds and the impacts of aggregator location and fault distance, resulting primarily in zone displacement in impedance estimation, leading to operation delays, affecting reliability and security parameters [36].
The Infeed and Outfeed effects and the implications of power oscillations were the main identified impacts. However, it is recognized that for the Outfeed effect due to load increase, other distribution system parameters, such as transformer or line overloads, must first be considered. The Infeed effect was identified as the primary impact caused by the GD aggregation, leading to the most significant complications in relay operation.
The use of different distance relay characteristic types can help mitigate the impacts of DER aggregation, with the quadrilateral characteristic being the most strongly recommended for implementing function 21 in distribution systems, allowing higher levels of aggregation and reducing over- and under-reach effects.
The use of the distance relay as the main protection in distribution lines is highly reliable and secure, owing to its excellent performance in instantaneous operation zones with DER aggregation. Unfortunately, the same cannot be guaranteed when it is used as backup protection due to the observed impacts on detecting and clearing faults in zones 2 and 3.
Author Contributions
Conceptualization, investigation, writing—original draft preparation, and methodology, D.R.G.-N. and E.G.-L.; Validation, formal analysis, writing—review & editing, E.G.-L. and J.C.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| DER | Distributed energy resources |
| DG | Distributed generation |
| DR | Distance relay |
| LDS | Local distribution system |
| NTS | National transmission system |
| PD | Protection device |
| PV | Solar photovoltaic panel |
| QUAD | Quadrilateral characteristic |
| RTS | Regional transmission system |
| SG | Synchronous generator |
| WT | Wind turbine |
| Z1 | Protection zone 1 |
| Z2 | Protection zone 2 |
| Z3 | Protection zone 3 |
| Symbols | |
| ° | Degree |
| Ω | Ohm |
References
- Muhammad, B.; Khan, S. Understanding the relationship between natural resources, renewable energy consumption, economic factors, globalization and CO2 emissions in developed and developing countries. In Natural Resources Forum; Wiley: Hoboken, NJ, USA, 2021; Volume 45, pp. 138–156. [Google Scholar] [CrossRef]
- REN21. REN21—Building the Sustainable Energy Future with Renewable Energy. Available online: https://www.ren21.net/ (accessed on 31 August 2024).
- International Energy Agency. Unlocking the Potential of Distributed Energy Resources Power System Opportunities and Best Practices. Available online: https://www.iea.org/reports/unlocking-the-potential-of-distributed-energy-resources (accessed on 21 February 2023).
- De La Cruz, J.; Gómez-Luna, E.; Ali, M.; Guerrero, J.M. Fault Location for Distribution Smart Grids: Literature Overview, Challenges, Solutions, and Future Trends. Energies 2023, 16, 2280. [Google Scholar] [CrossRef]
- Ndahepele, L.; Chowdhury, S. Impact of Distributed Generation on Traditional Protection in Distribution and Transmission Systems: A Review. In Proceedings of the 2020 IEEE PES/IAS PowerAfrica, Nairobi, Kenya, 25–28 August 2020; IEEE: New York, NY, USA, 2020; Volume 4, pp. 1–5. [Google Scholar] [CrossRef]
- Gómez-Luna, E.; De La Cruz, J.; Vasquez, J.C. New Approach for Validation of a Directional Overcurrent Protection Scheme in a Ring Distribution Network with Integration of Distributed Energy Resources Using Digital Twins. Energies 2024, 17, 1677. [Google Scholar] [CrossRef]
- Manditereza, P.T.; Bansal, R. Renewable distributed generation: The hidden challenges—A review from the protection perspective. Renew. Sustain. Energy Rev. 2016, 58, 1457–1465. [Google Scholar] [CrossRef]
- Mirsaeidi, S.; Said, D.M.; Mustafa, M.W.; Habibuddin, M.H.; Ghaffari, K. Progress and problems in micro-grid protection schemes. Renew. Sustain. Energy Rev. 2014, 37, 834–839. [Google Scholar] [CrossRef]
- Cummins Inc. Types of Distributed Energy Resources. Available online: https://onx.la/7656f (accessed on 24 June 2023).
- Mahadanaarachchi, V.P.; Ramakuma, R. Impact of distributed generation on distance protection performance—A review. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; IEEE: New York, NY, USA, 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Bloomberg. La Energía Solar y Eólica Alcanzó el 67% de la Capacidad Nueva de Energía Eléctrica Agregada a Nivel Mundial en 2019. Available online: https://onx.la/8842d (accessed on 24 June 2023).
- Chaitusaney, S.; Yokoyama, A. Reliability Analysis of Distribution System with Distributed Generation Considering Loss of Protection Coordination. In Proceedings of the 2006 International Conference on Probabilistic Methods Applied to Power Systems, Stockholm, Sweden, 11–15 June 2006; IEEE: New York, NY, USA, 2006; pp. 1–8. [Google Scholar] [CrossRef]
- Gómez-Luna, E.; Candelo-Becerra, J.E.; Vasquez, J.C. A New Digital Twins-Based Overcurrent Protection Scheme for Distributed Energy Resources Integrated Distribution Networks. Energies 2023, 16, 5545. [Google Scholar] [CrossRef]
- Escobar-Orozco, L.F.; Gómez-Luna, E.; Marlés-Sáenz, E. Identification and Analysis of Technical Impacts in the Electric Power System Due to the Integration of Microgrids. Energies 2023, 16, 6412. [Google Scholar] [CrossRef]
- Pan, Y.; Voloh, I.; Ren, W. Protection issues and solutions for protecting feeder with distributed generation. In Proceedings of the 2013 66th Annual Conference for Protective Relay Engineers, College Station, TX, USA, 8–11 April 2013; pp. 92–111. [Google Scholar] [CrossRef]
- Enel X S.r.l. ¿Cómo Funciona la Respuesta a la Demanda y por Qué es Importante? Available online: https://onx.la/306e6 (accessed on 24 June 2023).
- Velasco-Gomez, S.; Perez-Londono, S.; Mora-Florez, J. Application of Distance Protection on Active Distribution Networks: A Quantitative Comparison. In Proceedings of the 2022 IEEE ANDESCON: Technology and Innovation for Andean Industry, ANDESCON 2022, Barranquilla, Colombia, 16–19 November 2022; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Sinclair, A.; Finney, D.; Martin, D.; Sharma, P. Distance protection in distribution systems: How it assists with integrating distributed resources. IEEE Trans. Ind. Appl. 2014, 50, 2186–2196. [Google Scholar] [CrossRef]
- Nikolaidis, V.C.; Arsenopoulos, C.; Safigianni, A.S.; Vournas, C.D. A distance based protection scheme for distribution systems with distributed generators. In Proceedings of the 19th Power Systems Computation Conference, PSCC 2016, Genoa, Italy, 20–24 June 2016; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Lin, H.; Liu, C.; Guerrero, J.M.; Vasquez, J.C. Distance protection for microgrids in distribution system. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; IEEE: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Voima, S.; Kauhaniemi, K. Using distance protection in smart grid environment. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Europe, Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Pandakov, K.; Høidalen, H.K.; Marvik, J.I. Implementation of Distance Relaying in Distribution Network with Distributed Generation. In Proceedings of the 13th International Conference on Development in Power System Protection 2016 (DPSP), Edinburgh, UK, 7–10 March 2016; Institution of Engineering and Technology: London, UK, 2016. [Google Scholar] [CrossRef]
- Powerfactory, D. IEEE 13 Node Test Feeder. Available online: www.digsilent.de (accessed on 31 August 2024).
- Shadaei, M.; Jarrahi, M.A.; Bagheri, A.A.; Samet, H. A comprehensive investigation on performance of distance relays in transmission lines connected to wind farms. In Proceedings of the 2020 15th International Conference on Protection and Automation of Power Systems, IPAPS 2020, Shiraz, Iran, 30–31 December 2020; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Gers, J.; Holmes, E. Protection of Electricity Distribution Networks, 4th ed.; The Institution of Ingeneering and Technology: London, UK, 2021. [Google Scholar]
- Baluja, O.P.; Breffe, O.E.T.; Padrón, L. La protección de distancia y las condiciones de prefalla. In Revista de Ingeniería Energética; Universidad Tecnológica de La Habana: La Habana, Cuba, 2019; Volume 40, pp. 103–111. Available online: http://rie.cujae.edu.cu/index.php/RIE (accessed on 7 August 2023).
- Martin, D.; Sharma, P.; Sinclair, A.; Finney, D. Distance protection in distribution systems: How it assists with integrating distributed resources. In Proceedings of the 2012 65th Annual Conference for Protective Relay Engineers, College Station, TX, USA, 2–5 April 2012; IEEE: New York, NY, USA, 2012; pp. 166–177. [Google Scholar] [CrossRef]
- Yusoff, N.; Abidin, A.F.; Mahadan, M.E. The impact of Power Swing to the operation of Distance Relay. In Proceedings of the 2015 5th IEEE International Conference on System Engineering and Technology (ICSET), Shah Alam, Malaysia, 10–11 August 2015. [Google Scholar]
- Gómez, S.M.V.; Londoño, S.M.P.; Flórez, J.J.M. A Qualitative Comparison of Distance-Based Protection Approaches for Active Distribution Networks. Rev. Tecnura 2021, 25, 146–165. [Google Scholar] [CrossRef]
- Comisión de Regulación de Energía Y Gas. Concepto CREG 52808 de 2005. Available online: https://gestornormativo.creg.gov.co/gestor/entorno/docs/concepto_creg_0052808_2005.htm (accessed on 23 May 2024).
- Cummins Inc. What Are Distributed Energy Resources and How Do They Work? Available online: https://onx.la/34fd0 (accessed on 24 June 2023).
- Campos, J.T.L.S.; Sanca, H.S.; Costa, F.B.; De Souza, B.A. Distance Protection Analysis Applied for Distribution System with Distributed Generation. Prz. Elektrotechniczny 2018, 94, 13–17. [Google Scholar] [CrossRef]
- Sahbeni, N.; Meddeb, A.; Amor, N.; Chebbi, S. Distance Protection Behavior during Integration of Distributed Generation: Case Study Tunisian Transmission Network. In Proceedings of the 2019 International Conference on Advanced Systems and Emergent Technologies (IC_ASET), Hammamet, Tunisia, 19–22 March 2019; IEEE: New York, NY, USA, 2019; Volume 77, pp. 144–147. [Google Scholar] [CrossRef]
- Adrianti, A.; Firdaus, S.M.; Nasir, M. The Effect of Wind Power Generation on Distance Relay Performance. Andalas J. Electr. Electron. Eng. Technol. 2022, 2, 1–6. [Google Scholar] [CrossRef]
- Adrianti, A.; Sijabat, A.R.; Nasir, M. Analyzing Performance of Distance Relay in Protecting Distribution Lines with Distributed Generation. In Proceedings of the 2019 International Conference on Electrical Engineering and Computer Science (ICECOS), Batam, Indonesia, 2–3 October 2019; IEEE: New York, NY, USA, 2019; pp. 283–286. [Google Scholar] [CrossRef]
- George, N.; Naidu, O.D. Distance protection issues with renewable power generators and possible solutions. In Proceedings of the 16th International Conference on Developments in Power System Protection (DPSP 2022), Newcastle, UK, 7–10 March 2022; Institution of Engineering and Technology: New York, NY, USA, 2022; pp. 373–378. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).