Short-Term Forecast of Photovoltaic Solar Energy Production Using LSTM
Abstract
1. Introduction
- The prediction of photovoltaic solar energy over a 60-min horizon (with data collected every 1 min) using only meteorological variables;
- The construction of a model with a simple architecture utilizing LSTM layers and fully connected layers (DENSE);
- The evaluation of the prediction accuracy of the model for various values of model hyperparameters and different input variables;
- The training, validation, and testing of the model for various seasons of the year and a comparison of the results using performance indicators, namely mean absolute errors (MAEs), RMSE, and the coefficient of determination ();
- A comparison of the model’s accuracy with other simple architectures (BiLSTM, gated recurrent units (GRUs), and an RNN) and hybrid architectures (CNN + LSTM).
2. State of the Art
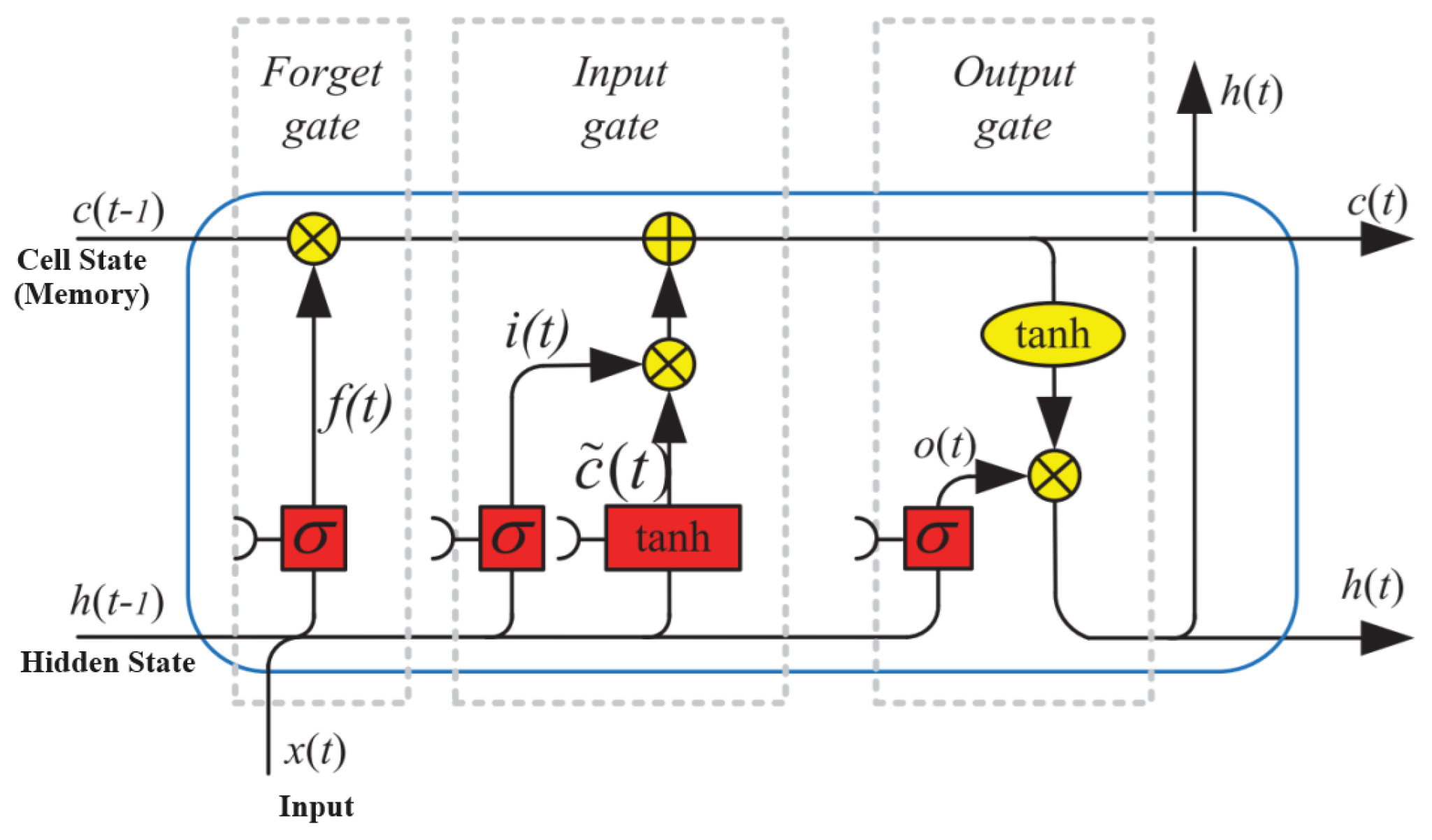
2.1. LSTM Network
2.2. How an LSTM Cell Works
2.3. Performance Indicators
3. Data Sets SunLAB Faro
4. System Development
4.1. Data Processing
4.1.1. Analyzing the Solar Energy Production Data Set
4.1.2. Analyzing the Weather Station Data Set
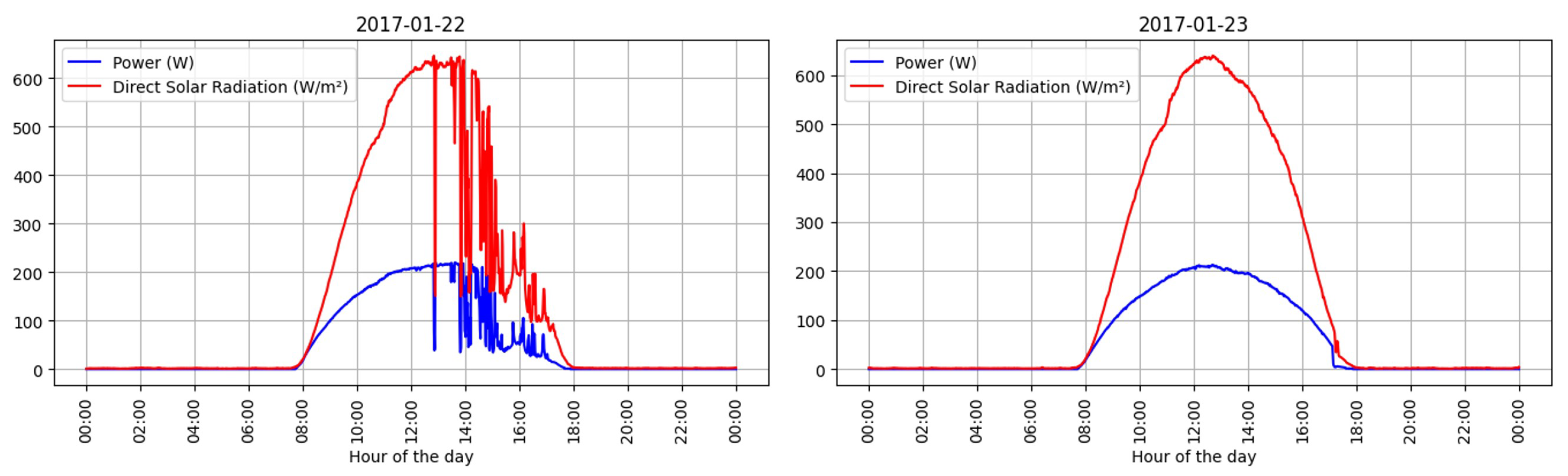
4.1.3. Analysis after Integrating the Solar Energy Production and Weather Station Data Sets
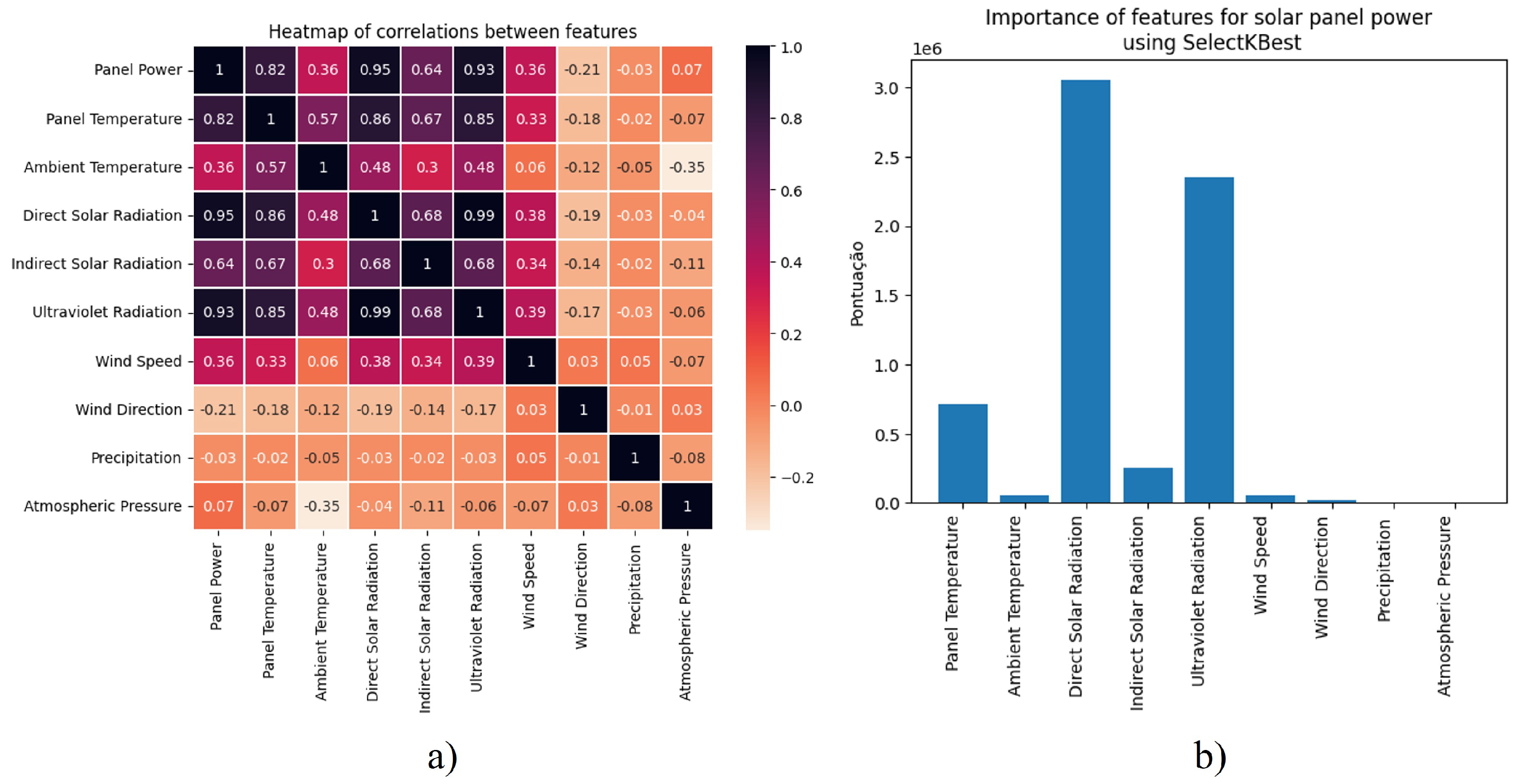
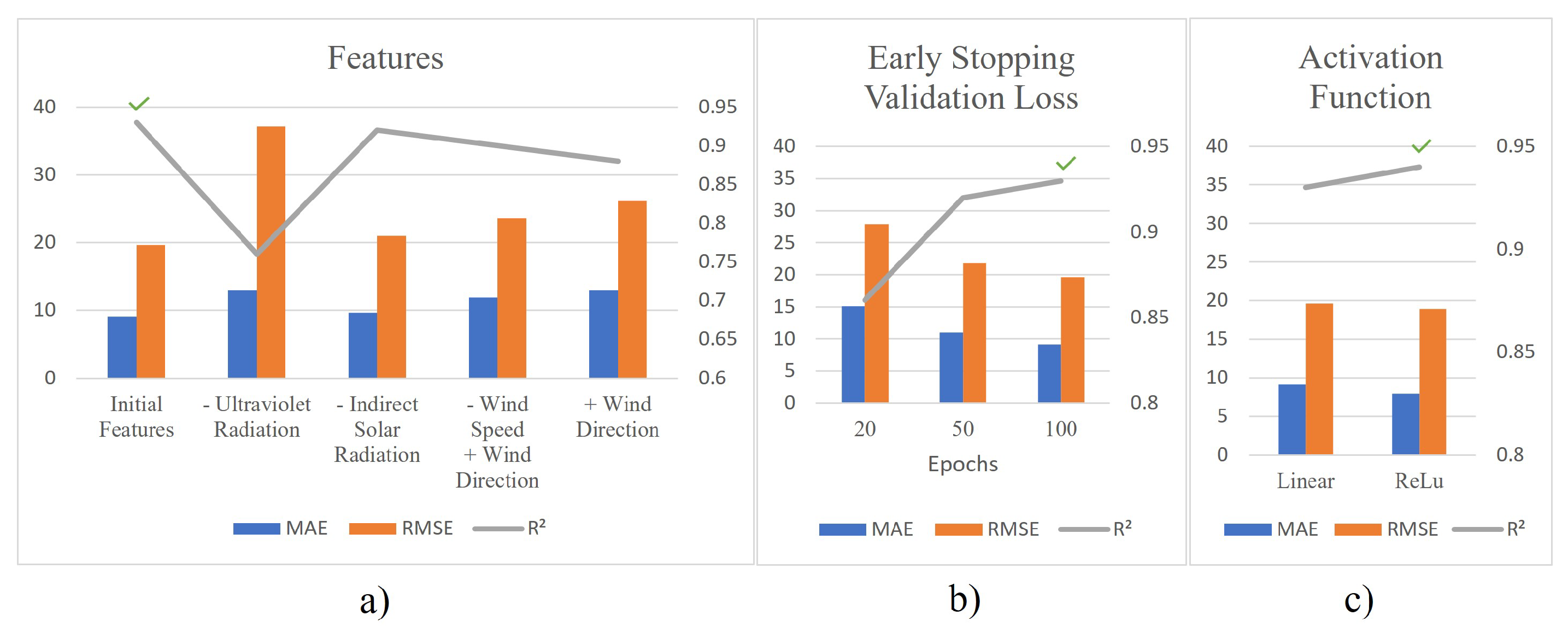
4.2. Choosing the Best Features
4.3. Data Set Division
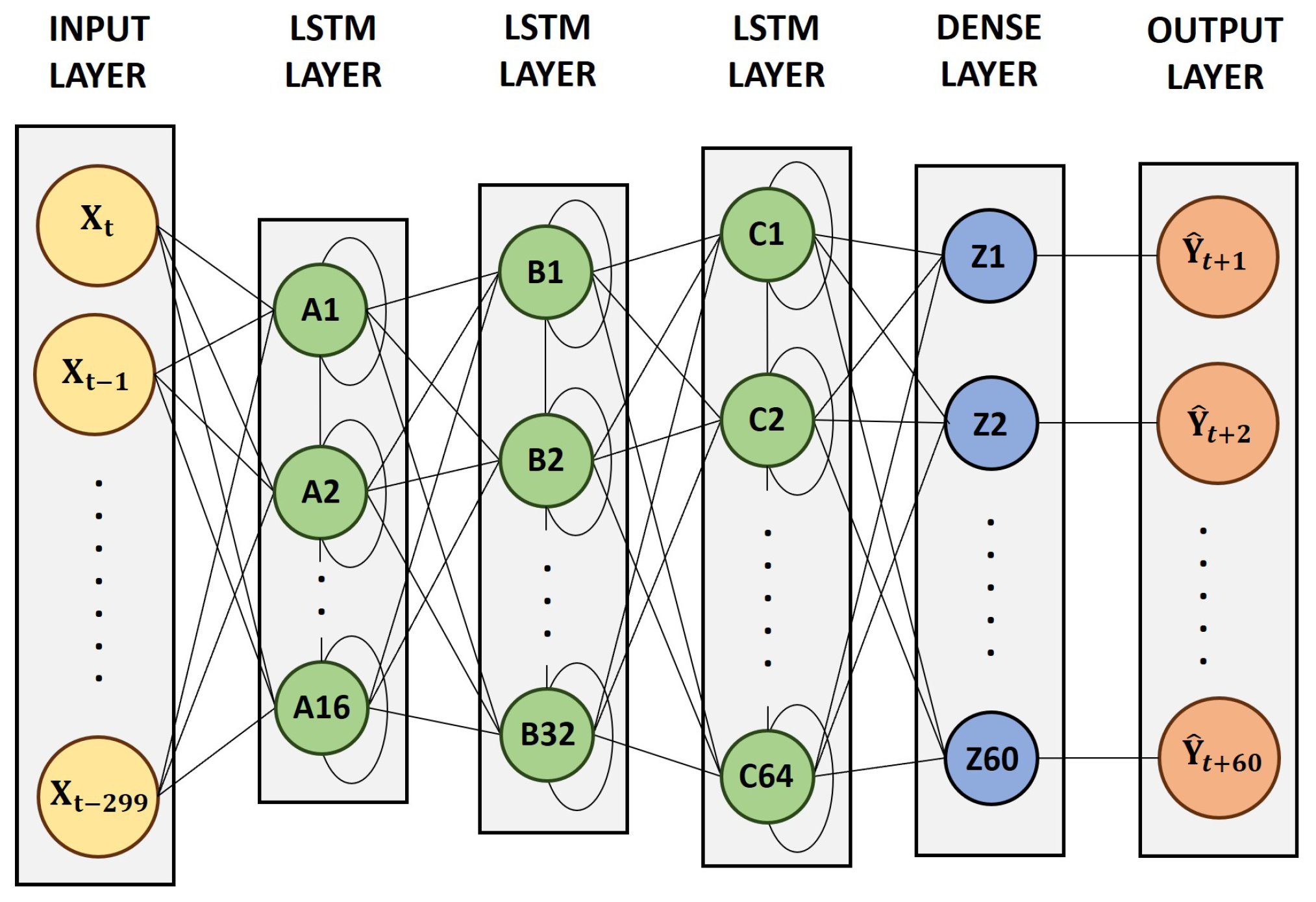
4.4. Neural Network Architecture
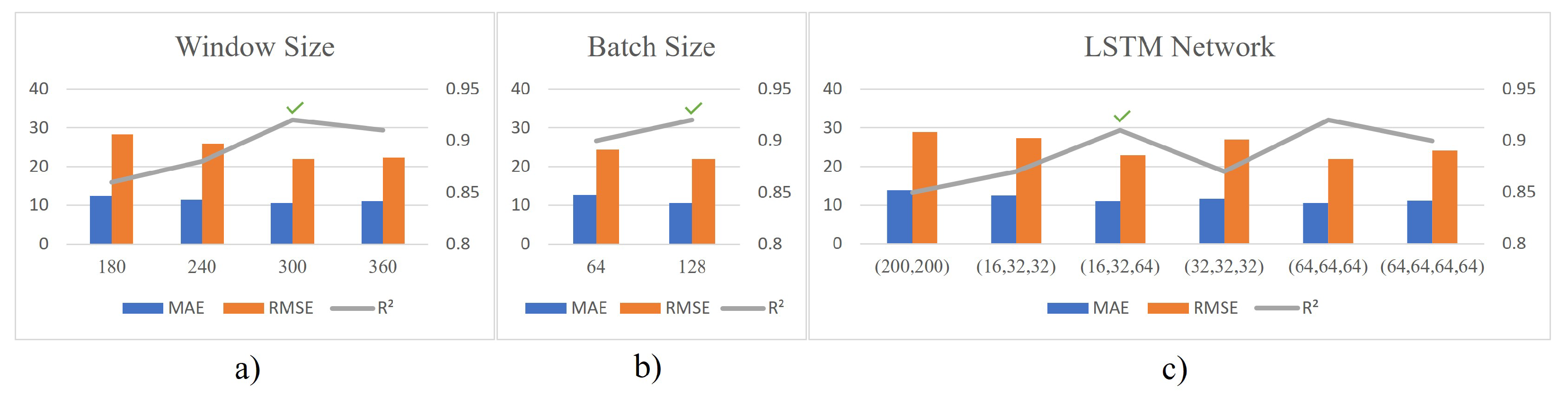
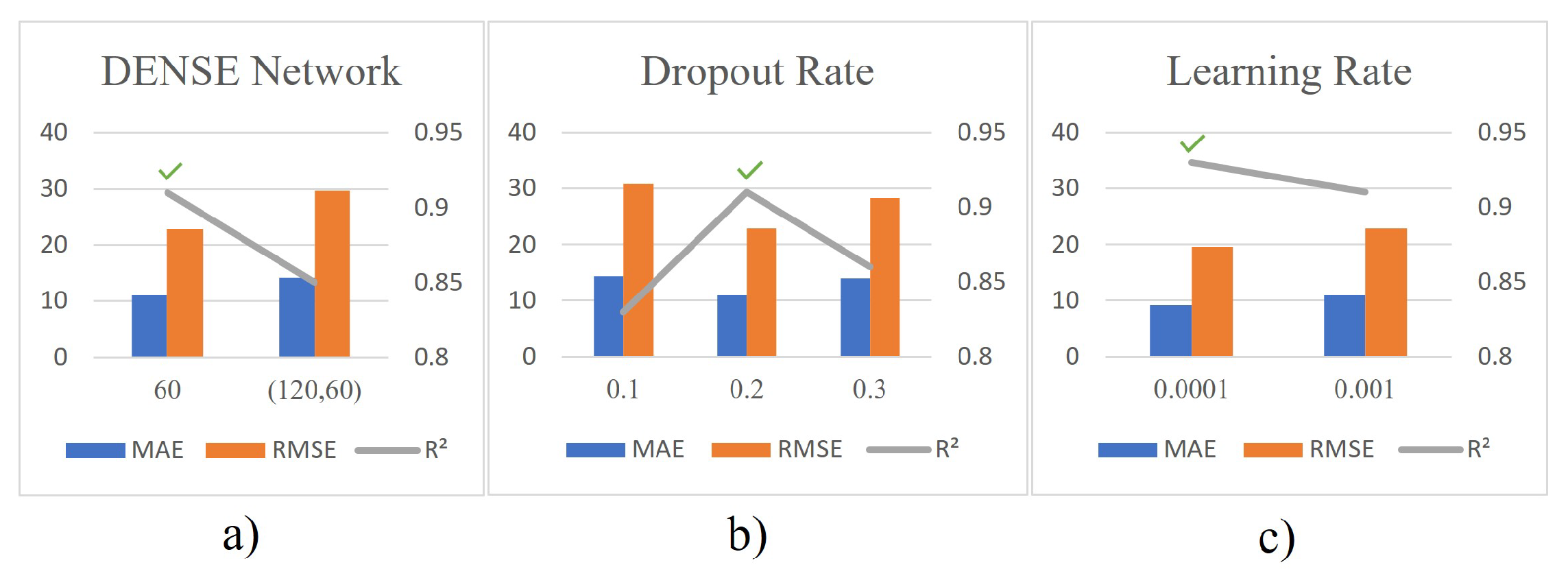
4.5. Choosing the Best Hyperparameters
5. Results
5.1. Interpretation of Performance Indicators
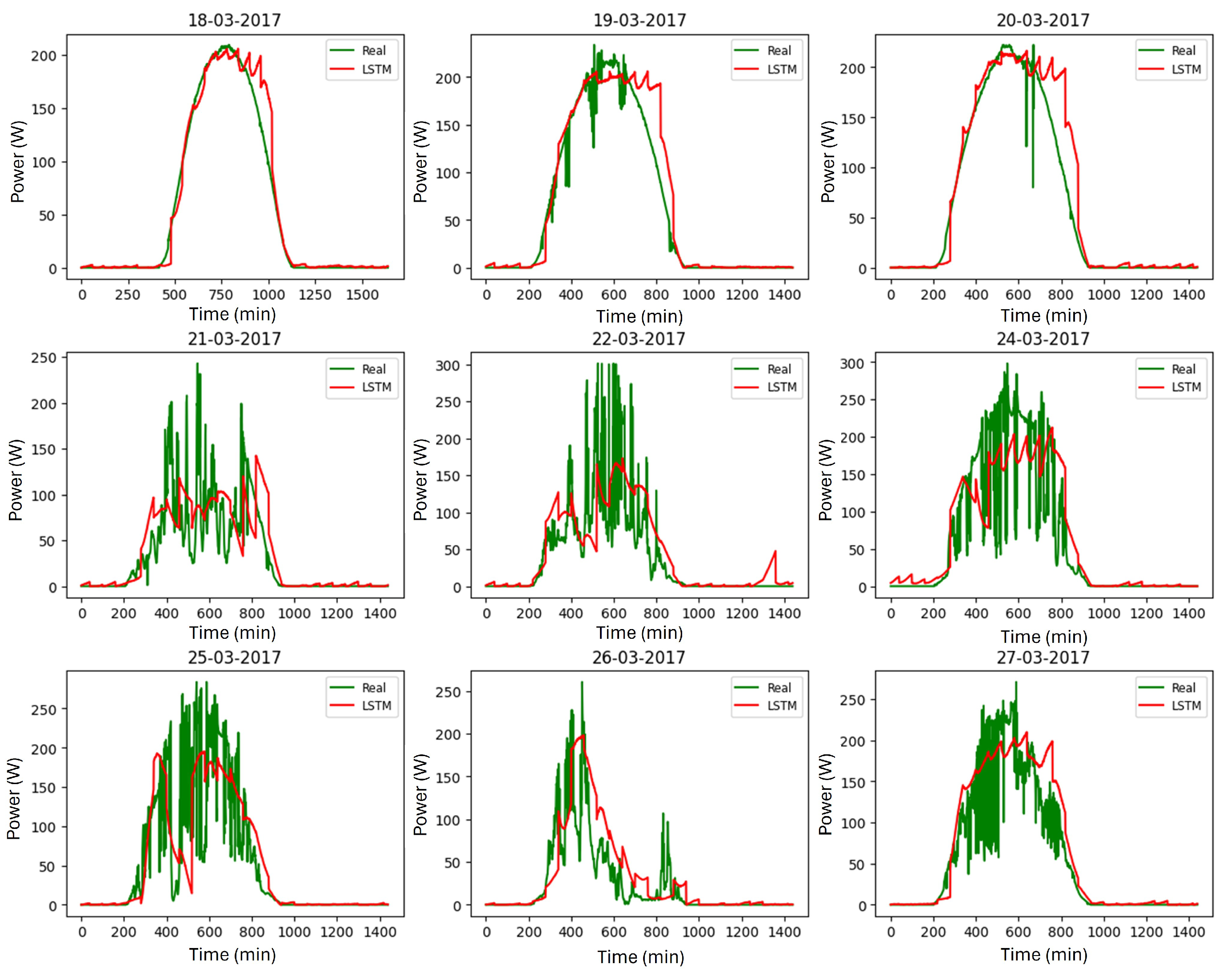
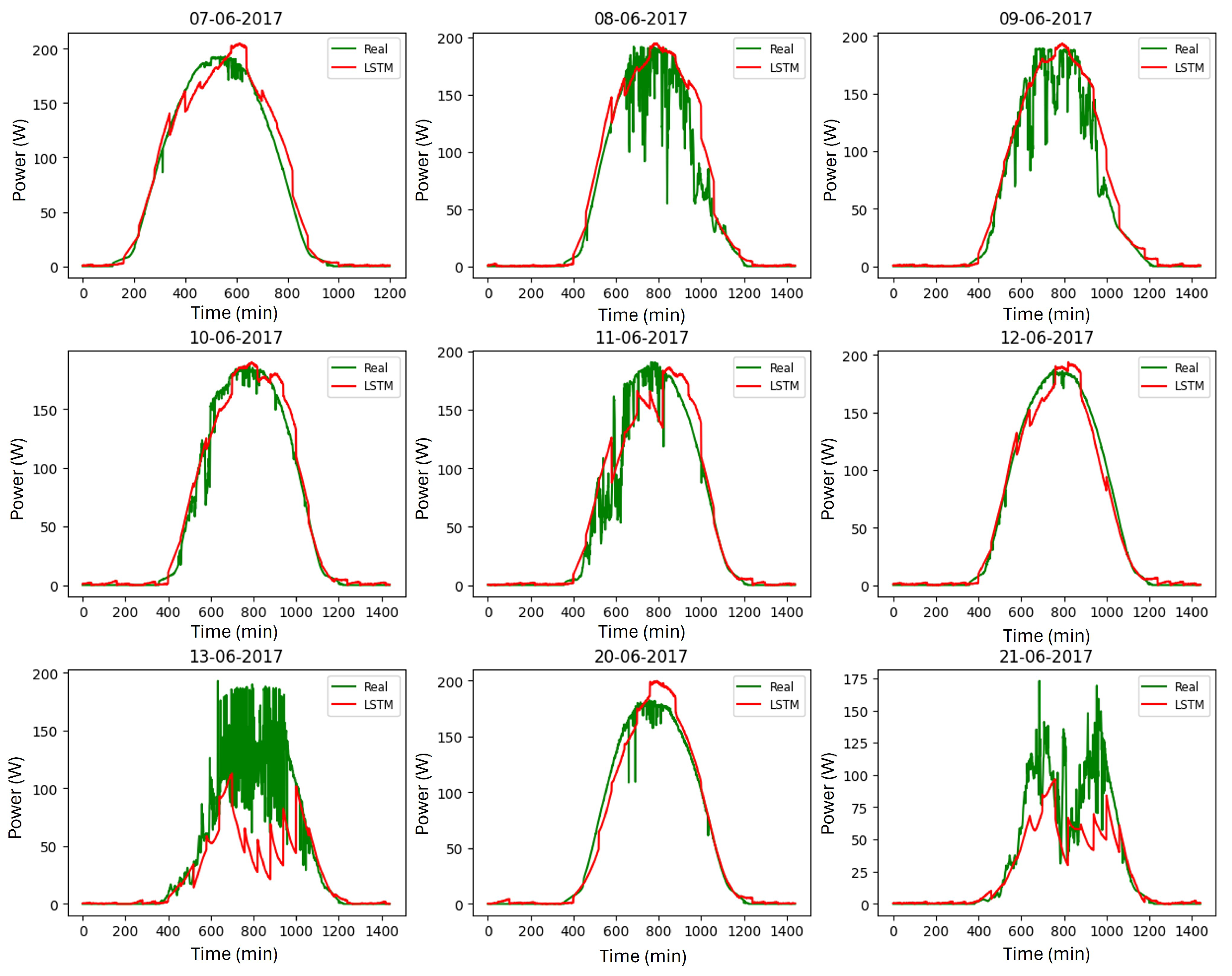
5.2. Graphical Results for Forecasting Solar Energy Production
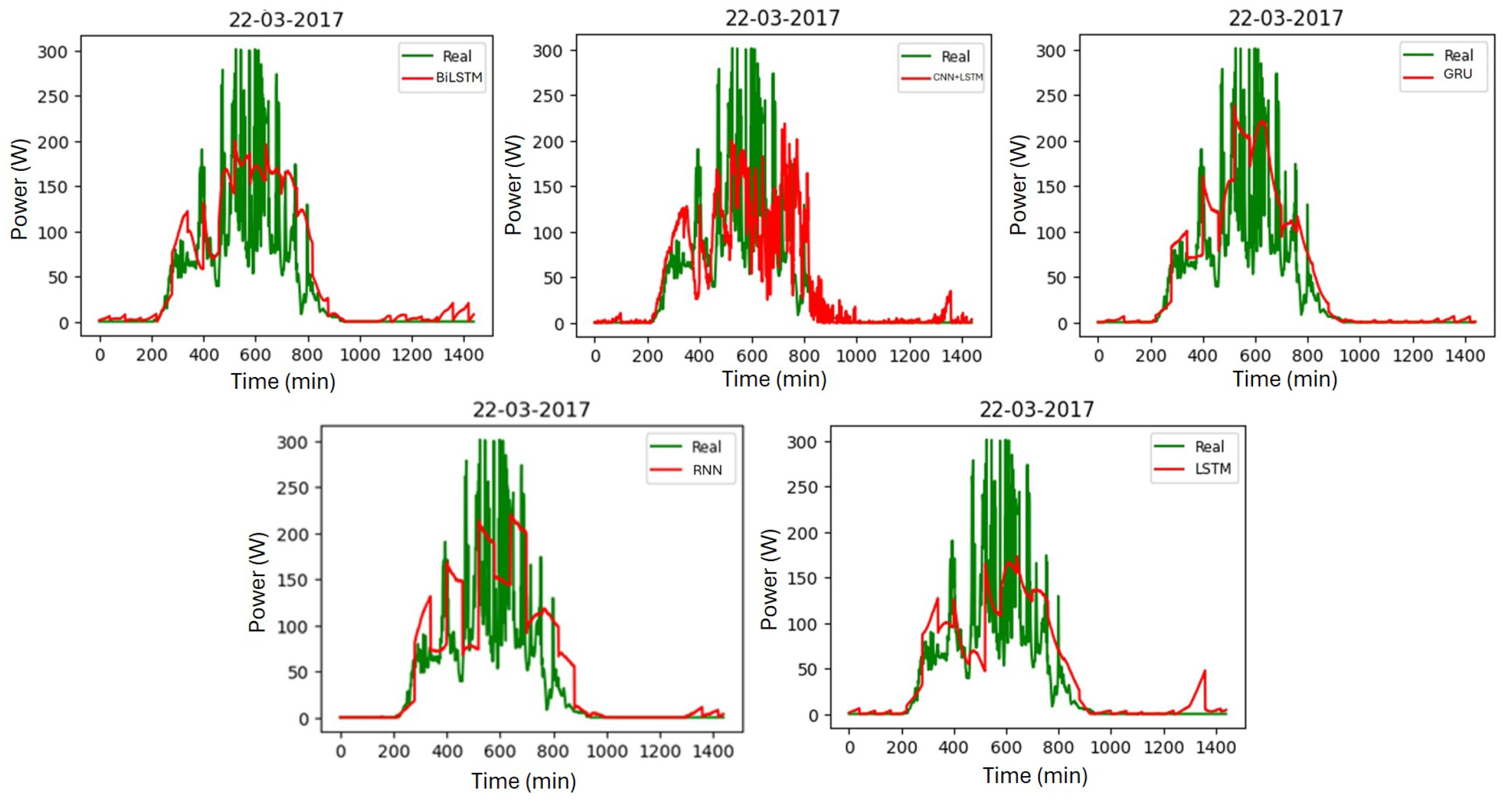
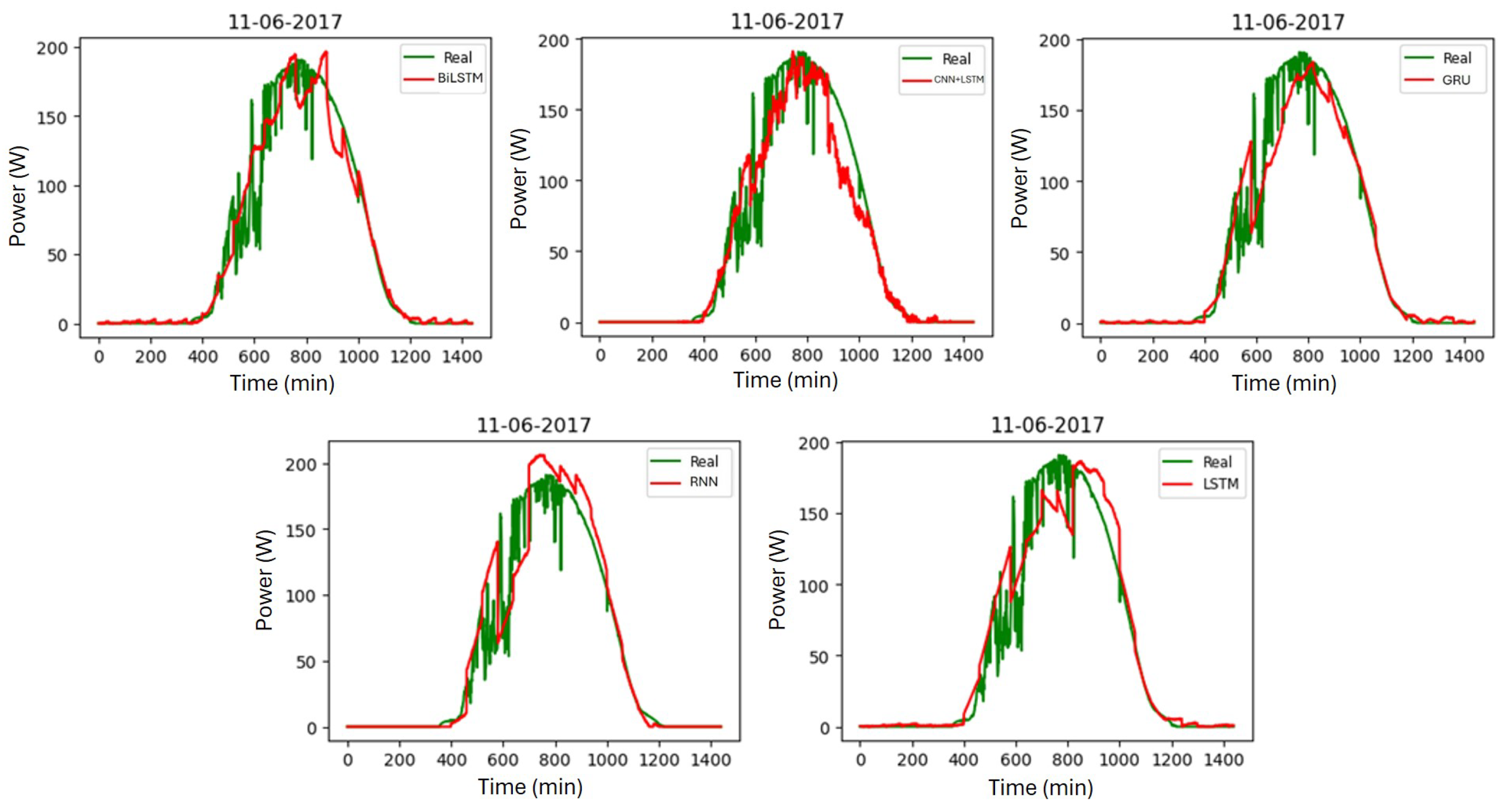
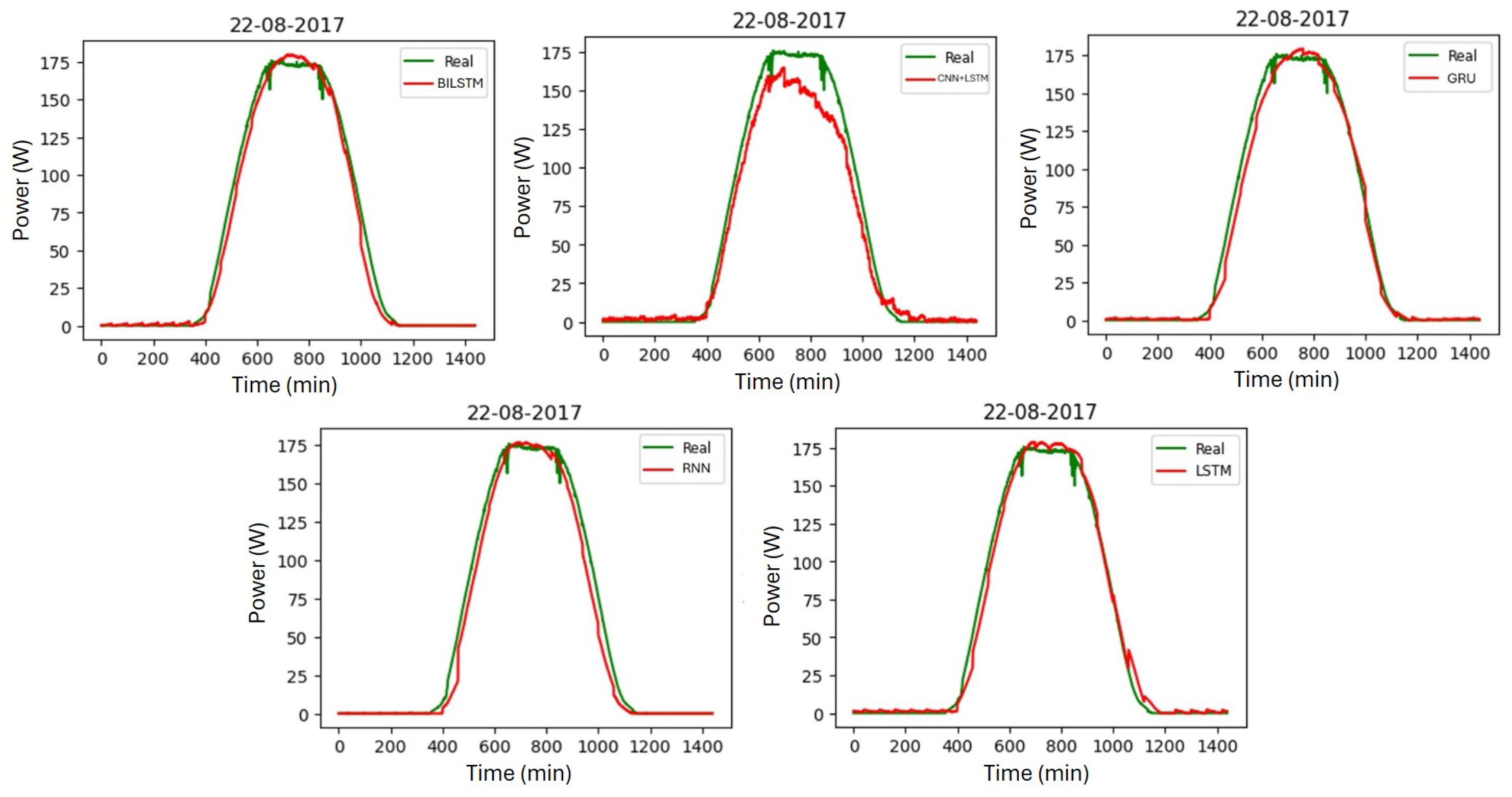
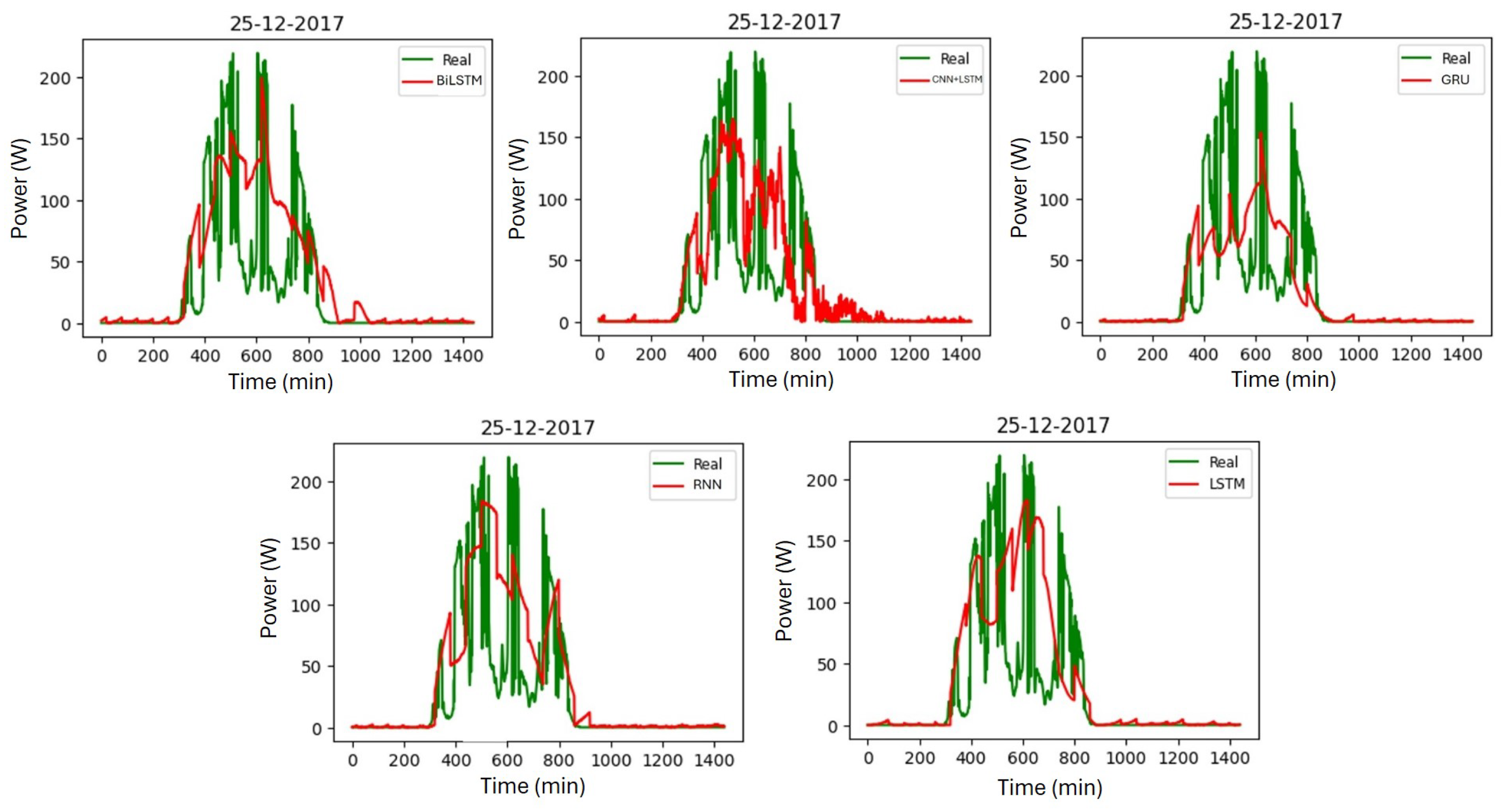
6. Comparison with Other Networks
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Causes and Effects of Climate Change. Available online: https://www.un.org/en/climatechange/science/causes-effects-climate-change (accessed on 24 January 2024).
- Dhaked, D.K.; Dadhich, S.; Birla, D. Power output forecasting of solar photovoltaic plant using LSTM. Green Energy Intell. Transp. 2023, 2, 100113. [Google Scholar] [CrossRef]
- Rocha, H.R.; Fiorotti, R.; Fardin, J.F.; Garcia-Pereira, H.; Bouvier, Y.E.; Rodríguez-Lorente, A.; Yahyaoui, I. Application of AI for short-term pv generation forecast. Sensors 2023, 24, 85. [Google Scholar] [CrossRef]
- Jailani, N.L.M.; Dhanasegaran, J.K.; Alkawsi, G.; Alkahtani, A.A.; Phing, C.C.; Baashar, Y.; Capretz, L.F.; Al-Shetwi, A.Q.; Tiong, S.K. Investigating the power of LSTM-based models in solar energy forecasting. Processes 2023, 11, 1382. [Google Scholar] [CrossRef]
- Lateko, A.A.; Yang, H.T.; Huang, C.M. Short-term PV power forecasting using a regression-based ensemble method. Energies 2022, 15, 4171. [Google Scholar] [CrossRef]
- Jlidi, M.; Hamidi, F.; Barambones, O.; Abbassi, R.; Jerbi, H.; Aoun, M.; Karami-Mollaee, A. An Artificial Neural Network for Solar Energy Prediction and Control Using Jaya-SMC. Electronics 2023, 12, 592. [Google Scholar] [CrossRef]
- Alharkan, H.; Habib, S.; Islam, M. Solar Power Prediction Using Dual Stream CNN-LSTM Architecture. Sensors 2023, 23, 945. [Google Scholar] [CrossRef] [PubMed]
- Mahesh, B. Machine learning algorithms-a review. Int. J. Sci. Res. (IJSR) 2020, 9, 381–386. [Google Scholar]
- Jung, S.M.; Park, S.; Jung, S.W.; Hwang, E. Monthly electric load forecasting using transfer learning for smart cities. Sustainability 2020, 12, 6364. [Google Scholar] [CrossRef]
- Svozil, D.; Kvasnicka, V.; Pospichal, J. Introduction to multi-layer feed-forward neural networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Chang, R.; Bai, L.; Hsu, C.H. Solar power generation prediction based on deep learning. Sustain. Energy Technol. Assess. 2021, 47, 101354. [Google Scholar] [CrossRef]
- Colah, C. Understanding LSTM Networks. Available online: https://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 4 February 2024).
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, R. Know the Best Evaluation Metrics for Your Regression Model! Available online: https://www.analyticsvidhya.com/blog/2021/05/know-the-best-evaluation-metrics-for-your-regression-model/ (accessed on 20 December 2023).
- de Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean Absolute Percentage Error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
- EDP Open Data. Available online: https://www.edp.com/en/innovation/open-data/data (accessed on 4 January 2024).
- Mirzabekov, S. Method of orientation of solar panels of solar power plant. In Proceedings of the E3S Web of Conferences, Tashkent, Uzbekistan, 26–28 April 2023; EDP Sciences. Volume 401, p. 04018. [Google Scholar]
- Randles, B.M.; Pasquetto, I.V.; Golshan, M.S.; Borgman, C.L. Using the Jupyter Notebook as a Tool for Open Science: An Empirical Study. In Proceedings of the 2017 ACM/IEEE Joint Conference on Digital Libraries (JCDL), Toronto, ON, Canada, 19–23 June 2017; pp. 1–2. [Google Scholar]
- Arnold, T.B. kerasR: R Interface to the Keras Deep Learning Library. J. Open Source Softw. 2017, 2, 296. [Google Scholar] [CrossRef]
- Pang, B.; Nijkamp, E.; Wu, Y.N. Deep learning with tensorflow: A review. J. Educ. Behav. Stat. 2020, 45, 227–248. [Google Scholar] [CrossRef]
- Bisong, E. Building Machine Learning and Deep Learning Models on Google Cloud Platform; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Belorkar, A.; Guntuku, S.C.; Hora, S.; Kumar, A. Interactive Data Visualization with Python: Present Your Data as an Effective and Compelling Story; Packt Publishing Ltd.: Birmingham, UK, 2020. [Google Scholar]
- Climate and Average Weather Year Round in Calendário Portugal. Available online: https://weatherspark.com/y/32466/Average-Weather-in-Calend%C3%A1rio-Portugal-Year-Round (accessed on 27 January 2024).
- Anguita, D.; Ghelardoni, L.; Ghio, A.; Oneto, L.; Ridella, S. The ‘K’ in K-fold Cross Validation. In Proceedings of the ESANN, Bruges, Belgium, 25–27 April 2012; pp. 441–446. [Google Scholar]
- Chollet, F. Deep Learning with Python, 2nd ed.; Manning: Shelter Island, NY, USA, 2021. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Google Colab—Online Interactive Notebook Environment. Available online: https://colab.research.google.com/ (accessed on 12 February 2024).
- Global Solar Atlas. Available online: https://globalsolaratlas.info/map (accessed on 5 February 2024).






| Season | Considered Interval |
|---|---|
| Winter | 1 January to 31 March |
| Spring | 1 April to 30 June |
| Summer | 1 July to 30 September |
| Autumn | 1 October to 31 December |
| Initial Model | Final Model | |
|---|---|---|
| Features | Direct Solar Radiation | |
| Indirect Solar Radiation | ||
| Ultraviolet Radiation | ||
| Ambient Temperature | ||
| Wind Speed | ||
| Learning Rate | 0.001 | 0.0001 |
| Window Size | 180 | 300 |
| Prediction Window Size | 60 | 60 |
| Batch Size | 128 | 128 |
| Number of Training Epochs | 350 | 350 |
| Number of Epochs to Stop Training if validate loss does not decrease | 100 | 100 |
| Dropout Rate | 0.2 | 0.2 |
| Size and Number of LSTM Neurons | (64, 64, 64) | (16, 32, 64) |
| Size and Number of DENSE Neurons | 60 | 60 |
| DENSE Activation Function | Linear | ReLu |
| MAE | 12.52 | 7.95 |
| RMSE | 28.37 | 18.97 |
| R2 | 0.86 | 0.94 |
| Winter | Spring | Summer | Autumn | |
|---|---|---|---|---|
| MAE | 16.47 | 9.44 | 8.49 | 12.99 |
| RMSE | 31.18 | 19.76 | 18.03 | 30.78 |
| R2 | 0.84 | 0.92 | 0.92 | 0.76 |
| Method | Season | MAE | RMSE | R2 |
|---|---|---|---|---|
| BiLSTM | Winter | 17.17 | 32.44 | 0.83 |
| Spring | 9.31 | 19.22 | 0.91 | |
| Summer | 8.94 | 18.46 | 0.92 | |
| Autumn | 12.69 | 28.57 | 0.77 | |
| CNN | Winter | 13.84 | 28.75 | 0.86 |
| +LSTM | Spring | 10.03 | 20.00 | 0.90 |
| Summer | 12.12 | 19.74 | 0.88 | |
| Autumn | 12.31 | 27.50 | 0.75 | |
| GRU | Winter | 14.27 | 30.42 | 0.85 |
| Spring | 9.20 | 21.20 | 0.90 | |
| Summer | 7.98 | 17.13 | 0.93 | |
| Autumn | 11.05 | 26.87 | 0.78 | |
| RNN | Winter | 15.71 | 30.78 | 0.86 |
| Spring | 9.34 | 18.77 | 0.93 | |
| Summer | 8.44 | 15.90 | 0.94 | |
| Autumn | 11.99 | 27.31 | 0.80 | |
| LSTM | Winter | 16.47 | 31.18 | 0.84 |
| Spring | 9.44 | 19.76 | 0.92 | |
| Summer | 8.49 | 18.03 | 0.92 | |
| Autumn | 12.99 | 30.78 | 0.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campos, F.D.; Sousa, T.C.; Barbosa, R.S. Short-Term Forecast of Photovoltaic Solar Energy Production Using LSTM. Energies 2024, 17, 2582. https://doi.org/10.3390/en17112582
Campos FD, Sousa TC, Barbosa RS. Short-Term Forecast of Photovoltaic Solar Energy Production Using LSTM. Energies. 2024; 17(11):2582. https://doi.org/10.3390/en17112582
Chicago/Turabian StyleCampos, Filipe D., Tiago C. Sousa, and Ramiro S. Barbosa. 2024. "Short-Term Forecast of Photovoltaic Solar Energy Production Using LSTM" Energies 17, no. 11: 2582. https://doi.org/10.3390/en17112582
APA StyleCampos, F. D., Sousa, T. C., & Barbosa, R. S. (2024). Short-Term Forecast of Photovoltaic Solar Energy Production Using LSTM. Energies, 17(11), 2582. https://doi.org/10.3390/en17112582







