What Is the Optimal Solution for Scheduling Multiple Energy Systems? Overview and Analysis of Integrated Energy Co-Dispatch Models

Abstract

With increasing dual pressure from global large energy consumption and environmental protection, multiple integrated energy systems (IESs) can provide more effective ways to achieve better energy utilization performance. However, in actual circumstances, many challenges have been brought to coupling multiple energy sources along with the uncertainty of each generated power to achieve efficient operation of IESs. To resolve this problem, this article reviews primary research on integrated energy optimization and scheduling technology to give constructive guidance in power systems. Firstly, the conceptual composition and classification of IESs are presented. Secondly, the coupling relationship between multiple energy sources based on mathematical expression is studied deeply. Thirdly, the scheduling of IESs with different types and regions is classified, analyzed, and summarized for clarification. Fourthly, on this basis, potential solutions for applications of key optimization technologies involved in the scheduling process in IESs can be found systematically. Finally, the future development trends to optimize scheduling integrated energy systems is explored and prospected in depth.

1. Introduction

Amid the increasingly scarce global energy resources and the increasingly severe environmental pollution, the development of green, low-carbon, and sustainable energy has become the common pursuit of all countries [1]. The 26th Conference of the Parties to the United Nations Framework Convention on Climate Change (UNFCCC COP26) in 2021 called for more urgent climate action from all countries. It aimed to halve global greenhouse gas emissions by 2030 and achieve net zero by 2050, thereby controlling the global temperature rise within 1.5 °C. However, currently, various energy sources are not closely coupled, and energy networks such as power grids, transportation grids, heat grids, natural gas networks, etc. are relatively independent. This phenomenon results in low overall energy utilization efficiency [2]. Under the global climate emergency, one of the crucial issues is to enhance the performance of traditional energy systems. For this issue, the IES is considered an effective solution in energy conservation and emission reduction by integrating multiple energy sources such as electricity, heat, and natural gas [3]. Optimized scheduling of IESs can integrate renewable energy sources like wind and solar energy, effectively responding to uncertainties in the system operation. However, some key technologies such as large-scale energy storage technology, multi-energy conversion equipment, and multi-scale control are not yet mature or are costly [4]. On the other hand, the lack of mature market mechanisms and policy support, such as an electricity pricing policy and carbon trading mechanism, may hinder the commercialization and large-scale development of IESs [5]. In IES optimization, the volatility of loads and renewable energy sources should be taken into account simultaneously, including the coupling of multiple energy sources [6]. Accordingly, an IES-based scheduling optimization method was proposed for better economy and stability in power systems [7]. Alternatively, a hierarchical optimization scheme was developed by considering the reconfigurable capability of the distribution network among the energy service providers (ESPs). Therefore, multi-energy coupling efficiency was addressed in the IES [8]. A hybrid time-scale optimal scheduling model to reduce uncertainty of the power system operation was thus constructed [9]. A multi-objective particle swarm optimization algorithm for scheduling process in a regionally integrated energy system was reported [10]. Also, a reserve scheduling model based on dynamic multistage robust optimization (DMRO) for the integrated electrical heating system (IEHS) was proposed to harness the potential of uncertain renewable energy sources [11]. A nested Benders decomposition algorithm was therefore used to obtain the global optimum. Another coordinated optimal scheduling method for IES clusters based on an improved multi-agent deep deterministic policy gradient (MADDPG) algorithm with a compression mechanism of initial state space was developed recently [12]. It faster increased the solving speed by 40 times than the alternating direction method of multipliers (ADMMs) distributed algorithm while ensuring the convergence and optimality of the process.

To comply with the global energy demand and promote the development of integrated energy system optimal scheduling, it is crucial to systematically investigate and summarize models in scheduling strategies. For this reason, this paper starts from the concept, composition, and classification of IESs. Based on the mathematical expressions, the coupling relationship between different energy sources is also unveiled and discussed in depth [13], which reveals the effective integration of energy sources in practical applications. Secondly, IES scheduling using different source types and regions is classified, analyzed, and summarized in detail. This allows the researchers to have a deeper understanding of the optimization of IES operation under various conditions. Potential solutions to the uncertainty and coupling problems in IES operation are also presented. Finally, the future IES optimal scheduling is envisioned to promote the improvement of system digital intelligence and resilience, thus realizing the efficient energy utilization with regional autonomy.

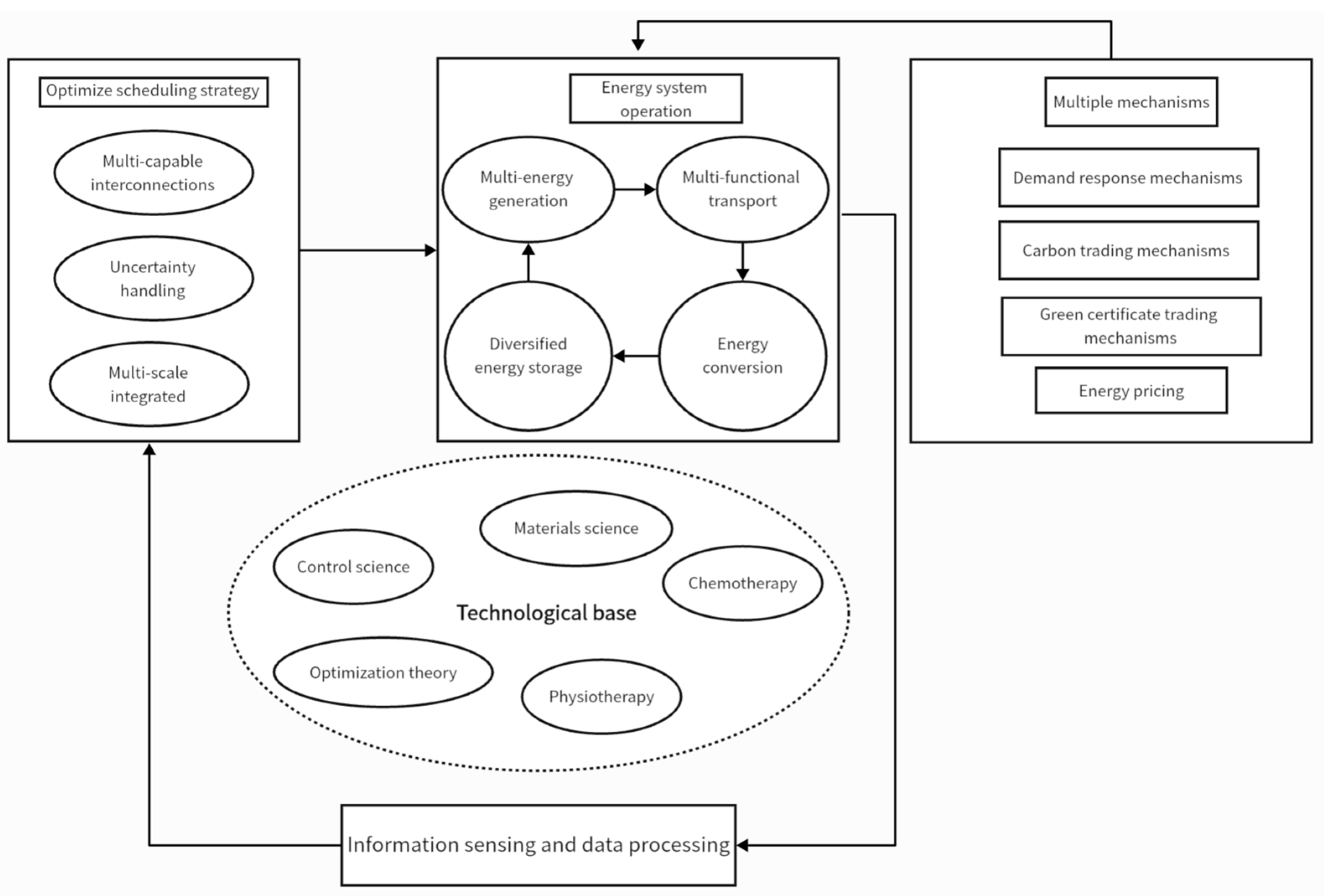
2. Overview of Optimized IES Scheduling

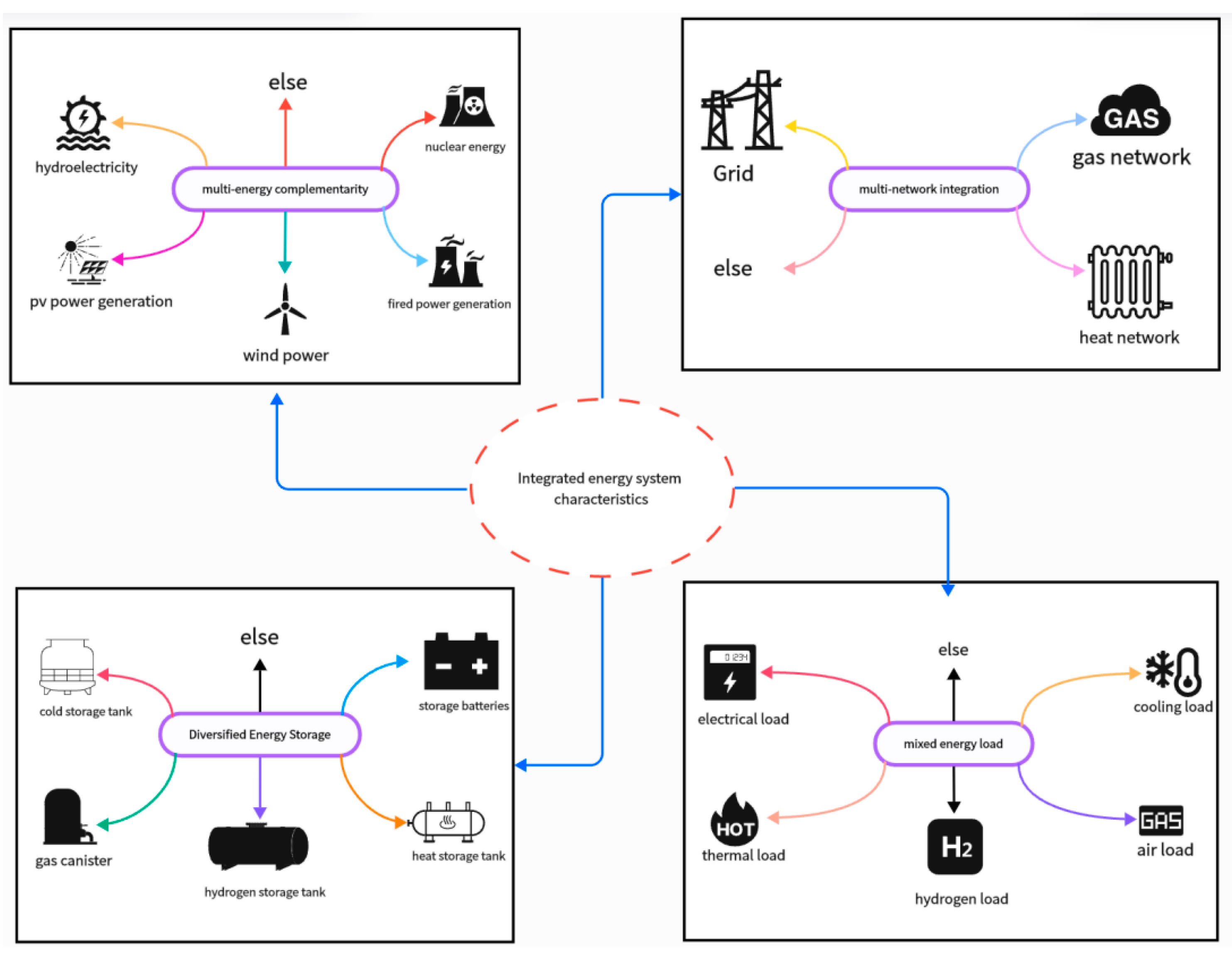
2.1. Conceptual Components of IESs

IESs can increase the power utilization efficiency of renewable energy, covering generation, transmission, conversion, storage, and distribution in multiple energy sources. According to the complementary characteristics of electricity, heat, gas, and other types of energy, the multi-energy system needs unified planning and coordinated optimization operation among integrated energy production, supply, and consumption integration systems [14]. In general, in the typical IES structure, as shown in Figure 1, the energy supply part consists of electricity, heat, gas, and other energy sources and the use of their energy characteristics through the type of equipment to achieve a variety of heterogeneous energy subsystems between the coordinated planning, optimization of the operation, and complementary mutual aid [15]. The source side is used to integrate power supply, gas supply, cooling, and heat supply to meet the user’s demand for multiple types of energy [16].

In addition to the grid power supply, IESs can also carry out the conversion of gas to electricity through gas turbine equipment, thereby providing electrical energy. The power-to-gas (P2G) equipment is used to perform the conversion of electric–gas energy. At the same time, the gas turbine, through a heat exchanger, provides heat energy, effectively utilizing the energy produced by preheating. IESs can also link with combined heat and power (CHP) units to generate electricity and heat. Through the electric boiler, heat pumps electricity–heat energy conversion for the supply of heat. The use of absorption chillers, electric chillers, and heat–cold energy provides energy to the cold load via electricity–cold energy conversion. When energy supply and demand are in imbalance, the excess/insufficient energy is stored/released through the energy storage equipment (electricity storage, gas storage, heat storage, cold storage, etc.) to maintain the dynamic balance of the system energy. The IES system can realize the energy balance and make energy more effectively through the mutual coupling of energy sources, conversion of energy, distributed energy storage, and other technologies.

2.2. Classification of IESs

IESs can be categorized into inter-regional, regional, and user level based on the geographic situation and energy generation, transmission, distribution, and use characteristics [6]. The integration characteristics of the integrated energy system are shown in Figure 2. The inter-regional integrated energy system is mainly involved in two energy forms, i.e., electricity and gas. It should be able to produce large-scale energy with long-distance transmission. It consists of centralized wind and solar power stations, large-scale integrated energy stations retrofitted with carbon capture equipment as energy production units, seasonal energy storage equipment as energy storage units, and long-distance energy transmission units such as transmission lines, gas pipelines, and transportation networks. User-level IESs provide energy services directly to end-users, and their components include small-scale wind power generation systems, geothermal energy, small-scale electric energy storage devices, and heat storage tanks. Due to the significant changes in the energy users’ behavior, these systems often suffer from “source-load” volatility and randomness. Regional-level IESs [17] realize energy transmission, distribution, conversion, and balancing by coupling power distribution systems, medium and low-voltage natural gas systems, and functional networks such as heating, cooling, and water supply systems. They cover a variety of heterogeneous energy sources, combines multifaceted energy storage devices, and forms a deeply coupled electricity, gas, heat, and cold energy transmission network.

Existing IES studies have been focused on the regional level, especially for industrial or technology parks. The coverage of regional-level IESs is moderate, and it can reflect the complexity and diversity of energy systems [18]. In contrast, inter-regional level systems have large-scale energy production and long-distance transmission with many uncertainties and variables, making the research more difficult. However, IESs at the regional level have significant advantages in dealing with energy optimization, resource allocation, economics, and environmental benefits, enhancing regional energy efficiency and sustainability [19]. Regional-level IES modeling is relatively simple, with sufficient empirical data support, while inter-regional-level and user-level IESs modelling are more complex and have big challenges due to the volatility and stochasticity of energy sources [20].

3. Models of IES

3.1. New Energy Generators

In an integrated energy system, wind and photovoltaic (PV) are known as major power generators. Wind energy relies on wind speed, blade radius, air density, and the wind turbine’s geographic location and performance attributes [21,22]. As a result, wind turbine modelling is determined by influential factors such as cut-in wind speed, cut-out wind speed, rated wind speed, and actual wind speed [23]. On the other hand, the PV system modelling should consider a variety of factors, including the cleanliness of the PV panels, solar irradiance, the mounting area of the PV panels [24], the operating temperature, the angle of incidence of light, and the inverter efficiency [25].

3.2. Modeling of Energy-Coupled Equipment

An integrated energy system is a system that couples multiple energy systems, such as electricity, heat, cooling, and natural gas to achieve complementary and synergistic optimization of energy sources. Therefore, the efficiency, security and flexibility of energy utilization can be improved or enhanced in the of energy supply. At the same time, environmental pollution and lower energy costs can be reduced considerably. Typical physical models applied in energy systems are reviewed more specifically as follows.

3.2.1. Modeling of Gas–Electric Coupled Equipment Units

Gas turbines in gas–electric coupled devices convert the chemical energy of natural gas into electrical and thermal energy, while hydrogen fuel cells convert the chemical energy of hydrogen directly into electrical energy. The gas turbine model is focused on power generation efficiency and air consumption, and it is usually used to generate the electrical power for a period of time. However, the energy conversion efficiency and cost can be directly affected by its efficiency, and it is usually applied to integrated energy systems. On the other hand, the hydrogen fuel cell model simulates the hydrogen consumption to be applicable to clean energy demand scenarios such as renewable energy systems, microgrids, and electric vehicle charging stations.

(1) Gas turbine model

The gas turbine (GT) generates power in an integrated energy system through the process of combustion of fuel and compression of air, of which the typical physical model is the following equation [26]:

$${\mathrm{P}}_{\mathrm{G}\mathrm{T}}\left(\mathrm{t}\right)={\mathsf{\eta }}_{\mathrm{G}\mathrm{T},\mathrm{e}}{\mathrm{G}}_{\mathrm{G}\mathrm{T}}\left(\mathrm{t}\right)$$

(1)

where ${\mathrm{P}}_{\mathrm{G}\mathrm{T}}\left(\mathrm{t}\right)$is the output electric power of the gas turbine at time period $\mathrm{t}$, ${\mathsf{\eta }}_{\mathrm{G}\mathrm{T},\mathrm{e}}$is the power generation efficiency of the GT, and ${\mathrm{G}}_{\mathrm{G}\mathrm{T}}\left(\mathrm{t}\right)$is the power consumed by the air in the T cycle.

(2) Hydrogen fuel cell model

Hydrogen fuel cells (HFCs) utilize the chemical energy present in hydrogen to generate electricity efficiently and cleanly. The cell relies on a constant supply of fuel and an oxidizer (usually oxygen) to maintain the reactions that power the electricity generation process. Thus, fuel cells have the ability to generate electricity continuously as long as a steady supply of fuel and oxygen is maintained. A typical physical model of this is [27]:

$${\mathrm{P}}_{\mathrm{t}}^{\mathrm{H}\mathrm{F}\mathrm{C}}={\mathsf{\eta }}^{\mathrm{H}\mathrm{F}\mathrm{C}}{\mathsf{\delta }}^{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}{\mathrm{M}}_{\mathrm{t}}^{{\mathrm{t}\mathrm{k}}_{\mathrm{f}\mathrm{c}}}$$

(2)

where ${\mathrm{P}}_{\mathrm{t}}^{\mathrm{H}\mathrm{F}\mathrm{C}}$ is the output electric power, ${\mathsf{\eta }}^{\mathrm{H}\mathrm{F}\mathrm{C}}$denotes the combustion hydrogen discharge efficiency, ${\mathsf{\delta }}^{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}$denotes the transfer coefficient between the electric energy and the weight of hydrogen, and ${\mathrm{M}}_{\mathrm{t}}^{\mathrm{t}\mathrm{k}\_\mathrm{f}\mathrm{c}}$ denotes the weight of the hydrogen output from the hydrogen storage tank to the fuel cell at time $\mathrm{t}$.

3.2.2. Modeling of Electric–Gas Coupled Equipment Units

Electric–gas coupling equipment is used for electrical energy to be converted to hydrogen by electrolyzing water. Subsequently, the hydrogen can be used in a fuel cell to generate electricity or burned directly in a gas turbine, completing the cycle of electric–gas energy conversion and storage. The electrolyzer efficiently breaks down water into hydrogen by utilizing electricity, and its efficiency and generation rate depend on the power, operating voltage, and efficiency of the electrolyzer. The performance efficacy of the electrolyzer directly affects the production of hydrogen and the energy conversion efficiency in the entire system. Hydrogen storage tanks, on the other hand, are responsible for storing this hydrogen, and their capacity and hydrogen volume are affected by the temperature, pressure and ideal gas constants. The design and operating conditions of hydrogen storage tanks are critical to ensure storage efficiency and system stability.

(1) Electrolyzer

An electrolyzer is a place where excess electricity generated by a solar wind system is utilized to convert water into hydrogen. Typical physical model equations for the rate of hydrogen production in an electrolyzer are [28]:

$${\dot{\mathrm{M}}}_{\mathrm{H}2}^{\mathrm{i}\mathrm{n}}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{e}\mathrm{l}\mathrm{z}}}{\frac{1}{2}\ast \mathrm{F}\ast {\mathrm{U}}_{\mathrm{e}\mathrm{l}\mathrm{z}}}}$$

(3)

where ${\mathrm{P}}_{\mathrm{e}\mathrm{l}\mathrm{z}}$and ${\mathrm{U}}_{\mathrm{e}\mathrm{l}\mathrm{z}}$ represent the power and operating voltage of the electrolyzer, respectively, 1/2 is the reciprocal of the molar mass of hydrogen, and $\mathrm{F}$ is the Faraday constant. The variable ${\dot{\mathrm{M}}}_{\mathrm{H}2}^{\mathrm{i}\mathrm{n}}$ (g/s) represents the mass flow rate of hydrogen produced in the electrolyzer. ${\mathrm{U}}_{\mathrm{e}\mathrm{l}\mathrm{z}}$ is given by the efficiency of the electrolyzer ${\mathsf{\eta }}_{\mathrm{e}\mathrm{l}\mathrm{z}}$, defined in the equation as:

$${\mathsf{\eta }}_{\mathrm{e}\mathrm{l}\mathrm{z}}={\displaystyle \frac{1.25}{{\mathrm{U}}_{\mathrm{e}\mathrm{l}\mathrm{z}}}}$$

(4)

(2) Hydrogen storage tank

Hydrogen tanks are used to store hydrogen produced by the electrolyzer, computed using ${\mathrm{M}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{k}}\left(\mathrm{t}\right)$ at specific time period $\mathrm{t}$ [28]:

$${\mathrm{M}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{k}}\left(\mathrm{t}\right)={\mathrm{M}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{k}}\left(\mathrm{t}-1\right)+{\dot{\mathrm{M}}}_{\mathrm{H}2}^{\mathrm{i}\mathrm{n}}-{\dot{\mathrm{M}}}_{\mathrm{H}2}^{\mathrm{o}\mathrm{u}\mathrm{t}}$$

(5)

where ${\dot{\mathrm{M}}}_{\mathrm{H}2}^{\mathrm{o}\mathrm{u}\mathrm{t}}$ is the flow rate of hydrogen discharged in the electrolyzer. The volume of hydrogen stored, ${\mathrm{V}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{k}}$, is given via the equation [28]:

$${\mathrm{V}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{k}}={\displaystyle \frac{{\mathrm{M}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{k}}\ast {\mathrm{T}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{k}}\ast \mathrm{R}}{{\mathrm{P}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{k}}}}$$

(6)

where ${\mathrm{T}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{k}}$, ${\mathrm{P}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{k}}$, and R are the temperature (K) and pressure (Mpa) in the hydrogen tank and the ideal gas constant (J/(mol∗K)).

3.2.3. Modeling of Electric–Thermal Coupling Equipment Unit

The electric–thermal coupling equipment is an electric boiler that directly converts the electric power into thermal energy to produce hot water. The heat pump using electric power extracts heat from the environment to realize the electric power conversion to thermal energy. In the electric heat boiler model, the input electric power and energy production efficiency are taken into account to calculate the thermal power produced in a specific time period. Its efficiency directly affects the system’s ability to convert electric energy into thermal energy, which has a significant impact on the energy utilization efficiency and operating costs, and is particularly suitable for district heating and hot water supply during times of excess electricity or low electricity prices. The heat pump model, on the other hand, is focused on power input and performance coefficients, including both cooling and heating modes, and is used to calculate the cooling and heating output of the heat pump in a specific time period. The energy efficiency in the heating and cooling modes is determined by its performance coefficients. Its application is crucial to achieve efficient energy usage and minimize the energy consumption, especially in areas with variable climates.

(1) Electric Boiler Model

An electric boiler (EB) produces hot water by consuming electricity, and its typical physical model is defined as [26]:

$${\mathrm{Q}}_{\mathrm{E}\mathrm{B}}\left(\mathrm{t}\right)={\mathsf{\eta }}_{\mathrm{E}\mathrm{B}}{\mathrm{P}}_{\mathrm{E}\mathrm{B}}\left(\mathrm{t}\right)$$

(7)

where ${\mathrm{P}}_{\mathrm{E}\mathrm{B}}\left(\mathrm{t}\right)$ is the input electric power of the EB, ${\mathrm{Q}}_{\mathrm{E}\mathrm{B}}\left(\mathrm{t}\right)$ is the output thermal power of the EB, and ${\mathsf{\eta }}_{\mathrm{E}\mathrm{B}}$ is the energy production efficiency of the EB.

(2) Heat pump model

The typical physical model of a heat pump (HP) for the required cooling power, ${\mathrm{P}}_{\mathrm{H}\mathrm{P},\mathrm{c}}^{\mathrm{o}\mathrm{u}\mathrm{t},\mathrm{t}}$, and heating output, ${\mathrm{P}}_{\mathrm{H}\mathrm{P},\mathrm{h}}^{\mathrm{o}\mathrm{u}\mathrm{t},\mathrm{t}}$, is expressed as [29]:

$${\mathrm{P}}_{\mathrm{H}\mathrm{P},\mathrm{c}}^{\mathrm{o}\mathrm{u}\mathrm{t},\mathrm{t}}=\mathrm{C}\mathrm{O}{\mathrm{P}}_{\mathrm{H}\mathrm{P}}^{\mathrm{c}}{\mathrm{P}}_{\mathrm{H}\mathrm{P}}^{\mathrm{i}\mathrm{n},\mathrm{t}}$$

(8)

$${\mathrm{P}}_{\mathrm{H}\mathrm{P},\mathrm{h}}^{\mathrm{o}\mathrm{u}\mathrm{t},\mathrm{t}}=\mathrm{C}\mathrm{O}{\mathrm{P}}_{\mathrm{H}\mathrm{P}}^{\mathrm{h}}{\mathrm{P}}_{\mathrm{H}\mathrm{P}}^{\mathrm{i}\mathrm{n},\mathrm{t}}$$

(9)

where ${\mathrm{P}}_{\mathrm{H}\mathrm{P}}^{\mathrm{i}\mathrm{n},\mathrm{t}}$ is the power input of the heat pump at time t, and $\mathrm{C}\mathrm{O}\mathrm{P}$ denotes the coefficient of performance.

3.2.4. Modeling of Gas–Heat Coupled Equipment Unit

The gas–heat coupled equipment consists of a gas boiler (GB) that generates heat by consuming natural gas. The model describes the heat generation of the boiler through heat output, gas consumption, and thermal efficiency. It can be used for calculating the required heat output of a gas boiler when there is insufficient heat in the system. The thermal efficiency and boiler gas consumption have a direct impact on the energy consumption and operating costs of the system, which in turn determines the efficiency of energy utilization. This model ensures the provision of reliable heat not only in residential and commercial buildings, but also in district heating systems when the energy supply is unstable. Moreover, it can optimize system performance to reduce heating costs and improve the energy efficiency and system reliability. When GB is activated and the heat energy produced, it is calculated as follows [30]:

$${\mathrm{Q}}_{\mathrm{G}\mathrm{B}}={\mathrm{V}}_{\mathrm{G}\mathrm{B}}{\mathsf{\eta }}_{\mathrm{G}\mathrm{B}}$$

(10)

where ${\mathrm{Q}}_{\mathrm{G}\mathrm{B}}$, ${\mathrm{V}}_{\mathrm{G}\mathrm{B}}$, and ${\mathsf{\eta }}_{\mathrm{G}\mathrm{B}}$ represent the heat output, gas consumption, and thermal efficiency of the gas boiler plant, respectively.

3.2.5. Modeling of Heat–Cooling Coupling Equipment Unit

In the heat–cooling coupling system, the absorption chiller (AC) uses high-temperature heat energy to drive the refrigeration cycle. It transfers heat from the low-temperature side to the high-temperature side, thus generating cold energy for refrigeration and discharging heat energy at the same time. The model considers the output refrigeration capacity and input heat capacity as well as the energy efficiency ratio of the equipment. This type of chiller is suitable for scenarios with a stable heat input, such as industrial waste heat recovery, a solar thermal collector, or renewable energy systems. It can achieve an efficient cooling process through low-grade thermal energy, thereby increasing the energy utilization of integrated energy systems and reducing the reliance on conventional electrical energy for cooling. Absorption chillers utilize thermal energy to drive the cooling effect through the exchange and circulation of refrigerant between the absorber and the generator. They are widely used in industrial and commercial locations and are particularly suitable for those that can provide thermal energy as a power source, such as the utilization of waste heat in industrial facilities or solar thermal collectors. Its typical physical modeling equations are expressed as follows [31]:

$${\mathrm{C}}_{\mathrm{A}\mathrm{C}}\left(\mathrm{t}\right)=\mathrm{E}\mathrm{E}{\mathrm{R}}_{\mathrm{A}\mathrm{C}}\times {\mathrm{Q}}_{\mathrm{A}\mathrm{C}}\left(\mathrm{t}\right)$$

(11)

where ${\mathrm{C}}_{\mathrm{A}\mathrm{C}}\left(\mathrm{t}\right)$ and ${\mathrm{Q}}_{\mathrm{A}\mathrm{C}}\left(\mathrm{t}\right)$ are the output cooling capacity and input heat capacity of the absorption chiller, kW, respectively; $\mathrm{E}\mathrm{E}{\mathrm{R}}_{\mathrm{A}\mathrm{C}}$ is the energy efficiency ratio of the absorption chiller.

3.2.6. Modeling of Electricity–Cooling Coupling Equipment Unit

In the electric–cooling coupling system, the electric chiller consumes electrical energy to generate cold energy, part of which is used directly for the cooling demand, while the remainder is stored in a storage tank by releasing cold energy during peak demand to balance the cooling load. The electric chiller model considers the input electric power and the refrigeration coefficient to calculate the output refrigeration power for a specific period of time. The refrigeration coefficient directly determines the energy efficiency, system’s energy consumption, and operating costs. It is suitable for commercial buildings, data centers, and industrial refrigeration, etc., where high refrigeration efficiency is required. The cold storage tank model is focused on the heat storage residual, heat loss rate, and charging and discharging power. It is used to simulate the thermal energy storage and release process of the cold storage tank. Its efficiency and heat loss rate have a significant impact on the system’s energy efficiency and thermal energy management. It is applicable to the district cooling system and the storage of cold energy in large-scale buildings, especially in the low valley of the energy load.

(1) Electric chiller

The electric chiller (EC) utilizes the phase change of refrigerant in different pressure states to absorb and release heat to achieve the cooling effect. Typical physical model equations are as follows [32]:

$${\mathrm{Q}}_{\mathrm{c}}^{\mathrm{E}\mathrm{C}}\left(\mathrm{t}\right)=\mathrm{C}\mathrm{O}{\mathrm{P}}_{\mathrm{E}\mathrm{C}}^{\mathrm{c}}{\mathrm{E}}_{\mathrm{E}\mathrm{C}}\left(\mathrm{t}\right)$$

(12)

where ${\mathrm{Q}}_{\mathrm{c}}^{\mathrm{E}\mathrm{C}}\left(\mathrm{t}\right)$, and ${\mathrm{E}}_{\mathrm{E}\mathrm{C}}\left(\mathrm{t}\right)$ are the EC output cooling power and input electric power, respectively, and $\mathrm{C}\mathrm{O}{\mathrm{P}}_{\mathrm{E}\mathrm{C}}^{\mathrm{c}}$ represents the EC cooling coefficient.

(2) Cooling storage tank

Cold storage tanks store the cold energy converted from the excess of other energy loads during the trough to improve the efficiency of energy utilization. The commonly used media for cold storage tanks are water and ice, which are clean, safe, and easily accessible, and their typical physical models are shown below [33]:

$${\mathrm{Q}}_{\mathrm{C}}\left(\mathrm{t}\right)=\left(1-{\mathsf{\mu }}_{\mathrm{c}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right){\mathrm{Q}}_{\mathrm{c}}\left({\mathrm{t}}_0\right)+\left({\mathrm{Q}}_{\mathrm{c}\mathrm{c}\mathrm{h}}\left(\mathrm{t}\right){\mathsf{\eta }}_{\mathrm{c}\mathrm{c}\mathrm{h}}-{\displaystyle \frac{{\mathrm{Q}}_{\mathrm{c}\mathrm{d}\mathrm{i}\mathrm{s}}}{{\mathsf{\eta }}_{\mathrm{c}\mathrm{d}\mathrm{i}\mathrm{s}}}}\right)\mathsf{\Delta }\mathrm{t}$$

(13)

where ${\mathrm{Q}}_{\mathrm{C}}\left(\mathrm{t}\right)$ and ${\mathrm{Q}}_{\mathrm{c}}\left({\mathrm{t}}_0\right)$denote the heat storage residual quantity of the accumulator at the time of $\mathrm{t}$ and ${\mathrm{t}}_0$, respectively, ${\mathsf{\mu }}_{\mathrm{c}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$ denotes the heat loss rate of the accumulator, ${\mathrm{Q}}_{\mathrm{c}\mathrm{c}\mathrm{h}}$ and ${\mathrm{Q}}_{\mathrm{c}\mathrm{d}\mathrm{i}\mathrm{s}}$ denote the heat charging and discharging power of the accumulator between the time of ${\mathrm{t}}_0$ and $\mathrm{t}$, respectively, and ${\mathsf{\eta }}_{\mathrm{c}\mathrm{c}\mathrm{h}}$ and ${\mathsf{\eta }}_{\mathrm{c}\mathrm{d}\mathrm{i}\mathrm{s}}$ denote the heat charging and discharging efficiency of the accumulator, respectively.

3.2.7. Modeling of Electricity–Heat–Gas Coupled Plant Unit

Electricity–heat–gas coupled equipment is a cogeneration unit that produces electricity and heat energy through simultaneous production of electricity and heat. The CHP unit in the electricity–heat–gas coupled system takes into account a number of factors, such as power generation, heat production, gas consumption, and start/stop status, and parameters such as the conversion efficiency, the heat exchange coefficient, the heat loss coefficient, and the gas-to-heat ratio. CHP systems are suitable for scenarios that require a stable supply of electricity and heat, such as industrial areas, commercial complexes, and urban residential areas, especially during peak energy demand. Such systems enhance energy security by reducing dependence on external energy sources, while lowering energy costs and environmental impacts. The flexibility of CHP allows it to adjust the ratio of power and heat output according to actual demand, ensuring system stability and reliability. Cogeneration units are classified into two types: a back-pressure type and steam extraction type. The coupling model of the back-pressure type cogeneration unit refers to a system that simultaneously utilizes a gas engine or a steam turbine to generate electricity, where the heat energy is used for heating or other industrial purposes through heat recovery equipment. It is highly economical and suitable for occasions with stable heat loads, taking the back-pressure type cogeneration unit as an example. Assuming that the relationship between power generation and power generation is constant, the energy conversion can be expressed as [34]:

$$\left\{\begin{array}{l}{\mathrm{p}}_{\mathrm{i},\mathrm{t}}^{\mathrm{CHP}}{\mathrm{I}}_{\mathrm{i},\mathrm{t}}^{\mathrm{CHP}}={\mathsf{\eta }}^{\mathrm{g}2\mathrm{e}}{\mathrm{g}}_{\mathrm{i},\mathrm{t}}^{\mathrm{CHP}}\\ {\mathrm{q}}_{\mathrm{i},\mathrm{t}}^{\mathrm{CHP}}{\mathrm{I}}_{\mathrm{i},\mathrm{t}}^{\mathrm{CHP}}={\mathsf{\eta }}^{\mathrm{g}2\mathrm{h}}{\mathrm{g}}_{\mathrm{i},\mathrm{t}}^{\mathrm{CHP}}={\mathsf{\eta }}^{\mathrm{HE}}\left(1-{\mathsf{\eta }}^{\mathrm{g}2\mathrm{e}}-{\mathsf{\eta }}^{\mathrm{L}}\right){\mathrm{g}}_{\mathrm{i},\mathrm{t}}^{\mathrm{CHP}}\end{array}\right.,\forall \mathrm{t}=\mathrm{T}$$

(14)

where ${\mathrm{p}}_{\mathrm{i},\mathrm{t}}^{\mathrm{CHP}}$, ${\mathrm{q}}_{\mathrm{i},\mathrm{t}}^{\mathrm{CHP}}$, and ${\mathrm{g}}_{\mathrm{i},\mathrm{t}}^{\mathrm{CHP}}$ denote the hourly power generation, heat production, and gas consumption of the CHP unit, kW; the binary variables, ${\mathrm{I}}_{\mathrm{i},\mathrm{t}}^{\mathrm{CHP}}$, denote the start-stop state of the CHP unit; the parameters, ${\mathsf{\eta }}^{\mathrm{g}2\mathrm{e}}$, ${\mathsf{\eta }}^{\mathrm{HE}}$, ${\mathsf{\eta }}^{\mathrm{L}}$, and ${\mathsf{\eta }}^{\mathrm{g}2\mathrm{e}}$ denote the conversion efficiency, heat transfer coefficient, heat loss coefficient, and gas-to-heat ratio of the CHP unit.

3.2.8. Modeling of Cooling-Heat–Power-Gas Coupling

The coupled cooling-heat–power-gas model (CCHPG) integrates the conversion and synergistic optimization between electricity, natural gas, heat, and cold energy, where the electricity, heat, and cooling loads and natural gas are involved. The conversion efficiency between different energy sources, such as natural gas to electricity and electricity to cooling, by means of the coupling coefficient, is also described. It is suitable for situations where multiple energy inputs and outputs need to be managed in an integrated manner, such as smart cities, industrial parks, and large commercial complexes. This model improves the energy utilization efficiency, reduces waste, lowers operating costs, and enhances system reliability and resilience. Application scenarios are wide-ranging, including smart grids, district heating and cooling networks, and integrated energy services. In a multi-energy system, the inputs are electricity and natural gas, and the outputs are electricity, heat, and cooling to meet different load requirements. Based on the concept of energy hubs and energy conservation, the relationship between inputs and outputs can be quantified via the following model [35]:

$$\left[\begin{array}{c}{\mathrm{E}}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\\ {\mathrm{Q}}_{\mathrm{h},\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\\ {\mathrm{Q}}_{\mathrm{c},\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\end{array}\right]=\left[\begin{array}{cc}{\mathrm{f}}_{\mathrm{e}\mathrm{e}}& {\mathrm{f}}_{\mathrm{g}\mathrm{e}}\\ {\mathrm{f}}_{\mathrm{e}\mathrm{h}}& {\mathrm{f}}_{\mathrm{g}\mathrm{h}}\\ {\mathrm{f}}_{\mathrm{e}\mathrm{c}}& {\mathrm{f}}_{\mathrm{g}\mathrm{c}}\end{array}\right]\left[\begin{array}{c}{\mathrm{E}}_{\mathrm{i}\mathrm{n}}\\ {\mathrm{G}}_{\mathrm{i}\mathrm{n}}\end{array}\right]-\left[\begin{array}{ccc}{\mathsf{\eta }}_{\mathrm{e}}& 0& 0\\ 0& {\mathsf{\eta }}_{\mathrm{h}}& 0\\ 0& 0& {\mathsf{\eta }}_{\mathrm{c}}\end{array}\right]\left[\begin{array}{c}\Delta {\mathrm{E}}_{\mathrm{s}\mathrm{t}\mathrm{o}}\\ \Delta {\mathrm{Q}}_{\mathrm{h},\mathrm{s}\mathrm{t}\mathrm{o}}\\ \Delta {\mathrm{Q}}_{\mathrm{c},\mathrm{s}\mathrm{t}\mathrm{o}}\end{array}\right]-\left[\begin{array}{c}0\\ {\mathrm{q}}_{\mathrm{h},\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}}\\ 0\end{array}\right]$$

(15)

where ${\mathrm{E}}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$, ${\mathrm{Q}}_{\mathrm{h},\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$, and ${\mathrm{Q}}_{\mathrm{c},\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$ denote the loads of electricity, heat, and cooling on the user side, respectively; ${\mathrm{E}}_{\mathrm{i}\mathrm{n}}$ and ${\mathrm{G}}_{\mathrm{i}\mathrm{n}}$ denote the inputs of electricity and natural gas, respectively; $\mathrm{f}$ denotes the coupling coefficients between different types of energy sources, e.g., ${\mathrm{f}}_{\mathrm{g}\mathrm{e}}$ denotes the efficiency of the conversion from natural gas to electricity, including that of the gas turbine and the absorption chiller efficiency; ${\mathrm{f}}_{\mathrm{e}\mathrm{e}}$ denotes the transformer efficiency from photovoltaic/wind/grid to electric energy; ${\mathrm{f}}_{\mathrm{e}\mathrm{c}}$ denotes the efficiency of the absorption chiller; $\mathsf{\eta }$ denotes the storage efficiency of electric, heat, and cold energy; $\mathsf{\Delta }\mathrm{E}$denotes the increase in energy storage; and ${\mathrm{q}}_{\mathrm{h},\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}}$denotes the unrecovered heat discard, which distinguishes the present model from a typical energy hub model.

3.2.9. Modeling of Dynamic Energy Hub

The dynamic energy hub (DEH) model in the literature [36] was constructed to more accurately simulate the energy conversion in the power system, especially considering the variations of different load rates such as the energy conversion efficiency, load factor, and performance data of the equipment. The model is suitable for applications in smart grids, distributed energy systems, and energy management in industrial parks. Literature [37] further developed a multi-timescale optimization strategy based on the DEH model from literature [36] to adapt to the efficiency changes of equipment under different operating conditions. An efficiency correction algorithm was developed to determine the time-varying coupling factor. In this study, the relationship between the equipment efficiency and load factor was built up for day-ahead, intraday and real-time scheduling. Such a modeling framework can better deal with the uncertainty and time dispersion in the energy supply and also improve the accuracy of the system operation and scheduling. Alternatively, for different energy conversion devices, the literature [37] fits a polynomial to obtain a specific expression for the efficiency as a function of the load factor. It is suitable for complex energy systems that require optimal scheduling on multiple time scales, especially in environments with high fluctuations. The energy conversion coupling can be expressed via a polynomial model, as follows [37]:

$${\mathsf{\eta }}_{\mathsf{\alpha }\mathsf{\beta }}=\mathrm{f}\left({\mathrm{R}}_{\mathsf{\alpha }\mathsf{\beta }}\right)$$

(16)

where ${\mathsf{\eta }}_{\mathsf{\alpha }\mathsf{\beta }}$ is the efficiency of the energy conversion device, and ${\mathrm{R}}_{\mathsf{\alpha }\mathsf{\beta }}$ is the load factor of the energy conversion device, i.e., the output capacity ratio.

$$\left[\begin{array}{c}{\mathrm{L}}_{\mathsf{\alpha }}\\ {\mathrm{L}}_{\mathsf{\beta }}\\ ⋮\\ {\mathrm{L}}_{\mathrm{n}}\end{array}\right]=\left[\begin{array}{cccc}\mathrm{f}\left({\mathrm{R}}_{\mathsf{\alpha }\mathsf{\alpha }}\right)& \mathrm{f}\left({\mathrm{R}}_{\mathsf{\beta }\mathsf{\alpha }}\right)& \cdots & \mathrm{f}\left({\mathrm{R}}_{\mathrm{n}\mathsf{\alpha }}\right)\\ \mathrm{f}\left({\mathrm{R}}_{\mathsf{\alpha }\mathsf{\beta }}\right)& \mathrm{f}\left({\mathrm{R}}_{\mathsf{\beta }\mathsf{\beta }}\right)& \cdots & \mathrm{f}\left({\mathrm{R}}_{\mathrm{n}\mathsf{\beta }}\right)\\ ⋮& ⋮& \ddots & ⋮\\ \mathrm{f}\left({\mathrm{R}}_{\mathsf{\alpha }\mathrm{n}}\right)& \mathrm{f}\left({\mathrm{R}}_{\mathsf{\beta }\mathrm{n}}\right)& \cdots & \mathrm{f}\left({\mathrm{R}}_{\mathrm{n}\mathrm{n}}\right)\end{array}\right]\left[\begin{array}{c}{\mathrm{P}}_{\mathsf{\alpha }}\\ {\mathrm{P}}_{\mathsf{\beta }}\\ ⋮\\ {\mathrm{P}}_{\mathrm{n}}\end{array}\right]-\left[\begin{array}{cccc}{\mathrm{s}}_{\mathsf{\alpha }\mathsf{\alpha }}& {\mathrm{s}}_{\mathsf{\beta }\mathsf{\alpha }}& \cdots & {\mathrm{s}}_{\mathrm{n}\mathsf{\alpha }}\\ {\mathrm{s}}_{\mathsf{\alpha }\mathsf{\beta }}& {\mathrm{s}}_{\mathsf{\beta }\mathsf{\beta }}& \cdots & {\mathrm{s}}_{\mathrm{n}\mathsf{\beta }}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathrm{s}}_{\mathsf{\alpha }\mathrm{n}}& {\mathrm{s}}_{\mathsf{\beta }\mathrm{n}}& \cdots & {\mathrm{s}}_{\mathrm{n}\mathrm{n}}\end{array}\right]\left[\begin{array}{c}{\mathrm{E}}_{\mathsf{\alpha }}\\ {\mathrm{E}}_{\mathsf{\beta }}\\ ⋮\\ {\mathrm{E}}_{\mathrm{n}}\end{array}\right]$$

(17)

where α, β…$\mathrm{n}$ are the elements of the energy form set, such as electricity, heat, cold, gas, etc., $\mathrm{L}$ is the output power vector, $\mathrm{P}$ is the input power vector, $\mathrm{s}$ is the attribution coefficient matrix of the energy storage device, $\mathrm{E}$ is the actual charging and discharging energy vector of the energy storage device, and ${\mathrm{R}}_{\mathsf{\alpha }\mathsf{\beta }}$ is the loading coefficient of the energy converting device, i.e., the output capacity ratio; the charging energy of the energy charging device is positive, and the energy charging device’s discharging energy is negative.

4. Optimization Scheduling of IESs

Multiple heterogeneous energy networks such as the power grid energy network, gas energy network, cold energy network, and heat energy network are involved in IESs. Interdisciplinary technologies include physics, chemistry, materials science, control science, artificial intelligence technology, optimization theory, economic principles, etc. Key techniques for comprehensive demonstration are concluded in Figure 3. More detailed analysis is presented in the following subsections.

IESs can be categorized by multiple time scales, including the day-ahead, intraday, and real-time stages. The coupling of green certificates and carbon trading mechanisms was considered under the diversified utilization of hydrogen energy [38]. The regulation level of renewable energy with the coupling mechanism is more effective in achieving economy and low carbon. Multi-spatial scale classification is conducted based on regional characteristics and divided into multi-region, park, and user levels. According to the system structure, it is classified as distributed, hierarchical, and centralized. The basic framework of interaction between typical parks and regional energy internet was introduced [39]. Therefore, the stratification phenomenon under geographical factors, scheduling factors, and energy management factors can be elaborated. The day-ahead optimization scheduling model was therefore proposed. The optimization objectives include cost minimization, energy efficiency maximization, carbon emission minimization, reliability optimization, etc. The demand-side response classification and resource integration in the participation of new energy were summarized [40]. Consequently, an integrated energy system optimization model and scheduling algorithm considering the demand response was proposed to achieve single-objective optimization under dual-carbon targets. A multi-objective optimization method for a park-level integrated energy system (PIES) was also reported [41]. Numerical simulation under different scenarios indicates that the proposed multi-objective optimal scheduling model can provide different scheduling strategies to achieve multi-objective optimization, including random optimization, robust optimization, and multi-scenario optimization. A stochastic optimization scheduling model considering extreme scenarios was proposed using extreme scenario weights combined with traditional stochastic optimization for scenario analysis [42]. CPLEX solver in MATLAB was used to achieve the goals of day-ahead economic efficiency and daily stability. A hybrid interval optimization method for interactive power management among distribution networks was proposed [43], considering building parameters, renewable energy, and load uncertainty. According to the classification of cooperative optimization, the cooperative optimization model emphasizes the coordination between different energy sources and energy systems to achieve the optimal operation of the entire system. A low-carbon optimal scheduling method combining hydropower, wind power, PV, and heat power was developed [44]. Through cascade carbon trading, the peak power load can be reduced without increasing operating cost so that the consumption of renewable energy can be thus alleviated. A two-stage collaborative optimization method that considers both long-term operation and short-term operation scheduling of the system was proposed [45]. It can achieve capacity optimization under long-term operation and good interaction with the power grid during daytime scheduling.

4.1. Multi-Time Scale Optimization Scheduling Model

Multi-timescale techniques are capable of handling multiple dynamic processes ranging from fast changing to slow evolving, providing IESs with a more refined and flexible scheduling approach for the system to be more skillfully scheduled through the accuracy of forecasts. The day-ahead phase usually relies on long-term forecasts, while on the contrary, the intraday and real-time phases to optimize the daily schedule rely on short-term and real-time forecasts. Multiple mechanisms such as demand response, carbon trading, and green certificate trading are considered to develop a multi-timescale model to respond to changes in customer demand and market price fluctuations. Multi-mechanism technology is suitable for energy market environments that require a high degree of flexibility and responsiveness, such as electricity markets, district heating and cooling systems, smart cities, and industrial zones, etc. By integrating different market and operational mechanisms, it provides IESs with a more flexible and cost-effective way to respond to changes in energy supply and the uncertainty of market conditions. Literature [46] proposed an IES model and a multi-timescale optimal scheduling method based on a demand response mechanism by introducing electric heating/cooling complementary substitution and horizontal time-shift demand at different stages of scheduling. A quantum sparrow search algorithm (QSSA) was applied to minimize the cost of adjusting the output power of the equipment. Literature [47] offset part of the carbon emissions through joint carbon trading and green certificate trading. It fully united the source-side and load-side flexible response resources, and effectively improved the level of wind power consumption under multiple time scales. Using hydrogen and carbon capture, a multi-timescale optimal scheduling model with a coupling device is constructed to realize the mutual conversion and complementarity between different energy systems. Literature [48] proposed an electricity–heat–hydrogen supply/demand balance model, where hydrogen energy can be dispatched and utilized in multiple microgrids. It effectively mitigated the effects of prediction errors by using model predictive control (MPC)-based rolling scheduling. On the other hand, literature [49] established a multi-timescale model by analyzing the real-time characteristics of cogeneration creep constraints, carbon capture equipment operation, and photovoltaic (PV) power generation. It used a fully neurodynamics-based optimization algorithm to compute one day ahead for an integrated urban energy system. A two-stage time-scale optimal scheduling model for hybrid energy storage was developed [50]. It solved the multi-timescale problem of heterogeneous energy sources and the co-operation of a hybrid energy storage system. For example, a mixed integer linear programming (MILP) problem can be solved via rolling optimization such as cutting-plane algorithms, branch-and-bound algorithms, and so on. Alternatively, a multi-timescale optimal scheduling model based on distributed model predictive control (DMPC) is a new type of control strategy [51,52]. It transforms the online optimization problem of a large-scale system into the optimal solution of each subsystem. The control strategy of each subsystem not only contains optimal control of itself, but also ensures it meets the requirements of the economic conditions through interactions with other subsystems. In order to realize the flexibility of multi-energy coordination and optimization, a multi-timescale optimal scheduling model was established to improve the flexibility of the power system [53]. It can effectively enhance the flexibility of the system operation by coordinating the output of the equipment, thus smoothing out the power fluctuation of electric heat and gas energy in different time scales.

Among the solution methods, the quantum sparrow search algorithm and improved particle swarm optimization can deal with complex and nonlinear problems under multiple regimes, with high dimensional and multi-peak problems. The system model with carbon capture was enhanced using a distributed neural dynamics optimization algorithm by considering reliability, robustness, flexibility, and privacy in the economic dispatch of integrated energy systems. MILP mainly deals with linear functions and integer and continuous variable optimization problems, and it is very flexible in modeling and is able to describe more complex real-world problems, but the solution complexity increases significantly with the size of the problem. On the other hand, the core idea of MPC is rolling time-domain optimization. It aims to predict the trajectory of the system in the time domain, where it is able to optimize the control strategy in real time by updating the prediction model and the optimization objective in a rolling fashion. However, it is very sensitive to prediction accuracy, and larger computational resources are required. When the system is complex and computationally intensive, it can be divided into multiple subsystems, from which DMPC is derived. The computational system chunking can be thus simplified for optimization. Simultaneously, it is able to balance the local control decision with the global optimization objective while reducing the centralized computational burden. Here, effective communication and coordination mechanisms are required to ensure consistency of decision-making among the subsystems. Furthermore, mixed integer linear programming models are able to describe more complex real-world problems, but the solution complexity is highly related to the problem size. The multi-time scale models are classified and summarized in this paper, as presented in

Table A1. Proposes and solves multi-time scale optimization scheduling models.

Model	Time Scale	Solved Problem	Solution Method	Remark
Multi-time scale optimal scheduling model under multiple mechanisms	Multiple mechanisms are considered for scheduling and demand response strategy optimization day-ahead, intraday and real-time stages	Considers demand response and market mechanisms such as carbon trading and green certificate trading and adapt to the flexibility and uncertainty of both supply and demand	Quantum sparrow search algorithm (QSSA), improved particle swarm optimization, mixed integer linear programming (MILP)	[46,47]
Multi-time scale optimal scheduling model with a coupling device	Based on the constructed coupling model, power is balanced and carbon trading costs are taken into account in the day-ahead, intraday and real-time processes	Considers hydrogen energy using carbon capture to achieve low-carbon operation	Model predictive control methods (MPC), fully distributed optimization algorithms	[48,49]
Multi-time scale optimal scheduling model based on hybrid energy storage	Based on the hybrid energy storage system (composed of battery and hydrogen storage), a two-stage time-scale model of fast and slow is established	Energy storage equipment optimization to improve energy efficiency and stability	MPC, MILP	[50]
Multi-time scale optimal scheduling model based on distributed model predictive control	Based on the MPC strategy, the basic scheduling plan is determined before the day, and the rolling optimization and feedback correction are carried out in real time within the day	Renewable energy and load demand uncertainty, computational efficiency, and system stability	Distributed model predictive control (DMPC)	[51,52]
Multi-time scale optimal scheduling model for multi-energy coordination	Day-ahead scheduling can coordinate the output of the equipment, and day-long real-time scheduling can smooth the power fluctuations of the electric hot gas on different time scales	Flexibility for coordinated optimization	MATLAB/YALMIP toolbox combined with GUROBI solver	[53]

of the Appendix.

4.2. Multi-Spatial Scale Optimization Scheduling Model

An IES is often very complex and encompasses a variety of energy forms and conversion techniques. Multi-spatial scale technologies are concerned with data representation and analysis at different spatial resolutions or scales. Regional integrated energy systems are intrinsically characterized by multiple levels and multiple subjects. Through the division of spatial scales, complex problems are decomposed into smaller and more manageable sub-problems. The micro-scale focuses more on local energy efficiency, while the macro-scale focuses more on the operation of large-scale energy networks and inter-regional energy exchange. The multi-spatial scale optimal scheduling model aims to achieve optimal energy allocation from local to global through centralized scheduling, distributed scheduling, and hierarchical scheduling. In centralized scheduling, a central controller is responsible for global decision-making; in distributed scheduling, decision-making is delegated to subsystems, which improves flexibility but requires coordination to avoid conflicts. In order to minimize the daily operating cost, a load cost optimization model of a regional distributed energy system for cooling and heating electricity consumption was constructed [54]. The distributed energy system consists of multiple energy conversion devices and related coupling units, which are coupled and converted to satisfy the multiple energy demands of the end-users. Literature [55] proposed a distributed optimal scheduling method based on an improved ADMM to reduce the system cost, being focused on the distributed optimal scheduling in an integrated electricity–gas–heat regional energy system. Hierarchical scheduling combines the advantages of distributed and centralized scheduling. For example, a hierarchical optimal scheduling method based on distributed autonomous and centralized coordinated design architecture was proposed [56]. A dynamic economic scheduling model was established in the upper layer, and an opportunity constraint model for autonomous energy management in multi-energy microgrids was established in the lower layer. The upper and lower layers were decoupled based on analytical target cascading (ATC), and only boundary electric power and thermal power need to be exchanged to obtain the global solution. The global optimal strategy was obtained through parallel microgrid computation based on iterative solving between layers. Literature [57] proposed a hierarchical distributed optimal scheduling decision-making method for a regional integrated energy system based on the cascade of analytical objectives. The upper layer was used by the regional integrated energy system operator (DIESO) for interacting with different energy networks, and the lower layer was used by the DIESO for interacting with subsystems and sub-subsystems. Literature [58] studied the joint optimal scheduling of multi-region IESs and the influence of the district heating network on the joint scheduling and established a two-layer model for the joint scheduling of multi-region IESs. The heat network provided a path to absorb excess energy so that the influence of heat load movement on IESs can be reduced. It ensured the independence of individual IESs while efficiently optimizing the energy scheduling between IESs. Literature [59] proposed a two-layer optimization model for multi-park distributed cooperation that did not depend on the accurate prediction of uncertainties such as source loads and tariffs. In the upper layer, the predictive decision-making in integrated scheduling can be achieved via the communication neural network. On the other hand, the lower layer adopted ADMM can be used to optimize the distribution of energy storage equipment, while protecting the privacy of data in each park. The performance is close to the theoretical optimal strategy under the premise of protecting the privacy of each park’s data.

Among the above algorithms, ATC mainly solves objective and constraint optimization problems with multiple layers, where it decouples the upper and lower layers by increasing the augmented Lagrange penalty function. It can simplify the problem structure, improve the computational efficiency, and identify and deal with the dependencies between different layers. On the other hand, the ADMM mainly deals with large-scale optimization problems and allows distributed computation and parallel processing by means of the separation and coordination strategy. Its solving process has better convergence, but it may be affected by the step size and convergence speed. Via the spatial structure, the integrated scale optimization scheduling models can be classified into regional distributed, regional layered, regional layered distributed, multi-regional layered distributed, and multi-park distributed, as shown in

Table A2. Proposes and solves the multi-spatial scale optimization scheduling models.

Model Type	Spatial Scale	Intended Solution	Method	Remark
Regional distributed optimal scheduling model	Energy systems within a single area	Improve the coupling and collaboration between energy systems in the region and reduce regional energy costs and CO2 emissions	Alternating direction method of multipliers (ADMM), MATLAB/YALMIP toolbox combined with CPLEX solver	[54,55]
Regional hierarchical optimal scheduling model	A hierarchy is added to a single region, which may include a regional control center on the upper level and a local control unit on the lower level	The upper level is responsible for overall optimization and coordination, while the lower level is responsible for specific energy supply and demand response	Analytical target cascading (ATC)	[56]
Regional layered distributed optimal scheduling model	Combining the characteristics of stratification and distribution, optimal scheduling is not only carried out at the regional level but also involves the distributed decision-making of different sub-regions or subsystems within the region	Problems such as data privacy, conflict of interest, and interactive power mismatch exist among multiple entities and better deal with heterogeneity and dynamics within the region	ATC	[57]
A multi-region hierarchical distributed optimal scheduling model	It involves energy scheduling and collaboration between multiple regions, each of which may adopt a hierarchical distributed structure	Deal with inter-regional energy trading, transmission, and coordination among different areas to achieve a more extensive range of optimization	ATC	[58]
Multi-park distributed optimal scheduling model	Optimization of energy systems across multiple campuses, such as various university campuses, residential complexes, or business parks	Each park can manage energy independently, while energy exchange and collaborative optimization can be carried out between parks	Communication neural networks (CommNet) enhance imitation learning and alternate direction multiplier method (ADMM) for two-layer optimization	[59]

of Appendix A.

4.3. Multi-Objective Optimal Scheduling Model

In order to improve energy efficiency and reduce costs, multi-objective optimal dispatch models have been developed to achieve optimal dispatch of IESs in recent years. Literature [60] constructed a multi-objective optimal dispatch model by combining multi-objective beluga whale optimization (MOBWO) with a price-based demand response (PDR) mechanism. It exhibited more a robust search capability and faster convergence to minimize the operating costs and maximize the environmental benefits, using non-dominated sorted beluga whale optimization (NSBWO). It combined the non-dominated sorted genetic algorithm II (NSGA-II) and the beluga whale optimization (BWO) algorithm. Literature [61] proposed a Q-learning-based multi-population dung beetle optimizer for multi-objective scheduling in hybrid integrated energy systems. It can dynamically and adaptively adjust the number of populations to enhance the information exchange between different sub-populations. Literature [62] proposed a multi-objective optimization model for regional integrated energy systems (RIES) from the perspective of external gas analysis of user satisfaction. Literature [63] established a multi-objective optimization method for integrating rural distributed IES solar collectors with air source heat pumps to achieve economic and environmentally friendly operation. Literature [64] proposed a multi-objective interaction scheduling optimization model for energy interaction scheduling and price optimization in a regional multi-intelligent IES body. It is based on Nash bargaining cooperative game theory to achieve economic and stable operation of each body, giving the whole region the objectives of economy, flexibility, and carbon emission. Literature [65], in the field of marine renewable energy, established a multi-energy complementary system using multi-objective optimization to achieve efficient energy use of ocean temperature difference energy, wind energy, and solar energy. For large ships, literature [66] proposed a combined cooling and heating power generation system with energy storage. The multi-objective grey wolf optimization (MOGWO) algorithm was applied to optimize the three objectives of total power, total cost, and annual CO2 emission reduction. Literature [67] investigated smart home energy management through a multi-objective optimization approach to balance the energy payment cost, user satisfaction, and self-sufficiency.

Multi-objective dung beetle optimization with q-learning (MODBO-QL) is suitable for dealing with complex and high-dimensional decision space problems [30]. With the adaptive capability gained through reinforcement learning, the multi-population strategy leads to a better balance between global search and local exploration. At the same time, a large number of iterations are required to learn an effective strategy. Nash bargaining cooperative game theory provides a fair and theoretically effective solution to the multi-objective problem by seeking the Pareto-optimal allocation [64]. However, it may receive multiple equilibrium solutions, making it difficult to predict the final negotiation outcome in practical applications. In the multi-objective grey wolf optimizer (MOGWO), it simulates the perceptual abilities of gray wolves, including smell, vision, and hearing [66]. Behaviors such as searching, tracking, and aggregation can be facilitated during the optimization process. Compared with traditional heuristic stochastic search algorithms, the MOGWO algorithm requires fewer parameters and converges faster so that it is suitable for solving high-dimensional optimization problems. NSGA-II can effectively maintain the diversity of the population and guide the search direction to find a more uniformly distributed solution set in multi-objective problems, but its computational complexity is high [68]. In the future, AI technologies, especially machine learning and deep learning, can be applied to optimize the operation and maintenance of IESs by analyzing a large amount of data [69]. Therefore, the energy demand, power generation costs, and market prices can be predicted to optimize the allocation of resources and reduce the operating costs. Objectives and solutions from the multi-objective optimal scheduling models are as shown in

Table A3. Proposes and solves the multi-objective optimal scheduling models.

Research Object	Optimization Objective	Intended Solution	Method	Remark
Integrated energy system for industrial park	Minimize operating costs and maximize environmental benefits	Achieve low-carbon economic dispatch and improve the consumption rate of renewable energy	Non-dominated sorting genetic algorithm II (NSGA-II) and beluga whale optimization (BWO)	[60]
Hybrid integrated energy system	Minimize economic costs and polluting gas emissions	Lower economic costs and reduce carbon emissions	Multi-objective dung beetle optimization with q-learning (MODBO-QL)	[61]
Integrated district energy systems	Economy, carbon emissions, and activity efficiency	Adapt to changing energy supply, demand, and the impact of customer-side load fluctuations on the system	NSGA-II	[62]
Integrated rural energy systems	Economic and environmental protection	Rural energy consumption is characterized by sloppy management, poor economics, and high gas emissions	NSGA-II with dynamic crowding distance	[63]
Integrated multi-regional energy systems	Economy, flexibility, and carbon emissions	Combine multiple energy types interact with each other for stable operation, including economic and environmental improvement throughout the region	Alternate direction multiplier method (ADMM)	[64]
Integrated offshore energy systems	Improve the economic viability and reliability of the system in providing energy and freshwater supplies	The goal is to reduce energy waste, achieve high conversion efficiency and minimize equipment investment	NSGA-II	[65]
Cold, heat, and power cogeneration system for large marine vessels	Thermal performance, economy, and environmental friendliness	Promote sustainable development and emission reduction in the maritime industry	Improved multi-objective grey wolf optimizer (IMOGWO)	[66]
Smart home integrated energy system	Optimizing energy payments, end-user satisfaction, and end-user self-sufficiency preferences	Multiple technologies, including electrical energy storage systems and electric vehicles (EVs), are considered	Mixed integer linear programming (MILP), general algebraic modeling system (GAMS) combined with CPLEX solver	[67]

of the Appendix A.

4.4. Uncertainty Optimization Scheduling Model

In the planning and operation of IESs, uncertainty analysis is crucial to ensure system reliability and efficiency. Uncertainty handling techniques allow the system to adapt to the changing energy environment and effectively improve the resilience and reliability in the power system [70]. However, they may introduce additional computational complexity and model uncertainty, especially in the context of global climate change and energy transition. In stochastic optimization methods, some parameters in the model are considered as random variables with known probability distributions. Literature [71] proposed a multi-stage stochastic optimization model based on a scenario tree for an AC-DC hybrid distribution network in response to PV intermittent uncertainty. The day-ahead discrete decision variables of the multi-stage stochastic optimization model can be adaptively adjusted with the change of uncertainty information in intraday and real-time stages. It is more in line with the operational requirements of an AC-DC hybrid distribution network under actual high percentage of PV penetration. Accordingly, the in situ consumption of PV and the peak shaving and valley filling of the system can be realized in applications. In this study, the second-order cone relaxation technique was used to transform the nonlinear model into a linear model, and the mixed-integer second-order cone planning model was used to solve the model more efficiently. Literature [72] established a two-stage stochastic optimization method based on scenario analysis by considering the uncertainty of source loads in a multi-energy hybrid grid. Probabilistic analysis and an improved K-means clustering algorithm were used to reduce the generated scenarios. The scheduling plans were developed to flexibly cope with the uncertainty based on different risk preferences using a mixed-integer second-order conical programming model. The robust optimization approach focuses on performance in order to find a solution in the worst case scenario. It does not rely on the probability distribution of random variables, but solves for the limit or range of uncertainty. For example, literature [73] proposed a two-stage robust allocation optimization model with multiple uncertainties. The multiple uncertainties in PV, wind, electricity, heat, and cooling loads were considered, and the fluctuations of the uncertainty parameters by means of adjustable robustness metrics were described. The decision maker can adjust the robustness parameters according to the risk preference to make the system more robust. In this study, the column and constraint generation algorithm (C&CG) was used to solve the two-stage robust optimal allocation model. Literature [74] established a network model suited for the electricity–gas–heat energy system under the extreme cases of the day-ahead and real-time phases. With the largest load and wind forecast errors, the iterative method was used to solve the master problem and sub-problems by utilizing the C&CG algorithm and strong binary theory. Literature [75] proposed a two-stage robust optimal scheduling model for a multi-energy complementary system under dual uncertainty of source and load. By constructing the moment uncertainty sets of load and wind power output, the two-stage robust model carries out a dyadic dynamic transformation using a dyadic dynamic planning algorithm. Literature [76] used a data-driven distributional robust optimization method, combining kernel density estimation and integrated paradigm constraints, to construct an uncertainty set for PV and wind power. A distributed robust optimization (DRO) approach was used for optimal scheduling under the worst case of random variables. Also, a linear programming solver was used to solve the DRO model and obtain the optimal allocation solution. Multi-scenario optimization deals with uncertainty by considering a series of possible scenarios, each with a corresponding probability of occurrence. All scenarios are considered together in the optimization process, so the expected value or weighted average is used to find a solution under multiple scenarios. Literature [77] used a day-ahead multi-scenario stochastic optimization algorithm and an intraday fuzzy opportunity constrained optimization algorithm to model the uncertainty of load and PV forecast errors. To reach the minimum in the operation cost, carbon emission cost, and adjustment cost, the scheduling plan within the day ahead is adjusted using flexible adjustment (FAD). In solving the uncertainty problem, the nonlinear model is usually transformed into a linear model so that it can be solved via the mixed-integer second-order conic programming model; the C&CG algorithm solves the uncertainty problem by decomposing it into the main problem and sub-problems, where the optimal solution can be found through continuous iteration. Various methods have been adopted to deal with these uncertainties, including stochastic optimization, robust optimization, and multi-scenario optimization, as shown in

Table A4. Uncertainty optimal scheduling models proposed and solving methods.

Method Class	Model	Uncertainties	Intended Solution	Method	Remark
Stochastic optimization	Multi-stage stochastic optimization model	Generating PV output scenarios using Monte Carlo with improved k-means clustering for scenario reduction	Reducing decision bias and realizing system economy and flexibility based on PV uncertainties	Mixed-integer second-order cone programming	[71]
	A two-stage stochastic optimization approach based on scenario analysis	Probabilistic analysis of source load forecast errors using mixed and conditional distributions	Flexibility to cope with uncertainty by developing scheduling plans based on different risk appetites	Mixed-integer second-order cone programming	[72]
Robust optimization	Two-stage robust configuration optimization model	Constructing PV, wind, and multi-load uncertainty sets	Improve system reliability and reduce load loss	Column and constraint generation algorithm (C&CG), big M method	[73]
	The two-stage robust optimization model	Constructing uncertainty ensembles for wind power and load forecast errors	Improve system robustness, wind power consumption capacity, and reduce additional costs due to fluctuations in electricity prices	C&CG	[74]
	A two-stage robust optimization scheduling model	Modeling wind power and load uncertainty using moment uncertainty ensemble	Improve the robustness of the system while overcoming the problem of over-conservatism and the risks associated with uncertainty	Pairwise dynamic programming algorithms	[75]
Distributed robust optimization	Distributed robust optimal scheduling model	Modeling of PV and wind power output uncertainty using kernel density estimation and latin hypercube sampling methods	Maintain optimal balance between economic efficiency and operational robustness, carbon emission reduction	A data-driven robust optimization approach	[76]
Multi-scene optimization	Day-ahead multi-scenario stochastic optimization model, intraday fuzzy chance-constrained optimization model	Uncertainty modeling of load and PV forecast errors via multi-scenario techniques and fuzzy theory	Mobilize system energy flexibility and overcome the impact of uncertainty on scheduling	Linear solver	[77]

of the Appendix A.

4.5. Collaborative Optimization Scheduling Model

Multi-energy synergistic optimization technology achieves efficient utilization and optimal dispatch of energy by considering the interactions and conversions between different energy systems, e.g., electricity, heat, natural gas, cold energy, etc. The crucial issue is to solve the coupling problem between different energy systems. The overall energy efficiency and economy can be therefore improved by coordinating different energy systems. Multi-energy interconnection coordination using optimization technology is suitable for areas with diverse energy demands and supply conditions. It can benefit from multi-energy interconnection when multiple energy supplies are demanded in places such as large industrial parks, smart cities, university campuses, etc. To better guide the practice of IES optimal scheduling, cooperative scheduling between different energy systems can be supplemented to ensure the stability and reliability of the whole system, especially in the case of an unstable energy supply. Source–load cooperative optimization is the coordination between the energy supply side (source) and the demand side (load). Literature [78] proposed a source–load cooperative optimal scheduling strategy to optimize energy production and consumption by predicting and responding to the dynamics of both parties. Shared energy storage cooperative optimization considers the role of the energy storage system as a buffer between energy supply and demand. Literature [79] reported a new energy sharing framework that considers hydrogen trading, where shared energy storage operators (SESOs) can facilitate hydrogen trading by setting time-of-day (TOD) pricing. A hierarchical optimization scheduling method was also proposed based on the Stackelberg game. It simplifies the complex Stackelberg game process into an information interaction problem between the upper and lower layers. Additionally, a two-tier optimization method via combining particle swarm optimization (PSO) and MILP is suitable for scenarios like residential, industrial, and commercial RIES structures. Source–load–storage co-optimization also considers the energy supply, demand, and storage segments. Literature [80] established a two-tier scheduling model for source–load–storage co-operation with a double game at the system level and the hydrogen production level, reaching balance between economic conflicts and consistency in absorbing wind power. Multi-energy subsystem co-optimization is for the integrated energy system containing multiple energy subsystems, through optimizing the conversion and interaction between different energy subsystems, to achieve integrated management and gradient utilization of energy. Literature [81] proposed a regional multi-energy system optimal scheduling model based on the cloud edge synergy theory, which can effectively improve the scheduling data processing capacity and the economics of regional multi-energy system scheduling. Literature [82] reported a two-tier optimal scheduling model for regional multi-energy systems with the cloud service application layer and the edge computing layer as the upper and lower optimal scheduling layers. The model was solved using a multi-objective whale optimization algorithm with the objectives in the optimal scheduling cost and minimum scheduling data transmission. Accordingly, it can effectively improve the scheduling data processing capacity and achieve economy of regional multi-energy system scheduling. Co-optimization of distributed energy systems emphasizes local energy self-sufficiency and nearby consumption. Literature [83] established a distributed cooperative optimization scheduling strategy for IESs based on edge computing and a consistency algorithm, which returns the optimization results of distributed cooperative computing at the edge layer to the cloud and device layers to achieve optimal scheduling, and proposed the distributed group consistency algorithm (DGCA), which uses two consistency protocols to solve the electricity, heat, and gas coupling problems. The reliability and anti-interference capability can be improved by optimizing the distribution and operation of distributed energy sources.

In the above methods, MILP is used in combination with PSO to simplify the multivariate and large-scale nonlinear optimization problem into a linear optimization problem, which reduces the complexity of Stackelberg’s game problem and improves the accuracy and speed of the computed solution. For the multi-objective whale algorithm, it mainly deals with multi-objective optimization problems. It is superior in its global search ability and has better convergence performance so that multiple high-quality Pareto solution sets can be found. However, the parameter selection and adjustment may be more complicated. On the other hand, the DGCA is used in multiple distributed energy units, achieving group consistency by exchanging information among distributed individuals. It can reduce the dependence on centralized control, but faces challenges in communication efficiency and information synchronization. The models and solutions for cooperative optimal scheduling are provided in

Table A5. Cooperative optimal scheduling models and solutions.

Model	Co-Optimization	Intended Solution	Method	Remark
Source–load cooperative optimal scheduling model	Increase electricity-to-gas technology installations on the source side to increase the space for wind power output and establish time-of-day tariffs and demand response models on the load side	Solve problems of inefficient and irrational energy use in rural areas and optimal low-carbon economic dispatching	MATLAB/YALMIP toolbox combined with CPLEX solver	[78]
Collaborative optimized dispatch model for shared energy storage	Optimization of IES connected to shared energy storage	Increase utilization of RESs and effective reduction of operating costs of systems	Particle swarm optimization (PSO), mixed integer linear programming (MILP)	[79]
Source–load–storage cooperative optimal scheduling model	Renewable energy at the source to meet user demand, natural gas at the load side to the cogeneration unit to meet the user’s cooling and heating needs, and each storage device will be excess electricity, heat, cooling, gas storage	Consider fine-grained demand response and source–load–storage synergistic hydrogen production to increase large-scale wind power consumption	MATLAB/YALMIP toolbox combined with CPLEX solver	[80]
Multi-energy subsystem synergistic optimal scheduling model	Integration and coordination of energy subsystems such as electricity, heat, natural gas, and cooling for efficient energy conversion and distribution	Satisfy higher data processing requirements for energy equipment and loads, complexity of operating status of multiple energy equipment	Mathematical planning methods, multi-objective whale optimization algorithm	[81,82]
Cooperative optimization scheduling model for distributed energy systems	When there are multiple independent operating entities or energy production and consumption units, decisions can be made independently and overall optimization can be achieved through coordination mechanisms	Solve the IES optimization scheduling problem in electrical, thermal, and gas coupling	Distributed group consistency algorithm (DGCA)	[83]

of the Appendix A.

5. Future Challenges and Prospects

IES faces a number of challenges in terms of technical limitations, storage capacity, conversion efficiency, and infrastructure requirements. Firstly, with the frequent occurrence of extreme weather in recent years, existing studies are more mature regarding modeling the coupling of multiple forms of energy in IESs under normal operating conditions. However, there is still insufficient modeling and analysis for possible failure events in the coupled system. Secondly, how to tap the passive carbon reduction in addition to active CO₂ capture needs to be addressed in different energy segments. With the access of large-scale renewable energy, its intermittency and volatility lead to energy storage technology development in the storage capacity. Improving the efficiency of energy conversion equipment such as CHP and P2G is crucial to reduce overall energy consumption and carbon emissions. Hydrogen in the hydrogen-containing integrated energy system serves as an important medium for the conversion of various energy sources, and the efficiency and economy of the various types of conversion technologies associated with it directly affects the development of the system as a whole. The technologies of electric hydrogen production and hydrogen fuel cells are still not sufficiently mature due to the low degree of commercialization and high cost. In terms of infrastructure, the expansion and optimization of natural gas pipeline networks and heat networks are crucial to the realization of multi-directional flow and complementary use of energy; at the same time, the convergence of transportation and information networks provides new resources of flexibility for the energy system, but it puts forward higher requirements for the construction and management of infrastructure. The effective operation of IESs requires the integration of advanced information and communication technologies (ICT) to achieve rapid data transmission and processing, which places higher demands on the ICT infrastructure. In response to these challenges, the following outlook is proposed to optimize the scheduling of the IES to enhance the reliability and economy of the system.

(1) Improvement of IES resilience

The enhancement of IES resilience has become particularly urgent in the global climate change. IES resilience involves the ability of the grid to withstand, recover, and adapt in the face of extreme weather events. To meet this challenge, future IESs will rely more on the application of intelligent and automated technologies. This includes real-time monitoring using advanced sensors and smart monitoring systems, as well as the use of adaptive control techniques to automatically adjust grid operations to maintain stability. Internet of things (IoT) and AI algorithms will play a key role in data collection, analysis, and forecasting, improving the system’s responsiveness to extreme weather events and decision-making efficiency. In addition, the construction of a diversified energy structure, such as the integration of wind, solar, and energy storage devices, will enhance the IES’s regulation and emergency backup capabilities to ensure the security of energy supply under extreme weather conditions.

(2) Zoning and layering balance

The future development trend in IESs is to develop the model for zonal autonomy and local balancing. It emphasizes the efficient use and optimal dispatch of energy in the region through intelligent energy management and control technologies. Zonal autonomy means dividing the IES into smaller zones, each of which is able to produce, distribute, and consume energy independently, thus increasing the flexibility and responsiveness of the system. In situ balancing, on the other hand, is focused on achieving optimal matching of energy supply and demand within these regions. It can promote the synergistic optimization of distributed energy resources, such as distributed power generation, energy storage, and demand response. Furthermore, the establishment of inter-regional energy trading will find the optimal allocation and complementarity of energy sources and improve overall energy efficiency. User-side participation and response are also encouraged to realize a more dynamic and interactive energy management system.

(3) Digital intelligence advancement

The application of emerging technologies and digital intelligence is becoming a key force in driving industry progress. The application of artificial intelligence, IoT, big data analytics, and cloud computing in IESs is promoting the intelligent and digital transformation of the industry. Advances in energy storage technology provide IESs with greater regulation capabilities, enabling them to respond more effectively to fluctuations in supply and demand and extreme weather events. The development of internet of energy (IoE) technology enhances energy interconnection and improves the efficiency of energy management and dispatch. The application of artificial intelligence and big data technologies, on the other hand, provides powerful support in energy demand forecasting and resource planning and management, making energy dispatch more accurate and efficient. The integration of these technologies not only increases the operational efficiency of the energy system, but also strengthens the reliability and flexibility of the system. With the continuous progress of technology, the future energy system will rely more on data-driven decision-making and automated operation to achieve optimal allocation and efficient use of energy.

6. Conclusions

In the face of the double pressure in global energy consumption and environmental protection, the emergence of IESs provides an innovative solution for realizing the efficient energy utilization and the balance between supply and demand. This paper reviews the main research in IES optimal scheduling technology. The concept, composition, and classification of an integrated energy system is firstly introduced. Then, the coupling relationship between multiple energy sources is investigated and studied in depth. Based on the coupling transformation and complementary utilization between heterogeneous energy flows, the electricity/heat/gas/cold in the system equipment unit can maintain its own unique energy quality attributes when coupling with other energy equipment. Different types of integrated energy system scheduling in different regions are categorized and evaluated. It covers many points such as dynamic scheduling in time scale, block control in space scale, simultaneous realization of multiple objectives, uncertainty analysis and treatment of the system, and synergistic optimization of source network, load, and storage, etc. The study exhibits that different types of optimal scheduling strategies can effectively improve the reliability and economy of the system; however, the efficient operation of the IES is faced with some problems, e.g., the complexity of energy coupling, the low efficiency of energy conversion, the lack of energy efficiency, the immature and costly technology, the poor adaptability in the face of unexpected conditions, etc. To address these issues, this paper discusses emerging technologies in the optimal IES scheduling process. It also provides important information in utilizing artificial intelligence and big data to promote energy interconnection, improve system resilience, and achieve efficient energy use with zonal autonomy.