Research on Temperature-Rise Characteristics of Motor Based on Simplified Lumped-Parameter Thermal Network Model

Abstract

The thermal management of a driving motor is related to the performance and economy of the vehicle. The lumped-parameter thermal network (LPTN) method can provide a model basis for motor temperature-rise control and effectively shorten the development cycle of motor thermal performance design. In this study, an 80 kw water-cooled permanent magnet synchronous motor was used and the accurate thermal model of a motor was built using the LPTN. On the basis of the accurate thermal model, the simplified thermal model of a motor was obtained by reducing the complexity of the model. The temperature-rise test of the end winding and magnetic steel of the motor was carried out under some working conditions. The test conditions were selected according to continuous external characteristics and operating characteristics of the motor. Compared with the experimental results, the temperature-rise error of the two thermal models was less than 5%. The temperature-rise error of the simplified thermal model was less than 3% compared with the accurate thermal model. Therefore, the simplified thermal model can be used to quickly predict the temperature rise of the motor.

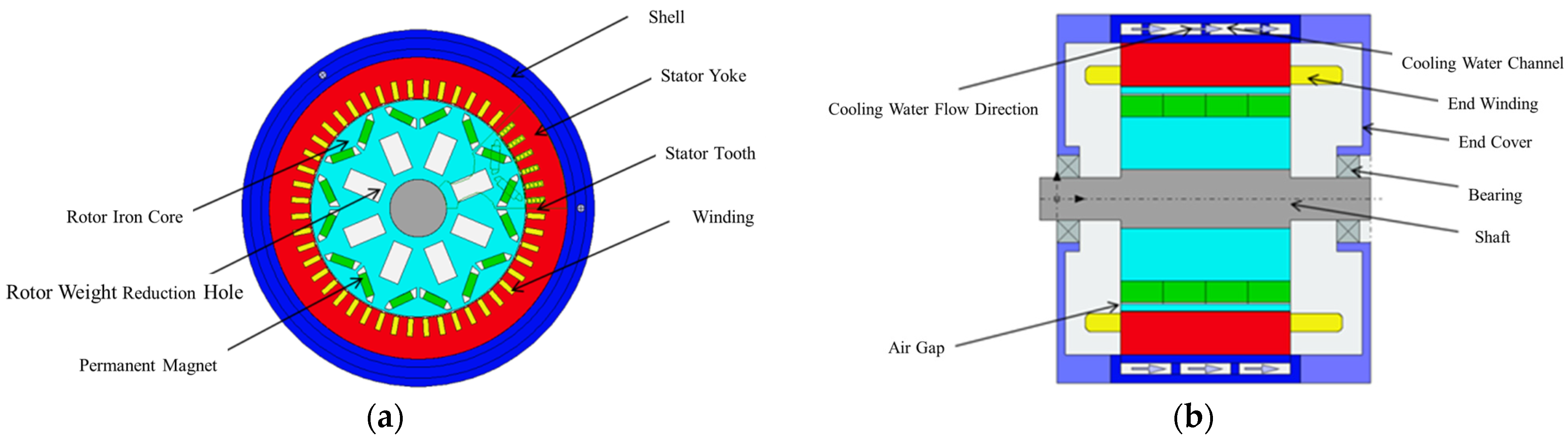
1. Introduction

The permanent magnet synchronous motor (PMSM) has attracted widespread attention due to its advantages of low vibration noise, good torque stability, high control accuracy, and high torque density [1,2]. The permanent magnet is easily affected by temperature. In order to ensure the stability and service life of the permanent magnet synchronous motor, it is necessary to cool the motor efficiently. The cooling methods of the motor mainly include air cooling, water cooling, and oil cooling, among which water cooling is widely used [3]. It is necessary to study the thermal characteristics of water-cooled permanent magnet synchronous motors.

The main calculation methods of motor temperature-rise characteristics include finite element analysis (FEA) [4,5,6,7,8], computational fluid dynamics (CFDs) [9,10,11], and the lumped-parameter thermal network (LPTN) [12,13,14]. The FEA mainly solves the motor model through the heat transfer equation to accurately simulate the thermal distribution of each part of the motor [15]. Compared with the LPTN, the FEA has the advantage of being able to handle more complex geometries [16,17]. Its disadvantages are that the processing time is too long, the thermal model needs to be simplified for easier use [18], and the temperature result of the FEA solution is highly dependent on the quality of meshing. The CFDs method uses the heat transfer equation and the fluid dynamics equation. The application object is broadened to dynamic fluid, and the convective heat transfer between the end winding and the air and the convective heat transfer between the shell and the air can be analyzed [19,20]. The accuracy of the CFDs method is quite high [21], and the cooling method can be optimized by simulating the temperature distribution of the fluid [22]. The disadvantages of the CFDs method are that the simulation requires a longer processing time and requires higher meshing quality, which poses challenges for a user’s hardware level and modeling experience.

The LPTN method performs a fast thermal parametric analysis of the study object by dividing it into a number of basic thermal elements. These basic thermal elements are usually represented by thermal nodes and thermal resistances. The LPTN method can be used to quickly predict the effect of different factors on the temperature rise of the motor and to analyze the electrical characteristics of the motor for different motor temperature rises [23,24,25]. But the LPTN relies on empirical formulas for high-precision modeling, and the heat conduction between solid components is simulated well. The disadvantage is that the convective heat transfer coefficient cannot be solved. In early research, researchers considered both the radial and axial heat transfer paths of the motor and the obtained model was more complicated [26,27]. In order to solve the problem that the axial thermal network model of the motor was too complex, Boglietti A et al. [28] ignored the axial heat conduction of the motor and only considered the radial heat conduction of the motor. In the research process, a simplified thermal network model of the motor was established, most of the thermal resistance calculation formulas were given, and the final error was less than 2.5%. Mellor et al. [26] divided the induction motor into 10 key nodes, and the obtained model can be used to estimate the temperature online. Amitav Tikadar et al. considered the temperature distribution of the air gap between the stator and the rotor when modeling but neglected to accommodate for the fact that the air-gap thickness would change at high temperatures [14]. Based on the research of Boglietti A, many researchers have carried out formula derivation and experimental verification on key thermal resistance and difficult-to-calculate thermal resistance [29,30]. Volkswagen AG comprehensively summarizes the heat transfer mechanism of motors with different cooling methods and builds LPTN models according to different cooling methods. The simulation results verify the wide applicability of the lumped-parameter method [31].

The LPTN represents the components of the motor with lumped parameters such as interconnected thermal resistance and thermal capacitance [32], which make the model simpler and faster. The disadvantage is that the temperature distribution of any point of the motor cannot be obtained. Some studies have simplified the LPTN model, highlighting the simple and fast advantages of the LPTN model, but the verification conditions used are relatively simple and different from the actual conditions [33,34]. With its fast and reliable characteristics, the LPTN model can also be coupled with electromagnetic field simulation to improve the simulation accuracy of the temperature field and electromagnetic field [35,36].

At present, most of the motor thermal circuit analyses analyze the main parts of the motor and rarely analyze all the parts. The thermal circuit analysis rarely considers the circumferential temperature transfer path of the components and lacks the prediction of the temperature rise of the important components of the motor when it is running under typical operating conditions. This paper studies a water-cooled automotive permanent magnet synchronous motor with a rated power of 80 kW, and based on the literature [26,27,30,37,38,39,40,41,42,43,44,45], the accurate thermal network and simplified thermal network models are constructed by considering the circumferential temperature transfer effects of the casing, the rotor, the stator core, and the permanent-magnet components. Under the typical test conditions of the whole vehicle, the accuracy of the constructed one-dimensional thermal network model in predicting the temperature rise of important parts of the motor is validated. Firstly, a one-dimensional accurate thermal model of the motor is established by the LPTN. Considering the circumferential conduction thermal resistance, the heat exchange model at the air gap and the equivalent thermal resistance calculation of the winding in the slot are optimized. The rotor structure is divided in detail and finally, a simplified motor thermal model is obtained.

2. Motor

A water-cooled flat wire interior permanent magnet synchronous motor (modified and manufactured by Jilin University) is taken as the research object. The water channel structure is a spiral water channel with a rectangular section, and the winding is a flat copper wire wrapped with an insulating layer. The convective heat transfer coefficients brought about by the flow of cooling water in the internal runners of the motor casing are solved by fluid simulation calculations using STAR CCM+ 17.04.

Table 1. Motor parameters.

Parameters	Value	Unit
Rated Torque	150	N m
Rated Speed	5000	RPM
Rated Power	80	kW
Max Speed	15,000	RPM
Number of Poles	8	-
Number of Stator Slots	48	-
Air-Gap Thickness	0.7	mm
Shell Cushion Diameter	220	mm
Outer Diameter	260	mm
Shaft Diameter	42	mm

shows the motor parameters.

Each pole of the motor rotor (each pole accounts for a 45° central angle) is installed inside the rotor by two pairs of magnetic strips, and there is a weight-reducing hole on each pole rotor. Figure 1 shows the radial and axial structure of the motor.

3. Establishment of Accurate Thermal Model

The simulation runs on a PC with an i7-10700 CPU @ 2.90 GHz core and 16 GB of RAM. AMESim (2020.1). The simulation running parameters are shown in

Table 2. Simulation running parameters.

Parameters	Value/Description	Units
Print interval	1	s
Sampling frequency	1	Hz
Simulation type	Single run	-
Integrator type	Standard integrator	-
Tolerance	1 × 10−7	-
Simulation mode	Dynamic	-
Solver type	Regular	-
Error type	Mixed	-

.

The thermal network model constructed by the thermal circuit analysis method needs to divide the motor into several units, and each unit consists of one or more nodes. In order to successfully apply the LPTN to build a thermal model, the following assumptions need to be made for the motor:

(1)

The heat source of the motor is continuously and evenly distributed.

(2)

Mechanical loss is ignored in the thermal model.

(3)

The motor is a barrel motor.

(4)

The heat transfer time constant does not change with time.

(5)

The thermal conductivity and heat capacity are fixed values.

In the operation of the motor, convection heat transfer in contact with the fluid, the conduction cooling of the parts themselves, and the contact heat conduction and heat dissipation of the parts are mainly generated. Therefore, the main thermal resistance includes convective thermal resistance, conductive thermal resistance, and contact thermal resistance. The key to building a thermal model by thermal circuit analysis is to solve the thermal resistance of each component.

Table 3. Thermal resistance calculation formula of motor parts [26,30,37,38,39,40,41,42,43,44].

Motor Parts	Thermal Resistance	Computing Formula
Shell	Convective heat transfer coefficient with cooling water	$h={\displaystyle \frac{\mathrm{N}\mathrm{u}\mathsf{\lambda }}{D_{hy}}}$
	Radial thermal resistance	$R_{sh}={\displaystyle \frac{1}{2\pi {\lambda }_{sh}l}}ln\left({\displaystyle \frac{D_{sh}/2}{\frac{D_{sh}}{2}-T{h}_{sh}}}\right)$
Stator	The contact thermal resistance with the shell	$R_{ho\_air}={\displaystyle \frac{{Th}_{ho\_air}}{{\lambda }_{air}{A}_{air}}}$
	Radial conduction thermal resistance of yoke	$R_{ra\_sy}={\displaystyle \frac{1}{2\pi {\lambda }_{ra\_si}{l}_{si}}}ln\left({\displaystyle \frac{{Do}_{si}}{{Do}_{si}-\frac{{Th}_{sy}}{2}}}\right)$
	Axial conduction thermal resistance of yoke	$R_{ax\_sy}={\displaystyle \frac{l_{si}}{\pi {\lambda }_{ax}\left[{Do}_{si}^2-{\left({Do}_{si}-{Th}_{si}\right)}^2\right]}}$
	Radial conduction thermal resistance of tooth	$R_{ra\_st}={\displaystyle \frac{1}{r_{ta\_ca}·2\pi {\lambda }_{ra\_si}{l}_{si}}}ln\left({\displaystyle \frac{{Di}_{sy}}{{Di}_{st}}}\right)$
	Axial conduction thermal resistance of tooth	$R_{ax\_st}={\displaystyle \frac{l_{si}}{{\lambda }_{ax\_si}{H}_{st}{W}_{st}{N}_{ss}}}$
Winding	Thermal resistance between winding and stator iron core	$R_{ax\_st}={\displaystyle \frac{Th{E}_{im\_air}}{{\lambda }_{im\_air}{Ai}_{slot}{N}_{slots}}}$
Air gap	Equivalent thermal resistance	$R_{air}={\displaystyle \frac{1}{h_{air}{A}_{air}}}$
Internal air	Convective heat transfer coefficient between fluid and solid interface	$h_{fas}=C_{cur1}\left(1+C_{cur2}ve{l}^{C_{cur3}}\right)$

shows the calculation method for the main motor components. Abbreviations of the variables are shown in Nomenclature.

Based on reference [40], this paper considers the circumferential thermal resistance of the rotor and provides an equivalent division of the rotor section with two magnetic stripes per pole. The equivalent thermal resistance of the rotor part needs to be divided into several different approximate hollow cylinders, and then the equivalent thermal resistance is used to solve the problem. Figure 2 shows the approximate structure of each stage rotor before and after equivalence.

The equivalent thermal resistance is calculated according to the hollow cylinder:

$$R={\displaystyle \frac{2\pi }{\varphi }}{\displaystyle \frac{\mathrm{l}\mathrm{n}\left(\frac{r_o}{r_i}\right)}{2\pi \lambda l}}$$

(1)

where r_i and r_o are, respectively, the inner and outer diameters of the hollow cylinder; l is the length of the hollow cylinder; ϕ is the angle of the center of the component; and λ is the thermal conductivity of the material.

4. Establishment of Simplified Thermal Model

After the construction of the accurate thermal model of the motor, the number of nodes exceeds 150. The temperature-rise characteristics of the motor can be predicted by using the accurate thermal model, but the model is more complicated. Compared with the accurate thermal model, the simplified thermal model reduces the number of nodes for calculating the axial temperature transfer of the motor and mainly considers the radial and circumferential temperature transfer of the motor. The simplified thermal model considers the circumferential equivalent thermal resistance of the stator yoke and the rotor and further divides the two parts on the basis of the accurate thermal model. The simplified thermal model also calculates the equivalent thermal resistance between the winding in the slot and the stator teeth by a new method and considers the influence of rotor thermal expansion and contraction on the air-gap thickness and influence of temperature on the thermal physical parameters of the air-gap.

4.1. Simplified Stator Yoke Part

The stator yoke is regarded as a hollow cylinder. Considering that the temperature change near the stator tooth and slot of the stator yoke will inevitably cause the circumferential temperature to change in the stator yoke, the circumferential thermal resistance is calculated. For a hollow cylinder or a hollow cylindrical section, the heat flow path is defined as a line along the average radius, and its integral basis can be written as an θ angle and swept along the full ϕ angle of the cylindrical section. For constant cross-sectional area A(θ) = (r_o − r_i), the calculation formula of circumferential thermal resistance of hollow cylinder is as follows:

$$R={\displaystyle \frac{\delta }{\lambda A}}={\int }_0^{\varphi }{\displaystyle \frac{1}{\lambda \left(r_o-r_i\right)l}}d\theta {\displaystyle \frac{r_o+r_i}{2}}={\displaystyle \frac{\varphi }{2\lambda l}}{\displaystyle \frac{r_o+r_i}{r_o-r_i}}$$

(2)

The integral and associated variables are shown in Figure 3.

The division of the stator yoke is shown in Figure 4 [45].

4.2. Simplified Winding Part

The equivalent thermal resistance of the winding is calculated according to the method introduced in the literature [27]. The stator slot is equivalent to a rectangular slot, and the insulation material outside the copper wire and the air is divided into two layers, which are evenly distributed on the outer side of the winding. The thicknesses of the two sides are d_i and d_a, respectively. The sum of the two is expressed in d, h is the height of the rectangular slot, and b is the width of the rectangular slot.

The total thermal resistance between the groove and the surrounding nodes is as follows:

$$R_{ix}={\displaystyle \frac{d_i}{h{\lambda }_i}}+{\displaystyle \frac{d_a}{h{\lambda }_a}}, R_{iy}={\displaystyle \frac{d_i}{w{\lambda }_i}}+{\displaystyle \frac{d_a}{w{\lambda }_a}}$$

(3)

$$R_{x0}={\displaystyle \frac{b}{h{\lambda }_{smix}}}, R_{y0}={\displaystyle \frac{h}{b{\lambda }_{smix}}}$$

(4)

$$R_x=0.5\left(R_{ix}+{\displaystyle \frac{R_{x0}}{6}}\right), R_y=0.5\left(R_{iy}+{\displaystyle \frac{R_{y0}}{6}}\right)$$

(5)

$$R_s={\displaystyle \frac{R_x{R}_y}{Q_{s}l\left(R_x+R_y\right)}}\left(1-{\displaystyle \frac{R_{x0}{R}_{y0}}{720R_x{R}_y}}\right)$$

(6)

Q_s is the specific volume power in the rectangular slot. The total thermal resistance of the connection between the node and the groove can be calculated by the following formula:

$$R_{s\text{-}node}=R_s{\displaystyle \frac{{\mathrm{\Phi }}_{sTot}}{{\mathrm{\Phi }}_{s\text{-}node}}}$$

(7)

In the formula, Φ_sTot is the total circumference of the slot and Φ_s-node is the length of the connection surface between the slot and the stator teeth and the stator yoke.

4.3. Rotor and Air Gap Part

The rotor part is further divided and the circumferential conduction thermal resistance is considered. The structure of each rotor is divided as shown in Figure 5. Considering the real situation, the influence of the thermal expansion and contraction of the rotor on the air-gap thickness is increased. The air-gap thickness has the following relationship with temperature:

$$\mathsf{\delta }={\delta }_0-k_{Fe}{r}_m\mathsf{\Delta }T$$

(8)

In the formula, δ₀ is the initial thickness of the air gap and k_Fe is the thermal expansion coefficient of iron, which is 10.4 × 10⁻⁶.

4.4. Simplified Thermal Model

The permanent magnet synchronous motor mainly consists of a case, cooling-water jacket, stator core, windings, air gap, rotor core, magnets, shaft, internal air, and front and rear end caps. The simplified thermal network model in the establishment process, the rotor, stator, windings, and air gap are divided in detail before the thermal circuit equivalent. The nodes of the heat path after the equivalence represent the average temperature of the components. The heat path model usually consists of heat capacity and thermal resistance, and losses are added for heat-generating components. Then, according to the direction of heat flow in the motor, the thermal circuit model of each component is connected to form the overall thermal circuit model of the motor. The model can be defined in terms of parameters by using global variables, formulas, or expressions. The simplified thermal network model has no more than 20 nodes, which is greatly reduced compared with the accurate thermal model. Figure 6 shows the simplified thermal model built in AMESim and

Table 4. Number of motor model nodes.

Motor Parts	Accurate Thermal Model	Simplified Thermal Model
Shell	20	2
Stator	48	6
Winding	32	4
Rotor	32	7
Internal air	2	-
Revolution axis	20	-
Grand total	154	19

shows the number of model nodes before and after simplification.

5. Experimental and Simulation Results

5.1. Test Conditions and Setup

Figure 7 displays the diagram of the motor test bench. During the test, the dynamometer was maintained at a constant speed mode according to test conditions, the dynamometer was powered by the frequency converter cabinet, the motor was powered by the battery simulator, and the motor-cooling water was provided by the cooling-water circulators. The data-acquisition box collected parameters such as motor torque, speed, thermocouple sensor temperature, bus voltage, inverter cabinet voltage, battery simulator power, voltage and current, dynamometer speed and torque, and power. And there were 11 thermocouples arranged to measure the temperature of the motor end windings and magnets.

The test conditions were selected according to the continuous external characteristics of the motor. Figure 8 shows the distribution of the test conditions of the motor. For the stator, in-slot windings, and end windings, the highest temperatures generally occurred at the end windings due to the heat dissipation path. In addition, when the motor was running at low speed and high torque, the winding current was higher and the loss was higher. When the motor was running at a high speed in the constant power region, the core losses were higher. Therefore, when selecting the test conditions for the end winding, according to the maximum external characteristic curve of the motor, take the rated speed as the reference, select two low-speed and high-torque working conditions on its left side, and select two constant power and high-speed working conditions on its right side. The experiment was completed by using a type K thermocouple to measure the temperature of the end winding, and the measured temperature results were collected and analyzed by a data-acquisition system. The accuracy of temperature measurement is ±(0.05% rdg. +0.5 °C), and the digital display resolution of the temperature measuring instruments is 0.01 °C. During the test measurement, two temperature sensors were firstly arranged at the two neutral points of the end winding, and then five temperature sensors were evenly arranged on the surface of the end winding to measure the temperature. The test points of the end winding are shown in

Table 5. Transient condition points of motor end winding.

Test Points	Speed (RPM)	Torque (N m)	Time (s)
1	2967	104	1800
2	4775	125	3600
3	6679	80	1800
4	9000	80	3600

.

The temperature of the magnet steel is generally slightly lower than the rotor temperature near the air gap. In this paper, the temperature of the thermal model rotor is verified by the temperature of the magnet steel. Two low-speed and high-torque conditions points were selected on the left side of the rated speed, and a constant power and high-speed conditions point was selected on the right side of the rated speed. During the rotor magnet temperature measurement test, the temperature sensor arrangement was as shown in Figure 9. Temperature sensors were arranged in the third and fourth layers of the magnet to measure the temperature of the magnet at three operating points. The thermocouple wires were introduced through wire holes drilled in the rotor laminations, to the motor rotor shaft, glued to the walls of the rotor shaft cavity, through the hollow rotor shaft of the motor, and finally connected to the temperature data acquisition card. The thermocouple sampling frequency was one temperature value per second. The experimental conditions of magnet steel are shown in

Table 6. Transient conditions points of motor magnet.

Test Points	Speed (RPM)	Torque (N m)	Time (s)
5	2000	135	2964
6	4000	140	3255
7	12,000	50	2459

.

5.2. Results Comparison

The three-dimensional electromagnetic field loss analysis is carried out through the three-dimensional electromagnetic field simulation software JMAG 21.0, which fully considers the influence of magnet segmentation and skin effect on the loss solution, thus improving the accuracy of the copper consumption, iron consumption, and magnet eddy current loss solution, providing accurate heat source input for the motor thermal network model. The electric power and winding losses at the input of the motor are derived directly and indirectly through tests, respectively, and the friction losses of the motor are derived through empirical formulas, thus indirectly deriving the iron losses of the motor. The experimental motor iron losses are compared with the iron losses obtained through the JMAG simulation, the simulated iron losses are corrected, and finally, the loss of each part of the motor is obtained. Figure 10 shows the accurate thermal model and simplified thermal model temperature rise diagram of the end winding.

It can be seen from Figure 10 that for the test point 1 of the end winding, the simulated temperature-rise curve and the experimental curve of the two thermal models have good following performance when the break point is ignored, and the errors of the two models are very close. For test point 2, the error of the accurate thermal model is smaller in the temperature-rise stage, and the accuracy of the simplified thermal model is higher in the motor-cooling process. At test point 3, the simulation accuracy of the accurate thermal model is higher, but the error of the simplified thermal model is still less than 5%. Under the condition of test point 4, the temperature-rise curve error of the simplified thermal model is larger, and the error is basically about 2%, which is 50% higher than the maximum absolute error of the accurate thermal model.

Figure 11 is the temperature-rise diagram of the accurate thermal model and the simplified thermal model of the magnet steel. It can be seen in Figure 11 that the absolute error of the accurate thermal model is maintained at about 4% at test point 5 and the absolute error of the simplified thermal model is slightly higher at about 5%. Under the second test conditions, the error of the accurate thermal model is kept within 5% and the error of the simplified thermal model is about 6%. The absolute error of the simplified thermal model is about 2% and the simulation error of the accurate thermal model is about 3%. At test points 6 and 7, the reason for the higher accuracy of the simplified thermal model is that the simplified thermal model only reflects the average temperature of the key components of the motor, while the accurate thermal model has more hot nodes and predicts a wider range of temperature points, so the error may be slightly larger after averaging.

6. Conclusions

In this paper, an 80 kw water-cooled permanent magnet synchronous motor was used to build a model of the motor by the LPTN method to study the temperature-rise characteristics. Based on the accurate thermal model, the simplified thermal model was optimized. The two models were verified by the end winding of the motor and the conditions experiment of the magnet steel. The conclusions are as follows:

(1)

The simulation results of the two models for the end winding and the magnet are basically consistent with the experiment results. The simplified thermal model is obtained on the basis of the accurate thermal model. The number of thermal network nodes is greatly reduced, but the error of the temperature-rise curve is not much different. It is proved that the simplified thermal model is not only simple but can also predict the temperature rise of the motor well.

(2)

In the end winding experiment and simulation, the temperature difference of the two thermal models basically increased with the running time. The temperature difference error of the two thermal models was large only at the speed of 4775 r/min and the torque of 125 Nm, and at the speed of 6679 r/min and the torque of 80 Nm. In general, the accurate thermal model has slightly less error in the temperature simulation results for the end winding compared to the simplified thermal model.

(3)

In the experiment and simulation of magnet steel, the simulation error of the accurate thermal model for low speed and high torque is smaller, and the simulation results of the simplified thermal model for high speed and low torque are more consistent with the experimental data. In general, the simulation error of the two models for magnet steel is not much different.