Optimised Two-Layer Configuration of SESS-CCHP System Considering Wind and Light Output Correlation and Load Sensitivity

Abstract

With the gradual depletion of fossil energy sources and the diversification of users’ energy demand, combined cooling, heating and power (CCHP) microgrids have become a hot technology to improve energy efficiency and promote efficient and synergistic energy operation. However, the uncertainty and correlation of wind power and photovoltaic (PV) outputs have posed a great challenge to the reliability of CCHP system operation, so CCHP systems are often equipped with energy storage devices to improve system flexibility to ensure the reliability of energy supply. However, system-owned reserves still have shortcomings such as high investment O&M costs and large space requirements. As an emerging model, “shared energy storage” can reduce the investment pressure of users and open up new ways for the economic and stable operation of CCHP systems. Therefore, based on the scenario of wind and solar power correlation and considering different types of load flexibility, this paper proposes to construct a shared energy storage station (SESS)-CCHP double-layer synergistic optimal allocation model. The model incorporates the consideration of the actual operation strategy of the CCHP system in the planning stage of energy storage. An example analysis shows that SESS reduces the total operating cost of the CCHP system by 25.96% and improves the new energy consumption rate by 10.46% compared with no energy storage. Compared with the system independently configured with energy storage, the cost saving is 2.14%, thus validating the effectiveness of the proposed model.

1. Introduction

With the current global energy and environmental problems, vigorously promoting the development of clean energy, and actively exploring a new form of energy industry, has become the focus of attention at home and abroad. Based on the resource endowment, it is urgent to promote energy revolution, ensure energy supply and achieve energy structure transformation [1,2]. The cold, heat and power (combined cooling heating and power (CCHP)) system as one of the important ways of distributed power generation, based on the physical framework of the traditional microgrid into the cold, heat and gas three forms of energy, to the core of the electric power system, breaking the power supply, cooling and heating system separate planning, operation of the existing model, fully exploiting the form of energy use of diversity and flexibility and efficiently achieving the stepwise use of primary energy can be widely used in shopping centres, schools, industrial parks and other regional integrated energy systems, and is of great significance in promoting energy reform [3,4]. However, CCHP microgrid application is gradually accompanied by the complex diversification of energy structure and energy demand, and CCHP microgrids are facing the problem of a significantly weakened system flexible regulation capability while ensuring energy supply. In order to cope with this problem, considering that the user-side cold, heat and electricity loads of CCHP microgrids can participate in system dispatch as flexible loads, and the flexibility of the three types of loads participating in dispatch at the same time will be higher compared to the power demand response [5], if integrated demand response (IDR) is introduced at the user side of the microgrid, it will help to improve the energy utilisation and reduce the cost of energy supply and use [6,7]. Therefore, it is important to study the economic optimal scheduling and planning problem for CCHP microgrids containing IDR. There are many research results in this area, and reference [8] demonstrates that in CCHP microgrids, the IDR mechanism that considers multiple types of loads can enhance CCHP flexibility and new energy consumption to a greater extent than the demand response that only considers a single-load type. Reference [9] presents an optimisation framework for energy management of CCHP customers that incorporates demand response. It considers how CCHP customers can flexibly participate in IDR through load aggregators or energy management centres in the context of electricity market reforms, and investigates the role of IDR in improving system economics and promoting renewable energy consumption. The findings imply that while IDR resource involvement enhances the microgrid’s economy and self-sufficiency, the robust optimisation model strengthens the system’s capacity to manage uncertainty risk. Reference [10] investigates how CCHP microgrids engage with the grid through participation in demand response initiatives, highlighting the significance of demand response in microgrid coordination with the broader grid. These studies have shown that IDR plays an important role in improving the clean energy utilisation and economics of the system.

At the same time, energy storage technology, with its characteristics at both ends of the ‘source-charge’, can smooth the fluctuation of clean energy output, which provides an important support for the development of a multi-energy complementary microgrid system. The CCHP microgrid structures discussed in the references [5,6,7,8,9,10] all demonstrate the role of the energy storage system in smoothing the new energy generation curve, which highlights the core position of energy storage technology in the CCHP system. Nevertheless, existing studies mainly focus on the impact of energy storage on the operating cost of CCHP systems, while insufficient attention has been paid to the comparison between the economic benefits brought by energy storage and the high investment cost, and the long-term payback cycle of energy storage also poses a challenge in practical applications [11]. Inspired by sharing economy enterprises such as Uber and Airbnb, the ‘shared energy storage’ model combines the concept of a sharing economy with large-scale energy storage power plants, which promotes the efficient use of energy by emphasising the right of use rather than ownership, and by taking advantage of the aggregation effect of centralised energy storage and the complementary nature of load behaviors, which may become a new way to solve the current challenges [12]. Currently, the research on a shared energy storage model is still in the preliminary stage. Reference [13] introduced the concept of ‘energy storage capacity rental’, in which the renter stores the surplus electricity to the provider, who charges according to the rented capacity and time. Aiming at the limitations of the operation mode of the energy storage provider, reference [14] proposed a new mode combining self-operated power and shared energy storage, and established a cooperative scheduling model of the distribution network including the Shared Energy Storage System (SESS), which effectively reduces the difference between the peaks and valleys of net loads in the distribution network, and verified the effectiveness of the method through case studies. Reference [15] studied how to optimise the allocation of new energy power station clusters according to the performance characteristics of different energy storage systems when adopting the shared energy storage trading model. The study evaluates the positive impact of this model on improving the use efficiency of energy storage equipment, enhancing the absorption capacity of new energy sources and economic benefits. The above literature demonstrates the importance of the SESS service model in promoting the widespread adoption of energy storage technologies by considering the three key dimensions of system operation flexibility, energy absorption capacity and economics.

From the above studies, it is clear that, while independent studies of IDR and SESS have been more than sufficient, there are relatively few cases of applying the combination of these two to CCHP. For example, reference [16] explores the application of SESS in CCHP microgrids without addressing the impact of demand response on loads or evaluating the comparative advantages of SESS versus individual self-built energy storage, limiting the wider application of the findings. IDR has a significant impact on the optimal operation of microgrids and energy storage allocation strategies; therefore, it is particularly important to study the synergy between IDR and SESS and its impact on microgrid systems. In addition, most of the existing studies perform optimal scheduling and allocation in deterministic wind power scenarios, ignoring the uncertainty of wind power, which may weaken the practicality of decision making. Therefore, it is necessary to incorporate the study of wind power uncertainty. A common approach is to predict the future wind power output through certain probability indicators based on existing wind power (WT) and photovoltaic (PV) output data, and to obtain a large number of samples using sampling techniques, and then to obtain representative scenarios through scenario reduction techniques in order to assess the impact of uncertainty on the optimal operation of the system [17,18]. At the same time, there is a correlation between the natural properties of wind and solar energy, and this correlation is particularly evident in wind turbines and photovoltaic power generation in the same region [19]. Considering this correlation of wind and solar output can improve the accuracy of typical output scenarios [20]. Reference [21] analysed the correlation between PV output and prediction error through an Archimedean Copula function, demonstrating ways to incorporate correlation in prediction models to improve prediction accuracy. However, many microgrid optimal scheduling and allocation studies often ignore this correlation between new energy generation, resulting in a failure to achieve optimal decision making.

A comprehensive analysis shows that the optimisation research considering the integration of IDR and SESS for CCHP microgrid optimisation is still in its infancy, and there are research gaps in various aspects. As shown in

Table 1. Status of studies on the correlation of IDR with SESS and renewable energy output.

Ref.	IDR	SESS	WT and PV Output Correlation
[5,6,7,8,9,10]	🗸	🗴	🗴
[11,12,15,16]	🗴	🗸	🗴
[17,18,21,22]	🗴	🗴	🗸
Proposed	🗸	🗸	🗸

, the shortcomings of the existing literature are mainly focused on the following key aspects: (1) there is a relative lack of research cases on the integration of IDR and SESS in CCHP microgrid optimisation; (2) research on SESS services in CCHP microgrids tends to overemphasise the operating costs of the system, while the payback of the SESS operator is relatively underexamined; (3) in the optimal dispatch and planning studies of microgrids, the relationship between wind power and PV power generation is considered, and in planning studies, the correlation between wind power and PV power generation is not sufficiently considered, which may affect the accuracy of decision making and the economics of the system.

Therefore, this paper proposes a two-layer cooperative optimal configuration model for the SESS-CCHP system based on the influence of the correlation of wind power output. Firstly, the non-parametric kernel density estimation and Copula function are used to generate the scenarios of wind power output with correlation, which is used as the basis for planning the SESS-CCHP system. Then, a two-layer synergistic optimal configuration model is constructed, which integrates the demand response of power, heat and cold energy to achieve the synergistic optimisation of SESS and CCHP microgrids. Finally, a simulation case is used to validate the solution strategy of the model and to analyse the impact of load flexibility within the microgrid on energy storage planning and total system cost. The main research work of this paper is as follows:

(1)

The Copula function is used to generate the output scenarios considering the correlation of wind and solar power generation, which provides the basic data for the subsequent system optimisation.

(2)

Based on the wind and solar power output correlation scenarios, a two-layer collaborative optimal allocation model of the SESS-CCHP system considering IDR is proposed to be constructed, and the validity of the model is verified by comparing different scenarios.

(3)

The impact of the base pricing of SESS services on its payback period and profitability is explored, which provides a reference of pricing strategy for SESS operators.

(4)

The impact of the degree of integrated demand response on SESS planning and total system cost is assessed, revealing the role of demand response in system economics.

The work allocation of this study is specified as follows. Section 2 focuses on the WP and PV output correlation scenario generation method, which provides the basic data for system optimisation. Section 3 describes the main structure of the SESS-CCHP system. The Section 4 establishes a two-layer cooperative optimisation configuration model for the SESS-CCHP system. Section 5 verifies the validity and practicality of the model through real case analysis. Section 6 summarises the main findings and conclusions of this study, providing guidance for future research directions and practical applications.

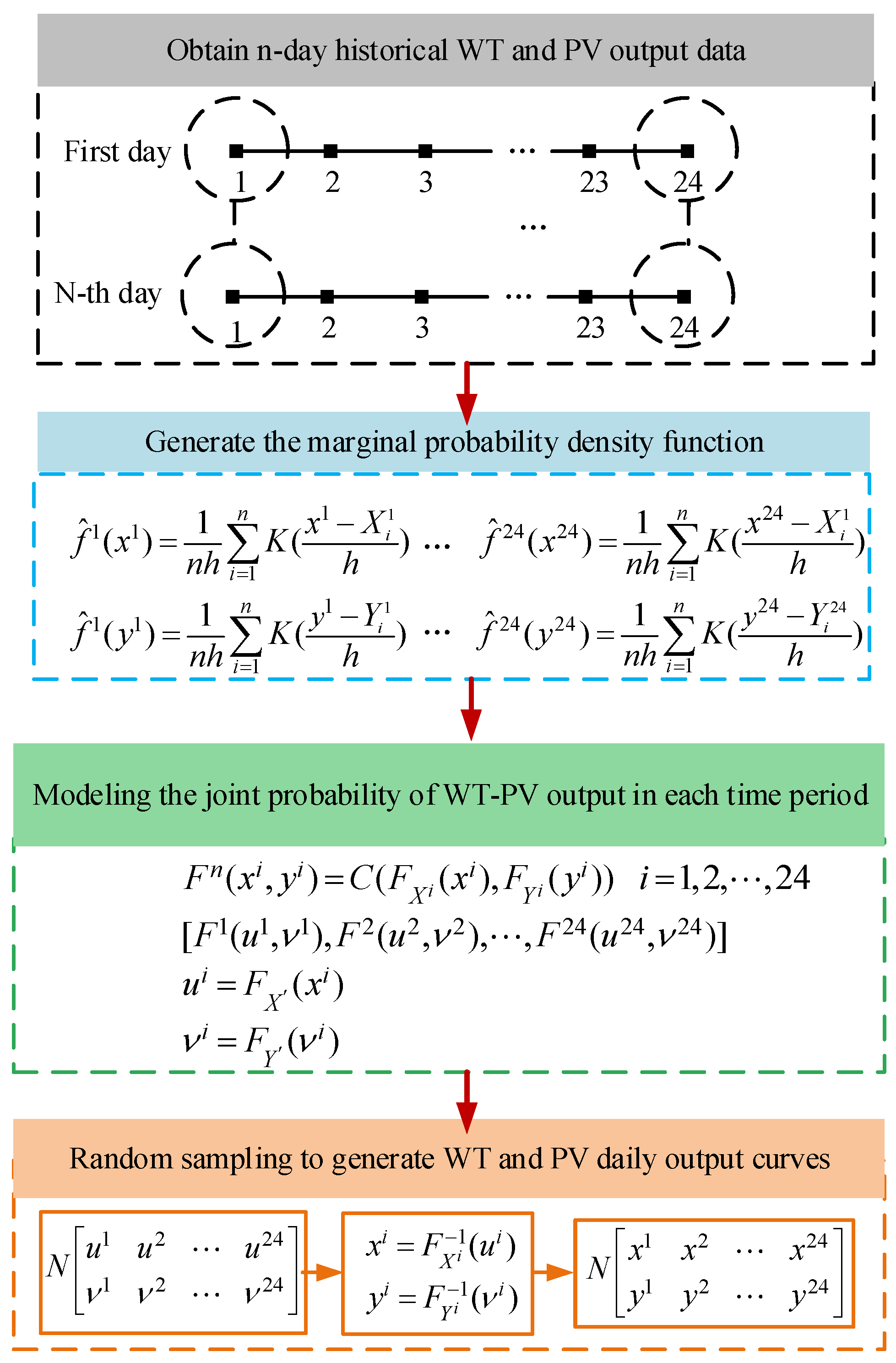
2. Scenario Generation Methods That Take into Account the Relevance of Scenery

There will always be a degree of uncertainty in the production of WT and PV electricity because of the inherent fluctuations in solar and wind energy. Furthermore, these two energy sources have a high correlation in a particular location. To ensure the stable and secure functioning of a multi-CCHP system, it is imperative to take into account the stochastic fluctuations of various renewable energy sources and their interconnections throughout the planning and operating phases.

By utilising the individual distribution functions of each variable to determine the combined distribution function, the Copula function describes the link between random variables [22]. The simulation results are significantly influenced by the type of Copula function that is used. The two families into which copula functions are primarily divided are the elliptic distribution family, which includes Normal-Copula and t-Copula, and the Archimedean distribution family, which includes Frank-Copula, Gumbel-Copula and Clayton-Copula [23]. Which Copula function effectively captures the relationship between the two variables depends on the specifics of WT and PV generation in the planning zone. We evaluated the correlation between wind and solar outputs by computing the Empirical-Copula function, and we utilised the Euclidean distance, the Kendall rank correlation coefficient and the Spearman rank correlation coefficient to identify which Copula function was most appropriate [24,25]. When there is a small Euclidean distance between the Empirical-Copula function and the optimum Copula function, their rank correlation coefficients are shown to be closely aligned. After selecting the best Copula function, we generate scenarios that include the correlations between WT and PV outputs using the scenario generating technique shown in Figure 1.

The procedures for creating situations with WT and PV outflow correlation are as follows, as illustrated in Figure 1:

(1)

Historical WT and PV output data were collected, ensuring that the data were presented in hourly time points ($x$ and $y$ represent WT and PV output).

(2)

A Gaussian kernel function was used to create the probability density functions of the WT and PV outputs for each time interval throughout the course of a 24-h period using the kernel density estimation approach.

(3)

The joint probability distribution function of WT and PV generation for each time period based on the preferred Copula function was constructed (in the figure, ($F_{X^i}(x^i)$ represents the cumulative distribution function of WT for each time period and $F_{Y^i}(Y^i)$ represents the cumulative distribution function of PV output for each time period).

(4)

In order to generate the typical daily curves, which take into account the correlation and stochasticity of the wind and light outputs, the joint probability distribution function for each time period must be sampled. Based on the sampling results, the inverse transformation method is used to obtain the WT and PV outputs for each time period.

Due to the large number of direct samples and low computational efficiency, we used the K-means clustering algorithm to cluster the $N$ sets of sampling results in order to generate representative typical day scenes and calculate the probability of occurrence of each scene.

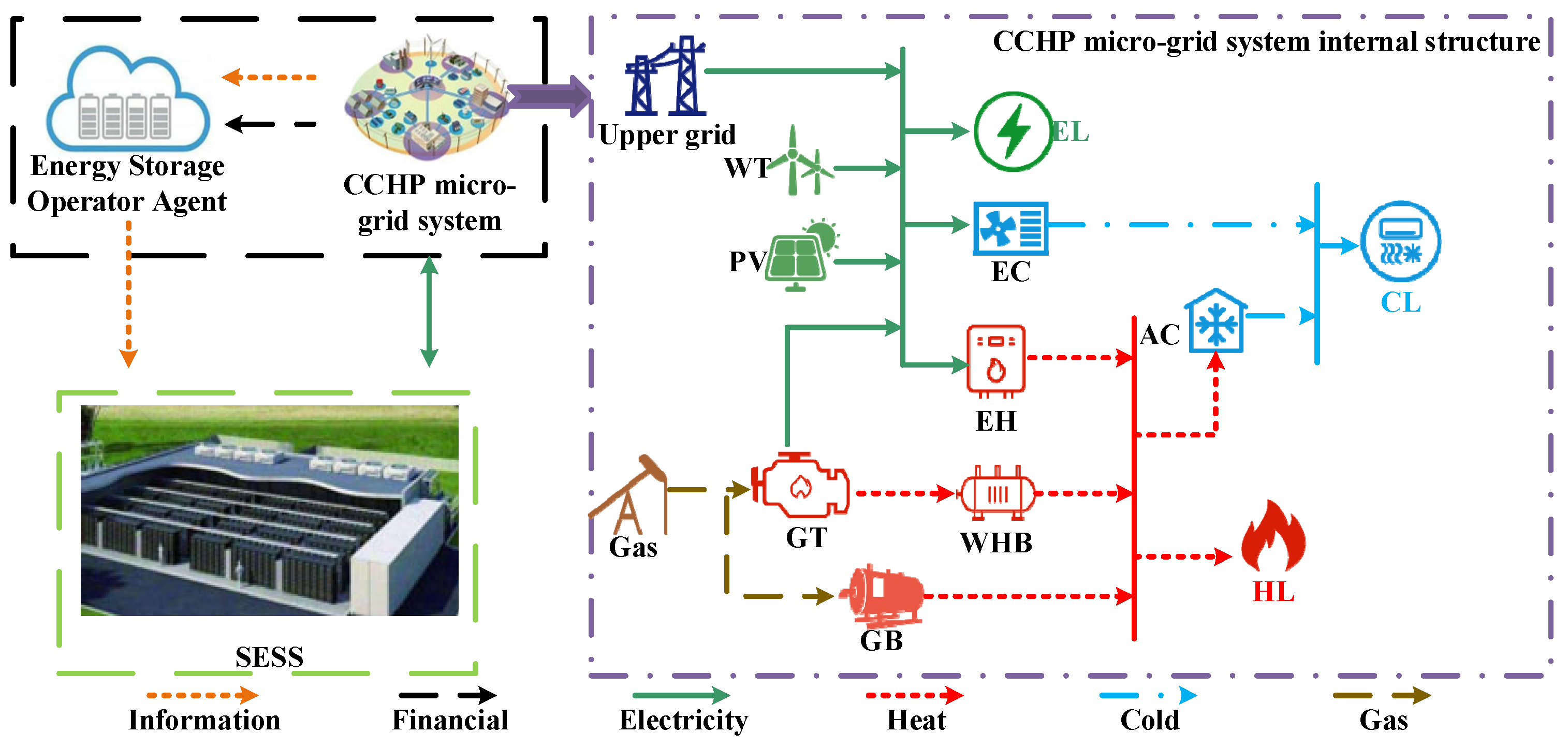
3. SESS-CCHP System Structure

The CCHP microgrid is made up of different types of loads, energy conversion devices for heating and cooling and renewable energy power producing units [26,27]. Through multi-energy complementarity, these components cooperate to provide three types of energy: cooling, heating and electricity. They also function in tandem with the SESS to ensure the effective use of integrated energy. The thermal energy bus is where waste heat boilers (WHB) absorb high-temperature waste smoke from GT power generation and produce thermal energy. Natural gas is used by gas boilers (GB) to produce thermal energy, whereas electric energy is used by electric heat (EH) equipment. On the electrical energy bus, renewable energy generators prioritise power supply, gas turbines (GT) consume natural gas to generate electrical energy and energy storage stations and grids fill the electrical energy deficit. On the cold energy bus, absorption chillers (AC) transform heat energy into cold energy, whereas electric chillers (EC) transform electrical energy into cold energy. Furthermore, the SESS operator invests in and builds the SESS and is in charge of managing and operating the system. Users pay a service fee for the use of the energy storage system, which is usually determined by the cost of charging and discharging the shared energy storage. The SESS-CHP system’s structure is depicted in Figure 2.

4. SESS-CCHP Two-Layer Synergistic Optimal Configuration Model

The SESS-CCHP system configuration model proposed in this study uses a two-tier planning strategy. The strategy involves two levels of models, each with independent objective functions and constraints. In the decision-making process, the upper-level model first makes a choice and subsequently passes its decision to the lower-level model. Based on the decisions of the upper level, the lower-level model defines its feasible solution space and performs an optimisation process to achieve the optimal value of the objective function. Once the optimisation is complete, the bottom layer model feeds the results back to the top layer, where the optimal solution and its associated values are finalised through an iterative process. The upper-layer problem depends on the optimal solution of the lower-layer problem, and the optimal solution of the lower layer problem is constrained by the decision variables of the upper layer. The core of two-layer planning is to consider the interests of both the upper and lower layers to ensure that the upper layer’s perspective is taken into account, while the lower layer maintains a certain degree of decision-making freedom within the framework of the top layer’s decision making.

4.1. Upper-Layer SESS Optimised Configuration Model

The upper-level model is responsible for solving the configuration problem of the energy storage plant over a longer time horizon during the planning period; the decision variables include the capacity configuration of the SESS and the maximum charging and discharging power.

4.1.1. Upper-Level Model Objective Function

Equation (1) illustrates that the SESS investment cost and SESS service benefit are included in the upper-level model objective function

$$\min C_{up}=C_{inv}-C_{serve}$$

(1)

where $C_{inv}$ is the annual value of SESS investment and O&M costs, etc.; and $C_{serve}$ is the annual return on SESS services.

(1)

SESS investment and O&M costs

The time value of money should be taken into account when calculating the investment cost of a shared energy storage power plant, so the equal annual value of the investment cost can be expressed as follows: SESS investment includes the one-time investment in the construction of the power station equal annual value and annual fixed investment costs for maintenance

$$C_{inv,w}={\displaystyle \frac{r{(1+r)}^y}{{(1+r)}^y-1}}\cdot ({\delta }_p{P}_{sess}^{\max }+{\delta }_E{E}_{sess}^{\max })+{\delta }_M{P}_{sess}^{\max }$$

(2)

where $r$ is the discount rate; $y$ is the SESS life cycle; ${\delta }_p$ is the investment cost per unit of power; ${\delta }_E$ is the investment cost per unit of capacity; $P_{sess}^{\max }$ and $E_{sess}^{\max }$ are the rated power and rated capacity of the SESS; and ${\delta }_M$ is the maintenance cost per unit of power of the SESS.

(2)

SESS service gains

$$\left\{\begin{array}{l}{C}_{serve,w}={\delta }_{\theta }\cdot (P_{sess,abs,w}+P_{sess,relea,w})\\ C_{serve}=365{\displaystyle \sum _{w=1}^W\pi (w)\cdot C_{serve,w}}\end{array}\right.$$

(3)

where $C_{serve,w}$ is the service revenue of SESS under typical day scenario $w$; ${\delta }_{\theta }$ is the service base price matrix of SESS; $\pi (w)$ is the probability of occurrence of typical day scenario $w$; $P_{sess,abs,w}(t)$ and $P_{sess,relea,w}(t)$ are the SESS charging and discharging power matrices under scenario $w$; and $\mathrm{T}$ is the transpose of the matrix.

4.1.2. Upper Level Constraint

The upper level constraints are mainly SESS-related constraints

$$\left\{\begin{array}{l}{E}_{\mathrm{sess},w}(t)=E_{\mathrm{sess},w}(t-1)+[{\eta }^{\mathrm{abs}}{P}_{\mathrm{sess},\mathrm{abs},w}(t)-{\displaystyle \frac{1}{{\eta }^{\mathrm{relea}}}}{P}_{\mathrm{sess},\mathrm{relea},w}(t)]\Delta t\\ E_{\mathrm{sess},w}(0)=E_{\mathrm{sess},w}(24)=0.2E_{\mathrm{sess}}^{\max }\\ 10\%E_{\mathrm{sess}}^{\max }\le E_{\mathrm{sess},w}(t)\le 90\%E_{\mathrm{sess}}^{\max }\\ 0\le P_{\mathrm{sess},\mathrm{abs},w}(t)\le U_{\mathrm{abs},w}(t)P_{\mathrm{sess}}^{\max }\\ 0\le P_{\mathrm{sess},\mathrm{relea},w}(t)\le U_{\mathrm{relea},w}(t)P_{\mathrm{sess}}^{\max }\\ U_{\mathrm{abs},w}(t)+U_{\mathrm{relea},w}(t)\le 1\end{array}\right.$$

(4)

where $E_{\mathrm{sess},w}(t)$ at the $t$ scheduling time slot charging state of the SESS under scenario $w$; ${\eta }^{\mathrm{abs}}$ and ${\eta }^{\mathrm{relea}}$ are the charging efficiency and discharging efficiency of the SESS; $E_{\mathrm{sess},w}(0)$ is the initial charging state of the SESS; and $U_{\mathrm{abs},w}(t)$ and $U_{\mathrm{relea},w}(t)$ represent the $t$ scheduling time slot charging and discharging identification bits of the SESS under scenario $w$.

4.2. Lower-Level CCHP Microgrid Optimisation Scheduling Model

The lower-level model is responsible for solving the optimal operation plan of the CCHP microgrid system in each scenario, with the optimisation objective of minimising the annual operating cost of the microgrid system, and the decision variables being the output power of the GT and GB, the AC output cooling power, the electrical power consumed by the EC, the electrical power consumed by the electric heating unit, the power purchased by the grid and the microgrid’s power exchanges with the SESS.

4.2.1. Lower-Level Optimisation Objective Function

In Equation (5)

$$\min C_{down}=C_{grid}+C_{fuel}+C_{serve}+C_{DG}+C_{IDR}$$

(5)

where $C_{grid}$ represents the annual expenditure on electricity purchased from the grid for the CCHP microgrid; $C_{fuel}$ represents cost of natural gas purchased on behalf of CCHP microgrids; $C_{DG}$ represents the cost of abandonment penalties of the CCHP microgrids; and $C_{IDR}$ represents the annual compensation cost for IDR for the CCHP microgrid.

(1)

Expenditure on electricity purchased from the grid

$$\left\{\begin{array}{l}{C}_{DG,w}={\tau }_{DG}\cdot (P_{ab,WT,w}+P_{ab,PV,w}{)}^{\mathrm{T}}\\ C_{DG}=365{\displaystyle \sum _{w=1}^W\pi (w)\cdot C_{DG,w}}\end{array}\right.$$

(6)

where $C_{grid,w}$ is the cost of power purchased by the microgrid from the grid under scenario $w$; ${\tau }_{grid}$ is the grid time-of-day tariff matrix; and $P_{grid,w}$ is the power matrix of power purchased by the CCHP from the grid under scenario $w$.

(2)

Cost of natural gas purchased on behalf

$$\left\{\begin{array}{l}{C}_{fuel,w}={\tau }_{gas}\cdot [{\displaystyle \frac{P_{GT,w}}{{\eta }_{GT}{L}_{NG}}}+{\displaystyle \frac{Q_{GB,w}}{{\eta }_{GB}{L}_{NG}}}{]}^{\mathrm{T}}\\ C_{fuel}=365{\displaystyle \sum _{w=1}^W\pi (w)\cdot }{C}_{fuel,w}\end{array}\right.$$

(7)

where $C_{fuel,w}$ represents the cost of gas purchased from the gas grid by the microgrid under scenario $w$; $P_{GT,w}$ is the GT electric power matrix under scenario $w$; $Q_{GB,w}$ is the GB thermal power matrix under scenario $w$; ${\eta }_{GT}$ and ${\eta }_{GB}$ are the operating efficiencies of GT and GB; and $L_{NG}$ is the calorific value of natural gas.

(3)

Annual penalty cost of CCHP microgrid power abandonment

$$\left\{\begin{array}{l}{C}_{DG,w}={\tau }_{DG}\cdot (P_{ab,WT,w}+P_{ab,PV,w}{)}^{\mathrm{T}}\\ C_{DG}=365{\displaystyle \sum _{w=1}^W\pi (w)\cdot C_{DG,w}}\end{array}\right.$$

(8)

where $C_{DG,w}$ is the microgrid waiver penalty cost under scenario $w$; $P_{ab,WT,w}$ and $P_{ab,PV,w}$ are the microgrid waiver wind and waiver light power matrices under scenario $w$; and ${\tau }_{DG}$ is the waiver penalty base price matrix.

(4)

CCHP microgrid IDR annual compensation cost.

IDR mechanisms can respond to imbalances between system supply and demand by providing incentives to change the energy use behavior of the user, improving the flexibility and reliability of the system

$$\left\{\begin{array}{l}{C}_{IDR,w}={\displaystyle \sum _{k\in \left\{e,h,c\right\}}[{\tau }_{DR}^{tran}\cdot \left|P_{k,w}^{tran}\right|]}\\ C_{IDR}=365{\displaystyle \sum _{w=1}^W\pi (w)\cdot C_{IDR,w}}\end{array}\right.$$

(9)

where $\left\{e,h,c\right\}$ denotes electrical, thermal and cooling loads, respectively; $P_{k,w}^{tran}$ is the transfer volume matrix for the $k$ class of loads under scenario $w$; and ${\tau }_{DR}^{tran}$ is the compensation base price matrix for the transferable loads.

4.2.2. Lower Level Constraint

(1)

Energy-balanced restraints

The energy balance constraint mainly consists of three forms of energy, namely electricity, heat and cold, as shown in Equations (10)–(12)

$$P_{GT,w}+P_{DG,w}+P_{grid,w}-P_{EC,w}-P_{EH,w}-P_{ele,w}=0$$

(10)

$$Q_{GB,w}+{\eta }_{EH}\cdot P_{EH,w}+P_{GT,w}{\gamma }_{GT}{\eta }_{WHB}-{\displaystyle \frac{Q_{AC,w}}{{\eta }_{AC}}}-P_{heat,w}=0$$

(11)

$${\eta }_{EC}\cdot P_{EC,w}+Q_{AC,w}-P_{cool,w}=0$$

(12)

where $P_{DG,w}$ is the clean energy output matrix under scenario $w$; $P_{EC,w}$ is the EC consumption electric power matrix under scenario $w$; $P_{EH,w}$ is the EH consumption electric power matrix under scenario $w$; $Q_{AC,w}$ is the AC output cooling power matrix under scenario $w$; ${\eta }_{EH}$ is the EH heating efficiency; ${\eta }_{WHB}$ is the WHB waste heat recovery efficiency; ${\gamma }_{GT}$ is the GT heat-to-electricity ratio; ${\eta }_{AC}$ is the AC cooling efficiency; ${\eta }_{EC}$ is the EC cooling efficiency; and $P_{ele,w}$, $P_{heat,w}$ & $P_{cool,w}$ are the electric, heat and cooling load matrices after demand response under scenario $w$.

(2)

CCHP microgrid system equipment output constraints

$$\begin{array}{l}{P}_{GT}^{\min }\le P_{GT,w}\le P_{GT}^{\max }\\ Q_{AC}^{\min }\le Q_{AC,w}\le Q_{AC}^{\max }\\ P_{EC}^{\min }\le P_{EC,w}\le P_{EC}^{\max }\\ Q_{GB}^{\min }\le P_{GB,w}\le Q_{GB}^{\max }\\ P_{EH}^{\min }\le P_{EH,w}\le P_{EH}^{\max }\end{array}$$

(13)

where $P_{GT}^{\min }$ and $P_{GT}^{\max }$ are the boundaries of the range of GT forces; $Q_{AC}^{\min }$ and $Q_{AC}^{\max }$ are the boundaries of the range of AC force; $P_{EC}^{\min }$ and $P_{EC}^{\max }$ are the boundaries of the range of EC force; $Q_{GB}^{\min }$ and $Q_{GB}^{\max }$ are the boundaries of the range of GB force; and $P_{EH}^{\min }$ and $P_{EH}^{\max }$ are the boundaries of the range of EH force.

(3)

Transferable load constraints

$$\left\{\begin{array}{l}{P}_{k,w}^{\mathrm{tran}}(t)=U_{k,w}^{\mathrm{in}}(t)\cdot P_{k,w}^{\mathrm{in}}(t)-U_{k,w}^{\mathrm{out}}(t)\cdot P_{k,w}^{\mathrm{out}}(t)\\ U_{k,w}^{\mathrm{in}}(t)+U_{k,w}^{\mathrm{out}}(t)=1\\ {\displaystyle \frac{\left|P_{k,w}^{\mathrm{tran}}(t)\right|}{P_{\mathrm{load},k,w}(t)}}\le \epsilon \\ {\displaystyle \sum _{t=1}^T{P}_{k,w}^{\mathrm{tran}}(t)=0}\end{array}\right.$$

(14)

where $k\in \left\{e,h,c\right\}$, $P_{k,w}^{\mathrm{tran}}(t)$ can be composed of the introduced auxiliary variables $P_{k,w}^{\mathrm{in}}(t)$ and $P_{k,w}^{\mathrm{out}}(t)$, which represent the increment and curtailment of the kth class of load at time t, respectively; $U_{k,w}^{\mathrm{in}}(t)$ and $U_{k,w}^{\mathrm{in}}(t)$ denote the kth class of load demand response state variables at time t, respectively; $P_{\mathrm{load},k,w}(t)$ represents the base load of load category $k$ in time period t under scenario $w$; and $\epsilon$ represents the adjusted upper limit of transferable load in each time period.

5. Arithmetic Simulation and Analysis

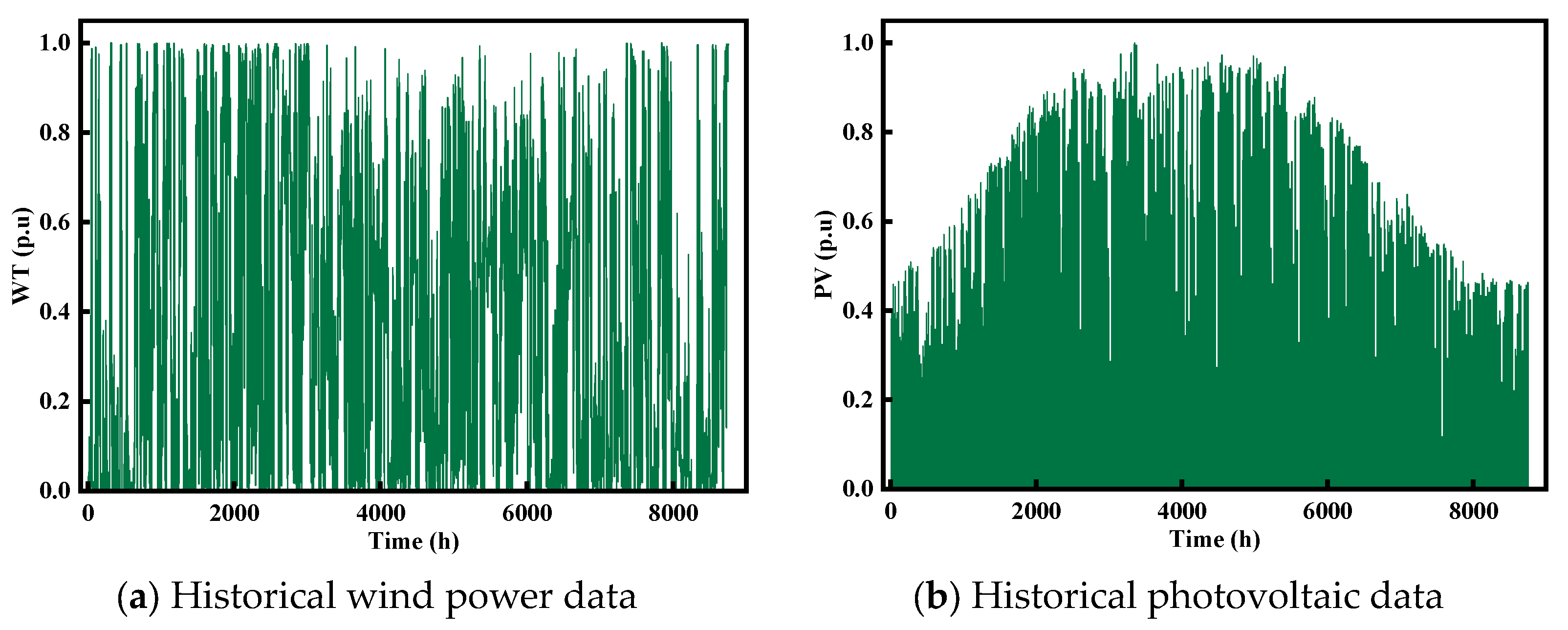
5.1. Results of the Generation of Scenarios of Wind and Light Outputs

A case study was chosen from a CCHP microgrid system located in Northwest China. Figure 3 displays the microgrid’s annual standardised PV and wind turbine output data for 2022. A variety of Copula models were applied to fit the data, and an additional computation was made to determine the Empirical-Copula function of the solar and wind production.

Table 2. Ordinal correlation coefficient and European distances.

Copula Function	Kendall	Spearman	Euclidean Square Distance
Empirical-Copula	−0.1240	−0.1854	0
$\mathrm{Gaussian}-\mathrm{Copula}$	−0.0889	−0.1330	0.20225
$\mathrm{t}-\mathrm{Copula}$	−0.1134	−0.1631	0.19332
$\mathrm{Gumbel}-\mathrm{Copula}$	1.3575 × 10−6	2.051 × 10−6	0.5462
$\mathrm{Clayton}-\mathrm{Copula}$	0.1117	0.1715	0.6811
$\mathrm{Frank}-\mathrm{Copula}$	−0.1235	−0.1860	0.1009

summarises the results of deriving and comparing the rank correlation coefficients of each model with the Euclidean distance of the Empirical-Copula function.

Table 2 shows that the Frank-Copula function best describes the distribution function of the combined wind and landscape flows. The best simulation results are produced by this function, which is why it was chosen. The scenario-generating approach proposed in Section 2 is applied to 10,000 groups of everyday situations, considering the correlation of scenic power. To accommodate for computation speed and accuracy, the 10,000 data groups are concurrently clustered into four typical everyday situations of scenic power. After inverse normalisation, the final scenic power possibilities are produced; the outcomes are shown in Figure 4.

Figure 4 displays the four PV and wind output possibilities that resulted from clustering reduction. The scenarios are labeled $\mathrm{WT}1~\mathrm{WT}4$ and $\mathrm{PV}1~\mathrm{PV}4$, respectively, with the probability of each scenario’s occurrence placed in parentheses. A correlation analysis between the production of PV, electricity and wind energy in each instance reveals a negative link between the two variables. This outcome is in line with Table 1’s negative rank correlation coefficients. Significant differences across the scenarios also highlight the significant seasonal fluctuations. In the first scenario, photovoltaic production begins early in the day and maintains its maximum output for the duration. However, in contrast to the other scenarios, the wind generation output is much higher, indicating the usual summertime characteristics. In Scenario 2, winter features are shown by the lowest PV power production at noon and the lowest wind power output. However, the overall power production of Scenarios 3 and 4 falls in between the first two, demonstrating the characteristics of a transitional season. Overall, the reliability of the system planning may be improved by precisely replicating the correlation and stochasticity of solar and wind power output in the planning area via the design of scenarios.

5.2. Calculation Data and Optimisation Results

Figure 5 displays the typical energy, heating and cooling performance of the chosen microgrid system together with load data from the electrical grid at different times of the day, shown in the standard view. The SESS design and operation of the CCHP microgrid system are improved in this study via the use of two-way communication and the development configuration of the SESS-CCHP system.

Table 3. System-related parameters.

Parameters	Value	Parameters	Value
$P_{\mathrm{GT}}^{\min }\left(\mathrm{kW}\right)$	0	$P_{\mathrm{GT}}^{\max }\left(\mathrm{kW}\right)$	600
$P_{\mathrm{EC}}^{\min }\left(\mathrm{kW}\right)$	0	$P_{\mathrm{EC}}^{\max }\left(\mathrm{kW}\right)$	400
$P_{\mathrm{EH}}^{\min }(\mathrm{kW})$	0	$P_{\mathrm{EH}}^{\max }\left(\mathrm{kW}\right)$	200
$Q_{\mathrm{GB}}^{\min }(\mathrm{kW})$	0	$Q_{\mathrm{GB}}^{\max }\left(\mathrm{kW}\right)$	1000
$Q_{\mathrm{AC}}^{\min }(\mathrm{kW})$	0	$Q_{\mathrm{AC}}^{\max }\left(\mathrm{kW}\right)$	500 kW
${\gamma }_{\mathrm{GT}}$	1.46	${\eta }_{\mathrm{GT}}$	0.3
$L_{\mathrm{NG}}{(\mathrm{kWh}/\mathrm{m}}^3)$	9.7	${\eta }_{\mathrm{GB}}$	0.9
${\tau }_{\mathrm{DR}}^{\mathrm{tran}}$ (Y/kWh)	0.2	${\eta }_{\mathrm{EC}}$	4
${\tau }_{\mathrm{DG}}$ (Y/kWh)	0.5	${\eta }_{\mathrm{EH}}$	3
${\tau }_{gas}$ (Y/m3)	2.2	${\eta }_{\mathrm{AC}}$	1.2
${\delta }_{\mathrm{p}}$ (Y/kW)	1000	${\eta }_{\mathrm{WHB}}$	0.8
${\delta }_{\mathrm{s}}$ (Y/kW)	1000	$r$	0.08
${\delta }_M$ [Y/(a · kW)]	78	$y(a)$	10

shows the relevant device parameters within the microgrid [26,27,28]. In order to solve the two-layer model proposed in this paper, the Karush–Kuhn–Tucker (KKT) condition and the large M method are used to transform the model into a single-layer, mixed-integer linear programming model and then the GUROBI solver is invoked to solve the model, and the flow of the solution process is shown in Figure 6, and the model-specific transformation method is shown in reference [28].

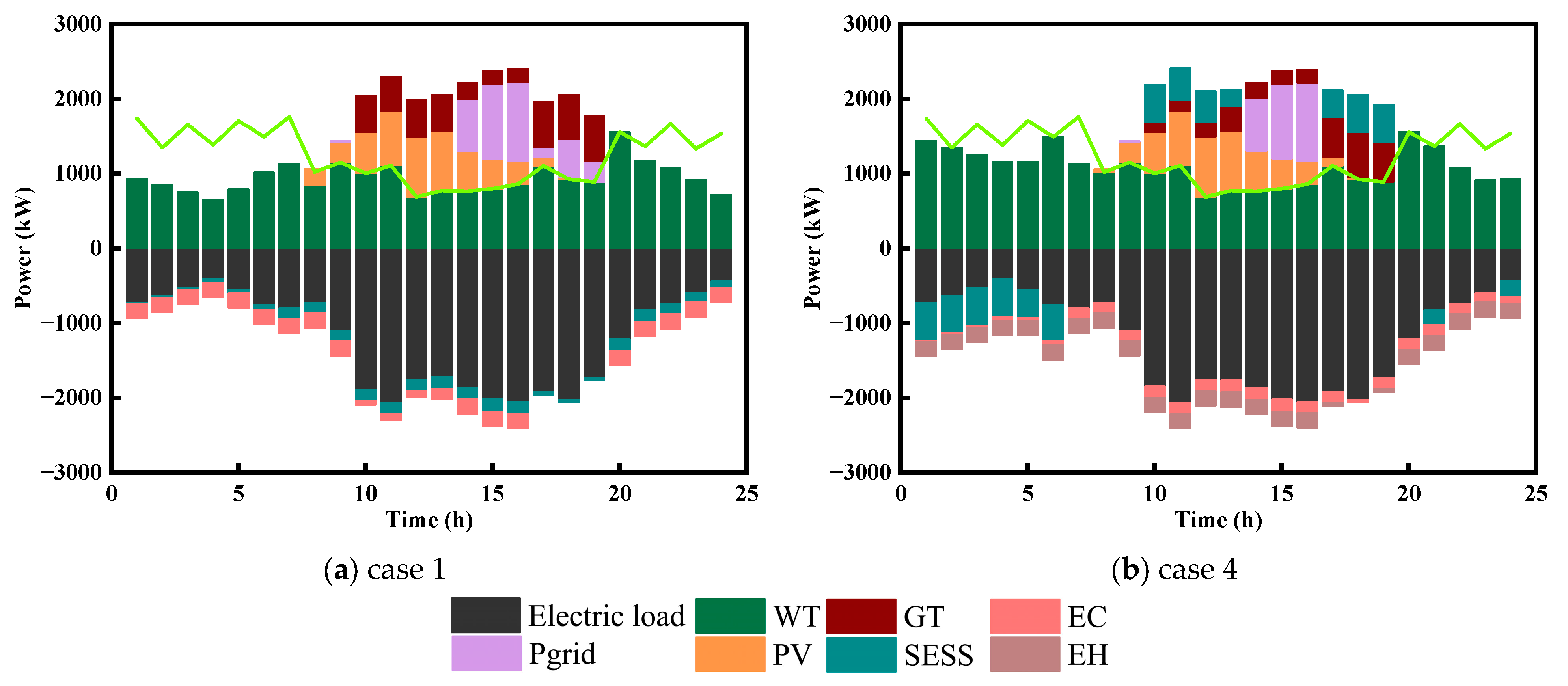
5.2.1. Analysis of the Results of Two-Layer Synergistic Optimisation

Four scenarios are prepared for comparative study in order to confirm the superiority of the two-layer cooperative optimisation and allocation technique suggested in this research. They are built up as follows:

Case 1: The CCHP system does not take energy storage into account; it only takes the demand-side response mechanism into account.

Case 2: Electricity abandonment is permitted, the user constructs their own energy storage, and the CCHP system takes the demand side response mechanism into account.

Case 3: The CCHP system does not permit power abandonment and takes user-built energy storage and demand-side response systems into account.

Case 4: Demand-side response techniques are taken into account by the CCHP system, which also takes part in shared energy storage services.

The user-built energy storage falls into one of the following two cases under the four previously mentioned scenarios: either it is configured for optimal system economy or it does not allow for the phenomenon of power abandonment, in which case it is configured for the system’s maximum new energy consumption rate.

Table 4. Optimised scheduling results for the four scenarios.

Parametric	Case 1	Case 2	Case 3	Case 4
Maximum power of energy storage$/\mathrm{kW}$	/	662.31	1304.36	505.90
Maximum capacity of energy storage$/\mathrm{kWh}$	/	5152.64	19,191.68	3881.12
New energy consumption rate$/\mathrm{RMB} 10,000$	84.71%	97.31%	100%	95.17%
Abandonment penalty cost$/\mathrm{RMB} 10,000$	85.49	16.31	0	35.5
Cost of purchased electricity$/\mathrm{RMB} 10,000$	125.95	71.48	94.6	28.41
Cost of gas purchase$/\mathrm{RMB} 10,000$	191.30	130.31	47.35	147.44
Demand response costs$/\mathrm{RMB} 10,000$	12.92	7.54	2.37	10.81
Service cost$/\mathrm{RMB} 10,000$	0	0	0	49.21
Annual investment cost of energy storage$/\mathrm{RMB} 10,000$	0	91.82	315.62	69.32
Total costs$/\mathrm{RMB} 10,000$	415.66	317.49	459.42	307.75

displays the best scheduling outcomes for each scenario. Figure 7 displays the optimisation results as well as the capacity distribution of the SESS charging and discharging behaviours under four typical day scenarios. Charging takes place when the SESS charging and discharging power is positive; discharging happens when it is negative.

The following three conclusions can be obtained from Table 4:

(1)

The maximum power and capacity of the energy storage configured in scenario 2 are 662.31 kW and 5152.64 kW.h; the maximum power and capacity of the energy storage configured in scenario 3 are 1304.36 kW and 19,191.68 kW.h; and the maximum power and capacity of the energy storage configured in scenario 4 are 505.90 kW and 3881.12 kW.h. The power and capacity of the energy storage configuration under scenario 4 is the smallest, scenario 2 is the second largest, and scenario 3 is the largest.

(2)

The total system cost of Scenario 2 is reduced by 23.61% (i.e., RMB 981,700) compared with Scenario 1. This is due to the introduction of the energy storage device in Scenario 2, and the penalty cost for power abandonment, cost of purchasing electricity, cost of purchasing gas and cost of demand response of the system are all significantly reduced, so that the system’s overall economic performance is greatly improved despite the increase in the investment cost of the energy storage device and the system’s new energy consumption rate has reached 97.31%, compared with Scenario 1, which is 12.6% higher than that of Scenario 1. In Scenario 3, although the new energy consumption rate in the system reaches 100%, the investment cost of energy storage for the system to fully consume the new energy increases by 243.73% (i.e., RMB 2,238,000) compared to Scenario 2, which greatly increases the cost burden of the system, resulting in an increase in the total cost of the system in this scenario compared to Scenario 1 and Scenario 2 by 10.52% (i.e., RMB 437,600) and 44.7% (i.e., USD 1,419,300). Therefore, it can be seen that appropriate abandonment of part of the new energy generation can help the system significantly reduce the power and capacity cost of the energy storage configuration while maintaining a high new energy consumption rate.

(3)

The total system cost under Scenario 4 is RMB 3,077,500,000, which decreases by 25.96% (i.e., RMB 1,079,100,000) relative to Scenario 1, and the new energy consumption rate increases by 10.46%. Meanwhile, the service revenue of the shared energy storage operator in Scenario 4 is RMB 492,100, the total investment cost of shared energy storage is RMB 4,387,000, and the annual operation and maintenance cost is RMB 39,400. The static payback period of the energy storage plant is 9.69 years, and the operator has room for profit. In addition, it can be found that the new energy consumption rate under Scenario 4 has decreased by 2.14% compared to Scenario 2. The reason for this phenomenon is that if the CCHP system wants to achieve the full consumption of new energy, the total cost of the shared energy storage configuration will be too high, and the energy storage operator will need to significantly increase the service fee if it wants to have profitability margins, which, in turn, will result in a rapid increase in the cost of the system. Therefore, this configuration strategy is to further improve the new energy consumption rate of the CCHP system under the premise of taking into account the common interests of operators and users.

In summary, the introduction of the shared energy storage model can help the CCHP system to improve the new energy consumption capacity while relieving the users of the burden of energy storage investment costs. At the same time, the shared energy storage operators charge a certain service fee to make their own use of a certain profit margin. Therefore, this chapter proposes a two-layer synergistic optimal allocation strategy for CCHP systems considering shared energy storage that takes into account the interests of both the operator and the users, and the strategy is theoretically feasible and provides a reference for the promotion and application of energy storage.

The distribution pattern of the shared energy storage’s daily maximum charging and discharging times is shown in Figure 6. This suggests that at least once in every regular day scenario, the stored energy experiences maximum charging and discharging behaviour. Moreover, the SESS charges mostly during nighttime, between 00:00 and 08:00, when wind power output is at its highest. To maintain a stable power system and balance supply and demand, it discharges between 09:00 and 13:00 and 16:00 and 19:00 during times of low generating power. As a result, during times of strong renewable energy output, the shared energy storage system efficiently stores energy and releases it as required. This increases the pace at which additional energy is used and improves the overall power system’s operating stability.

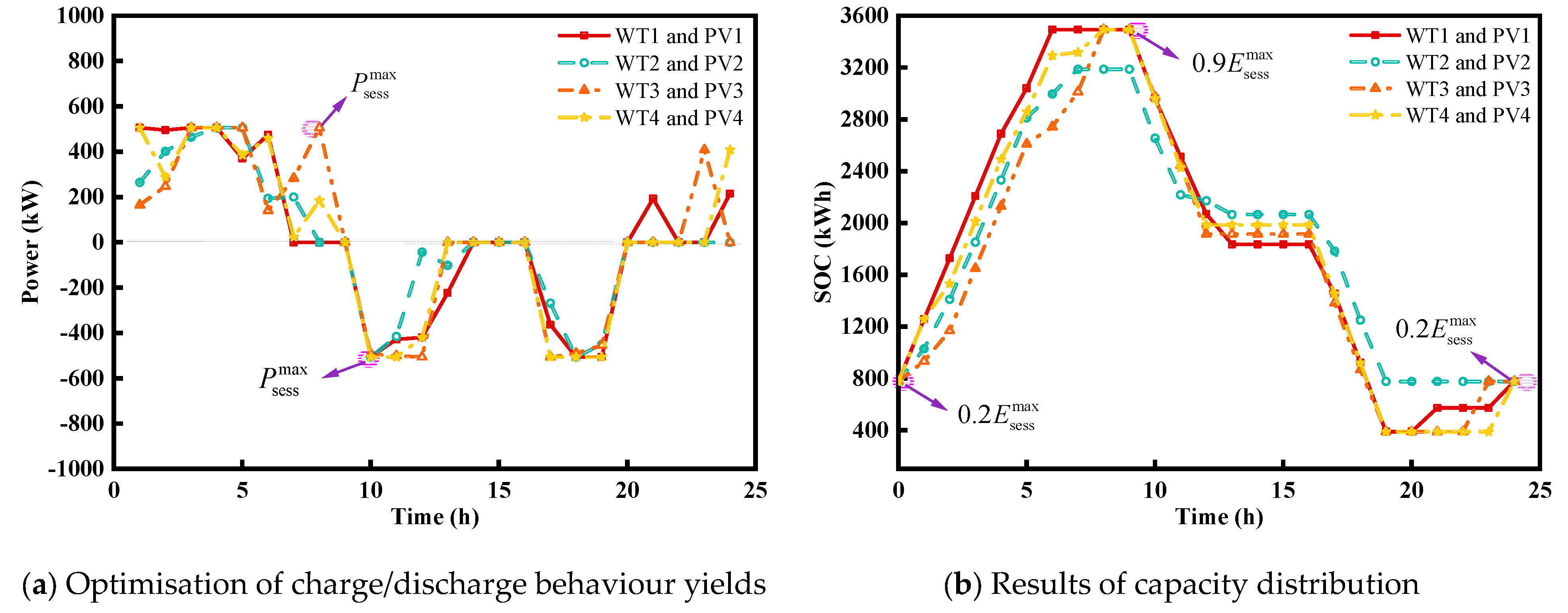
5.2.2. Analysis of Optimal Scheduling of Microgrids under SESS Services

Figure 8 displays the outcomes of the CCHP system’s optimum scheduling under Scenarios 1 and 4, based on the summer wind power production scenarios WT1 and PV1. The figure’s green line segments represent each scenario’s expected wind power production.

As shown in Figure 8, the system is charged with shared energy storage to reduce wind abandonment during 0:00–07:00, and then discharged during the peak hours of 10:00–13:00 and 17:00–19:00, which reduces the gas turbine output and the power purchased from the grid during the peak hours of the CCHP system, and reduces the cost of the system’s gas and the cost of the grid’s power purchased from the grid. Therefore, it can be obtained that after the introduction of shared energy storage, the wind abandonment phenomenon of the CCHP system is significantly improved, the environmental friendliness of the system is enhanced, and the penalty cost of the system due to wind abandonment is reduced. At the same time, the shared energy storage eases the power purchased from the grid during the peak period and reduces the burden of grid operation. This series of effects fully proves the superiority and practical application value of the shared energy storage model in energy management and environmental protection.

5.2.3. SESS Power and Capacity Sensitivity Analysis

To evaluate the influence of SESS operational characteristics on the microgrid system’s economics, a sensitivity analysis of the impacts of different charging and discharging power and capacity on the CCHP system’s cost and the SESS income is carried out. The particular outcomes are shown in Figure 9, where the pre-set ranges for SESS capacity and charging and discharging power are [3000, 4200], with a step size of 100 kWh, and [100, 700], with a step size of 50 kW, respectively. The sensitivity analysis of the impacts of several SESS operational characteristics on the microgrid system’s economics is carried out in the following parts of this research.

Figure 9a illustrates that when the SESS charge–discharge power is in the range of [100, 500], the SESS gain gradually improves and the overall operating cost of the CCHP microgrid gradually reduces as the maximum charge–discharge power increases. However, the shared energy storage gain and the overall cost of the CCHP system exhibit a consistent trend when the SESS charge–discharge power is within the range of (500, 700).

The overall cost of the CCHP system tends to drop as the energy storage capacity steadily grows, while the benefit of the SESS increases proportionally, as Figure 8b illustrates when the SESS capacity is between [3000, 3900]. On the other hand, the benefits of the SESS and the total cost of the CCHP microgrid start to stabilise when the SESS capacity is between (3900, 4200).

The microgrid system’s restricted ability to produce wind electricity is the cause of the aforementioned outcomes. The microgrid system can use its own wind power generation and can stop utilising the SESS service excessively once the charging and discharging power and capacity of the SESS reach an optimal value. Increasing the SESS’s power and capacity further can only result in resource waste and higher investment expenditures for the SESS operator. In general, 500 kW and 3900 kWh, respectively, are the optimal SESS charging and discharging powers and capacities. These numbers show that the proposed collaborative optimal configuration model is valid because they closely match the optimal configuration results in Table 4.

5.2.4. Base Price Sensitivity Analysis for Shared Energy Storage Services

The operator’s main source of revenue is the invoicing of SESS services, and the pricing approach it uses has a significant impact on both the operational cost-effectiveness of SESS and client usage patterns. The results of a thorough analysis that took into consideration the SESS payback period and the subscriber’s cost of use are presented in Figure 10.

The data shown in Figure 10 suggest a positive relationship between the annual operating cost of the CCHP system and the base price of SESS services. On the other hand, there is a negative correlation between the SESS payback duration and the base price. Concurrently, SESS can only turn a profit if the service base price is higher than 0.22 RMB/(kWh); if it is more than 0.275 RMB/(kWh), the CCHP system’s annual operating expenses will be higher than those of the user’s own energy storage. CCHP systems and energy storage operators benefit from the SESS service base pricing range of [0.22, 0.275] because of this.

5.2.5. Sensitivity Analysis of Transferable Load Share

This study performs a sensitivity analysis of the transferable loads in order to investigate the effects of the fraction of transferable loads on the SESS configuration alternatives and the total operating expenses of the CCHP system. The analysis’s findings are displayed in Figure 11.

Figure 11 illustrates how the load transfer rate increases and how the annual investment cost of the energy storage system and the total cost of the CCHP system both drop dramatically. This is because the CCHP system can regulate the resources needed to use fresh energy as the quantity of load transferred rises, lowering the cost of purchase and energy waste in the system. In order to minimise energy storage waste and lower investment costs, manufacturers are reducing the supply and storage capacity of energy storage, while the system itself has become more flexible, reducing the demand for energy storage. As a result, before designing an adequate energy storage system, the flexibility of the system needs must be taken into account.

6. Conclusions

In this paper, a typical daily output scenario generation method for WT and PV is constructed based on the Copula theory, and a two-layer synergistic optimal configuration model of the SESS-CCHP system that closely integrates planning and operation is constructed based on the two-layer planning theory. Through this model, the positive role of SESS in enhancing the new energy absorption capacity of the CCHP microgrid system as well as improving the system economics is confirmed. The impact of demand-side flexibility on SESS planning decisions and total system cost is also explored, and the following main conclusions are drawn:

(1)

The wind power scenario generation method based on historical data proposed in this study can accurately reflect the stochasticity and correlation of wind power, which helps to make more reasonable decisions in the planning stage.

(2)

Compared with no energy storage configuration, the new energy consumption rate of the CCHP system with SESS is increased by 10.46%, and the total system cost is decreased by 25.96%.

(3)

Compared with the self-built energy storage mode, the new energy consumption rate under the SESS service mode decreases by 2.14%, but the total cost of the CCHP is the lowest, at RMB 3,077,500, which is the result of taking into account the interests of both the SESS and the CCHP users. At the same time, SESS operators can achieve mutual benefits for both operators and users through reasonable pricing, and the optimal service base price ranges from 0.22 RMB/kWh to 0.275 RMB/kWh.

(4)

Demand-side flexibility has a significant impact on energy storage planning decisions. Therefore, the evaluation of demand-side flexibility resources in the CCHP system is especially critical before making relevant decisions.

In this study, the impact of the carbon trading market has not yet been fully incorporated in the design of shared energy storage solutions for CCHP systems. Considering ‘carbon emissions’ as a widespread concern, it is crucial to consider carbon emissions in future CCHP system optimisation and shared energy storage plant (SESS) deployment strategies, which will be a priority in our research agenda. In addition, while this study mainly analyses the potential of SESS in enhancing the economic efficiency of CCHP systems, SESS, as a business model with great potential for energy storage, has also demonstrated its importance in medium- and long-term power trading, power system peaking, frequency regulation services and spot-market trading, which is also an area of research that deserves to be further explored.