Multi-Objective Optimization Analysis of Electromagnetic Performance of Permanent Magnet Synchronous Motors Based on the PSO Algorithm
Abstract
1. Introduction
2. Electromagnetic Field Analysis of PMSM
2.1. Structure and Parameters
2.2. Rated No-Load Electromagnetic Calculation
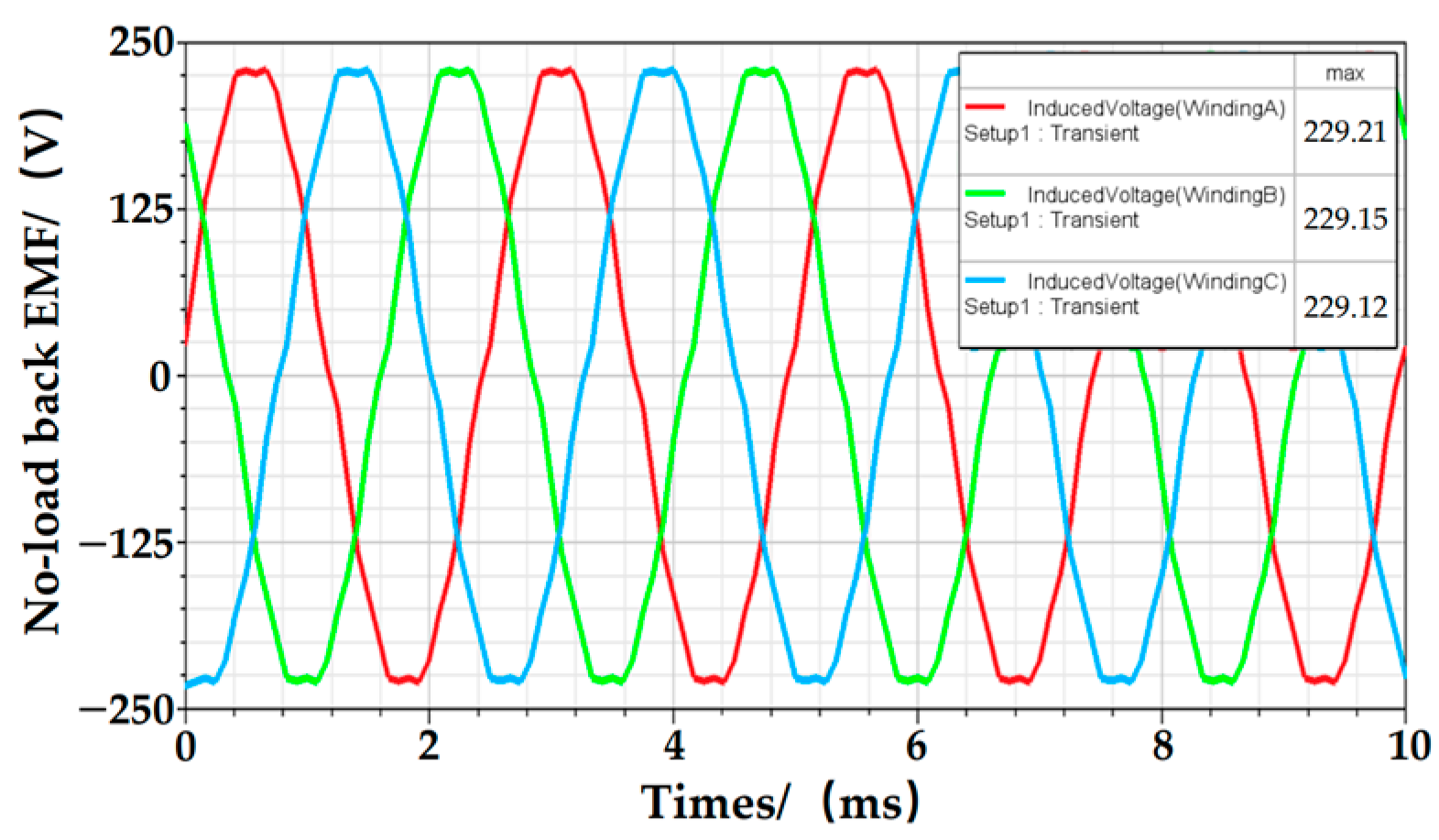
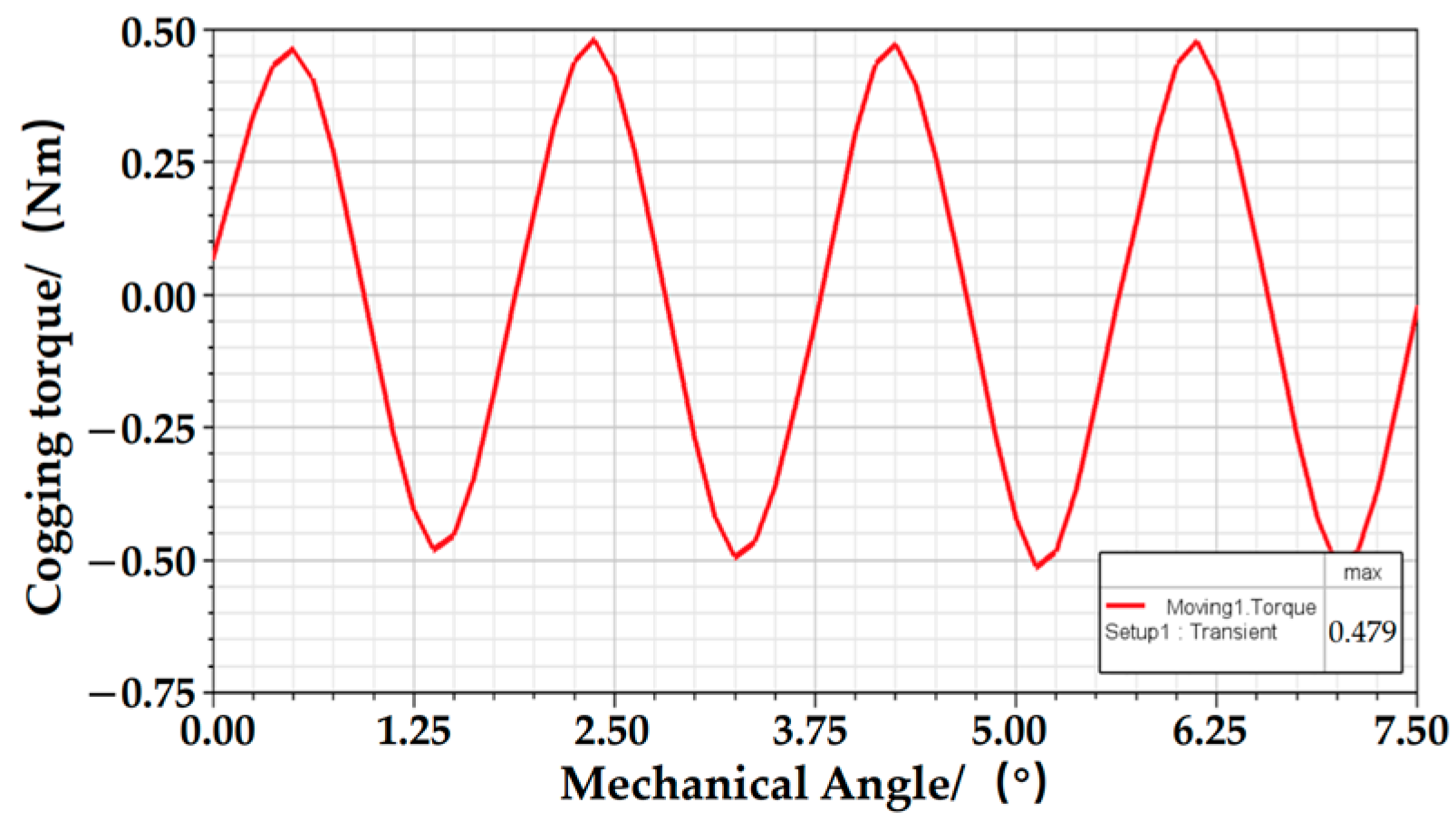
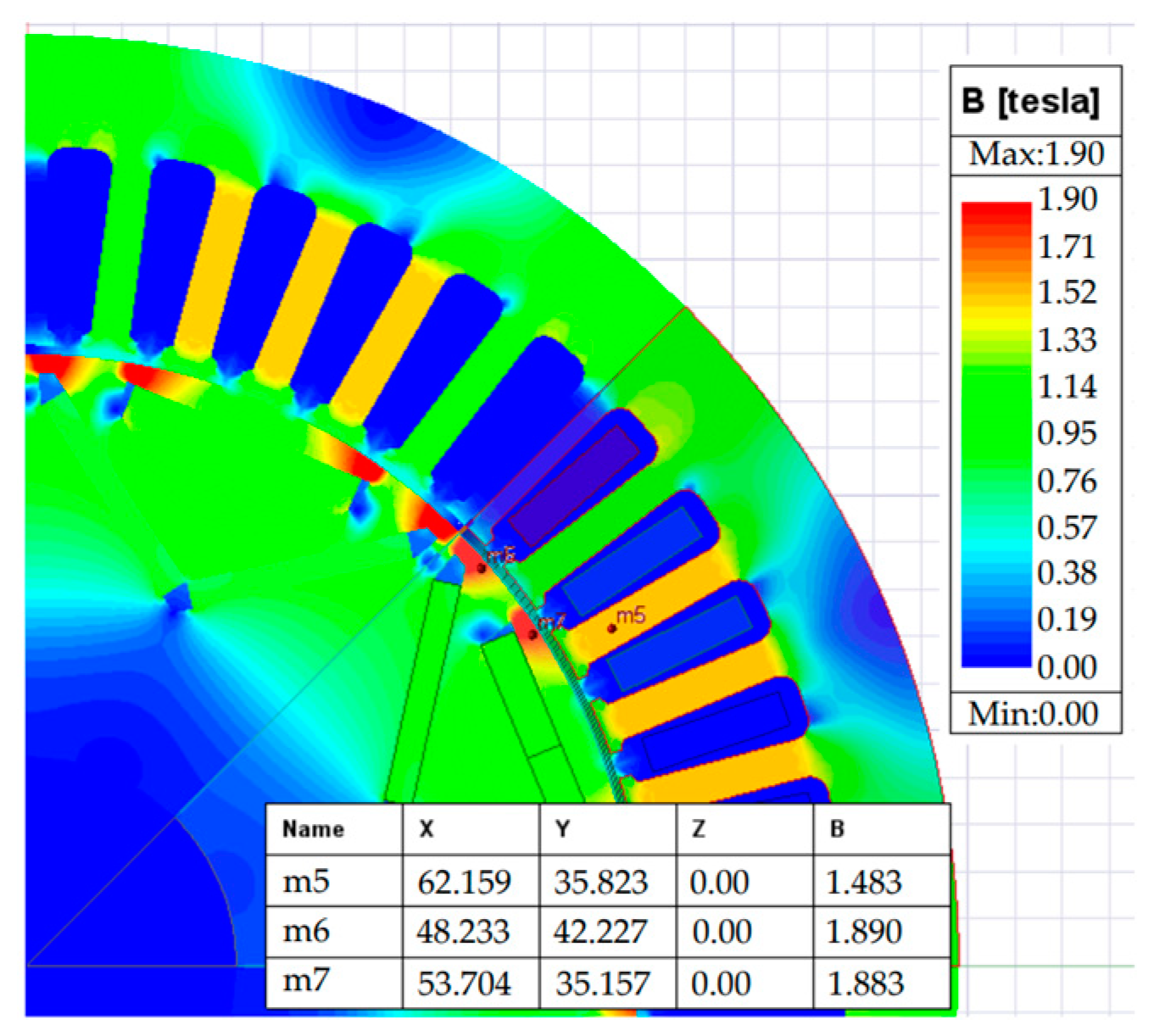
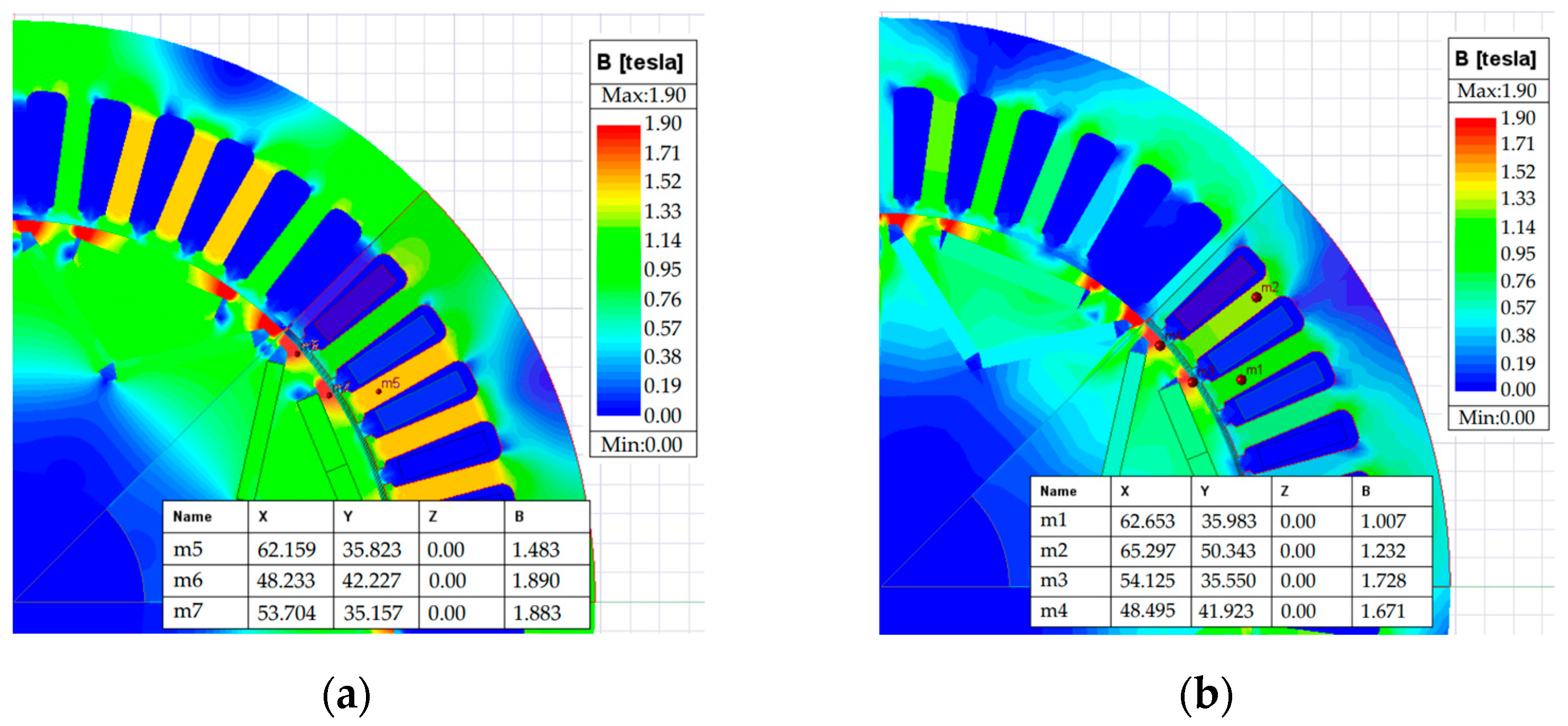
2.3. Rated No-Load Electromagnetic Field Simulation
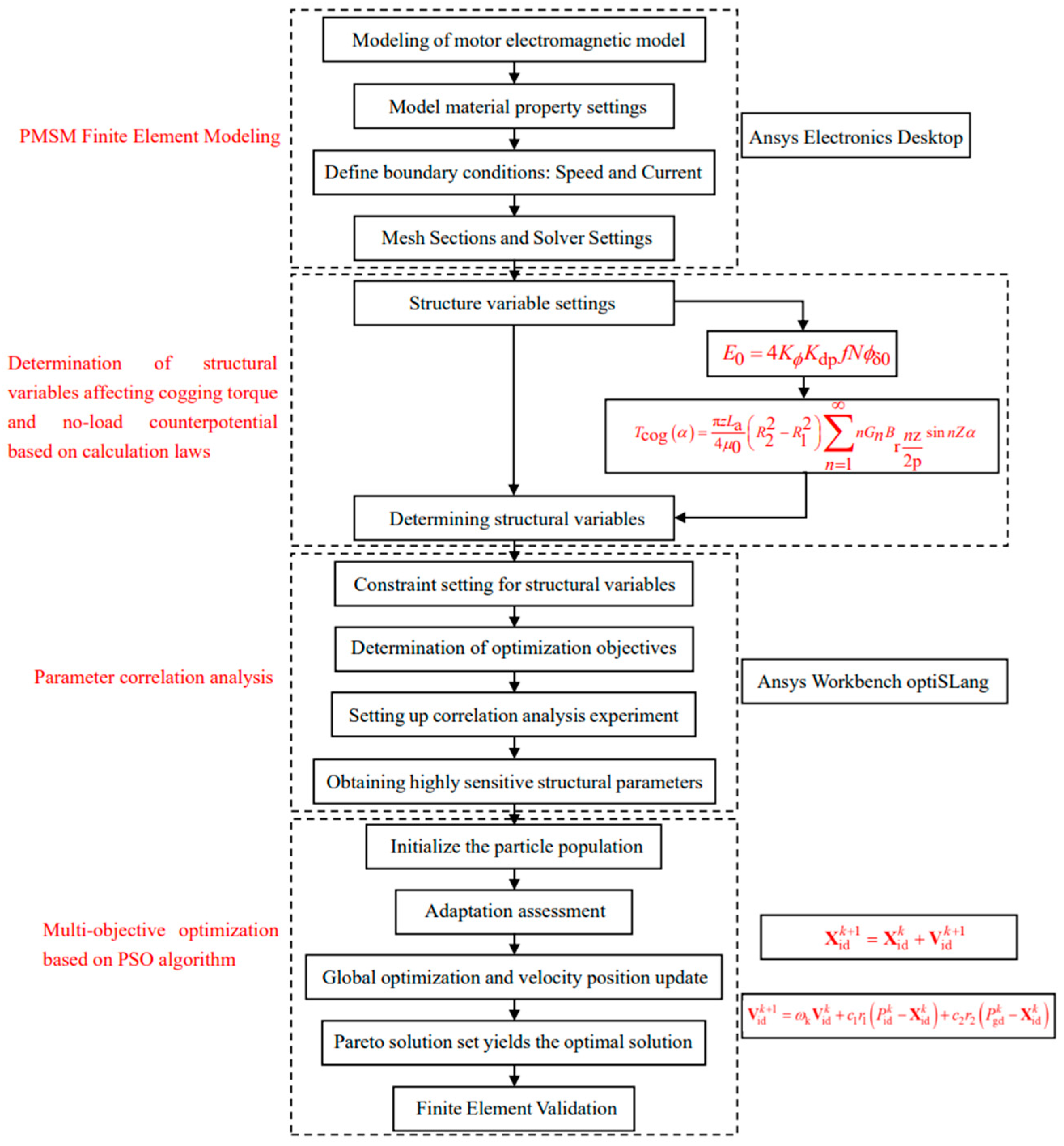
3. Multi-Objective Optimization Based on the PSO Algorithm
3.1. Structural Parameterized Model
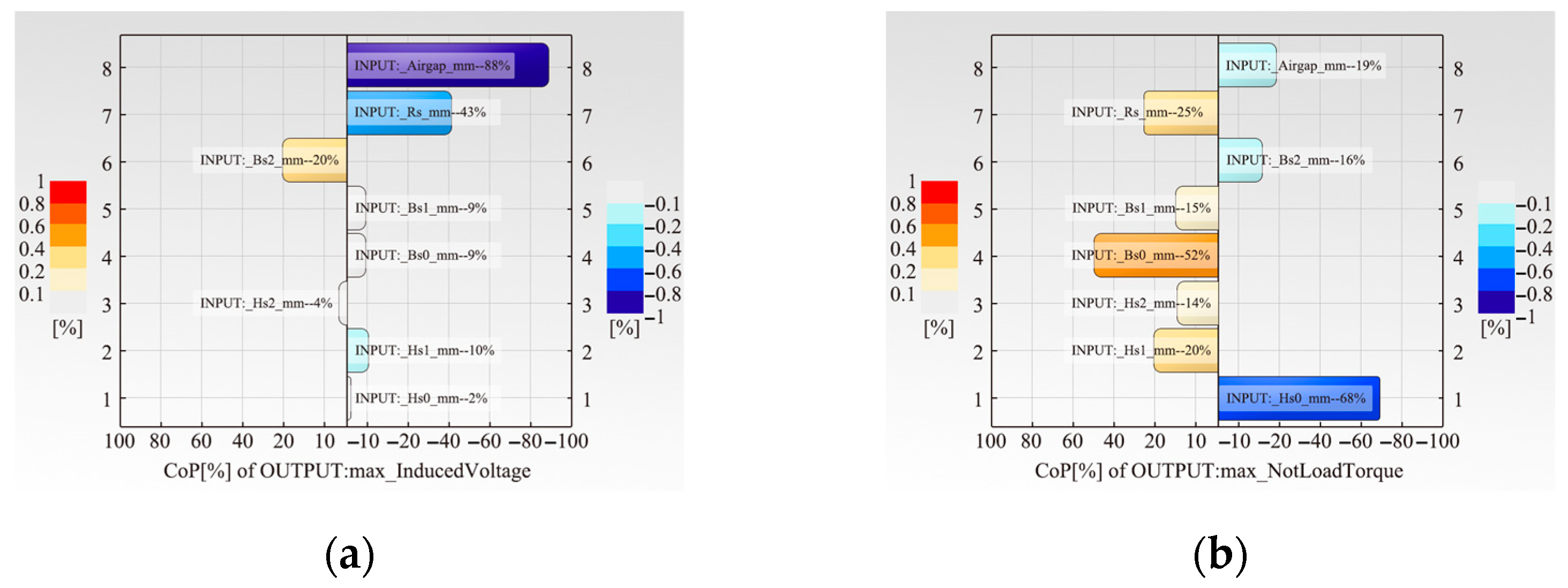
3.2. Construction of the Optimization Function
3.3. PSO Algorithm Optimization Model
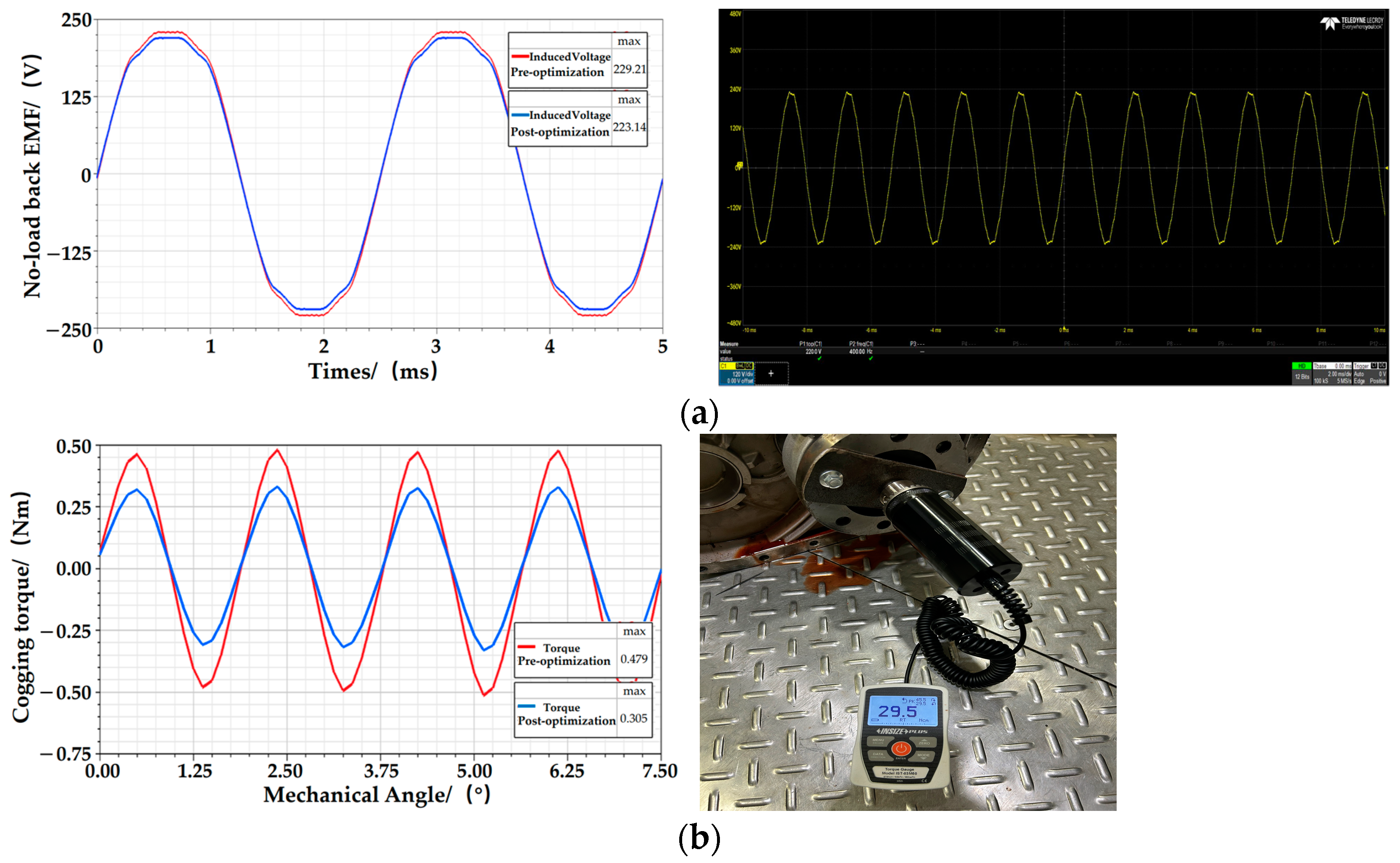
4. Experimental Validation
5. Conclusions
- (1)
- Significant improvements in the motor’s electromagnetic performance were achieved by globally optimizing the structural parameters using the PSO algorithm-based multi-objective optimization strategy. The peak value of no-load back EMF decreased by 2.65%, and the peak value of cogging torque decreased by 36.33%. Moreover, the magnetic flux density remained within a reasonable range.
- (2)
- The finite element validation of the results obtained from the optimization strategy was carried out, and it was concluded that the error between the values of the optimization results and the values after the finite element validation was within a reasonable range, thus verifying the reliability of the computational results.
- (3)
- The experimental tests carried out on the structurally optimized motor show that the experimental values are very close to the theoretical values derived from the simulation, and the errors between the simulated and experimental values for the peak cogging torque and the peak no-load back EMF are 5.36% and 3.38%, respectively, which proves the accuracy of the multi-objective optimization strategy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.J.; Ye, Q.J.; Zhao, X.C.; Jiang, Z.; Zhu, J.A. Cogging torque reduction method of permanent magnet motor based on optimization of stator structure. Micromotors 2024, 57, 6–9+17. [Google Scholar] [CrossRef]
- Jiang, C.; Xue, X.H.; Zhang, L. Electromagnetic optimization design of permanent magnet motor for high-speed train based on torque compensation. Mech. Des. Manuf. Eng. 2022, 51, 74–78. [Google Scholar] [CrossRef]
- Gu, H.J.; Huang, W.M.; Wang, C.; Gao, J.W. Influence of stator teeth notching on cogging torque of interior permanent magnet motor. Electr. Mach. Control Appl. 2016, 43, 40–45. [Google Scholar] [CrossRef]
- Ye, X.B.; Wu, B.C. Cogging torque optimization design in interior-type permanent magnet synchronous motor. Micromotors 2019, 52, 12–14+51. [Google Scholar] [CrossRef]
- Ren, D.J.; Huang, Q.; Li, J.J.; Wu, N. Optimal analysis on cogging torque of the built-in permanent magnet synchronous motors. Explos.-Proof Electr. Mach. 2019, 54, 4–7+43. [Google Scholar] [CrossRef]
- Wang, H.M.; Zhong, S.C.; Zhang, W.; Guo, L.Y. Optimal designing of air flux barrier to reduce torque ripple of interior permanent magnet synchronous motor. Micromotors 2021, 54, 18–22. [Google Scholar] [CrossRef]
- Qiu, R.L.; Hua, Q.S.; Zhang, H.X.; Shi, C.L. Optimal design of permanent magnet synchronous motor rotor based on Taguchi method. J. Qingdao Univ. (Eng. Technol. Ed.) 2020, 35, 57–61+82. [Google Scholar] [CrossRef]
- Qiu, M.S.; Hua, Q.S. Electromagnetically optimized design for high-speed permanent magnet synchronous motor by Taguchi iteration. J. Beijing Norm. Univ. (Nat. Sci.) 2022, 58, 713–719. [Google Scholar] [CrossRef]
- Cao, Y.J.; Feng, L.L.; Mao, R.; Yu, L.; Jia, H.Y.; Jia, Z. Multi-objective stratified optimization design of axial-flux permanent magnet memory motor. Proc. CSEE 2021, 41, 1983–1992. [Google Scholar] [CrossRef]
- Chen, Q.; Liao, J.H.; Qian, W.; Zhao, W.X.; Liu, G.H.; Chen, X.; Xu, G. Design and optimization a new spoke-type flux-modulation machine with inverted T-shape permanent magnets. IEEE Trans. Energy Convers. 2022, 38, 203–217. [Google Scholar] [CrossRef]
- Li, Y.K.; Wu, Y.S.; Hu, Y.L. Design and optimization of a novel canned Halbach array permanent-magnet motor. Micromotors 2023, 56, 1–8. [Google Scholar] [CrossRef]
- Wang, C.; Huang, J.; Jiang, M.; Han, J.B.; Zhang, Z.R. Multi-objective optimization and design of flux-concentrating permanent magnet in-wheel motor. Proc. CSEE 2024, 44, 1173–1184. [Google Scholar] [CrossRef]
- Xie, B.C.; Zhang, Y.; Xu, Z.Y.; Zhang, F.G.; Liu, W.H. Review on multidisciplinary optimization key technology of electrical machine based on surrogate models. Trans. China Electrotech. Soc. 2022, 37, 5117–5143. [Google Scholar] [CrossRef]
- Huang, R.; Zheng, D. Multi-objective optimization design of unequal-thickness permanent magnet motor based on Kriging proxy model and particle swarm optimization. Small Spec. Electr. Mach. 2020, 48, 19–23. [Google Scholar] [CrossRef]
- Jin, Y.X.; Wang, A.Y.; Wang, T.; Sun, J. Multi-objective optimization design of nuclear canned induction motor based on particle swarm optimization. Electr. Mach. Control Appl. 2019, 46, 53–57. [Google Scholar] [CrossRef]
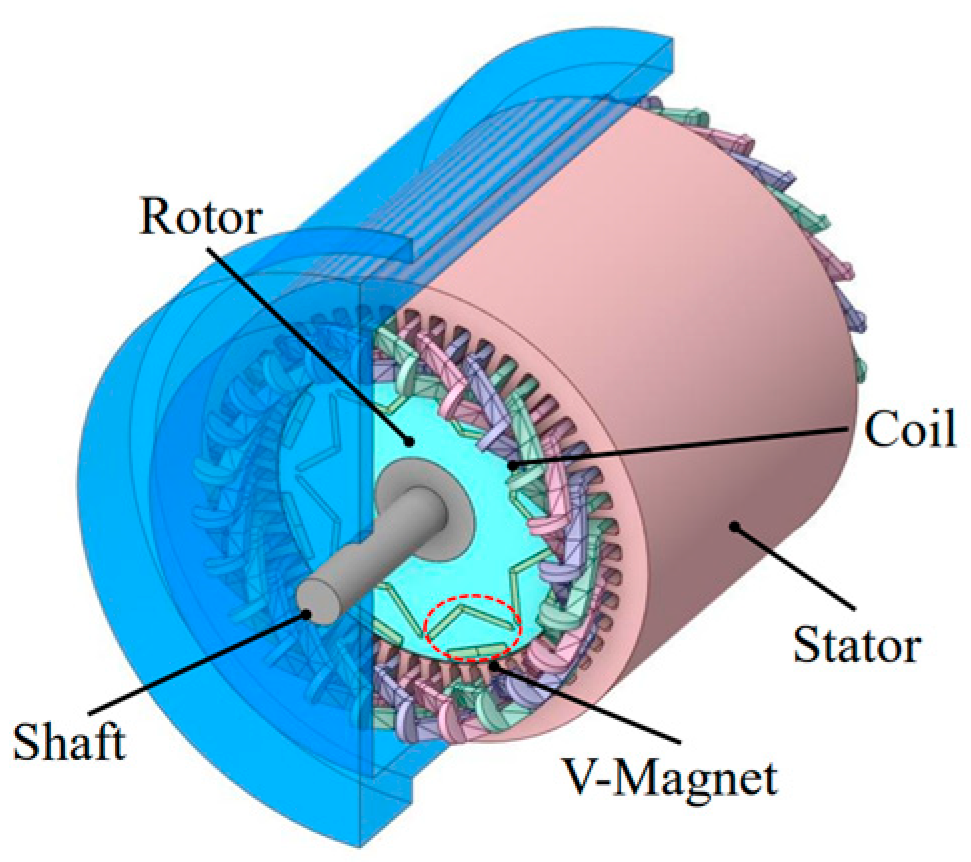





| Parameter | Value |
|---|---|
| Outer diameter of stator | 198 mm |
| Inner diameter of stator | 132 mm |
| Outer diameter of rotor | 130 mm |
| Inner diameter of rotor | 44.5 mm |
| Number of poles | 8 |
| Number of slots | 48 |
| Air-gap length | 1 mm |
| Axial length of rotor core | 160 mm |
| Structure Name | Structural Parameter | Initial Value (mm) | Variable Range (mm) |
|---|---|---|---|
| Slot opening height | Hs0 | 1.2 | 0.80~1.32 |
| Slot wedge height | Hs1 | 0.48 | 0.42~0.52 |
| Slot body height | Hs2 | 17.29 | 16.56~18.01 |
| Slot opening width | Bs0 | 2.81 | 2.20~3.10 |
| Slot width at the top | Bs1 | 4.71 | 4.45~5.05 |
| Slot width at the bottom | Bs2 | 6.98 | 6.25~7.65 |
| Slot fillet radius | Rs | 2 | 1.80~2.20 |
| Air-gap length | Airgap | 1 | 0.80~1.10 |
| Structural Parameter | Original Design (mm) | Final Optimized Design (mm) |
|---|---|---|
| Hs0 | 1.2 | 0.98 |
| Hs1 | 0.48 | 0.46 |
| Hs2 | 17.29 | 17.29 |
| Bs0 | 2.81 | 2.80 |
| Bs1 | 4.71 | 4.71 |
| Bs2 | 6.98 | 7.08 |
| Rs | 2 | 2.09 |
| Airgap | 1 | 1.03 |
| Electromagnetic Performance | Before Optimization | After Optimization | Variation |
|---|---|---|---|
| Peak no-load back EMF | 229.21 V | 223.14 V | −2.65% |
| Peak cogging torque | 0.479 N·m | 0.305 N·m | −36.33% |
| Structural Parameter | Optimization Results (mm) | Finite Element Verification Results (mm) |
|---|---|---|
| Hs0 | 0.98 | 1.05 |
| Hs1 | 0.46 | 0.44 |
| Hs2 | 17.29 | 17.29 |
| Bs0 | 2.80 | 2.80 |
| Bs1 | 4.71 | 4.71 |
| Bs2 | 7.08 | 7.01 |
| Rs | 2.09 | 2.13 |
| Airgap | 1.03 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cen, Y.; Shen, H.; Wang, X.; Wu, Y.; Du, J. Multi-Objective Optimization Analysis of Electromagnetic Performance of Permanent Magnet Synchronous Motors Based on the PSO Algorithm. Energies 2024, 17, 4637. https://doi.org/10.3390/en17184637
Cen Y, Shen H, Wang X, Wu Y, Du J. Multi-Objective Optimization Analysis of Electromagnetic Performance of Permanent Magnet Synchronous Motors Based on the PSO Algorithm. Energies. 2024; 17(18):4637. https://doi.org/10.3390/en17184637
Chicago/Turabian StyleCen, Yufei, Haoyu Shen, Xiaoyuan Wang, Yongming Wu, and Jingjuan Du. 2024. "Multi-Objective Optimization Analysis of Electromagnetic Performance of Permanent Magnet Synchronous Motors Based on the PSO Algorithm" Energies 17, no. 18: 4637. https://doi.org/10.3390/en17184637
APA StyleCen, Y., Shen, H., Wang, X., Wu, Y., & Du, J. (2024). Multi-Objective Optimization Analysis of Electromagnetic Performance of Permanent Magnet Synchronous Motors Based on the PSO Algorithm. Energies, 17(18), 4637. https://doi.org/10.3390/en17184637








