1. Introduction
At present, the problem of ash blockage in a rotary air preheater of the coal-fired power plant is very common, which is mainly caused by the loose ash and cohesive ash deposited in the rotary air preheater [
1,
2]. It seriously affects the safe and economic operation of the coal-fired generating units. Therefore, it is vital to solve the ash-blocking problem caused by the fly ash deposition on the surface of the air preheater. In the past few years, many researchers from all over the world have researched the formation mechanism and the influencing factors of ash deposition on the air preheater through numerical simulation or experimental methods. The blend deposition of ammonium bisulfate (ABS) and fly ash is affected by many factors, such as the concentrations of NH
3 and SO
3, the ash particle sizes, and the flue gas temperature [
3]. The operation practice of coal-fired boilers shows that the blend deposition degree of ABS and fly ash on the surface of the air preheater is related to the working conditions [
4,
5], with which the position and the intensity of ash deposition can change. The soot blowing using high temperature and high-pressure steam is considered a common approach to alleviate the ash blocking of the air preheater [
6]. A certain amount of heat carried by high-temperature steam can enhance the temperature of the corrugated plates, and a certain amount of momentum of steam sprayed into the space of the air preheater can cause the ash layer to peel off. However, the effects of steam soot blowing vary greatly due to the different working conditions. The soot-blowing effects and the service life of the corrugated plates can be affected by the soot-blowing operation time, the operation frequency, and the soot-blowing position, which further affects the safe operation of the air preheater. Therefore, it is necessary to study the influences of the flow field and the temperature field in the air preheater and the parameters of soot blowing on the ash deposition under the conditions of steam soot blowing.
Numerical simulation is a common method to study the flow field and the temperature field in the air preheater. Koray et al. [
7] performed the numerical simulation of the temperature field in the air preheater model based on the flow resistance coefficient and the convective heat transfer coefficient in the single channel. Armin et al. [
8] simulated the flow field and the temperature field of the heat storage plate in the air preheater using the porous medium model in Ansys Fluent software. Shah et al. [
9] established a heat transfer calculation model considering the air leakage based on the principles of dimensionless length and time and obtained the temperature distributions in the inlet and outlet of the flue gas side and the air side. Yan et al. [
10] established a non-thermal equilibrium model of a tri-sectional rotary air preheater and simulated the three-dimensional temperature distribution of the air preheater. Chen et al. [
11] constructed a three-dimensional numerical calculation model for the quad-sectional air preheater using the software of Ansys Fluent 2021R1 and calculated the detailed temperature field distribution. The above research provides useful theoretical guidance to study the flow field and the temperature field in the rotary air preheater. However, it is still relatively rare to perform the numerical simulation study on the flow field and temperature field in the rotary air preheater, considering the influences of the steam soot-blowing.
In this study, taking the tri-sectional rotary air of a 600 MW coal-fired power plant boiler as the research object, the relevant numerical calculation models are established, and the mesh model of the flue gas side of the air preheater considering the influence of steam soot-blowing is established using the Gambit 2.4.6 software. Under the varied operation conditions, including the boiler loads and the steam soot-blowing parameters, the velocity field and the temperature field in the air preheater are simulated using the software Ansys Fluent 2021R1. The influences of the boiler load, the operation parameters of the steam soot blower, and the running and outage of the soot blower on the flue gas velocity distribution in the depth direction of the corrugated plates, the soot-blowing coverage area, the inlet flue gas velocity, and the inlet flue gas temperature of the corrugated plates are analyzed. The research results are helpful to further explore the ash deposition characteristics and then optimize the soot blowing strategy in order to effectively solve the ash blockage in the rotary air preheater.
2. Numerical Simulation Models and Methods
It is a prerequisite for studying the influences of a steam soot blower on the ash deposition in the corrugated plates that the characteristics of the flow field and the temperature field in the air preheater, including the steam soot blower, are investigated first. The flue gas flow with lots of fly ash particles in the air preheater is a typical two-phase flow. The two-phase flow mathematical models mainly involve the flow and heat transfer mathematical models. The related sub-models mainly include the basic control equations, the turbulence models, the discrete phase models, and the heat transfer models. The numerical calculation models and methods are as follows.
2.1. Numerical Simulation Models
2.1.1. Basic Control Equations
The flue gas flow inside the air preheater abides by the basic control equations, including the mass conservation equation, the momentum conservation equation, and the energy conservation equation.
- (1)
Mass conservation equation
The mass conservation equation is shown in Equation (1), which can be used for compressible and incompressible flows.
Here, ρ—the flue gas density, kg/m3; —the overall velocity vector of flue gas, m/s; t—the time, s.
- (2)
Momentum conservation equations
The momentum conservation equations along the three coordinate axes in the rectangular coordinate system are shown in Equations (2)–(4), respectively.
Here, vx, vy, and vz—the fluid velocity component in the direction of x-axis, y-axis, and z-axis, m/s; µ—the flue gas dynamic viscosity, N·s/m2; θ—the stress on the flue gas, N; Sx, Sy, and Sz—the deformation velocity tensor in the direction of x-axis, y-axis, and z-axis, respectively.
In Equations (2)–(4), the symbolic meanings of other variables are the same as those in Equation (1).
- (3)
Energy conservation equation
The energy conservation equation is listed in Equation (5).
Here, cp—the fluid-specific heat at constant pressure, J/(kg·K); λ—the flue gas thermal conductivity, W/(m·K); T—the thermodynamic temperature, K; ST—the fluid viscous dissipation term. Other variable meanings are described above.
2.1.2. Gas-Phase Turbulence Models
The flow of flue gas and water vapor in the rotary air preheater is in a turbulent state. In this study, there may exist a local turbulence phenomenon in the area where the flue gas and the soot-blowing steam meet for the air preheater, but the area accounting for the whole space is not large. Hence, the turbulent process in the air preheater can be described by the standard
k-ε model that includes the
k equation of the turbulent kinetic energy and the
ε equation of the turbulent dissipation rate, as shown in Equation (6) and Equation (7), respectively.
Here, ui, uj—the fluid velocity component in the direction of the x-axis and y-axis, respectively, m/s; k—the turbulence kinetic energy, J; ε—the dissipation rate of turbulence kinetic energy,%; μ—the turbulent viscosity of the fluid in the standard state, kg/(m·s); μt—the turbulent viscosity of the fluid at a temperature(t), kg/(m·s); σk, σε—the Prandtl constant of k and ε, respectively; Gk—the volume generation rate of turbulent kinetic energy, m2/s2.
The calculation formula of turbulent kinetic energy volume generation rate (
Gk) and other related quantity calculation formulas are as follows:
There are multiple coefficients in the standard
k-ε model describing the turbulent process in the air preheater, the values of which are listed in
Table 1.
2.1.3. Gas–Solid Two-Phase Flow Models
The mixed flow of flue gas and fly ash in the air preheater is a typical gas–solid two-phase flow, so it can be described using the Discrete Phase Model (DPM) based on the Euler–Lagrangian method in Fluent software. The DPM is suitable for the numerical simulation of gas–solid two-phase flow with particle volume fraction less than 12%. In this study, the ash volume content of flue gas in the air preheater is below 8%, so the DPM model is used to track the particle movement and predict the ash deposition on the surface of the corrugated plates. When the fly ash particles, along with the flue gas, skim over the surface of the heat exchanger elements, they are easily subject to multiple forces, e.g., gravity, thermophoresis force, drag force, and Basset force [
13].
Because the particle size of fly ash particles is in the range of 1–100 μm and there is a large temperature difference in the flue gas, the drag force, the gravity, and the thermophoretic force on the fly ash particles are considered in the numerical simulation [
14]. The motion equation of a single particle is shown in Equation (11) [
13].
Here, the subscript p—the fly ash particle; t—the time, s; g—the gravitational acceleration, m/s2; u—the flue gas velocity, m/s; up—the fly ash particle velocity, m/s; FD(u−up)—the drag force on the fly ash particles, N; —the gravity on the fly ash particles, N; —the density of fly ash particles, kg/m3; Fth—the thermophoretic force on the fly ash particles, N. Other variables are described above.
- (1)
Drag force calculation
When moving with the flue gas, the velocity of the fly ash particles is less than the flue gas velocity, so the fly ash particles are subjected to the drag force. The calculation models of drag force and other associated parameters are as follows:
Here, dp—the fly ash particle size, μm; CD—the drag coefficient; Rep—the Reynolds number; ds0—the characteristic particle size, μm; n—the distribution index of ash particle size. Other variables are described above.
- (2)
Gravity calculation
The fly ash particles are subjected to gravity during the movement process, which has a great influence on the ash deposition. So, the gravity of the fly ash particles cannot be ignored. Its calculation is shown in Equation (16).
- (3)
Thermophoretic force calculation
When the flue gas flows through the air preheater, there is heat transfer. There is a certain temperature gradient between the fly ash particles and the flue gas. Therefore, the effect of the thermophoresis force should be considered in the simulation calculation. Its calculation models involved are shown in Equations (17) and (18).
Here, Cs—the heat slip coefficient, Cs = 1.17; Cm—Momentum slip coefficient, Cm = 1.14; Ct—the temperature step coefficient, Ct = 2.18; λp—the thermal conductivity of fly ash particle, W/(m·K); L—the mean free path of flue gas, m; mp—the quality of fly ash particle, kg; Other variables are described above.
2.1.4. Heat Transfer Models
Heat transfer occurs when flue gas with fly ash particles flows through the air preheater. The heat transfer process mainly includes the convection heat transfer between the flue gas and the heat exchanger elements, as well as the convection heat transfer between the flue gas and the fly ash particles.
- (1)
Convective heat transfer quantity between the flue gas and the air preheater
The quantity of convective heat transfer between the flue gas and the air preheater is calculated according to Equation (19).
Here, Qc1—the heat convection quantity between the flue gas and the air preheater, W/m2; hg—the convective heat transfer coefficient between the flue gas and the heat-exchanger elements of the air preheater, W/(m2·K); Tw—the wall temperature of the heat-exchanger elements, K; Tg—the temperature of flue gas, K.
- (2)
Convective heat transfer quantity between the flue gas and the fly ash particles
The calculation equations involved in the convective heat transfer quantity between the flue gas and the fly ash particles are listed below [
15].
Here, Qc2—the convective heat transfer quantity between the flue gas and the fly ash particles, W/m2; hgp—the convective heat transfer coefficient between the flue gas and the fly ash particles, W/(m2·K); λg—the flue gas thermal conductivity, W/(m·K); Tp—the temperature of the fly ash particles, K; Nup—the Neusselt number of the fly ash particle; αg, αp—the equivalent absorption rate of the flue gas and the fly ash particle, respectively; Prg—the Prandtl number of the flue gas. Other variables are described above.
2.2. Geometric Modeling and Grid Division of the Rotary Air Preheater
2.2.1. Geometric Modeling of the Rotary Air Preheater
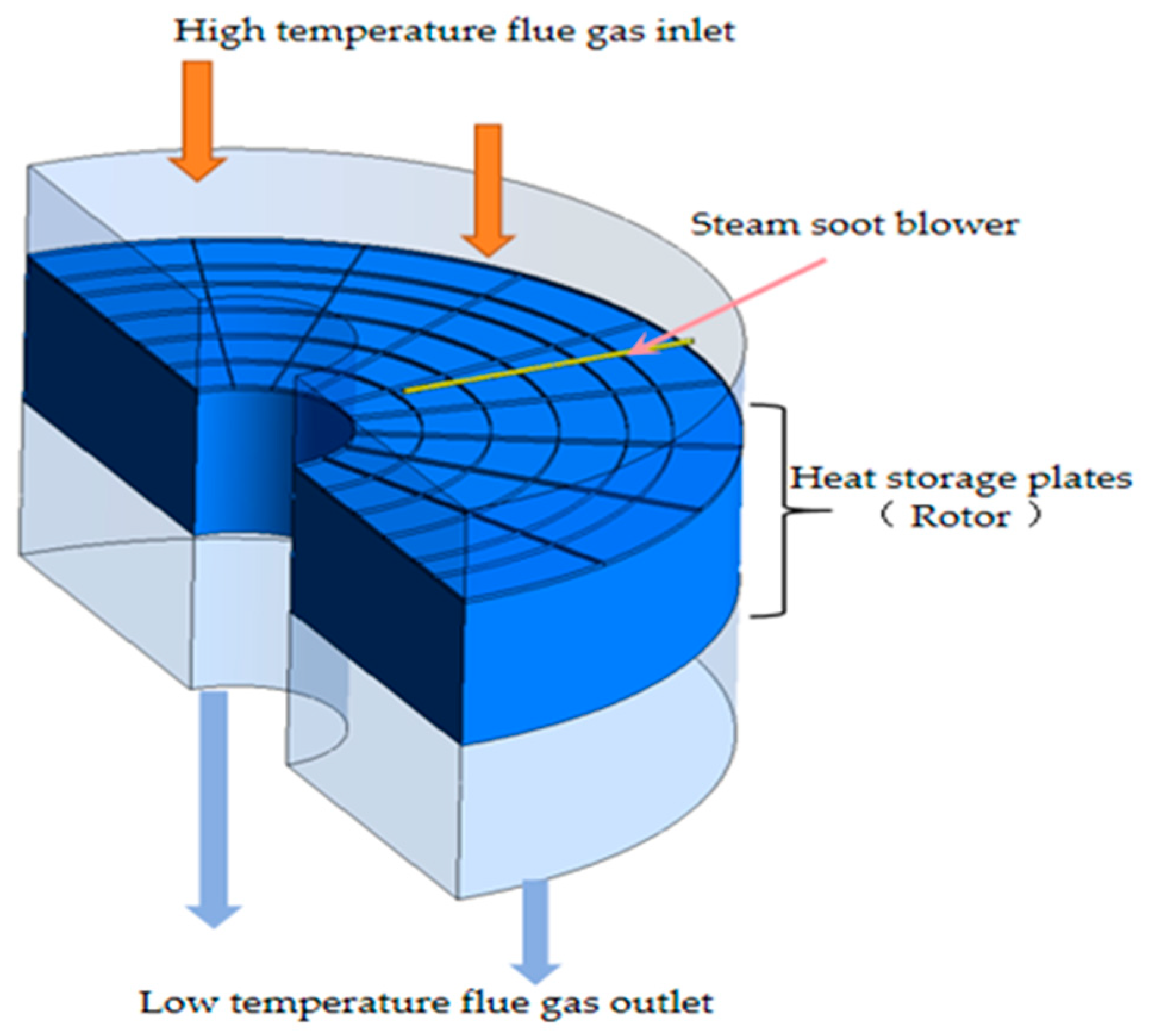
The research object is a tri-sectional rotary air preheater of a 600 MW coal-fired power plant boiler in this study. When modeling the flue gas side of the air preheater, the influences of the steam soot blowing on the flow of the flue gas in the air preheater have been considered. According to the actual structure and the size of the rotary air preheater, a three-dimensional geometric model at a ratio of 1:1 is established. The geometric model of the flue gas side of the rotary air preheater is shown in
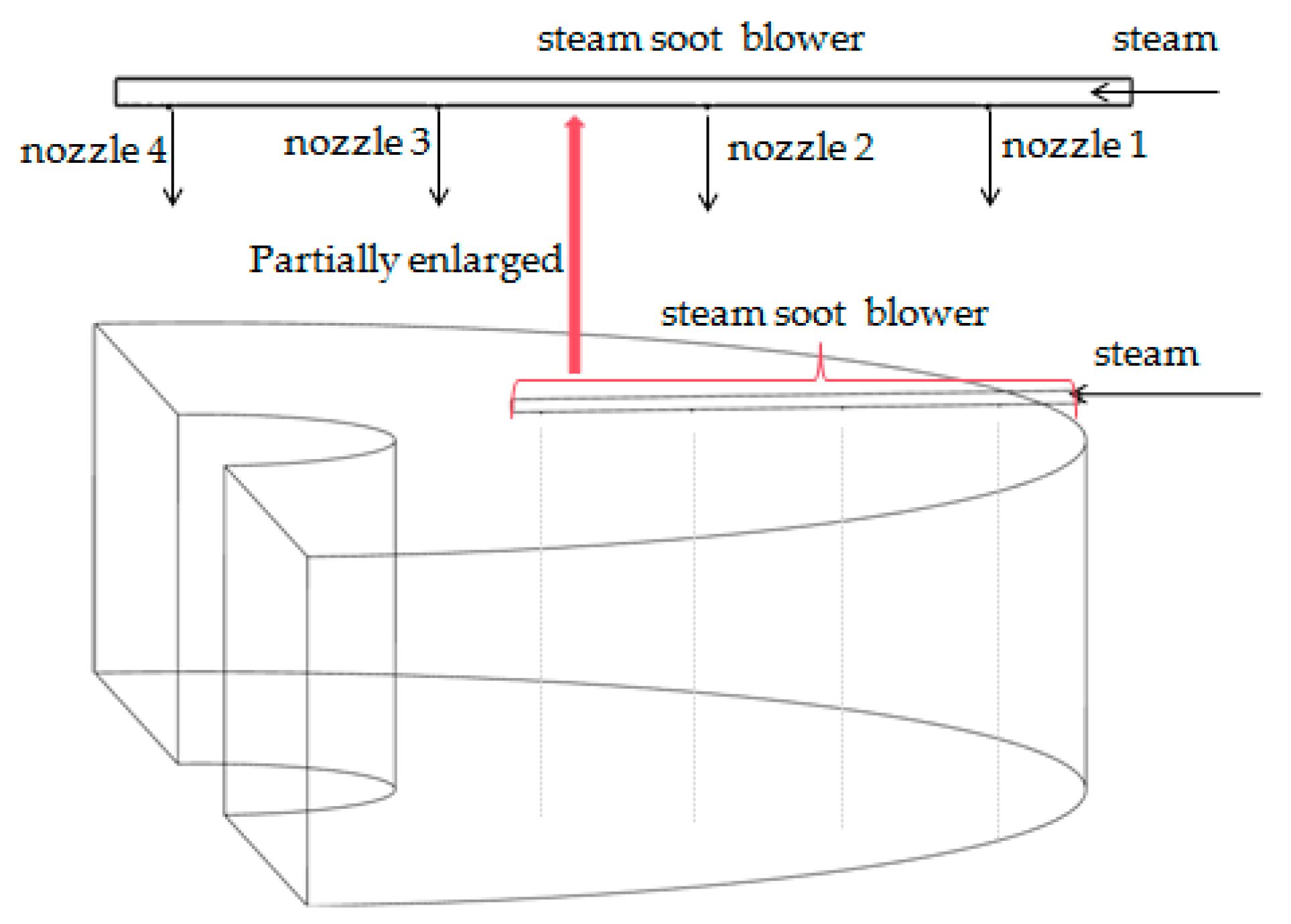
Figure 1. From the upper inlet, the high-temperature flue gas enters the rotary air preheater. The height between the soot blower and the hot end inlet of the corrugated plates is 0.25 m. The height of the corrugated plates in the flow direction of flue gas is 2.81 m. The total length of the steam soot blower is 4.5 m, and there are four steam nozzles numbered 1, 2, 3, and 4, respectively, as shown in
Figure 2. The steam soot blower is partially magnified in
Figure 2 in order to show the arrangement of the four nozzles. The distance between two adjacent nozzles is 1.15 m, as shown in
Figure 2. The ejecting direction of soot-blowing steam is the same as the flow direction of flue gas. The overall traveling distance of the steam soot blower inside the air preheater is 1.5 m. The cross-section of the corrugated plates (that is, the rotor) is the fan shape with an angle of 180° cut by the ring with an outer diameter of 13.4 m and an inner diameter of 2.9 m. In this study, the rotor composed of a large number of corrugated plates is regarded as a porous medium.
2.2.2. Grid Division and Grid Independence Validation
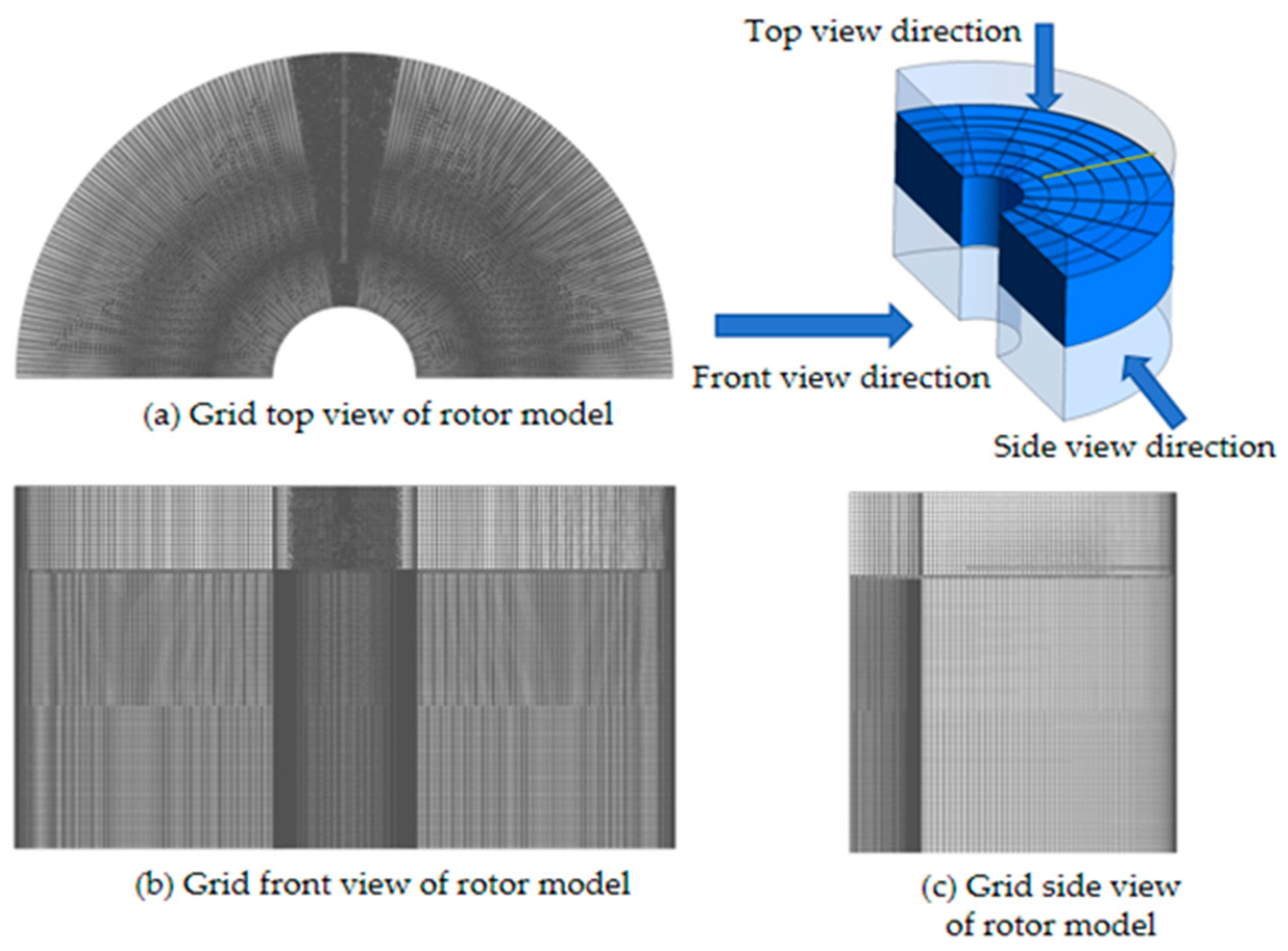
Based on the partition grid division method, the geometric model of the air preheater studied is meshed by the software Gambit 2.4.6, as shown in
Figure 3.
Figure 3a–c are the grid top view, the grid front view, and the grid side view of the the rotor model, respectively. Due to the relatively complex structure, the unstructured regular tetrahedron grids are used for the square-to-circular irregular body of the flue gas inlet section and the semi-ring body containing the soot blower. Because the structure size of the soot blower is small, its grid size is also reduced accordingly, and the mesh in this area is dense, as shown in
Figure 3a. The structure of the corrugated plates is simple, so the structured, regular hexahedron grids are adopted in order to improve the quality of the grid division and facilitate the convergence of the steady-state field calculation.
The quantity of grids greatly influences the accuracy of the numerical simulation results and the computation speed. In this study, four meshing schemes were used based on a test method of grid-independent [
16,
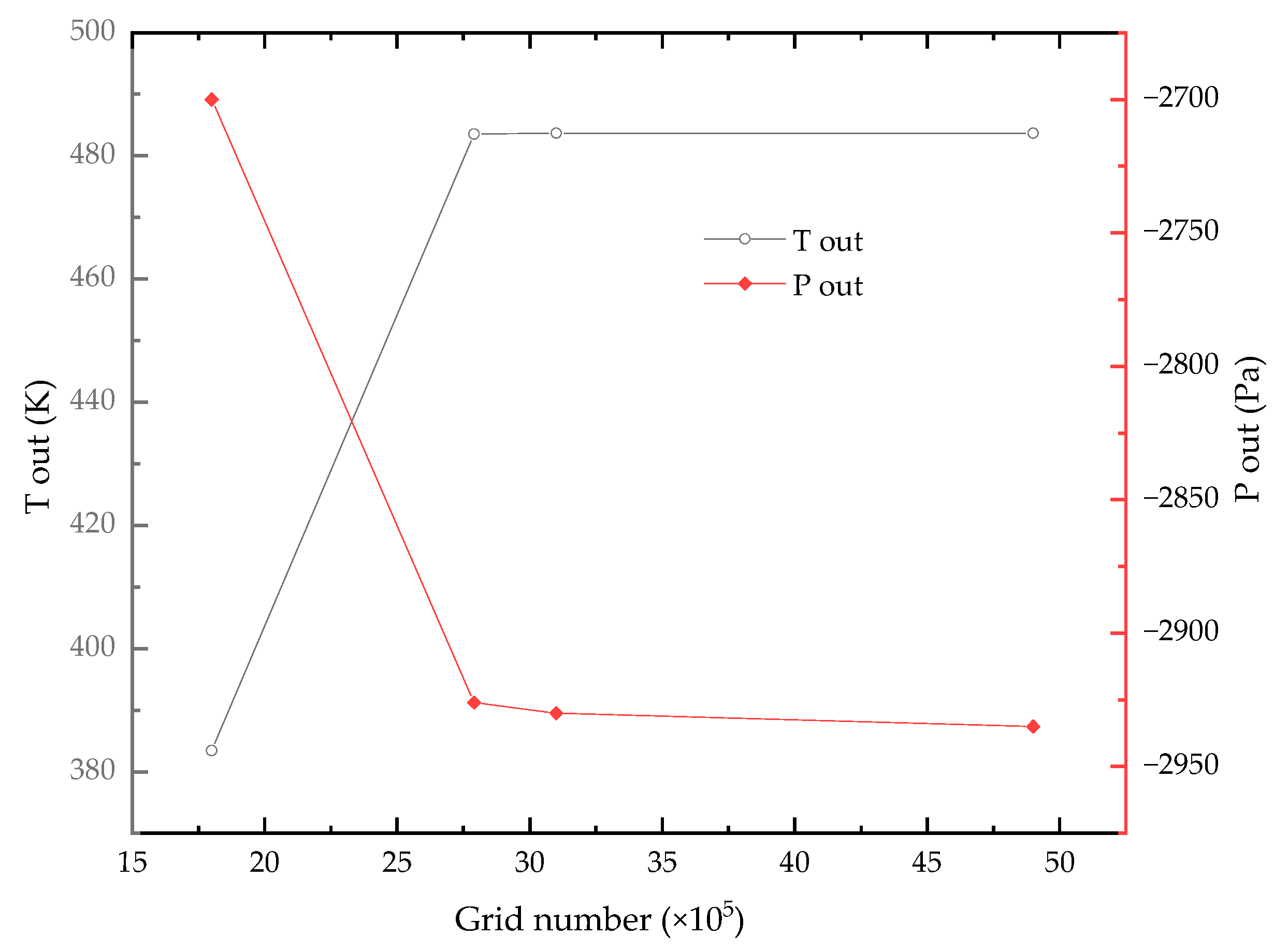
17]. The grids number are 4.94 million, 3.10 million, 2.79 million, and 1.89 million, respectively. The main differences in the grid quantity result from the difference between the unstructured grid size of the inlet section and the structured grid size of the corrugated plates. The number of grids used in the soot blower part is basically the same in four meshing schemes. The models with different numbers of grids have been numerically solved, and the values of fluid temperature and pressure varying with the number of grids at the outlet of the air preheater are shown in
Figure 4. It can be seen from
Figure 4 that when the number of grids is separately 4.94 million, 3.10 million, and 2.79 million, the fluid temperature and pressure at the outlet change little, but the fluid temperature and the fluid pressure at the outlet change greatly when the number of grids is reduced to 1.89 million. Therefore, on the premise of ensuring calculation accuracy, the grid division scheme with 3.10 million grid cells has been adopted in order to improve the calculation speed.
2.3. Setting of the Boundary Conditions
In this study, the boiler maximum continuous rating (BMCR: 600 MW) is taken as the base operation condition; meanwhile, the steam soot blowers in the air preheater are in operation normally. In order to better simulate the heat transfer of the corrugated plates of the air preheater and attain the outlet temperature of the air preheater closer to the measured value, it is necessary to introduce the internal heat source term in the corrugated plates according to the actual heat transfer situation of the air preheater [
18]. The main operation parameters of the air preheater and the steam soot blower set are listed in
Table 2.
Additionally, the velocity inlet boundary condition and the pressure outlet boundary condition are adopted separately in the inlet boundary condition settings and in the outlet boundary condition settings of flue gas and soot-blowing steam. The wall temperature of the air preheater model is set at 300 K, and the outer wall temperature of the soot blower pipe is set at the flue gas temperature.
2.4. Calculation Methods
The software of Ansys Fluent 2021R1 is employed to simulate numerically the flow and heat transfer in the corrugated plates of the air preheater, considering the influences of steam soot-blowing. The standard
k-ε double-equation mode is adopted to analyze the turbulent process, and the SIMPLE algorithm is used for the velocity–pressure coupling. The cell-based Green-Gaussian algorithm is selected for the gradient interpolation. The convection terms of the governing equations are discretized with the second-order upwind scheme, and a simple scheme is adopted for pressure–velocity coupling. The convection terms of the governing equations are discretized with a second-order upwind scheme. The condition for calculating convergence is that the sum (
RΦ) of standard residuals is less than the set value (σ). The value of σ in the energy equation is set at 10
−6, and the values of σ for the remaining variables are all set at 10
−3. The calculation formula for
RΦ is as follows:
Here, Φ—the local variable; RΦ—the residual of the equation corresponding to the variable of Φ; CV—the control volume of the unit cell.
3. Results and Discussion
In this section, the numerical calculation of the flow field and the temperature field in the air preheater, including the steam soot blower, under different working conditions is performed based on the established geometric models and mathematical models. The influences of the boiler loads, the operation parameters of the steam soot-blowers, and the running and shutdown of soot-blowers on the flue gas velocity in the corrugated depth direction, the soot-blowing coverage area, the inlet velocity, and the inlet temperature of the hot end of the corrugated plates are analyzed.
3.1. Settings of Simulated Working Conditions
The simulated working conditions include four boiler loads: 600 MW (100% BMCR), 450 MW (75% BMCR), and 300 MW (50% BMCR). The changes in the soot blower’s steam velocity include four running conditions: stopping the running of the soot blower (0 m/s), normal operation of the soot blower (25 m/s), reducing the steam velocity of the soot blower (20 m/s), and increasing steam velocity of the soot blower (30 m/s). The steam temperature of the soot blower is set at three working conditions: normal temperature (621 K), reducing steam temperature (601 K), and increasing steam temperature (641 K). The working parameters of the air preheater under different working conditions are listed in
Table 3. The working condition No.1 is defined as the base operation condition. The working conditions numbered 1–3 are the comparison conditions of changing flue gas parameters. The working conditions numbered 1, 4, and 5 are the conditions for changing the inlet steam velocity of the soot blower steam pipe under the high load of 600 MW. The working conditions numbered 3, 8, and 9 are the conditions for changing the inlet steam velocity of the soot blower steam pipe under the low load of 300 MW. Due to the high temperature of flue gas in working condition No.1, the influences of inlet steam temperature cannot be observed. Therefore, working condition No.3 is used as the comparison working condition of working conditions No.6 and No.7 (changing the inlet steam temperature). The working conditions No.10 and No.11 are used as the reference working conditions when the soot blower stops working under the conditions of 100% BMCR and 50% BMCR, respectively. There are 11 working conditions in total.
3.2. Numerical Simulation of the Base Working Condition
3.2.1. The Flue Gas Velocity Distribution in the Depth Direction of the Corrugated Plates
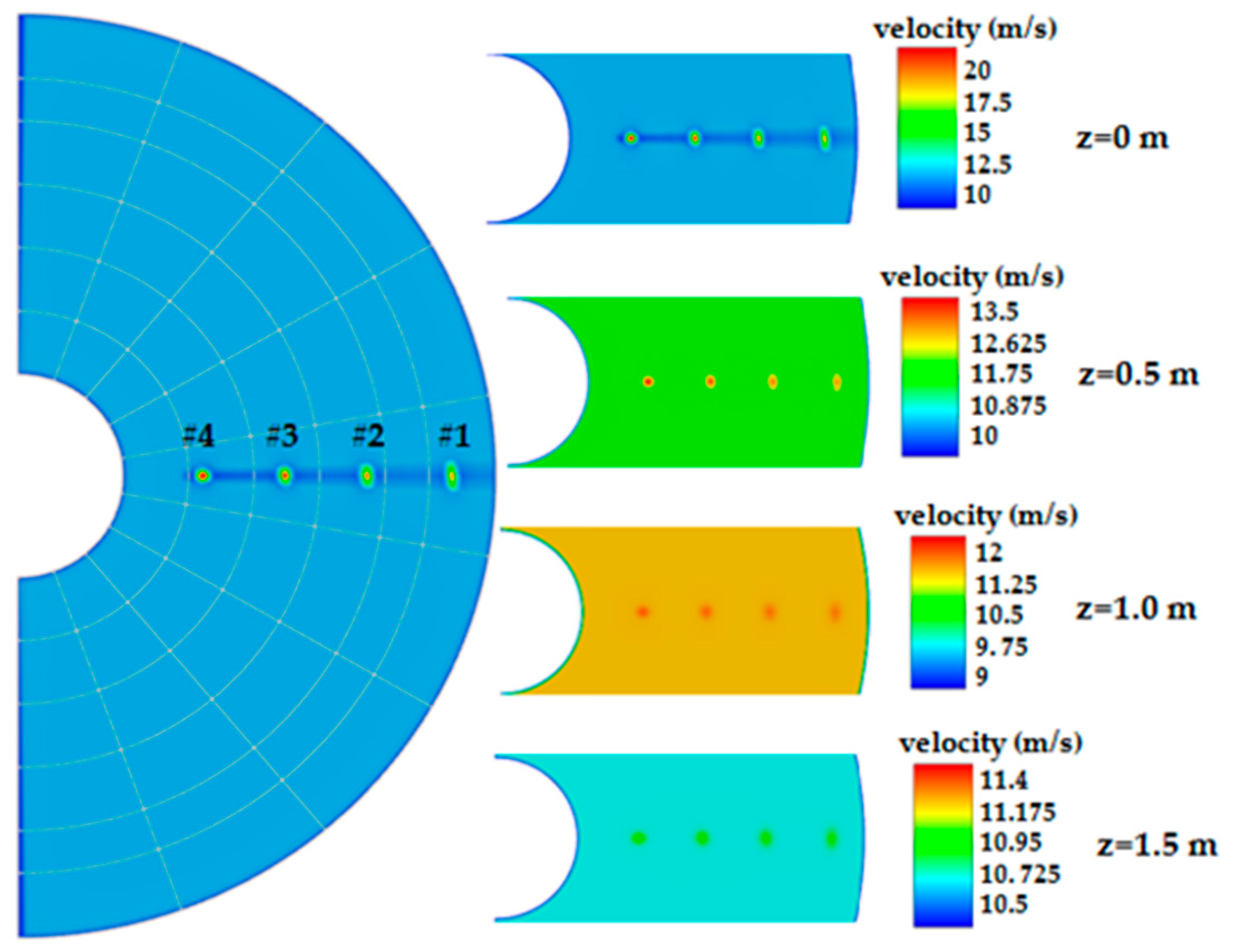
The numerical simulation results of the flue gas velocity distribution in the depth direction of the corrugated plates are shown in
Figure 5 and
Figure 6 after the flue gas is mixed with soot-blowing steam under the base working condition. In
Figure 5, the letter Z represents the depth coordinate of the air preheater corrugated plates, and the value of Z equal to 0 m represents the hot end inlet plane of the corrugated plates of the air preheater. The flue gas velocity distribution on four planes is shown in
Figure 5. On the plane of
Z equal to 0 m, because the steam with a high velocity is mixed into the flue gas, an obvious high-speed area can be observed below each nozzle, and the velocity difference on this plane is relatively large. With an increase in the longitudinal depth, the velocity difference between the area below the soot blower and the surrounding area gradually decreases. When the flue gas reaches the plane of
Z equal to 1.5 m, the relative change rate of the flue gas velocity on this plane is about 7.9% (<10%), and the average flue gas velocity is about 11.0 m/s accordingly.
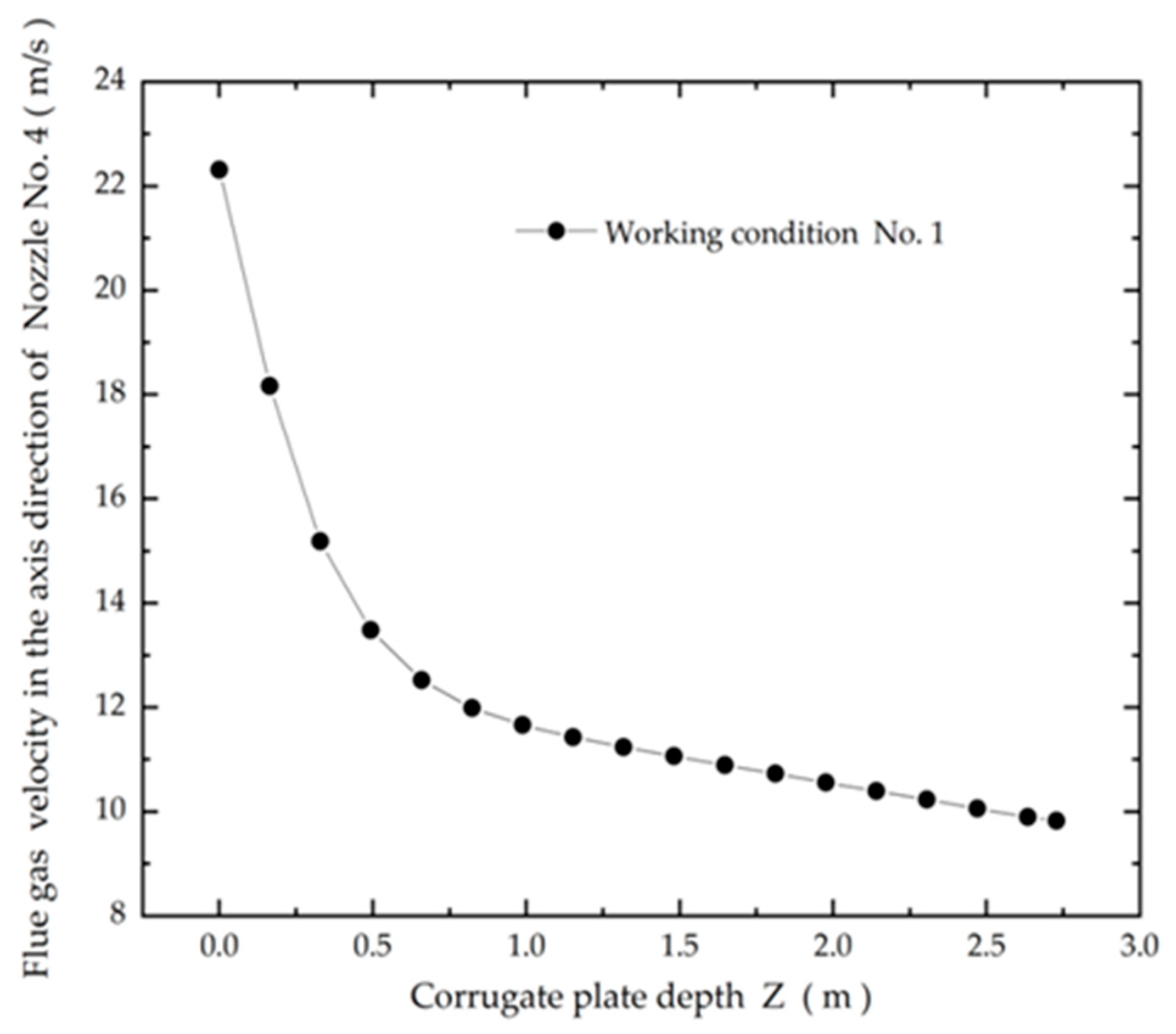
The variation in flue gas velocity in the axis direction of the nozzle is illustrated in
Figure 6, taking Nozzle No.4 as a representative example. According to the simulated data, the flue gas velocities at the inlet and outlet of corrugated plates are, respectively, 22.31 m/s and 9.82 m/s along the axial direction of Nozzle No.4. It can be seen from
Figure 6 that the flue gas velocity decreases rapidly in the axis when the value of Z is less than 1.0 m, and then it decreases slowly with almost equal slope with an increase in corrugated plate depth. The flue gas velocity calculated is 11.06 m/s at the value of Z equal to 1.5 m, dropping by about 50.4% compared with the inlet flue gas velocity.
3.2.2. Definition of Soot-Blowing Coverage Area (Ai)
The soot-blowing coverage area (Ai) is considered a soot-blowing plane characteristic parameter of the hot end inlet of the corrugated plates. Here, the letter i represents the working condition number. Taking the base working condition as an example, the physical meaning of the soot-blowing coverage area (Ai) is described.
The soot-blowing coverage area of the single nozzle (
Aij) is defined as the maximum area where there exists the velocity difference (when the relative variation rate of the flue gas velocity is greater than 10%) caused by the soot-blowing steam on the plane of Z equal to 0 under the working condition numbered
i. Here, the letter
j represents the steam nozzle number. There are four soot-blowing steam nozzles in
Figure 5, numbered 1, 2, 3, and 4, respectively. The soot-blowing coverage area (
Ai) under a certain working condition is defined as the sum of four coverage areas (
Ai,j) caused by four nozzles of the steam soot blower on the plane of Z equal to 0.
Under the base working condition, the approximate circle diameters of the coverage areas caused by four steam nozzles on the plane of Z equal to 0 are 0.303 m (d11), 0.303 m (d12), 0.352 m (d13), and 0.351 m (d14), respectively. The corresponding four coverage areas are 0.072 m2 (A11), 0.072 m2 (A12), 0.097 m2 (A13), and 0.097 m2 (A14), respectively. Hence, the soot-blowing coverage area (A1) of the base working condition is 0.338 m2 according to the above definition. The corresponding approximate circle diameter (d1) is 0.656 m.
3.3. Effects of Boiler Load on the Relevant Parameters
3.3.1. Effects of Boiler Load on the Longitudinal Flue Gas Velocity
It can be seen from
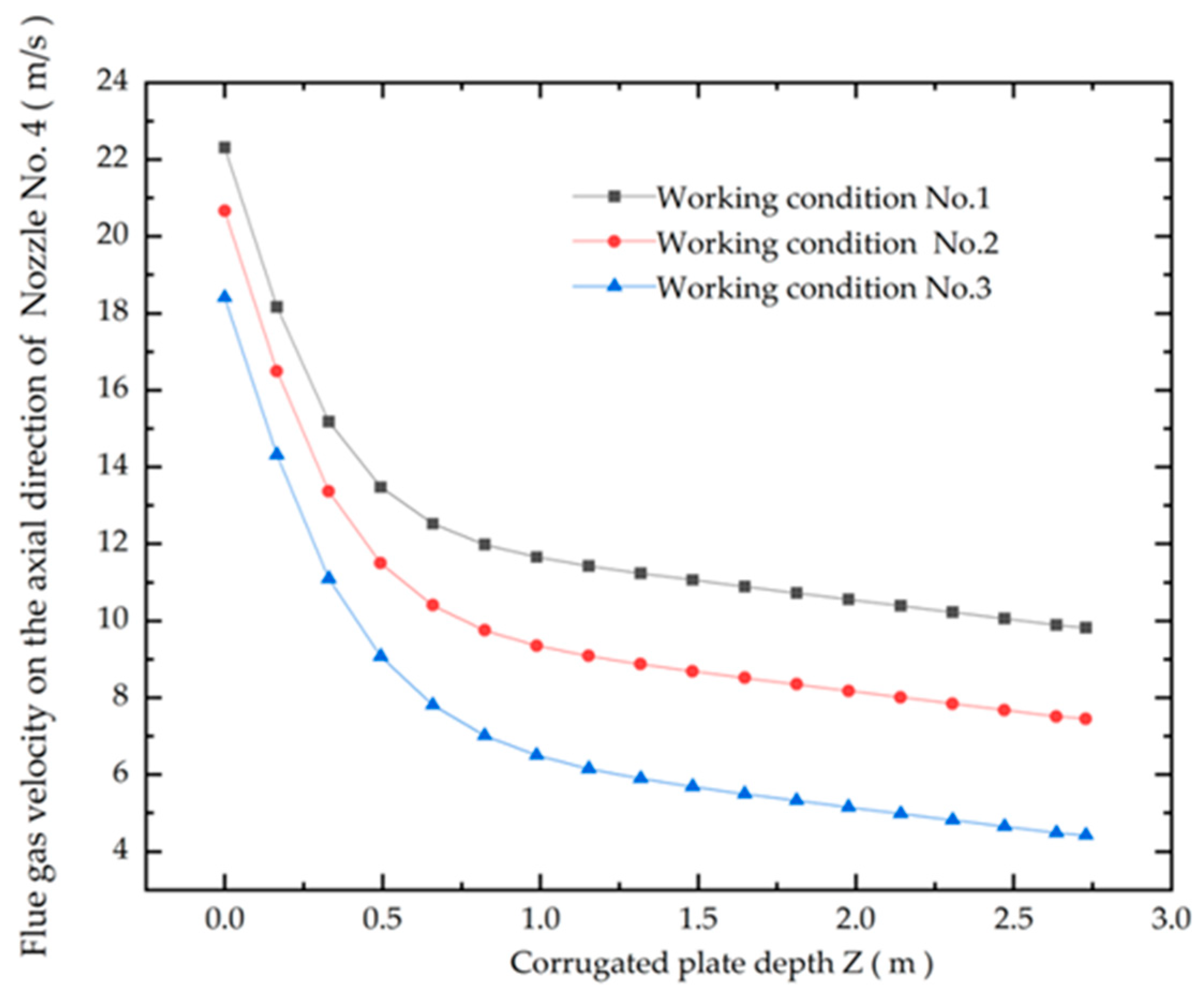
Table 3 that the flue gas velocity entering the air preheater is significantly reduced from 12.29 m/s to 6.98 m/s, with the boiler load decreasing from 600 MW to 300 MW. Therefore, the flue gas velocity entering the corrugated plates is obviously reduced. Taking Nozzle No.4 as an example, as shown in
Figure 7, the flue gas velocities simulated at the inlet of the corrugated plates on the axis of the nozzle under working conditions No.1–No.3 are 22.31 m/s, 20.66 m/s, and 18.40 m/s, respectively. Accordingly, the flue gas velocities at the outlet of the corrugated plates are, respectively, 9.82 m/s, 7.45 m/s, and 4.40 m/s. It can be seen from
Figure 7 that the flue gas velocity on the axis of the nozzle obviously decreases when decreasing the boiler load. The reduction in flue gas velocity increases with an increase in corrugated plate depth. The inlet and outlet flue gas velocities on the axis of the nozzle, respectively, reduce by 17.5% and 55.0% when the boiler load declines from 600 MW to 300 MW. It indicates that the average flue gas velocity in the space of corrugated plates under the working condition of a low boiler load is significantly lower than that under the condition of a high boiler load. So, the deposition of the fly ash easily occurs on the surface of corrugated plates under the condition of low boiler load.
3.3.2. Effects of Boiler Load on the Soot-Blowing Coverage Area
According to the algorithm described in the above definition of the soot-blowing coverage area (Ai), the corresponding values of Ai under working conditions No.1–No.3 can be calculated, namely A1 = 0.338 m2, A2 = 0.363 m2, and A3 = 0.422 m2. Additionally, the corresponding approximate circle diameters can be calculated, namely d1 = 0.656 m, d2 = 0.680 m, and d3 = 0.733 m. It is obvious that the soot-blowing coverage area on the inlet plane of the corrugated plates is negatively correlated with the boiler load. The soot-blowing coverage area increases by 24.9%, with the boiler load decreasing from 600 MW to 300 MW. The flue gas velocity decreases when the boiler load drops. Therefore, the velocity difference between the flue gas and the soot-blowing steam becomes larger, which enhances the mixing strength of the flue gas and steam. So, the soot-blowing coverage area increases with the boiler load decreasing. This means that the velocity attenuation of soot-blowing steam at low boiler load is faster than that at high boiler load. However, the rapid attenuation of soot-blowing steam velocity is not conducive to the removal of ash deposition on the cold end of the corrugated plates in the air preheater.
3.4. Effects of the Soot-Blowing Steam Velocity on the Relevant Parameters
3.4.1. Effects of Soot-Blowing Steam Velocity on the Longitudinal Flue Gas Velocity
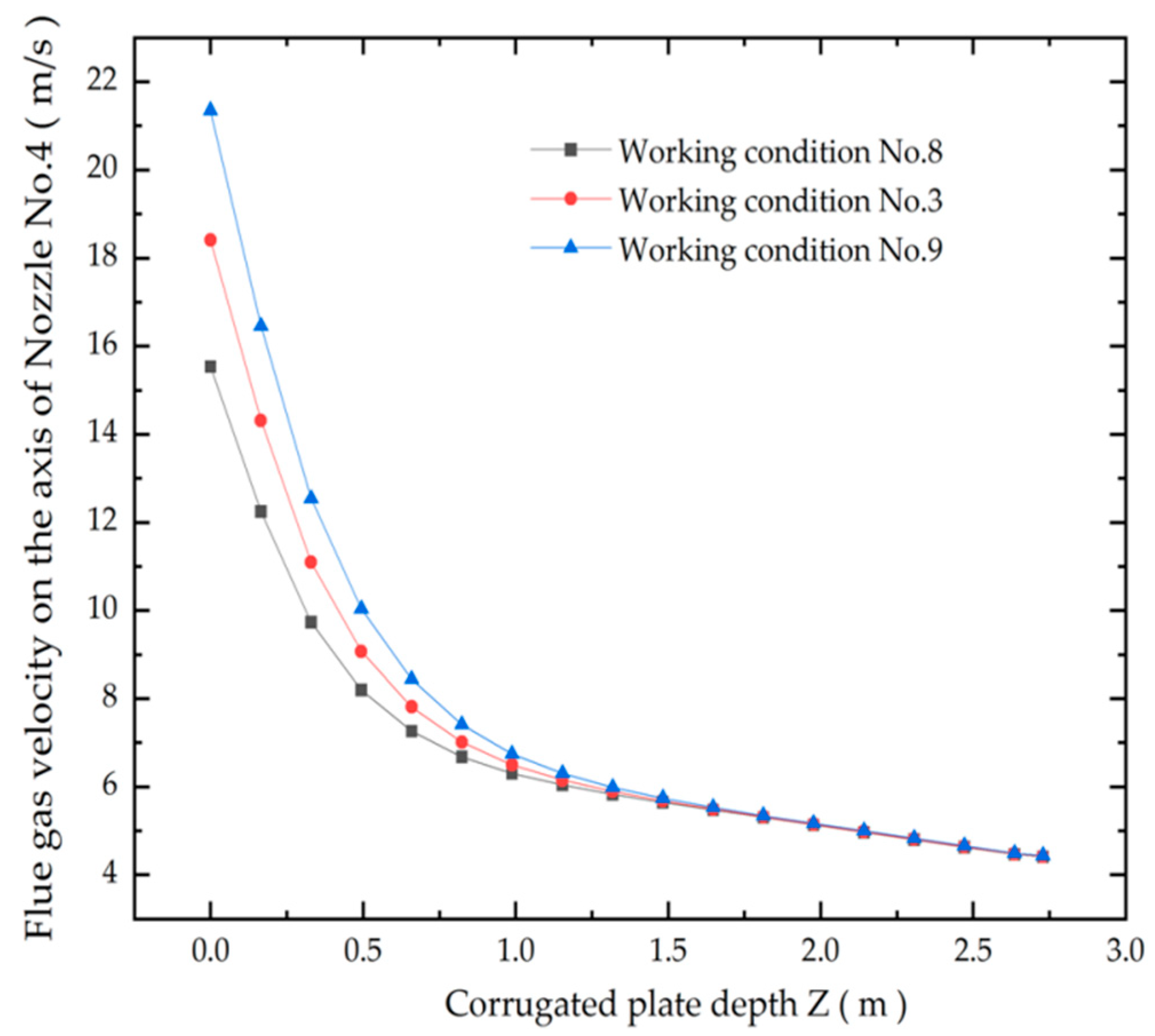
In this study, the effects of changing soot-blowing steam velocity on the longitudinal flue gas velocity are investigated under high load (600 MW) and low load (300 MW). Working condition No.1 and working condition No.3 are used as the comparison conditions for changing the steam velocity under the conditions of high and low boiler loads, respectively. Still taking Nozzle No.4 as an example, when changing the soot-blowing steam velocity, the flue gas velocity variations along the corrugated plate depth are separately indicated in
Figure 8 and
Figure 9 at high load (600 MW) and low load (300 MW). It can be seen from
Figure 8 and
Figure 9 that the flue gas velocity on the axis of the nozzle increases with the soot-blowing steam velocity increasing, whether under high load conditions or low load conditions on the whole. However, an increase in flue gas velocity decreases gradually with an increase in the corrugated plate depth, and the flue gas velocity is almost not affected by the change in steam velocity when the value of Z is greater than 1.5 m. It can be inferred that it is difficult to perform effective ash removal on the surface of the medium and low-temperature ends of the corrugated plates only by raising the soot-blowing steam velocity above the air preheater.
3.4.2. Effects of the Soot-Blowing Steam Velocity on the Soot-Blowing Coverage Area
The influence laws of the soot-blowing steam velocity on the soot-blowing coverage area are shown in
Table 4. Under the condition of a 600 MW boiler load, almost all the relative change rates of the nozzle coverage area and the total coverage area are not more than 10% when the steam velocity changes by 20%, except that the coverage area relative change rate of Nozzle No.2 increases by 34.5% when the steam velocity increases by 20% (working condition No.5). The relative change rates of nozzle coverage area and total coverage area are also are less than 10% under the condition of 300 MW boiler load except that the coverage area relative change rate of Nozzle No.3 reduces by 23.0% when the steam velocity reduces by 20% (working condition No.8). On the whole, the total soot-blowing coverage area of four nozzles has a slight positive correlation with the steam velocity of soot blower.
3.5. Effects of Different Working Condition Parameters on the Inlet Flue Gas Velocity of the Corrugated Plates on the Axis of Nozzle
The effects of different boiler loads, different inlet steam velocities of the soot blower, and other parameters on the inlet flue gas velocity of the corrugated plates on the axis of each nozzle are shown in
Table 5. With the decrease in boiler load (working condition No.1–No.3), the average inlet flue gas velocity of the corrugated plates has an obvious downward trend. The average inlet flue gas velocity decreases by 21.7% when the boiler load is reduced by 50%. It can be inferred that the average flue gas velocity in the medium and low-temperature ends of the corrugated plates is further reduced due to the flow resistance of the corrugated plates. Therefore, the ash deposition is likely to occur on the corrugated plate surface under the condition of low boiler load.
Compared with the working condition No.1, when the inlet steam velocity of soot blower is reduced by 5 m/s under the working condition No.4, the average inlet flue gas velocity decreases from 19.12 m/s to 17.15 m/s, with a decrease of 10.3%. Under working condition No.5, when the inlet steam velocity increases by 5 m/s, the average inlet flue gas velocity increases from 19.12 m/s to 21.16 m/s, with an increase of 10.6%. For every 5 m/s variation in the inlet steam velocity, the inlet flue gas velocity can change by about 10% in the same direction at a high boiler load. Meanwhile, the effects of the inlet steam velocity variation on the inlet flue gas velocity of the corrugated plates are studied under the working condition of 50% BMCR, namely the working conditions No.3, No.8, and No.9. For every 5 m/s variation in the inlet steam velocity, the average inlet flue gas velocity of the corrugated plates changes by about 14% in the same direction at low boiler load.
When the soot-blowing steam temperature is changed in working conditions No.3, No.6, and No.7, the average inlet gas velocities of the corrugated plates are basically the same. Additionally, it can be seen from the data in
Table 5 that under the condition of not starting the soot blowers (working condition No.10 and working condition No.11), the inlet gas velocities of the corrugated plates below the nozzles are in the range of 6–12 m/s, which are obviously lower than those under the conditions of starting soot blower and the same boiler load (working conditions No.1–No.9). It is indicated that whether the soot blower is put into operation or not has an obvious effect on the hot end inlet gas velocity of the corrugated plates.
3.6. Effects of Different Working Condition Parameters on the Inlet Flue Gas Temperature of the Corrugated Plates
When the steam soot blower is put into operation, the inlet flue gas temperature of the corrugated plates is determined by the parameters of the original flue gas and soot-blowing steam. The inlet flue gas temperatures of the corrugated plates below four nozzles under different working conditions are listed in
Table 6. It can be seen from
Table 6 that the inlet flue gas temperatures below four nozzles under the same working conditions are very close. According to the data of working conditions No.1–No.3, the variations of the boiler load obviously influence the inlet flue gas temperature of the corrugated plates. When the boiler load is reduced from 100% BMCR to 50% BMCR, the average inlet flue gas temperature of the corrugated plates reduces by 44.2 K. It is predicted that the outlet flue gas temperature of the corrugated plates obviously decreases with decreasing the boiler load, which can promote the potential adhesive ash deposition caused by ABS.
Comparing the working conditions No.1 to No.10, the soot-blowing steam temperature is 2.0 K higher than the temperature of flue gas entering the air preheater, so the inlet average flue gas temperature of the corrugated plates increases by 1.5 K after the steam is mixed with the original flue gas. Comparing the working conditions No.3 to No.11, the inlet average flue gas temperature of the corrugated plates increases by 7.5 K because the steam temperature is 50 K higher than the temperature of flue gas entering the air preheater when the steam soot-blower is put into operation. It can be seen from
Table 6 that when the temperature of flue gas entering the air preheater is lower than the soot-blowing steam temperature, running the steam soot blower can increase the inlet flue gas temperature of the corrugated plates, especially under the condition of low boiler load. In theory, an increase in inlet temperature is helpful to improve the average flue gas temperature of the cold end of the corrugated plates to alleviate the ash deposition to a certain extent.
Under the working condition of 50% BMCR, compared with working condition No.3, the average inlet flue gas temperature of the corrugated plates decreases by 1.8 K when the soot-blowing steam temperature decreases by 20 K under working condition No.6. Under working condition No.7, when the steam temperature increases by 20 K, the average inlet flue gas temperature of the corrugated plates increases by 1.7 K. It can be seen that the inlet flue gas temperature of the corrugated plates is positively correlated with the soot blowing steam temperature, but it does not change much.
4. Conclusions
Based on the analysis and discussion of the numerical simulation results, some conclusions are summarized as follows:
(1) The simulation results of the base working condition show that there is an obvious high-speed zone on the inlet plane of the corrugated plates. With an increase in the corrugated plate depth, the plane velocity difference gradually decreases. When the value of Z is greater than 1.5 m, the plane velocity distribution tends to be uniform. When the value of Z is less than 1.0 m, the flue gas velocity on the axis of the nozzle decreases rapidly with the increasing value of Z, and then it decreases slowly with an almost equal slope.
(2) The longitudinal flue gas velocity has a positive correlation with the boiler load. The longitudinal flue gas velocity obviously decreases when the boiler load is decreased, and its reduction significantly increases with an increase in corrugated plate depth. The inlet and outlet flue gas velocities on the axis of the No.4 nozzle, respectively, reduce by 17.5% and 55.0% when the boiler load declines from 600 MW to 300 MW. It means that the ash deposition is prone to occur on the cold end of corrugated plates under the condition of low boiler load.
(3) The soot-blowing coverage area is negatively correlated with the boiler load. The soot-blowing coverage area increases by 24.9% when the boiler load is reduced by 50%. It means that the velocity attenuation of soot-blowing steam at low boiler load is faster than that at high boiler load, which is not conducive to the removal of ash deposition on the cold end of the corrugated plates. Additionally, the total soot-blowing coverage area of four nozzles has a slight positive correlation with the steam velocity of the soot blower on the whole.
(4) The longitudinal flue gas velocity on the axis of the nozzle increases on the whole when the soot-blowing steam velocity increases. However, the increase in axial flue gas velocity decreases gradually with an increase in the corrugated plate depth, and it is almost not affected by the change in steam velocity when the corrugated plate depth is greater than 1.5 m. So, it is difficult to perform effective ash removal on the surface of the cold end of the corrugated plates only by raising the soot-blowing steam velocity above the air preheater. Adding a steam soot blower at the outlet of the corrugated plates may be an option to solve the ash deposition of the corrugated plates.
(5) The inlet flue gas velocity of the corrugated plates has a positive correlation with the boiler load and the inlet steam velocity of the soot blower. The average inlet flue gas velocity decreases by 21.7% when the boiler load is reduced by 50%. For every 5 m/s variation in the inlet steam velocity, the inlet flue gas velocity changes by about 10% at high boiler load and about 14% at low boiler load in the same direction, respectively. Additionally, whether the soot blower is put into operation or not has an obvious effect on the inlet gas velocity of the corrugated plates.
(6) The inlet flue gas temperature of the corrugated plates is positively correlated with the boiler load. When the boiler load is reduced from 100% BMCR to 50% BMCR, the average inlet flue gas temperature of the corrugated plates is reduced by 44.2 K. It can be predicted that the outlet flue gas temperature of the corrugated plates obviously decreases with decreasing the boiler load, which can promote the potential adhesive ash deposition caused by ABS. When the temperature of flue gas entering the air preheater is lower than the soot-blowing steam temperature, running the steam soot blower can increase the inlet flue gas temperature of the corrugated plates, especially under the condition of low boiler load. Additionally, the inlet flue gas temperature of the corrugated plates has a small positive correlation with the soot-blowing steam temperature. When the soot-blowing steam temperature varies by 20 K, the average inlet temperature of the corrugated plates varies by about 1.8 K in the same direction. It can be inferred that it is difficult to enhance the cold end flue gas temperature of the corrugated plates only by raising the soot-blowing steam temperature at a low boiler load.
In conclusion, the results of numerical simulation are conducive to further designing reasonable steam soot-blowing parameters and optimizing the steam soot-blowing strategy according to different working conditions in order to effectively solve the ash blockage in the rotary air preheater.
Author Contributions
Conceptualization, L.Z.; Methodology, H.Z.; Software, Y.C.; Validation, Y.W.; Formal analysis, Y.C., B.C. and H.Z.; Investigation, B.C.; Resources, Y.C. and L.Z.; Data curation, Y.W.; Writing—original draft, Y.C.; Writing—review & editing, H.Z.; Supervision, L.Z.; Project administration, L.Z.; Funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the science and technology project of Jiangsu Frontier Electric Technology Co., Ltd. (KJ202303).
Data Availability Statement
Data is contained within the article.
Acknowledgments
We thank the experimental boiler and the operating data provided by the science and technology project of Jiangsu Frontier Electric Technology Co., Ltd. We thank the Big Data Computing Center of Southeast University for providing the facility support on the numerical calculation in this paper.
Conflicts of Interest
Authors Youfu Chen, Yaou Wang and Bo Chen were employed by the company Jiangsu Frontier Electric Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The authors declare that this study received funding from Jiangsu Frontier Electric Technology Co., Ltd. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
References
- Menasha, J.; Dunn-Rankin, D.; Muzio, L.; Stallings, J. Ammonium bisulfate formation temperature in a bench-scale single-channel air preheater. Fuel 2011, 90, 2445–2453. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, L.; Deng, Y.; Ma, S. Research progress on ammonium bisulfate formation and control in the process of selective catalytic reduction. Environ. Prog. Sustain. 2016, 35, 1664–1672. [Google Scholar] [CrossRef]
- Ni, Y.; Rong, Y.; Yu, X.; Huang, S.; Xue, X.; Zhou, H. Experimental study on the effects of reheat temperatures on the ammonium bisulfate and ash blend deposition. Fuel 2022, 324, 124719. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y.G.; Zhao, Q.X.; Chen, Z.; Zhang, J. Experimental investigation of ash deposition on low temperature heating surfaces in a coal-fired boiler. Proc. CSEE 2015, 35 (Suppl. S1), 118–124. [Google Scholar]
- Lei, J.; Zhao, L.L. Study on cohesive ash accumulation characteristics of ammonium bisulfate in air preheater under variable boiler load. J. Eng. Therm. Energy Power 2021, 36, 107–113. [Google Scholar]
- You, L.Z. Application of high intensity sonic soot blower in air preheater of 600 MW units. Electr. Power Technol. Environ. Prot. 2016, 32, 40–41. [Google Scholar]
- Özdemir, K.; Serincan, M.F. A computational fluid dynamics model of a rotary regenerative heat exchanger in a flue gas desulfurization system. Appl. Therm. Eng. 2018, 143, 988–1002. [Google Scholar] [CrossRef]
- Heidari-Kaydan, A.; Hajidavalloo, E. Three-dimensional simulation of rotary air preheater in steam power plant. Appl. Therm. Eng. 2014, 73, 399–407. [Google Scholar] [CrossRef]
- Shah, R.K.; Skiepko, T. Influence of leakage distribution on the thermal performance of a rotary regenerator. Appl. Therm. Eng. 1999, 19, 685–705. [Google Scholar] [CrossRef]
- Yan, S.L.; Cao, B.X. Three-dimensional numerical simulation on temperature field in rotary air preheater. Therm. Power Gener. 2020, 49, 51–57. [Google Scholar]
- Chen, C.X. Numerical Simulation of the Thermal Performance of Quad-Sectional Air Preheater and Research on the System’s Dynamic Characteristics. Ph.D. Thesis, Shandong University, Jinan, China, 2016. [Google Scholar]
- Wang, H.X. Numerical Study on the Abrasion and Ash Deposition Characteristics of a New Type Economizer Tubes. Master’s Thesis, North China Electric University, Baoding, China, 2018. [Google Scholar]
- Li, J.B.; Wang, P.L.; Cheng, L. Characteristics of ash deposition on a novel heat transfer surface. CIESC J. 2016, 67, 3598–3606. [Google Scholar]
- Yang, Q.; Wang, H.; Cao, W.; Wei, X.; Cai, Y.; Wu, S. A review of boiler fly ash deposition with numerical method. Energy Conserv. Technol. 2015, 33, 495–502+508. [Google Scholar]
- Nabwey, H.A.; Armaghani, T.; Azizimehr, B.; Rashad, A.M.; Chamkha, A.J. A Comprehensive Review of Nanofluid Heat Transfer in Porous Media. Nanomaterials 2023, 13, 937. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhou, Y. Numerical optimization of the influence of multiple deep air-staged combustion on the NOx emission in an opposed firing utility boiler using lean coal. Fuel 2020, 269, 116996. [Google Scholar] [CrossRef]
- Yi, Z.; Hu, X. Numerical simulation of by-product fuel combustion in a tangential gas-fired boiler: Effect of proportion and angle on coke oven gas. J. Energ. Eng. 2022, 148, 04022006. [Google Scholar] [CrossRef]
- Yan, W.P.; Li, H.Y. Numerical Method on Heat Transfer in Tri-sectional Regenerative Air Heater. J. Power Eng. 2009, 29, 841–845. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).