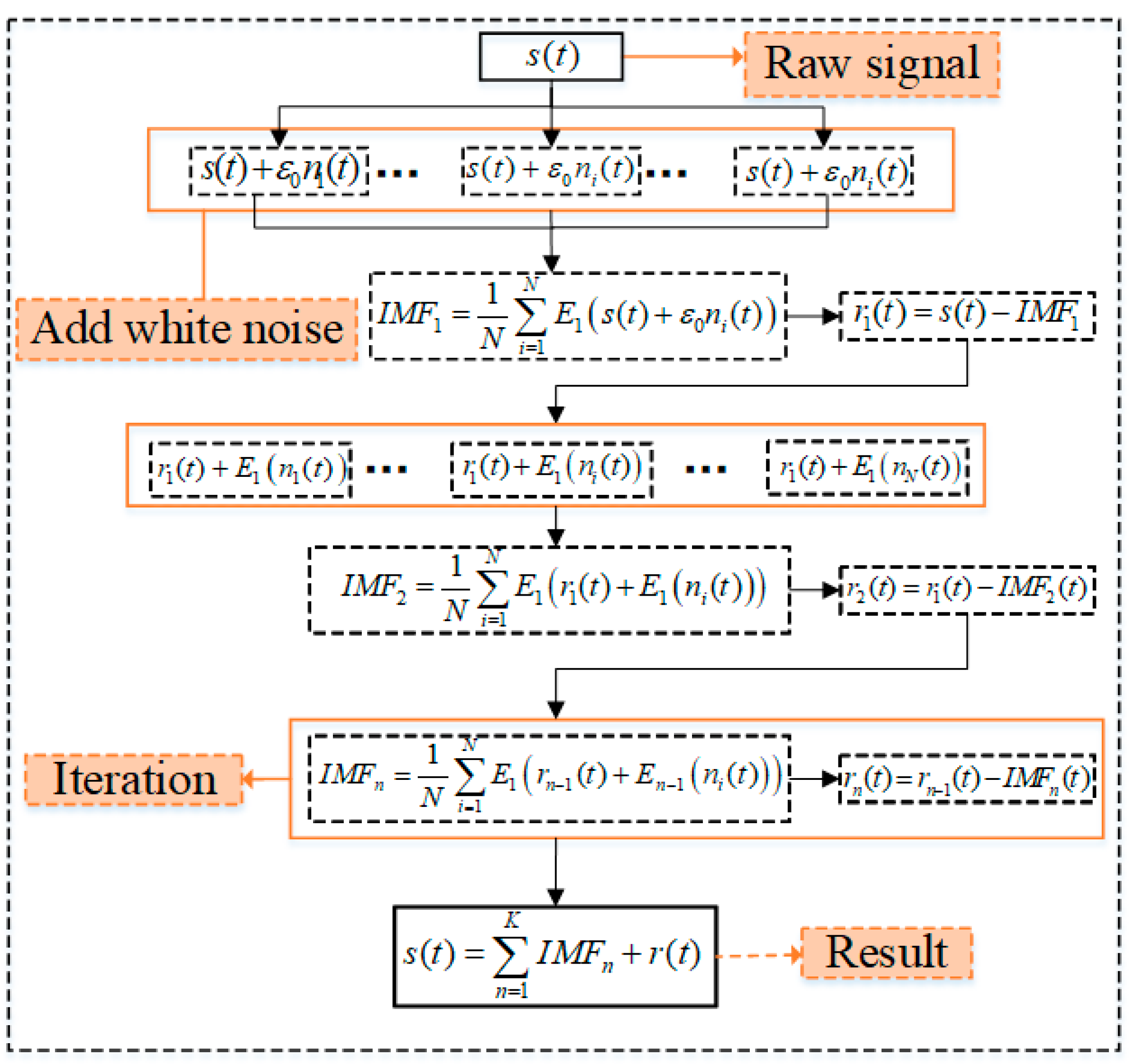
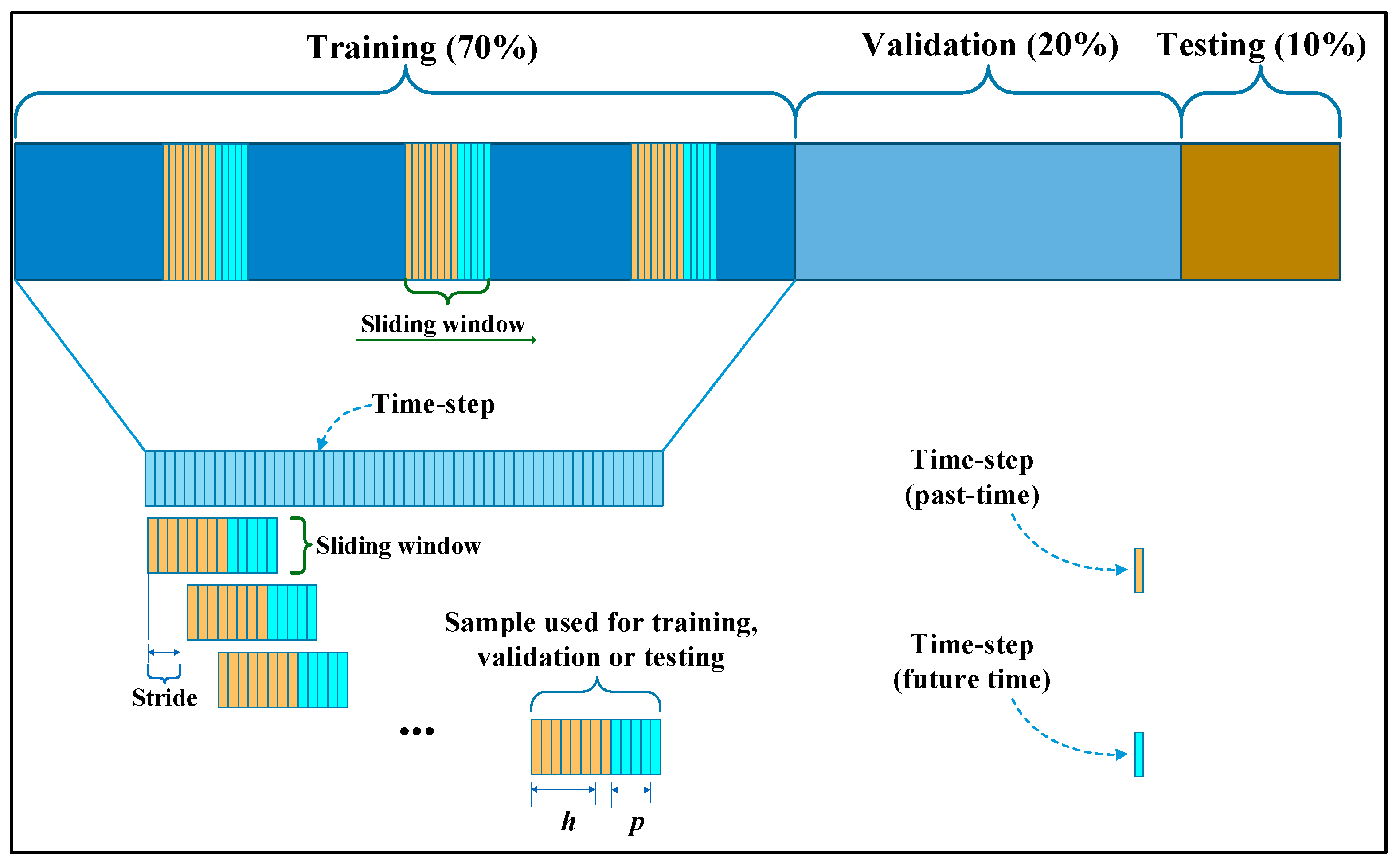
This section uses two cases to evaluate the effectiveness of the proposed CEEMDAN-LSTM method. Then, the study utilizes statistical tests to assess the significance of the performance differences between our proposed model and the benchmark models. Finally, a sensitivity analysis is conducted to identify the most critical factors affecting the proposed CEEMDAN-LSTM model’s performance.
4.1. Experiment 1: Wind Speed in Austria
Figure 11 demonstrates the strong forecasting performance of the CEEMDAN-LSTM model for IMF2 through IMF9 and the Residual component, which show impressive alignment with the actual values. It indicates the model’s ability to capture the underlying patterns in these components effectively. The only exception is IMF1, in which the forecasts deviate visibly from the original data. This divergence is understandable given the high-frequency fluctuations in IMF1 that are inherently difficult to predict. Then, by summing up all IMFs and Res, the reconstructed wind speed curve can be obtained, as shown in
Figure 12. For reconstructed wind speed, CEEMDAN-LSTM has a good overall fitting ability.
To evaluate the predicted performance of the reconstructed wind speed and every IMF with more accuracy, eight evaluated metrics, including R
2, MAE, MSE, RMSE, HMAE, HMSE, MAPE, and NRMSE, are selected in
Table 5. For the reconstructed wind speed, CEEMDAN-LSTM, with a strong correlation (R
2 = 0.7952), shows a high prediction accuracy. Then, the error metrics of MAE in 0.4557, MSE in 0.3285, RMSE in 0.5732, MAPE in 0.2241, and NRMSE in 0.2020 are relatively low in absolute terms, showing that the model produces minor forecasting errors. The Harmonic HMAE in 0.1579 and HMSE in 0.0394 values are also relatively small, further indicating the model generates low errors for predicting wind speed. In addition, for other IMF components, IMF1 stands out with a relatively weak correlation (R
2 = 0.0509) in prediction due to the high-frequency fluctuations that are inherently difficult to predict. IMF2 shows a strong correlation (R
2 = 0.7956) and high accuracy. IMF3 to IMF8 show an almost perfect correlation (R
2 ≈ 1) and outstanding accuracy, indicating that the model’s ability to capture the variations in these components accurately. In addition, the Res components exhibit a strong correlation (R
2 = 0.9829), which demonstrates high accuracy. Overall, the CEEMDAN-LSTM demonstrates promising predictive abilities for wind speed.
To validate the performance of the CEEMDAN-LSTM model, comparative analyses are conducted against various benchmark models, namely DTR, SVR, DNN, LSTM, GRU, EMD-CNN, EMD-LSTM, and CEEMDAN-CNN. The testing dataset is utilized to evaluate the predictive capabilities of each model.
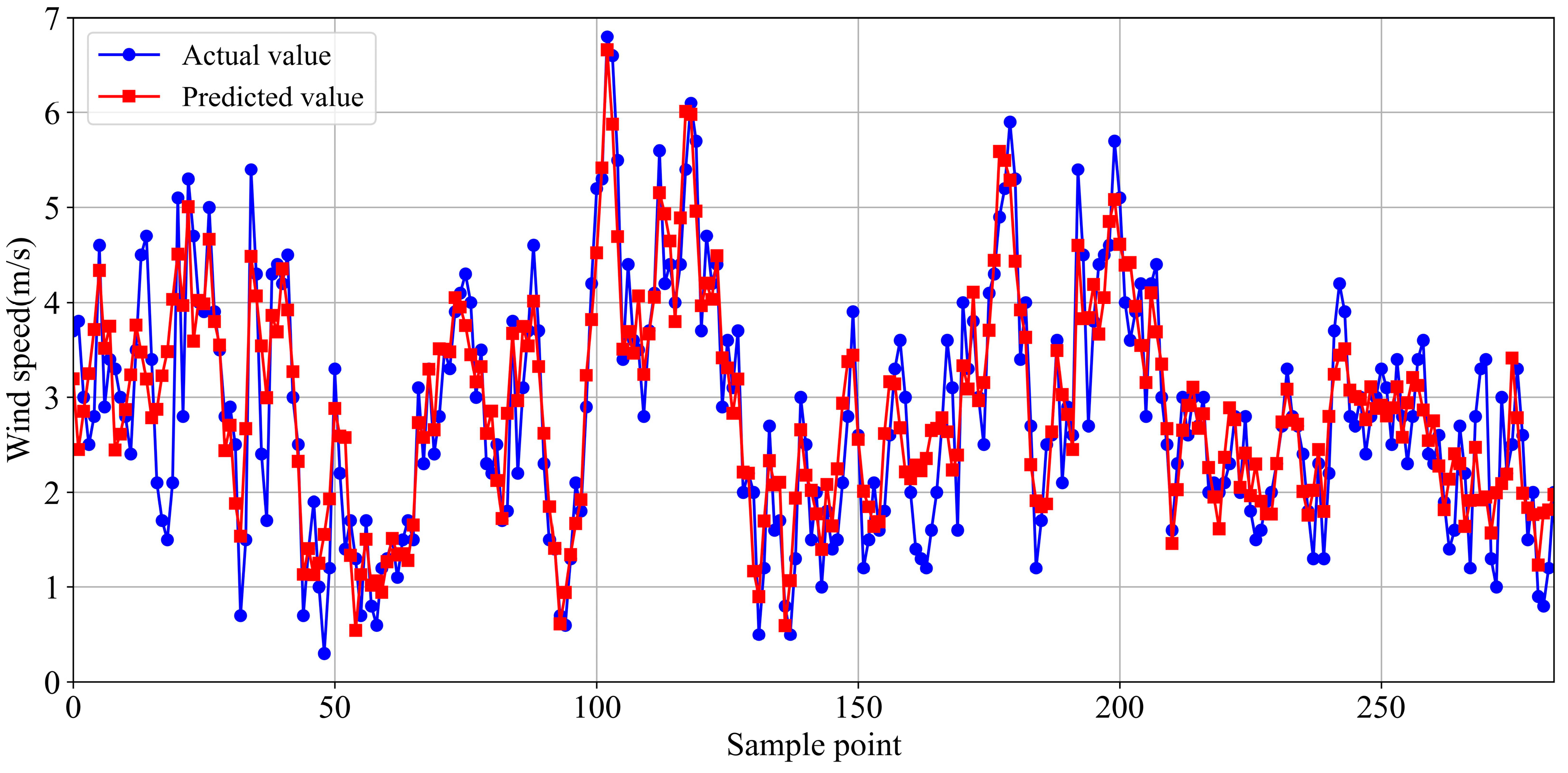
Figure 13 displays the wind speed prediction results of the nine models. The upper part of the figure shows the predicted wind speeds (lines in different colors) and the actual wind speeds (blue line). To observe the prediction performance of the different models in detail, the lower part of the figure plots the scatter diagrams of the actual values versus the predicted values, which intuitively exhibits the prediction effectiveness of each model. For scatter diagrams, the red dot represents wind speed value and blue dash indicates the slope. The blue dashed line indicates a slope of 1, and the closer the scatters is to the blue dashed line, the closer the predicted values are to the actual values. The R
2 values of the different prediction models are shown in the upper left corner of the scatter plots. From the R
2 metric, it can be seen that the CEEMDAN-LSTM model achieves the best prediction performance, followed by CEEMDAN-CNN (R
2 = 0.7716), EMD-LSTM (R
2 = 0.7562), and EMD-CNN (R
2 = 0.7526). Compared with these hybrid models, single modes, including DTR, SVR, DNN, LSTM, and GRU, have a general accuracy in predicting wind speed. Specifically, the GRU, LSTM, and DNN models attained R
2 values of 0.5075, 0.5108, and 0.5027, respectively, indicating a moderate degree of fit between the forecasted and observed wind speed data. Conversely, the SVR and DTR models demonstrated the lowest R
2 values of 0.4961 and 0.4360, respectively, which suggests a relatively limited efficacy. It can be found from the experimental results that these sequences, based on the CEEMDAN method decomposition, provide a better explanation of both long-term and short-term factors affecting power variations. The final wind speed prediction result is obtained by summing these predictions, which can improve the accuracy of the forecast compared with methods based on the original wind speed.
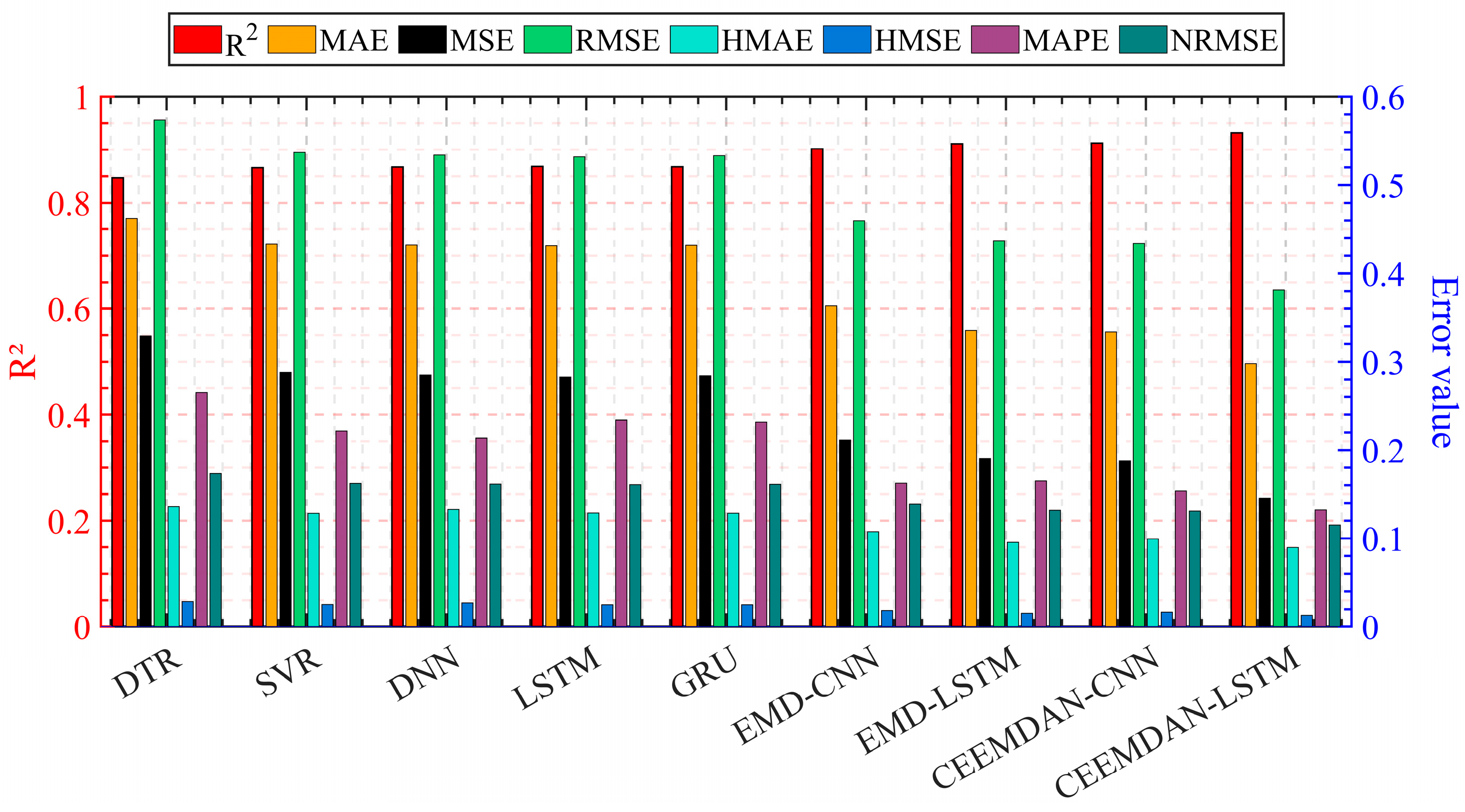
Some performance indicators are selected to verify the predicted result of different models, such as R
2, MAE, MSE, RMSE, HMAE, HMSE, MAPE, and NRMSE in
Figure 14 and
Table 6. CEEMDAN-LSTM has the highest R
2 score of 0.7952 and lowest values for MAE, MSE, RMSE, HMAE, HMSE, MAPE, and NRMSE, suggesting that it has the best overall performance among all the models listed. For the other hybrid models, it is observed that the CEEMDAN-CNN model achieves an R² value of 0.7716, while the EMD-LSTM and EMD-CNN models demonstrate comparable performance with R
2 values of 0.7562 and 0.7526, respectively. These results indicate a close similarity in predictive accuracy. For LSTM and GRU, the two models have low performance with R
2 scores of around 0.51, and relatively higher error rates than CEEMDAN-LSTM. DNN has an R
2 score of 0.5027, which is slightly lower than that of LSTM and GRU. The SVR model has a slightly lower R
2 score of 0.4961 compared to DNN, LSTM, and GRU. DTR has the lowest R
2 score of 0.4360 and the highest error rates among all the models listed. Based on these metrics, the CEEMDAN-LSTM model demonstrates superior performance compared to the other models evaluated. This can be attributed to CEEMDAN’s ability to decompose the original wind speed data into a series of IMFs and a residual trend component. Such decomposition effectively breaks down the complex wind speed signal into simpler oscillatory modes that capture variations across different time scales, thereby allowing for the representation of both long-term trends and short-term fluctuations.
4.2. Experiment 2: Wind Speed in Almeria
The predicted results of CEEMAN-LSTM are shown in
Figure 15. The left half of the figure shows the comparison curve between the predicted wind speed (blue curve) and the actual wind speed (red curve). The closer the blue and red curves are, the better the prediction effect. The right side of the figure shows the loss curves of the components in the training and validation sets. As the number of iterations increases, the loss curve shows a decreasing trend and converges within 100 iterations. It is evident from the figure that the predicted values for IMF3 through IMF7 align closely with their actual values, while the predictions for IMF1 and IMF2 show discrepancies with the actual values. By summing all IMFs and Res obtained from CEEMDAN decomposition, the reconstructed wind speed is obtained in
Figure 16.
To comprehensively analyze the prediction results of IMFs, Res, and reconstructed wind speed, eight evaluation metrics (R
2, MAE, MSE, RMSE, HMAE, HMSE, MAPE, and NRMSE) are selected to evaluate the predictive capabilities of the CEEMDAN-LSTM model.
Table 7 shows that IMF1 exhibits a minimal correlation with the actual data, as evidenced by its R
2 value of merely 0.0017, suggesting a limited predictive prowess for high frequency. Then, a marked improvement in predictive accuracy is observed from IMF2 through IMF9. Notably, the R
2 values for IMF3 to IMF7 are strikingly close to 1, indicating near-perfect predictions for these components. The Res component, with an R
2 value of 0.9951, effectively captures the residual fluctuations, further emphasizing the model’s robustness. The error metrics for this reconstruction wind speed, with values such as MAE at 0.2980, MSE at 0.1455, and RMSE at 0.3815, are low, further highlighting the model’s high predictive precision.
To further investigate the effectiveness of the CEEMDAN-LSTM model in wind speed prediction, it is compared with different models, including DTR, SVR, DNN, LSTM, GRU, EMD-LSTM, EMD-CNN, and CEEMDAN-CNN. These models are evaluated using the same wind speed data to measure their predictive capabilities. The prediction results for each model are shown in
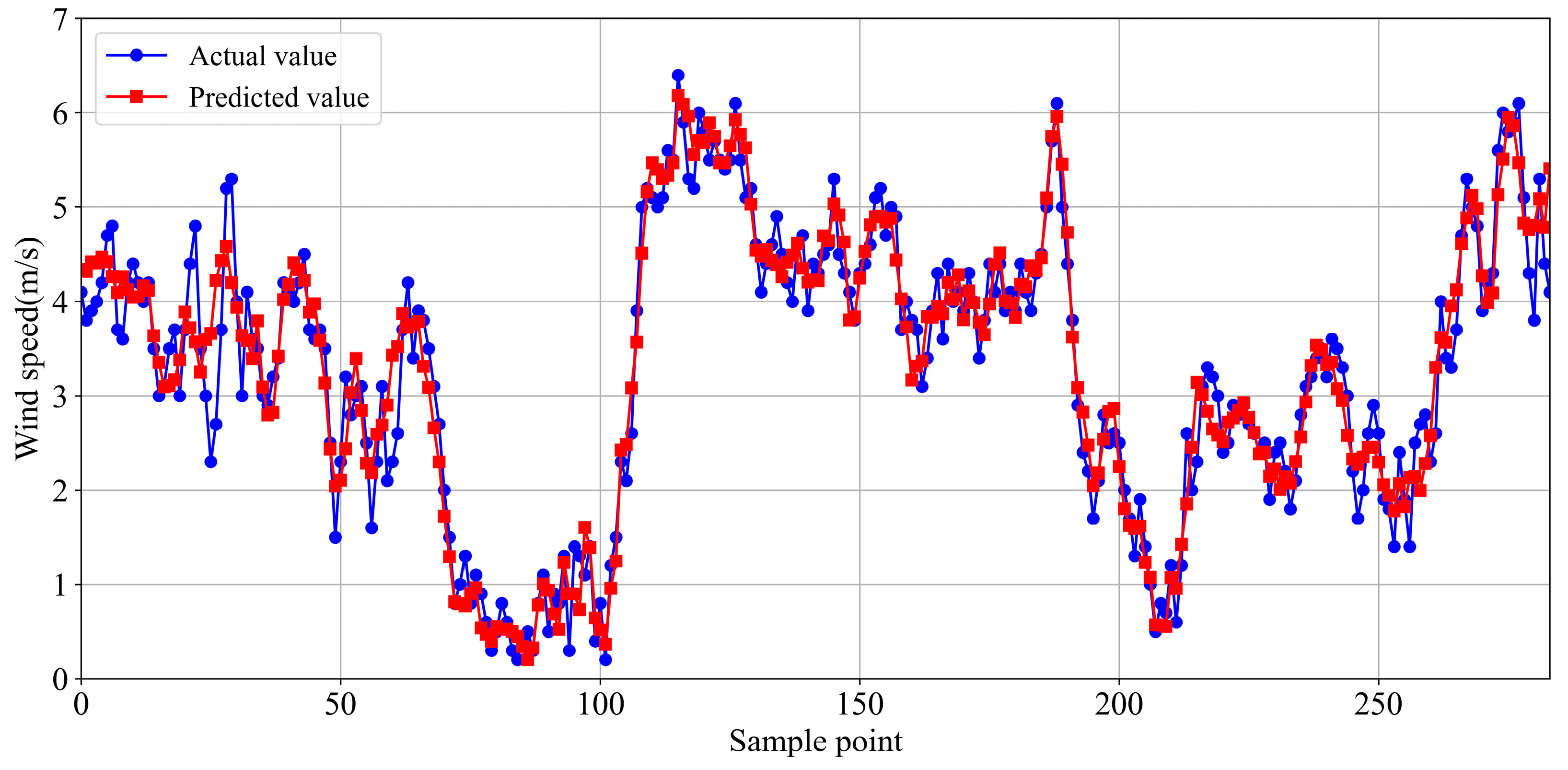
Figure 17. The upper part of the figure displays the prediction trends of the different models on the test set, along with the actual wind speed data line plot. It can be observed that all models have performed well, with no significant deviations from the actual values. To further assess the prediction performance of each model, scatter plots of the predicted values versus the actual values are plotted below the figure. The scatter points are closer to the blue dashed line with a slope of 1, and the predicted values are closer to the actual values. Additionally, the scatter plot in the upper left corner marks the corresponding R
2 value for each model, allowing for a straightforward comparison of the superiority of the CEEMDAN-LSTM in wind speed prediction. Experimental result shows that CEEMDAN-LSTM exhibits the highest R
2 values of 0.9323 among all the models. Based on the above results, it can be observed that traditional methods struggle to predict future wind speed information from wind speed signals. Therefore, it is necessary to decompose complex nonlinear signals into several physically meaningful single-component signals, which enhances the frequency-domain resolution of signal analysis and improves the accuracy of wind speed prediction.
Detailed evaluation data for all the models on the test dataset are presented in
Figure 18 and
Table 8. The CEEMDAN-LSTM model achieved the best overall performance, with the highest R
2 value of 0.9323 and the lowest error values across all metrics. This indicates that it had the best fit and accuracy in modeling the dataset. Subsequently, hybrid modes, including EMD-LSTM, EMD-CNN, and CEEMDAN-CNN, obtain better results for wind speed prediction. Specifically, the EMD-LSTM model achieves accuracy with an R
2 value of 0.9112, effectively capturing wind speed variations. The CEEMDAN-CNN model, with the lowest relative error (HMSE of 0.0168), demonstrates superior stability and accuracy. The EMD-CNN model has a slightly lower performance, with an R
2 value of 0.9017 and higher errors. In comparison, single models (such as DNN, LSTM, and GRU) have low prediction accuracy. The LSTM and GRU models, with R
2 values of 0.8684 and 0.8678, are worse than CEEMDAN-LSTM. The DNN model performed similarly to LSTM and GRU. The SVR and DTR models achieved worse results across all metrics than the deep learning models. Their R
2 values of 0.8660 and 0.8469 are the lowest, while their error values like MAE, MSE, and HMSE are the highest. In addition, when comparing the predictive performance of a single LSTM model with that of a combined model decomposed by the CEEMDAN algorithm, it was found that the hybrid model performed better. This is because wind speed data exhibits time series characteristics, and LSTM is more adept at capturing this relationship. Therefore, after multimodal decomposition, LSTM can better utilize the time series properties for prediction, learning features related to time dependency, and intermodal relationships from different IMF data. Thus, it can improve the prediction accuracy.
4.3. Statistical Analysis of Different Models
To assess the significance of performance differences, this study employs both the paired T-test [
47] and the Wilcoxon signed-rank test [
48] to compare the proposed CEEMDAN-LSTM model with various benchmark models, DTR, SVR, DNN, LSTM, GRU, EMD-CNN, EMD-LSTM, and CEEMDAN-CNN. Before proceeding with the statistical analyses, it is essential to verify whether the error distributions of each model meet the assumption of normality. The error is defined as follows:
where
and
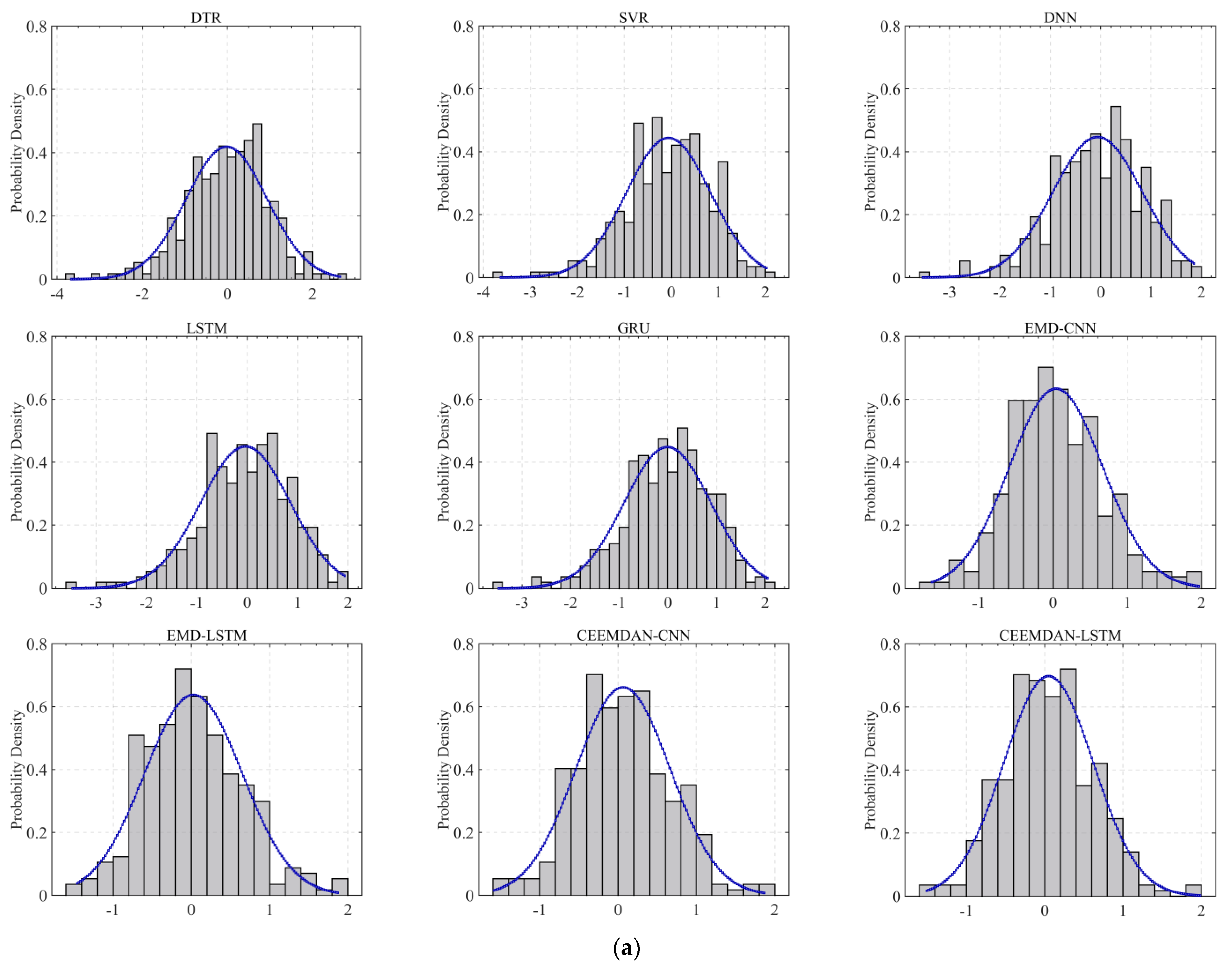
denote the prediction value and actual value. If the error distribution satisfies the normal distribution, the paired T-test can be applied to determine whether there are significant differences between the model performances. Conversely, if the normality assumption is violated, the non-parametric Wilcoxon signed-rank test is conducted. The results of the normality tests for the different models’ error distributions are depicted in
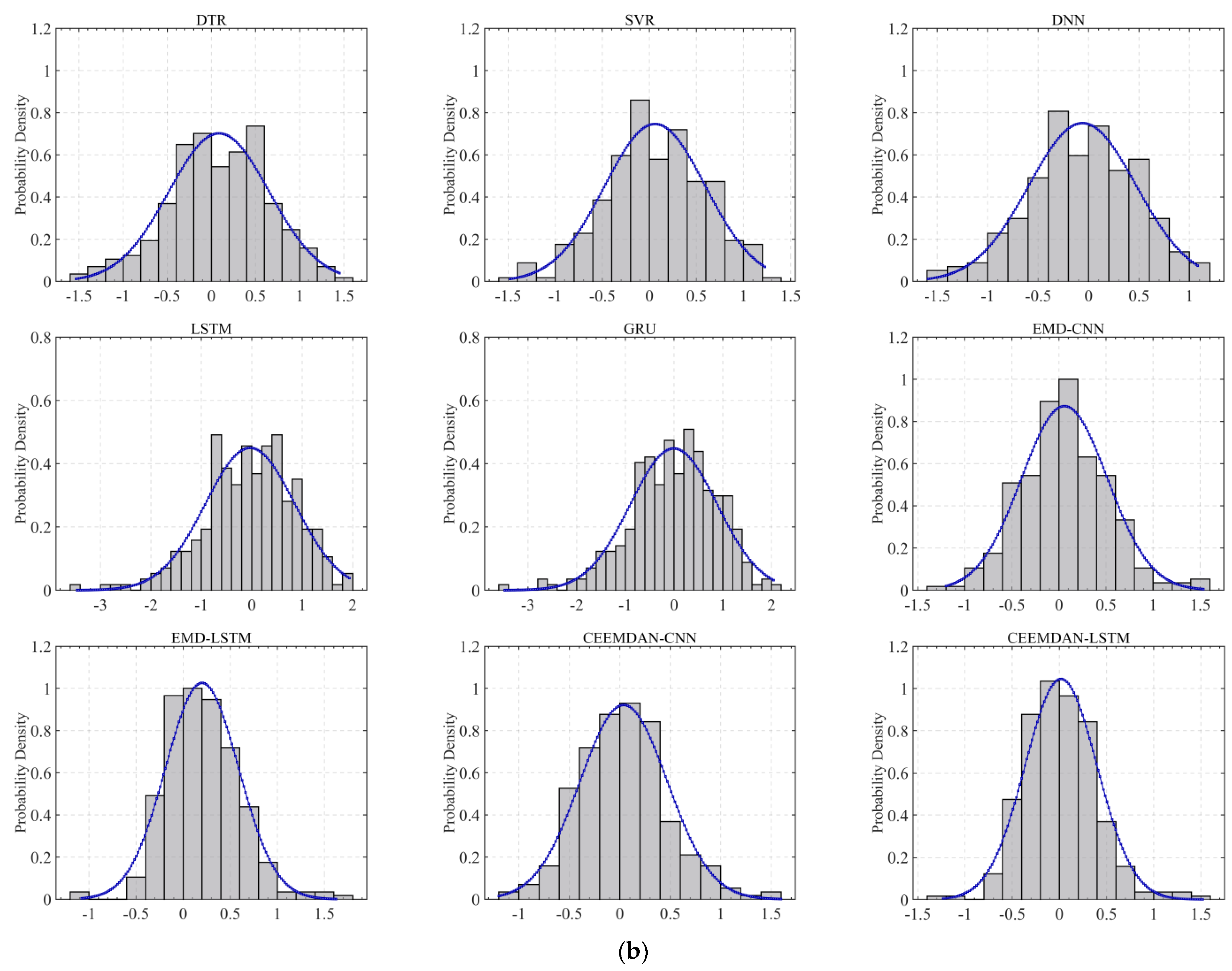
Figure 19 and
Table 9.
Figure 19 shows error distribution on the testing dataset using different models, where the blue line represents fit curve.
Table 9 shows the performance of different methods based on Paired
t-test. Firstly, for the Austria dataset, the error distributions of CEEMDAN-CNN and CEEMDAN-LSTM meet the normality assumption, with
p-values of 0.2461 and 0.2284, respectively. These
p-values indicate that, at the 95% confidence level, the null hypothesis of normality cannot be rejected. In contrast, the error distributions of DTR, SVR, DNN, LSTM, GRU, EMD-CNN, and EMD-LSTM do not satisfy the normality assumption, as their
p-values are all below the 0.05 threshold (0.0112, 0.0039, 0.0062, 0.0041, 0.0036, 0.0436, and 0.0429, respectively). Therefore, for these models, the Wilcoxon signed-rank test should be applied to determine the significance of the performance differences due to the violation of normality.
For the Almeria dataset, the error distributions of DTR, SVR, DNN, LSTM, GRU, and EMD-CNN satisfy the normality assumption, as indicated by their p-values (0.1083, 0.0999, 0.1825, 0.2689, 0.3194, and 0.0807, respectively), which are above the 0.05 threshold. However, EMD-LSTM, CEEMDAN-CNN, and CEEMDAN-LSTM show p-values of 0.0005, 0.0076, and 0.0003, respectively, indicating non-normal distributions. In summary, for models that satisfy the normality assumption, the paired T-test is appropriate, while for those that do not, the Wilcoxon signed-rank test is more suitable.
For most models, including DTR, SVR, DNN, LSTM, GRU, EMD-CNN, CEEMDAN-CNN, and CEEMDAN-LSTM, the p-values are greater than 0.05 for both datasets. This indicates that there is no statistically significant difference in the performance between these models and the baseline models. However, the EMD-LSTM model shows a very low p-value (2.9684 × 10−15) on the Almeria dataset, suggesting a highly significant difference compared to the baseline.
In addition, the proposed CEEMDAN-LSTM model stands out due to its robust performance across both datasets in
Table 10. Specifically, the CEEMDAN technique decomposes the complex nonlinear signals into several physically meaningful single-component signals, leading to more reliable features for the LSTM model to learn. This is particularly adept at handling time series data; the proposed CEEMDAN-LSTM model can capture long-term dependencies and temporal patterns effectively. While other models show similar performance levels, the proposed CEEMDAN-LSTM model consistently demonstrates non-significant differences (
p > 0.05), indicating that its performance is comparable to or better than that of existing methods without introducing additional variance or bias.
4.4. Computational Efficiency and Sensitivity Analysis
Table 11 presents a comparative analysis of the prediction times of various models for the testing datasets, highlighting the performance differences across several machine learning and deep learning algorithms. The models include DTR, SVR, DNN, LSTM, GRU, EMD-CNN, EMD-LSTM, CEEMDAN-CNN, and CEEMDAN-LSTM.
Among these models, the proposed CEEMDAN-LSTM model, which integrates the CEEMDAN and LSTM networks, demonstrates a competitive prediction time, particularly in relation to other deep learning models. For the Austria dataset, CEEMDAN-LSTM exhibits a prediction time of 0.228 s, which is shorter than both the standalone LSTM (0.256 s) and GRU (0.241 s), and comparable to EMD-LSTM (0.231 s). For the Almeria dataset, CEEMDAN-LSTM achieves a prediction time of 0.227 s, outperforming LSTM (0.303 s) and GRU (0.294 s), and again showing similar efficiency to EMD-LSTM (0.229 s).
These results suggest that the CEEMDAN-LSTM model strikes a favorable balance between computational efficiency and model complexity, potentially offering superior performance in scenarios in which both accuracy and prediction speed are crucial. The integration of CEEMDAN in the model architecture enhances the decomposition process, which could contribute to its relatively lower computational time compared to other LSTM-based approaches. Thus, the CEEMDAN-LSTM model is a promising candidate for time-sensitive predictive modeling tasks.
Table 12 presents the experimental results of the CEEMDAN-LSTM model on the Austria and Almeria datasets, where three key hyperparameters—sliding window size, number of neurons in the LSTM layer, and number of neurons in the fully connected layer—are varied. The model’s performance is evaluated using four metrics: R
2, HMSE, MAPE, and NRMSE.
The results reveal that the model’s predictive performance is highly sensitive to the choice of these parameters. Notably, the optimal results are achieved when the Window size is set to 15, the number of neurons in the LSTM layer is 16, and the number of neurons in the fully connected layer is 5. Under these specific configurations, the CEEMDAN-LSTM model achieves the highest R2 values (0.7952 for the Austria dataset and 0.9323 for the Almeria dataset), indicating the best goodness-of-fit between the predicted and actual values. Simultaneously, the lowest error metrics, HMSE (0.0394 for Austria, 0.0131 for Almeria), MAPE (0.2241 for Austria, 0.1323 for Almeria), and NRMSE (0.2020 for Austria, 0.1152 for Almeria), suggest that the CEEMDAN-LSTM model is both accurate and reliable in its predictions.
When the Window size is set to values other than 15 (e.g., 5, 10, 20, and 30), a notable decrease in R2 and an increase in error metrics are observed across both datasets. This suggests that a Window size of 15 captures the temporal dependencies in the time series data more effectively, balancing model complexity and overfitting. Similarly, variations in the number of neurons in the LSTM layer show that 16 neurons result in the most effective learning capacity, optimizing the balance between underfitting and overfitting. Lower or higher values (e.g., 10, 32, 50, and 64) lead to slightly decreased R2 values and higher error metrics, indicating less optimal model performance. Furthermore, the number of neurons in the fully connected layer is critical for achieving optimal results. With a value of 5, the model achieves the best performance metrics on both datasets. Increasing or decreasing the number of neurons (e.g., 3, 10, 15, and 30) results in marginally lower performance, suggesting that five neurons provide the necessary network capacity to adequately map the features extracted by the LSTM layer to the final output without unnecessary complexity.
The specific combination of a Window size of 15, 16 neurons in the LSTM layer and five neurons in the fully connected layer achieves a balance that minimizes prediction errors while maximizing the R2, thus offering a robust model configuration for both the Austria and Almeria datasets.