Abstract
Recently, the increasing concern for climate control has led to the widespread application of grid-connected inverter (GIC)-based renewable-energy systems. In addition, the increased usage of non-linear loads and electrification of the transport sector cause ineffective grid-frequency management and the introduction of harmonics. These grid conditions affect power quality and result in uncertainty and inaccuracy in monitoring and measurement. Incorrect measurement leads to overbilling/underbilling, ineffective demand and supply forecasts for the power system, and inefficient performance analysis. To address the outlined problem, a novel, three-phase frequency component extraction and power measurement method based on Digital Lock-in Amplifier (DLIA) and Digital Lock-in Amplifier–Frequency-Locked Loop (DLIA–FLL) is proposed to provide accurate measurements under the conditions of harmonics and frequency offset. A combined filter, with a lowpass filter and notch filter, is employed to improve computation speed for DLIA. A comparative study is performed to verify the effectiveness of the proposed power measurement approach, by comparing the proposed method to the windowed interpolated fast Fourier transform (WIFFT). The ZERA COM 3003 (a commercial high-accuracy power measurement instrument) is used as the reference instrument in the experiment.
1. Introduction
Over the past decade, the global population has increased, coupled with increasingly severe weather conditions, leading to a significant rise in energy demand. The growth in energy demand results in increased production of electrical energy from fossil fuels, contributing to the deteriorating global warming crisis [1]. As a result, new policies related to decarbonization have been introduced by the global stakeholders to control and limit the worsening situation. The transition from conventional transportation means to electric vehicles (EVs) represents a significant step toward achieving the decarbonization goals for governments worldwide [2]. In addition, the penetration of grid-connected inverter (GCI)-based renewable-energy systems in the power system is increasing over time. Such increased integration results in reduced power system inertia, which creates grid-frequency management issues. The increased usage of grid-connected renewable-energy systems, non-linear loads, and electrification of the transport sector results in non-sinusoidal grid conditions with harmonic injection and grid-frequency deviations [3,4,5,6,7]. The non-sinusoidal grid conditions can result in the transformer overheating, tripping of the power system equipment, and non-reliable power measurement by the conventional power measurement method used in watt–hour meters [6,7,8], and inefficient performance analysis of power electronics applications. For non-sinusoidal signals consisting of extra frequency components, component extraction is a critical part of achieving accurate power measurement and performance analysis. Therefore, it is necessary to extract frequency components accurately [9,10,11].
Digital power measurement methods are becoming famous these days. This type of method records the samples of voltage and current and then calculates the instantaneous power in the time domain. It provides real-time measurement, stores big sizes of data, and is highly protected from tempering. Although electronic power measurement methods offer numerous advantages, they are not ideal for measuring the power of signals with harmonic frequency components and frequency deviations. This is due to an accuracy in zero-crossing detection, which results in inaccurate power measurement outcomes [12,13,14,15]. In addition, it struggles to distinguish between different frequency components, such as fundamental, harmonics, noise, and interharmonics. Ref. [16] presents error analysis for digital input electricity meters, which utilize a time-domain approach for power measurement by taking the integration of input signal over time, which demonstrates a maximum power measurement error of 2% for a frequency offset of ±0.5 Hz, as shown in Figure 1. Where the red and blue color shows the maximum error in positive and negative direction, respectively.
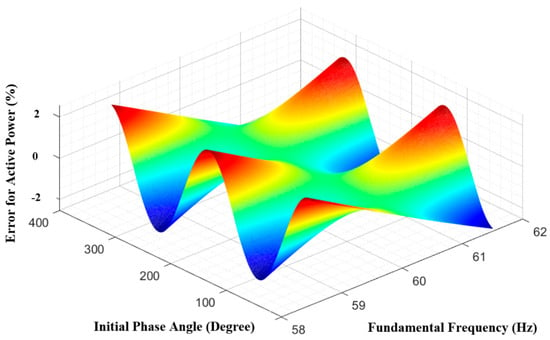
Figure 1.
Error curves for digital input electricity meters under the condition of ±0.5 Hz frequency offset error in real power.
Fast Fourier transform (FFT) is another extensively used method for the extraction of frequency components and using the extracted components for power calculation. The FFT method is very accurate when applied under the conditions of synchronous sampling [3,9]. However, the fundamental frequency deviation and introduction of harmonics make it difficult to maintain synchronous sampling in real-world applications. This results in inaccurate measurement [17,18,19].
The literature introduced windowed FFT (WFFT) to reduce the effect of spectral leakage. In WFFT, different window functions are multiplied by the input signal, followed by FFT calculation. The ideal window should have a low main lobe width and high roll-off for the side lobes to attain higher attenuation and better frequency resolution. There are different types of windows, such as Hanning, Hamming, Blackman window, triangular self-convolution window, etc. Although the use of WFFT improves the measurement results, the accuracy is still low, as the ideal window cannot be selected because of the trade between the main lobe width and the side lobe attenuation [18,19].
Another solution proposed in the literature is the combined use of spectral correction technique and window function to reduce the effect of picket fencing and spectral leakage known as windowed interpolated FFT (WIFFT). In this method, the window function is applied to obtain the FFT result, and then the spectral lines (double-spectrum-line or triple-spectrum-line) with maximum amplitude in the WFFT result are used to calculate the correction factors for the amplitude, frequency, and phase. The WIFFT contains higher measurement accuracy as compared to the WFFT. However, WIFFT still has limitations: if the frequency change is very fast, in that case, the result is inaccurate, and the use of window function with higher-order combined windows requires the solving of complex equations. Due to frequency deviations and harmonic injections in the power system, these limitations FFT-based methods result in unreliable power measurements [19,20,21].
The Digital Lock-in Amplifier (DLIA) is an alternative method employed for power measurement by extracting the voltage and current components for different frequencies. It has better performance in terms of component extraction as compared to the FFT [22,23,24,25]. In addition, the conventional DLIA has less computational burden as compared to FFT, as FFT works for a large range of evenly distributed frequency components and mostly requires complex window functions and interpolation. Table 1 shows the comparison of the computational burden of FFT and conventional DLIA for (N = 10,000) [26]. However, the DLIA has a limitation: in case of frequency deviation, the measurement accuracy reduces [22,23,24,25].

Table 1.
Comparison of computational burden of FFT and conventional LIA.
The literature demonstrates that many power measurement methods utilize feedback loops based on tracking frequency or phase for tracking and synchronization purposes. The (Phase Locked Loop) PLL methods include park transformation-based PLL and SOGI-PLL. The PLL-based method performs better around nominal grid frequency and for higher-order harmonics. However, the performance degrades for input signals with DC offset and low-order harmonics [27]. The (Frequency-Locked Loop) FLL has more advantages as compared to PLL, including the absence of a voltage control oscillator, which leads to reduced computational burden. However, it is observed that its performance deteriorates when subjected to conditions like DC offset and high total harmonic distortion (THD) [28]. A second-order, generalized, integrator-based FLL (SOGI-FLL) is introduced with an offset estimation and rejection loop [29]. However, it has the limitation that a slightly wrong offset estimation results in measurement errors. Two more FLL-based methods, multiple adaptive vectorial filter-based FLL (MAVF-FLL) and reduced-order, generalized, integrator-based FLL (ROGI-FLL), are proposed for frequency tracking. These methods are susceptible to DC offset and distorted input signals.
A method is proposed to estimate the phase and frequency, which is based on prefilter [30,31], which relies on an additional frequency estimation technique to provide frequency information to be used by the prefilter. This additional loop resulted in increased complexity and computational burden. Similarly, ref. [32] proposed a multi-circular limit cycle oscillator (multi-CLO-FLL). It also requires a prefilter to achieve harmonic attenuation. The currently available synchronization techniques face limitations and performance deterioration in an environment with noise, like DC component and high THD. The solutions proposed to remove DC components and attenuate harmonics resulted in increased complexity and computational burden. Therefore, it is essential to develop a power measurement method that addresses the shortcomings of traditional methods and provides accurate results under conditions involving frequency variations and harmonics.
This article proposes a novel frequency component extraction and three-phase power measurement method as an extension of the method proposed in conference publication [33]. It is based on DLIAs and Digital Lock-in Amplifier–Frequency-Locked Loop (DLIA–FLL) with combined filters to obtain accurate power measurement results for signals with harmonic frequency components and frequency deviations. The DLIA–FLL tracks the fundamental frequency component of the input signal, followed by the generation of reference signals using tracked frequency. The DLIA uses the generated reference signals to extract the accurate amplitude and phase information for the fundamental and harmonic frequency components from the input voltage and current signals. These extracted parameters give accurate measurement results for electrical power parameters. To validate the advantages of the proposed method compared to conventional methods, a power measurement experiment is conducted for an input signal with 25% THD and variable frequency conditions. The experimental study utilizes a printed circuit board consisting of sensors with dc offset in the output and microcontroller units (MCUs).
2. Proposed Frequency Component Extraction and Power-Monitoring Method by Using DLIA and DLIA–FLL
The proposed component extraction method uses DLIA to extract the magnitude and phase information accurately for the fundamental and harmonic components present in the input signal. However, under the condition of frequency variation, the accuracy of the DLIA decreases because of the difference between the frequency of reference signal and input signal. To cope with this limitation, the proposed DLIA–FLL tracks any change in the frequency of input signal and generates the reference signals with new frequency which are used by the DLIA for the component extraction. There are n number of DLIAs for voltage and current each, where n is the number of frequency components to be extracted. Figure 2 shows the complete architecture of the proposed method for power measurement consisting of DLIA and DLIA–FLL.
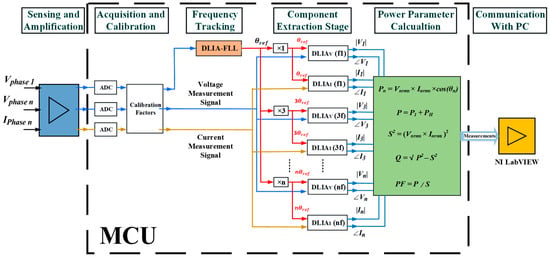
Figure 2.
Block diagram of the proposed component extraction and power measurement method with the Digital Lock-in Amplifier Frequency-Locked Loop (DLIA–FLL).
The voltage measurement signal that comes from the sensing and amplification stage, through ADC of the MCU, acts as the input for the proposed DLIA–FLL, which utilizes this input to track the fundamental frequency. In the next stage, these tracked frequency and measurement signals (voltage and current) that come from sensing and amplification stage, through ADCs of the MCU, act as the inputs for the DLIAs (DLIA1–DLIAn), which utilize these inputs to extract the fundamental and harmonic frequency components. The extracted information of frequency components is represented in terms of magnitude and phase, which is further utilized to calculate the rms voltage, rms current, real power, reactive power, apparent power, phase difference, and power factor. In the final stage, the measurement results for voltage, current, frequency, and power are transferred to the PC (NI LabVIEW 2022Q3) through UART-Serial communication protocol.
Further explanation on the working principle of each component of the proposed power measurement method is given in Sub-Sections below.
2.1. Digital Lock-In Amplfier Working Principle
The DLIA contains three sections, Phase Sensitive Detector (PSD), Combined Filter (CF), and Phase and Amplitude extraction. Figure 3 shows the block diagram for DLIA.
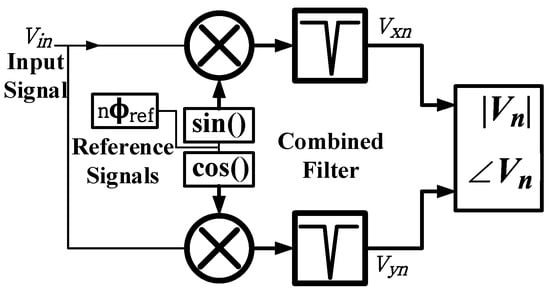
Figure 3.
Block diagram for Digital Lock-in Amplifier (DLIA) with proposed combined filter (Lowpass Filter + Notch Filter).
In PSD, dual modulation Lock-in is achieved by multiplying the input signal with reference sine and cosine signals that match the input signal’s frequency. Equation (1) shows the input voltage signal with fundamental and n odd harmonics.
where represents the peak amplitude of the fundamental component; denotes the amplitude ratio of the nth harmonic with the amplitude of the fundamental component; and and are the frequency and phase of the fundamental component, respectively. would be (0, 120, 240 degrees) for the three-phase system.
Equation (2) shows the reference signals for DLIA, where k defines the harmonic order of the reference, and and are the frequency and phase of the reference signal, respectively.
The dual-modulation Lock-in results in two signals, and , by using the trigonometric identity. Equations (3) and (4) show the simplified expression for and . These signals contain the amplitude of the concerned frequency component from the input signal at DC (0 Hz) and at twice the frequency of the concerned frequency component (120 Hz in this case) from the input signal.
The combination of single-order low pass filter and the second-order notch filter is employed to extract the DC component from the and .
Equation (5) shows the transfer function for the combined filter, where is the cut-off frequency, and is the order of low pass filter. is the natural frequency for the notch filter. and are the damping factors selected according to the condition (≪ ).
The natural frequency of the notch filter is selected (120 Hz) as the lowest frequency component to be attenuated to twice the grid frequency. To attenuate the higher order frequency components, a single-order (k = 1), low pass filter with a cut-off frequency () of 10 Hz is employed. Figure 4 shows the bode plot for the designed combined filter.
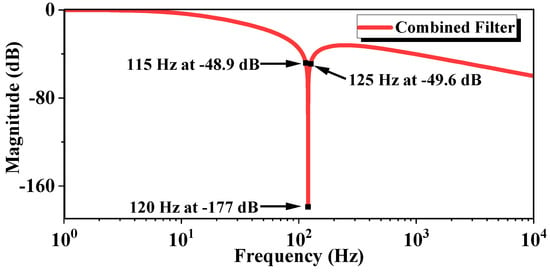
Figure 4.
Bode plot for the combined filter consisting of notch filter and lowpass filter.
For the notch filter and the low pass filter, 120 Hz is selected as the natural and cut-off frequency. As the fundamental frequency component in the system for which the measurement is performed is 60 Hz, then the lowest frequency component generated by the lock-in modulation would be 2 f1, which is 120 Hz in this case. So, the filters are designed to attenuate the lowest-possible frequency component.
Furthermore, the damping factors and are used to adjust the width and depth of the notch filter, respectively. affects the bandwidth and stability of the notch filter. A large value of results in a wider notch but with less sharp attenuation at notch frequency. However, a smaller narrows the notch, making it more selective but potentially less stable. affects the depth of the notch filter. The attenuation at notch frequency can be adjusted using . A smaller value of results in a deeper notch filter response, which means higher attenuation at notch frequency. It is useful for effectively rejecting specific frequencies. However, the filter might become more sensitive to variations in the input. The values of both the damping factors are selected to have the desired depth and bandwidth without compromising the robustness and stability. The filter design procedure begins by selecting initial values for all variables involved in the filter transfer function, which are then optimized using MATLAB 2018a to achieve the desired filter response. The continuous-time domain transfer function is defined in MATLAB using the optimized values for the above-defined variables. Following that, this continuous-time domain transfer function is converted to the discrete-time domain transfer function using MATLAB. Finally, the discrete-time transfer function is re-arranged into a form suitable for implementation in the hardware setup, ensuring the filter operates correctly in a digital system.
The application of the notch filter allowed the elimination of the lowest frequency component. As a result, a lowpass filter with reduced order and high cut-off frequency can be used. This proposed combined filter with low order and high cut-off leads to less computational burden and faster filter response [26]. It is important because computational burden is a critical factor in effective practical implementation of measurement method.
Equations (6) and (7) show the signals at the output of the combined filters. These signals contain just DC component and 120 Hz. The other higher-frequency components are attenuated.
In the last section of the DLIA, the output signal from the combined-filter stage is utilized to determine the component-specific information consisting of magnitude and phase. Equations (8) and (9) are employed to compute the frequency-component-specific information consisting of phase and amplitude.
2.2. Digital Lock-In Amplfier–Frequency-Locked Loop (DLIA–FLL)
The primary goal of the proposed DLIA–FLL is to monitor and follow the change in the grid-frequency to provide correct frequency and phase . This frequency and phase information is used to obtain the correct reference signals for the DLIA to provide accurate extraction. Figure 5 shows the block diagram for the proposed DLIA–FLL.
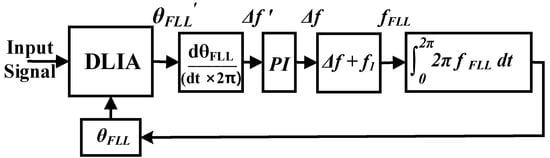
Figure 5.
Block diagram for proposed reference signal synchronization method with DLIA–FLL.
The working principle of the DLIA–FLL is defined as the DLIA provides the phase output using the output of the combined filter section shown in (10) that is further simplified to obtain (11).
Equation (12) is used to find the difference in the frequency by taking the derivative of phase with respect to time.
The resultant difference in frequency is passed through a PI controller, which provides the updated difference in frequency ∆f. This difference in frequency is added into the grid frequency (60 Hz in this case) to obtain tracked grid frequency , as shown in (13).
Equation (14) is used to calculate the phase of FLL, which is then used to update the reference signals of the DLIA.
2.3. Component Extraction and Power Measurement by Proposed DLIA–FLL
As detailed in the previous Sections, the DLIA–FLL tracks the grid-frequency and uses this information to update the reference signals for the DLIAs used in component extraction. The number of DLIAs are equal to the number of frequency components (DLIA1–DLIAn). These DLIAs extract the accurate amplitude and phase information for all the frequency components (fundamental and harmonics) input signals. The frequency-component-specific information for voltage and current input is utilized to obtain results for power parameters.
Equations (15)–(20) are used to estimate the power and power factor for non-sinusoidal conditions according to the standard formulas defined by IEEE Std 1459-2010 [34]. The power measurement results obtained using the proposed method are then transmitted from microcontroller unit (MCU) to the LabVIEW interface using UART communication to display the power measurement results.
3. Experimental Implementation and Results
A power measurement study is performed to evaluate the performance of the proposed method. A three-phase setup is used to conduct measurement for the condition of 25% THD and two different input signal fundamental frequencies (60 Hz, and 61.5 Hz). The ZERA COM3003 is used as the reference measurement instrument in this experiment. The measurement results by the proposed method are compared with the WIFFT (classical power measurement method). The following Sections outline the evaluation setup and present the experimental results.
3.1. Experimental Equipment and Setup Configuration
Figure 6 illustrates the arrangement and configuration employed for the experimental testing. Chroma 61704 is used as the AC source in this setup. It is adjusted with parameters for the voltage (220 V per phase), current (4.48 A per phase), frequency (60 Hz, and 61.5 Hz), and harmonic profile for 25% THD.
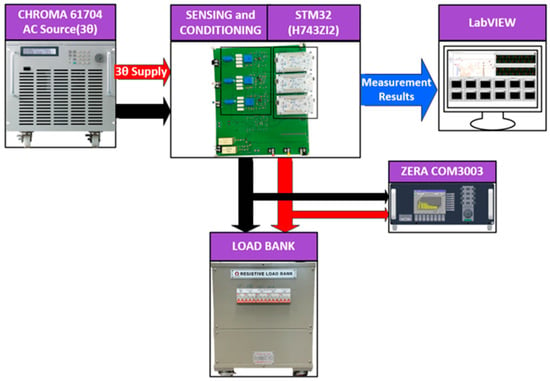
Figure 6.
Experimental setup used for power measurement experiment.
After configuration, the output of the three-phase AC supply is connected to the input of the sensing and amplification circuit on the designed PCB. The developed sensor interface circuitry is based on LV 25-P for voltage sensing and LAH 50-P for current sensing. A 1.5 V DC offset is added to the bipolar measurement signals of voltage and current sensors to convert the signal into unipolar form. The sensors are calibrated before the power measurement to remove the sensing and amplification stage error to the maximum. The temperature trends for sensors and sensor resistors are recorded, which leads to the selection of a consistent temperature (44 degrees Celsius for sensors and 40 degrees Celsius for sensing resistors) to avoid temperature-related drift in sensor performance during the experimentation.
The output of the sensing and amplification circuit is a unipolar voltage signal transmitted to the ADC of the STM32 MCU. There are three MCUs based on the (H743ZIT6U) ARM Cortex-M7 digital signal processor. The MCU features an operating clock frequency of 480 MHz, 16-bit ADC, 2 MB of flash, and 1 MB of RAM [35]. In addition, it offers a wide range of peripherals, including UART, SPI, I2C, and USB, which makes it a suitable MCU for applications involving complex operations.
Each STM32 MCU has an algorithm based on the DLIA and DLIA–FLL for precise three-phase power measurement and frequency tracking. The input capture feature of the timer configuration in STM32 MCU is utilized to read external clock signal that helps to synchronize the interrupt generation and ADC acquisition of all the MCUs.
Figure 7 shows the flow chart for the algorithm inside STM32 MCU. At the start, there is an initialization of variables, ADCs, and interrupts. The MCU1 acts as a master and generates a pulse signal at general purpose input–output pin (GPIO), which is read by two other slave MCUs to maintain the synchronized operation of all three MCUs. Following that, the ADCs start the acquisition of voltage and current signals coming from the sensing and amplification circuit. The DLIA–FLL part of the algorithm uses the acquired signal amplitude to track the frequency of the input signal. Phase-1 voltage is used as the source of DLIA–FLL for all three phases. This process continues until 200 ms is completed. After that, the component extraction algorithm based on DLIA uses the acquired signals and tracked frequency from DLIA–FLL to extract the amplitude and phase for the fundamental and harmonic components.
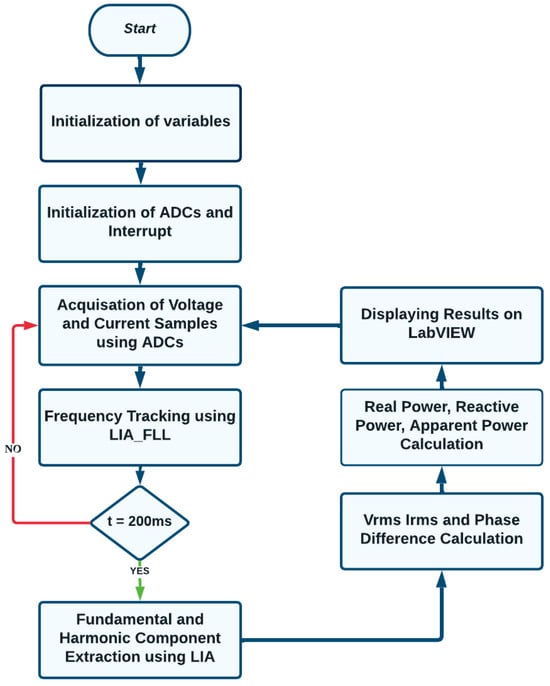
Figure 7.
Flowchart for the proposed power measurement algorithm implemented in MCU.
The extracted information is used to calculate the rms voltage, rms current, and phase difference. This calculation leads to the calculation of power parameters. All these power measurement results are then transferred to the LabVIEW interface with the help of UART communication. The LabVIEW interface displays the measurement result for each phase to validate and compare the performance.
The three-phase output of the PCB is connected to the load bank and ZERA COM3003. The ZERA COM3003, a commercial reference instrument, is connected in parallel to the load. It measures the power and harmonics to provide the reference values for percentage error calculations during comparative analysis. The percentage error calculation allows us to validate the effectiveness and reliability of the proposed method with DLIA–FLL.
3.2. Frequency-Tracking Results by the Proposed DLIA–FLL
The performance of the proposed DLIA–FLL is presented in this Section. The experimental setup defined before is used, with a sampling frequency of 40.02 kHz and 25% THD. This experiment is performed with two different cases of input signal frequency. In case a, the frequency of the input signal is fixed at 60 Hz, and in case b, the frequency of the input signal is changed to 61.5 Hz. The deviation in the frequency is selected according to the frequency deviation standard of ±1.5 Hz defined by the Korea Electric Power Company (KEPCO), South Korea [36]. The tracking results show that the developed DLIA–FLL algorithm inside the STM32 MCU further tracks the frequency deviation in 151 ms. Figure 8 shows the frequency-tracking results for frequency deviation indicating frequency tracking time utilizing green dashed line, which works well.
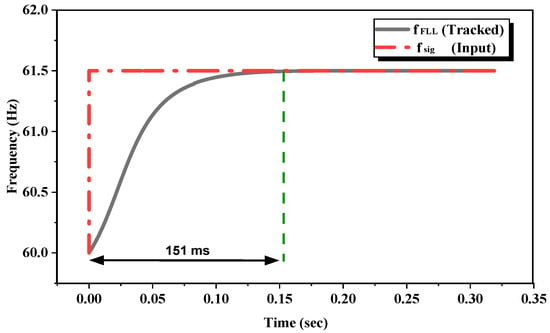
Figure 8.
Frequency-tracking performance achieved by the proposed system with DLIA–FLL.
3.3. Component Extraction and Power Measurement by the Proposed DLIA–FLL and ZERA COM3003
This Section explains the power measurement experiment performed with ZERA COM3003 and the proposed three-phase component extraction and power measurement method using the experimental setup explained before. After the definition of voltage, current, frequency, and THD profile, with 25% THD, the Chroma AC power supply is used to provide the three-phase supply to the load through the designed PCB. The input signal frequency is set to 60 Hz. Figure 9 shows the three-phase voltage and current signals generated by chroma.
Figure 9.
Three-phase voltage (a) and current (b) signals generated by chroma supply.
Simultaneously, ZERA COM3003 from the experimental setup is used to perform the power measurement as well. Table 2 shows the THD measurement for three-phase system voltage using ZERA COM3003. It verifies that the generated THD is according to the defined THD profile.

Table 2.
Total harmonic distortion (THD) measurement results by ZERA COM3003 for three-phase voltage.
The proposed algorithm defined inside the STM32 MCU detects the voltage and current signals through the sensing and amplification circuit and performs the frequency tracking, followed by component extraction and power calculation. The power measurement results are then sent to the LabVIEW interface through UART communication to display the results.
As explained earlier, the ZERA COM3003 is connected to the experimental setup as the reference power measurement instrument. The comparison involves calculating the percentage error by evaluating the power measurement results from the proposed method with DLIA–FLL against those obtained from the ZERA COM3003. The above-explained procedure is again repeated, with the input signal frequency changed to 61.5 Hz under similar testing conditions of supply voltage, current, load, and THD.
Table 3 and Table 4 show the comparative analysis results between the power measurement results obtained by the proposed DLIA–FLL and ZERA COM3003 for an input signal frequency of 60 Hz and 61.5 Hz, respectively. The results show that the power measurement accuracy is ±0.019% (accuracy class 0.02). The frequency-tracking error under the frequency deviation is ±0.005%.

Table 3.
Measurement results by the proposed DLIA–FLL for 60 Hz fundamental signal.

Table 4.
Measurement results by the proposed DLIA–FLL for 61.5 Hz fundamental signal.
3.4. Component Extraction and Power Measurement by WIFFT
Power measurement methods are generally based on different FFT methods. The WIFFT is a proposed method in recent literature to reduce the effect of picket-fencing and spectral leakage. The power measurement experiment is performed under the same testing conditions of voltage, current, load, and 25% THD. The input signal frequency is set to 60 Hz first and then changed to 61.5 Hz for the second measurement.
The WIFFT algorithm (with 1 Hz resolution) is defined in the MCU, which receives the voltage and current signals through a sensing and amplification circuit. WIFFT first calculates the WFFT and then uses the two spectral points with maximum amplitude to obtain the correction factors, which are applied to obtain the amplitude, phase, and frequency of the voltage and current signal. These parameters lead to power calculation. The power measurement results are again sent to the same LabVIEW interface, using UART communication to display the power measurement results. Table 5 and Table 6 show the percentage error obtained by comparing the power measurement results obtained by WIFFT, with the results obtained by ZERA COM3003. The results show that the power measurement error under the deviation is 0.051%, and the frequency-tracking error under the frequency deviation is ±0.013%.

Table 5.
Measurement results by WIFFT for 60 Hz fundamental signal.

Table 6.
Measurement results by WIFFT for 61.5 Hz fundamental signal.
The comparison shows that for an input signal frequency of 60 Hz, the proposed method has better performance as compared to WIFFT. However, under the condition of frequency deviation (61.5 Hz), the proposed method has much better performance (0.019%) as compared to WIFFT (0.051%). The reason for the deterioration in the performance of WIFFT is the fact that the 61.5 Hz causes the spectral leakage; as the resolution is set to 1 Hz, with the (1 s) data set, the resolution is a non-integer multiple of input frequency, which results in incorrect results despite the window function and interpolation.
In case the frequency resolution observes variation, the magnitude percentage error for WIFFT varies and follows the principle that if the resolution is an integer multiple of the input signal frequency, the resultant error is minimum, and in cases of non-integer multiples, the error will be maximum. In between these two extreme conditions, the magnitude of error will depend upon the degree of farness from integer multiple.
The results discussed above show that under the condition of frequency deviation and high THD, the proposed component extraction and three-phase power measurement method based on DLIA and DLIA–FLL has good performance under the frequency deviation ±1.5 Hz and 25% THD. Although, the proposed method is less accurate compared to the reference standard ZERA COM3003. However, this method is being developed for KEPCO to provide a cost-effective alternative compared to high-end power measurement devices with enough accuracy for applications such as inspection and performance analysis of devices, such as wattmeter, inverters, and motor drives, for different conditions of frequency and THD focusing on power measurement and power quality.
4. Conclusions
In this article, a novel frequency component extraction method based on DLIA and DLIA–FLL, implemented inside the STM32 MCU is proposed to obtain accurate component extraction and power measurement results under the conditions of harmonics and frequency fluctuations. The proposed method addresses the limitation, performance deterioration in the presence of disturbances such as frequency deviation, dc components, and harmonics, exhibited by conventional frequency component extraction and frequency-locked loop methods. The proposed DLIA–FLL is based on the combined filter consisting of lowpass and notch filter. The introduction of a combined filter leads to a lower computational burden, which means less sampling frequency and faster computation. The proposed method offers following advantages:
- The proposed method does not require any filter in the Orthogonal Signal Generator stage unlike other FLLs.
- Unlike the updated version of the conventional FLLs (SOGI-FLL/ROGI-FLL), the proposed method does not require any complex structure to remove dc components or estimate the frequency of the input to tune its parameters.
- It is immune to disturbances in the input signal, such as harmonics, dc components, and frequency deviations.
- It does not require any complex window function, unlike other FFT-based methods, to avoid picket-fencing or spectral leakage effect.
The validity and effectiveness of the proposed method are verified by conducting a power measurement experiment under the condition of 25% THD and two different input signal’s fundamental frequencies (60 Hz and 61.5 Hz). The experimental setup consists of the PCB with sensing and amplification circuit and STM32 MCUs (containing proposed component extraction and measurement algorithm). The sensors are calibrated, and the temperature environment is kept consistent to mitigate any performance dynamics exhibited by sensing and conditioning circuit. The power measurement results are sent from MCUs to the LabVIEW interface through UART communication. The measurement results of the proposed method are compared with WIFFT and the reference instrument ZERA COM3003. The comparison validates that the proposed method demonstrated better measurement accuracy compared to conventional methods, such as WIFTT, for a frequency variation of ±1.5 Hz and under a 25% THD condition.
Author Contributions
Conceptualization, A.R., T.A. and W.C.; methodology, A.R., T.A. and W.C.; software, A.R.; validation, A.R., T.A. and W.C.; formal analysis, A.R.; investigation, A.R.; resources, A.R.; data curation, A.R.; writing—original draft preparation, A.R.; writing—review and editing, A.R.; visualization, A.R., T.A. and W.C.; manuscript revision and supervision, W.C.; project administration, A.R.; funding acquisition, W.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xiu, L.; He, J.; Li, M.; Song, H. Fast and Stable Detection Scheme of Point of Common Coupling Voltage for Renewable Energy Systems Tied to Distortion Grids. IEEE Trans. Ind. Inform. 2023, 19, 7876–7884. [Google Scholar] [CrossRef]
- Teng, F.; Ding, Z.; Hu, Z.; Sarikprueck, P. Technical Review on Advanced Approaches for Electric Vehicle Charging Demand Management, Part I: Applications in Electric Power Market and Renewable Energy Integration. IEEE Trans. Ind. Appl. 2020, 56, 5684–5694. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, X.; Hu, Z.; Moura, S.J. Sustainable plug-in electric vehicle integration into power systems. Nat. Rev. Electr. Eng. 2024, 1, 35–52. [Google Scholar] [CrossRef]
- Tiwari, V.K.; Umarikar, A.C.; Jain, T. Field Programmable Gate Array-Based Measurement System for Real-Time Estimation of Single-Phase Electric Power Quantities. IEEE Sens. J. 2019, 19, 5086–5097. [Google Scholar] [CrossRef]
- Vorobev, P.; Greenwood, D.M.; Bell, J.H.; Bialek, J.W.; Taylor, P.C.; Turitsyn, K. Deadbands, Droop, and Inertia Impact on Power System Frequency Distribution. IEEE Trans. Power Syst. 2019, 34, 3098–3108. [Google Scholar] [CrossRef]
- Li, J.; Yao, W.; Wang, G.; Liang, C.; Hong, D.; Lin, H. A simple and fast measurement algorithm for power system flicker severity evaluation. Electr. Eng. 2024, 1–13. [Google Scholar] [CrossRef]
- Liao, K.; Pang, B.; Yang, J.; He, Z. Output Current Quality Improvement for VSC With Capability of Compensating Voltage Harmonics. IEEE Trans. Ind. Electron. 2023, 71, 9087–9097. [Google Scholar] [CrossRef]
- Kannan, S.; Meyer, J.; Rens, J.; Schegner, P. A Novel Extended Noninvasive Harmonic Resonance Detection Technique for Public Low-Voltage Networks. IEEE Trans. Instrum. Meas. 2022, 71, 9002711. [Google Scholar] [CrossRef]
- Babuta, A.; Gupta, B.; Kumar, A.; Ganguli, S. Power and energy measurement devices: A review, comparison, discussion, and the future of research. Measurement 2021, 172, 108961. [Google Scholar] [CrossRef]
- Morello, R.; De Capua, C.; Fulco, G.; Mukhopadhyay, S.C. A Smart Power Meter to Monitor Energy Flow in Smart Grids: The Role of Advanced Sensing and IoT in the Electric Grid of the Future. IEEE Sens. J. 2017, 17, 7828–7837. [Google Scholar] [CrossRef]
- Dirik, H.; Duran, I.U.; Gezegin, C. A Computation and Metering Method for Harmonic Emissions of Individual Consumers. IEEE Trans. Instrum. Meas. 2019, 68, 412–420. [Google Scholar] [CrossRef]
- Paris, J.; Donnal, J.S.; Remscrim, Z.; Leeb, S.B.; Shaw, S.R. The Sinefit Spectral Envelope Preprocessor. IEEE Sens. J. 2014, 14, 4385–4394. [Google Scholar] [CrossRef]
- Ikram, M.K.; Amrr, S.M.; Asghar, M.S.J.; Islam, T.; Iqbal, A. Voltage Independent Reactive Current Based Sensor for Static VAr Control Applications. IEEE Sens. J. 2023, 23, 10023–10031. [Google Scholar] [CrossRef]
- Marais, Z.; Brom, H.E.v.D.; Kok, G.; van Veghel, M.G.A. Reduction of Static Electricity Meter Errors by Broadband Compensation of Voltage and Current Channel Differences. IEEE Trans. Instrum. Meas. 2020, 70, 1501511. [Google Scholar] [CrossRef]
- Cetina, Q.; Roscoe, R.A.J.; Wright, P. Challenges for Smart Electricity Meters due to Dynamic Power Quality Conditions of the Grid: A Review. In Proceedings of the 2017 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Liverpool, UK, 20–22 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Yan, Z.; Wen, H. Performance Analysis of Electricity Theft Detection for the Smart Grid: An Overview. IEEE Trans. Instrum. Meas. 2021, 71, 2502928. [Google Scholar] [CrossRef]
- Wu, W.; Xu, Q.; Mu, X.; Ji, F.; Bao, J.; Ouyang, Z. Effect of Frequency Offset on Power Measurement Error in Digital Input Electricity Meters. IEEE Trans. Instrum. Meas. 2018, 67, 559–568. [Google Scholar] [CrossRef]
- Li, W.; Zhang, G.; Chen, M.; Zhong, H.; Geng, Y. Dynamic Harmonic Phasor Estimator Considering Frequency Deviation. IEEE Sens. J. 2021, 21, 24453–24461. [Google Scholar] [CrossRef]
- Testa, A.; Gallo, D.; Langella, R. On the Processing of Harmonics and Interharmonics: Using Hanning Window in Standard Framework. IEEE Trans. Power Deliv. 2004, 19, 28–34. [Google Scholar] [CrossRef]
- Qian, H.; Zhao, R.; Chen, T. Interharmonics Analysis Based on Interpolating Windowed FFT Algorithm. IEEE Trans. Power Deliv. 2007, 22, 1064–1069. [Google Scholar] [CrossRef]
- Belega, D.; Dallet, D.; Petri, D. Accuracy of Sine Wave Frequency Estimation by Multipoint Interpolated DFT Approach. IEEE Trans. Instrum. Meas. 2010, 59, 2808–2815. [Google Scholar] [CrossRef]
- Wen, H.; Zhang, J.; Meng, Z.; Guo, S.; Li, F.; Yang, Y. Harmonic Estimation Using Symmetrical Interpolation FFT Based on Triangular Self-Convolution Window. IEEE Trans. Ind. Inform. 2015, 11, 16–26. [Google Scholar] [CrossRef]
- Ferreira, J.A.; Petraglia, A. Analog integrated lock-in amplifier for optical sensors. IEEE Instrum. Meas. Mag. 2017, 20, 43–50. [Google Scholar] [CrossRef]
- Ashraf, M.N.; Khan, R.A.; Choi, W. A Novel Selective Harmonic Compensation Method for Single-Phase Grid-Connected Inverters. IEEE Trans. Ind. Electron. 2020, 68, 4848–4858. [Google Scholar] [CrossRef]
- Choudhury, B.K.; Jena, P. A Digital Lock-In Amplifier Assisted Active Islanding Detection Technique for DC Microgrids. IEEE Trans. Ind. Appl. 2023, 59, 377–391. [Google Scholar] [CrossRef]
- Fu, X.; Colombo, D.M.; Alamdari, H.H.; Yin, Y.; El-Sankary, K. Lock-In Amplifier for Sensor Application Using Second Order Harmonic Frequency with Automatic Background Phase Calibration. IEEE Sens. J. 2022, 22, 16067–16080. [Google Scholar] [CrossRef]
- Jana, S.K.; Srinivas, S. A Computationally Efficient Harmonic Extraction Algorithm for Grid Applications. IEEE Trans. Power Deliv. 2022, 37, 146–154. [Google Scholar] [CrossRef]
- Xie, M.; Wen, H.; Zhu, C.; Yang, Y. DC Offset Rejection Improvement in Single-Phase SOGI-PLL Algorithms: Methods Review and Experimental Evaluation. IEEE Access 2017, 5, 12810–12819. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Musavi, F.; Vasquez, J.C. Single-Phase Frequency-Locked Loops: A Comprehensive Review. IEEE Trans. Power Electron. 2019, 34, 11791–11812. [Google Scholar] [CrossRef]
- Vazquez, S.; Sanchez, J.A.; Reyes, M.R.; Leon, J.I.; Carrasco, J.M. Adaptive Vectorial Filter for Grid Synchronization of Power Converters Under Unbalanced and/or Distorted Grid Conditions. IEEE Trans. Ind. Electron. 2014, 61, 1355–1367. [Google Scholar] [CrossRef]
- Sahoo, A.; Ravishankar, J.; Jones, C. Phase-Locked Loop Independent Second-Order Generalized Integrator for Single-Phase Grid Synchronization. IEEE Trans. Instrum. Meas. 2021, 70, 9004409. [Google Scholar] [CrossRef]
- Ahmed, H.; Bierhoff, M.; Benbouzid, M. Multiple Nonlinear Harmonic Oscillator-Based Frequency Estimation for Distorted Grid Voltage. IEEE Trans. Instrum. Meas. 2020, 69, 2817–2825. [Google Scholar] [CrossRef]
- Rehman, A.; Cho, K.; Ali, H.; Choi, W. A Novel Power Measurement Method Using Lock-in Amplifiers with a Frequency-Locked Loop. In Proceedings of the 2023 11th International Conference on Power Electronics and ECCE Asia (ICPE 2023-ECCE Asia), Jeju Island, Republic of Korea, 22–25 May 2023. [Google Scholar]
- IEEE Std 1459; IEEE Standard Definitions for the Measurement of Electric Power Quantities Under Sinusoidal, Nonsinusoidal, Balanced, or Unbalanced Conditions. IEEE: New York, NY, USA, 2010; pp. 1–50. [CrossRef]
- ST Microelectronics. Getting Started with the STM32H7 Series MCU 16-bit ADC. 2020 March. Available online: https://www.st.com/resource/en/application_note/an5354-getting-started-with-the-stm32h7-series-mcu-16bit-adc-stmicroelectronics.pdf (accessed on 10 June 2024).
- CyberKEPCO. Available online: https://cyber.kepco.co.kr/ckepco/front/jsp/CO/H/htmlView/COHAHP00908.jsp# (accessed on 1 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).