Analysis of the Distillation Column of a Catalytic Cracking Unit Using Fuzzy Input Information

Abstract

The aim of this work is to analyze and model the performance of the distillation column of a catalytic cracking plant using fuzzy initial information. A system of mathematical models of the studied columns was developed, and we discussed the issues of modeling the distillation column of a catalytic cracking plant operating in conditions of fuzzy initial information. The system of mathematical models of the studied columns was developed on the basis of statistical and fuzzy information. The mathematical models of columns K-1, K-2 and K-3 were identified with regression and fuzzy regression equations, i.e., combined models of the main columns of the catalytic cracking plant were constructed. The purpose of this study was to create an optimal control system for the distillation column of a catalytic cracking unit using a mathematical model of the process. The results obtained in this work can be helpful during the design, modernization and optimization of equipment and installations, especially those used in the chemical and petrochemical industries. They can be useful both from a scientific and practical point of view, and they are also significant in terms of environmental protection, economy and mechanical engineering.

1. Introduction

For the last decade, the main development trends in oil refining, as well as the modernization of oil refining production in almost all countries of the world, have been determined by environmental requirements aimed at reducing emissions resulting from the combustion of motor fuels. One of the main sources of air pollution is the gases released from motor vehicles.

Reducing the toxicity of exhaust gasses coming from vehicles is carried out in various ways: by improving the design and performance of the engine; by fitting cars with retention systems and catalytic converters neutralizing harmful emissions; and by improving the organization of traffic as well as improving the environmental properties of gasoline used.

For countries that support international trends in gasoline production, this means that refineries must produce commercial gasoline that meets modern world standards in terms of quality characteristics.

Complex methods of solving these problems are proposed on the basis of fuzzy set theory, taking into account the unclear information that represents human knowledge and experience—production personnel, specialist experts, etc.

The goal of this article is to study the problems of the development of mathematical models and the optimization of chemical–technological systems of oil refineries, which are often characterized by a lack of basic information and vagueness. The main approaches to the construction of mathematical models of aggregates are theoretical, experimental–statistical and involve the application of fuzzy set theory approaches and mixed approaches.

The oil refining industry makes an important contribution to the emissions of industrial volatile organic compounds (VOC). With the development of industry, atmospheric pollution is a growing problem. The most important anthropogenic emissions relative to the gas chemistry of the troposphere are nitrogen- and carbon-containing compounds. Emissions of volatile organic compounds are a major atmospheric pollutant, consisting of a wide range of compounds. In [1], a fundamental work on the control of volatile organic compounds, these sources are exhaust gases from automobiles, refineries, plastics plants, synthetic resins and solvents.

In order to reduce the amount of harmful emission in the air, it is better to use petrol that meets the international standard Euro-5 C high-octane number. EURO-5 fuel has a lower sulfur content than fourth-generation fuel, so it is better to use it. EURO-5 gasoline has a high-octane number, and AI-92 refined gasoline can be EURO-5. Its octane number is 92. At the same time, 95 octane petrol may be classified in the EURO-4 environmental standard due to the presence of different impurities.

A cracking reaction, mainly represented by a C—C bond break, refers to an endothermic reaction: the higher the temperature, the higher the reaction speed. Cracking reactions are one of the most important types of reactions in catalytic cracking. The higher the molecular weight of a hydrocarbon in the homological series, the faster the reaction rate. However, compared with alkanes that have the same carbon number, alkenes still have the greatest susceptibility to cracking. Following alkenes, the hydrocarbons with the greatest propensity to the cracking reaction are polymethylene hydrocarbons, isoparaffin, the long side-chain of aromatic hydrocarbons (side-chain cracking), alkalis of normal structure, and aromatic hydrocarbons.

Isomerization is an important reaction of the catalytic cracking process. As a result of the mechanism of the carbonate ion reaction of catalytic cracking, isomerization embodies the isomeric hydrocarbon molecule through the deflection and stripping of carbon and hydrogen atoms on the carbonate ion. The displacement of hydrogen atoms leads to isomerization of the double bond of alkenes. Isoparaffinic acid contains fairly high concentrations of MON (OCmm) and RON (OCC); therefore, in the context of the constant tightening of control requirements for the content of alkenes in gasoline, a maximum increase in the level of isomerization of hydrocarbon molecules is very important for maintaining a high-octane gasoline number.

Due to the tightening of the concentration control of alkenes in gasoline, high-temperature short-contact technology, which was previously widely used in classical catalytic cracking plants, is no longer able to meet modern requirements for the quality control of gasoline. The hydrogen transport reaction is the main mechanism for the creation of cracking products—the transformation of alkenes into limited hydrocarbons. Reducing the concentration of alkenes in gasoline requires rational engineering and technological solutions to determine the correct ratio of the activity of catalysts and working parameters. One of the methods to solve these problems is to generate and use initial fuzzy (qualitative) information about the characteristics of the work of the objects under study [2].

The authors of [3] offer an algorithm for the synthesis of mathematical models with consideration of the fuzziness of the output parameters of an object. Based on this algorithm, the model structure is identified as fuzzy multiple regression equations with fuzzy coefficients. The article offers a method for the parametric identification of fuzzy coefficients of regression and the proposed algorithm and methodology have been tested in the development of mathematical models.

Building a Linguistic Model (LM):

The algorithm takes into account the fuzziness of input ${\tilde{x}}_i,i=\overline{1,n}$ and output ${\tilde{y}}_j\in {\tilde{B}}_j,j=\overline{1,m}$ parameters.

• Select the input ${\tilde{x}}_i\in {\tilde{A}}_i,i=\overline{1,n}$ and output ${\tilde{y}}_j\in {\tilde{B}}_j,j=\overline{1,m}$ parameters of the object, which are linguistic variables (${\tilde{A}}_i\in X{\tilde{B}}_j\in Y$–fuzzy subsets).
• On the basis of expert procedures to assess parameter values ${\tilde{x}}_i,{\tilde{y}}_j,$ construct a term set $T\left({\tilde{X}}_i,{\tilde{Y}}_j\right)$.
• Construct ownership functions of the fuzzy parameters ${\mu }_{Ai}({\tilde{x}}_i),{\mu }_{Bi}({\tilde{y}}_j)$.
• Construct a linguistic model of the system and formalize fuzzy mappings defining the relationship between ${\tilde{x}}_i$ and ${\tilde{y}}_{j-Rij}$.
• Define fuzzy values of the output parameters of an object and select their numerical values from the fuzzy set of solutions.
• Check the condition of adequacy of the model. If the condition is met, the model is recommended for use when optimizing and managing the object; otherwise, define and return to the previous points to refine the model.

It is necessary to choose parameters which characterizes the quality of the cracking installation. For convenience, the ranges of fuzzy parameters are defined as segments, with minimum (x^min, y^min) and maximum (x^max, y^max) values. These depend on the discussion of experts, divided into several intervals (quanta), for example

$$x_j^{\min }=x_j^1\prec x_j^2\prec \dots \prec x_j^n=x_j^{\max };y_j^{\min }=y_j^1\prec y_j^2\prec \dots \prec y_j^n=y_j^{\max }.$$

(1)

To construct a term set of states, each quantum of the selected parameters is characterized by corresponding fuzzy terms, and they can be described by the following terms:

$${\tilde{y}}_i=\left\{\mathrm{NB}, \mathrm{NS}, \mathrm{N}, \mathrm{PS}, \mathrm{and} \mathrm{PB}\right\}$$

where NB—negative big, NS—negative small, N—normal, PS—positive small, and PB—positive big.

The accepted term set is a set of values of linguistic variables describing the work of the object under study. Each sampling interval is characterized by a specific thermometer. This term corresponds to the fuzzy set described by the affiliation function at its corresponding grading level.

The construction of the fuzzy parameter belonging function is one of the main steps in modeling complex objects using fuzzy set theory methods. The main way to restore this function is to plot a curve of the degree of belonging of a parameter corresponding to an odd set.

The goal of the control of the catalytic cracking is to make decisions based on choosing optimal values of the regime parameters $x=(x_1,x_2,x_3,x_4,x_5)$ of the gasoline production complex, providing extreme values of control criteria when applying the imposed unclear restrictions, which allows one to run the process in a stable and reliable mode. In production environments, when there are problems with the uncertainty and ambiguity of the initial information that complicate the process of formalization and prevent solving the problems by taking optimal values of the control parameters, a more efficient and convenient approach, as already noted, is the application of methods of theories of fuzzy sets based on formalization and the use of the experience, knowledge and intuition of experts in the subject area [4].

The technological complex of catalytic cracking and the tasks of modeling its operation modes are characterized by complexity. A characteristic feature of traditionally existing production facilities is a limited amount of information about the properties, structures and parameters of processed materials, which is associated with both the logic of production processes and the limited availability of measuring devices for obtaining reliable information about technological processes. On the other hand, the management of such production systems is more complicated in cases where the operating conditions of the system are not clearly defined, caused by the drift of the parameters and the control system, changes in working conditions, the influence of time-varying external factors and operating conditions on the management process, uncertainty of management alternatives and their selection criteria, etc.

A large share of the total output of chemical production is taken by products processed in multi-column rectification plants. The efficiency of rectification columns significantly affects the purity and, as a result, the quality of products. Existing distillation columns are characterized by relatively high technological costs, which significantly reduce the profitability of production and lead to higher product prices. To ensure the contact of steam (gas) and liquid flows in the processes of rectification and absorption, devices of various designs are used, among which vertical column-type devices are the most common [5,6].

In rectification columns, the steam and liquid phases come into contact on special devices—the nozzle layer, grid, and poppet structures are required for the clarity of separation into components. The term “rectification” refers to the process of separation of the homogeneous binary and multicomponent mixtures of volatile liquids due to two-way mass transfer and heat exchange between non-equilibrium gaseous (vapor) and liquid phases moving opposite each other. During the rectification of the separated mixture, partial evaporation and condensation processes occur simultaneously. The separation of mixtures is usually carried out in countercurrent column apparatuses with contact elements (nozzles and plates) with multiple or continuous phase contact. At each contact of the phases, a low-boiling component that enriches the vapors mainly evaporates from the liquid separated mixture, and from the vapor phase there is condensation and the component with the highest boiling point transitions to liquid.

Rectification is one of the most important technological processes in the chemical industry. The scope of rectification in chemical technology is constantly expanding. This process is especially important in the production of high-purity substances. Rectification is the process of separating liquid inhomogeneous mixtures into practically pure components, or fractions that have different boiling points. The physical essence of rectification carried out during oil distillation is two-way mass and heat exchange between liquid and steam flows, with significant turbulence of the contacting phases [7].

The simplest design of rectification devices is a column in which the movement of liquid from one stage of contact to another occurs under the influence of gravity. The main apparatus of oil distillation units is a vertical cylindrical distillation column. Inside it, plates are placed one above the other. On their surface, the vapor and liquid phases come into contact. Moreover, the lightest components during liquid irrigation evaporate and rush up together with the vapors, while the heaviest components condense and remain in the liquid.

As a result, evaporation and condensation proceed continuously in the distillation column. In stepwise rectification, liquid–vapor contact can occur in direct current, countercurrent, and crosscurrent forms. With continuous rectification in the entire volume of the column, the contact of liquid and steam during the movement of both phases occurs only in the countercurrent. Rectification columns are widely used in various industries, in particular in oil and gas processing for the separation of oil and fuel oil at primary oil distillation plants (ABT), gasoline at secondary distillation plants, hydrocarbon gasses at gas fractionating plants (HFC), and reaction products at chemical processing plants of hydrocarbon raw materials (catalytic cracking, thermal cracking, hydrocracking, coking, etc.) [8].

Thus, in the distillation column, the product is divided into the components of the mixture (oil, tar, chemical products, etc.), depending on their temperature and pressure in the processes of evaporation and condensation.

The main distillation column of the catalytic cracking unit is designed to separate the reaction products that come directly from the reactor into several fractions—gas, light gasoline, light catalytic gas oil, heavy catalytic gas oil and the remainder (Figure 1) [9].

Catalytic gas oils have a wider fractional composition than the products of the atmospheric column. In its composition, light catalytic gas oil is approximately equal to a mixture of light and heavy diesel fuels. Gas and gasoline leave from the top of the column, and catalytic gas oils are obtained in the form of side pods taken from the rebound sections. Due to the fact that the raw material enters the column from the reactors in the form of superheated steam with catalyst dust, the lower part of the column is a section of circulating irrigation designed for cooling the raw material vapors, washing them from the catalyst dust, condensing the heaviest part of the raw material and stripping light fractions from it. Cascade wash plates are installed in this section. At the bottom of the column and in the steam columns, a condenser–refrigerator is installed for the partial condensation of vapors of the upper product; the height of the column has one or two circulation irrigation systems, one of them is located at the top of the column.

Each side shoulder strap from the main column is sent to the stripper column, where light fractions are stripped from it. From the steam columns, the vapors are returned to the main column, and the liquid is taken as target fractions. Since the vapors returned to the main column have a lower temperature compared to the liquid entering the steamer, they are returned to the column one or two plates above the output of the side selection. At the top, the main column has a condenser–refrigerator and an irrigation tank in the form of a three-phase separator. Acute irrigation is applied to the upper plate of the column; the height of the columns undergoes 2–3 more circulation irrigations in the form of intermediate refrigerators with liquid circulating in them.

The products of the distillation column of the catalytic cracking unit are gas; light gasoline; light catalytic gas oil; heavy catalytic gas oil; heavy catalytic gas oil residue. It should be noted that due to the use of heat from the hot products of the rectification columns and heat from the circulating irrigation, it is possible to preheat oil to 200–210 °C. Thanks to the use of steam columns and circulating irrigation, the process of oil rectification at KK installations is characterized by high thermodynamic efficiency.

A characteristic feature of the technological scheme of a column is the absence of a heater or a hot jet that is supplied to the lower part of the column, which means that almost all the heat is supplied to the column with raw materials. This circumstance makes it possible to determine the thermal loads and phlegm flows along the column from the heat balance of the column with sufficient accuracy, without resorting to a complex potential calculation of material and heat balances.

2. Problem Statement

Oil refining is a complex process of chemical technology. Various approaches are used to develop models and control methods. However, optimization results are often inadequate for the current technological situation. An attempt to obtain more accurate models by taking into account additional factors leads to a large dimension of issues and to the complexity of accounting for non-formalized or difficult-to-formalize requirements. One of the ways to partially overcome these difficulties is to use the fuzzy set approach to formalize and process high-quality information [10].

The authors of the study [11,12] aim to predict the optimal management of complex oil processing processes operating in the uncertain background of the information. They explore the prospective use of artificial intelligence techniques, neural networks and fuzzy control, defined as a management strategy based on empirically acquired knowledge of the operation of the object (process) presented in linguistic form as a set of rules. The focus of this work is the Primary Oil Refinery Division, which requires the quick definition of a number of quality indicators to maintain its product quality. One of the most important indicators is the fractional composition of the deflection fractions at certain temperature ranges.

Special analyzers are used to measure individual indicators of product quality in industrial installations. The use of analyzers as sensors for the automatic stabilization of quality indicators is difficult for a number of reasons. First of all, analyzers introduce a large delay in the control system. According to the author of [13], the delay in the reaction of a boiling point analyzer installed on the object compared to the change in the boiling limit of the fraction in the column is of the order of 1–4 h. For end-of-boiling analyzers, this figure will be even higher. The delay is caused by the inertia of the sampling and heating system as well as the transport delay between the sampling point (usually at the outlet of the corresponding pump) and the location of the side sampling. Another factor that calls into question the feasibility of using analyzers in process optimization is the imperfection of sampling systems, which is aggravated by the high content of catalyst dust in cracking products. All this leads to the unreliable operation of the analyzers. Finally, the third reason is the design complexity of the analyzers, which makes it difficult to repair and maintain them.

In connection with the above, it is particularly important to develop mathematical models that link the quality indicators of raw materials with the mode in the devices of the catalytic cracking unit. When developing mathematical models for determining quality indicators, you can use the experience of the decision maker.

To build the model, we will use statistical and experimental data obtained from the various sensors of the system and will also apply the idea of regression serial inclusion methods (for structural identification).

3. Problem Definition

The integration of individual models of assemblies into a single system occurs according to the progress of the process of installation. The output of one model (calculation results) will be the input to another model. For example, the output of the K-1 column models is the input of K-2 columns, and the results of this column modeling will be the raw data for K-3 column modeling; then, this continues to the chain of K-6 and P-2 and K-7, at the end of which a finished product will be produced.

Thus, the main criteria we use for selecting the type of aggregate models, in addition to the necessary accuracy and efficiency of their application in computer modeling and optimization decision systems, include the convenience of combining them into a single system, that is, the coincidence of output and input variables models related to each other [2,6].

Each object model in the system is derived from a set of models, such as statistical, fuzzy and mixed. The integration of models of different aggregates into one system is carried out by the means of system modeling [7,8,9]. After analyzing the pros and cons of each model, selection criteria for the cost of aggregates, accuracy and model designation were developed, and the principles of integration of models were defined. To this end, the analysis of different typical models of the main units of the catalytic cracking plant was carried out. Based on the results of the studies of the aggregates of the catalytic cracking plant and the specifications of the processes, experimental data and expert evaluation were analyzed and evaluated, as well as approaches to the modeling of similar aggregates. The results are presented in

Table 1. Analysis and evaluation of possible types of models of elements and subsystems of production systems.

Stripping Column and Absorbers	Criterion	Types of Models
		Determined	Statistical	Fuzzy	Combined
Columns (K-1—stripping; K-2—absorber; K-3—absorber)	Availability of necessary information	3.5	4	4.5	5
	Cost of development	1.5	4	4	3.5
	Model accuracy	4.5	3.5	3.5	4.5
	Applicability according to designation	4	4	4	5
	Possibility of unification into a package	4.5	4	4	4.5
		18	19.5	20	22.5

. For the assessment of model type (ranking), a five-point scale was used.

Based on the above studies, we developed mathematical characteristics and models of aggregates. The mathematical model of the K-1 column was based on the statistical data and expert information processed by methods of fuzzy set theory, as well as on equations of material and thermal balances [6].

In the given table, ($i=\overline{1, 4}$-model type, $j=\overline{1, 5}$-model evaluation criteria, $k=\overline{1, N}$-object number (system element)) the i-th model-type evaluation was explored according to j-th criterion for k-th object, which was convenient to evaluate by a point (for example five points) scale.

A fuzzy estimate is allowed, i.e., ${\tilde{\alpha }}_{ijk}$ is a fuzzy variable from a given term set that can be described by the function of belonging to ${\mu }_{\tilde{A}}\left({\tilde{\alpha }}_{ijk}\right); {\tilde{\alpha }}_{ijk}\in \tilde{A}, \tilde{A}$—a fuzzy subset.

Based on the results of the expert evaluation shown in Table 1, a multi-criteria selection of model type (alternatives) of the system objects was carried out.

4. Mathematical Models of the Column and Reactor

The mathematical model of the kolon and reactor was based on statistical data and expert information processed by the methods of fuzzy set theory.

As a result of processing experimental and statistical data, expert data and the idea of the sequential inclusion of regression, and by mathematically modeling various types of information, the following system structure of equations of multiple, qualitative regression and conditional logical conclusion, which are models of the investigated columns, was obtained:

$$y_j=a_{0j}+{\displaystyle \sum _{i=1}^4{a}_{ij}{x}_{ij}+{\displaystyle \sum _{i=1}^4{\displaystyle \sum _{k=i}^4{a}_{ikj}{x}_{ij}{x}_{kj},j=\overline{1}\overline{,3}}}}$$

(2)

$${\tilde{y}}_j={\tilde{a}}_{0j}+{\displaystyle \sum _{i=1}^4{\tilde{a}}_{ij}{x}_{ij}+{\displaystyle \sum _{i=1}^4{\displaystyle \sum _{k=i}^4{\tilde{a}}_{ikj}{x}_{ij}{x}_{kj},j=\overline{4,6}}}}$$

(3)

x₁—loading—input of raw materials;

x₂—temperature;

x₃—irrigation flow in K-1;

x₄—pressure;

y₁—output of products (hydrogenate from K-1);

y₂—output of hydrogenous gas (HGG) (from K-2);

y₃—output of hydrocarbon gas (HCG) (from K-3);

$\tilde{y}$₄—content of total sulfide compounds in hydrogenate (K-1);

$\tilde{y}$₅—composition of hydrogenous gas (from K-2);

$\tilde{y}$₆—content of hydrocarbon gas (HCG) (from K-3).

As can be seen, the models describing the output of the block products have a multiple regression, respectively, identified by the experimental–statistical methods. The sulfur quality estimation models are like fuzzy equations of multiple regression, and they are based on qualitative information from experts.

For the identification of unknown fuzzy coefficients ${\tilde{a}}_{0j}, {\tilde{a}}_{ij}(i=\overline{4,6})$ and ${\tilde{a}}_{ikj}(i,k=\overline{1,4}, j=\overline{4,6})$ in Equation (2), the odd sets describing qualitative indicators of production were broken down into the following set levels: α = 0.5; 0.75; 1. According to the selected level, the input x_ij and output ${\tilde{y}}_3$, ${\tilde{y}}_4$ parameters were observed at each level $a_q(q=\overline{1,3})$.

For each level of α and q models of the qualitative indicators of the output products (2), it is possible to present a system of multiple regression equations; then, the task of identification of their coefficients $a_{ij}^{aq}(i=\overline{1,4}), j=\overline{4,6}, q=\overline{1,3})$ is reduced to classical tasks of evaluation of the parameters of multiple regression. To solve the problem, one can use well-known algorithms or standard programs of multiple regression. We have used the MatLab R2014a system.

The results of the parametric identification of the models determining the dependence of the hydrogenation output on the column are as follows (4)–(6):

$$\begin{array}{l}{y}_1=f_1(x_{11},x_{21},x_{31},x_{41})=-3.65+0.24400x_{11}+0.036500x_{21}+1.825x_{31}-1.327272727x_{41}+0.00180247x_{11}^2+\\ 0.0000913x_{21}^2+0.1140625x_{31}^2-0.06033058x_{41}^2+0.0004056x_{11}{x}_{21}+0.020277778x_{11}{x}_{31}+0.004562500x_{21}{x}_{31}\end{array}$$

(4)

$$\begin{array}{l}{y}_2=f_2(x_{12},x_{22},x_{42})=84.999999998+0.298245614x_{12}+2.833333333x_{22}-2.428571429x_{42}+0.000116275x_{21}^2+\\ 0.0944444440x_{22}^2-0.0693877550x_{42}^2+0.006627680x_{12}{x}_{22}+0.002840434x_{12}{x}_{42}+0.242857143x_{22}{x}_{42}\end{array}$$

(5)

$$\begin{array}{l}{y}_3=f_3(x_{13},x_{23},x_{43})=83.499999998+0.297329377x_{13}+2.783333333x_{23}-7.590909091x_{33}+0.000117638x_{13}^2+\\ 0.0927777780x_{23}^2-0.6900826450x_{33}^2+0.0066073190x_{13}{x}_{23}+0.009009981x_{13}{x}_{33}+0.759090909x_{23}{x}_{33}\end{array}$$

(6)

The quality of the product is determined by the content of unsaturated hydrocarbons in the hydrogen [not more (1%)]; content of sulfur in the hydrogen [0.00005%]; and content of water-soluble acids and alkalis in the hydrogen [0%]. In fact, quality indicators are characterized by limitations such as “no more” and “about”, i.e., they are fuzzy.

To determine the optimum temperature of the water purification process dependent on the quality of raw material based on expert information, logical inference rule and knowledge base, a linguistic model was built. This model implements the following linguistic dependence: “If the raw material is heavy, then the optimum is low temperature; otherwise, if the raw material is light, then the optimal is high temperature”. On the basis of expert procedures and methods of fuzzy set theory, the functions of belonging describing fuzzy sets were defined:

-

μ_A(m) = exp(|(m − 185)0.5|)—heavy raw materials—direct gasoline;

-

μ_A(λ) = exp(|l − 165)0.5|)—light raw materials;

-

μ_B($\mathcal{H}$) = exp(|n − 300)0.7|)—low temperature;

-

μ_B(ϐ) = exp(|h − 400)0.7|)—high temperature.

In practice, we want the output to be bigger and the quality to be better. However, criteria are often contradictory, and it is often impossible to improve them at the same time. The task is to find the optimal compromise solution that depends on the production situation and planning, and that also satisfies the decision maker.

Thus, using the given statements of decision-making problems, the problem of optimizing the hydrotreating process of a catalytic cracking plant can be formalized and set as follows:

Let $f(x)=\mu (f(x))={\mu }_0^1(x)$, the normalized criterion to measure the output of the hydrogenated feed, be separated. Let us assume that for each fuzzy constraint describing product quality indicators ${\phi }_q(x)\tilde{\ge }{b}_q, q=1\overline{,3}$, the membership function of its execution is constructed ${\mu }_q(x)$, $q=\overline{1,3}.$ Either a set of priorities for restrictions is known $I_R=\{1,2,3\}$, or a weight vector reflects the mutual importance of these constraints $\beta =({\beta }_1,{\beta }_2,{\beta }_3)$ [13].

The criteria and restrictions depend on the vector of parameters ($x_1$—loading of raw materials; $x_2$, $x_3$—pressure and temperature in the reactor; $x_4$—volume feed rate of raw materials; $x_5$—hydrogen/hydrocarbons ratio).

The formalized problem of making a decision, under conditions of multi-criteria and fuzziness, can be written as the following problem of fuzzy mathematical programming:

$$\underset{x\in X}{\max } {\mu }_0^1(x),$$

(7)

$$X=\{x:\arg \underset{x\in \Omega }{\max }{\displaystyle \sum _{q=1}^3{\beta }_q{\mu }_q(x)\wedge {\displaystyle \sum _{q=1}^3{\beta }_q=1\wedge {\beta }_q\ge 0, }} q=\overline{1,3}$$

(8)

To solve the multi-criteria task of determining the optimal mode of operation of the catalytic tuning installation, the following dialog algorithm is proposed for working in an unclear environment, based on modification of the principles of the main criterion (MC) (for the criterion, if it is possible to select a main criterion) and Pareto optimality (PO). FMC + PO algorithm:

• Set $p_q, q=\overline{1,L}$ —the number of steps per q coordinate and the priority series for local criteria $I_k=\{1,\dots ,m\}$ (the main criterion must have priority 1)—and enter the value of the constraint weight vector ${\beta }^1, {\beta }^2,\dots ,{\beta }^N$, taking into account the importance of local constraints.
• The decision maker sets the boundary values (limits) of local criteria.
• Determine $h_q=1/p_q, q=\overline{1,L}$—the steps to change the coordinate of the weight vector β.
• Determines the set of weight vectors ${\beta }^1, {\beta }^2,\dots ,{\beta }^N$.
• Defines the term set $T(X,Y)$ and constructs the functions of the constraint execution membership ${\mu }_q(x), q=\overline{1,L}$.

The main criterion is maximized on a set of X, and the current solution is determined: $x({\mu }_R^i,\beta ), {\mu }_0^1(x({\mu }_R^i,\beta )),\dots ,{\mu }_0^m(x({\mu }_R^i,\beta ));$ ${\mu }_1(x({\mu }_R^i,\beta )),\dots ,$ ${\mu }_L(x({\mu }_R^i,\beta )),$ $i=\overline{2,m}$. The decision is presented to the person making the decision. If the current results do not meet, new values are assigned ${\mu }_R^i(x), i=\overline{2,m}$ and (or) values are adjusted.

The following membership functions are built, and constraints are defined by the specified algorithm:

μ₁(x) = exp(0.50000000|y₂ − 0.8000000)0.55|);

(9)

μ₂(x) = exp(0.00002000|y₃ − 0,0000400)0.85|);

(10)

μ₃(x) = exp(0.00000001|y₄ − 0.0000001)1.00|);

(11)

where y₂, y₃, and y₄ output fuzzy values reflecting product quality.

• Based on expert evaluation methods, the values of the weight vector for constraints are determined $\beta =({\beta }_1,{\beta }_2,{\beta }_3), {\displaystyle \sum _{q=1}^3{\beta }_q=1, {\beta }_q\ge 0, q=\overline{1,3}}$, in our case β = (0.3, 0.4, 0.3).
• To solve the maximization problem on the set X defined by expression, define solution $x(\beta ), {\mu }_0^1(x(\beta )),$ ${\mu }_1(x(\beta )),{\mu }_2(x(\beta )),{\mu }_3(x(\beta )).$
• The decision shall be presented to the decision maker. If the current results do not satisfy the decision maker, they are assigned new values β and returned to point 2.

The search for a solution stops, and the results of the final choice of the decision maker are displayed: optimal values of the regime parameters $x^{*}(\beta )$; values of the criterion y1 y₁ − ${\mu }_0^1(x^{*}(\beta )),$; values of fuzzy restrictions, i.e., the degree of fulfillment (membership function) of restrictions ${\mu }_1(x^{*}(\beta )),{\mu }_2(x^{*}(\beta )),{\mu }_3(x^{*}(\beta )).$

These results are shown in

Table 2. Comparison of optimization results based on the proposed algorithm, deterministic method, and experimental data.

№	Criteria and Restrictions Values	Deterministic Method (Literature Data)	The Proposed Algorithm Is Fuzzy Mathematic Program (FKMM + PO)	Experimental Data (Atyrau Oil Refinery)
1	The output of the hydrogenated feed is separated criterion y1	74.5	79.5	76.5
2	The content of unsaturated hydrocarbons in the hydrogenated feed is separated (${\tilde{y}}_2$)	0.85	0.70	(0.85) l
3	The sulfur content of the hydrogenated feed is separated (${\tilde{y}}_3$)	0.000050	0.0000463	(0.000047) l
4	The content of water-soluble acids and alkalis in the hydrogenated feed is separated (${\tilde{y}}_4$)	0.1 × 10−5	0.3 × 10−6	(0.3 × 10−6) l
5	Membership function for executing a fuzzy constraint on ${\tilde{y}}_2$ − ${\mu }_1(x^{*}(\beta ))$	-	1.0	-
6	Membership function for executing a fuzzy constraint on ${\tilde{y}}_3$ − ${\mu }_2(x^{*}(\beta ))$	-	1.0	-
7	Membership function for executing a fuzzy constraint on ${\tilde{y}}_4$ − ${\mu }_3(x^{*}(\beta ))$	-	0.95	-
8	The optimal values of input parameters and operating conditions $x^{*}=(x_1^{*},x_2^{*},x_3^{*},x_4^{*},x_5^{*})$? x1*—loading of raw materials;	80	80	80
9	x2*—hydrotreating pressure;	26	35	32
10	x3*—the temperature of hydrotreating;	340	320	320
11	x4*—volume feed rate of raw materials;	3.5	3	3
12	x5*—hydrogen/hydrocarbon ratio.	415	390	400

Note: the input and mode parameters of the process taken are approximately the same, and ^l means that they are obtained by the laboratory.

.

Analysis of the data presented in Table 2 gives grounds to draw the following conclusions:

• The proposed algorithm is more efficient than the deterministic method and more accurately matches the experimental data.
• When solving optimization problems based on the proposed algorithms, the adequacy of solving the production problem increases, since additional fuzzy information (experience, knowledge) that more fully describes the real situation without idealization is taken into account.
• The fuzzy mathematical programming algorithm (FKMM + PO) allows you to determine the degree of fulfillment (membership function) of a particular fuzzy constraint, i.e., the degree of correctness of the obtained solutions.
• The results of modeling show that increased requirements for product quality decrease the volume of the output, i.e., the decision maker chooses a satisfactory compromise between quality and quantity.

If the adequacy condition is met, S = |y_M − y_E| ≤ S_D, where S, SD, respectively, is the criterion and its acceptable value, y_M and y_E, are the output values obtained experimentally by model with identical input values. The developed models are recommended for the research and determination of optimal modes of operation of the objects—elements of the production facility and system as a whole. Otherwise, the cause of the inadequacy must be determined, and the relevant paragraphs must be returned to address the issue of model adequacy.

Based on the logical rule of conditional inference and knowledge base, linguistic models describing the effect of the reactor temperature of catalytic cracking on the output of the catalyst and the stability of the catalyst are built [14,15].

$$\begin{gathered} \mathrm{If} \tilde{x}\in \tilde{A}(NB), \mathrm{then} {\tilde{y}}_1\in {\tilde{B}}_1(PB), {\tilde{y}}_3\in {\tilde{B}}_3(NB), {\tilde{y}}_3\in {\tilde{B}}_3(NB); \\ \mathrm{if} \tilde{x}\in \tilde{A}(N), \mathrm{then} {\tilde{y}}_1\in {\tilde{B}}_1(PS), {\tilde{y}}_2\in {\tilde{B}}_2(PS), {\tilde{y}}_3\in {\tilde{B}}_3(PS); \mathrm{and} \\ \mathrm{if} \tilde{x}\in \tilde{A}(\mathrm{PB}), \mathrm{then} {\tilde{y}}_1\in {\tilde{B}}_1(NB), {\tilde{y}}_2\in {\tilde{B}}_2(\mathrm{PB}), {\tilde{y}}_3\in {\tilde{B}}_3(\mathrm{PM}). \end{gathered}$$

where PB—positive big; PS—positive small; N—norm; NS—negative small; NB—negative big; $\tilde{x},{\tilde{y}}_1,{\tilde{y}}_2,{\tilde{y}}_3$, respectively, are the input and the output linguistic variables; ($\tilde{x}$) is the catalyst (${\tilde{y}}_1$) and hydrogen (${\tilde{y}}_2$) volume and quality of the catalyst (${\tilde{y}}_3$); and $\tilde{A}$, ${\tilde{B}}_j$, $\tilde{x}$, ${\tilde{y}}_j, j=\overline{1,3}$ are the fuzzy sets characterizing linguistic variables.

To determine the optimum temperature of the water purification process depending on the quality of raw material based on expert information, logical inference rule and knowledge base, a linguistic model was built. This model implements the following linguistic dependence: “If the raw material is heavy, then the optimum is low temperature, otherwise, if the raw material is light, then the optimal is high temperature”. 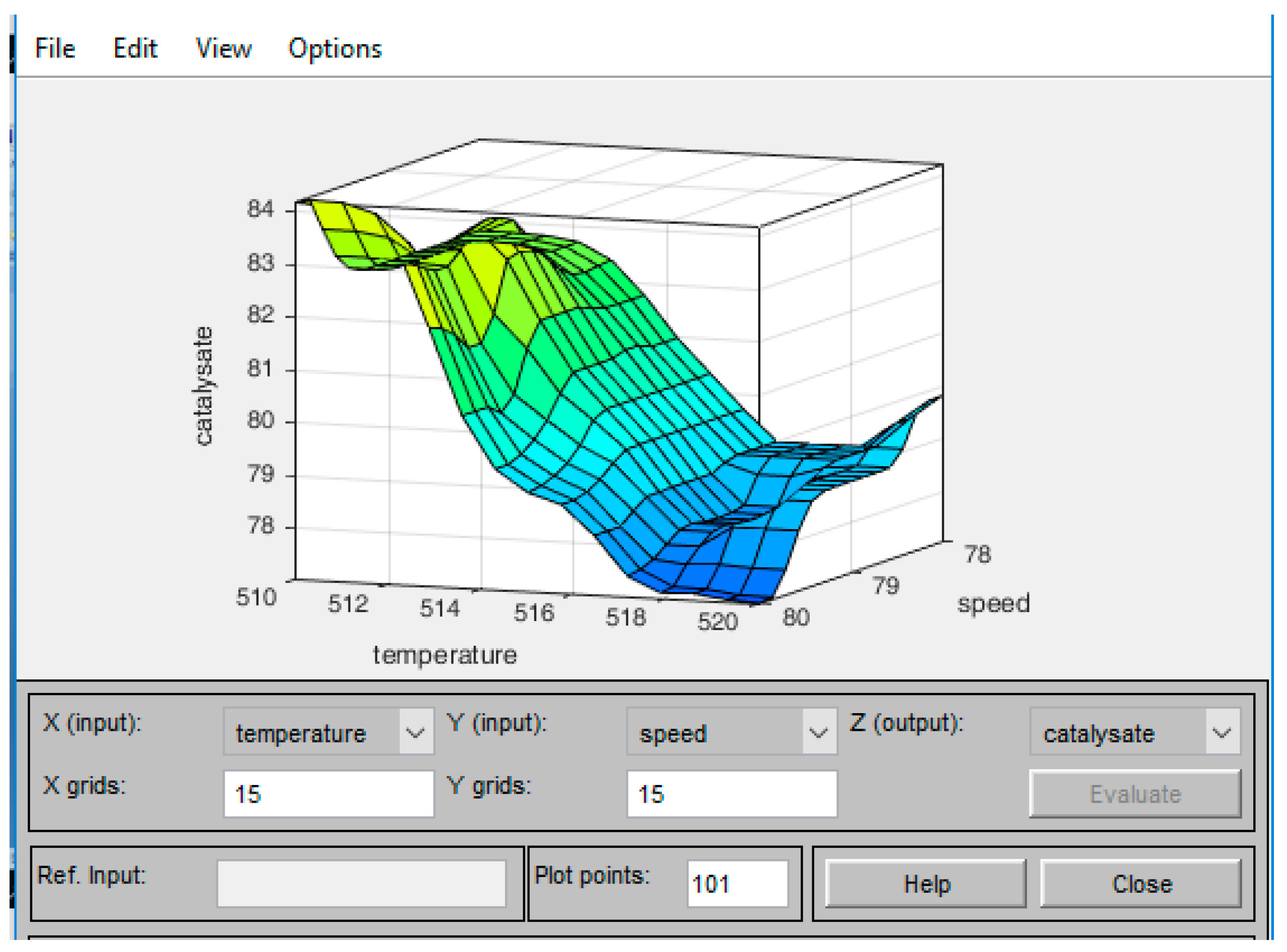Figure 2 shows the use of the Rule editor window.

Speed dependence on the temperature shown in (Figure 3).

With the help of this system, models can be used to determine the optimal operating modes of the facility by simulating the operation of the Atyrau catalytic cracking unit in a refinery to solve optimization tasks and develop recommendations for the effective management of the reforming process [16]. The results of the simulation of the work of the object, their comparison with other known results, and experimental production data are shown in Table 2.

It is very difficult and not always possible to estimate the quality of the products by one number. The quality of the product is determined by the content of unbiased hydrocarbons in hydrogenates [not more than ($\tilde{\le }$) 1%]. Qualitative indicators are characterized by limitations of type «not more than» and «about», i.e., they are unclear. The FKMM + PO algorithm allows one to determine the degree of fulfillment (belonging function) of a fuzzy restriction, i.e., the degree of correctness of obtained decisions. Thus, the proposed methodology of building models is based on information on the different nature and methods of model synthesis in an unclear environment based upon systems theory and fuzzy sets, probabilistic methods, methods of expert assessments, and developed mathematical models of the main aggregates of a catalytic cracking plant.

When solving multi-criteria optimization problems on the basis of the proposed algorithm, the adequacy of solving the production problem is increased since additional qualitative information (experience, knowledge of the decision maker, experts) is taken into account, more fully describing the real situation without idealization.

The proposed and used algorithm makes it possible to determine the degree (function) of belonging for the execution of a fuzzy restriction, i.e., the degree of correctness of the obtained solutions.

The reliability of the obtained results and conclusions is confirmed by the correctness of the methods of research, based on the scientific provisions of the theory of optimization, the theories of fuzzy sets, and methods of expert estimation; and sufficient convergence of the calculation and model (theoretical) and experimental (experimental-industrial) results of the study (relative error not more than 3%).

5. Conclusions

Based on the proposed algorithm, the decision-making tasks are formalized in order to select the optimal values of the regime parameters for the installation of catalytic cracking. The novelty of the obtained problems’ solution as a fuzzy mathematical programming problem consists of being set and solved in an unclear environment and not converting them to deterministic tasks, that is, keeping available information of an unclear nature. This approach, based on the knowledge and experience of experts, allows us to obtain adequate solutions to complex production tasks. To solve the problems of multicriteria, ideas of compromise schemes and principles of optimality were used, and they were modified in case of ambiguity of the initial information. A new kind of principle of optimality was obtained—quasi-maximin principle.

Based on the conducted studies, the structure and parameters of the mathematical models of the column and the reactor of the catalytic cracking plant were identified.

The simulation results have high precision and are consistent with real (experimental) data. On the basis of the models obtained, it is possible to determine qualitative performance in a fuzzy environment, which is not possible by traditional modeling methods.

Thus, new decision-making tasks are obtained for optimizing the regime parameters of catalytic cracking installation, and they are set and solved in an unclear environment without conversion to equivalent deterministic variants, developing heuristic algorithms for their solutions. The developed algorithms are based on the modification and combination of various principles of optimality; they are modified on the basis of methods of fuzzy mathematics to work in an unclear environment. The construction method of mathematical models of technological systems under uncertainty conditions takes into account unclear information which was implemented in the development of a system of models of technological aggregates from the catalytic cracking plant of Atyrau oil refinery. The developed models are used in making decisions on the selection of optimal modes of operation of the object under investigation.