A Comprehensive Review on Molecular Dynamics Simulations of Forced Convective Heat Transfer in Nanochannels
Abstract
:1. Introduction
2. Fundamentals of the MD Simulation Method in FCHT-NC
2.1. Step 1: Initial Preparation
2.1.1. Selection of Nanochannel Wall and Fluid Materials
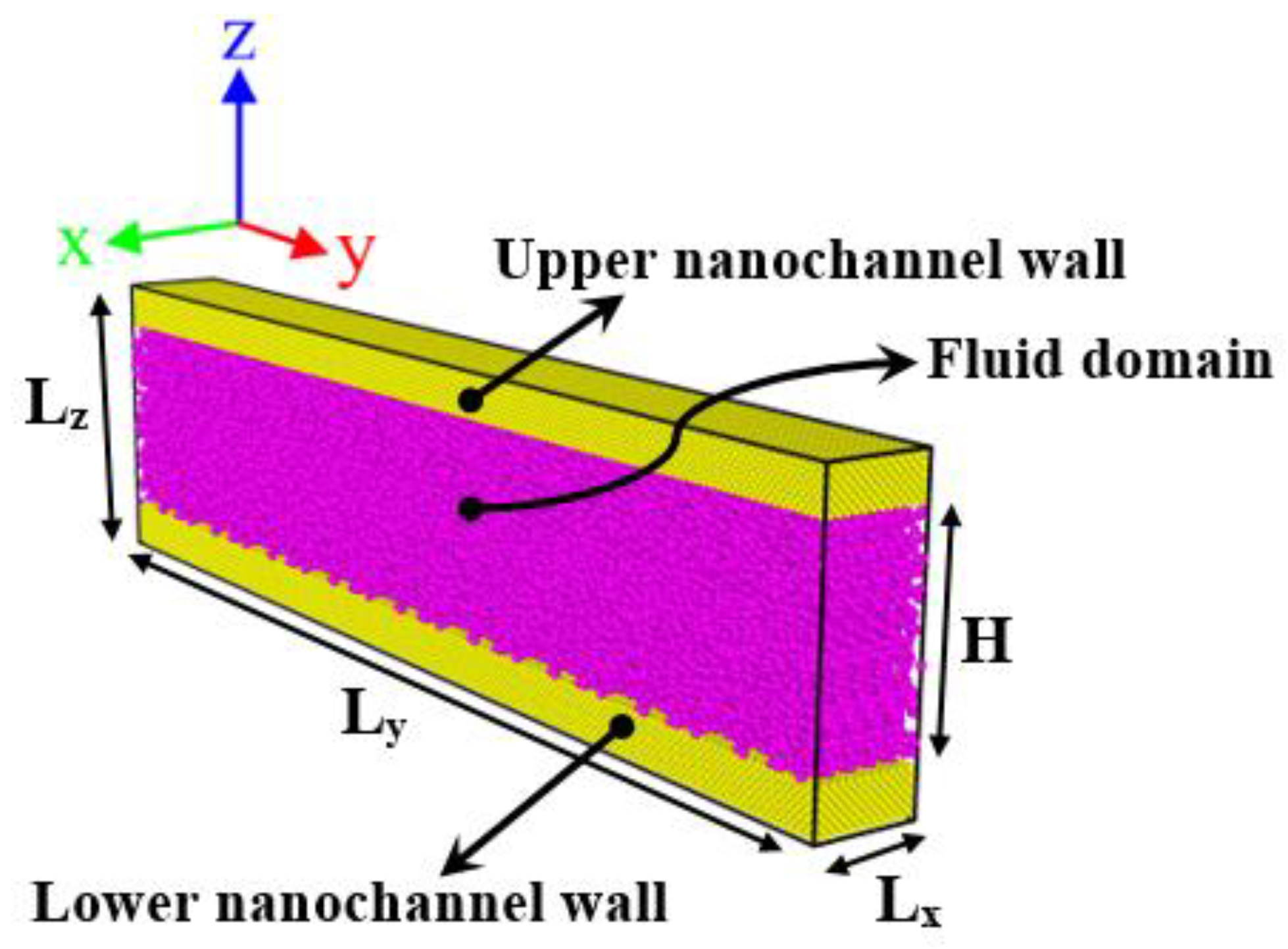
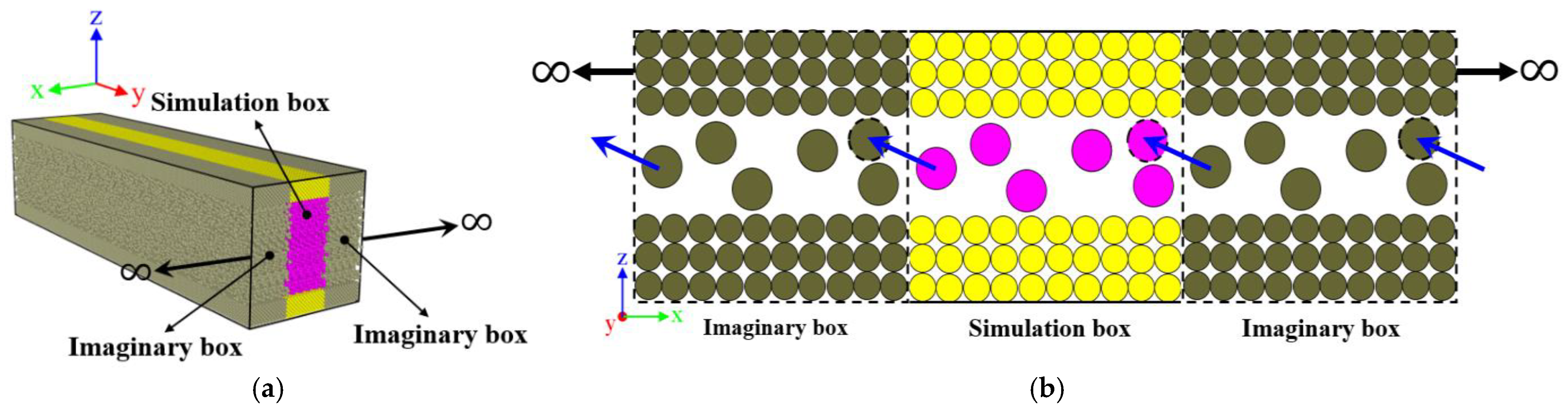
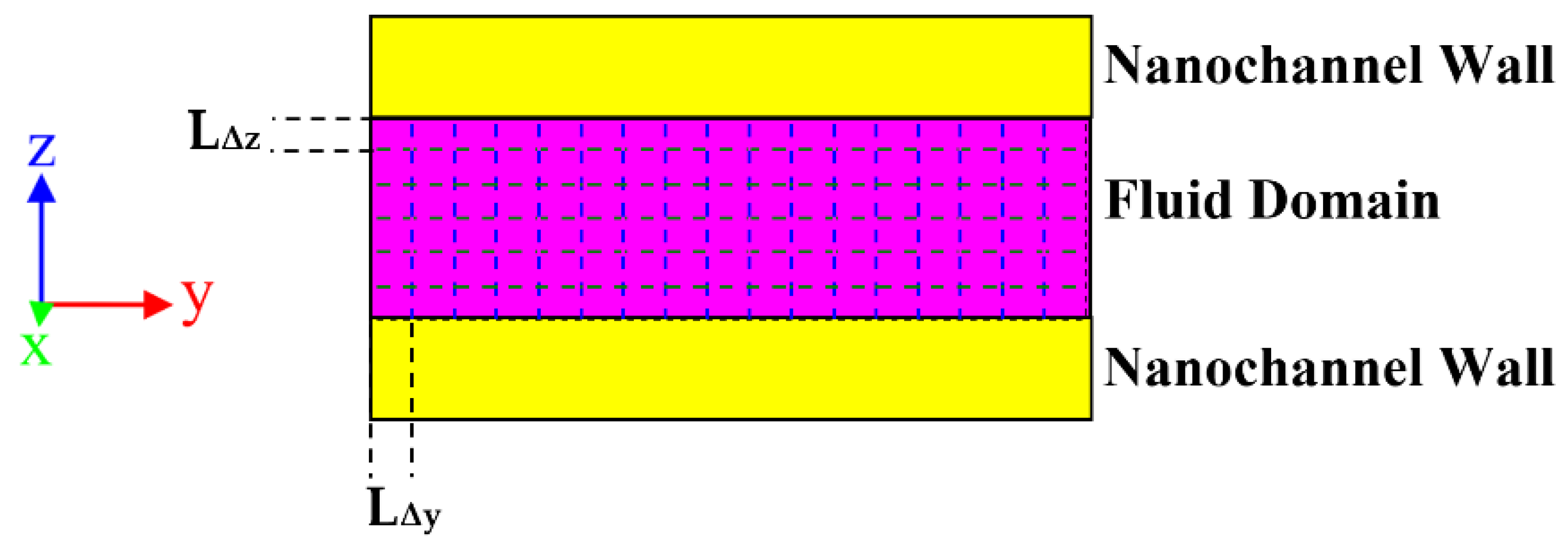
2.1.2. Construction of the Initial Simulation Box
2.1.3. Determination of Suitable Potential Energy Functions
2.2. Step 2: Geometry Optimization
2.3. Step 3: Equilibrium MD (EMD) Simulation
2.3.1. Definition of Ensembles
2.3.2. Definition of Initial Velocities
2.4. Step 4: Non-Equilibrium MD (NEMD) Simulation
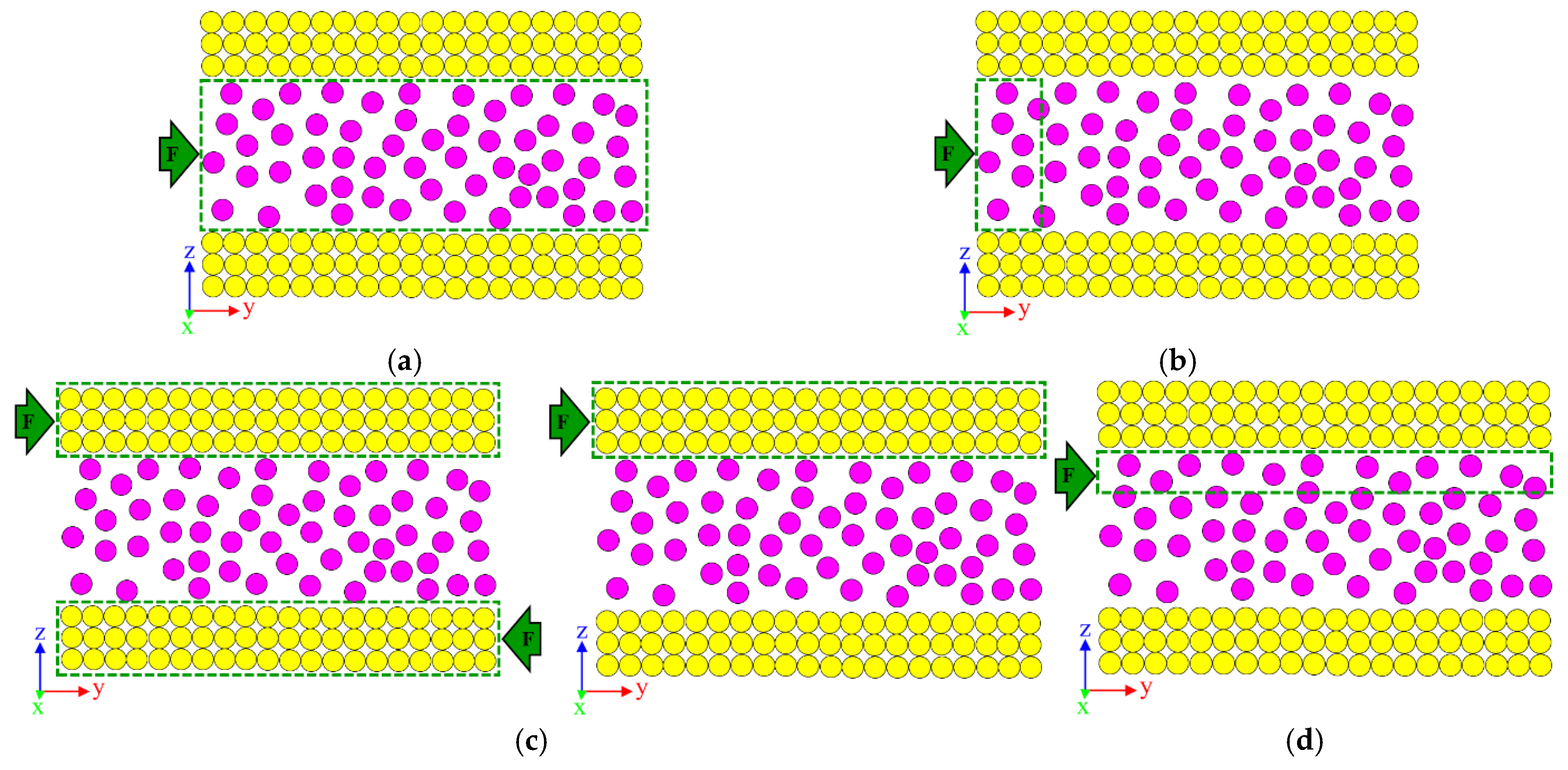
2.4.1. Flow Creation
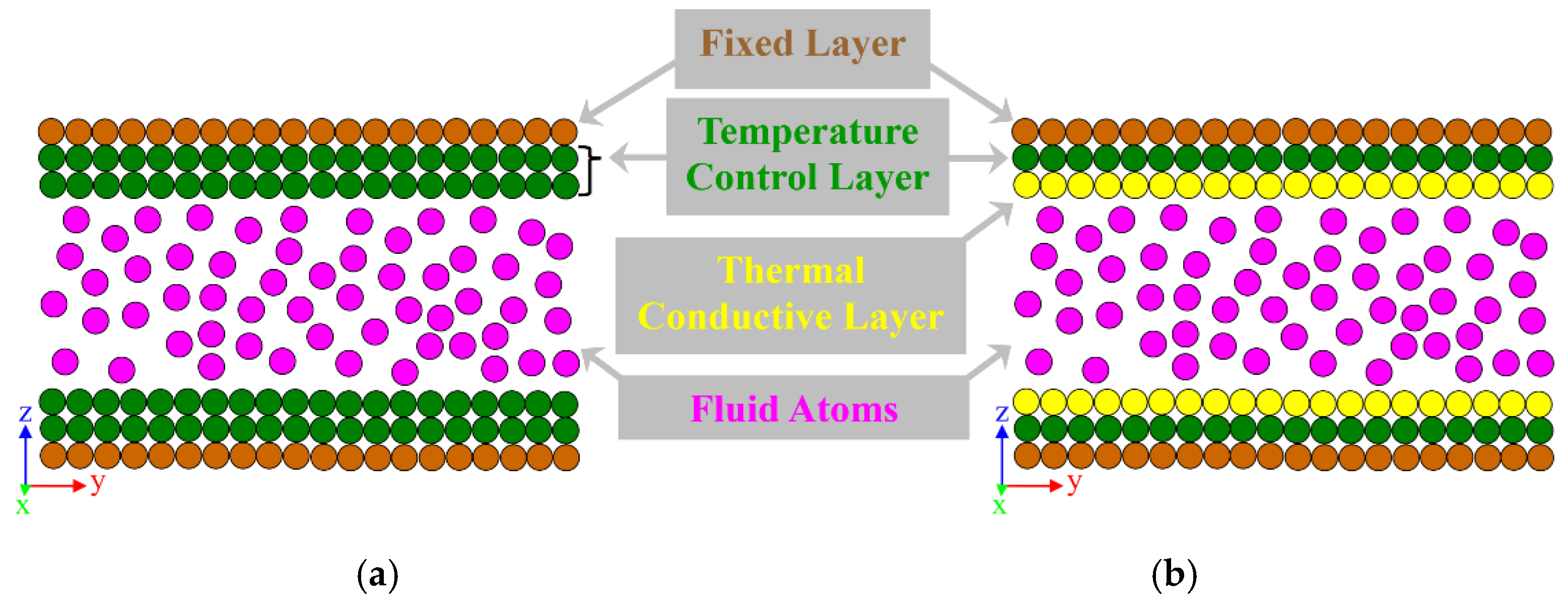
2.4.2. Heat Generation
- All-wall thermostat model (or cold-wall model): in this model, all nanochannel wall layers are selected as the region where the thermostat is applied to induce heat flux (see Figure 8a).
- Partial-wall thermostat model (or thermal wall model): in this model, a small number of wall layers, called “temperature control layers,” which are sufficiently distant from the solid–fluid interface, are chosen as the region where a thermostat is applied. The next inner layers, called “thermal conductive layers,” interact freely with the neighboring atoms under an NVE ensemble (see Figure 8b).
3. Analysis of the MD Simulation of FCHT-NC
3.1. Basic Governing Equations
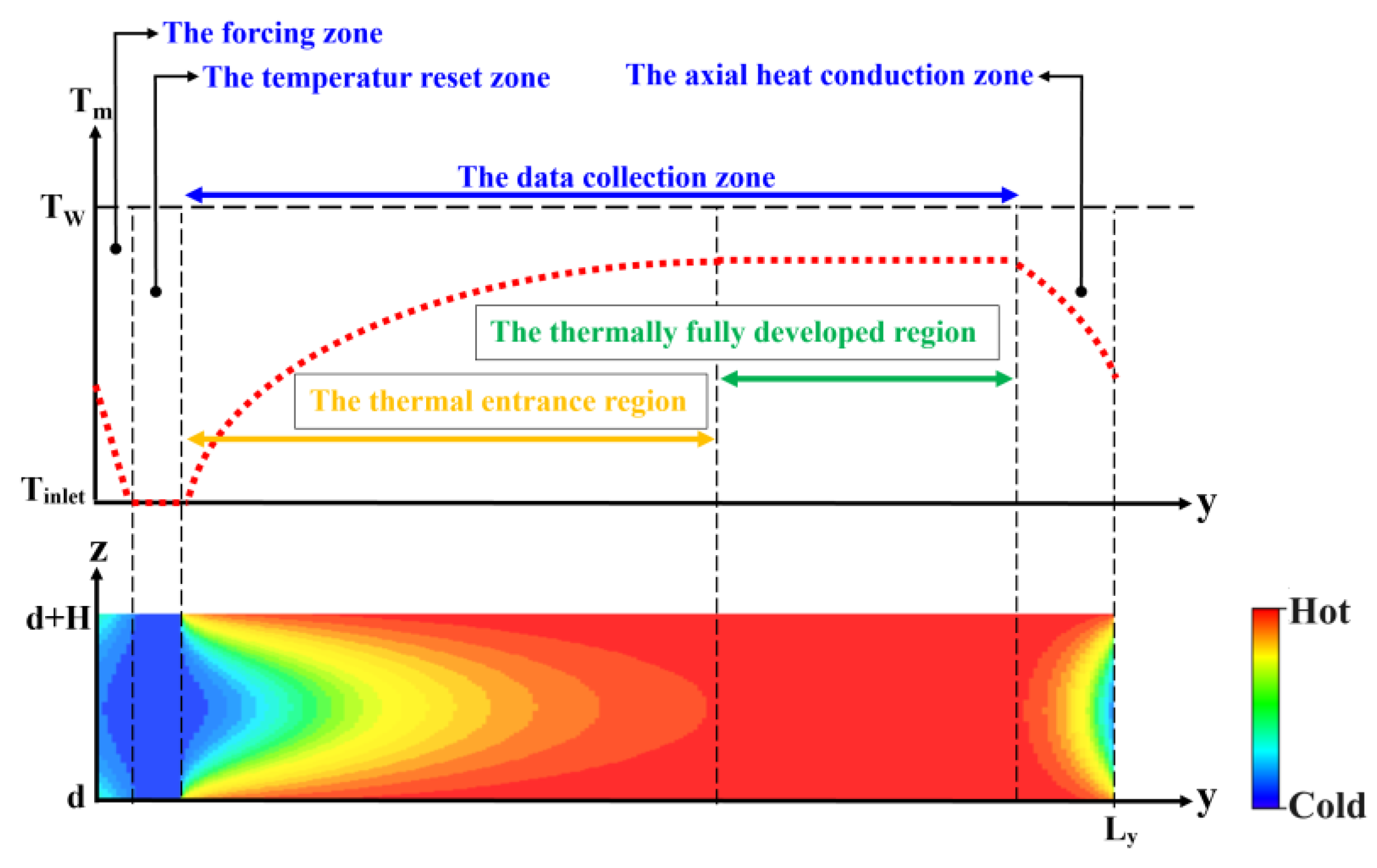
3.2. Overall Heat Transfer Performance
3.3. Influencing Parameters on FCHT-NC
3.3.1. Effect of Surface Wettability
3.3.2. Effect of Nanochannel Wall Material
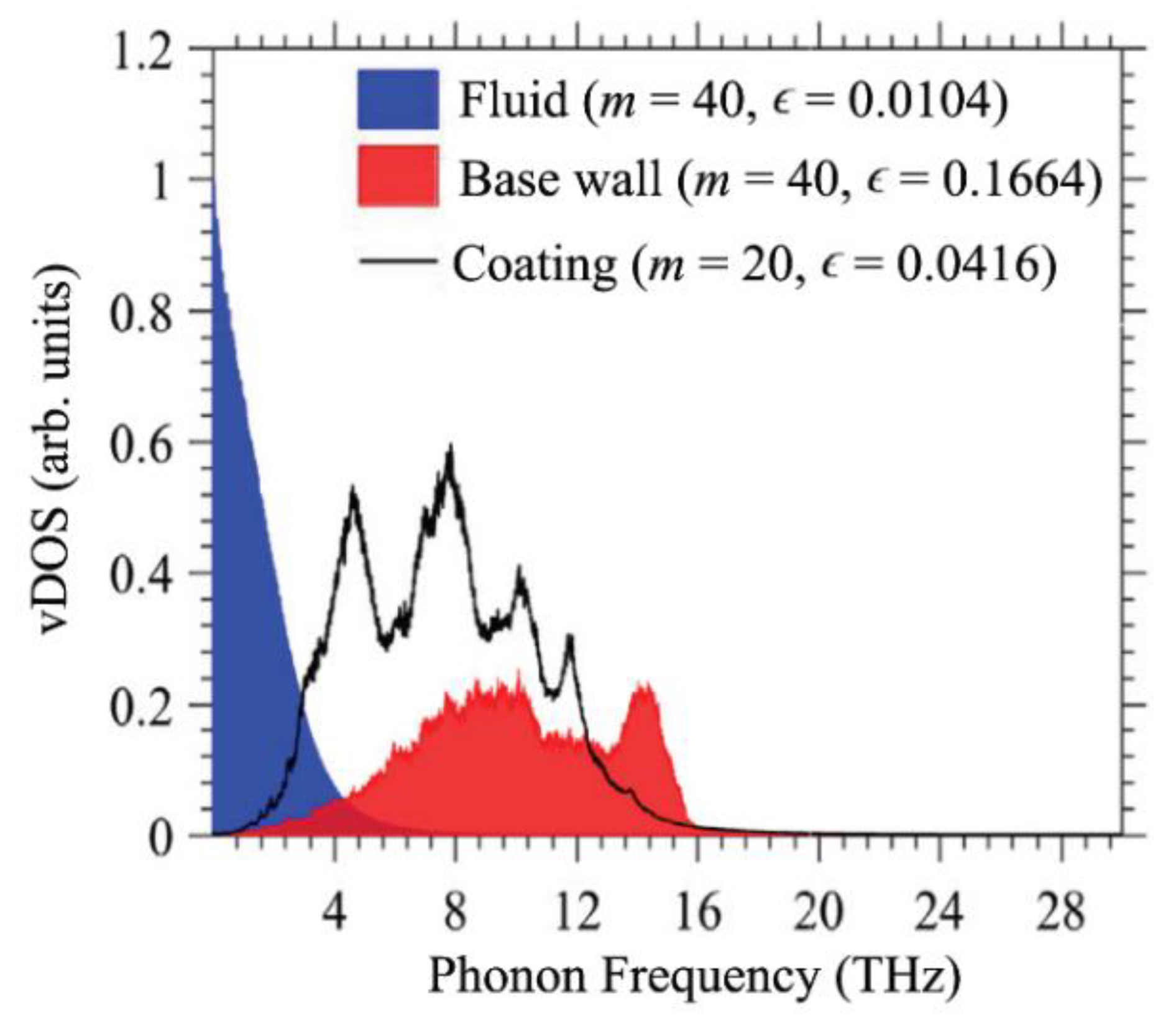
3.3.3. Effect of Surface Coating
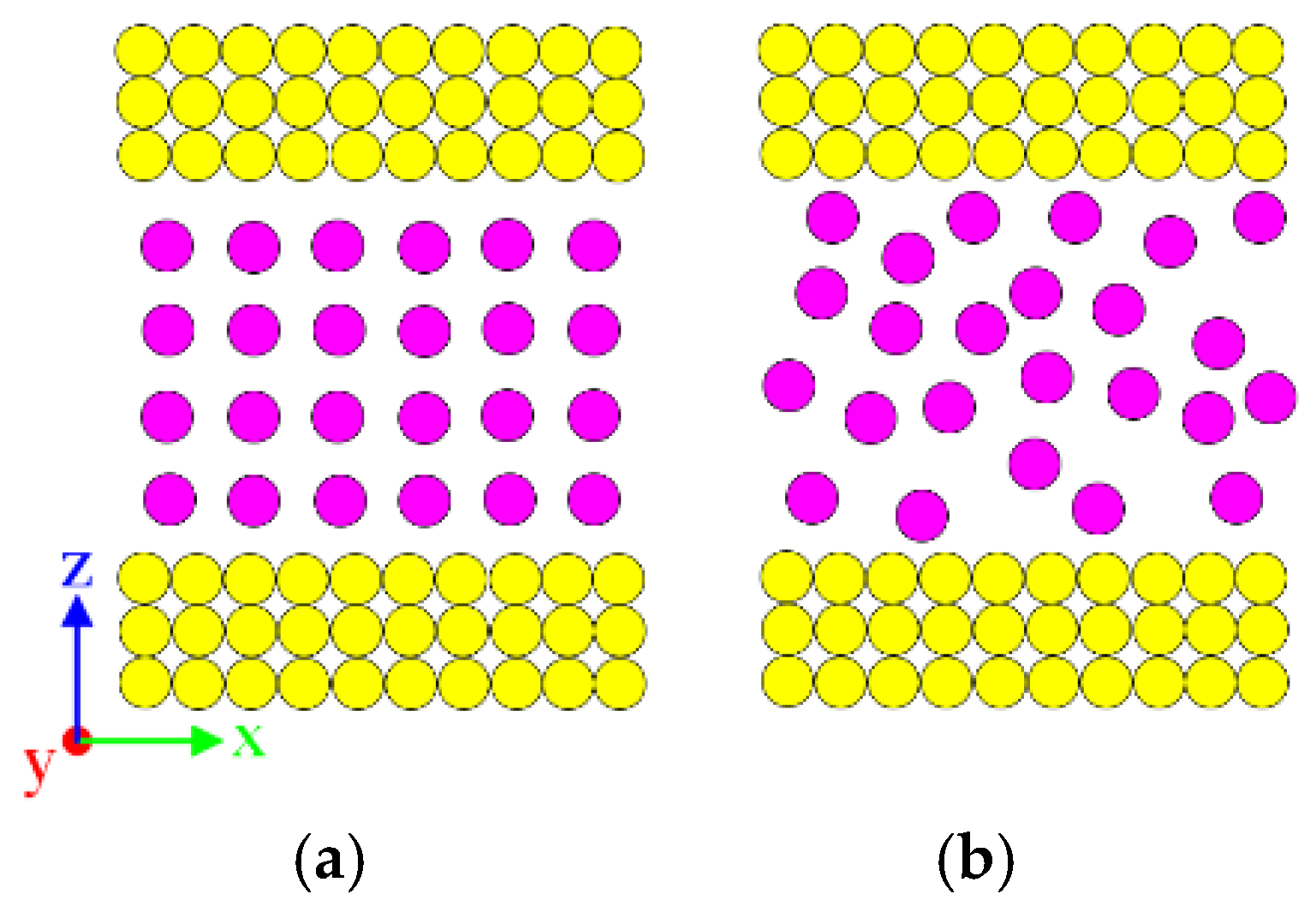
3.3.4. Effect of Surface Roughness
3.3.5. Effect of Adding Nanoparticles
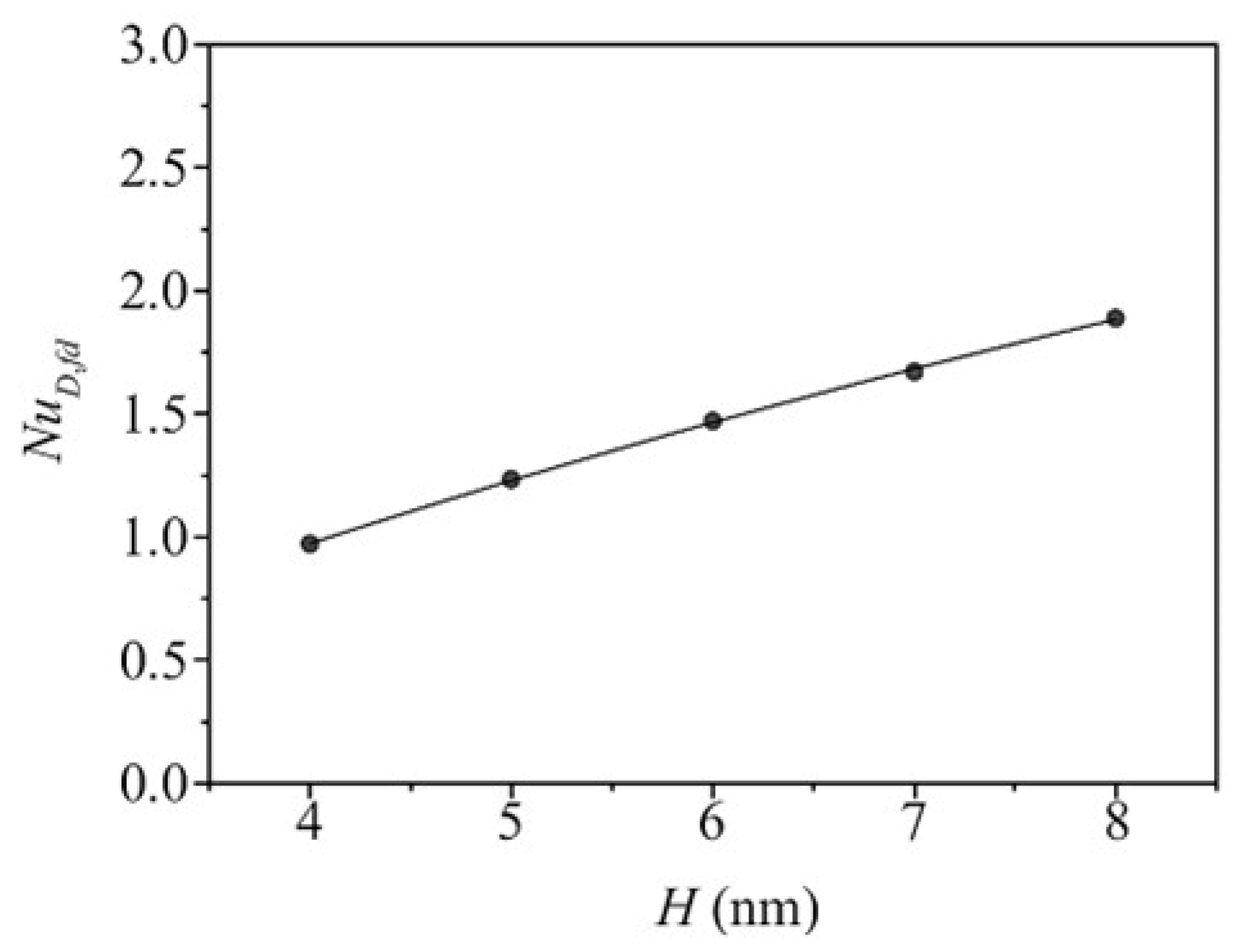
3.3.6. Effect of Channel Height
3.3.7. Effect of Fluid Velocity
3.3.8. Effect of Nanochannel Wall Temperature
4. Conclusions: Challenges and Future Directions
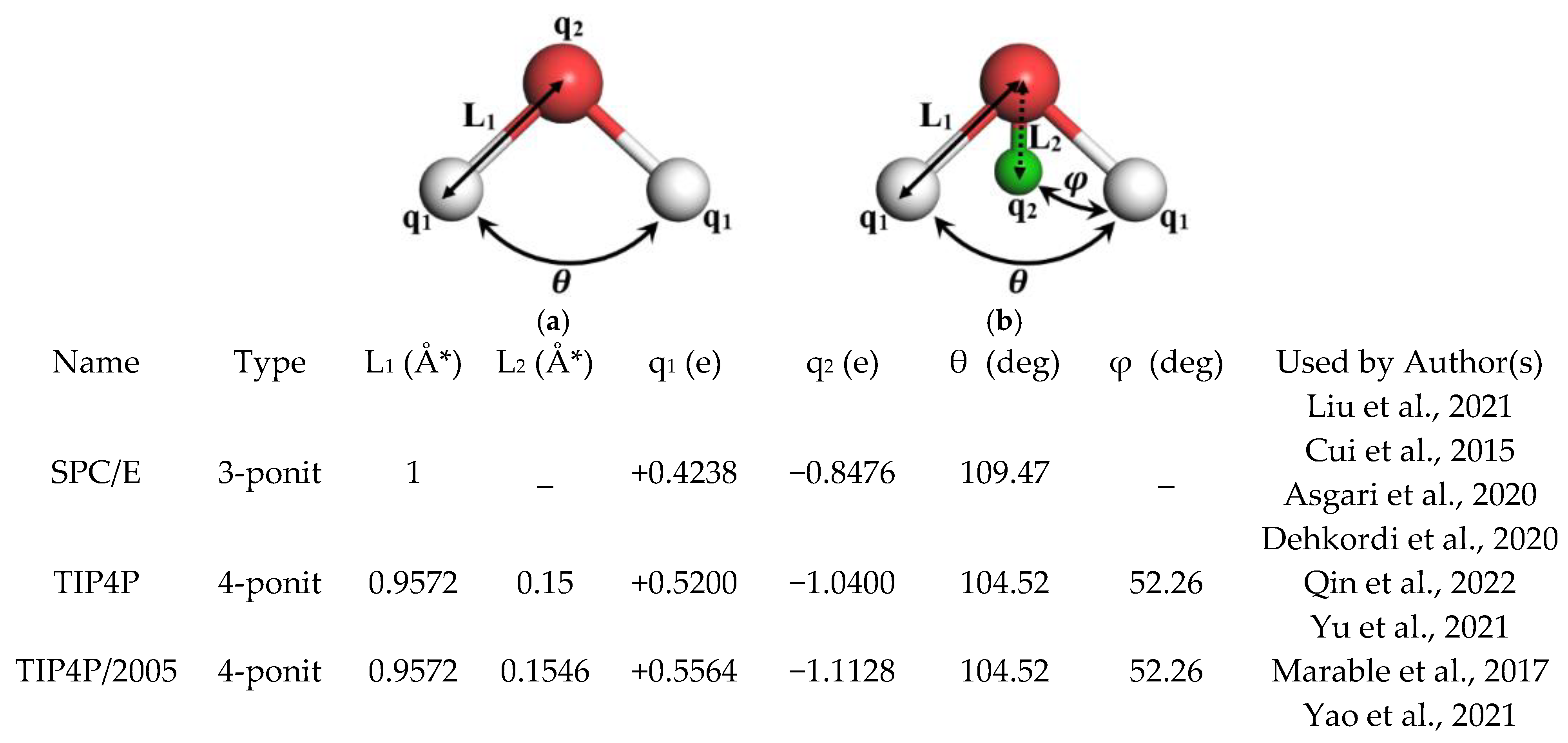
- While various water models such as SPC/E, TIP4P, and TIP4P/2005 are typically utilized to simulate the fluid domain, five-site water models like TIP5P-Ew are anticipated to provide more accurate representations for future research.
- Although Cu and Pt are frequently used as nanochannel wall materials mainly due to being practically applicable and simple, silicon, as a more commonly used material in practical applications, should receive greater attention.
- Generally, researchers apply the LJ 12–6 and EAM potentials to represent the interactions between solid-solid nanochannel wall atoms. On one hand, the common length and energy parameters in the LJ 12–6 potential for metallic solid wall materials cannot account for the strong bonding and thermal motion of metallic solid atoms. On the other hand, using the EAM potentials may require significant computational resources. Meanwhile, Heinz et al. [65] introduced parameters for the LJ 12–6 potentials, which would be effectively employable and an excellent alternative.
- In MD simulations of FCHT-NC using the Poiseuille flow model, two distinct arrangements for the forcing zone and temperature reset zone order, referred to as the “thermal pump method”, have been implemented: the Markvoort method and the Ge method. Although the Ge method has become the most common and demonstrates effective control of the inlet fluid temperature, it results in unrealistic axial heat conduction. Consequently, improvements to the Ge thermal pump method are essential for future studies.
- More studies are required to gain a comprehensive understanding of the complex relationship between the flowing fluid velocity and FCHT, particularly on nanostructured surfaces.
- Using more complex morphologies (such as random surface roughness [116,117,118]) instead of these simple morphologies would be more realistic. Furthermore, since researchers have recently focused on using nanoporous materials to improve microchannel performance (refer to Refs. [119,120], for example), it would be intriguing to investigate their impact on the FCHT-NC system’s performance.
- Recent studies indicate that adding nanoparticles into base fluids significantly improves the heat transfer efficiency. Future research should be carried out to explore commonly used nanoparticles like SiO2, CuO, TiO2, and Al2O3 for an optimal heat transfer performance.
- Some research shows that raising the channel height can improve FCHT performance by lowering the Kapitza resistance. Others, however, show no significant effect or even negative impact. Therefore, conducting more research is necessary to comprehend the connection between the channel height and the FCHT efficiency.
- The fluid velocity in nanochannels can be regulated by external forces, with MD simulations showing speeds of ~3 to ~300 m/s. While some studies suggest that higher velocities do not enhance the FCHT-NC performance and may even hinder it, experimental evidence does not support these claims. Therefore, the relationship between fluid velocity and the FCHT efficiency in nanochannels remains uncertain and requires more study.
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, X.; Ji, Z.; Wang, J.; Lv, X. Research progress on structural optimization design of microchannel heat sinks applied to electronic devices. Appl. Therm. Eng. 2023, 235, 121294. [Google Scholar] [CrossRef]
- Jana, K.K.; Srivastava, A.; Parkash, O.; Avasthi, D.K.; Rana, D.; Shahi, V.K.; Maiti, P. Nanoclay and swift heavy ions induced piezoelectric and conducting nanochannel based polymeric membrane for fuel cell. J. Power Sources 2016, 301, 338–347. [Google Scholar] [CrossRef]
- Bigham, A.; Hassanzadeh-Tabrizi, S.A.; Rafienia, M.; Salehi, H. Ordered mesoporous magnesium silicate with uniform nanochannels as a drug delivery system: The effect of calcination temperature on drug delivery rate. Ceram. Int. 2016, 42, 17185–17191. [Google Scholar] [CrossRef]
- Akbari, O.A.; Saghafian, M.; Shirani, E. Investigating the effect of obstacle presence on argon fluid flow characteristics in rough nanochannels using molecular dynamics method. J. Mol. Liq. 2023, 386, 122462. [Google Scholar] [CrossRef]
- Atofarati, E.O.; Sharifpur, M.; Meyer, J.P. Pulsating nanofluid-jet impingement cooling and its hydrodynamic effects on heat transfer. Int. J. Therm. Sci. 2024, 198, 108874. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Ghachem, K.; Albalawi, H.; Alshammari, B.M.; Labidi, T.; Kolsi, L. Effects of using magnetic field and double jet impingement for cooling of a hot oscillating object. Case Stud. Therm. Eng. 2024, 60, 104791. [Google Scholar] [CrossRef]
- Forster, M.; Ligrani, P.; Weigand, B.; Poser, R. Experimental and numerical investigation of jet impingement cooling onto a rib roughened concave internal passage for leading edge cooling of a gas turbine blade. Int. J. Heat Mass Transf. 2024, 227, 125572. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Benabdallah, F.; Ghachem, K.; Albalawi, H.; Alshammari, B.M.; Kolsi, L. Effects of using sinusoidal porous object (SPO) and perforated porous object (PPO) on the cooling performance of nano-enhanced multiple slot jet impingement for a conductive panel system. Propuls. Power Res. 2024, 13, 166–177. [Google Scholar] [CrossRef]
- Tian, J.; Li, B.; Wang, J.; Chen, B.; Zhou, Z.; Wang, H. Transient analysis of cryogenic cooling performance for high-power semiconductor lasers using flash-evaporation spray. Int. J. Heat Mass Transf. 2022, 195, 123216. [Google Scholar] [CrossRef]
- Tian, J.; He, C.; Chen, Y.; Wang, Z.; Zuo, Z.; Wang, J.; Chen, B.; Xiong, J. Experimental study on combined heat transfer enhancement due to macro-structured surface and electric field during electrospray cooling. Int. J. Heat Mass Transf. 2024, 220, 125015. [Google Scholar] [CrossRef]
- Qenawy, M.; Wang, J.; Tian, J.; Li, B.; Chen, B. Investigation of unsteady flow behavior of cryogen-spray coupled with cold air jet. Appl. Therm. Eng. 2023, 235, 121406. [Google Scholar] [CrossRef]
- Karimipour, A.; D’Orazio, A.; Shadloo, M.S. The effects of different nano particles of Al2O3 and Ag on the MHD nano fluid flow and heat transfer in a microchannel including slip velocity and temperature jump. Phys. Rev. E 2017, 86, 146–153. [Google Scholar] [CrossRef]
- Okechi, N.F. Stokes slip flow in a rough curved microchannel with transversely corrugated walls. Chin. J. Phys. 2022, 78, 495–510. [Google Scholar] [CrossRef]
- Nagayama, G.; Matsumoto, T.; Fukushima, K.; Tsuruta, T. Scale effect of slip boundary condition at solid-liquid interface. Sci. Rep. 2017, 7, 43125. [Google Scholar] [CrossRef]
- Dey, R.; Das, T.; Chakraborty, S. Frictional and heat transfer characteristics of single-phase microchannel liquid flows. Heat Transf. Eng. 2011, 33, 425–446. [Google Scholar] [CrossRef]
- Roy, P.; Anand, N.K.; Banerjee, D. Liquid slip and heat transfer in rotating rectangular microchannels. Int. J. Heat Mass Transf. 2013, 62, 184–199. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, L.; Zhou, W.; Wei, J.A. Study of convective heat transfer by using the hybrid MD-FVM method. J. Mol. Liq. 2021, 340, 117178. [Google Scholar] [CrossRef]
- Kandlikar, S.G. Boiling and evaporation in microchannels. In Encyclopedia of Microfluidics and Nanofluidics, 1st ed.; Li, D., Ed.; Springer Science & Business Media: New York, NY, USA, 2008; pp. 158–159. [Google Scholar]
- Yao, S.; Wang, J.; Jin, S.; Tan, F.; Chen, S. Atomistic insights into the microscope mechanism of solid–liquid interaction influencing convective heat transfer of nanochannel. J. Mol. Liq. 2023, 371, 121105. [Google Scholar] [CrossRef]
- Thekkethala, J.F.; Sathian, S.P. The effect of graphene layers on interfacial thermal resistance in composite nanochannels with flow. Microfluid. Nanofluid. 2015, 18, 637–648. [Google Scholar] [CrossRef]
- Markvoort, A.J.; Hilbers, P.A.J. Molecular dynamics study of the influence of wall-gas interactions on heat flow in nanochannels. Phys. Rev. 2005, 71, 066702. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.; Wang, J. Effect of rough morphology on the flow and heat transfer in nanochannel. In Proceedings of the International Conference on Applied Energy, Bangkok, Thailand, 1–10 December 2020. [Google Scholar]
- Yao, S.; Wang, J.; Liu, X. The influence of wall properties on convective heat transfer in isothermal nanochannel. J. Mol. Liq. 2021, 324, 115100. [Google Scholar] [CrossRef]
- Yao, S.; Wang, J.; Liu, X. Role of wall-fluid interaction and rough morphology in heat and momentum exchange in nanochannel. Appl. Energy 2021, 298, 117183. [Google Scholar] [CrossRef]
- Yao, S.; Wang, J.; Liu, X. Influence of nanostructure morphology on the heat transfer and flow characteristics in nanochannel. Int. J. Therm. Sci. 2021, 165, 106927. [Google Scholar] [CrossRef]
- Yao, S.; Wang, J.; Liu, X. The impacting mechanism of surface properties on flow and heat transfer features in nanochannel. Int. J. Heat Mass Transf. 2021, 176, 121441. [Google Scholar] [CrossRef]
- Yao, S.; Wang, J.; Jin, S.; Tan, F.; Chen, S. Effect of surface coupling characteristics on the flow and heat transfer of nanochannel based on the orthogonal test. Int. J. Therm. Sci. 2024, 203, 109161. [Google Scholar] [CrossRef]
- Yao, S.; Wang, J.; Liu, X. The Influencing mechanism of surface wettability on convective heat transfer in copper nanochannel. In Proceedings of the International Conference on Applied Energy, Bangkok, Thailand, 29 November–5 December 2021. [Google Scholar]
- Song, Z.; Cui, Z.; Cao, Q.; Lio, Y.; Li, J. Molecular dynamics study of convective heat transfer in ordered rough nanochannels. J. Mol. Liq. 2021, 337, 116052. [Google Scholar] [CrossRef]
- Song, Z.; Cui, Z.; Lio, Y.; Cao, Q. Heat transfer and flow characteristics in nanochannels with complex surface topological morphology. Appl. Therm. Eng. 2022, 201, 117755. [Google Scholar] [CrossRef]
- Song, Z.; Shang, X.; Cui, Z.; Lio, Y.; Cao, Q. Investigation of surface structure-wettability coupling on heat transfer and flow characteristics in nanochannels. Appl. Therm. Eng. 2023, 218, 119362. [Google Scholar] [CrossRef]
- Motlagh, M.B.; Kalteh, M. Molecular dynamics simulation of nanofluid convective heat transfer in a nanochannel: Effect of nanoparticles shape, aggregation and wall roughness. J. Mol. Liq. 2020, 318, 114028. [Google Scholar] [CrossRef]
- Motlagh, M.B.; Kalteh, M. Simulating the convective heat transfer of nanofluid Poiseuille flow in a nanochannel by molecular dynamics method. Int. Commun. Heat Mass Transf. 2020, 111, 104478. [Google Scholar] [CrossRef]
- Motlagh, M.B.; Kalteh, M. Investigating the wall effect on convective heat transfer in a nanochannel by molecular dynamics simulation. Int. J. Therm. Sci. 2020, 156, 106472. [Google Scholar] [CrossRef]
- Assadi, S.; Kalteh, M.; Motlagh, M.B. Investigating convective heat transfer coefficient of nanofluid Couette flow in a nanochannel by molecular dynamics simulation. Mol. Simul. 2022, 48, 702–711. [Google Scholar] [CrossRef]
- Chatterjee, S.; Paras, H.H.; Chakraborty, M.A. Review of nano and microscale heat transfer: An experimental and molecular dynamics perspective. Processes 2023, 11, 2769. [Google Scholar] [CrossRef]
- Ran, Y.; Bertola, V. Achievements and prospects of molecular dynamics simulations in thermofluid sciences. Energies 2024, 17, 888. [Google Scholar] [CrossRef]
- Kim, B.H.; Beskok, A.; Cagin, T. Viscous heating in nanoscale shear driven liquid flows. Microfluid. Nanofluid. 2010, 9, 31–40. [Google Scholar] [CrossRef]
- Bao, L.; Priezjev, N.V.; Hu, H.; Luo, K. Effects of viscous heating and wall-fluid interaction energy on rate-dependent slip behavior of simple fluids. Phys. Rev. E 2017, 96, 033110. [Google Scholar] [CrossRef]
- Dinh, Q.V.; Vo, T.Q.; Kim, B. Viscous heating and temperature profiles of liquid water flows in copper nanochannel. J. Mech. Sci. Technol. 2019, 33, 3257–3263. [Google Scholar] [CrossRef]
- AbdulHussein, W.A.; Abed, A.M.; Mohammad, D.B.; Smaisim, G.F.; Baghaei, S. Investigation of boiling process of different fluids in microchannels and nanochannels in the presence of external electric field and external magnetic field using molecular dynamics simulation. Case Stud. Therm. Eng. 2022, 35, 102105. [Google Scholar] [CrossRef]
- Wang, M.; Sun, H.; Cheng, L. Flow condensation heat transfer characteristics of nanochannels with nanopillars: A molecular dynamics study. Langmuir 2021, 37, 14744–14752. [Google Scholar] [CrossRef]
- Wang, M.; Sun, Q.; Yang, C.; Cheng, L. Molecular dynamics simulation of thermal de-icing on a nanochannel with hot fluids. J. Mol. Liq. 2022, 354, 118859. [Google Scholar] [CrossRef]
- Wang, M.; Sun, H.; Cheng, L. Enhanced heat transfer characteristics of nano heat exchanger with periodic fins: A molecular dynamics study. J. Mol. Liq. 2021, 341, 116908. [Google Scholar] [CrossRef]
- Sun, H.; Li, F.; Wang, M.; Xin, G.; Wang, X. Molecular dynamics study of convective heat transfer mechanism in a nano heat exchanger. RSC Adv. 2020, 10, 23097. [Google Scholar] [CrossRef]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation, 1st ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Pal, S.; Ray, B.C. Molecular Dynamics Simulation of Nanostructured Materials: An Understanding of Mechanical Behavior, 1st ed.; Taylor & Francis Group: Abingdon, UK, 2020. [Google Scholar]
- Sadus, R.J. Molecular Simulation of Fluids: Theory, Algorithms, Object-Orientation, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Gonzalez, I.; Law, D. Effect of single nanoparticle diameter on a nanochannel fluid flow and heat transfer. In Proceedings of the ASME 2022 Fluids Engineering Division Summer Meeting, Toronto, ON, Canada, 3–5 August 2022. [Google Scholar]
- Tang, Y.; Fu, T.; Mao, Y.; Zhang, Y.; Yuan, W. Molecule dynamics simulation of heat transfer between argon flow and parallel copper plates. J. Nanotechnol. Eng. Med. 2014, 5, 034501. [Google Scholar] [CrossRef]
- Guillot, B.A. Reappraisal of what we have learnt during three decades of computer simulations on water. J. Mol. Liq. 2002, 101, 219–260. [Google Scholar] [CrossRef]
- Kargar, S.; Baniamerian, Z.; Moran, J.L. Molecular dynamics calculations of the enthalpy of vaporization for different water models. J. Mol. Liq. 2024, 393, 123455. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Abascal, J.L.F.; Vega, C.A. General purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef]
- Cui, W.; Shen, Z.; Yang, J.; Wu, S. Flow and heat transfer behaviors of water-based nanofluids confined in nanochannel by molecular dynamics simulation. Dig. J. Nanomater. Biostructures 2015, 10, 401–413. [Google Scholar]
- Asgari, A.; Nguyen, Q.; Karimipour, A.; Bach, Q.; Hekmatifar, M.; Sabetvand, R. Develop molecular dynamics method to simulate the flow and thermal domains of H2O/Cu nanofluid in a nanochannel affected by an external electric field. Int. J. Thermophys. 2020, 41, 126. [Google Scholar] [CrossRef]
- Dehkordi, R.B.; Toghraiea, D.; Hashemian, M.; Aghadavoudi, F.; Akbari, M. Molecular dynamics simulation of ferro-nanofluid flow in a microchannel in the presence of external electric field: Effects of Fe3Oe nanoparticles. Int. Commun. Heat Mass Transf. 2020, 116, 104653. [Google Scholar] [CrossRef]
- Qin, Y.; Zhao, J.; Liu, Z.; Wang, C.; Zhang, H. Study on effect of different surface roughness on nanofluid flow in nanochannel by using molecular dynamics simulation. J. Mol. Liq. 2022, 346, 117148. [Google Scholar] [CrossRef]
- Yu, H.; Tao, Y.; Zhao, Y.; Sha, J. The effect of flow velocity on the convection in nanochannel. In Proceedings of the International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale, Xi’an, China, 2–6 August 2021. [Google Scholar]
- Marable, D.C.; Shin, S.; Nobakht, A.Y. Investigation into the microscopic mechanisms influencing convective heat transfer of water flow in graphene nanochannels. Int. J. Heat Mass Transf. 2017, 109, 28–39. [Google Scholar] [CrossRef]
- Kusalik, P.G.; Svishchev, I.M. The spatial structure in liquid water. Science 1994, 265, 1219–1221. [Google Scholar] [CrossRef] [PubMed]
- Mahoney, M.W.; Jorgensen, W.L. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys. 2000, 112, 8910–8922. [Google Scholar] [CrossRef]
- González, M.A.; Abascal, J.L.F. The shear viscosity of rigid water models. J. Chem. Phys. 2010, 132, 096101. [Google Scholar] [CrossRef]
- Vega, C.; Abascal, J.L.F. Simulating water with rigid non-polarizable models: A general perspective. Phys. Chem. Chem. Phys. 2011, 13, 19663–19688. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, J. Transport properties of bulk water at 243–550 K: A comparative molecular dynamics simulation study using SPC/E, TIP4P, and TIP4P/2005 water models. Mol. Phys. 2018, 117, 1926–1933. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, Y. Thermal conductivity, shear viscosity and specific heat of rigid water models. Chem. Phys. Lett. 2012, 542, 37–41. [Google Scholar] [CrossRef]
- Rick, S.W. A reoptimization of the five-site water potential (TIP5P) for use with Ewald sums. J. Chem. Phys. 2004, 120, 6085–6093. [Google Scholar] [CrossRef]
- Luo, K.; Li, W.; Ma, J.; Chang, W.; Huang, G.; Li, C. Silicon microchannels flow boiling enhanced via microporous decorated sidewalls. Int. J. Heat Mass Transf. 2022, 191, 122817. [Google Scholar] [CrossRef]
- Chakraborty, P.; Ma, T.; Cao, L.; Wang, Y. Significantly enhanced convective heat transfer through surface modification in nanochannels. Int. J. Heat Mass Transf. 2019, 136, 702–708. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, B. Molecular Dynamic Simulation: Fundamentals and Applications, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Rosa, P.; Karayiannis, T.G.; Collins, M.W. Single-phase heat transfer in microchannels: The importance of scaling effects. Appl. Therm. Eng. 2009, 29, 3447–3468. [Google Scholar] [CrossRef]
- Alavi, S. Molecular Simulations: Fundamentals and Practice, 1st ed.; Wiley-VCH: Weinheim, Germany, 2020; pp. 79–81. [Google Scholar]
- Ge, S.; Gu, Y.; Chen, M. A molecular dynamics simulation on the convective heat transfer in nanochannels. Mol. Phys. 2014, 113, 703–710. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2001; pp. 34–35. [Google Scholar]
- Li, L.; Liu, Z.; Qi, R. Molecular dynamics simulations in hydrogel research and its applications in energy utilization: A review. Energy Rev. 2024, 3, 100072. [Google Scholar] [CrossRef]
- Gennes, P.G. Wetting: Statics and dynamics. Rev. Mod. Phys. 1985, 57, 827. [Google Scholar] [CrossRef]
- Wang, M.; Sun, H.; Cheng, L. Investigation of convective heat transfer performance in nanochannels with fractal Cantor structures. Int. J. Heat Mass Transf. 2021, 171, 121086. [Google Scholar] [CrossRef]
- Tucker, Q.J.; Ivanov, D.S.; Zhigilei, L.V.; Johnson, R.E.; Bringa, E.M. Molecular dynamics simulation of sputtering from a cylindrical track: EAM versus pair potentials. NIM-B 2005, 228, 163–169. [Google Scholar] [CrossRef]
- Sekerka, R.F. Thermal Physics: Thermodynamics and Statistical Mechanics for Scientists and Engineers, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2015; pp. 273–274. [Google Scholar]
- Sun, H.; Liu, Z.; Xin, G.; Xin, Q.; Zhang, J.; Cao, B.Y.; Wang, X. Thermal and flow characterization in nanochannels with tunable surface wettability: A comprehensive molecular dynamics study. Numer. Heat Transf. Part A Appl. 2020, 78, 231–251. [Google Scholar] [CrossRef]
- Fallahzadeh, R.; Bozzoli, F.; Cattani, L.; Azam, M.W. Effect of cross nanowall surface on the onset time of explosive boiling: A molecular dynamics study. Energies 2024, 17, 1107. [Google Scholar] [CrossRef]
- Daw, M.S.; Foiles, S.M.; Baskes, M.I. The embedded-atom method: A review of theory and applications. Mater. Sci. Rep. 1993, 9, 251–310. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Tian, C.; Meng, X. Numerical experiments on evaporation and explosive boiling of ultra-thin liquid argon film on aluminum nanostructure substrate. Nanoscale Res. Lett. 2015, 10, 158. [Google Scholar] [CrossRef] [PubMed]
- Daw, M.S.; Chandross, M. Simple parameterization of embedded atom method potentials for FCC metals. Acta Mater. 2023, 248, 118771. [Google Scholar] [CrossRef]
- Heinz, H.; Vaia, R.A.; Farmer, B.L.; Naik, R.R. Accurate simulation of surfaces and interfaces of face-centered cubic metals using 12-6 and 9-6 Lennard-Jones potentials. J. Phys. Chem. C 2008, 112, 17281–17290. [Google Scholar] [CrossRef]
- Din, X.D.; Michaelides, E.E. Kinetic theory and molecular dynamics simulations of microscopic flows. Phys. Fluids. 1997, 9, 3915–3925. [Google Scholar] [CrossRef]
- Barrat, J.L.; Bocquet, L. Large slip effect at a nonwetting fluid-solid interface. Phys. Rev. Lett. 1999, 82, 4671. [Google Scholar] [CrossRef]
- Hagler, A.T.; Lifson, S.; Dauber, P. Consistent force field studies of intermolecular forces in hydrogen-bonded crystals. 2. a benchmark for the objective comparison of alternative force fields. J. Am. Chem. Soc. 1979, 101, 5122–5130. [Google Scholar] [CrossRef]
- Hagler, A.T.; Huler, E.; Lifson, S. Energy functions for peptides and proteins. I. Derivation of a consistent force field including the hydrogen bond from amide crystals. J. Am. Chem. Soc. 1974, 96, 5319–5327. [Google Scholar] [CrossRef]
- Waldman, M.; Hagler, A.T. New combining rules for rare gas van der Waals parameters. J. Comput. Chem. 1993, 14, 1077–1084. [Google Scholar] [CrossRef]
- Delhommelle, J.; Millie, P. Inadequacy of the Lorentz-Berthelot combining rules for accurate predictions of equilibrium properties by molecular simulation. Mol. Phys. 2001, 99, 619–625. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Jiang, H.; Patel, A.J. Recent advances in estimating contact angles using molecular simulations and enhanced sampling methods. Curr. Opin. Chem. Eng. 2019, 23, 130–137. [Google Scholar] [CrossRef]
- Debye, P.; Erich, H. The theory of electrolytes. I. Freezing point depression and related phenomena. Phys. Z. 1923, 24, 185–206. [Google Scholar]
- Nichita, D.V.; Petitfrere, M. Phase equilibrium calculations with quasi-Newton methods. Fluid Phase Equilib. 2015, 406, 194–208. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bur. Stand. 1952, 49, 2379. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Chen, W.-H.; Wu, C.-H.; Cheng, H.-C. Modified Nosé-Hoover thermostat for solid state for constant temperature molecular dynamics simulation. J. Comput. Phys. 2011, 230, 6354–6366. [Google Scholar] [CrossRef]
- Rowlinson, J.S. The maxwell–Boltzmann distribution. Mol. Phys. 2005, 103, 2821–2828. [Google Scholar] [CrossRef]
- Hu, C.; Bai, M.; Lv, J.; Li, X. An investigation on the flow and heat transfer characteristics of nanofluid by nonequilibrium molecular dynamics simulations. Numer. Heat Transf. Part B 2016, 70, 152–163. [Google Scholar] [CrossRef]
- Ashurst, W.T.; Hoover, W.G. Dense-fluid shear viscosity via nonequilibrium molecular dynamics. Phys. Rev. A 1975, 11, 658. [Google Scholar] [CrossRef]
- Khare, R.; de Pablo, J.; Yethiraj, A. Molecular simulation and continuum mechanics study of simple fluids in non-isothermal planar couette flows. J. Chem. Phys. 1997, 107, 2589–2596. [Google Scholar] [CrossRef]
- Zheng, B.; Huang, Z.; Zheng, Z.; Chen, Y.; Yan, J.; Cen, K.; Yang, H.; Ostrikov, K. Accelerated ion transport and charging dynamics in more ionophobic sub-nanometer channels. Energy Storage Mater. 2023, 59, 102797. [Google Scholar] [CrossRef]
- Fallahzadeh, R.; Bozzoli, F.; Cattani, L. Effect of closed-loop nanochannels on the onset of explosive boiling: A molecular dynamics simulation study. J. Phys. Conf. Ser. 2024, 2685, 012013. [Google Scholar] [CrossRef]
- Hu, H.; Lu, Y.; Guo, L.; Chen, X.; Wang, Q.; Wang, J.; Li, Q. Effects of system pressure on nucleate boiling: Insights from molecular dynamics. J. Mol. Liq. 2024, 402, 124745. [Google Scholar] [CrossRef]
- Barisik, M.; Beskok, A. Boundary treatment effects on molecular dynamics simulations of interface thermal resistance. J. Comput. Phys. 2012, 231, 7881–7892. [Google Scholar] [CrossRef]
- Qin, S.; Chen, Z.; Wang, Q.; Li, W.; Xing, H. Effect of surface structure on fluid flow and heat transfer in cold and hot wall nanochannels. Int. J. Heat Mass Transf. 2024, 151, 107257. [Google Scholar] [CrossRef]
- Schneider, T.; Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 1978, 17, 1302. [Google Scholar] [CrossRef]
- Berendsen, H.J.; Postma, J.V.; Van Gunsteren, W.F.; DiNola, A.R.H.J.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Thomas, T.M.; Vinod, N. Convective heat transfer between liquid argon flows and heated carbon nanotube arrays using molecular dynamics. J. Appl. Fluid Mech. 2019, 12, 971–980. [Google Scholar] [CrossRef]
- Gu, Y.W.; Ge, S.; Chen, M. A molecular dynamics simulation of nanoscale convective heat transfer with the effect of axial heat conduction. Mol. Phys. 2016, 114, 1922–1930. [Google Scholar] [CrossRef]
- Yu, F.; Wang, T.; Zhang, C. Effect of axial conduction on heat transfer in a rectangular microchannel with local heat flux. J. Therm. Sci. Technol. 2018, 13, JTST0013. [Google Scholar] [CrossRef]
- Cole, K.D.; Çetin, B. The effect of axial conduction on heat transfer in a liquid microchannel flow. Int. J. Heat Mass Transf. 2011, 54, 2542–2549. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y. Studying the influence of surface roughness with different shapes and quantities on convective heat transfer of fluid within nanochannels using molecular dynamics simulations. J. Mol. Model. 2024, 30, 42. [Google Scholar] [CrossRef]
- Stojanovic, N.; Maithripala, D.H.S.; Berg, J.M.; Holtz, M.J.P.R. Thermal conductivity in metallic nanostructures at high temperature: Electrons, phonons, and the Wiedemann-Franz law. Phys. Rev. B 2010, 82, 075418. [Google Scholar] [CrossRef]
- Heino, P.; Ristolainen, E. Thermal conduction at the nanoscale in some metals by MD. Microelectron. J. 2003, 34, 773–777. [Google Scholar] [CrossRef]
- Stamper, C.; Cortie, D.; Yue, Z.; Wang, X.; Yu, D. Experimental confirmation of the universal law for the vibrational density of states of liquids. J. Phys. Chem. Lett. 2022, 13, 3105–3111. [Google Scholar] [CrossRef] [PubMed]
- Peethan, A.; Unnikrishnan, V.K.; Chidangil, S.; George, S.D. Laser-Assisted tailoring of surface wettability-fundamentals and applications: A critical review. Prog. Adhes. Adhesives. 2020, 5, 331–365. [Google Scholar] [CrossRef]
- Zhang, C.B.; Xu, Z.L.; Chen, Y.P. Molecular dynamics simulation on fluid flow and heat transfer in rough nanochannels. Acta Phys. Sin. 2014, 63, 214706. [Google Scholar] [CrossRef]
- Zhang, T.; Cui, T. Enhanced wetting properties of silicon mesh microchannels coated with SiO2/SnO2 nanoparticles through layer-by-layer self-assembly. Sens. Actuators B Chem. 2011, 157, 697–702. [Google Scholar] [CrossRef]
- Wu, H.Y.; Cheng, P. An experimental study of convective heat transfer in silicon microchannels with different surface conditions. Int. J. Heat Mass Transf. 2003, 46, 2547–2556. [Google Scholar] [CrossRef]
- Toghraie, D.; Mokhtari, M.; Afrand, M. Molecular dynamic simulation of Copper and Platinum nanoparticles Poiseuille flow in a nanochannels. Physica. E 2016, 84, 152–161. [Google Scholar] [CrossRef]
- Fu, T.; Wang, Q. Effect of nanostructure on heat transfer between fluid and copper plate: A molecular dynamics simulation study. Mol. Simul. 2018, 44, 697–702. [Google Scholar] [CrossRef]
- Liu, H.; Deng, W.; Ding, P.; Zhao, J. Investigation of the effects of surface wettability and surface roughness on nanoscale boiling process using molecular dynamics simulation. Nucl. Eng. Des. 2021, 382, 111400. [Google Scholar] [CrossRef]
- Liu, H.; Qin, X.; Ahmad, S.; Tong, Q.; Zhao, J. Molecular dynamics study about the effects of random surface roughness on nanoscale boiling process. Int. J. Heat Mass Transf. 2019, 145, 118799. [Google Scholar] [CrossRef]
- Fallahzadeh, R.; Bozzoli, F.; Cattani, L.; Pagliarini, L.; Naeimabadi, N.; Azam, M.W. A molecular dynamics perspective on the impacts of random rough surface, film thickness, and substrate temperature on the adsorbed film’s liquid-vapor phase transition regime. Sci 2024, 6, 33. [Google Scholar] [CrossRef]
- Piekiel, N.W.; Morris, C.J.; Currano, L.J.; Lunking, D.M.; Isaacson, B.; Churaman, W.A. Enhancement of on-chip combustion via nanoporous silicon microchannels. Combust. Flame 2014, 161, 1417–1424. [Google Scholar] [CrossRef]
- Morshed, A.M.; Rezwan, A.A.; Khan, J.A. Two-phase convective flow in microchannel with nanoporous coating. Procedia Eng. 2014, 90, 588–598. [Google Scholar] [CrossRef]
- Ahmad, S.; Deng, W.; Liu, H.; Khan, S.A.; Chen, J.; Zhao, J. Molecular dynamics simulations of nanoscale boiling on mesh-covered surfaces. Appl. Therm. Eng. 2021, 195, 117183. [Google Scholar] [CrossRef]
- Ahmad, S.; Khan, S.A.; Ali, H.M.; Huang, X.; Zhao, J. Molecular dynamics study of nanoscale boiling on double layered porous meshed surfaces with gradient porosity. Appl. Nanosci. 2022, 12, 2997–3006. [Google Scholar] [CrossRef]
- Guan, S.Y.; Zhang, Z.H.; Wu, R.; Gu, X.K.; Zhao, C.Y. Boiling on nano-porous structures: Theoretical analysis and molecular dynamics simulations. Int. J. Heat Mass Transf. 2022, 191, 122848. [Google Scholar] [CrossRef]
- Islam, M.A.; Rony, M.D.; Hasan, M.N. Thin film liquid-vapor phase change phenomena over nano-porous substrates: A molecular dynamics perspective. Heliyon 2023, 9, e15714. [Google Scholar] [CrossRef]
- Gürdal, M.; Arslan, K.; Gedik, E.; Minea, A.A. Effects of using nanofluid, applying a magnetic field, and placing turbulators in channels on the convective heat transfer: A comprehensive review. Renew. Sustain. Energy Rev. 2022, 162, 112453. [Google Scholar] [CrossRef]
- Wen, D.; Ding, Y. Experimental investigation into convective heat transfer of nanofluids at the entrance region under laminar flow conditions. Int. J. Heat Mass Transf. 2004, 47, 5181–5188. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Z.G.; Grulke, E.A.; Anderson, W.B.; Wu, G. Heat transfer properties of nanoparticle-in-fluid dispersions (nanofluids) in laminar flow. Int. J. Heat Mass Transf. 2005, 48, 1107–1116. [Google Scholar] [CrossRef]
- Sun, H.; Wang, M. Atomistic insights into heat transfer and flow behaviors of nanofluids in nanochannels. J. Mol. Liq. 2022, 345, 117872. [Google Scholar] [CrossRef]
- Hashemi, S.M.H.; Fazeli, S.A.; Zirakzadeh, H.; Ashjaee, M. Study of heat transfer enhancement in a nanofluid-cooled miniature heat sink. Int. Commun. Heat Mass Transf. 2012, 39, 877–884. [Google Scholar] [CrossRef]
- Sakanova, A.; Keian, C.C.; Zhao, J. Performance improvements of microchannel heat sink using wavy channel and nanofluids. Int. J. Heat Mass Transf. 2015, 89, 59–74. [Google Scholar] [CrossRef]
- Rahimi-Gorji, M.; Pourmehran, O.; Hatami, M.; Ganji, D.D. Statistical optimization of microchannel heat sink (MCHS) geometry cooled by different nanofluids using RSM analysis. Eur. Phys. J. Plus. 2015, 130, 22. [Google Scholar] [CrossRef]
- Shahrestani, M.I.; Maleki, A.; Shadloo, M.S.; Tlili, I. Numerical investigation of forced convective heat transfer and performance evaluation criterion of Al2O3/water nanofluid flow inside an axisymmetric microchannel. Symmetry 2020, 12, 120. [Google Scholar] [CrossRef]
- Lin, X.; Mo, S.; Jia, L.; Yang, Z.; Chen, Y.; Cheng, Z. Experimental study and Taguchi analysis on LED cooling by thermoelectric cooler integrated with microchannel heat sink. Appl. Energy 2019, 242, 232–238. [Google Scholar] [CrossRef]




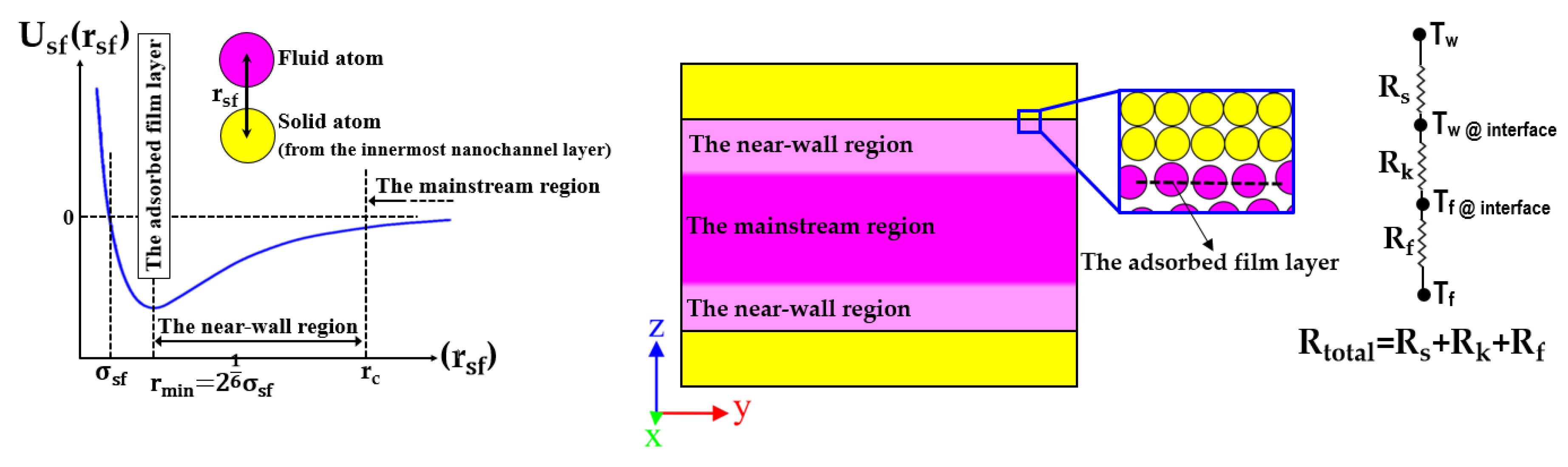




| Atom Pair | Reference | ||
|---|---|---|---|
| Cu-Cu | 2.340 Å | 0.4096 eV * | [31] |
| Pt-Pt | 2.475 Å | 0.521 eV * | [78] |
| Atom Pair | Water Model | Reference | ||
|---|---|---|---|---|
| Ar-Ar | - | 3.405 Å | 0.01043 eV | [27] |
| O-O | SPC/E | 3.166 Å | 0.650 kJ/mol | [62] |
| TIP4P | 3.15365 Å | 0.6480 kJ/mol | [63] | |
| TIP4P/2005 | 3.1589 Å | 0.7749 kJ/mol | [55] |
| Nature of the Surface | Contact Angle (Degree) |
|---|---|
| Super-hydrophilic | |
| Hydrophilic | |
| Neutral | |
| Hydrophobic | |
| Super-hydrophobic |
| Author(s)/Year | Fluid/Wall Materials | Nature of the Studied Surfaces |
|---|---|---|
| Markvoort et al. [21]/2005 | CLJ/CLJ | Super-hydrophilic, Hydrophobic |
| Ge et al. [74]/2014 | Ar/CLJ | Super-hydrophilic, Neutral |
| Cheng-Bin et al. [120]/2014 | CLJ/CLJ | Super-hydrophilic, Neutral, Hydrophobic |
| Gu et al. [112]/2016 | Ar/Pt | Super-hydrophilic, Hydrophilic, Neutral |
| Marable et al. [71]/2017 | water/graphene | Super-hydrophilic, Hydrophilic, Neutral, Hydrophobic |
| Yao and Wang [22]/2020 | Ar/Pt | Super-hydrophilic, Hydrophobic |
| Sun et al. [81]/2020 | Ar/Cu | Super-hydrophilic, Hydrophilic, Hydrophobic |
| Yao et al. [23]/2021 | Ar/CLJ | Super-hydrophilic, Neutral |
| Yao et al. [24]/2021 | Ar/Pt | Super-hydrophilic, Hydrophobic |
| Wang et al. [78]/2021 | Ar/Pt | Super-hydrophilic, Hydrophilic |
| Yao et al. [25]/2021 | Ar/Pt | Super-hydrophilic, Hydrophobic |
| Yao et al. [26]/2021 | Ar/Pt | Super-hydrophilic, Hydrophobic |
| Yao et al. [28]/2021 | water/Cu | Hydrophilic, Hydrophobic |
| Song et al. [31]/2023 | Ar/Cu | Super-hydrophilic, Hydrophilic, Hydrophobic |
| Yao et al. [19]/2023 | Ar/Pt | Super-hydrophilic, Hydrophilic, Neutral, Hydrophobic |
| Yao et al. [27]/2024 | Ar/Pt | Super-hydrophilic, Hydrophilic, Neutral, Hydrophobic |
| Author(s)/Year | Fluid/Wall Materials | Coating Material |
|---|---|---|
| Thekkethala and Sathian [20]/2015 | Ar/Cu | graphene |
| Chakraborty et al. [70]/2019 | Ar/CLJ | CLJ |
| Yao et al. [23]/2021 | Ar/CLJ | CLJ |
| Yao et al. [27]/2024 | Ar/CLJ | CLJ |
| Author(s)/Year | Wall Material | Surface Roughness Morphology |
|---|---|---|
| Cheng-Bin et al. [120]/2014 | CLJ | Uniform rectangle nanostructure |
| Toghraie et al. [123]/2016 | Pt | Uniform rectangle nanostructure |
| Fu and Wang [124]/2018 | Cu | Uniform rectangle nanostructure |
| Chakraborty et al. [70]/2019 | CLJ | Uniform rectangle nanostructure Non-uniform rectangle nanostructure |
| Motlagh and Kalteh [32]/2020 | Cu | Uniform rectangle nanostructure |
| Motlagh and Kalteh [34]/2020 | Cu | Uniform rectangle nanostructure |
| Yao and Wang [22]/2020 | Pt | Uniform rectangle nanostructure |
| Asgari et al. [57]/2020 | Cu | Uniform hemispherical nanostructure |
| Song et al. [29]/2021 | Cu | Simple periodic sinusoidal nanostructure |
| Yao et al. [24]/2021 | Pt | Uniform rectangle nanostructure |
| Yao et al. [25]/2021 | Pt | Uniform rectangle nanostructure |
| Wang et al. [78]/2021 | Pt | Non-uniform rectangle nanostructure |
| Yao et al. [26]/2021 | Pt | Uniform rectangle nanostructure |
| Song et al. [29]/2022 | Cu | Simple periodic sinusoidal nanostructure Subdivided periodic sinusoidal nanostructure |
| Song et al. [31]/2023 | Cu | Simple periodic sinusoidal nanostructure Subdivided periodic sinusoidal nanostructure |
| Qin et al. [108]/2024 | Pt | Uniform rectangle nanostructure Uniform triangular nanostructure |
| Chen and Li [115]/2024 | Cu | Uniform rectangle nanostructure Uniform triangular nanostructure Uniform hemispherical nanostructure |
| Yao et al. [27]/2024 | Pt | Uniform rectangle nanostructure |
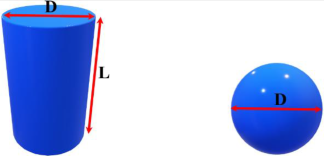 | |||||
| Cylindrical nanoparticle | Spherical nanoparticle | ||||
| Author(s)/Year | Base Fluid/Wall Materials | Nanoparticles | |||
| Material | Shape | Dimensions (Å) | Number of Nanoparticles | ||
| Cui et al. [56]/2015 | water/Cu | Cu | sphere | D = 40 | 1 |
| Hu et al. [102]/2016 | Ar/Cu | Cu | sphere | D = 20, 24 and 30 | 1 and 3 |
| Toghraie et al. [123]/2016 | Ar/Pt | Cu and Pt | sphere | D 60 | 2, 3 and 4 |
| Motlagh and Kalteh [33]/2020 | Ar/Cu | Cu | sphere | D = 8, 10 and 12.6 | 1, 2, 3 and 4 |
| Motlagh and Kalteh [32]/2020 | Ar/Cu | Cu | cylinder | L = 9.5 and D = 6 | 4 |
| Dehkordi et al. [58]/2020 | /Cu | Fe3O4 | sphere | D = 250, 500 and 700 | 1, 2 and 3 |
| Assadi et al. [35]/2020 | Ar/Cu | Cu | sphere | D = 12.64, 15 and 16 | 3, 4 and 5 |
| Gonzalez and Law [49]/2022 | Ar/Cu | Cu | sphere | D = 8, 10, 15, 17.5 and 20 | 1 |
| Sun and Wang [137]/2022 | Ar/Cu | Cu | sphere | D 7 | 40 and 80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fallahzadeh, R.; Bozzoli, F.; Cattani, L.; Naeimabadi, N. A Comprehensive Review on Molecular Dynamics Simulations of Forced Convective Heat Transfer in Nanochannels. Energies 2024, 17, 4352. https://doi.org/10.3390/en17174352
Fallahzadeh R, Bozzoli F, Cattani L, Naeimabadi N. A Comprehensive Review on Molecular Dynamics Simulations of Forced Convective Heat Transfer in Nanochannels. Energies. 2024; 17(17):4352. https://doi.org/10.3390/en17174352
Chicago/Turabian StyleFallahzadeh, Rasoul, Fabio Bozzoli, Luca Cattani, and Niloofar Naeimabadi. 2024. "A Comprehensive Review on Molecular Dynamics Simulations of Forced Convective Heat Transfer in Nanochannels" Energies 17, no. 17: 4352. https://doi.org/10.3390/en17174352
APA StyleFallahzadeh, R., Bozzoli, F., Cattani, L., & Naeimabadi, N. (2024). A Comprehensive Review on Molecular Dynamics Simulations of Forced Convective Heat Transfer in Nanochannels. Energies, 17(17), 4352. https://doi.org/10.3390/en17174352







