A Review of Flow Field and Heat Transfer Characteristics of Jet Impingement from Special-Shaped Holes
Abstract
1. Introduction
2. Overview of Jet Impingement Cooling from Special-Shaped Holes
2.1. Comparison of Special-Shaped and Circular Jet
2.2. Performance Parameters of Jet Impingement Cooling from Special-Shaped Holes
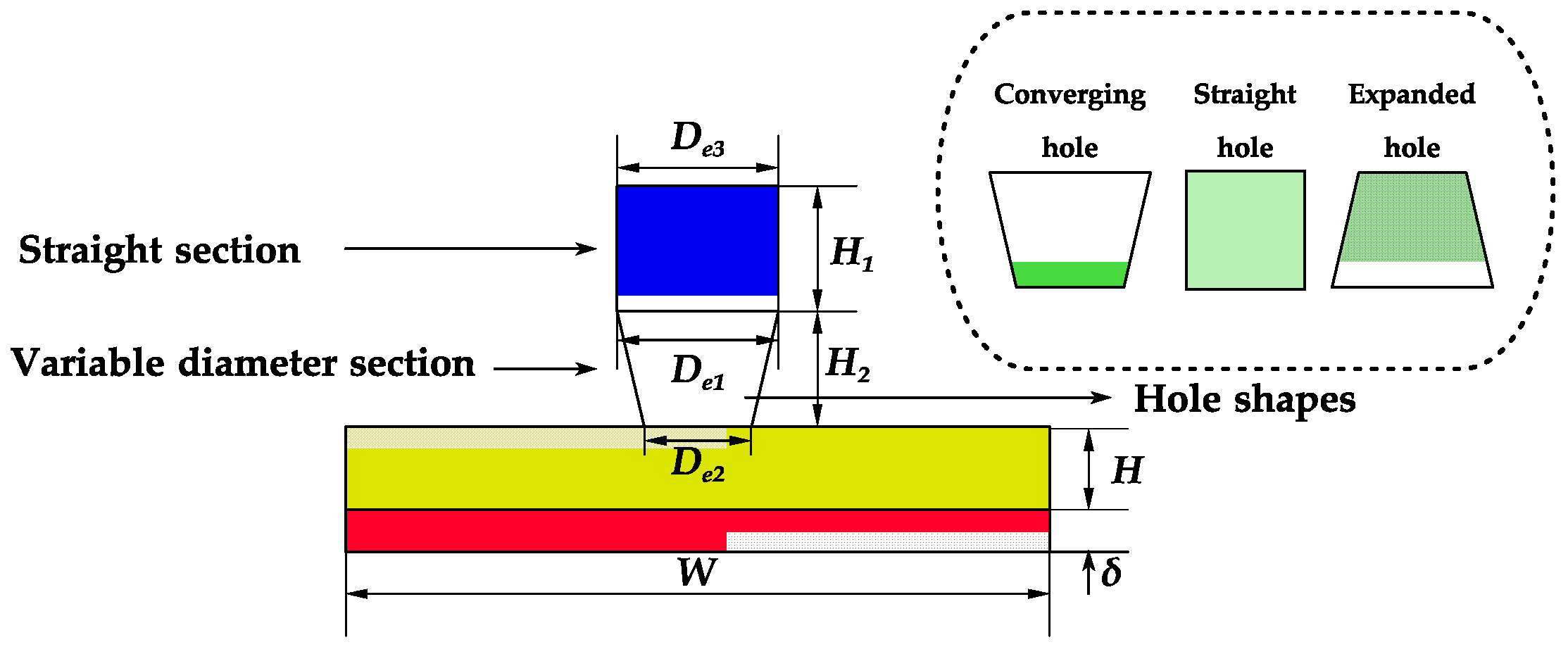
3. Variable-Diameter Holes
4. Irregularly Geometrical Holes
4.1. Chevron Nozzle
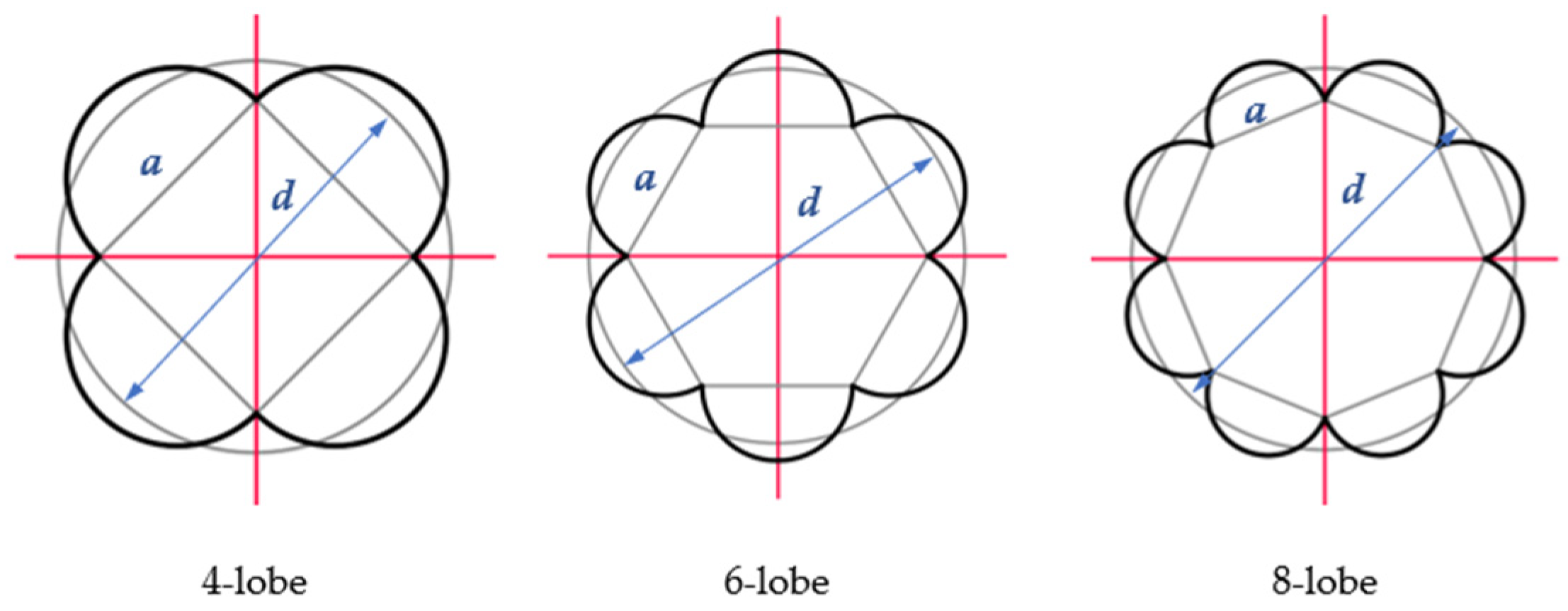
4.2. Lobed Nozzle
4.3. Cross-Shaped Nozzle
4.4. Racetrack-Shaped Nozzle
5. Swirl Nozzles
5.1. Inserting Twisted Tape
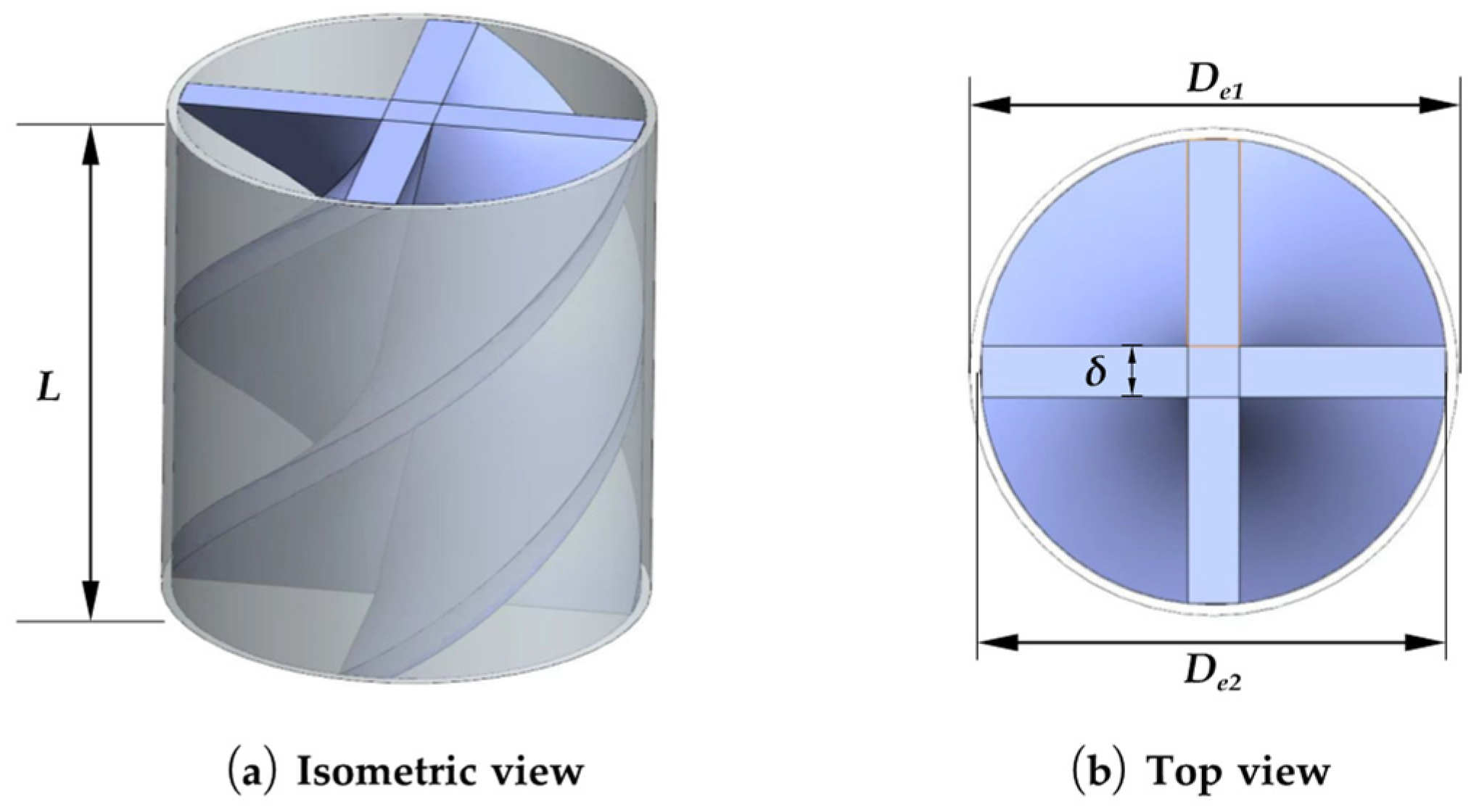
5.2. Installing a Spiral Rod
5.3. Inserting Guide Vane
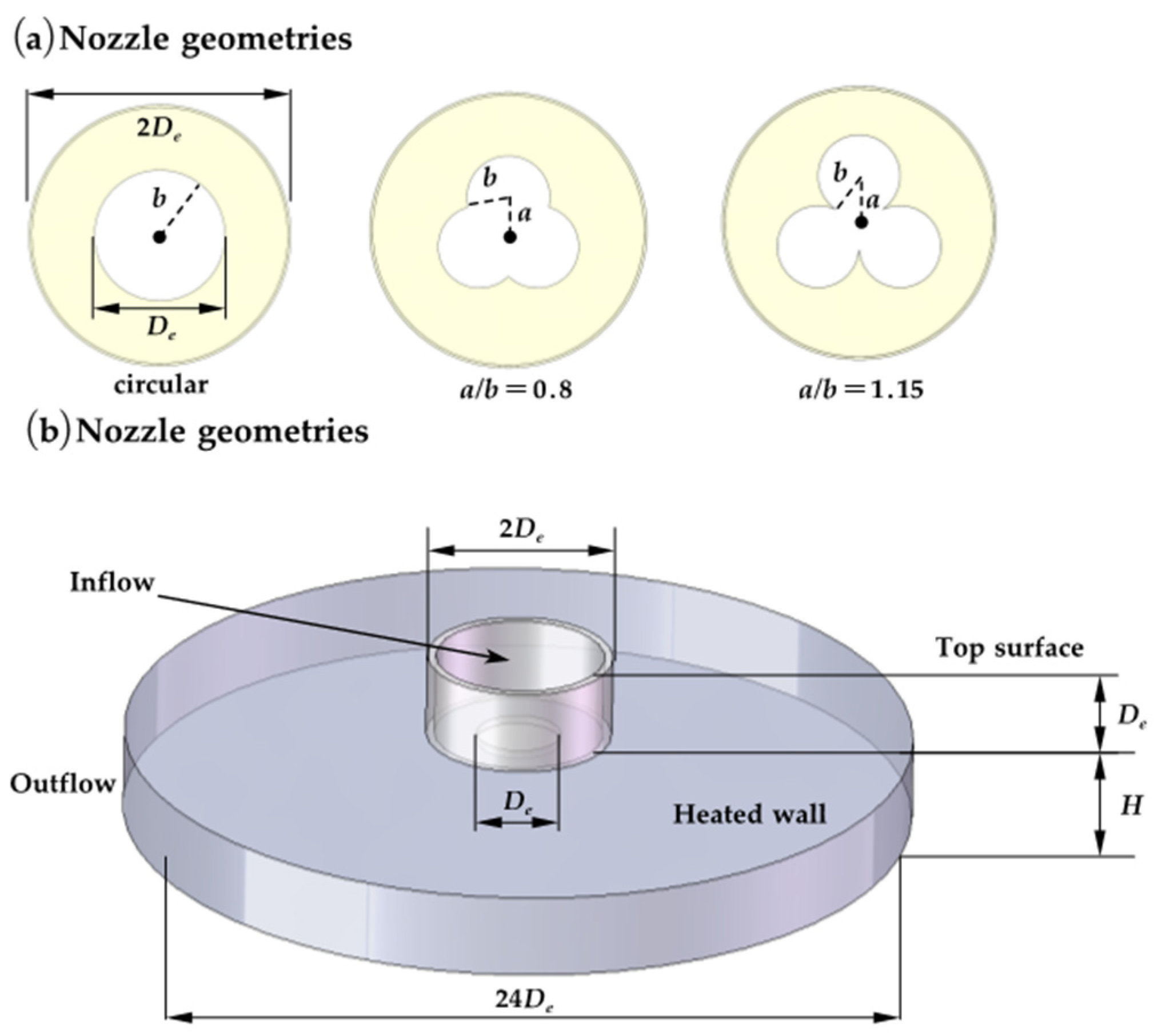
6. Special-Shaped Hole Arrays
6.1. Impact of Nozzle Geometry
6.2. Impact of Array Method
7. Conclusions and Outlook
- (1)
- The variable diameter nozzle is a relatively simple item to produce, which has resulted in it being used more widely than other special-shaped nozzles. Among these, the conical nozzle is the most prevalent type of variable-diameter nozzle, and the cone angle represents the primary determinant of its performance. The current research indicates that a 20° cone angle has the most effective cooling effect; however, it is not yet clear whether this is the optimal angle. The main method used to optimise the nozzle structure is the agent model combined with an optimisation algorithm.
- (2)
- The implementation of nozzles with specially shaped jet holes has been demonstrated to markedly enhance the heat transfer characteristics in comparison to those of circular jets, particularly at smaller distances between the nozzle and the plate. The correlation between different geometric parameters and nozzle performance has been less well studied than the optimisation of nozzle performance itself, despite the latter being a well-researched topic. Furthermore, there is a paucity of research examining the parameters that characterise flow properties, such as pressure drop.
- (3)
- The main special-shaped nozzles for generating rotating jets have been shown to provide a significant improvement in the uniformity of heat transfer distribution, particularly in terms of the local Nusselt number distribution in the radial direction, in comparison to the direct current jet. In the case of nozzles incorporating Nusselt elements, the number of twisted bands and the twist ratio represent the primary parameters influencing their performance. In the case of nozzles embedded with helical rods and guide vanes, the current studies have concentrated on examining the impact of the swirl angle and lobed nozzle angle. However, this research has not yet fully addressed the subject. The complexity of its structure has resulted in a relatively low current usage of optimisation algorithms.
- (4)
- Currently, there is a paucity of studies on special-shaped hole arrays, with the majority of research focusing on the impact of modifying jet hole geometry. In comparison to single jets, the impact of alterations in the jet-to-plate distance is relatively minimal, whereas there is a pronounced correlation between the jet spacing and the resulting outcomes. In contrast to circular jets, the orientation of the main axis of the special-shaped jet holes represents a significant factor influencing the efficacy of impingement cooling. In contrast, SSHs are predominantly arranged in square and staggered arrays, with a paucity of research on alternative array methods.
- (1)
- The combination of different types of nozzles, such as conical-lobed nozzles or embedded twisted belt-chevron nozzles. However, there is currently insufficient literature to prove the feasibility of this approach.
- (2)
- The optimal geometrical parameters of the various special-shaped nozzles have yet to be determined, necessitating a structure-integrated optimisation approach. The performance of the optimised results must then be verified by experimental and numerical methods.
- (3)
- The majority of specialised cooling holes are currently employed in the aerospace industry. However, with the growing demand for enhanced cooling capabilities in electronic devices, the necessity for a wider range of specialised cooling holes for use in electronic chips is becoming increasingly apparent.
- (4)
- Despite the enhanced thermal performance of special-shaped nozzles, their manufacturing complexity and cost are greater than those of conventional nozzles. Consequently, a more comprehensive set of evaluation criteria is required to ascertain whether special-shaped nozzles can fulfil the requisite specifications for replacing round-hole nozzles.
- (5)
- The use of nanofluids as workmasses has the potential to enhance thermal conductivity and reduce pumping efficiency. However, there is a paucity of research on the use of these fluid workmasses in special-shaped nozzles. Consequently, further verification of the applicability of these new workmasses is required in the future.
- (6)
- The majority of published results have focused on the evaluation of performance enhancement in jet cooling. However, further performance evaluations are required for more complex cooling methods, such as composite cooling.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| SSHs | Special-shaped holes |
| CIJ | Circular impinging jet |
| PIV | Particle image velocimetry |
| LDV | Laser Doppler velocimetry |
| LES | Large Eddy Simulation |
| CO/H | Cross-hole nozzle |
| CO/P | Cross-hole nozzle on the plane |
| Sh | Sherwood number |
| Nu | Nusselt number |
| Re | Reynolds number |
| Nuave | Average Nusselt number |
| r | Radial length |
| d | The diameter of the hole (mm) |
| H/d | Nozzle-to-plate distance |
| S/d | Distance between nozzles |
| h1 | Heat transfer coefficient (W/m2·K) |
| λ | Thermal conductivity of the fluid (W/m·K) |
References
- Garimella, S.V.; Nenaydykh, B. Nozzle-geometry effects in liquid jet impingement heat transfer. Int. J. Heat Mass Transf. 1996, 39, 2915–2923. [Google Scholar] [CrossRef]
- Brignoni, L.A.; Garimella, S.V. Effects of nozzle-inlet chamfering on pressure drop and heat transfer in confined air jet impingement. Int. J. Heat Mass Transf. 2000, 43, 1133–1139. [Google Scholar] [CrossRef]
- Oyakawa, K.; Yaga, M.; Nasu, K.; Senaha, I.; Matsuda, S.; Azama, T. Impingement heat transfer by jet issuing from a cross-shaped nozzle. Heat Transf.-Jpn. Res. Co-Spons. Soc. Chem. Eng. Jpn. Heat Transf. Div. ASME 1998, 27, 192–204. [Google Scholar] [CrossRef]
- Herrero Martin, R.; Buchlin, J.M. Jet impingement heat transfer from lobed nozzles. Int. J. Therm. Sci. 2011, 50, 1199–1206. [Google Scholar] [CrossRef]
- Violato, D.; Scarano, F. Three-dimensional evolution of flow structures in transitional circular and chevron jets. Phys. Fluids 2011, 23, 124104. [Google Scholar] [CrossRef]
- Barewar, S.D.; Joshi, M.; Sharma, P.O.; Kalos, P.S.; Bakthavatchalam, B.; Chougule, S.S.; Habib, K.; Saha, S.K. Optimization of jet impingement heat transfer: A review on advanced techniques and parameters. Therm. Sci. Eng. Prog. 2023, 39, 101697. [Google Scholar] [CrossRef]
- Sarkar, S.; Gupta, R.; Roy, T.; Ganguly, R.; Megaridis, C.M. Review of jet impingement cooling of electronic devices: Emerging role of surface engineering. Int. J. Heat Mass Transf. 2023, 206, 123888. [Google Scholar] [CrossRef]
- Hussain, L.; Khan, M.M.; Masud, M.; Ahmed, F.; Rehman, Z.; Amanowicz, L.; Rajski, K. Heat Transfer Augmentation through Different Jet Impingement Techniques: A State-of-the-Art Review. Energies 2021, 14, 6458. [Google Scholar] [CrossRef]
- Ekkad, S.V.; Singh, P. A Modern Review on Jet Impingement Heat Transfer Methods. J. Heat Transf. Asme 2021, 143, 064001. [Google Scholar] [CrossRef]
- Xu, L.; Lan, J.; Ma, Y.; Gao, J.; Li, Y. Numerical study on heat transfer by swirling impinging jets issuing from a screw-thread nozzle. Int. J. Heat Mass Transf. 2017, 115, 232–237. [Google Scholar] [CrossRef]
- Xi, L.; Ruan, Q.; Gao, Y.; Gao, J.; Xu, L.; Li, Y. Study on flow and heat transfer performance of single jet impingement cooling through variable-diameter hole. Therm. Sci. 2024, 116. [Google Scholar] [CrossRef]
- Sodjavi, K.; Montagné, B.; Meslem, A.; Byrne, P.; Serres, L.; Sobolik, V. Passive control of wall shear stress and mass transfer generated by submerged lobed impinging jet. Heat Mass Transf. 2016, 52, 925–936. [Google Scholar] [CrossRef]
- Colucci, D.W.; Viskanta, R. Effect of nozzle geometry on local convective heat transfer to a confined impinging air jet. Exp. Therm. Fluid Sci. 1996, 13, 71–80. [Google Scholar] [CrossRef]
- Ram, C.; Seralathan, S.; Premkumar, T.; Venkatesan, H. Computational study of leading edge jet impingement cooling with a conical converging hole for blade cooling. ARPN J. Eng. Appl. Sci. 2017, 12, 6397–6406. [Google Scholar]
- Zielinski, A.J.; Solovitz, S.A. Flow Analysis of the Impingement of a Variable-Diameter Synthetic Jet. J. Flow Vis. Image Process. 2019, 26, 127–148. [Google Scholar] [CrossRef]
- Shuja, S.Z.; Yilbas, B.S.; Budair, M.O. Jet impingement onto a limited-area heated plate: Conical nozzle considerations. J. Enhanc. Heat Transf. 2005, 12, 301–313. [Google Scholar] [CrossRef]
- Markal, B.; Avci, M.; Aydin, O. Conical coaxial impinging air jets: Angle effect on the heat transfer performance. Heat Mass Transf. 2020, 56, 3135–3146. [Google Scholar] [CrossRef]
- Sathish, S.; Seralathan, S.; Ch, M.S.N.; Rizwan, V.M.; Varma, U.P.; Kumar, K.N.M. Influence of converging conical hole angles on jet impingement blade cooling of gas turbine blade leading edge. AIP Conf. Proc. 2022, 2385, 120003. [Google Scholar] [CrossRef]
- Subrahmanyam, P.; Krishnamoorthy, A.; Harvest, J. Flow Field Characteristics of Multiple Impinging Tapered Nozzles in Confined Channels for High Heat Flux Applications. In Proceedings of the 2018 17th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), San Diego, CA, USA, 29 May 2018–1 June 2018; pp. 436–448. [Google Scholar]
- Kansy, J.; Kalmbach, T.; Loges, A.; Treier, J.; Wetzel, T.; Wiebelt, A. Determination of effective heat transfer area on vertical surfaces subject to spray and impinging jet. Appl. Therm. Eng. 2021, 184, 116303. [Google Scholar] [CrossRef]
- Talapati, R.J.; Hiremath, N.S.; Katti, V.V. Influence of nozzle geometry on wall static pressure coefficient of the submerged turbulent jet impinging on a smooth flat surface. Int. J. Ambient. Energy 2023, 44, 1959–1968. [Google Scholar] [CrossRef]
- Shuja, S.Z.; Yibas, B.S.; Khan, S.A. Flow emerging from annular-conical nozzle combinations and impinging onto a cylindrical cavity. Int. J. Therm. Sci. 2009, 48, 975–984. [Google Scholar] [CrossRef]
- Abdel-Fattah, A.; Abou-Taleb, F.S.; Moustafa, G.H. Behavior of Air Jet Impinging on Curved Surfaces. J. Aerosp. Eng. 2014, 27, 04014029. [Google Scholar] [CrossRef]
- Chi, Z.R.; Liu, H.Q.; Zang, S.S. Geometrical optimization of nonuniform impingement cooling structure with variable-diameter jet holes. Int. J. Heat Mass Transf. 2017, 108, 549–560. [Google Scholar] [CrossRef]
- Das, S.; Biswas, A.; Das, B. Parametric investigation on the thermo-hydraulic performance of a novel solar air heater design with conical protruded nozzle jet impingement. Appl. Therm. Eng. 2023, 219, 119583. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, X.R.; Yuan, G.; Li, Z.L.; Zhang, F.B. Structure optimization of straight cone nozzle and its effect on jet impingement heat transfer. Numer. Heat Transf. Part A Appl. 2023, 13. [Google Scholar] [CrossRef]
- Whitt, R.; Huitink, D. Variable Area Jet Impingement for High Voltage Power Electronics. In Proceedings of the Asme 2023 International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems, Interpack 2023, San Diego, CA, USA, 24–26 October 2023. [Google Scholar]
- Limaye, M.D.; Gulati, P.; Vedula, R.P.; Prabhu, S.V. Effect of the profile of a convergent nozzle on heat transfer distribution of a flat plate impinged by an under-expanded jet. Exp. Therm. Fluid Sci. 2013, 45, 75–91. [Google Scholar] [CrossRef]
- Sanjai, P. Jet Impingement on a Flat Plate with Different Plate Parameters. Int. J. Res. Eng. Sci. Manag. 2018, 1, 49–51. [Google Scholar]
- Violato, D.; Ianiro, A.; Cardone, G.; Scarano, F. Investigation on Circular and Chevron Impinging Jets by Ir Thermography and Time-Resolved Tomographic Piv. In Proceedings of the Asme/Jsme/Ksme Joint Fluids Engineering Conference 2011, Hamamatsu, Japan, 24–29 July 2011; Volume 1, Parts A–D. pp. 3075–3086. [Google Scholar]
- Violato, D.; Ianiro, A.; Cardone, G.; Scarano, F. Three-dimensional vortex dynamics and convective heat transfer in circular and chevron impinging jets. Int. J. Heat Fluid Flow. 2012, 37, 22–36. [Google Scholar] [CrossRef]
- Horra, S.; Nemouchi, Z.; Khezzar, L. Effects of the Shape of a Nozzle with Chevrons on the Dynamics of Turbulent Impinging Jet. In Proceedings of the Asme International Mechanical Engineering Congress and Exposition, Phoenix, AZ, USA, 11–17 November 2016; Volume 7. [Google Scholar]
- Vinze, R.; Chandel, S.; Limaye, M.D.; Prabhu, S.V. Local heat transfer distribution between smooth flat surface and impinging incompressible air jet from a chevron nozzle. Exp. Therm. Fluid Sci. 2016, 78, 124–136. [Google Scholar] [CrossRef]
- Du, X.; Yang, Z.; Jin, Z.; Xia, C.; Bao, D. A comparative study of passive control on flow structure evolution and convective heat transfer enhancement for impinging jet. Int. J. Heat Mass Transf. 2018, 126, 256–280. [Google Scholar] [CrossRef]
- Gao, Q.H.; Zhang, J.Z.; Lyu, Y.W.; Sun, W.J. An Experimental Investigation of Chevron-Nozzle Jet Impingement Heat Transfer on a Confined Conical-Concave Surface. J. Enhanc. Heat Transf. 2021, 28, 19–33. [Google Scholar] [CrossRef]
- Guan, T.; Zhang, J.-z.; Shan, Y.; Hang, J. Conjugate heat transfer on leading edge of a conical wall subjected to external cold flow and internal hot jet impingement from chevron nozzle—Part 1: Experimental analysis. Int. J. Heat Mass Transf. 2017, 106, 329–338. [Google Scholar] [CrossRef]
- Guan, T.; Zhang, J.-z.; Shan, Y. Conjugate heat transfer on leading edge of a conical wall subjected to external cold flow and internal hot jet impingement from chevron nozzle—Part 2: Numerical analysis. Int. J. Heat Mass Transf. 2017, 106, 339–355. [Google Scholar] [CrossRef]
- Lyu, Y.-w.; Zhang, J.-z.; Liu, X.-c.; Shan, Y. Experimental Investigation of Impinging Heat Transfer of the Pulsed Chevron Jet on a Semicylindrical Concave Plate. J. Heat Transf. 2019, 141, 032201. [Google Scholar] [CrossRef]
- Lyu, Y.-w.; Zhang, J.-z.; Liu, X.-c.; Tan, X.-m. Experimental investigation on convective heat transfer induced by piston-driven synthetic jet with a transmission pipe. Experimental Thermal and Fluid Science 2019, 104, 26–42. [Google Scholar] [CrossRef]
- Crispo, C.M.; Greco, C.S.; Avallone, F.; Cardone, G. On the flow organization of a chevron synthetic jet. Exp. Therm. Fluid Sci. 2017, 82, 136–146. [Google Scholar] [CrossRef]
- Crispo, C.M.; Greco, C.S.; Cardone, G. Convective heat transfer in circular and chevron impinging synthetic jets. Int. J. Heat Mass Transf. 2018, 126, 969–979. [Google Scholar] [CrossRef]
- Crispo, C.M.; Greco, C.S.; Cardone, G. Flow field features of chevron impinging synthetic jets at short nozzle-to-plate distance. Exp. Therm. Fluid Sci. 2019, 106, 202–214. [Google Scholar] [CrossRef]
- Boulenouar, M.; Meslem, A.; Imine, B.; Nastase, I. Numerical study of a turbulent jet flow issued from lobed diffuser. Mechanika 2011, 17, 168–171. [Google Scholar] [CrossRef]
- Panse, S.S.; Madhavan, S.; Singh, P.; Ekkad, S.V. Impingement Heat Transfer of Various Lobe-Shaped Nozzles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 11–14 November 2019; p. V008T009A037. [Google Scholar]
- Lyu, Y.W.; Zhang, J.Z.; Wang, B.Y.; Tan, X.M. Convective heat transfer on flat and concave surfaces subjected to an impinging jet form lobed nozzle. Sci. China Technol. Sci. 2020, 63, 116–127. [Google Scholar] [CrossRef]
- He, C.X.; Liu, Y.Z. Jet impingement heat transfer of a lobed nozzle: Measurements using temperature-sensitive paint and particle image velocimetry. Int. J. Heat Fluid Flow 2018, 71, 111–126. [Google Scholar] [CrossRef]
- He, C.X.; Liu, Y.Z.; Gan, L. Dynamics of the jet flow issued from a lobed Nozzle: Tomographic particle image velocimetry measurements. Int. J. Heat Fluid Flow 2021, 89, 108795. [Google Scholar] [CrossRef]
- Lyu, Y.W.; Zhang, J.Z.; Tan, J.W.; Shan, Y. Impingement heat transfer on flat and concave surfaces by piston-driven synthetic jet from planar lobed orifice. Int. J. Heat Mass Transf. 2021, 167, 120832. [Google Scholar] [CrossRef]
- Lyu, Y.W.; Zhao, Y.D.; Zhang, J.Z.; Zhang, J.Y.; Shan, Y. Large eddy simulation of temperature-variation effect of impinging planar lobed synthetic jet on flat plate and the semi-cylindrical concave plate. Int. J. Therm. Sci. 2023, 184, 107981. [Google Scholar] [CrossRef]
- Trinh, X.T.; Fénot, M.; Dorignac, E. Flow and heat transfer of hot impinging jets issuing from lobed nozzles. Int. J. Heat Fluid Flow 2017, 67, 185–201. [Google Scholar] [CrossRef]
- Kristiawan, M.; Meslem, A.; Nastase, I.; Sobolik, V. Wall shear rates and mass transfer in impinging jets: Comparison of circular convergent and cross-shaped orifice nozzles. Int. J. Heat Mass Transf. 2012, 55, 282–293. [Google Scholar] [CrossRef]
- Chin, D.T.; Tsang, C.H. Mass Transfer to an Impinging Jet Electrode. J. Electrochem. Soc. 1978, 125, 1461. [Google Scholar] [CrossRef]
- Rau, M.J.; Dede, E.M.; Garimella, S.V. Local single- and two-phase heat transfer from an impinging cross-shaped jet. Int. J. Heat Mass Transf. 2014, 79, 432–436. [Google Scholar] [CrossRef]
- Sodjavi, K.; Montagné, B.; Bragança, P.; Meslem, A.; Bode, F.; Kristiawan, M. Impinging cross-shaped submerged jet on a flat plate: A comparison of plane and hemispherical orifice nozzles. Meccanica 2015, 50, 2927–2947. [Google Scholar] [CrossRef]
- Trinh, X.T.; Fénot, M.; Dorignac, E. The effect of nozzle geometry on local convective heat transfer to unconfined impinging air jets. Exp. Therm. Fluid Sci. 2016, 70, 1–16. [Google Scholar] [CrossRef]
- Taslim, M.; Setayeshgar, L. Experimental Leading-Edge Impingement Cooling Through Racetrack Crossover Holes. In Proceedings of the Turbo Expo 2001: Power for Land, Sea, and Air, New Orleans, LA, USA, 4–7 June 2001; 2001; p. V003T001A036. [Google Scholar]
- Jordan, C.N.; Wright, L.M.; Crites, D.C. Impingement Heat Transfer on a Cylindrical, Concave Surface with Varying Jet Geometries. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; Volume 4, Parts A and B. pp. 335–346. [Google Scholar]
- Jordan, C.N.; Elston, C.A.; Wright, L.M.; Crites, D.C. Leading Edge Impingement with Racetrack Shaped Jets and Varying Inlet Supply Conditions. In Proceedings of the Asme Turbo Expo: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013; Volume 3a. [Google Scholar]
- Harmon, W.V.; Elston, C.A.; Wright, L.M. Experimental Investigation of Leading Edge Impingement under High Rotation Numbers with Racetrack Shaped Jets. In Proceedings of the Asme Turbo Expo: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; Volume 5a. [Google Scholar]
- Wang, J.S.; Liu, J.; Wang, L.; Sundén, B.; Wang, S.T. Conjugated heat transfer investigation with racetrack-shaped jet hole and double swirling chamber in rotating jet impingement. Numer. Heat Transf. Part A Appl. 2018, 73, 768–787. [Google Scholar] [CrossRef]
- Harmon, W.V.; Wright, L.M.; Crites, D.C.; Morris, M.C.; Riahi, A. Combined Effects of Jet Plate Thickness and Fillet Radius on Leading Edge Jet Impingement with Round and Racetrack Shaped Jets. In Proceedings of the Asme Turbo Expo: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; Volume 5a. [Google Scholar]
- Kulkarni, R.V.; Wright, L.M. Heat Transfer and Pressure Loss Correlations for Leading Edge, Jet Impingement Using Racetrack-Shaped Jets With Filleted Edges. ASME J. Heat Mass Transf. 2023, 145, 121801. [Google Scholar] [CrossRef]
- Wen, M.-Y.; Jang, K.-J. An impingement cooling on a flat surface by using circular jet with longitudinal swirling strips. Int. J. Heat Mass Transf. 2003, 46, 4657–4667. [Google Scholar] [CrossRef]
- Fu, Y.; Zhou, J.; Yang, Y. Experimental research on compulsive cooling of swirling jet impingement. In Proceedings of the Conference on High Density Microsystem Design and Packaging and Component Failure Analysis, HDP’06, Shanghai, China, 27–28 June 2006; pp. 137–140. [Google Scholar]
- Kunnarak, K.; Somravysin, P.; Eiamsa-ard, S.; Chuwattanakul, V. Impingement Cooling by Round Jets with a Longitudinal Swirling Strip. Int. J. Mech. Eng. Robot. Res. 2016, 7, 179–183. [Google Scholar] [CrossRef]
- Ianiro, A.; Violato, D.; Scarano, F.; Cardone, G. Three dimensional features in swirling impinging jets. In Proceedings of the 15th International Symposium on Flow Visualization, Minsk, Belarus, 25–28 June 2012; pp. 25–28. [Google Scholar]
- Nuntadusit, C.; Wae-Hayee, M.; Bunyajitradulya, A.; Eiamsa-Ard, S. Visualization of flow and heat transfer characteristics for swirling impinging jet. Int. Commun. Heat Mass Transf. 2012, 39, 640–648. [Google Scholar] [CrossRef]
- Nanan, K.; Wongcharee, K.; Nuntadusit, C.; Eiamsa-ard, S. Forced convective heat transfer by swirling impinging jets issuing from nozzles equipped with twisted tapes. Int. Commun. Heat Mass Transf. 2012, 39, 844–852. [Google Scholar] [CrossRef]
- Salman, S.D.; Kadhum, A.A.H.; Takriff, M.S.; Mohamad, A.B. Experimental and Numerical Investigations of Heat Transfer Characteristics for Impinging Swirl Flow. Adv. Mech. Eng. 2014, 6, 631081. [Google Scholar] [CrossRef]
- Kumar, S.S.; Hindasageri, V.; Prabhu, S.V. Local heat transfer distribution on a flat plate impinged by a swirling jet generated by a twisted tape. Int. J. Therm. Sci. 2017, 111, 351–368. [Google Scholar] [CrossRef]
- Zeiny, E.; Farhadi, M.; Sedighi, K. Numerical investigation of the simultaneous influence of swirling flow and obstacles on plate in impinging jet. Int. J. Heat Technol. 2017, 35, 59–66. [Google Scholar] [CrossRef]
- Khanmohammad, S.; Mazaher, N. Second law analysis and multi-criteria optimization of turbulent heat transfer in a tube with inserted single and double twisted tape. Int. J. Therm. Sci. 2019, 145, 105998. [Google Scholar] [CrossRef]
- Eiamsa-ard, S.; Nanan, K.; Wongcharee, K. Heat transfer visualization of co/counter-dual swirling impinging jets by thermochromic liquid crystal method. Int. J. Heat Mass Transf. 2015, 86, 600–621. [Google Scholar] [CrossRef]
- Nasirzadeh, H.; Yazdi, M.E.; Lavasani, A.M. Heat transfer and fluid flow of swirling impinging jets ejected from nozzles with different twisted tapes. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 498. [Google Scholar] [CrossRef]
- Ajour, M.N.; Jahangiri, S.; Al-Shati, A.S.; Abu-Hamdeh, N.H.; Mostafa, M.E.; Jasim, D.J.; Hekmatifar, M. Numerical investigation of the effect of swirling flow caused by twisted tape in impinging jet’s nozzle on heat transfer: Application in cooling of electronic components and turbine blades. J. Taiwan Inst. Chem. E 2023, 150, 105058. [Google Scholar] [CrossRef]
- Hindasageri, V.; Vedula, R.P.; Prabhu, S.V. Heat transfer distribution of swirling flame jet impinging on a flat plate using twisted tapes. Int. J. Heat Mass Transf. 2015, 91, 1128–1139. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, Y.; Yang, D.; Li, H.W. Experimental study on heat transfer characteristics of hybrid nanofluid impinging jets. Appl. Therm. Eng. 2019, 151, 556–566. [Google Scholar] [CrossRef]
- Wongcharee, K.; Chuwattanakul, V.; Eiamsa-ard, S. Heat transfer of swirling impinging jets with TiO2-water nanofluids. Chem. Eng. Process. Process Intensif. 2017, 114, 16–23. [Google Scholar] [CrossRef]
- Huang, L.; ElGenk, M.S. Heat transfer and flow visualization experiments of swirling, multi-channel, and conventional impinging jets. Int. J. Heat Mass Transf. 1998, 41, 583–600. [Google Scholar] [CrossRef]
- Bilen, K.; Bakirci, K.; Yapici, S.; Yavuz, T. Heat transfer from a plate impinging swirl jet. Int. J. Energy Res. 2002, 26, 305–320. [Google Scholar] [CrossRef]
- Lee, D.H.; Won, S.Y.; Kim, Y.T.; Chung, Y.S. Turbulent heat transfer from a flat surface to a swirling round impinging jet. Int. J. Heat Mass Transf. 2002, 45, 223–227. [Google Scholar] [CrossRef]
- Senda, M.; Inaoka, K.; Toyoda, D.; Sato, S. Heat transfer and fluid flow characteristics in a swirling impinging jet. Heat Transf. Asian Res. 2005, 34, 324–335. [Google Scholar] [CrossRef]
- Bakirci, K.; Bilen, K. Visualization of heat transfer for impinging swirl flow. Exp. Therm. Fluid Sci. 2007, 32, 182–191. [Google Scholar] [CrossRef]
- Fénot, M.; Dorignac, E.; Lalizel, G. Heat transfer and flow structure of a multichannel impinging jet. Int. J. Therm. Sci. 2015, 90, 323–338. [Google Scholar] [CrossRef]
- Markal, B. The effect of Total flowrate on the cooling performance of swirling coaxial impinging jets. Heat Mass Transf. 2019, 55, 3275–3288. [Google Scholar] [CrossRef]
- Chouaieb, S.; Kriaa, W.; Mhiri, H.; Bournot, P. Swirl generator effect on a confined coaxial jet characteristics. Int. J. Hydrog. Energy 2017, 42, 29014–29025. [Google Scholar] [CrossRef]
- Singh, P.; Chander, S. Study of flow field and heat transfer characteristics for an interacting pair of counter-rotating dual-swirling impinging flames. Int. J. Therm. Sci. 2019, 144, 191–211. [Google Scholar] [CrossRef]
- Mohamed Illyas, S.; Ramesh Bapu, B.R.; Venkata Subba Rao, V. Heat transfer and flow visualization of swirling impinging jet on flat surface using helicoid inserts. J. Vis. 2018, 21, 729–749. [Google Scholar] [CrossRef]
- Mohamed Illyas, S.; Ramesh Bapu, B.R.; Venkata Subba Rao, V. Experimental Analysis of Heat Transfer and Multi Objective Optimization of Swirling Jet Impingement on a Flat Surface. J. Appl. Fluid Mech. 2019, 12, 803–817. [Google Scholar] [CrossRef]
- Alekseenko, S.V.; Bilsky, A.V.; Dulin, V.M.; Markovich, D.M. Experimental study of an impinging jet with different swirl rates. Int. J. Heat Fluid Flow 2007, 28, 1340–1359. [Google Scholar] [CrossRef]
- Nozaki, A.; Igarashi, Y.; Hishida, K. Heat transfer mechanism of a swirling impinging jet in a stagnation region. Heat Transf. Asian Res. 2003, 32, 663–673. [Google Scholar] [CrossRef]
- Yang, H.Q.; Kim, T.; Lu, T.J.; Ichimiya, K. Flow structure, wall pressure and heat transfer characteristics of impinging annular jet with/without steady swirling. Int. J. Heat Mass Transf. 2010, 53, 4092–4100. [Google Scholar] [CrossRef]
- Brown, K.J.; Persoons, T.; Murray, D.B. Heat Transfer Characteristics of Swirling Impinging Jets. In Proceedings of the Asme International Heat Transfer Conference—2010, Washington, DC, USA, 8–13 August 2010; Volume 5, pp. 657–665. [Google Scholar]
- Ahmadvand, M.; Najafi, A.F.; Shahidinejad, S. An experimental study and CFD analysis towards heat transfer and fluid flow characteristics of decaying swirl pipe flow generated by axial vanes. Meccanica 2009, 45, 111–129. [Google Scholar] [CrossRef]
- Yang, H.; Kim, T.; Lu, T. Characteristics of annular impinging jets with/without swirling flow by short guide vanes. Sci. China Technol. Sci. 2011, 54, 749–757. [Google Scholar] [CrossRef]
- Liu, L.; Bai, B.F. Flow regime identification of swirling gas-liquid flow with image processing technique and neural networks. Chem. Eng. Sci. 2019, 199, 588–601. [Google Scholar] [CrossRef]
- Ali, K. Experimental and numerical investigation of impinging multi-jet system. Mechanics 2017, 23, 228–235. [Google Scholar] [CrossRef]
- Xu, L.; Xiong, Y.; Xi, L.; Gao, J.; Li, Y.; Zhao, Z. Numerical Simulation of Swirling Impinging Jet Issuing from a Threaded Hole under Inclined Condition. Entropy 2019, 22, 15. [Google Scholar] [CrossRef]
- Yang, T.; Sun, Y.; Xu, L.; Xi, L.; Gao, J.; Li, Y. Comparative study on flow and heat transfer characteristics of swirling impingement jet issuing from different nozzles. Int. J. Therm. Sci. 2023, 184, 107914. [Google Scholar] [CrossRef]
- Arjocu, S.C.; Liburdy, J.A. Identification of dominant heat transfer modes associated with the impingement of an elliptical jet array. J. Heat Transf. Asme 2000, 122, 240–247. [Google Scholar] [CrossRef]
- Attalla, M.; Maghrabie, H.M.; Qayyum, A.; Al-Hasnawi, A.G.; Specht, E. Influence of the nozzle shape on heat transfer uniformity for in-line array of impinging air jets. Appl. Therm. Eng. 2017, 120, 160–169. [Google Scholar] [CrossRef]
- Whelan, B.R.; Robinson, A.J. The effect of nozzle geometry on pressure drop and heat transfer to free surface liquid jet arrays. In Proceedings of the Asme/Jsme Thermal Engineering Summer Heat Transfer Conference 2007, Vancouver, BC, Canada, 8–12 July 2007; Volume 2, pp. 747–756. [Google Scholar]
- Marzec, K.; Kucaba-Pietal, A. Heat transfer characteristic of an impingement cooling system with different nozzle geometry. J. Phys. Conf. Ser. 2014, 530, 012038. [Google Scholar] [CrossRef]
- Yamane, Y.; Yamamoto, M.; Honami, S. Effect of Cross-Shaped Circular Jet Array on Impingement Heat Transfer. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; Volume 4, Parts A and B. pp. 89–97. [Google Scholar]
- Yamane, Y.; Yamamoto, M.; Motosuke, M.; Honami, S. Effect of Jet Shape of Square Array of Multi-Impinging Jets on Heat Transfer. In Proceedings of the Asme Turbo Expo: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013; Volume 3a. [Google Scholar]
- Wannassi, M.; Monnoyer, F. Fluid flow and convective heat transfer of combined swirling and straight impinging jet arrays. Appl. Therm. Eng. 2015, 78, 62–73. [Google Scholar] [CrossRef]
- Xu, L.; Yun, X.; Xi, L.; Gao, J.M.; Yang, T.; Li, Y.L. Heat transfer characteristics of single row of jets issuing from screw-thread nozzles impinging on a concave surface. Case Stud. Therm. Eng. 2021, 28, 101590. [Google Scholar] [CrossRef]
- Lyu, Y.W.; Zhang, J.Z.; Liu, X.C.; Shan, Y. Experimental study of single-row chevron-jet impingement heat transfer on concave surfaces with different curvatures. Chin. J. Aeronaut. 2019, 32, 2275–2285. [Google Scholar] [CrossRef]
- Wen, Z.X.; He, Y.L.; Cao, X.W.; Yan, C. Numerical study of impinging jets heat transfer with different nozzle geometries and arrangements for a ground fast cooling simulation device. Int. J. Heat Mass Transf. 2016, 95, 321–335. [Google Scholar] [CrossRef]
- Dano, B.P.E.; Liburdy, J.A.; Kanokjaruvijit, K. Flow characteristics and heat transfer performances of a semi-confined impinging array of jets: Effect of nozzle geometry. Int. J. Heat Mass Transf. 2005, 48, 691–701. [Google Scholar] [CrossRef]
- Dano, B.P.E.; Liburdy, J.A. Structure detection and analysis of non-circular impinging jets in a semi-confined array configuration. Exp. Therm. Fluid Sci. 2007, 31, 991–1003. [Google Scholar] [CrossRef]
- Nuntadusit, C.; Wae-hayee, M.; Tekasakul, P.; Eiamsa-ard, S. Local heat transfer characteristics of array impinging jets from elongated orifices. Int. Commun. Heat Mass Transf. 2012, 39, 1154–1164. [Google Scholar] [CrossRef]
- Fawzy, H.; Zheng, Q.; Jiang, Y.T. Impingement cooling using different arrangements of conical nozzles in a film cooled blade leading edge. Int. Commun. Heat Mass Transf. 2020, 112, 104506. [Google Scholar] [CrossRef]



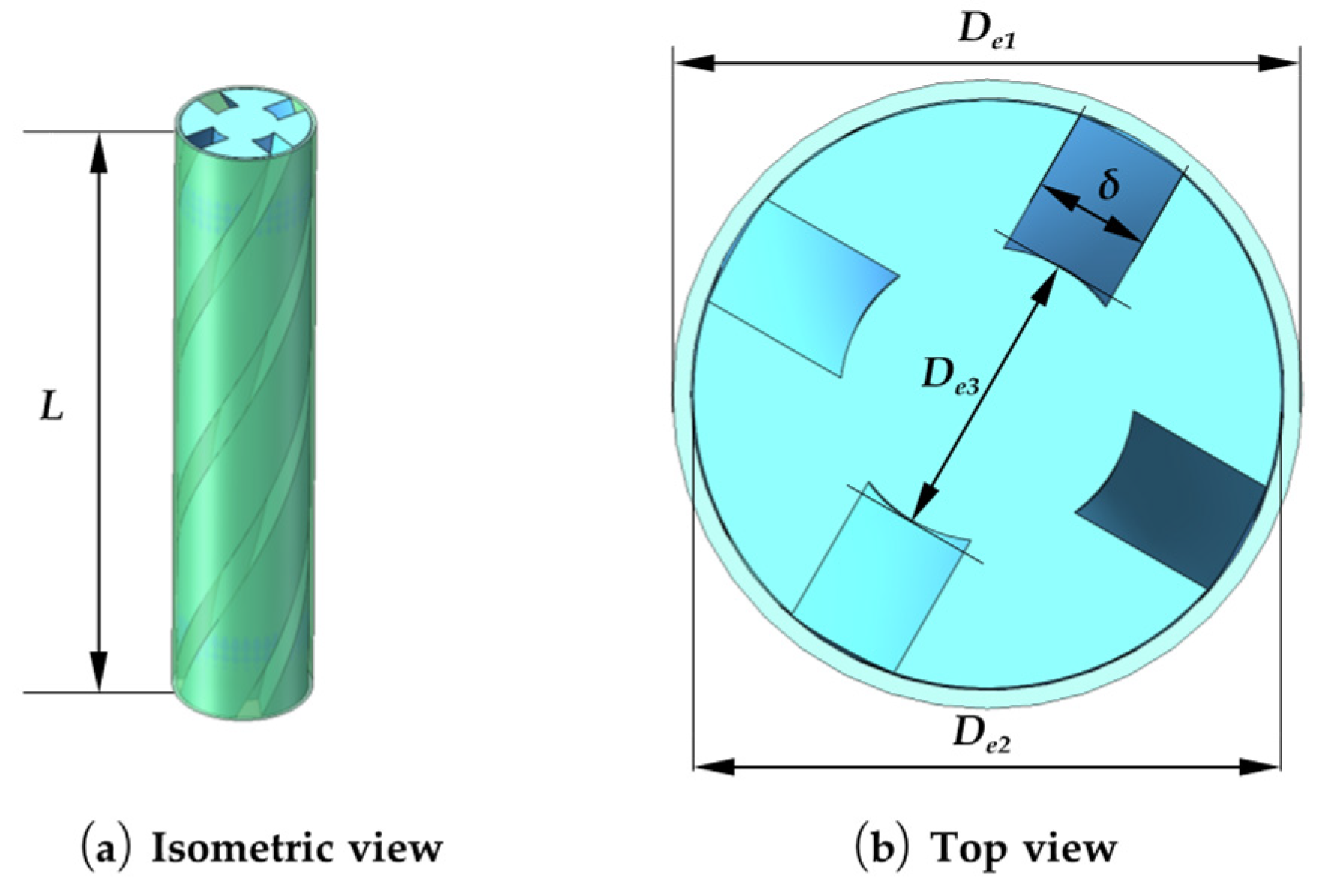
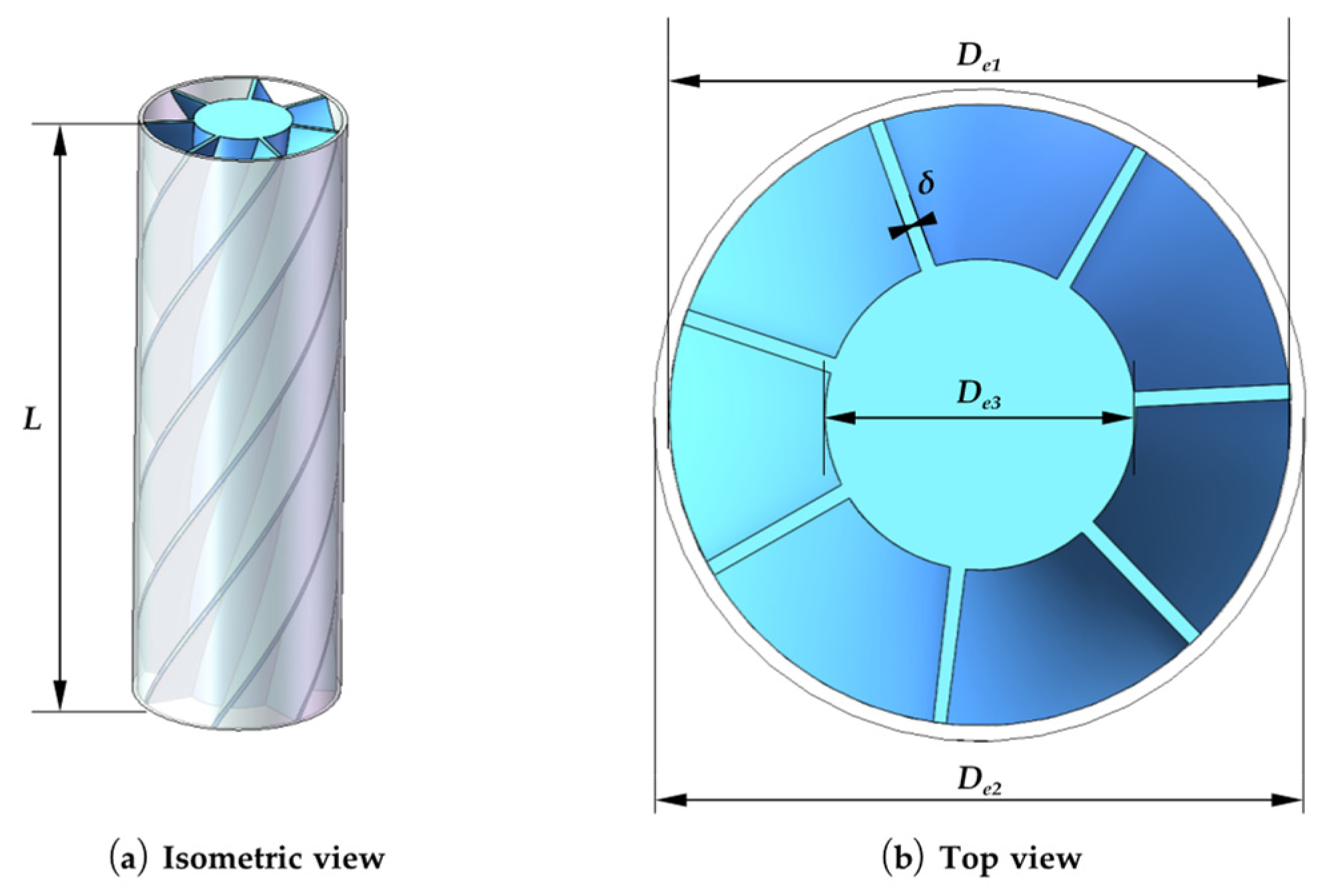
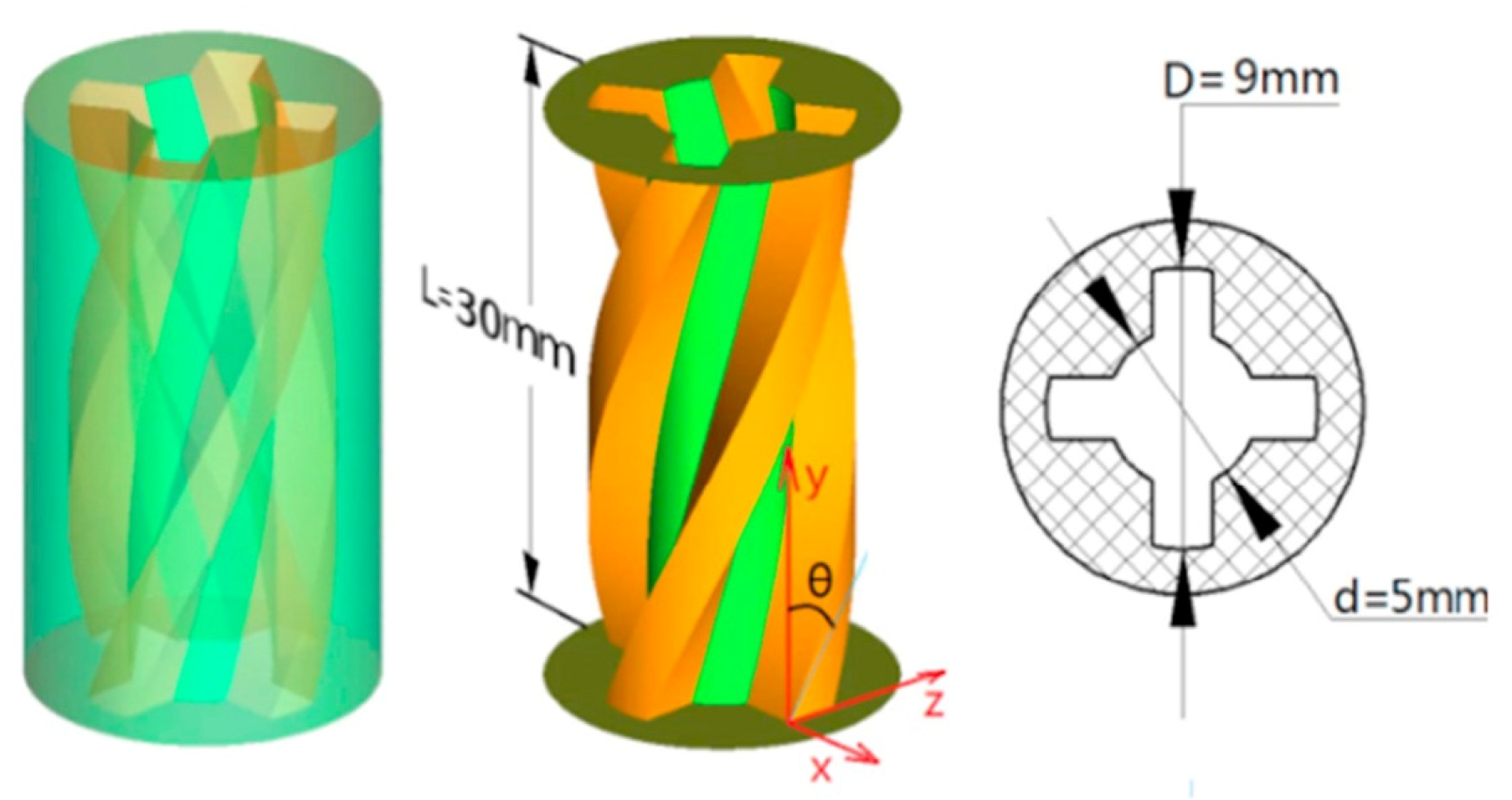
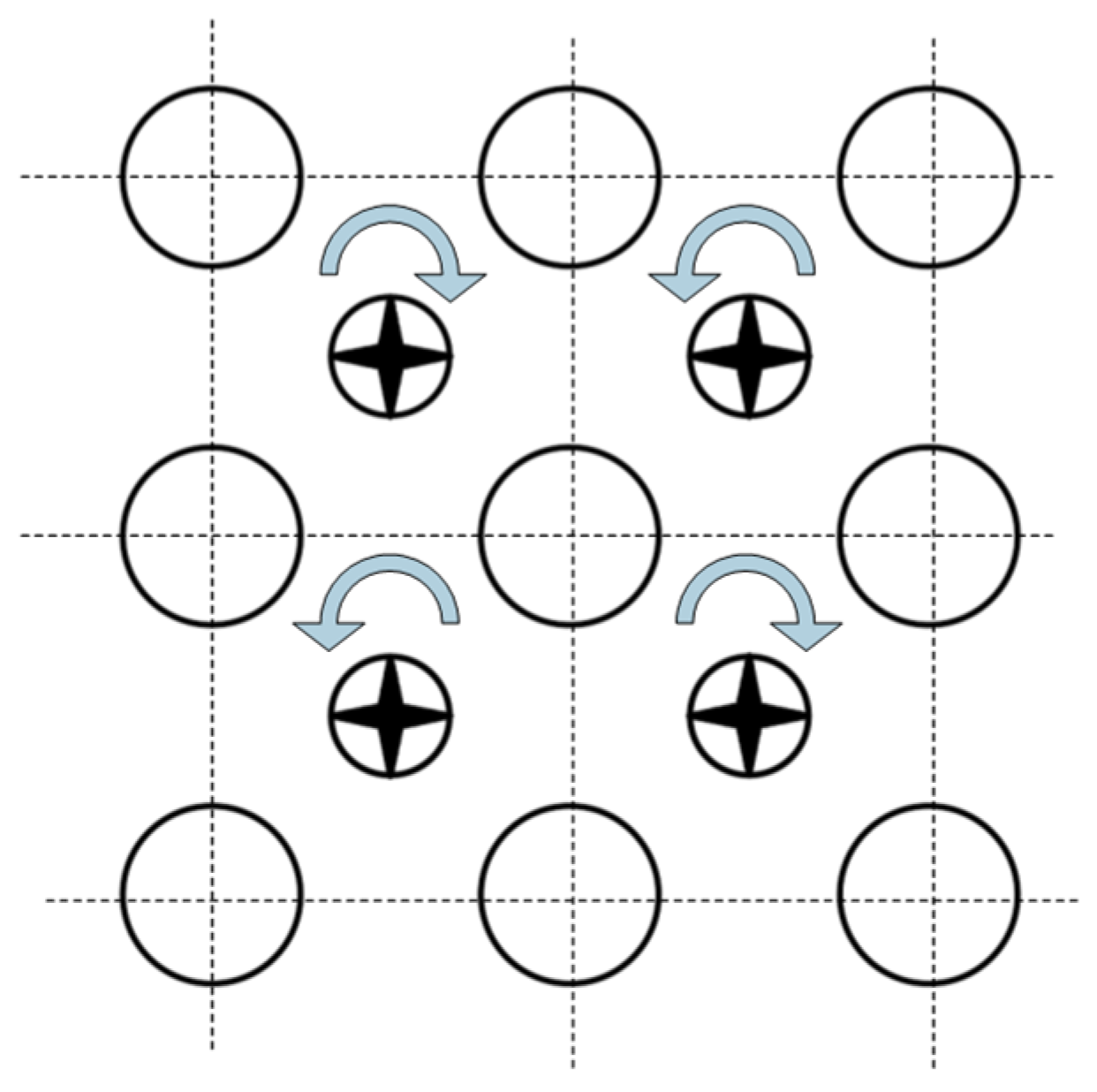
| Special-Shaped Holes | Types | Main Factors | Features |
|---|---|---|---|
| Variable-diameter holes | Tapered nozzles | H/d, Re | Broad application |
| Cone angle | Enhance heat transfer | ||
| aspect ratio | Good combined heat transfer and flow characteristics | ||
| Irregularly geometrical holes | Chevron nozzles | Number and angle of chevrons | Significantly improves heat transfer |
| Suitable for use in synthetic jet | |||
| Lobed nozzles | Number of lobes | Enhanced heat transfer in the stagnation zone | |
| Ratio of nozzle centre offset to radius | Excellent mass transfer performance | ||
| Cross-shaped nozzles | Hemispherical shaped outlet | Enhanced heat transfer in the stagnation zone | |
| Excellent mass transfer performance | |||
| Racetrack-shaped nozzles | More array jet applications | ||
| Swirl nozzles | Inserting twisted tape | Twist ratios | Significantly improves heat transfer uniformity |
| Number of tapes | |||
| Installing a spiral rod | Swirl angles | Relatively poor heat transfer in the centre of the stagnation zone | |
| Inserting guide vane. | Guide vane angles | Relatively complex nozzle geometry |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Hu, N.; Lin, H.; Xi, L.; Li, Y.; Gao, J. A Review of Flow Field and Heat Transfer Characteristics of Jet Impingement from Special-Shaped Holes. Energies 2024, 17, 4510. https://doi.org/10.3390/en17174510
Xu L, Hu N, Lin H, Xi L, Li Y, Gao J. A Review of Flow Field and Heat Transfer Characteristics of Jet Impingement from Special-Shaped Holes. Energies. 2024; 17(17):4510. https://doi.org/10.3390/en17174510
Chicago/Turabian StyleXu, Liang, Naiyuan Hu, Hongwei Lin, Lei Xi, Yunlong Li, and Jianmin Gao. 2024. "A Review of Flow Field and Heat Transfer Characteristics of Jet Impingement from Special-Shaped Holes" Energies 17, no. 17: 4510. https://doi.org/10.3390/en17174510
APA StyleXu, L., Hu, N., Lin, H., Xi, L., Li, Y., & Gao, J. (2024). A Review of Flow Field and Heat Transfer Characteristics of Jet Impingement from Special-Shaped Holes. Energies, 17(17), 4510. https://doi.org/10.3390/en17174510







