Research Methods for Transient Stability Analysis of Power Systems under Large Disturbances
Abstract
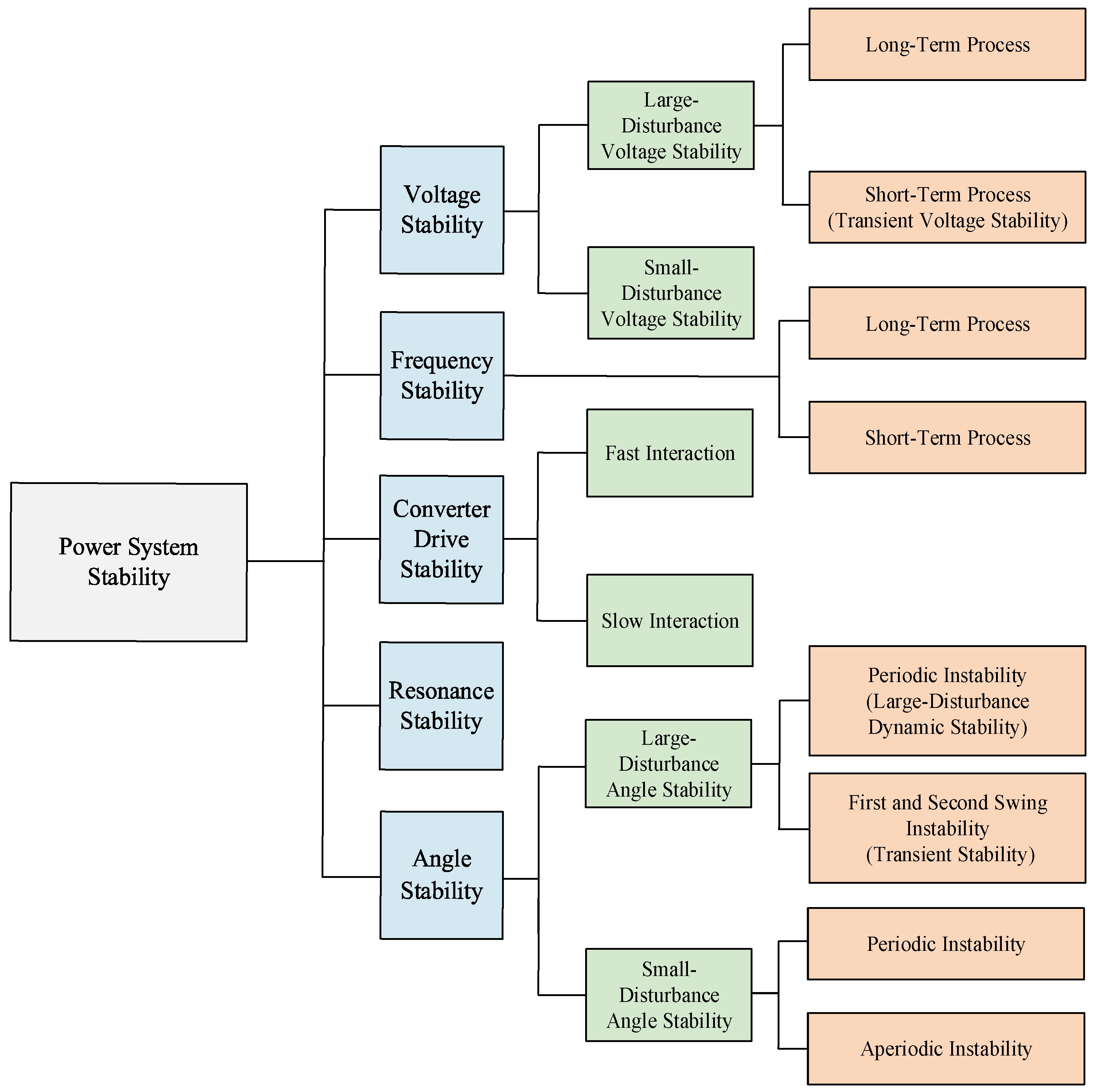
1. Introduction
2. Simulation Methods
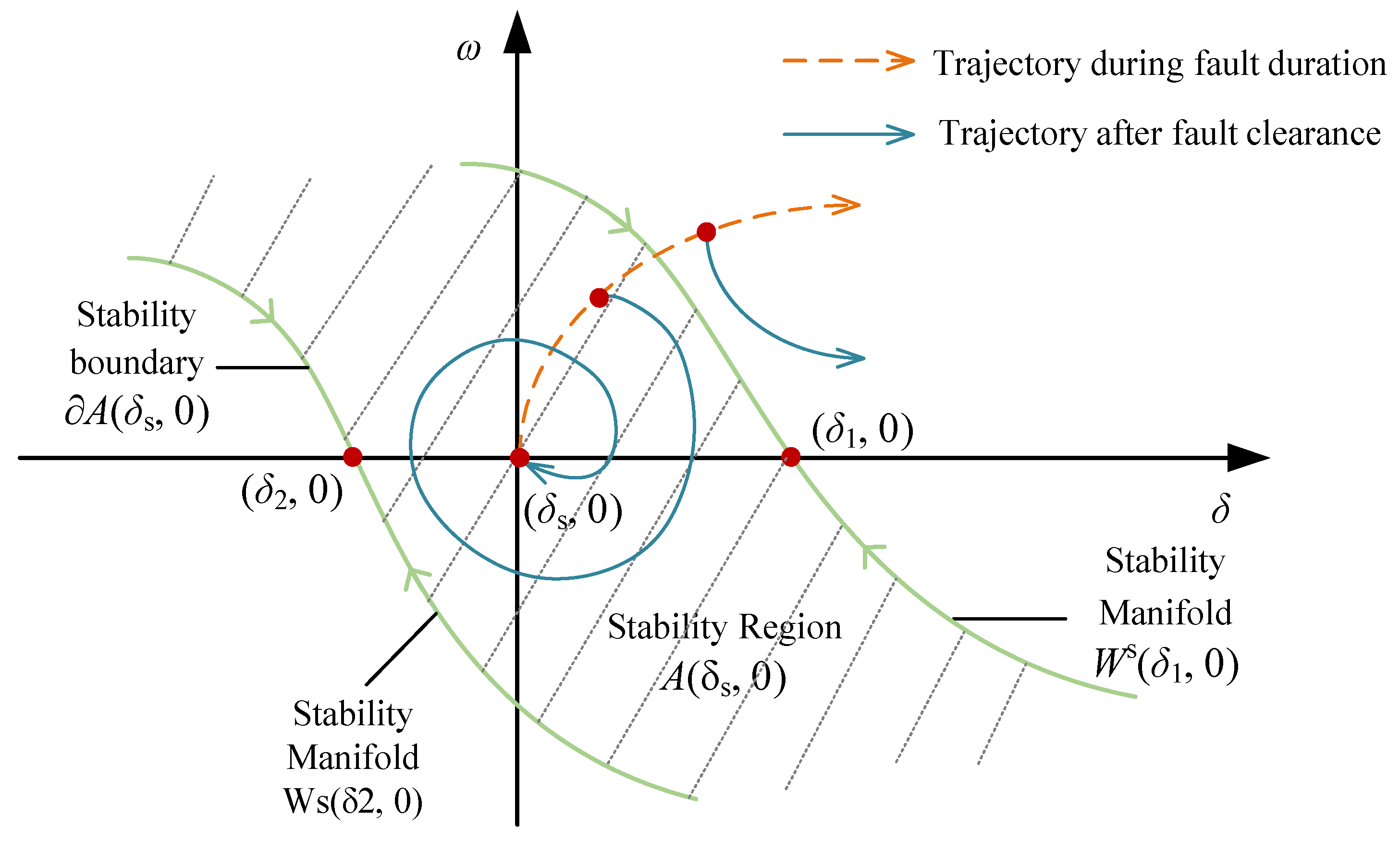
3. Direct Methods
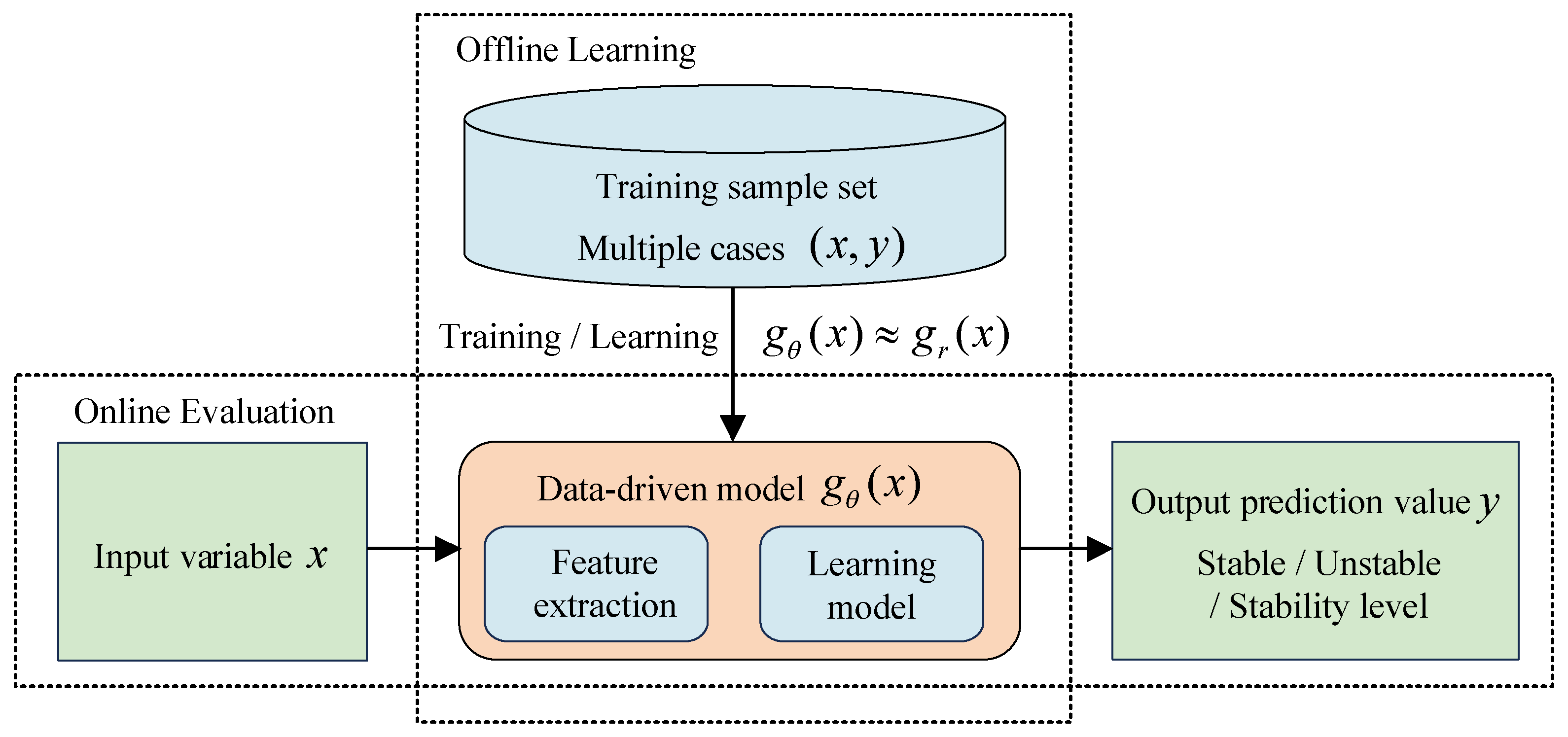
4. Data-Driven Methods
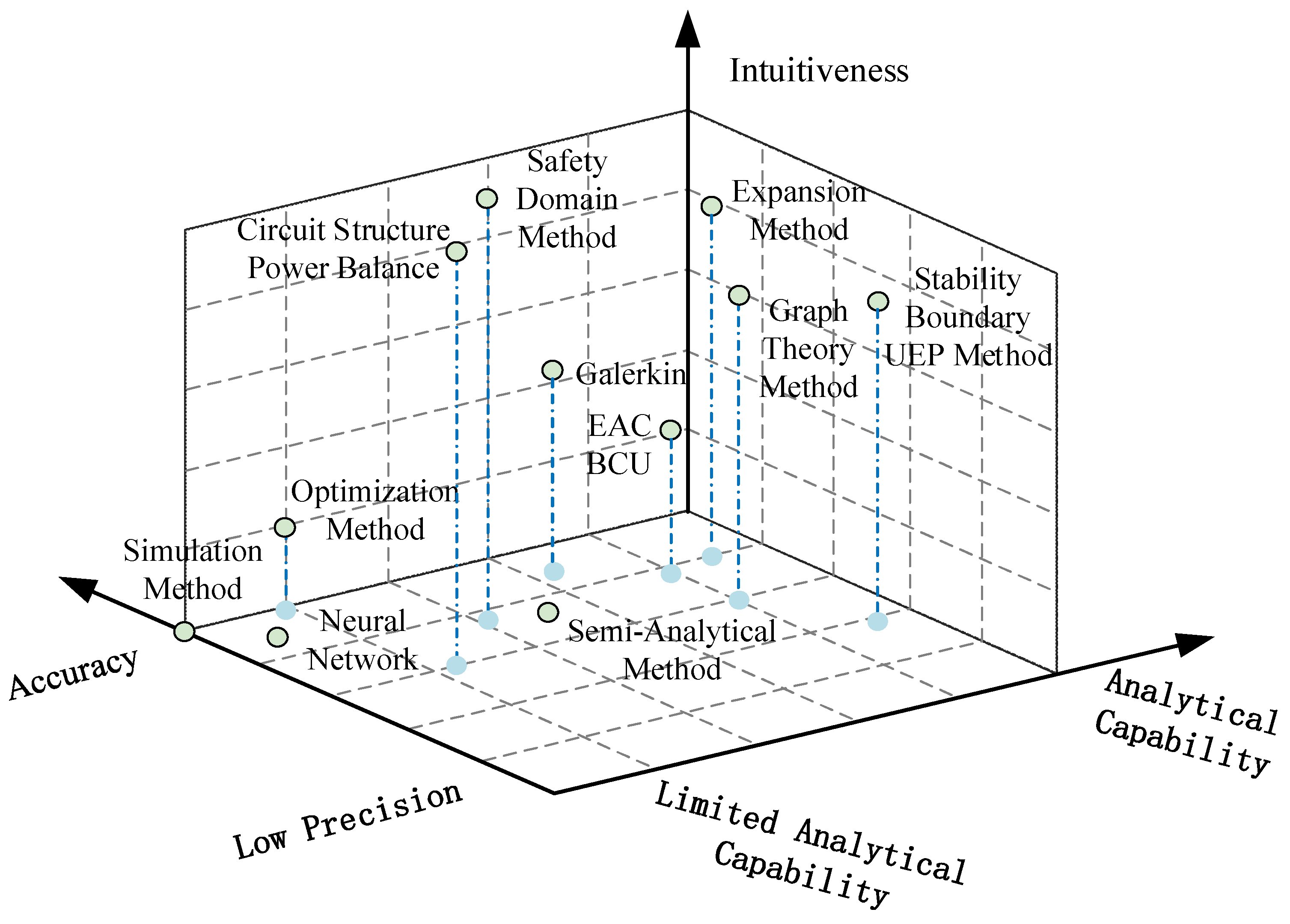
5. Analytical Methods
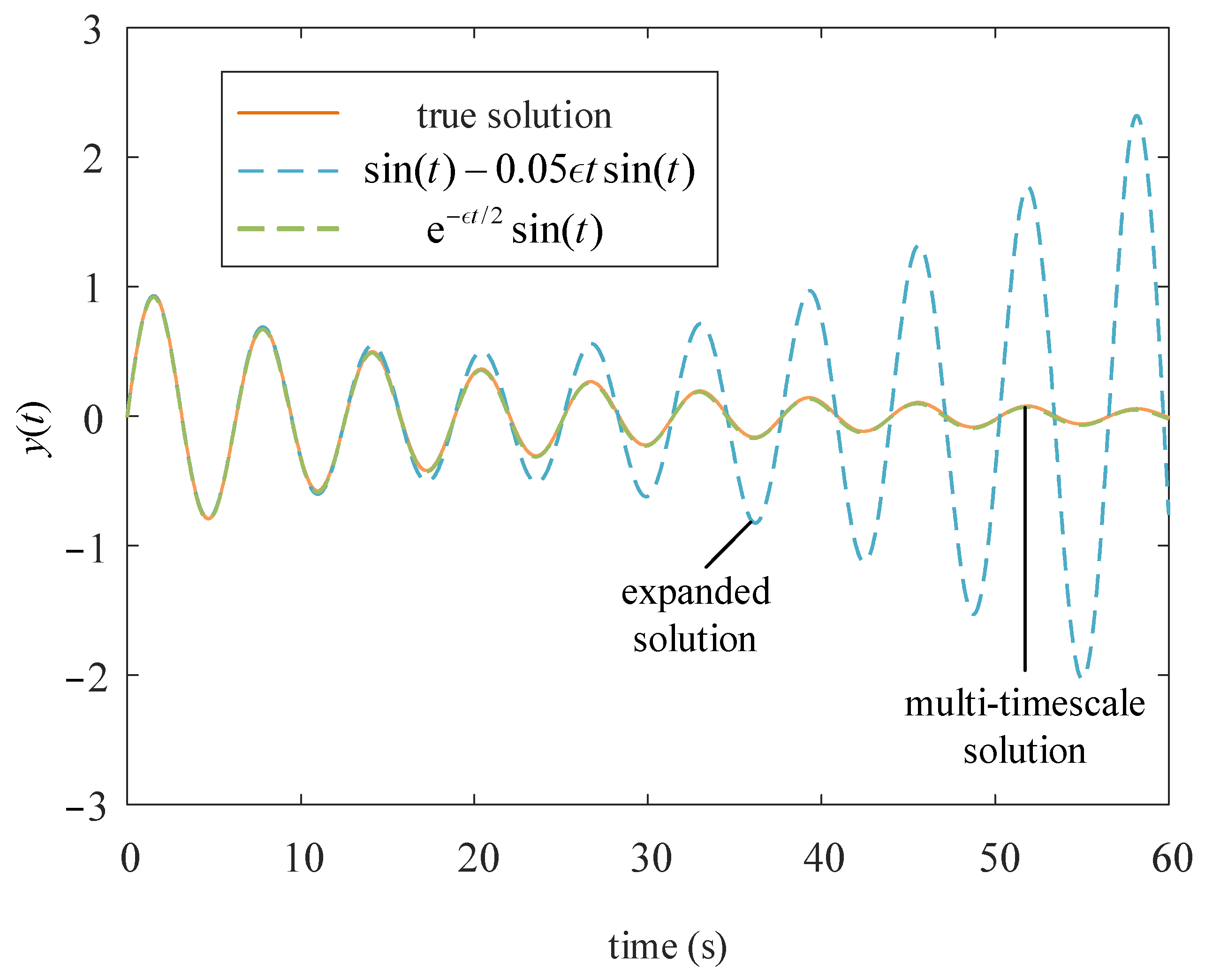
5.1. Asymptotic Expansion Method
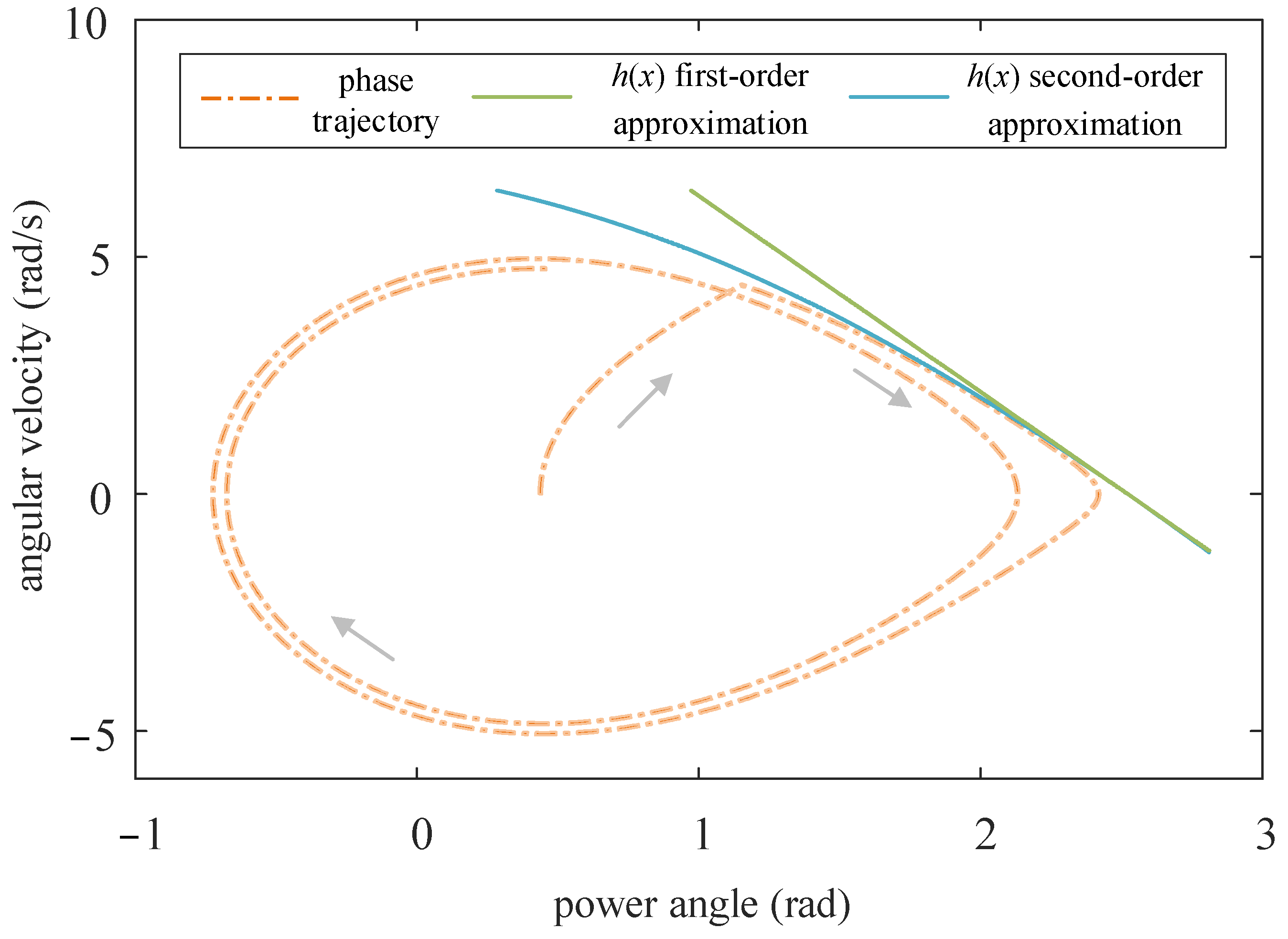
5.2. Intrusive Approximation Method
5.3. Other Analytical Methods
6. Other Methods
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, G.; Li, M.; Xu, T. System Protection and its Key Technologies of UHV AC and DC Power Grid. Autom. Electr. Power Syst. 2018, 42, 2–10. [Google Scholar]
- Li, M. Characteristic Analysis and Operational Control of Large-Scale Hybrid UHV AC/DC Power Grids. Power Syst. Technol. 2016, 40, 985–991. [Google Scholar]
- Yan, R.; Masood, N.-A.; Saha, T.K.; Bai, F.; Gu, H. The anatomy of the 2016 South Australia blackout: A catastrophic event in a high renewable network. IEEE Trans. Power Syst. 2018, 33, 5374–5388. [Google Scholar] [CrossRef]
- Nagpal, M.; Martinich, T.G.; Jiao, Z.; Manuel, S.-H.; Zhang, H.A.; Alimardani, A. Lessons learned from a regional system blackout and restoration in BC hydro. IEEE Trans. Power Deliv. 2018, 33, 1954–1961. [Google Scholar] [CrossRef]
- Guo, H.; Zheng, C.; Iu, H.H.-C.; Fernando, T. A critical review of cascading failure analysis and modeling of power system. Renew. Sustain. Energy Rev. 2017, 80, 9–22. [Google Scholar] [CrossRef]
- Maxwell, J.C. On governors. Proc. R. Soc. Lond. 1868, 16, 270–283. [Google Scholar]
- Kimbark, E.W. Power Systems Stability: Vol. I: Elements of Stability Calculation; Wiley and Sons: Hoboken, NJ, USA, 1953. [Google Scholar]
- Evans, R. Studies of transmission stability. Trans. Am. Inst. Electr. Eng. 1926, 45, 51–94. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, X.; Zhao, L. Feasibility study on new energy multi-feed direct current grid connection. Proc. Inst. Civ. Eng. Energy 2021, 174, 57–66. [Google Scholar] [CrossRef]
- Gunturu, U.B.; Schlosser, C.A. Characterization of wind power resource in the United States. Atmos. Chem. Phys. 2012, 12, 9687–9702. [Google Scholar] [CrossRef]
- Bullich-Massagué, E.; Cifuentes-García, F.-J.; Glenny-Crende, I.; Cheah-Mañé, M.; Aragüés-Peñalba, M.; Díaz-González, F.; Gomis-Bellmunt, O. A review of energy storage technologies for large scale photovoltaic power plants. Appl. Energy 2020, 274, 115213. [Google Scholar] [CrossRef]
- Mulder, F.M. Implications of diurnal and seasonal variations in renewable energy generation for large scale energy storage. J. Renew. Sustain. Energy 2014, 6, 033105. [Google Scholar] [CrossRef]
- Jiang, S.; Xu, Y.; Li, G.; Xin, Y.; Wang, L. Coordinated Control strategy of receiving-end fault ride-through for DC grid connected large-scale wind power. IEEE Trans. Power Deliv. 2021, 37, 2673–2683. [Google Scholar] [CrossRef]
- Shu, Y.; Tang, Y. Analysis and recommendations for the adaptability of China’s power system security and stability relevant standards. CSEE J. Power Energy Syst. 2017, 3, 334–339. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C. Definition and classification of power system stability–revisited and extended. IEEE Trans. Power Syst. 2020, 36, 3271–3281. [Google Scholar] [CrossRef]
- Martinez-Velasco, J.A. Transient Analysis of Power Systems: A Practical Approach; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Kuang, M.; Tian, Y.; Liu, Q. A Review of Control Strategies for Automatic Generation Control of Power Systems Containing New Energy Sources. Authorea Preprints 2023, 824, 1–23. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, X. Modelling and analysis of frequency-responsive wind turbine involved in power system ultra-low frequency oscillation. IEEE Trans. Sustain. Energy 2021, 13, 844–855. [Google Scholar] [CrossRef]
- Pavella, M.; Ernst, D.; Ruiz-Vega, D. Transient Stability of Power Systems: A Unified Approach to Assessment and Control; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Zheng, C.; Sun, H.; Li, H. Response based transient transmission capacity index and emergency control of branch circuits. Chin. J. Electr. Eng. 2021, 41, 581–592. [Google Scholar]
- Xia, Y.; Peng, Y.; Yang, P.; Yu, M.; Wei, W. Distributed coordination control for multiple bidirectional power converters in a hybrid AC/DC microgrid. IEEE Trans. Power Electron. 2016, 32, 4949–4959. [Google Scholar] [CrossRef]
- Wu, Q.H.; Lin, Y.; Hong, C. Transient stability analysis of large-scale power systems: A survey. CSEE J. Power Energy Syst. 2023, 9, 1284–1300. [Google Scholar]
- Marx, D.; Magne, P.; Nahid-Mobarakeh, B.; Pierfederici, S.; Davat, B. Large signal stability analysis tools in DC power systems with constant power loads and variable power loads—A review. IEEE Trans. Power Electron. 2011, 27, 1773–1787. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, L.; Xie, M.; Yu, J.; Qian, L.; Xu, K.; Chen, M.; Wang, Y. Advancements and Challenges in Power Cable Laying. Energies 2024, 17, 2905. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-oriented transient stability analysis of grid-connected converters with power synchronization control. IEEE Trans. Ind. Electron. 2018, 66, 6473–6482. [Google Scholar] [CrossRef]
- Zhong, T.; Yang, H.; Sun, C.; Liu, C.; Chen, J. Adaptive Band-Pass Filter and VMD-Esprit Based Multi-Mode Monitoring Method for Broadband Electromagnetic Oscillation in “Double High” Power Systems. Energies 2023, 16, 3110. [Google Scholar] [CrossRef]
- Ippolito, M.G.; Musca, R.; Sanseverino, E.R.; Zizzo, G. Frequency dynamics in fully non-synchronous electrical grids: A case study of an existing island. Energies 2022, 15, 2220. [Google Scholar] [CrossRef]
- Kuehni, H.P.; Lorraine, R.G. A new A-C network analyzer. Trans. Am. Inst. Electr. Eng. 1938, 57, 67–73. [Google Scholar] [CrossRef]
- Stagg, G.W.; El-Abiad, A.H. Computer Methods in Power System Analysis; McGraw-Hill: Columbus, OH, USA, 1968. [Google Scholar]
- Dommel, H.; Sato, N. Fast transient stability solutions. IEEE Trans. Power Appar. Syst. 1972, 4, 1643–1650. [Google Scholar] [CrossRef]
- Price, W.; Chiang, H.; Clark, H. Load representation for dynamic performance analysis. IEEE Trans. Power Syst. 1993, 8, 472–482. [Google Scholar]
- Amin, S.M. Smart grid: Overview, issues and opportunities. Advances and challenges in sensing, modeling, simulation, optimization and control. Eur. J. Control 2011, 17, 547–567. [Google Scholar] [CrossRef]
- Liu, J.; Wei, Z.; Fang, W.; Duan, C.; Hou, J.; Xiang, Z. Modified quasi-steady state model of DC system for transient stability simulation under asymmetric faults. Math. Probl. Eng. 2015, 2015, 103649. [Google Scholar] [CrossRef]
- Khan, I.; Zeb, K.; Din, W.U.; Islam, S.U.; Ishfaq, M.; Hussain, S.; Kim, H.-J. Dynamic modeling and robust controllers design for doubly fed induction generator-based wind turbines under unbalanced grid fault conditions. Energies 2019, 12, 454. [Google Scholar] [CrossRef]
- Han, P.; Lin, Z.; Wang, L.; Fan, G.; Zhang, X. A Survey on equivalence modeling for large-scale photovoltaic power plants. Energies 2018, 11, 1463. [Google Scholar] [CrossRef]
- Cui, J.; Li, Z.; He, P.; Gong, Z.; Dong, J. Electromechanical transient modeling of energy storage based on virtual synchronous machine technology. Arch. Electr. Eng. 2022, 71, 581–599. [Google Scholar] [CrossRef]
- Fan, M.; Li, Z.; Ding, T.; Huang, L.; Dong, F.; Ren, Z.; Liu, C. Uncertainty evaluation algorithm in power system dynamic analysis with correlated renewable energy sources. IEEE Trans. Power Syst. 2021, 36, 5602–5611. [Google Scholar] [CrossRef]
- Astic, J.; Bihain, A.; Jerosolimski, M. The mixed Adams-BDF variable step size algorithm to simulate transient and long term phenomena in power systems. IEEE Trans. Power Syst. 1994, 9, 929–935. [Google Scholar] [CrossRef]
- Hashim, N.; Hamzah, N.; Arsad, P.M.; Baharom, R.; Ismail, N.N.; Aminudin, N.; Johari, D.; Sallehhudin, A. Modeling of power system dynamic devices incorporated in dynamic computation for power systems for transient stability analysis. In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 15–18 May 2011; pp. 647–652. [Google Scholar]
- Decker, I.; Falcao, D.; Kaszkurewicz, E. Parallel implementation of a power system dynamic simulation methodology using the conjugate gradient method. IEEE Trans. Power Syst. 1992, 7, 458–465. [Google Scholar] [CrossRef]
- Geng, G.; Jiang, Q.; Sun, Y. Parallel transient stability-constrained optimal power flow using GPU as coprocessor. IEEE Trans. Smart Grid 2016, 8, 1436–1445. [Google Scholar] [CrossRef]
- Yu, J.; Pi, J. Influence of wind thermal power capacity ratio on transient stability of AC/DC transmission system. In Proceedings of the 2021 Power System and Green Energy Conference (PSGEC), Shanghai, China, 21–22 August 2021. [Google Scholar]
- Sun, J.; Li, X.; Bai, E.; Zhang, X.; Xu, J.; Yuan, P. Analysis of Transient Voltage Characteristics of Wind-Fire Bundling DC External Transmission System. In Proceedings of the 5th International Conference on Power and Energy Applications, Guangzhou, China, 18–20 November 2022. [Google Scholar]
- He, P.; Fang, Q.; Jin, H.; Ji, Y.; Gong, Z.; Dong, J. Coordinated design of PSS and STATCOM-POD based on the GA-PSO algorithm to improve the stability of wind-PV-thermal-bundled power system. Int. J. Electr. Power Energy Syst. 2022, 141, 108208. [Google Scholar] [CrossRef]
- Kunjumuhammed, L.; Kuenzel, S.; Pal, B. Simulation of Power System with Renewables; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Skilling, H.; Yamakawa, M.H. A graphical solution of transient stability. Electr. Eng. 1940, 59, 462–465. [Google Scholar] [CrossRef]
- Magnusson, P.C. The transient-energy method of calculating stability. Trans. Am. Inst. Electr. Eng. 1947, 66, 747–755. [Google Scholar] [CrossRef]
- Gless, G.E. Direct method of Liapunov applied to transient power system stability. IEEE Trans. Power Appar. Syst. 1966, PAS-85, 159–168. [Google Scholar] [CrossRef]
- El-Abiad, A.H.; Nagappan, K. Transient stability regions of multimachine power systems. IEEE Trans. Power Appar. Syst. 1966, PAS-85, 169–179. [Google Scholar] [CrossRef]
- Friedlander, G.D. The Northeast power failure-a blanket of darkness. IEEE Spectr. 1966, 3, 54–73. [Google Scholar] [CrossRef]
- Savulescu, S.C. Real-Time Stability in Power Systems: Techniques for Early Detection of the Risk of Blackout; Springer: London, UK, 2014. [Google Scholar]
- Chiang, H.D. Direct Methods for Stability Analysis of Electric Power Systems: Theoretical Foundation, BCU Methodologies, and Applications; Wiley: Berlin, Germany, 2011. [Google Scholar]
- Pai, M.A. Energy Function Analysis for Power System Stability; Springer: Greer, SC, USA; Cham, Switzerland, 2012. [Google Scholar]
- Moon, Y.H.; Cho, B.H.; Lee, Y.H. Energy conservation law and its application for the direct energy method of power system stability. In IEEE Power Engineering Society, Proceedings of the 1999 Winter Meeting, New York, NY, USA, 31 January–4 February 1999; IEEE: New York, NY, USA, 1999; Volume 1, pp. 695–700. [Google Scholar]
- Schultz, D.; Gibson, U.J. The variable gradient method for generating Liapunov functions. Trans. Am. Inst. Electr. Eng. 1962, 81, 203–210. [Google Scholar] [CrossRef]
- Jiang, N.; Chiang, H.-D. Energy function for power system with detailed DC model: Construction and analysis. IEEE Trans. Power Syst. 2013, 28, 3756–3764. [Google Scholar] [CrossRef]
- Kakimoto, N.; Ohsawa, Y.; Hayashi, M. Transient stability analysis of multimachine power system with field flux decays via Lyapunov’s direct method. IEEE Trans. Power Appar. Syst. 1980, 5, 1819–1827. [Google Scholar] [CrossRef]
- Chiang, H.-D.; Wu, F.; Varaiya, P. A BCU method for direct analysis of power system transient stability. IEEE Trans. Power Syst. 1994, 9, 1194–1208. [Google Scholar] [CrossRef]
- Kabalan, M.; Singh, P.; Niebur, D. Large signal Lyapunov-based stability studies in microgrids: A review. IEEE Trans. Smart Grid 2016, 8, 2287–2295. [Google Scholar] [CrossRef]
- Dy-Liacco, T.E. Control of Power Systems via the Multi-Level Concept; Case Western Reserve University: Cleveland, OH, USA, 1968. [Google Scholar]
- Sarajcev, P.; Kunac, A.; Petrovic, G.; Despalatovic, M. Artificial intelligence techniques for power system transient stability assessment. Energies 2022, 15, 507. [Google Scholar] [CrossRef]
- James, J.; Hill, D.J.; Lam, A.Y. Intelligent time-adaptive transient stability assessment system. IEEE Trans. Power Syst. 2017, 33, 1049–1058. [Google Scholar]
- Tan, B.; Zhao, J. Debiased uncertainty quantification approach for probabilistic transient stability assessment. IEEE Trans. Power Syst. 2023, 38, 4954–4957. [Google Scholar] [CrossRef]
- Zhu, L.; Wen, W.; Li, J.; Hu, Y. Integrated data-driven power system transient stability monitoring and enhancement. IEEE Trans. Power Syst. 2024, 39, 1797–1809. [Google Scholar] [CrossRef]
- Papadopoulos, P.N.; Milanović, J.V. Probabilistic framework for transient stability assessment of power systems with high penetration of renewable generation. IEEE Trans. Power Syst. 2016, 32, 3078–3088. [Google Scholar] [CrossRef]
- Konstantelos, I.; Sun, M.; Tindemans, S.H.; Issad, S.; Panciatici, P.; Strbac, G. Using vine copulas to generate representative system states for machine learning. IEEE Trans. Power Syst. 2018, 34, 225–235. [Google Scholar] [CrossRef]
- Krishnan, V.; McCalley, J.D.; Henry, S.; Issad, S. Efficient database generation for decision tree based power system security assessment. IEEE Trans. Power Syst. 2011, 26, 2319–2327. [Google Scholar] [CrossRef]
- Thams, F.; Venzke, A.; Eriksson, R.; Chatzivasileiadis, S. Efficient database generation for data-driven security assessment of power systems. IEEE Trans. Power Syst. 2019, 35, 30–41. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [PubMed]
- Bahbah, A.; Girgis, A. New method for generators’ angles and angular velocities prediction for transient stability assessment of multimachine power systems using recurrent artificial neural network. IEEE Trans. Power Syst. 2004, 19, 1015–1022. [Google Scholar] [CrossRef]
- Wehenkel, L.; Pavella, M.; Euxibie, E.; Heilbronn, B. Decision tree based transient stability method a case study. IEEE Trans. Power Syst. 1994, 9, 459–469. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, J.; Ji, L.; Yu, Z.; Lin, K.; Hao, L. Transient stability preventive control of power systems using chaotic particle swarm optimization combined with two-stage support vector machine. Electr. Power Syst. Res. 2018, 155, 111–120. [Google Scholar] [CrossRef]
- Li, J.; Jiang, S.; Li, H.; Chai, W.; Fo, J.; Luo, F.; Ge, N.; Wang, S. Research on fault self-healing control method of intelligent power distribution system based on deep learning. In Proceedings of the 2023 IEEE 7th Conference on Energy Internet and Energy System Integration (EI2), Hangzhou, China, 15–18 December 2023; pp. 2956–2962. [Google Scholar]
- Liu, X.; Ti, C.; Liang, G. Wide-band modelling and transient analysis of the multi-conductor transmission lines system considering the frequency-dependent parameters based on the fractional calculus theory. IET Gener. Transm. Distrib. 2016, 10, 3374–3384. [Google Scholar] [CrossRef]
- Wu, X.; Wu, H.; Shen, D.; Shi, Y.; Cao, L.; Gan, D. Polynomial approximation of transient stability region boundary in parameter space based on collocation method. IEEE Trans. Power Syst. 2021, 36, 5971–5974. [Google Scholar] [CrossRef]
- Watanabe, M.; Mitani, Y.; Tsuji, K. A numerical method to evaluate power system global stability determined by limit cycle. IEEE Trans. Power Syst. 2004, 19, 1925–1934. [Google Scholar] [CrossRef]
- Machlev, R.; Heistrene, L.; Perl, M. Explainable Artificial Intelligence (XAI) techniques for energy and power systems: Review, challenges and opportunities. Energy AI 2022, 9, 100169. [Google Scholar] [CrossRef]
- Sun, J.; Taylor, D.; Bollt, E.M. Causal network inference by optimal causation entropy. SIAM J. Appl. Dyn. Syst. 2015, 14, 73–106. [Google Scholar] [CrossRef]
- Poincaré, H.; Popp, B.D. The Three-Body Problem and the Equations of Dynamics: Poincaré’s Foundational Work on Dynamical Systems Theory; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Jazar, R.N. Perturbation Methods in Science and Engineering; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Mudavanhu, B.; O’malley, R.E., Jr.; Williams, D.B. Working with multiscale asymptotics: Solving weakly nonlinear oscillator equations on long-time intervals. J. Eng. Math. 2005, 53, 301–336. [Google Scholar]
- Cartmell, M.; Ziegler, S.; Khanin, R.; Forehand, D. Multiple scales analyses of the dynamics of weakly nonlinear mechanical systems. Appl. Mech. Rev. 2003, 56, 455–492. [Google Scholar] [CrossRef]
- Sethna, P.R. On averaged and normal form equations. Nonlinear Dyn. 1995, 7, 1–10. [Google Scholar] [CrossRef]
- Tao, M. Simply improved averaging for coupled oscillators and weakly nonlinear waves. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 1–21. [Google Scholar] [CrossRef]
- Ziane, M. On a certain renormalization group method. J. Math. Phys. 2000, 41, 3290–3299. [Google Scholar] [CrossRef]
- O’malley, R.E., Jr.; Williams, D.B. Deriving amplitude equations for weakly-nonlinear oscillators and their generalizations. J. Comput. Appl. Math. 2006, 190, 3–21. [Google Scholar] [CrossRef][Green Version]
- Abed, E.; Alexander, J. Approximation of faulted power system trjectories via averaging. In Proceedings of the 26th IEEE Conference on Decision and Control, Los Angeles, CA, USA, 9–11 December 1987; Volume 26, pp. 863–865. [Google Scholar]
- Gurrala, G.; Dinesha, D.L.; Dimitrovski, A.; Sreekanth, P.; Simunovic, S.; Starke, M. Large multi-machine power system simulations using multi-stage adomian decomposition. IEEE Trans. Power Syst. 2017, 32, 3594–3606. [Google Scholar] [CrossRef]
- Yao, R.; Sun, K.; Qiu, F. Vectorized efficient computation of padé approximation for semi-analytical simulation of large-scale power systems. IEEE Trans. Power Syst. 2019, 34, 3957–3959. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, K.; Yao, R.; Wang, B. Power system time domain simulation using a differential transformation method. IEEE Trans. Power Syst. 2019, 34, 3739–3748. [Google Scholar] [CrossRef]
- Peponides, G.; Kokotovic, P.; Chow, J. Singular perturbations and time scales in nonlinear models of power systems. IEEE Trans. Circuits Syst. 1982, 29, 758–767. [Google Scholar] [CrossRef]
- Shen, F.; Ju, P.; Shahidehpour, M.; Li, Z.; Wang, C.; Shi, X. Singular perturbation for the dynamic modeling of integrated energy systems. IEEE Trans. Power Syst. 2020, 35, 1718–1728. [Google Scholar] [CrossRef]
- Giraldi, L.; Liu, D.; Matthies, H.G.; Nouy, A. To be or not to be intrusive? The solution of parametric and stochastic equations—Proper generalized decomposition. SIAM J. Sci. Comput. 2015, 37, A347–A368. [Google Scholar] [CrossRef]
- Giraldi, L.; Litvinenko, A.; Liu, D. To be or not to be intrusive? The solution of parametric and stochastic equations—The “plain vanilla” Galerkin case. SIAM J. Sci. Comput. 2014, 36, A2720–A2744. [Google Scholar] [CrossRef][Green Version]
- Xia, B.; Wu, H.; Qiu, Y.; Lou, B.; Song, Y. A Galerkin method-based polynomial approximation for parametric problems in power system transient analysis. IEEE Trans. Power Syst. 2018, 34, 1620–1629. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Gan, D.; Wu, H. Harmonic solution of higher-dimensional second order Kuramoto oscillator network. IEEE Access 2024, 12, 33816–33831. [Google Scholar] [CrossRef]
- Shen, D.; Wu, H.; Xia, B.; Gan, D. Arbitrarily sparse polynomial chaos expansion for high-dimensional parametric problems: Parametric and probabilistic power flow as an example. IEEE Syst. J. 2021, 16, 4950–4961. [Google Scholar] [CrossRef]
- Qiu, Q.; Ma, R.; Kurths, J.; Zhan, M. Swing equation in power systems: Approximate analytical solution and bifurcation curve estimate. Chaos 2020, 30, 013110. [Google Scholar] [CrossRef]
- Tsolas, N.; Arapostathis, A.; Varaiya, P. A structure preserving energy function for power system transient stability analysis. IEEE Trans. Circuits Syst. 1985, 32, 1041–1049. [Google Scholar] [CrossRef]
- Sastry, S. Nonlinear Systems; Springer: New York, NY, USA, 1999. [Google Scholar]
- Thapar, J.; Vittal, V.; Kliemann, W.; Fouad, A. Application of the normal form of vector fields to predict interarea separation in power systems. IEEE Trans. Power Syst. 1997, 12, 844–850. [Google Scholar] [CrossRef]
- Lin, C.-M.; Vittal, V.; Kliemann, W.; Fouad, A. Investigation of modal interaction and its effects on control performance in stressed power systems using normal forms of vector fields. IEEE Trans. Power Syst. 1996, 11, 781–787. [Google Scholar] [CrossRef]
- Saha, S.; Fouad, A.; Kliemann, W.; Vittal, V. Stability boundary approximation of a power system using the real normal form of vector fields. IEEE Trans. Power Syst. 1997, 12, 797–802. [Google Scholar] [CrossRef]
- Cheng, D.; Ma, J.; Lu, Q.; Mei, S. Quadratic form of stable sub-manifold for power systems. Int. J. Robust Nonlinear Control 2004, 14, 773–788. [Google Scholar] [CrossRef]
- Cheng, D.; Ma, J. Calculation of stability region. In Proceedings of the 42nd IEEE International Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003. [Google Scholar]
- Cheng, D. Semi-tensor product of matrices and its applications to dynamic systems. In New Directions and Applications in Control Theory; Springer: Berlin/Heidelberg, Germany, 2005; pp. 61–79. [Google Scholar]
- Cheng, D.; Qi, H.; Xue, A. A survey on semi-tensor product of matrices. J. Syst. Sci. Complex. 2007, 20, 304–322. [Google Scholar] [CrossRef]
- Cheng, D.; Qi, H. Semi-Tensor Product of Matrices—Theory and Applications; Science Press: Beijing, China, 2007. [Google Scholar]
- Cheng, D.; Feng, J.-E.; Lv, H. Solving fuzzy relational equations via semitensor product. IEEE Trans. Fuzzy Syst. 2011, 20, 390–396. [Google Scholar] [CrossRef]
- Dorfler, F.; Bullo, F. Kron reduction of graphs with applications to electrical networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 60, 150–163. [Google Scholar] [CrossRef]
- Dörfler, F.; Bullo, F. Synchronization and transient stability in power networks and nonuniform Kuramoto oscillators. SIAM J. Control Optim. 2012, 50, 1616–1642. [Google Scholar] [CrossRef]
- Dörfler, F.; Chertkov, M.; Bullo, F. Synchronization in complex oscillator networks and smart grids. Proc. Natl. Acad. Sci. USA 2013, 110, 2005–2010. [Google Scholar] [CrossRef] [PubMed]
- Dörfler, F.; Bullo, F. Synchronization in complex networks of phase oscillators: A survey. Automatica 2014, 50, 1539–1564. [Google Scholar] [CrossRef]
- La Scala, M.; Lorusso, G.; Sbrizzai, R.; Trovato, M. A qualitative approach to the transient stability analysis [of power systems]. IEEE Trans. Power Syst. 1996, 11, 1996–2002. [Google Scholar] [CrossRef]
- Gan, D.; Thomas, R.J. Stability-constrained optimal power flow. IEEE Trans. Power Syst. 2000, 15, 535–540. [Google Scholar] [CrossRef]
- Liu, C.; Wang, B.; Sun, K. Fast power system simulation using semi-analytical solutions based on Pade approximants. In Proceedings of the 2017 IEEE Power and Energy Society General Meeting (PESGM), Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Anghel, M.; Milano, F.; Papachristodoulou, A. Algorithmic Construction of Lyapunov Functions for Power System Stability Analysis. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 2533–2546. [Google Scholar] [CrossRef]
- Prestel, A.; Delzell, C. Positive Polynomials: From Hilbert’s 17th Problem to Real Algebra; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Shen, Z.; Arraño-Vargas, F.; Konstantinou, G. Virtual testbed for development and evaluation of power system digital twins and their applications. Sustain. Energy Grids Netw. 2024, 38, 101331. [Google Scholar]
- Wang, Y.; Sun, H.; Xu, S.; Zhao, B. Transient Stability Analysis and Improvement for the Grid-Connected VSC System with Multi-Limiters. IEEE Trans. Power Syst. 2023, 39, 1979–1995. [Google Scholar] [CrossRef]
- Xing, G.; Chen, L.; Min, Y.; Tang, Y.; Li, Y.; Xu, S. Effects of PLL frequency limiters for synchronization stability of grid connected VSC and strategy to realize global stability. IEEE Trans. Energy Convers. 2023, 38, 2096–2107. [Google Scholar] [CrossRef]
- Shi, P.; Zhou, J.; Gan, D.; Wang, Z. A rational fractional representation method for wind power integrated power system parametric stability analysis. IEEE Trans. Power Syst. 2018, 33, 7122–7131. [Google Scholar] [CrossRef]




| Methods | Principles | Advantages | Disadvantages | Future Directions |
|---|---|---|---|---|
| Simulation Methods | Use step-by-step integration to directly obtain numerical solutions and capture the system’s nonlinear dynamics. |
|
| Develop tools with high-resolution relationships, systemic comprehensiveness, high levels of visualization, and robust stability analysis. |
| Direct Methods | Based on Lyapunov’s theory, it focuses on the initial conditions of faults to determine transient stability. |
|
| More convenient computations and more refined theories to enhance practical applicability. |
| Data-Driven Methods | Mine the mapping relationship between system operational state and stability condition from offline data. |
|
| Improve data generation techniques and labeling accuracy and enhance interpretability and predictive performance of intelligent algorithms. |
| Analytical Methods | Use mathematical techniques to derive approximate analytical expressions for system responses and stability. |
|
| Develop more robust techniques to handle highly nonlinear systems and combine analytical methods with other approaches for enhanced accuracy and applicability. |
| Other Methods | Combine various approaches to leverage their complementary strengths for stability analysis. |
|
| Further explore the integration of different methods for comprehensive stability analysis and develop hybrid approaches tailored for modern power systems with high penetration of renewable energy sources. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Li, J.; Yang, H. Research Methods for Transient Stability Analysis of Power Systems under Large Disturbances. Energies 2024, 17, 4330. https://doi.org/10.3390/en17174330
Wu H, Li J, Yang H. Research Methods for Transient Stability Analysis of Power Systems under Large Disturbances. Energies. 2024; 17(17):4330. https://doi.org/10.3390/en17174330
Chicago/Turabian StyleWu, Hao, Jing Li, and Haibo Yang. 2024. "Research Methods for Transient Stability Analysis of Power Systems under Large Disturbances" Energies 17, no. 17: 4330. https://doi.org/10.3390/en17174330
APA StyleWu, H., Li, J., & Yang, H. (2024). Research Methods for Transient Stability Analysis of Power Systems under Large Disturbances. Energies, 17(17), 4330. https://doi.org/10.3390/en17174330







