Distribution System State Estimation Based on Power Flow-Guided GraphSAGE

Abstract

Acquiring real-time status information of the distribution system forms the foundation for optimizing the management of power system operations. However, missing measurements, bad data, and inaccurate system models present a formidable challenge for distribution system state estimation (DSSE) in practical applications. This paper proposes a physics-informed graphical learning state estimation approach, to address these limitations by integrating power flow equations and GraphSAGE. The generalization ability of GraphSAGE for unknown nodes is used to perform inductive learning of measurement information. For unseen measurement points in the training set, the simulation proves that the proposed approach can still satisfactorily predict the state quantity. The training process is guided by power flow equations to ensure it has physical significance. Additionally, the possibility of applying the proposed approach to an actual distribution area is explored. Equivalent preprocessing of the three-phase voltage measurement data of the actual distribution area is conducted to improve the estimation accuracy of the transformer measurement points and simplify the computation required for state estimation.

1. Introduction

With the increasing amount of distributed renewable energy generation, flexible loads, and smart terminal devices being connected to the distribution system, the network state of the distribution system is becoming increasingly complex, and the real-time operation and control of the system require higher precision of the basic data. State estimation is an important task in system monitoring and it can use the received raw measurements to provide more reliable estimation data for the distribution system, to ensure safe and stable operation [1].

Currently, weighted least squares (WLS)-based state estimation is widely used in actual power grids. Under the assumption of ideal conditions where the measurement noise in the system consists solely of Gaussian white noise, WLS is an unbiased minimum variance estimator. However, unlike transmission grids, distribution grids suffer from inadequate measurements, complex topology, and inaccurate physical model parameters. Especially with the rising trend of promoting the high penetration of resources-based distributed energy, the uncertainty of the distribution grid increases, making it difficult to guarantee the observability of the active distribution grid [2,3,4], which can cause excessive iterations of the WLS or even non-convergence, resulting in a significant decrease in estimation accuracy [5]. To enhance robustness, there are generally two methods: one is to add a bad data identification module after the WLS estimation, such as the largest normalized residual (LNR) test or the estimation identification method; the other is to use robust estimation methods to improve the robustness and convergence of state estimation. In recent years, both domestic and foreign scholars have proposed the use of weighted least absolute value (WLAV), non-quadratic criteria (such as quadratic-linear, quadratic-constant), least median of squares (LMS), least trimmed squares (LTS), maximum normal measurement rate (MNMR), etc. However, these model-based algorithms are still limited by precise model parameters and difficult to apply in distribution systems with limited measurement information and low measurement accuracy.

The advancement of information levels in distribution systems, coupled with the rapid development of artificial intelligence technology, is driving the adoption of smart meters, phasor measurement units (PMUs), and other new measurement devices. These technologies are enabling the storage of increasing amounts of historical data in modern complex large-scale systems, forming measurement ‘big data’, which encompasses process information based on system parameters and noise characteristics. Because data-driven methods are not dependent on physical equations, they have become an attractive research direction. The main trend in these methods involves utilizing artificial neural networks (ANNs) to describe either a portion or the entirety of the power system [6]. The numerous models explored in various studies include multi-layer perceptrons (MLPs) [7,8,9]; recurrent neural networks (RNNs) employing gated mechanisms or long short-term memory (LSTM) for estimation and forecasting [10]; convolutional neural networks (CNNs) [11]; and generative adversarial networks (GANs) and autoencoders [12], as well as Bayesian deep learning for static DSSE [13,14]. Beyond ANNs, methods like kernel-weighted neighbors and kernel functions have also been utilized for estimating the current state of the power grid [15]. However, the data-driven methods mentioned above only capture the potential relationships between system quantities and state quantities. The absence of a physical model for the underlying system can cause overfitting in learning models [16], decreasing their resistance to abnormal conditions like missing measurements due to packet loss, or corrupted data from instrument miscalibration and smart meter manipulation [17].

Due to the limitations of the above methods, integrating model-based and data-driven approaches offers a promising solution. In [18], a physics regularization term was added to the loss function of deep neural networks (DNNs) to leverage physical knowledge. Reference [19] presents a physics-informed dynamic DSSE that incorporates power flow equations as a regularizer. Reference [10] introduces a state estimation approach using a prox-linear network that integrates physics-based optimization with neural networks for high computational efficiency. A real-time monitoring state estimator based on Gaussian–Newton unrolled neural networks is presented in [20]. Hybrid state estimation approaches using auto-encoders, where the decoder is replaced by a physical model, are discussed in [21,22]. Reference [23] proposes a physics-aware learning approach that embeds physical connections into neural networks. The work in [24] advances the field by pruning unnecessary connections. GNNs-based methods have also been proposed for parameter identification [25] and state estimation [26]. The authors of [27] present a deep learning model using GNNs that employs weakly supervised learning. By integrating power flow equations and physical penalty terms, this approach decreases data requirements and enhances robustness towards inaccurate measurements.

Although the above works enhance interpretation by embedding physical knowledge, they typically study DSSE under a fixed graph topology. In practical applications, distribution systems often undergo frequent topological changes [28]. This necessitates retraining learning-based methods to adapt to the new topology, a process that is both data intensive and time consuming, making these methods less cost-effective for handling minor node changes in large-scale systems.

Therefore, this paper proposes a DSSE approach based on power flow-guided GraphSAGE. The main contributions are summarized as follows:

(1)

By leveraging the generalization ability of GraphSAGE for unknown nodes, inductive learning is performed using measurement information. The simulation results show that even for measurement points not present in the training set, this approach can still qualitatively predict state variables.

(2)

The training process is guided by power flow equations, ensuring that the model remains physically meaningful.

(3)

The potential application of the proposed approach to real-world distribution systems is explored. Equivalent preprocessing of three-phase voltage measurement data is performed to improve the estimation accuracy at transformer measurement points and simplify the computation involved in DSSE.

The rest of this paper is organized as follows: Section 2 introduces the traditional solution form of the DSSE problem, as well as the approach proposed in this paper. Section 3 relates the development of a model for transformer nodes to enhance the estimation accuracy of transformer measurement points, particularly for actual distribution systems with widespread transformers and significant three-phase imbalance. Section 4 evaluates the performance of the proposed approach through the analysis of typical cases, including IEEE14, IEEE33, and an actual distribution area experiment. Finally, Section 5 concludes the work.

2. Methodology

This section presents three key elements of the proposed DSSE approach: a model-based method, GraphSAGE, and a novel fusion that leverages the strengths of both techniques through power flow-guided GraphSAGE.

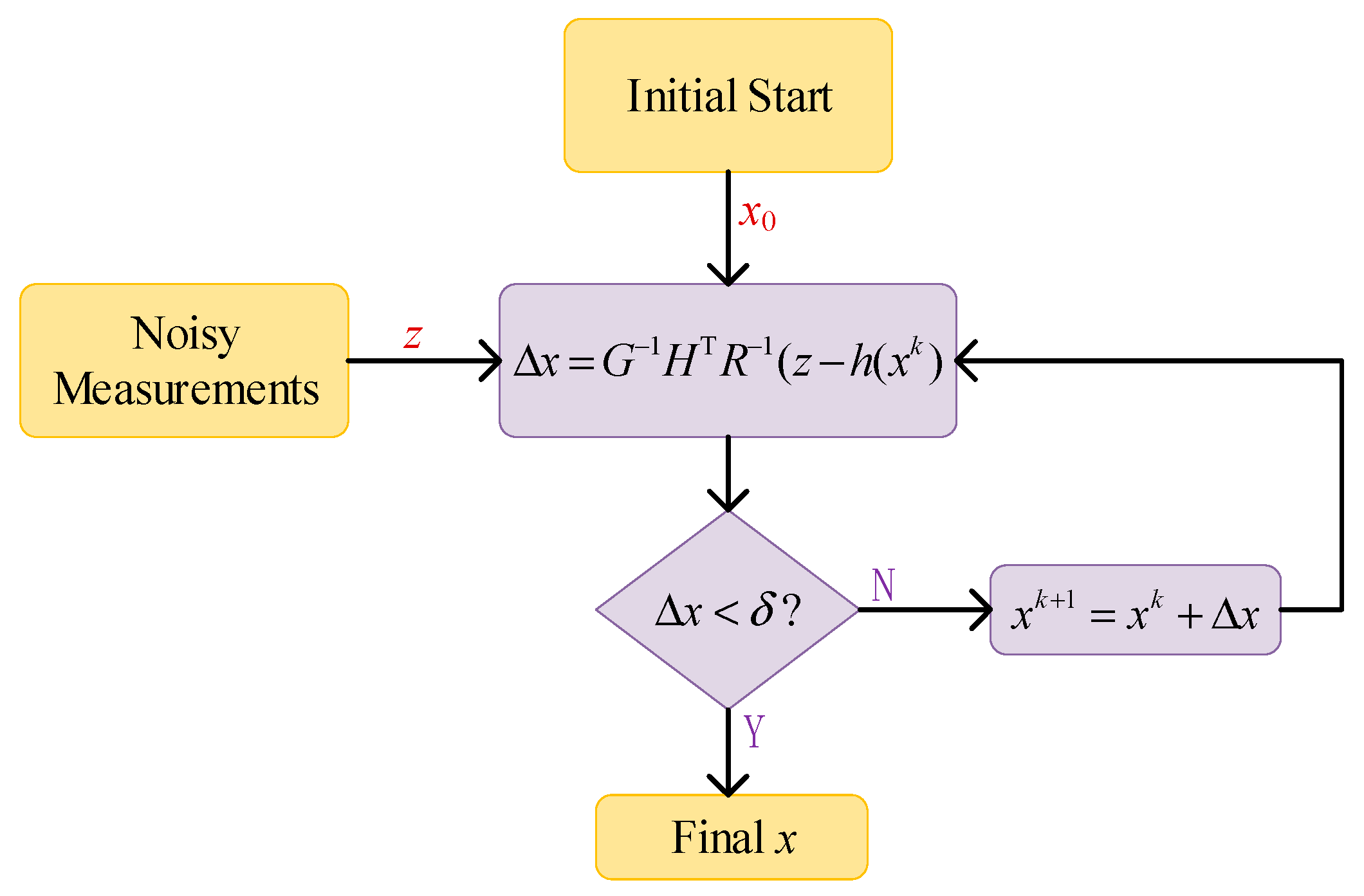
2.1. Traditional Model-Based Method

The physical model for DSSE is based on the relationships between the network topology, line parameters, state variables, and real-time measurements, which can be expressed as follows:

$$z=h(x)+\epsilon$$

(1)

where z is the measured variable, which usually includes bus voltages, bus power injections, branch power flows, etc.; h(∙) is the conversion function from the realized state to the measurement, which contains information about the system’s physical model parameters; x is the state variable, which is usually the magnitude and phase angle of the bus voltages; and ε is the measurement error.

Here, we take as an example the classic WLS method, shown in Figure 1, which aims to minimize the weighted residuals:

$$\min J(x)={[z-h(x)]}^{\mathrm{T}}W[z-h(x)]$$

(2)

where W is the measurement weight matrix and R is the covariance matrix corresponding to the measurement error, meaning that the solution to the above optimization problem is an unbiased estimate.

Since h(x) is a nonlinear function of x, the state variable x cannot be calculated directly, so the Newton method is used for the following iterative solution:

$$\Delta x={[H^{\mathrm{T}}(x)R^{-1}H(x)]}^{-1}{H}^{\mathrm{T}}(x)R^{-1}(z-h(x))$$

(3)

$$x^{k+1}=x^k+\Delta x$$

(4)

where $H(x)=\partial h(x)/\partial x$ is the Jacobian matrix measurement and k is the iteration number; until the convergence criterion is satisfied, the system’s state estimation value can be obtained.

There is a minimum amount of required measurements necessary for the regression to be mathematically possible. This method necessitates having at least as many measurements as state variables, i.e., m ≥ 2n − k, where n is the number of buses and k is the number of defined slack buses. However, meeting this requirement without providing sufficient redundancy can seriously affect the accuracy of the estimation. In practice, m ≈ 4n yields satisfactory results. This is almost sufficient for transmission grids, but the iterative process may fail to converge under conditions of poor observability or high measurement noise, rendering it unsuitable for distribution systems.

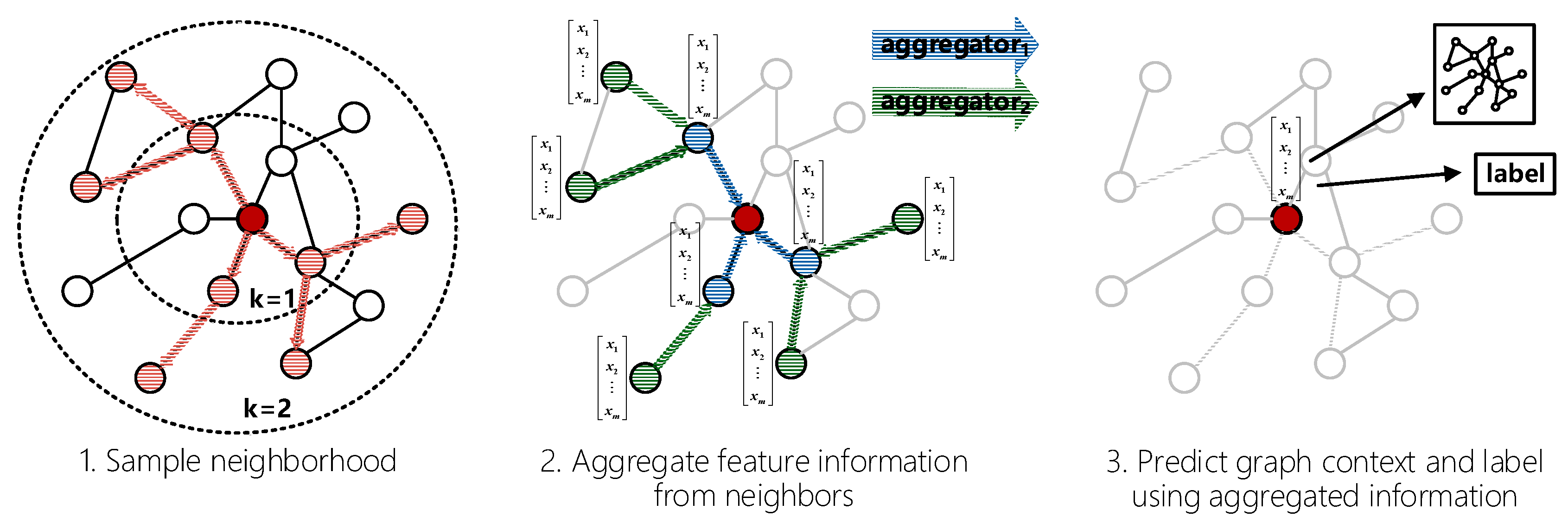
2.2. GraphSAGE

Traditional graph embedding algorithms, such as those based on matrix decomposition and random walks, require the use of all node information during the iterative process and must learn vector representations for all nodes. These methods are inherently transductive, meaning they cannot naturally generalize to unseen nodes. When new nodes are added, the entire network must be recalculated.

In contrast, GraphSAGE, proposed by William L. Hamilton et al., is an inductive framework that can efficiently generate embeddings for unseen nodes by leveraging node feature information [29]. GraphSAGE is designed to learn a method for node representation, specifically how to sample and aggregate node features from a node’s local neighborhood, rather than training separate embeddings for each node. Unlike previous methods that store the mapped results, GraphSAGE stores the mapping function that generates embeddings, making it more scalable. This makes GraphSAGE particularly well suited for the node-rich topologies of distribution systems, allowing new nodes to be directly represented based on the aggregation of their neighbors’ features without the need to iterate the entire network again. As illustrated in Figure 2, the algorithm consists of three main steps: (1) node sampling; (2) neighbor aggregation; and (3) node representation learning based on the aggregated information.

In practical applications, the buses of the distribution system can be treated as nodes, and the lines as connections between points, to construct a graph topology. The measurement information from the buses, such as voltage magnitude, phase angle, and active and reactive power, can be used as input features for the nodes.

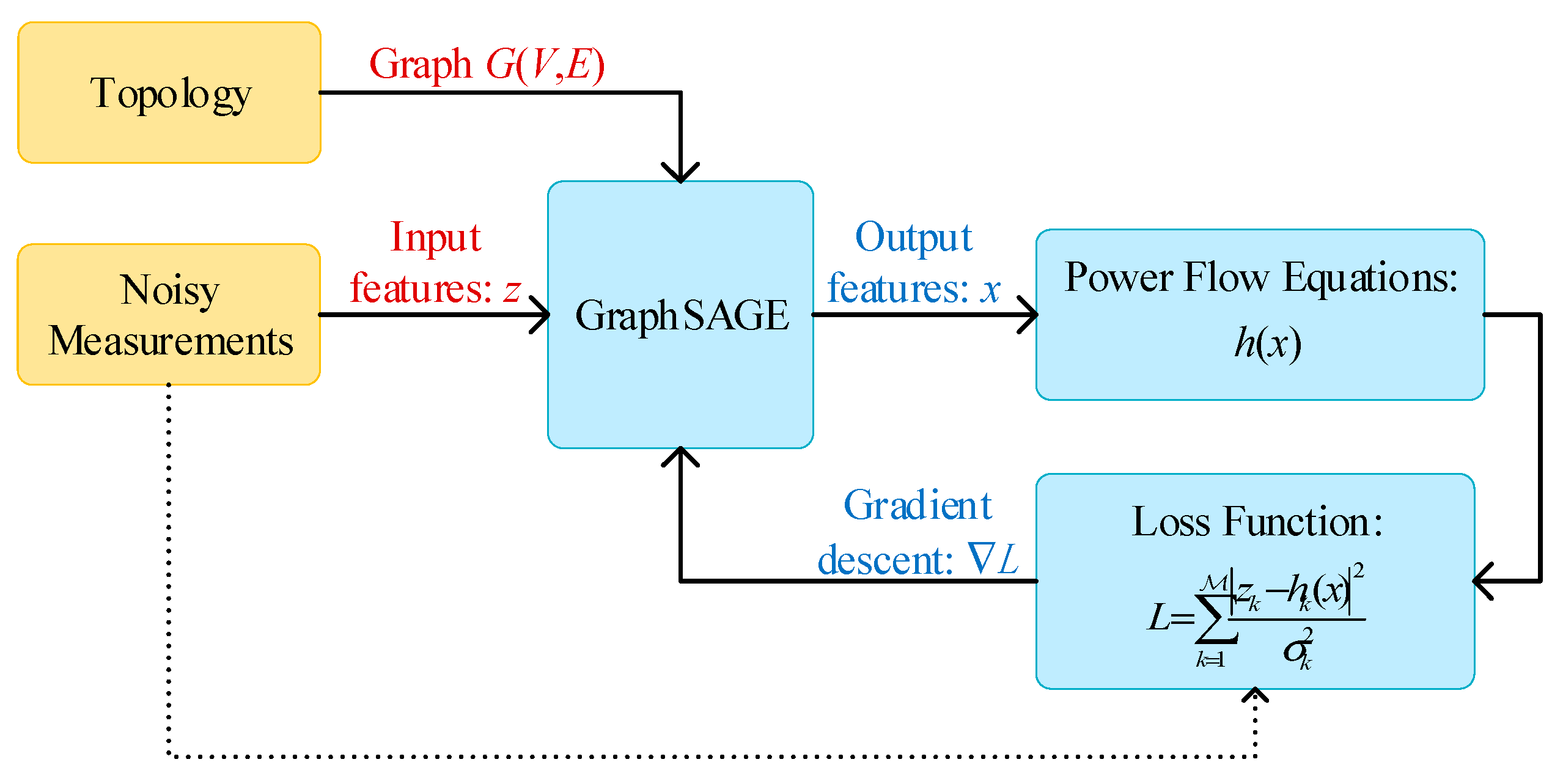
2.3. Proposed Approach

To ensure that the estimation has physical meaning, this paper proposes a DSSE approach using power flow-guided GraphSAGE, as illustrated in Figure 3. The GraphSAGE algorithm takes the graph $\mathcal{G}$ and the measurement vector z as inputs, and outputs an estimated state vector x, which is subsequently used to calculate the estimated values h(x). The model’s loss function is set to minimize the objective of the WLS method.

In actual operating conditions, issues such as inaccurate system parameters, variable topology, unbalanced three-phase power, and poor observability make it impossible to obtain true label data. In this paper, the measurement function h(x) uses the following power flow equations:

$$h(x)=\{\begin{array}{c}{V}_i=V_i\\ {\theta }_{ij}={\theta }_i-{\theta }_j\\ P_i={\displaystyle \sum _{j\in i}{V}_i{V}_j(G_{ij}\cos {\theta }_{ij}+B_{ij}\sin {\theta }_{ij})}\\ Q_i={\displaystyle \sum _{j\in i}{V}_i{V}_j(G_{ij}\sin {\theta }_{ij}+B_{ij}\cos {\theta }_{ij})}\end{array}$$

(5)

where V_i and V_j are the voltage magnitudes at the starting and ending nodes of branch ij; θ_ij is the phase angle difference between the voltages at both ends of branch ij; G_ij and B_ij are the real and imaginary parts of element ij in the admittance matrix; and P_i and Q_i are the active and reactive power injections of bus i derived from the power flows.

The training process for the PF-GraphSAGE approach involves four steps:

• The GraphSAGE algorithm estimates the state vector x from the input topological graph $\mathcal{G}$ and the measurement vector z;
• The state vector x is used to derive the network values through the power flow equations h(x);
• The estimated values h(x) are compared to the actual measurements z using the WLS loss function, with each estimation error weighted by the inverse of its measurement variance;
• The gradient descent method is applied to the loss function L to adjust the GraphSAGE model based on the computed partial derivatives.

Algorithm 1 presents the pseudocode for GraphSAGE. In summary, the algorithm primarily includes five parts: initialization, sampling neighborhoods, aggregating features, skip connections, and normalization.

Algorithm 1: GraphSAGE Algorithm

Input: Graph $\mathcal{G}$($\mathcal{V}$, ε); depth K; input features zi{Vi, σVi, θi, σθi, Pi, σPi, Qi, σQi}, ∀i ∈ $\mathcal{V}$ ; weight matrices Wk, ∀k ∈ {1, …, K}; non-linearity ϕ; differentiable aggregator functions AGGREGATEk, ∀k ∈ {1, …, K}; neighborhood function $\mathcal{N}$: i→2 $\mathcal{V}$

Output: output features xi {Vi, θi, ∀i ∈ $\mathcal{V}$}

In this algorithm, $\mathcal{G}$($\mathcal{V}$, ε) represents the topological graph; K is the number of layers in the network, which also corresponds to the number of hops that each vertex can use to aggregate its neighboring nodes, as each additional layer allows the aggregation of more distant neighbors; z_i, ∀i ∈ $\mathcal{V}$ represents the feature vector of node i and serves as an input; ${\mathrm{h}}_j^{k-1}$, ∀j ∈ $\mathcal{N}$(i) represents the embedding of node j, the neighbor of node i, in layer k; ${\mathrm{h}}_{\mathcal{N}\left(i\right)}^k$ represents the feature representation of all neighboring nodes of node i in layer k; ${\mathrm{h}}_i^k$, ∀i ∈ ν is the feature representation of node i in layer k; $\mathcal{N}$(i) is defined as uniformly sampling a fixed number of elements from the set {j ∈ i: (j,$\mathcal{V}$) ∈ ε}, i.e., the node neighbors in each layer of GraphSAGE are sampled from the previous layer network, with not all neighbors participating, and the number of sampled neighbors is fixed; the final output state variable is x_i; and the Aggregation functions include the Mean aggregator, LSTM aggregator, and Pooling aggregator. For more information, please refer to the original article.

3. Distribution System Three-Phase Data Preprocessing

In practical power grids, distribution systems are equipped with a large number of intelligent fusion terminals, which can collect power, voltage magnitude, and current magnitude measurement information, enriching the measurement configuration. The measurement configuration in the marketing system is relatively sufficient, and it is generally able to achieve full coverage of the measurement of distribution transformers. The connection of these devices is usually adopted in the form of three-phase metering. The types of measurement are as follows: three-phase voltage magnitude $V_i^d$, d ∈ a{a,b,c}; three-phase injected current magnitude $I_i^d$; three-phase injected active power $P_i^d$; and three-phase injected reactive power $Q_i^d$ (all relative to the neutral point).

To improve the accuracy of DSSE, this study conducts mathematical modeling for transformers operating under three-phase unbalanced conditions. In this model, the measured voltages at the transformer points are equivalent to voltage sources. The equivalent circuit is shown in Figure 4. The three points A, B, and C marked in the figure are the collection points on the low-voltage side of the distribution transformer; E_A, E_B, and E_C are three-phase voltage sources, and the collected three-phase voltages and three-phase currents are U_A, U_B, and U_C and I_A, I_B, and I_C. The short-circuit impedance of the distribution transformer is composed of resistance and reactance components, which are, respectively, represented as R_A, R_B, and R_C and X_A, X_B, and X_C. The zero-sequence impedance in the figure is also composed of resistance and reactance components, which are, respectively, represented as R_n and X_n. Z_A, Z_B, and Z_C in the figure represent the load impedance of the distribution transformer. I_n is the neutral current in the equivalent circuit of the transformer.

The voltage loop equations of each phase are written, respectively, according to the real part and the imaginary part:

$$\{\begin{array}{c}{E}_{Ar}=U_{Ar}+R_A\cdot I_A\cdot \cos {\beta }_A-X_A\cdot I_A\cdot \sin {\beta }_A+R_{\mathrm{n}}{I}_{nr}-X_{\mathrm{n}}\left(I_A\cdot \cos {\beta }_A+I_B\cdot \cos {\beta }_B+I_C\cdot \cos {\beta }_C\right)\\ E_{Ai}=U_{Ai}+R_A\cdot I_A\cdot \sin {\beta }_A+X_A\cdot I_A\cdot \cos {\beta }_A+R_{\mathrm{n}}{I}_{ni}+X_{\mathrm{n}}\left(I_A\cdot \cos {\beta }_A+I_B\cdot \cos {\beta }_B+I_C\cdot \cos {\beta }_C\right)\\ E_{Br}=U_{Br}+R_B\cdot I_B\cdot \cos {\beta }_B-X_B\cdot I_B\cdot \sin {\beta }_B+R_{\mathrm{n}}{I}_{nr}-X_{\mathrm{n}}\left(I_A\cdot \cos {\beta }_A+I_B\cdot \cos {\beta }_B+I_C\cdot \cos {\beta }_C\right)\\ E_{Bi}=U_{Bi}+R_B\cdot I_B\cdot \sin {\beta }_B+X_B\cdot I_B\cdot \cos {\beta }_B+R_{\mathrm{n}}{I}_{ni}+X_{\mathrm{n}}\left(I_A\cdot \cos {\beta }_A+I_B\cdot \cos {\beta }_B+I_C\cdot \cos {\beta }_C\right)\\ E_{Cr}=U_{Cr}+R_C\cdot I_C\cdot \cos {\beta }_C-X_C\cdot I_C\cdot \sin {\beta }_C+R_{\mathrm{n}}{I}_{nr}-X_{\mathrm{n}}\left(I_A\cdot \cos {\beta }_A+I_B\cdot \cos {\beta }_B+I_C\cdot \cos {\beta }_C\right)\\ E_{Ci}=U_{Ci}+R_C\cdot I_C\cdot \sin {\beta }_C+X_C\cdot I_C\cdot \cos {\beta }_C+R_{\mathrm{n}}{I}_{ni}+X_{\mathrm{n}}\left(I_A\cdot \cos {\beta }_A+I_B\cdot \cos {\beta }_B+I_C\cdot \cos {\beta }_C\right)\end{array}$$

(6)

where β = α − θ is the angle between the voltage at the three-phase measurement point and the voltage source; α is the angle between the voltage at the three-phase measurement point, ${\alpha }_A+{\alpha }_B+{\alpha }_C=0$; and θ is the angle between the voltage and current at the three-phase measurement point (i.e., the power factor angle):

$$\{\begin{array}{c}{\theta }_A=\arctan \left(Q_A/P_A\right)\\ {\theta }_B=\arctan \left(Q_B/P_B\right)\\ {\theta }_C=\arctan \left(Q_C/P_C\right)\end{array}.$$

(7)

Since the equivalent three-phase voltage sources have equal values, we have the following:

$$E=E_A=E_B=E_C.$$

(8)

This mathematical model is a set of multivariate nonlinear equations, which are difficult to solve directly. Therefore, the model can be expressed as an optimization problem to solve for the equivalent voltage E, with constraints applied to the network state.

The intelligent optimization algorithm adopted in this paper is the Chaos Game Optimization (CGO) Algorithm [30]. The objective functions and constraints of the optimization problem are set as follows:

$$\min F\left({\alpha }_A,{\alpha }_B,{\alpha }_C,R_n,X_n,E\right)={\displaystyle \sum _{i=1}^6\left|f_{\mathrm{i}}\left({\alpha }_A,{\alpha }_B,{\alpha }_C,R_n,X_n,E\right)\right|}$$

(9)

$$\{\begin{array}{c}-60\le {\alpha }_A\le 60\\ -180\le {\alpha }_B\le -60\\ 60\le {\alpha }_C\le 180\\ 0\le R_n\le 10\\ 0\le X_n\le 10\\ 0.8\le E\le 1.2\end{array}.$$

(10)

This paper takes as an example a 10 kV substation in a certain area of northeastern China, as shown in Figure 5, below. The three-phase measured voltage and its equivalent effect of voltage during a certain time period are shown in Figure 6, below, aligning with the observed trend.

4. Case Studies

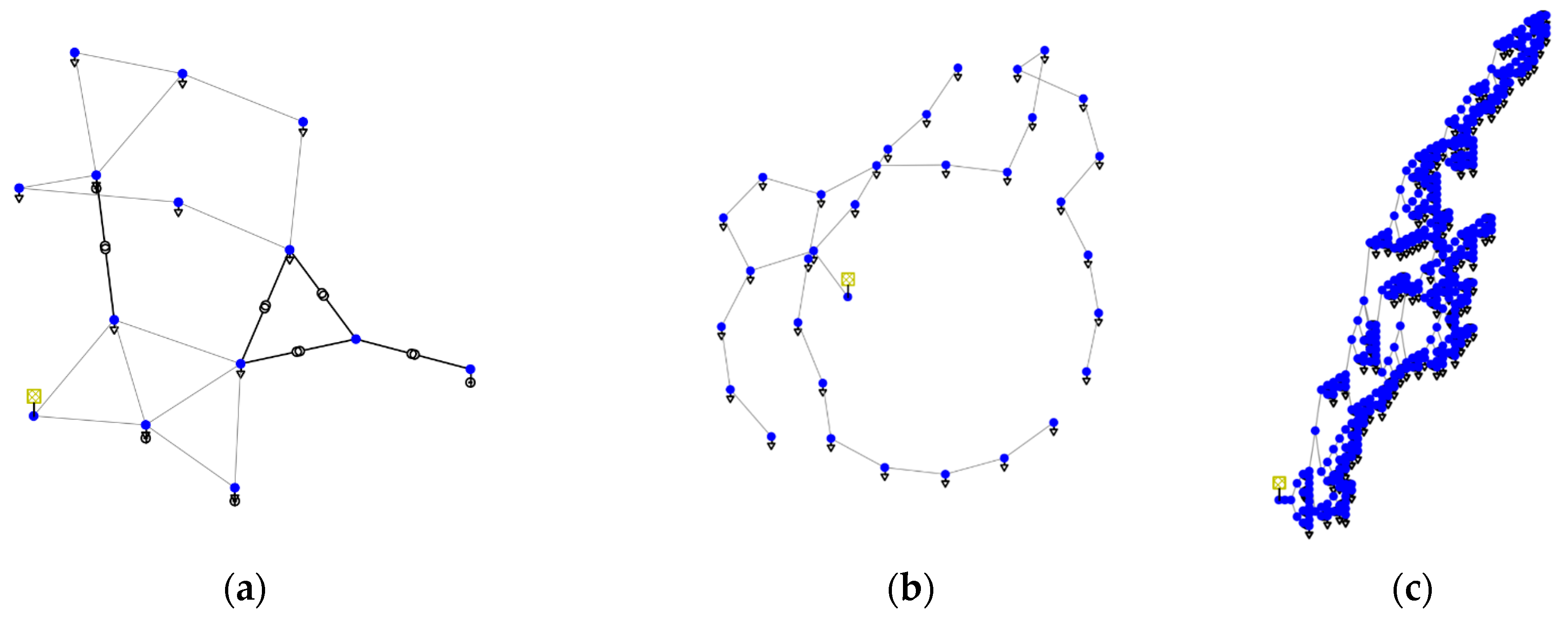
4.1. Test Systems

The data for the distribution system operation used in the case studies are categorized into two types: Monte Carlo simulations and actual power system databases. Data processing for both types is conducted using Python 3.9 with Pandapower 2.13 [31]. The CPU used is an Intel(R) Core(TM) i5-13400 with a clock speed of 2.50 GHz.

• Monte Carlo simulation

This paper mainly describes the looped network IEEE 14-bus system and the radial network IEEE 33-bus system, as shown in Figure 7a,b. Each load scenario consists of 24 hourly samples for all network loads. Load and DG scenarios are derived from Monte Carlo sampling of standard load profiles and DG outputs from [32], and consider a 50% uncertainty.

In general, the measurement accuracy of voltage magnitude, branch power, and current magnitude is above 99%, while the injection power at the buses in the distribution system comprises almost entirely spurious measurements, and the measurement accuracy of spurious measurements is generally below 50%. Therefore, an error of 1% is set for the measured voltage, an error of 50% is set for the measured power, and the pseudo-measurement noise is modeled as uniformly distributed noise. The actual measurement simulates Gaussian white noise with zero mean, between 0.5% and 2% standard deviations were assumed for the voltage and current measurement noise, and between 1% and 5% were assumed for the active and reactive power measurement errors.

• Actual power system database

The test was conducted using a 10 kV distribution area in northeastern China, referred to as CNEDA404 in this paper, which has a total of 404 buses, as shown in Figure 7c, and 108 measurement points. The measured quantities are voltage U, current I, active power P, and reactive power Q. The data from 5 days in August and September 2021, with a 15-min interval as one sample section, resulted in a total of 480 sample sections. The measurement accuracy of voltage and current is more than 99%, and the measurement accuracy of power injection is more than 50%.

The dataset was divided into training, validation, and test sets, with an 80/10/10 split.

4.2. Simulation Setup

The network parameters of GraphSAGE are set as shown in

Table 1. Experiment results in IEEE 14-bus test system.

Parameter	Case (IEEE14, IEEE33)	Actual (CNEDA404)
epochs	500	1000
batch_size	64	64
hidden_layers	3	3
internal_dim	48	48
sample_nums	5	5
training_steps	20	20
learning_rate	0.01	0.006
dropout_rate	0.4	0.4
time_iterations	30 × 24	5 × 96

, and the aggregation is performed using the Mean aggregator.

The evaluation index adopts the Root Mean Squared Error (RMSE):

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{m}}{\displaystyle \sum _{i=1}^m{\left(y_i-{\widehat{y}}_i\right)}^2}}$$

(11)

where $y_i$ and ${\widehat{y}}_i$ are the actual and predicted values of the ith observation—per unit voltage (p.u.) is used in this paper—and m is the total number of observations. The trend of RMSE in the validation set during training is shown in Figure 8, below. The RMSE of the voltage curve decreases slowly with each epoch.

4.3. Analysis

Due to the lack of trained labels for comparison with supervised learning, this study selected the widely used WLS and linear LAV algorithms for comparative analysis, and assessed the method’s performance by simulating missing measurements and introducing substantial measurement noise. We removed the value calculation indices that did not meet the required confidence level.

At the same time, the WLS method proved unstable in large, noisy networks, resulting in poor convergence rates. Noisy measurements can constrain the Newton–Raphson solver, causing divergence [33]. To address these issues, we compared the accuracy and computation times of PF-GraphSAGE with WLS, utilizing actual measurements and pseudo-measurements to enhance convergence rates (WLS*).

4.3.1. Accuracy and Computation Speed

The evaluation metrics include voltage RMSE, confidence, and computation time. The results for the three test systems under normal operating conditions are presented in

Table 2. Experiment results in the IEEE 14-bus test system under normal conditions.

Evaluation Index	WLS	LAV	PF-GraphSAGE
Voltage RMSE mean	10.630	9.8945	3.243
(standard deviation) [10−3]	(0.58)	(0.23)	(0.17)
Voltage RMSE max [10−3]	17.332	12.358	4.274
Convergence [%]	100	100	100
Computation time [ms]	453.049	93.738	9.764

,

Table 3. Experiment results in the IEEE 33-bus test system under normal conditions.

Evaluation Index	WLS	LAV	PF-GraphSAGE
Voltage RMSE mean	11.844	6.233	4.031
(standard deviation) [10−3]	(0.76)	(0.28)	(0.19)
Voltage RMSE max [10−3]	17.307	7.982	6.499
Convergence [%]	100	87.5	100
Computation time [ms]	501.57	109.42	11.65

and

Table 4. Experiment results in the CNEDA404 bus test system under normal conditions.

Evaluation Index	WLS*	LAV	PF-GraphSAGE
Voltage RMSE mean	12.14	12.36	1.653
(standard deviation) [10−3]	(0.45)	(0.31)	(0.04)
Voltage RMSE max [10−3]	16.12	14.72	3.628
Convergence [%]	100	91.66	100
Computation time [ms]	671.74	2440.71	41.92

. In small systems, PF-GraphSAGE achieves a voltage RMSE that is 1.5 to 3 times better than the traditional methods, with a computation time 10 times faster than that of LAV. In large systems, due to the increased network information, PF-GraphSAGE shows a voltage RMSE performance that is more than 10 times better and a computation time more than 15 times faster than that of WLS.

Regarding errors and convergence, when the network experiences random noise, the traditional method LAV fails to satisfy convergence, as illustrated by the example of two buses in Figure 9. The approach proposed in this paper, guided by power flow equations, is closer to the true value of power flow than WLS. Notably, in larger systems, both WLS and LAV require additional pseudo-measurements to achieve convergence, highlighting the advantage of PF-GraphSAGE.

For computation speed, WLS is relatively slow, while LAV exhibits a linear advantage in small networks but becomes very inefficient with large datasets. The trained PF-GraphSAGE model demonstrates a significant advantage in computation time.

4.3.2. Generalization and Robustness

We removed the measurement data of bus 3 from the training set, i.e., by setting bus 3 as a missing node, and enlarged the measurement noise of bus 8 in the test set, i.e., by setting bus 8 as an abnormal data node.

Aggregating the graph information, the simulation results are shown in Figure 10. It can be seen that the error of bus 3 in the PF-GraphSAGE approach is the largest; bus 3 is the newly generated embedding in the network, but its error is still within the acceptable range—this is because bus 3 has learned the mapping generated by the bus. The prediction of bus 8 is limited by the information of the neighbor bus and, therefore, no anomaly occurs. The proposed voltage RMSE of PF-GraphSAGE is three times lower than that of WLS, and 70% of the buses using the proposed approach fall within the satisfactory range, while the remaining 30% are in the acceptable range. In contrast, more than half of the nodes are deemed unacceptable with the traditional WLS and LAV methods.

4.3.3. Actual Distribution System Testing

This paper validates data from actual distribution systems, highlighting the advantages of PF-GraphSAGE. It outperformed both WLS and LAV across all metrics in larger networks. PF-GraphSAGE benefits from local operations around buses and can extrapolate to other areas, improving accuracy with more buses and lines. Figure 11 and Figure 12 show the voltage level estimates in the CNECA404 bus system over a sampling period.

As shown in Figure 11, taking bus 35 and bus 248 as examples, the proposed approach is closer to the true value under normal conditions.

Despite achieving high accuracy in noisy measurements, the model’s adaptability to network topology changes is limited. Figure 12 shows the electricity data from August, which is when power consumption peaks each summer. Meanwhile, the large distribution area results in lower overall voltage at buses farther from the substation. The early predictions were normal, but after 6 PM, a line failure occurred, leading to the temporary rerouting of bus 293 and a sharp drop in voltage. Since the method primarily focuses on learning node information and has limited awareness of line parameters, the results deviate from the actual values. The DSSE did not restore its function until after 11 PM, when the line was repaired. An advantage is that the local errors of this method do not affect the global errors, for example, buses 83 and 107 do not show any large errors.

5. Conclusions

This paper proposes a state estimation approach for distribution systems using power flow-guided graph feature learning. By generating typical IEEE14 and IEEE33 datasets based on the Pandapower library, as well as performing simulations and verification with actual measurement data from distribution areas, we reached the following conclusions:

(1)

The approach proposed in this paper effectively fits the state variables under non-Gaussian noise and demonstrates tolerance for faulty data, exhibiting strong adaptability and robustness.

(2)

The method does not require true values as labels and has a certain degree of generalization for unseen data.

(3)

Through guidance with power flow equations rather than simple numerical analysis, the method becomes more in line with distribution systems’ physical characteristics.

Graph networks have strong potential for handling distribution systems with natural graph properties. However, the proposed approach primarily focuses on node learning and does not fully capture edge features; future work could explore embedding line information. Additionally, DSSE could be further accelerated through advancements in graph computing and linearization, as well as by conducting deeper investigations into three-phase imbalance, transformer ratios, and topology changes.