Identification and Evaluation of Vulnerable Links in a Distribution Network with Renewable Energy Source Based on Minimum Discriminant Information

Abstract

With the increase in the proportion of photovoltaic and wind power access, the scale and form of distribution networks are becoming more and more complex. The traditional single distribution network vulnerability assessment method is difficult to use to identify the vulnerable links in the distribution network. Therefore, this paper proposes a method for identifying and evaluating vulnerable links in distribution networks based on minimum discriminant information. First, considering the influence of distributed grid connection, an improved probabilistic power flow calculation method is proposed, which improves the calculation efficiency and accuracy. Second, considering the correlation degree, transmission capacity, and voltage stability of branches in the distribution network, the identification index of vulnerable lines is defined. Based on power quality and operating state, the identification index of vulnerable nodes in a distribution network is defined. Finally, based on the indicators of vulnerable nodes and vulnerable lines, the vulnerable links in the distribution network are comprehensively evaluated based on the principle of minimum discriminant information, and the vulnerable links of the entire distribution network are evaluated according to different degrees of vulnerability. The rationality and effectiveness of the proposed method are verified via an example analysis of actual power grid data.

1. Introduction

With the rapid development of power systems as an important infrastructure, the economy and power quality of the power supply have been greatly improved. However, the increasing integration of renewable energy sources contributes to heightened randomness and complexity within the power system, posing significant challenges to its safe operation [1]. The current distribution network faces many challenges, including the aging of traditional infrastructure, the difficulty of integrating renewable energy and distributed generation resources, the increasing complexity of demand side management, and the increasing demand for grid protection and automation [2]. With the increasing demand for electricity and the acceleration of electrification, the reliability and resilience of distribution networks have been tested. In addition, power grid security and the ability to combat severe weather events have also become important issues. Enhancing the operational safety and disaster resilience of distribution networks is therefore crucial. Conducting effective vulnerability assessments and identifying vulnerable links for reinforcement are essential steps in achieving this goal [3].

Currently, research on grid vulnerability predominantly focuses on transmission networks both domestically and internationally, with limited exploration into distribution networks. Existing studies primarily revolve around constructing vulnerability assessment systems, developing assessment methodologies, and exploring coupled system vulnerability assessments. Complex network theory serves as a foundational approach in deriving vulnerability assessment indices for distribution networks [4,5]. Notably, indices like electrical betweenness and enhanced line betweenness are commonly used indicators in vulnerability assessments [6,7]. Reference [8] introduces metrics such as dielectric constant and power flow transfer entropy to evaluate distribution network state vulnerability, employing methods like the analytic hierarchy process (AHP) and entropy weight methods to derive comprehensive weight matrices for vulnerability indices. Reference [9] redefines electrical betweenness metrics, considering the impact of bidirectional power flow following distributed energy integration, thereby proposing a method by which to evaluate vulnerable grid lines using complex network metrics. Additionally, references [10,11,12] integrate probabilistic methods into power system analysis, enhancing understanding of system operation states through consideration of equipment failure rates and system state probabilities. Bayesian models and line betweenness metrics, as described in reference [13], are utilized to assess grid line importance. Reference [14] introduces complex network theory indices into energy storage planning for line vulnerability evaluation, pioneering new approaches for identifying vulnerable links. Reference [15] explores grid vulnerability from an overload mechanism perspective, analyzing grid fault adjacency. With the rapid increase in the proportion of renewable energy, such as wind and light energy in the modern energy system, the impact of renewable energy source on the vulnerability of the distribution network cannot be ignored [16]. Reference [17] establishes models for integrated wind/PV/storage systems, using fault mode and Monte Carlo analyses to compute reliability under various scenarios. In reference [18], the distribution network integrated with distributed energy and electric vehicles is studied, and the evaluation index and evaluation method based on the deep learning algorithm are proposed. Considering the influence of extreme weather on the distribution network, reference [19] studied and summarized the general vulnerability assessment methods of distribution networks and the enhancement of power system resilience. In reference [20], a voltage quality assessment method for distribution networks is proposed to stimulate the active/online management of voltage quality problems.

However, the current research on the vulnerability of distribution networks mainly focuses on local performance, and there is no in-depth evaluation of the effectiveness of the index system, nor does it combine the comprehensive evaluation with the local and overall network perspective. This limitation hampers efforts to capture distribution network dynamics fully and establish widely applicable evaluation standards [21]. This paper addresses these gaps by comprehensively considering node operational status, voltage violations, transformer overloads, three-phase imbalances, and new energy integration impacts. These factors are quantified into corresponding indicators to establish a model for identifying vulnerable lines. Utilizing the principle of minimum discriminant information, comprehensive index weights [22] are derived to facilitate distribution network line vulnerability assessments.

Through this study, we achieve the identification and comprehensive vulnerability assessment of vulnerable links within actual distribution networks. The contributions of this research are multifaceted.

First, we propose an improved semi-invariant probabilistic power flow calculation method to better assess distribution network risks under varying renewable energy source outputs and loads, enhancing power flow calculation efficiency and accuracy.

Second, we define identification indices for vulnerable links in distribution networks, including node and line vulnerability indices. The node vulnerability index utilizes the GWO-Elman model to predict load voltage data for the next period and establishes indices for transformer overloads, voltage violations, and three-phase imbalances to assess node vulnerability comprehensively. The line vulnerability index employs complex network theory, introducing improved branch degree and branch electrical transmission betweenness based on branch power supply matrices. Considerations of node degree and voltage stability further enhance comprehensive line vulnerability identification.

Finally, we establish an evaluation method for vulnerable links based on the principle of minimum discriminant information. This method integrates subjective weight vectors derived from the G1 order relation analysis method with objective weight vectors obtained through an enhanced entropy method. The combination of these weights using the principle of minimum discriminant information yields comprehensive weights used to assess distribution network line vulnerabilities.

The following is the structure of the remaining sections of the article. Section 2 identifies the vulnerable links of the distribution network with renewable energy source by defining the indicators of vulnerable nodes and vulnerable lines. In Section 3, the minimum discriminant information principle is used to combine the subjective and objective weights in order to obtain the comprehensive weight so as to realize the vulnerability assessment of the distribution network line. In Section 4, the power distribution data of a line in Liaoning Province are used for simulation, which verifies that the evaluation method of vulnerable links is reasonable. Section 5 provides the research conclusions and suggestions for future research.

2. Identification of Vulnerable Links in Distribution Network with Renewable Energy Source

The commonly used identification indices of vulnerable links in a distribution network include the degree index, betweenness index, path length index, aggregation coefficient, and cohesion index [23]. The identification of vulnerable links in a distribution network with renewable energy source is more complicated. Given the increasingly obvious phenomenon of voltage limit violation and power flow limit violation after distributed power access to a distribution network, this paper defines the identification indices of vulnerable links in a distribution network with renewable energy source, including the vulnerable line node index and vulnerable line identification index.

2.1. Vulnerable Node Identification

This paper primarily addresses aspects of power quality and the vulnerability analysis of power supply links in the context of integrating renewable energy source sources. Defined within are indices for identifying vulnerable nodes, including the node voltage over-limit, the transformer heavy overload, and the three-phase voltage imbalance.

2.1.1. Improved Semi-Invariant Probabilistic Power Flow Calculation

When renewable energy source sources are integrated into the distribution network, numerous uncertainties arise within the system. Traditional deterministic power flow calculations are time-consuming and may fail to provide comprehensive results. By employing probabilistic methods to address the random variables in the distribution network and utilizing a probabilistic power flow algorithm, the evaluation time can be reduced, efficiency improved, and the problem effectively resolved.

Current probabilistic power flow algorithms include analytical and simulation methods. This paper adopts an improved semi-invariant method to compute the probabilistic power flow. First, based on the Rosenblatt transform, the output power between wind farms and wind–solar farms is independently converted. Second, the semi-invariant of the independent data is calculated, and the probabilistic power flow calculation of the semi-invariant method is carried out. Finally, the output probability density function is solved by the Gram–Charlier series.

The core concept of the semi-invariant method is to simplify complex convolution operations into straightforward arithmetic operations between semi-invariants, significantly reducing calculation complexity. The semi-invariants of the input random variables are mapped to those of the output variables through the Jacobian matrix and sensitivity matrix, facilitating the transfer and transformation of the probability distribution.

The relationship between node voltage change $\Delta U$, branch power change $\Delta S$, and node injection power change $\Delta X$ is shown in the following formula.

$$\{\begin{array}{l}\Delta U=J_0^{-1}\Delta X\\ \Delta S=G_0{J}_0^{-1}\Delta X\end{array},$$

(1)

where $J_0$ and $G_0$ are the partial derivatives of the node injection power imbalance and the branch power to the node voltage amplitude $V$ and phase angle $\delta$, respectively.

Instead of relying on convolution operations, the semi-invariant property is used to convert the semi-invariant of the node injection power. This approach yields the k-order semi-invariants of the node voltage and branch power, as demonstrated in the following formula:

$$\{\begin{array}{l}\Delta U^{\left(k\right)}={\left(J_0^{-1}\right)}^k\Delta X^{\left(k\right)}\\ \Delta S^{\left(k\right)}={\left(G_0{J}_0^{-1}\right)}^k\Delta X^{\left(k\right)}\end{array}.$$

(2)

The cumulative probability distribution function of output variables (node voltage, branch power flow) is obtained via the Gram–Charlier series, where ${\mu }_x$ is the expected value of the random variable, and ${\sigma }_x$ is the standard deviation. By standardizing random variables by $\overline{X}={\displaystyle \frac{X-{\mu }_x}{{\sigma }_x}}$, we obtain its probability density function $f(\overline{x})$.

$$\begin{array}{c}f(\overline{x})=\phi (\overline{x})+{\displaystyle \frac{1}{6}}{{\rm Y}}_3({\phi }^2(\overline{x})-1)\\ \hspace{1em}+{\displaystyle \frac{1}{24}}{{\rm Y}}_4({\phi }^3(\overline{x})-3\phi (\overline{x}))\\ \hspace{1em}\hspace{1em}\hspace{1em} -{\displaystyle \frac{1}{36}}{{\rm Y}}_3^2(2{\phi }^3(\overline{x})-5\phi (\overline{x}))+\cdots \end{array},$$

(3)

where $\phi \left(\overline{x}\right)$ is the probability density function, and ${{\rm Y}}_k$ is the k-order semi-invariant.

In this paper, samples of wind power and photovoltaic output obtained through sampling are input into the probabilistic power flow calculation using the improved semi-invariant method. The power flow calculation results are then statistically analyzed to obtain the final probabilistic power flow outcomes. Figure 1 illustrates the flow chart of the improved semi-invariant probabilistic power flow calculation process.

2.1.2. Node Voltage Over-Limit Identification

As the penetration of photovoltaic and wind power increases in the distribution network, one major risk to the low-voltage distribution system is the potential for node voltage to exceed acceptable limits. When a substantial amount of renewable energy source sources are integrated into the grid, the traditional radial network transforms into a multi-power network. The increased output from distributed power sources raises the access point voltage, causing the node voltage amplitude to surpass specified thresholds. Therefore, the degree of node voltage over-limit is also one of the indicators by which to identify vulnerable nodes. The voltage over-limit index based on the relevant power supply voltage quality standards given by

$$R_{volt}=\sum _{i\in {\Omega }_i}prob\left(V_i\right)\cdot sev\left(V_i\right),$$

(4)

where $R_{volt}$ represents the node voltage over-limit index; $prob\left(V_i\right)$ represents the probability of node $i$ voltage exceeding the limit; $sev\left(V_i\right)$ represents the voltage offset threshold of node $i$. $sev\left(\underset{\_}{V_i}\right)$ and $sev(\overline{V_i})$ represent the severity of the upper and lower limits of the node, respectively. The expressions of $sev\left(\underset{\_}{V_i}\right)$ and $sev(\overline{V_i})$ are as follows:

$$sev\left(\underset{\_}{V_i}\right)=\{\begin{array}{cc}{\displaystyle \frac{V_{i,\min }-V_i}{V_{i,\min }}},& V_i<V_{i,\min }\\ 0,& V_i\ge V_{i,\min }\end{array},$$

(5)

$$sev(\overline{V_i})=\{\begin{array}{cc}{\displaystyle \frac{V_{i,\max }-V_i}{V_{i,\max }}},& V_i>V_{i,\max }\\ 0,& V_i\le V_{i,\max }\end{array},$$

(6)

where $V_i$ is the voltage amplitude of node $i$, $V_{i,\min }$ is the lower limit of node $i$ voltage, and $V_{i,\max }$ is the upper limit of node $i$ voltage.

2.1.3. Transformer Heavy Overload Identification

The state with a load rate below 60% is regarded as a normal operation state, and the state with a load rate above 60% is regarded as high risk. Therefore, the heavy overload risk loss value and risk degree of the node transformer are defined as Formula (7) and Formula (8), respectively.

$$L_{bo}=\{\begin{array}{cc}L-0.3,& L>0.6\\ 0,& L\le 0.6\end{array},$$

(7)

$$R_{bo}=e^{\max (L_{bo})}-1,$$

(8)

where $L_{bo}$ is the risk loss value of transformer heavy overload; $R_{bo}$ is the risk of heavy overload; $L$ is the transformer load rate.

2.1.4. Three-Phase Voltage Imbalance Identification

The accurate calculation method of three-phase voltage unbalance is

$$R_{ub}={\displaystyle \frac{1-e^{-\epsilon }}{1-e^{-1}}},$$

(9)

$$L={\displaystyle \frac{U_a^4+U_b^4+U_c^4}{{\left(U_a^2+U_b^2+U_c^2\right)}^2}},$$

(10)

$$\epsilon =\sqrt{{\displaystyle \frac{1-\sqrt{3-6L}}{1+\sqrt{3-6L}}}}\times 100\%,$$

(11)

where $R_{ub}$ represents the three-phase voltage imbalance; and $U_a$, $U_b$, and $U_c$ are the voltage of the A phase, B phase, and C phase, respectively.

2.2. Vulnerable Line Identification

Based on the conditions of a distribution network line in Liaoning Province, this study defines the improved node degree, improved line degree, improved branch electrical transmission betweenness, and the line voltage stability index. These metrics are used to rank the vulnerability of the distribution network lines, thereby enabling the identification of the most vulnerable lines.

2.2.1. Node Degree Identification Based on Improved Branch Power Supply Matrix

The degree index is typically utilized for node analysis and evaluation. It examines the number of side roads connected to a node by introducing the branch power supply correlation matrix for analysis. In the branch power supply correlation matrix, the column represents each node in the network, and the row represents each side road. Corresponding to the number of all the “1”s in each column, the connection of each node can be known. The degree of the node can be obtained by counting the number of “1”s in each column. A higher number indicates a more critical power supply role for the node in the network. By incorporating the branch power supply correlation matrix, an improved node degree formula is proposed, as demonstrated in Formula (12):

$$N_{bi}={\displaystyle \frac{d_i}{{\overline{d}}^2}}\underset{l\in N_{bi}}{{\displaystyle \Sigma }}{d}_l,$$

(12)

where $N_{bi}$ is the set of all edge paths connected by $i$ nodes; and $d_i$ is the node degree of $i$ node.

2.2.2. Branch Degree Identification Based on Improved Branch Power Supply Matrix

The node plays the role of transit in the power supply line. When describing the branch of the power system, the influence of the node on the line cannot be ignored. For a single-loop radial distribution network, node failure may cause subsequent lines to fail to supply power normally. In addition, the distributed power supply can form an island power supply form, or there is a tie line that can cut off the off-supply node and transfer it to the adjacent branch to ensure normal power supply. Therefore, this paper considers both the branch degree and the influence of the node degree and proposes an improved branch degree index. The formula is shown in Formula (13):

$$R_{lbi}={\displaystyle \frac{\left|Z_{ij}\cdot l_{ij}\right|}{\overline{d}}}\sqrt{N_{bi}\cdot N_{bj}},$$

(13)

where $R_{lbi}$ is the branch degree index; $Z_{ij}$ is the unit line impedance of the wire or cable between node $i$ and node $j$ and the value of the unit line impedance of different wires is different; $l_{ij}$ is the line length between node $i$ and node $j$; $\left|Z_{ij}\cdot l_{ij}\right|$ is the line impedance modulus between node $i$ and node $j$, and $\left|Z_{ij}\cdot l_{ij}\right|=\sqrt{R_{ij}^2+X_{ij}^2}\cdot l_{ij}$.

2.2.3. Identification of Branch Electrical Transmission Betweenness

With the integration of a large number of renewable energy source sources, the main risk impact on the low-voltage distribution network is not only the node voltage exceeding the limit but also the line power flow exceeding the threshold. Due to the access of renewable energy source, the line power flow may change from one-way flow to two-way flow, and the traditional concept of betweenness is no longer applicable. Therefore, based on the combination of active power flow and reactive power flow, this paper proposes the definition of electrical transmission betweenness to better describe the problem of power flow in power system.

Therefore, the improved branch electrical transmission betweenness is defined as Formula (14):

$$R_{\chi ij}=\sqrt{{\displaystyle \frac{{\rho }_P\times E_{\chi Pij}^2+{\rho }_Q\times E_{\chi Qij}^2}{E_{\chi Pij}^2+E_{\chi Qij}^2}}},$$

(14)

where $R_{\chi ij}$ is the branch electrical transmission betweenness index; ${\rho }_P$ is the weight of the active power flow transmission factor; and ${\rho }_Q$ is the weight of the active power flow transmission factor. When ${\rho }_P=1$ and ${\rho }_Q=0$, the system focuses on active power flow transmission; when ${\rho }_P=0.5$ and ${\rho }_Q=0.5$, the system attaches the same importance to active power flow transmission and reactive power flow transmission; and when ${\rho }_P=0$ and ${\rho }_Q=1$, the system focuses on reactive power flow transmission.

2.2.4. Line Voltage Stability Identification in the Distribution Network

In the process of line identification, voltage stability is also a factor that we need to consider. Therefore, the line voltage stability index is defined as one of the indicators for the assessment of vulnerable links, as shown in Formula (15):

$$R_{vs}={\displaystyle \frac{4Q_k{\left|Z_{ik}\right|}^2}{{\left(X_{ik}\cos {\theta }_k+R_{ik}\sin {\theta }_k\right)}^2{U}_i^2}},$$

(15)

where $R_{vs}$ is the voltage stability index; $Q_k$ is the reactive power of the terminal node; $Z_{ik}$ is the line impedance between node $i$ and node $k$; $X_{ik}$ is the line reactance; $R_{ik}$ is the line resistance; $U_i$ is the voltage amplitude of the head node $i$; and ${\theta }_k$ is the power factor angle of the terminal node $k$. The line voltage stability index can use distribution information to accurately identify the voltage stability of the 10 kV bus through the index. When the evaluation index $0\le R_{vs}\le 1$, the distribution network line voltage is in a stable operating state. When $R_{vs}>1$, the distribution network line voltage is unstable.

3. Vulnerable Link Assessment Based on the Principle of Minimum Discriminant Information

Utilizing defined metrics for vulnerable nodes and lines, corresponding weights are assigned. Vulnerable links in the distribution network are identified using the minimum discriminant information principle. Commonly employed subjective and objective weighting methods include the analytic hierarchy process, fuzzy comprehensive evaluation method, G1 order relationship analysis method, and entropy weight method. Among these, the G1 order relationship analysis method stands out for its simplicity and intuitive nature, significantly reducing computational complexity and improving speed. Not requiring a judgment matrix eliminates the need for consistency testing and imposes no limits on the number of elements per level, ensuring the order of each element [24]. The entropy weight method determines the index weights based on variation degrees of index values, mitigating human bias but potentially diverging from expected results, thus overlooking decision makers’ subjective intentions. Therefore, this study integrates the strengths and weaknesses of both methods, utilizing the G1 order relationship analysis method for subjective weighting and the entropy weight method for objective weighting, and ultimately applying the minimum discriminant information principle to compute comprehensive weights.

The vulnerability objective function, guided by the principle of minimum discriminant information, is formulated in Formula (16):

$$\{\begin{array}{l}\min F(\omega )={\displaystyle \sum _{i=1}^m}\left({\omega }_i\ln {\displaystyle \frac{{\omega }_i}{{\omega }_{zgi}}}+{\omega }_i\ln {\displaystyle \frac{{\omega }_i}{{\omega }_{kgi}}}\right)\hfill \\ \mathrm{s}.\mathrm{t}.{\displaystyle \sum _{i=1}^m}{\omega }_i=1,{\omega }_i\ge 0,i=1,2,\cdots ,m\hfill \end{array},$$

(16)

where $F(\omega )$ is the objective function to make the comprehensive weight ${\omega }_i$ as close to the subjective and objective weight as possible; ${\omega }_i$ is the comprehensive weight of the $i$ index; and ${\omega }_{zgi}$ is the subjective weight coefficient of the $i$ index and the calculation formulae are as follows:

$${\omega }_{zgi}={\left(1+\underset{i=2}{\overset{m}{{\displaystyle \Sigma }}}\underset{k=i}{\overset{m}{{\displaystyle \Pi }}}{r}_k\right)}^{-1},$$

(17)

$${\omega }_{zgi}=r_{i+1}{\omega }_{zgi+1},$$

(18)

$$r_i={\displaystyle \frac{{\omega }_{zgi}}{{\omega }_{zgi+1}}}.$$

(19)

The $r_i$ values are 1, 1.2, 1.4, 1.6, and 1.8. The larger the $r_i$ value, the greater the importance of index $i$ than index $i+1$.

${\omega }_{kgi}$ is the objective weight coefficient of the $i$ index, and the calculation formulae are as follows:

$${\omega }_{kgi}={\displaystyle \frac{\underset{i=1}{\overset{n}{{\displaystyle \Sigma }}}{h}_i+3m-2-3m{h}_i}{\underset{i=1}{\overset{n}{{\displaystyle \Sigma }}}\left(\underset{i=1}{\overset{n}{{\displaystyle \Sigma }}}{h}_i+3m-2-3m{h}_i\right)}},$$

(20)

$$h_i=-{\displaystyle \frac{1}{\ln n}}\left(\sum _{i=1}^m{y}_i\ln y_i\right),$$

(21)

$${\varphi }_i={\displaystyle \frac{1-h_i}{{\displaystyle \sum _{i=1}^n}\left(1-h_i\right)}},\hspace{1em}{\varphi }_i\in [0,1],$$

(22)

where ${\omega }_{kgi}$ satisfies ${\displaystyle \Sigma }\omega =1$; $m$ is the number of indicators; and $h_i$ is the entropy of the index and satisfies $0\le h_i\le 1$.

The vulnerability objective function based on the Lagrange function is solved as follows. To determine the optimal solution for the problem at hand, we construct the Lagrangian function.

$$L=\sum _{i=1}^m\left({\omega }_i\ln {\displaystyle \frac{{\omega }_i}{{\omega }_{zgi}}}+{\omega }_i\ln {\displaystyle \frac{{\omega }_i}{{\omega }_{kgi}}}\right)+\lambda \left(\sum _{i=1}^m{\omega }_i-1\right).$$

(23)

Let $\partial L/\partial {\omega }_i=0$, $\partial L/\partial \lambda =0$, then

$$\{\begin{array}{l}{\displaystyle \frac{\partial L}{\partial {\omega }_i}}=2\ln {\omega }_i+2-\ln {\omega }_{zgi}{\omega }_{kgi}+\lambda =0\hfill \\ {\displaystyle \frac{\partial L}{\partial \lambda }}={\displaystyle \sum _{i=1}^m}{\omega }_i-1=0\hfill \end{array}.$$

(24)

The comprehensive weight is obtained from Formula (25):

$${\omega }_i={\displaystyle \frac{\sqrt{{\omega }_{zgi}{\omega }_{kgi}}}{e}}.$$

(25)

By substituting the indicators of vulnerable nodes and vulnerable lines, the comprehensive evaluation results of vulnerable links in the distribution network can be obtained.

$$R_{vul}={\omega }_i{R}_i,$$

(26)

where $R_{vul}$ is the comprehensive evaluation value of vulnerable links; and $R_i$ is the value of each index, and $R_i\in \left\{R_{bo},R_{volt},R_{ub},R_{lbi},R_{\chi ij},R_{vs}\right\}$. The larger the value of $R_{vul}$, the higher the vulnerability caused by the quality of the power supply.

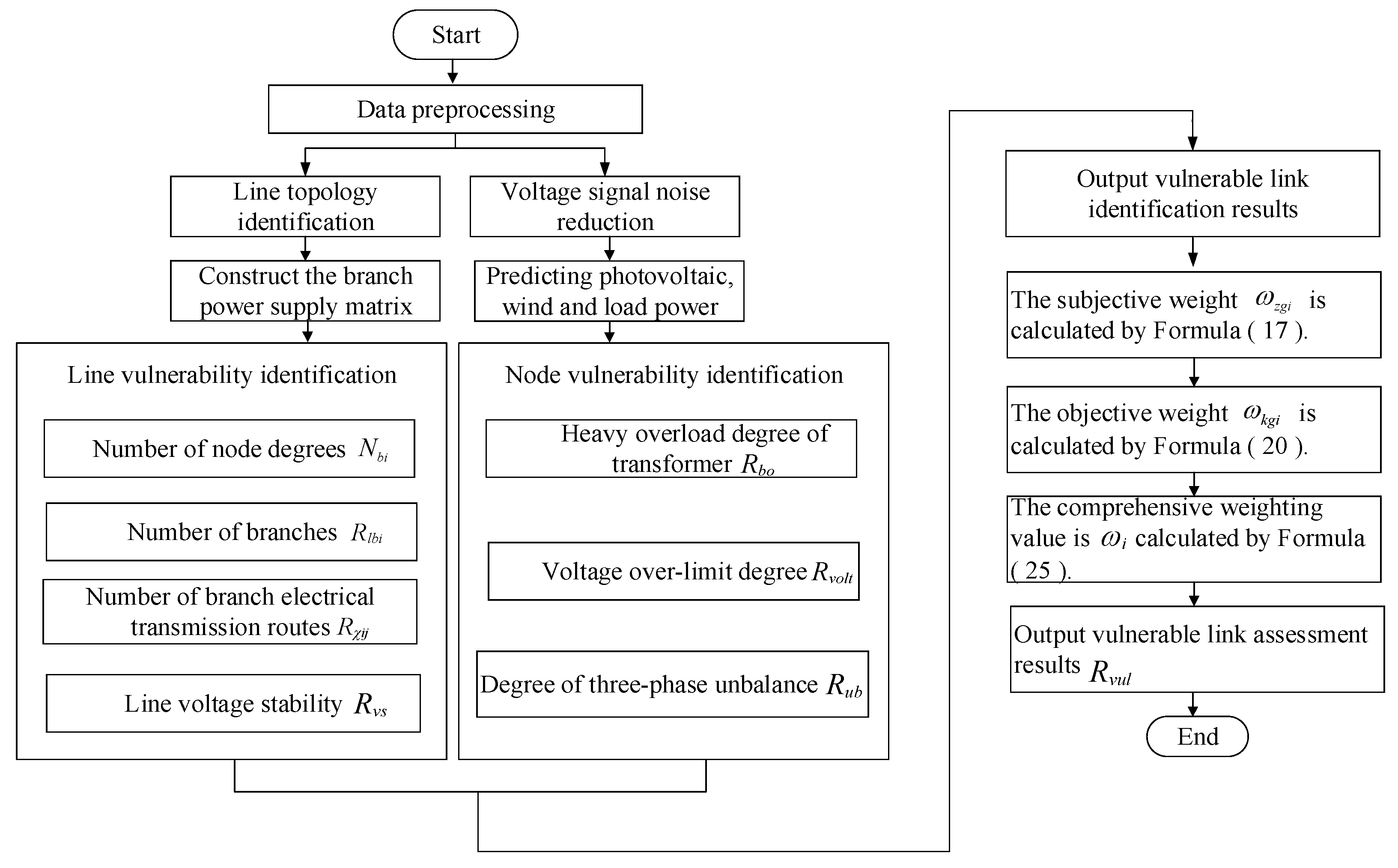
The identification and evaluation process of vulnerable links in the distribution network with renewable energy source is shown in Figure 2.

First, before proceeding with data utilization, it is imperative to perform preprocessing to maximize data authenticity. Incomplete datasets are processed accordingly to ensure data integrity.

In the identification of vulnerable nodes, empirical mode decomposition is employed to denoise the voltage signal, thereby reducing noise interference and aligning predictions more closely with actual development trends. Subsequently, the grey wolf algorithm (GWO) optimizes the parameters of the Elman neural network, enabling the GWO-Elman model to forecast load voltage data [25]. Additionally, an adaptive kernel density estimation method establishes a wind–solar output model. Finally, criteria such as transformer heavy overload, voltage limits exceeding, and three-phase voltage imbalance are defined to pinpoint vulnerable nodes.

In the identification of vulnerable lines, the relationship between nodes and branches in the directed graph is established by using the correlation matrix method of graph theory. Then, the branch power supply matrix is derived via matrix derivation. Second, the concept of degree and betweenness of a complex network is adopted to integrate electrical parameters into a complex network to better describe the correlation degree, power transmission, and voltage stability of branches in the distribution network. Then, all lines are analyzed and compared using vulnerable line identification, and then, vulnerable lines are sorted according to different vulnerabilities.

Finally, leveraging indicators from both vulnerable nodes and lines, the G1 sequence relation analysis method is applied to determine subjective weight values, while an enhanced entropy weight method calculates objective weight values. These are combined using the principle of minimum discriminant information to compute comprehensive weights, facilitating a thorough assessment of vulnerable links in the distribution network.

4. Example Analysis

This paper utilizes distribution and consumption data from a distribution network line located in Liaoning Province for the example analysis. The Maiwang line spans a total length of 13.097 km and encompasses 805 nodes, including 243 distribution transformers. The combined capacity of these transformers is 23.245 MVA, with the main transformer reaching a peak load rate of 51.5%. Nodes 182 and 386 serve as photovoltaic access points, while nodes 610 and 710 serve as wind power access points. The installed capacity of the photovoltaic power station is 500 KW, and the total area of the photovoltaic module is $A={800 \mathrm{m}}^2$. The Homer version 2.81 software is used to generate the light intensity sequence of China’s Liaoning region (118°53′ E, 38°43′ N). The shape parameters $\alpha =0.6579$ and $\beta =1.7263$ of the Beta distribution and the photoelectric conversion efficiency $\eta =0.13$ are calculated. The wind speed data are also taken from the Weibull distribution with the scale parameter of 7.39 and the shape parameter of 3 in Liaoning area. The cut-in wind speed is 3 m/s, the constant power wind speed is 10 m/s, the cut-out wind speed is 23 m/s, and the rated power of each wind turbine is 500 KW. Figure 3 shows the local branch diagram of the 10 kV Maiwang line.

4.1. Calculation Results and Analysis of 10 kV Side Power Flow

Figure 4 illustrates the power flow calculations for the Maiwang line, different colored lines in the figure represent different moments. The figure indicates that in certain instances, the voltage level on the 10 kV side meets the specified requirements; while in most instances, it remains in a state close to the lower limit. The power supply capacity from some nodes to the end branch is insufficient. If the load rate is too large, the current in the line will be too large, so the line loss of the main line will rise sharply. The calculation result of the line loss of the Maiwang line based on the power correction module is shown in Figure 5. The main line closer to the PowerPoint will lead to too large a line loss in the interval due to too large a current. On the contrary, the line diameter of the end node is too small, and the current is relatively small compared with the node close to the substation, so the loss is relatively small.

4.2. Identification and Analysis of Vulnerable Nodes

Figure 6 depicts the operational status of the system, with node data collected at 15-min intervals, totaling 96 data points daily. Figure 7 presents voltage data for the subsequent moment, derived from processed data using GWO-Elman neural network predictions. Singular value decomposition is then applied to determine periodic singular values, followed by entropy theory to calculate singular value entropy. Evaluating the system’s operational state is based on maximum and minimum entropy values; lower entropy values indicate greater stability and less variation. As shown in Figure 6, the degree values for each node hover around 0.7, indicating a state of stable operation. Vulnerable nodes are evaluated based on the operation status of the distribution network system.

The heavy overload degree of the transformer is obtained by the transformer heavy overload index $R_{bo}$, that is, Formula (8). Figure 8 shows the degree of heavy overload of the transformer at 18:00, which is also the moment when the number of heavy overloads is the largest throughout the day. The degree of heavy overload of the transformer is obtained by the load rate undertaken by the transformer.

From the three-phase imbalance index $R_{ub}$, the three-phase imbalance degree of the node is obtained. Figure 9 displays the degree of three-phase imbalance for nodes on the Maiwang line. The figure illustrates that the number of nodes experiencing significant three-phase imbalance is minimal, indicating minimal impact on the system.

From the voltage over-limit index $R_{volt}$, the node voltage over-limit degree is obtained. In Figure 10, the node voltage over-limit degree for the Maiwang line is depicted. It is observed that during daytime hours, there is a notable occurrence of nodes exceeding voltage limits, predominantly located at the line’s terminus. This is attributed to increased load rates during daytime hours, leading to compromised power quality at these end nodes. Therefore, it is imperative to implement appropriate measures to ensure uninterrupted electricity supply for end node users.

4.3. Identification and Analysis of Vulnerable Lines

The node degree is the number of edge paths connected by the node. The higher the number of edges, the more important the power supply role of the node in the network. Figure 11 presents the evaluation results for node degrees along the Maiwang line. Nodes located on the main line exhibit higher importance, reflected in their higher node degrees. Similarly, branch line nodes, which also carry significant responsibilities, demonstrate higher node degrees compared to end nodes.

From the branch degree index $R_{lbi}$, the branch degree evaluation result is obtained. Figure 12 displays the assessment outcomes regarding the branching degree of the Maiwang line. It is evident from the figure that branch 483 exhibits a higher degree, with a length measuring 1554 m and a conductor model of LGJ00035. In terms of electrical parameters, the branch conductor is characterized by excessive length and thinness, which adversely impacts the power supply to subsequent nodes, thereby justifying its higher branching degree.

From the transmission betweenness index $R_{\chi ij}$, the evaluation result of branch transmission betweenness is obtained. Figure 13 shows the evaluation results of the transmission betweenness of the Maiwang line branch. The transmission betweenness of the main line and the branch line is relatively high because these lines are closely related to the nodes and other branches. The branch connected by the end node has a small number of connected nodes, so the transmission betweenness of such branches is small.

From the voltage stability index $R_{vs}$, the evaluation results of branch voltage stability are obtained. Figure 14 presents the assessment results regarding the voltage stability of branches on the Maiwang line. Specifically, branches 172 and 649 exhibit poor stability. Branch 172 is linked to a specialized distribution transformer serving the quarry, while branch 649 is connected to a specialized distribution transformer serving the Hexi farm. Both the quarry’s heavy equipment and the farm’s aquaculture equipment consume substantial electrical energy and are sensitive to the start–stop cycles of large loads in their respective environments, contributing to voltage instability along these branches. Additionally, the figure illustrates that voltage instability is prevalent at the line’s terminus, likely due to undersized wiring and some degree of line aging. When the load rate increases, the loss shows a nonlinear change, which leads to the instability of the line voltage. According to the actual field investigation, the users at the end of the line are in a low voltage state for a long time, which makes the household appliances unable to work normally or even operate, which is very inconvenient for production and life. However, the voltage stability of most branches of the line does not exceed 0.1, and the voltage is relatively stable under normal operation.

4.4. Vulnerable Link Assessment Results of the Distribution Network

In terms of subjective evaluation, the six groups of indicators are ranked based on frontline operators’ experience. The order of importance is as follows: branch voltage stability, node voltage over-limit degree, node transformer heavy overload degree, node three-phase imbalance, branch electrical transmission betweenness, and branch degree. For objective weighting, the improved entropy weight method is employed. This method determines index weights based on each index’s variation, thereby mitigating biases introduced by subjective human judgment. Hence, the objective weighting method selects the improved entropy weight method for comprehensive analysis and evaluation.

Table 1. Subjective weight value based on G1 order relation method.

Index	Branch Voltage Stability	Degree of Node Voltage Over-Limit	Transformer Heavy Overload Degree	Node Three-Phase Unbalance	Branch Electrical Transmission Betweenness	Branch Degree
Subjective weights	0.2606	0.2105	0.177	0.1292	0.1165	0.1062

presents the subjective weight values obtained through the G1 order relation method for each index, while

Table 2. Objective weight value based on improved entropy weight method.

Index	Branch Voltage Stability	Degree of Node Voltage Over-Limit	Transformer Heavy Overload Degree	Node Three-Phase Unbalance	Branch Electrical Transmission Betweenness	Branch Degree
Objective weights	0.1925	0.1239	0.1767	0.1712	0.1595	0.1762

shows the objective weight values derived from the improved entropy weight method.

By calculating the comprehensive weight based on the principle of minimum discriminant information and substituting each index of vulnerable nodes and vulnerable lines, the comprehensive evaluation results of vulnerable links in the distribution network can be obtained, as shown in Figure 15. The diagram indicates the Maiwang line’s overall stable operation, with a few nodes exhibiting anomalies.

Table 3. Assessment of fragile links on the Maiwang Line.

Link	172	649	11	14	49
Evaluation result	0.679	0.411	0.370	0.280	0.224

details links identified with higher vulnerability.

4.5. Comparison of Evaluation Methods

The link with the comprehensive vulnerability ranking in the top 5 is selected and compared with the results of scheme 1 and scheme 2, as shown in

Table 4. Comparison of evaluation results of vulnerable links in the distribution network.

Ranking of Vulnerable Links	Method of This Article	Scheme 1	Scheme 2
1	172	172	172
2	649	649	11
3	11	11	649
4	14	49	14
5	49	285	483

.

Scheme 1 is to use the general degree, betweenness, path length, aggregation coefficient, and cohesion index to evaluate the vulnerable links of the distribution network.

Scheme 2 is based on complex network theory and risk theory. The node and line vulnerability indices are proposed, and the analytic hierarchy process is used to sum the weights of each index to obtain the comprehensive vulnerability index and evaluate the vulnerable links.

Compared with scheme 1, the method in this paper identifies four vulnerable links, and the identification results are basically similar, but the ranking is slightly different. The reason is that there are differences in the indicators considered by the two evaluation methods. Link 14 is the vulnerable link identified in this paper rather than the vulnerable link identified in scheme 1, and link 285 is the vulnerable link identified in scheme 1 rather than the vulnerable link identified in this paper. Although the vulnerability of link 14 in node degree is lower than 285, the transmission betweenness and voltage stability of link 14 branch are higher than those of link 285. Therefore, considering the above factors, the vulnerability of link 14 is higher than that of link 285.

Compared with scheme 2, the method in this paper identifies four vulnerable links, and the identification results are basically similar, but the ranking is slightly different. The reason is that there are differences in the comprehensive weighting methods considered by the two evaluation methods. Link 49 is the vulnerable link identified in this paper rather than the vulnerable link identified in scheme 2, and link 483 is the vulnerable link identified in scheme 2 rather than the vulnerable link identified in this paper. Although the vulnerability of link 49 in branch degree evaluation is lower than that of link 483, the node degree evaluation and voltage stability of link 49 are higher than those of link 483. Therefore, considering the above factors, the vulnerability of link 49 is higher than that of link 483.

5. Conclusions

The research goal of this paper is to propose a method for evaluating the vulnerable links of the distribution network with renewable energy source, which can quantify the risk of the distribution network and then identify the vulnerable links of the distribution network in combination with the grid structure information of the distribution network. It is helpful to monitor and warn, in a timely manner, of the risk of the distribution network after the distributed power supply is connected to the grid and provide theoretical support for system planning and scheduling operation. In this paper, the combination of theoretical modeling and simulation analysis is used to evaluate the vulnerable links of the distribution network with renewable energy source and identify the vulnerable links. The main results are as follows:

• When dealing with a distribution network with a high proportion of distributed energy, the traditional probabilistic power flow calculation method has problems such as low accuracy and long calculation time, which need to be improved and optimized. Therefore, considering the random output characteristics of renewable energy source and load, this paper proposes an improved semi-invariant probabilistic power flow calculation method, which improves the efficiency and accuracy of power flow calculation and can more accurately evaluate the safety and stability of power system.
• The evaluation index system of vulnerable links in a distribution network with renewable energy source is established. The reliability indices of traditional distribution network at home and abroad are extracted. These indices reflect the power supply capacity of the distribution network for a long time and lack the investigation of node voltage and line power flow in the distribution network. With the access of a high proportion of renewable energy source, the identification of vulnerable links in a distribution network is more complicated. In view of the increasingly obvious phenomenon of voltage over-limit and power flow over-limit after the access of distributed generation to a distribution network, this paper defines the identification index of vulnerable links in a distribution network with renewable energy source, including vulnerable line node index and vulnerable line identification index, which improves the traditional reliability index system and considers it more comprehensively.
• Aiming at the comprehensive evaluation of the vulnerable links of the distribution network, this paper uses the subjective and objective weighting method to analyze each index subjectively and objectively. Then, the comprehensive weighting method based on the minimum discriminant information theory is adopted to evaluate the vulnerable links of the distribution network comprehensively, which makes the evaluation results more reasonable. The distribution and utilization information of the Maiwang line is used for example analysis. From the simulation results, it can be seen that the overall operation of the Maiwang line is relatively stable, and the evaluation of vulnerable links is more reasonable. Some theoretical calculation methods and governance strategies have been applied in actual projects, and the feasibility of theoretical research has been further verified by actual results.

In addition, this paper does not consider the impact of electric vehicle clusters and network attacks on the vulnerability of distribution networks. With the rapid development and popularization of electric vehicles, the impact of electric vehicle access on the distribution network is becoming more and more obvious. In the future, large-scale electric vehicle access to the distribution network will be considered, the distribution of vehicle-network energy flow will be analyzed, and the vulnerability assessment of the distribution network will be carried out.