Decentralized Robust Power System Stabilization Using Ellipsoid-Based Sliding Mode Control
Abstract
1. Introduction
1.1. Survey of the Related Publications
1.2. Contributions
- Control decentralization is achieved by splitting the multi-machine system into subsystems. For each machine, a controller is installed using only the local states. For a specific machine, the influence of the rest of the system is seen as an external disturbance that must be minimized.
- The SMC design for power system excitation control is based on the methodology described in [9]. It is predicated on choosing the sliding surface correctly using the invariant ellipsoid approach. Unlike the conventional SMC, which cannot eliminate the effects of unmatched disturbances, the proposed SMC ensures minimizing the effects of the unmatched disturbances on system state trajectories in a sliding mode.
- The ellipsoidal SMC method in [9] is extended to a decentralized excitation stabilization design. The proposed decentralized design is unlike the conventional centralized control, which requires a costly communication network associated with its time-delay that might cause system instability.
- The proposed design can be applied to large power systems because of its decentralized structure. This is accomplished by decomposing the large system into small size subsystems for which a controller can be easily obtained for each.
- A simple design process that does not call for costly computational techniques.
- Using the features of Lyapunov functions, the closed-loop stability is ensured.
- The theoretical conclusions are validated by the simulation results on a multi-machine IEEE test system.
1.3. Notations
2. Power System Model and Problem Formulation
3. SMC by the Invariant Ellipsoid Method
3.1. Invariant Ellipsoid Method [9]
3.2. System Decomposition and Main Result
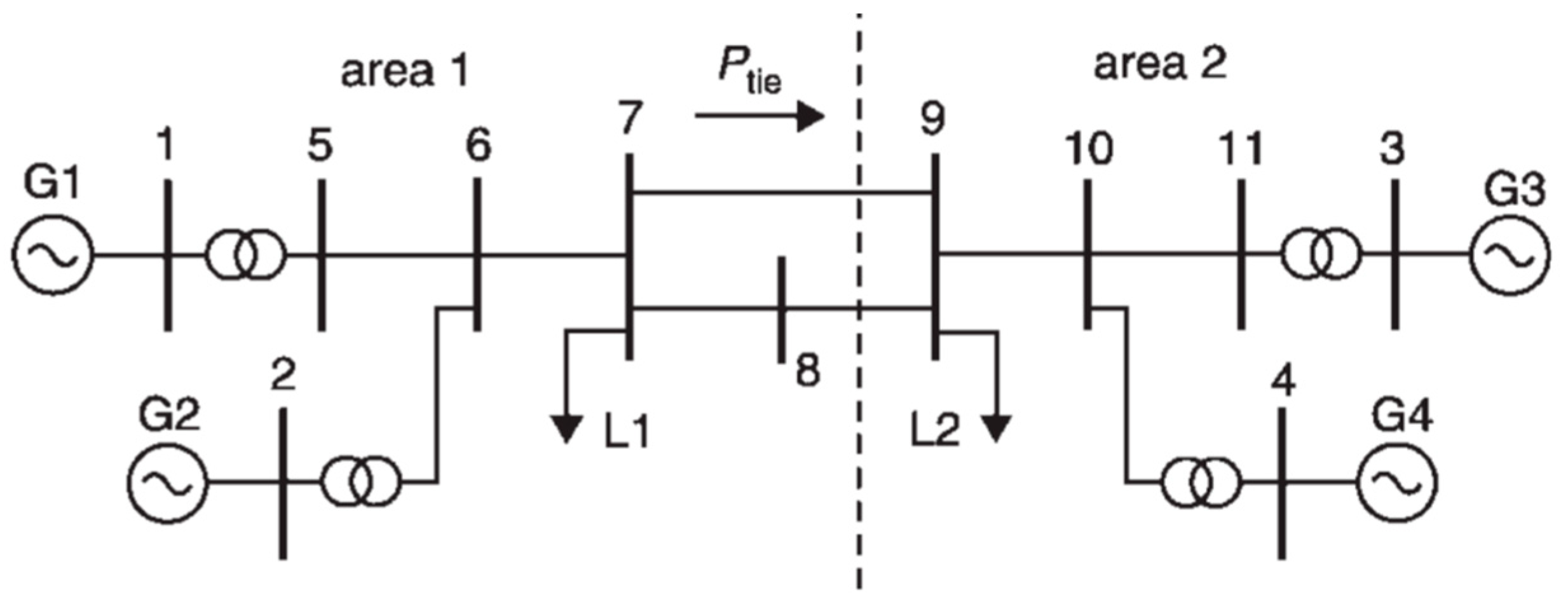
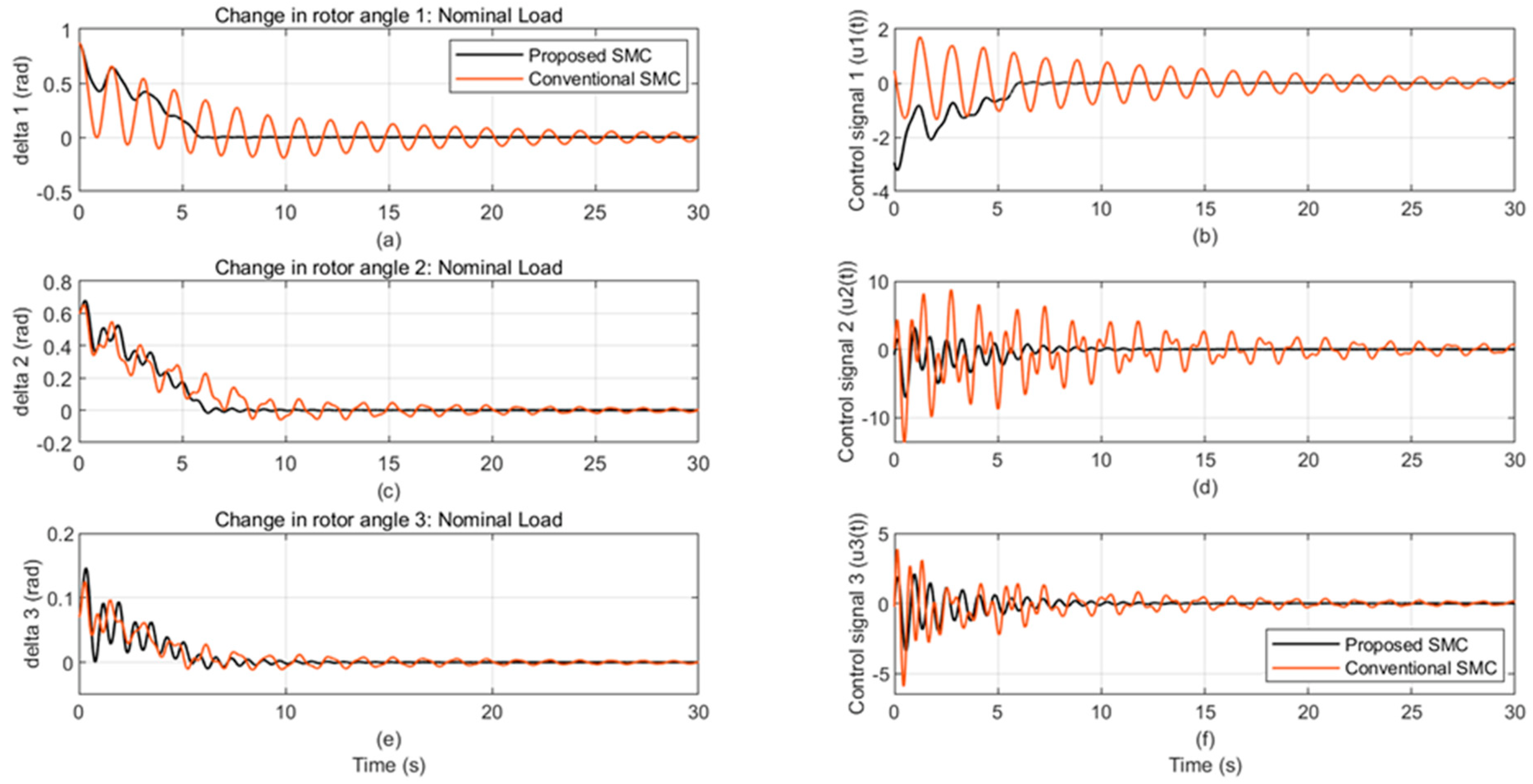
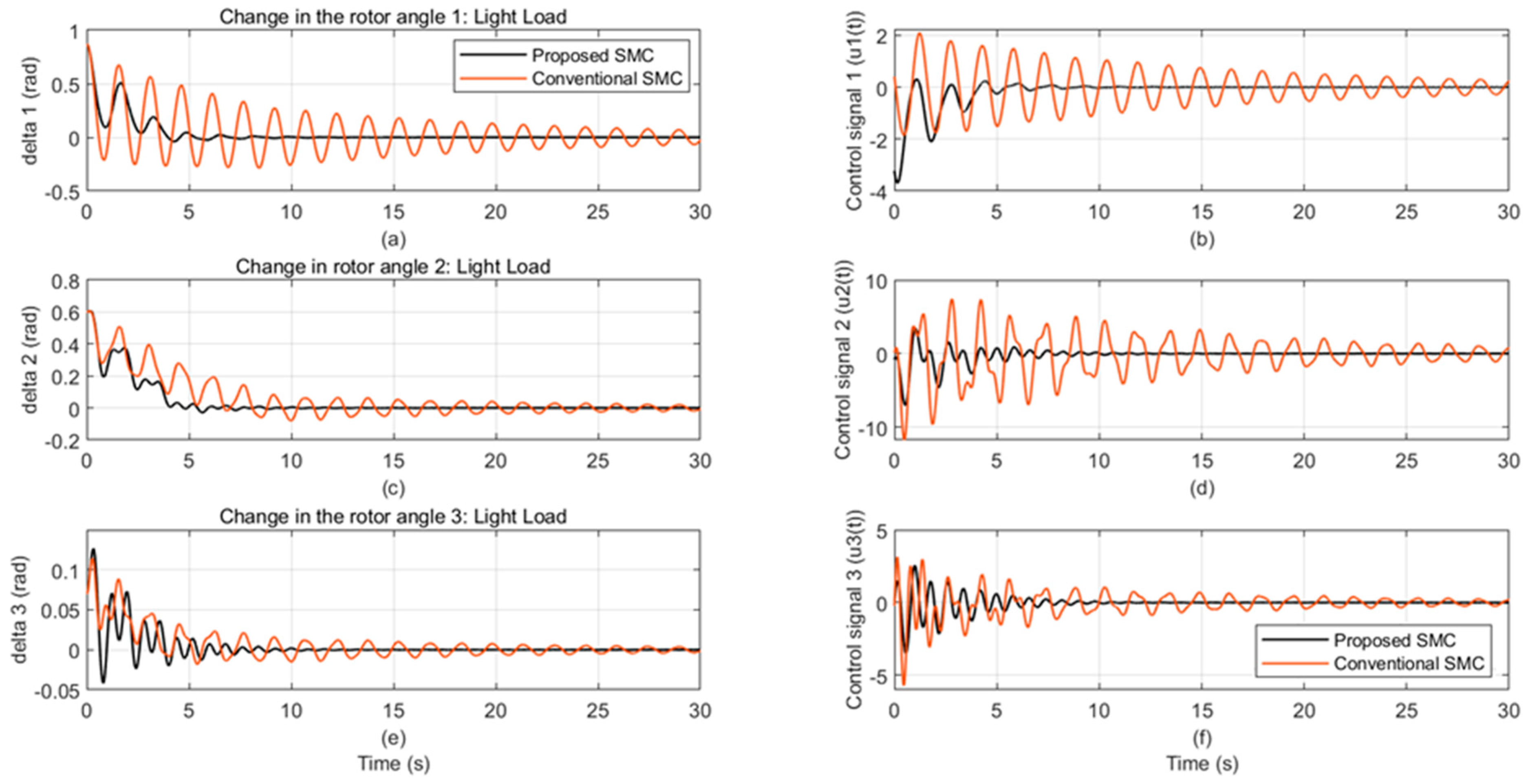
4. Simulation Validation
4.1. Simulation of Multi-Machine Power System
4.2. Robustness Assessment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Multi-Machine Model
- (i)
- Machine # 1
- (ii)
- Machine # 2
- (iii)
- Machine # 3
References
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill Education: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Soliman, H.M.; Benzaouia, A.; El-Sheikhi, F.A.; Buyukatak, K. Grid Frequency Stabilization under Magnitude and Generation Rate Constraints. Int. J. Model. Identif. Control. 2024, 44, 174–180. [Google Scholar] [CrossRef]
- Sauer, P.W.; Pai, M.A.; Chow, J.H. Power System Dynamics and Stability: With Synchro phasor Measurement and Power System Toolbox; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Dudgeon, G.J.W.; Leithead, W.E.; Dysko, A.; O’Reilly, J.; McDonald, J.R. The effective role of AVR and PSS in power systems: Frequency response analysis. Power Syst. IEEE Trans. 2007, 22, 1986–1994. [Google Scholar] [CrossRef]
- Mrad, F.; Karaki, S.; Copti, B. An adaptive fuzzy-synchronous machine stabilize. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2000, 30, 131–137. [Google Scholar] [CrossRef]
- Sarkar, D.U.; Prakash, T. A Recent Review on Approaches to Design Power System Stabilizers: Status, Challenges and Future Scope. IEEE Access 2023, 11, 34044–34061. [Google Scholar] [CrossRef]
- Rigatos, G.; Siano, P. Design of robust electric power system stabilizers using Kharitonov’s theorem. Math. Comput. Simul. 2011, 82, 181–191. [Google Scholar] [CrossRef]
- Garcia-Sanz, M.; Houpis, C.H. Wind Energy Systems: Control Engineering Design; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Poznyak, A.; Polyakov, A.; Azhmyakov, V. Attractive Ellipsoids in Robust Control; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Boukas, E.; AL-Sunni, F.M. Mechatronic Systems Analysis, Design and Implementation; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Yaghooti, A.; Buygi, M.O.; Shanechi, M.H.M. Designing coordinated power system stabilizers: A reference model based controller design. IEEE Trans Power Syst. 2016, 31, 1–11. [Google Scholar] [CrossRef]
- Abido, M.A.; Abdel-Magid, Y.L. Optimal design of power system stabilizers using evolutionary programming. IEEE Trans. Energy Con. 2002, 17, 429–436. [Google Scholar] [CrossRef]
- Sarkar, D.U.; Prakash, T. A Neural Network Approach to Design Power System Stabilizer for Damping Power Oscillations. In Proceedings of the 22nd National Power Systems Conference (NPSC), New Delhi, India, 17–19 December 2022. [Google Scholar]
- Hussein, T.; Saad, M.S.; Elshafei, A.L.; Bahgat, A. Damping inter-area modes of oscillation using an adaptive fuzzy power system stabilizer. Electr. Power Syst. Res. Dec. 2010, 80, 1428–1436. [Google Scholar] [CrossRef]
- Saoudi, K.; Harmas, M.N. Enhanced design of an indirect adaptive fuzzy sliding mode power system stabilizer for multi-machine power systems. I.J. Electr. Power Energy Syst. 2014, 54, 425–443. [Google Scholar] [CrossRef]
- Ju, P. Stochastic Dynamics of Power Systems; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Ye, K.; Zhao, J.; Duan, N.; Maldonado, D.A. Stochastic Power System Dynamic Simulation and Stability Assessment Considering Dynamics from Correlated Loads and PVs. IEEE Trans. Ind. Appl. 2022, 58, 7764–7775. [Google Scholar] [CrossRef]
- Lu, Z.; Lu, S.; Xu, M.; Cui, B. A robust stochastic stability analysis approach for power system considering wind speed prediction error based on Markov model. Comput. Stand. Interfaces 2021, 75, 103503. [Google Scholar] [CrossRef]
- Poznyak, A.S.; Alazki, H.; Soliman, H.M. Invariant-set Design of Observer-based Robust Control for Power Systems Under Stochastic Topology and Parameters Changes. I. J. Electr. Power Energy Syst. 2021, 131, 107112. [Google Scholar] [CrossRef]
- Poznyak, A.; Alazk, H.; Soliman, H. Attractive ellipsoidal design for robust stabilization of time-delay stochastic power systems under a series of lightning surges. Comput. Electr. Eng. 2024, 116, 109228. [Google Scholar] [CrossRef]
- Poznyak, A.S.; Soliman, H.M.; Alazki, H.; Bayoumi, E.H.E.; De Santis, M. Decentralized passivity-based voltage tracker for islanded DC-microgrids: Attracting ellipsoid approach. Energies 2024, 17, 1529. [Google Scholar] [CrossRef]
- Bayoumi, E.H.E. Sliding Mode Position Control of Synchronous Motor with Parameters and Load Uncertainties. Electromotion Sci. J. 2010, 17, 99–106. [Google Scholar]
- Edwards, C.; Spergeon, S. Sliding Mode Control: Theory and Applications; Taylor and Francis: Abingdon, UK, 1998. [Google Scholar]
- Utkin, V.I.; Guldner, J.; Shi, J. Sliding Modes in Electromechanical Systems; Taylor and Francis: London, UK, 1999. [Google Scholar]
- The MathWorks Inc. MATLAB, Version: 9.13.0 (R2023b); The MathWorks Inc.: Natick, Massachusetts, 2023; Available online: https://www.mathworks.com (accessed on 2 August 2024).
- Available online: https://yalmip.github.io/ (accessed on 19 August 2024).
- Available online: https://sedumi.ie.lehigh.edu/?page_id=58 (accessed on 19 August 2024).
- Jin, P.; Li, Y.; Li, G.; Chen, Z.; Zhai, X. Optimized hierarchical power oscillations control for distributed generation under unbalanced conditions. Appl. Energy 2017, 194, 343–352. [Google Scholar] [CrossRef]

| Machine # | R | ||
|---|---|---|---|
| 1 | 0.6592 | [6.8119, −1.0325 × 10−13, 6.6887 × 10−13 −1.0325 × 10−13, 6.8119, −7.6312 × 10−13 6.6887 × 10−13, −7.6312 × 10−13, 6.8119] | [−0.98782 −99.5610 8] |
| 2 | 0.58687 | [6.4499, 6.4696 × 10−13, 8.0441 × 10−13 6.4696 × 10−13, 6.4499, −4.0267 × 10−13 8.0441 × 10−13, −4.0267 × 10−13, 6.4499] | [−24.71 −42.9985 8] |
| 3 | 0.63266 | [6.6725, 2.7361 × 10−12, −7.2498 × 10−12 2.7361 × 10−12, 6.6725, −3.1488 × 10−12 −7.2498 × 10−12, −3.1488 × 10−12, 6.6725] | [−72.22 −109.310 8] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayoumi, E.H.E.; Soliman, H.M.; El-Sheikhi, F.A. Decentralized Robust Power System Stabilization Using Ellipsoid-Based Sliding Mode Control. Energies 2024, 17, 4249. https://doi.org/10.3390/en17174249
Bayoumi EHE, Soliman HM, El-Sheikhi FA. Decentralized Robust Power System Stabilization Using Ellipsoid-Based Sliding Mode Control. Energies. 2024; 17(17):4249. https://doi.org/10.3390/en17174249
Chicago/Turabian StyleBayoumi, Ehab H. E., Hisham M. Soliman, and Farag A. El-Sheikhi. 2024. "Decentralized Robust Power System Stabilization Using Ellipsoid-Based Sliding Mode Control" Energies 17, no. 17: 4249. https://doi.org/10.3390/en17174249
APA StyleBayoumi, E. H. E., Soliman, H. M., & El-Sheikhi, F. A. (2024). Decentralized Robust Power System Stabilization Using Ellipsoid-Based Sliding Mode Control. Energies, 17(17), 4249. https://doi.org/10.3390/en17174249







