Numerical Simulation of Corona Discharge Plasma Affecting the Surface Behavior of Polymer Insulators
Abstract
1. Introduction
2. Description of the Numerical Simulation Model
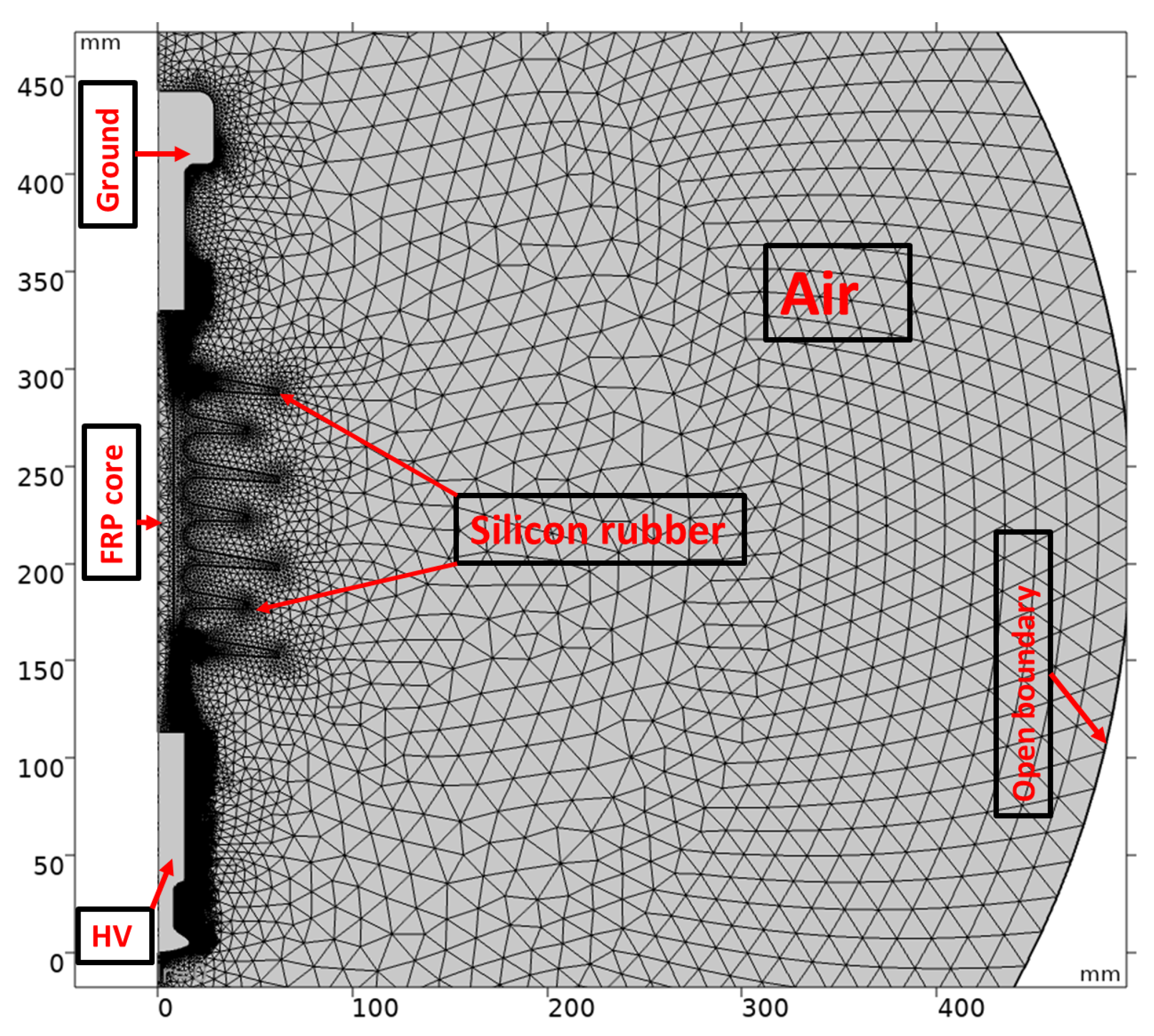
2.1. Geometric and Numerical Model
2.2. Corona Discharge in Air
3. Results and Discussion
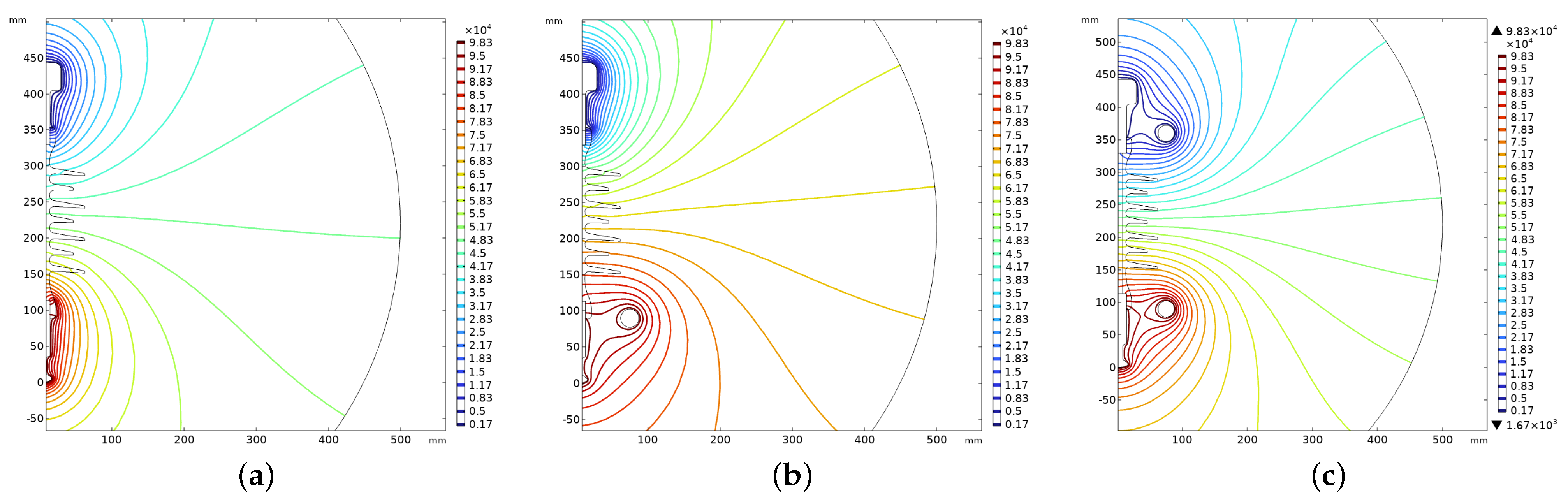
3.1. Equipotential and Electric Field Distributions
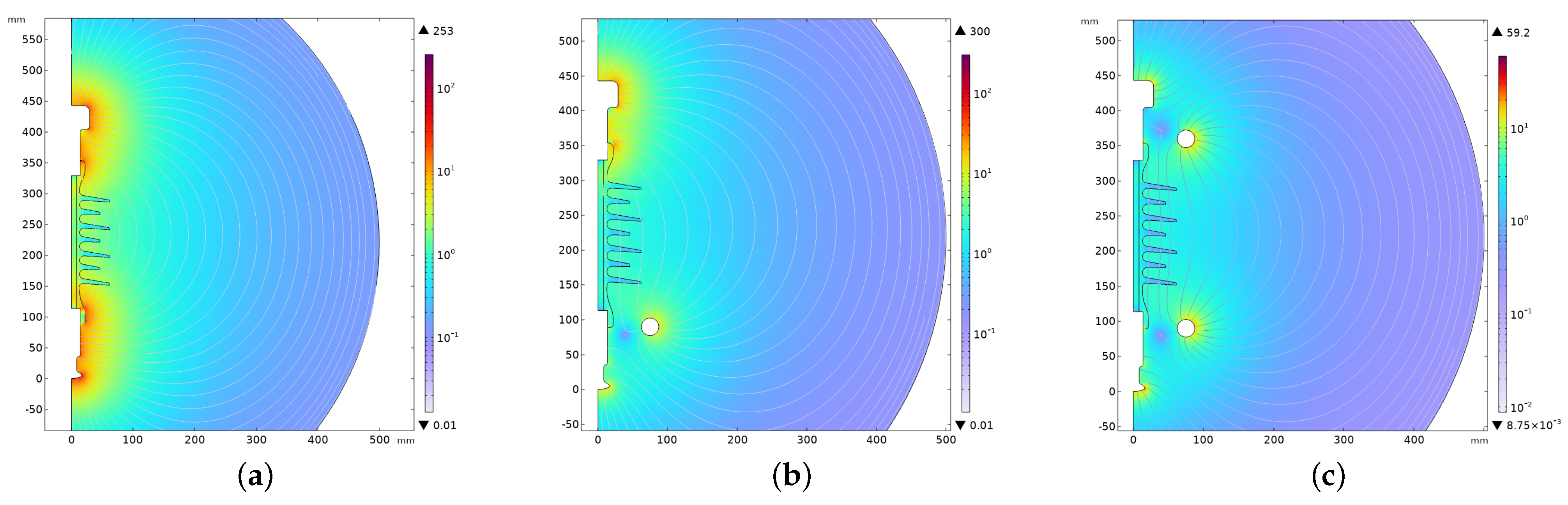
3.2. Electron Density Distribution
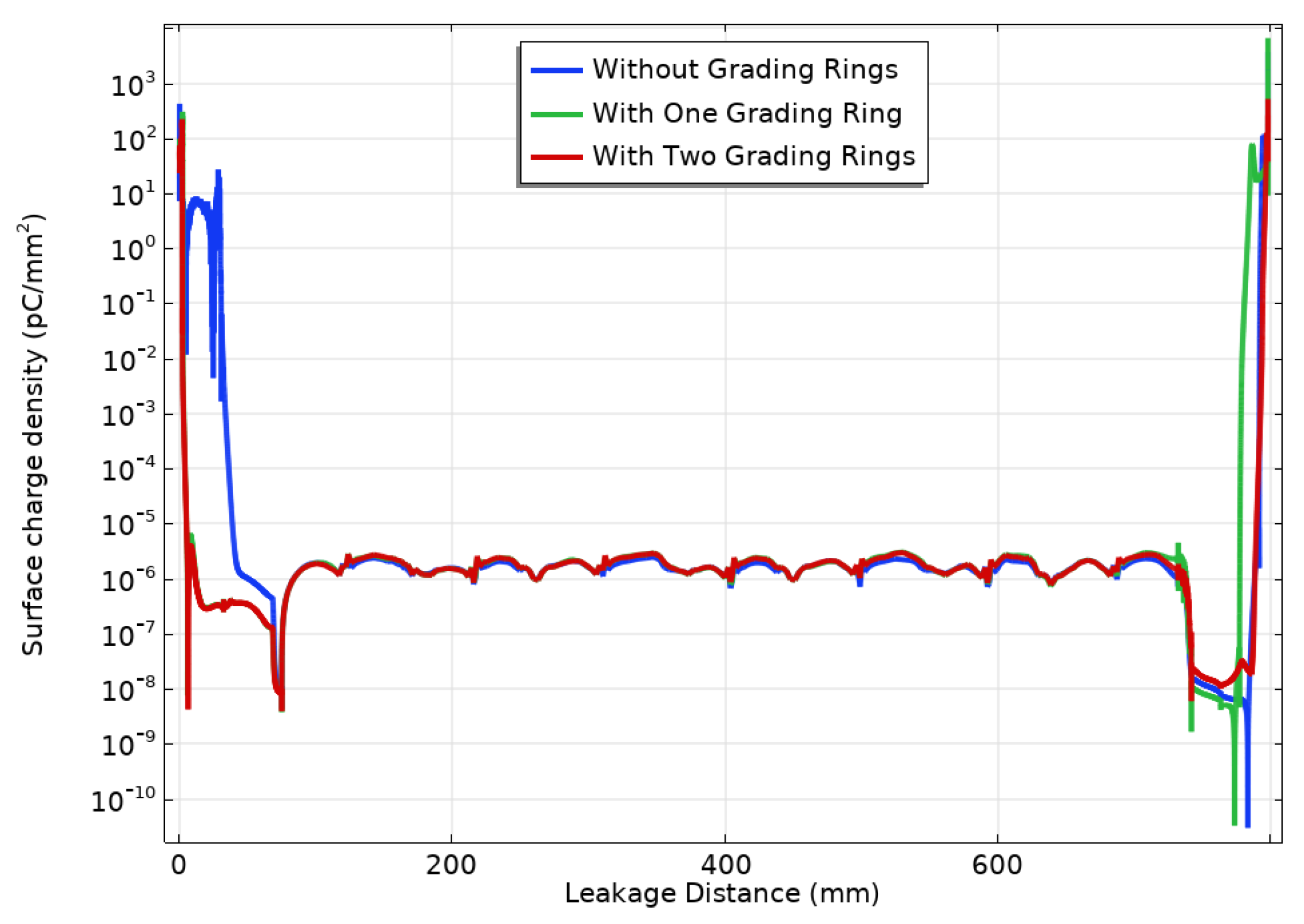
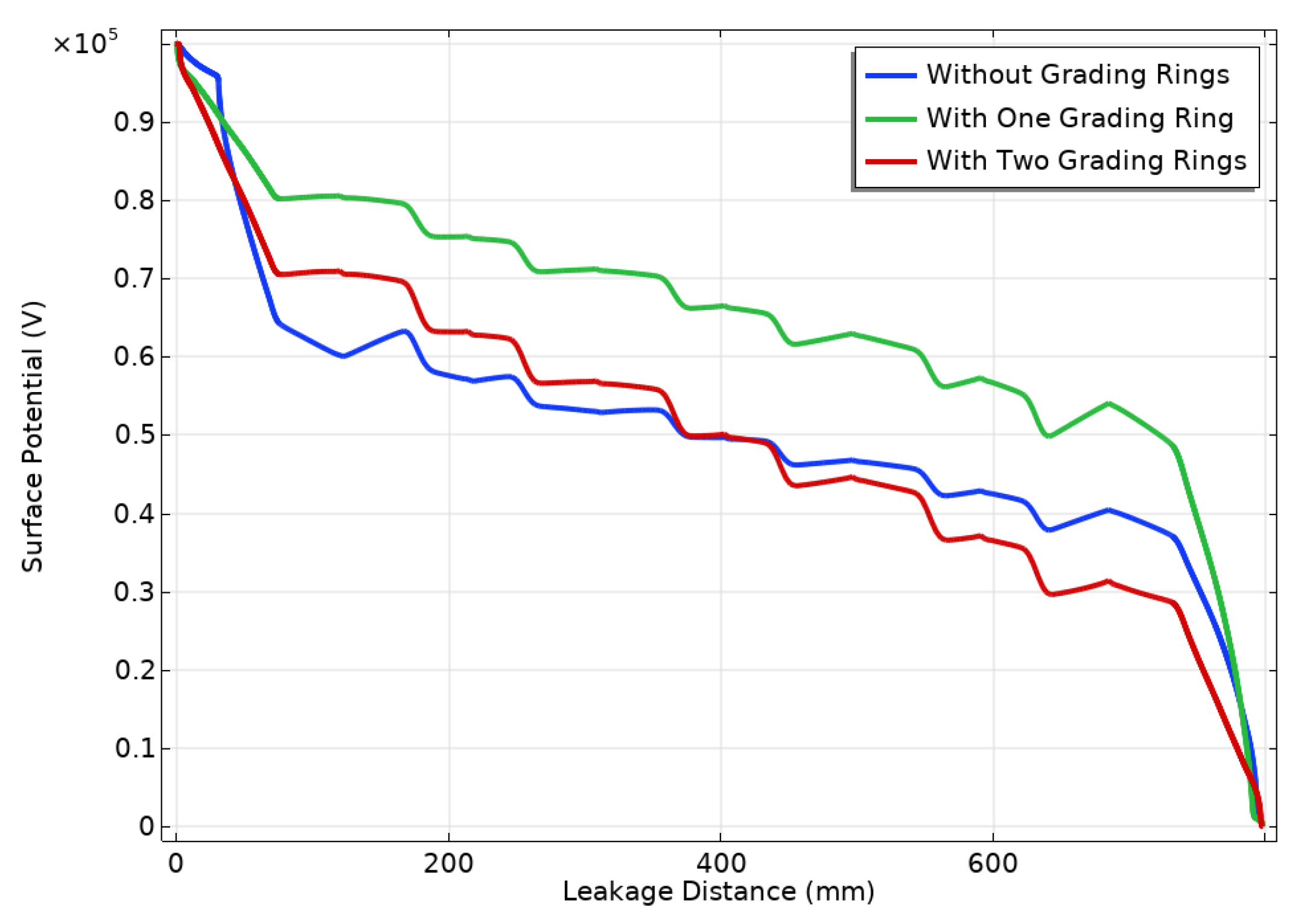
3.3. Surface Charge Density and Surface Potential
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cherney, E.A. 50 years in the development of polymer suspension-type insulators. IEEE Electr. Insul. Mag. 2013, 29, 18–26. [Google Scholar] [CrossRef]
- Mahmoodi, J.; Mirzaie, M.; Akmal, A.A.S. Surface charges on silicon rubber (SiR) insulator and their effect on potential and electric field distribution. Electr. Eng. 2018, 100, 2695–2705. [Google Scholar] [CrossRef]
- Learning from Service Experience with Composite Line Insulators. INMR: 2020. Available online: http://www.inmr.com/learning-from-service-experience-with-composite-line-insulators-2/ (accessed on 10 May 2024).
- Zheng, Y.; Wang, L.; Wang, D.; Jia, S. Numerical study of the effect of the needle tip radius on the characteristics of Trichel pulses in negative corona discharges. Phys. Plasmas 2017, 24, 063515. [Google Scholar] [CrossRef]
- Tarasenko, V.F.; Kh Baksht, E.; Vinogradov, N.P.; Kozyrev, A.V.; Kokovin, A.S.; Kozhevnikov, V.Y. On the Mechanism of Generation of Trichel Pulses in Atmospheric Air. JETP Lett. 2022, 115, 667–672. [Google Scholar] [CrossRef]
- Saifutdinova, A.A.; Timerkaev, B.A.; Saifutdinov, A.I. Numerical Computations of Transition Processes in Direct Current Corona Microdischarge. Russ. Phys. J. 2022, 65, 156–168. [Google Scholar] [CrossRef]
- Saifutdinov, A.I. Numerical study of various scenarios for the formation of atmospheric pressure DC discharge characteristics in argon: From glow to arc discharge. Plasma Sources Sci. Technol. 2022, 31, 094008. [Google Scholar] [CrossRef]
- Reddy, B.S. Corona degradation of the polymer insulator samples under different fog conditions. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 359–367. [Google Scholar] [CrossRef]
- Reddy, B.S.; Marathe, M. Corona studies on polymeric insulator samples used in high voltage transmission. In Proceedings of the IEEE International WIE Conference on Electrical and Computer Engineering (WIECON-ECE), Pune, India, 19–21 December 2016; pp. 160–163. [Google Scholar]
- Yuan, Z.; Tu, Y.; Wang, C. Temperature Rise Prediction on Silicone Rubber Housing of Composite Insulator in High Humidity Environment. In Proceedings of the IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; pp. 1–4. [Google Scholar]
- Belhiteche, E.H.; Rondot, S.; Dony, P.; Moudoud, M.; Jbara, O. Effect of Aging Time on the Hydrophobicity of Polymers Subjected to Corona Discharge. In Proceedings of the International Conference of Advanced Technology in Electronic and Electrical Engineering (ICATEEE), M’sila, Algeria, 26–27 November 2022; pp. 1–5. [Google Scholar]
- Ghiasi, Z.; Faghihi, F.; Shayegani-Akmal, A.A. FEM analysis of electric field distribution for polymeric insulator under different configuration of non-uniform pollution. Electr. Eng. 2021, 103, 2799–2808. [Google Scholar] [CrossRef]
- Kone, G.; Volat, C.; Ezzaidi, H. Numerical investigation of electric feld distortion induced by internal defects in composite insulators. IET High Volt 2017, 2, 253–260. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, J.; Zhang, L.; Wang, Y.; Li, X. Numerical simulation of surface discharge characteristics on silicone rubber insulators with different surface roughness. IEEE Access 2021, 9, 104898–104907. [Google Scholar]
- Liu, H.; Liu, Q.; Wang, Z.; Zhang, L. Numerical simulation and analysis of corona discharge in a coaxial cylindrical system under high-altitude environment. IEEE Trans. Plasma Sci. 2021, 49, 3984–3994. [Google Scholar]
- Li, Y.; Li, X.; Li, D.; Xie, W. Numerical simulation of surface charge accumulation on silicone rubber insulator based on corona discharge model. IEEE Access 2020, 8, 165004–165014. [Google Scholar]
- Shanmugam, G.; Karakkad, S. Influence of the insulator geometry on the streamer propagation characteristics in polymeric insulators under positive polarity lightning impulse voltages. IET Sci. Meas. Technol. 2018, 12, 1082–1088. [Google Scholar] [CrossRef]
- Zogning, C.; Lobry, J.; Moiny, F. Comparison between Positive and Negative Corona Discharges by Hydrodynamic Plasma Simulations. In Proceedings of the International Symposium on Electrical Insulating Materials (ISEIM), Tokyo, Japan, 13–17 September 2020; pp. 552–560. [Google Scholar]
- Sima, W.; Liu, C.; Yang, M.; Shao, Q.; Xu, H.; Liu, S. Plasma model of discharge along a dielectric surface in N2/O2 mixtures. Phys. Plasmas 2016, 23, 063508. [Google Scholar] [CrossRef]
- Zogning, C.; Lobry, J.; Moiny, F. Simulation of Positive Corona Discharge in Atmospheric-pressure Air by Plasma Hydrodynamic Model. In Proceedings of the 12th National Conference on High Voltage Engineering CNHT, Sidi Bel-Abbès, Algeria, 4–6 October 2022. [Google Scholar]
- Hagelaar, M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722. [Google Scholar] [CrossRef]
- Zhelezniak, M.B.; Mnatsakanian, A.K.; Sizykh, S.V. Photoionization of nitrogen and oxygen mixtures by radiation from a gas discharge. High Temp. 1982, 20, 357–362. [Google Scholar]
- Bourdon, A.; Pasko, V.P.; Liu, N.Y.; Célestin, S.; Ségur, P.; Marode, E. Efficient models for photoionization produced by non-thermal gas discharges in air based on radiative transfer and the Helmholtz equations. Plasma Sour. Sci. Technol. 2007, 16, 656–678. [Google Scholar] [CrossRef]
- Kossyi, I. Kinetic scheme of the non-equilibrium discharge in nitrogen-oxygen mixture. Plasma Sources Sci. Technol. 1992, 1, 207. [Google Scholar] [CrossRef]
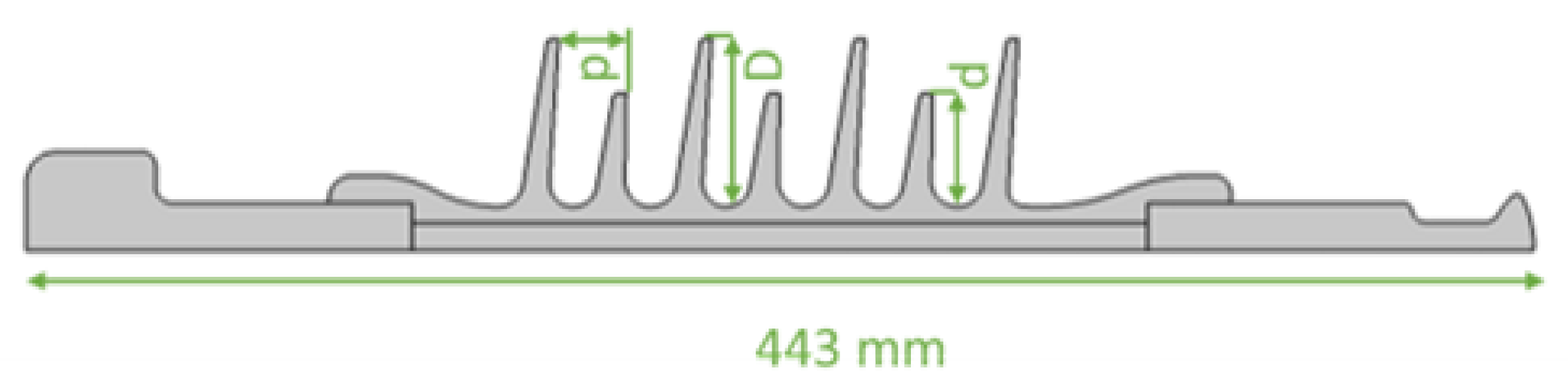


| Leakage distance | 800 mm |
| Dry arcing distance | 265 mm |
| Large shed radius (D) | 48.9 mm |
| Small shed radius (d) | 33.2 mm |
| Space between two sheds (p) | 24.7 mm |
| Shed number | 7 |
| Materials | Electrical Conductivity (S/m) | Relative Permittivity |
|---|---|---|
| Air | 1.0 | |
| Fiber glass | 7.2 | |
| Silicon rubber | 4.3 | |
| Metal fittings | 1.0 |
| Reaction Type | Reaction | Rate Expression |
|---|---|---|
| Impact ionization | Townsend coefficients (Bolsig+ code) | |
| Impact ionization | Townsend coefficients (Bolsig+ code) | |
| Electron attachment | ||
| production | ||
| Three-body recombination | ||
| Three-body recombination | ||
| Impact dissociation | ||
| Photoionization | Calculated by Helmholtz equation set |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zogning, C.; Lobry, J.; Moiny, F. Numerical Simulation of Corona Discharge Plasma Affecting the Surface Behavior of Polymer Insulators. Energies 2024, 17, 4247. https://doi.org/10.3390/en17174247
Zogning C, Lobry J, Moiny F. Numerical Simulation of Corona Discharge Plasma Affecting the Surface Behavior of Polymer Insulators. Energies. 2024; 17(17):4247. https://doi.org/10.3390/en17174247
Chicago/Turabian StyleZogning, Calvin, Jacques Lobry, and Francis Moiny. 2024. "Numerical Simulation of Corona Discharge Plasma Affecting the Surface Behavior of Polymer Insulators" Energies 17, no. 17: 4247. https://doi.org/10.3390/en17174247
APA StyleZogning, C., Lobry, J., & Moiny, F. (2024). Numerical Simulation of Corona Discharge Plasma Affecting the Surface Behavior of Polymer Insulators. Energies, 17(17), 4247. https://doi.org/10.3390/en17174247







