Numerical Modeling and Optimization of a Quasi-Resonant Inverter-Based Induction Heating Process of a Magnetic Gear

Abstract

Induction heating is a clear, cheap, and highly effective technology used for many industrial and commercial applications. Generally, a time-varying magnetic field produces the required heat in the workpiece with a specially designed coil. The efficiency of the heating process depends highly on the coil design and the geometrical arrangement. A detailed and accurate finite element analysis of the induction heating process usually needs to resolve a coupled thermoelastic–magnetic problem, whose parameters values depend on the solution of another field. The paper deals with a shrink-fitting process design problem: a gear should be assembled with an axe. The interesting part of this case study is given the prescribed low limits for critical stress, the temperature of the gear material, and the heat-treated wearing surfaces. A coupled finite-element-based model and a genetic algorithm-based parameter determination methodology were presented. A thermal imaging-based measurement validated the presented numerical model and parameter determination task. The results show that the proposed methodology can be used to calibrate and validate the numerical model and optimize an induction heating process.

1. Introduction

Induction heating is a widely used, clean, and environment-friendly technology in the industry. It can be applied for many processes from shrink-fitting, forging, melting, hardening, brazing, or creating an appropriate heat treatment for the workpieces in a mass manufacturing process [1,2,3,4,5]. Applying an assembly process using induction heating requires precise planning and experimentation, as the process is susceptible to the geometry of the coil and workpiece to be heated and to the parameters of the materials used. The physical model of the process requires the solution of a coupled thermoelastic and electromagnetic problem, whose parameters are typically nonlinear and whose values depend on the solution of another field [6,7,8].

Due to its complexity, many recent papers published on the topic, which present novel numerical methodologies for the coupled field analysis [4,6,9,10,11,12,13]. In [14], the authors reported numerical modeling and experimental validation of an induction heating system with a thermographic camera. This paper published a coupled magneto–thermal numerical model examining a steel workpiece with both temperature-dependent and independent material properties. Bay et al. [15] proposed a coupled thermoelastic electromagnetic numerical model of the induction heating problem, which can accurately used to model simple, inductionally heated systems. Dolezel et al. [16] proposed a hp-adaptive numerical solution to an attractive, coupled magneto–thermoelastic problem. Here, the thermoelastic phenomenon was used to control the heating rods’ position in a reactor accurately. In [17], the authors proposed a fully coupled electromagnetic and heat transfer model for modeling thin wall injection molding. The authors in [18] shown a coupled, finite element-based numerical model for a triangle heating experiment on a rolled plate, whose methodology can overcome the influence of edge effect on temperature distribution and transverse shrinkage. The resulting numerical model was applicable to examine the temperature characteristics and deformation behavior in moveable triangle heating. Due to the challenging solution of the induction heating problem involving different physical domains, the COMPUMAG Society proposes a benchmark problem to test novel numerical methods on a nonlinear induction heating problem [19,20]. Selecting an accurate and fast numerical solver is necessary to resolve this task and the connecting inverse coil design problem. Some analytical formulations have also been developed recently to accelerate the solution of the time-consuming optimization task [2]. These new formulas’ goal is to take into consideration the geometry of the modeled workpiece, which was limited previously [21,22].

In [23], the authors proposed a numerical model-based parameter determination method for a rarely examined alloy of bismuth (32.5%), tin (16.5%), and indium (51.0%). The proposed methodology showed how an optimization method could be used with an accurate numerical model to determine the missing parameters, which was the material’s specific heat capacity in the case study. The proposal used the fact that the melting point of this material is very low, around 60 °C, and the necessary information can be determined from the melting process. A weakly coupled magneto–thermal model was applied during this optimization task, where the missing parameters were searched with a genetic algorithm. Afzal et al. [24] applied a neural network and a genetic algorithm-based process to determine the optimal values of the parameters on a pipe induction heating problem. Bao et al. described an online methodology to estimate the inductance parameters for precise control of an inductive heating system [25]. Pánek [26] proposed a finite element model and a coupled hp-adaptive FEM-based methodology to find out the optimal material parameters and create an appropriate model for perforated sheet-based materials of the intentionally brazed evaporator. Barman et al. [27] used analytical, numerical, and experimental methods to determine a multi-layered induction heating coil’s frequency-dependent inductance and resistance parameters. It was obtained during the simulation that, however, the capacitance of the coil does not affect the steady-state conditions; it significantly impacts the calculations. Spateri et al. [28] published a novel optimization framework using novel parametrization formulation together with set membership global optimization method for designing the coil configurations in induction heating applications [29,30].

The accurate solution to the induction heating’s numerical problem can be used to design a fast and accurate process with cheap, easily accessible tools for a specific problem, where it is necessary to determine the missing parameters of the heating process. The paper deals with a case study problem, where a steel gear should be heated to reach the required expansion for a shrink-fitting process while its hotspot temperature is limited to not hurt the heat treatment of the material. The importance and the originality of this study is that it proposes a numerical analysis of an induction heating process of a steel workpiece, which has strict temperature limitations. It demonstrates that using novel numerical methods, the missing parameters can be determined by a numerically, reducing the cost of the measurements. The applied FEM model solves the partial differential equations of the coupled magnetic, thermal, and elastic problem with an open-source hp-adaptive finite element method-based tool: Agros Suite. The correctness of the numerical model was validated by infrared thermography and thermal resistance-based measurements. The proposed process, with the connection measurement methodology methods, demonstrates how to determine the missing thermal flow parameters for the simulation, apply the given numerical model for design, and optimize the size and the layout using standardized flat-shaped windings. Simulation and experimental results were evaluated and discussed at the end of the paper.

2. Materials and Methods

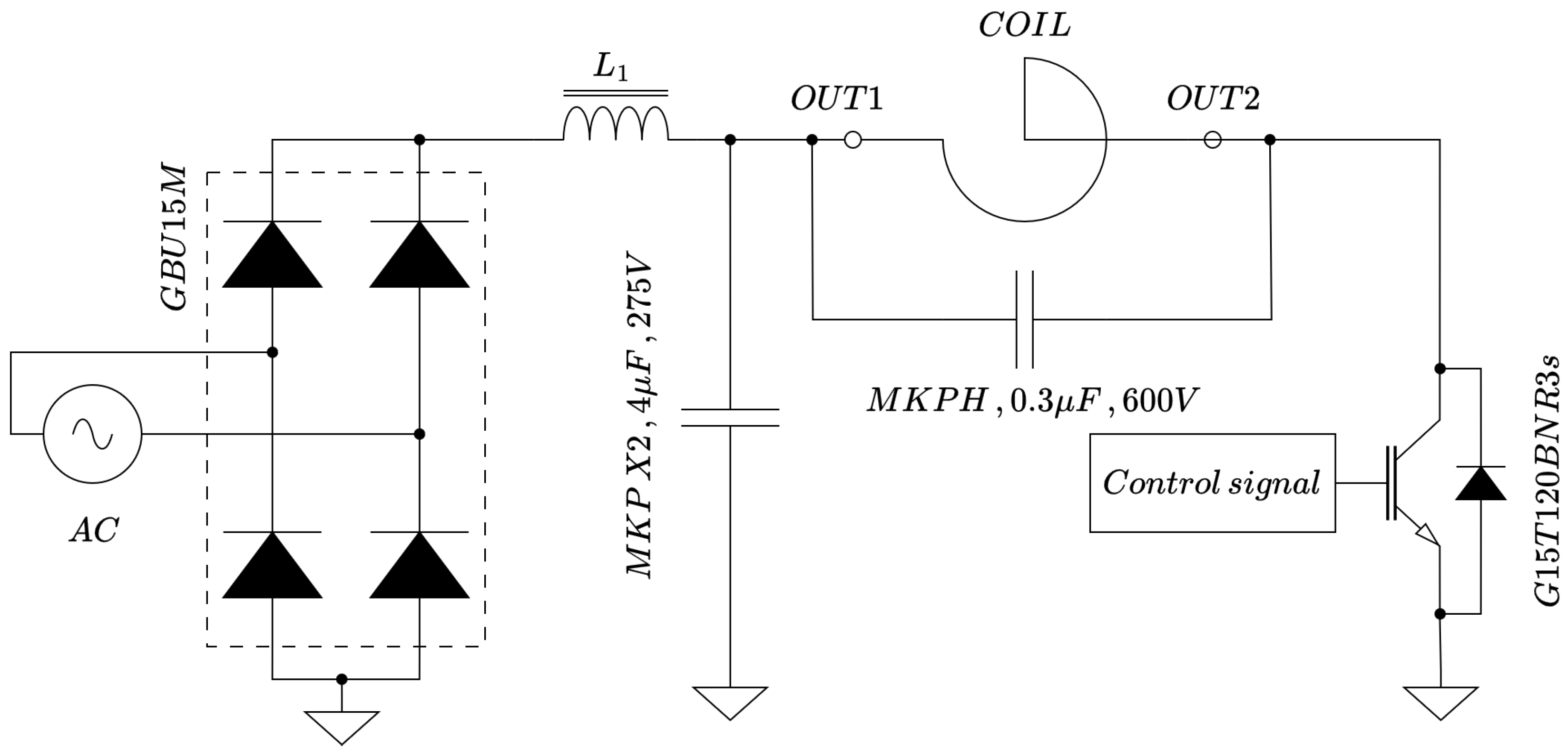
2.1. Problem Description and Experimental Test

The engineering task aims to provide a simple layout for the induction heating-based assembly process, where a gear should be placed on the axe with shrink fitting. The proposed process’s maximum length should be less than eight minutes to replace the current assembly methodology. This is not a strict criterion for an inductive heating process. However, the hotspot of the temperature should be lower than 200 °C during the assembly process to not degrade the heat-treated surface of the gear. The heating power must not be arbitrarily high so that the material of the heated workpiece does not suffer permanent deformation during the assembly process. Another problem during this assembly process is that all the applied material parameters are unknown. A measurement setup was created to estimate the missing parameters and validate the proposed numerical model. The installation is depicted in Figure 1a, where the gears are blurred due to confidential reasons. The experiment included a portable, long-wave (between 7.5 and 14 µm) professional-grade uncooled microbolometer thermal imager (Testo 885-2, Titisee-Neustadt, Germany) with 240 × 320 pixel resolution, adjustable focus, <30 mK thermal sensitivity at 30 °C, and capability to measure up to 1200 °C. The thermal imager was equipped with a 30° × 23° lens with 1.7 mrad geometric resolution (IFOV) which is ideal for measuring close objects and was set up on a tripod to record a fully radiometric video during the heating process using 24 fps. Besides the thermal imager, three NiCr-Ni K-type thermocouples (Ahlborn T-190-0, Holzkirchen, Germany) were fixed to the gear with measurement tapes. The thermocouples are class 2 with limiting deviation of ±2.5 K, the wires and sheath are glass fiber insulated, and their operating temperature is between −1 °C and 400 °C. Measurements from the thermocouples were recorded every 5 s using a portable precision measuring instrument and data logger (Ahlborn Almemo 2890-9, Holzkirchen, Germany) with internal memory. The data logger is AA precision class, capable of up to 100 measuring operations per second (mops) with a system accuracy of 0.02% at 2.5 mops. The thermocouples were connected to the data logger using the data logger’s connectors (Ahlborn Almemo ZA9020FS, Holzkirchen, Germany), which provides 0.1 K resolution and ±0.05 K accuracy on the measured temperatures. The gear was heated using a simple inductive heater (Esperanza EKH011, Ożarów Mazowiecki, Poland) adjustable between 200 W to 2000 W, which uses a quasi-resonant converter with a simple pancake coil (Figure 1b). Different tapes were applied to the measured reflective metal surface to obtain more accurate infrared thermographic measurements [31]. The reflected temperature was set to 20 °C since the laboratory temperature was maintained at this constant temperature. The appropriate measurement tape was selected during calibration, and the emissivity factor was calibrated. One tape was used to attach the three K-type thermocouples to the three distinct parts of the gear: one fixed near the head, one in the middle region, and one near the wearing surface. The fourth thermocouple was used to monitor the air temperature, which should be constant during the measurements because it was made in a tempered laboratory room.

The induction heating during the experiments was carried out with a low-cost quasi-resonant induction heating circuit. Given the shape and size of the prototype and the financial constraints, the simplest solution was an induction hob, which is also used in households. As well known, a high excitation current is needed to create the largest possible magnetic field. A resonant solution achieves a reasonable efficiency. Although the circuit is fed from the mains, without the resonant solution, the high operating current of the semiconductor would cause significant conduction losses (which would also increase the cost of the circuit). The resonant design increases efficiency and reduces the circuit is size and weight, allowing a more compact design. It was essential for our experiments [32].

The circuit is resonant frequency depends on the material and the desired heating power. Up to a power of a few kW, it is about 20–50 kHz. In this lower frequency range, IGBTs (Insulated-Gate Bipolar Transistors) are the preferred switching elements. The resonant process allows the semiconductor to be switched by ZZero Voltage Switching) and ZCS (Zero Current Switching). The induction cooker applies a quasi-resonant process, where the resonant tank circuit is used only to create a ZVS or ZCS condition to turn the performing semiconductor switch on or off [33]. In addition to the convenience electronics, the structure of the device is simple: it includes a pancake coil and quasi-resonant electronics, which can also be seen in Figure 2. Accordingly, the topology consists of a single IGBT with an anti-parallel diode connected to the resonant tank. The coil forms the resonant tank shown in Figure 2 and is parallel to it by the high-voltage MKPH capacitor.

Using the rotational symmetry of the gear, the 3D geometric deformations can be modeled by a 2D axisymmetric fem model, which resolves the coupled magnetic–thermal and elastic fields to calculate the deformations and the temperature distribution in the gear. The purpose of the numerical model is to determine those excitation setups and temperature distributions, which are necessary to create the 85 μm and larger expansion in the inner hole of the gear. Due to the 3D deformation of the shape of the gear during the heating process, this calculation is not easy in itself; however, the second difficulty is that the proposed temperature limit (200 °C) is only 10–20 °C higher than we need for this expansion in the ideal case. Firstly, we can investigate the feasibility of the task by calculating the maximal thermal expansion with the proposed data in

Table 1. The known material parameters of the applied carbon steel material of the gear and the axe.

Quantity	Value	Dimension
Thermal Conductivity	45	${\displaystyle \frac{\mathrm{W}}{\mathrm{mK}}}$
Specific heat capacity	470	${\displaystyle \frac{\mathrm{J}}{\mathrm{kg}\mathrm{K}}}$
Thermal Expansion coefficient	$11.5·{10}^{-6}$	${\displaystyle \frac{\mathrm{m}}{\mathrm{K}}}$
Density	7800	${\displaystyle \frac{\mathrm{kg}}{{\mathrm{m}}^3}}$
Young’s modulus	210	GPa
Poisson ratio	$0.3$	[-]
Heat Transfer coefficient	25	${\displaystyle \frac{\mathrm{W}}{{\mathrm{m}}^2\mathrm{K}}}$

.

The following formula can be used to calculate the thermal expansion of the gear:

$$\mathrm{\Delta }d=d_0\alpha \mathrm{\Delta }T,$$

(1)

where $\mathrm{\Delta }d$ is the thermal expansion, $\alpha$ is the linear thermal coefficient, and $\mathrm{\Delta }T$ is the greatest permissible temperature difference during the heating process is 170 K. Calculating with this values, the resulting $\mathrm{\Delta }T$ is 107.5 μm, which is only 26% higher than the necessary 85 μm. This temperature difference can be increased if it is possible to cool down the axe during the assembly process, but in this paper, we are not considering this scenario.

2.2. Numerical Model of the Related Physical Fields

The mathematical model of an induction heating-based shrink-fitting process is based on the solution of three connecting partial differential equations describing the distribution of the magnetic and the temperature field. In contrast, its solution provides the input parameters for the elasticity problem, which provides expansion of the gear, for which calculations are necessary to resolve the original engineering problem.

The magnetic vector potential $\mathit{A}$ can describe the magnetic field. The following equation can describe its distribution in the system [34,35]:

$$\nabla \times \nabla \times \mathit{A}+j·\sigma \mu \omega \mathit{A}=\mu {\mathit{J}}_{\mathit{ext}},$$

(2)

where $\omega =2\pi f$ stands for the angular velocity, where f describes the frequency of the field current, $sigma$ is the electrical conductivity of the modeled materials, $\mu$ represents the magnetic permeability, and ${\mathit{J}}_{\mathit{ext}}$ represents the field current density. A Dirichlet condition is applied around the modeled area with $\mathit{A}=0$.

The heat transfer equation can describe the distribution of the temperature field in the following form:

$$\nabla ·(\lambda \nabla T)=\rho c_p{\displaystyle \frac{\partial T}{\partial t}}-w_j$$

(3)

where $\lambda$ is the thermal conductivity of the material, $\rho$ is the specific mass, and $c_p$ represents the specific heat capacity of the material. Both of these physical quantities depend on the temperature of the material; while $w_j$ represents the time average of the generated Joule losses, its value can be calculated by the following expression:

$$w_j={\displaystyle \frac{\left|\right|{{\mathit{J}}_{\mathit{eddy}}\left|\right|}^2}{2\sigma }},$$

(4)

where ${\mathit{J}}_{\mathit{eddy}}$ denotes the phasor of the amplitude of the current density, it can be expressed by ${\mathit{J}}_{\mathit{ind}}=\omega \sigma \mathit{A}$.

The boundary condition can be written in the following format for this heat convection problem:

$$-\lambda {\displaystyle \frac{\partial T}{\partial \mathit{n}}}=\alpha (T_{ext}-T).$$

(5)

where $T_{ext}$ is the external temperature, measured at the outer surface of the gear, while $\mathit{n}$ denotes the outward normal to the surface. Due to the relatively low temperatures, the radiation component can be neglected.

The solution of the Lamé equation can resolve the thermoelasticity problem of the gear [16,36]:

$$(\varphi +\psi )·\nabla (\nabla ·\mathit{u})+\psi ·\mathrm{\Delta }\mathit{u}-(3\varphi +2\psi )·{\alpha }_T\nabla T+\mathit{f}=0$$

(6)

where $\varphi \ge 0$, $\psi >0$ are coefficients that can be determined by the following assumptions:

$$\varphi ={\displaystyle \frac{\nu ·E}{(1+\nu )(1-2\nu )}},$$

(7)

$$\psi ={\displaystyle \frac{E}{2·(1+\nu )}}.$$

(8)

In Equation (7) and in Equation (8), E denotes the Young’s modulus of the material, while $\nu$ is the Poisson coefficient of the contraction. Moreover, $\mathit{u}$ describes the displacement, ${\alpha }_T$ is the material’s linear thermal dilatability, and $\mathit{f}$ vector describes the internal forces. These vectors contain the gravitational and the Lorentz forces, which are negligible during the calculations because they are very small compared to the thermoelastic stresses [16].

This mathematical model was resolved by Agros Suite, using a 2D axisymmetric model of the geometry, which used the geometrical symmetries to create a simplified FEM model. Agros Suite (version. 2020.9.15.64726) is an open source software, under GNU General Public License, which supports the weakly coupled solution of the above-shown partial differential equation system, with the aid of a state-of-the-art numerical solver, supports hp-adaptive mesh generation, and provides the possibility to create an optimization problem using Ᾱrtap framework, which contains many evolutionary and artificial-intelligence-based optimization methods [37].

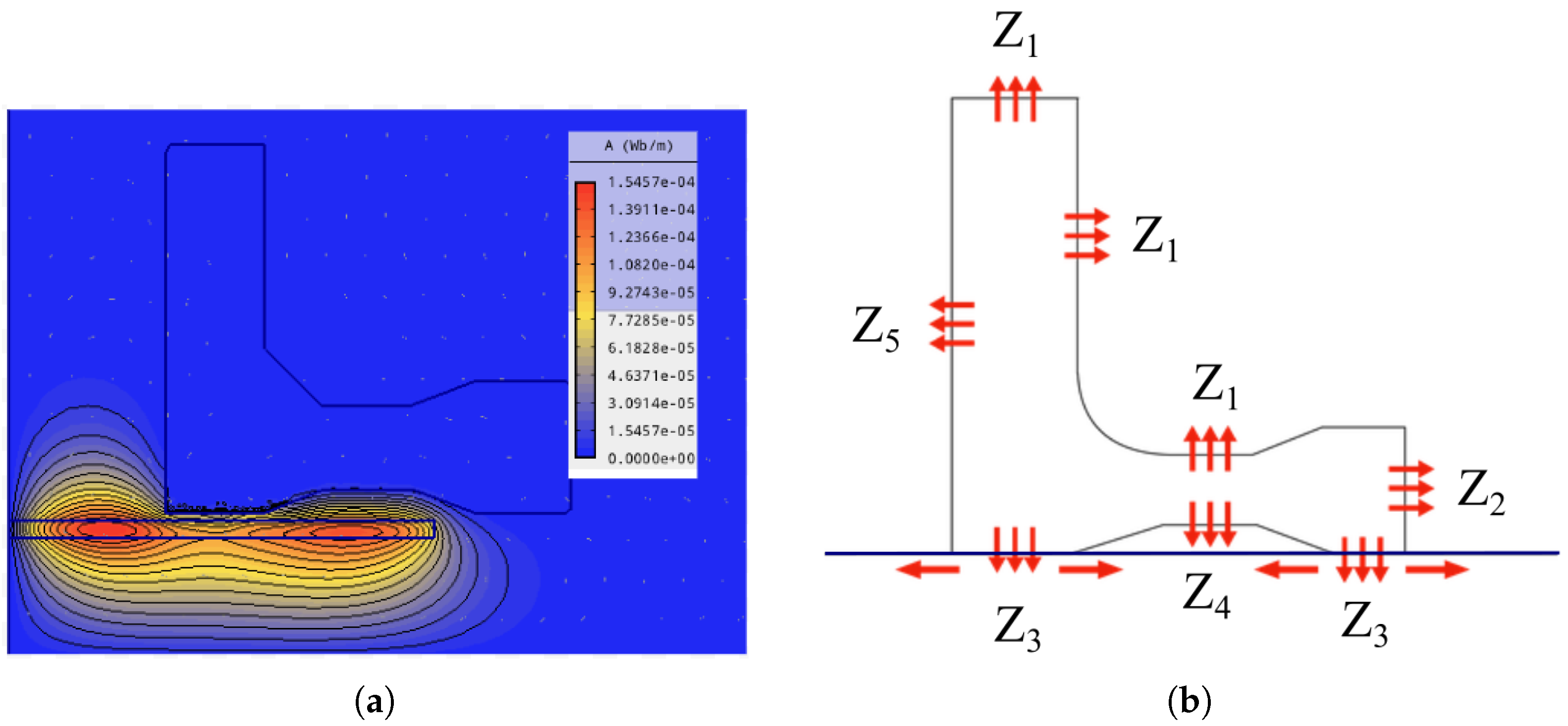
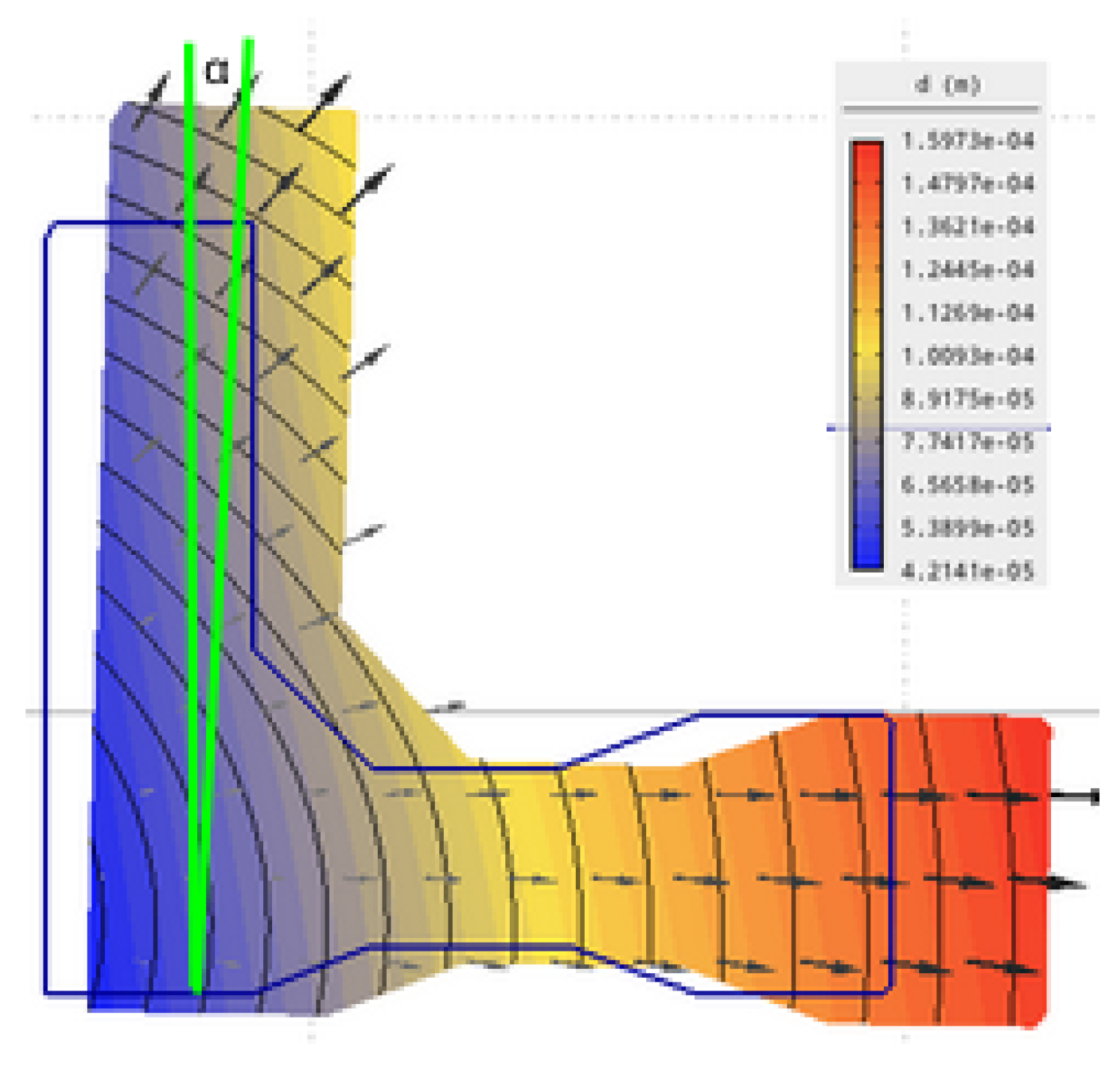
2.3. Numerical Model of the Gear

The 2D axisymmetric model of the gear, created in Agros Suite, is a simple yet accurate representation. The pancake coil of the induction hob (Figure 1b) is modeled by the copper filling factor of the winding, which is represented by a simple rectangle. While this model may not be suitable for accurately modeling the eddy current loss in the windings, it is simple and accurate enough to model and calculate the resulting magnetic field distribution with the required precision. The frequency of the exciting current in the winding was set to 50 kHz in our calculations, while the exciting current is 2000 Amperturns, and the filling factor is around 0.6, wound from stranded wires. The electrical conductivity of the examined steel is $\sigma =10$ MS/m. A scalar hysteresis measurement device measured the magnetic permeability of the gear. During the measurements, we created a primary coil around the gear, which was excited by a current generator, while the secondary current was measured by using a National Instruments Data Acquisition (NI-DAQ) card. The results were post-processed by Labview-based software [38,39]. The magnetic permeability of the gear material was ${\mu }_r$ = 50 at 200 Hz. This means that this special steel does not have good magnetic properties. It can be modeled with ${\mu }_r$ = 1 at the used excitation frequencies.

The used thermal model parameters of the gear are summarized in Table 1; however, determining the heat loss via the boundaries between the gear and the different surfaces is not obvious. The following simplifications and five distinct heat loss zones are introduced with the following assumptions (see in Figure 3b):

• $Z_1$: this is a free surface connected directly to the air.
• $Z_2$: Area of the teeth, the modeled surface replaces the original surface by the mean surface of the teeth; this parameter is higher than the heat exchange between the gear material and the air in reality due to the real surface of the teeth being larger than in the applied model.
• $Z_3$: The contact area between the bottom of the gear and the insulation glass, which separates the induction heating coil from the gear. This area has a low heat conductivity, which is considered a small value in the model.
• $Z_4$: This is an air-gear contact area, where the bottom of the gear contacts with the air. However, this zone is closed by the insulator glass; due to the lack of air circulation, this parameter is much lower than $Z_1$.
• $Z_5$: Shaft connection area (the inner hole). This area is closed from the bottom. Therefore, air circulation is lower in the modeled region than in the free outer surface of the gear. Thus, the air temperature will be higher here than in the other areas. This region should be considered by smaller heat loss than the other free surfaces ($Z_1$) connected to the free air.

These boundary parameters will be estimated from the following measurements. The Poisson ratio and Young’s modulus are also given in Table 1, which is a necessary input to resolve the partial differential equation of the elasticity problem. The maximum stress during the heating process should not be higher than 100 MPa in order to prevent permanent deformation after the heating process.

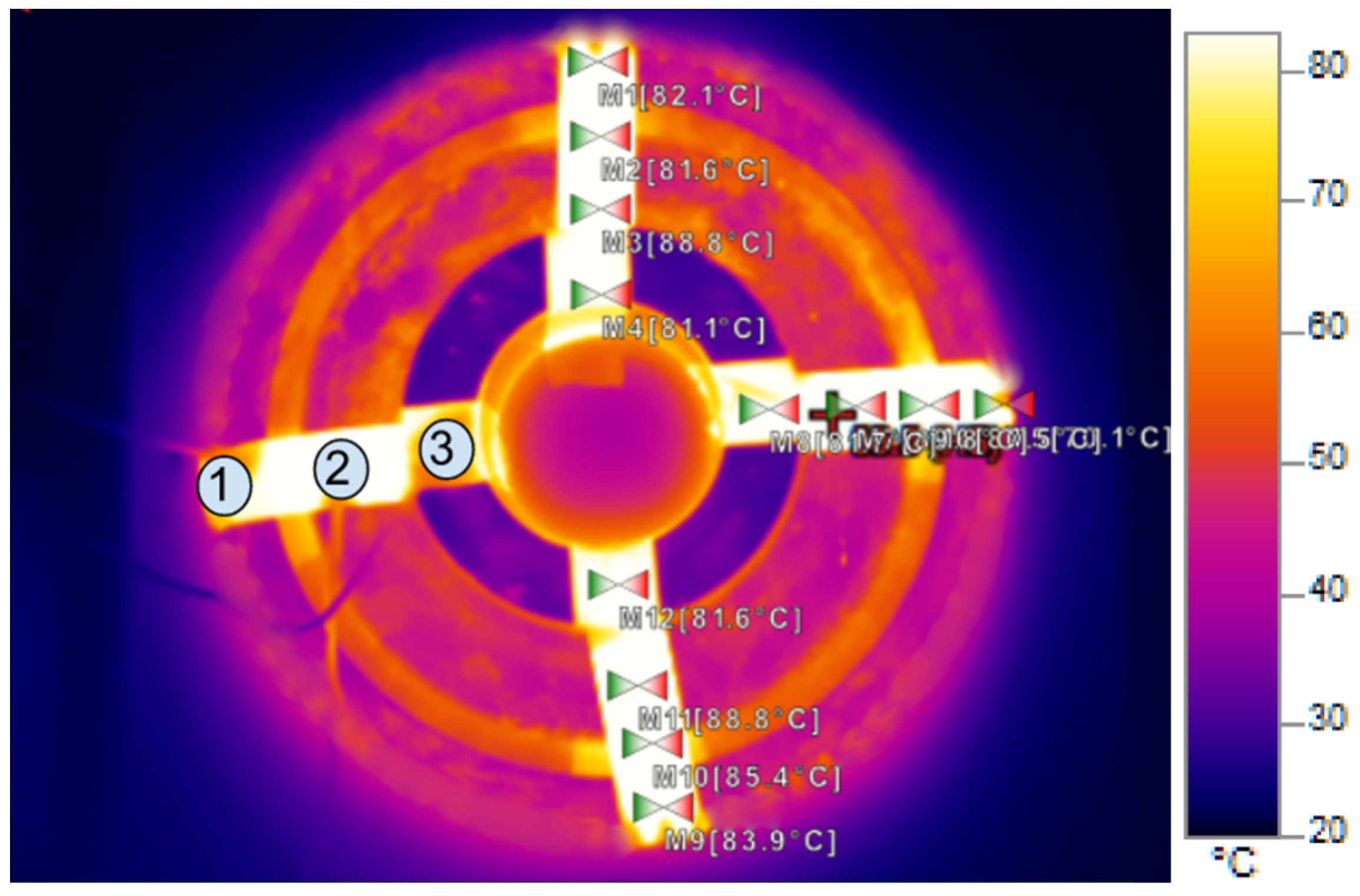
3. Measurements and Numerical Results

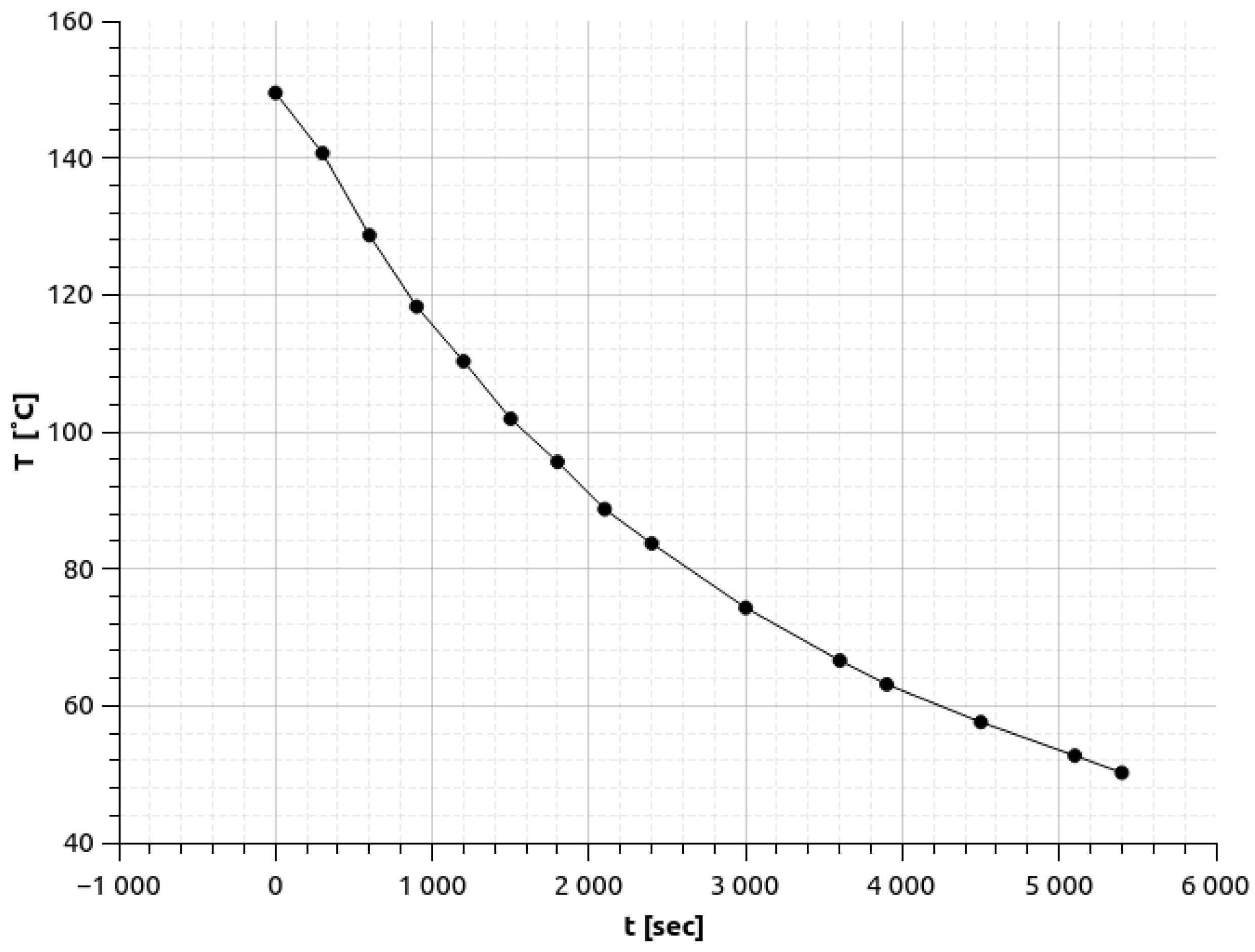
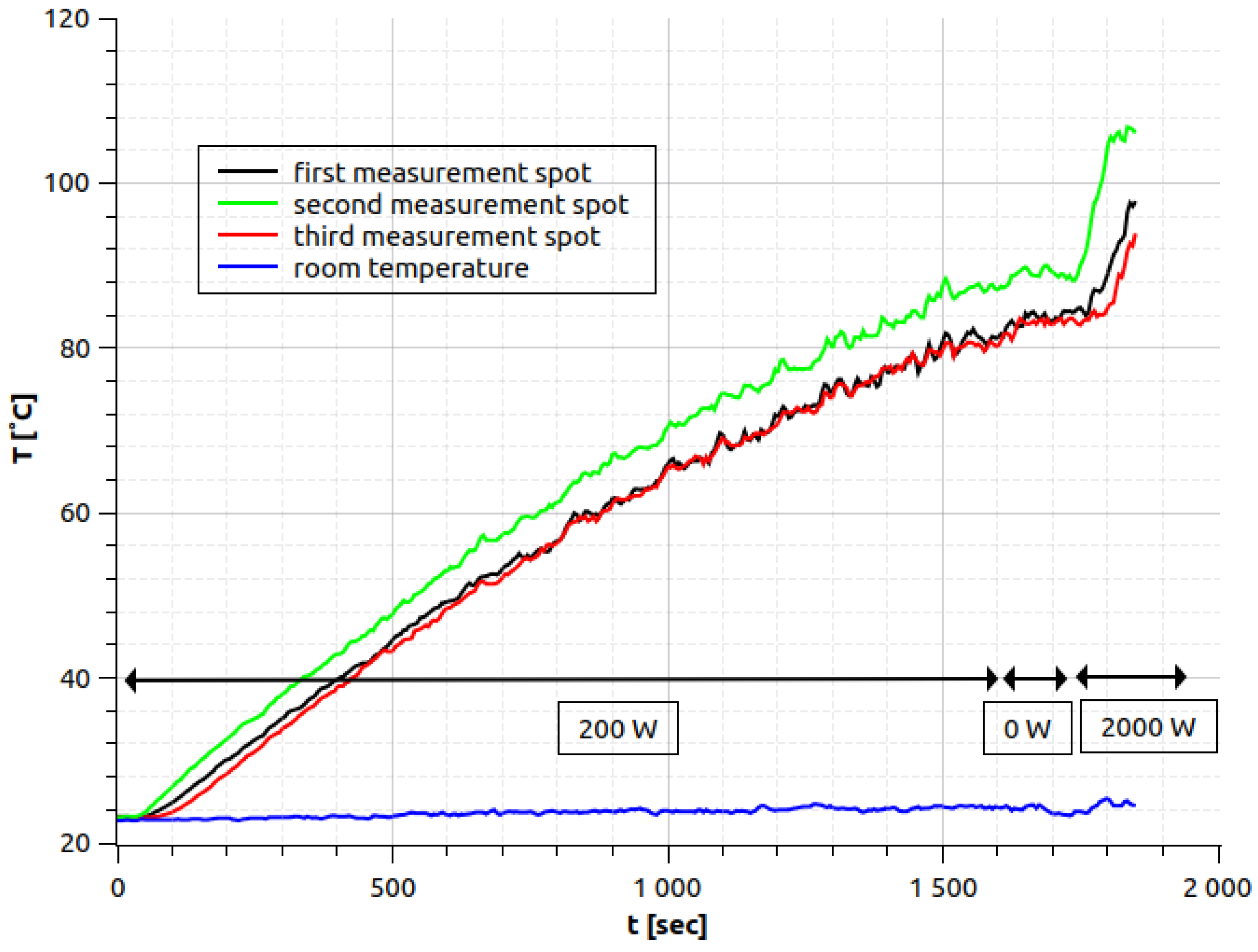
3.1. Thermal Equilibrium

The first measurement aimed to determine the temperature of the thermal equilibrium condition when 200 W excitation power was set on the induction heater. In this case, the heating process was very slow; reaching the thermal equilibrium temperature at 149.5 ± 1 °C took hours. At this point, we waited more than five minutes to check that the temperature did not change, and we can assume that the temperature distribution was homogenised in the heated part. Using this assumption that the heating temperature is equal to the heat loss at this temperature, we can calculate from the applied numerical model that the effective heating power means about 135 ± 10 W in this layout, which agrees with our expectations. From this point, we can estimate the average heat loss from the measured values and the total surface of the gear ($9.03·{10}^{-2}{\mathrm{m}}^2$), as a rule of thumb. The average heat loss results in 12.1 ${\displaystyle \frac{\mathrm{W}}{{\mathrm{m}}^2\mathrm{K}}}$ for the whole gear.

3.2. Cooling and Heating Characteristics

From the thermal equilibrium, the gear’s cooling down was also measured at the three different points and with the thermal camera. It took about one and a half hours to decrease the temperature to 50 °C at the measurement points. The results of the measurements in the third measurement point are depicted in Figure 4.

These data from the temperature decay at the third measurement curve can be used for parameter fitting and testing the accuracy of the modeled parameters by using the resulting curves of the second measurement. Figure 5 shows the resulting curves of the measurement in the three measurement spots and the air temperature near the measurements. The position of the three measurement spots and the temperature distribution during the measurements can be seen in Figure 6. The first measurement sensor was placed on one tooth of the crown, the second measurement spot was placed in the middle part, and the third spot was placed at the top of the gear’s inner ring. All of them were inserted under the masking tape.

At the start of the measurement, the gear temperature was the same as the ambient air temperature at all three measurement spots. From this point, the measurement was started by setting the induction plate to 200 W. This power was used to heat the gears for 1600 s. The inductor was switched off, and after waiting 200 s, the inductor was switched on again at a maximum power of 2000 W. This gave another, much steeper heating curve. The power value used for induction heating was indicated in Figure 5 in the different sections marked by arrows. We used different excitations during the curve measurement to validate our fitted parameters, i.e., our numerical model with missing heat transfer coefficients.

It can be seen from the measured curves (Figure 5) and the thermal image (Figure 6) that the highest temperatures can be measured at the second measurement spot and its nearby area. One explanation for the fact that the temperature at this point is the highest in the whole measurement is that the thickness of the material is the smallest, and the heat cannot dissipate downwards due to the lack of airflow in the $Z_4$ area.

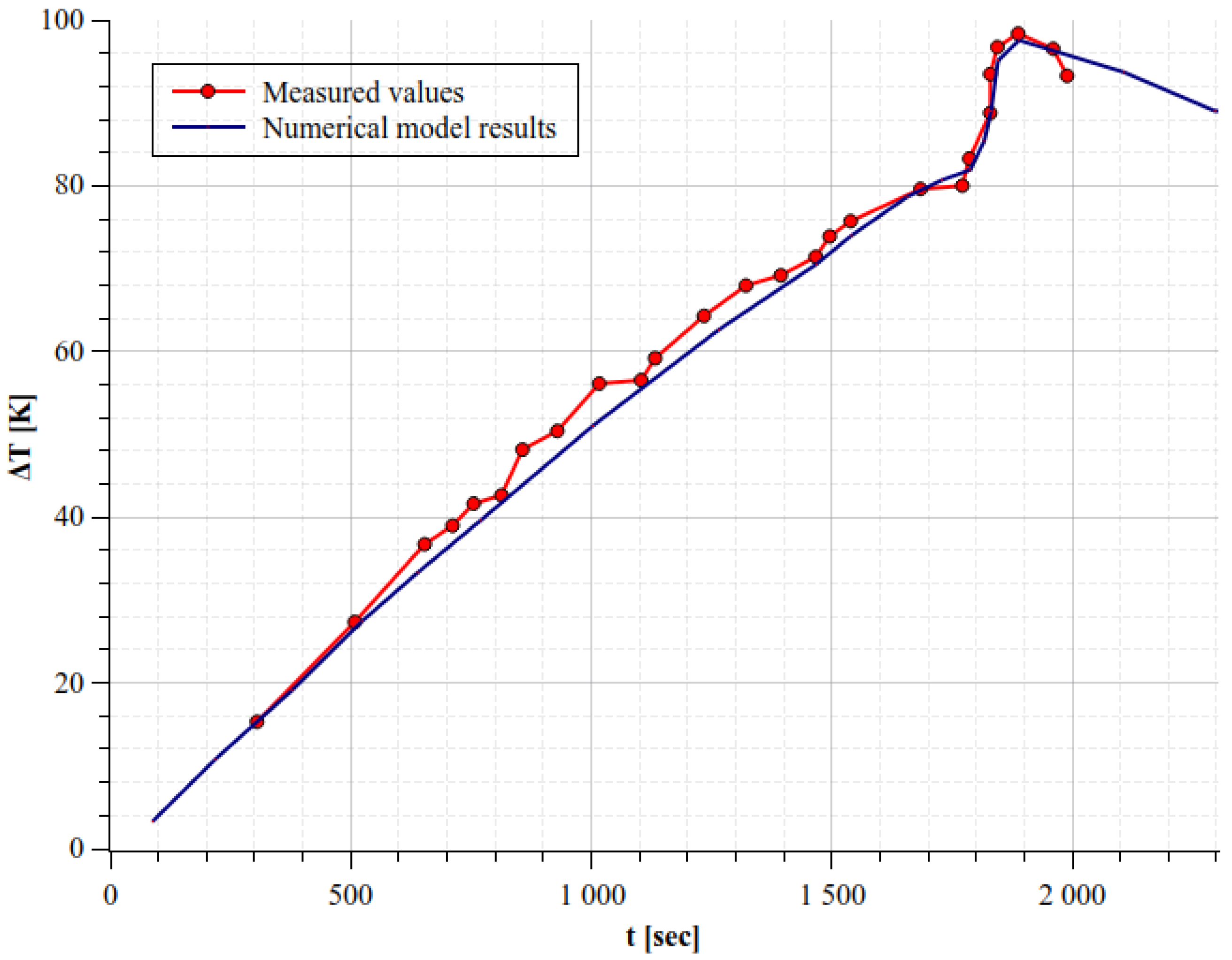
3.3. Parameter Fitting and Numerical Model Validation

A genetic algorithm-based fitting process was introduced to find the most appropriate values for the heat loss parameters at the different heat loss zones from $Z_1$ to $Z_5$. The optimization was realized in Artap framework, which provides a Python interface to Agros Suite and many built-in genetic and evolutionary optimization algorithms, which can be used to solve the wide range of optimization tasks [37].

The current optimization problem can be formulated as a single-objective optimization problem and can be resolved by a genetic algorithm, as depicted in Figure 7. The goal function aims to minimize the difference between the measurement points and the numerical calculation values, and the following mathematical formulae can define it:

$$\mathrm{\Delta }y=\Sigma {(y_i-m_i)}^2,$$

(9)

where $m_i$ represents the ith measurement point, which will be the measured temperature value at the third measurement spot. Similarly, $x_i$ denotes the numerically calculated temperature value at the given position of the gear. The goal of the optimization algorithm was to minimize the $\mathrm{\Delta }y$ value.

The parameter fitting task has five independent variables ($Z_1$ to $Z_5$), whose values are searched during the optimization. These parameters are contained by the x vector, which is the input parameter for the following numerical analysis (Figure 7). The applied genetic algorithm selects these values from the initially defined limits. Then, the FEM model calculates the temperature rise at the first measurement point during the heating test (Figure 5), where two different heating powers are set up during the process. Both of them are considered in the calibration of the numerical model. After evaluating the goal function for the full population, the genetic algorithm creates the new population by applying the mutation and the crossover operations. The population contained 30 individuals, and the full calculation process was made for 30 generations for this calibration task.

After all the 900 evaluations, the following settings seem to be the most appropriate for the different zones of the gear:

• $Z_1=12.0{\displaystyle \frac{\mathrm{W}}{{\mathrm{m}}^2\mathrm{K}}}$;
• $Z_2=18.0{\displaystyle \frac{\mathrm{W}}{{\mathrm{m}}^2\mathrm{K}}}$;
• $Z_3=2.0{\displaystyle \frac{\mathrm{W}}{{\mathrm{m}}^2\mathrm{K}}}$;
• $Z_4=1.0{\displaystyle \frac{\mathrm{W}}{{\mathrm{m}}^2\mathrm{K}}}$;
• $Z_5=10.0{\displaystyle \frac{\mathrm{W}}{{\mathrm{m}}^2\mathrm{K}}}$.

A comparison between the values calculated with the calibrated numerical model and the measured values is shown in Figure 8. The efficiency of the heating layout can be identified from this parameter fitting methodology. Due to the high frequency-based excitation, the skin depth is minimal, as can be seen on Figure 3a. The resulting joule loss is about 130 W in the gear during heating. Therefore, the effectivity is about 65% in the first case, when the pancake coil was excited by 200 W; if we changed the nominal power of the circuit to 2000 W, the effective joule loss in the material increased to 900 W, which means a decreased, 45% efficiency.

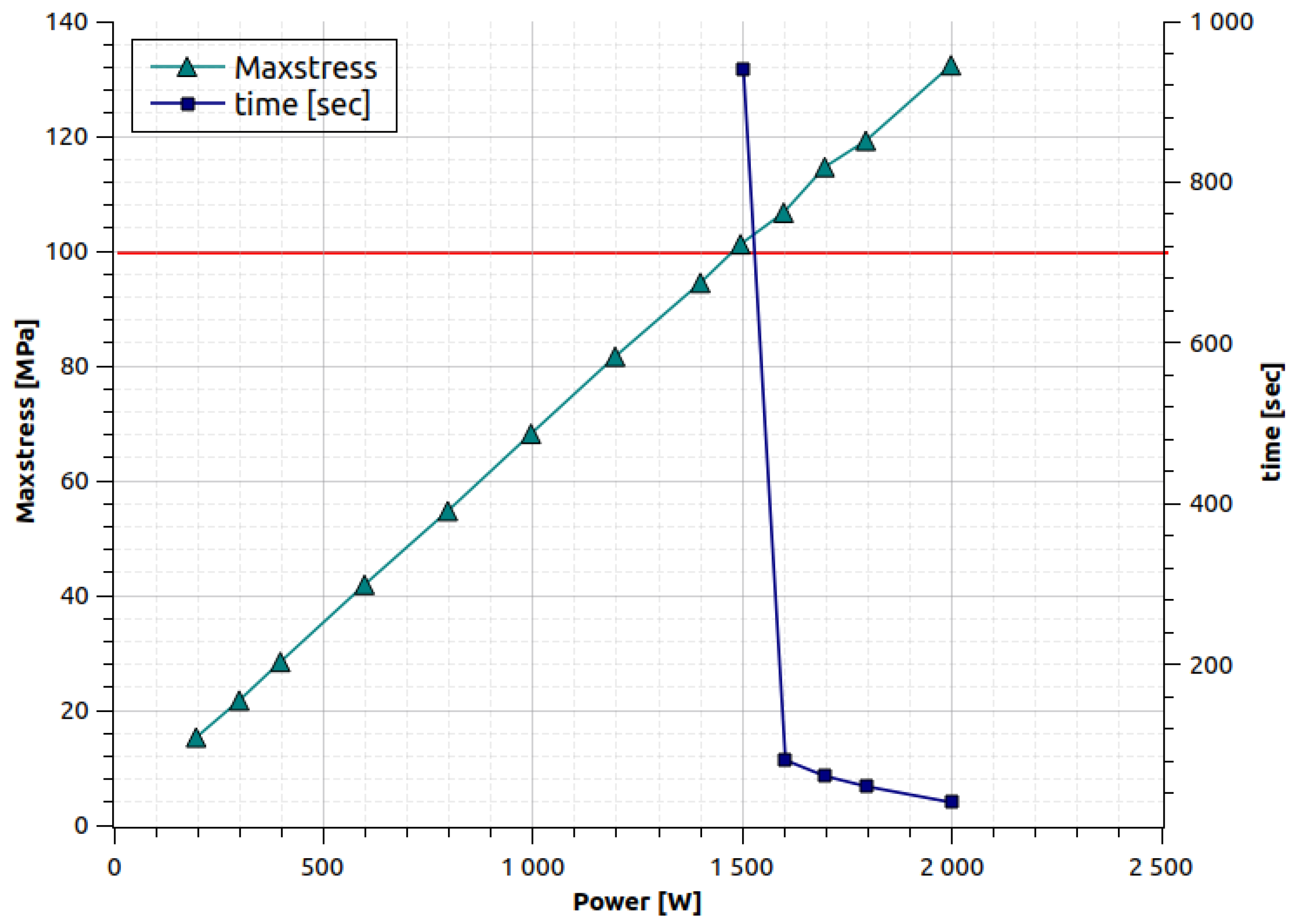
4. Discussion of the Calibrated Model Results

Using the calibrated FEM model, we can calculate the maximal permissible heating power at the given pancake-coil-based layout. The final step of one calculation is depicted in Figure 9, which shows the magnetic field distribution, the temperature distribution, and the resulting displacement in the heated workpiece. The bottom of the gear is encircled in Figure 9b, which marks the critical part, where the temperature can reach the previously defined 200 °C limit.

This inhomogeneity in the resulting temperature distribution and the low heat conductivity of the applied carbon steel material cause a deformation in the inner hole geometry. This current geometry causes an asymmetric expansion in the gear material, represented by $\alpha$ in Figure 10. This effect can handled by overheating the bottom part of the gear, which can cause problems in the heat-treated wearing surface of the gear and create high stresses in the steel, causing permanent material change. To avoid this phenomenon, other coil arrangements can be used, or a multi-stage heating process can be developed, allowing time for the temperature distribution to homogenize by resting the workpiece for a sufficient time between the heating phases.

For this process development, the calibrated simulations can estimate the maximal allowable heating time in a given power. These calculations were made from 200 W to 2000 W power; the results are depicted in Figure 11. The horizontal red line represents the maximal permitted value of the internal stress (100 MPa), while the green line represents the resulting maximal stress value. The blue line represents that time, which is spent from the beginning of the heating until it reaches the allowable 100 MPa. It can be seen that around 1450 W heating power can be permissible with the given layout. Using this value, the minimal length of the process time without dividing heating and relaxing phases can be calculated, which results in about 5 min. This processing time fulfills the original requirements. However, it can be reduced further if we use a 30-s heating phase with a 10–30-s relaxation phase, switching them until we reach the required 45 μm expansion of the inner hole at the bottom of the gear.

The proposed methodology can provide a solid basis for further investigation of different coil-gear layouts; for example, the role of another coil above the heated gear can be examined to determine how it can reduce the processing time. The parameter fitting steps and the proposed calibration methodology can be used for that and other similar projects to simply identify the missing numerical parameters and create a validation for a design process. The proposed numerical methods can be used to train machine learning and artificial-intelligence-based methods to reduce the computation demand of the optimization process.

5. Conclusions

The numerical modeling of an induction heating-based workflow is a complex task due to the need to model the three connecting physical fields. This problem has been the subject of many papers. Due to the sensitivity of the material parameters, the knowledge of the exact geometrical and material properties is necessary to create a reliable mass manufacturing process that does not damage the assembled parts and minimizes waste production. This paper presents a simple approach to dealing with a case study for numerical modeling and parameter determination for an induction heating process design. The focus is on carbon steel gear that needs to be rapidly heated within strict temperature limits to avoid damaging the heat-treated wearing surface. This limitation means that the achievable maximum expansion of the hole is only 20 μm larger than required for the assembly process. Heat exchange parameters need to be determined from measurements. The proposed paper has shown simple quasi-resonant induction heater-based measurements, which can be used to determine the missing parameters for a coupled magneto–thermoelastic simulation. Other measurements used to validate the simulation and its results can be used to determine the limits and create a more optimal workflow. These measurements confirmed that the simulation results has the required precision to apply for a design and analysis of the examined layout. The proposed methodology and the shown open source tools can be succesfully used for design, optimization and parameter determination of other induction heating design problems with different geometrical and material properties.