Using Advanced Metering Infrastructure Data from MV/LV Substations to Minimize Reactive Energy Supply Cost to Final Consumers
Abstract
1. Introduction
- minimizing the total costs of active energy losses due to reactive energy flows in the distribution network and simultaneously the costs of compensation of reactive energy consumption carried by consumers;
- determining the optimal level of customer factors tgφ in the case of reactive energy consumption and generation which may further serve as a basis for DSO tariff decisions;
- use of long-term power flow measurements registered in the basic period of settlement of the electricity market via AMI for customers, as well as by AMI balance meters in the MV/LV substations that supply these customers, to determine the network and load parameters necessary to calculate the optimal tgφ factor according to the methodology presented.
2. Reactive Energy Flow Control in Polish Distribution Networks
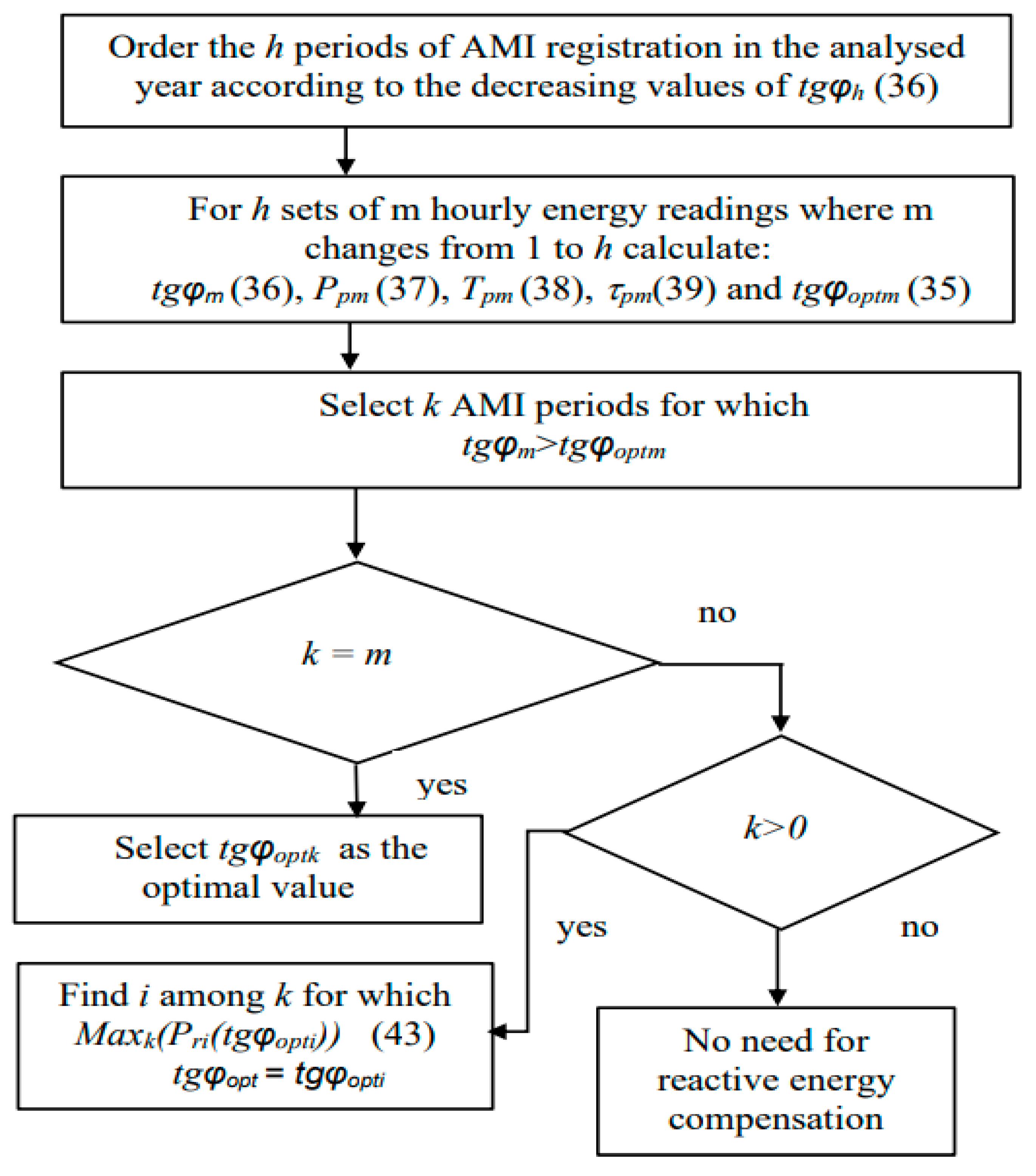
3. Determining the Optimal Level of Reactive Energy Compensation for Consumers Based on AMI Measurements
- data from smart meters are available, allowing for the balance of active energy flow at the voltage levels of the distribution network for the period of determining the optimal compensation parameters;
- equivalent resistances for calculating active energy losses due to the flow of the current of receivers are determined based on annual energy losses, maximum loads, and load characteristics reflecting their changes over time for parts of the distribution network supplying the receivers according to [52];
- the optimal parameters of the compensation devices for tariff purposes in the case of many receivers connected to the LV network can be calculated as averages for all receivers supplied from the MV/LV station, without taking into account their individual location within the LV network.
3.1. Network Losses in Supply Cables Due to Reactive Power Flow
3.2. Influence of Reactive Load Power Compensation
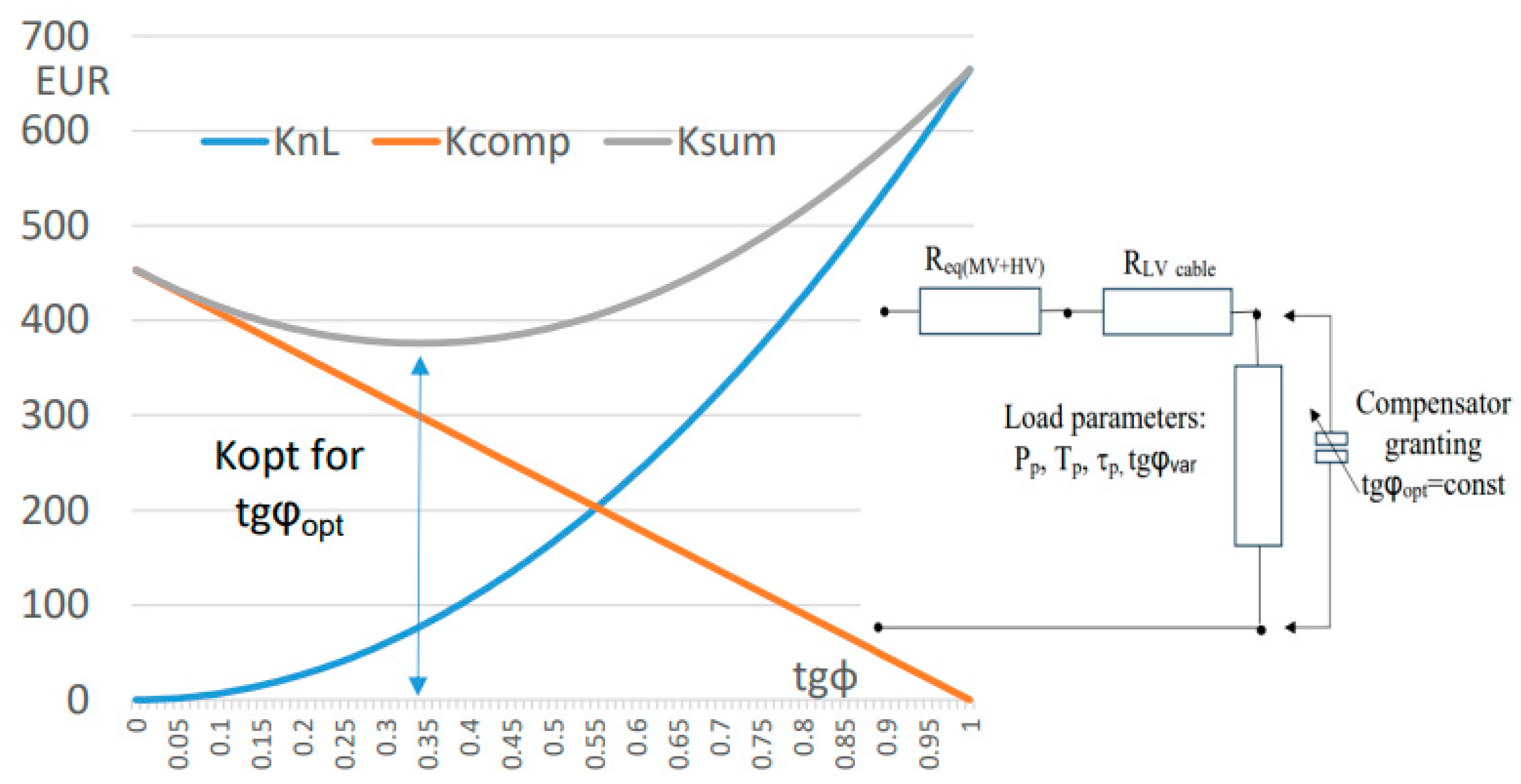
3.3. Optimal Compensation Granting Minimum Costs for the Network Operator and Customer
3.4. Calculation of Compensation Parameters for the LV Supply Area Based on Data Registered in a Smart Metering System
4. Analysis of Optimal Reactive Energy Compensation Levels for MV/LV Substations Based on AMI Measurements
5. Discussion of Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
| AMI | advanced metering infrastructure |
| CCB | controlled capacitor bank |
| DSO | distribution system operator |
| HV | high voltage |
| MV | medium voltage |
| LV | low voltage |
| PV | photovoltaic |
| RPC | reactive power compensator |
| SVG | static var generator |
References
- Sorokin, A.; Rebennack, S.; Pardalos, P.M.; Iliadis, N.A.; Pereira, M.V.F. (Eds.) Handbook of Networks in Power Systems I; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Blinov, I.; Zaitsev, I.O.; Kuchanskyy, V.V. Problems, Methods and Means of Monitoring Power Losses in Overhead Transmission Lines. Stud. Syst. Decis. Control. 2020, 298, 123–136. [Google Scholar] [CrossRef]
- Kulczycki, J. Straty Energii Elektrycznej w Sieciach Dystrybucyjnych. (Electricity Losses in Distribution Networks); PTPiREE: Poznań, Poland, 2009. [Google Scholar]
- Kaloudas, C.G.; Ochoa, L.F.; Marshall, B.; Majithia, S.; Fletcher, I. Assessing the Future Trends of Reactive Power Demand of Distribution Networks. IEEE Trans. Power Syst. 2017, 32, 4278–4288. [Google Scholar] [CrossRef]
- Dong, M.; Meira, P.C.M.; Xu, W.; Chung, C.Y. Non-intrusive signature extraction for major residential loads. IEEE Trans. Smart Grid 2013, 4, 1421–1430. [Google Scholar] [CrossRef]
- Anderson, H.C.; al Hadi, A.; Jones, E.S.; Ionel, D.M. Power Factor and Reactive Power in US Residences—Survey and EnergyPlus Modeling. In Proceedings of the 10th IEEE International Conference on Renewable Energy Research and Applications, ICRERA 2021, Istanbul, Turkey, 26–29 September 2021; pp. 418–422. [Google Scholar] [CrossRef]
- Statistics Poland. Energy Consumption in Households in 2018; Statistics Poland: Warsaw, Poland, 2019. [Google Scholar]
- Commission Regulation (EU) 2019/2020 of 1 October 2019 laying down ecodesign requirements for light sources and separate control gears pursuant to Directive 2009/125/EC of the European Parliament and of the Council and repealing Commission Regulations (EC) No 244/2009, (EC) No 245/2009 and (EU) No 1194/2012 Text with EEA relevance. n.d. Off. J. Eur. Union. 2019, 315, 209–240.
- Winder, S. Nonisolated Power Factor Correction Circuits. In Power Supplies for LED Driving; Elsevier: Amsterdam, The Netherlands, 2017; pp. 155–187. [Google Scholar] [CrossRef]
- Heffernan, W.J.B.; Watson, N.R.; Watson, J.D. Heat-pump performance: Voltage dip/sag, under-voltage and over-voltage. J. Eng. 2014, 2014, 640–657. [Google Scholar] [CrossRef]
- IEC 61000-3-2:2018/AMD1:2020 Electromagnetic Compatibility (EMC)—Part 3-2: Limits—Limits for Harmonic Current Emissions (Equipment Input Current ≤16 A per Phase) n.d. Available online: https://webstore.iec.ch/publication/63492 (accessed on 16 July 2022).
- Batarseh, I.; Wei, H. Power Factor Correction Circuits. In Power Electronics Handbook; Elsevier Inc.: Amsterdam, The Netherlands, 2011. [Google Scholar] [CrossRef]
- Cortezzi, F.C.M.; da Silva Jota, P.R. Residential Load Curve Analysis during Electric Vehicle Charging. J. Power Energy Eng. 2017, 5, 49–61. [Google Scholar] [CrossRef][Green Version]
- Gayatri, M.T.L.; Parimi, A.M.; Pavan Kumar, A.V. A review of reactive power compensation techniques in microgrids. Renew. Sustain. Energy Rev. 2018, 81, 1030–1036. [Google Scholar] [CrossRef]
- Sarkar, M.N.I.; Meegahapola, L.G.; Datta, M. Reactive power management in renewable rich power grids: A review of grid-codes, renewable generators, support devices, control strategies and optimization Algorithms. IEEE Access 2018, 6, 41458–41489. [Google Scholar] [CrossRef]
- Pothirasan, N.; Rajasekaran, M.P.; Muneeswaran, V. Real time reactive power compensation for battery/photovoltaic hybrid power source for internet of hybrid electric vehicle system. Cogn. Syst. Res. 2018, 52, 473–488. [Google Scholar] [CrossRef]
- Golshannavaz, S. Cooperation of electric vehicle and energy storage in reactive power compensation: An optimal home energy management system considering PV presence. Sustain. Cities Soc. 2018, 39, 317–325. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W. Dynamic active and reactive power compensation in distribution networks with batteries: A day-ahead economic dispatch approach. Comput. Electr. Eng. 2020, 85, 106710. [Google Scholar] [CrossRef]
- Guchhait, P.K.; Banerjee, A.; Mukherjee, V. Comparative study using soft computing techniques for the reactive power compensation of a hybrid power system model. Ain Shams Eng. J. 2020, 11, 87–98. [Google Scholar] [CrossRef]
- Águila Téllez, A.; López, G.; Isaac, I.; González, J.W. Optimal reactive power compensation in electrical distribution systems with distributed resources. Heliyon 2018, 4, e00746. [Google Scholar] [CrossRef]
- Vlahinić, S.; Franković, D.; Komen, V.; Antonić, A. Reactive Power Compensation with PV Inverters for System Loss Reduction. Energies 2019, 12, 4062. [Google Scholar] [CrossRef]
- Li, H.; Wen, C.; Chao, K.-H.; Li, L.-L. Research on Inverter Integrated Reactive Power Control Strategy in the Grid-Connected PV Systems. Energies 2017, 10, 912. [Google Scholar] [CrossRef]
- Arnold, G.; Valov, B.; Reimann, T.; Stetz, T.; Braun, M. Optimal Reactive Power Supply in Distribution Networks—Technological and Economic Assessment for PV-Systems. In Proceedings of the 24th European Photovoltaic Solar Energy Conference, Hamburg, Germany, 21–25 September 2009; pp. 3872–3881. [Google Scholar] [CrossRef]
- Rezaei, F.; Esmaeili, S. Decentralized reactive power control of distributed PV and wind power generation units using an optimized fuzzy-based method. International J. Electr. Power Energy Syst. 2017, 87, 27–42. [Google Scholar] [CrossRef]
- Layate, Z.; Bahi, T.; Abadlia, I.; Bouzeria, H.; Lekhchine, S. Reactive power compensation control for three phase grid-connected photovoltaic generator. Int. J. Hydrogen Energy 2015, 40, 12619–12626. [Google Scholar] [CrossRef]
- Schultis, D.L.; Ilo, A.; Schirmer, C. Overall performance evaluation of reactive power control strategies in low voltage grids with high prosumer share. Electr. Power Syst. Res. 2019, 168, 336–349. [Google Scholar] [CrossRef]
- Hamrouni, N.; Younsi, S.; Jraidi, M. A Flexible Active and Reactive Power Control Strategy of a LV Grid Connected PV System. Energy Procedia 2019, 162, 325–338. [Google Scholar] [CrossRef]
- Jakušenoks, A.; Laizāns, A. Impact of household electric energy usage trends on electrical power supply net power factor. Res. Rural. Dev. 2015, 1. Available online: https://losses.ukpowernetworks.co.uk/losses/static/pdfs/strategies-for-reducing-losses-in-distribution-networks.d1b2a6f.pdf (accessed on 28 November 2021).
- Strbac, G.; Djapic, P.; Pudjianto, D.; Konstantelos, I.; Moreira, R. Strategies for Reducing Losses in Distribution Networks; Imperial College London: London, UK, 2018. [Google Scholar]
- Benchmarking Smart Metering Deployment in the EU-28—Publications Office of the EU n.d. Available online: https://op.europa.eu/en/publication-detail/-/publication/b397ef73-698f-11ea-b735-01aa75ed71a1/language-en (accessed on 28 November 2021).
- Tufon, C.; Isemonger, A.; Kirby, B.; Kueck, J.; Li, F. A tariff for reactive power. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, PSCE 2009, Seattle, WA, USA, 15–18 March 2009. [Google Scholar] [CrossRef]
- Raap, M.; Raesaar, P.; Tiigimägi, E. Reactive power pricing in distribution networks. Oil Shale 2011, 28, 223–239. [Google Scholar] [CrossRef]
- Wilczyński, A.; Bućko, P. Reactive Energy Billing in Operator Tariffs in Poland. Acta Energetica 2015, 4–9. [Google Scholar] [CrossRef]
- Kolenc, M.; Papič, I.; Blažič, B. Coordinated reactive power control to achieve minimal operating costs. Int. J. Electr. Power Energy Syst. 2014, 63, 1000–1007. [Google Scholar] [CrossRef]
- Coman, C.M.; Florescu, A.; Oancea, C.D. Improving the Efficiency and Sustainability of Power Systems Using Distributed Power Factor Correction Methods. Sustainability 2020, 12, 3134. [Google Scholar] [CrossRef]
- Mahdavi Tabatabei, N.; Jafari Aghbolaghi, A.; Bizon, N.; Blaabjerg, F. Reactive Power Control in AC Power Systems; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Sauer, P.W. Reactive Power and Voltage Control Issues in Electric Power Systems. In Applied Mathematics for Restructured Electric Power Systems; Springer: Berlin/Heidelberg, Germany, 2005; pp. 11–24. [Google Scholar] [CrossRef]
- Gandhi, O.; Rodríguez-Gallegos, C.; Reindl, T.; Srinivasan, D. Competitiveness of PV Inverter as a Reactive Power Compensator considering Inverter Lifetime Reduction. Energy Procedia 2018, 150, 74–82. [Google Scholar] [CrossRef]
- Bisanovic, S.; Hajro, M.; Samardzic, M. One approach for reactive power control of capacitor banks in distribution and industrial networks. Int. J. Electr. Power Energy Syst. 2014, 60, 67–73. [Google Scholar] [CrossRef]
- Ahmadi, H.; Martí, J.R.; Dommel, H.W. A Framework for Volt-VAR Optimization in Distribution Systems. IEEE Trans. Smart Grid 2015, 6, 1473–1483. [Google Scholar] [CrossRef]
- Stanelyte, D.; Radziukynas, V. Review of Voltage and Reactive Power Control Algorithms in Electrical Distribution Networks. Energies 2019, 13, 58. [Google Scholar] [CrossRef]
- Amiel, I.; Rajput, S.; Averbukh, M. Capacitive reactive power compensation to prevent voltage instabilities in distribution lines. Int. J. Electr. Power Energy Syst. 2021, 131, 107043. [Google Scholar] [CrossRef]
- Yang, C.F.; Lai, G.G.; Lee, C.H.; Su, C.T.; Chang, G.W. Optimal setting of reactive compensation devices with an improved voltage stability index for voltage stability enhancement. Int. J. Electr. Power Energy Syst. 2012, 37, 50–57. [Google Scholar] [CrossRef]
- Molina-García, Á.; Mastromauro, R.A.; García-Sánchez, T.; Pugliese, S.; Liserre, M.; Stasi, S. Reactive Power Flow Control for PV Inverters Voltage Support in LV Distribution Networks. IEEE Trans. Smart Grid 2017, 8, 447–456. [Google Scholar] [CrossRef]
- Jay, D.; Swarup, K.S. A comprehensive survey on reactive power ancillary service markets. Renew. Sustain. Energy Rev. 2021, 144, 110967. [Google Scholar] [CrossRef]
- Braun, M. Provision of Ancillary Services by Distributed Generators: Technological and Economic Perspective; Kassel University Press GmbH: Kassel, Germany, 2009. [Google Scholar]
- Anaya, K.L.; Pollitt, M.G. Reactive power procurement: A review of current trends. Appl. Energy 2020, 270, 114939. [Google Scholar] [CrossRef]
- Albuquerque, F.L.; Moraes, A.J.; Guimarães, G.C.; Sanhueza, S.M.R.; Vaz, A.R. Photovoltaic solar system connected to the electric power grid operating as active power generator and reactive power compensator. Solar Energy 2010, 84, 1310–1317. [Google Scholar] [CrossRef]
- Reiman, A.P.; Somani, A.; Alam, M.J.E.; Wang, P.; Wu, D.; Kalsi, K. Power factor correction in feeders with distributed photovoltaics using residential appliances as virtual batteries. IEEE Access 2019, 7, 99115–99122. [Google Scholar] [CrossRef]
- Prasad, V.; Jayasree, P.R.; Sruthy, V. Active Power Sharing and Reactive Power Compensation in a Grid-tied Photovoltaic System. Mater. Today Proc. 2018, 5, 1537–1544. [Google Scholar] [CrossRef]
- Baghban-Novin, S.; Mahzouni-Sani, M.; Hamidi, A.; Golshannavaz, S.; Nazarpour, D.; Siano, P. Investigating the impacts of feeder reforming and distributed generation on reactive power demand of distribution networks. Sustain. Energy Grids Netw. 2020, 22, 100350. [Google Scholar] [CrossRef]
- Andruszkiewicz, J.; Lorenc, J.; Weychan, A. Determination of the Optimal Level of Reactive Power Compensation That Minimizes the Costs of Losses in Distribution Networks. Energies 2024, 17, 150. [Google Scholar] [CrossRef]
- European Norm EN 50160; Voltage Characteristics of Electricity Supplied by Public Distribution Systems. CENELEC: Brussels, Belgium, 1999.
- Rozporządzenie Ministra Gospodarki z Dnia 4 Maja 2007 r. w Sprawie Szczegółowych Warunków Funkcjonowania Systemu Elektroenergetycznego n.d. (Regulation of the Minister of Economy of 4 May 2007 on Detailed Conditions for the Operation of the Electricity System). Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=wdu20070930623 (accessed on 13 July 2022).
- Rozporządzenie Ministra Energii z Dnia 6 Marca 2019 r. w Sprawie Szczegółowych Zasad Kształtowania i Kalkulacji Taryf Oraz Rozliczeń w Obrocie Energią Elektryczną n.d. (Regulation of the Minister of Energy of 6 March 2019 on Detailed Principles for Shaping and Calculating Tariffs and Settlements in Electricity Trading). Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20190000503 (accessed on 13 July 2022).
- Ustawa z 10 Kwietnia 1997 r.—Prawo Energetyczne—Tekst Jednolity (Act of 10 April 1997—Energy Law—Consolidated Text). Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20220001385 (accessed on 15 March 2024).
- ARE. Statystyka Elektroenergetyki Polskiej (Statistics of the Polish Power Industry) 2019; ARE: Warszawa, Poland, 2020. [Google Scholar]
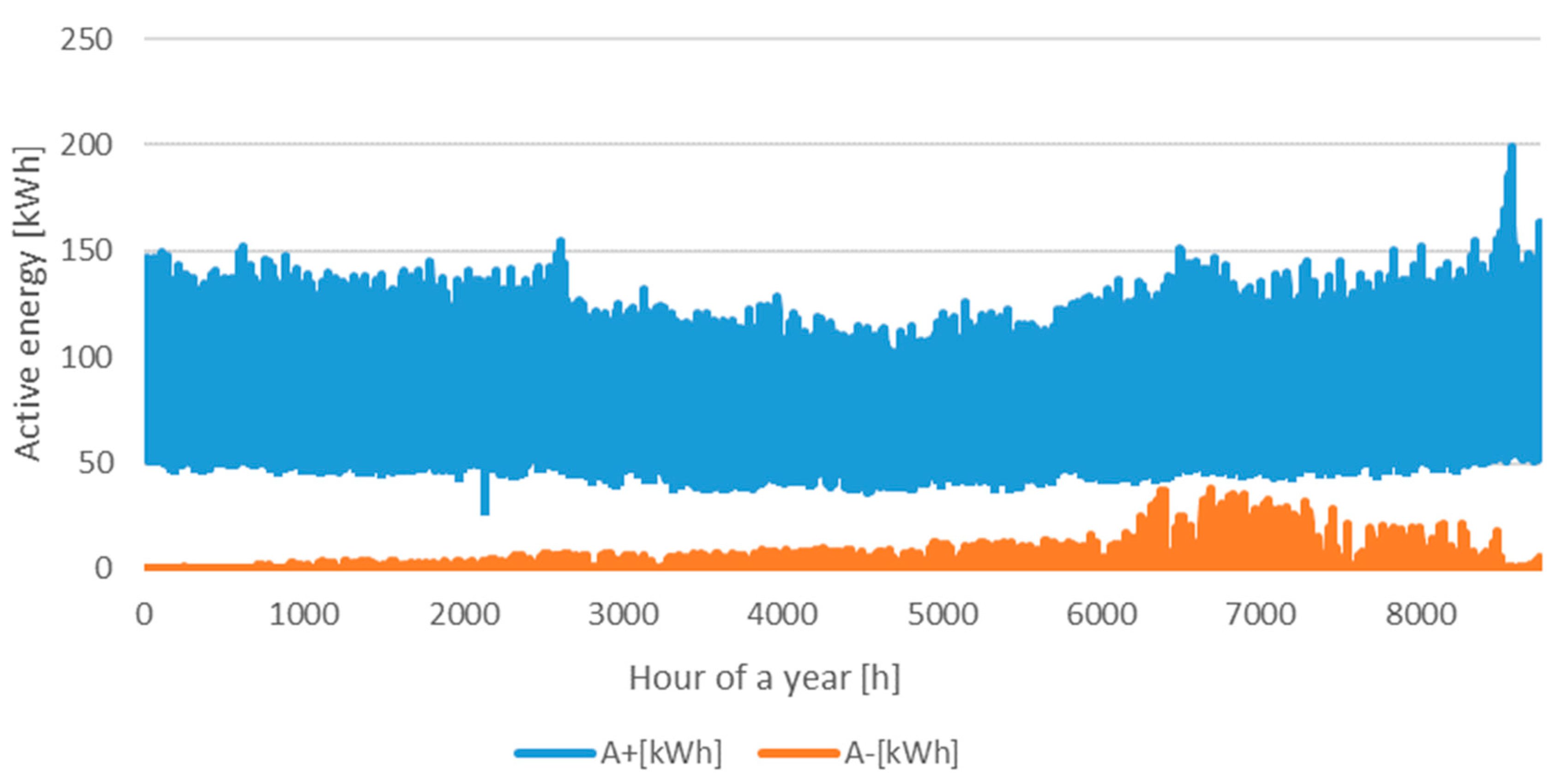
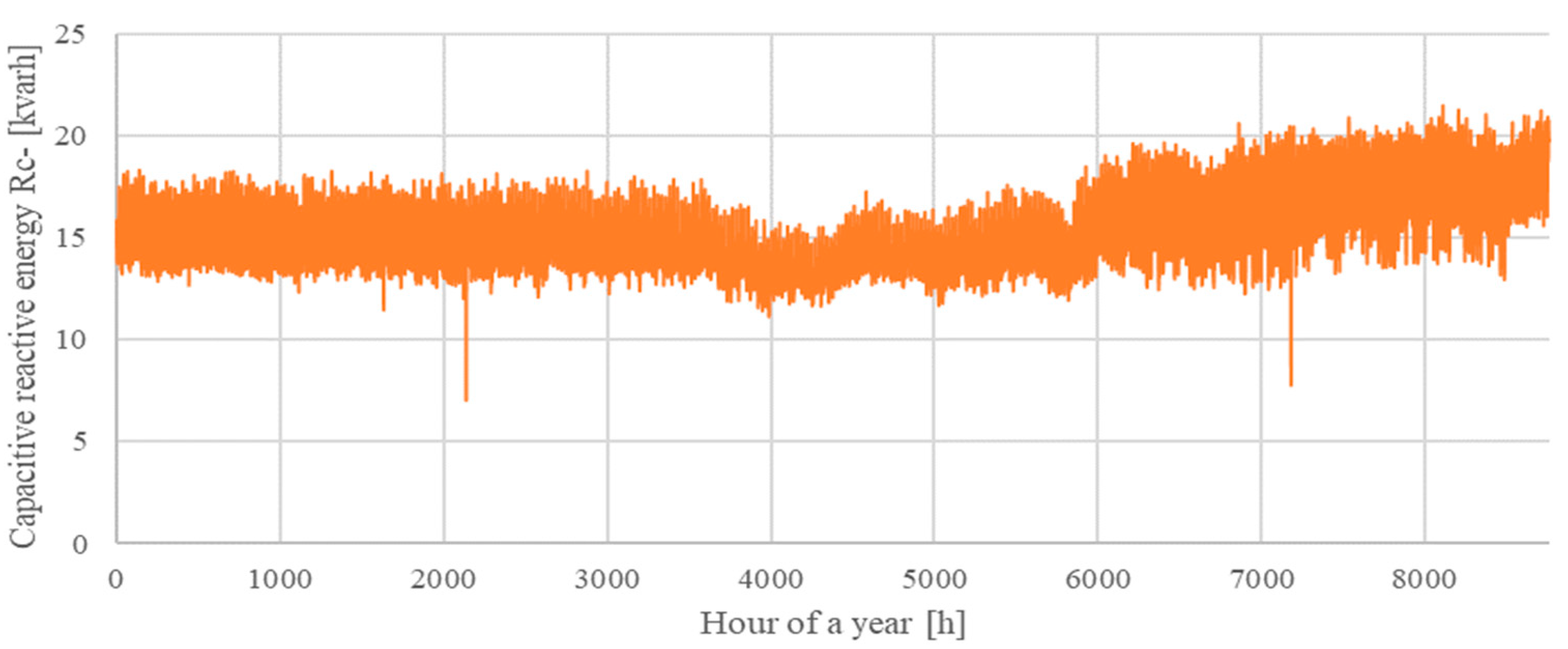
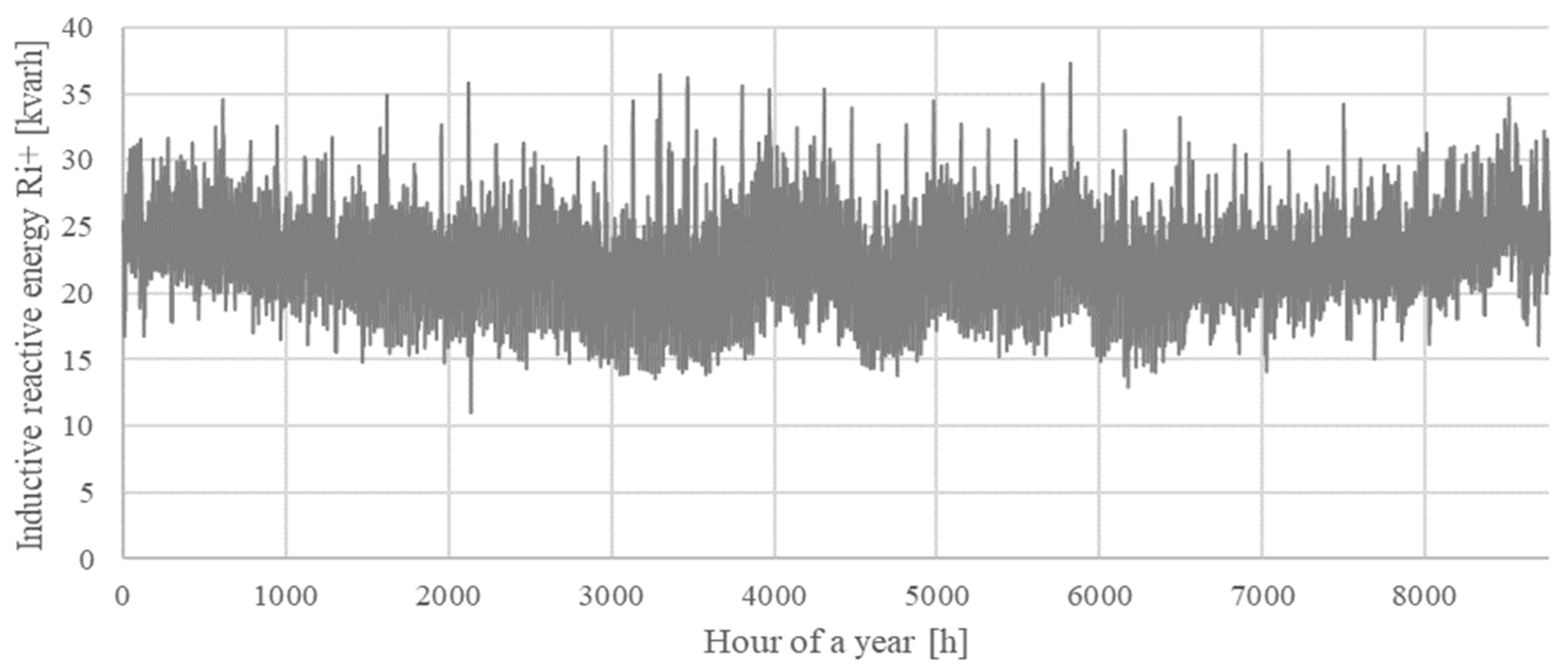
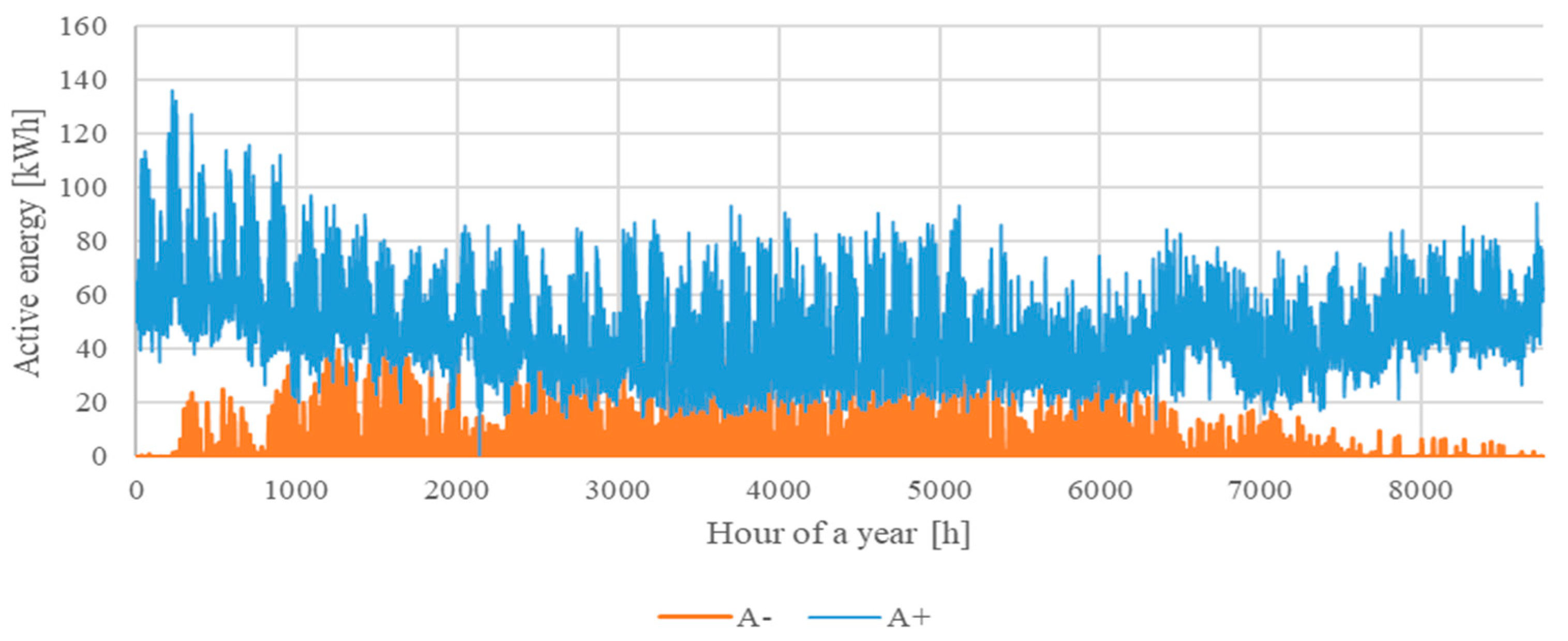
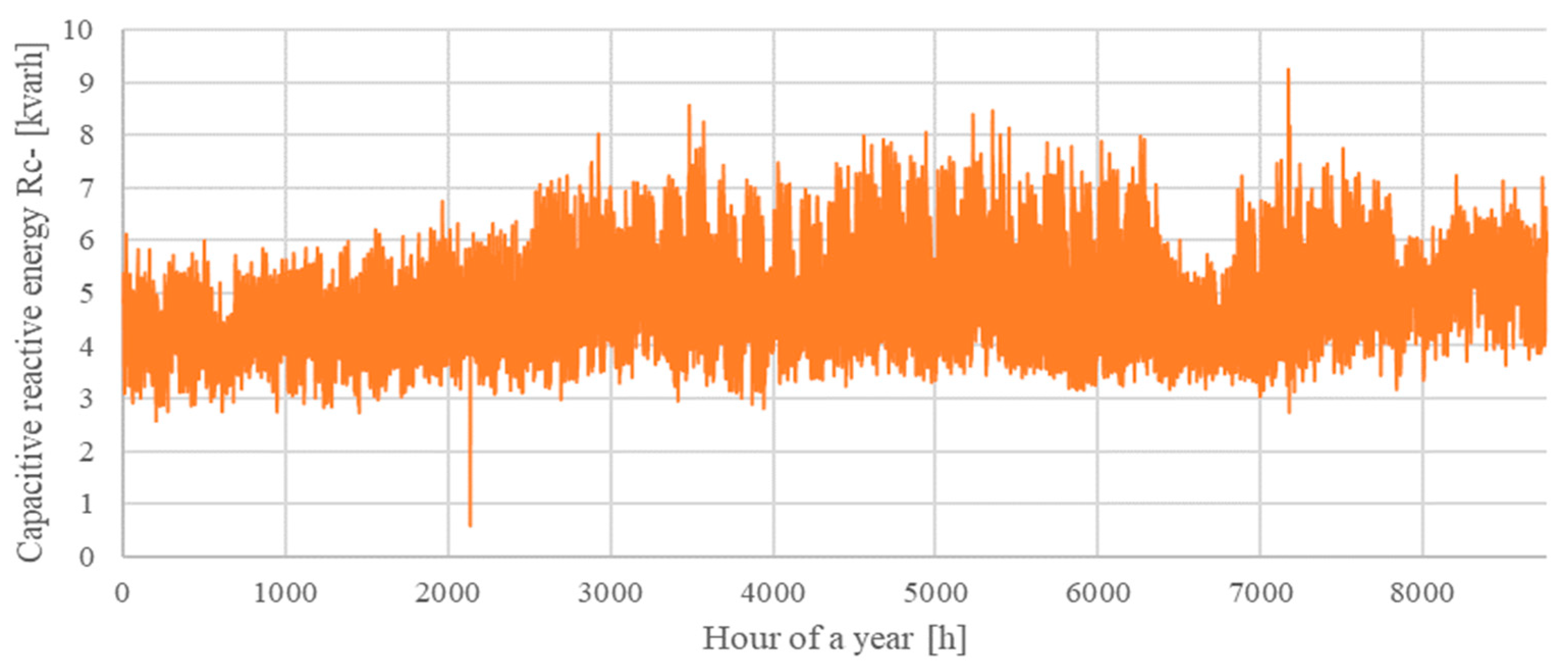
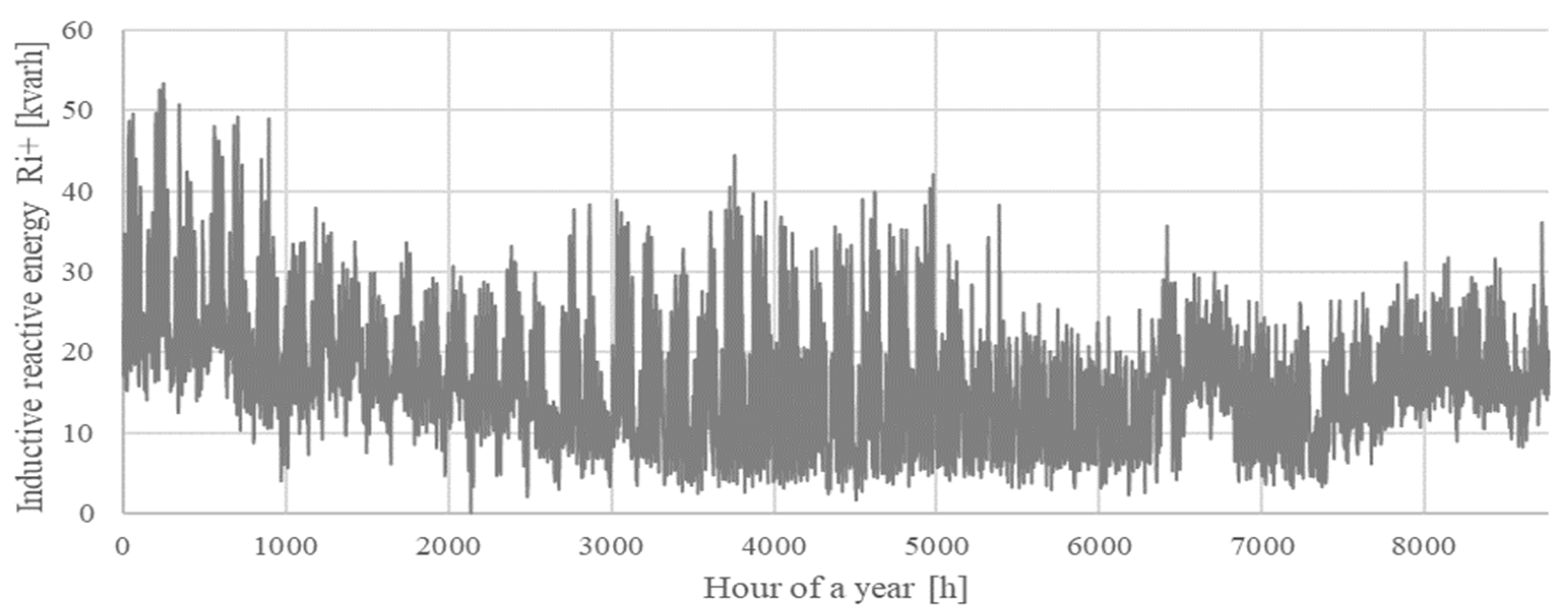
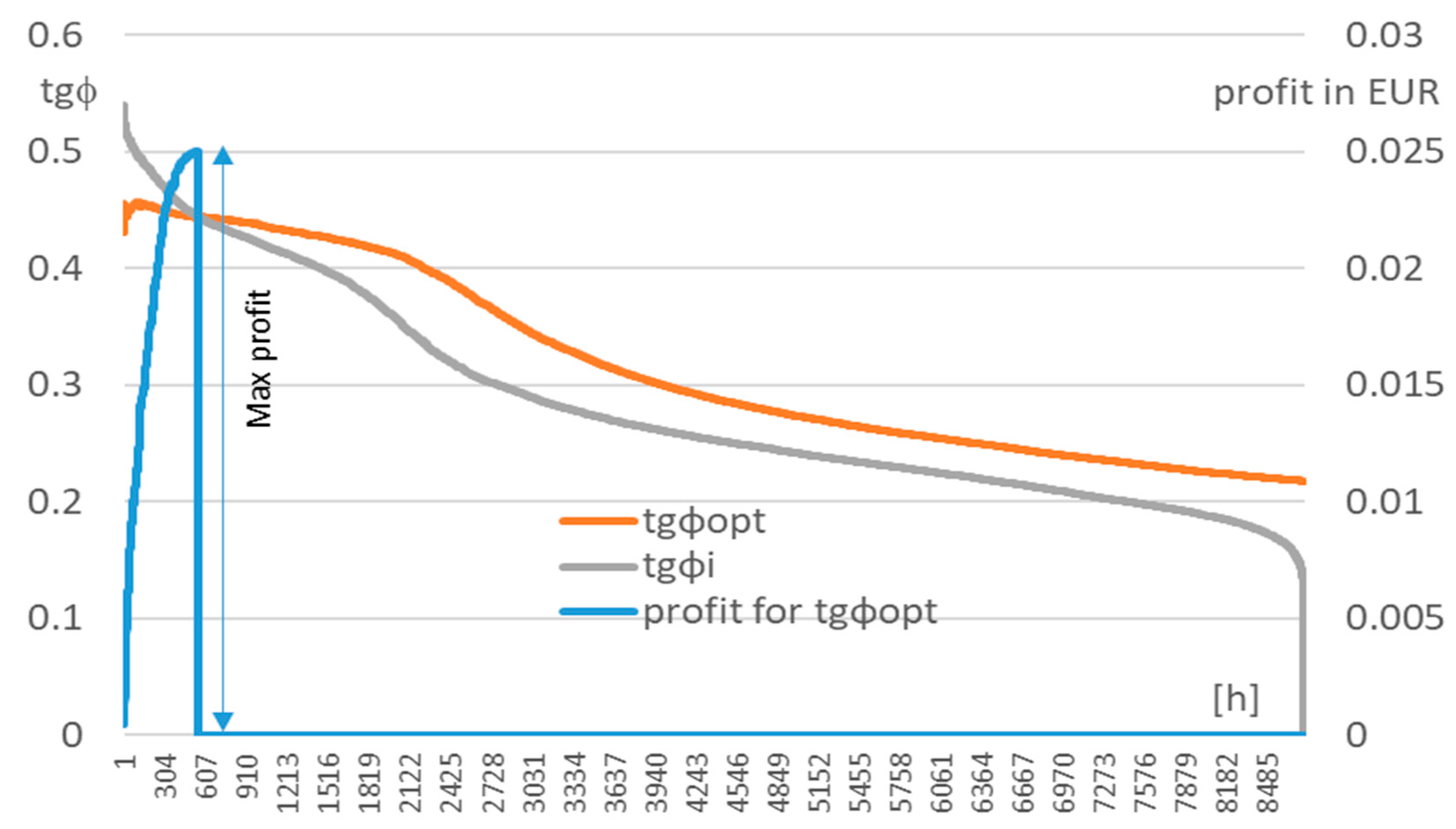
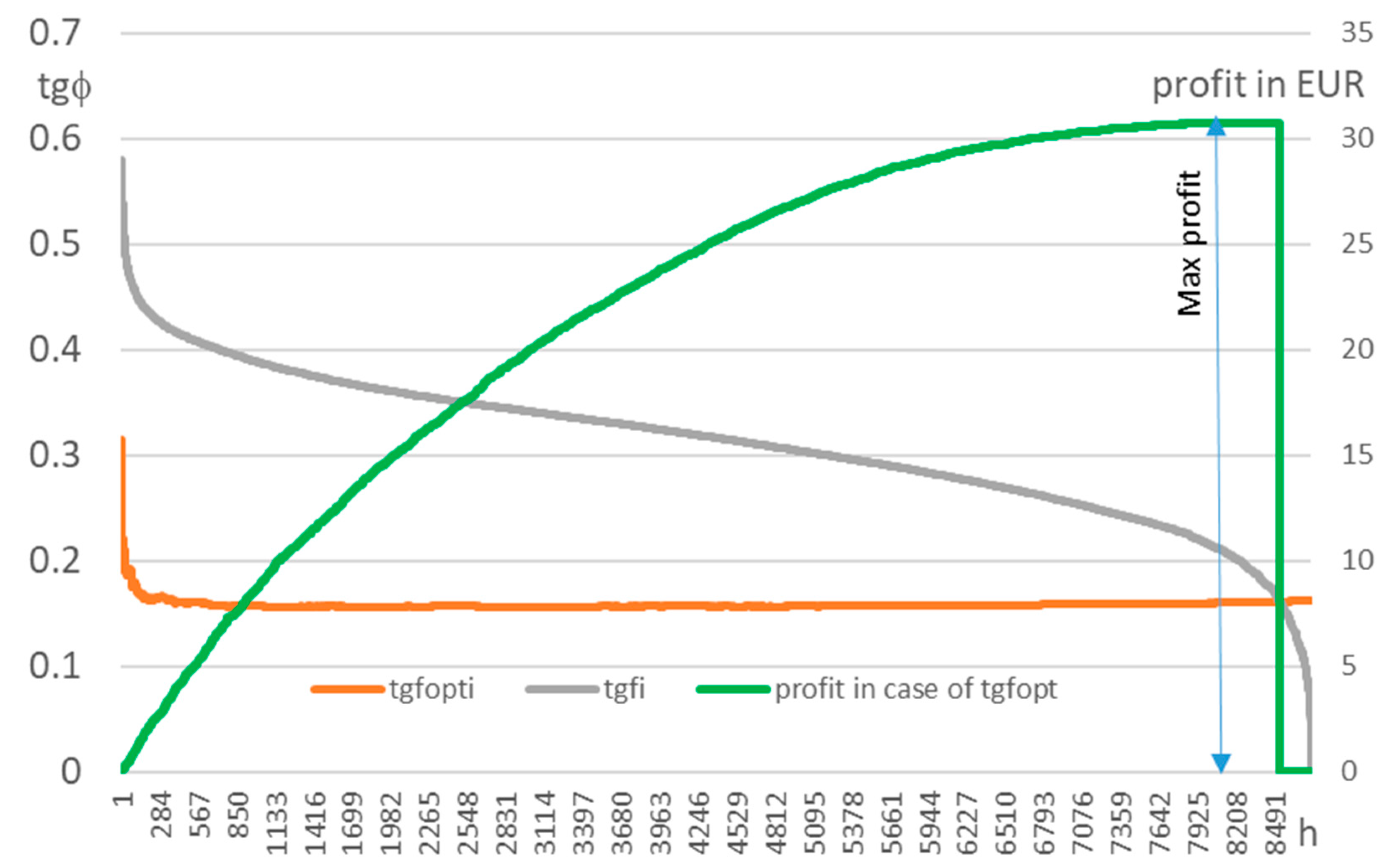
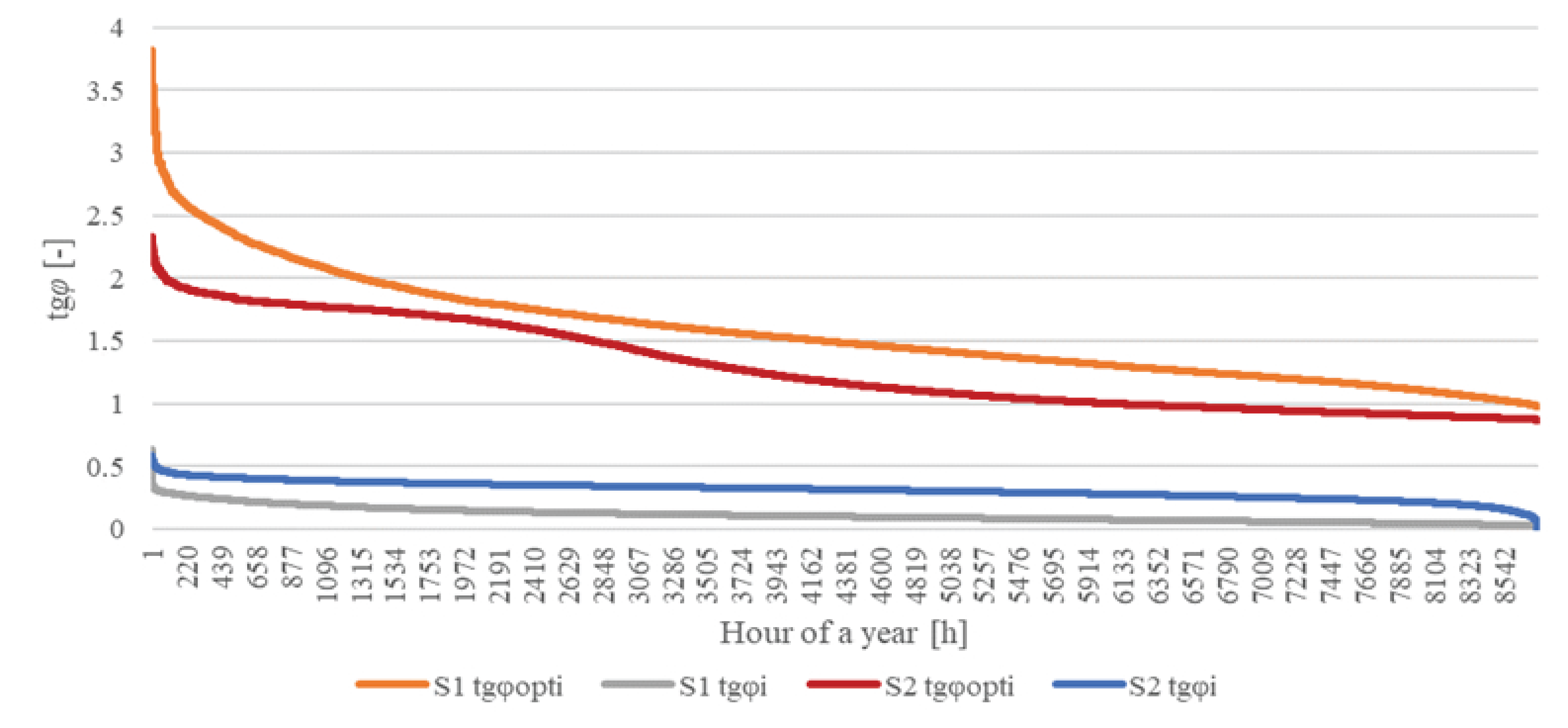
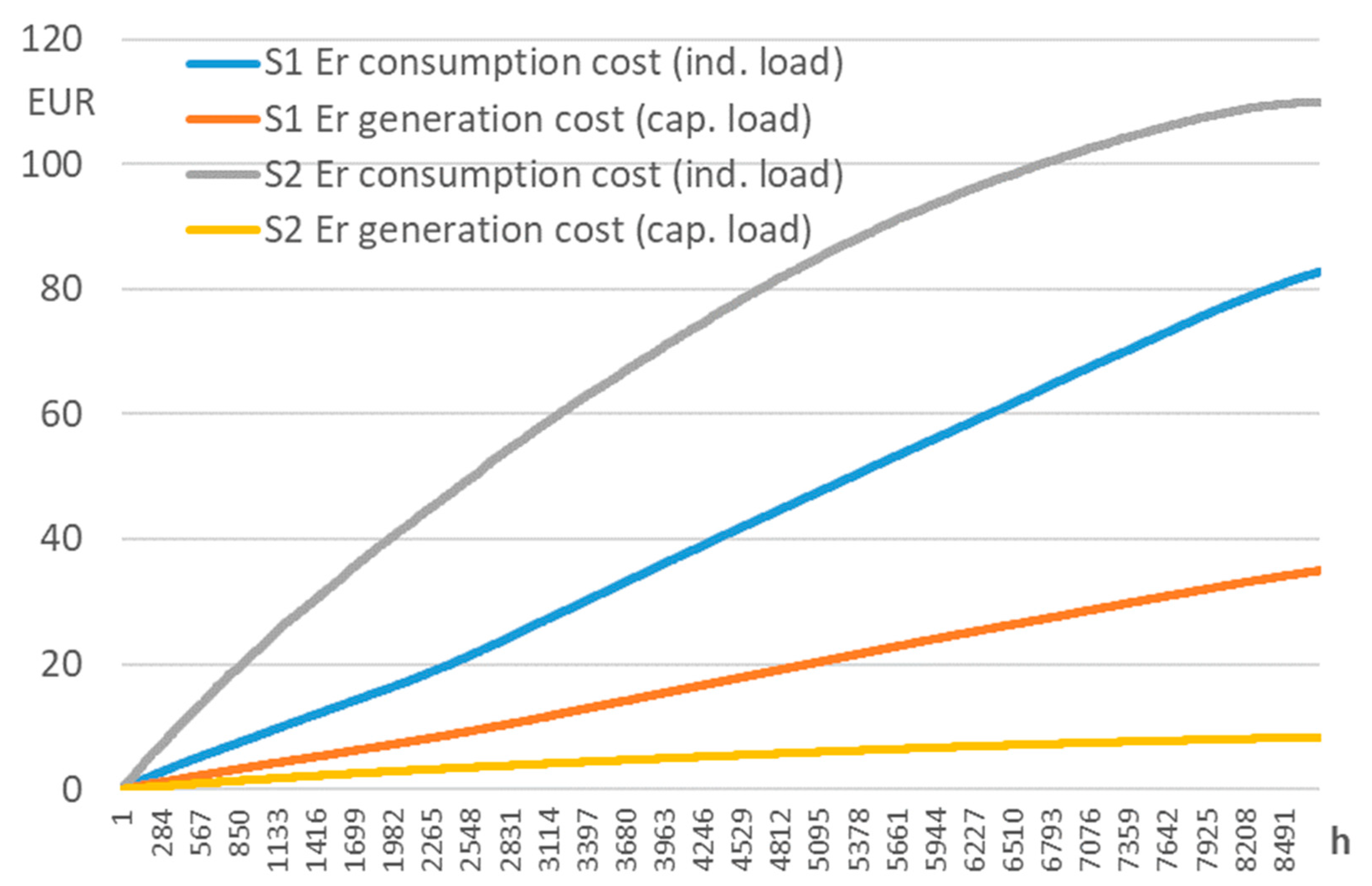
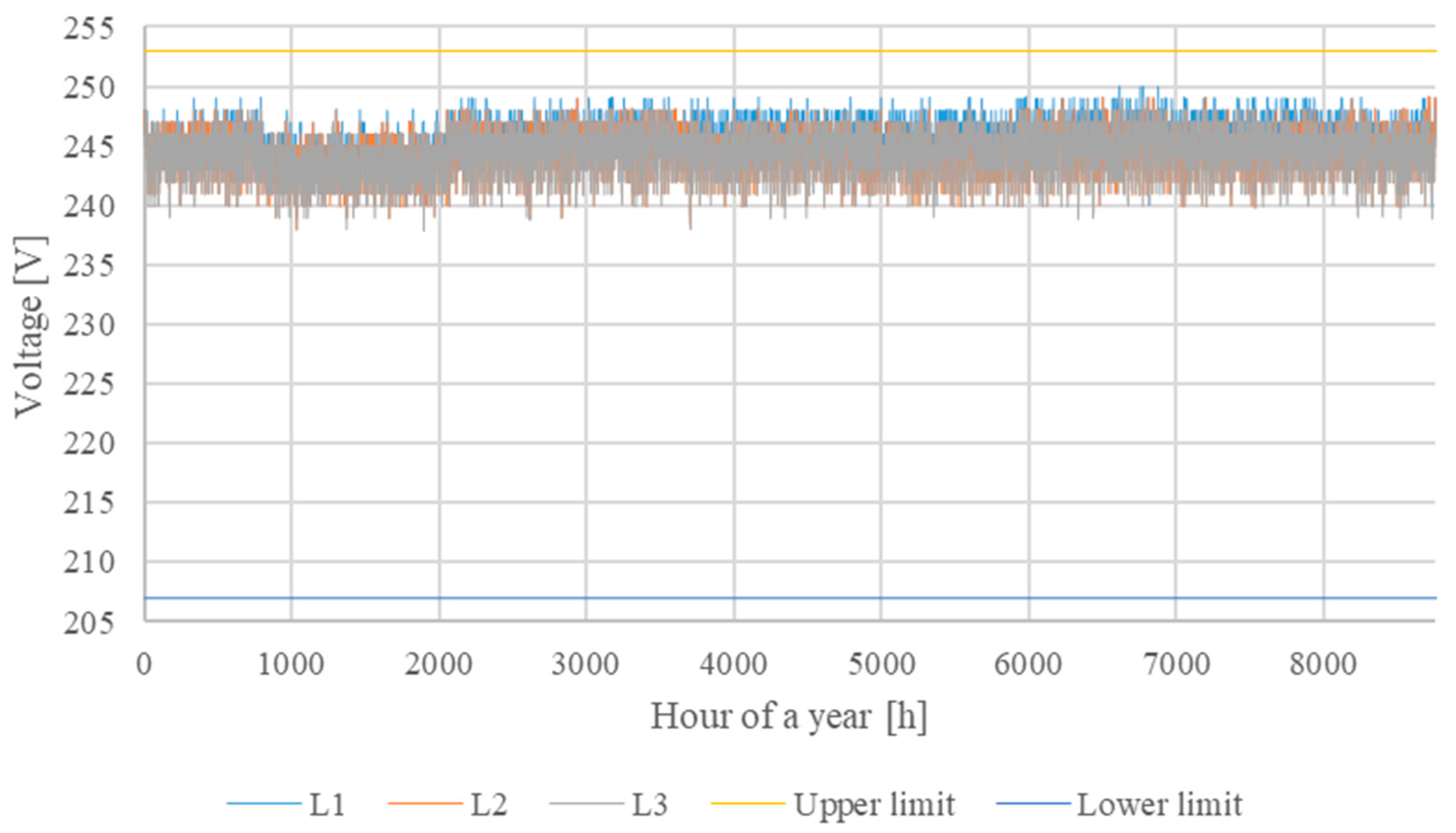
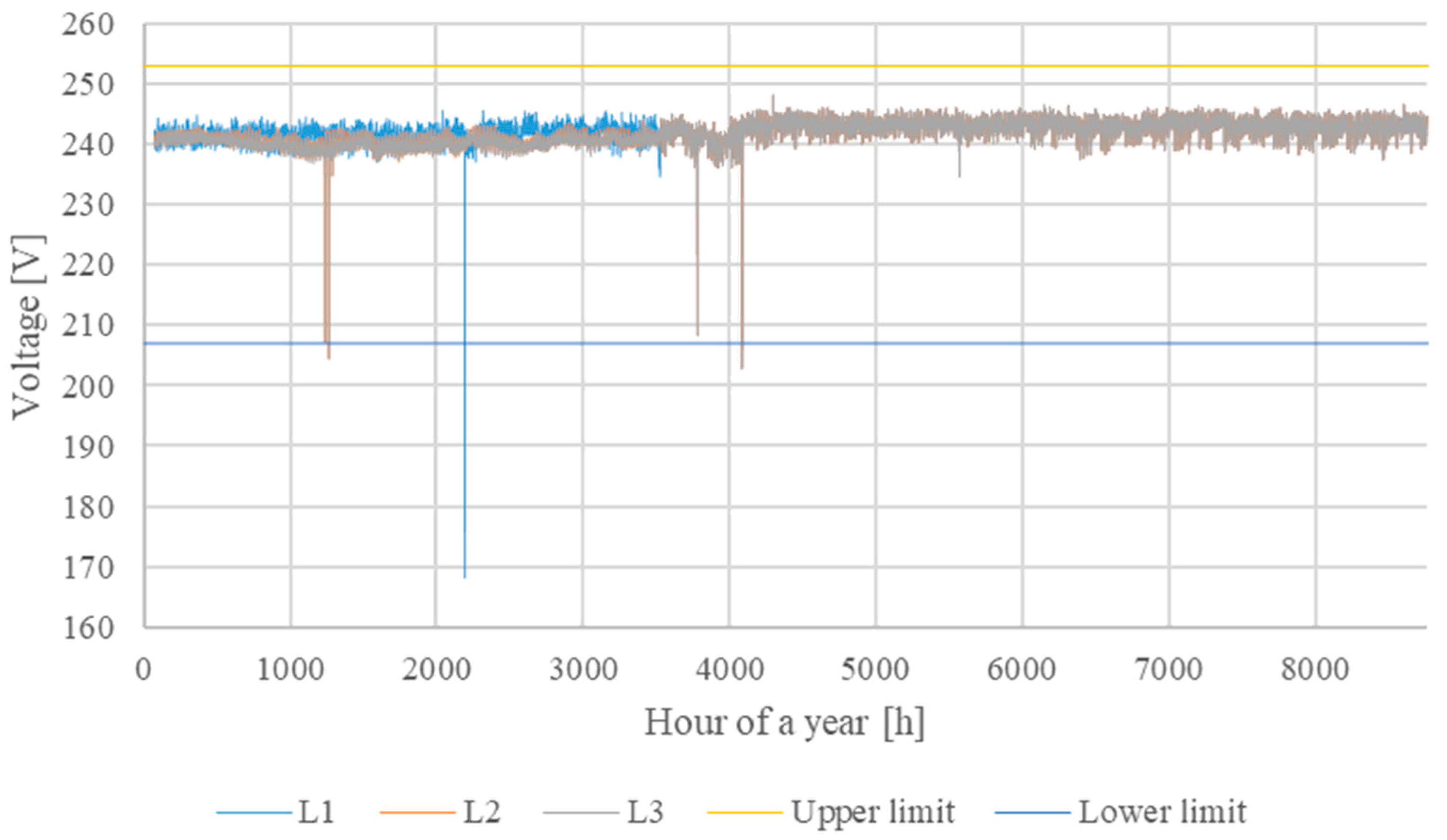
| MV/LV Substation | S1 | S2 |
|---|---|---|
| Sn tr MV/LV [kVA] | 400 | 160 |
| LV network | urban | rural |
| Conductors | cable | OHL |
| Dominant cross section [mm2] | 120/150 | 70 |
| LV network length [km] | 5.1 | 2.9 |
| Eaa(+)st [kWh] | 767,191.4 | 394,352.8 |
| ∑Eaa(+) cust [kWh] | 761,398.3 | 412,540.9 |
| Eaa(−)st [kWh] | 0.0 | 2542.8 |
| ∑Eaa(−)cust [kWh] | 15,946.9 | 37,199.2 |
| ΔEaaLV [kWh] | 21,740.0 | 16,468.3 |
| ρLV [%] | 2.86 | 3.99 |
| ∑Earind cust [kvarh] | 200,706.8 | 141,963.8 |
| ∑Earcap cust [kvarh] | 130,845.6 | 42,173.3 |
| MV/LV Substation | S1 | S2 |
|---|---|---|
| Cmp [EUR/MWh] | 61.36 | 61.36 |
| Sp cust LV [kVAh/h] | 202.0 | 145.9 |
| Pp cust LV [kWh/h] | 199.0 | 136.96 |
| Tp cust LV [h] | 3826 | 3032 |
| τeq custLV [h] | 2023 | 1391 |
| τp [h] | 1917 | 1417 |
| ReLV [Ω] | 0.0431 | 0.0970 |
| Req(HV+MV) [Ω] | 0.0028 | 0.0047 |
| SVG LCOEr [EUR/kvarh] | 0.003 | 0.003 |
| CCB LCOEr [EUR/kvarh] | 0.001 | 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andruszkiewicz, J.; Lorenc, J.; Weychan, A. Using Advanced Metering Infrastructure Data from MV/LV Substations to Minimize Reactive Energy Supply Cost to Final Consumers. Energies 2024, 17, 4116. https://doi.org/10.3390/en17164116
Andruszkiewicz J, Lorenc J, Weychan A. Using Advanced Metering Infrastructure Data from MV/LV Substations to Minimize Reactive Energy Supply Cost to Final Consumers. Energies. 2024; 17(16):4116. https://doi.org/10.3390/en17164116
Chicago/Turabian StyleAndruszkiewicz, Jerzy, Józef Lorenc, and Agnieszka Weychan. 2024. "Using Advanced Metering Infrastructure Data from MV/LV Substations to Minimize Reactive Energy Supply Cost to Final Consumers" Energies 17, no. 16: 4116. https://doi.org/10.3390/en17164116
APA StyleAndruszkiewicz, J., Lorenc, J., & Weychan, A. (2024). Using Advanced Metering Infrastructure Data from MV/LV Substations to Minimize Reactive Energy Supply Cost to Final Consumers. Energies, 17(16), 4116. https://doi.org/10.3390/en17164116






