Dynamic Radiant Barrier for Modulating Heat Transfer and Reducing Building Energy Usage
Abstract
1. Introduction
2. Experimental Procedures
2.1. Materials and Manufacturing
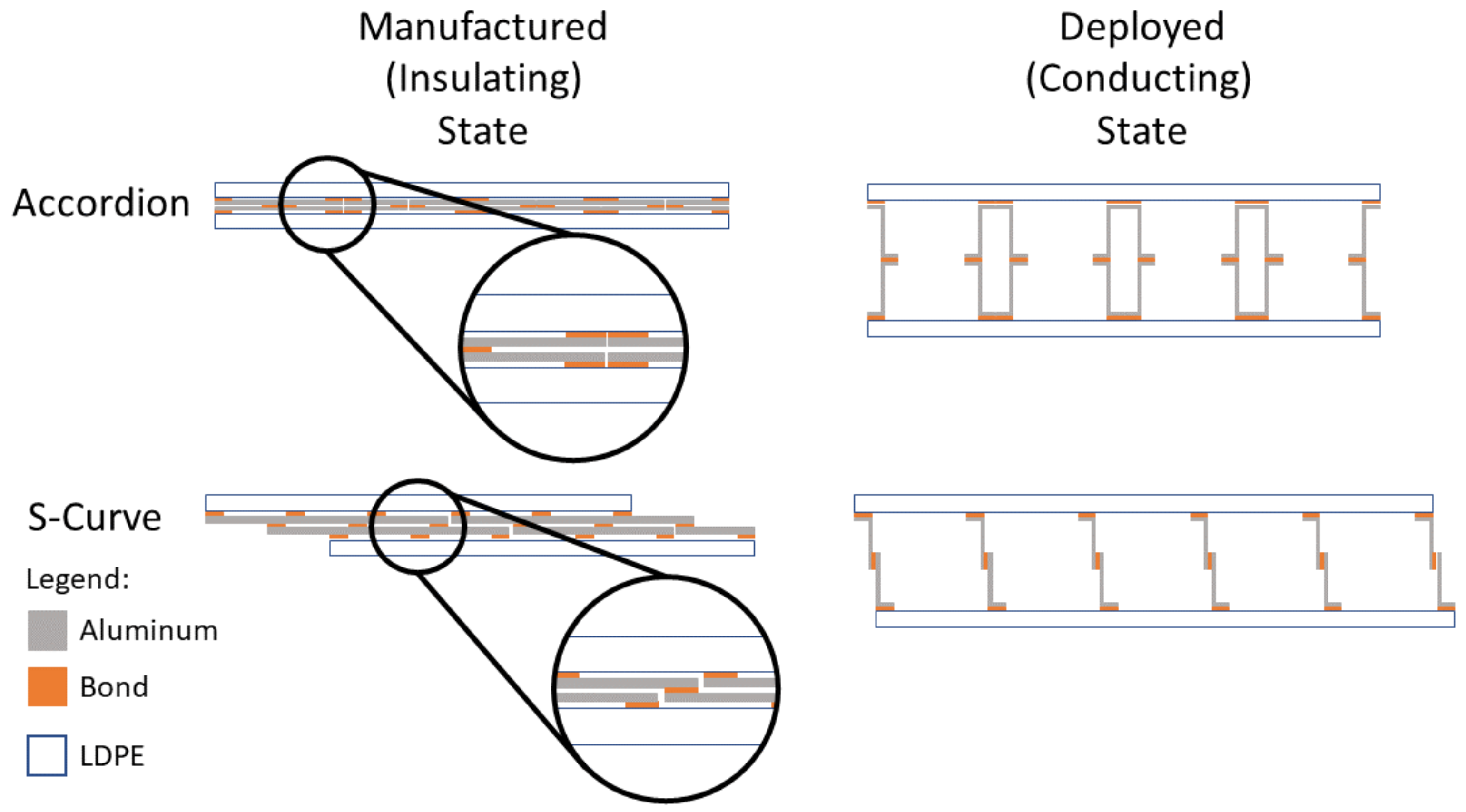
2.1.1. DRB Concept
2.1.2. Fabrication
2.2. Hotbox Testing
Measurement Uncertainty
2.3. Finite Element Analysis
- (1)
- Heat conduction through the system.
- (2)
- Free convection in the interior cavity between particleboards.
- (3)
- Radiation exchange between the underside of the top particleboard and the surfaces in the cavity using the hemicube surface-to-surface method.
3. Results and Discussion
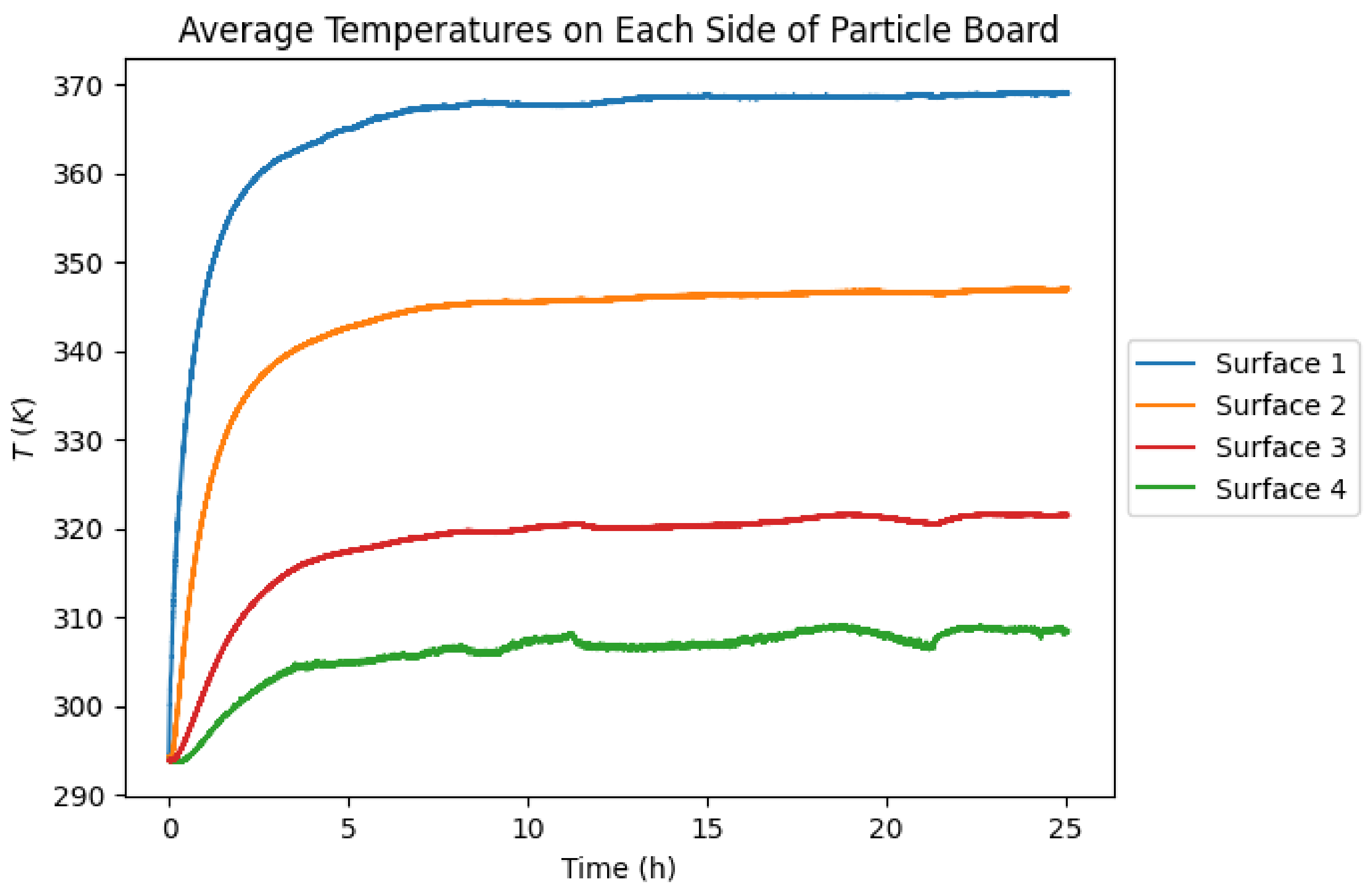
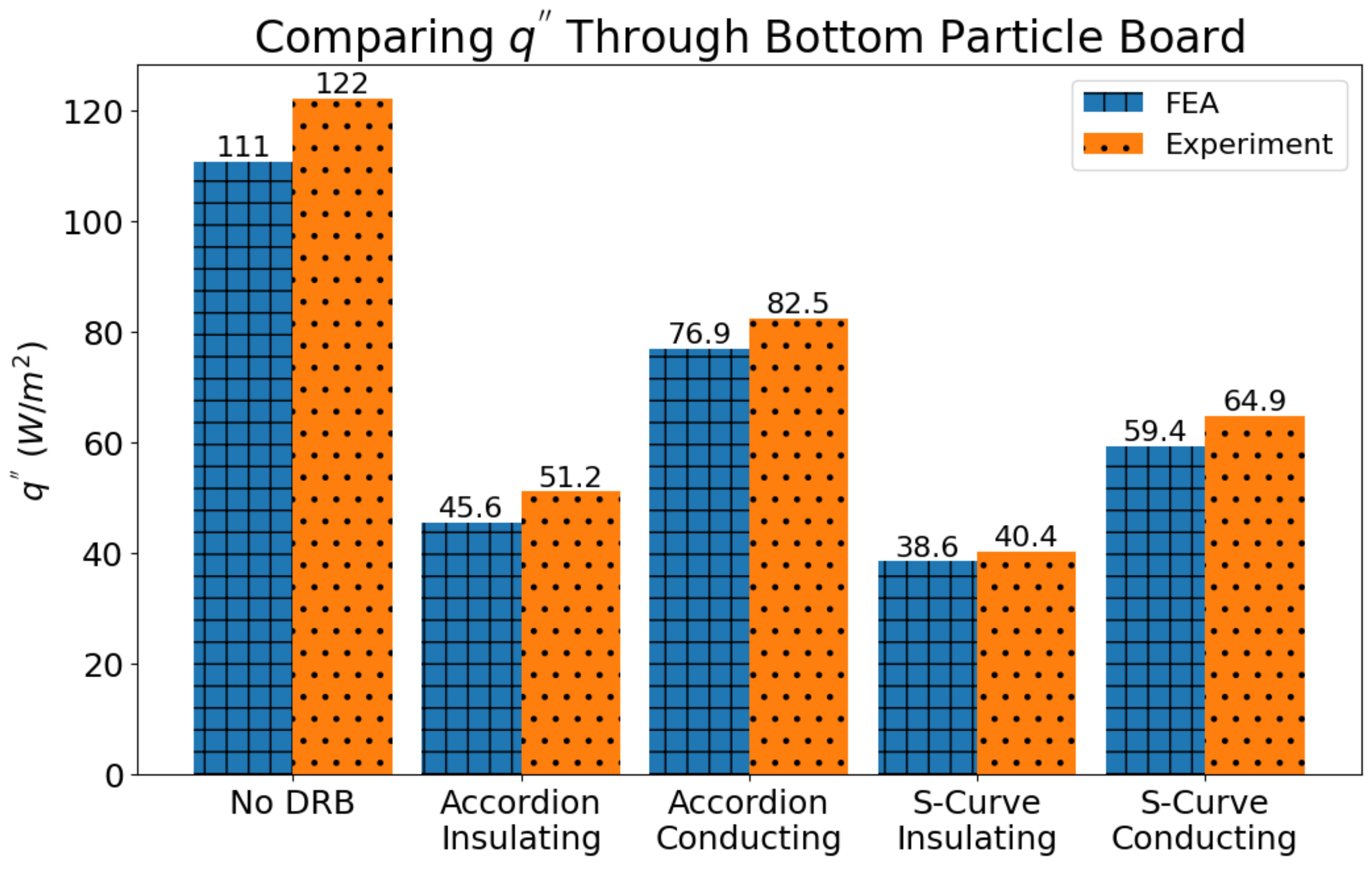
3.1. DRB Performance
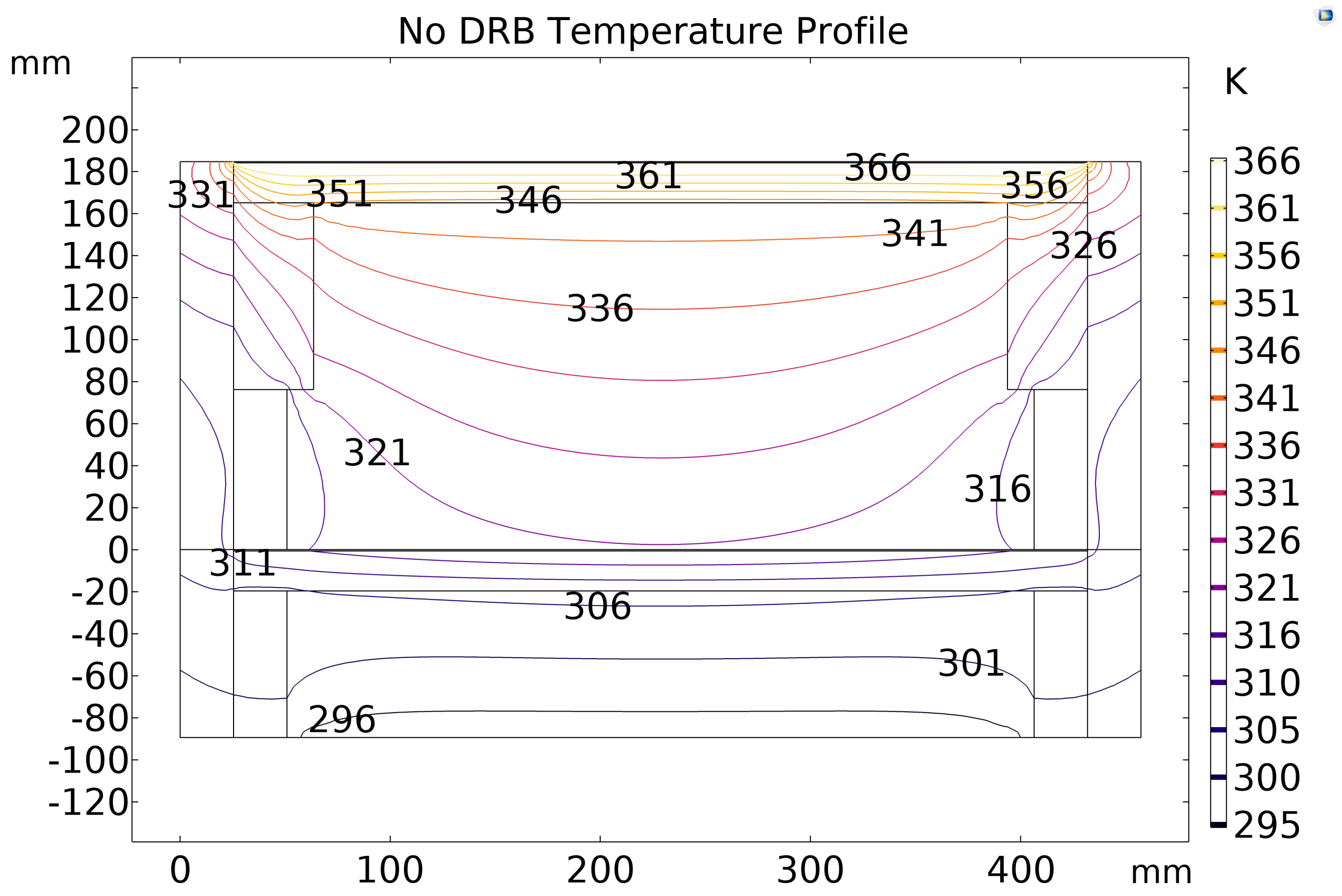
3.2. FEA Results
3.3. Design Considerations
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| heat capacity at constant pressure | |
| difference in averaged temperatures on surfaces i and j | |
| DRB | dynamic radiant barrier |
| emissivity | |
| FEA | finite element analysis |
| h | convection coefficient |
| k | thermal conductivity |
| LDPE | low-density polyethylene |
| n | number of measurements |
| heat flux | |
| heat flux through paired thermocouples | |
| averaged heat flux through surfaces i and j | |
| conducting heat flux | |
| insulating heat flux | |
| thermal resistance of the cavity between the particleboards | |
| conducting thermal resistance | |
| insulating thermal resistance | |
| R2R | roll-to-roll |
| SEM | standard error of the mean |
| standard deviation | |
| temperature on surface i | |
| u | uncertainty |
| uncertainty of measured thermocouple error | |
| x | thickness of particleboard |
References
- US Department of Energy. Quadrennial Technology Review: An Assessment of Energy Technologies and Research Opportunities; US Department of Energy: Washington, DC, USA, 2015.
- U.S. Energy Information Administration. Annual Energy Outlook 2023 (AEO2023); U.S. Energy Information Administration: Washington, DC, USA, 2023.
- United Nations Environment Programme Buildings and Climate Change: Summary for Decision Makers; United Nations Environment Programme: Paris, France, 2009.
- Directorate-General For Energy European Commission. Commission ‘Digitalising the Energy System—EU Action Plan’; Technical Report; European Commission: Brussels, Belgium, 2022. [Google Scholar]
- Federal Information & News Dispatch, LLC. Building a Better Grid Initiative to Upgrade and Expand the Nation’s Electric Transmission Grid to Support Resilience, Reliability, and Decarbonization; Technical Report; Federal Information & News Dispatch, LLC: Lanham, MD, USA, 2022. [Google Scholar]
- Butt, O.M.; Zulqarnain, M.; Butt, T.M. Recent advancement in smart grid technology: Future prospects in the electrical power network. Ain Shams Eng. J. 2021, 12, 687–695. [Google Scholar] [CrossRef]
- Tan, K.M.; Babu, T.S.; Ramachandaramurthy, V.K.; Kasinathan, P.; Solanki, S.G.; Raveendran, S.K. Empowering smart grid: A comprehensive review of energy storage technology and application with renewable energy integration. J. Energy Storage 2021, 39, 102591. [Google Scholar] [CrossRef]
- Hagentoft, C.E. Introduction to Building Physics, 1st ed.; Studentlitteratur: Lund, Sweden, 2001. [Google Scholar]
- Pinteric, M. Building Physics: From Physical Principles to International Standards, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Heat and Mass Transfer in Buildings. Available online: https://www.staff.dtu.dk/-/media/staff/menqin/heat-and-mass-transfer-in-buildings.pdf (accessed on 20 June 2024).
- DRAFT Research and Development Opportunities Report for Opaque Building Envelopes. Available online: https://www.energy.gov/sites/prod/files/2020/05/f74/bto-20200505_Draft_Envelope_RDO_0.pdf (accessed on 20 June 2024).
- Burdajewicz, F.; Korjenic, A.; Bednar, T. Bewertung und Optimierung von dynamischen Dämmsystemen unter Berücksichtigung des Wiener Klimas. Bauphysik 2011, 33, 49–58. [Google Scholar] [CrossRef]
- Nicol, K. The thermal effectiveness of various types of window coverings. Energy Build. 1986, 9, 231–237. [Google Scholar] [CrossRef]
- Le-Thanh, L.; Le-Duc, T.; Ngo-Minh, H.; Nguyen, Q.H.; Nguyen-Xuan, H. Optimal design of an Origami-inspired kinetic façade by balancing composite motion optimization for improving daylight performance and energy efficiency. Energy 2021, 219, 119557. [Google Scholar] [CrossRef]
- Krarti, M. Optimal energy performance of dynamic sliding and insulated shades for residential buildings. Energy 2023, 263, 125699. [Google Scholar] [CrossRef]
- Viereck, V.; Ackermann, J.; Li, Q.; Jakel, A.; Schmid, J.; Hillmer, H. Sun glasses for buildings based on micro mirror arrays: Technology, control by networked sensors and scaling potential. In Proceedings of the 2008 5th International Conference on Networked Sensing Systems, Kanazawa, Japan, 17–19 June 2008; pp. 135–139. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, S. Thermal insulation solutions for opaque envelope of low-energy buildings: A systematic review of methods and applications. Renew. Sustain. Energy Rev. 2022, 167, 112738. [Google Scholar] [CrossRef]
- Menyhart, K.; Krarti, M. Potential energy savings from deployment of Dynamic Insulation Materials for US residential buildings. Build. Environ. 2017, 114, 203–218. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration. Annual Energy Outlook 2018 (AEO2018); Technical Report; U.S. Energy Information Administration: Washington, DC, USA, 2018.
- Stevens, T.R.; Crane, N.B.; Mulford, R.B. Topology Morphing Insulation: A Review of Technologies and Energy Performance in Dynamic Building Insulation. Energies 2023, 16, 6978. [Google Scholar] [CrossRef]
- Dehwah, A.H.A.; Krarti, M. Cost-benefit analysis of retrofitting attic-integrated switchable insulation systems of existing US residential buildings. Energy 2021, 221, 119840. [Google Scholar] [CrossRef]
- Lee, S.W.; Lim, C.H.; Salleh, E.I.B. Reflective thermal insulation systems in building: A review on radiant barrier and reflective insulation. Renew. Sustain. Energy Rev. 2016, 65, 643–661. [Google Scholar] [CrossRef]
- Desjarlais, A.O. Radiant Barrier Fact Sheet; Technical Report; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2010. [Google Scholar]
- Fairey, P. The measured side-by-side performance of attic radiant barrier systems in hot, humid climates. In Proceedings of the Nineteenth International Thermal Conductivity Conference, Cookville, TN, USA, 20–23 October 1985; pp. 481–496. [Google Scholar]
- Medina, M.A. A comprehensive review of radiant barrier research including laboratory and field experiments. ASHRAE Trans. 2012, 118, 400. [Google Scholar]
- United States Department of Energy. Radiant Barriers. 2016. Available online: https://www.energy.gov/energysaver/radiant-barriers%7D. (accessed on 20 June 2024).
- Dehwah, A.H.A.; Krarti, M. Impact of switchable roof insulation on energy performance of US residential buildings. Build. Environ. 2020, 177, 106882. [Google Scholar] [CrossRef]
- Chang, P.C.; Chiang, C.M.; Lai, C.M. Development and preliminary evaluation of double roof prototypes incorporating RBS (radiant barrier system). Energy Build. 2008, 40, 140–147. [Google Scholar] [CrossRef]
- AustuteAnalytica. Global Fiberglass Market Is Poised to Reach US $23,217.3 Million by 2031, Says Astute Analytica. 2013. Available online: https://finance.yahoo.com/news/global-fiberglass-market-poised-reach-133000622.html (accessed on 8 August 2023).
- United States Department of Energy. Guide to Home Insulation. 2010. Available online: https://www.energy.gov/sites/prod/files/guide_to_home_insulation.pdf (accessed on 20 June 2024).
- Greener, J. Roll-to-Roll Manufacturing. In Roll-to-Roll Manufacturing: Process Elements and Recent Advances; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018; pp. 1–17. [Google Scholar] [CrossRef]
- Howell, L.L. Compliant Mechanisms; John Wiley & Sons Ltd: Hoboken, NJ, USA, 2001. [Google Scholar]
- Yarbrough, D.W. Assessment of Reflective Insulations for Residential and Commercial Applications; Technical Report; Oak Ridge National Lab: Oak Ridge, TN, USA, 1983. [Google Scholar] [CrossRef]
- Finckenor, M.M.; Dooling, D. Multilayer Insulation Material Guidelines; Technical Report; NASA: Washington, DC, USA, 1999.
- Smith, C.; Mckinley, I.; Ramsey, P.; Rodriguez, J. Performance of multi-layer insulation for spacecraft instruments at cryogenic temperatures. In Proceedings of the 46th International Conference on Environmental Systems, Vienna, Austria, 10 July 2016. [Google Scholar]
- Morgan, J.; Magleby, S.P.; Howell, L.L. An Approach to Designing Origami-Adapted Aerospace Mechanisms. J. Mech. Des. 2016, 138, 052301. [Google Scholar] [CrossRef]
- Thrall, A.P.; Quaglia, C.P. Accordion shelters: A historical review of origami-like deployable shelters developed by the US military. Eng. Struct. 2014, 59, 686–692. [Google Scholar] [CrossRef]
- Klotz, A. Origami-shaped conducting polymer stretches like an accordion. MRS Bull. 2018, 43, 400. [Google Scholar] [CrossRef]
- American Wood Council. 2024 Wood Frame Construction Manual (WFCM) for One- and Two-Family Dwellings; American Wood Council: Leesburg, VA, USA, 2023. [Google Scholar]
- International Code Council. 2021 International Residential Code; International Code Council: Nappanee, IN, USA, 2021. [Google Scholar]
- Association, A.T.E.W. APA Engineered Wood Construction Guide. 2019. Available online: https://osb.westfraser.com/wp-content/uploads/2020/01/E30X.pdf (accessed on 20 June 2024).
- Ndegwa, N.G.; Ndiritu, F.G.; Hussein, G.S.A.; Kamweru, P.K.; Kagia, J.K.; Muthui, Z.W. Reflectance, Transmittance and Absorptance of HDPE, LDPE, Glass and Sand Layer Used in a SAH. Int. J. Appl. Phys. Math. 2014, 4, 406–416. [Google Scholar] [CrossRef][Green Version]
- Carrobé, A.; Martorell, I.; Solé, C.; Castell, A. Transmittance analysis for materials suitable as radiative cooling windshield and aging study for polyethylene. In Proceedings of the EuroSun 2020, Athens, Greece, 29 September–1 October 2020. [Google Scholar] [CrossRef]
- Pozzobon, V.; Levasseur, W.; Do, K.V.; Palpant, B.; Perré, P. Household aluminum foil matte and bright side reflectivity measurements: Application to a photobioreactor light concentrator design. Biotechnol. Rep. 2020, 25, e00399. [Google Scholar] [CrossRef]
- Fairey, P.W. Effects of Infrared Radiation Barriers on the Effective Thermal Resistance of Building Envelopes. In Proceedings of the ASHRAE/DOE Conference on Thermal Performance of the Exterior Envelopes of Buildings II, Clearwater, FL, USA, 1–5 December 1982. [Google Scholar]
- ASTM C518-21; Standard Test Method for Steady-State Thermal Transmission Properties by Means of the Heat Flow Meter Apparatus. ASTM International: West Conshohocken, PA, USA, 2021. [CrossRef]
- RMax. Sika® Rmax® Pro Select Polyiso Insulation Board. 2023. Available online: https://usa.sika.com/dms/getdocument.get/137e484c-d2c9-4fc2-bc25-2a7b2e4dc52a/Sika-Rmax-Pro-Select-R-Matte-Plus-3-Product-Data-Sheet.pdf (accessed on 20 June 2024).
- Fricker, J.M. Computational Analysis of Reflective Air Spaces. Airah J. 1997, 51, 29–32. [Google Scholar]
- Asadi, S.; Hassan, M.M.; Beheshti, A. Performance evaluation of an attic radiant barrier system using three-dimensional transient finite element method. J. Build. Phys. 2013, 36, 247–264. [Google Scholar] [CrossRef]
- Robinson, H.E.; Powlitch, F.J. The Thermal Insulating Value of Air Spaces; Technical Report; National Bureau of Standards: Gaithersburg, MD, USA, 1954.
- Aremco. Electrically and Thermally Conductive Adhesives and Coatings. Available online: https://www.aremco.com/wp-content/uploads/2018/05/A08_S1_18.pdf (accessed on 20 June 2024).
- Sonderegger, W.; Niemz, P. Thermal conductivity and water vapour transmission properties of wood-based materials. Eur. J. Wood Wood Prod. 2009, 67, 313–321. [Google Scholar] [CrossRef]
- Nakos, J.T. Uncertainty Analysis of Thermocouple Measurements Used in Normal and Abnormal Thermal Environment Experiments at Sandia’s Radiant Heat Facility and Lurance Canyon Burn Site; Technical Report; Sandia National Laboratories: Livermore, CA, USA, 2004. [Google Scholar] [CrossRef]
- ISO; BIPM; OIML. Guide to the Expression of Uncertainty in Measurement (GUM), BIPM, IEC, IFCC, ISO, IUPAC, IUPAP, OIML; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Farrance, I.; Frenkel, R. Uncertainty of Measurement: A Review of the Rules for Calculating Uncertainty Components through Functional Relationships. Clin. Biochem. Rev. 2012, 33, 49–75. [Google Scholar] [PubMed]
- Eggers, A.J. One-Dimensional Flows of an Imperfect Diatomic Gas; Technical Report; NASA: Washington, DC, USA, 1949.
- Yost, B.; Weston, S. State-of-the-Art Small Spacecraft Technology; Technical Report; NASA: Washington, DC, USA, 2024.
- Fantucci, S.; Serra, V. Experimental Assessment of the Effects of Low-Emissivity Paints as Interior Radiation Control Coatings. Appl. Sci. 2020, 10, 842. [Google Scholar] [CrossRef]
- Anderson, K.; Weritz, J.; Kaufman, J.G. (Eds.) 1xxx Aluminum Alloy Datasheets. In Properties and Selection of Aluminum Alloys; ASM International: Detroit, MI, USA, 2019; Volume 2B. [Google Scholar] [CrossRef]
- Zhang, A.; Li, Y. Thermal Conductivity of Aluminum Alloys—A Review. Materials 2023, 16, 2972. [Google Scholar] [CrossRef] [PubMed]
- Sonnier, R.; Ferry, L.; Gallard, B.; Boudenne, A.; Lavaud, F. Controlled Emissivity Coatings to Delay Ignition of Polyethylene. Materials 2015, 8, 6949. [Google Scholar] [CrossRef] [PubMed]
- Gauthier, M.M. Thermal Analysis and Properties of Polymers; Engineered Materials Handbook Desk Edition; ASM International: Detroit, MI, USA, 1995. [Google Scholar] [CrossRef]
- Lopes, C.M.A.; Felisberti, M.I. Thermal conductivity of PET/(LDPE/AI) composites determined by MDSC. Polym. Test. 2004, 23, 637–643. [Google Scholar] [CrossRef]
- Yousefi, Y.; Tariku, F. Thermal Conductivity and Specific Heat Capacity of Insulation materials at Different Mean Temperatures. J. Phys. Conf. Ser. 2021, 2069, 12090. [Google Scholar] [CrossRef]
- Ross, R.J.; Laboratory, F.P.U.F.S. Wood Handbook: Wood as an Engineering Material; Technical Report; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Washington, DC, USA, 2010. [CrossRef]
- Czajkowski, L.; Olek, W.; Weres, J.; Guzenda, R. Thermal properties of wood-based panels: Specific heat determination. Wood Sci. Technol. 2016, 50, 537–545. [Google Scholar] [CrossRef]
- Long, L.; Ye, H. The roles of thermal insulation and heat storage in the energy performance of the wall materials: A simulation study. Sci. Rep. 2016, 6, 24181. [Google Scholar] [CrossRef]




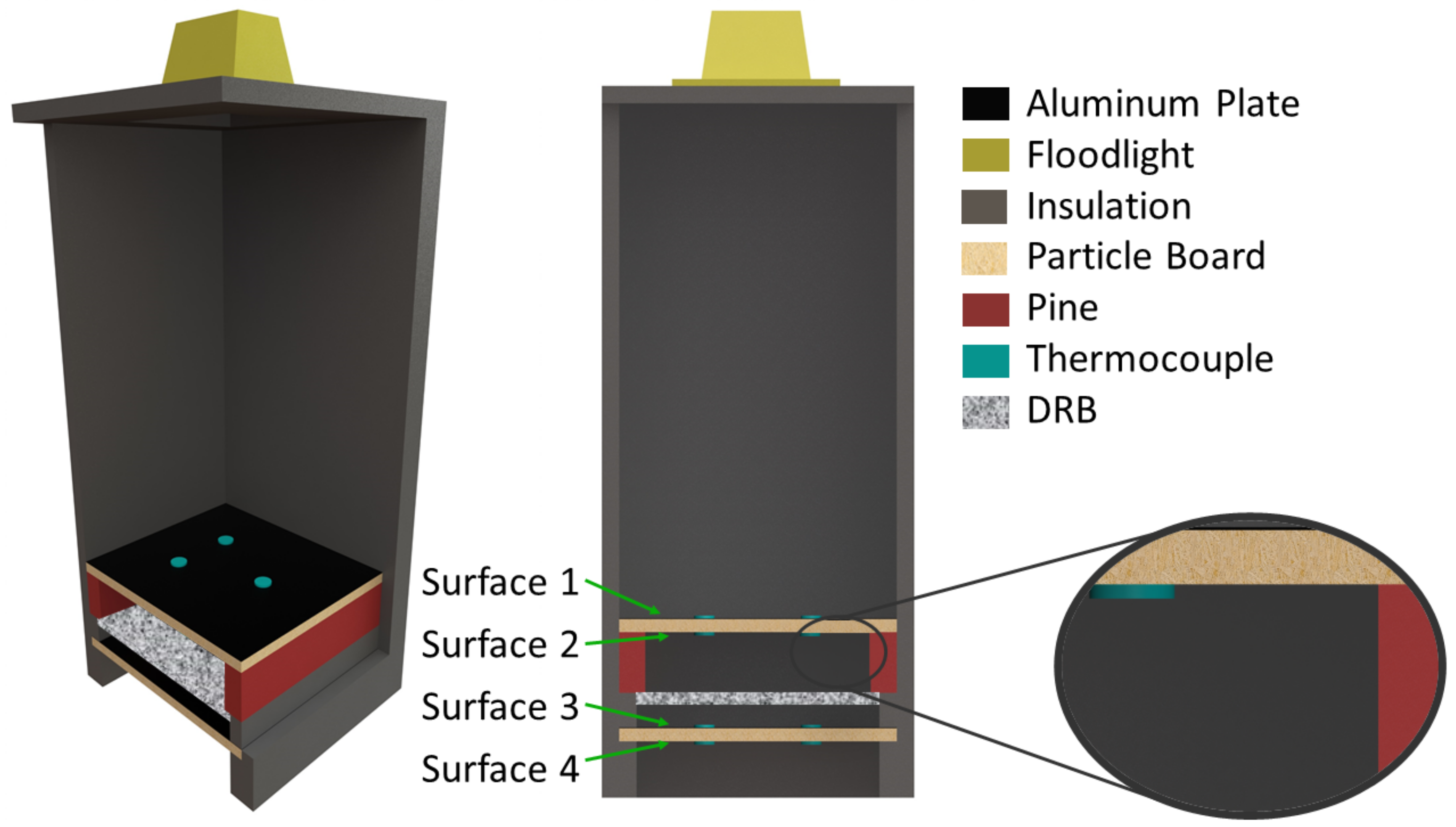
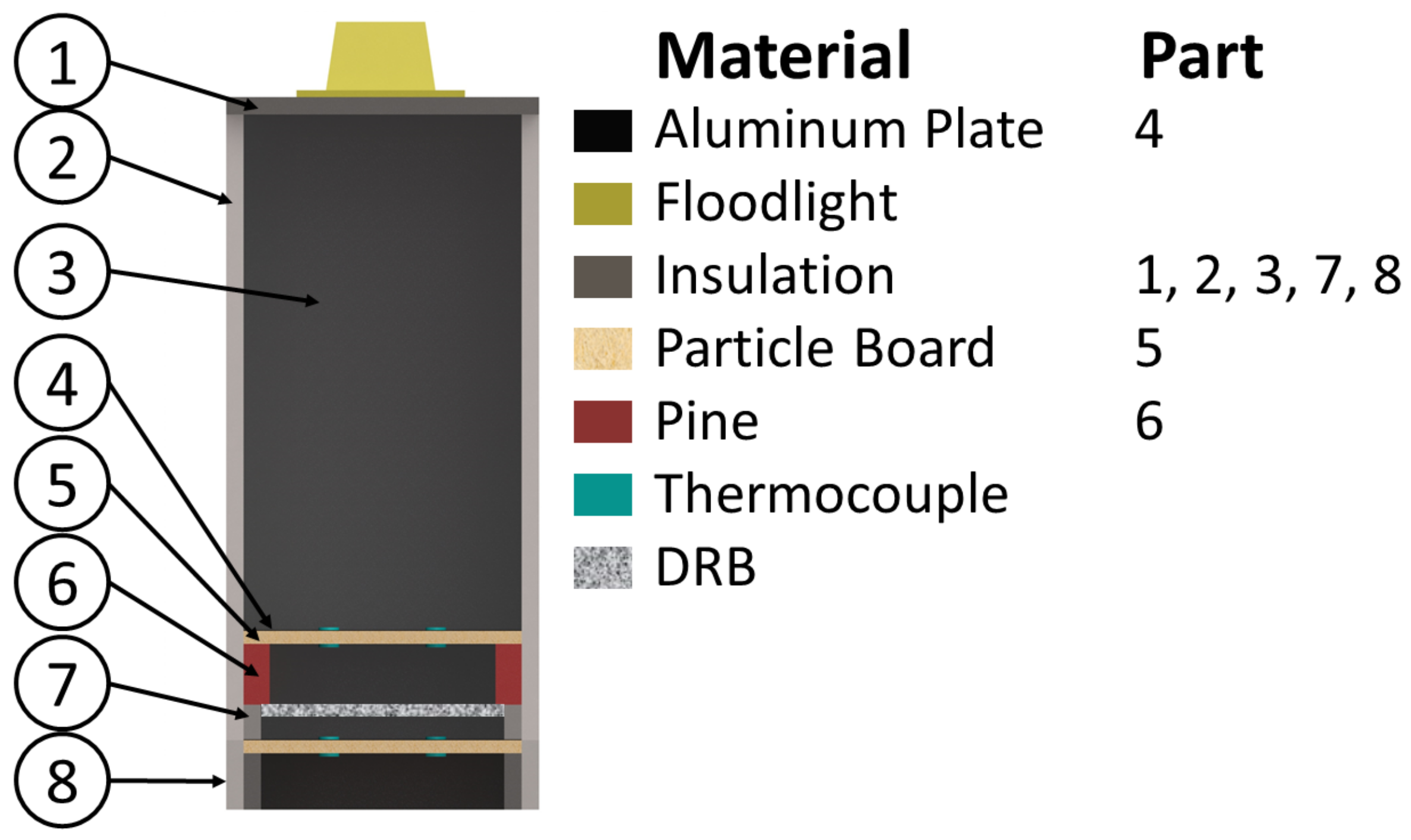


| Component | Material | Dimensions | ||
|---|---|---|---|---|
| Length (mm) | Width (mm) | Thickness (mm) | ||
| 1 | Insulation | 460 | 460 | 25.4 |
| 2 | Insulation | 914 | 406 | 25.4 |
| 3 | Insulation | 914 | 406 | 51 |
| 4 | Aluminum Plate | 406 | 406 | 0.6 |
| 5 | Particleboard | 406 | 406 | 19 |
| 6 | Pine | 406 | 38 | 89 |
| 7 | Insulation | 406 | 25.4 | 90 |
| 8 | Insulation | 406 | 25.4 | 111 |
| Material | Properties | ||
|---|---|---|---|
| (J/kg·K) | (W/m K) | ||
| Aluminum | 0.85 [57]/0.04 [58] * | 900 [59] | 237 [60] |
| LDPE | 0.92 [61] | 2300 [62] | 0.33 [63] |
| Foam Board | - | 1700 [64] | 0.87 [47] |
| Particleboard | 0.8 [65] | 1420 [66] | 0.12 [52] |
| Pine | 0.95 [65] | 2850 [67] | 0.12 [65] |
| Simulation | Temperature (K) of Surface | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| No DRB | 369 | 347 | 321 | 309 |
| Accordion Insulating | 358 | 346 | 303 | 298 |
| Accordion Conducting | 355 | 341 | 310 | 301 |
| S-Curve Insulating | 349 | 340 | 302 | 298 |
| S-Curve Conducting | 342 | 330 | 307 | 300 |
| Experiment | (m2 K/W) | (m2 K/W) | (W/m2) | (W/m2) | ||
|---|---|---|---|---|---|---|
| No DRB | 0.21 | 122 | ||||
| Accordion | 0.37 | 0.84 | 2.23 | 82.5 | 51.2 | 0.62 |
| S-Curve | 0.36 | 0.94 | 2.58 | 64.9 | 40.4 | 0.62 |
| Simulation | Temperature (K) of Surface | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| No DRB | 369 | 345 | 318 | 307 |
| Accordion Insulating | 358 | 346 | 304 | 299 |
| Accordion Conducting | 355 | 338 | 312 | 303 |
| S-Curve Insulating | 349 | 339 | 302 | 298 |
| S-Curve Conducting | 342 | 329 | 307 | 301 |
| Simulation | Temperature (K) of Surface | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| No DRB | 369 | 345 | 318 | 307 |
| DRB Insulating | 369 | 354 | 306 | 300 |
| Accordion Conducting | 369 | 346 | 316 | 306 |
| S-Curve Conducting | 369 | 348 | 316 | 306 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stevens, T.R.; Parsi, B.; Mulford, R.B.; Crane, N.B. Dynamic Radiant Barrier for Modulating Heat Transfer and Reducing Building Energy Usage. Energies 2024, 17, 3959. https://doi.org/10.3390/en17163959
Stevens TR, Parsi B, Mulford RB, Crane NB. Dynamic Radiant Barrier for Modulating Heat Transfer and Reducing Building Energy Usage. Energies. 2024; 17(16):3959. https://doi.org/10.3390/en17163959
Chicago/Turabian StyleStevens, Tyler R., Behzad Parsi, Rydge B. Mulford, and Nathan B. Crane. 2024. "Dynamic Radiant Barrier for Modulating Heat Transfer and Reducing Building Energy Usage" Energies 17, no. 16: 3959. https://doi.org/10.3390/en17163959
APA StyleStevens, T. R., Parsi, B., Mulford, R. B., & Crane, N. B. (2024). Dynamic Radiant Barrier for Modulating Heat Transfer and Reducing Building Energy Usage. Energies, 17(16), 3959. https://doi.org/10.3390/en17163959






