A Parallel Prediction Model for Photovoltaic Power Using Multi-Level Attention and Similar Day Clustering
Abstract
1. Introduction
- (1)
- Improved Clustering and Data Quality: Employing similar day selection and an improved ISODATA clustering algorithm improves the clustering impact, categorizing the dataset by different seasons and climate types. This approach reduces the amount of data required for prediction and improves data quality.
- (2)
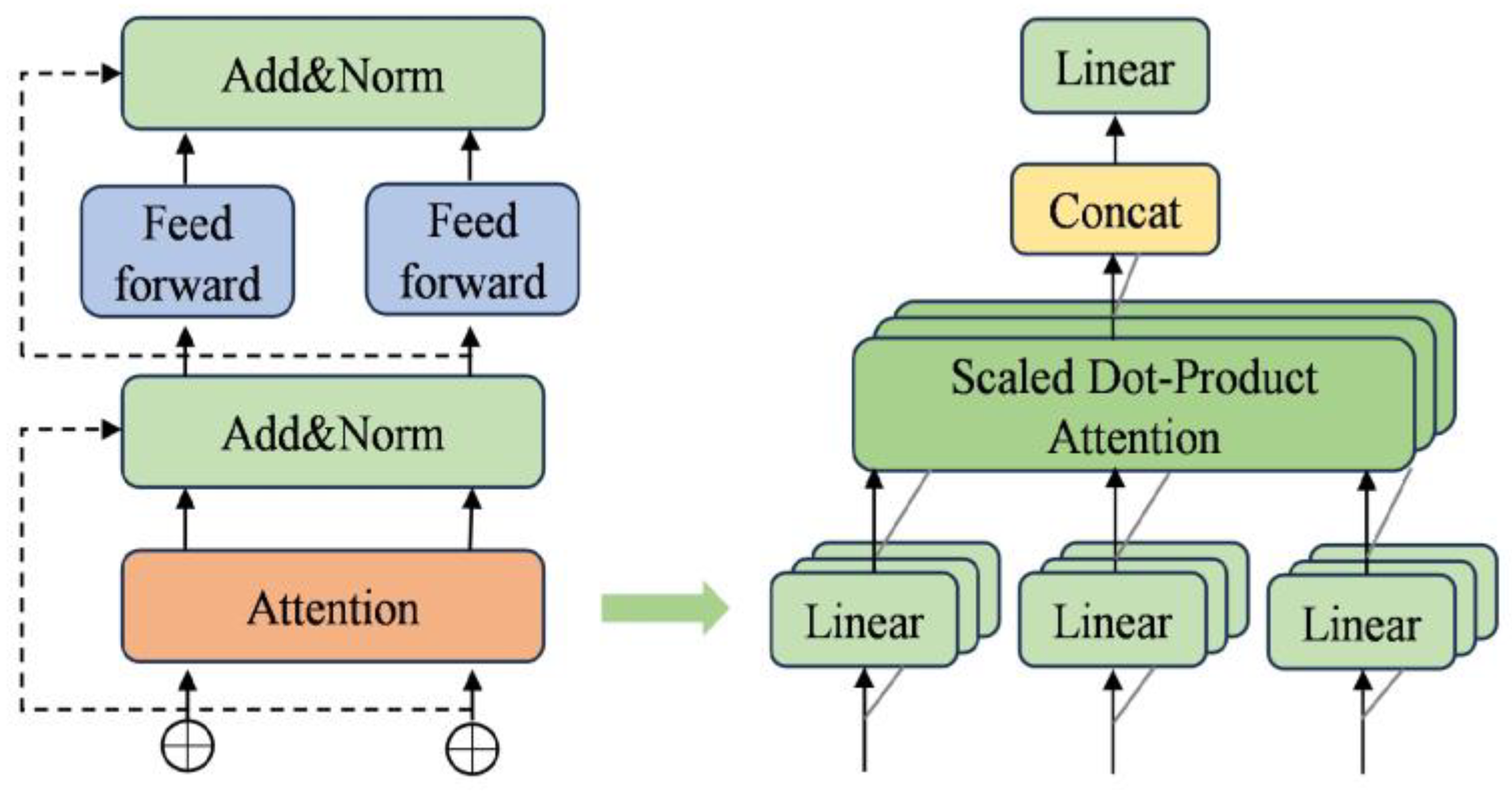
- Transformer Encoder Layer: Dependencies between different positions in the sequence are extracted and global contextual information is captured using a Transformer encoder layer with a multi-head attention mechanism. Additionally, a parallel structure is implemented to accelerate model training and inference.
- (3)
- BiGRU with Global Attention: A BiGRU network, optimized with Global Attention, captures global temporal features, enhancing the model’s ability to perceive time-domain characteristics of multi-feature sequences.
- (4)
- Cross Attention for Feature Fusion: Cross Attention is employed to fuse information from different sources, enhancing the representation capability of features and achieving high-accuracy predictions.
2. Meteorological Data Processing
2.1. Data Preprocessing
- (1)
- It must be ensured that data recording intervals, feature labels, and timestamps are uniformly formatted;
- (2)
- For noncontinuous missing data, interpolation methods can be used for estimation. Given the strong periodicity of load data, the Lagrangian interpolation method is employed to estimate missing values and fill in the gaps [27];
- (3)
- Evident errors and repeatability issues, such as sudden zero values or extremely high values exceeding system capacity, should be identified and corrected. Invalid data must be discarded or replaced, as PV systems are expected to operate normally with slow, gradual changes in power. Invalid data points can be replaced by the average value of the preceding and succeeding time points.
2.2. Similar Day Selection
- (1)
- Meteorological feature vectors are developed based on the selected meteorological features M:where denotes the average daily irradiance; denotes the average daily temperature; denotes the average daily wind speed; and denotes the average daily humidity.
- (2)
- After processing each component, the meteorological feature vectors for the forecast day and d day are and , respectively.
- (3)
- The correlation coefficients of and in the s (s = 1, 2, …, 4) classification, , are determined as follows:where r denotes the resolution coefficient, which takes a value between [0,1]. In this study, r = 0.5.
- (4)
- The correlation coefficient of each component is synthesized, and the similarity between and is defined as .where m denotes the total number of components of the meteorological eigenvectors.
2.3. Improved ISODATA Clustering Algorithm
2.3.1. Optimization of Initial Clustering Centers
- (1)
- A random sample from the dataset is selected to serve as the first initial clustering center.
- (2)
- For each remaining sample xi, its distance from each existing clustering center is calculated, and the shortest distance d(xi), is recorded.
- (3)
- The probability of each sample xi being selected as the next clustering center is proportional to . Samples with larger d(xi) have a higher probability of being selected.
- (4)
- Step 2 is repeated until k initial clustering centers are selected.
2.3.2. Kernel Method
2.3.3. Evaluation Criteria
3. Multi-Level Attention Parallel Prediction Model
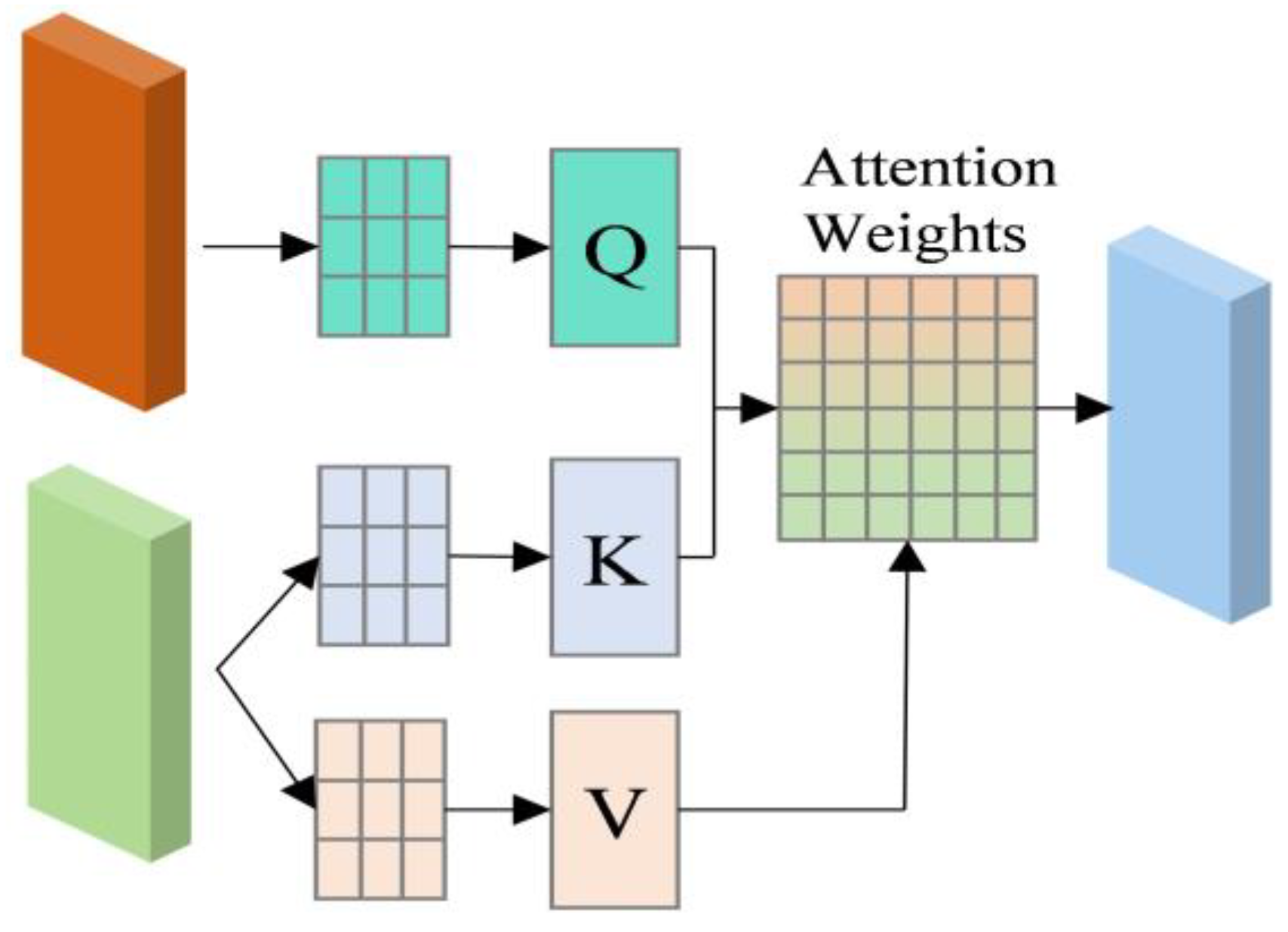
3.1. Transformer–Multi-Head Attention
3.2. BiGRU-Global Attention
3.3. Cross Attention
3.4. Framework of This Paper
4. Calculus Analysis
4.1. Data Sources
4.2. Clustering Impact Analysis
4.3. Comparative Analysis of Predictive Models
5. Conclusions
- (1)
- The training set data were selected through a similar day analysis, reducing the complexity of the model training set and shortening the prediction time.
- (2)
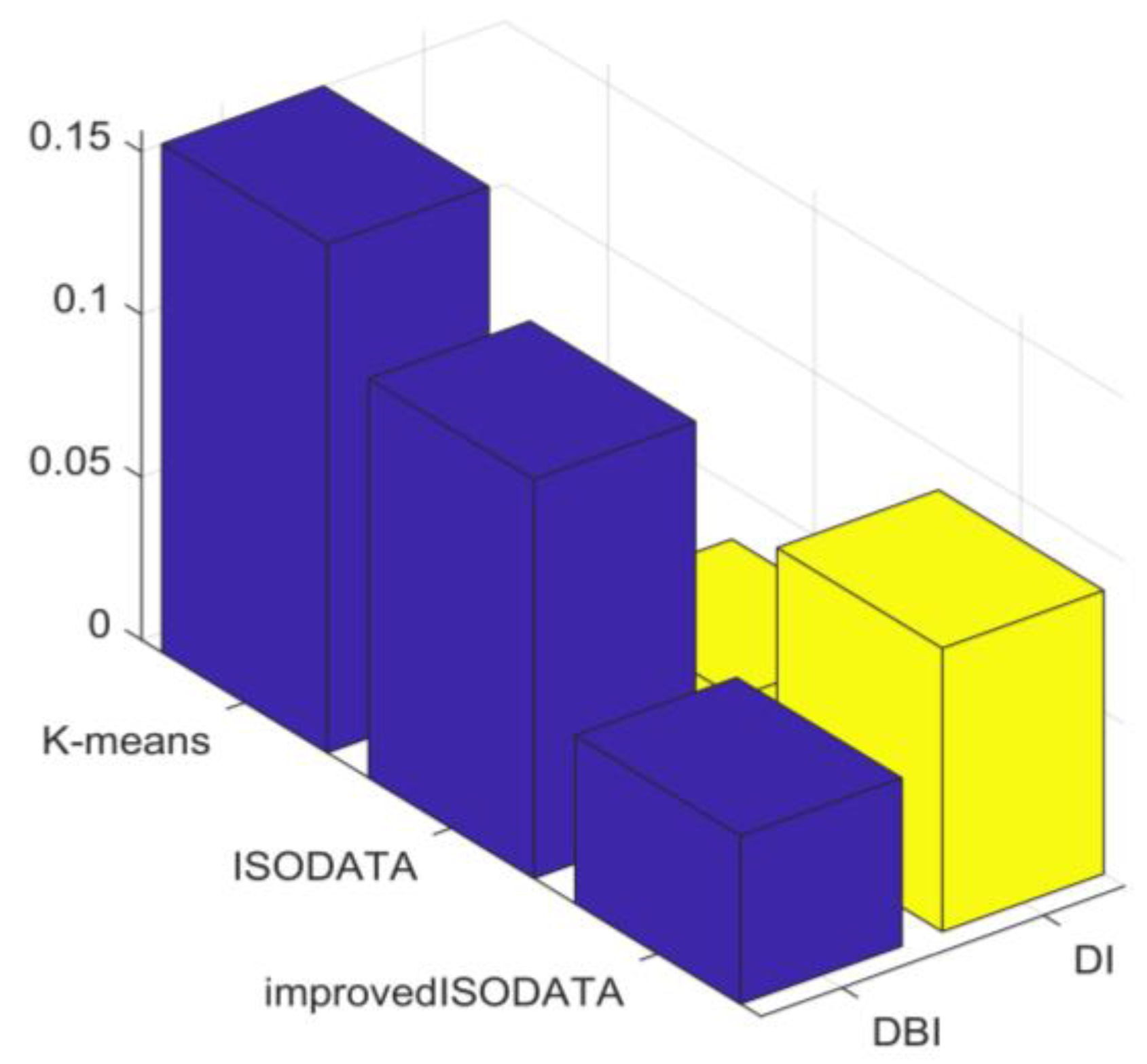
- An improved ISODATA algorithm was proposed to optimize the configuration of initial clustering centers and Euclidean distances, enhancing the clustering impact and speed. This further optimizes the similar day dataset and guarantees prediction accuracy.
- (3)
- A parallel prediction model with a multi-level attention mechanism was proposed to synthesize the advantages of networks such as Transformer, BiGRU, Global Attention, and Cross Attention. This allows the model to integrate information from different feature subspaces, achieving better prediction results under various climate types compared to the basic model, as validated experimentally.
- (4)
- The forecasting method in this study focused on the temporal correlation of PV series. Future research will consider mining and utilizing more hidden spatial correlation information from the historical load series to further improve forecasting accuracy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stua, M. Evidence of the clean development mechanism impact on the Chinese electric power system’s low-carbon transition. Energy Policy 2013, 62, 1309–1319. [Google Scholar] [CrossRef]
- Lupangu, C.; Bansal, R. A review of technical issues on the development of solar photovoltaic systems. Renew. Sustain. Energy Rev. 2017, 73, 950–965. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Venkateswari, R.; Sreejith, S. Factors influencing the efficiency of photovoltaic system. Renew. Sustain. Energy Rev. 2019, 101, 376–394. [Google Scholar] [CrossRef]
- Gaviria, J.F.; Narváez, G.; Guillen, C.; Giraldo, L.F.; Bressan, M. Machine learning in photovoltaic systems: A review. Renew. Energy 2022, 196, 298–318. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. Solar photovoltaic system modeling and performance prediction. Renew. Sustain. Energy Rev. 2014, 36, 304–315. [Google Scholar] [CrossRef]
- Jo, K.-Y.; Go, S.-I. Operation Method of PV–Battery Hybrid Systems for Peak Shaving and Estimation of PV Generation. Electronics 2023, 12, 1608. [Google Scholar] [CrossRef]
- Fara, L.; Diaconu, A.; Craciunescu, D.; Fara, S. Forecasting of energy production for photovoltaic systems based on ARIMA and ANN advanced models. Int. J. Photoenergy 2021, 2021, 6777488. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, J.; Song, Y.; Xu, Z.; Lin, J.; Hu, Z. Photovoltaic and solar power forecasting for smart grid energy management. CSEE J. Power Energy Syst. 2015, 1, 38–46. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Congedo, P.M.; Malvoni, M. Photovoltaic power forecasting using statistical methods: Impact of weather data. IET Sci. Meas. Technol. 2014, 8, 90–97. [Google Scholar] [CrossRef]
- Mohamad Radzi, P.N.L.; Akhter, M.N.; Mekhilef, S.; Mohamed Shah, N. Review on the Application of Photovoltaic Forecasting Using Machine Learning for Very Short-to Long-Term Forecasting. Sustainability 2023, 15, 2942. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine learning and deep learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Khortsriwong, N.; Boonraksa, P.; Boonraksa, T.; Fangsuwannarak, T.; Boonsrirat, A.; Pinthurat, W.; Marungsri, B. Performance of Deep Learning Techniques for Forecasting PV Power Generation: A Case Study on a 1.5 MWp Floating PV Power Plant. Energies 2023, 16, 2119. [Google Scholar] [CrossRef]
- Miraftabzadeh, S.M.; Colombo, C.G.; Longo, M.; Foiadelli, F. A Day-Ahead Photovoltaic Power Prediction via Transfer Learning and Deep Neural Networks. Forecasting 2023, 5, 213–228. [Google Scholar] [CrossRef]
- Ying, C.; Wang, W.; Yu, J.; Li, Q.; Yu, D.; Liu, J. Deep learning for renewable energy forecasting: A taxonomy, and systematic literature review. J. Clean. Prod. 2023, 384, 135414. [Google Scholar] [CrossRef]
- Rodríguez, F.; Martín, F.; Fontán, L.; Galarza, A. Ensemble of machine learning and spatiotemporal parameters to forecast very short-term solar irradiation to compute photovoltaic generators’ output power. Energy 2021, 229, 120647. [Google Scholar] [CrossRef]
- Di Piazza, A.; Di Piazza, M.C.; Vitale, G. Solar and wind forecasting by NARX neural networks. Renew. Energy Environ. Sustain. 2016, 1, 39. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y.; Ali, I.H.O. CNN-LSTM: An efficient hybrid deep learning architecture for predicting short-term photovoltaic power production. Electr. Power Syst. Res. 2022, 208, 107908. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, K.; Zhang, S.; Zhang, Z. Photovoltaic power forecasting: A hybrid deep learning model incorporating transfer learning strategy. Renew. Sustain. Energy Rev. 2022, 162, 112473. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, F.; Lv, J.; Duan, Y.; Qin, Z.; Li, G.; Tian, G. Do RNN and LSTM have long memory? In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; PMLR: New York, NY, USA, 2020; pp. 11365–11375. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf (accessed on 1 June 2024).
- Kim, J.; Obregon, J.; Park, H.; Jung, J.-Y. Multi-step photovoltaic power forecasting using transformer and recurrent neural networks. Renew. Sustain. Energy Rev. 2024, 200, 114479. [Google Scholar] [CrossRef]
- Moon, J. A Multi-Step-Ahead Photovoltaic Power Forecasting Approach Using One-Dimensional Convolutional Neural Networks and Transformer. Electronics 2024, 13, 2007. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. In Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; pp. 11106–11115. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Zhang, Y.; Yan, J. In Crossformer: Transformer utilizing cross-dimension dependency for multivariate time series forecasting. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Claridge, D.E.; Chen, H. Missing data estimation for 1–6 h gaps in energy use and weather data using different statistical methods. Int. J. Energy Res. 2006, 30, 1075–1091. [Google Scholar] [CrossRef]
- Kim, G.G.; Choi, J.H.; Park, S.Y.; Bhang, B.G.; Nam, W.J.; Cha, H.L.; Park, N.; Ahn, H.K. Prediction Model for PV Performance With Correlation Analysis of Environmental Variables. IEEE J. Photovolt. 2019, 9, 832–841. [Google Scholar] [CrossRef]
- Gopi, A.; Sharma, P.; Sudhakar, K.; Ngui, W.K.; Kirpichnikova, I.; Cuce, E. Weather impact on solar farm performance: A comparative analysis of machine learning techniques. Sustainability 2022, 15, 439. [Google Scholar] [CrossRef]
- Pang, X.; Sun, W.; Li, H.; Wang, Y.; Luan, C. Short-term power load forecasting based on gray relational analysis and support vector machine optimized by artificial bee colony algorithm. PeerJ Comput. Sci. 2022, 8, e1108. [Google Scholar] [CrossRef] [PubMed]
- Cheng, K.; Guo, L.M.; Wang, Y.K.; Zafar, M.T. Application of clustering analysis in the prediction of photovoltaic power generation based on neural network. IOP Conf. Ser. Earth Environ. Sci. 2017, 93, 012024. [Google Scholar] [CrossRef]
- Karthik; Shivakumar, B.R. Land Cover Mapping Capability of Chaincluster, K-Means, and ISODATA techniques—A Case Study. In Advances in VLSI, Signal Processing, Power Electronics, IoT, Communication and Embedded Systems; Springer: Singapore, 2021; pp. 273–288. [Google Scholar]
- Deborah, L.J.; Baskaran, R.; Kannan, A. A survey on internal validity measure for cluster validation. Int. J. Comput. Sci. Eng. Surv. 2010, 1, 85–102. [Google Scholar] [CrossRef]
- Domhan, T. In How Much Attention Do You Need? A Granular Analysis of Neural Machine Translation Architectures. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Melbourne, Australia, 15–20 July 2018. [Google Scholar]
- Niu, D.; Yu, M.; Sun, L.; Gao, T.; Wang, K. Short-term multi-energy load forecasting for integrated energy systems based on CNN-BiGRU optimized by attention mechanism. Appl. Energy 2022, 313, 118801. [Google Scholar] [CrossRef]
- Liu, Y.; Shao, Z.; Hoffmann, N. Global attention mechanism: Retain information to enhance channel-spatial interactions. arXiv 2021, arXiv:2112.05561. [Google Scholar]
- Lin, H.; Cheng, X.; Wu, X.; Shen, D. In Cat: Cross attention in vision transformer. In Proceedings of the 2022 IEEE International Conference on Multimedia And Expo (ICME), Taipei, Taiwan, 18–22 July 2022; pp. 1–6. [Google Scholar]
- Yang, D.; Alessandrini, S.; Antonanzas, J.; Antonanzas-Torres, F.; Badescu, V.; Beyer, H.G.; Blaga, R.; Boland, J.; Bright, J.M.; Coimbra, C.F.M.; et al. Verification of deterministic solar forecasts. Sol. Energy 2020, 210, 20–37. [Google Scholar] [CrossRef]
- Sabadus, A.; Blaga, R.; Hategan, S.-M.; Calinoiu, D.; Paulescu, E.; Mares, O.; Boata, R.; Stefu, N.; Paulescu, M.; Badescu, V. A cross-sectional survey of deterministic PV power forecasting: Progress and limitations in current approaches. Renew. Energy 2024, 226, 120385. [Google Scholar] [CrossRef]




| Meteorological Factors | Pearson Coefficient |
|---|---|
| Irradiance | 0.989 |
| Temperature | 0.519 |
| Humidity | 0.504 |
| Wind speed | 0.346 |
| Wind direction | 0.109 |
| Air pressure | 0.058 |
| Algorithm | DBI | DI | Time |
|---|---|---|---|
| K-means | 0.156 | 0.020 | 0.670 |
| ISODATA | 0.123 | 0.033 | 0.860 |
| Improved ISODATA | 0.057 | 0.087 | 0.530 |
| Weather | Model | Pavg | RMSE | MSE | MAE | R2 | IAE | RE | Score |
|---|---|---|---|---|---|---|---|---|---|
| Sunny | BiGRU | 46.622 | 3.388 | 11.479 | 2.429 | 0.995 | 218.717 | 40.953 | 0.221 |
| Transformer | 45.867 | 3.512 | 12.335 | 2.934 | 0.995 | 265.230 | 63.827 | 0.193 | |
| BiGRU–Global Attention | 45.393 | 3.186 | 10.153 | 2.651 | 0.996 | 199.101 | 38.190 | 0.268 | |
| CNN-LSTM | 46.166 | 3.393 | 11.511 | 2.682 | 0.995 | 244.016 | 46.183 | 0.220 | |
| NARX | 46.312 | 3.307 | 10.936 | 2.639 | 0.995 | 240.162 | 53.984 | 0.240 | |
| informer | 46.078 | 3.324 | 11.046 | 2.806 | 0.995 | 255.299 | 62.639 | 0.236 | |
| Crossformer | 45.792 | 3.178 | 10.101 | 2.498 | 0.996 | 227.352 | 54.673 | 0.270 | |
| Multi-level attention | 45.565 | 3.154 | 9.945 | 2.053 | 0.996 | 184.917 | 25.730 | 0.275 | |
| Cloudy | BiGRU | 24.297 | 4.221 | 17.821 | 3.184 | 0.975 | 283.404 | 45.191 | 0.037 |
| Transformer | 25.357 | 4.189 | 17.547 | 3.092 | 0.975 | 289.245 | 53.719 | 0.045 | |
| BiGRU–Global Attention | 23.627 | 4.049 | 16.397 | 2.691 | 0.977 | 242.632 | 31.818 | 0.077 | |
| CNN-LSTM | 23.995 | 4.099 | 16.800 | 2.902 | 0.976 | 264.090 | 37.420 | 0.065 | |
| NARX | 24.351 | 4.440 | 19.713 | 3.019 | 0.976 | 293.897 | 44.912 | −0.013 | |
| informer | 24.492 | 3.951 | 15.614 | 2.865 | 0.978 | 260.734 | 40.393 | 0.099 | |
| Crossformer | 24.812 | 3.758 | 14.124 | 2.688 | 0.980 | 244.639 | 38.199 | 0.143 | |
| Multi-level attention | 24.082 | 3.727 | 13.889 | 2.198 | 0.980 | 196.012 | 18.979 | 0.150 | |
| Rainy | BiGRU | 13.953 | 3.746 | 14.031 | 2.644 | 0.959 | 232.934 | 41.589 | 0.042 |
| Transformer | 13.536 | 3.703 | 13.709 | 2.646 | 0.959 | 231.802 | 44.003 | 0.053 | |
| BiGRU–Global Attention | 14.923 | 2.843 | 8.082 | 2.049 | 0.976 | 185.543 | 43.276 | 0.273 | |
| CNN-LSTM | 14.471 | 3.469 | 12.032 | 2.461 | 0.965 | 223.913 | 47.399 | 0.113 | |
| NARX | 14.008 | 3.941 | 15.528 | 2.708 | 0.954 | 246.430 | 39.696 | −0.008 | |
| informer | 14.230 | 3.075 | 9.455 | 2.140 | 0.972 | 194.692 | 38.050 | 0.214 | |
| Crossformer | 14.403 | 2.822 | 7.965 | 1.974 | 0.977 | 179.616 | 35.327 | 0.278 | |
| Multi-level attention | 13.913 | 2.788 | 7.774 | 1.692 | 0.977 | 150.891 | 24.904 | 0.287 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Su, X.; Kim, C.; Cao, K.; Jung, H. A Parallel Prediction Model for Photovoltaic Power Using Multi-Level Attention and Similar Day Clustering. Energies 2024, 17, 3958. https://doi.org/10.3390/en17163958
Gao J, Su X, Kim C, Cao K, Jung H. A Parallel Prediction Model for Photovoltaic Power Using Multi-Level Attention and Similar Day Clustering. Energies. 2024; 17(16):3958. https://doi.org/10.3390/en17163958
Chicago/Turabian StyleGao, Jinming, Xianlong Su, Changsu Kim, Kerang Cao, and Hoekyung Jung. 2024. "A Parallel Prediction Model for Photovoltaic Power Using Multi-Level Attention and Similar Day Clustering" Energies 17, no. 16: 3958. https://doi.org/10.3390/en17163958
APA StyleGao, J., Su, X., Kim, C., Cao, K., & Jung, H. (2024). A Parallel Prediction Model for Photovoltaic Power Using Multi-Level Attention and Similar Day Clustering. Energies, 17(16), 3958. https://doi.org/10.3390/en17163958






