Optimal Design of an Interior Permanent Magnet Synchronous Motor for Electric Vehicle Applications Using a Machine Learning-Based Surrogate Model
Abstract
1. Introduction
2. Model of IPMSM with the Addition of Ferrite
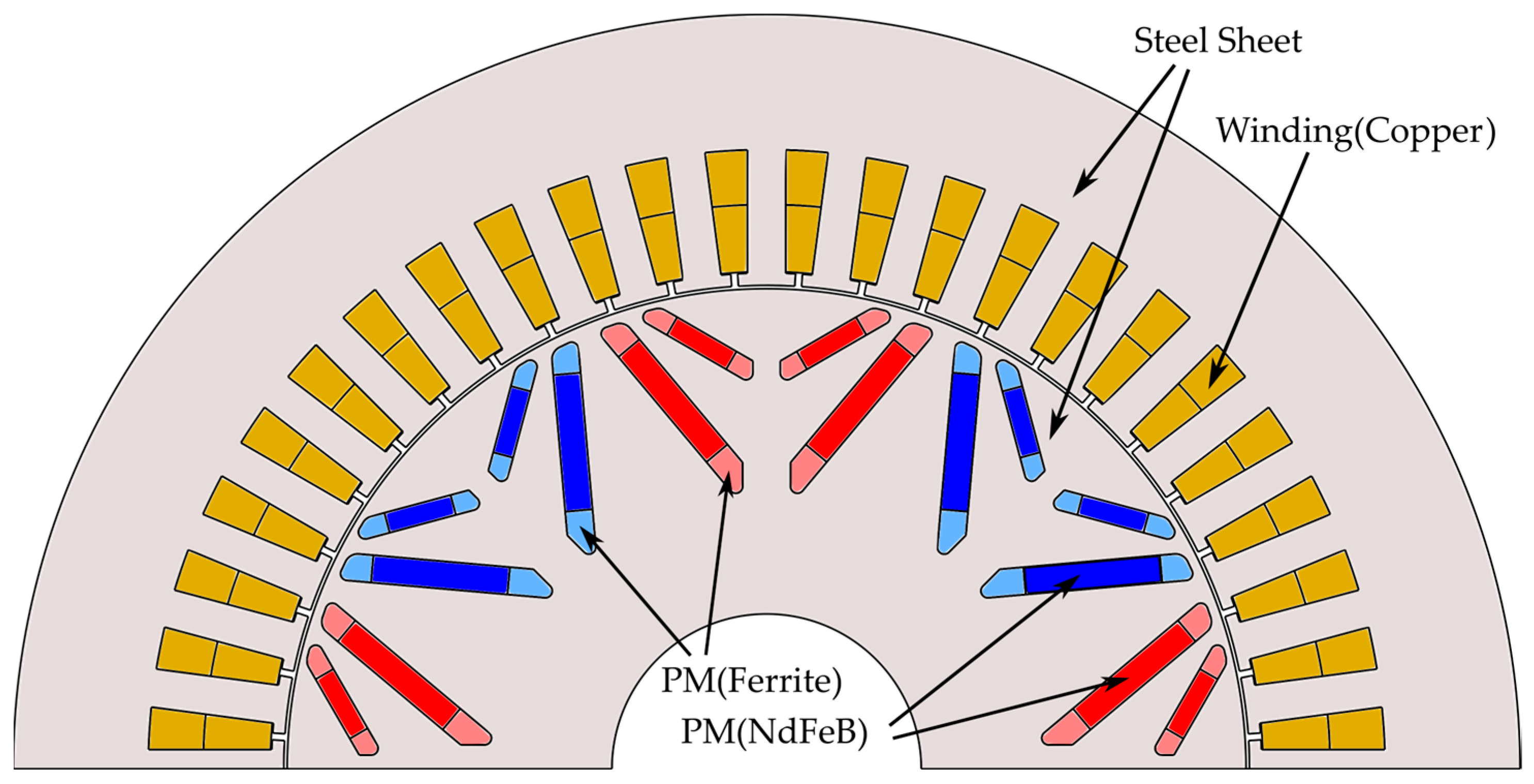
2.1. Motor Structure
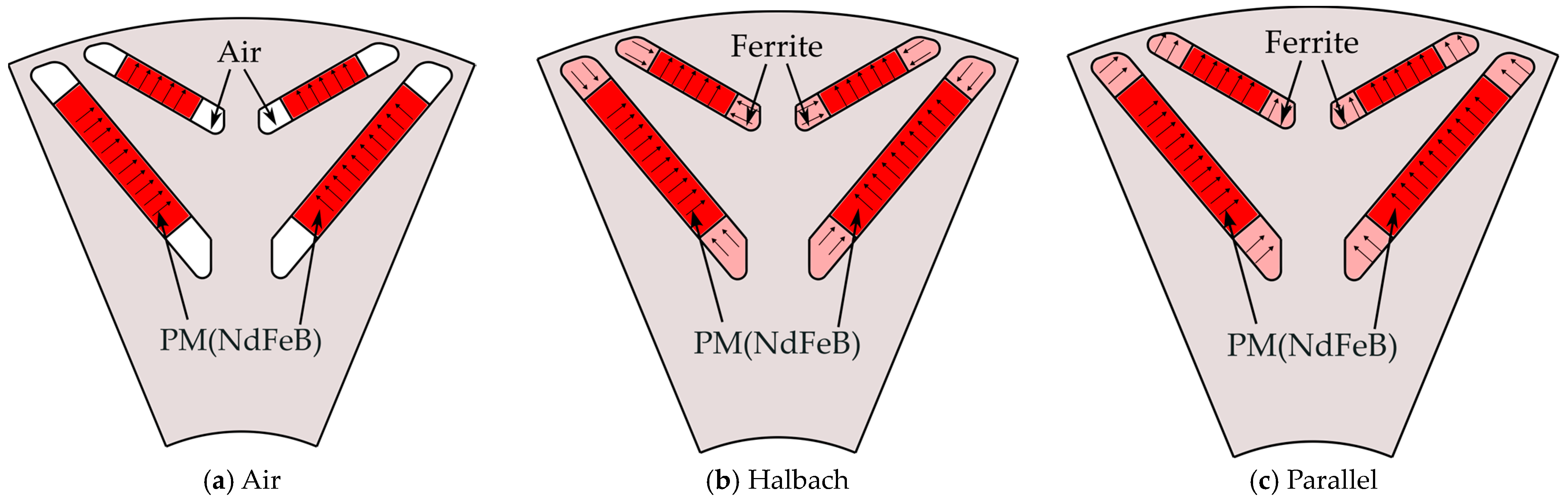
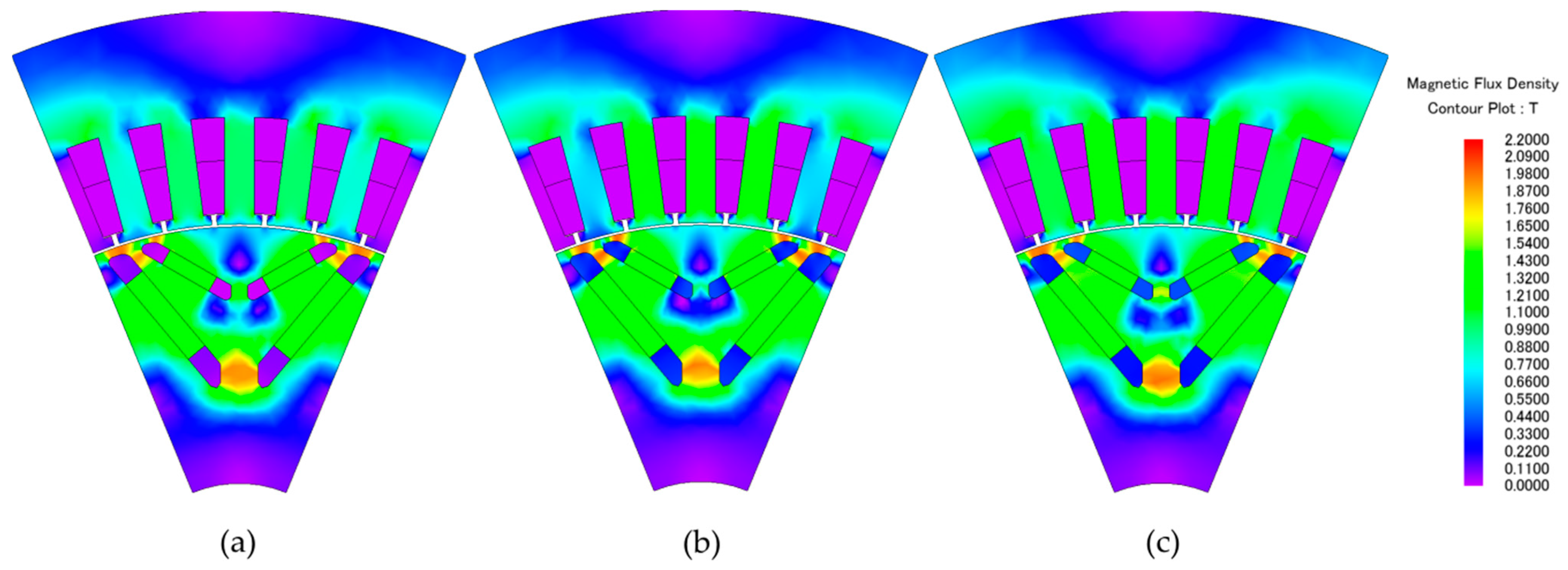
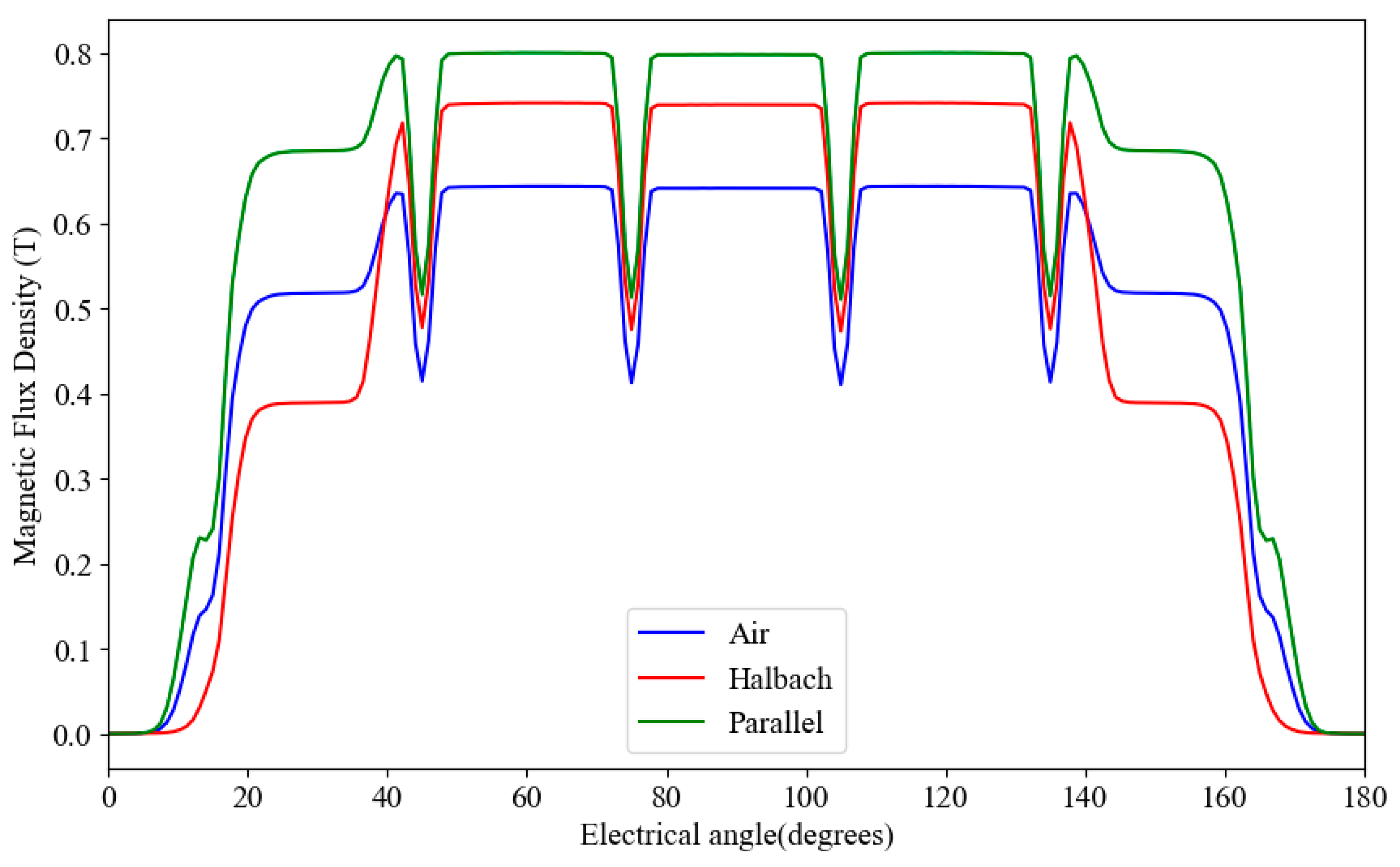
2.2. Structure Selection and Analysis
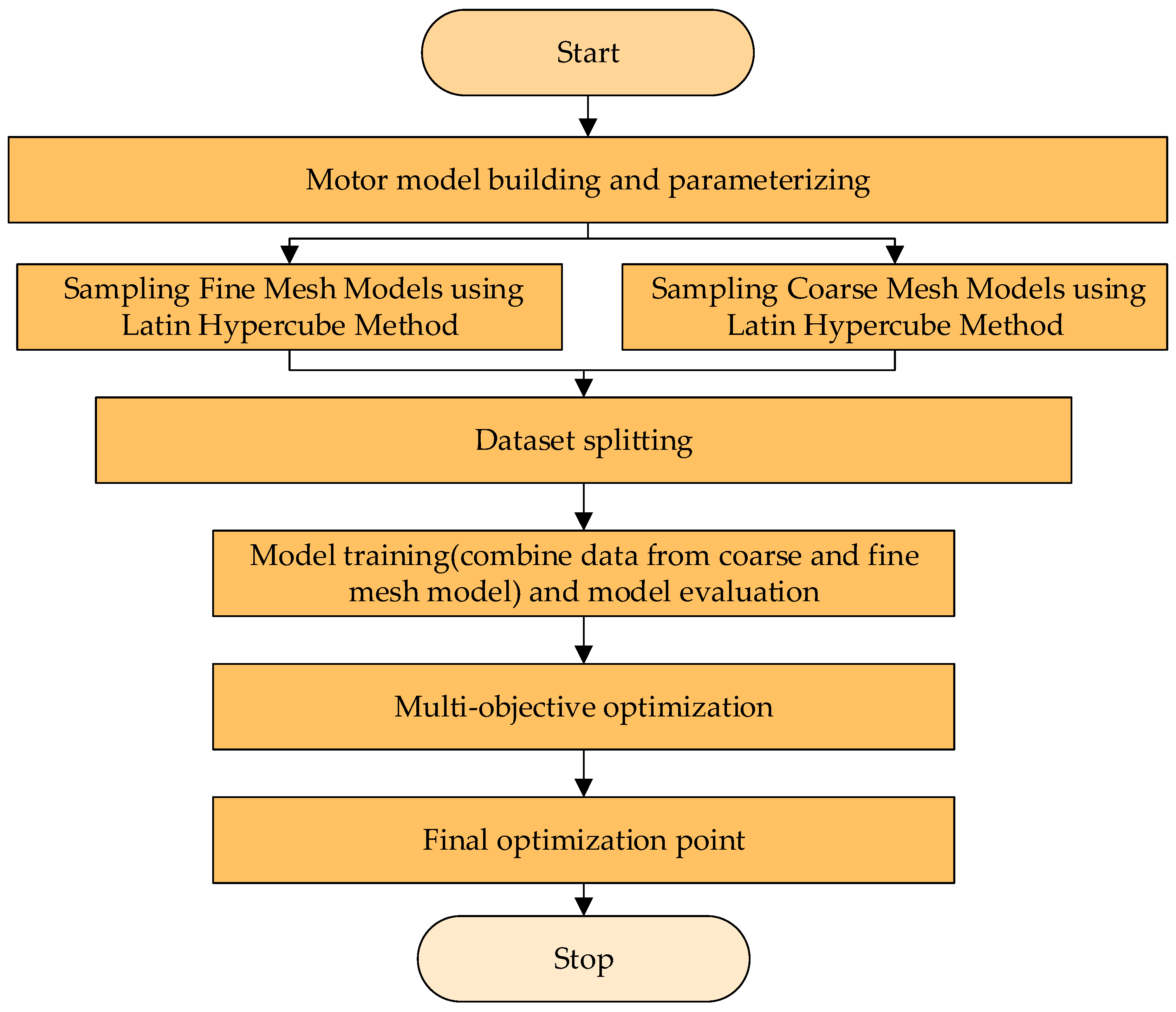
3. Methodology
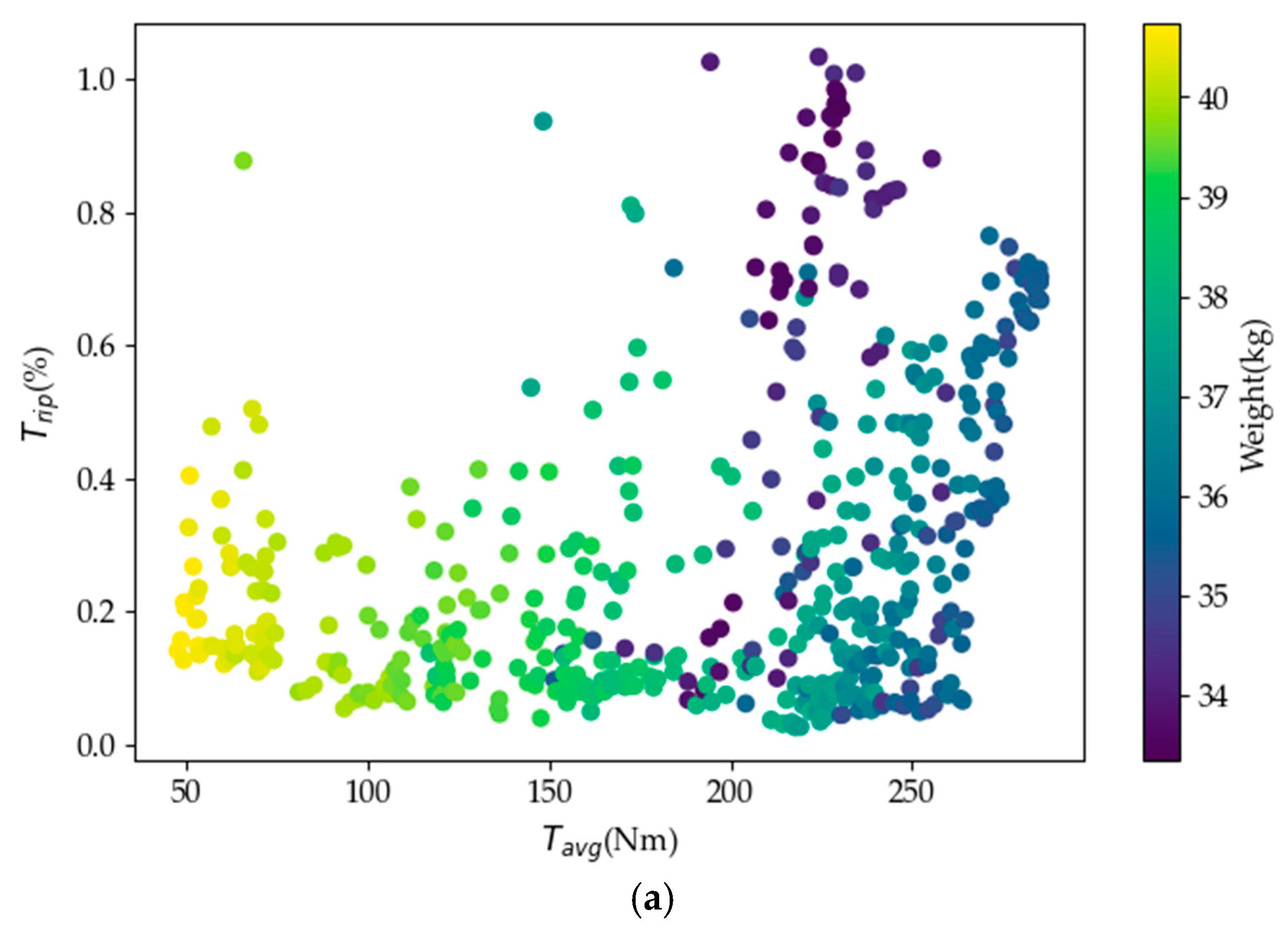
3.1. Model Design Variables and Optimal Objectives
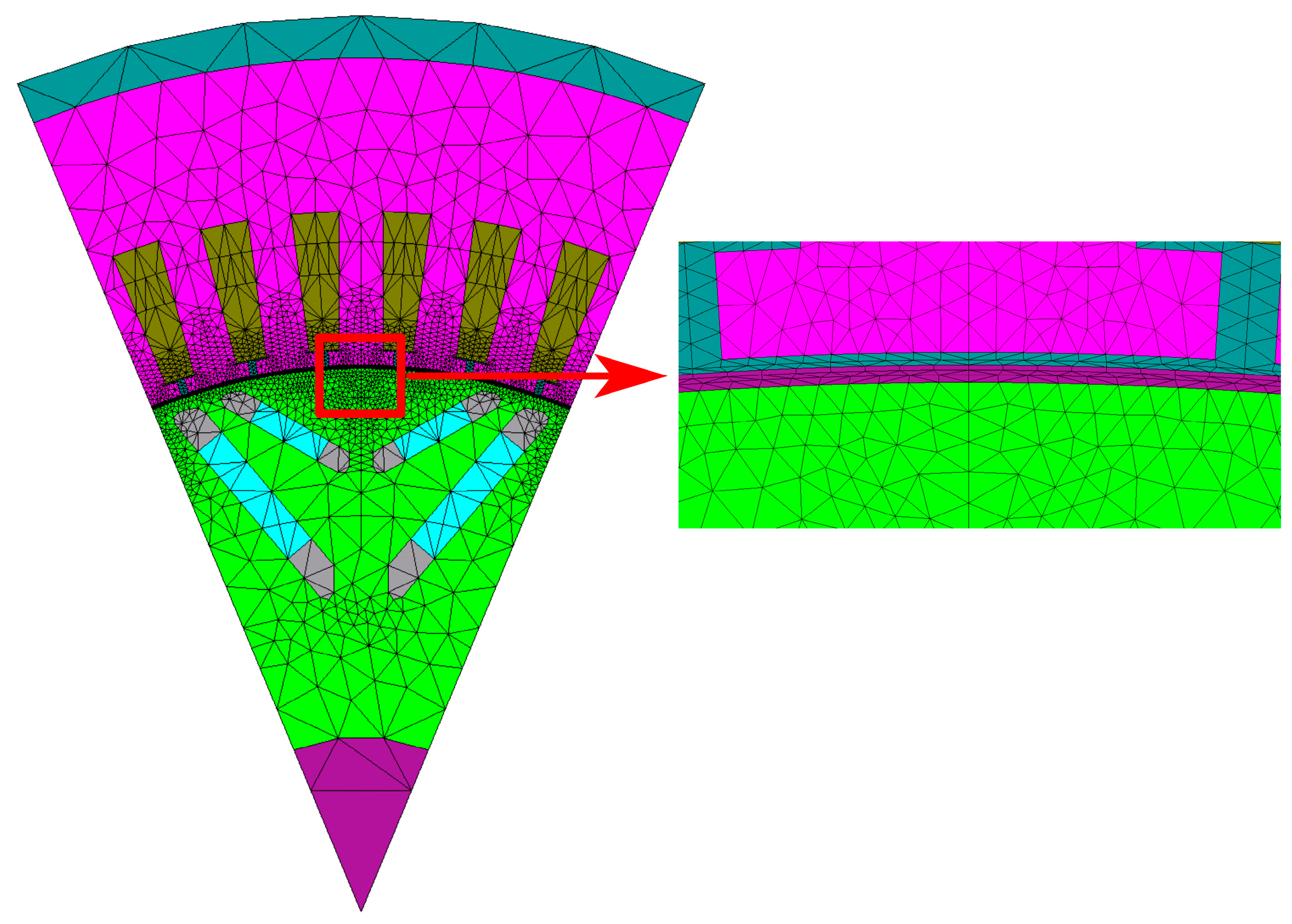
3.2. Sampling Method
3.3. Surrogate Model
3.3.1. Model Training Strategy
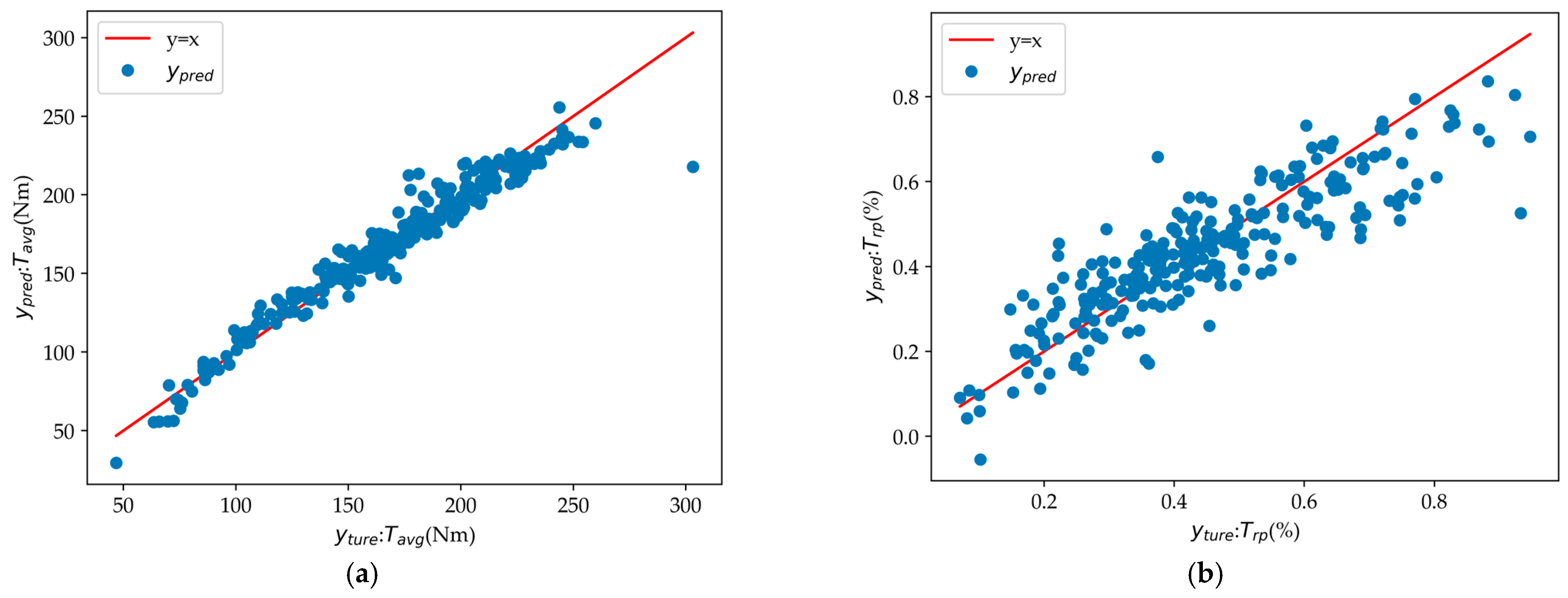
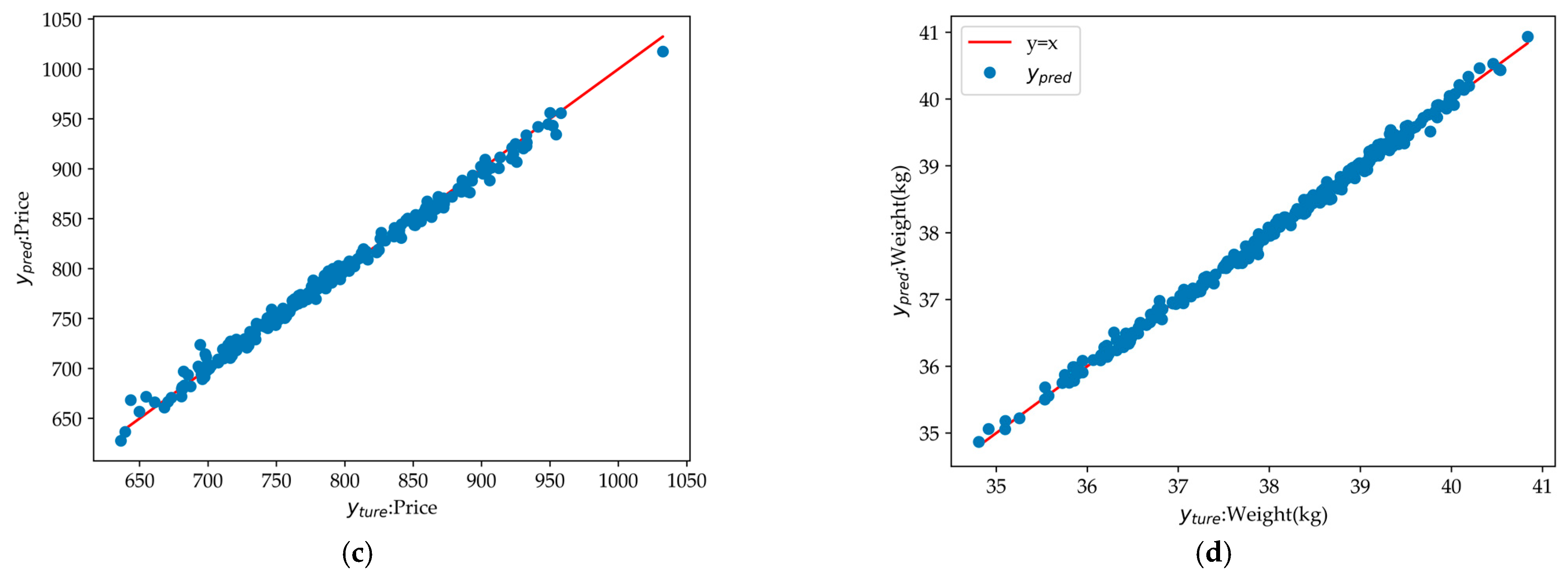
3.3.2. Discussion
3.3.3. Model Construction
3.3.4. Optimization
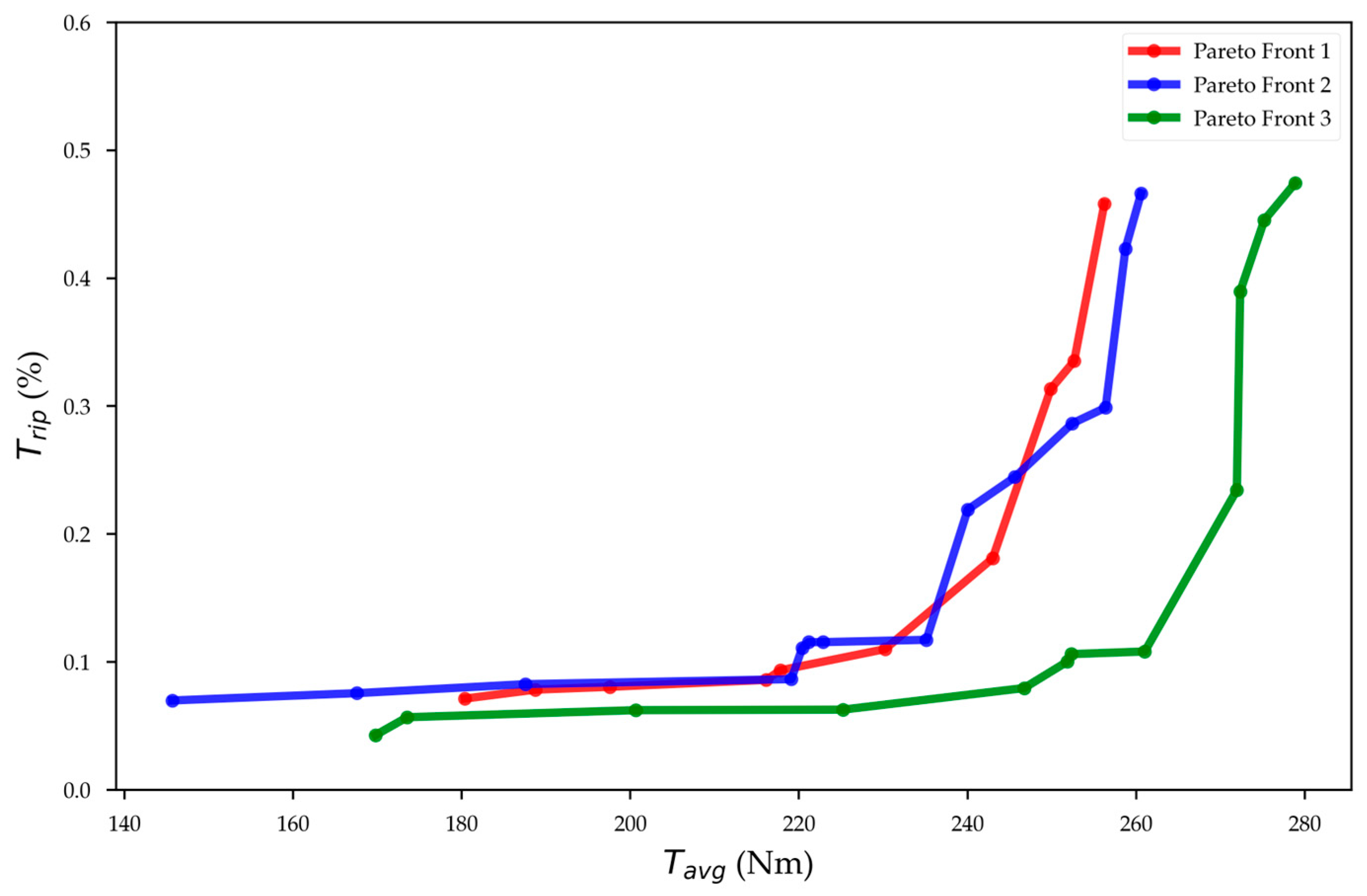
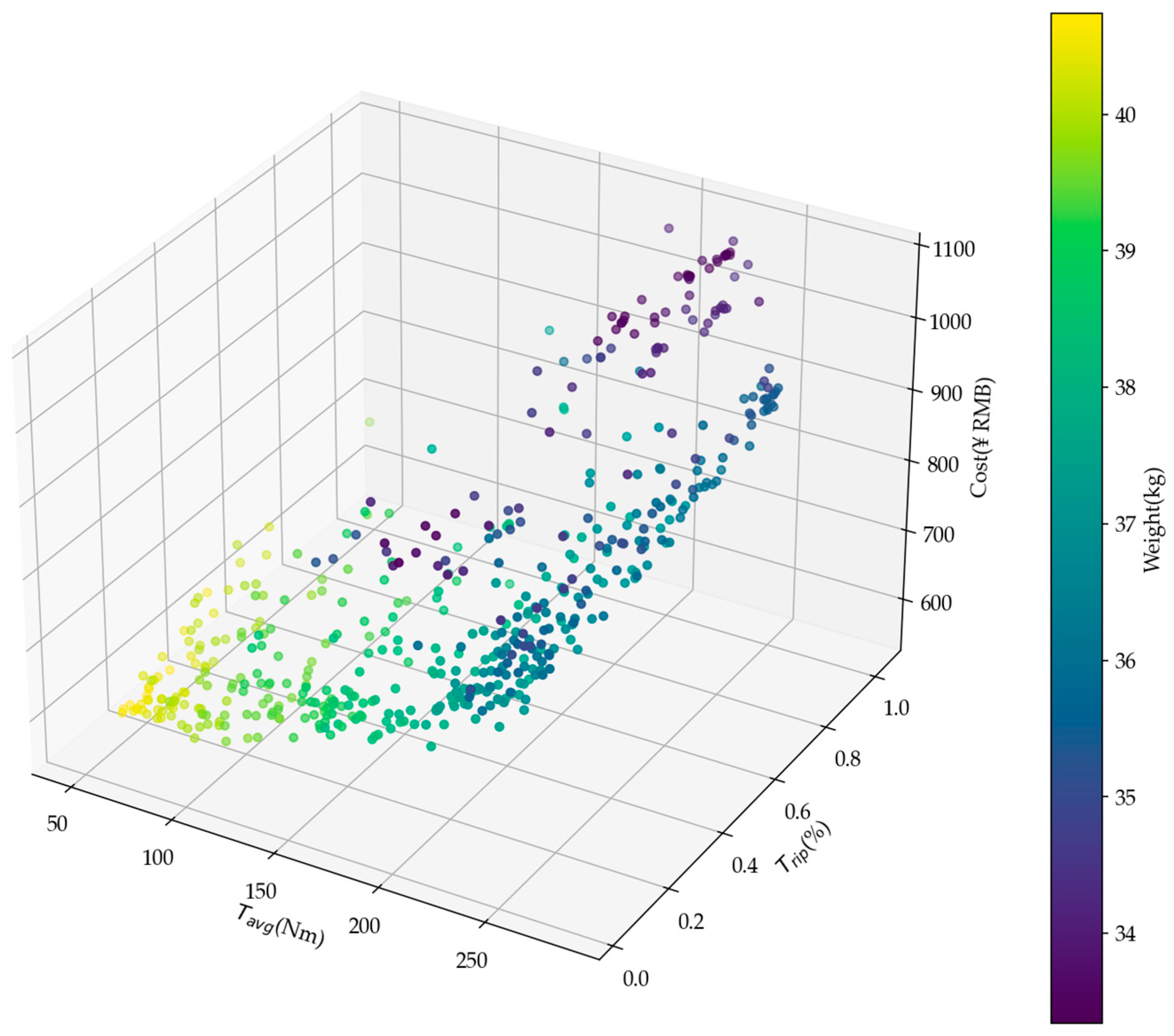
3.3.5. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kurian, A.G.; Thakur, S.K.; Kunde, S.; Sankpal, K.; Wagh, S. Challenges in Electric Vehicle NVH. In Proceedings of the 2021 IEEE Transportation Electrification Conference (ITEC-India), New Delhi, India, 16–19 December 2021. [Google Scholar]
- Hu, Y.; Wang, Z.; Li, X. Impact of policies on electric vehicle diffusion: An evolutionary game of small world network analysis. J. Clean. Prod. 2020, 265, 121703. [Google Scholar] [CrossRef]
- Kaarlela, T.; Villagrossi, E.; Rastegarpanah, A.; San-Miguel-Tello, A.; Pitkäaho, T. Robotised disassembly of electric vehicle batteries: A systematic literature review. J. Manuf. Syst. 2024, 74, 901–921. [Google Scholar] [CrossRef]
- Malozyomov, B.V.; Martyushev, N.V.; Kukartsev, V.A.; Kukartsev, V.V.; Tynchenko, S.V.; Klyuev, R.V.; Zagorodnii, N.A.; Tynchenko, Y.A. Study of Supercapacitors Built in the Start-Up System of the Main Diesel Locomotive. Energies 2023, 16, 3909. [Google Scholar] [CrossRef]
- Zhao, N.; Schofield, N. An Induction Machine Design With Parameter Optimization for a 120-kW Electric Vehicle. IEEE Trans. Transp. Electrif. 2020, 6, 592–601. [Google Scholar] [CrossRef]
- Dianati, B.; Kahourzade, S.; Mahmoudi, A. Optimization of Axial-Flux Induction Motors for the Application of Electric Vehicles Considering Driving Cycles. IEEE Trans. Energy Convers. 2020, 35, 1522–1533. [Google Scholar] [CrossRef]
- Guan, Y.; Zhu, Z.Q.; Afinowi, I.A.A.; Mipo, J.C.; Farah, P. Design of synchronous reluctance and permanent magnet synchronous reluctance machines for electric vehicle application. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 1853–1859. [Google Scholar]
- Credo, A.; Fabri, G.; Villani, M.; Popescu, M. Adopting the Topology Optimization in the Design of High-Speed Synchronous Reluctance Motors for Electric Vehicles. IEEE Trans. Ind. Appl. 2020, 56, 5429–5438. [Google Scholar] [CrossRef]
- Nardo, M.D.; Calzo, G.L.; Galea, M.; Gerada, C. Design Optimization of a High-Speed Synchronous Reluctance Machine. IEEE Trans. Ind. Appl. 2018, 54, 233–243. [Google Scholar] [CrossRef]
- Jeong, C.-L.; Kim, Y.-K.; Hur, J. Optimized Design of PMSM With Hybrid-Type Permanent Magnet for Improving Performance and Reliability. IEEE Trans. Ind. Appl. 2019, 55, 4692–4701. [Google Scholar] [CrossRef]
- Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Multi-Objective Design Optimization of an IPMSM Based on Multilevel Strategy. IEEE Trans. Ind. Electron. 2021, 68, 139–148. [Google Scholar] [CrossRef]
- Cho, S.-K.; Jung, K.-H.; Choi, J.-Y. Design Optimization of Interior Permanent Magnet Synchronous Motor for Electric Compressors of Air-Conditioning Systems Mounted on EVs and HEVs. IEEE Trans. Magn. 2018, 54, 8204705. [Google Scholar] [CrossRef]
- Jung, J.-W.; Lee, S.-H.; Lee, G.-H.; Hong, J.-P.; Lee, D.-H.; Kim, K.-N. Reduction Design of Vibration and Noise in IPMSM Type Integrated Starter and Generator for HEV. IEEE Trans. Magn. 2010, 46, 2454–2457. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, C.; Dong, Z.; Huang, R.; Li, X. Design and Optimization of a Magnetic-Geared Direct-Drive Machine With V-Shaped Permanent Magnets for Ship Propulsion. IEEE Trans. Transp. Electrif. 2022, 8, 1619–1633. [Google Scholar] [CrossRef]
- Li, X.; Wei, Z.; Zhao, Y.; Wang, X.; Hua, W. Design and Analysis of Surface-Mounted Permanent-Magnet Field-Modulation Machine for Achieving High Power Factor. IEEE Trans. Ind. Electron. 2024, 71, 4375–4386. [Google Scholar] [CrossRef]
- Zhu, X.; Wu, W.; Quan, L.; Xiang, Z.; Gu, W. Design and Multi-Objective Stratified Optimization of a Less-Rare-Earth Hybrid Permanent Magnets Motor With High Torque Density and Low Cost. IEEE Trans. Energy Convers. 2019, 34, 1178–1189. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, C.; Song, Z.; Wang, W. Exact Modeling and Multiobjective Optimization of Vernier Machines. IEEE Trans. Ind. Electron. 2021, 68, 11740–11751. [Google Scholar] [CrossRef]
- Liu, C.; Chau, K.T.; Lee, C.H.T.; Song, Z. A Critical Review of Advanced Electric Machines and Control Strategies for Electric Vehicles. Proc. IEEE 2021, 109, 1004–1028. [Google Scholar] [CrossRef]
- Hwang, C.C.; Cho, Y.H. Effects of leakage flux on magnetic fields of interior permanent magnet synchronous motors. IEEE Trans. Magn. 2001, 37, 3021–3024. [Google Scholar] [CrossRef]
- Cheng, M.; Zhao, X.; Dhimish, M.; Qiu, W.; Niu, S. A Review of Data-driven Surrogate Models for Design Optimization of Electric Motors. IEEE Trans. Transp. Electrif. 2024. [Google Scholar] [CrossRef]
- Ren, Z.; Ma, J.; Qi, Y.; Zhang, D.; Koh, C.S. Managing Uncertainties of Permanent Magnet Synchronous Machine by Adaptive Kriging Assisted Weight Index Monte Carlo Simulation Method. IEEE Trans. Energy Convers. 2020, 35, 2162–2169. [Google Scholar] [CrossRef]
- Zhang, Z.; Rao, S.; Zhang, X. Performance Prediction of Switched Reluctance Motor Using Improved Generalized Regression Neural Networks for Design Optimization. CES Trans. Electr. Mach. Syst. 2018, 2, 371–376. [Google Scholar] [CrossRef]
- Dhulipati, H.; Ghosh, E.; Mukundan, S.; Korta, P.; Tjong, J.; Kar, N.C. Advanced Design Optimization Technique for Torque Profile Improvement in Six-Phase PMSM Using Supervised Machine Learning for Direct-Drive EV. IEEE Trans. Energy Convers. 2019, 34, 2041–2051. [Google Scholar] [CrossRef]
- Raia, M.R.; Ruba, M.; Nemes, R.O.; Martis, C. Artificial Neural Network and Data Dimensionality Reduction Based on Machine Learning Methods for PMSM Model Order Reduction. IEEE Access 2021, 9, 102345–102354. [Google Scholar] [CrossRef]
- Demir, U.; Akgun, G.; Akuner, M.C.; Pourkarimi, M.; Akgun, O.; Akinci, T.C. An Innovative Approach to Electrical Motor Geometry Generation Using Machine Learning and Image Processing Techniques. IEEE Access 2023, 11, 48651–48666. [Google Scholar] [CrossRef]
- Dlala, E. Hybrid Rotor Assembly. US20200412190A1, 31 December 2020. [Google Scholar]
- Liu, K.; Yin, M.; Hua, W.; Ma, Z.; Lin, M.; Kong, Y. Design and Analysis of Halbach Ironless Flywheel BLDC Motor/Generators. IEEE Trans. Magn. 2018, 54, 8109305. [Google Scholar] [CrossRef]
- Wang, X.; Wu, L.; Zhou, S.; Hu, C.; Zhao, M. Optimization Design of In-wheel Motor Based on Halbach (Ce,Nd)FeB Magnet. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–4. [Google Scholar]
- Yu, J.; Liu, C.; Liu, S.; Zhao, H. Comparative Study of Double-Stator Interior-PM Vernier Machines Based on Electromagnetic-Structural Coupling Analysis. IEEE Trans. Ind. Electron. 2021, 68, 10510–10520. [Google Scholar] [CrossRef]
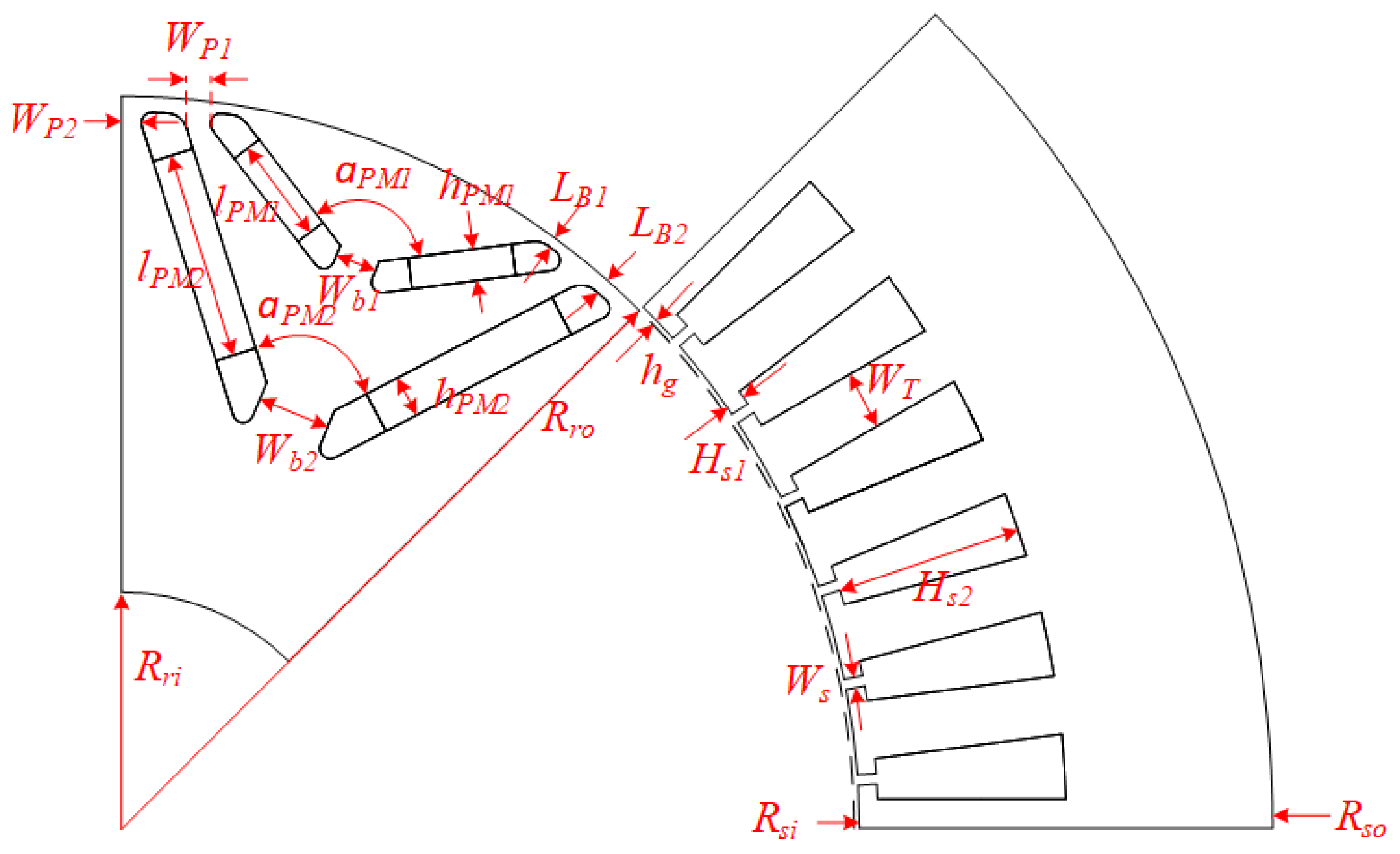
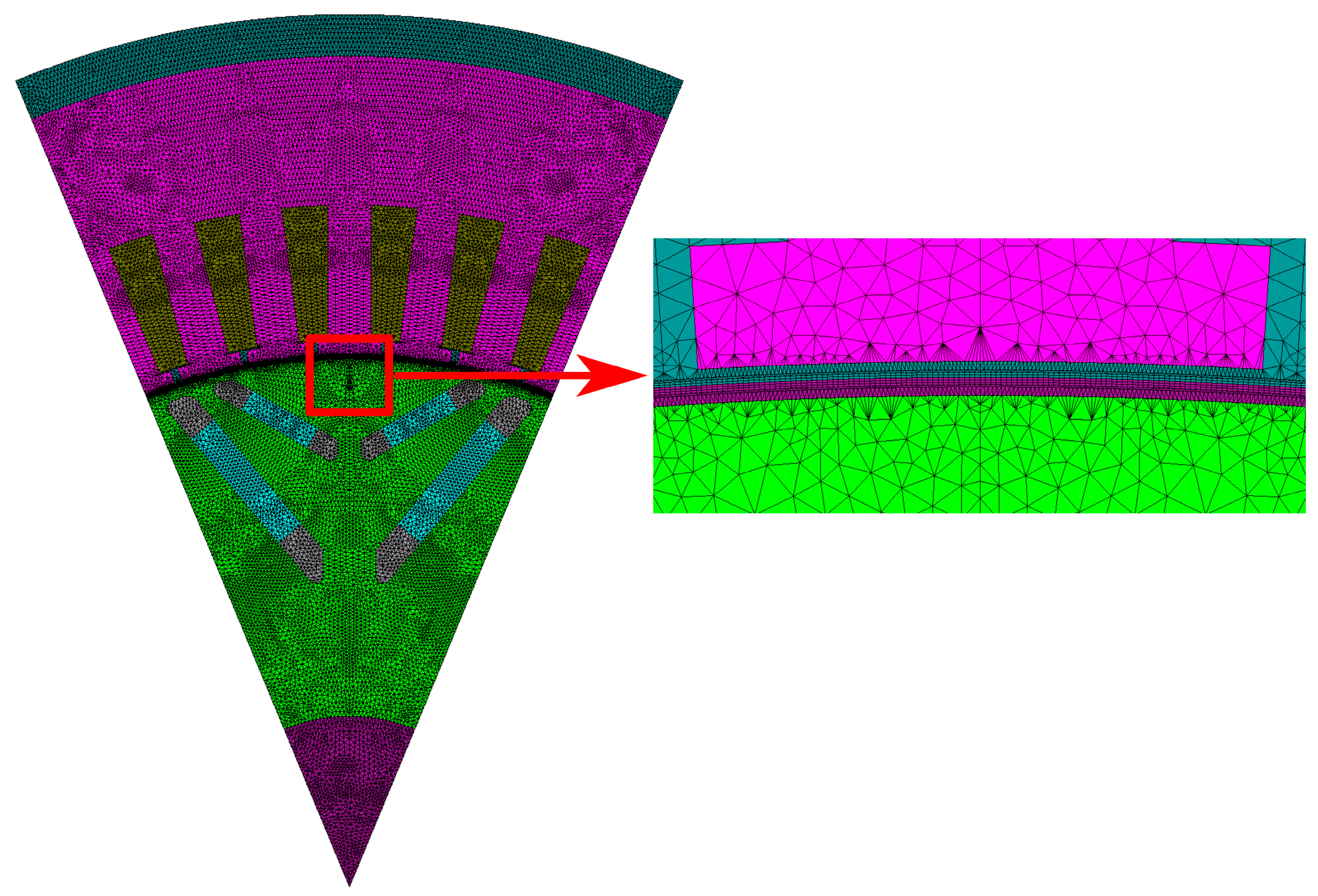
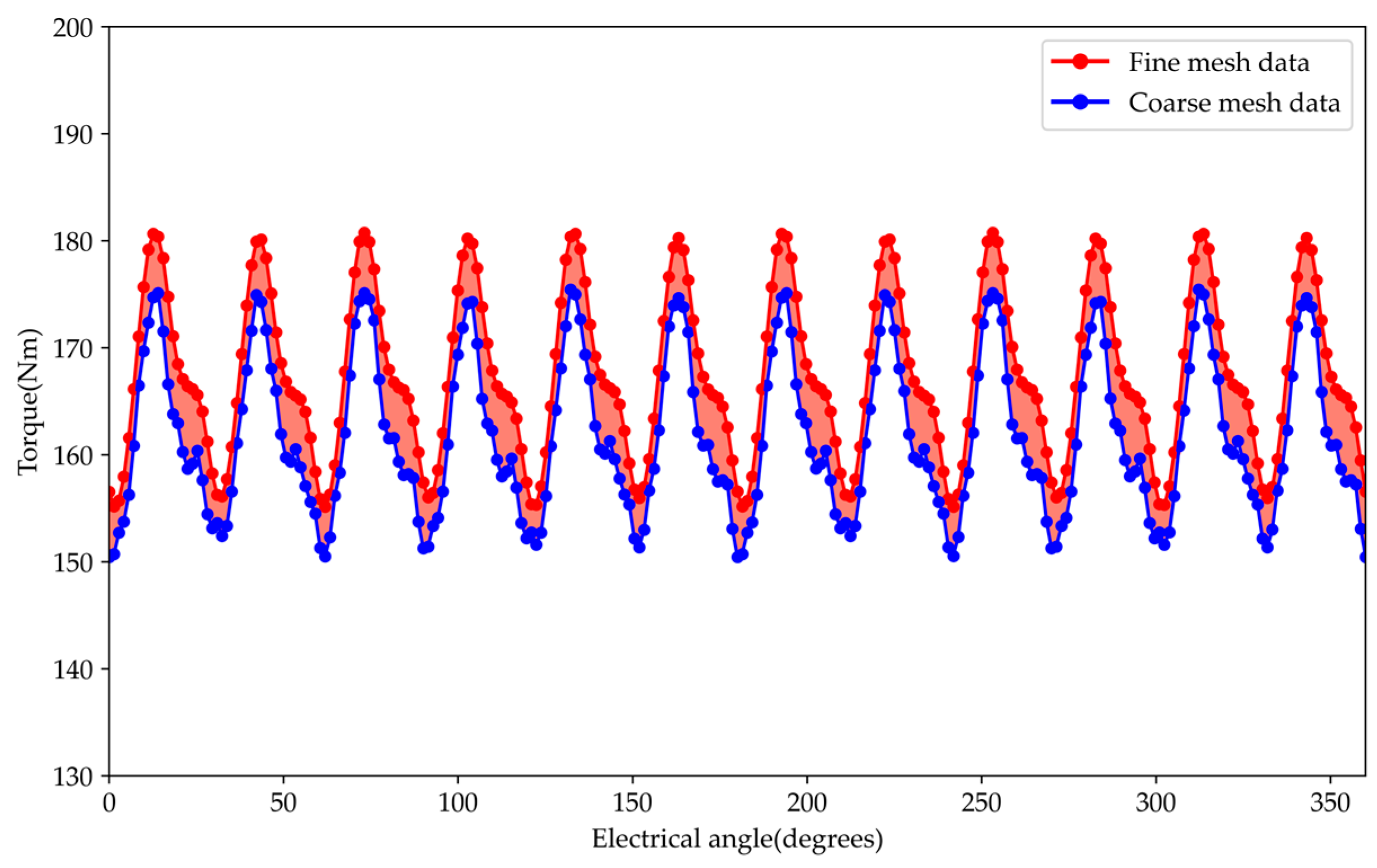


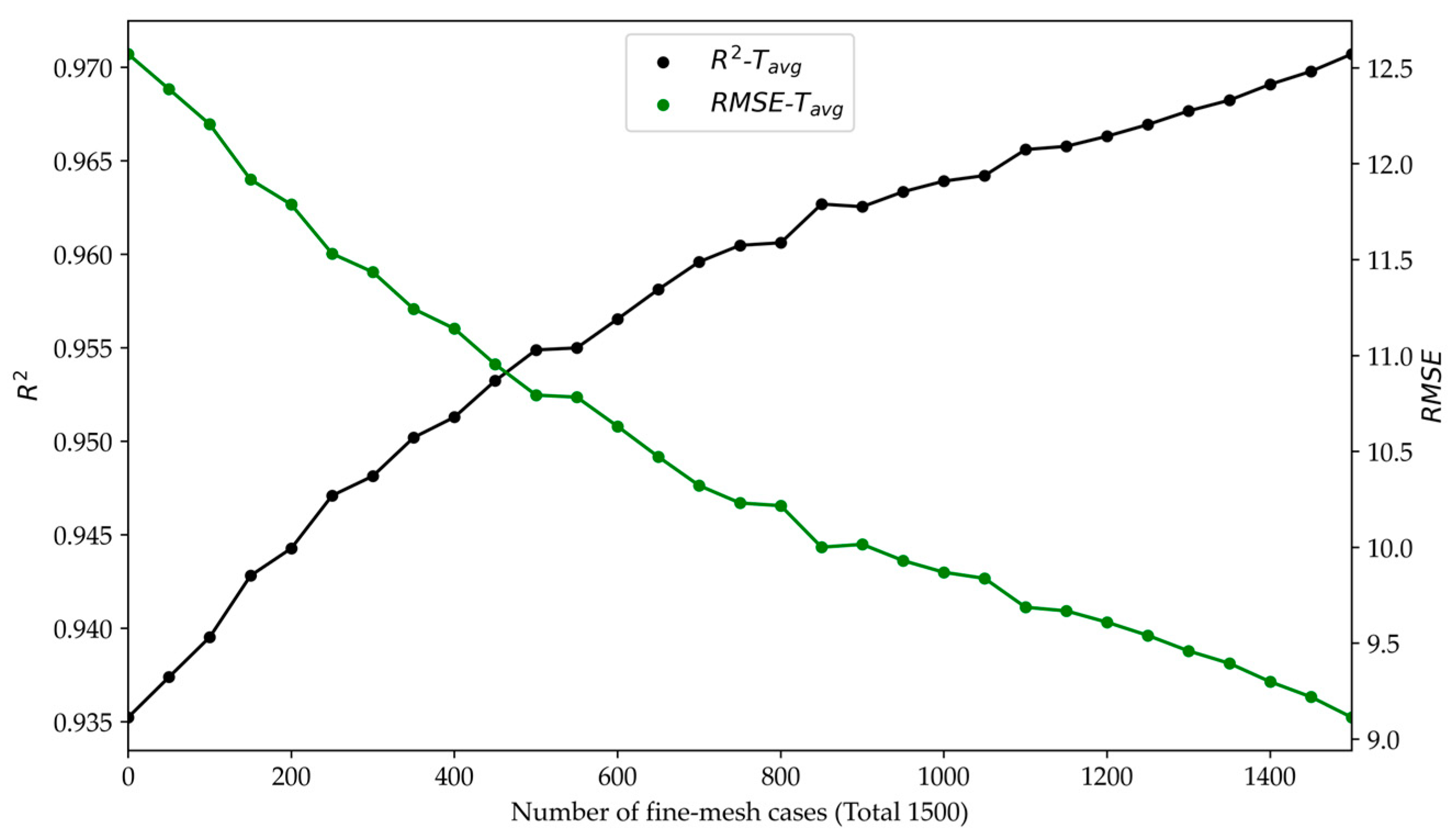
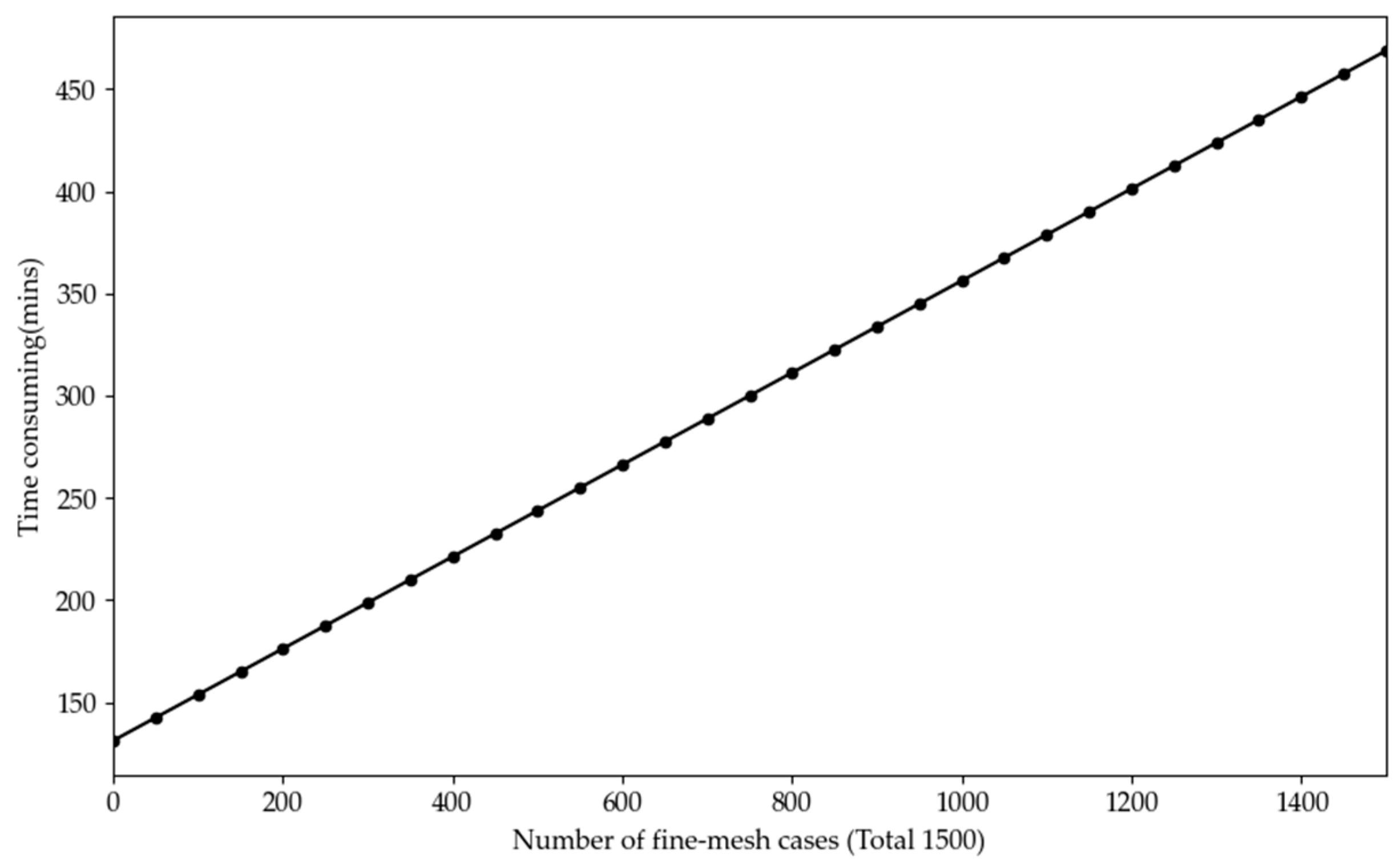

| Design Parameters | Unit | Description | Range/Value |
|---|---|---|---|
| Rri | mm | Rotor inner radius | 23 |
| Rro | mm | Rotor outer radius | 70 |
| Rsi | mm | Stator inner radius | 70.5 |
| Rso | mm | Stator outer radius | 110 |
| hg | mm | Air gap length | 0.5 |
| WT | mm | Tooth width | 2–8 |
| Ws | mm | Slot opening width | 1–4 |
| Hs1 | mm | Slot opening depth | 0–5 |
| Hs2 | mm | Slot depth | 15–25 |
| lPM1 | mm | PM1 length | 8–10 |
| lPM2 | mm | PM2 length | 15–18 |
| hPM1 | mm | PM1 height | 3–5 |
| hPM2 | mm | PM2 height | 3–5 |
| LB1 | mm | Bridge length | 1–2 |
| LB2 | mm | Bridge length | 1–2 |
| WP1 | mm | PM Web width | 1–2 |
| WP2 | mm | PM Web width | 1–2.5 |
| Wb1 | mm | Magnet post width | 2–3 |
| Wb2 | mm | Magnet post width | 3–7 |
| αPM1 | deg | PM1 V shape angle | 110–135 |
| αPM2 | deg | PM2 V shape angle | 70–110 |
| Material | Density (kg/m3) | Cost (RMB/kg) |
|---|---|---|
| N50-NdFeb | 7500 | 229.460 |
| Steel-50CS1000 | 7850 | 5.050 |
| Copper | 8960 | 70.700 |
| Ferrite | 5000 | 3.715 |
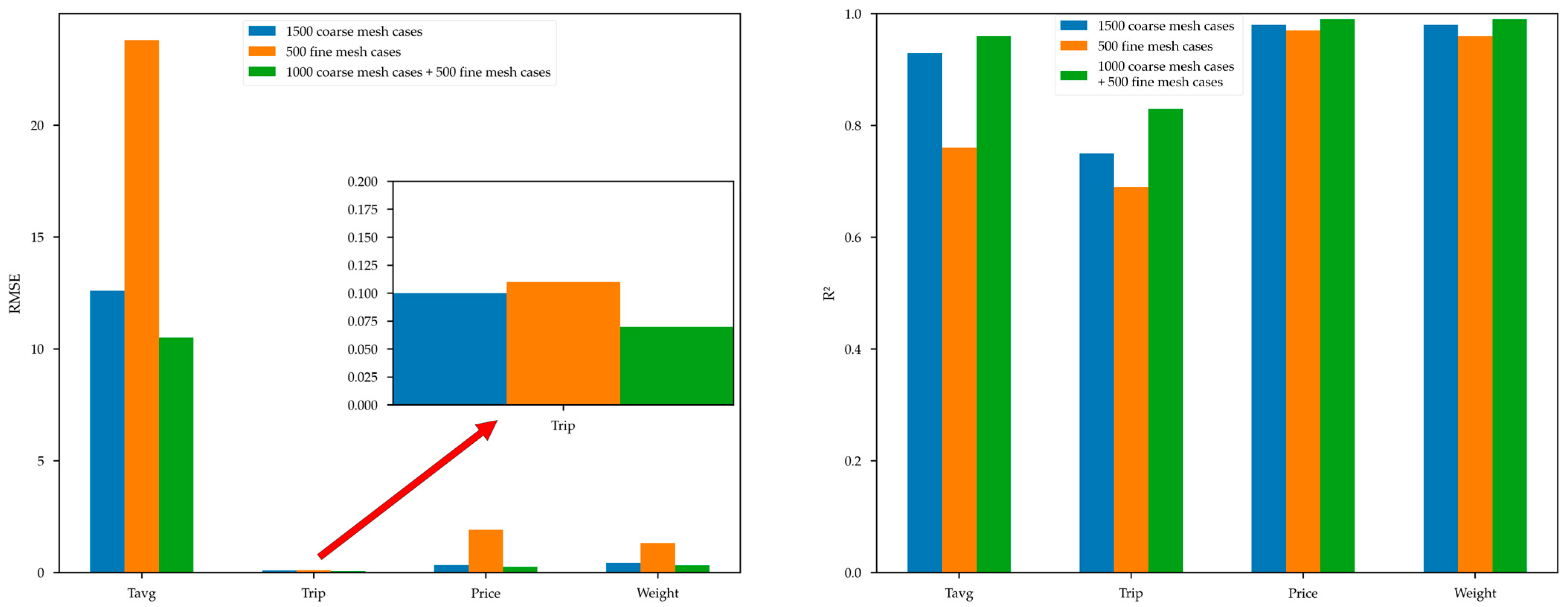
| Group | f(x) | RMSE | R2 |
|---|---|---|---|
| 1500 coarse mesh cases | Tavg | 12.6 | 0.93 |
| Trip | 0.10 | 0.75 | |
| Cost | 0.33 | 0.98 | |
| Weight | 0.43 | 0.98 | |
| 500 fine mesh cases | Tavg | 23.8 | 0.76 |
| Trip | 0.11 | 0.69 | |
| Cost | 1.92 | 0.97 | |
| Weight | 1.32 | 0.96 | |
| 1000 coarse mesh cases + 500 fine mesh cases | Tavg | 10.5 | 0.96 |
| Trip | 0.07 | 0.83 | |
| Cost | 0.26 | 0.99 | |
| Weight | 0.32 | 0.99 |
| Parameters | Initial Design | Final Optimized by FEA Method | Final Optimized by Surrogate Method | Finite Element Verification Calculation | Unit | |
|---|---|---|---|---|---|---|
| Design variables | WT | 5.6 | 3.69 | 3.06 | 3.06 | mm |
| Ws | 1 | 1.73 | 1.33 | 1.33 | mm | |
| Hs1 | 1.8 | 1.84 | 3.39 | 3.39 | mm | |
| Hs2 | 18 | 24.92 | 17.84 | 17.84 | mm | |
| lPM1 | 10 | 9.92 | 9.94 | 9.94 | mm | |
| lPM2 | 20 | 15.32 | 17.36 | 17.36 | mm | |
| hPM1 | 3 | 3.41 | 3.87 | 3.87 | mm | |
| hPM2 | 4 | 4.11 | 4.26 | 4.26 | mm | |
| LB1 | 1 | 1.35 | 1.13 | 1.13 | mm | |
| LB2 | 1.5 | 1.67 | 1.82 | 1.82 | mm | |
| WP1 | 1.5 | 1.08 | 1.66 | 1.66 | mm | |
| WP2 | 1.5 | 1.24 | 1.73 | 1.73 | mm | |
| Wb1 | 3 | 2.12 | 2.46 | 2.46 | mm | |
| Wb2 | 7 | 5.62 | 3.66 | 3.66 | mm | |
| αPM1 | 120 | 121.22 | 129.41 | 129.41 | deg | |
| αPM2 | 80 | 77.81 | 101.47 | 101.47 | deg | |
| Objectives | Tage | 169.49 | 271.25(↑1 60.03%) | 270.52(↑59.61%) | 271.13 | Nm |
| Trip | 17.16 | 10.36(↓2 39.62%) | 9.23(↓46.21%) | 9.08 | % | |
| Cost | 793.64 | 772.12(↓2.71%) | 782.34(↓1.42%) | 782.50 | RMB | |
| Weight | 39.14 | 36.73(↓6.15%) | 35.99(↓7.99%) | 36.12 | kg |
| Optimization Strategy | CPU Type | Time Spent for Step | Total Time Consumed |
|---|---|---|---|
| Proposed method | Intel core i9-13980hx (Intel, Santa Clara, CA, USA) @2400 MHz 24 Cores with 32 Processors | 1. Case evaluation by FEA 1000 + 500 = 1500 cases (4 h) 2. Model construction and fitting (10 min) 3. Using NSGA-II solve MOOP and find the Pareto frontier, 10,000 cases (10 min) | 4.2 h |
| FEA-based optimization | Direct global optimization by NSGA-II, 5000 cases | 70 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Su, X.; Zhao, H. Optimal Design of an Interior Permanent Magnet Synchronous Motor for Electric Vehicle Applications Using a Machine Learning-Based Surrogate Model. Energies 2024, 17, 3864. https://doi.org/10.3390/en17163864
Guo S, Su X, Zhao H. Optimal Design of an Interior Permanent Magnet Synchronous Motor for Electric Vehicle Applications Using a Machine Learning-Based Surrogate Model. Energies. 2024; 17(16):3864. https://doi.org/10.3390/en17163864
Chicago/Turabian StyleGuo, Song, Xiangdong Su, and Hang Zhao. 2024. "Optimal Design of an Interior Permanent Magnet Synchronous Motor for Electric Vehicle Applications Using a Machine Learning-Based Surrogate Model" Energies 17, no. 16: 3864. https://doi.org/10.3390/en17163864
APA StyleGuo, S., Su, X., & Zhao, H. (2024). Optimal Design of an Interior Permanent Magnet Synchronous Motor for Electric Vehicle Applications Using a Machine Learning-Based Surrogate Model. Energies, 17(16), 3864. https://doi.org/10.3390/en17163864







