Discovering the Properties of a Problem of Scheduling Battery Charging Jobs to Minimize the Total Time with the Use of Harmonic Numbers

Abstract

In this work, we consider a problem from the field of power-aware scheduling in which a fleet of electric vehicles have to be charged in a minimum time. Each vehicle is equipped with a lithium-ion battery of a given capacity. The initial power used for charging each battery is known, whereas it is assumed that the power drops to zero at the moment when the battery gets fully loaded. The power usage function is linear and decreasing. The charging jobs are nonpreemptable and independent, whereas the total available amount of power is limited. The objective is to minimize the schedule length. In this paper, we analyze the case of a problem with identical jobs that already cover a wide variety of practical situations. By employing inverses of natural numbers, similar to harmonic series, we prove two properties of this case, and we also discuss the phenomenon of the stabilization of the difference between the start times of two successive jobs in a schedule. We also take under examination a few special cases of the problem. Some conclusions and directions for future research are given.

1. Introduction

Harmonic numbers are a mathematical concept that arise from the harmonic series, which is the sum of the inverses of the successive positive integers (i.e., natural numbers). Harmonic numbers represent the partial sums of this series, denoted by $H_n$, where $n$ is a positive integer. As $n$ grows larger, $H_n$ approaches the natural logarithm of $n$, making them useful in approximating certain logarithmic functions.

Harmonic numbers find applications in various areas of mathematics and beyond. They often serve as a fundamental tool in various scientific disciplines, aiding in the analysis, modeling, and understanding of diverse phenomena. In number theory, they are used in the analysis of the distribution of prime numbers and in understanding properties of certain number sequences. Harmonic numbers appear in combinatorial problems, such as analyzing the expected number of trials needed until a specific event occurs in probabilistic scenarios. They have applications in financial mathematics, particularly in the calculation of certain types of averages and in understanding the behavior of interest rates over time. They are also encountered in physics when dealing with problems involving oscillatory phenomena, such as in the analysis of vibrations and waveforms. In music theory, harmonic numbers play a crucial role in understanding the structure and relationships between musical intervals and frequencies. They provide a theoretical framework for understanding the fundamental principles of sound production, harmony, and timbre in music. They are essential for composers, musicians, and audio engineers in creating and analyzing musical compositions and performances. In computer science, harmonic numbers are relevant in the design and analysis of algorithms for optimization problems, particularly in approximation algorithms and the analysis of algorithms with random components. In algorithm analysis, they help in determining the time complexity of algorithms, particularly in cases involving nested loops or recursive functions.

In this paper, we will show how employing inverses of successive natural numbers, similar to those appearing in the harmonic series, can help in analysis and discovering the properties of a scheduling problem. We consider a problem of scheduling jobs of charging batteries of electric vehicles. The jobs are nonpreemptable and independent, and all are available at the start of the process. Each job requires some amount of power and consumes a certain amount of energy during its processing. We also assume that the power usage of each job linearly decreases with time, which is the case when Li-ion batteries are being charged. The initial power usage and the capacity of each battery are known in advance, whereas the total available amount of power is limited and also known. The objective is to minimize the total time of charging the entire fleet of vehicles. For this research, we assume that the jobs are identical, i.e., their capacities and initial power usages are equal.

Notice that this simple case is already quite practical and covers a great variety of real-life applications. These are situations where, e.g., a municipal communication company charges its transport vehicles at night, which are usually identical or very similar. Another example may concern a parcel company having a fleet of identical delivery vans. The vans run all day long with parcels, and during the night, their batteries have to be charged. In both cases, the company has a charging terminal to its disposal with a limited power delivery. Situations of this kind are also typical for other companies using a fleet of identical or quite similar electric vehicles, not only buses or vans but also cars, bikes, taxis, drones, etc. The company wants to charge its vehicles within a minimum time so that they are ready to go for the next day.

The considered problem can be placed in the field of so-called power-aware scheduling. Problems from this field concerning scheduling of jobs of charging batteries of electric vehicles have been studied in a huge number of papers up to now. For comprehensive surveys of models, approaches, applications, solutions, challenges, and future trends, we refer the reader to review papers, e.g., [1,2,3]. A most recent, highly extensive, and structured survey on electric vehicle scheduling is given in [4]. In the paper, the collected studies are grouped on the basis of their main features. Operational research aspects and problem-specific properties are discussed in detail, and representative mathematical model formulations are also presented. A variety of future research opportunities are also included.

The novelty of this paper consists of the fact that we identify cases of problems of scheduling battery charging jobs having such an advantage that they can be solved analytically. Although we consider identical jobs at this stage of the research, the presented methodology, however, may be applied to more complex models of practical situations where, e.g., before the final scheduling process, all charging jobs are grouped into subsets of identical jobs. If we treat each of such subset as single jobs of the length defined analytically, it may lead to much more effective approaches to finding solutions of the entire problem by using some heuristic algorithms. Considering such more general cases and designing heuristic methods for solving them will be a direction for further research.

The paper is organized as follows. In Section 2, we define harmonic numbers and give a sketch of their applications in the field of computer science. The considered scheduling problem is mathematically formulated in Section 3. In Section 4, we formulate and prove a property of the case of a problem with identical jobs in which harmonic numbers appear, and we also discuss the issue of the stabilization of the difference between the start time of two consecutive jobs in a schedule. The main results of this research are presented in Section 5. First, we present a proposition concerning the case of a problem with at most two jobs processed simultaneously, and we then analyze a few special cases of a problem in which harmonic numbers are involved. Section 6 contains conclusions and some directions for future research.

2. Harmonic Numbers

2.1. Definition

As is commonly known, in mathematics, the $n$-th harmonic number $H_n$ is defined as the sum of the inverses of the first $n$ natural numbers, according to the following formula [5]:

$$H_n=1+{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{4}}+\dots +{\displaystyle \frac{1}{n}}={\displaystyle \sum }_{k=1}^n{\displaystyle \frac{1}{k}}$$

(1)

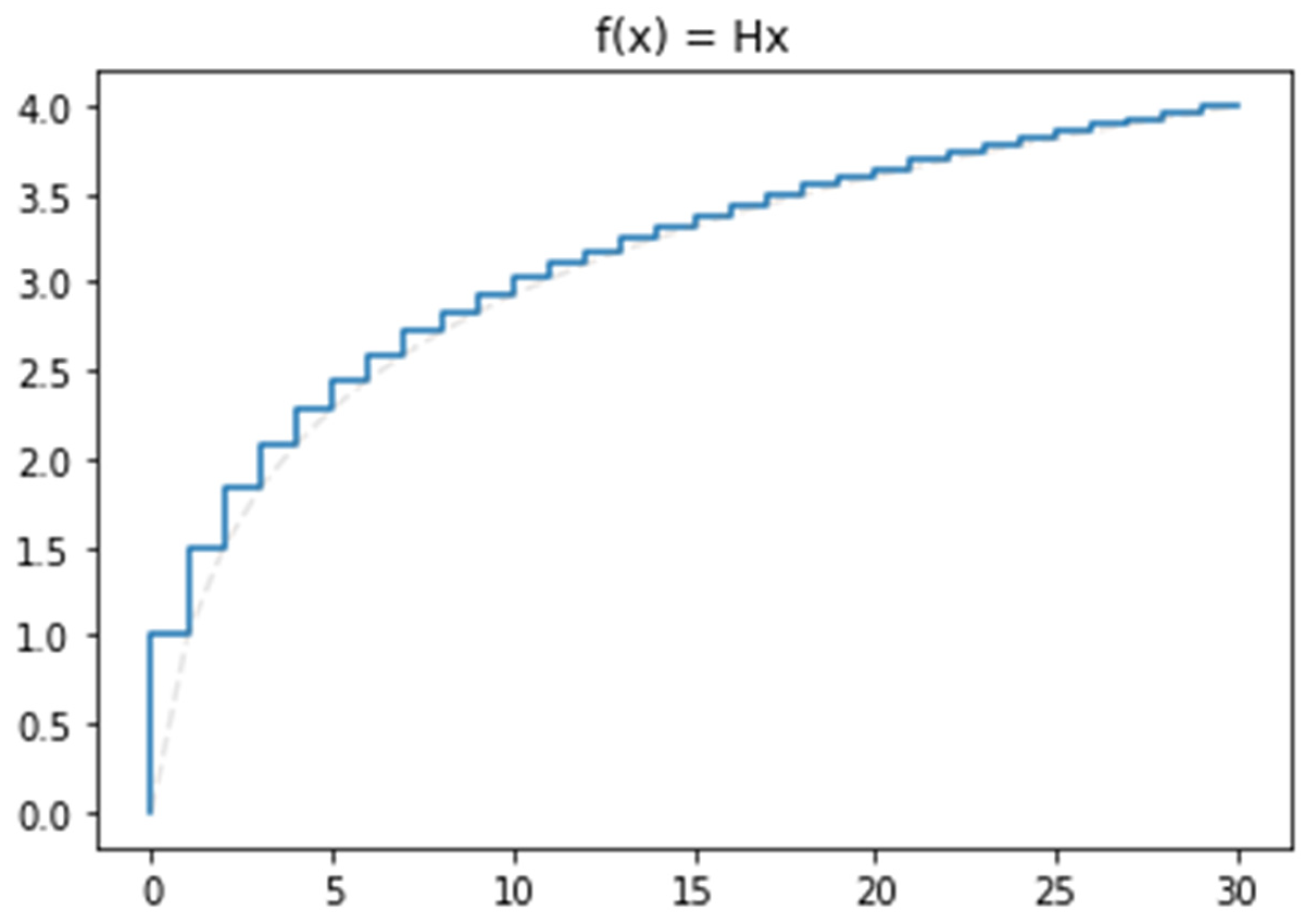
The harmonic series is an infinite series formed by harmonic numbers. It is an ascending, divergent series, as shown in Figure 1.

The harmonic numbers roughly approximate the natural logarithm function, as given by the Euler–Maclaurin formula:

$$H_n=\ln n+\gamma +{\displaystyle \frac{1}{2n}}-{\epsilon }_n$$

(2)

where $\gamma \approx 0.5772$ is the Euler–Mascheroni constant and $0\le {\epsilon }_n\le {\displaystyle \frac{1}{8n^2}}$, which approaches 0 when $n$ goes to infinity [6].

It is also implied by the Bertrand–Chebyshev theorem that, except for the case $n=1$, the harmonic numbers are never integers [7].

2.2. Computer Science Applications

As mentioned in the Section 1, harmonic numbers have a wide range of applications in numerous scientific areas, including various fields of mathematics (especially number theory, combinatorics, optimization) but also in physics, economy, music theory, and many others. In this section, we will sketch some applications in the area of computer science.

2.2.1. Algorithm Analysis

Harmonic numbers find applications in algorithm analysis, particularly in estimating the time complexity of algorithms involving loops. In algorithms where the number of iterations depends on the harmonic series (e.g., some greedy algorithms or algorithms with nested loops), harmonic numbers help in understanding the overall time complexity. For instance, in certain approximation algorithms, the convergence rate can be analyzed using harmonic numbers to determine how quickly the algorithm approaches the optimal solution. Moreover, harmonic numbers are utilized in the analysis of certain data structures and their associated operations, providing insights into their efficiency and performance characteristics.

A good example is the well-known Quicksort algorithm used for sorting an $n$-element array. As is known, the pessimistic (worst) number of operations executed by the algorithm is $n^2$. However, the average number $C_n$ of comparisons performed is given as:

$$C_n=2\left(n+1\right){\displaystyle \sum }_{k=1}^n{\displaystyle \frac{1}{k+1}}$$

(3)

which can be expressed by harmonic numbers:

$$C_n=2\left(n+1\right)H_n-2n$$

(4)

2.2.2. Computer Graphics

In computer graphics, harmonic numbers are employed in various contexts such as image processing, texture mapping, and rendering. One application is in the analysis and optimization of antialiasing techniques, where harmonic numbers aid in understanding the distribution of pixel samples and optimizing sampling patterns for smoother images. Additionally, they play a role in analyzing the frequency content of signals in Fourier analysis, which is fundamental in tasks like image compression and signal processing, contributing to the efficient representation and manipulation of graphical data. Furthermore, harmonic numbers are utilized in the design of filters and shaders, enabling the creation of visually appealing effects and realistic simulations by controlling the amplitude and phase of harmonic components in graphical elements (see, e.g., [8]).

2.2.3. Machine Learning

In machine learning, harmonic numbers find applications in various areas such as model evaluation, optimization algorithms, and regularization techniques. For example, in the analysis of convergence rates of optimization algorithms, harmonic numbers help in understanding the convergence behavior and stability of iterative optimization procedures. Moreover, they play a role in regularization methods like the Tikhonov regularization, where they contribute to controlling the trade-off between fitting the training data and preventing overfitting, leading to more robust and generalizable models. In addition, harmonic numbers are utilized in the evaluation of model performance metrics, aiding in the analysis of learning curves and understanding the behavior of learning algorithms as the training dataset size increases. They are also used for improving the performance of the Support Vector Machine (SVM) algorithm, as shown, e.g., in [9,10].

2.2.4. Scheduling Theory

In scheduling theory, harmonic numbers are applied in analyzing and optimizing scheduling algorithms for various systems such as CPU scheduling, task scheduling in parallel and distributed systems, and scheduling in manufacturing processes. One application is in the analysis of scheduling policies, where harmonic numbers help in estimating the average waiting times and response times of tasks under different scheduling algorithms. In addition, harmonic numbers are used in scheduling periodic tasks or jobs with deadlines, aiding in the determination of feasible schedules and meeting deadlines while minimizing resource contention. Apart from that, harmonic numbers appear in analyzing the performance of scheduling algorithms in real-time systems, where tasks have strict timing requirements, ensuring that tasks are scheduled efficiently and deadlines are met to maintain system correctness and reliability. For applications of harmonic numbers in scheduling problems see, e.g., [11,12,13,14,15].

3. Problem Formulation

In this section, we consider a problem of charging a fleet of EVs (electric vehicles) equipped with Li-ion batteries. For extensive surveys regarding the development of high-energy Li-ion batteries for EVs, we refer to [16,17]. The charging profile of such batteries reported in the literature (see, e.g., [18]) shows that in the last stage of the process, the power used for charging drops linearly with time from an initial value. We assume that this initial power usage, as well as the capacity of each battery, is known in advance. Without loss of generality, it is additionally assumed that the power usage drops to 0 at the moment when a battery is fully loaded. Problems of this type were previously discussed in [19,20]. Let us recall below the mathematical formulation of the general version of the problem.

Let us assume that $N$ nonpreemptable, independent jobs are to be scheduled, where each job requires for its processing a certain amount of power and consumes some amount of energy during its execution. A charging job $i,i=1,2,\dots ,N$, is characterized by its power usage function $p_i\left(t\right)$, initial power usage $P_{0i}$, and its size $e_i$ being the amount of energy consumed by the job. As mentioned earlier, the function $p_i\left(t\right)$ is linear and decreasing, while it is known that $p_i\left(s_i\right)=P_{0i}$ and $p_i\left(c_i\right)=0$, where $s_{i, } c_i$ are the starting and completion times of job $i$, respectively. 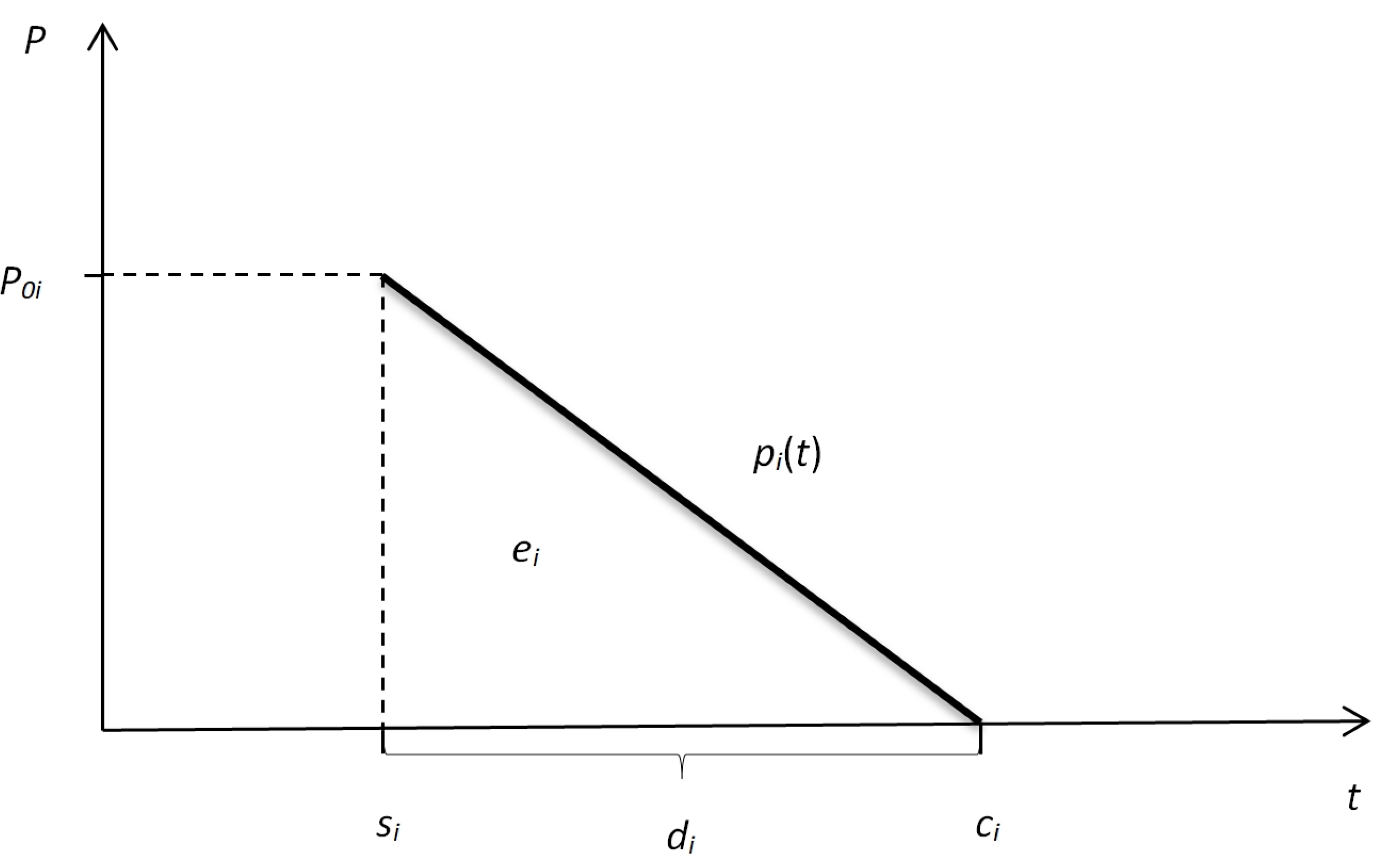In Figure 2, we present a graphical interpretation of the job model under the above assumptions.

From Figure 2, it is easy to see that the power usage function of each charging job $i$ can be mathematically defined by Formula (5):

$$p_i\left(t\right)=\left\{\begin{array}{c}0 for t<s_i\\ P_{0i}-{\displaystyle \frac{P_{0i}}{d_i}}\left(t-s_i\right) for s_i\le t\le c_i\\ 0 for t>c_i\end{array}\right.$$

(5)

It can be also easily observed from Figure 2 that:

$$e_i={\displaystyle \frac{1}{2}}{P}_{0i}{d}_i$$

(6)

and thus, the processing time $d_i$ of job $i$ can be immediately calculated as:

$$d_i=2e_i/P_{0i}$$

(7)

The objective is to minimize the length of the schedule of the charging jobs under an amount of power limited by $P$. Obviously, it has to be assumed that ${\mathrm{V}}_{i=1,\dots ,n}{P}_{0i}\le P$, since otherwise at least one charging job cannot be executed and no feasible schedule exists.

In [19], a fundamental theorem was proven for the scheduling problem defined above. According to the theorem, for a defined job list, an optimal schedule is obtained by scheduling each successive job $i$ from the list at the earliest possible time when the required amount of power $P_{0i}$ becomes available. Obviously, a few (at least one) first jobs from the list will start at time 0, as long as the sum of their initial power usages does not exceed the total available power $P$. Then, it was also shown in [19] that the starting time $s_j$ of each next job $j$ can be calculated as:

$$s_j={\displaystyle \frac{P_{0j}-P+{{\displaystyle \sum }}_{i\in A_t}{P}_{0i}+{{\displaystyle \sum }}_{i\in A_t}\frac{P_{0i}}{d_i}{s}_i}{{{\displaystyle \sum }}_{i\in A_t}\frac{P_{0i}}{d_i}}}$$

(8)

where $A_t$ is the set of jobs processed at time $t$.

For a special case of the problem, where jobs are identical, i.e., $P_{0i}=P_0, d_i=d, i=1,2,\dots ,N$, Formula (8) takes a simpler form. Since in this case we can treat all jobs as unit-time ones, i.e., it can be assumed that $d_i=d=1, i=1,2,\dots ,n$, the starting time of the next job $j$ is given by [19]:

$$s_j={\displaystyle \frac{1-\frac{P}{P_0}+{{\displaystyle \sum }}_{i\in Z_k}{s}_i}{N_k}}+1$$

(9)

where $N_k$ is the number of elements in combination $Z_k$, and $Z_k$ is the set of jobs currently processed.

Let us stress that Formula (9) defines the first non-zero starting time of a job, since some of the jobs, as mentioned above, will start at time 0. The number $N_1$ of jobs starting at time 0, i.e., processed in the first combination $Z_1$, can easily be found from the following equation:

$$N_1=\lfloor {\displaystyle \frac{P}{P_0}}\rfloor$$

(10)

As a result, the first $N_1$ jobs will start at time 0, i.e., ${\mathrm{V}}_{i=1,\dots ,N_1}{s}_i=0$. Moreover, it is obvious that in the considered case, the order of jobs on the input list is of no importance, as they all are identical. As a result, the jobs can be scheduled in an arbitrary order, e.g., according to their increasing indices. Starting successive jobs at times given by Formula (9) will lead to an optimal schedule for a particular instance.

4. Materials and Methods

In this section, we formulate a property of the special case of the problem defined in Section 3, where all jobs are identical (Section 4.1). Then, in Section 4.2, we analyze and discuss the phenomenon of the stabilization of the difference between start time of two consecutive jobs, which will be our main focus through the remainder of the paper.

4.1. Property of the Identical Jobs Case

Below, we will show and prove an interesting property of the considered problem in which inverses of successive natural numbers, similarly as they occur in the harmonic series, are directly involved for the first time. The property defines the lengths of the intervals between the start times of successive jobs until the first job (or jobs) is completed.

 Property 1. 

For the case of identical jobs, until the first job (or jobs) is completed, the intervals between the start times of successive jobs depend neither on $P$ nor on $P_0$ and are equal to the inverses of the numbers of jobs being currently executed.

 Proof of Property 1. 

Let us analyze the situation presented in Figure 3, where $N_1$ is the number of jobs started at time $t=0$, and $N_x$ is the total number of jobs being performed at time $s_{N_x}$.

It was shown and proven in [19] that each job starts as soon as the required amount of power is available. Thus, at the moment of starting a job $N_x$, the total available amount $P$ of power is used. This means that:

$$P=N_1\left(P_0-P_0{s}_{N_x}\right)+{\displaystyle \sum }_{i=N_1+1}^{N_x}(P_0-P_0\left(s_{N_x}-s_i\right))$$

(11)

Then, after a time $x$, exactly the same condition holds, when a successive $\left(N_x+1\right)$-st job is being started. The following equation is true:

$$P=N_1\left(P_0-P_0\left(s_{N_x}+x\right)\right)+{\displaystyle \sum }_{i=N_1+1}^{N_x}(P_0-P_0\left(s_{N_x}-s_i+x\right))+P_0-P_{0}x$$

(12)

By comparing the right-hand sides of Equations (11) and (12), we obtain:

$$-N_{1}x-{\displaystyle \sum }_{i=N_1+1}^{N_x}x+1-x=0$$

(13)

which is equivalent to:

$$-N_{1}x-(N_x-\left(N_1+1\right))x+1-x=0$$

(14)

and thus:

$$x={\displaystyle \frac{1}{N_x}}$$

(15)

Equation (15) means that each successive job is started after a time defined as the inverse of the number of jobs currently executed. □

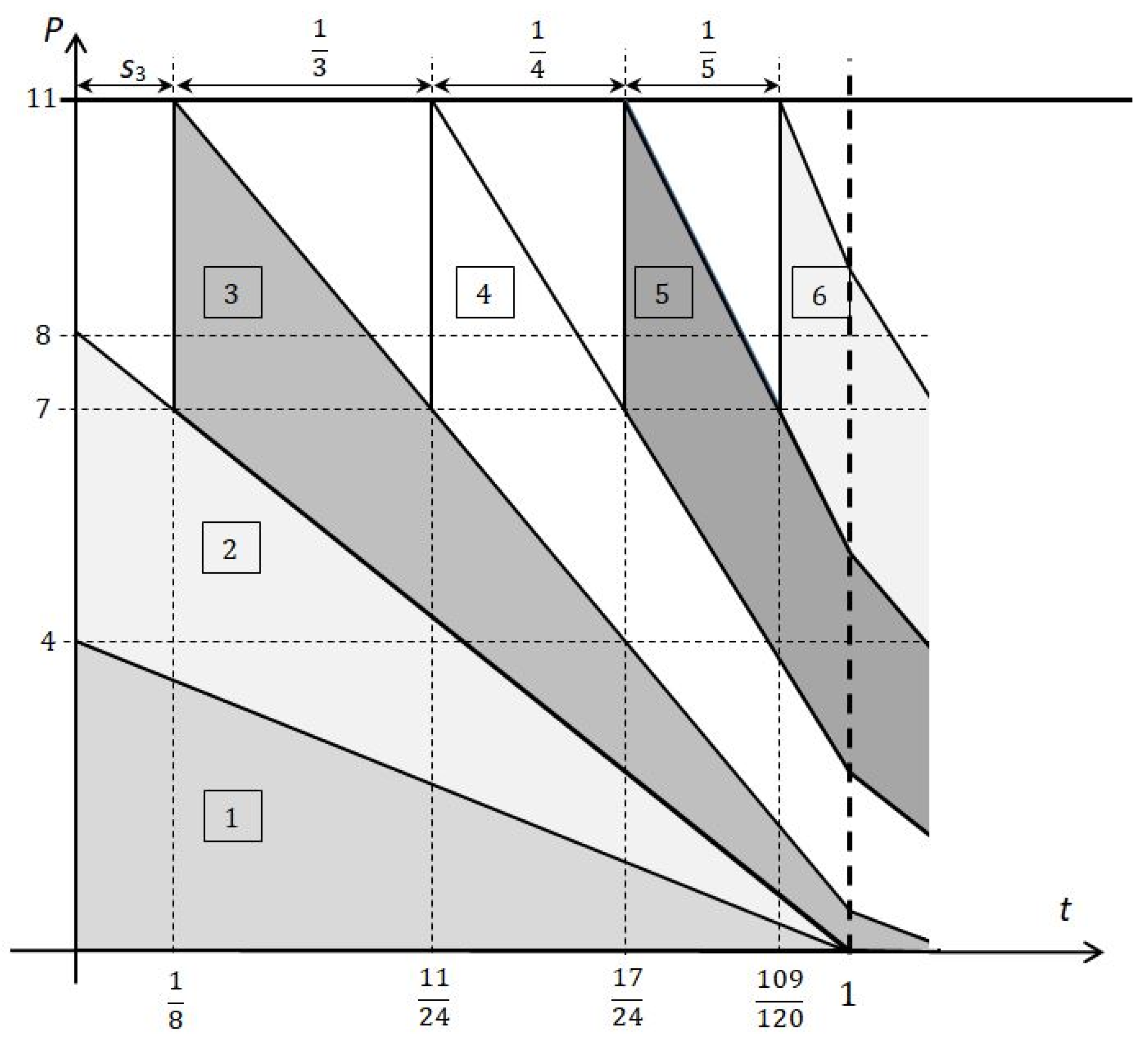
Let us consider the following instance of the problem in which $P=11 \mathrm{and} P_0=4$. The schedule where consecutive jobs are started until the completion of the first job is presented in Figure 4. As can be seen, the two first jobs may start at time $t=0$. The starting time of the third job is calculated from Equation (9) as follows:

$$s_3={\displaystyle \frac{1-\frac{11}{4}}{2}}+1={\displaystyle \frac{1}{8}}$$

After $s_3$ is found, the next starting times are calculated as the sum of $s_3$ and the successive inverses of natural numbers, as is the case in the harmonic series. Obviously, in our case, the sum begins with ${\displaystyle \frac{1}{3}}$, since the third job is the first with a non-zero starting time. For example, the starting time of job #6 is calculated as:

$$s_3+{\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{4}}+{\displaystyle \frac{1}{5}}={\displaystyle \frac{1}{8}}+{\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{4}}+{\displaystyle \frac{1}{5}}={\displaystyle \frac{109}{120}}$$

4.2. Start Times Difference Stabilization

In order to use harmonic numbers to discover the properties of the considered scheduling problem, some preliminary computational experiments were carried out. In the experiments, we assumed that the initial power usage of each job is a known fraction of the total available amount of power, i.e.,

$$P_0=aP$$

(16)

where $a\in \left(0;1\right)$.

Notice that for $a=1$, the problem is trivial, since the schedule has to be sequential, and therefore any order of jobs (with no idle times) gives the schedule of the same length.

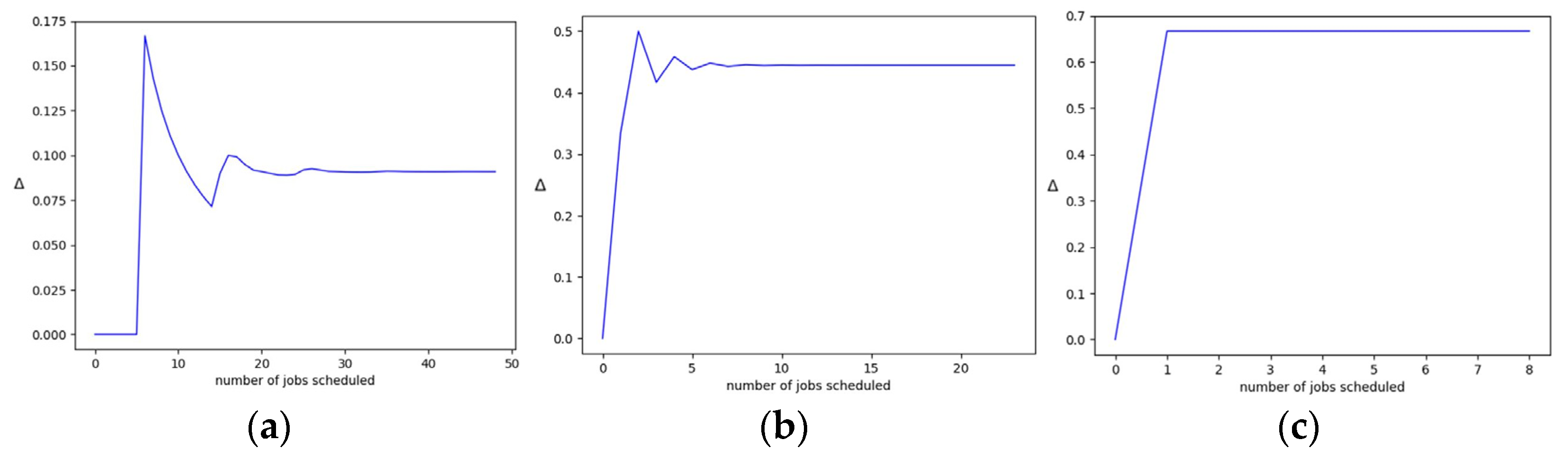
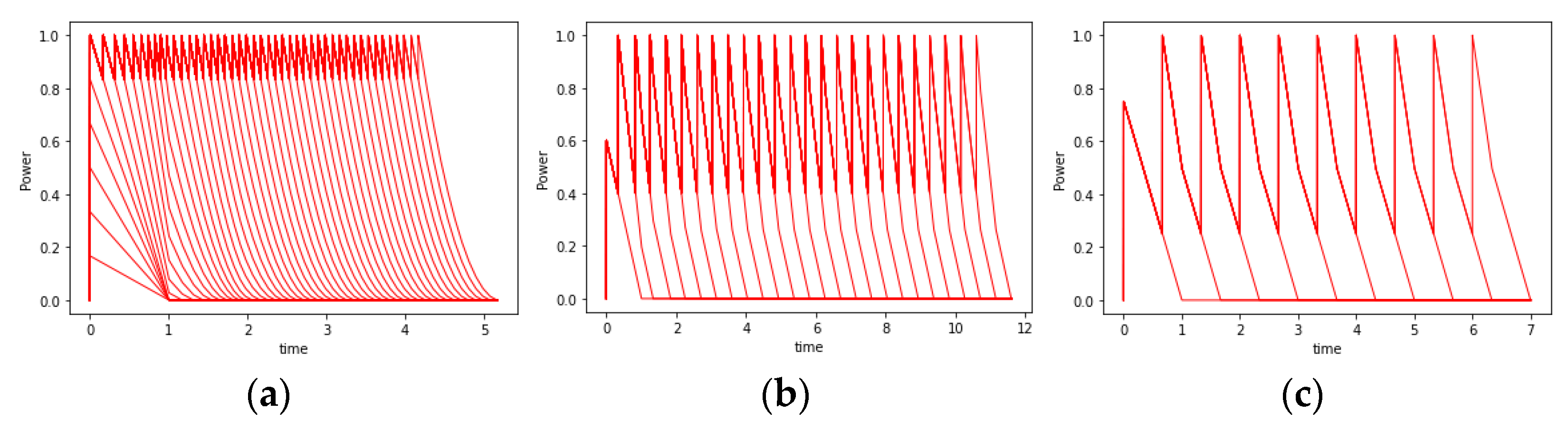
The experiments were performed for various values of $a$ in order to observe a stabilization process ongoing in the schedules. Gantt charts of exemplary problems with growing value of $a$ are presented in Figure 5. The charts show that for each value of the $a$ parameter, the difference $\Delta$ between the start times of two consecutive jobs stabilizes after some time. The stabilization occurs sooner when the $a$ parameter grows. It can be seen in Figure 5c that the chart stabilizes already at time 1, i.e., after the completion of the first job. In Figure 6, we present the relation of $\Delta$ versus the number of jobs already scheduled. The diagrams confirm the observation that the stabilization of the difference happens the sooner the greater the value of $a$. In the third diagram (Figure 6c), it is visible that the difference in the starting times becomes fixed along with the scheduling of the second job.

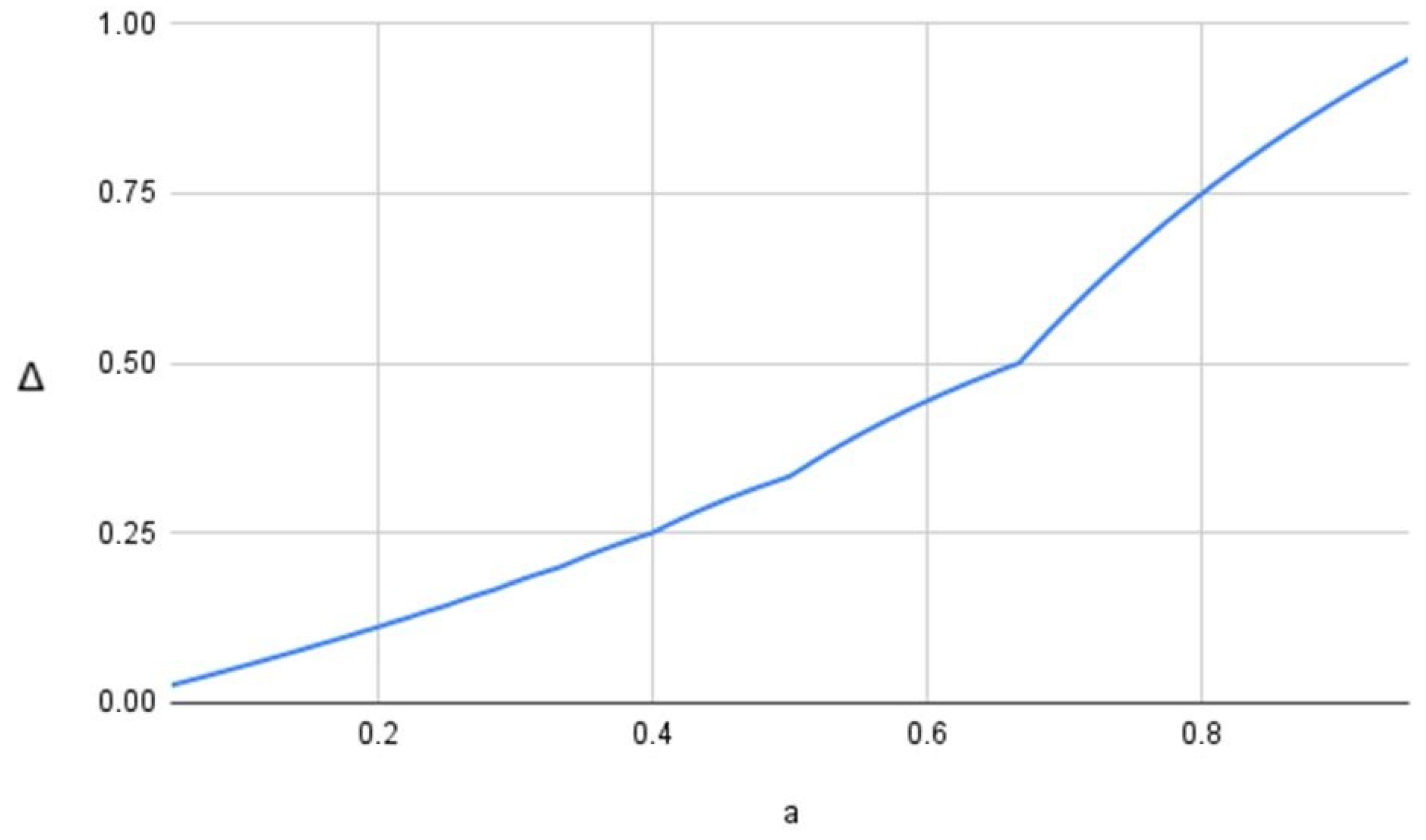
Generally, for each examined value of parameter $a$, the difference between the start times of two successive jobs converges to a constant. The relation between the stabilized start time differences and the value of the $a$ parameter is presented in Figure 7.

On the basis of the obtained results, we can conclude that when scheduling identical jobs, the difference between the start times of consecutive jobs stabilizes and will be the same after a certain time. As a consequence, it is possible to define the time of completion of a set of jobs, i.e., the length of the entire schedule, having known the number of scheduled jobs after which the difference stabilizes, as well as the value of difference in the stable start times. This can be expressed by the following formula:

$$c_{max}=s_r+\left(N-r\right)\Delta +1$$

(17)

where:

-

$r$ is the number of jobs after the scheduling of which the difference between the start times of the jobs is already constant (i.e., stabilization occurs).

-

$s_r$ is the start time of job $r$.

-

$\Delta$ is the difference in the stabilized start times.

-

$N$ is the number of all jobs.

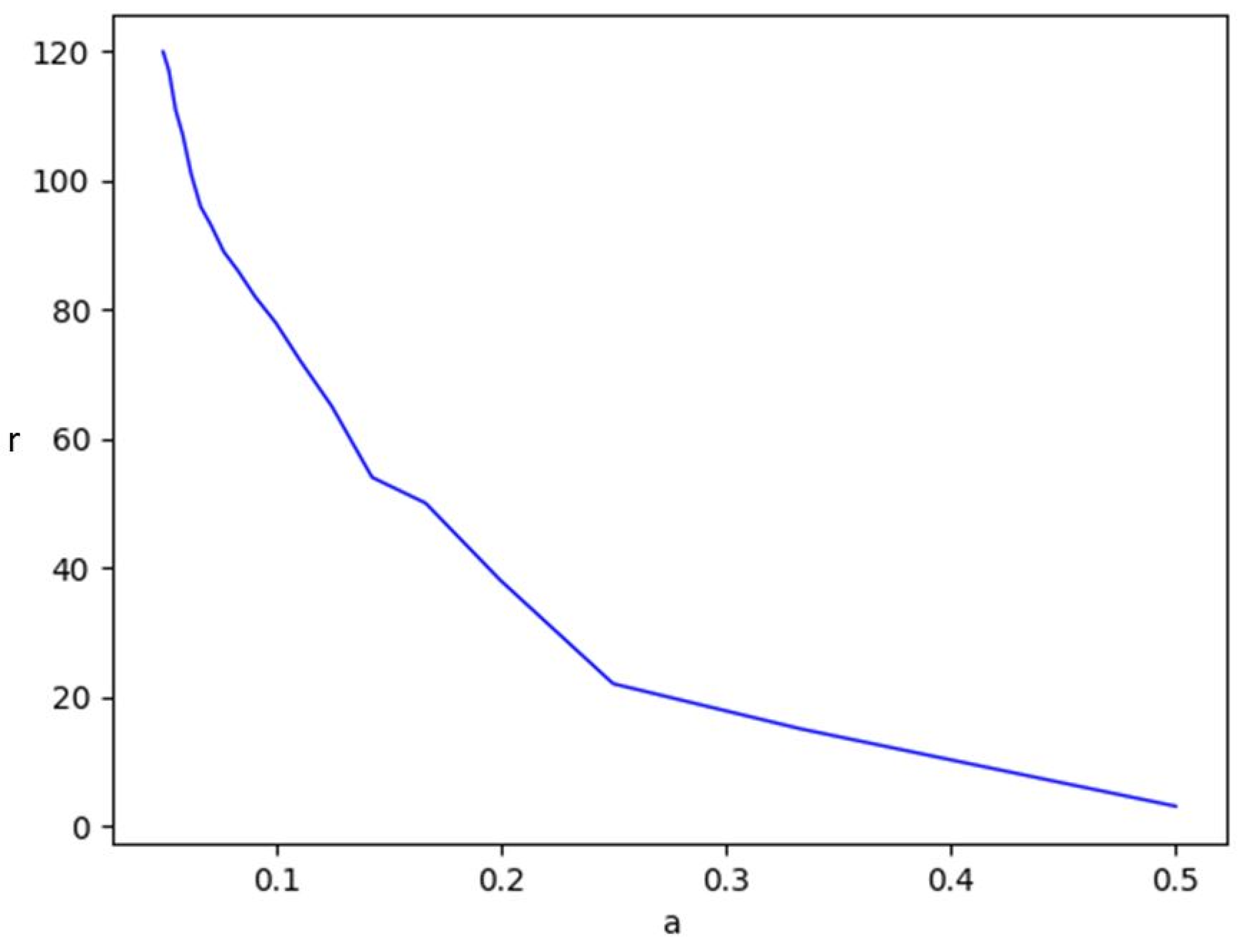
In Figure 8, we present the relation between the number of jobs that are scheduled before the stabilization of the difference between the start times of two consecutive jobs appears. As maintained before, this number goes down when the $a$ parameter grows.

In

Table 1. Notation.

Symbol	Description
$n,m,k$	natural numbers
$H_n$	$n$-th harmonic number
$\mathbb{N}$	set of natural numbers
$N$	number of charging jobs
$p_i\left(t\right)$	power usage function of job $i,i=1,2,\dots ,N$
$P_{0i}$	initial power usage of job $i,i=1,2,\dots ,N$
$e_i$	size of job $i,i=1,2,\dots ,N$
$d_i$	processing time (duration) of job $i,i=1,2,\dots ,N$
$s_i$	starting time of job $i,i=1,2,\dots ,N$
$c_i$	completion time of job $i,i=1,2,\dots ,N$
$c_{max}$	schedule length (makespan)
$P$	power limit
$P_0$	initial power usage in the case of identical jobs
$d$	job duration in the case of identical jobs
$A_t$	set of jobs processed at time $t$
$Z_k$	$k$-th combination of jobs processed in parallel
$N_k$	number of jobs processed in combination $Z_k$
$a\in \left(0;1\right)$	power ratio, $P_0=aP$
$r$	number of jobs scheduled before stabilization
$\Delta$	difference in stabilized start times

, we summarize all the introduced notations.

5. Results and Discussion

In this section, we present the main results of this research. In Section 5.1, the primary result obtained for the case of at most two charging jobs processed in parallel at a time is given in a form of a proposition. Section 5.2 contains analyses of some special cases of the problem with a particular use of harmonic numbers.

5.1. Primary Result for the Case of at Most Two Parallel Jobs

In this section, we present the basic results obtained for the case of identical jobs and a certain range of the $a$ parameter. Moreover, in the following analysis, we make an assumption that at most two jobs are processed in parallel at a given time. For more than two jobs executed at a time, it seems too hard to generate analytical results because of mathematical complications. The proposition given in this section is mainly derived from the discussion conducted in Section 4.2. In order to formulate the proposition, let us first perform some computational analysis for the case when identical jobs are sequentially being scheduled in an arbitrary order. As previously mentioned, we assume $N$ identical jobs of unit-time durations and an initial power usage of the form given by Formula (16).

1. First of all, let us notice that if $a>{\displaystyle \frac{1}{2}}$, then only one job can start at the beginning of the process, i.e., at time $t=0$. Thus, job #1 being scheduled is assigned $s_1=0$ and $c_1=1$. The combination of the currently processed jobs is as follows:

$$Z_1=\left[\begin{array}{ccc}i& s_i& c_i\\ 1& 0& 1\end{array}\right]$$

For simplicity, we will omit the headers of the columns $\left[i s_i c_i\right]$ in the following combinations.

2. Now, the starting time of job #2 can be calculated from Formula (9) as follows:

$$s_2={\displaystyle \frac{1-\frac{P}{aP}+0}{1}}+1=2-{\displaystyle \frac{1}{a}}$$

Since $a\in \left(0;1\right)$, then $s_2<1$, and thus job #2 starts before job #1 ends, which means two jobs will be executed in parallel in the current (second) combination:

$$Z_2=\left[\begin{array}{ccc}1& 0& 1\\ 2& 2-{\displaystyle \frac{1}{a}}& 3-{\displaystyle \frac{1}{a}}\end{array}\right]$$

3. The starting time of job #3 is calculated from Formula (9):

$$s_3={\displaystyle \frac{1-\frac{1}{a}+2-\frac{1}{a}}{2}}+1={\displaystyle \frac{5a-2}{2a}}$$

Now, since we assume at most two jobs executed in parallel at a time, the starting time of job #3 has to be greater or equal to the completion time of the job that was started the earliest from among the jobs currently processing, which in this case is job #1. As a result, we obtain the following condition:

$${\displaystyle \frac{5a-2}{2a}}\ge 1$$

and hence:

$$a\ge {\displaystyle \frac{2}{3}}$$

Firstly, let us notice that the above condition is compatible to the previously made assumption $a>{\displaystyle \frac{1}{2}}$. Secondly, it is easy to observe that the condition $a\ge {\displaystyle \frac{2}{3}}$ implies in itself that at most two jobs are processed simultaneously at a given time, since there will be not enough power at any stage of the schedule to start a third job in the same interval.

Let us now take a look at the schedule from the other side. After the completion of job#1, which takes place at time $t=1$, the combination of the jobs currently processed takes the form:

$$Z_3=\left[\begin{array}{ccc}2& 2-{\displaystyle \frac{1}{a}}& 3-{\displaystyle \frac{1}{a}}\end{array}\right]$$

If we now recalculate the starting time of job #3 from Formula (9), we obtain:

$$s_3={\displaystyle \frac{1-\frac{1}{a}+2-\frac{1}{a}}{1}}+1=4-{\displaystyle \frac{2}{a}}=2\left(2-{\displaystyle \frac{1}{a}}\right)=2s_2$$

and the combination describing the two currently processed jobs—job #2 and job #3—takes the following form:

$$Z_4=\left[\begin{array}{ccc}2& s_2=2-{\displaystyle \frac{1}{a}}& 3-{\displaystyle \frac{1}{a}}\\ 3& 2s_2=4-{\displaystyle \frac{2}{a}}& 5-{\displaystyle \frac{2}{a}}\end{array}\right]$$

4. The starting time of job #4 is calculated from Formula (9) as:

$$s_4={\displaystyle \frac{1-\frac{1}{a}+2-\frac{1}{a}+4-\frac{2}{a}}{2}}+1={\displaystyle \frac{9a-4}{2a}}$$

And now, as previously, comparing starting time $s_4$ to completion time $c_2$, we obtain:

$${\displaystyle \frac{9a-4}{2a}}\ge 3-{\displaystyle \frac{1}{a}}$$

which gives again:

$$a\ge {\displaystyle \frac{2}{3}}$$

The current combination of jobs is:

$$Z_5=\left[\begin{array}{ccc}3& 4-{\displaystyle \frac{2}{a}}& 5-{\displaystyle \frac{2}{a}}\end{array}\right]$$

After recalculating time $s_4$ for the new combination $Z_5$, we obtain:

$$s_4={\displaystyle \frac{1-\frac{1}{a}+4-\frac{2}{a}}{1}}+1=6-{\displaystyle \frac{3}{a}}=3\left(2-{\displaystyle \frac{1}{a}}\right)=3s_2$$

and the next combination is:

$$Z_6=\left[\begin{array}{ccc}3& 2s_2=4-{\displaystyle \frac{2}{a}}& 5-{\displaystyle \frac{2}{a}}\\ 4& 3s_2=6-{\displaystyle \frac{3}{a}}& 7-{\displaystyle \frac{3}{a}}\end{array}\right]$$

5. Let us calculate the starting time of job #5:

$$s_5={\displaystyle \frac{1-\frac{1}{a}+4-\frac{2}{a}+6-\frac{3}{a}}{2}}+1={\displaystyle \frac{13a-6}{2a}}$$

and compare it to completion time of job #3:

$${\displaystyle \frac{13a-6}{2a}}\ge 5-{\displaystyle \frac{2}{a}}$$

from which we obtain:

$$a\ge {\displaystyle \frac{2}{3}}$$

The current combination of jobs is:

$$Z_7=\left[\begin{array}{ccc}4& 6-{\displaystyle \frac{3}{a}}& 7-{\displaystyle \frac{3}{a}}\end{array}\right]$$

and the corresponding starting time of job #5 is:

$$s_5={\displaystyle \frac{1-\frac{1}{a}+6-\frac{3}{a}}{1}}+1=8-{\displaystyle \frac{4}{a}}=4\left(2-{\displaystyle \frac{1}{a}}\right)=4s_2$$

As a result of the computational analysis presented above, we can formulate the following proposition:

 Proposition 1. 

For the case of   $N$  identical jobs and   $a\in \left[{\displaystyle \frac{2}{3}};1\right)$, the starting time of$i$-th job is given by:

$$s_i=\left(i-1\right)\left(2-{\displaystyle \frac{1}{a}}\right)$$

(18)

whereas the difference in the start times of each two consecutive jobs is equal to:

$$\Delta =2-{\displaystyle \frac{1}{a}}$$

(19)

The schedule length (or the makespan) can be calculated in advance as:

$$c_{max}=\left(N-1\right)\left(2-{\displaystyle \frac{1}{a}}\right)+1$$

(20)

 Proof of Proposition 1. 

On the basis of the calculations presented above, it can be observed that at any stage of the scheduling process, each even-indexed combination $Z_{2k}, k=1,2,\dots$, looks as follows:

$$Z_{2k}=\left[\begin{array}{c}k\\ k+1\end{array}\left|\begin{array}{c}\left(k-1\right)\left(2-{\displaystyle \frac{1}{a}}\right)\\ k\left(2-{\displaystyle \frac{1}{a}}\right)\end{array}\right|\begin{array}{c}\left(k-1\right)\left(2-{\displaystyle \frac{1}{a}}\right)+1\\ k\left(2-{\displaystyle \frac{1}{a}}\right)+1\end{array}\right]$$

Then, the starting time of the next job, which is, in fact, job $k+2$, is calculated as:

$$s_{k+2}={\displaystyle \frac{1-\frac{1}{a}+\left(k-1\right)\left(2-\frac{1}{a}\right)+k\left(2-\frac{1}{a}\right)}{2}}+1$$

which, after proper reductions, gives:

$$s_{k+2}={\displaystyle \frac{\left(4k+1\right)a-2k}{2a}}$$

Now, the condition $s_{k+2}\ge c_k$ takes the form:

$${\displaystyle \frac{\left(4k+1\right)a-2k}{2a}}\ge \left(k-1\right)\left(2-{\displaystyle \frac{1}{a}}\right)+1$$

which simplifies to the condition that:

$$a\ge {\displaystyle \frac{2}{3}}$$

Continuing, the next odd-indexed combination $Z_{2k+1}$ is now the following:

$$Z_{2k+1}=\left[k+1\left|k\left(2-{\displaystyle \frac{1}{a}}\right)\right|k\left(2-{\displaystyle \frac{1}{a}}\right)+1\right]$$

and if we recalculate starting time $s_{k+2}$, we obtain:

$$s_{k+2}={\displaystyle \frac{1-\frac{1}{a}+k\left(2-\frac{1}{a}\right)}{2}}+1$$

which finally gives:

$$s_{k+2}=\left(k+1\right)\left(2-{\displaystyle \frac{1}{a}}\right)$$

(21)

From (21), the calculations of $\Delta$ and $c_{max}$ are obvious. □

Let us stress again that Proposition 1 holds for the case of $a\ge {\displaystyle \frac{2}{3}}$, which, as mentioned earlier, implies that at least two jobs are processed in parallel at a given time. For a larger number of jobs executed simultaneously, the problem of analytically finding the moment of stabilization, the stabilized different between start times of two consecutive jobs, the starting times of successive jobs, or the length of the entire schedule is too complex to derive general formulas.

5.2. Properties of Special Cases

In this section, we will present some results obtained for special cases of the considered problem when computational investigations were carried out. In particular, during the computational analyses of those cases, it was observed that for certain values of parameter $a$, the difference in the start times of two consecutive jobs tends to approach specific constants. In the special cases of the problem discussed below, harmonic numbers will be utilized for discovering the properties of those cases.

5.2.1. The Case of $a={\displaystyle \frac{1}{n}}$

The first analyzed case concerns the $a$ parameter taking values of the inverses of successive natural numbers, similarly as they appear in the harmonic series (see Section 2.1).

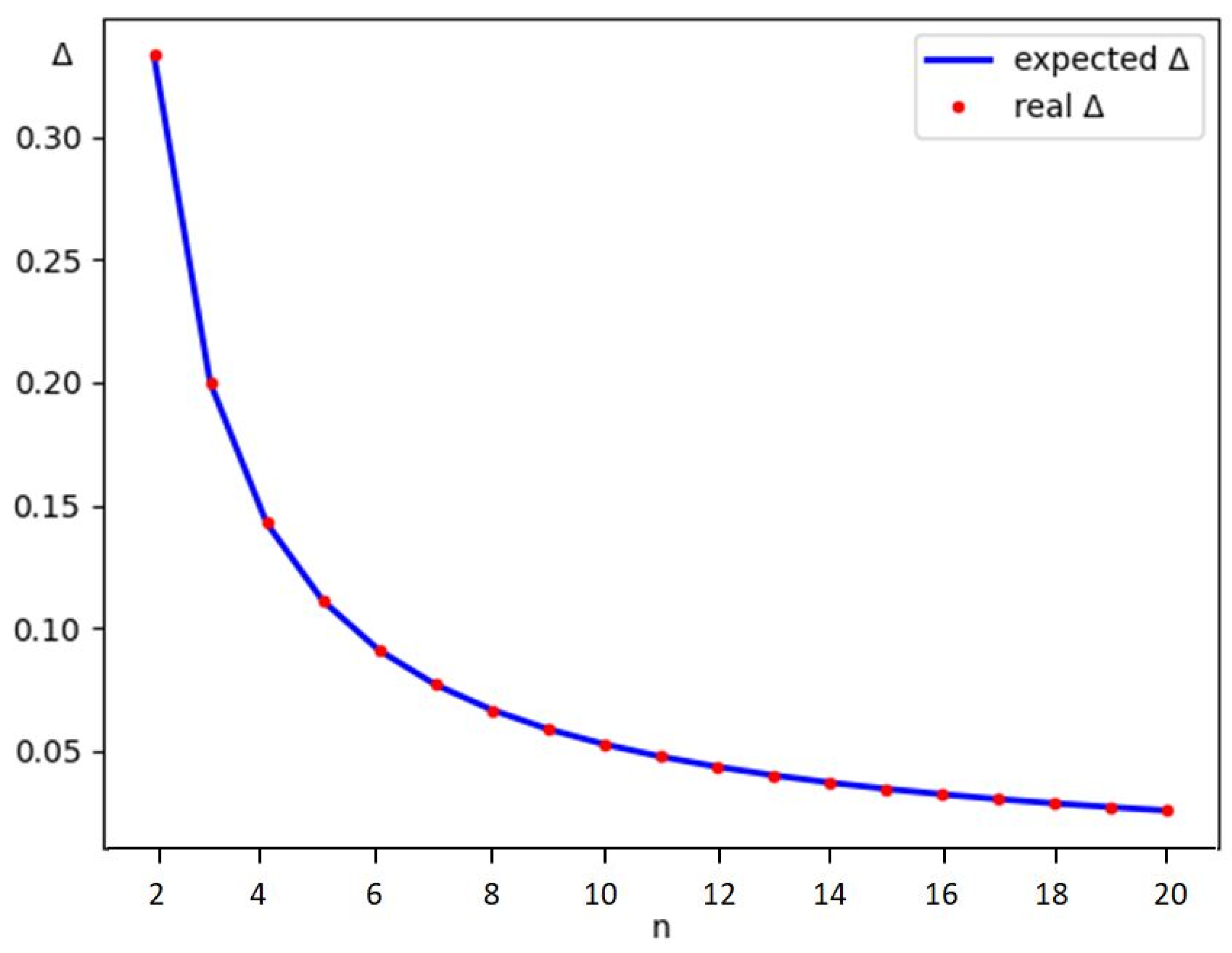
 Observation 1. 

For $a$ taking values according to the formula:

$$a={\displaystyle \frac{1}{n}} , n\in \mathbb{N}\setminus \left\{1\right\}$$

(22)

the difference $\Delta$ between the start times of two consecutive jobs approaches the value:

$$\Delta ={\displaystyle \frac{1}{2n-1}}$$

(23)

In Figure 9, we present the value of $\Delta$ obtained as a result of applying the scheduling procedure versus the expected value of $\Delta$, i.e., calculated from Formula (23). The results show that for larger number of jobs $N$, which consequently implies smaller values of a, some differences between the obtained and expected values of $\Delta$ appear; however, they are of the order of 10⁻⁷. Such small deviations are insignificant and may be neglected. As a result, we can state that Formula (23) has been empirically confirmed.

5.2.2. The Case of $a={\displaystyle \frac{2}{n}}$

 Observation 2. 

For:

$$a={\displaystyle \frac{2}{n}} , n\in \mathbb{N}\setminus \left\{1,2\right\}$$

(24)

the difference in the start times converges to:

$$\Delta ={\displaystyle \frac{1}{n-1}}$$

(25)

The obtained and expected values of $\Delta$ for this case are shown in Figure 10. As in Section 5.2.1, the computational results here are also almost identical to the expected values, and the differences are negligible. This fact confirms empirically the validity of Formula (25).

5.2.3. The Case of $a={\displaystyle \frac{n-1}{n}}$

 Observation 3. 

For   $a$  taking the values given by formula:

$$a={\displaystyle \frac{n-1}{n}} , n\in \mathbb{N}\setminus \left\{1,2\right\}$$

(26)

the difference $\Delta$ reaches the value:

$$\Delta ={\displaystyle \frac{n-2}{n-1}}$$

(27)

Notice that in this case, we can refer to Proposition 1. As it is assumed that $n\in \mathbb{N}\setminus \left\{1,2\right\}$, the smallest possible value of $a$ is ${\displaystyle \frac{2}{3}}$. The next values, i.e., ${\displaystyle \frac{3}{4}}, {\displaystyle \frac{4}{5}}, {\displaystyle \frac{5}{6}}$,… etc., are all greater than ${\displaystyle \frac{2}{3}}$, so we can use Proposition 1 to examine this case analytically.

By substitution of $a={\displaystyle \frac{n-1}{n}}$ from (26) into Formula (19), we obtain:

$$\Delta =2-{\displaystyle \frac{n}{n-1}}={\displaystyle \frac{2n-2-n}{n-1}}={\displaystyle \frac{n-2}{n-1}}$$

which is the value given by (27).

As a result, for a particular instance characterized by the number of jobs $N$ and the value of the parameter $n$, we can immediately calculate the value of the makespan from (20) as follows:

$$c_{max}=\left(N-1\right){\displaystyle \frac{n-2}{n-1}}+1$$

(28)

Let us stress again that the analyses of this case are valid for $n\ge 3$, since if $n=2$, then $\Delta =0$ would be obtained from (27), whereas the right value is $\Delta ={\displaystyle \frac{1}{3}}$.

5.2.4. The Case of $a={\displaystyle \frac{n-m}{n}}$

Firstly, it is easy to see that the case considered in the previous section (Section 5.2.3) is a special case of this one when $m=1$. However, the case of $a={\displaystyle \frac{n-m}{n}}$ is also very interesting, since it can generate values of the $a$ parameter that are unreachable for the previous three variants.

Secondly, after we performed some preliminary computational experiments, we observed that the stabilization of $\Delta$ occurs when, again, $a\ge {\displaystyle \frac{2}{3}}$. For values of ${\displaystyle \frac{n-m}{n}}<{\displaystyle \frac{2}{3}}$, we did not observe any particular value to which $\Delta$ would be convergent. As a result, for analyzing this case, we make an assumption that $a\ge {\displaystyle \frac{2}{3}}$, which, as was the case in Section 5.2.3, allows us to take advantage of Proposition 1 again.

The consequence of the assumption that $a\ge {\displaystyle \frac{2}{3}}$ implies obviously that ${\displaystyle \frac{n-m}{n}}\ge {\displaystyle \frac{2}{3}}$, which means that $n\ge 3m$. This leads to the following observation:

 Observation 4. 

For   $a$  equal to:

$$a={\displaystyle \frac{n-m}{n}}, n,m\in \mathbb{N}, n\ge 3m$$

(29)

the difference in the start times $\Delta$ takes the value of:

$$\Delta ={\displaystyle \frac{n-2m}{n-m}}$$

(30)

In order to justify Observation 4, let us substitute $a$ from (29) into Formula (19):

$$\Delta =2-{\displaystyle \frac{n}{n-m}}={\displaystyle \frac{2n-2m+n}{n-m}}={\displaystyle \frac{n-2m}{n-m}}$$

Similarly, as was the case in Section 5.2.3, having the value of $\Delta$ means that we can calculate the makespan from Formula (20) as:

$$c_{max}=\left(N-1\right){\displaystyle \frac{n-2m}{n-m}}+1$$

(31)

for a particular problem instance where $N, n, \mathrm{and} m$ are all known.

6. Conclusions

In this paper, a power-aware scheduling problem was considered for a case where a fleet of EVs are to be charged. Each EV is equipped with the same type of battery, i.e., the capacity of the battery as well as the initial power used for charging it and the power usage characteristic is identical in each vehicle. The charging jobs are assumed to be nonpreemptable and independent. The objective is to minimize the makespan under a limited amount of power available at a time.

In the research described in this paper, we used a theorem proved in [19], which constitutes that each job should be scheduled as soon as the required amount of power is available and defines the starting time of each job (Formula (9)). Obviously, in the case of identical jobs, the order of the jobs being scheduled is of no importance. In this research, we related the analysis to so-called harmonic numbers, where inverses of successive natural numbers occur.

In this paper, we formulated and proved two important properties of the considered problem. The first property says that before the first job is completed, the intervals between the start times of successive jobs are equal to the inverses of the numbers of the jobs being currently executed. The second property of the problem is formulated as a proposition that allows for calculating the starting time of each job, the difference in the start times of each two consecutive jobs, and the length of the entire schedule for the case of the initial power usage ratio being in a given range. Then, we analyzed a few special cases of the problem. For various forms of dependency of the initial power usage ratio from successive natural numbers, we showed that the start time difference between two consecutive jobs is equal to a certain value. In two cases, we demonstrated this fact empirically; in another two, we showed it analytically by using the previously proven property.

In future research, we plan to continue the exploration of the properties of the considered problem both with identical jobs and its generalizations and extensions. Firstly, the extensions may concern the following: a case with identical battery capacities but different initial power usages, a case with different capacities but identical initial power usages, or a case where each battery has different characteristics. Secondly, other charging models can be considered including, e.g., fast and slow charging, etc. Thirdly, the randomness of some events can be taken into account, for example, breakdowns, disturbances, interruptions of the charging process, or similar problems. Fourthly, economic conditionings may also affect the charging procedure, e.g., discounts, bonuses, extras, or other financial incentives with respect to electricity tariffs, etc. Finally, such extensions as repetitive sets of tasks, time constraints for task execution, or limitations on the number of concurrently performed tasks seem to be attractive. The dual problem is interesting too, where there is a deadline imposed on the time executing the entire set of tasks and where the objective is to meet the deadline while using the minimum amount of power.