Dynamic K-Decay Learning Rate Optimization for Deep Convolutional Neural Network to Estimate the State of Charge for Electric Vehicle Batteries
Abstract
1. Introduction
1.1. Literature Survey
1.2. Contributions
- (1)
- Advanced optimization technique: The paper proposes an advanced optimization technique, the advanced dynamic k-decay learning rate scheduling method, to enhance training efficiency. This technique dynamically adjusts the learning rate during training based on changes in validation loss, optimizing the training process and improving prediction accuracy. This contribution enhances the effectiveness of SoC estimation models, leading to more reliable battery management systems.
- (2)
- Experimental validation: The effectiveness of the proposed CNN architecture and optimization technique is validated through extensive experimentation. Experimental validation is conducted across various drive cycles and temperature conditions, spanning a range of real-world scenarios. Additionally, dynamic temperature generation and Gaussian noise injection are integrated into the dataset to enhance realism and robustness. The results demonstrate the superior performance of the proposed approach in accurately predicting SoC across different battery types and operating conditions.
1.3. Organization of Paper
2. Proposed CNN Model with Learning Rate Optimization
2.1. Proposed CNN Architecture
2.2. Advanced Dynamic K-Decay Learning Rate Optimization
- (1)
- Decay Rule
- (2)
- Sharp Decay Rule
3. Experiment Setup Dataset and Initial Results Explanation
3.1. Data Preprocessing
- (1)
- Obtaining Dynamic Temperature Data
- (2)
- Adding Gaussian Noise for Robustness
3.2. Dataset Description
3.3. Hyperparameter Tuning and Training Process
3.4. Computational Framework
4. Final Result and Analysis
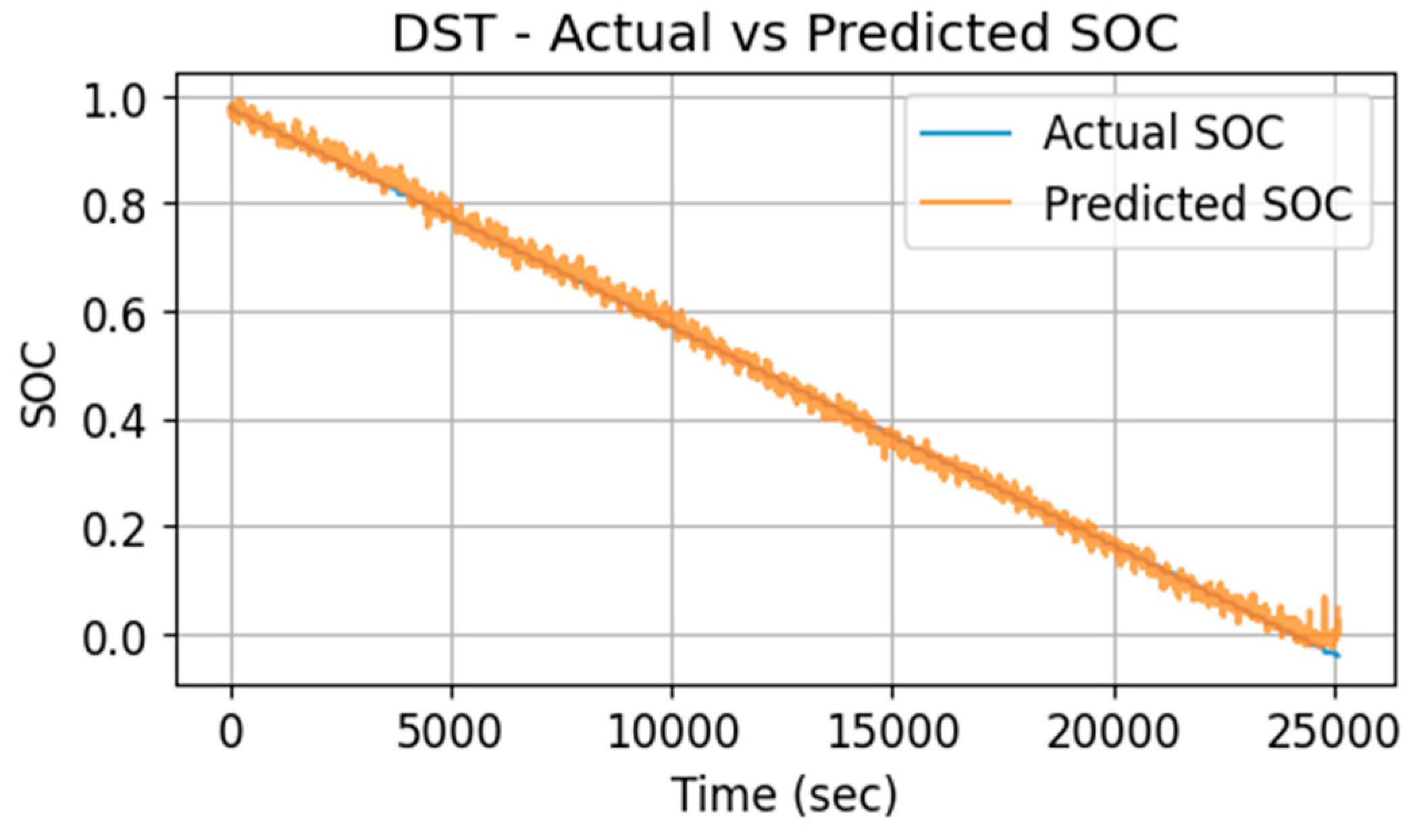
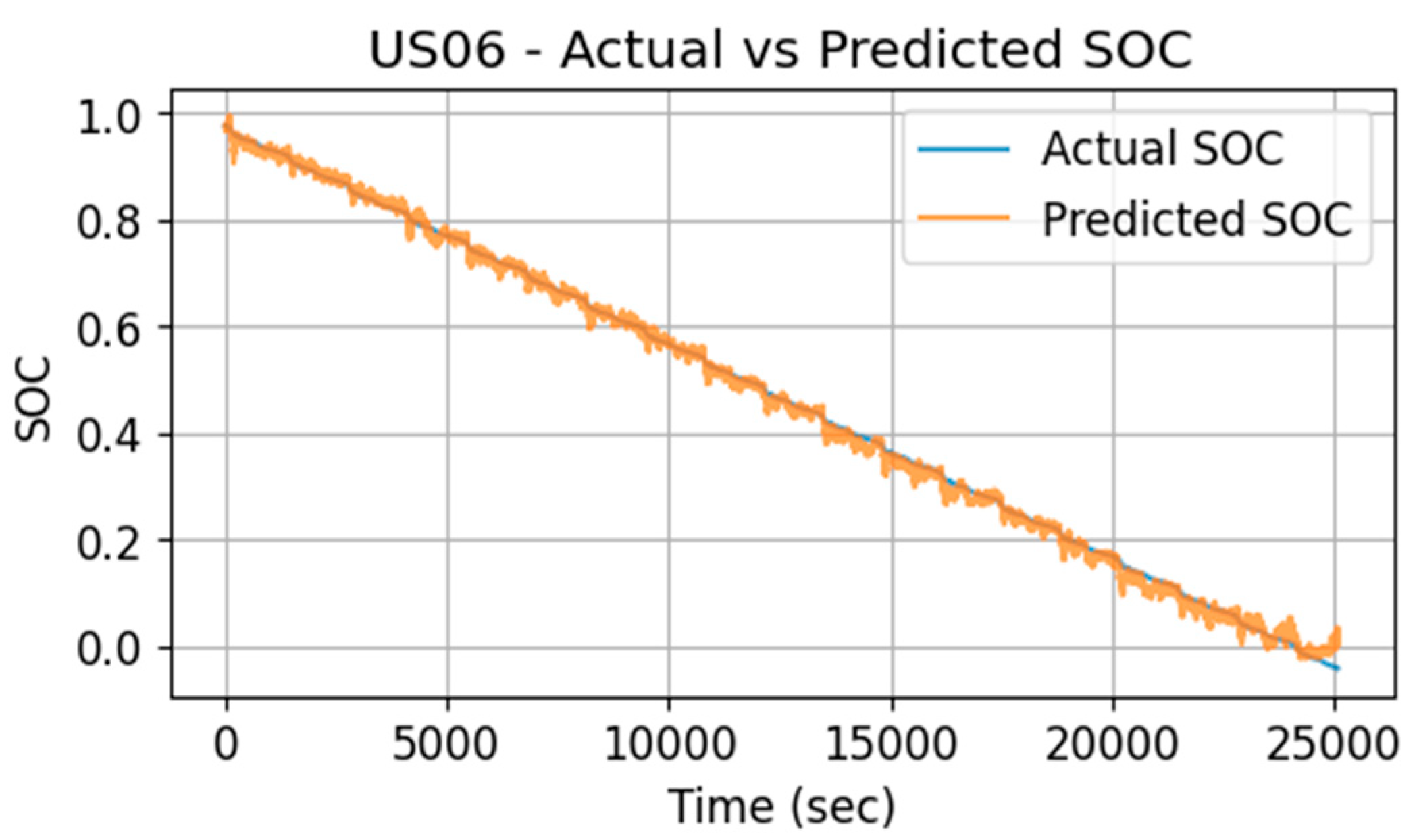
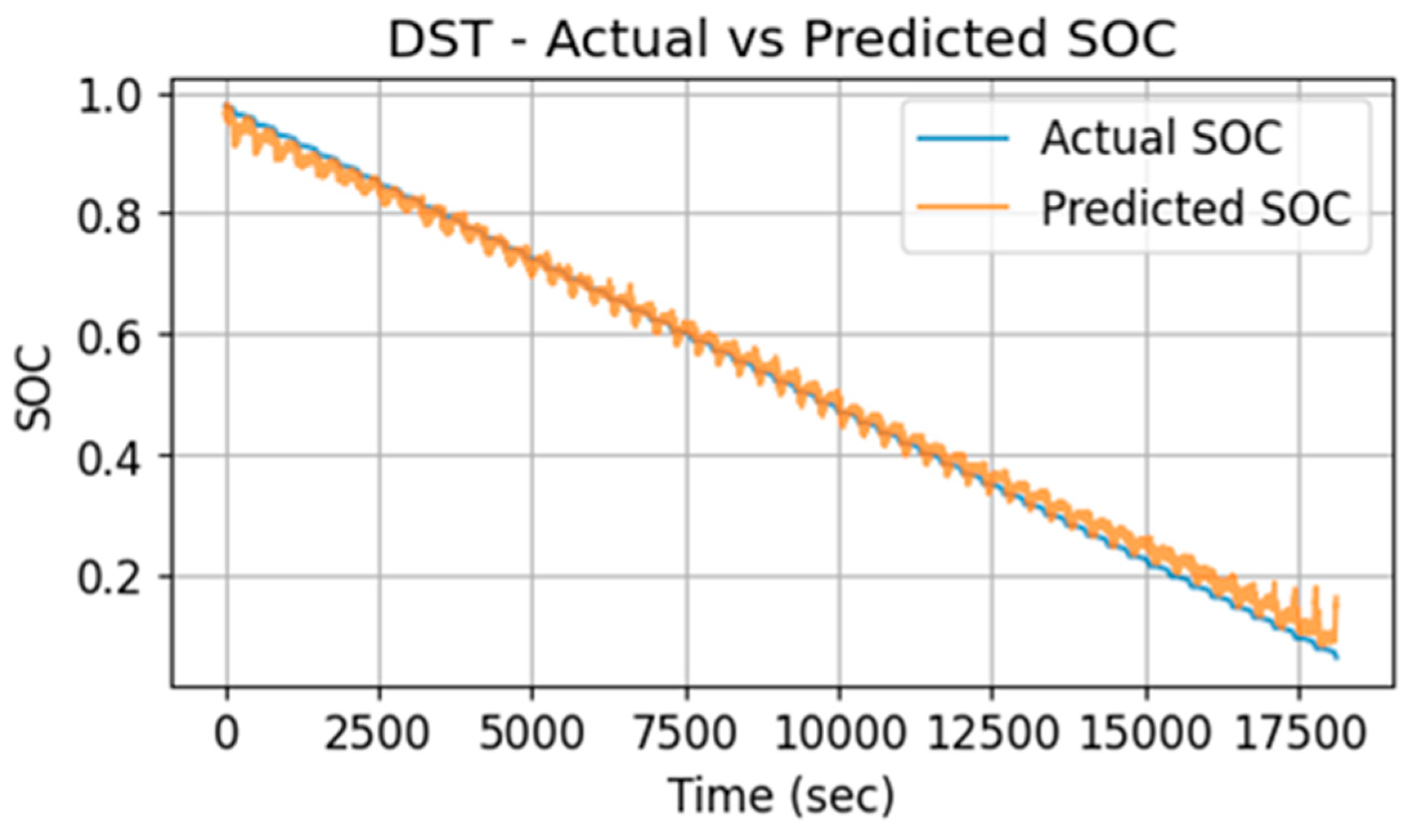
4.1. SoC Prediction at Ambient and Variable Temperatures
- (1)
- Test error of DST drive cycle
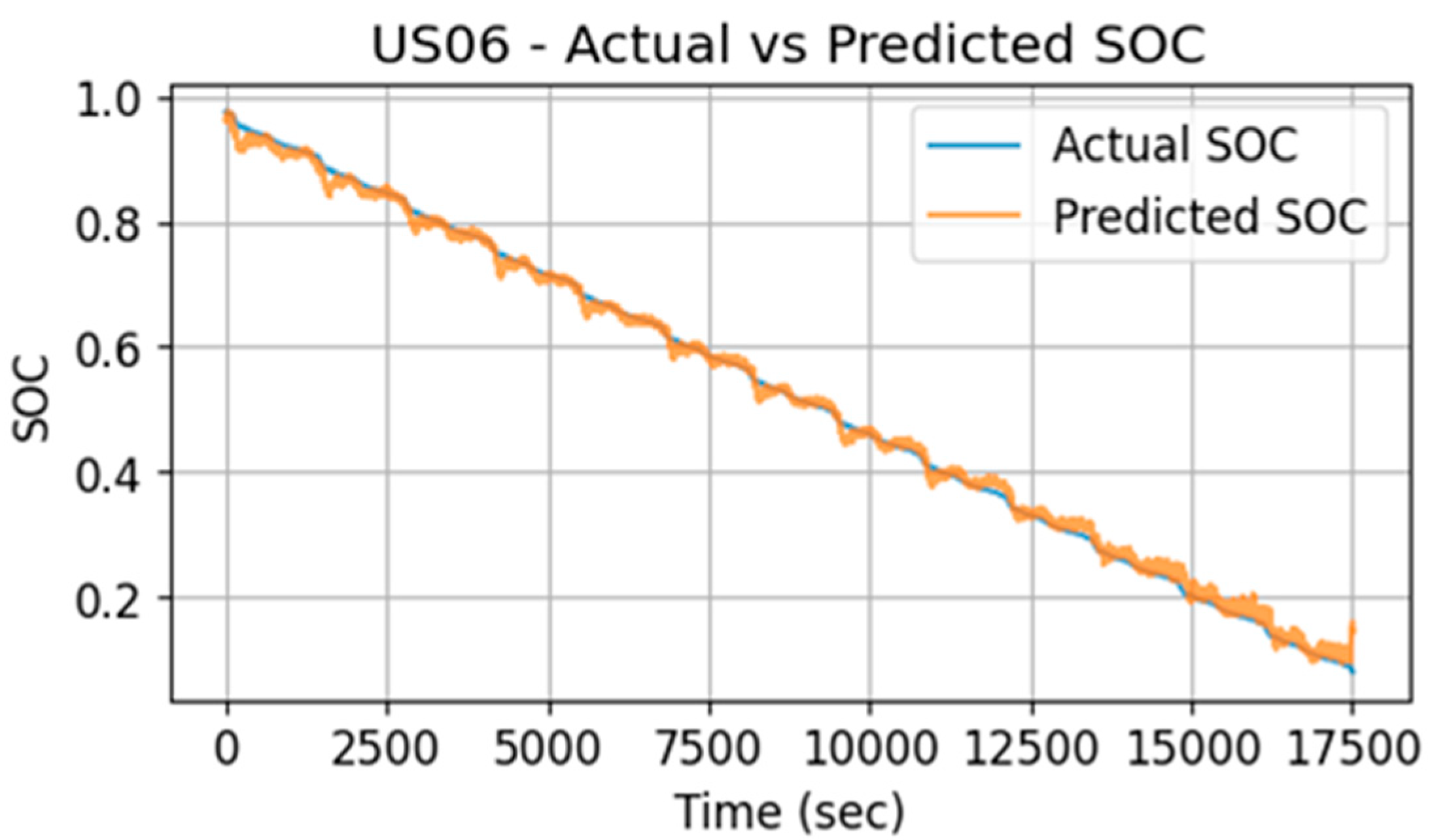
- (2)
- Test error at US06.
4.2. Comparison of Architecture and Computational Cost
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, K.; Wei, F.; Tseng, K.J.; Soong, B.-H. A Practical Lithium-Ion Battery Model for State of Energy and Voltage Responses Prediction Incorporating Temperature and Ageing Effects. IEEE Trans. Ind. Electron. 2018, 65, 6696–6708. [Google Scholar] [CrossRef]
- Wu, F.; Wang, S.; Liu, D.; Cao, W.; Fernandez, C.; Huang, Q. An improved convolutional neural network-bidirectional gated recurrent unit algorithm for robust state of charge and state of energy estimation of new energy vehicles of lithium-ion batteries. J. Energy Storage 2024, 82, 110574. [Google Scholar] [CrossRef]
- Bockrath, S.; Lorentz, V.; Pruckner, M. State of health estimation of lithium-ion batteries with a temporal convolutional neural network using partial load profiles. Appl. Energy 2023, 329, 120307. [Google Scholar] [CrossRef]
- Qin, P.; Zhao, L. A novel transfer learning-based cell SOC online estimation method for a battery pack in complex application conditions. IEEE Trans. Ind. Electron. 2023, 71, 1606–1615. [Google Scholar] [CrossRef]
- Wadi, A.; Abdel-Hafez, M.; Hashim, H.A.; Hussein, A.A. An Invariant Method for Electric Vehicle Battery State-of-Charge Estimation Under Dynamic Drive Cycles. IEEE Access 2023, 11, 8663–8673. [Google Scholar] [CrossRef]
- Mazzi, Y.; Ben Sassi, H.; Errahimi, F. Lithium-ion battery state of health estimation using a hybrid model based on a convolutional neural network and bidirectional gated recurrent unit. Eng. Appl. Artif. Intell. 2024, 127, 107199. [Google Scholar] [CrossRef]
- Wang, Q.; Ye, M.; Wei, M.; Lian, G.; Li, Y. Deep convolutional neural network based closed-loop SOC estimation for lithium-ion batteries in hierarchical scenarios. Energy 2023, 263, 125718. [Google Scholar] [CrossRef]
- Wang, X.; Hao, Z.; Chen, Z.; Zhang, J. Joint prediction of li-ion battery state of charge and state of health based on the DRSN-CW-LSTM model. IEEE Access 2023, 11, 70263–70273. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long Short-Term Memory Networks for Accurate State-of-Charge Estimation of Li-ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6730–6739. [Google Scholar] [CrossRef]
- Shu, X.; Li, G.; Zhang, Y.; Shen, S.; Chen, Z.; Liu, Y. Stage of Charge Estimation of Lithium-Ion Battery Packs Based on Improved Cubature Kalman Filter with Long Short-Term Memory Model. IEEE Trans. Transp. Electrif. 2021, 7, 1271–1284. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Lipu, M.S.H.; Sahari, K.S.M.; Ker, P.J.; Muttaqi, K.M. State-of-Charge Estimation of Li-Ion Battery in Electric Vehicles: A Deep Neural Network Approach. IEEE Trans. Ind. Appl. 2020, 56, 5565–5574. [Google Scholar] [CrossRef]
- Zhao, R.; Kollmeyer, P.J.; Lorenz, R.D.; Jahns, T.M. A Compact Methodology Via a Recurrent Neural Network for Accurate Equivalent Circuit Type Modeling of Lithium-Ion Batteries. IEEE Trans. Ind. Appl. 2019, 55, 1922–1931. [Google Scholar] [CrossRef]
- Hannan, M.A.; How, D.N.T.; Lipu, M.S.H.; Ker, P.J.; Dong, Z.Y.; Mansur, M.; Blaabjerg, F. SOC Estimation of Li-ion Batteries with Learning Rate-Optimized Deep Fully Convolutional Network. IEEE Trans. Power Electron. 2020, 36, 7349–7353. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, B. Accurate state-of-charge estimation approach for lithium-ion batteries by gated recurrent unit with ensemble optimizer. IEEE Access 2019, 7, 54192–54202. [Google Scholar] [CrossRef]
- Song, X.; Yang, F.; Wang, D.; Tsui, K.-L. Combined CNN-LSTM Network for State-of-Charge Estimation of Lithium-Ion Batteries. IEEE Access 2019, 7, 88894–88902. [Google Scholar] [CrossRef]
- Bian, C.; Yang, S.; Miao, Q. Cross-Domain State-of-Charge Estimation of Li-Ion Batteries Based on Deep Transfer Neural Network with Multiscale Distribution Adaptation. IEEE Trans. Transp. Electrif. 2020, 7, 1260–1270. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Verma, A.; Mishra, S.; Saha, T.K. Estimating State of Charge for xEV Batteries Using 1D Convolutional Neural Networks and Transfer Learning. IEEE Trans. Veh. Technol. 2021, 70, 3123–3135. [Google Scholar] [CrossRef]
- Shu, X.; Shen, J.; Li, G.; Zhang, Y.; Chen, Z.; Liu, Y. A Flexible State-of-Health Prediction Scheme for Lithium-Ion Battery Packs with Long Short-Term Memory Network and Transfer Learning. IEEE Trans. Transp. Electrif. 2021, 7, 2238–2248. [Google Scholar] [CrossRef]
- Qin, Y.; Adams, S.; Yuen, C. Transfer Learning-Based State of Charge Estimation for Lithium-Ion Battery at Varying Ambient Temperatures. IEEE Trans. Ind. Inform. 2021, 17, 7304–7315. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, X.; Li, X.; Yu, Q. An intelligent fusion estimation method for state of charge estimation of lithium-ion batteries. Energy 2024, 286, 129462. [Google Scholar] [CrossRef]
- Demirci, O.; Taskin, S.; Schaltz, E.; Demirci, B.A. Review of battery state estimation methods for electric vehicles—Part I: SOC estimation. J. Energy Storage 2024, 87, 111435. [Google Scholar] [CrossRef]
- Hu, X.; Liu, X.; Wang, L.; Xu, W.; Chen, Y.; Zhang, T. SOC Estimation Method of Lithium-Ion Battery Based on Multi-innovation Adaptive Robust Untraced Kalman Filter Algorithm. In Proceedings of the 2023 5th International Conference on Power and Energy Technology, ICPET 2023, Tianjin, China, 27–30 July 2023; pp. 321–328. [Google Scholar] [CrossRef]
- Ghaeminezhad, N.; Ouyang, Q.; Wei, J.; Xue, Y.; Wang, Z. Review on state of charge estimation techniques of lithium-ion batteries: A control-oriented approach. J. Energy Storage 2023, 72, 108707. [Google Scholar] [CrossRef]
- Tang, A.; Huang, Y.; Xu, Y.; Hu, Y.; Yan, F.; Tan, Y.; Jin, X.; Yu, Q. Data-physics-driven estimation of battery state of charge and capacity. Energy 2024, 294, 130776. [Google Scholar] [CrossRef]
- Korkmaz, M. A novel approach for improving the performance of deep learning-based state of charge estimation of lithium-ion batteries: Choosy SoC Estimator (ChoSoCE). Energy 2024, 294, 130913. [Google Scholar] [CrossRef]
- Smith, L.N. Cyclical learning rates for training neural networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 464–472. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic gradient descent with warm restarts. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017—Conference Track Proceedings, Toulon, France, 24–26 April 2017; pp. 1–16. [Google Scholar]
- Bengio, Y. Practical recommendations for gradient-based training of deep architectures. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2012; pp. 437–478. [Google Scholar]
- Zhang, T.; Li, W. k-decay: A New Method for Learning Rate Schedule. arXiv 2020, arXiv:2004.05909. [Google Scholar]
- Sherkatghanad, Z.; Ghazanfari, A.; Makarenkov, V. A self-attention-based CNN-Bi-LSTM model for accurate state-of-charge estimation of lithium-ion batteries. J. Energy Storage 2024, 88, 111524. [Google Scholar] [CrossRef]
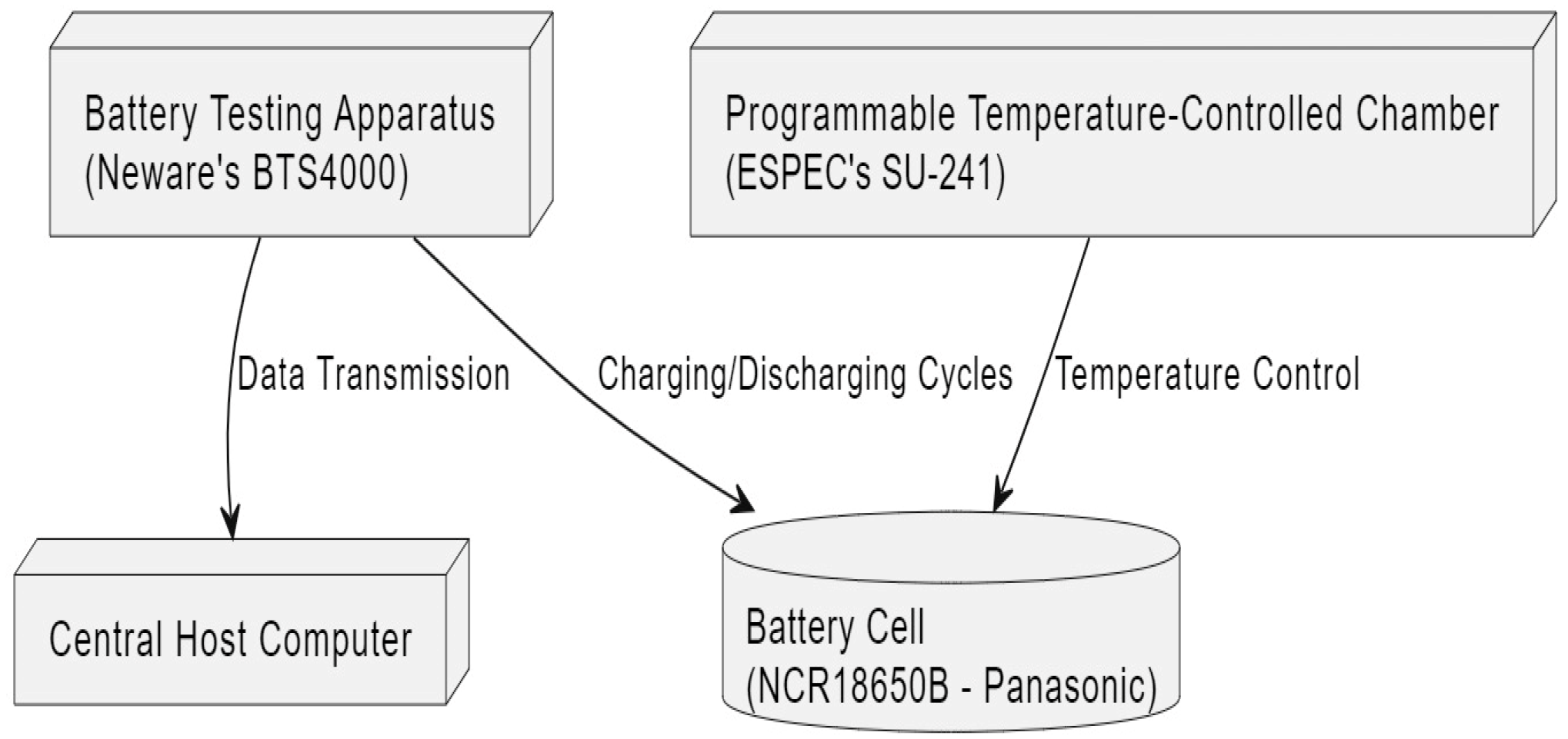


| Specification | NCR18650B (Panasonic) |
|---|---|
| Chemistry | NCA |
| Nominal Voltage | 3.6 V |
| Cut-off Voltage (Discharge-Charge) | 2.5–4.2 V |
| Nominal Capacity | 3400 mAh |
| Max Continuous Discharge | 4.87 A |
| Cycle Life | 500 |
| Model | Ambient Temperature (25 °C) | Ambient Temperature (45 °C) | Ambient Temperature (5 °C) | Ambient Temperature (−5 °C) | ||||
|---|---|---|---|---|---|---|---|---|
| Test Error (%) | Test Error (%) | Test Error (%) | Test Error (%) | |||||
| MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| Original CNN | 1.2 | 1.6 | 2.4 | 3.1 | 1.6 | 3.37 | 2.1 | 2.5 |
| K-decay optimize CNN | 0.91 | 1.3 | 1.9 | 2.3 | 0.93 | 1.2 | 1.5 | 1.8 |
| Model | Ambient Temperature (25 °C) | Ambient Temperature (45 °C) | Ambient Temperature (5 °C) | Ambient Temperature (−5 °C) | ||||
|---|---|---|---|---|---|---|---|---|
| Test Error (%) | Test Error (%) | Test Error (%) | Test Error (%) | |||||
| MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| Original CNN | 1.2 | 1.3 | 1.9 | 2.3 | 2.1 | 2.5 | 1.5 | 1.8 |
| K-decay-optimized CNN | 0.80 | 0.95 | 1.0 | 1.2 | 0.78 | 1.0 | 0.90 | 1.2 |
| Model | Number of Parameters | Training Time (min) | ||
|---|---|---|---|---|
| Test Error (%) | ||||
| MAE | RMSE | |||
| Original CNN | 1.2 | 1.3 | 12,033 | 10.81 (648.59 s) |
| Dynamic K-decay-optimized CNN | 0.80 | 0.95 | 12,033 | 5.40 (324.14 s) |
| LSTM | 0.90 | 1.54 | 15,900 | 55 |
| Bi-LSTM | 0.90 | 1.50 | 42,701 | 60 |
| CNN-LSTM | 0.80 | 1.37 | 56,849 | 130 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhushan, N.; Mekhilef, S.; Tey, K.S.; Shaaban, M.; Seyedmahmoudian, M.; Stojcevski, A. Dynamic K-Decay Learning Rate Optimization for Deep Convolutional Neural Network to Estimate the State of Charge for Electric Vehicle Batteries. Energies 2024, 17, 3884. https://doi.org/10.3390/en17163884
Bhushan N, Mekhilef S, Tey KS, Shaaban M, Seyedmahmoudian M, Stojcevski A. Dynamic K-Decay Learning Rate Optimization for Deep Convolutional Neural Network to Estimate the State of Charge for Electric Vehicle Batteries. Energies. 2024; 17(16):3884. https://doi.org/10.3390/en17163884
Chicago/Turabian StyleBhushan, Neha, Saad Mekhilef, Kok Soon Tey, Mohamed Shaaban, Mehdi Seyedmahmoudian, and Alex Stojcevski. 2024. "Dynamic K-Decay Learning Rate Optimization for Deep Convolutional Neural Network to Estimate the State of Charge for Electric Vehicle Batteries" Energies 17, no. 16: 3884. https://doi.org/10.3390/en17163884
APA StyleBhushan, N., Mekhilef, S., Tey, K. S., Shaaban, M., Seyedmahmoudian, M., & Stojcevski, A. (2024). Dynamic K-Decay Learning Rate Optimization for Deep Convolutional Neural Network to Estimate the State of Charge for Electric Vehicle Batteries. Energies, 17(16), 3884. https://doi.org/10.3390/en17163884









