Abstract
The hybrid AC/DC grid, based on a significant share of renewable energy sources, is gradually becoming an essential aspect of the modern energy system. The integration of intermittent renewable generators into contemporary energy systems is accompanied by the decommissioning of power plants containing synchronous generators. Consequently, this leads to a reduction in system inertia and an increase in the risk of stability disruption. The abrupt disconnection of the primary generator or power line can result in an unanticipated mismatch between power generation and consumption. This discrepancy can trigger substantial and swiftly evolving alterations in power distribution, angular speed, load flow, and the frequency of generators. The risks of an energy system collapse can be mitigated through automation, enabling rapid adjustments to generation and load capacities, as well as power flows, in the electrical network. This article justifies the utilisation of a power control method for high-voltage power line interconnections. The technology of hydro storage power plants and measurements of voltage phasors are employed. The potential for easing power flow restrictions and realising substantial economic benefits is supported by the results obtained using simplified dynamic model of the Baltic power system and Nord Pool electricity market model.
1. Introduction
1.1. Motivation
The urgency of the climate crisis demands immediate action to implement mitigation measures and reduce greenhouse gas emissions [1]. A pivotal strategy for achieving this involves the widespread development of renewable energy sources (RESs). The integration of intermittent RES into modern power systems is rapidly increasing, aligning with the decommissioning of fossil fuel energy plants. Some countries already have RES capacity capable of meeting more than 100% of demand [2]. However, the widespread adoption of RESs exacerbates challenges related to reliability, stability, and adequacy, demanding comprehensive solutions [3,4,5]. The intermittent nature of RES generation, combined with the variable and challenging-to-control nature of consumption, emphasises the need for capital-intensive energy reserve and storage. This intricacy further complicates the delicate balance between generation and consumption. Consequently, the widespread adoption of RESs necessitates substantial efforts and investments to simultaneously achieve four key objectives: system adequacy, reliability, stability, and economic effectiveness [6].
In power systems (PSs) with an extensive share of RESs, inertia can exhibit large variations over time and across different regions. PSs are permanently subjected to a variety of troubles, such as a short circuit in a transmission grid, a fault in and damage to a large generator, etc. Large disturbances occur relatively rarely; however, they can lead to loss of synchronism among generators and damage to PS equipment, resulting in enormous economic and social consequences [7,8]. The transition from synchronous generators to renewables significantly reduces system inertia [2,4,5,9]. Low-inertia zones are particularly predisposed to the loss of dynamic and transient stability, increased rates of change of frequency (ROCOFs), reduced frequency stability, an increased likelihood of cascading outages, and a decrease in the number of generation units available for primary and secondary frequency regulation [3,10,11]. On one hand, with the reduction in total system inertia and the associated faster frequency dynamics, the existing emergency control and Under-Frequency Load Shedding (UFLS) schemes are becoming obsolete [12]. The increased risk manifests itself as an increased probability of load shedding, transmission power line tripping, and generation outages. This challenge is even more pronounced in cases of the limited power capacity of interconnecting lines [2,8]. The stability of AC power systems, encompassing frequency [13], transient voltage, angular, and thermal stabilities [10], etc., forms the bedrock of secure and reliable operation in contemporary power systems. The importance of stability is particularly high in power systems of relatively small volume connected to neighbouring power systems by lines with a limited transmission capacity. Figure 1 depicts a power system consisting of several subsystems: PS1 is a relatively small power system, connected by a high-voltage AC transmission line (TL) to PS2 and by high-voltage direct current (HVDC) lines to the subsystem PS3.
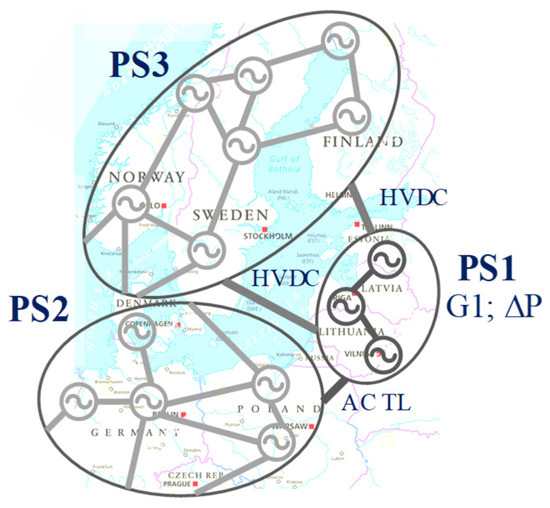
Figure 1.
Interconnected power systems.
Normally, operators of the considered system are obligated to ensure its functionality in the event of the sudden failure (disconnection) of any of the major elements (the N-1 criterion [14]). Let us assume that the failure leads to a reduction in generation in subsystem PS1 by an amount represented by . To justify the admissibility of the power jump, the operator, in accordance with the N-1 criterion, employs dynamic models of the energy system containing synchronous generators based on equations in the following form [15]:
where, , and are the mechanical, electrical, and accelerating power (per unit), respectively; since PS1 is an importing PS, the accelerating power is negative or decelerating. is the synchronous (angular) speed, is the total system inertia, and is the angular acceleration of the rotor; in our case, a negative value represents deceleration.
Equations (1) and (2) delineate a process triggered by a disturbance in balance capable of instigating a frequency drop or power oscillations between generators and potentially resulting in the collapse of the power system. We can conclude that the rates of changes in system frequency and rotor angle deviation are inversely proportional to the total system inertia. Fluctuations in the angular speed and frequency of generators over time can cause significant alterations in the power flow within the transmission network. This may result in the overloading of power transmission lines, ultimately leading to their disconnection. We can see that the loss of system inertia causes faster falls in frequency and rotor angle change for the same power imbalance (1) and increases the risk of large-scale accidents and blackouts [16]. The risk of potential cascading events and catastrophic blackouts can be reduced by using three distinct methods: Firstly, by augmenting the overall system inertia , attained by incorporating additional synchronous machines (such as synchronous condensers) or by introducing synthetic inertia [17,18]. Secondly, by minimizing the value of achieved through constraining the power from the energy sources in use. It is worth noting that adherence to this constraint often necessitates the use of less profitable generators. Thirdly, by immediately reducing imbalances during dangerous processes [19]. To attain this goal, two primary steps must be undertaken: (a) employing suitable automation and measurement methods to identify unforeseen disconnections of energy sources and assess the magnitude of imbalance between production and consumption; (b) taking corrective actions by influencing generators or loads to promptly rectify the power mismatch between energy production and energy consumption. The implementation of the first two measures listed is often blocked by substantial costs since enhancement can be attained through either constraining the influence of economically efficient sources or reinforcing the capacity of power transmission lines. A more economically appealing option emerges with the deployment of Special Protection Systems (SPSs) or Remedial Action Schemes (RASs), used when carrying out the above measures is considered impractical or undesirable. A rapid reduction in can be achieved through timely remedial actions, including, but not limited to, load shedding [20], system segment isolation [8], generator tripping, generator reconnection, and the utilisation of braking resistors [19,21,22]. SPSs are designed to take fixed, remedial action to preserve system integrity and ensure suitable system performance [23].
While the rapid connection or disconnection of spare capacities to and from the network can address the need for stability, it introduces challenges related to connection speed. The maximum allowable time for taking stability assurance measures depends on the type of the problem. Angular and frequency stability issues typically require the fastest resolution [24], at least within a few cycles, but usually in less than one second. Actions to alleviate steady-state stability problems and slow voltage collapse may have an available time period of several seconds. Thermal overload issues may allow several minutes before action is required. The connection of significant generation capacities takes time, typically measured in tens of seconds or more. As noted in [25], generally, hydro turbines are much faster than conventional steam turbine coal plants, which exhibit typical ramp rates of 1% of rated power in MW/min. In fact, hydro turbines have a response comparable to heavy duty and aero-derivative gas turbines, providing up to 20 and 30 MW/min per unit, respectively. The Dinorwig power plant is one of the fastest ramping pumped hydroelectric storage power plants (PHSPPs) in the world and is able to increase power from 0 to 1320 MW in 12 s [26]. At the same time, the switching of loads can be performed much more rapidly, typically within a time of approximately ten milliseconds. To address this task, load shedding schemes are commonly employed. The cutting off of loads requires prompt identification of threats associated with emergency processes. To achieve this, emergency automation features such as UFLS and out-of-step protection (OSP) are employed most widely [27,28,29,30]. However, it is important to recognise that the UFLS method leads to economic and social losses, since it is implemented by disconnecting energy consumers from the network. Additionally, UFLS identifies the need for load shedding by detecting a decrease in system frequency. However, the time required to make a decision may become unacceptably long, considering the need to ensure angular stability conditions and prevent the occurrence of asynchronous modes, for whose elimination out-of-step protection automation is employed. The standard OSP automation method divides the power system into segments, which ultimately leads to an imbalance and the disconnection of a portion of consumers. OSP automation identifies stability disruption by using PMU and measuring phasors’ angles [31]. In this case, restoring the power system to a stable state is achieved through disconnecting consumers, resulting in economic losses due to power interruptions.
It should be noted that the ongoing electrification of specific engineering infrastructures is causing notable rises in both the quantity and capacity of consumers who are highly sensitive to interruptions in power supply, particularly in terms of economic losses. Involving consumers who are sensitive to operational pauses can impede efforts to prevent the development of frequency breakdowns, thus significantly restricting the available options for implementing UFLS and OSP in emergency modes. Fortunately, along with these challenges, new opportunities emerge to address or circumvent them. The development of rapid communication networks presents promising opportunities for the distribution and transmission of information, as well as for control actions. Wide area protection and phasor measurement systems are extensively discussed in the scientific literature [32]. These technological advancements offer a way to improve the coordination and efficiency of energy management and control systems, especially when considering increased sensitivity among specific consumers. In addition, the significance and capacities of energy storage systems are experiencing growth. Experts unanimously emphasise that green hydrogen is an inevitable component of the future solution [33]. Concurrently, various other types of energy storage are either in use or under study [34]. These technologies include but are not limited to the following: pumped hydroelectric storage power plants (currently the most widely used technology [35]), battery energy storage systems [36,37], compressed air stations, and synchronous condenser technology [18]. Energy storage can be used for the rapid substitution of an unplanned power outages [38]; however, achieving this requires ensuring sufficient speed and cost-effectiveness in managing the storage operation. In the featured article [38], a feedback control strategy that modulates the real power injected or absorbed by distributed energy-storage devices is proposed. Regrettably, the analysis has been carried out under the assumption that there are no physical constraints on the operational rate of the system.
Dynamic braking [22,39] uses an artificial load near generators during a fault in a grid to consume the power of the generators in order to reduce rotor acceleration. Shunt resistors have been used by switching resistors for about 0.5 s following a fault. The dynamic braking method is not suitable in cases of a power deficit.
The integration of joint management operations for energy storage and flows of HV TLs has been thoroughly analysed in [29,40]. It has been pointed out [41] that such a structure makes possible the utilisation of reserves from neighbouring PSs and provides additional opportunities for management, control, and the electricity market. The potential benefits of this approach depend on the transmission capacities of power lines, emphasising the importance of increasing its maximum capacity as a key factor in achieving stability goals. Dynamic Line Rating (DLR) technology represents a method for enhancing line capacity [42]. It is important to recognise that the effectiveness of DLR technology relies on the line conductor thermal capacity limit and is applicable when this element is the weakest one in the route. However, long transmission lines with high nominal voltages often face constraints due to their impact on transient or post-contingency system stability. This recognition emphasises the need for a comprehensive approach to enhancing line capacity, considering both thermal limitations and concerns about system stability.
1.2. Research Problem’s Definition, Aim, and Contribution
Summarising the above, the urgency of the climate crisis demands the rapid development and deployment of RES technologies to reduce greenhouse gas emissions. However, integrating intermittent RESs into power systems, while decommissioning fossil fuel plants, poses challenges to system reliability, stability, and adequacy due to the reduced system inertia and variability in energy sources. Existing emergency control schemes, such as UFLS and OOS protection, are becoming less effective. Alternatives, like SPS and RAS, are cost-effective for rapid responses to disturbances. Advancements in fast communication networks, measurement systems, and energy-storage technologies offer new opportunities for improving system stability and control. To address these issues, we propose a new mode of operation for pumped hydroelectric storage plants, involving the simultaneous running of the pump and the generator. While this mode increases energy consumption, it also makes it possible to recover the disrupted balance, thus allowing for a higher power flow in interconnected power lines. This can compensate for energy losses and can be economically viable.
The assumption of the technical and economic viability of simultaneous use of the pump and generation modes of a PSHPP forms the main hypothesis, the justification of which constitutes the core of this article. The purpose of the paper is to demonstrate how the proposed technology would detect additional transmission capacity on an interconnection transmission line and how utilities and regional transmission operators might incorporate such a DLR into real-time operations.
To validate the above-stated hypothesis, we set and complete the following tasks:
- By using a simple dynamic model of the power system, we demonstrate the potential for increasing the maximum allowable power of a TL connecting two PSs;
- Via an abridged dynamic model and the parameters of the power systems of the Baltic Sea region, we show the possibility of maintaining stability during sudden outages of large energy sources;
- By utilising data from the Nordic Power Exchange (Nord Pool) market [43], we conduct an example of assessing the economic efficiency of the proposed approach.
It is worth noting that a brief disconnection of the pump of a pumped storage hydroelectric power plant operating in combined pump and generator mode during a stability threat can be easily implemented, incurring acceptable economic losses, and is practically feasible.
1.3. The Structure of the Paper
The structure of this paper is as follows: Section 2 lays out the fundamentals of the proposed control method, elucidating the instability phenomenon through the Equal Area Criterion and detailing the proposed operational mode of pumped storage plants. In Section 3, case studies are presented to substantiate the efficacy of the proposed strategy. Finally, Section 4 offers concluding remarks to end the paper.
2. Materials and Methods
2.1. Instability Arising from Generation Surges
Let us return to the analysis of the PS, comprising two subsystems interconnected by a transmission line (AC TL; please refer to Figure 1), and consider a scenario where each subsystem is composed of a single synchronous generator harmoniously matched with its respective load. Moreover, within the subsystem, PS1 holds the distinction of being the predominant primary energy source, while the maximum allowable capacity of the power line has been definitively determined and set. The sudden and unplanned disconnection of both of these elements could potentially lead to instability in the analysed system. The transmission system operators (TSOs) of subsystems PS1 and PS2 are responsible for ensuring stability, setting constraints when choosing the operating modes for each subsystem and the transmission lines between them. Additionally, let us assume that both subsystems, PS1 and PS2, are part of a single electricity market and are managed by an Electricity Market Operator (EMO) whose main task is to provide consumers with the cheapest energy offered by generating companies. Ultimately, the operating mode was determined by formulating and solving an optimisation problem with two primary objectives:
- Minimising the risk of instability [10,41];
- Minimising energy generation costs while adhering to specified constraints, some of which relate to stability conditions.
The mentioned bi-objective problem was decomposed into two separate tasks. Firstly, there was a search for operating modes that are acceptable in terms of stability. Secondly, there was a minimisation of costs while considering the constraints obtained from the first step.
To elucidate and elaborate on the proposed method, we employed a widely used approach that included the dependence of transmitted power on the phase angle between the voltages of equivalent generators in two interconnected power systems (see Figure 2a). We assumed that the first subsystem (PS1) has limited inertia and power capacity and acts as an importer of energy from the second subsystem (PS2). When synthesising the model of the system, we used the assumption that all the components of subsystems PS1 and PS2 are located in one node (copperplate model, [44]). We supposed that the model satisfied the power balance equation at any point in time. We examined two modes: (1) a steady-state one, characterised by power balance Equation (3), and (2) a transient one, determined by (4), assuming that a power outage occurred in subsystem PS1.
where represents the aggregated generation in PS1, stands for a power outage, denotes the exchange with the neighbouring subsystem, represents the aggregated load, and denotes the decelerating power in PS1.
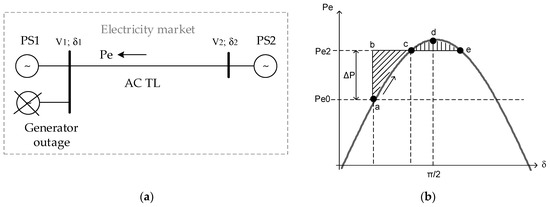
Figure 2.
(a) A simplified diagram of the interconnected power system and (b) a representation of a sudden outage using the EAC.
The power losses due to transmission and distribution were neglected. A power outage introduced angular changes, which are described by (2). Because of the highly nonlinear behaviour, it was difficult to obtain pure analytical solutions to the system equations, and the graphical method, also known as the Equal Area Criterion (EAC), was often used to determine whether or not the system would lose stability after a disturbance [45].
For the system presented in Figure 2a, it was assumed that PS1 is a power-deficient system, with the generators of PS1 operating at their maximum capacity.
The PS1 deficit was overcome by importing power from PS2 over the TL (point a in Figure 2b). For a sudden outage of the major generation source in PS1, power deficit occurred, and a number of things happened. Immediately after the generation loss, the power deficit was redistributed among the remaining generators of PS1 and PS2. The kinetic energy of the rotational mass of the generators’ rotors ensured power balance at the very first moment but, as the inertial response decayed, the generators started to decelerate and the system frequency started to decline. In response to the frequency decline, the generators gradually increased their power, but the generators of PS1 were already operating at their maximum power and, thus, the power transfer over the TL was gradually increased by the amount (from point a to point c, Figure 2b). In case the acceleration energy of generator PS2 (area abc in Figure 2b) needed to regain power balance in point c became greater than the maximum available deceleration energy (area cde in Figure 2b), angular instability may have arisen between the generators of PS1 and PS2, resulting in the loss of synchronism and an out-of-step condition along the transmission line.
To avoid the out-of-step condition, the power transfer over the TL had to be reduced from to (Figure 3a,b), thus increasing the deceleration areas cde and cdef (Figure 3a,b). This was achieved by disconnecting some load in PS1 (an undesirable method) or by the fast injection of a significant amount of power in PS1.

Figure 3.
Representation of (a) the fast injection of additional power in PS1 on a rising slope and (b) fast injection of additional power in PS1 on a falling slope using the EAC.
Such fast injection of additional power in PS1 was implemented on a rising slope of the power–angle curve (Figure 3a), or even on a falling slope, when the angle exceeded π/2 (Figure 3b). Fast injection of power assumes that there must be generation capacities in the PS1 system that are already in operation, being synchronised with the system but without supplying any power.
2.2. Fixing a Large-Scale Imbalance: Out-of-Step Protection
To detect the threat of instability, we utilised methods commonly used in SPSs. There are two main types of special protection schemes: event-based and response-based schemes [23,46,47]. Event-based SPSs initiate the shedding of low-priority loads or generators as soon as a forced outage of one or more power generators or loads occurs. The distinction between event-based and response-based SPSs, along with their limitations, can be summarised as follows:
- An event-based special protection scheme is typically activated by changes in the position of switches, promptly disconnecting loads or generators immediately after a predetermined outage occurs [42]. In contrast, a response-driven special protection scheme incorporates measurement elements that introduce time delays.
- An event-based SPS typically necessitates a communication system for transmitting control signals, whereas a response-driven scheme, such as a UFLS, conducts local parameter measurements and initiates local shedding actions. Both schemes involve the shedding of loads or generators and can be implemented either together or separately.
It is possible to combine both of the mentioned approaches. To ensure the stability of high-voltage power transmission lines, protections against out-of-step conditions were adopted. One method of such protection involves monitoring the angle between the voltages of equivalent generators connected to opposite ends of the line [48,49,50]. This approach was implemented by using local protective terminals (see Figure 4; [51]) or a system of phasor measurement units of voltage vectors.

Figure 4.
Angle-control-based OSP.
As described in [51], each terminal models/determines equivalent generator electromotive force vectors according to (5). It is supposed that is equivalent to the emf of the power plant, which, in turn, may consist of several generator units.
where are the voltages at the station buses, are the total currents of the generation sources, and are the equivalent impedances of the generation sources.
Phasor measurement units (PMUs) were strategically deployed throughout the network to conduct real-time synchronised measurements of phase angles. The collected data were subsequently aggregated and processed by the SPS. In the event of a significant disturbance, the SPS detected anomalies based on real-time angle differences, which allowed us to initiate adjustments or line disconnections when instability becomes imminent. Using Equation (5), it is a straightforward task to identify the threat of stability disruption. For example, when angle exceeds the preset maximum threshold
2.3. A Pumped Hydroelectric Storage Plant as a Rapid Power Injection System
Pumped hydroelectric storage power plants represent the world’s most widely used storage technology with a total capacity reaching 159.5 GW [34,35,52,53,54]. PHSPP systems are designed to efficiently transfer water from a lower reservoir to an upper reservoir during periods of low-cost power generation, such as windy and sunny days [55]. Conversely, during times of increased demand or supply shortages, such as during the evening, the water is returned to the lower reservoir through a turbine, enabling electricity generation. PHSPPs have relatively swift response times (from zero to nominal power in a time span of 20 s to a few minutes. Typically, hydropower plants have from 2 to 10 (or more) runners, and the power of the units can reach hundreds of megawatts, while the round-trip efficiency can reach 0.8 [25,54]. It is important to emphasise that these units typically operate either in pump mode or in generator mode, and these two cannot function simultaneously (see Figure 5), as highlighted by Natalia Naval [52]. However, the restriction on the simultaneous operation of these modes is driven by economic considerations, as in this case, the energy consumed by the pump exceeds the energy generated by the generator, leading to seemingly unjustified economic losses.
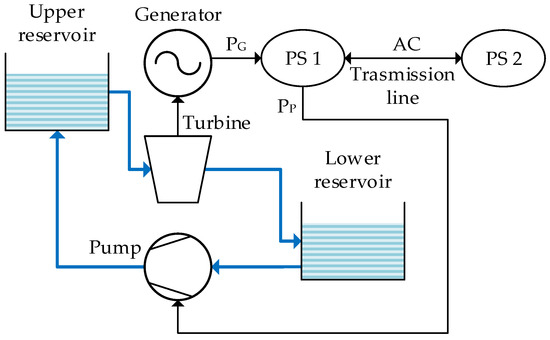
Figure 5.
Structural block diagram of a system with a PSHPP.
The situation changes significantly when we consider the ability of the above mode to swiftly adjust the PS operation in response to a sudden imbalance in PS1. To succeed in this, deactivating the pump of the PSHPP (as shown in Figure 5) is a feasible option.
In such a scenario, it becomes possible to execute the transition depicted in Figure 3, moving from Figure 3a to Figure 3b and ultimately selecting a higher volume of permissible energy imports ( in Figure 3) for enhanced stability. Given favourable prices for imported energy, the costs associated with implementing the aforementioned mode are justified.
2.4. Modelling Methodology and Tools
The selection of operational modes for power systems in many countries is governed by the regulations and guidelines established by electricity market rules, such as those of Nord Pool. The selection process typically involves the following main steps:
- Preparation of bids from generators and consumers [42,56];
- Determination of commitments for generator units;
- Verification of compliance with technical and environmental restrictions.
The first step is carried out by numerous energy retailers [57,58], while the second and third steps are performed by market and transmission system operators (TSOs). Typically, this problem is addressed by considering restrictions established by the TSO and minimising the costs of energy demand. Detailed power system models are necessary for the performance of the above procedures, particularly for the study of electromechanical processes and energy system stability. Even for simulating minor electromechanical transition processes in PSs, solving high-order systems of differential equations and having a comprehensive database of real PS element parameters are necessary. Industrial software (such as ETAP version 12.5) is used to create these models. The models embody mathematical descriptions of specific PS components: generators, transformers, high-voltage lines, loads, and automatic control actions (in the form of differential-algebraic equations [42,56]). To analyse the stability control method under consideration, we can utilise the above software and draw upon the existing experience of the operators, as the PS is only slightly modified by adding one generator and load. However, we need to compare the energy costs of two cases (see Figure 6):
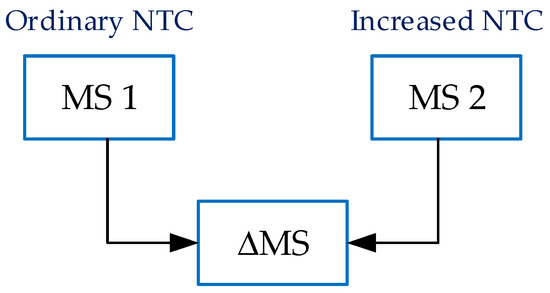
Figure 6.
The assessment structure of the impact of restrictions on the estimation of consumption costs (MS1–market simulation: case 1; MS–simulation of power market; case 2; ΔMS–cost difference).
- A simulation of the system without the simultaneous operation of the generator and pump of the PHSPP (ordinary Network Transfer Capacity (NTC));
- A system with simultaneous operation of the generator and pump of the PHSPP (increased NTC).
In the below case study, we present a portion of the Baltic power system. The full diagram includes elements of the Estonian, Latvian and Lithuanian power systems, as well as the connections with Finland, Sweden, and Poland.
3. Results: Case Studies
3.1. The Baltic Power System
The Baltic power system (BPS) has been chosen to demonstrate the proposed approach. The BPS combines the power systems of the three Baltic States, namely the Estonian, Latvian, and Lithuanian power systems. It is a relatively small PS with a peak load of 4683 MW (EE: 1552, LV: 1100, LT: 2031), historically operated synchronously with the Unified Power System of Russia (UPS), which provides vast frequency and inertia reserves. To improve energy independence and security, a political decision [59] was taken to disconnect the Baltic PS from the UPS and to establish a new synchronous interconnection with the Continental European network via Poland in 2025 (through one double-circuit 400 kV AC line) [20]. The integration process has been started by introducing new HVDC connections with Finland, Sweden, and Poland. There is an HVDC interconnection between Estonia and Finland consisting of two DC cables (Estlink 1 and Estlink 2, the total capacity is 1.05 GW) (in 2024). The LitPol Link is an electricity link between Poland and Lithuania that connects the Baltic transmission system to the synchronous grid of Continental Europe. It has a capacity of 500 MW, and since 2021, it can operate in a synchronous regime. Another HVDC interconnector, NordBalt, connects the PSs of Lithuania and Sweden; its maximum capacity is 700 MW. To strengthen the BPS, three synchronous condensers rated ca. 305 MVA each per each Baltic country will be installed by 2025 [60]. There are plans to build a 500 MW underground pumped hydro energy storage plant in Paldiski, Estonia by 2031. The planned storage capacity of 6 GWh during a 12 h storage cycle is equivalent to Estonian households’ average daily electricity consumption [61]. In the future, up to 2050, a major transformation of the existing system is planned: high-capacity solar, wind, and synthetic methane power plants will be built, and plants producing atmospheric CO2 emissions will be shut down. The Polish national energy and climate plan makes provisions for building nuclear power plants in the 2030s, as well as developing wind energy [6]. With regard to interconnections, it is important to note that the TSOs are planning to increase the import/export capacity of the synchronous interconnections with Germany, the Czech Republic, and Slovakia by 2000 MW.
As is presented in Figure 7, the electricity generation mix in the BPS includes hydro, biomass, wind, and solar power plants, comprising large PHSPPs and natural gas-fired CHP plants.

Figure 7.
The portfolio of the power plants and interconnections: pumped storage hydropower plant (PSHPP), hydropower plant (HPP), solar power plant (SPP), wind power plant (WPP), seasonal energy storage (SES), and combined heat and power plant (CHPP); electricity loads (demand) and interconnections.
The powerful PSHPP that actually exists in Lithuania (Kruonis PSHPP) is taken as the facility to be reviewed. The plant is connected to the 330 kV transmission grid, which does not impose restrictions when choosing plant operating modes. When planning the operation, we assume the following: the water levels in the upper reservoir at the beginning and at the end of the planning period are equal to the maximum permissible level and the pump–turbine units at each hour can work only with the rated power, and, furthermore, the combination of the generation mode and the pumping mode is impossible. The parameters of Kruonis PSHPP are presented in Table 1.

Table 1.
Parameters of Kruonis PSHPP [62].
3.2. Modelling of the Baltic Power Grid
To evaluate the transient processes and behaviour of the BPS in case of generation loss or major transmission line short circuits, ETAP version 12.5 was used [63]. A simplified 330/400 kV network model was created, representing each country with a single busbar with aggregated loads and equivalent generators (Figure 8). A diagram of the modelled grid is represented in Figure 8.

Figure 8.
Modelled Baltic power systems.
The generation of Estonia and Lithuania is represented by an equivalent synchronous turbo generator for each country. The generation of Latvia is represented by an equivalent HPP generator. The generation and load values for the simulation are taken from a typical spring situation in the BPS in the recent years—a situation in which full production from Latvian hydropower plants can be expected. The Estonian PS is importing electricity (250 MW), and the Lithuanian PS is importing energy from Sweden (700 MW) and Poland (700 MW or 1100 MW for different scenarios, S1–S6). Kruonis PSHPP of the Lithuanian PS is modelled with two synchronous generators (G1 and G3) and two synchronous motors operating in water pump mode (M2 and M4). The NordBalt HVDC link (L3) is represented with a dedicated busbar and transmission cable. Interconnection with Poland PS is accomplished by means of two AC transmission lines, L1 and L2. All Baltic generators’ angles are referenced to a Polish generator, which is chosen as the swing-generator. The parameters of the modelled AC transmission lines correspond to the equivalent of the real AC lines interconnecting the Baltic power grid. Table 2 summarises an overview of the parameters of the modelled system.

Table 2.
The main parameters of the modelled PS.
3.3. Validation of the Model
The model was developed using real power system parameters specific to the Baltic region. Its behaviour was rigorously tested against experimental data, including real-world short-circuit scenarios and the corresponding automation responses. Furthermore, the model has been extensively used for analysing transient stability in various studies. The results derived from the model were found to be trustworthy and consistent with those obtained from models used by experts, such as transmission system operators. This validation process ensures that the model accurately simulates the behaviour of the Baltic power system under diverse operational conditions. As a result, the model serves as a valuable tool for conducting thorough analysis and supporting decision-making in the fields of power system operation and planning.
Below, we present the results of calculating the most intriguing transient regimes for the selected scenarios.
3.4. Simulation Results
A brief description of the data and assumptions used are provided in Table 3. It presents two main cases as the most severe for the Baltic power system: the loss of generation due to the tripping of the 700 MW Sweden–Lithuania interconnection (L3) and a short circuit on a major transmission line (L1). For each case, we consider three scenarios:

Table 3.
The results of disturbances and the transient process.
- S1, S4—the absence of OSP protection and using the suggested control method to evaluate the dangers of the operation mode;
- S2, S5—the mode with OSP protection used to assess the BPS ability to withstand a disturbance;
- S3, S6—the implementation of the proposed control method to evaluate the system’s performance and the effectiveness of the suggested solution.
The right column of the table summarises the consequences of the transient process for each scenario in these test cases based on the modelling results presented in the subsequent Section 3.4.1 and Section 3.4.2. The transient process visualisation for each scenario includes the following:
- (a)
- Generator active power (MW) of the selected, most essential units;
- (b)
- Generator angle (electrical degrees) and system frequency relative to nominal (%);
- (c)
- Power flow through the selected line/s (MW).
3.4.1. Test Case Set: Loss of Generation (Scenarios S1, S2, and S3)
The first three scenarios, S1–S3, have been designed to assess PS stability in the case of the loss of a large generation source by tripping the NordBalt line between Lithuania and Sweden (L3) and disconnecting 700 MW of the power transferred to BPS at t = 0.5 s.
In Scenario S1 (see Figure 9c), the power deficit of 700 MW leads to a significant increase in the amount of power transmitted from Poland (L1 + L2), which, in turn, results in an out-of-step condition at 2.65 s (Figure 9a): power swings of Plavinas HPP and Polish generators; (Figure 9b): increasing divergence in the phase angles of the LV and PL generators; (Figure 9c): SW-LT interconnections power oscillations). The inability to transfer power due to the out-of-step condition results in a further frequency decline and the operation of five steps of UFLS at the following times: t = 3.278, 3.442, 3.545, 3.759, and 3.823 s (see (Figure 9b): change in the system frequency).
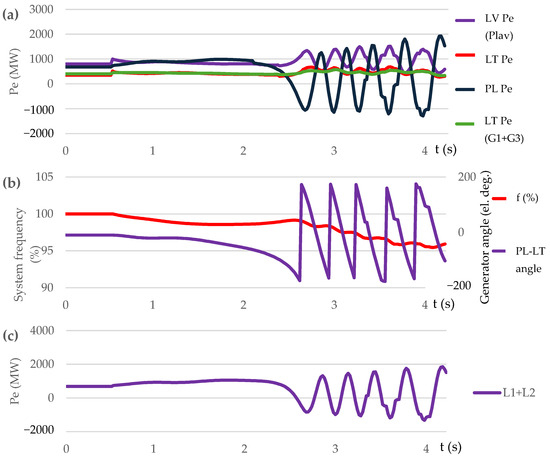
Figure 9.
Scenario S1: (a) generator active power (Pe) at Pļaviņas HPP (LV), Kruonis PSHPP (LT), and generation units at LT and PL; (b) generator angle and system frequency; (c) power flow through lines L1 and L2.
This case demonstrates that an excessive power transfer from Poland could potentially lead to angular instability, which is unacceptable, and such a regime should be avoided.
In Scenario S2 (see Figure 10), the operation of the OSP is simulated. The OSP disconnects transmission lines L1 and L2 as soon as the angle between Poland and the BPS exceeds 115 electric degrees at 2.4 s (see (Figure 10b,c)). As a result of the inability to meet the power deficit, six steps of UFLS have been triggered at the following times: t = 2.935 s, 3.025, 3.097, 3.161, 3.222, and 3.292 s (see (Figure 10a,b)). The BPS remains in operation ((Figure 10a): fading power oscillations) with a decreased system frequency of 47.5 Hz~0.95% fnom (see (Figure 10b)).


Figure 10.
Scenario S2: (a) generator active power (Pe) at Pļaviņas HPP (LV), Kruonis PSHPP (LT), and generation units at LT and PL; (b) generator angle and system frequency; (c) power flow through lines L1 and L2.
Scenarios S1 and S2 demonstrate that the power transfer over the Poland–BPS synchronous link (L1 + L2) must be intentionally limited to avoid the possible development of instability and significant load shedding actions. Additional simulations show that the angular and frequency stability of the BPS is preserved when the maximum power transfer from Poland is limited to 400 MW.
In Scenario S3 (see Figure 11), the proposed control automation disconnects pumps/motors (M2 and M4) of Kruonis PSHPP (0.5 s after tripping of L3) at t = 1.0 s, thus preventing development of dangerous processes such as an out-of-step condition along the lines L1 and L2 and consequent frequency instability of the BPS. Kruonis PSHPP generators G1 and G3 provide the power system with an additional 400 MW of power, thus stabilising the system frequency of the BPS ((Figure 11b): fading frequency oscillations; (Figure 11c): fading power oscillations).
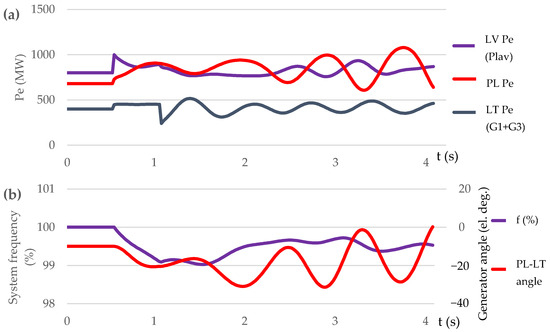

Figure 11.
Scenario S3: (a) generator active power (Pe) at Pļaviņas HPP (LV), Kruonis PSHPP (LT), and generation units at PL; (b) generator angle and system frequency; (c) power flow through line L4.
This case shows that fast actions, intended for the quick redirection of a significant amount of power from non-critical load (Kruonis PSHPP pumps) to the network, preventing hazardous scenarios with frequency instability. Therefore, the power transfer margin from Poland can be increased without the risk of losing stability.
3.4.2. Test Case Set: Short Circuit on Transmission Line (Scenarios S4, S5, and S6)
The next set of scenarios, S4–S6, demonstrates the performance of the proposed automation in the case of a short circuit in one of two Poland–BPS interconnecting lines (L1 and L2) and its impact on the stability of the BPS. The power transfer from Poland is close to the thermal and static stability margin.
In Scenario S4 (see Figure 12), a short circuit on L1 at t = 0.5 s is simulated. The short circuit was disconnected after 50 ms and the power transfer over the remaining line L1 resulted in an out-of-step condition at 2.6 s ((Figure 12a): power swings of generators; (Figure 12b): increasing divergence in the phase angles of the LT and PL generators; (Figure 12c): L2 power oscillations).


Figure 12.
Scenario S4: (a) generator active power (Pe) generation units at EE, LV, LT, and PL; (b) generator angle and system frequency; (c) power flow through lines L1 and L2.
In Scenario S5 (see Figure 13), a short circuit on L1 at t = 0.5 s is simulated. The short circuit has been disconnected after 50 ms and, to prevent an out-of-step condition, the OSP disconnects line L2 at 2.2 s ((Figure 13a): fading oscillations; (Figure 13b)). As a result of the significant power deficit, three steps of UFLS have been triggered. The PSs remain in operation with a decreased frequency of 48.75 Hz (97.5% fnom) (see (Figure 13b)).

Figure 13.
Scenario S5: (a) generator active power (Pe) generation units at EE, LV, LT, and PL; (b) generator angle and system frequency; (c) power flow through L1 and L2.
As was expected, the line short circuit leads to consequences similar to those in cases S1 and S2. The power transfer over lines L1 and L2 should be intentionally limited to avoid the angular and frequency instability of the BPS.
In Scenario S6 (see Figure 14), a short circuit on L1 at t = 0.5 s is simulated. The short circuit was disconnected after 50 ms, and the proposed control automation disconnects the pumps (400 MW) of Kruonis PSHPP at t = 1.0 s.

Figure 14.
Scenario S6: (a) generator active power (Pe) generation units at EE, LV, LT, and PL; (b) generator angle and system frequency; (c) power flow through line L2.
An additional injection of 400 MW from the Kruonis generators prevents an out-of-step condition along the remaining line L2 (see (Figure 14c)), thus preventing the development of frequency instability in the BPS.
Scenario S6 demonstrates the efficiency of the proposed approach in the prevention of angular and frequency instability even when the transmission link is operating close to it is maximal capacity. For all the simulated scenarios, if the proposed method is implemented, the restrictions of the power transfer limit can be relaxed without the risk of losing stability. For the cases presented, the power transfer over the Poland–BPS link could be increased from 400 MW up to 800 MW.
3.5. The Impact of the Line Capacity on the Market Price
Taking into consideration the fact that both the producers and consumers of the energy systems participate in the Nord Pool electricity market, let us examine the impact of increasing the TL capacity on the market price of electricity. All the participants are required to submit their bids for buying and selling electricity to the Electricity Market Operator (EMO). The market bids indicate how much the seller or the buyers are willing to buy or sell and for what price. Bid acceptance in Nord Pool is based on the market price formation and is managed by the EMO. The EMO aggregates all the bids and determines the accepted/rejected generation and consumption bids and sets a market clearing price (MCP) for each hour [64]. The selection of the cheapest generators is ensured, provided that there is guaranteed balance and adherence to energy flow limitations along the transmission lines. Generators’ bids with a price lower than the MCP and purchase bids with a price higher than the MCP are accepted, whereas the remaining bids are rejected. In this auction scheme, all the accepted participants are paid the market clearing price. Thus, the MCP determines the incomes of power plants and the costs of power consumers. The diagrams in Figure 15 illustrate the situations arising in cases of excess cheap energy in the Polish power system and a deficit in the Baltic power system (different market bids are represented by different colours in the figure).
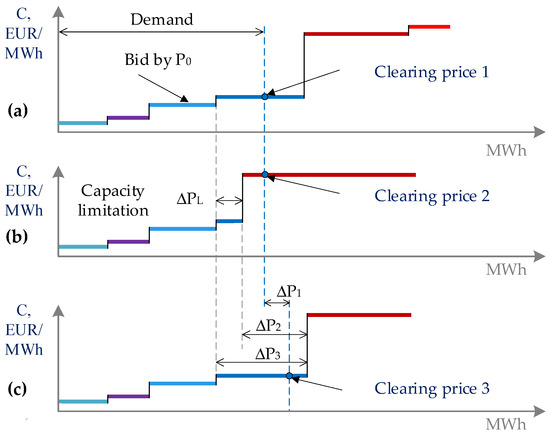
Figure 15.
Representation of the impact of the power limitations on the MCP: (a) without a power transmission limitation along the LitPol line/s; (b) with a limitation on the transmitted power along the LitPol line/s; (c) alleviating the limitation through simultaneous use of a pump and a generator at Kruonis PSHPP.
Figure 15a presents a diagram illustrating the scenario of generator selection in the absence of power transmission limitations along the LitPol line. We can see that, thanks to imports from Poland, a low MCP is established. Figure 15b depicts the scenario of generator selection in the presence of a limitation on the transmitted power along the LitPol line. Figure 15c illustrates the situation of alleviating the limitation on the transmitted power along the LitPol line through the simultaneous use of a pump and a generator at Kruonis PSHPP. We can observe an increase in the power consumed by the BPS by the amount and a significantly greater amount for the transmission capacity of the LitPol line (see Figure 15c). The economic gain in this case, denoted as , can be expressed as follows:
where parameters , , , and correspond to Figure 15.
To evaluate the scale of the gain, we will utilise the market prices registered in the Baltic region on 9 February 2024, as depicted in Figure 16.

Figure 16.
Nord Pool market prices on 9 February 2024.
Using the market price data from 9 February (Figure 16) and assuming that the transmission capacity of the LitPol line can be increased by 400 MW, based on the previous calculations, we obtain the diurnal gain (the number of hours when the prices are above 74% of the price in the PL area to observe efficiency: 12 h; average price difference: 80.4367 EUR/MWh.):
A similar situation (high prices in the LT area and low prices in the PL area) was observed in September 2023 (Figure 17). The difference in the day-ahead prices between the LT and PL areas is presented in Figure 18. The prices in the LT area were higher than in the PL area at 202 h (28%) during this period (the average difference was 62.3 EUR/MWh).

Figure 17.
Nord Pool day-ahead prices in the PL and LT areas in September 2023.
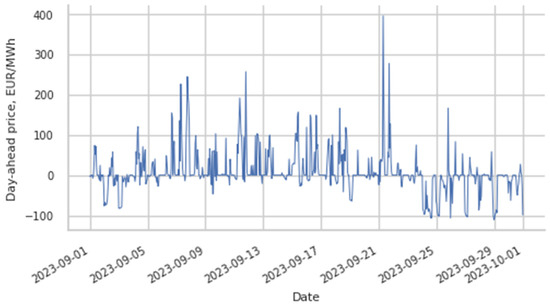
Figure 18.
The difference in the Nord Pool day-ahead prices between the LT and PL areas in September 2023.
To evaluate the economic gain of the proposed solution, we consider the hours with LT prices above 74% of the price in the PL area, thus taking into account the efficient cycle use rate of Kruonis PSHPP (Table 1). There were 113 h with LT prices above the 74% threshold; the distribution of the prices in the LT area above 74% of the price in the PL area is shown in Figure 19, and the average price difference for these hours was 95.03 EUR/MWh.

Figure 19.
The distribution of Nord Pool day-ahead prices in the LT area above 74% of the price in the PL area and the distribution of the differences between these prices in September 2023.
The economic gain for this period could be
The possibility of saving more than four million euros per month could be considered economically attractive, since the implementation of this solution only requires financing for constructing the automation.
4. Discussion and Conclusions
The hybrid AC/DC grid, incorporating a substantial proportion of intermittent renewables, is becoming a vital configuration in modern energy systems. The energy transition results in a reduction in system inertia, consequently elevating the risk of stability disruption. A sudden loss of large generation or cross-border interconnection can lead to an unexpected energy imbalance, posing significant challenges for grid stability and reliability. Therefore, power system operators restrict operating conditions, in particular by decreasing the transfer capacity of a weakly interconnected power system. One negative consequence of such restrictions under electricity market conditions is significant price variance between different price areas. We can observe similar market behaviour and price changes in cases when an important interconnection or generator has been disconnected.
In this paper, an analysis has been carried out to evaluate the technical feasibility and economic viability of leveraging pumped storage power plants. The proposed control automation allows for enhancing the stability of a weakly interconnected power system (in particular, the Baltic power system) and alleviates cross-border transfer capacity limitations due to a decrease in inertia. There are cases when the simultaneous operation of the generators and pumps of a PSHPP is feasible. The preliminary results (Section 3.4) have shown that it is possible and that power system stability can be enhanced by applying the proposed control automation, employing measurements of voltage phasors. The two most probable cases of disturbances were assessed: the loss of large-scale generation and tripping of cross-border interconnections due to a short circuit. In the first case (Scenario S3), the disconnection of the PSHPP’s pumps prevents the development of dangerous processes such as an out-of-step condition along the lines (L1 and L2) and the consequent frequency drop. The generators of Kruonis PSHPP (G1 and G3) provide the power system with an additional 400 MW of power, thus stabilising the BPS system frequency (the transient frequency deviation does not exceed 1%). In the second case (Scenario S6), the short circuit was eliminated by tripping the line (by relay protection) and the proposed control automation disconnects the pumps (400 MW) of Kruonis PSHPP. An additional injection of 400 MW from Kruonis generators prevents an out-of-step condition along the remaining line (L2), thus preventing the development of frequency instability in the BPS (the transient frequency remains in the range of 99.7–100.8%).
To evaluate the economic gain, the historical market prices have been used. The results obtained (Section 3.5) prove the economic viability of the proposed solution (the total saving could reach 4,295,356 EUR per month).
Future research will focus on refining the current model to enhance the effectiveness of our proposed method. This includes identifying optimal conditions for its application and further development of the method’s accuracy and reliability in diverse scenarios. Through iterative testing and analysis, we aim to establish clear guidelines for when and how to best utilise the proposed method for maximum impact.
Author Contributions
Conceptualisation, A.S.; methodology, A.S., A.U. and D.Ž.; software, A.U.; validation, A.U. and D.Ž.; formal analysis, A.S., A.U. and D.Ž.; writing—original draft preparation, A.S.; writing—review and editing, A.S., A.U. and D.Ž.; visualisation, A.U. and D.Ž.; supervision, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Latvian Council of Science, project No. Lzp–2023/1-0376 “Innovative emergency control of RES-dominated low-inertia power systems (INNOVA)”.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| AC | Alternate Current |
| BPS | Baltic power system |
| CHPP | Combined heat and power plant |
| DLR | Dynamic Line Rating |
| EAC | Equal Area Criterion |
| emf | Electromotive force |
| EMO | Electricity Market Operator |
| HPP | Hydropower plant |
| HVDC | High-voltage direct current |
| MCP | Market clearing price |
| MS | Market simulation |
| NTC | Network Transfer Capacity |
| OSP | Out-of-step protection |
| PMU | Phasor measurement unit |
| PHSPP | Pumped hydroelectric storage power plant |
| PS | Power system |
| RAS | Remedial Action Scheme |
| RESs | Renewable Energy Resources |
| ROCOFs | Rates of change of frequency |
| SES | Seasonal energy storage |
| SPP | Solar power plant |
| SPS | Special Protection System |
| TL | Transmission line |
| TSO | Transmission Systems Operator |
| UFLS | Under-Frequency Load Shedding |
| UPS | Unified Power System of Russia |
| WPP | Wind power plant |
References
- The European Council. The 2030 Climate and Energy Framework. Available online: https://www.consilium.europa.eu/en/policies/climate-change/2030-climate-and-energy-framework (accessed on 17 May 2024).
- Milano, F.; Dorfler, F.; Hug, G.; Hill, D.J.; Verbic, G. Foundations and Challenges of Low-Inertia Systems (Invited Paper). In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–25. [Google Scholar]
- Lavanya, L.; Swarup, K.S. Inertia Monitoring in Power Systems: Critical Features, Challenges, and Framework. Renew. Sustain. Energy Rev. 2024, 190, 114076. [Google Scholar] [CrossRef]
- Johnson, S.C.; Rhodes, J.D.; Webber, M.E. Understanding the Impact of Non-Synchronous Wind and Solar Generation on Grid Stability and Identifying Mitigation Pathways. Appl. Energy 2020, 262, 114492. [Google Scholar] [CrossRef]
- Prabhakar, K.; Jain, S.K.; Padhy, P.K. Inertia Estimation in Modern Power System: A Comprehensive Review. Electr. Power Syst. Res. 2022, 211, 108–222. [Google Scholar] [CrossRef]
- International Energy Agency. Available online: https://www.iea.org/ (accessed on 28 January 2024).
- Alhelou, H.H.; Hamedani-Golshan, M.E.; Njenda, T.C.; Siano, P. A Survey on Power System Blackout and Cascading Events: Research Motivations and Challenges. Energies 2019, 12, 682. [Google Scholar] [CrossRef]
- Zalostiba, D. Power System Blackout Prevention by Dangerous Overload Elimination and Fast Self-Restoration. In Proceedings of the IEEE PES ISGT Europe 2013, Lyngby, Denmark, 6–9 October 2013; pp. 1–5. [Google Scholar]
- Ørum, E.; Kuivaniemi, M.; Laasonen, M.; Bruseth, A.I.; Jansson, E.A.; Danell, A.; Elkington, K.; Modig, N. ENTSO Report—Future System Inertia; European Network of Transmission System Operators for Electricity: Brussels, Belgium, 2015. [Google Scholar]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and Classification of Power System Stability—Revisited & Extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar] [CrossRef]
- Guzs, D.; Utans, A.; Sauhats, A.; Junghans, G.; Silinevics, J. Resilience of the Baltic Power System When Operating in Island Mode. In Proceedings of the 2020 IEEE 61th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 5 November 2020; pp. 1–6. [Google Scholar]
- Markovic, U.; Stanojev, O.; Aristidou, P.; Vrettos, E.; Callaway, D.; Hug, G. Understanding Small-Signal Stability of Low-Inertia Systems. IEEE Trans. Power Syst. 2021, 36, 3997–4017. [Google Scholar] [CrossRef]
- Scherer, M.; Andersson, G. How Future-Proof Is the Continental European Frequency Control Structure? In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar] [CrossRef]
- Zbunjak, Z.; Bašić, H.; Pandžić, H.; Kuzle, I. Phase Shifting Autotransformer, Transmission Switching and Battery Energy Storage Systems to Ensure n-1 Criterion of Stability. J. Energy-Energ. 2015, 64, 285–298. [Google Scholar] [CrossRef]
- Machowski, J.; Bialek, J.W.; Bumby, J.R. Power System Dynamics. Stability and Control, 3rd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2012; ISBN 978-0-470-72558-0. [Google Scholar]
- Sauhats, A.; Chuvychin, V.; Bockarjova, G.; Zalostiba, D.; Antonovs, D.; Petrichenko, R. Detection and Management of Large Scale Disturbances in Power System. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2016; Volume 8985, pp. 147–152. ISBN 9783319316635. [Google Scholar]
- Ratnam, K.S.; Palanisamy, K.; Yang, G. Future Low-Inertia Power Systems: Requirements, Issues, and Solutions—A Review. Renew. Sustain. Energy Rev. 2020, 124, 109773. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Yang, G.; Nielsen, A.H.; Jensen, P.H. Combination of Synchronous Condenser and Synthetic Inertia for Frequency Stability Enhancement in Low-Inertia Systems. IEEE Trans. Sustain. Energy 2019, 10, 997–1005. [Google Scholar] [CrossRef]
- Ali, M.H.; Murata, T.; Tamura, J. Effect of Coordination of Optimal Reclosing and Fuzzy Controlled Braking Resistor on Transient Stability during Unsuccessful Reclosing. IEEE Trans. Power Syst. 2006, 21, 1321–1330. [Google Scholar] [CrossRef]
- Sauhats, A.; Utans, A.; Silinevics, J.; Junghans, G.; Guzs, D. Enhancing Power System Frequency with a Novel Load Shedding Method Including Monitoring of Synchronous Condensers’ Power Injections. Energies 2021, 14, 1490. [Google Scholar] [CrossRef]
- Elliott, R.T.; Choi, H.; Trudnowski, D.J.; Nguyen, T. Real Power Modulation Strategies for Transient Stability Control. IEEE Access 2022, 10, 37215–37245. [Google Scholar] [CrossRef]
- Saluja, R.; Ali, M.H. Novel Braking Resistor Models for Transient Stability Enhancement in Power Grid System. In Proceedings of the 2013 IEEE PES Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 24–27 February 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Power Systems Engineering Research Center. System Protection Schemes: Limitations, Risks, and Management; Power Systems Engineering Research Center: Tempe, AZ, USA, 2010. [Google Scholar]
- Tower, N. Special Protection Systems (SPS) and Remedial Action Schemes (RAS): Assessment of Definition, Regional Practices, and Application of Related Standards. 2013; pp. 1–48. Available online: https://www.nerc.com/pa/Stand/Prjct201005_2SpclPrtctnSstmPhs2/System_Protection_and_Control_Subcommittee_SPCS_20_SAMS-SPCS_SPS_Technic_02182014.pdf (accessed on 3 February 2024).
- Beevers, D.; Branchini, L.; Orlandini, V.; De Pascale, A.; Perez-Blanco, H. Pumped Hydro Storage Plants with Improved Operational Flexibility Using Constant Speed Francis Runners. Appl. Energy 2015, 137, 629–637. [Google Scholar] [CrossRef]
- Koritarov, V.; Ploussard, Q.; Kwon, J.; Balducci, P. A Review of Technology Innovations for Pumped Storage Hydropower. 2022. Available online: https://publications.anl.gov/anlpubs/2022/05/175341.pdf (accessed on 25 December 2023).
- Mahmoudi, M.M.; Kincic, S.; Zhang, H.; Tomsovic, K. Implementation and Testing of Remedial Action Schemes for Real-Time Transient Stability Studies. IEEE Power Energy Soc. Gen. Meet. 2018, 2018, 8274518. [Google Scholar] [CrossRef]
- Ojetola, S.; Wold, J.; Trudnowski, D.; Wilches-Bernal, F.; Elliott, R. A Real Power Injection Control Strategy for Improving Transient Stability. IEEE Power Energy Soc. Gen. Meet. 2020, 2020, 9281741. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.; Adiyabazar, C.; Martinez, E.V. Setting and Testing of the Out-of-Step Protection at Mongolian Transmission System. Energies 2021, 14, 8170. [Google Scholar] [CrossRef]
- Ojetola, S.; Wold, J.; Trudnowski, D. Multi-Loop Transient Stability Control via Power Modulation from Energy Storage Devices. IEEE Trans. Power Syst. 2021, 36, 5153–5163. [Google Scholar] [CrossRef]
- Sauhats, A.S.; Utans, A. Out-of-Step Relaying Principles and Advances. Scientific Monograph; RTU Press: Riga, Latvia, 2022. [Google Scholar]
- Rudez, U.; Mihalic, R. Trends in WAMS-Based under-Frequency Load Shedding Protection. In Proceedings of the IEEE EUROCON 2017—17th International Conference on Smart Technologies, Ohrid, Macedonia, 6–8 July 2017; pp. 782–787. [Google Scholar]
- What Is Green Hydrogen and Why Do We Need It? An Expert Explains. Available online: https://www.weforum.org/agenda/2021/12/what-is-green-hydrogen-expert-explains-benefits/ (accessed on 3 February 2024).
- Nikolaidis, P.; Poullikkas, A. A Comparative Review of Electrical Energy Storage Systems for Better Sustainability. J. Power Technol. 2017, 97, 220–245. [Google Scholar]
- Šćekić, L.; Mujović, S.; Radulović, V. Pumped Hydroelectric Energy Storage as a Facilitator of Renewable Energy in Liberalized Electricity Market. Energies 2020, 13, 6076. [Google Scholar] [CrossRef]
- Koltermann, L.; Drenker, K.K.; Celi Cortés, M.E.; Jacqué, K.; Figgener, J.; Zurmühlen, S.; Sauer, D.U. Potential Analysis of Current Battery Storage Systems for Providing Fast Grid Services like Synthetic Inertia—Case Study on a 6 MW System. J. Energy Storage 2023, 57, 106190. [Google Scholar] [CrossRef]
- Angenendt, G.; Zurmühlen, S.; Figgener, J.; Kairies, K.P.; Sauer, D.U. Providing Frequency Control Reserve with Photovoltaic Battery Energy Storage Systems and Power-to-Heat Coupling. Energy 2020, 194, 116923. [Google Scholar] [CrossRef]
- Ojetola, S.T.; Wold, J.; Trudnowski, D. Feedback Control Strategy for Transient Stability Application. Energies 2022, 15, 6016. [Google Scholar] [CrossRef]
- Ebadian, M.; Alizadeh, M. Improvement of Power System Transient Stability Using Fault Current Limiter and Thyristor Controlled Braking Resistor. In Proceedings of the 2009 International Conference on Electric Power and Energy Conversion Systems, (EPECS), Sharjah, United Arab Emirates, 10–12 November 2009; pp. 1–6. [Google Scholar]
- Guzmán, A.; Tziouvaras, D.A.; Schweitzer, E.O.; Martin, K. Local- and Wide-Area Network Protection Systems Improve Power System Reliability. In Proceedings of the 2006 Power Systems Conference: Advanced Metering, Protection, Control, Communication, and Distributed Resources, Clemson, SC, USA, 14–17 March 2006; pp. 174–181. [Google Scholar] [CrossRef]
- Dai, Y.; Preece, R.; Panteli, M. Risk Assessment of Cascading Failures in Power Systems with Increasing Wind Penetration. Electr. Power Syst. Res. 2022, 211, 108392. [Google Scholar] [CrossRef]
- ENTSO-E. Guideline for Cost Benefit Analysis of Grid Development Projects; Final—Approved by the European Commission; Entso-E: Brussels, Belgium, 2018. [Google Scholar]
- Nord Pool. Available online: https://www.nordpoolgroup.com (accessed on 17 February 2024).
- Hess, D.; Wetzel, M.; Cao, K.K. Representing Node-Internal Transmission and Distribution Grids in Energy System Models. Renew. Energy 2018, 119, 874–890. [Google Scholar] [CrossRef]
- Kimbark, E.W. Power System Stability, Volume I; IEEE Press Classic Reissue; John Wiley & Sons: Hoboken, NJ, USA, 1995; ISBN 978-0-780-31135-0. [Google Scholar]
- Hong, Y.Y.; Hsiao, C.Y. Event-based Under-frequency Load Shedding Scheme in a Standalone Power System. Energies 2021, 14, 5659. [Google Scholar] [CrossRef]
- Stanković, S.; Hillberg, E.; Ackeby, S. System Integrity Protection Schemes: Naming Conventions and the Need for Standardization. Energies 2022, 15, 3920. [Google Scholar] [CrossRef]
- Antonovs, D.; Sauhats, A.; Utans, A.; Svalovs, A.; Bochkarjova, G. Protection Scheme against Out-of-Step Condition Based on Synchronized Measurements. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–8. [Google Scholar] [CrossRef]
- Sauhats, A.; Svalova, I.; Svalovs, A.; Antonovs, D.; Utans, A.; Bochkarjova, G. Two-Terminal out-of-Step Protection for Multi-Machine Grids Using Synchronised Measurements. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Sauhats, A.; Utans, A.; Biela-Dailidovicha, E. Wide-Area Measurements-Based out-of-Step Protection System. In Proceedings of the 2015 56th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 14 October 2015; pp. 5–9. [Google Scholar] [CrossRef]
- Sauhats, A.; Utans, A.; Antonovs, D.; Svalovs, A. Angle Control-Based Multi-Terminal out-of-Step Protection System. Energies 2017, 10, 308. [Google Scholar] [CrossRef]
- Naval, N.; Yusta, J.M.; Sánchez, R.; Sebastián, F. Optimal Scheduling and Management of Pumped Hydro Storage Integrated with Grid-Connected Renewable Power Plants. J. Energy Storage 2023, 73, 108993. [Google Scholar] [CrossRef]
- Kougias, I.; Aggidis, G.; Avellan, F.; Deniz, S.; Lundin, U.; Moro, A.; Muntean, S.; Novara, D.; Pérez-Díaz, J.I.; Quaranta, E.; et al. Analysis of Emerging Technologies in the Hydropower Sector. Renew. Sustain. Energy Rev. 2019, 113, 109257. [Google Scholar] [CrossRef]
- Carrieann Stocks. Largest Pumped Storage Plants in Operation and Development. Available online: https://www.nsenergybusiness.com/features/largest-pumped-storage-plants/ (accessed on 3 February 2024).
- Harby, A.; Sauterleute, J.; Korpås, M.; Killingtveit, Å.; Solvang, E.; Nielsen, T. Pumped Storage Hydropower. In Transition to Renewable Energy Systems; Wiley Blackwell: Hoboken, NJ, USA, 2013; pp. 597–618. ISBN 9783527673872. [Google Scholar]
- Chiodi, A.; Deane, J.P.; Gargiulo, M.; Ó’Gallachóir, B.P. Modelling Electricity Generation—Comparing Results: From a Power Systems Model and an Energy Systems Model. In Proceedings of the 2011 International Energy Workshop, Stanford, CA, USA, 6–8 July 2011; Environmental Research Institute: Thurso, UK, 2011. Corpus ID: 7021600. pp. 1–25. Available online: https://api.semanticscholar.org/CorpusID:7021600 (accessed on 5 April 2024).
- Ottesen, S.Ø.; Tomasgard, A.; Fleten, S.E. Multi Market Bidding Strategies for Demand Side Flexibility Aggregators in Electricity Markets. Energy 2018, 149, 120–134. [Google Scholar] [CrossRef]
- Iria, J.; Soares, F.; Matos, M. Optimal Supply and Demand Bidding Strategy for an Aggregator of Small Prosumers. Appl. Energy 2018, 213, 658–669. [Google Scholar] [CrossRef]
- European Commission. Energy Security: The Synchronisation of the Baltic States’ Electricity Networks—European Solidarity in Action. Available online: https://ec.europa.eu/commission/presscorner/detail/en/IP_19_3337 (accessed on 17 February 2024).
- AST Synchronisation with Europe. Available online: https://www.ast.lv/en/projects/synchronisation-europe (accessed on 17 February 2024).
- Press Release: Estonia’s First Pumped Hydro Energy Storage Facility Has Issued an Invitation to Tender. Available online: https://zeroterrain.com/press-release-estonias-first-pumped-hydro-energy-storage-facility-invitation-to-tender/ (accessed on 5 April 2024).
- ignitis gamyba Kruonis Pumped Storage Hydroelectric Power Plant (KPSHP). Available online: https://ignitisgamyba.lt/en/our-activities/electricity-generation/kruonis-pumped-storage-hydroelectric-power-plant-kpshp/4188 (accessed on 5 April 2024).
- Etap Software. Available online: https://etap.com/ (accessed on 17 May 2024).
- Cai, T.; Dong, M.; Chen, K.; Gong, T. Methods of Participating Power Spot Market Bidding and Settlement for Renewable Energy Systems. Energy Rep. 2022, 8, 7764–7772. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).